Geodezja Wyższa i

Astronomia Geodezyjna

Dr inż. Magdalena Kłęk

Wyższa Szkoła Działalności Gospodarczej
Instytut Geodezji i Kartografii

Treść ćwiczeń

1.

Sfera niebieski, okręgi kół wielkich i małych, dwukąt
i trójkąt sferyczny, miara kątów i boków trójkąta
sferycznego, trójkąt biegunowy. Podstawowe wzory
trójkąta sferycznego.

2.

Transformacja układów współrzędnych jako przykład
rozwiązywania

trójkątów sferycznych.

3.

Zjawiska ruchu dobowego - analiza i obliczanie
efemeryd tych zjawisk.

4.

Zależność pomiędzy czasem słonecznym średnim a
gwiazdowym, zależność pomiędzy czasem
słonecznym średnim a czasem słonecznym
prawdziwym - równanie czasu.

5.

Rozwiązywanie małych trójkątów sferycznych.
Przenoszenie współrzędnych

zadanie wprost i

odwrotne.

6.

Przeliczanie współrzędnych ortokartezjańskich na
elipsoidalne i odwrotnie.

7.

Przeliczenie współrzędnych elipsoidalnych na
współrzędne płaskie w

wybranym odwzorowaniu.

8. Obliczenie poprawek odwzorowawczych do

pomierzonych kątów i długości.

9. Azymut astronomiczny, geodezyjny, kąt kierunkowy w

odwzorowaniu.

10.Transformacje pomiędzy przestrzennymi układami

odniesienia

stosowanymi w Polsce.

11.Obliczanie poprawek niwelacyjnych – ortometrycznej i

normalnej.

Treść ćwiczeń

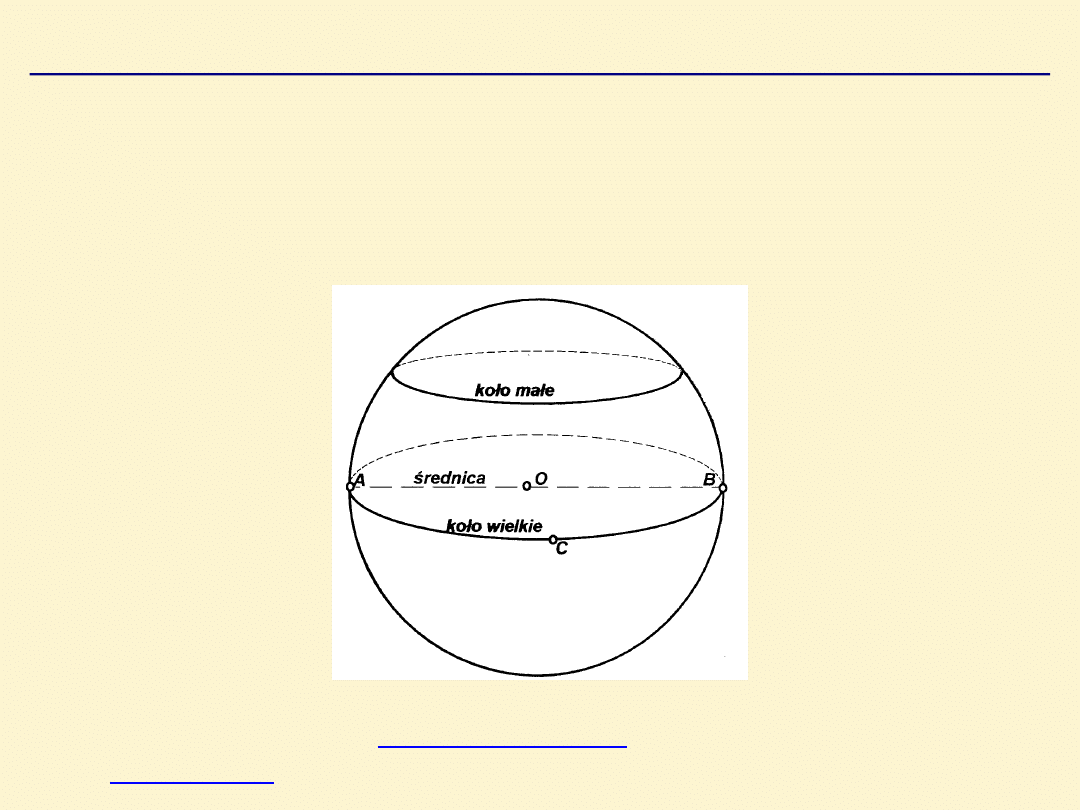
Geometria sfery

SFERA

– zbiór punktów przestrzeni, których

odległość r od pewnego obranego punktu o jest
stała. Odległość r jest promieniem sfery, punkt O –
środkiem sfery.

KOŁO

– przekrój powierzchni sfery płaszczyzną.

Jeżeli płaszczyzna sieczna przechodzi przez środek sfery to
przekrój nazywamy

kołem wielkim

, jeżeli nie – przekrojem

jest

koło małe

.

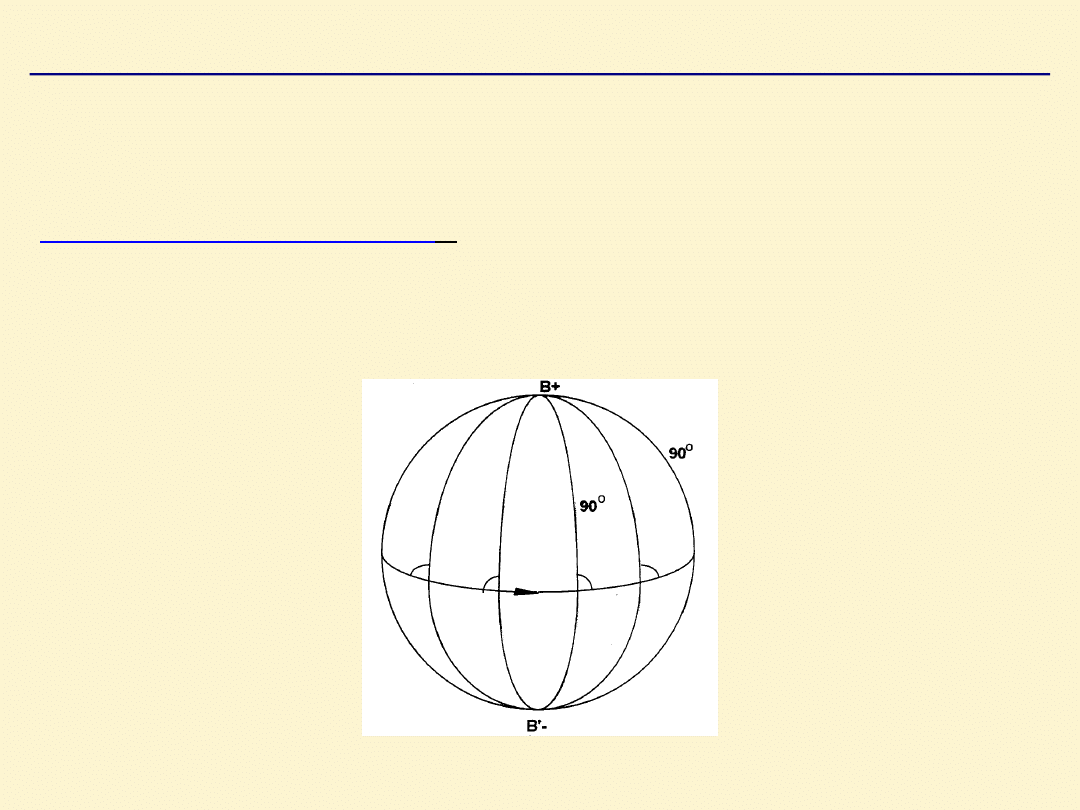
Geometria sfery

Biegun koła wielkiego

jest to miejsce geometryczne na

powierzchni sfery (kuli), którego odległość od danego koła
wielkiego wynosi 1/4 obwodu koła wielkiego

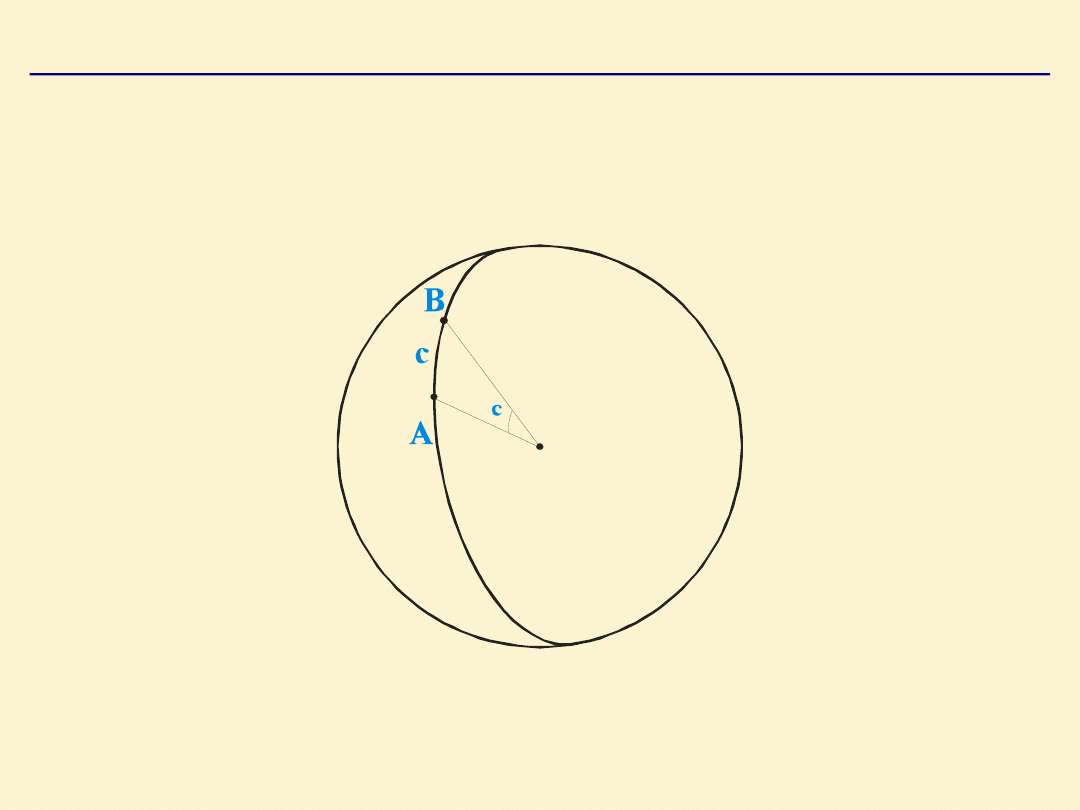
Geometria sfery

ODLEGŁOŚĆ SFERYCZNA

– długość mniejszego łuku koła

wielkiego przechodzącego przez dwa punkty leżące na
sferze.

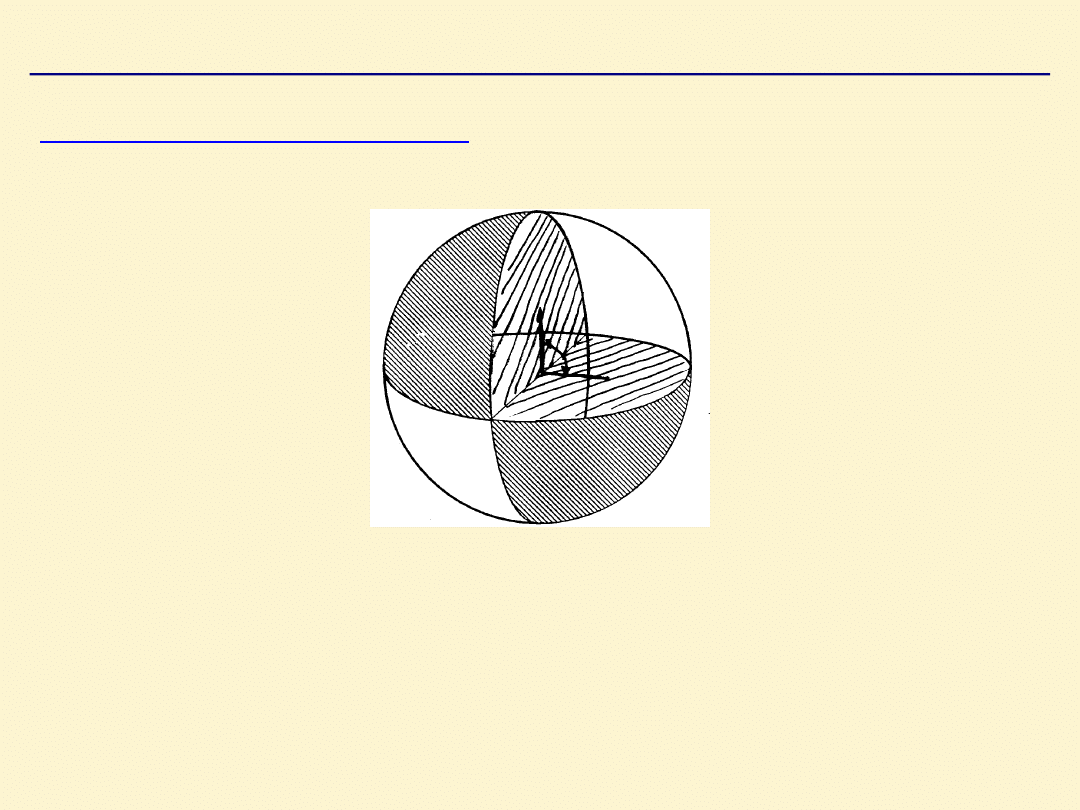
Geometria sfery

Dwukątem sferycznynym

nazywamy wycinek sfery (kuli)

który tworzą dwa przecinające się koła wielkie.

Dwa przecinające koła wielkie tworzą 4 dwukąty sferyczne.

Geometria sfery

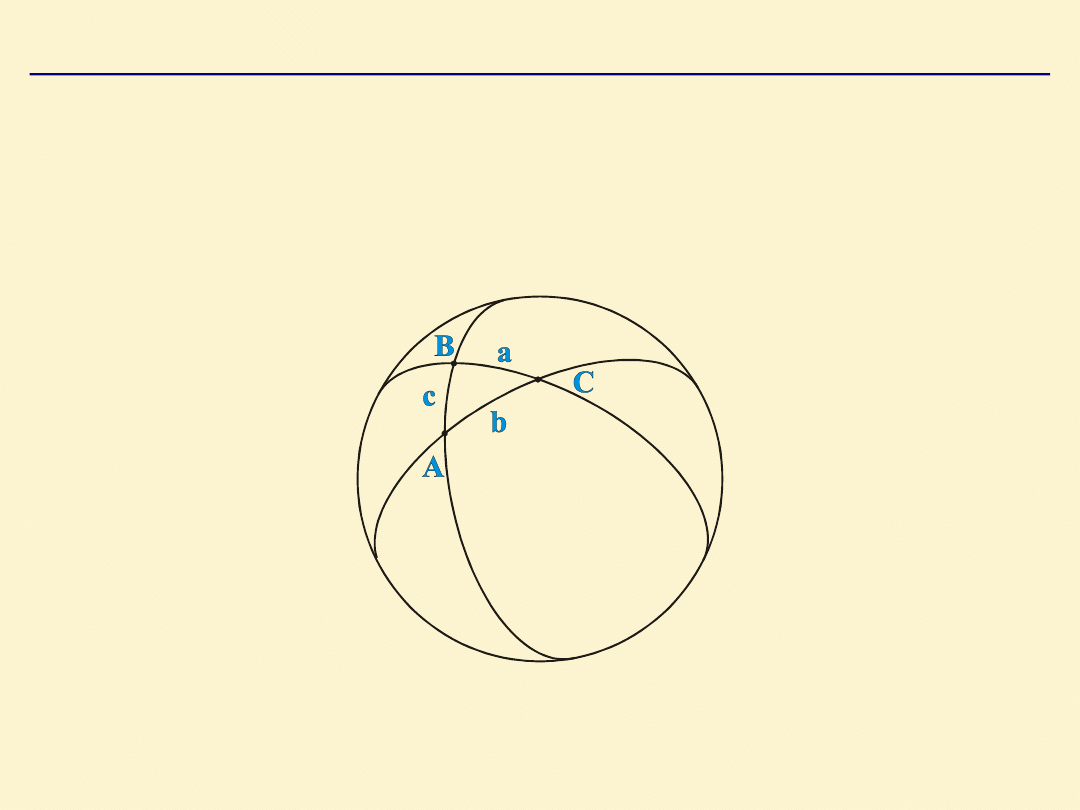
TRÓJKĄT SFERYCZNY

– część powierzchni sfery ograniczona

łukami trzech kół wielkich.

KĄT TRÓJKĄTA SFERYCZNEGO

– kąt pomiędzy

stycznymi do kół wielkich wychodzących z danego
wierzchołka.

Geometria sfery

Geometria sfery

1. w trójkącie sferycznym naprzeciw większego

(mniejszego) boku leży większy (mniejszy) kąt i
odwrotnie – naprzeciw większego (mniejszego) kąta leży
większy (mniejszy) bok.

2. w trójkącie sferycznym naprzeciw równych boków leżą

równe kąty: jeżeli a=b to A=B.

3. w trójkącie sferycznym suma dwóch boków jest większa

od boku trzeciego (a+b>c), zaś suma dwóch kątów jest
mniejsza od sumy kąta trzeciego i kąta półpełnego
(A+B<C+180°).

4. jeżeli w trójkącie sferycznym suma dwóch boków jest

większa, równa lub mniejsza od 180° to suma
pozostałych kombinacji boków jest również większa,
równa lub mniejsza od 180°.

WŁASNOŚCI TRÓJKĄTA SFERYCZNEGO:

TRÓJKĄTY EULERA

– trójkąty sferyczne o bokach i kątach mniejszych od 180°.

Geometria sfery

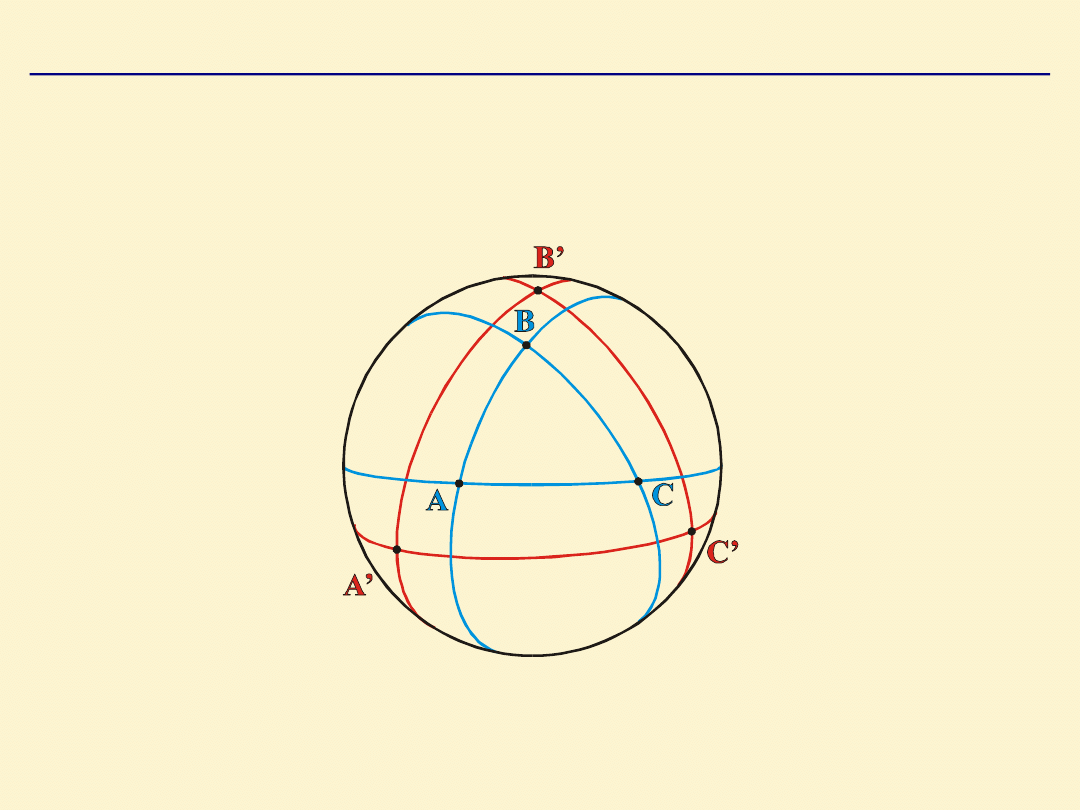
TRÓJKĄTEM BIEGUNOWYM A’B’C’

względem danego

trójkąta sferycznego ABC nazywamy trójkąt utworzony
przez bieguny kół wielkich, które tworzą boki trójkąta
danego.

Trójkąt wyjściowy jest trójkątem biegunowym dla
swojego trójkąta biegunowego.

Geometria sfery

Pomiędzy elementami trójkąta danego (bokami a, b, c i
kątami A, B, C), a elementami trójkąta biegunowego
(bokami a’, b’, c’ i kątami A’, B’, C’) zachodzą zależności:

a + A’ = 180°

A + a’ = 180°

b + B’ = 180°

B + b’ = 180°

c + C’ = 180°

C + c’ = 180°

NADMIAR SFERYCZNY:



= A + B + C –180°

0° <



< 180°

Geometria sfery

WARIANTY ROZWIĄZYWANIA

TRÓJKĄTÓW SFERYCZNYCH

DANE

OPIS DANYCH

SZUKANE

Wariant

1

a

b

c

3 boki

A

B

C

Wariant

2

a

b

C

2 boki i kąt

pomiędzy nimi

A

B

c

Wariant

3

a

b

A

2 boki i kąt

przyległy

do jednego z nich

B

C

c

Wariant

4

B

C

c

2 kąty i bok

przyległy

do jednego z nich

a

b

A

Wariant

5

A

B

c

2 kąty i bok

pomiędzy nimi

a

b

C

Wariant

6

A

B

C

3 kąty

a

b

c

Geometria sfery

Wzory do rozwiązywania trójkątów

WZÓR SINUSOWY

C

c

B

b

A

a

sin

sin

sin

sin

sin

sin





WZÓR COSINUSOWY (ALBATANIEGO)

C

b

a

b

a

c

B

c

a

c

a

b

A

c

b

c

b

a

cos

sin

sin

cos

cos

cos

cos

sin

sin

cos

cos

cos

cos

sin

sin

cos

cos

cos













Geometria sfery

C

a

b

a

b

B

c

C

b

a

b

a

A

c

B

a

c

a

c

C

b

B

c

a

c

a

A

b

A

b

c

b

c

C

a

A

c

b

c

b

B

a

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin

























WZÓR SINUSOWO-COSINUSOWY

WZORY PODSTAWOWE TRÓJKĄTA BIEGUNOWEGO

B

a

b

A

a

A

C

A

C

c

A

a

C

B

C

B

b

A

a

C

B

C

B

A

sin

sin

sin

sin

cos

cos

sin

sin

cos

cos

sin

cos

cos

sin

sin

cos

cos

sin

cos

sin

sin

cos

cos

cos

















Sfera niebieska

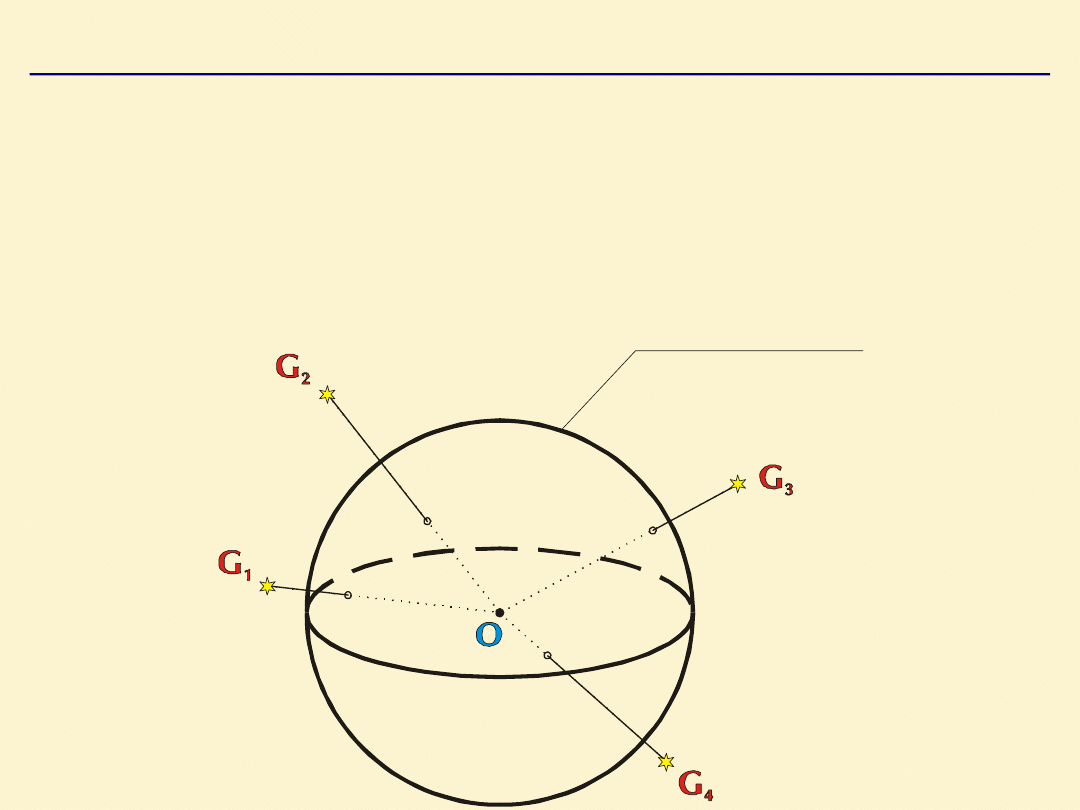
Sfera o nieskończenie wielkim, bliżej nieokreślonym
promieniu, której środek zależnie od potrzeb umieszcza się
np. w miejscu obserwacji, centrum mas Ziemi czy centrum
mas Słońca. Zamiast rozpatrywać pęk kierunków do ciał
niebieskich znajdujących się w przestrzeni w różnych
odległościach od obserwatora rozpatruje się ich rzuty na
sferę

niebieską,

będące

punktami

przecięcia

tych

kierunków ze sferą niebieską.

s f e r a n i e b i e s k a

Sfera niebieska

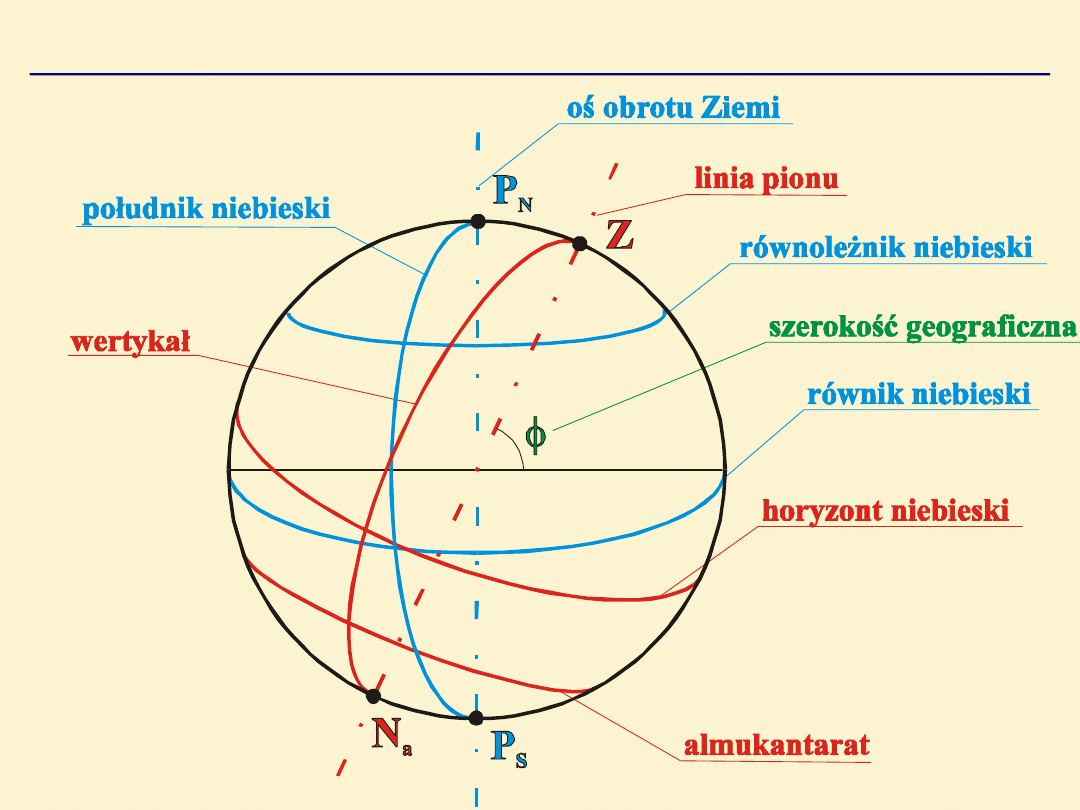
ZENIT I NADIR

(Z, Nd) – punkty przecięcia sfery

niebieskiej przez linię pionu wystawioną w miejscu
obserwacji.

HORYZONT NIEBIESKI

– linia przecięcia płaszczyzny

horyzontu ze sferą niebieską.

WERTYKAŁ

– linia przecięcia płaszczyzny przechodzącej

przez linię pionu ze sferą niebieską.

ALMUKANTARAT

– linia przecięcia płaszczyzny równoległej

do płaszczyzny horyzontu ze sferą niebieską.

BIEGUNY NIEBIESKIE (Pn, Ps)

– punkty przecięcia sfery

niebieskiej z osią obrotu Ziemi.

RÓWNIK NIEBIESKI

– linia przecięcia się płaszczyzny

równika ziemskiego ze sferą niebieską.

POŁUDNIK NIEBIESKI

– linia przecięcia się płaszczyzny

południka ziemskiego ze sferą niebieską.

RÓWNOLEŻNIK NIEBIESKI

– linia przecięcia się

płaszczyzny równoleżnika ziemskiego ze sferą niebieską.

Sfera niebieska

Sfera niebieska

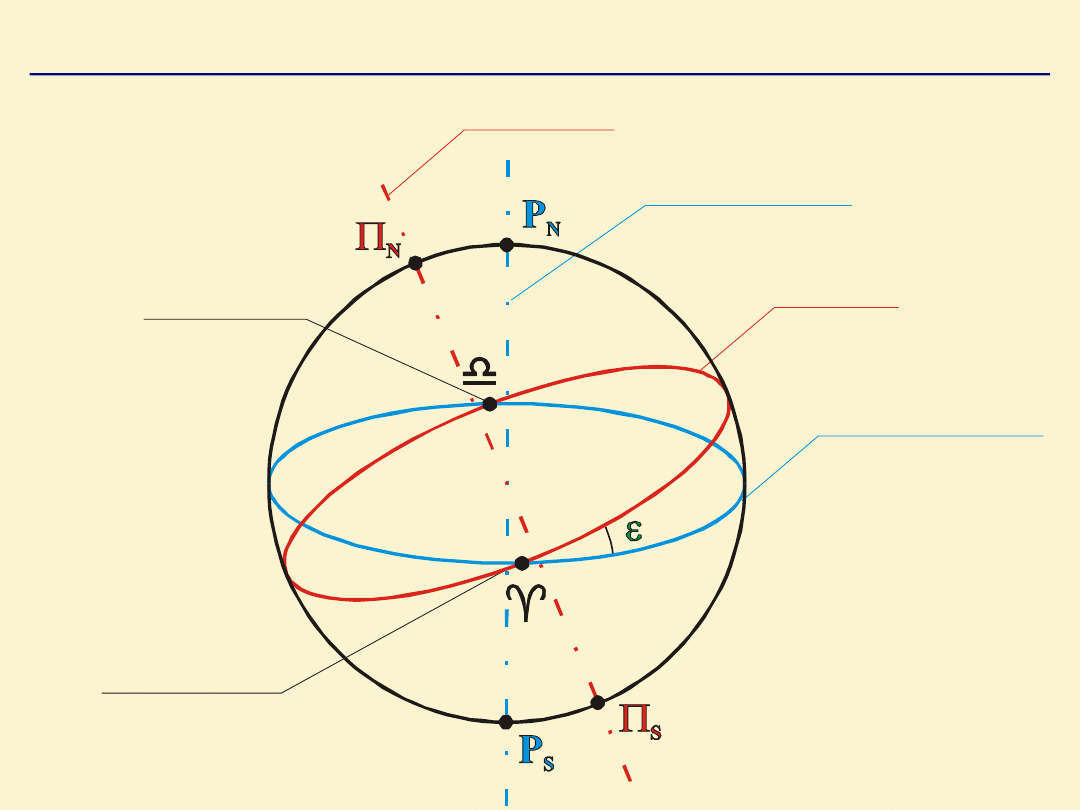
EKLIPTYKA

– linia przecięcia płaszczyzny

heliocentrycznej orbity Ziemi ze sferą niebieską.

BIEGUNY EKLIPTYKI

(



n,



s)

– punkty przecięcia się

linii prostopadłej do płaszczyzny ekliptyki i
przechodzącej przez środek sfery niebieskiej ze sferą.

POŁUDNIK MIEJSCOWY

– koło wielkie przechodzące

przez bieguny niebieskie oraz zenit i nadir.

I WERTYKAŁ

– wertykał prostopadły do południka

miejscowego.

STRONY ŚWIATA

– punkt południa (S) i punkt północy

(N): miejsca przecięcia się południka miejscowego i
horyzontu, punkt wschodu (E) i punkt zachodu (W)
miejsca przecięcia się I wertykału i horyzontu.

Sfera niebieska

r ó w n ik n ie b ie s k i

p u n k t B a r a n a

p u n k t W a g i

e k lip t y k a

o ś e k lip t y k i

o ś o b r o t u Z ie m i

Sfera niebieska