
Wykład III
Granice funkcji
:
f
R
A
R
,
A
przedział
A
x
0
,
f
określona w
0
0
0
\
,
0
x
x
x
S
x
Definicja 3.1 (definicja Cauchy’ego granicy funkcji)
g
x
f
x
x
g
x
f
x
x
D
x
x
x
f
)
(
:
lim
0
0
0
0
0
0
x
x
,
0
x
U
x
g
x
f
,
g
x
f
Inaczej:
x
f
U
x
g
x
f
x
x
D
x
x
ot
U
g
ot
x
x
f
0
0
0
:
lim
K
x
ot
U
x
M
x
ot
U
x
Granice niewłaściwe:
g
x
0
g
x
f
k
x
g
x
f
f
D
x
R
K
x
0
lim
K
x
f
M
x
x
f
f
D
x
R
M
R
K
x
lim
Def. 3.2. (definicja Heinego granicy funkcji)
g
x
f
x
x
g
x
f
n
n
n
n
x
x
D
x
x
x
n
f
n
lim
lim
:
lim
0
0
0
K
M
x
Definicja 3.3 (granice jednostronne)
granica lewostronna:
g
x
f
x
x
g
x
f
n
n
n
n
x
x
D
x
x
x
n
f
n
lim
lim
lim
0
0
0
granica prawostronna:
g
x
f
x
x
g
x
f
n
n
n
n
x
x
D
x
x
x
n
f
n
lim
lim
lim
0
0
0
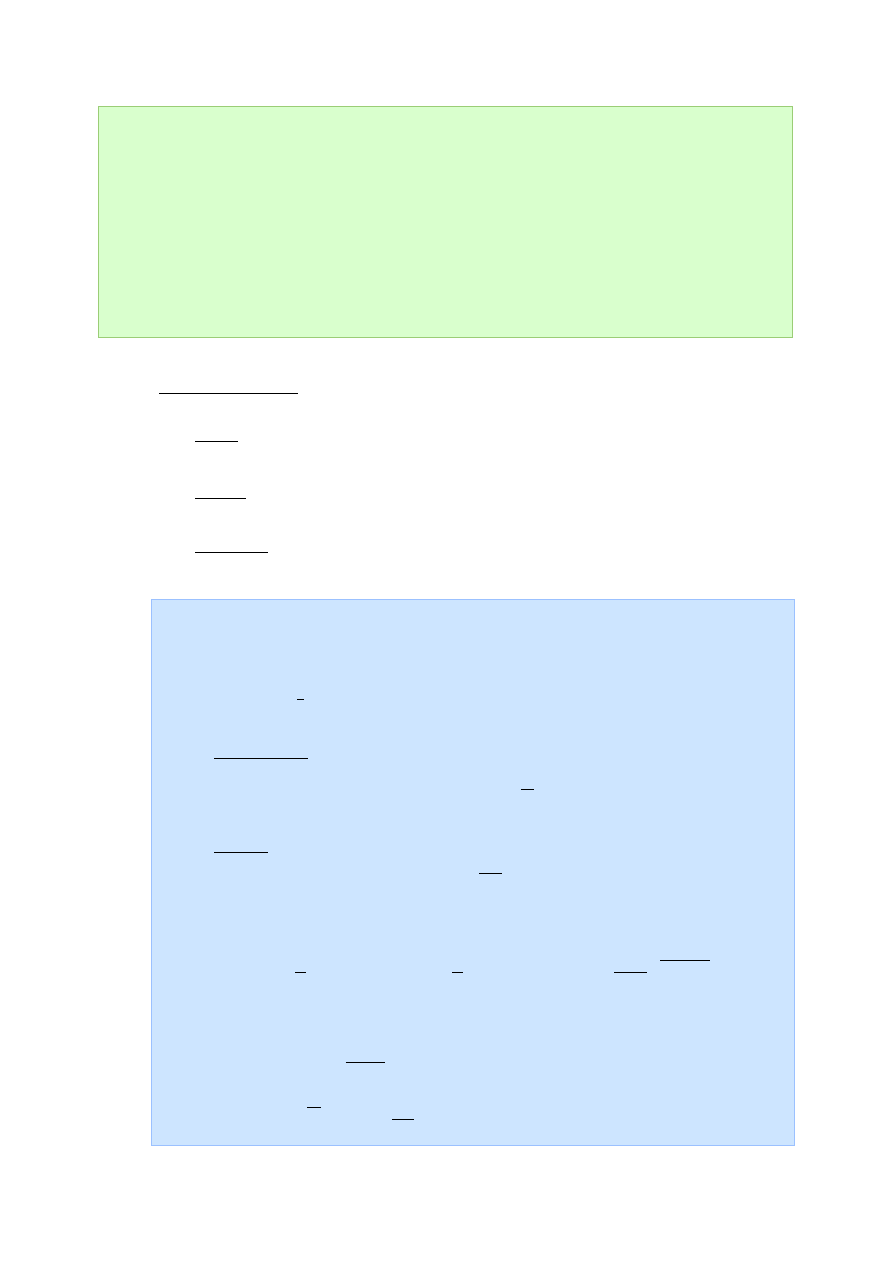
granice specjalne:
1)
1
sin
lim
0
2)
1
1
lim
0
e
3)
1
1
ln
lim
0
Przykład 3.1
a)
e
x
x
x
1
1
0
1
lim
uzasadnienie:
e
x
x
R
x
n
x
n
n
n
n
n
1
1
lim
0
lim
ogólnie:
e
x
f
x
f
x
f
x
x
x
x
1
0
0
1
lim
0
lim
b)
?
2
)
sin
(
sin
1
2
0
2
0
1
1
2
0
2
2
2
2
2
2
2
sin
1
lim
1
cos
1
lim
cos
lim
x
x
e
x
x
x
x
x
x
x
x
x
?:=
2
sin
2
lim
2
0
x
x
x
2
2
2
0
1
cos
lim
2
2
e
e
x
x
x
na podstawie definicji
Heinego granicy funkcji
c)
x
x
1
sin
lim
0
Podejrzewamy, że ciąg nie ma granicy.
n
x
n
2
2
1
1
2
sin
2
2
sin
n
n
x
n
2
2
1
Niech
0
2
2
1
n
n
n
x
1
2
2
sin
1
sin
n
n
n
n
x
x
f
0
1
n
n
n
x
0
sin
n
n
n
x
f
x
x
f
x
x
f
x
x
n
n
n
n
n
n
n
n
1
sin
lim
0
lim
0
1
lim
0
0
x
x
sin

Podstawowe twierdzenia dotyczące granic funkcji
Twierdzenie 3.1 (podstawowe własności granic funkcji)
Z definicji Heinego granicy funkcji i odpowiednich twierdzeń dotyczących granic
ciągów wynikają następujące własności:
(działania arytmetyczne)
Jeżeli:
g
f ,
określone w sąsiedztwie punktu
0
x
2
1
0
0
lim
lim
g
x
g
g
x
f
x
x
x
x
2
1
, g
g
granice właściwe
1°
2
1
0
lim
g
g
x
g
x
f
x
x
2°
2
1
0
lim
g
g
x
g
x
f
x
x
3°
2
1
0
lim
g
g
x
g
x
f
x
x
przy dodatkowym założeniu, że
0
x
g
w sąsiedztwie
0
2
0
g
x
Twierdzenie 3.2 (twierdzenie o 3-ch funkcjach)
Z.
0
x
ot
U
h
g
f
,
,
określone na
0
\ x
U
x
h
x
g
x
f
x
U
x
0
\
g
x
h
x
f
x
x
x
x
0
0
lim
lim
T.
g
x
g
x
x
0
lim
Przykład 3.2
Oblicz:
x
x
x
sin
lim
Ogólnie:
Z twierdzenia o 3-ch funkcjach wynika następująca własność:
Jeżeli lim
𝑥→𝑥
0
𝑓 𝑥 = 0 g-ograniczona w otoczeniu 𝑥
0
⇒ lim
𝑥→𝑥
0
𝑓 𝑥 ∗ 𝑔(𝑥) = 0
krótko:
0
lim
0
0
0
ogr
x
x
x
x
x
g
x
f
x
h
x
g
x
f
g
g
g
0
x
x
0
x
x
0
x
x
0
0
0
x
x
x
x
x
x
x
1
sin
1

W przykł. 3.2.:
0
sin
1
lim
0
ogr
x
x
x
Definicja 3.4 (ciągłość w punkcie)
f
określona w otoczeniu punktu
0
x
f
ciągła w
0
0
0
lim
x
f
x
f
x
x
x
inaczej:
f
ciągła w
0
0
0
3
lim
2
1
0
x
f
g
g
x
f
D
x
x
x
x
f
Ciągłość jednostronna:
f
lewostronnie (prawostronnie) ciągła w
0
)
(
0
0
3
lim
2
1
0
0
x
f
g
g
x
f
D
x
x
x
x
x
x
f
Przykład 3.3
Zbadać ciągłość w punkcie
2
x
w zależności od
m
.
2
dla
2
dla
1
1
2
1
x
m
x
e
x
f
x
m
f
2
1

R
m
x
x
x
x
x
x
f
e
x
f
e
x
f
x
x
2
0
2
2
2
2
lim
1
1
1
lim
lim
0
1
1
lim
lim
2
0
2
1
0
2
1
- dla
f
m
0
lewostronnie ciągła w punkcie
2
x
- dla
f
m 1
prawostronnie ciągła w punkcie
2
x
Definicja 3.5 (ciągłość na zbiorze)
f
ciągła na zbiorze ciągła zbioru X tzw. (jeżeli jest ciągła w każdym punkcie)
Wniosek 3.1
1
Suma, różnica, iloraz funkcji ciągłych jest funkcją ciągła.
Iloraz funkcji ciągłych jest funkcja ciągłą pod warunkiem, że
mianownik jest różny od 0.
2
Złożenie funkcji ciągłych jest funkcją ciągłą.
Własności funkcji ciągłych – c.d.
I. (twierdzenie o lokalnym zachowaniu znaku)
f
ciągła w
0
x
, określona w
0
0
0
0
x
f
x
ot
U
0
0
1
0
1
x
f
U
x
x
ot
U
0
x
by
f
była
ciągła w
2
x
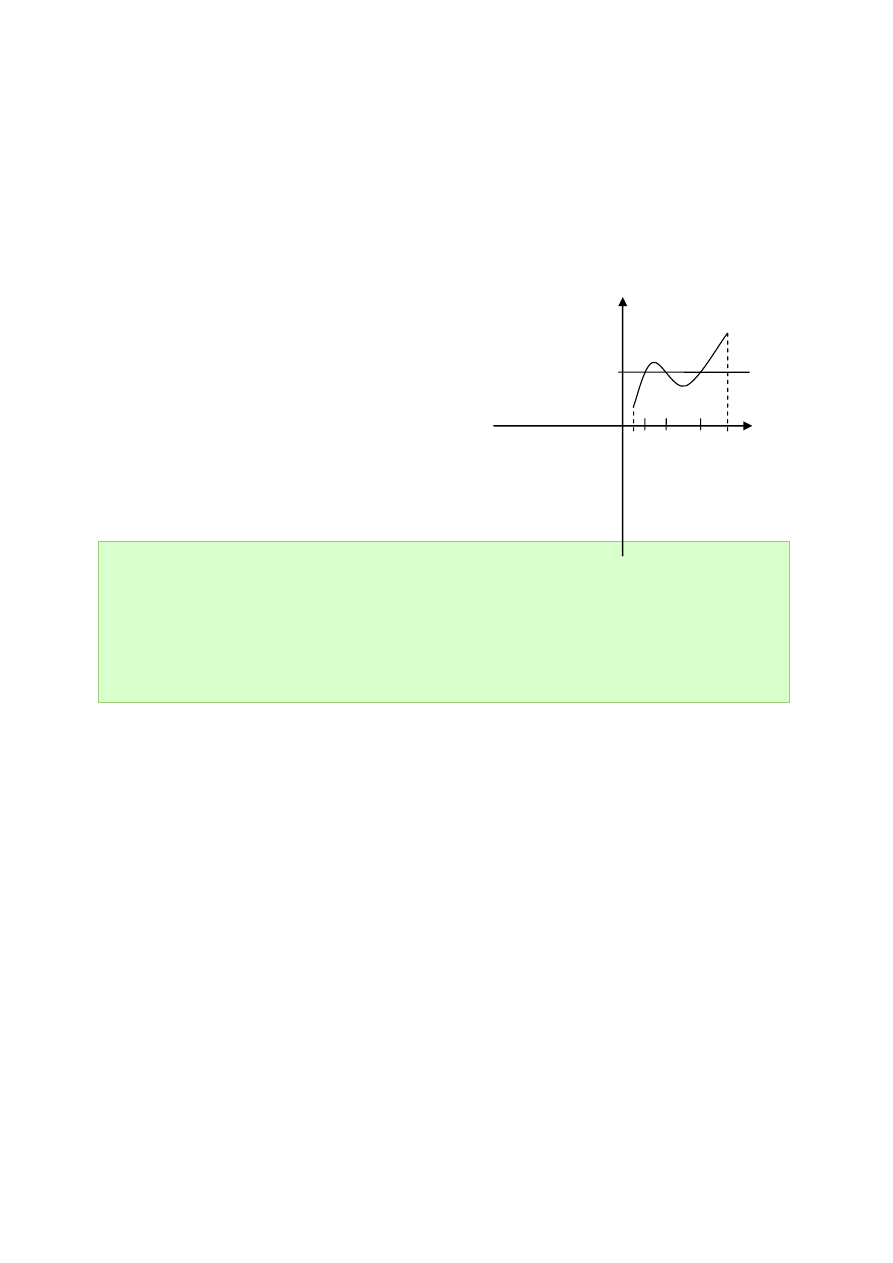
II. (własność Darboux)
b
f
a
f
C
f
b
a
,
, niech
c
liczba pomiędzy
a
f
i
b
f
c
x
f
b
a
x
0
)
,
(
0
Funkcja ciągła na przedziale domkniętym
i ograniczonym przyjmuje wszystkie
wartości pośrednie.
Definicja 3.6 (ograniczenie funkcji)
f
1
ograniczona z góry na zbiorze
M
x
f
X
X
x
R
M
:
f
2
ograniczona z dołu na zbiorze
m
x
f
X
X
x
R
m
:
0
x
0
x
0
x
a
b
c
Przykład 3.4
x
e
x
f
2
1
x
x
g
Definicja 3.7 (kresy funkcji)
M
x
f
M
x
f
x
f
M
X
x
X
x
X
x
0
2
1
:
sup
(czyt. supremum po
x
należącym do
X
z
x
f
)
1
x
y
0
inf
x
R
x
e
funkcja nie osiąga kresu dolnego
x
e
y
y
x
1
2
1
x
y
1
1
max
1
0
1
sup
2
2
x
f
x
R
x
R
x
funkcja osiąga kres górny → maksimum
m
x
f
m
x
f
x
f
m
X
x
X
x
X
x
0
2
1
:
inf
(czyt. infimum po
x
należącym do
X
z
x
f
)
III. (twierdzenie Weierstrassa)
Funkcja ciągła na przedziale domkniętym i ograniczonym osiąga swoje kresy.
x
f
x
f
x
f
x
f
C
f
b
a
x
b
a
x
b
a
x
x
b
a
,
2
,
1
,
,
,
sup
inf
2
1
Rachunek różniczkowy funkcji 1-ej zmiennej
Niech
f
określona na
0
x
ot
U
,
U
h
x
0
h
x
f
h
x
f
0
0
– iloraz różnicowy
Definicja 3.8 (pochodna)
Jeżeli
h
x
f
h
x
f
h
0
0
0
lim
to powiemy, że funkcja
f
jest różniczkowalna w punkcie
0
x
i wartość tej granicy
0
0
0
0
lim
x
f
h
x
f
h
x
f
h
nazywamy pochodną funkcji w
punkcie
0
x
.
y
x
h
x
f
0
0
x
f
0
x
h
h
x
0
0
0
x
f
h
x
f
n
l

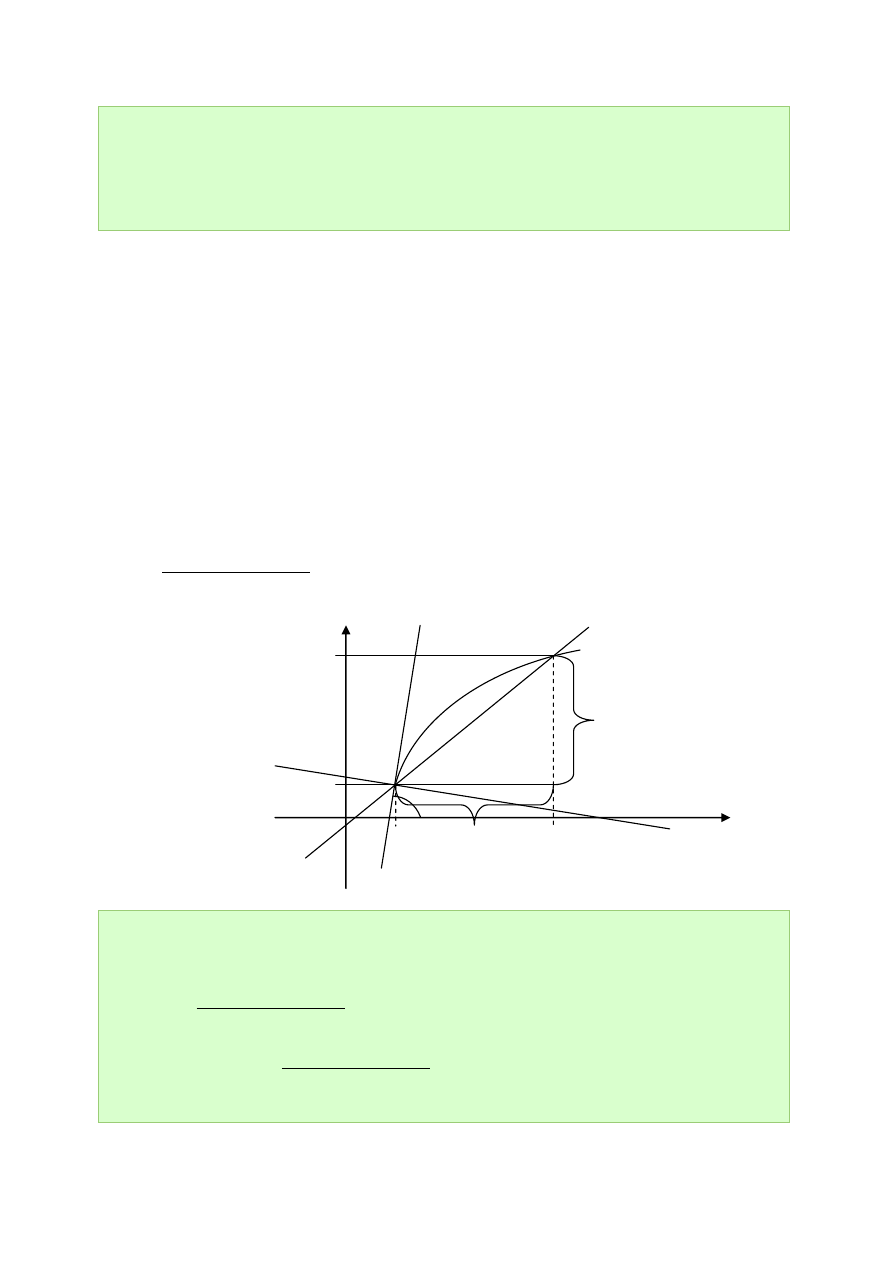
Interpretacja geometryczna pochodnej:
tg
x
f
0
kąt pomiędzy styczną do wykresu funkcji w punkcie
0
0
,
x
f
x
i dodatnim kierunkiem osi
X
0
Wniosek 3.2
0
0
0
:
x
x
x
f
x
f
y
l
– prosta styczna do wykresu w punkcie
0
,
0
x
f
x
Prosta do niej prostopadła nazywa się prostą normalną:
0
0
0
1
:
x
x
x
f
x
f
y
n
Definicja 3.9 (różniczkowalność na przedziale)
f
– różniczkowalna na
f
U
– różniczkowalna w każdym punkcie
U
x
x
f
x
X
f
:
Tw. 3.3 (działania arytmetyczne na pochodnych)
Z:
g
f ,
– różniczkowalne w
0
x
T:
1)
g
f
R
,
– różniczkowalna w
0
x
0
0
0
x
g
x
f
x
g
f
2)
g
f
– różniczkowalna w
0
x
0
0
0
0
0
0
x
g
x
f
x
g
x
f
x
g
x
f
3)
0
g
w pewnym
0
x
ot
U
g
f
– różniczkowalna w
0
x

2
0
0
0
0
0
0
0
x
g
x
g
x
f
x
g
x
f
x
g
x
f
D:
2)
x
g
x
f
x
g
x
f
h
x
g
h
x
g
x
f
h
x
g
h
x
f
h
x
f
h
x
g
x
f
h
x
g
x
f
h
x
g
x
f
h
x
g
h
x
f
h
x
g
x
f
h
x
g
h
x
f
x
g
x
f
x
g
x
f
h
h
h
0
0
0
lim
lim
lim
h
x
f
h
x
f
x
f
h
0
0
0
lim
0
0
0
lim
x
x
x
f
x
f
x
f
x
x
– drugi wzór na pochodną
Wyszukiwarka
Podobne podstrony:
kolos granice, pochodne
granice pochodna zadania
granice i pochodne
Granica i pochodne funkcji, Ekonomia- studia, matematyka
Granica i pochodna funkcji, Analiza matematyczna
kolos granice, pochodne
zadania z granic, pochodnych itp
Granice funkcji - pochodne, Prywatne, matna
zadania na kolos, macierze i pochodne granice jedn ciaglosc+
zadania na kolos, macierze i pochodne granice ciagow funkcji
pochodne granice
granice, ciagi, pochodzne, calki
Pochodną funkcji f w punkcie x nazywamy granicę, Matematyka, analiza
13 GRANICA CIAGLOSC POCHODNA, szkola technikum, matma, mata, zadania z liceum
BHP w sprawie?wek granicznych promieniowania jonizującego i wskaźników pochodnych określających zagr
więcej podobnych podstron