OBWODY ELEKTRYCZNE

i

Teoria Obwodów 1

Kurs powtórkowy

Kurs powtórkowy

Sierpie

ń

2011

Sierpie

ń

2011

w3

w3

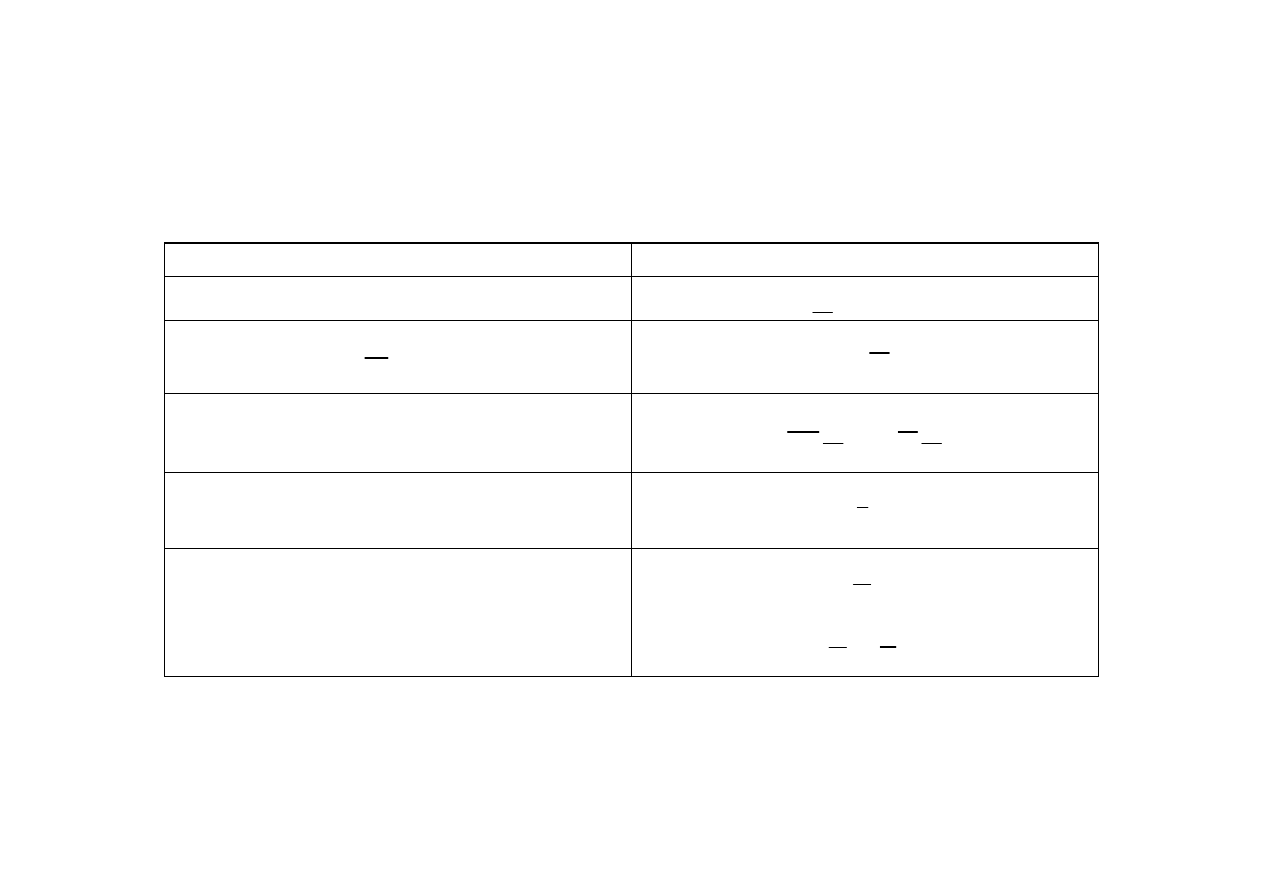
Metoda symboliczna

Domena czasowa

Domena zespolona

( )

sin(

)

m

X

x t

X

t

ω

=

+Ψ

X

j

X

Xe

Ψ

=

( )

d

x t

dt

j X

ω

( )

x t dt

∫

1

1

X

j

X

j

ω

ω

=−

( ) 0

k

k

i t

±

=

∑

0

k

k

I

± =

∑

( ) 0

k

k

u t

±

=

∑

( )

( ) 0

k

k

k

u t

e t

±

±

=

∑

0

k

k

U

± =

∑

0

k

k

k

U

E

± ± =

∑

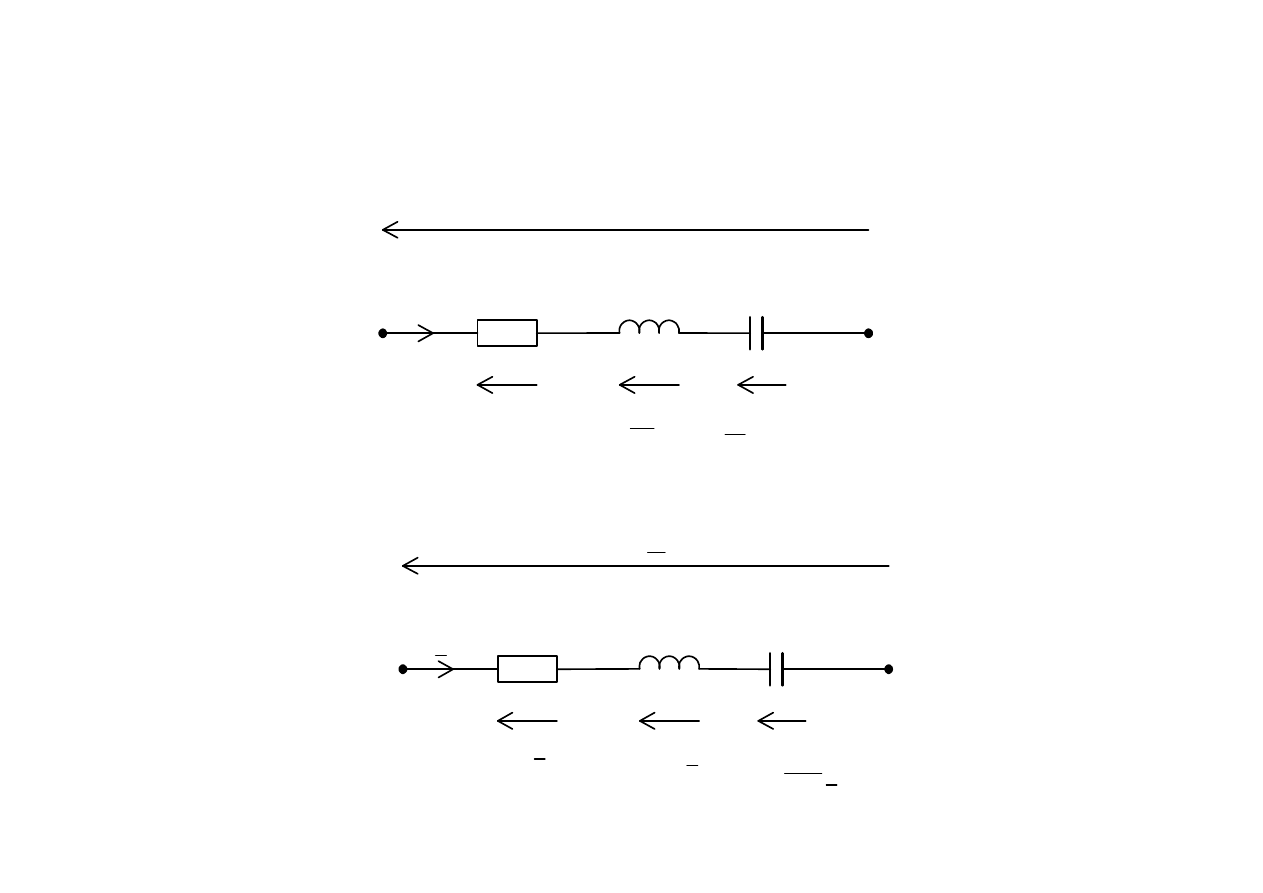
Metoda symboliczna

U

( )

u t

( )

i t

I

( )

Ri t

RI

( )

d

L

i t

dt

j LI

ω

1

( )

i t dt

C

∫

1

j

I

C

ω

−

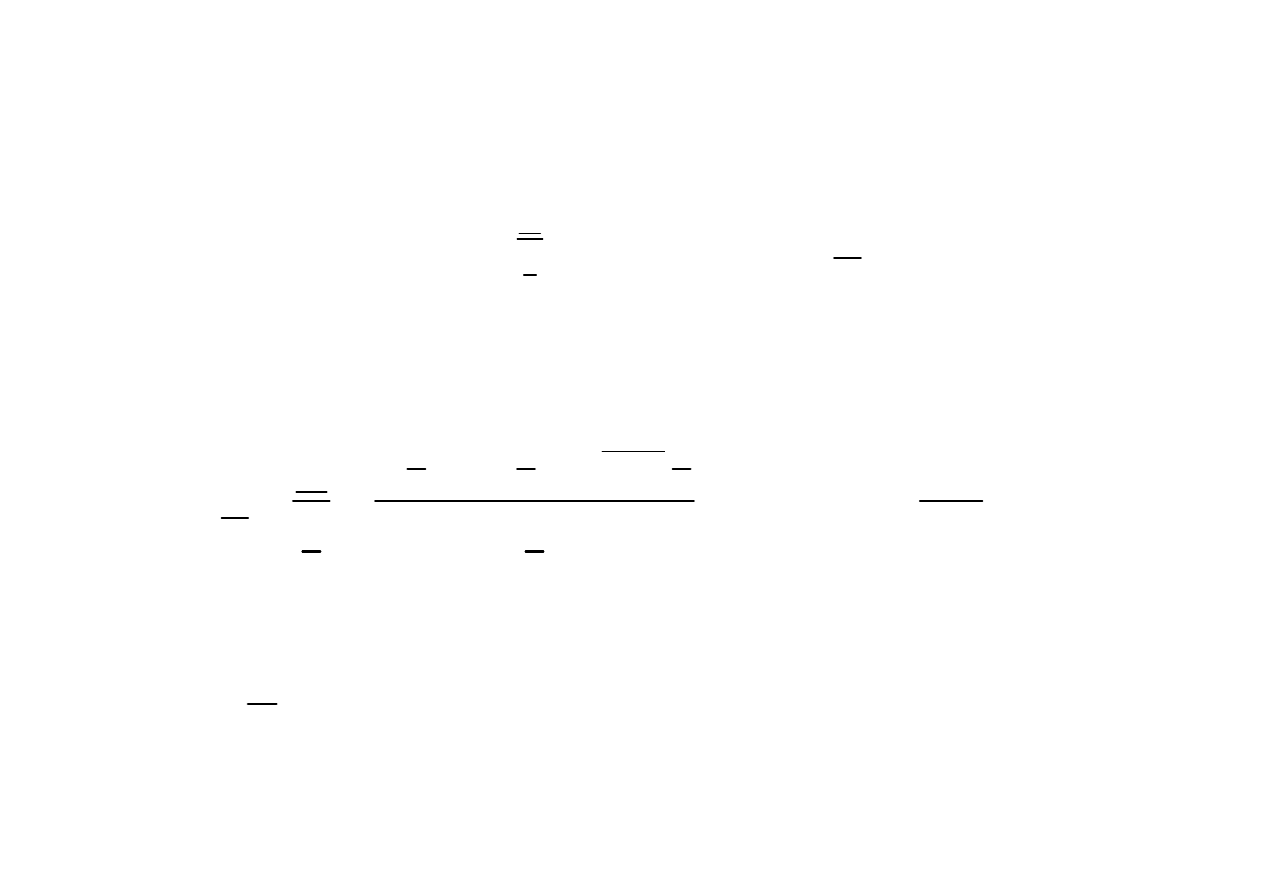
Impedancja

U

I

Z

1

1

RI

j I

j

I

U

C

Z

R

j

j

I

I

C

ω

ω

ω

ω

+

−

=

=

= +

−

Wprowadzamy dla gał

ę

zi iloraz i oznaczamy liter

ą

Wielko

ść

niezale

ż

na od amplitudy ani od fazy pocz

ą

tkowej pr

ą

du nazywa si

ę

impedancj

ą

zespolon

ą

( oporem pozornym )

Z

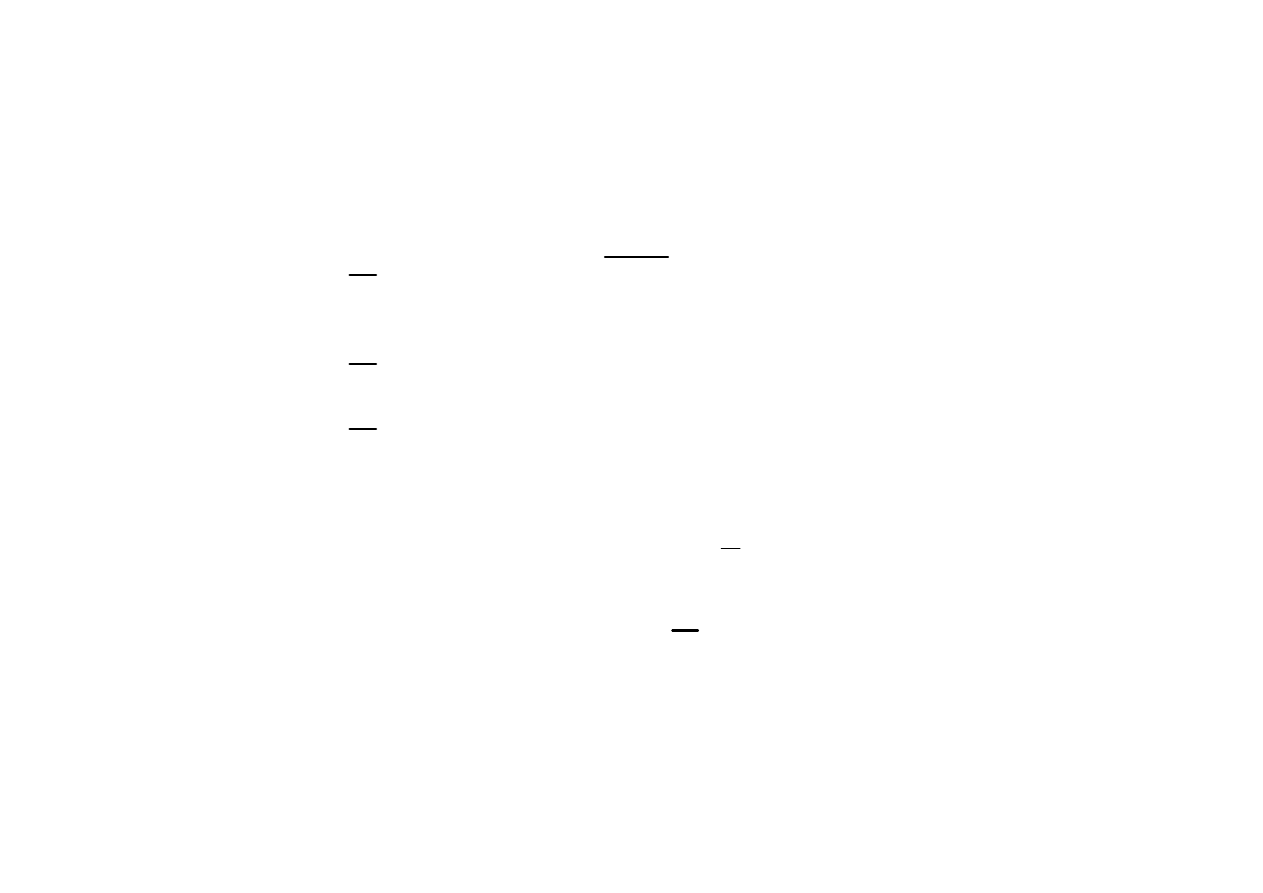
Impedancja

1

(

)

L

C

L

C

Z

R

j

j

R

jX

jX

C

Z

R

j X

X

Z

R

jX

ω

ω

= +

−

= +

−

= +

−

= +

Z

Z

R – rezystancja lub opór czynny - Re{ }

X – reaktancja lub opór bierny Im{ }

Impedancja

X=X

L

-X

C

X

L

>X

C

→

X>0

→

charakter indukcyjny gał

ę

zi

X

L

<X

C

→

X<0

→

charakter pojemno

ś

ciowy gał

ę

zi

X

L

=X

C

→

X=0

→

charakter rezystancyjny gał

ę

zi

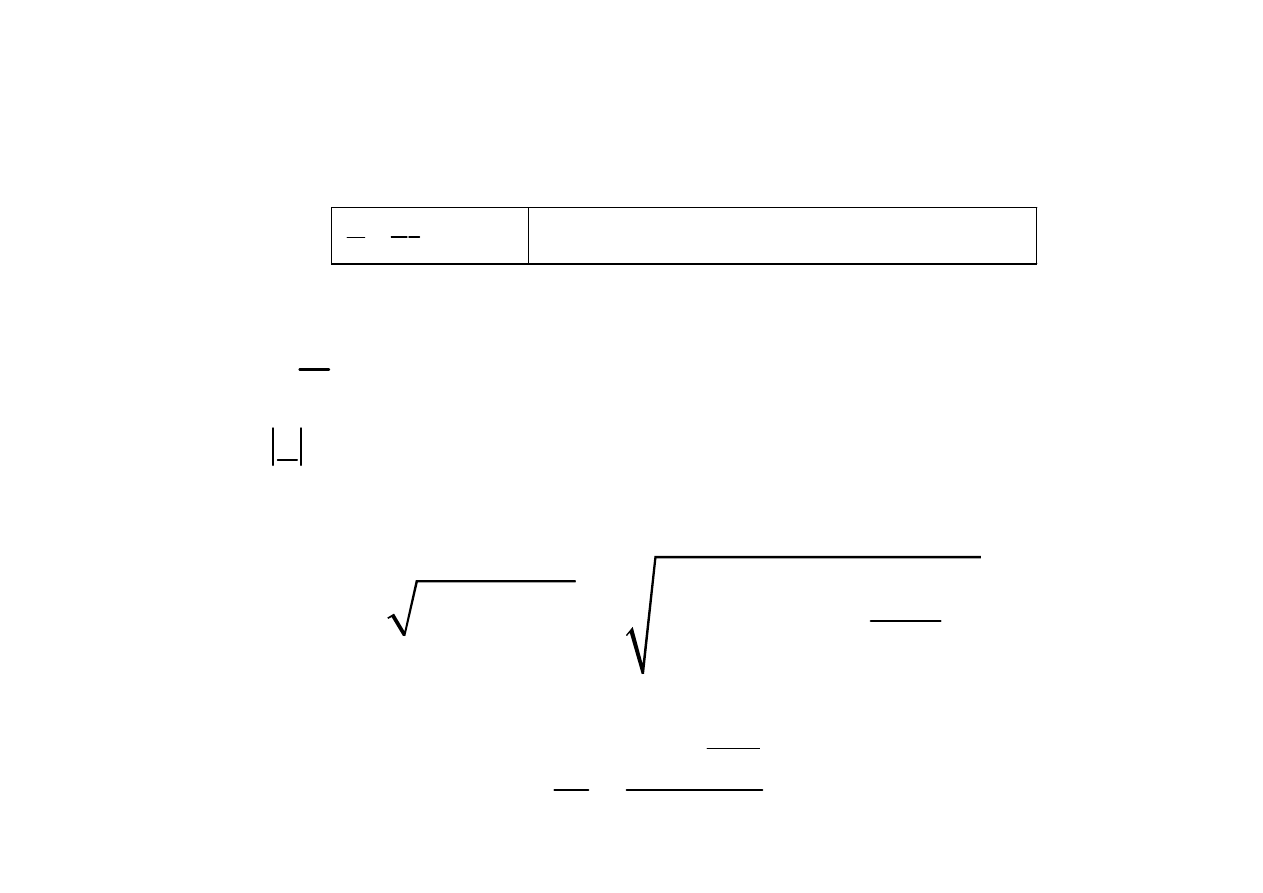
Prawo Ohma

U

Z I

=

prawo Ohma w zapisie zespolonym

cos

sin

j

Z

R

jX

Ze

Z

jZ

ϕ

ϕ

ϕ

= +

=

=

+

Z

Z

=

→

2

2

2

2

1

(

)

Z

R

X

R

L

C

ω

ω

=

+

=

+

−

1

L

X

C

tg

R

R

ω

ω

ϕ

−

=

=

moduł impedancji [Z]=1

Ω

φ

– argument impedancji

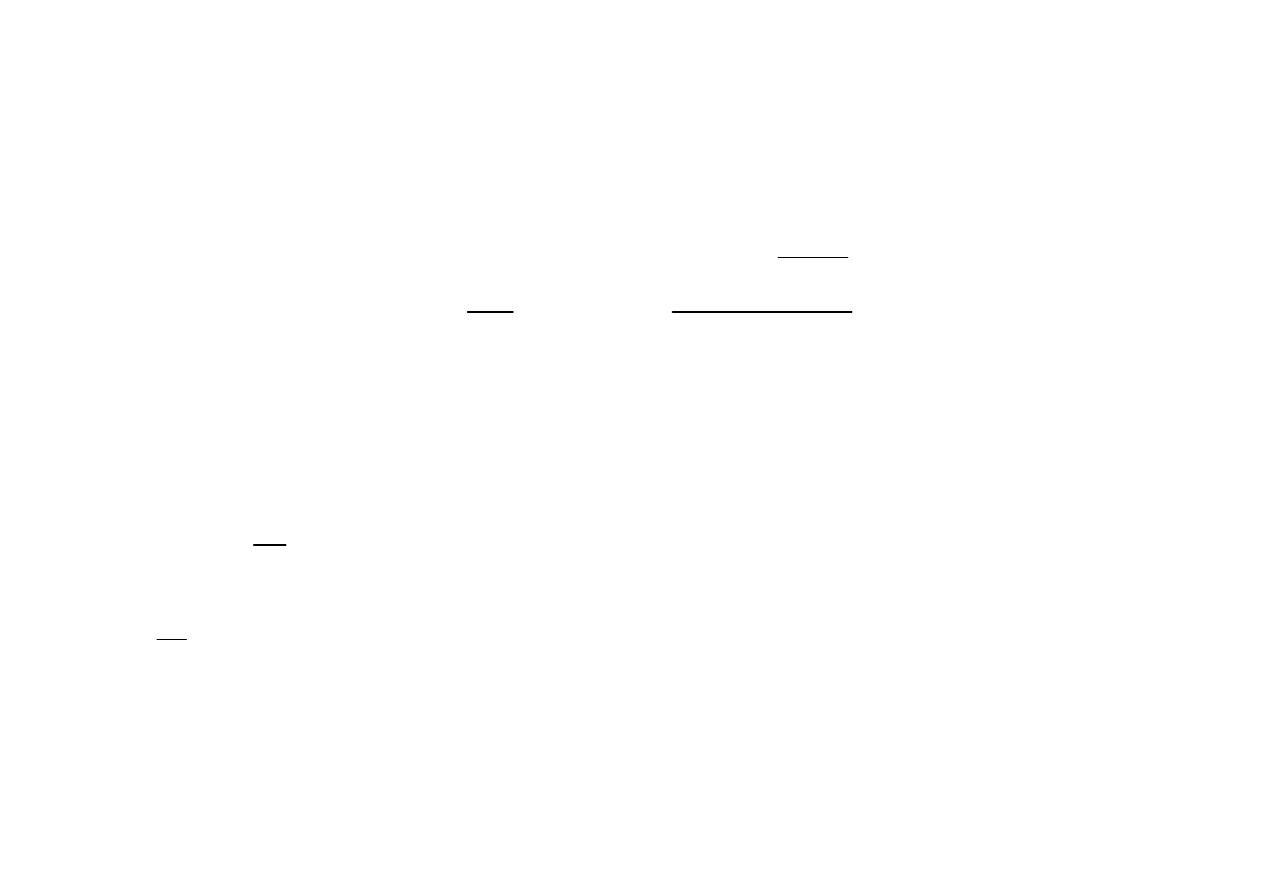
Impedancja

1

L

X

C

arctg

arctg

R

R

ω

ω

ϕ

−

=

=

1

arctg

tg

ϕ

ϕ

−

→

0

2

ϕ

Π

< ≤

0

2

ϕ

Π

− < ≤

0

ϕ

=

gdy X

L

>X

C

- charakter indukcyjny gał

ę

zi

gdy X

L

<X

C

- charakter pojemno

ś

ciowy gał

ę

zi

gdy X

L

=X

C

- charakter rezystancyjny gał

ę

zi

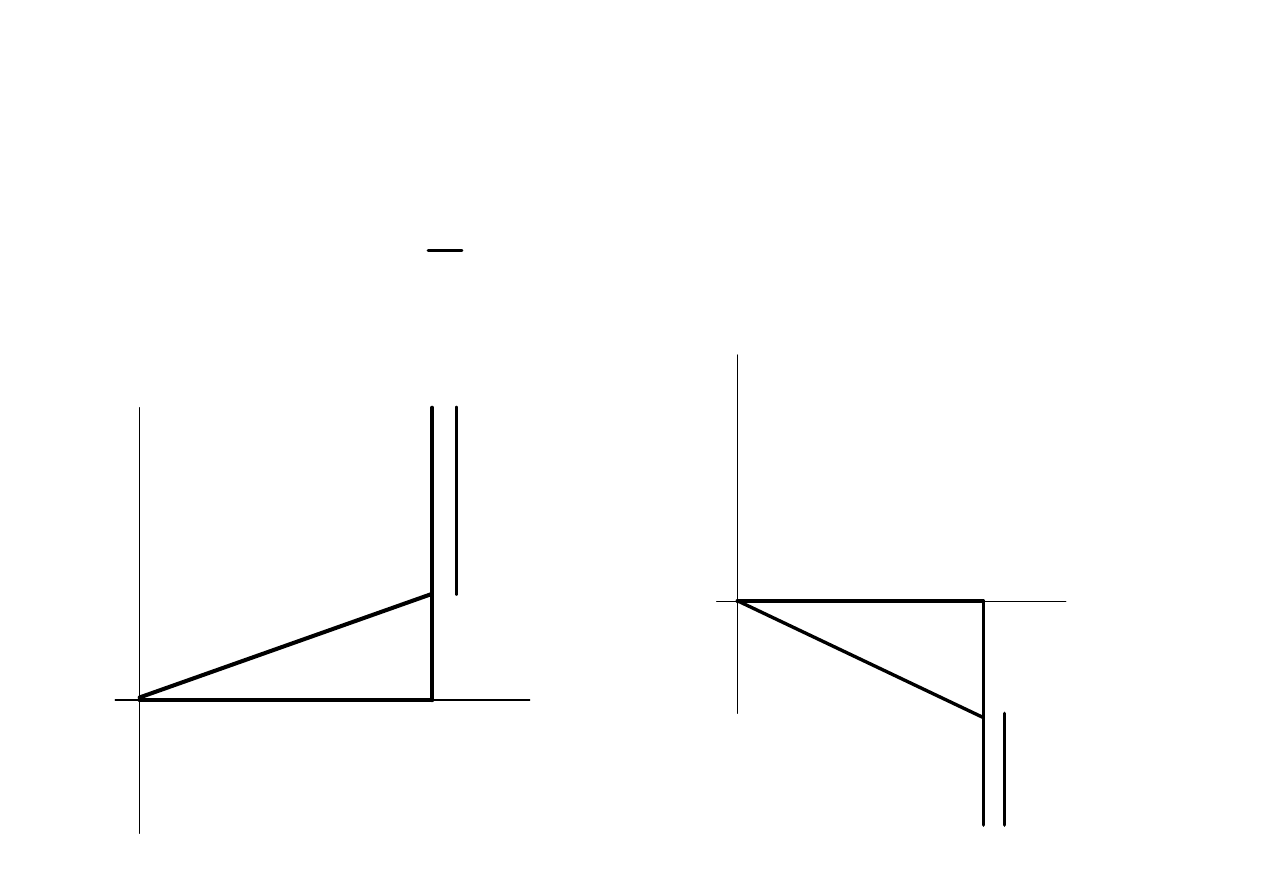
Trójk

ą

t impedancji

(

)

L

C

Z

R

j X

X

= +

−

}

ϕ

R

Z

jX

L

jX

C

jX

−

}

ϕ

R

Z

jX

−

L

jX

C

jX

−

gdy

φ

>0 charakter indukcyjny gał

ę

zi

φ

<0 charakter pojemno

ś

ciowy gał

ę

zi

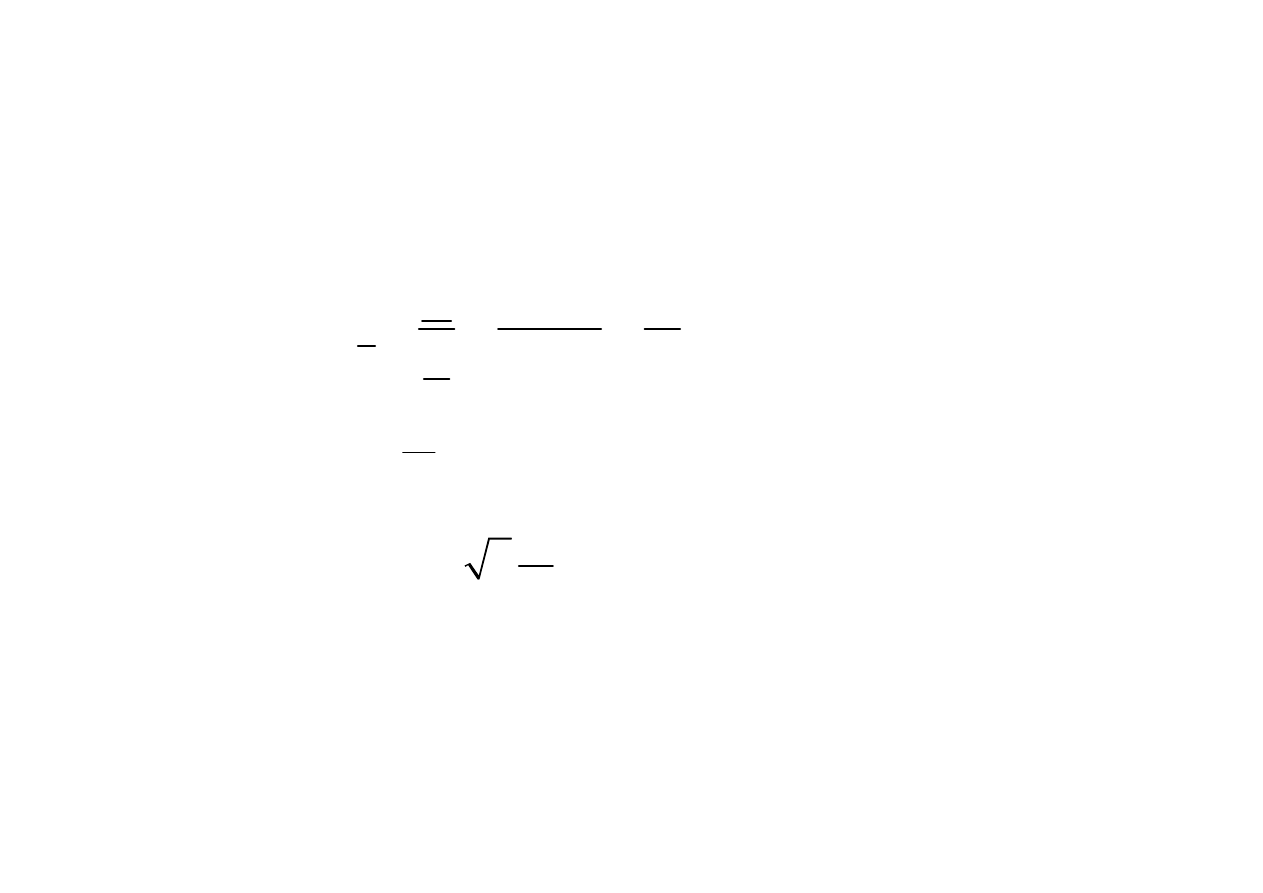
Impedancja

(

)

U

U

I

j

j

j

j

U

Ue

U

I

e

Ie

Z

Ze

Z

ϕ

ϕ

Ψ

Ψ −

Ψ

=

=

=

=

U

I

Z

=

I

U

ϕ

Ψ = Ψ −

( )

2

sin(

)

U

U

i t

t

Z

ω

ϕ

=

+ Ψ −

U

I

ϕ

= Ψ − Ψ

z prawa Ohma

st

ą

d

oraz

- k

ą

t przesuni

ę

cia fazowego

Impedancja

Ψ

U

>

Ψ

I

gdy

φ

>0 - charakter indukcyjny – napi

ę

cie

wyprzedza pr

ą

d lub pr

ą

d opó

ź

nia si

ę

wzgl

ę

dem

napi

ę

cia

Ψ

U

<

Ψ

I

gdy

φ

<0 - charakter pojemno

ś

ciowy –

napi

ę

cie opó

ź

nia si

ę

wzgl

ę

dem pr

ą

du lub pr

ą

d

wyprzedza napi

ę

cie

Ψ

U

=

Ψ

I

gdy

φ

=0 - charakter rezystancyjny – napi

ę

cie

i pr

ą

d s

ą

ze sob

ą

w fazie

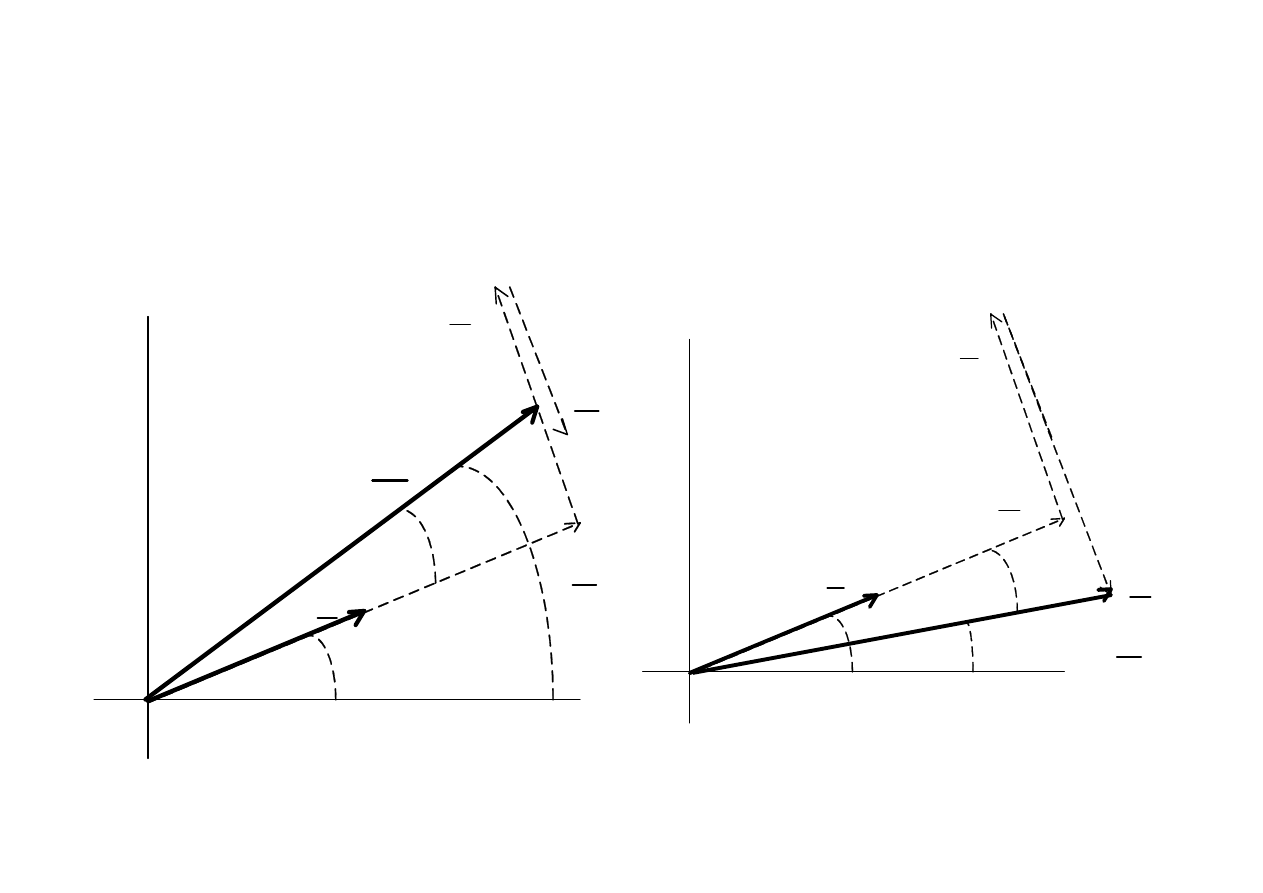
Trójk

ą

t napi

ęć

I

I

Ψ

ϕ

U

Ψ

U

L

U

C

U

R

U

0

ϕ

>

I

I

Ψ

ϕ

U

Ψ

U

L

U

C

U

R

U

0

ϕ

<

Admitancja

Z

Y

1

Y

G

jB

Z

=

= +

(

)(

)

2

2

2

2

2

2

1

1

R

jX

R

jX

R

X

R

X

Y

j

G

a

B

Z

R

jX

R

jX

R

jX

R

X

Z

Z

Z

Z

−

−

=

=

=

=

=

−

⇒

=

= −

+

+

−

+

Odwrotno

ść

nazywa si

ę

admitancj

ą

i oznacza jako

( przewodno

ść

pozorna, zespolona).

G – kondunktancja ( przewodno

ść

czynna )

B – susceptancja ( przewodno

ść

bierna )

Admitancja

1

1

1

1

j

j

j

Y

e

Ye

Y

Y

Z

Ze

Z

Z

ϕ

ϕ

ϕ

−

−

=

=

=

=

⇒

=

=

Y

?

Z

=

(

)(

)

2

2

2

2

2

2

1

1

G

jB

G

jB

G

B

G

B

Z

j

R

a

X

Y

G

jB

G

jB G

jB

G

B

Y

Y

Y

Y

−

−

= =

=

=

=

−

⇒

=

= −

+

+

−

+

1

1

1

1

j

j

j

Z

e

Ze

Z

Z

Y

Ye

Y

Y

ϕ

ϕ

ϕ

−

= =

=

=

⇒

=

=

Odwrotnie , dane obliczy

ć

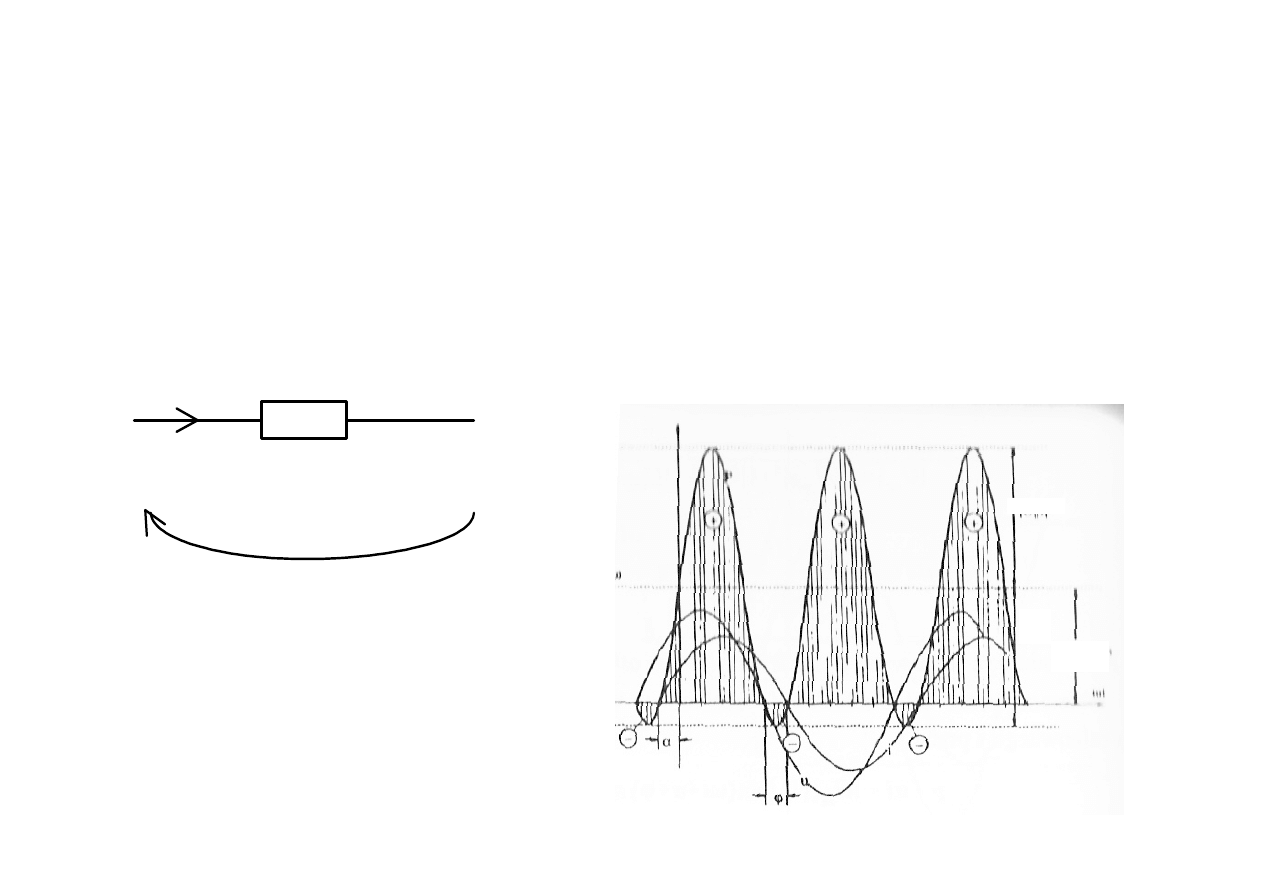
Moc czynna , bierna i pozorna

( )

( ) ( )

p t

u t i t

=

( )

i t

( )

u t

U I

U I

cos

UI

ϕ

Moc chwilowa na dowolnym dwójniku

p > 0 energia dopływa do odbiornika

P < 0 energia odpływa z odbiornika

Moc czynna , bierna i pozorna

2

2

2

2

2

2

sin (

)

1

1

1

cos(2

2

)

(1 cos(2

2

))

2

2

2

R

m

I

m

m

I

m

I

p

u i

Ri

RI

t

RI

RI

t

RI

t

ω

ω

ω

=

=

=

+ Ψ =

=

−

+ Ψ =

−

+ Ψ

2

2

sin(

)

sin(

)

2

1

sin(

) cos(

)

sin(2

2

)

2

L

m

I

m

I

m

I

I

m

I

p

u i

LI

t

I

t

LI

t

t

LI

t

ω

ω

ω

ω

ω

ω

ω

ω

Π

=

=

+ Ψ +

+ Ψ =

=

+ Ψ

+ Ψ =

+ Ψ

Rezystancja

Indukcyjno

ść

pojemno

ść

2

2

1

sin(

)

sin(

)

2

1

1

sin(

) cos(

)

sin(2

2

)

2

C

m

I

m

I

m

I

I

m

I

p

u i

I

t

I

t

C

I

t

t

I

t

C

C

ω

ω

ω

ω

ω

ω

ω

ω

Π

=

= −

+ Ψ +

+ Ψ =

= −

+ Ψ

+ Ψ = −

+ Ψ

Moc czynna , bierna i pozorna

Praktyczne znaczenie posiada energia

w okresie T wielkość energii wynosi

0

0

T

T

T

W

pdt

uidt

=

=

∫

∫

dla prądu stałego ( DC )

0

0

0

T

T

T

T

W

uidt

Pdt P dt PT

=

=

=

=

∫

∫

∫

Analogicznie wprowadzamy pojęcie mocy średniej zwanej mocą czynną

0

1

T

P

uidt

T

=

∫

Odpowiada ona energii jaka wydziela się w jednostce czasu na elemencie rezystancyjnym

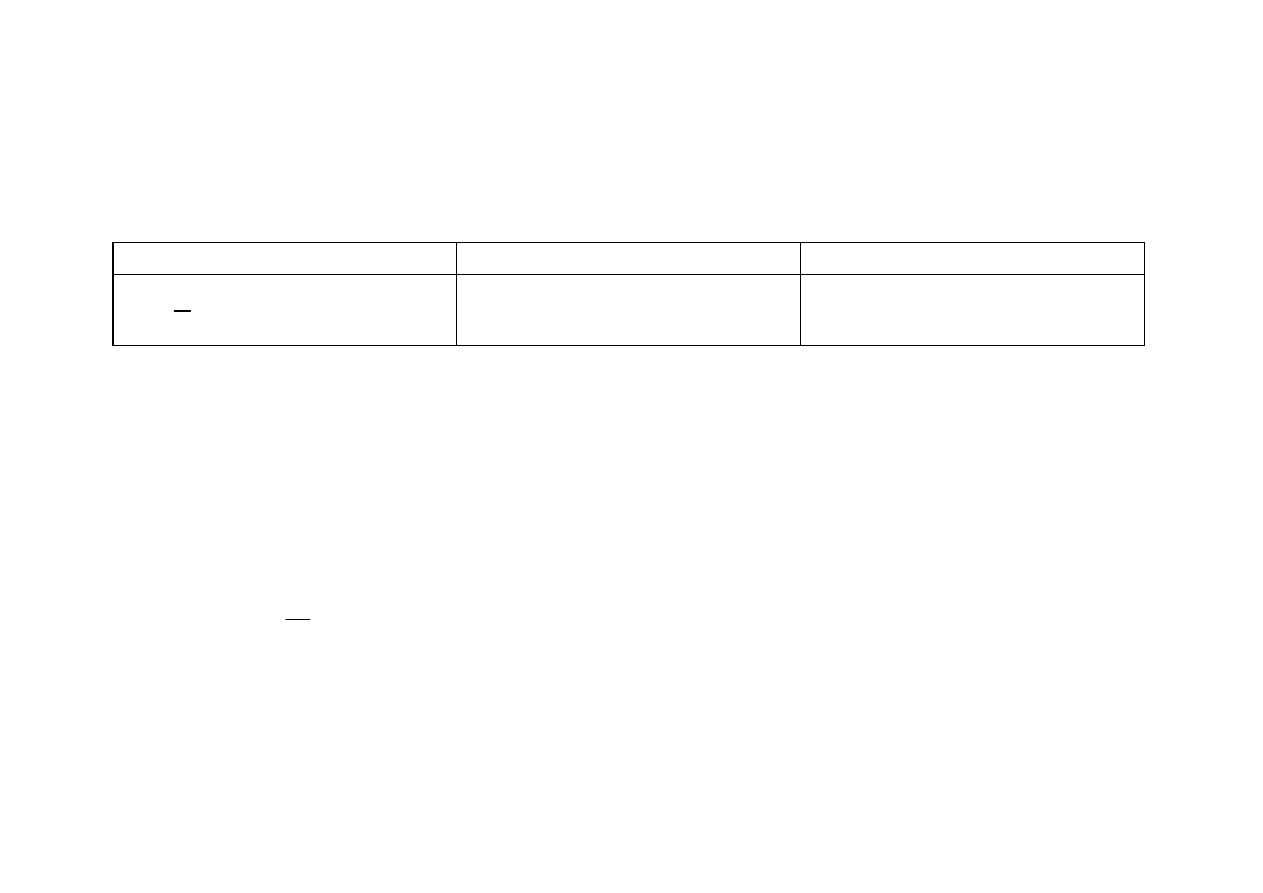
Moc czynna , bierna i pozorna

Rezystancja

Indukcyjność

pojemność

2

2

1

2

m

P

RI

RI

=

=

0

P

=

0

P

=

sin(

) sin(

)

1

cos(

) cos(2

)

2

cos( ) cos(2

)

m m

U

I

m m

U

I

U

I

U

I

ui

U I

t

t

U I

t

UI

t

ω

ω

ω

ϕ

ω

=

+ Ψ

+ Ψ =





=

Ψ − Ψ −

+ Ψ + Ψ

=









=

−

+ Ψ + Ψ





Przypadek ogólny

Moc czynna , bierna i pozorna

moc czynna

0

1

cos

cos(

)

T

U

I

P

uidt

UI

UI

T

ϕ

=

=

=

Ψ − Ψ

∫

Moc czynna równa się iloczynowi wartości skutecznych

napięcia i prądu oraz cosinusa kąta między nimi

Rezystancja

Indukcyjność

pojemność

φ

=0

φ

=Π/2

φ

=-Π/2

2

R

P

U I

RI

=

=

0

P

=

0

P

=

W celu policzenia energii pobranej w czasie t[s]

wystarczy pomnożyć

t

W

Pt

=

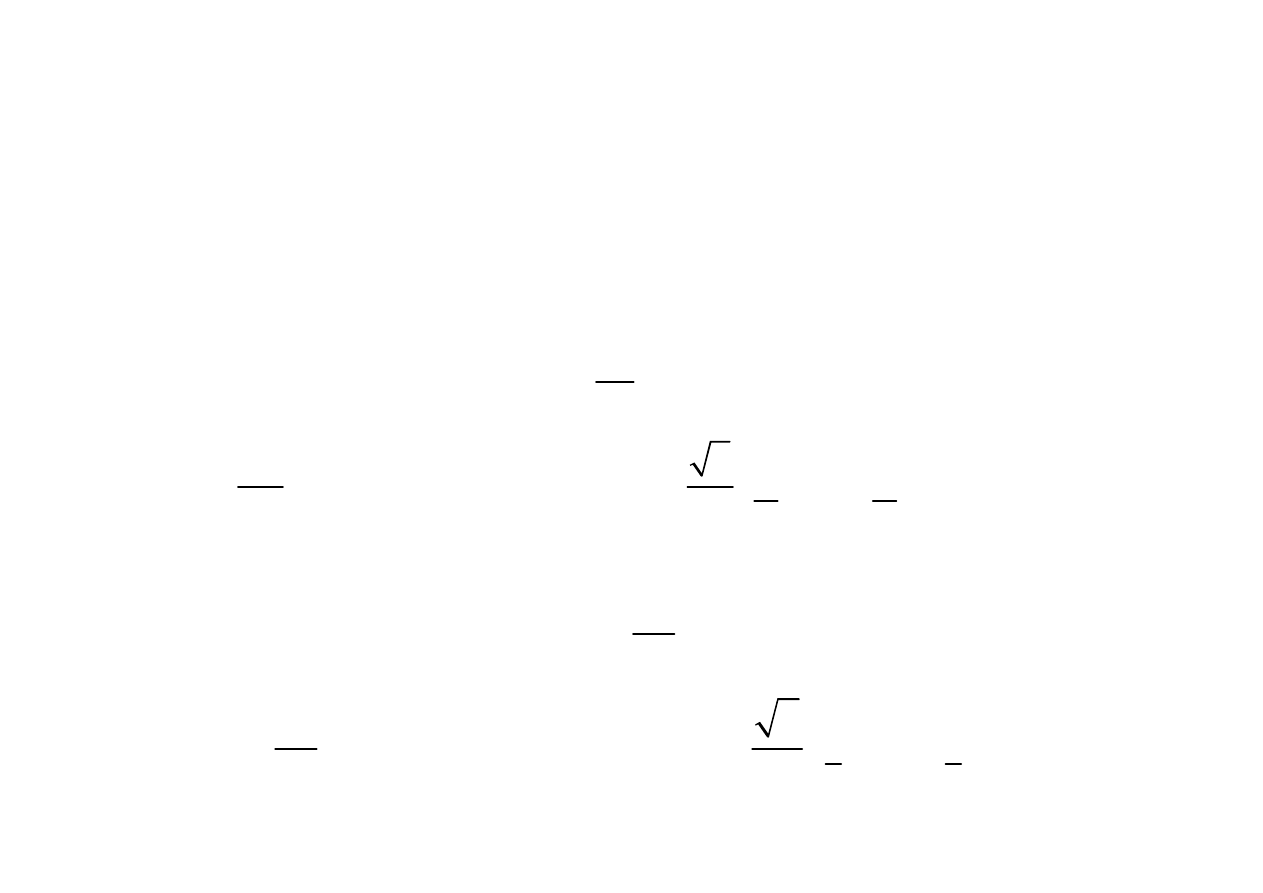
Moc czynna , bierna i pozorna

(

)

(

)

*

(

)

(

)

(

)

(

)

(

)

(

)

1

( )

sin(

)

2

2

2

2

U

U

U

U

j

t

j

t

m

U

m

j

j

j

t

j

t

j

t

j

t

m

u t

U

t

U

e

e

j

U

e

e

e

e

Ue

U e

j

j

ω

ω

ω

ω

ω

ω

ω

+Ψ

−

+Ψ

Ψ

− Ψ

−

−





=

+ Ψ =

−

=













=

−

=

−









(

)

(

)

*

(

)

(

)

(

)

(

)

(

)

(

)

1

( )

sin(

)

2

2

2

2

I

I

I

I

j

t

j

t

m

I

m

j

j

j

t

j

t

j

t

j

t

m

i t

I

t

I

e

e

j

I

e

e

e

e

Ie

I e

j

j

ω

ω

ω

ω

ω

ω

ω

+Ψ

−

+Ψ

Ψ

− Ψ

−

−





=

+ Ψ =

−

=













=

−

=

−









Moc czynna jest warto

ś

ci

ą

ś

redni

ą

mocy chwilowej.

Przebieg chwilowy napi

ę

cia mo

ż

na zapisa

ć

w postaci

analogicznie dla pr

ą

du

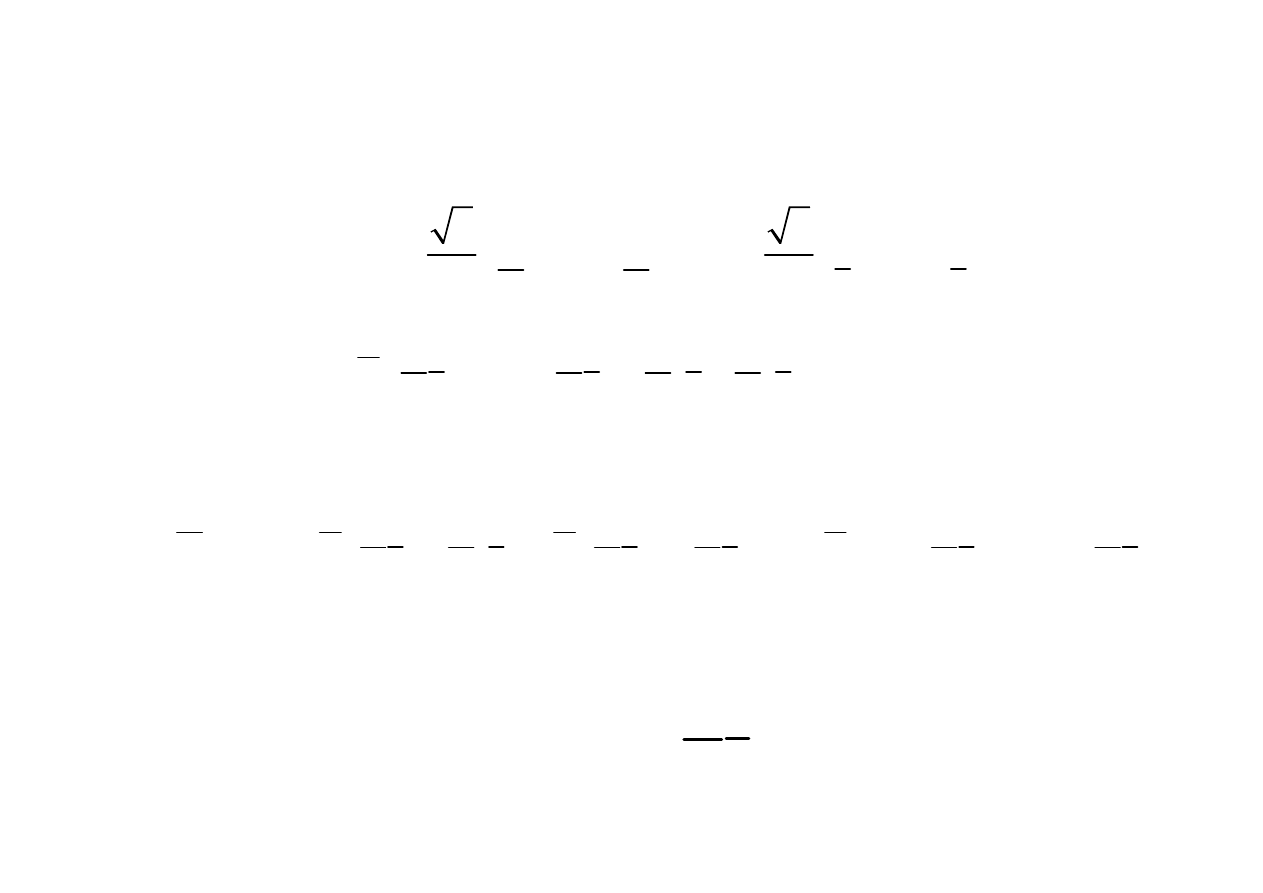
Moc czynna , bierna i pozorna

*

*

(

)

(

)

(

)

(

)

*

*

*

*

(2

)

(2

)

2

2

2

2

1

2

j

t

j

t

j

t

j

t

j

t

j

t

p

ui

Ue

U e

Ie

I e

j

j

U Ie

U I

U I

U I e

ω

ω

ω

ω

ω

ω

−

−

−









= =

−

−

=













= −

−

−

+





(

) (

)

{ } { }

*

*

*

*

*

*

*

0

1

1

1

1

(

)

2 Re

Re

2

2

2

T

P

uidt

U I

U I

U I

U I

U I

U I

T

=

=

+

=

+

=

=

∫

{ }

*

Re

P

U I

=

st

ą

d

st

ą

d moc czynna

a wi

ę

c

Moc czynna , bierna i pozorna

oznaczamy

*

S

U I

=

więc

{ }

Re

P

S

=

Wielkość

*

S

U I

=

nazywa się mocą pozorną w postaci

zespolonej.

Jej część rzeczywista jest mocą czynną.

Moduł

S

UI

=

- moc pozorna S , [S]=VA

Część urojona mocy pozornej zespolonej

{ }

{ }

*

Im

Im

S

U I

Q

=

=

nazywa się mocą bierną

[Q]=VAr

[P]= W

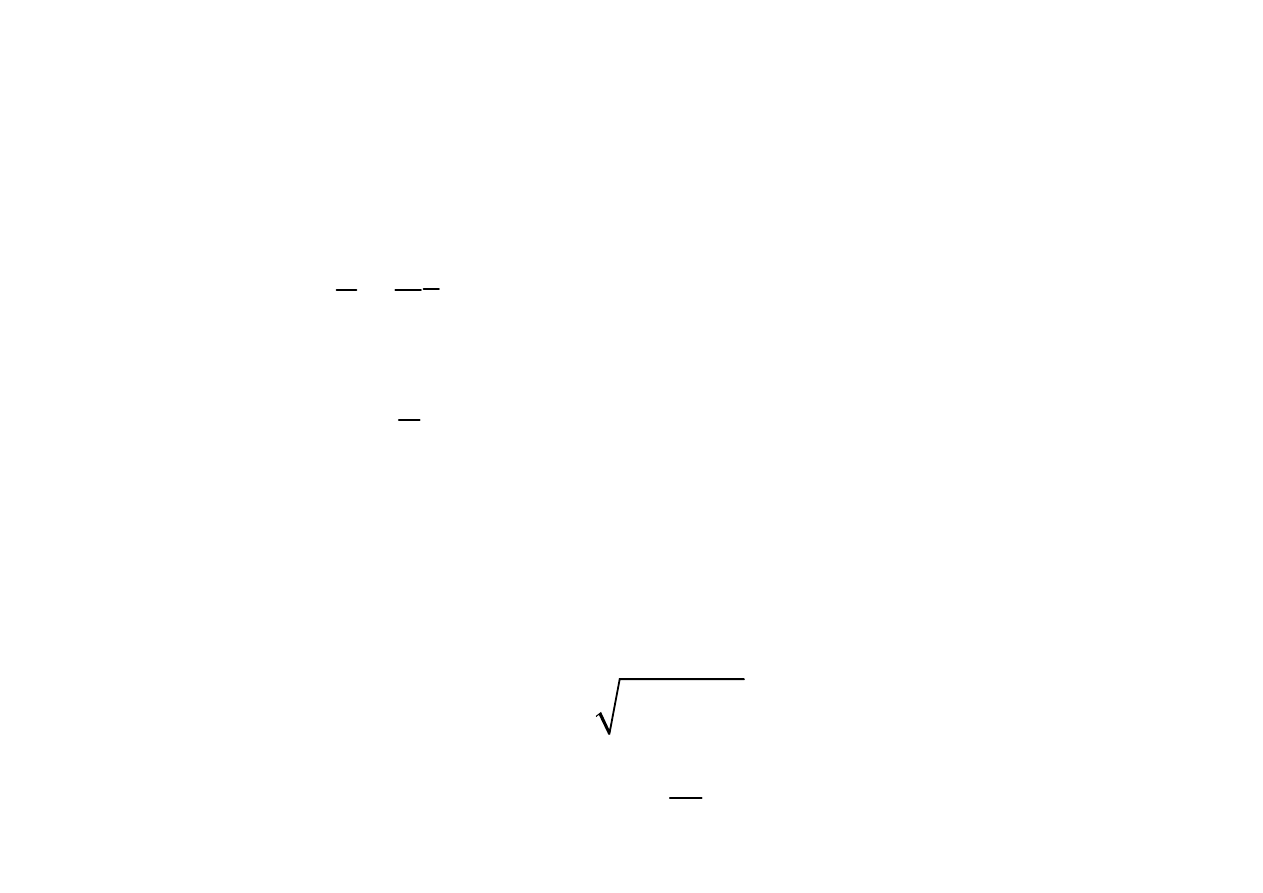
Moc czynna , bierna i pozorna

Rozpiszmy

*

(

)

U

U

I

I

j

j

j

S

U I

Ue

Ie

UIe

UIe

ϕ

Ψ

Ψ −Ψ

− Ψ

=

=

=

=

czyli

(cos

sin )

S

UI

j

P

jQ

ϕ

ϕ

=

+

= +

stąd

cos

cos

sin

sin

P UI

S

Q UI

S

ϕ

ϕ

ϕ

ϕ

=

=

=

=

2

2

S

P

Q

Q

tg

P

ϕ

=

+

=

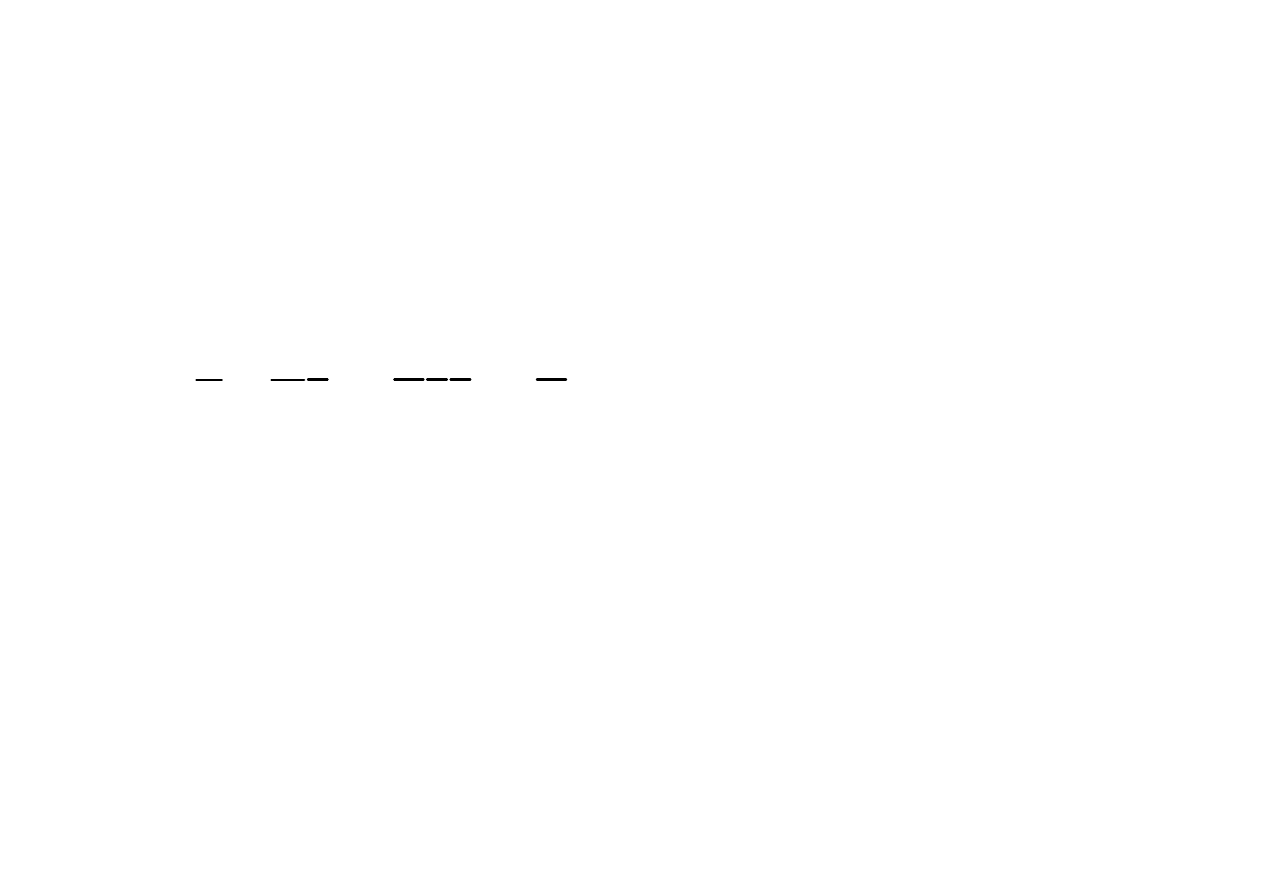
Moc czynna , bierna i pozorna

dalej

*

*

2

2

2

2

(

)

S

U I

Z I I

ZI

R

jX I

RI

jXI

=

=

=

=

+

=

+

zatem

2

2

2

P

RI

Q

XI

S

ZI

=
=
=

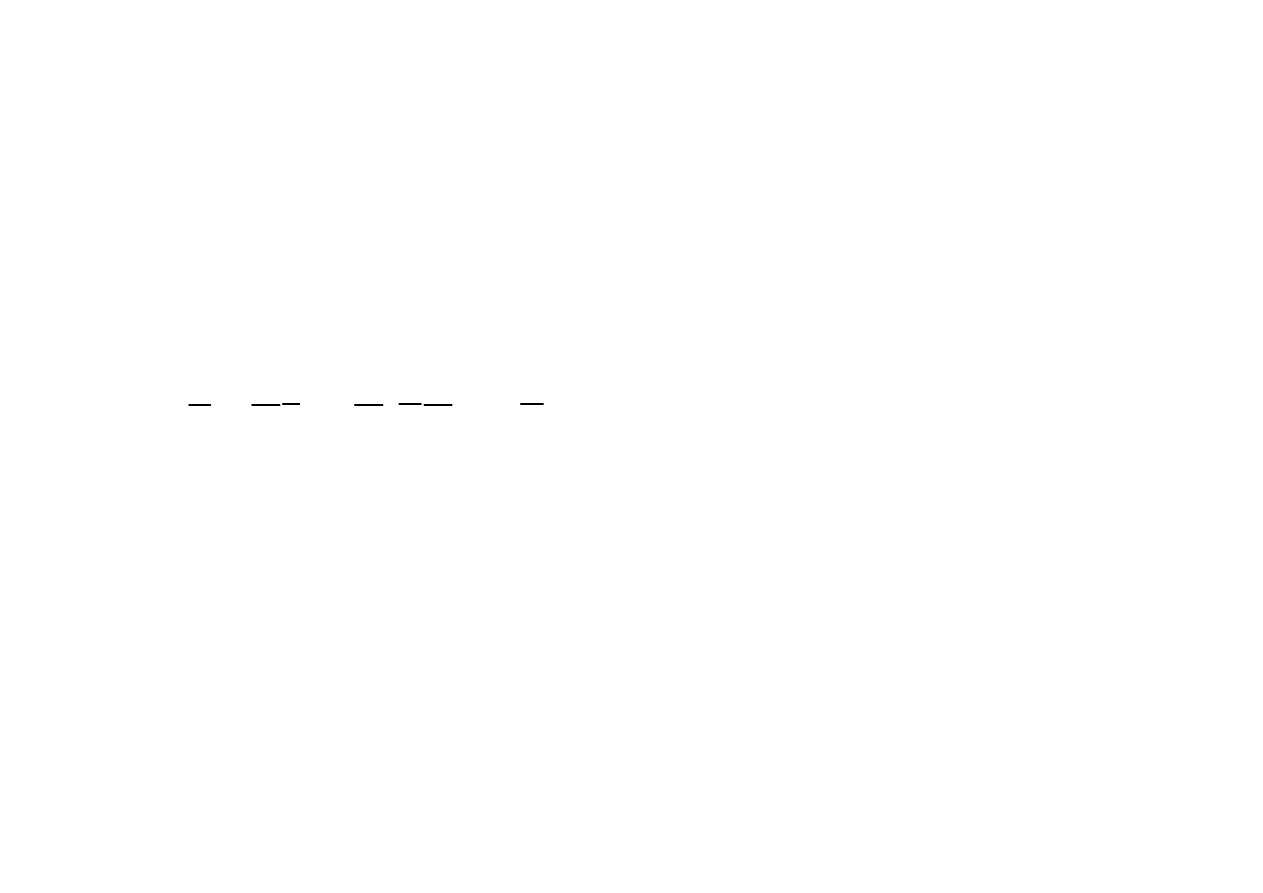
Moc czynna , bierna i pozorna

•

Analogicznie

*

*

*

2

2

2

2

(

)

(

)

S

U I

U YU

Y U

G

jB U

GU

jBU

=

=

=

=

−

=

−

zatem

2

2

2

P

GU

Q

BU

S

YU

=

= −

=

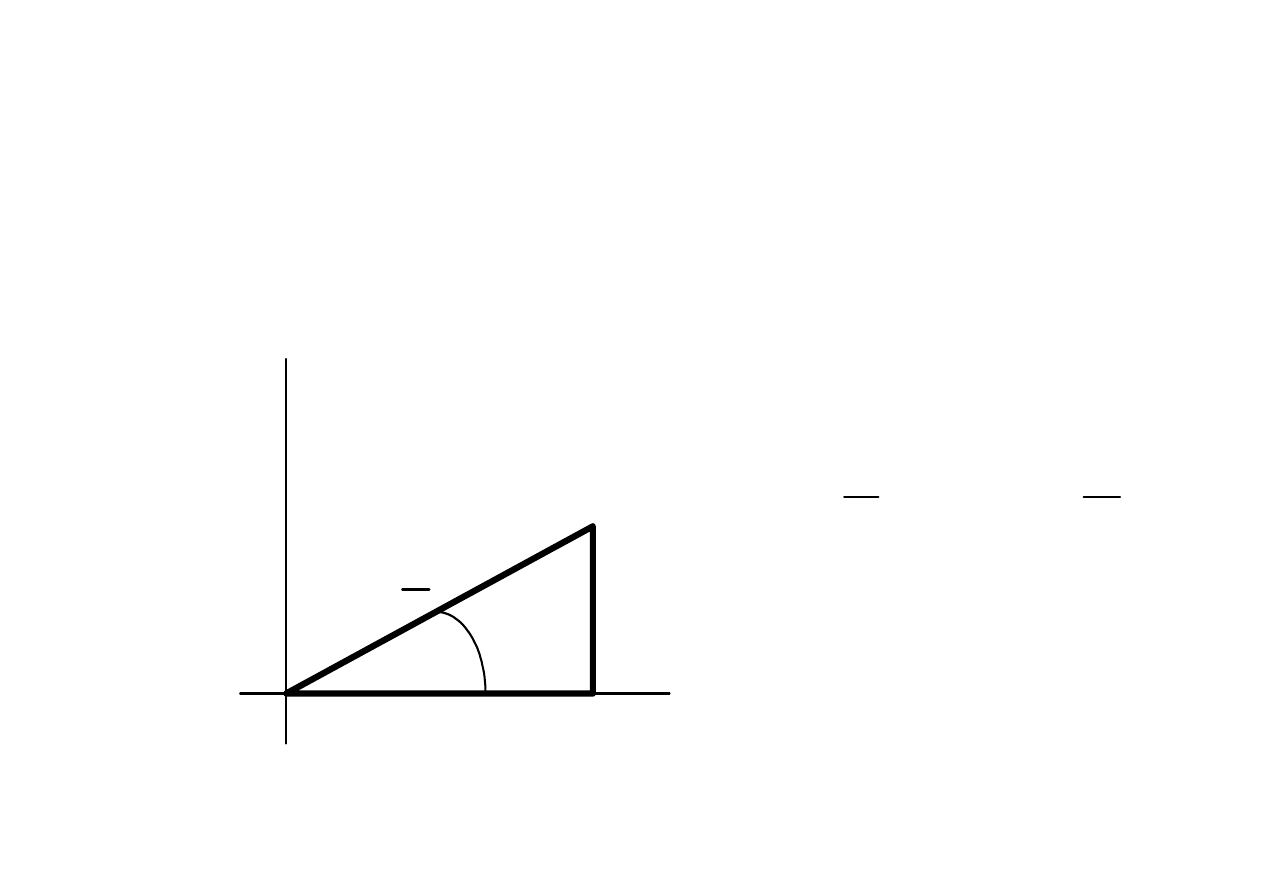
Trójk

ą

t mocy

S

P

Q

ϕ

z definicji moc bierna rezystora Q

R

=0

z definicji moc bierna cewki Q

L

>0

z definicji moc bierna kondensatora Q

C

<0

cos

,

P

Q

tg

S

P

ϕ

ϕ

=

=

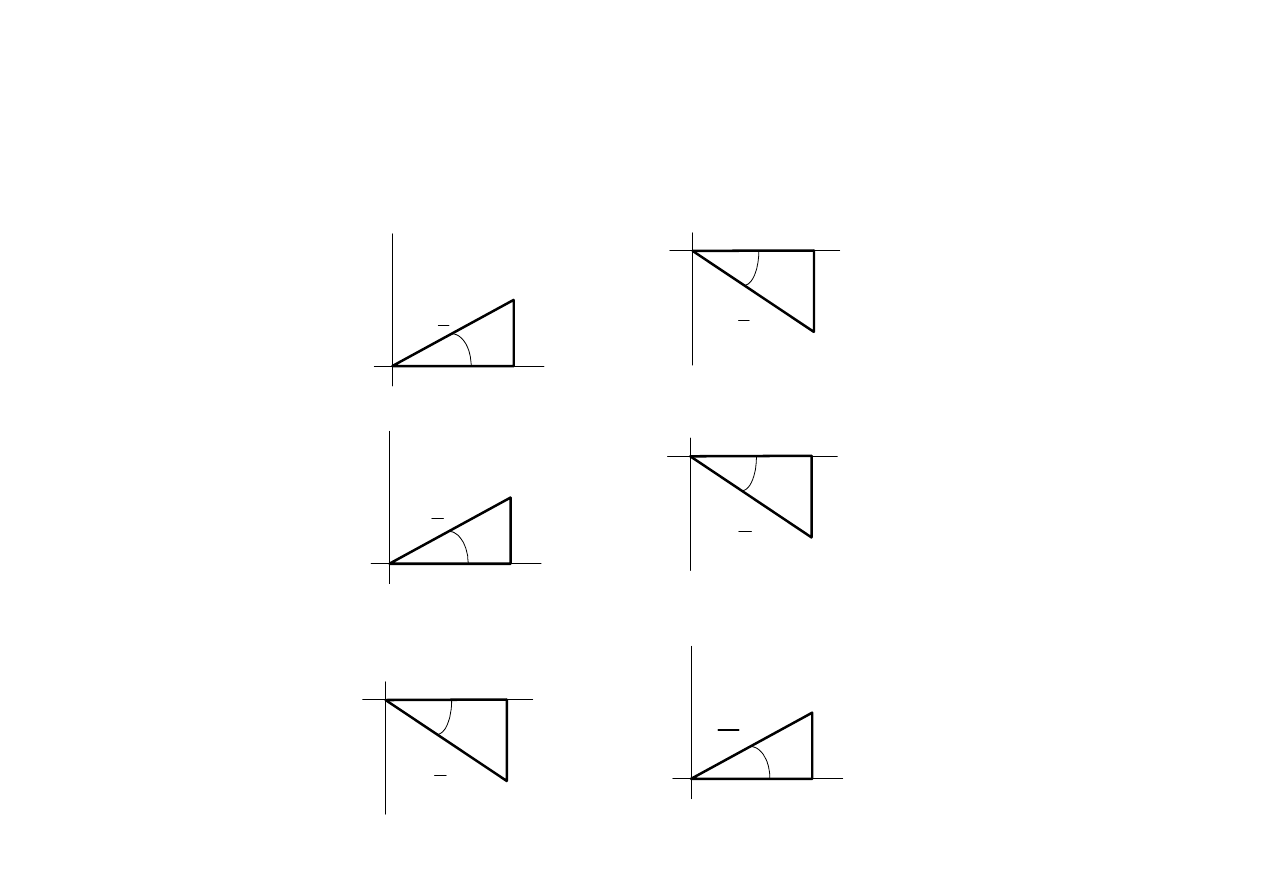
Trójk

ą

t mocy

0

ϕ

>

S

P

Q

ϕ

R

Z

X

ϕ

Y

G

B

ϕ

S

P

Q

ϕ

Z

R

X

ϕ

Y

G

B

ϕ

0

ϕ

<

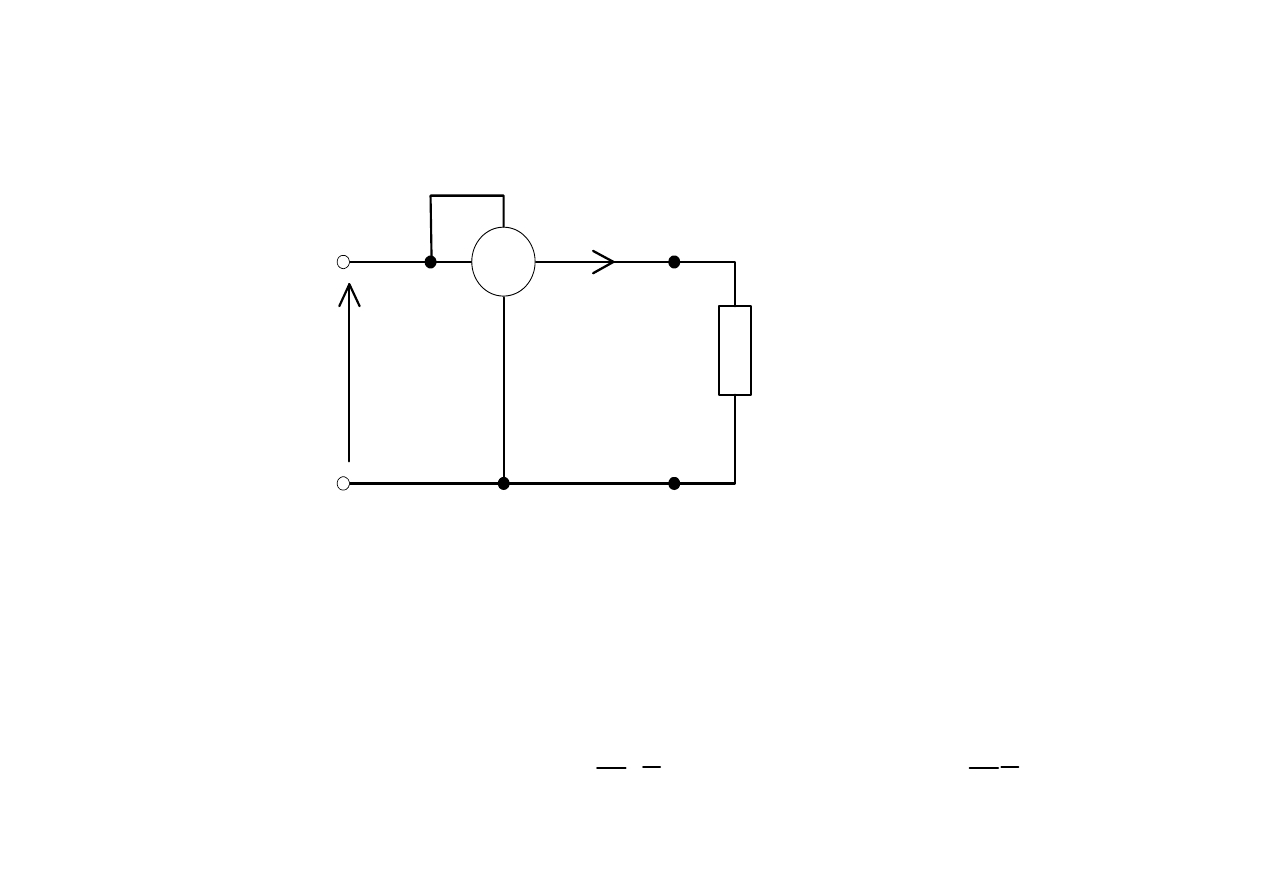
Pomiar mocy dwójnika

W

u

i

A

B

{ }

*

cos[ ( , )]

cos

Re

W

P

UI

U I

UI

U I

ϕ

=

=

=

∢

Watomierz wskazuje warto

ść

ś

redni

ą

iloczynu ui czyli moc czynn

ą

.

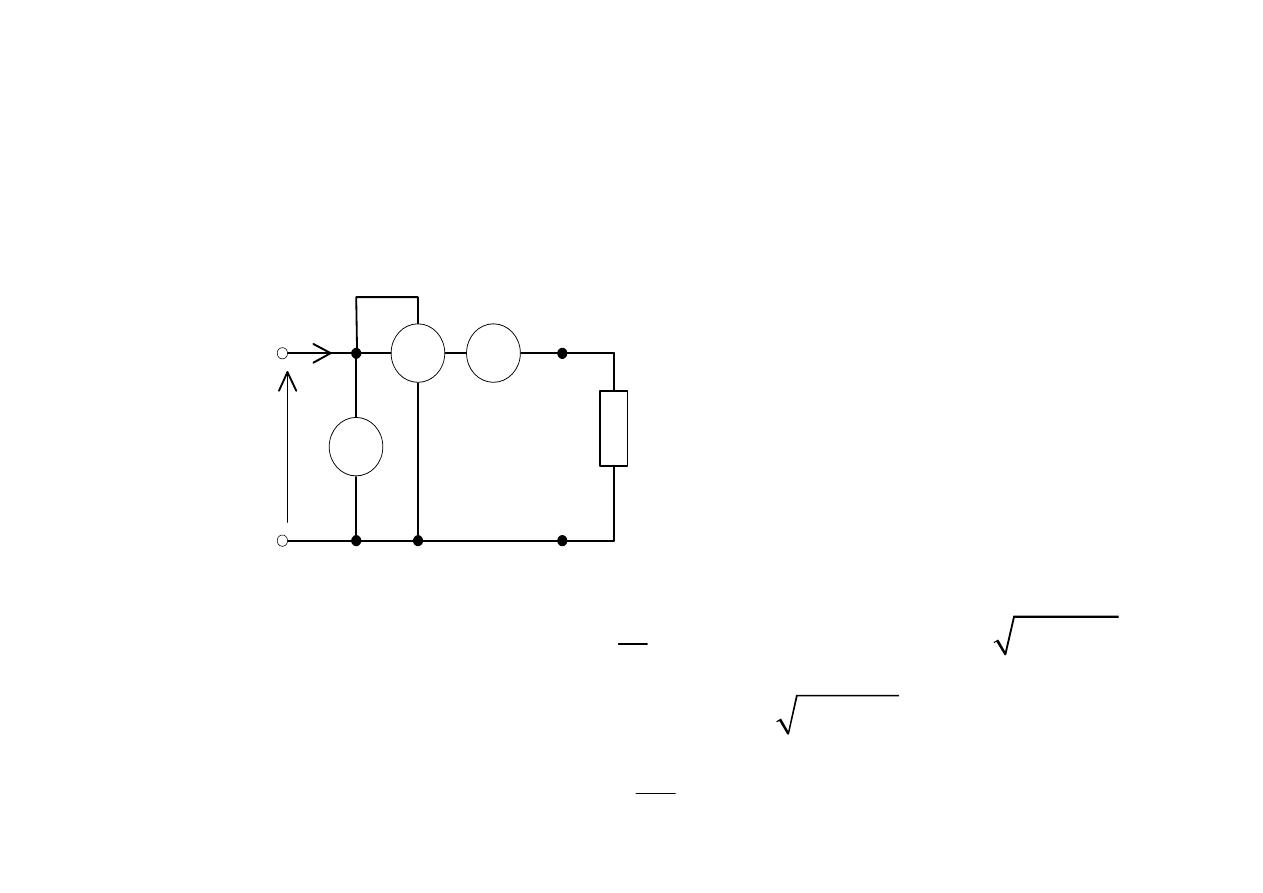
Pomiar mocy dwójnika

W

u

i

A

B

A

V

2

2

2

2

,

cos

,

cos

,

U

Z

R

Z

X

Z

R

I

S

UI

Q

S

P

P

UI

ϕ

ϕ

=

=

=

−

=

=

−

=

Cz

ę

sto zał

ą

czamy jeszcze amperomierz i woltomierz – metoda

techniczna pomiaru parametrów dwójnika

z pomiaru mamy P, U, I
st

ą

d

Składowe czynne i bierne napi

ę

cia i pr

ą

du

cos

;

cos ;

sin

;

sin ;

cz

cz

cz

b

b

b

P

P

UI

IU

U

U

U

RI

I

Q

Q

UI

IU

U

U

U

XI

I

ϕ

ϕ

ϕ

ϕ

=

=

=

= =

=

=

=

=

=

{ }

Re

cz

U

U

≠

U

cz

; U

b

– składowe czynne i bierne napi

ę

cia

Składowa czynna – rzut wskazu napi

ę

cia na kierunek wyznaczony przez

wskaz pr

ą

du.

Składowa bierna – rzut wskazu napi

ę

cia na kierunek prostopadły do

kierunku wyznaczonego przez wskaz pr

ą

du.

Ogólnie

Składowe czynne i bierne napi

ę

cia i pr

ą

du

cz

U

b

U

U

I

ϕ

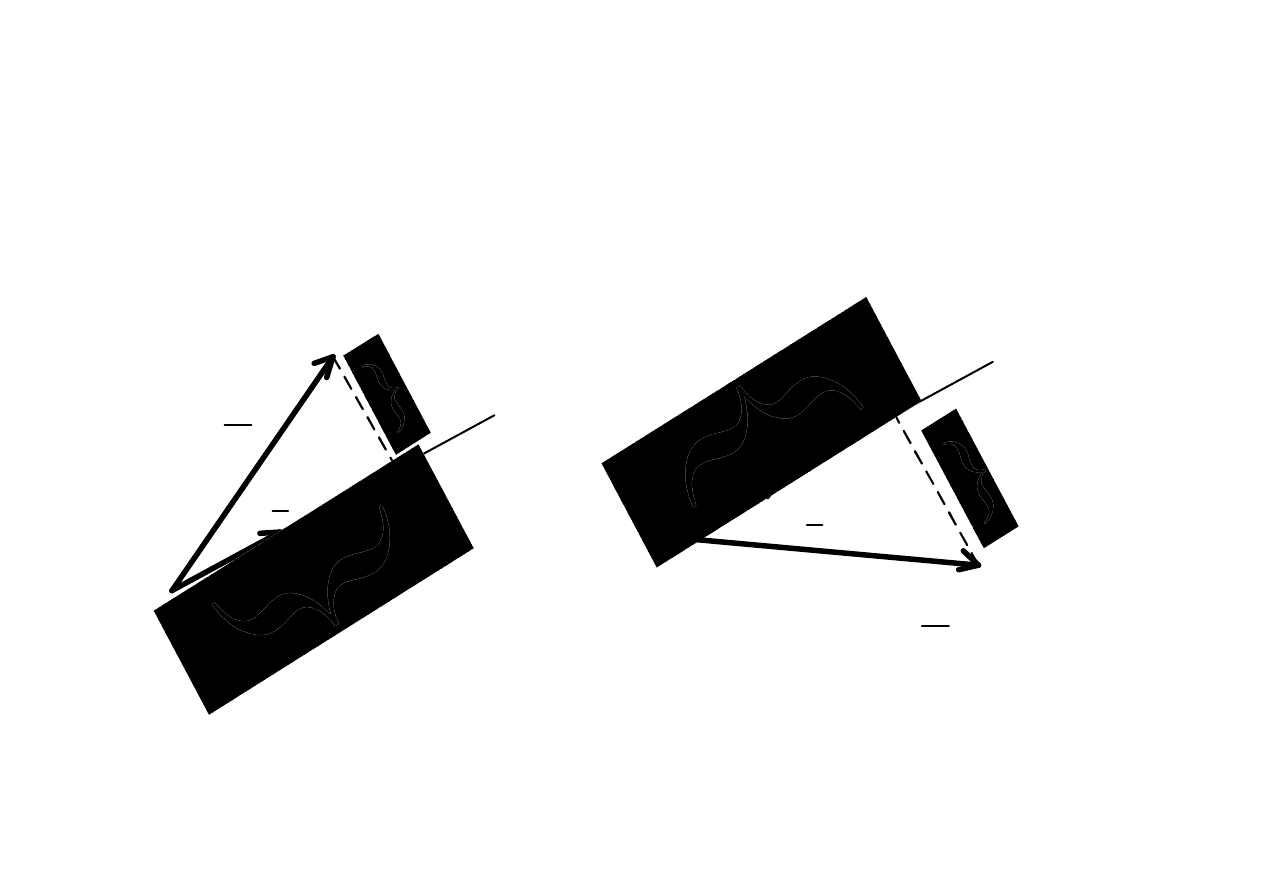
Składowe czynne i bierne napi

ę

cia i pr

ą

du

cz

U

0

b

U

>

U

I

ϕ

0

ϕ

>

cz

U

0

b

U

<

U

I

ϕ

0

ϕ

<

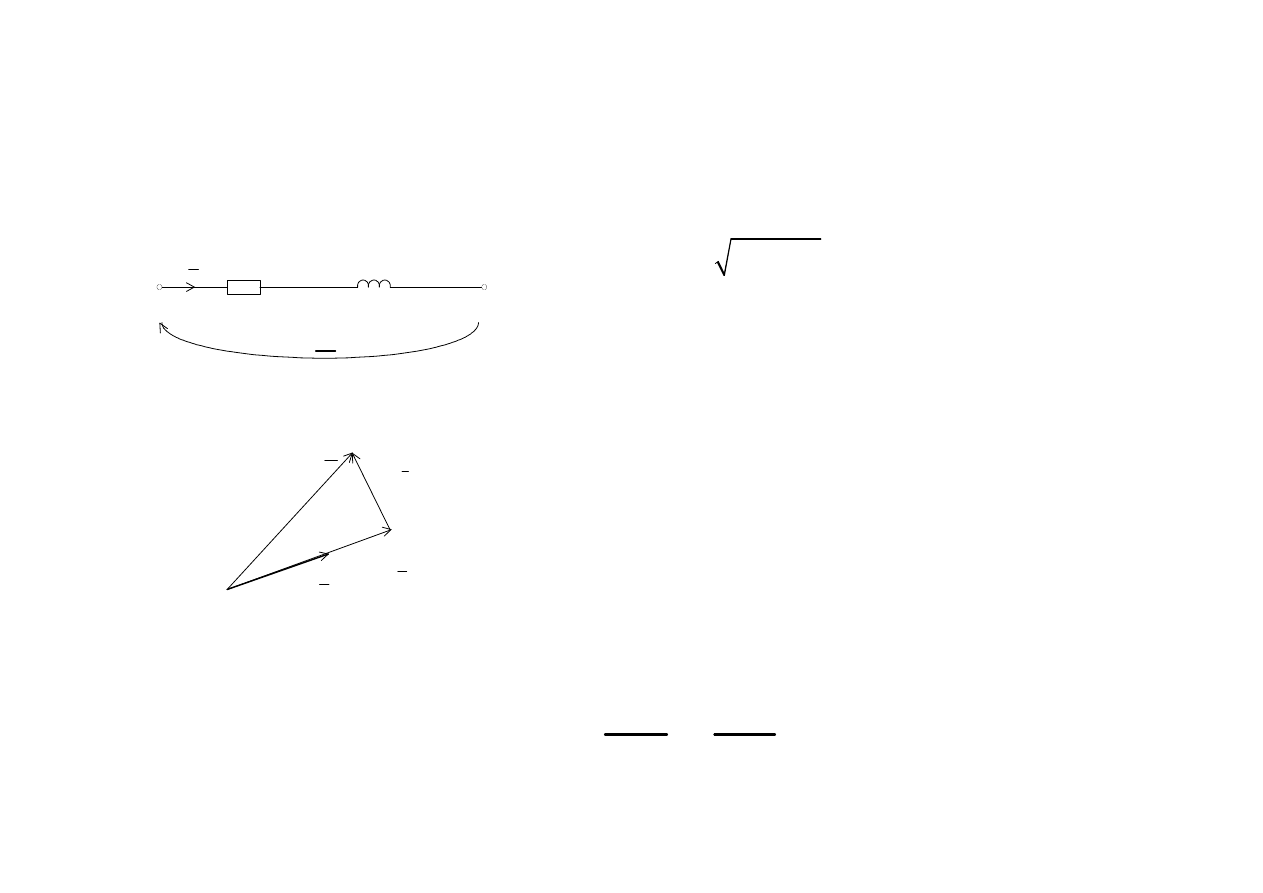
Składowe czynne i bierne napi

ę

cia i pr

ą

du

b

cz

L

U

L

U

R

ω

=

Np. cewka rzeczywista

I

U

L

R

L

X

I

RI

ϕ

U

L

jX I

2

2

cos

cos

sin

sin

L

cz

b

cz

L

R

b

L

L

U

ZI

U

U

U

U

IZ

IR

U

U

U

IZ

IX

U

ϕ

ϕ

ϕ

ϕ

=

=

+

=

=

=

=

=

=

=

=

Dobro

ć

cewki

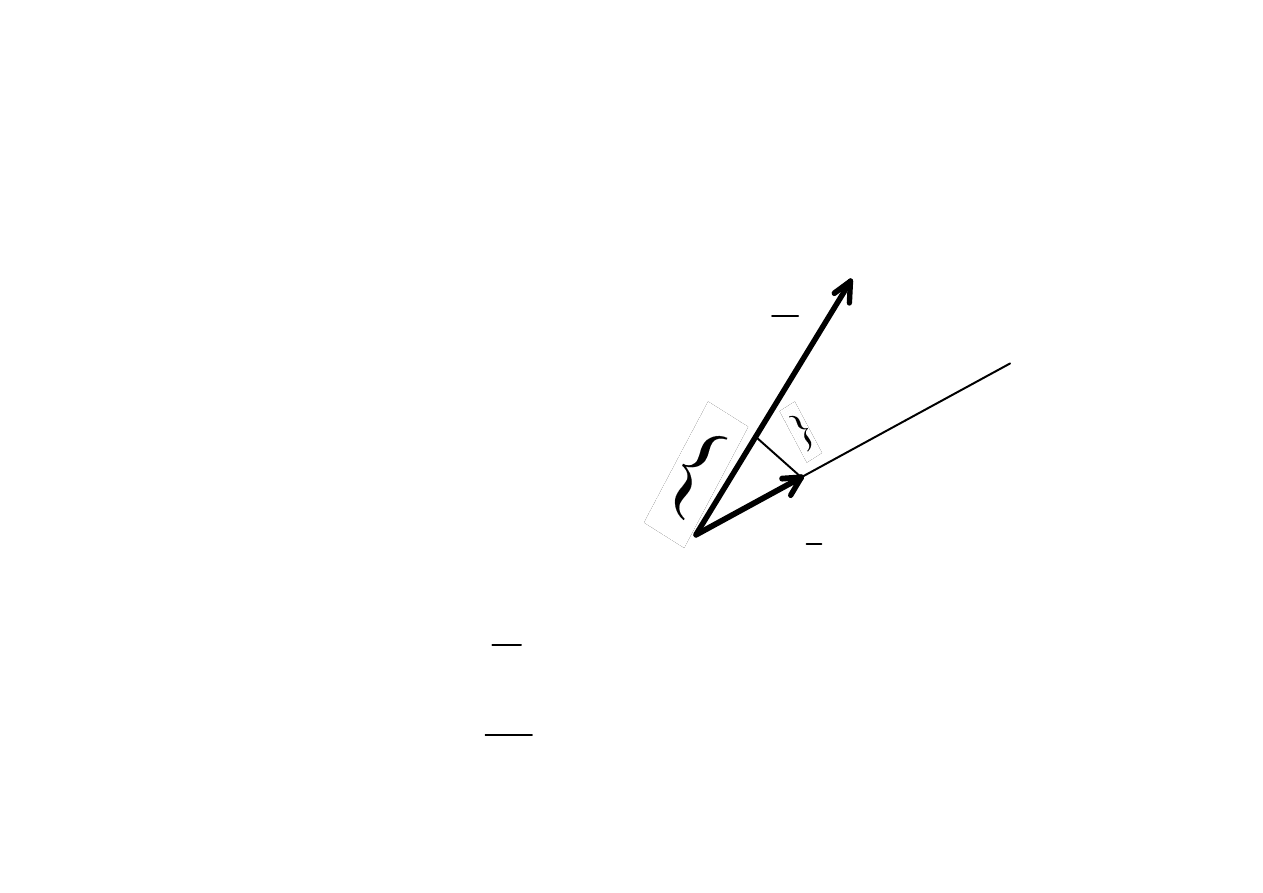
Składowe czynne i bierne napi

ę

cia i pr

ą

du

cz

I

0

b

I

<

U

I

ϕ

0

ϕ

>

cos ;

;

sin ;

cz

cz

cz

b

b

b

P

I

I

I

I

GU

U

Q

I

I

I

I

BU

U

ϕ

ϕ

=

=

=

−

= −

=

=

Analogicznie dla pr

ą

du

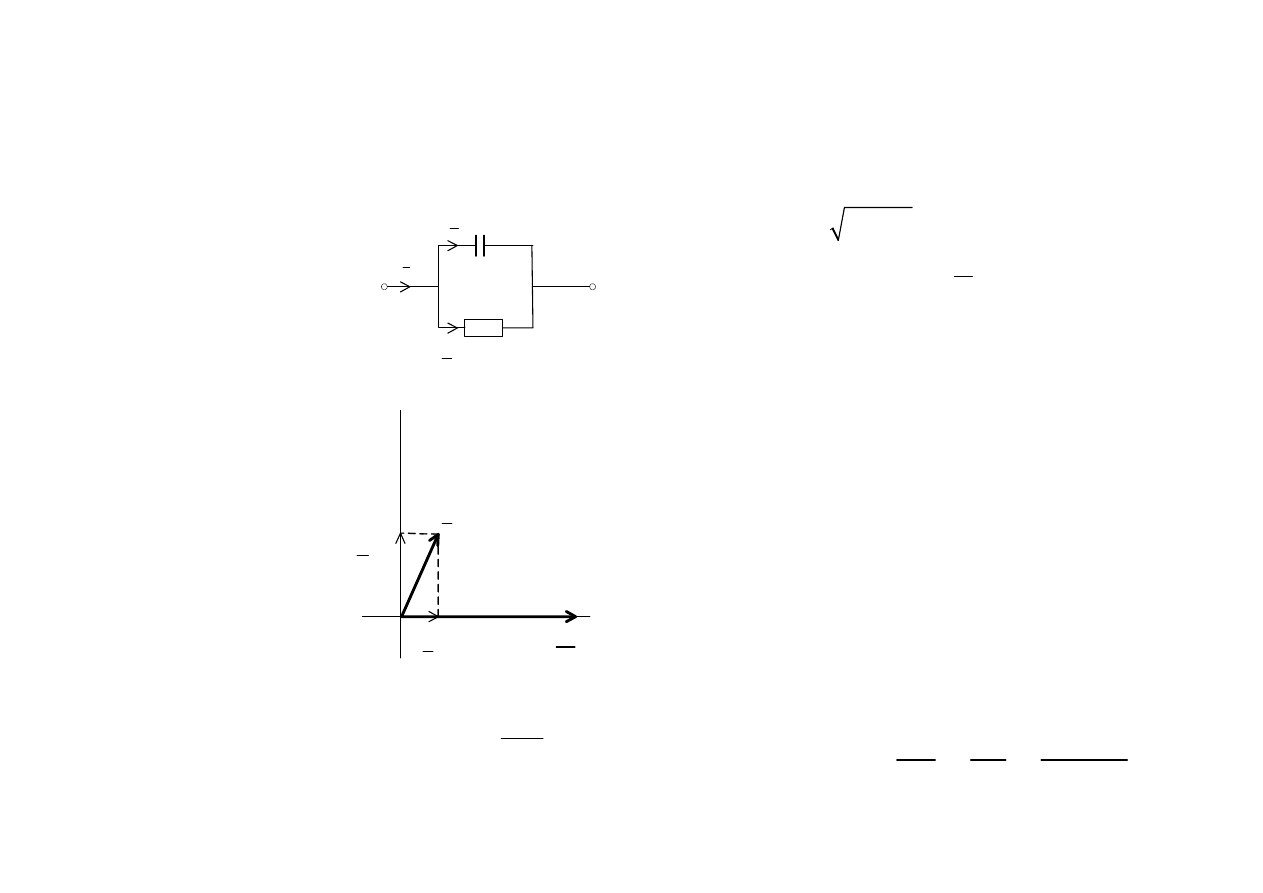
Składowe czynne i bierne napi

ę

cia i pr

ą

du

C

X

C

R

I

b

I

cz

I

ϕ

δ

I

U

cz

I

b

I

2

2

1

cos

cos

sin

sin

C

cz

b

cz

C

R

b

C

C

I

YU

I

I

I

I

UY

UG

U

I

R

I

I

UY

UB

U C

I

ϕ

ϕ

ϕ

ϕ

ω

=

=

+

=

=

=

=

=

=

=

=

=

=

b

C

cz

I

R C

I

ω

=

1

cz

R

b

C

C

I

I

tg

I

I

R C

δ

ω

=

=

=

np. rzeczywisty kondensator

Dobro

ć

kondensatora

współczynnik stratno

ś

ci

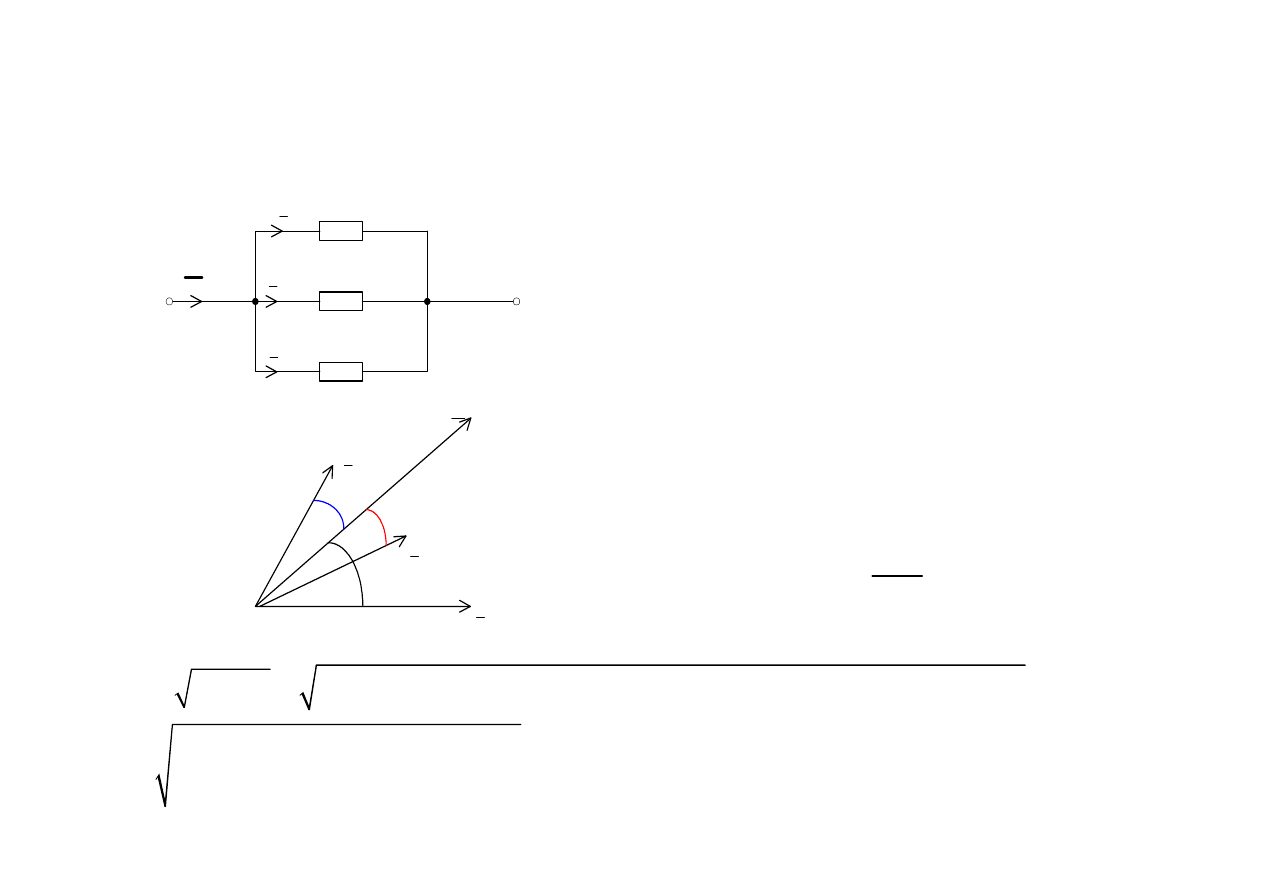
Składowe czynne i bierne napi

ę

cia i pr

ą

du

I

1

I

2

I

3

I

1

cos

ϕ

2

cos

ϕ

3

cos

ϕ

1

I

2

I

3

I

U

1

ϕ

2

ϕ

3

ϕ

(

) (

)

2

2

2

2

1

1

2

2

3

3

1

1

2

2

3

3

2

2

cos

cos

cos

sin

sin

sin

cos

sin

cz

b

k

k

k

k

k

k

I

I

I

I

I

I

I

I

I

I

I

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

=

+

=

+

+

+

+

+

=









=

+

















∑

∑

b

cz

I

tg

I

ϕ

=

Zastosowanie składowych