OBWODY ELEKTRYCZNE

i

Teoria Obwodów 1

Kurs powtórkowy

Kurs powtórkowy

Sierpie

ń

2011

Sierpie

ń

2011

w4

w4

Dopasowanie i sprawno

ść

ź

ródła

Elektrownia wodna w Malborku znajduje si

ę

na stopniu wodnym Rakowiec,

zbudowana 1909 roku.

Ź

ródłem energii jest oryginalny synchroniczny generator Siemensa o mocy 900

kVA, nap

ę

dzany przez turbin

ę

Kaplana o osi pionowej i przełyku 20 m

3

.

Elektrownia praktycznie produkuje energi

ę

elektryczn

ą

przez cały rok z wyj

ą

tkiem

bardzo rzadkich „ni

ż

ówek” na Wi

ś

le, kiedy poziom Nogatu jest wy

ż

szy od poziomu

Wisły w Białej Górze. Łatwo stwierdzi

ć

w Malborku kiedy to si

ę

dzieje, gdy

ż

Nogat

na całej szeroko

ś

ci robi si

ę

wówczas zielony.

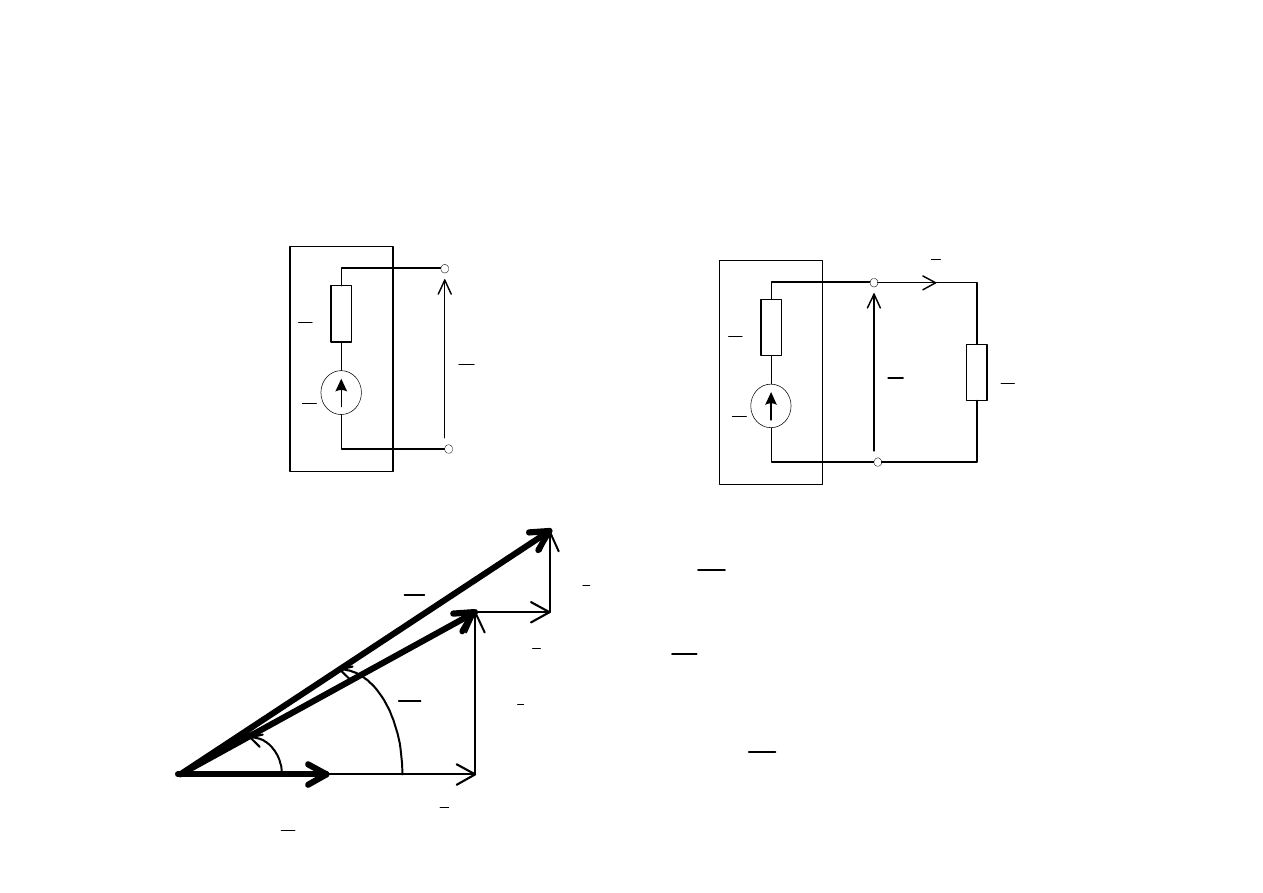
Siła elektromotoryczna SEM

E

g

Z

U

E

g

Z

I

odb

Z

U

g

g

g

Z

R

jX

=

+

odb

odb

odb

Z

R

jX

=

+

E

j

E

Ee

ϕ

=

E

U

g

R I

g

jX I

odb

R I

odb

jX

I

ϕ

E

ϕ

I

Moc zespolona-pozorna

ź

ródła

oddawana do odbiornika

(

) (

)

(

) (

)

2

2

2

2

2

2

odb

odb

odb

g

odb

g

odb

odb

odb

odb

odb

odb

g

odb

g

E R

P

R

R

X

X

S

P

jQ

E X

Q

R

R

X

X

=





+

+

+









=

+

⇒

=





+

+

+









max

0

odb

g

odb

odb

odb

g

X

X

P

P

gdy

R

R

+

=



=



=



(

)

(

) (

)

*

2

*

*

*

*

2

2

2

)

2

2

2

odb

odb

odb

odb

odb

odb

odb

odb

odb

g

odb

g

odb

g

U

U

S

U I

U

Z

Z

Z

I I

Z

I

E

E

Z

R

jX

Z

Z

R

R

X

X

=

=

=

=

=

=

=

=

=

+

+

+

+

+

Moc zespolona-pozorna

ź

ródła

odb

odb

odb

g

odb

g

P

R

P

P

R

R

η

=

=

+ ∆

+

P

odb

=P

odbmax

–

dopasowanie odbiornika do

ź

ródła

Moc czynna odbiornika

P

odb

=R

odb

I

2

Moc czynna całkowita

P

odb

+

∆

P

g

=( R

odb

+ R

g

) I

2

Sprawno

ść

ź

ródła

przy dopasowaniu

0, 5

50%

odb

odb

odb

R

R

R

η

η

=

=

⇒

=

+

Zast

ę

pcze

ź

ródło pr

ą

dowe

E

w

Z

U

I

w

w

zr

w

w

w

E U

NPK

U

E

I Z

I

Z

E

U

U

I

I

Z

Z

Z

−

⇒

= −

⇒

=

=

−

=

−

to odpowiada poł

ą

czeniu

w

Z

U

I

zr

I

w

U

Z

równoległe poł

ą

czenie idealnego

ź

ródła pr

ą

dowego z impedancj

ą

wewn

ę

trzn

ą

.

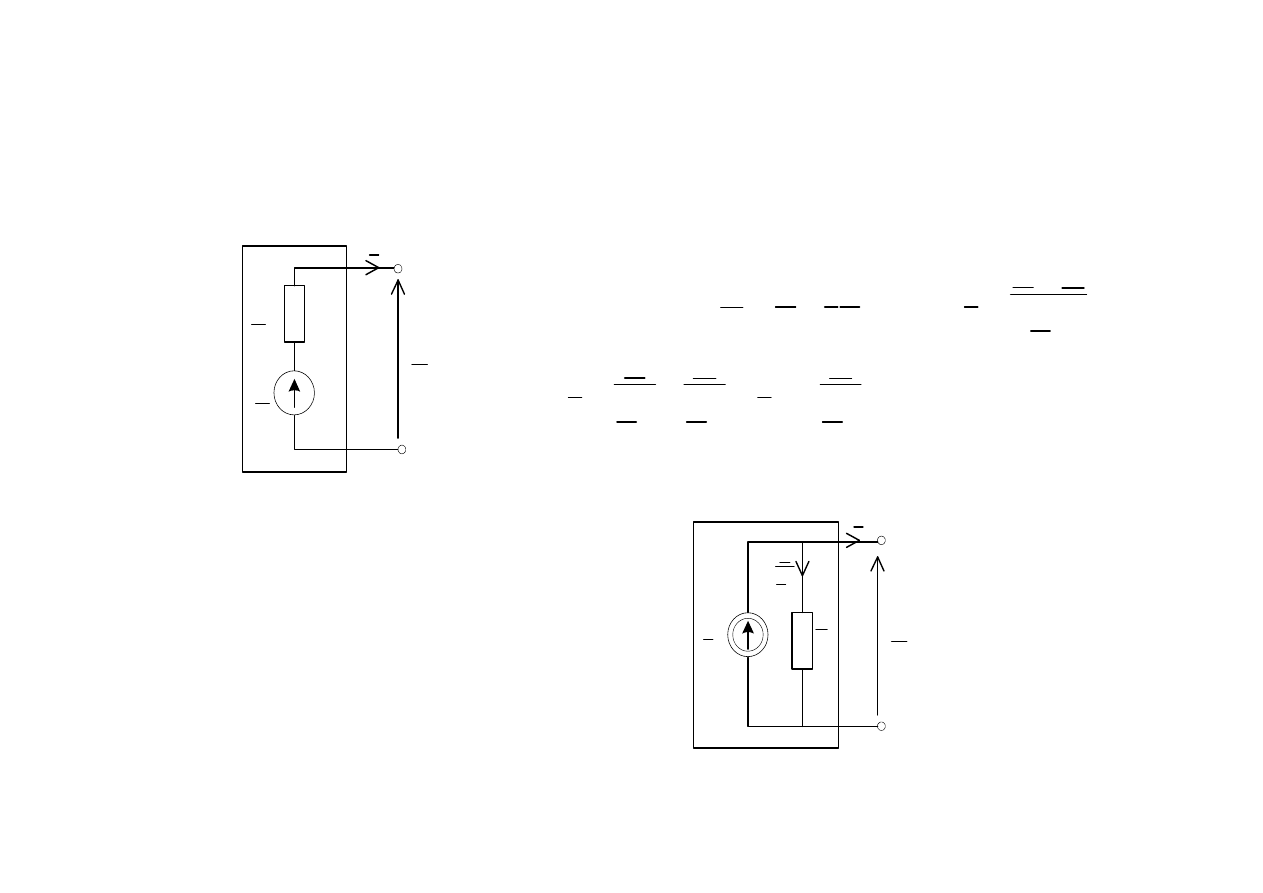
Odbiornik RL

E

w

Z

U

I

R

L

X

E

w

Z

U

I

R

L

X

R

U

L

U

(

) (

)

0

R

L

R

L

L

L

NPK

U

U

U

U

U

U

I R

I jX

I R

jX

⇒

−

−

=

⇒

=

+

=

+

=

+

I

R

U

L

U

U

ϕ

Re

Im

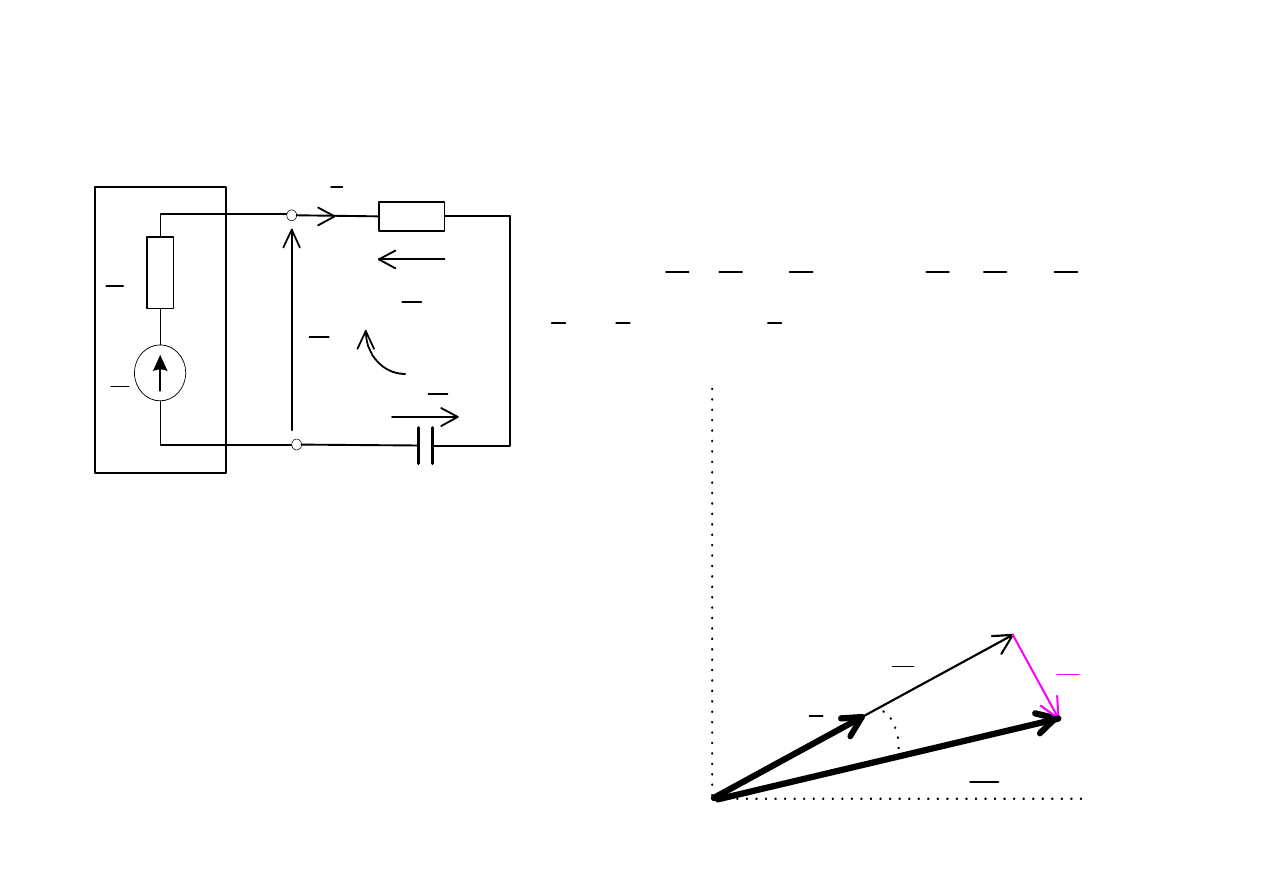
Odbiornik RC

E

w

Z

U

I

R

R

U

C

U

C

X

(

) (

)

0

R

C

R

C

C

C

NPK

U

U

U

U

U

U

IR

I

jX

I R

jX

⇒

−

−

=

⇒

=

+

=

+ −

=

−

I

R

U

C

U

U

ϕ

−

Re

Im

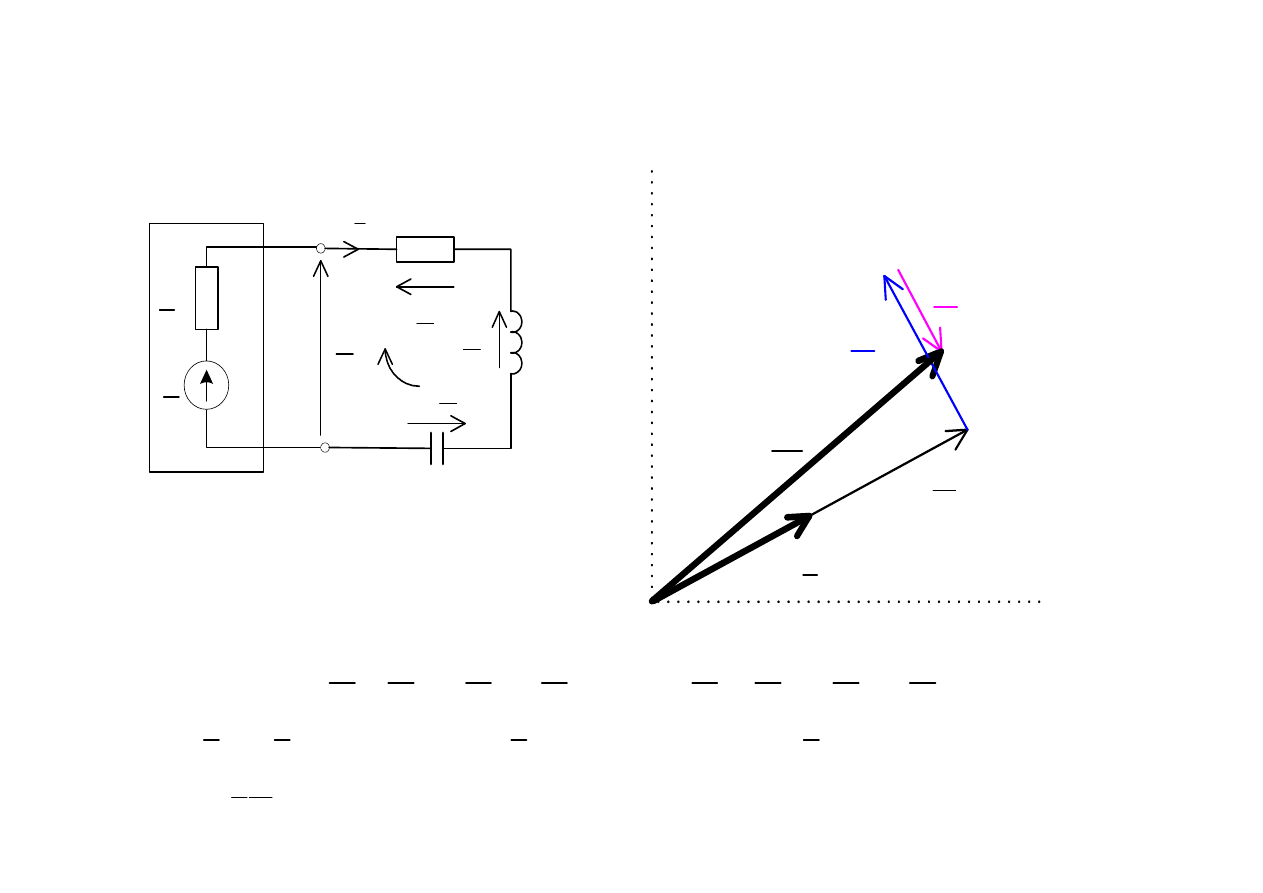
Odbiornik RLC

E

w

Z

U

I

R

R

U

C

U

C

X

L

U

(

) (

) (

)

0

(

)

R

L

C

R

L

C

L

C

L

C

L

C

odb

NPK

U

U

U

U

U

U

U

U

IR

I jX

jX

I R

jX

jX

I R

j X

X

I Z

⇒

−

−

−

=

⇒

=

+

+

=

+

−

=

+

−

=

+

−

=

=

I

R

U

C

U

U

ϕ

Im

L

U

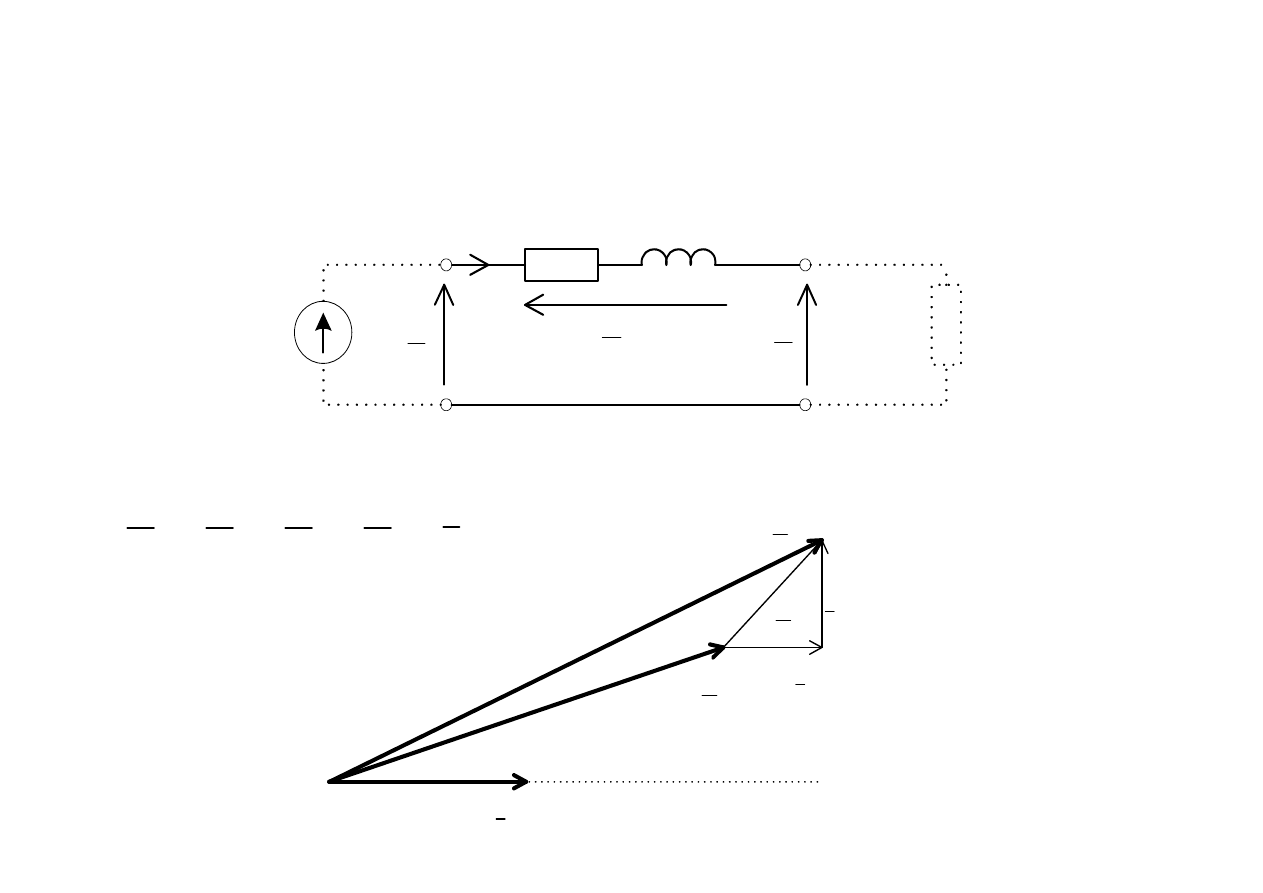
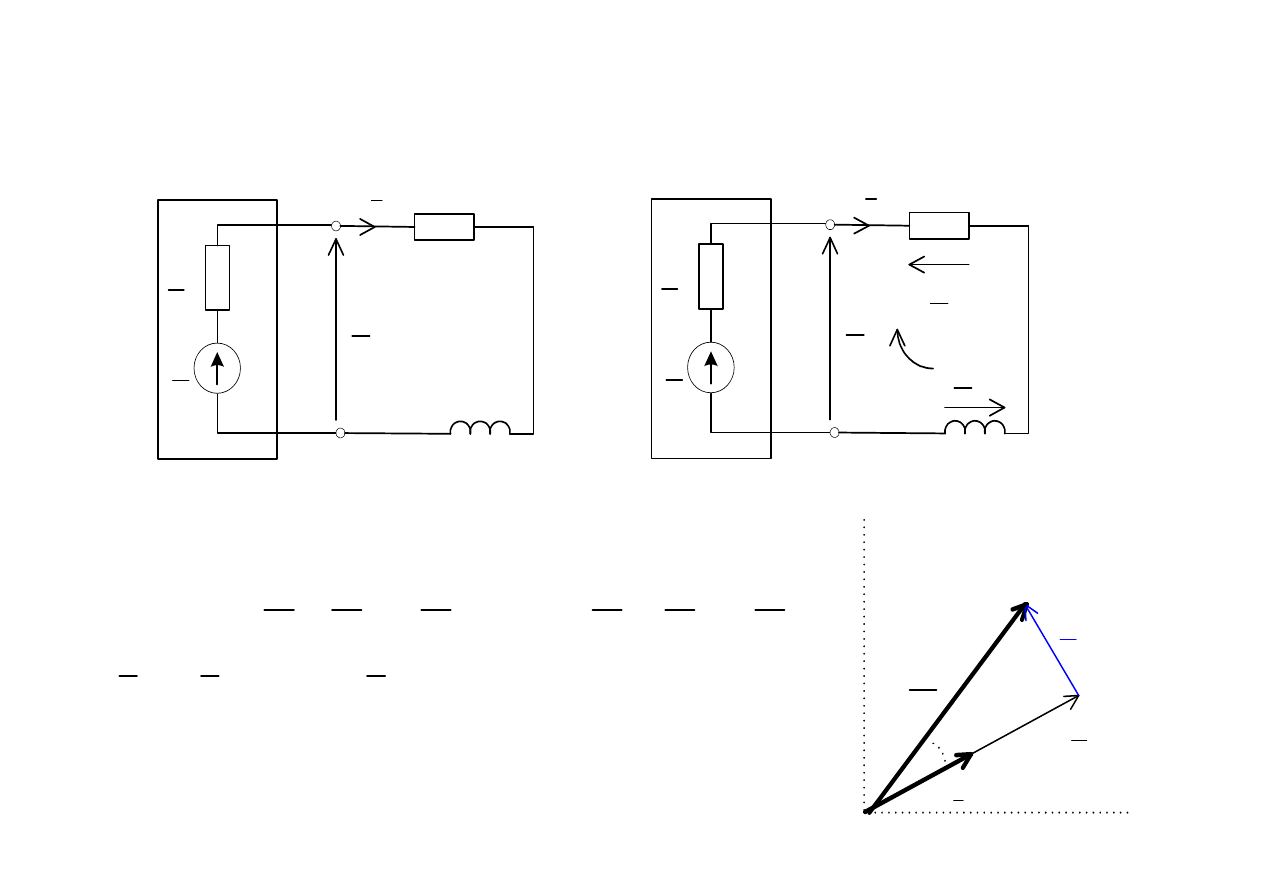
Spadek napi

ę

cia i strata mocy w linii

l

R

l

X

1

U

2

U

l

U

odb

(

)

1

2

2

l

l

l

U

U

U

U

I R

jX

=

+

=

+

+

I

2

U

1

U

l

U

IR

( )

l

I jX

spadek napi

ę

cia linii

1

2

U

U

U

∆ =

−

I

2

U

1

U

l

U

IR

( )

l

I jX

U

∆

2

ϕ

(

) (

)

2

2

1

2

2

2

2

2

2

cos

sin

l

l

U

U

U

U

R I

U

X I

U

ϕ

ϕ

∆ =

−

=

+

+

+

−

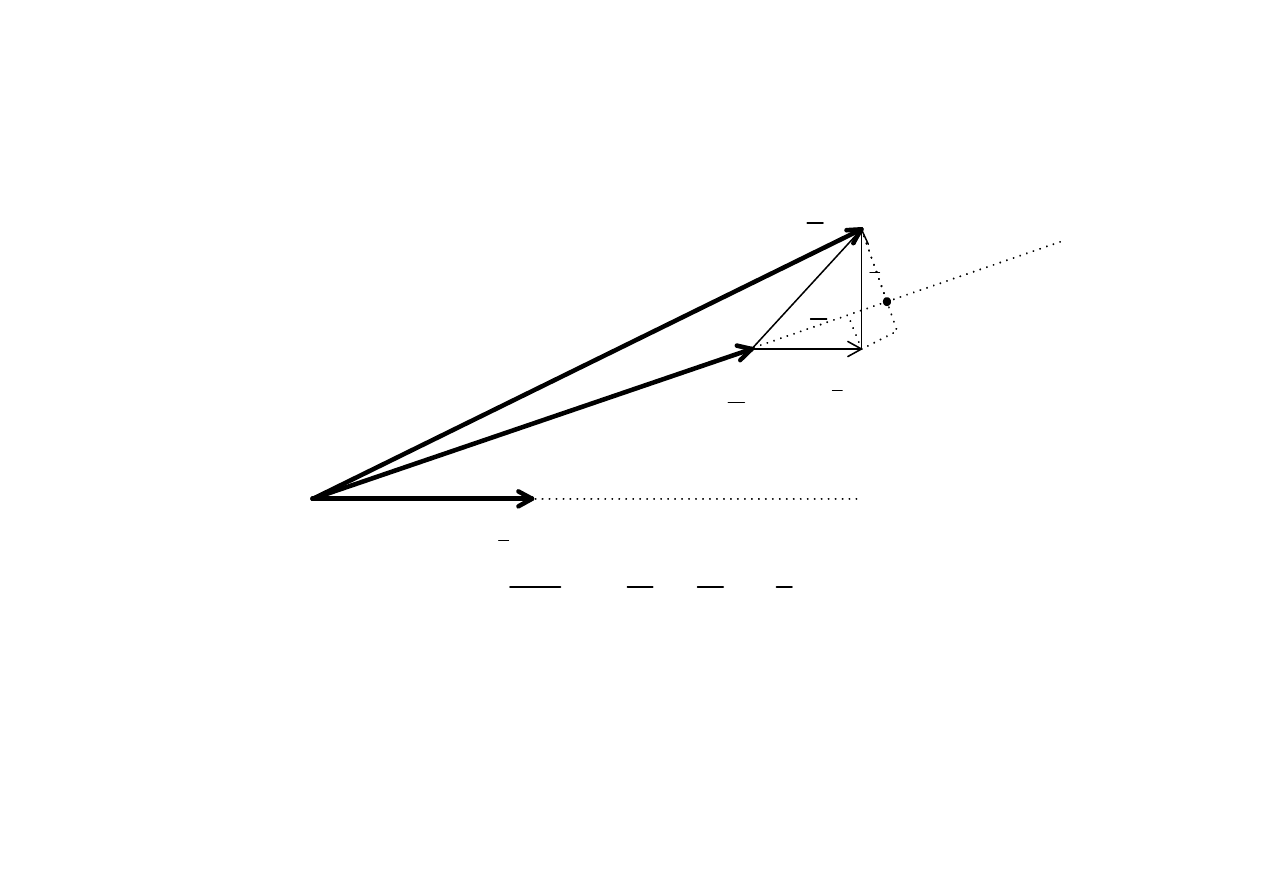
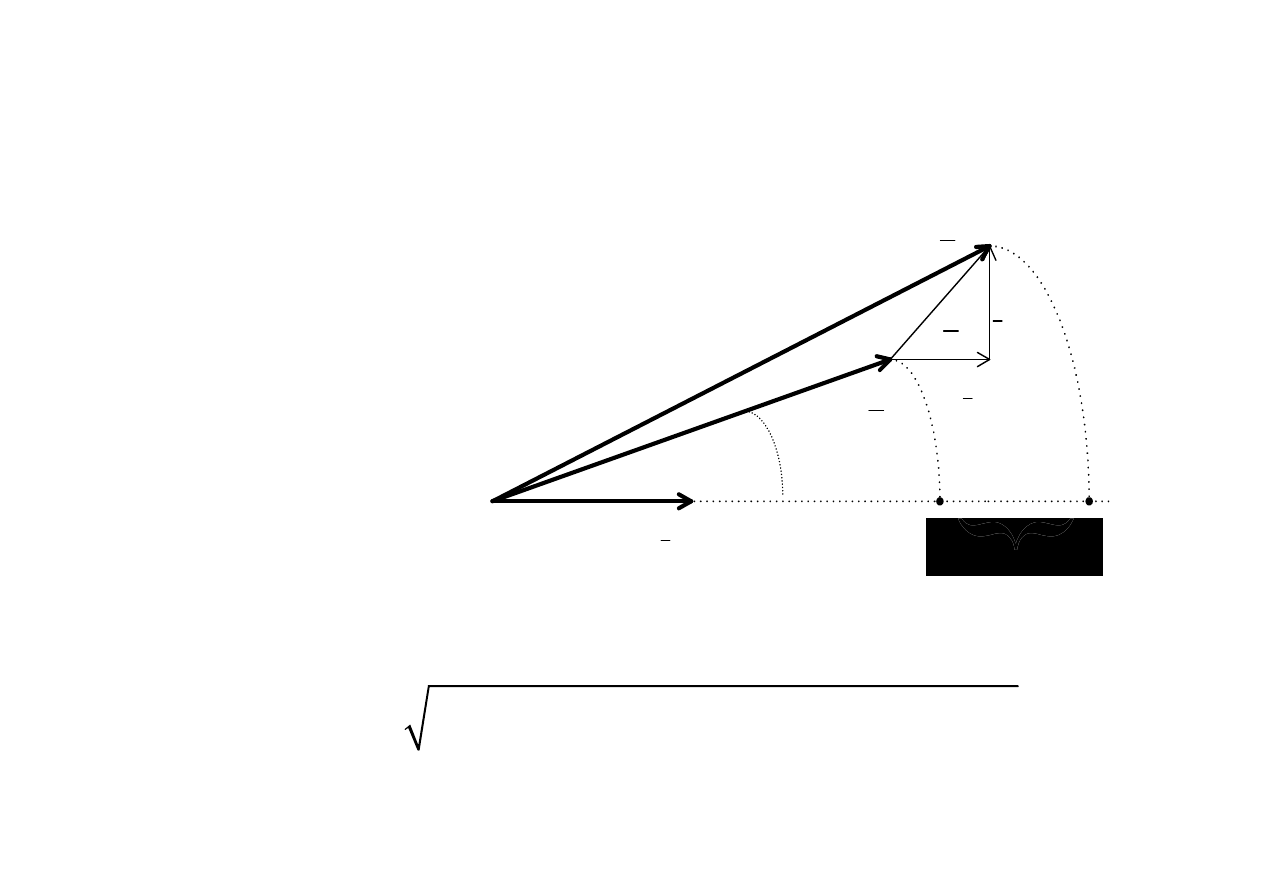
spadek napi

ę

cia linii

I

2

U

1

U

l

U

IR

( )

l

I jX

A

B

C

strata napi

ę

cia

strata podłu

ż

na ( AB )

= R

l

Icos

φ

2

+ X

l

Isin

φ

2

strata poprzeczna( BC )

=- R

l

Isin

φ

2

+ X

l

Icos

φ

2

(

)

1

2

str

l

l

U

U

U

I R

jX

∆

=

−

=

+

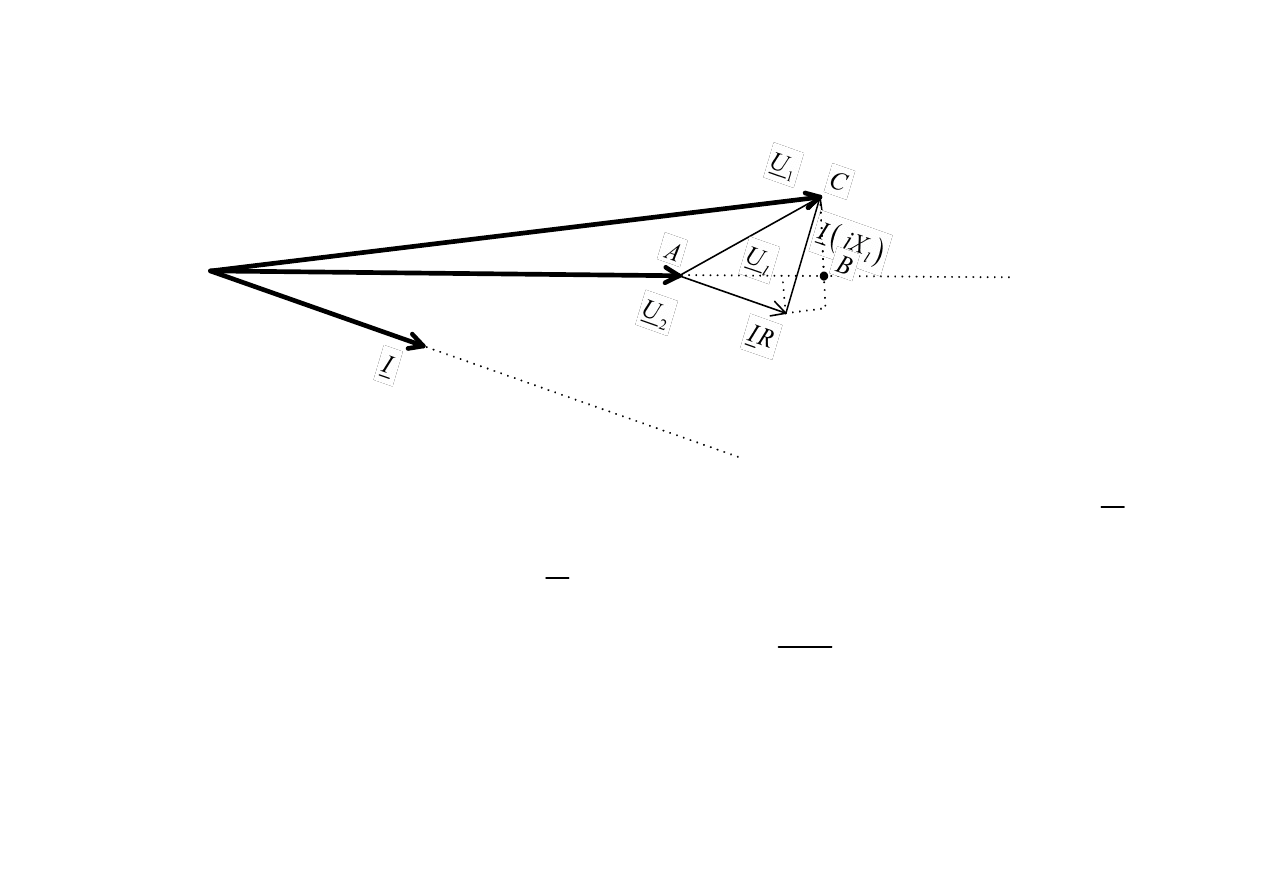
spadek napi

ę

cia linii

(

)

(

)

2

2

2

2

cos

sin

cos

sin

1

l

l

l

l

l

l

U

U

R I

X I

R I

X I

U

PR

QX

U

ϕ

ϕ

ϕ

ϕ

∆ ≈

+

=

+

=

=

+

w przybli

ż

eniu spadek napi

ę

cia

strata napi

ę

cia linii w %

strata mocy czynnej linii

2

l

l

P

R I

∆ =

(

)

%

2

2

100

%

L

L

U

PR

QX

U

∆

=

+

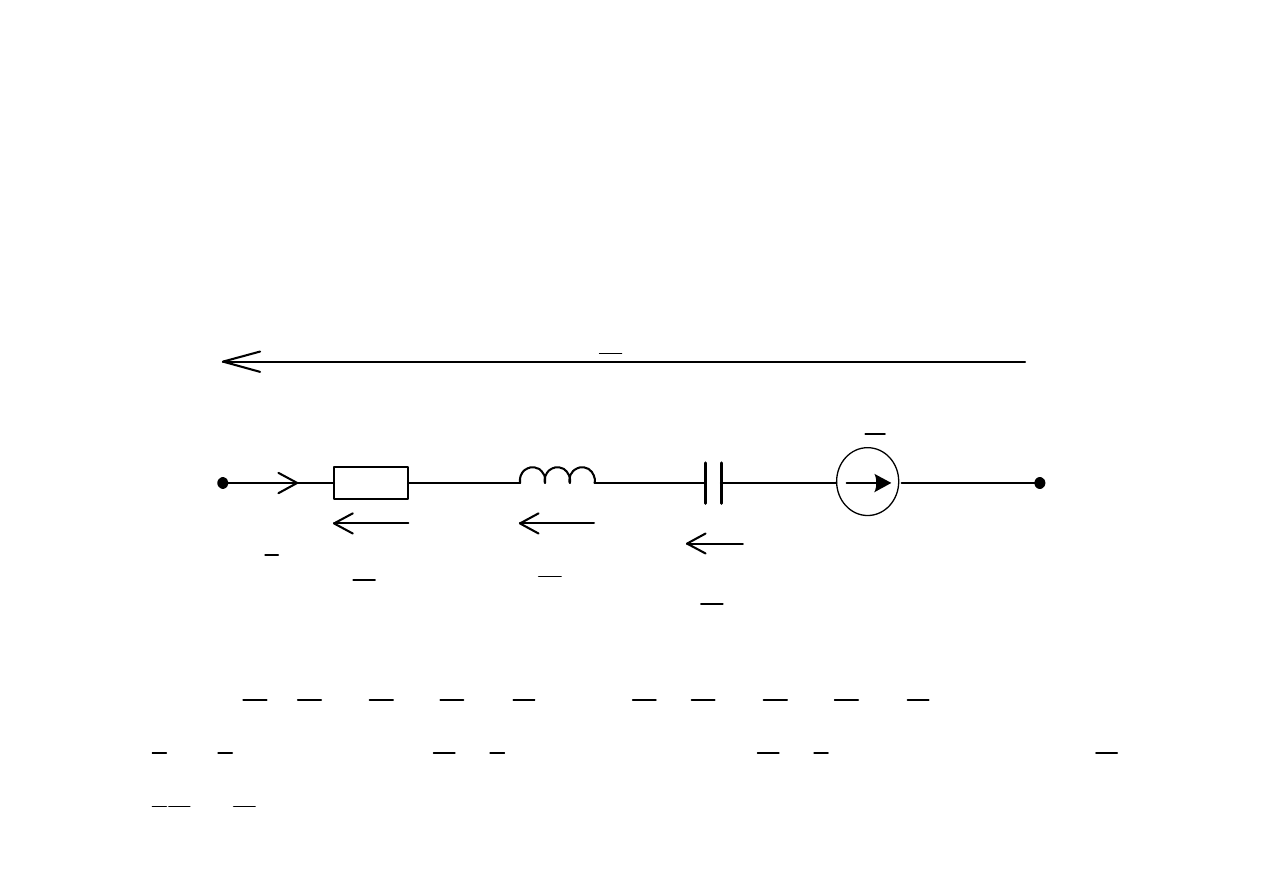
Prawo Ohma w zapisie

zespolonym

U

I

R

L

X

C

X

E

R

U

L

U

C

U

Dla dowolnej gał

ę

zi obwodu

(

)

(

)

(

)

0

(

)

R

L

C

R

L

C

L

C

L

C

L

C

NPK

U

U

U

U

E

U

U

U

U

E

I R

I jX

jX

E

I R

jX

jX

E

I R

j X

X

E

I Z

E

⇒

−

−

−

+ =

⇒

=

+

+

− =

=

+

−

− =

+

−

− =

+

−

− =

=

−

dla całego obwodu elektrycznego

1

1

1

1

1

1

1

1

1

1

0

0

j

j

j

j

j

j

j

n

n

n

n

n

n

n

j

j

j

n

n

n

U

Z I

E

Z I

E

U

Z I

E

Z I

E

U

Z I

E

Z I

E

Z

I

E

Z

I

E

Z

I

E

−











 













 



⋅

⋅

⋅

⋅











 













 



=

=

−

=

−











 



⋅

⋅

⋅

⋅











 













 



−







 









 

 





 

 



⋅

⋅

⋅



 

 





 

 



=

−



 

 



⋅

⋅

⋅



 

 





 

 





 

 



i

w zapisie macierzowym

[ ] [ ][ ] [ ]

U

Z

I

E

=

−

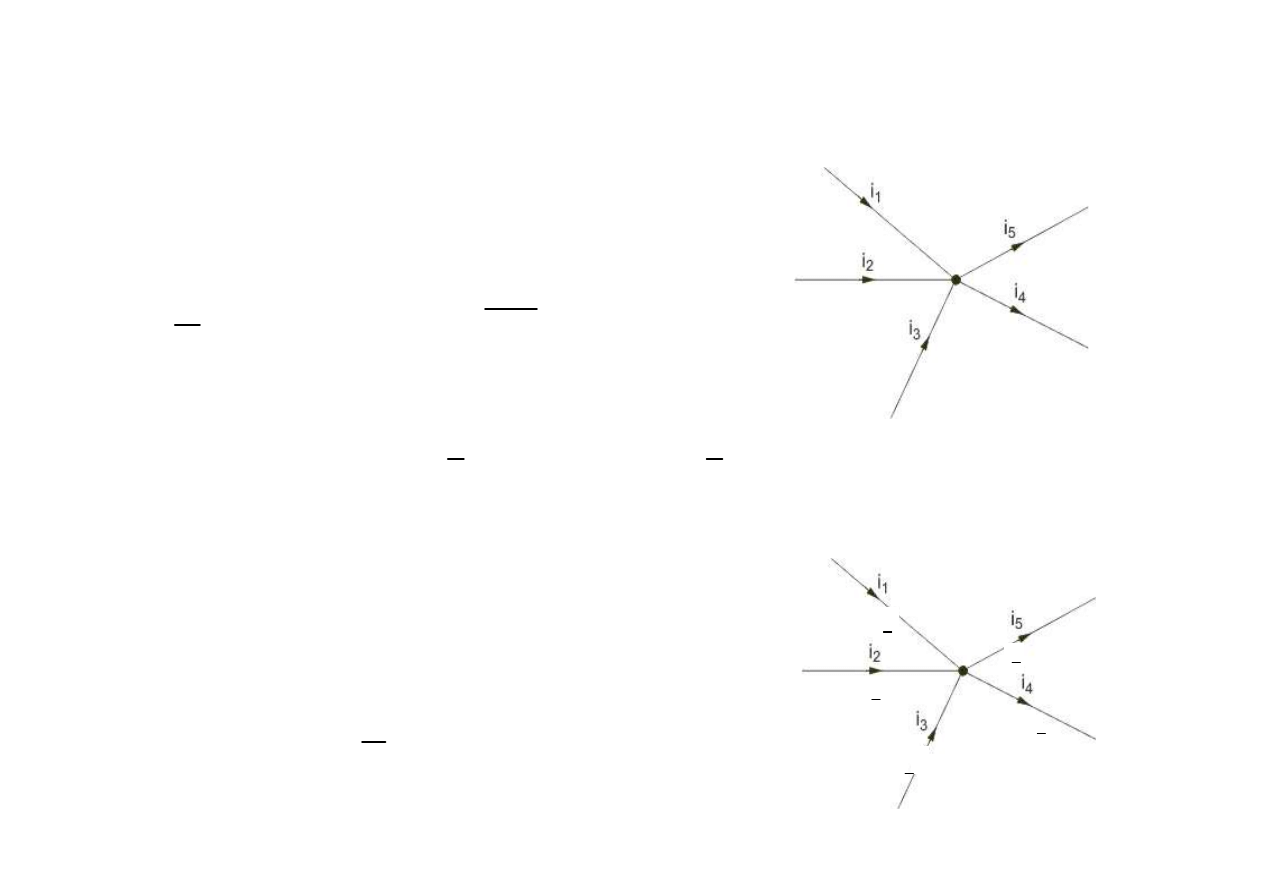
Równania w

ę

złowe Kirchhoffa w

zapisie zespolonym

[ ] [ ]

[ ]

[ ]

1

Z

R

j

L

D

j

ω

ω

=

+

+

macierz impedancji gał

ę

ziowych

⇓

1

I

2

I

3

I

4

I

5

I

0

( )

0

0

j

j

j

węzle

węzle

węzle

i

I t

I

± = →

±

= →

± =

∑

∑

∑

w zapisie macierzowym

[ ][ ] [ ]

0

A I

=

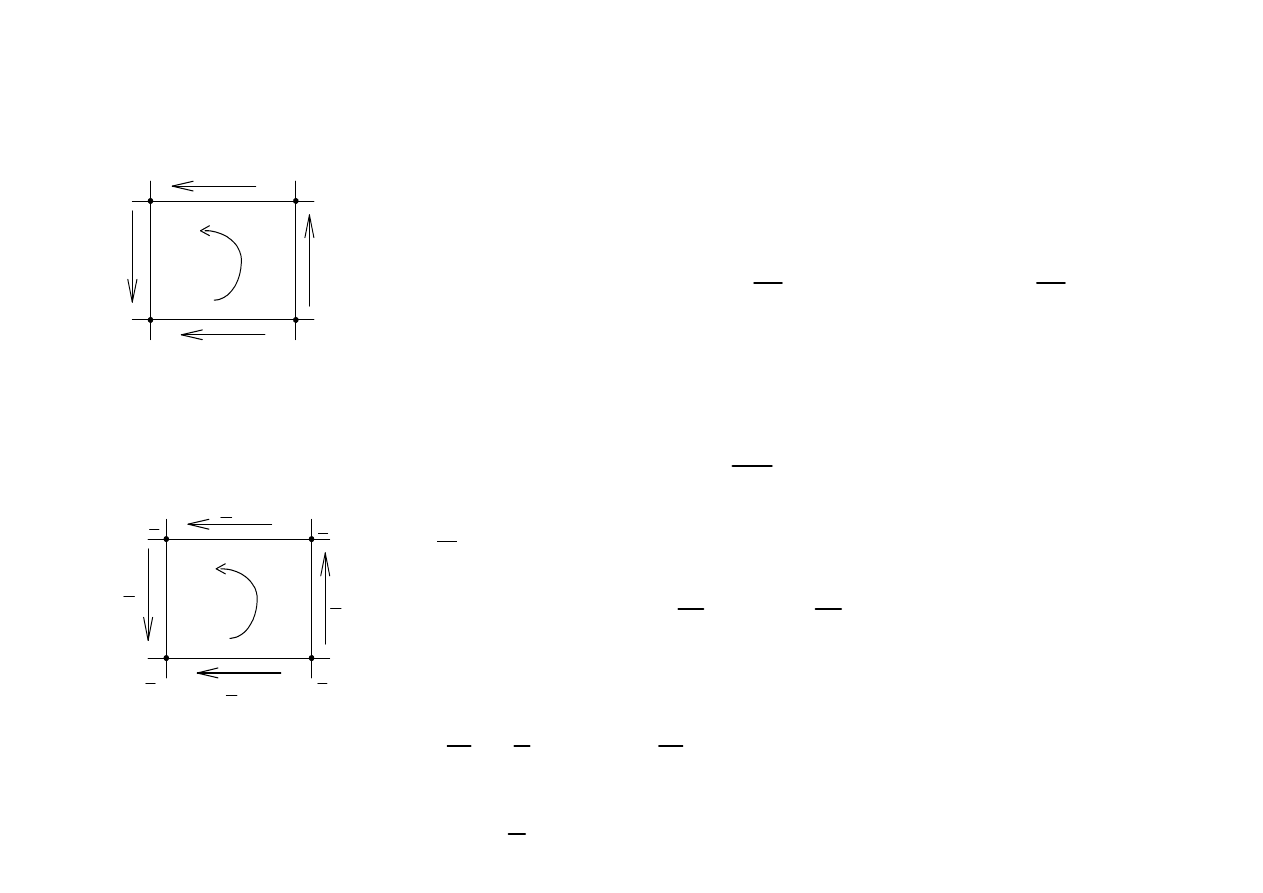
Równania oczkowe Kirchhoffa w

zapisie zespolonym

1

u

2

u

3

u

4

u

1

V

2

V

3

V

4

V

⇓

1

U

2

U

3

U

4

U

1

V

2

V

3

V

4

V

0

( )

0

0

j

j

j

oczko

oczko

oczko

u

U

t

U

± = →

±

= →

±

=

∑

∑

∑

[ ] [ ] [ ]

0

B

U

⋅

=

w zapisie macierzowym

[U] - macierz warto

ś

ci zespolonych napi

ęć

gał

ę

ziowych

ale

[ ] [ ][ ] [ ]

U

Z

I

E

=

−

st

ą

d

[ ] [ ] [ ] [ ] [ ]

1

B

Z

I

B

E

NPK

n

w

rownan

⋅

⋅

=

⋅

⇒

→ − +

[ ] [ ] [ ]

0

1

A

I

PPK

w

rownan

⋅

=

⇒

→ −

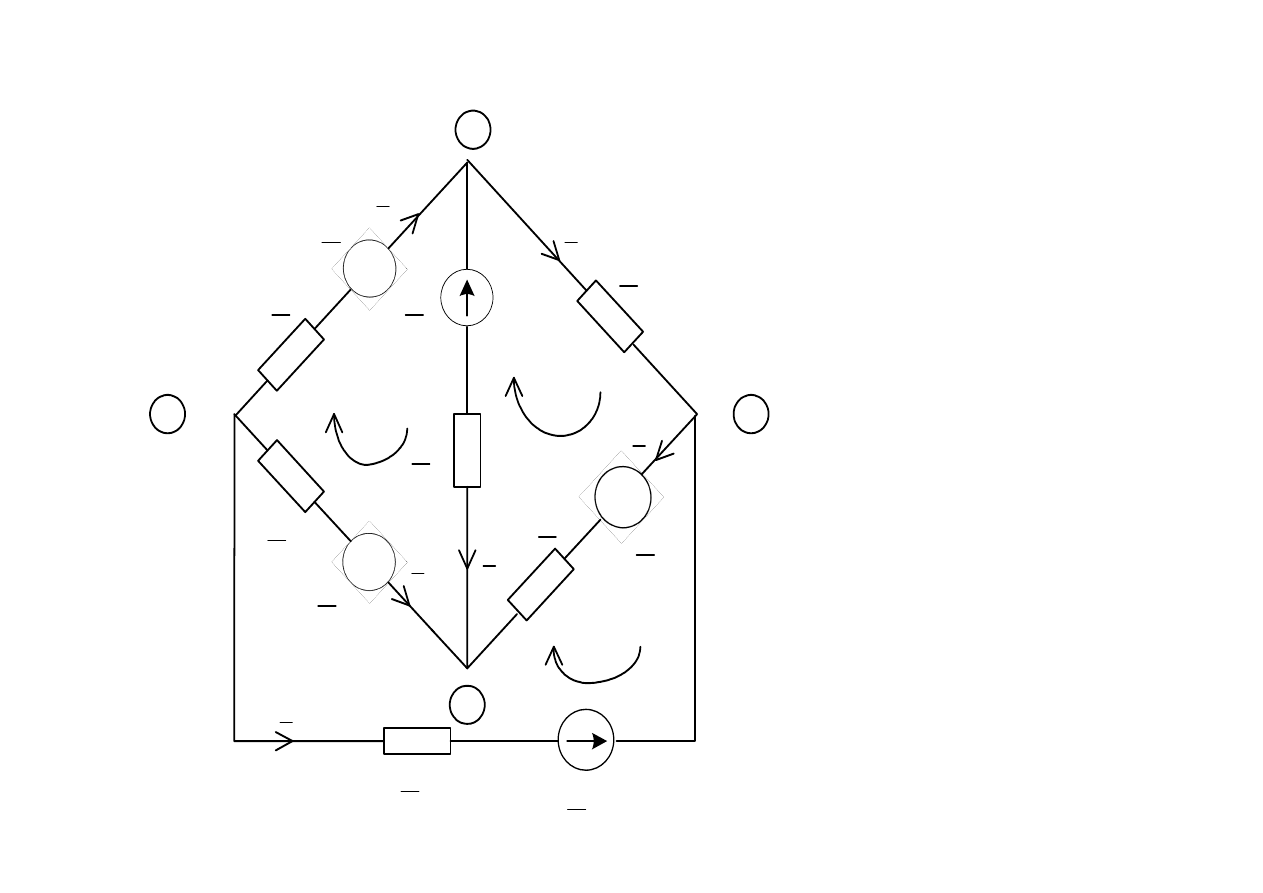
Przykład

1

I

2

I

3

I

4

I

5

I

6

I

1

Z

2

Z

3

Z

4

Z

5

Z

6

Z

1

E

3

E

4

E

5

E

6

E

1

2

3

4

I

II

III

g=6, w=4 to w

n

=w-1=3 to o=g-w

n

=3

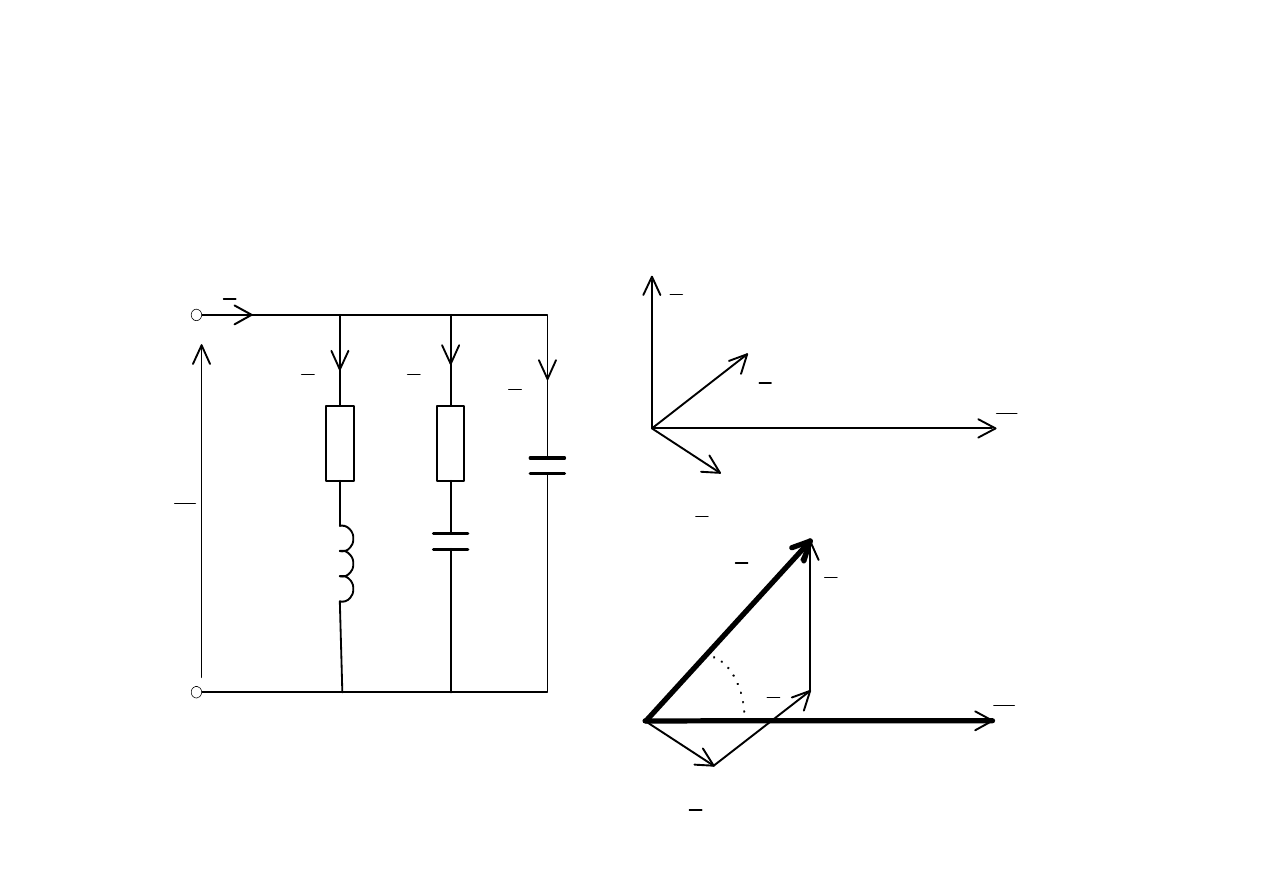
Konstrukcja wykresów wskazowych

na płaszczy

ź

nie zespolonej

U

I

1

I

2

I

3

I

1

R

2

R

1

L

2

C

3

C

U

1

I

2

I

3

I

U

1

I

2

I

3

I

I

ϕ

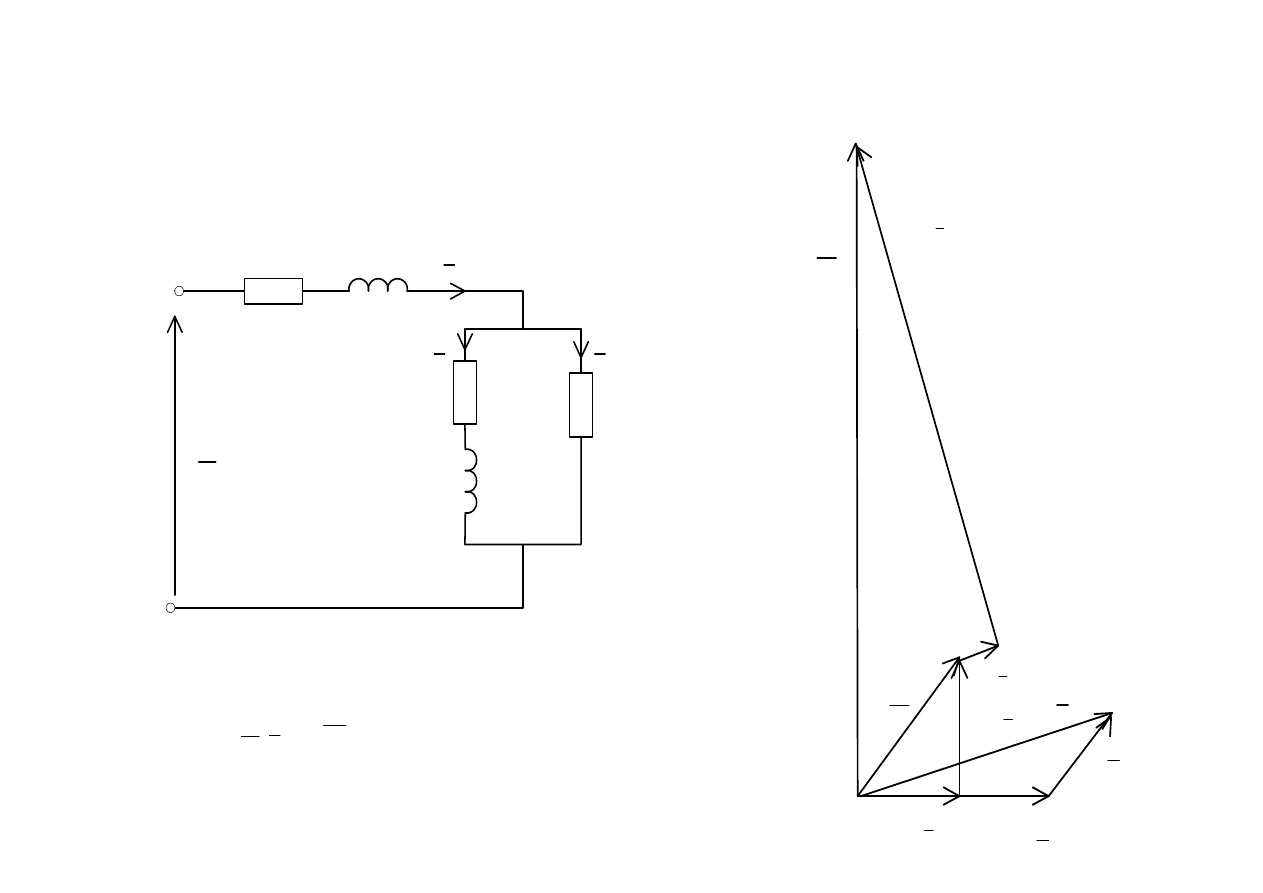
Obwody elektryczne

1

R

3

R

2

R

1

L

X

31

L

X

3

I

1

I

2

I

U

1

I

2

I

3

I

1

1

R I

3

3

R I

1

1

L

jX I

3

3

L

jX I

U

1

U

•

gdy to jest to tzw. układ Hummela

(

)

1

;

2

U I

Π

=

∢

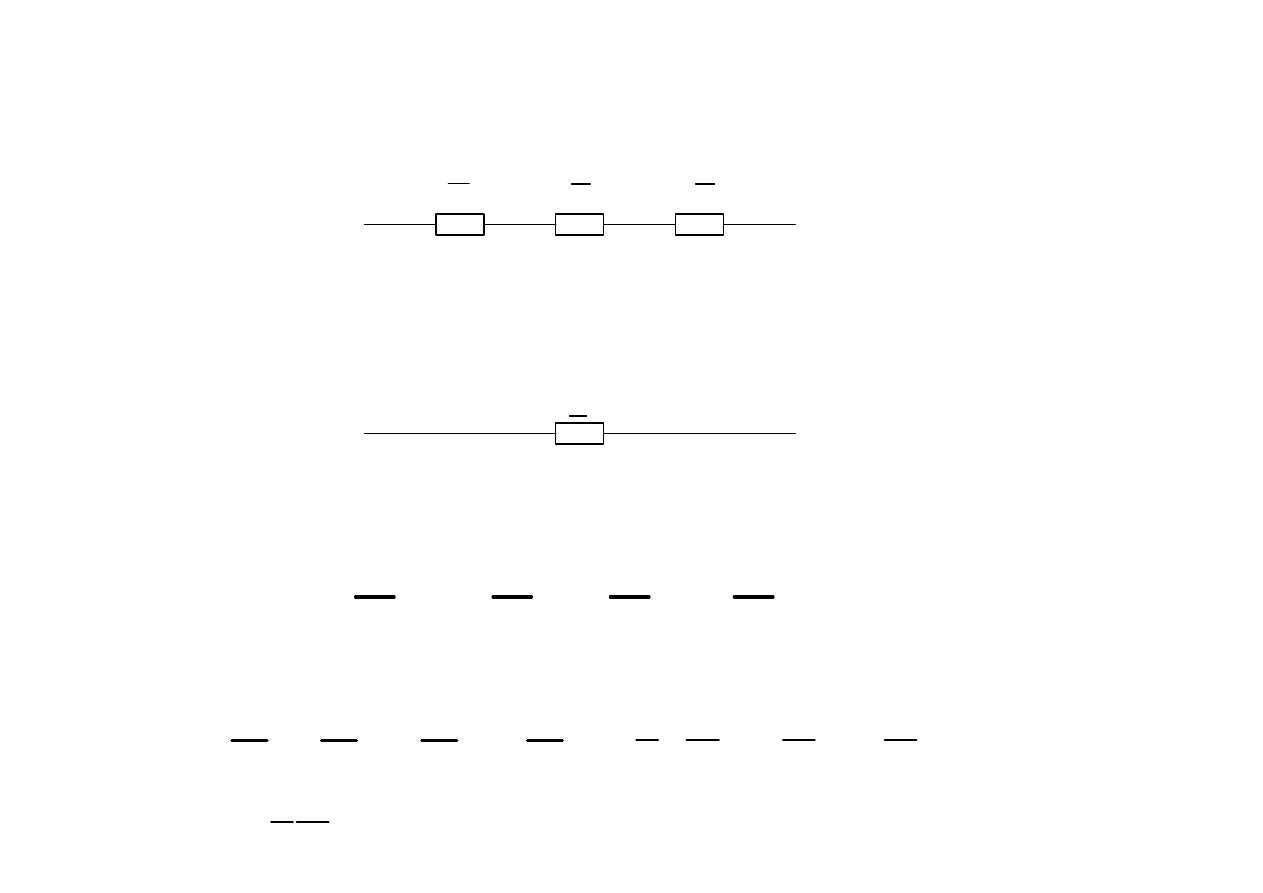
Układ zast

ę

pczy równowa

ż

ny

⇕

Z

Z

1

Z

2

Z

3

Z

1

2

3

Z

Z

Z

Z

Z

= + +

(

)

1

2

3

1

2

3

Z

U

U

U

U

I Z

Z

Z

I Z

=

+

+

=

+

+

=

=

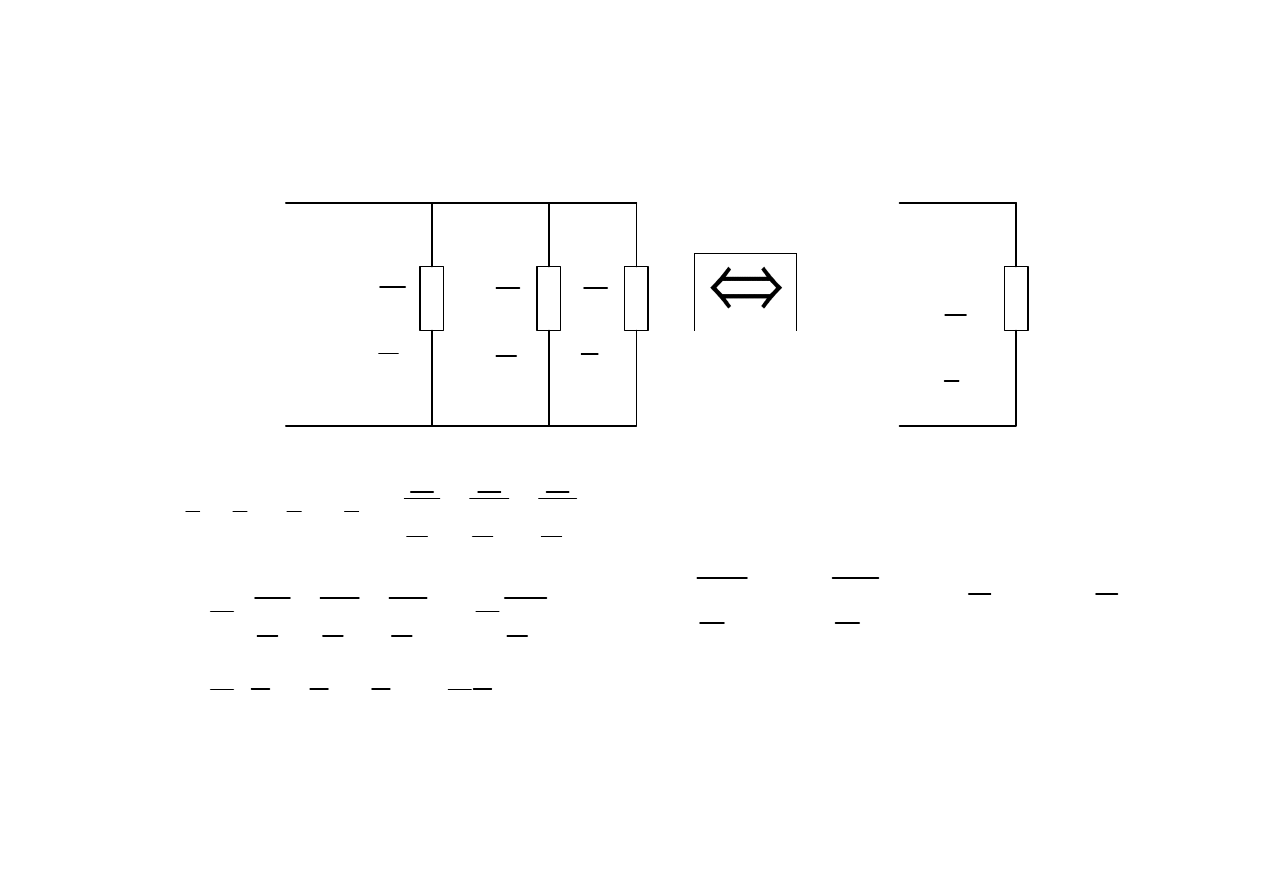
Układ zast

ę

pczy równowa

ż

ny

1

Z

2

Z

3

Z

Z

Z

1

Y

2

Y

3

Y

Z

Y

(

)

1

2

3

1

2

3

1

2

3

1

2

3

1

1

1

1

Z

Z

U

U

U

I

I

I

I

Z

Z

Z

U

U

Z

Z

Z

Z

U Y

Y

Y

U Y

= + + =

+

+

=





=

+

+

=

=









=

+

+

=

1

1

lub

Z

j

j

j

Z

j

Y

Y

Z

Z

=

=

∑

∑

w układach szeregowych sumuj

ą

si

ę

impedancje a

w układach równoległych sumuj

ą

si

ę

admitancje.

Równowa

ż

no

ść

zachodzi tylko przy danej pulsacji.

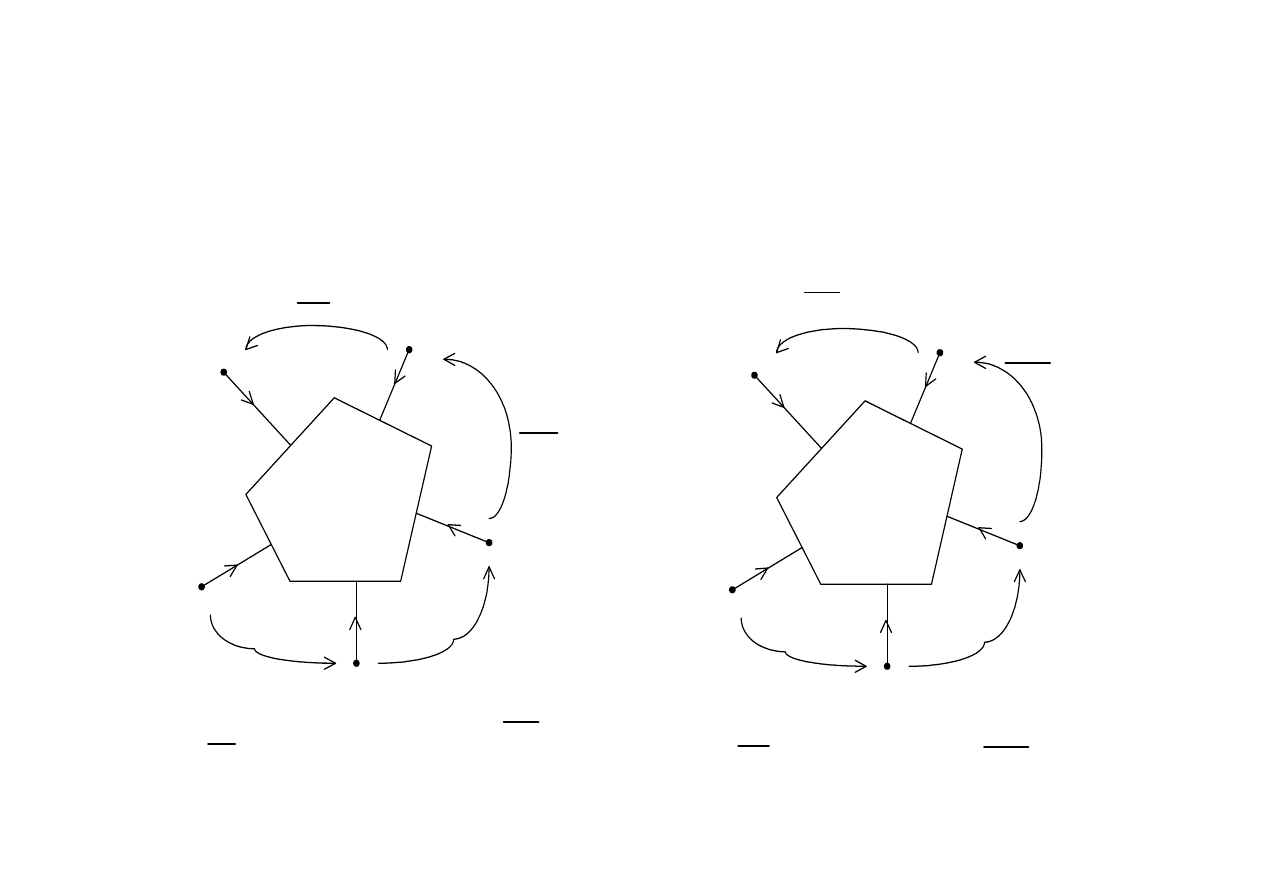
Równowa

ż

no

ść

n-biegunników

≡

1

2

3

n

12

U

23

U

34

U

1,

n

n

U

−

12

'

U

23

'

U

34

'

U

1,

'

n

n

U

−

1'

2'

'

n

3 '

Równowa

ż

no

ść

n-biegunników

Układy n-zaciskowe ( n-biegunniki ) s

ą

równowa

ż

ne gdy identyczne s

ą

zale

ż

no

ś

ci

mi

ę

dzy napi

ę

ciami:

U

12

, U

23

, U

34

,...U

k,k+1

,.....U

n-1,n

a pr

ą

dami niezale

ż

nymi

I

1

,I

2

,I

3

,....I

k

,....I

n-1

( gdy takie zwi

ą

zki daj

ą

si

ę

sprecyzowa

ć

).

Np.

U

k,k+1

=f

k,k+1

(I

1

,I

2

,I

3

,....I

k

,....I

n-1

); k= 1,2,3 .... n-1

Jest identyczne jak
U’

k,k+1

=f’

k,k+1

(I’

1

,I’

2

,I’

3

,....I’

k

,....I’

n-1

); k= 1,2,3 .... n-1

f

k,k+1

= f’

k,k+1

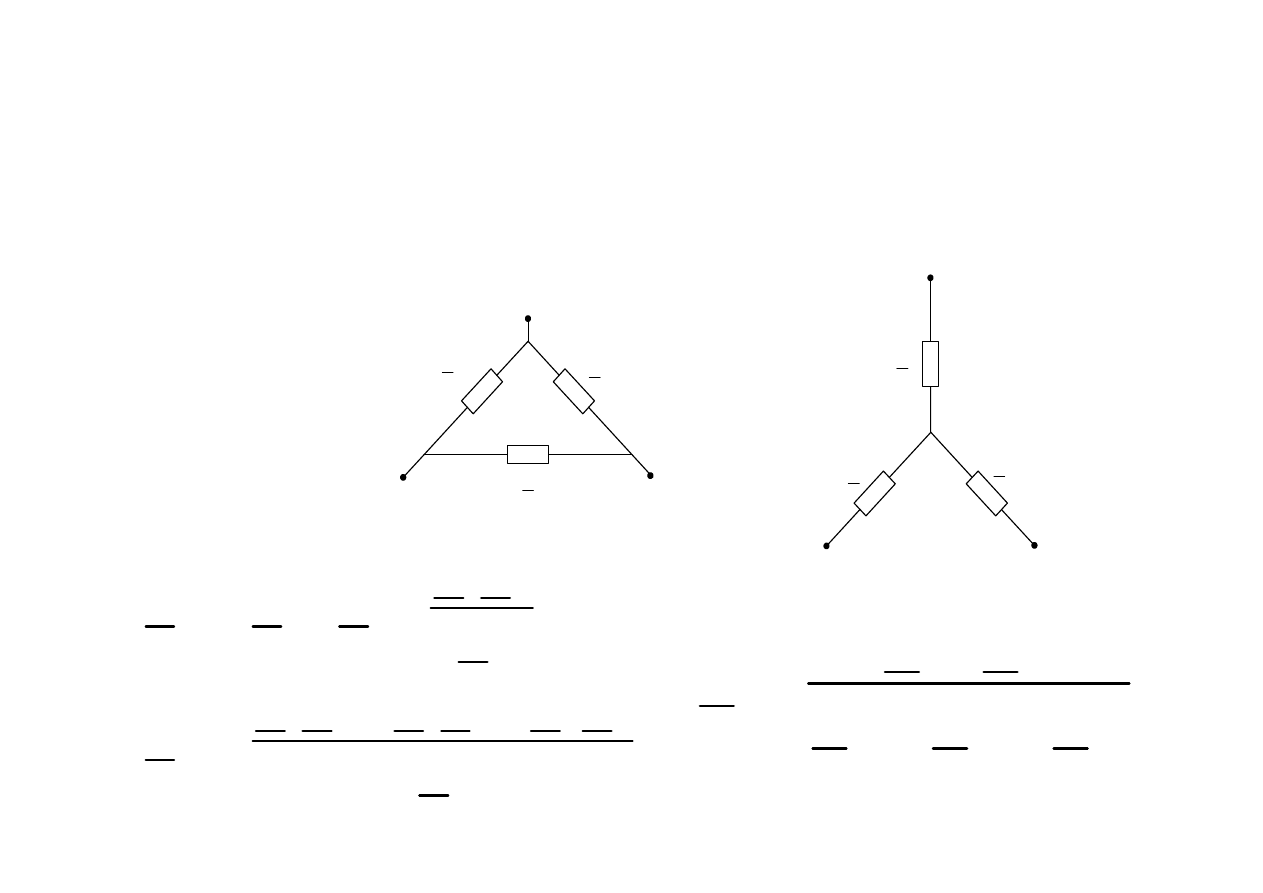
Przykład:

∆→Υ

1

2

3

12

Z

23

Z

31

Z

1'

2'

3'

1

Z

2

Z

3

Z

≡

na

ć

wiczeniach

1

2

12

1

2

3

1

2

1

3

2

3

12

3

Z Z

Z

Z

Z

Z

Z Z

Z Z

Z Z

Z

Z

=

+

+

+

+

=

12

31

1

12

31

23

Z

Z

Z

Z

Z

Z

⋅

=

+

+

Bilans mocy czynnej

[ ]

[ ] [ ] [ ]

[ ] [ ][ ] [ ] [ ][ ] [ ] [ ]

*

*

1

*

*

*

1

*

*

*

( )

( )

.

,..

,...

.

0

0

j

j

j

j

j j

j

j

j

T

T

T

j

n

j

n

T

T

T

u i

U t I t

U I

I

U

U

U

U

I

A

V

I

I

I

V

A I

V

A I

V

→

→

=

 

 

 

 





 





⋅

=

=

=





 





 

 

 

 

 





=

=

=

=





∑

∑

∑

Analogicznie jak dla przebiegów chwilowych

czyli

1

0

n

j

j

S

=

=

∑

bilans mocy pozornej zespolonej.

Obwody elektryczne

1

0

n

j

j

P

=

=

∑

St

ą

d z algebry liczb zespolonych

1

0

n

j

j

Q

=

=

∑

bilans mocy czynnej

bilans mocy biernej.

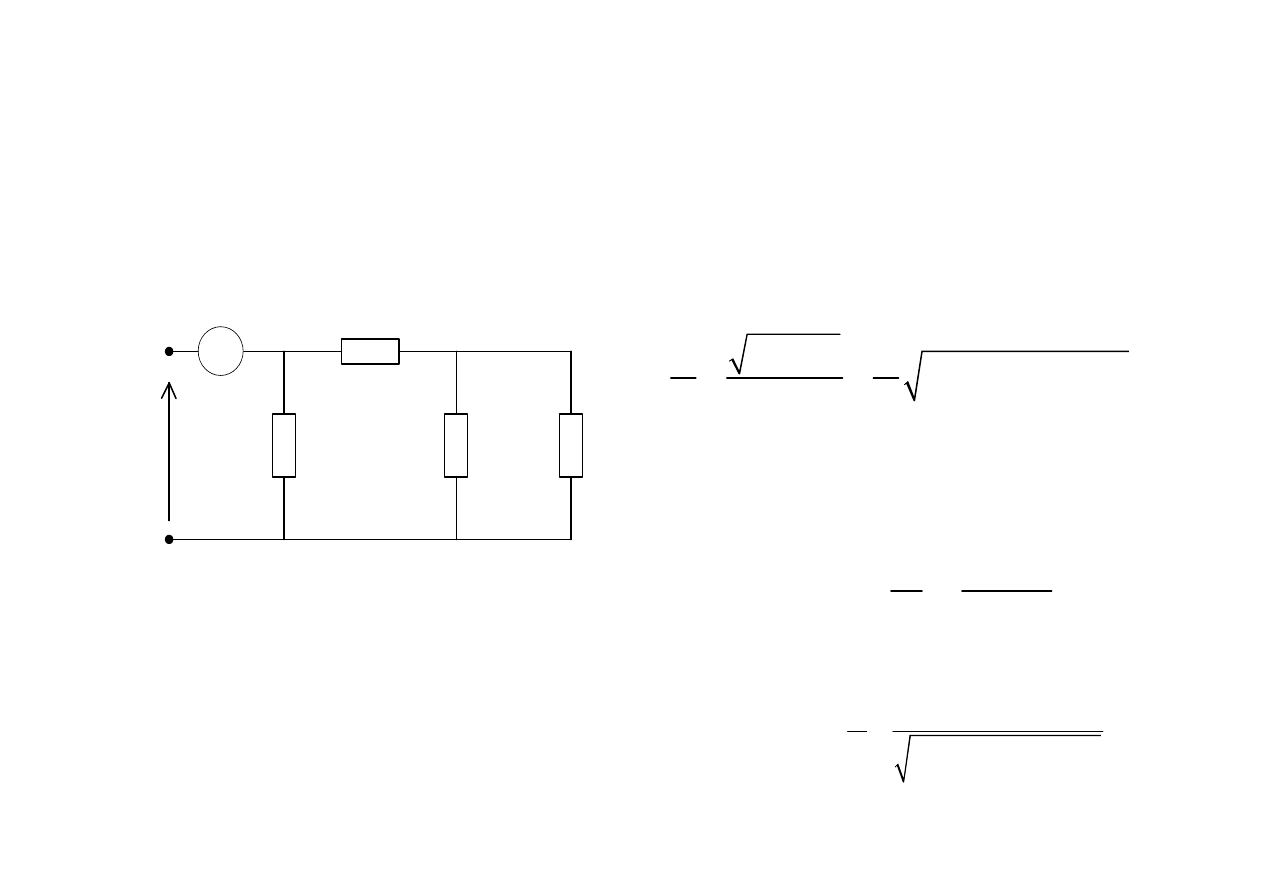
Zastosowanie bilansu mocy

A

1

1

cos

P

ϕ

4

4

cos

P

ϕ

2

2

cos

P

ϕ

3

3

cos

P

ϕ

U

j

j

j

Q

P tg

ϕ

=

(

) (

)

2

2

2

2

1

j

j

P

Q

S

I

P

Q

U

U

U

+

=

=

=

+

∑

∑

Obliczy

ć

pr

ą

d zasilaj

ą

cy

j

j

Q

Q

tg

P

P

ϕ

=

=

∑

∑

(

) (

)

2

2

cos

j

j

j

P

P

S

P

Q

ϕ

= =

+

∑

∑

∑

wypadkowy k

ą

t przesuni

ę

cia fazowego

φ

wypadkowy współczynnik mocy

cos

φ

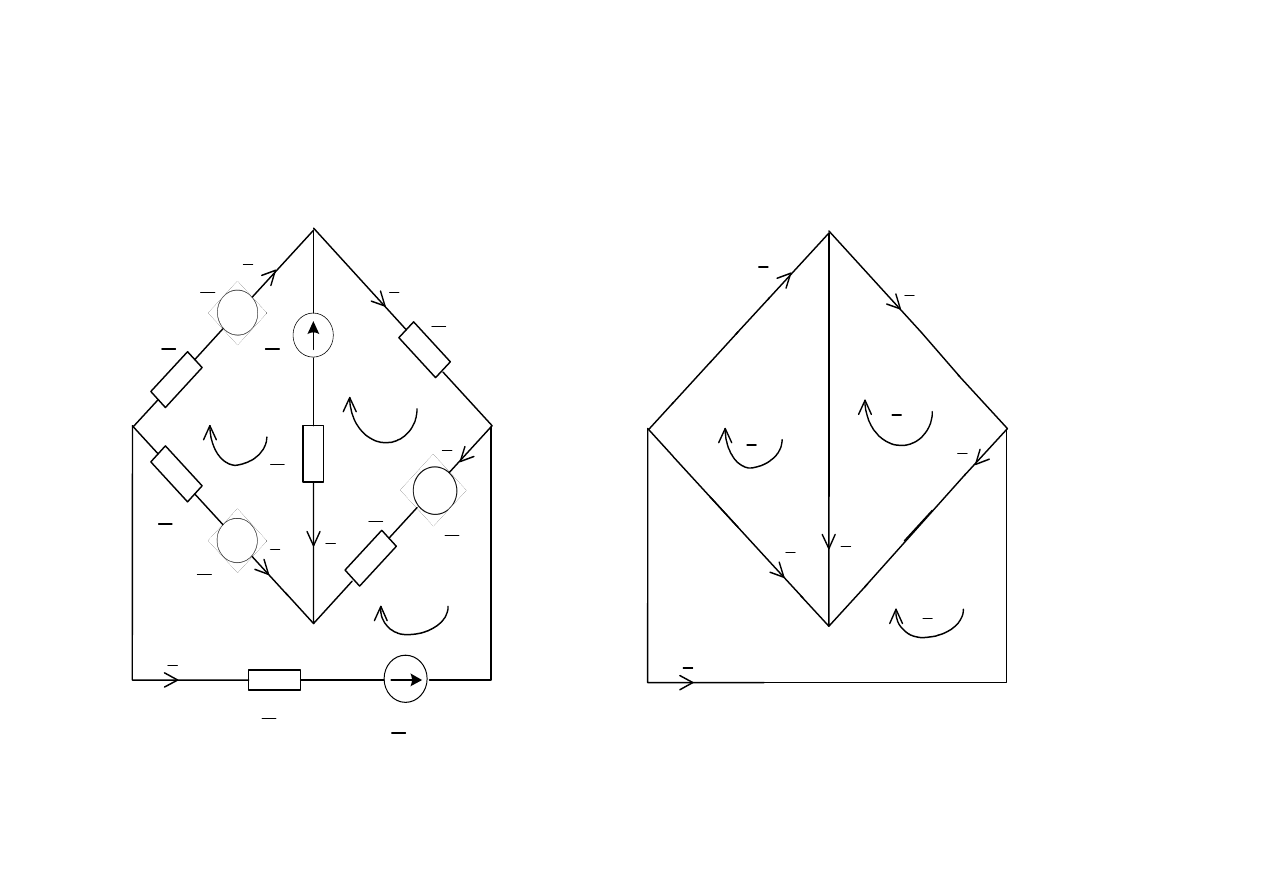
Metody obliczania obwodów

Metoda pr

ą

dów oczkowych ( pr

ą

dów konturowych, Maxwella )

1

I

2

I

3

I

4

I

5

I

6

I

1

Z

2

Z

3

Z

4

Z

5

Z

6

Z

1

E

3

E

4

E

5

E

6

E

I

II

III

1

I

2

I

3

I

4

I

5

I

6

I

1

o

I

2

o

I

3

o

I

Metoda pr

ą

dów oczkowych

1

1

2

1

2

3

2

4

3

1

5

3

2

6

3

;

;

;

;

;

o

o

o

o

o

o

o

o

o

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

=

=

−

=

=

−

=

−

= −

Pomysł:
Wprowadzenie nowych zmiennych- tzw. pr

ą

dów oczkowych ,

przyporz

ą

dkowanych poszczególnym oczkom niezale

ż

nym. ( o=g-w

n

).

Oczek niezale

ż

nych jest znacznie mniej ni

ż

gał

ę

zi, st

ą

d post

ę

powanie to

zmniejszy liczb

ę

niewiadomych równa

ń

.

Polega to na wyra

ż

eniu pr

ą

du danej gał

ę

zi przez pr

ą

dy oczek, do których nale

ż

y

dana gał

ąź

.

Np.

Warto

ś

ciom pr

ą

dów oczkowych przyporz

ą

dkowuje si

ę

warto

ś

ci pr

ą

dów w

gał

ę

ziach

I

j

o

j

I

Metoda pr

ą

dów oczkowych

[ ]

0

1

1

0

0

.

.

.

T

j

j

n

m

I

I

B

I

I

I

I





 





 





 





 

=





 





 





 

 









[ ] [ ] [ ]

T

o

I

B

I

=

a wi

ę

c

mno

ż

ymy obustronnie przez

[A]

[ ][ ] [ ][ ] [ ] [ ][ ]

0

0

T

o

o

A I

A B

I

I

=

=

=

a wi

ę

c wyra

ż

enie warto

ś

ci pr

ą

dów gał

ę

ziowych przez dowolne warto

ś

ci pr

ą

dów

oczkowych implikuje spełnienie równa

ń

w

ę

złowych.

Metoda pr

ą

dów oczkowych

[ ] [ ] [ ]

T

o

I

B

I

=

[ ][ ]

[ ][ ][ ] [ ][ ]

0

B U

B Z

I

B E

=

⇒

=

[ ][ ][ ] [ ] [ ][ ]

T

o

B Z

B

I

B E

=

Po podstawieniu

do napi

ę

ciowego równania Kirchhoffa

lub skróconym zapisie

[ ] [ ] [ ]

o

o

o

Z

I

E

=

przy czym

[ ]

o

Z

- kwadratowa macierz impedancji oczkowych

[ ] [ ]

;

o

o

I

E

- kolumnowe macierze pr

ą

dów i sił elektromotorycznych oczkowych

Metoda pr

ą

dów oczkowych

[ ] [ ] [ ]

o

o

o

Z

I

E

=

[ ]

[ ] [ ]

[ ][ ][ ] [ ][ ]

1

1

o

o

o

T

I

Z

E

B Z

B

B E

−

−









=

=









rozwi

ą

zanie równania

a nast

ę

pnie obliczamy

[ ] [ ] [ ]

T

o

I

B

I

=

równanie to równie

ż

spełnia równanie pr

ą

dowe Kirchhoffa

[A][I]=0

.

Metoda pr

ą

dów oczkowych

[ ]

o

kl

mxm

Z

Z





=





kk

kj

j

Z

Z

=

∑

,

kl

lk

kl j

k l

k l

j

Z

Z

Z

≠

≠

=

=

±

∑

Macierz impedancji oczkowych

przy czym

- suma impedancji w k-tym oczku lub impedancja własna
k-tego oczka

- suma ( lub ró

ż

nica ) impedancji granicznych mi

ę

dzy k-tym i

l-tym oczkiem ( + gdy pr

ą

dy oczkowe gał

ę

zi wspólnych maj

ą

zwroty zgodne, - w przypadku przeciwnym.

- macierz jest symetryczna.

[ ]

o

kl

mxm

Z

Z





=





o

k

E

- suma ( lub ró

ż

nica ) sił elektromotorycznych w k-tym oczku lub

siła elektromotoryczna własna k-tego oczka ( + gdy SEM zgodna z
pr

ą

dem oczkowym, - w przeciwnym przypadku ).

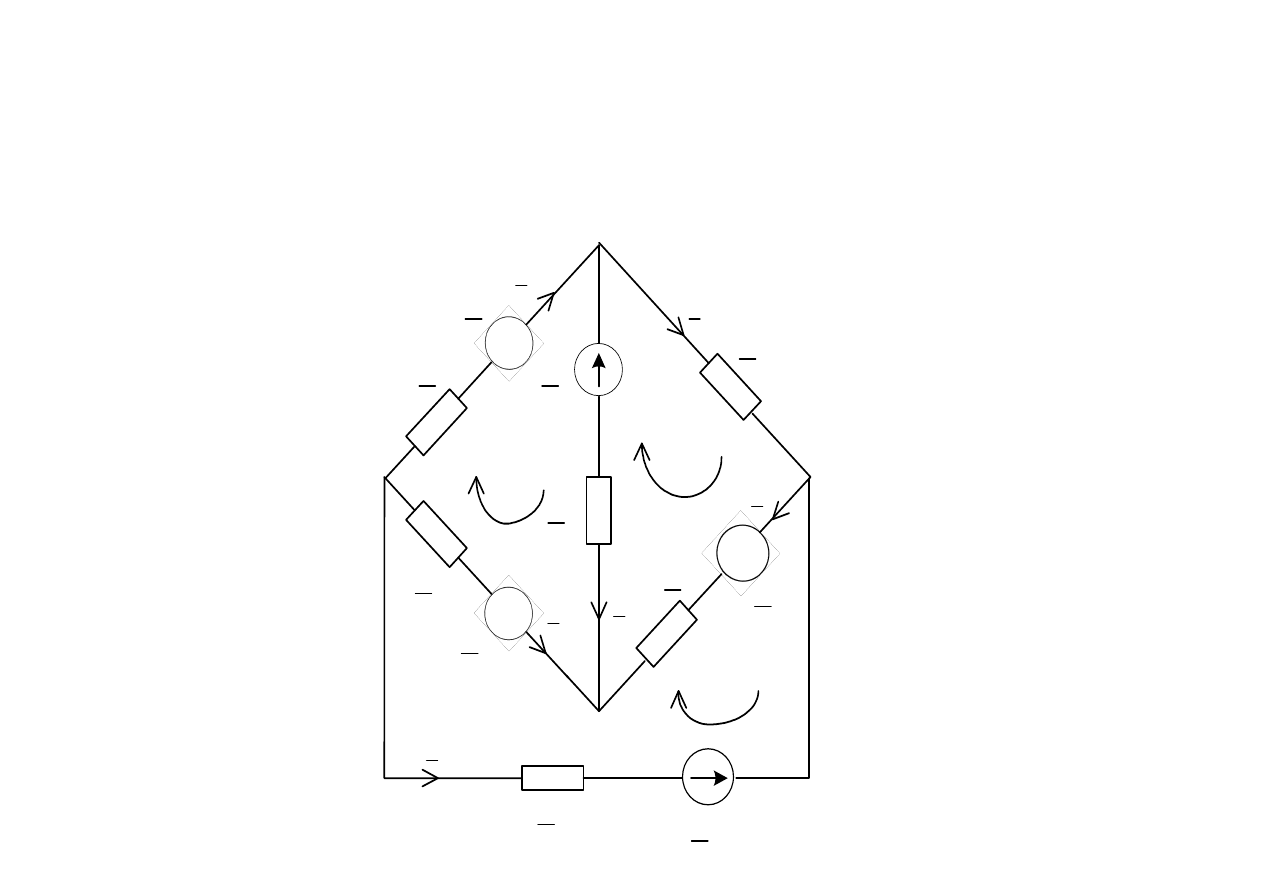
Metoda pr

ą

dów oczkowych

Przykład:

1

I

2

I

3

I

4

I

5

I

6

I

1

Z

2

Z

3

Z

4

Z

5

Z

6

Z

1

E

3

E

4

E

5

E

6

E

I

II

III