OBWODY ELEKTRYCZNE

i

Teoria Obwodów 1

Sierpień 2011

Sierpień 2011

wykład 9

wykład 9

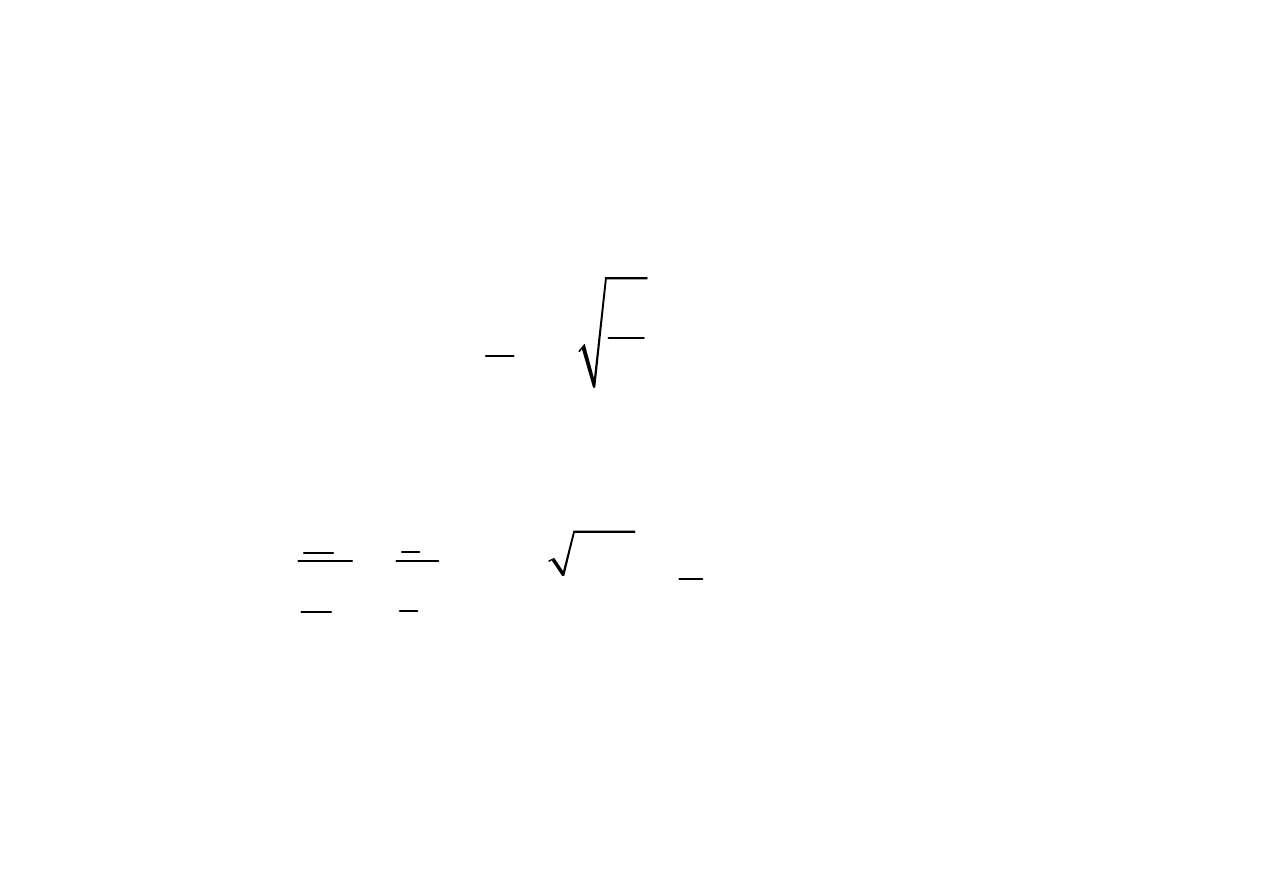
impedancja falowa

c

j

c

c

B

Z

Z e

C

ϕ

=

=

Współczynnik przenoszenia

1

1

2

2

g

a

jb

U

I

A

BC

e

e e

U

I

ϑ

=

= +

= =

=

g=

a

+j

b

- współczynnik przenoszenia

współczynnik tłumienia

współczynnik fazowy

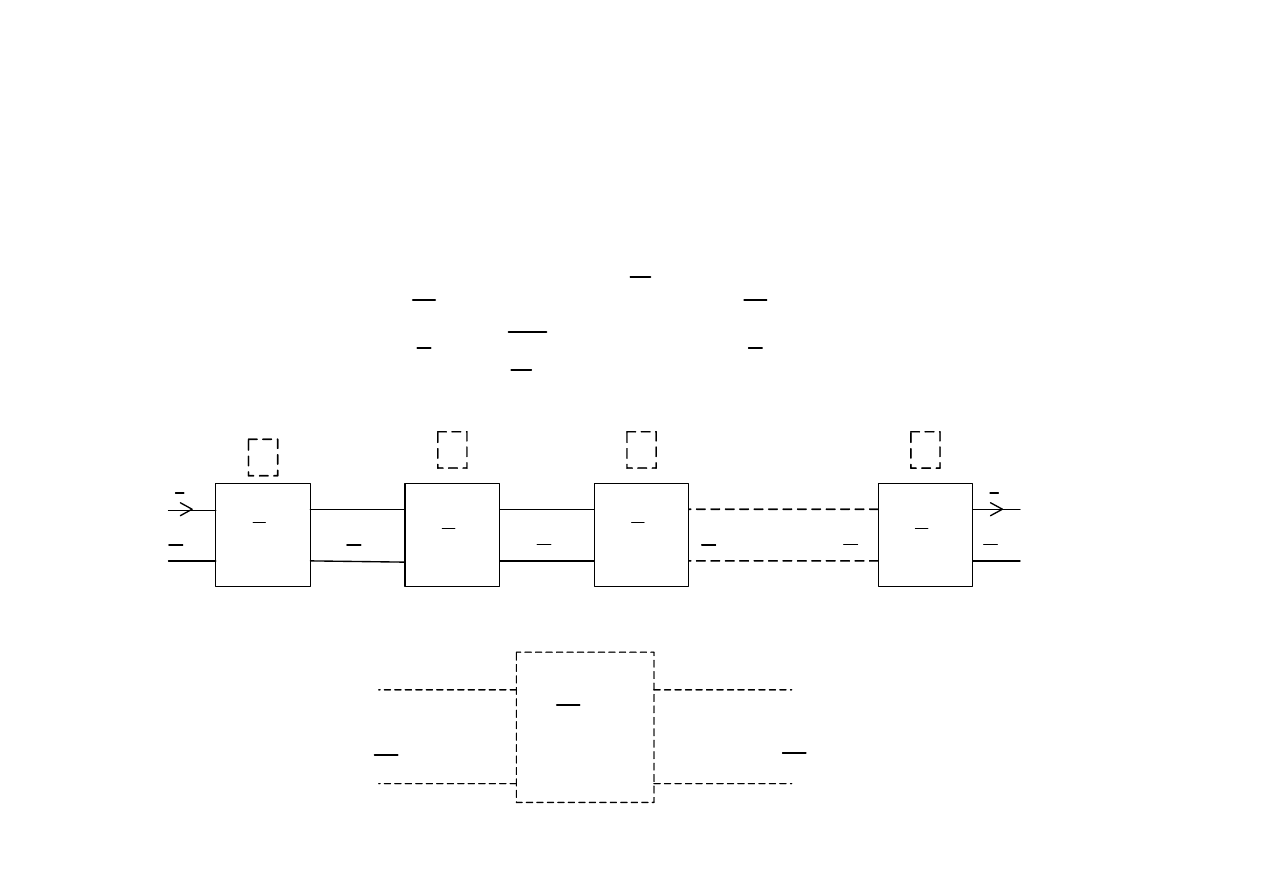
Czwórniki - postać hiperboliczna

1

2

1

2

1

c

c

chg

Z shg

U

U

shg

chg

I

I

Z

















=





























c

Z

g

c

Z

g

c

Z

g

c

Z

g

1

U

1

I

1

2

3

n

2

U

3

U

4

U

n

U

1

n

U

+

1

n

I

+

1

U

1

n

U

+

c

Z

ng

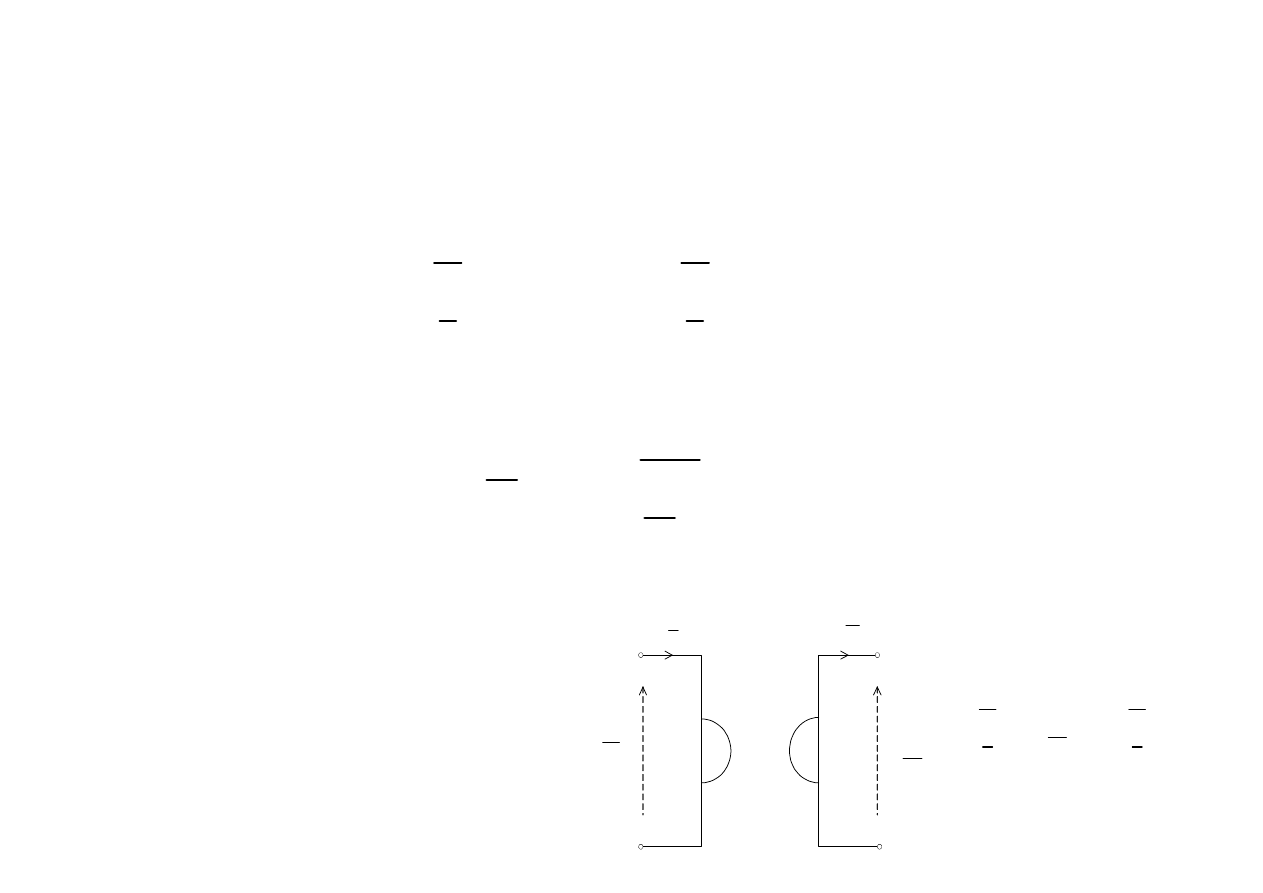
Inwertory impedancji

1

2

1

2

0

0

U

B

U

I

C

I







 



=







 









 



1

2

1

i

Z

K

Z

=

Oznaczmy

K

i

= B/C

- współczynnik inwersji ( dodatni lub ujemny )

znaczenie praktyczne: ( żyrator ).

1

2

1

2

0

1

0

R

U

U

I

I

R

















=

























1

U

2

U

1

I

2

I

R

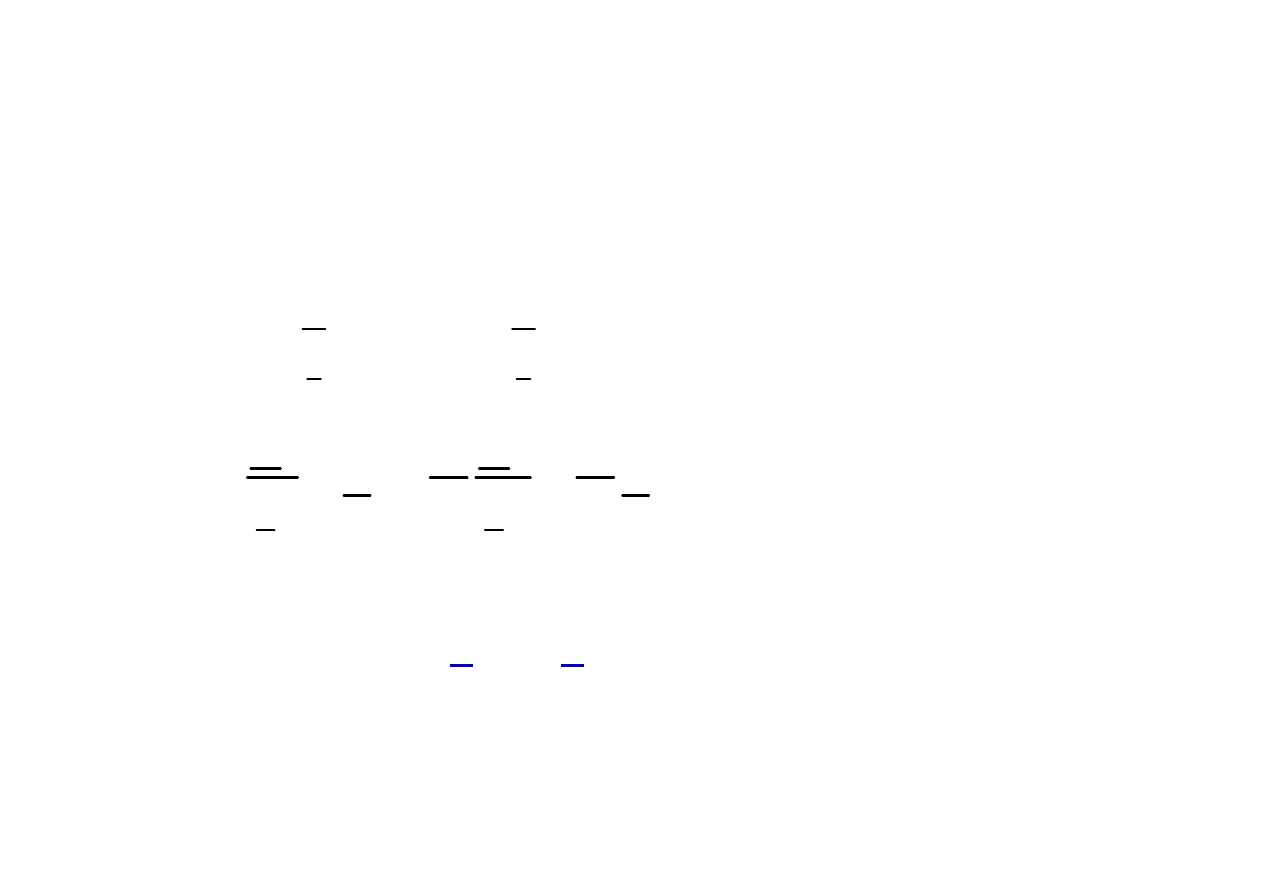
Konwertery impedancji

Czwórniki aktywne, których macierz łańcuchowa ma postać

1

2

1

2

0

0

U

A

U

I

D

I







 



=







 









 



czyli

B=C=0

1

2

1

2

1

2

U

A U

A

Z

Z

I

D I

D

=

=

=

K

k

=A/D

- współczynnik konwersji

Z

1

=K

k

Z

2

Impedancja wejściowa konwertera jest proporcjonalna do impedancji

obciążenia.

Konwertery impedancji

Ze względu na znak współczynnika konwersji dzielimy na:

PIC

( positive impedancje converter ) – konwerter dodatnio-impedancyjny,

K

k

>0

NIC

( negative impedancje converter ) – konwerter ujemno-impedancyjny,

K

k

<0

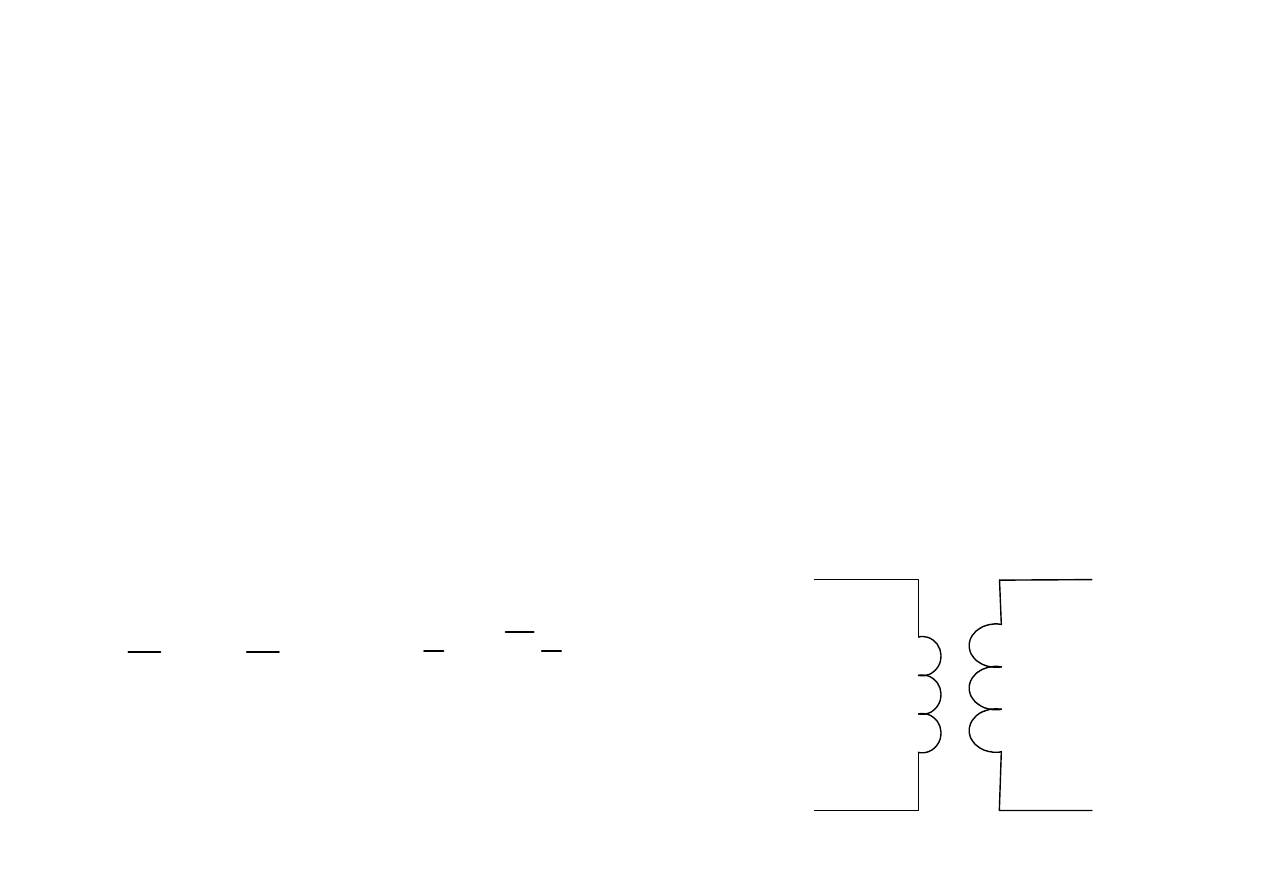
Przykładem konwertera PIC jest transformator idealny

n

1

2

1

2

1

U

nU

i

I

I

n

=

=

czyli

A=n a D= 1/n

Konwertery impedancji

Większe znaczenie praktyczne mają konwertery typu NIC

rozróżniamy dwa rodzaje:

V NIC ( U NIC )

C NIC ( I NIC )

zmiana znaku napięcia

zmiana znaku prądu

1

2

1

2

1

0

0

1

U

U

k

I

I





−













=

























1

2

1

2

1

0

1

0

U

U

I

I

k

















=













−













1

2

1

Z

Z

k

= −

1

2

Z

k Z

= −

Jest to czwórnik aktywny i nieodwracalny

Przekształca

R→ - R; L→ - L; C→ - C

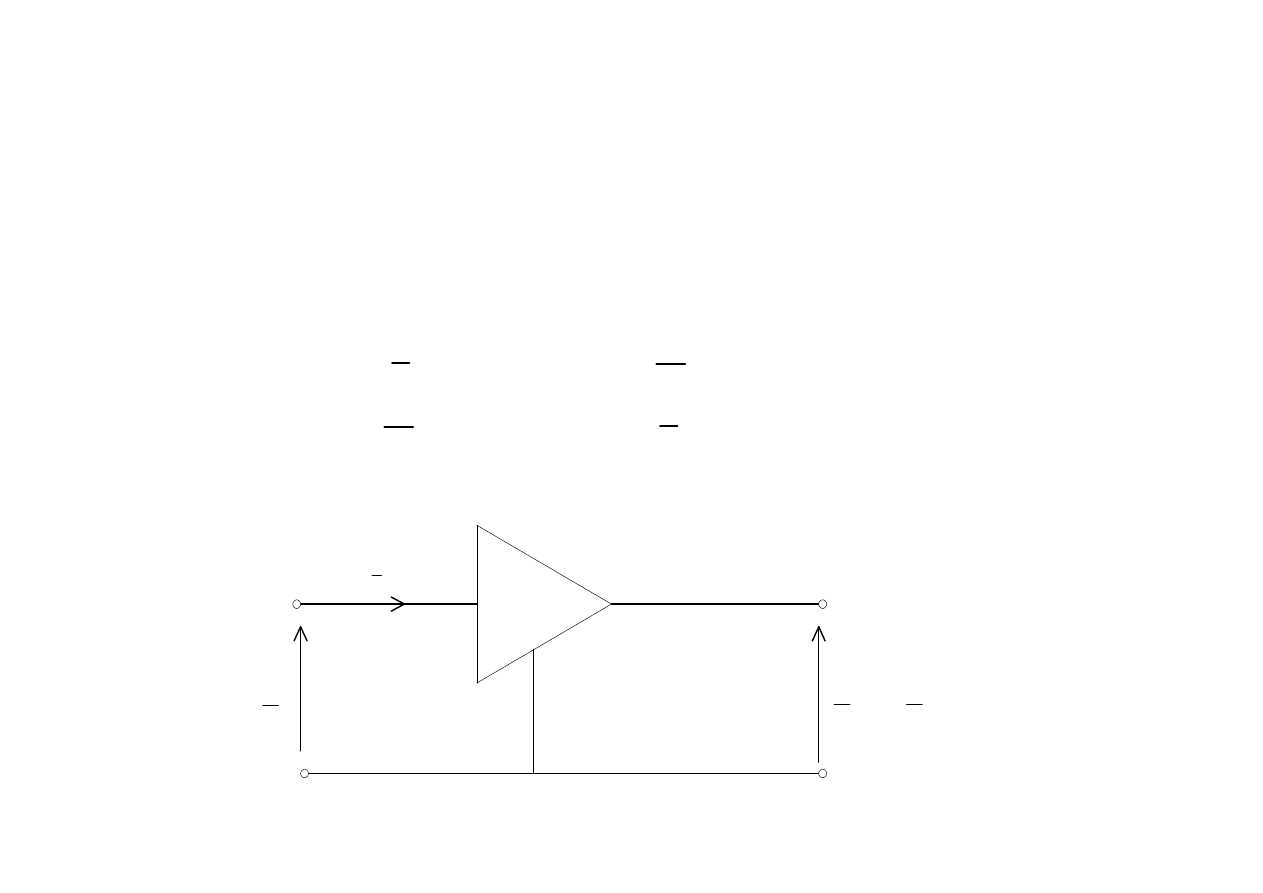
wzmacniacz napięciowy ( idealny )

Czwórnik aktywny opisany macierzą hybrydową

1

1

2

2

21

0

0

0

I

U

h

U

I













=

























1

U

2

1

21

U

h U

=

1

0

I

=

21

h

wzmacniacz napięciowy

Wynika że, idealny wzmacniacz napięciowy nie pobiera prądu

(impedancja wejściowa równa nieskończoności),

i przetwarza napięcie wejściowe

U

1

w wyjściowe

U

2

zgodnie z relacją

2

1

21

U

h U

=

1

0

I

=

1

U

2

1

21

U

h U

=

2

U

Wejście układu stanowi przerwę (

impedancja wejściowa równa nieskończoności

).

Na wyjściu istnieje jedynie idealne źródło napięcia sterowane napięciem U

1

.

Stąd

impedancja wyjściowa takiego układu jest równa zeru

.

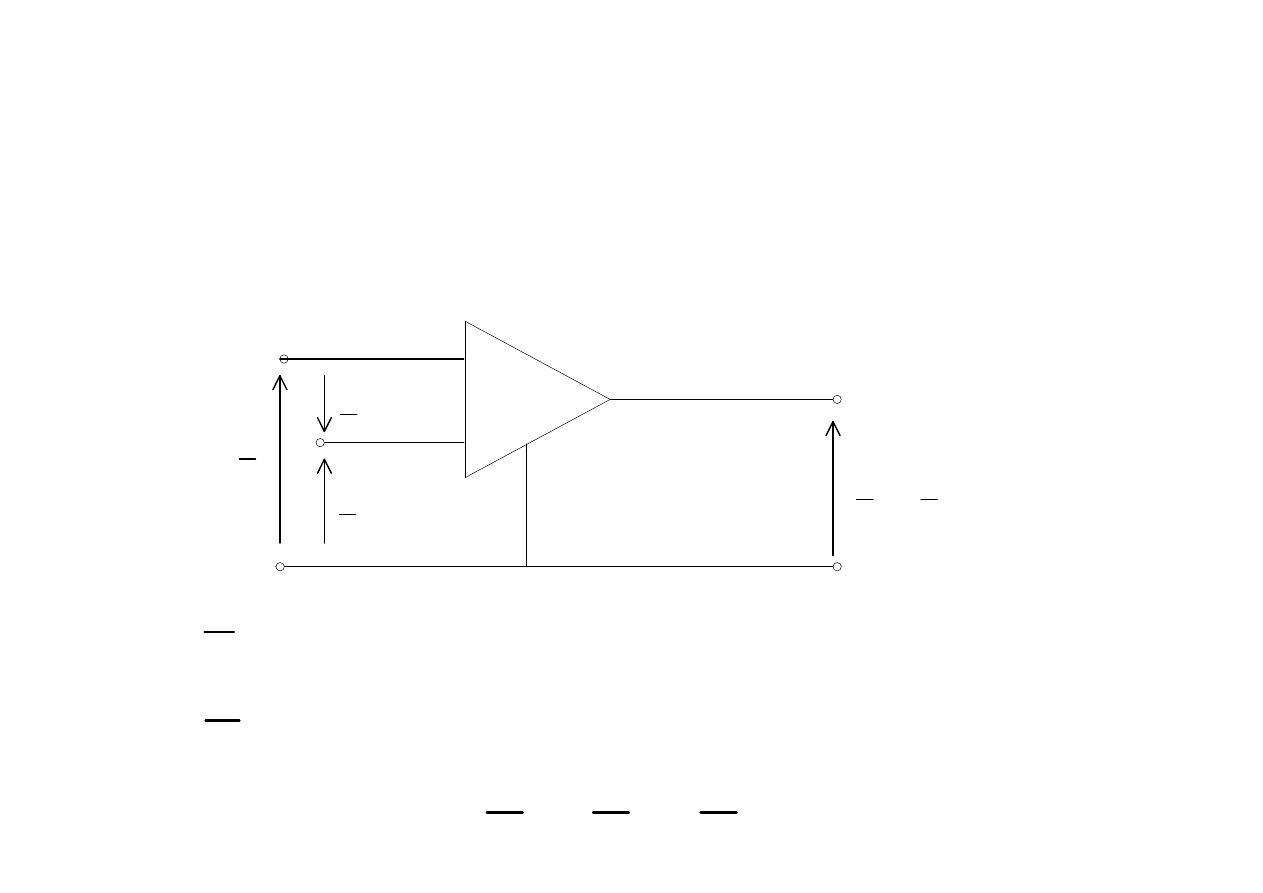
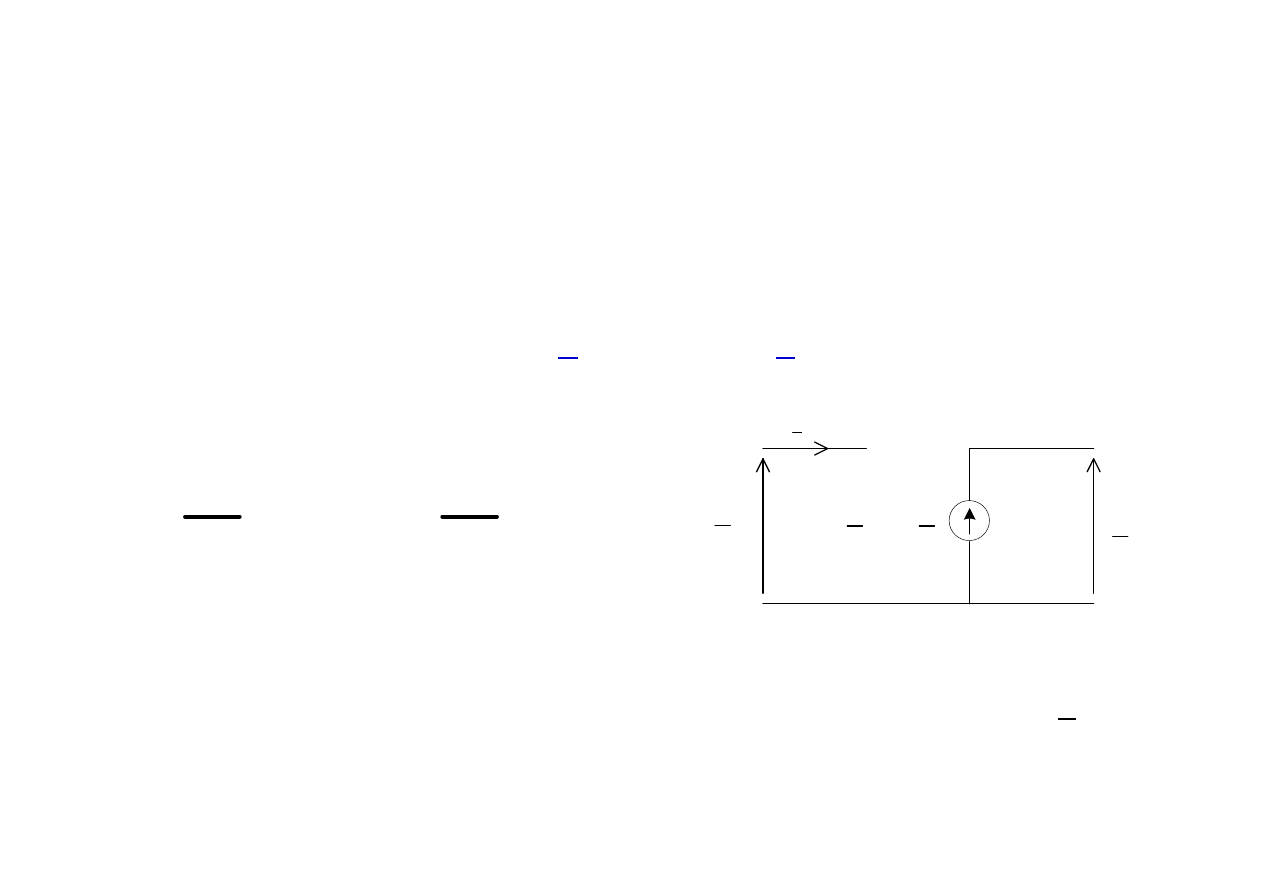
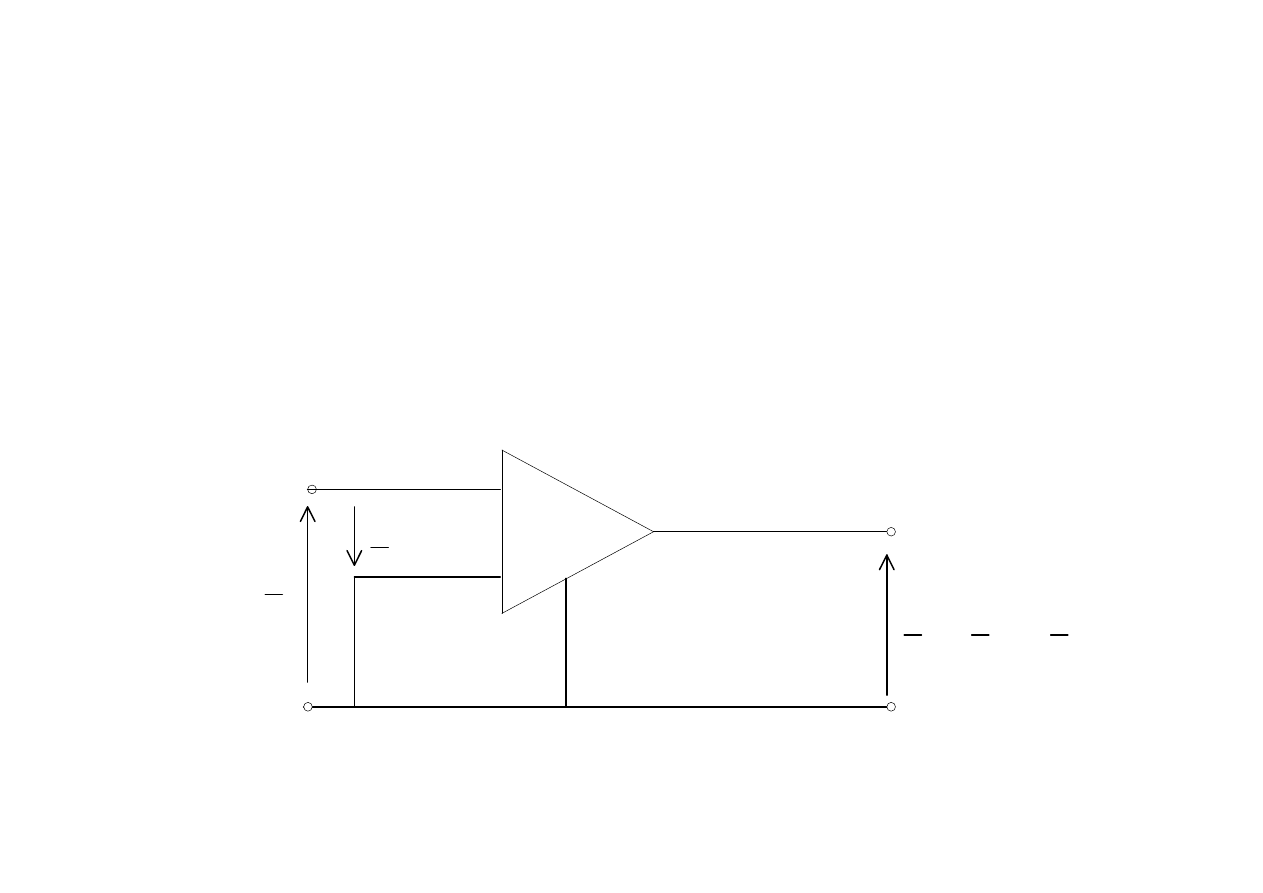
wzmacniacz operacyjny ( idealny )

Jest szczególnym przypadkiem wzmacniacza napięciowego

1

U

2

1

U

kU

=

k

+

_

U

+

U

−

jest napięciem wejścia nieodwracającego,

jest napięciem wejścia odwracającego wzmacniacza

U

+

U

−

1

U

U

U

+

−

=

−

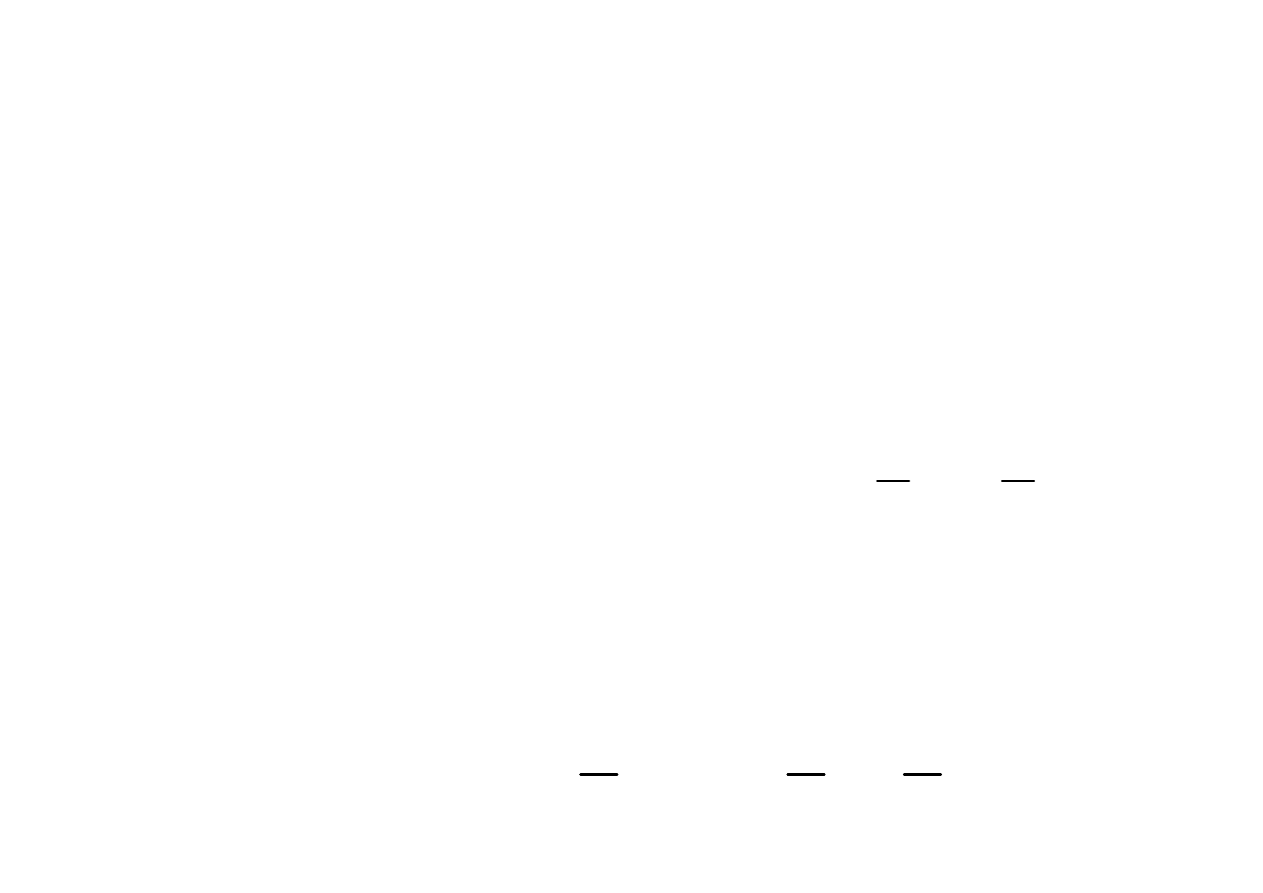
wzmacniacz operacyjny

Idealny wzmacniacz operacyjny posiada:

-

impedancję wejściową

równą nieskończoności,

-

napięcie wyjściowe

w zakresie pracy liniowej jest

proporcjonalne

do wejściowego napięcia różnicowego

,

2

1

U

kU

=

Przy założeniu idealności wzmacniacza operacyjnego wartość wzmocnienia

k

dąży do nieskończoności

.

Napięcie wyjściowe wzmacniacza może przyjmować jedynie wartości

skończone, to napięcie różnicowe w idealnym wzmacniaczu operacyjnym

musi być równe zeru.

1

0

U

U

U

+

−

= →

=

wzmacniacz operacyjny

Idealny wzmacniacz operacyjny charakteryzuje się:

-

nieskończoną wartością wzmocnienia napięciowego,

-

zerową wartością impedancji wyjściowej,

-

nieskończoną impedancją wejściowa,

- spełnia wszystkie powyższe cechy dla zakresu częstotliwości

od zera do nieskończoności.

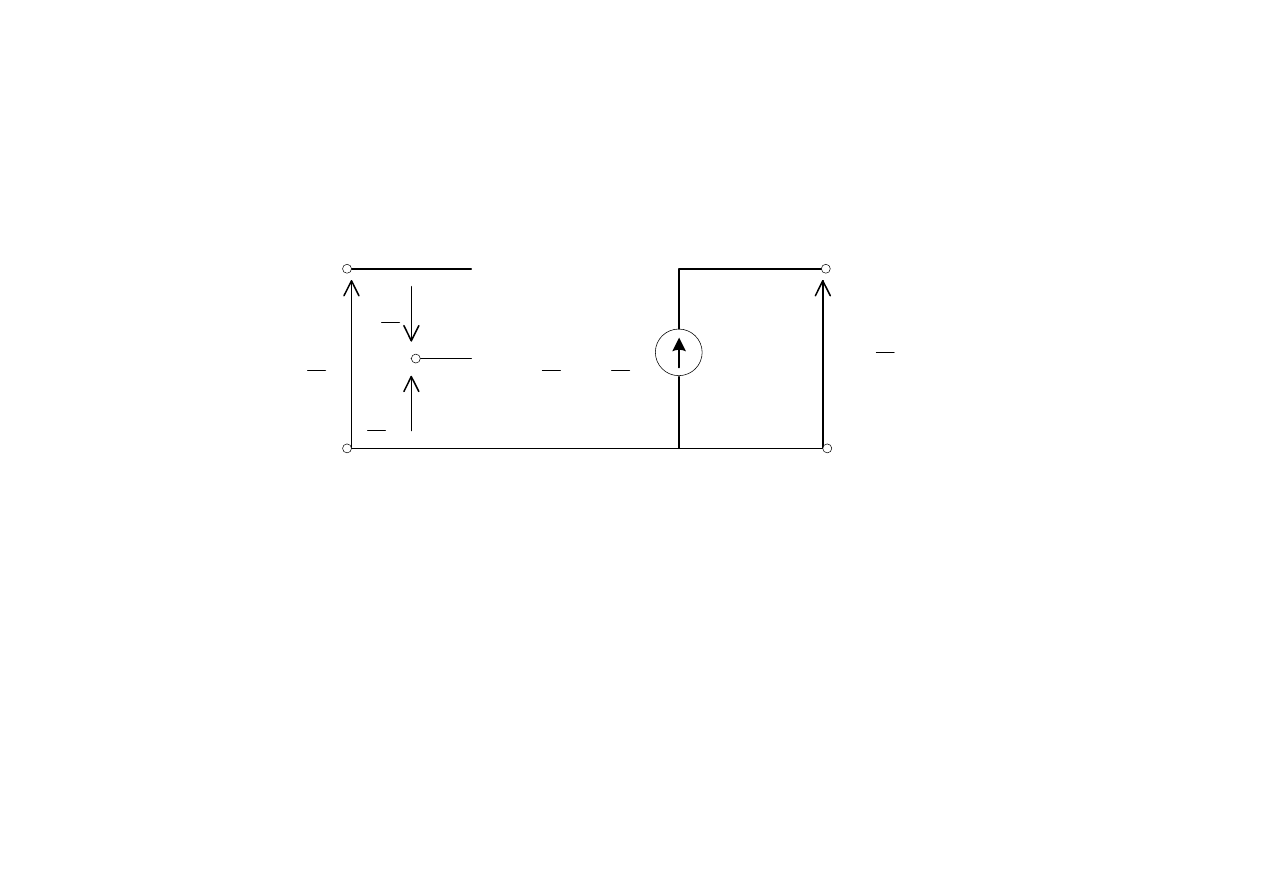
wzmacniacz operacyjny

Schemat zastępczy idealnego wzmacniacza operacyjnego

2

1

U

kU

=

2

U

U

−

1

U

U

+

Rzeczywisty wzmacniacz operacyjny wykonany w technologii scalonej ma:

- skończoną wartość impedancji wejściowej (bardzo dużą , rzędu 10

8

Ω

),

- skończoną wartość wzmocnienia napięciowego ( k > 10

4

V/V ),

- wzmocnienie napięciowe jest w istotny sposób zależne od częstotliwości,

- impedancja wyjściowa wzmacniacza rzeczywistego przyjmuje wartość około

kilkadziesiąt

Ω

zamiast wartości zerowej w przypadku idealnym.

W zakresie małych częstotliwości do 10 kHz rzeczywisty wzmacniacz

operacyjny może być traktowany jako idealny.

wzmacniacz operacyjny

Wzmacniacz operacyjny dzięki swoim cechom znalazł

szerokie zastosowania w technice elektronicznej.

Wzmacniacz napięcia

1

U

2

1

U

kU

kU

−

=

= −

k

+

_

U

−

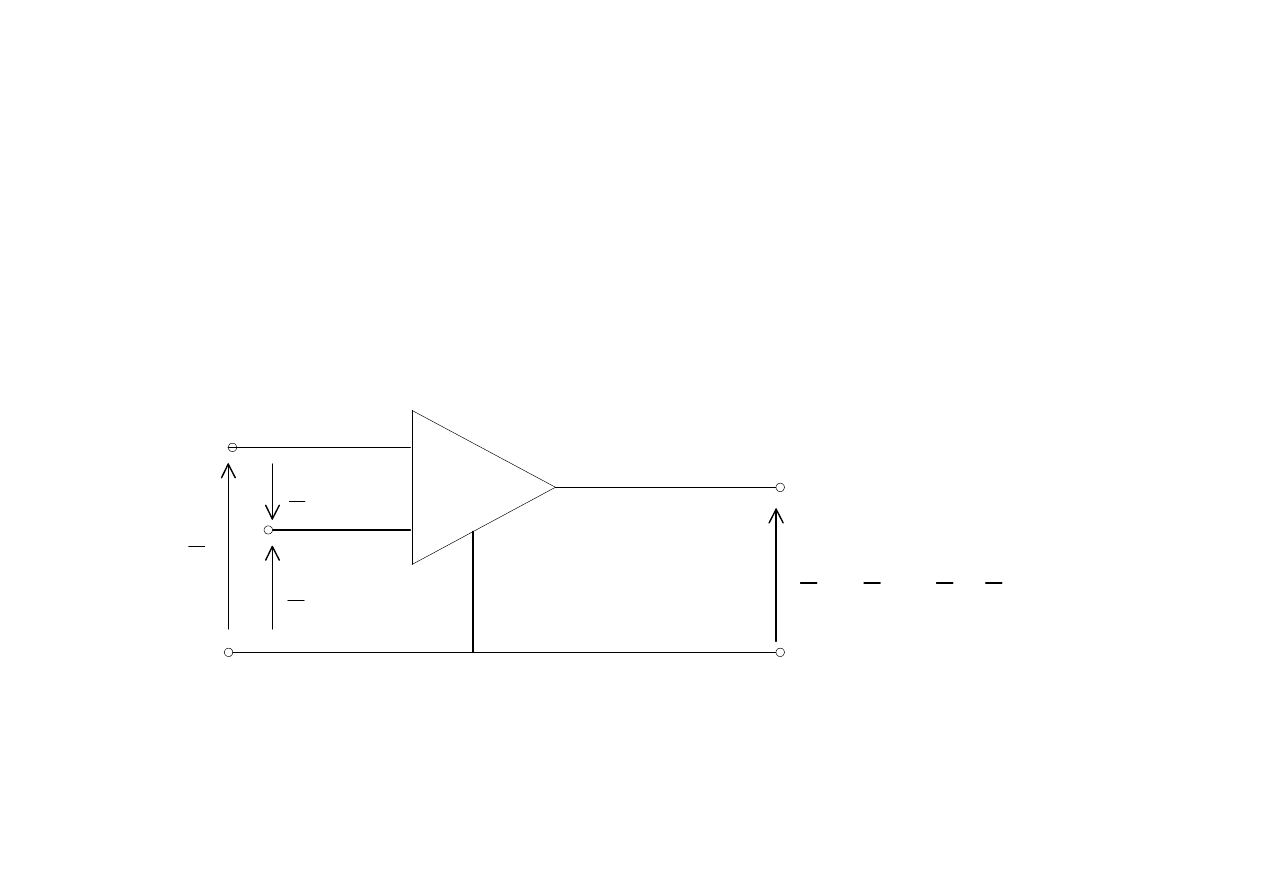
wzmacniacz operacyjny

Wzmacniacz różnicowy

1

U

(

)

2

1

U

kU

k U

U

+

−

=

=

−

k

+

_

U

+

U

−

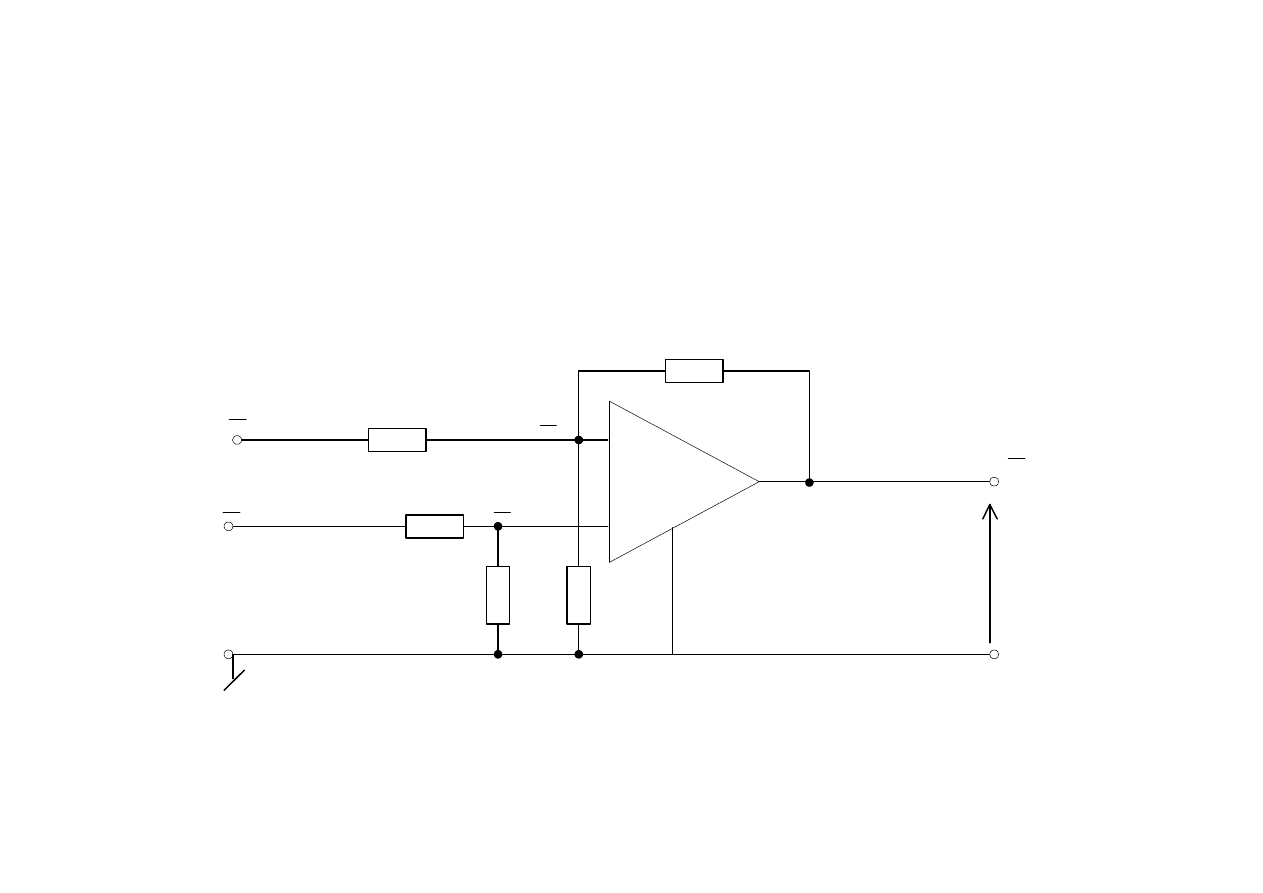
wzmacniacz operacyjny

sumator

3

U

k

+

_

U

−

U

+

1

R

2

R

s

R

0

R

+

0

R

−

2

U

1

U

wzmacniacz operacyjny

z PRK

(

)

(

)

(

)

2

2

0

1

3

1

0

1

1

1

1

1

s

U

U

U

R

R

U

U

U

U

U

R

R

R

+

+

+

−

−

−

−

−

=

−

=

+

−

wzmacniacz idealny to k=∞, to

rozwiązując

układ równań otrzymamy, że

(

)

0

U

U

U

U

+

−

+

−

−

=

⇒

=

0

2

2

0

R

U

U

R

R

+

+

+

=

+

wzmacniacz operacyjny

oraz

(

)

0

1

0

0

1

3

2

1

1

0

2

0

1

(

)

s

s

s

R

R R

R R

R R

R

U

U

U

R R R

R

R

+

−

−

−

+

+

+

=

−

+

czyli

3

1

2

1

2

U

k U

k U

=

+

sygnał wyjściowy jest sumą ważoną sygnałów wejściowych

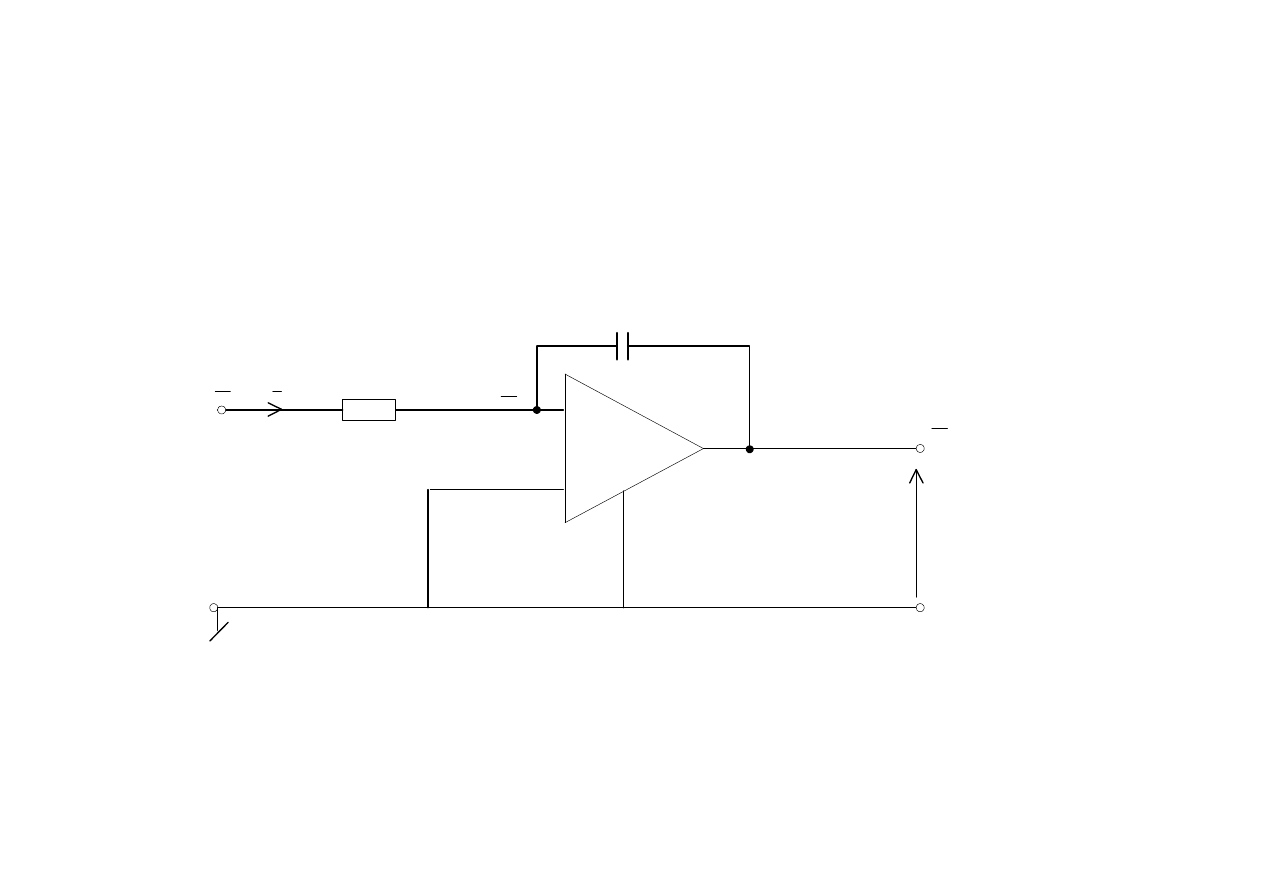
wzmacniacz operacyjny

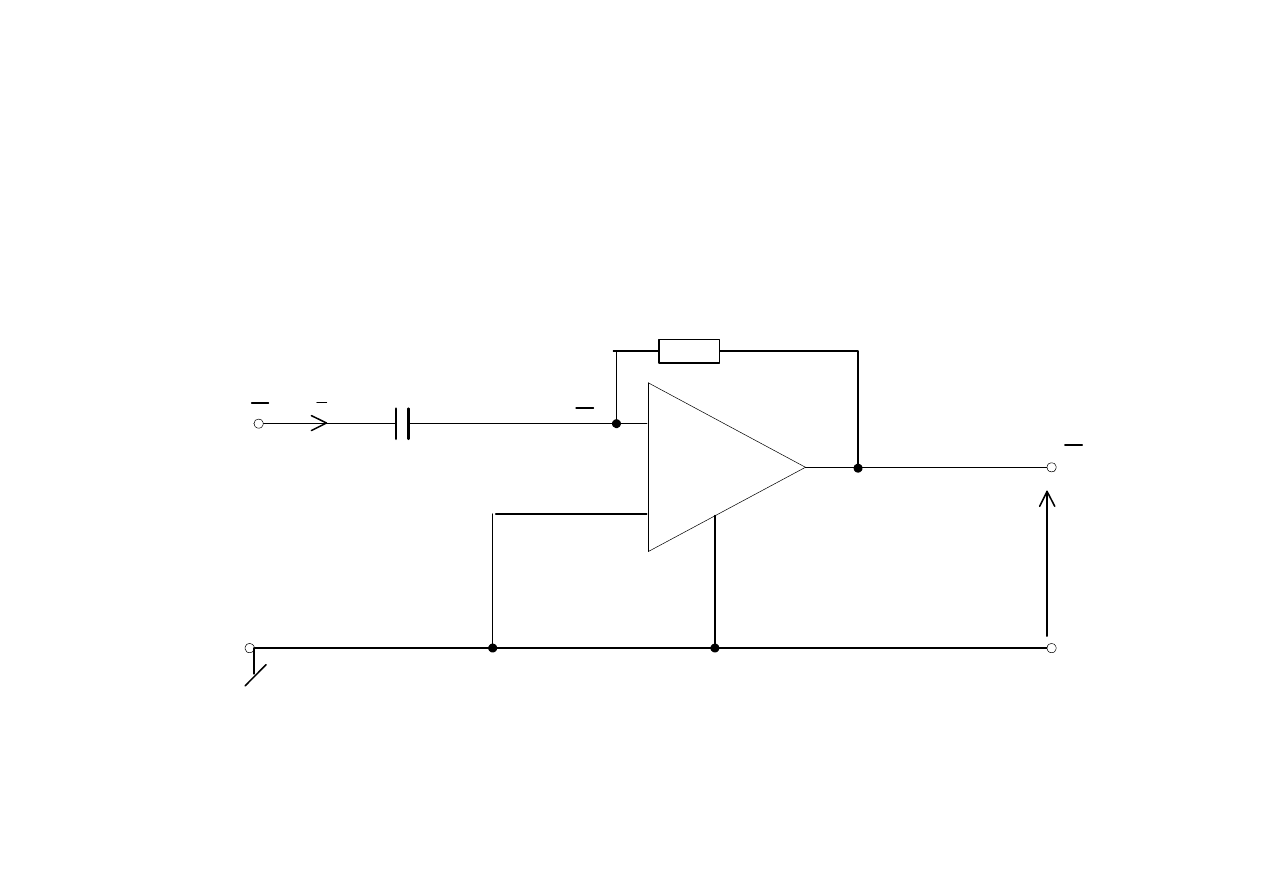
Układ całkujący

2

U

k

+

_

U

−

1

U

R

C

I

wzmacniacz idealny → wzmacniacz nie pobiera prądu→ napięcie różnicowe

jest równe zeru, otrzymuje się następujące równania opisujące układ

wzmacniacz operacyjny

1

U

RI

=

i

2

1

U

j

I

C

ω

=

transmitancja napięciowa układu równa się

2

1

1

U

T

U

j RC

ω

=

= −

a to realizuje operację całkowania sygnału

u

1

(t) ze współczynnikiem k=-1/RC

wzmacniacz operacyjny

Układ różniczkujący

2

U

k

+

_

U

−

1

U

R

C

I

wzmacniacz idealny → wzmacniacz nie pobiera prądu→ napięcie różnicowe

jest równe zeru,otrzymuje się następujące równania opisujące układ

wzmacniacz operacyjny

1

1

U

j

I

C

ω

= −

i

2

U

RI

= −

i

Transmitancja napięciowa układu równa się

2

1

U

T

j RC

U

ω

=

= −

a to realizuje operację różniczkowania sygnału u

1

(t)

ze współczynnikiem k= - RC

Filtry częstotliwościowe

Filtr przepuszcza sygnał bez tłumienia w określonym paśmie

częstotliwości a tłumi poza tym pasmem.

- bez tłumienia –

pasmo przepustowe ( przepuszczania )

- tłumione –

pasmo tłumieniowe ( tłumienia ) lub zaporowe

te pasma dzieli częstotliwość graniczna (odcięcia ) -

f

g

Filtry częstotliwościowe

0

g

f

f

0

g

f

f

0

1

g

f

f

2

g

f

Rozróżniamy filtry:

dolnoprzepustowe

górnoprzepustowe

0

1

g

f

f

2

g

f

pasmowe

zaporowe

Filtry częstotliwościowe

Szeroką klasę filtrów stanowią czwórniki symetryczne

reaktancyjne ( z cewek i kondensatorów )

1

2

1

2

1

c

c

chg

Z shg

U

U

shg

chg

I

I

Z

















=





























1

2

1

2

U

A

B

U

I

C

D

I







 



=







 









 



(

)

2

(cos

sin )

(

cos

s

cos

sin )

2

cos

sin

2

2

in

a jb

a jb

a

b

a

b

a

b

e

e

A

chg

ch a

jb

e

a

j

b

e

a

j

b

e

e

e

e

b

j

cha

b

jsha

b

b

A

+

− −

−

−

−

+

=

=

+

=

=

+

+

−

=

=

+

−

+

+

=

=

=

=

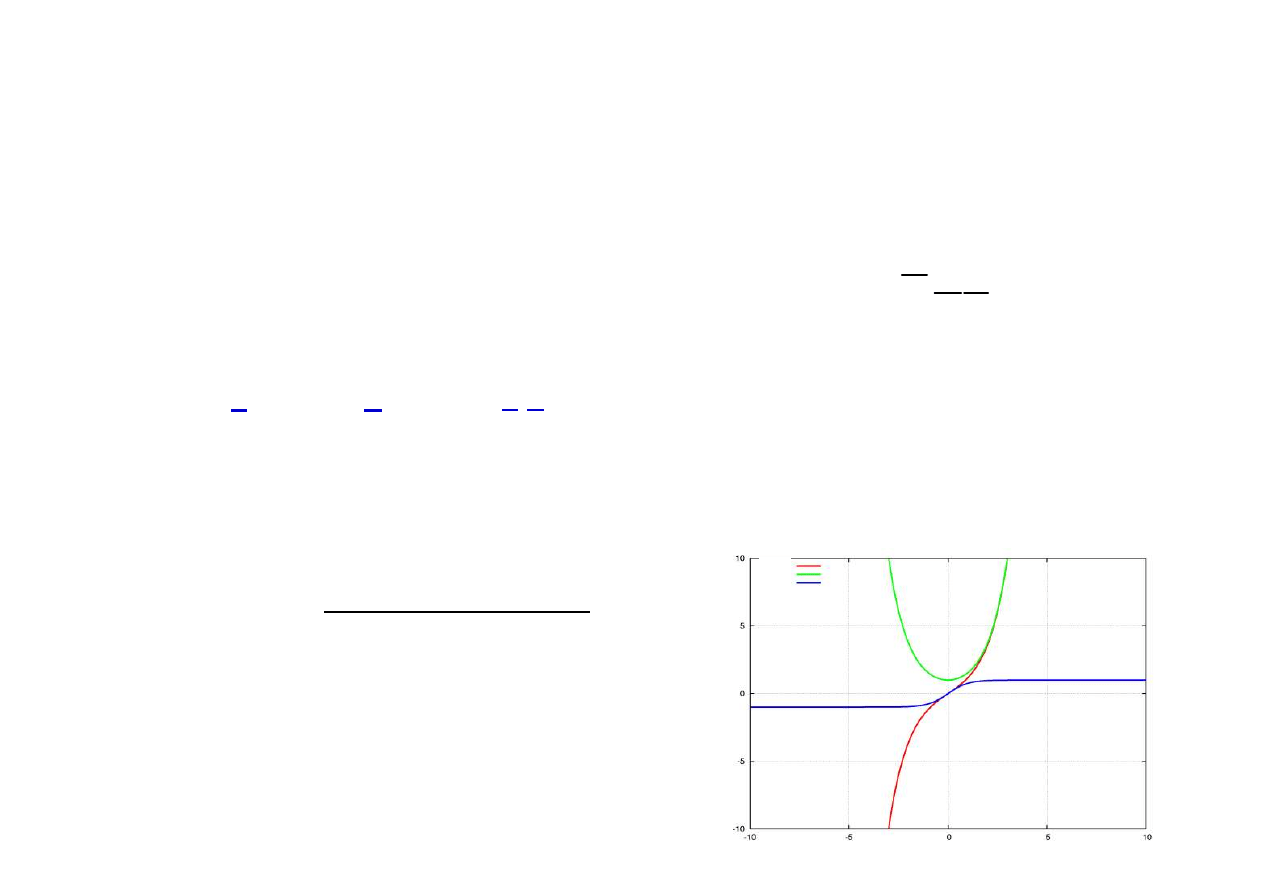
Filtry częstotliwościowe

dla czwórnika symetrycznego

1

1

2

A

D

ZY

= = +

jeżeli

Z=j X

a

Y=j B

to

Z Y

= liczba

rzeczywista

a więc

A – rzeczywiste

czyli

Re{A}=ch( a) cos( b ); Im{A}= sh( a )sin( b ) = 0

pasmo przepustowe

a = 0;

sha

=0

cha

=1

A = cosb czyli -1 ≤ A ≤ 1

shg

chg

thg

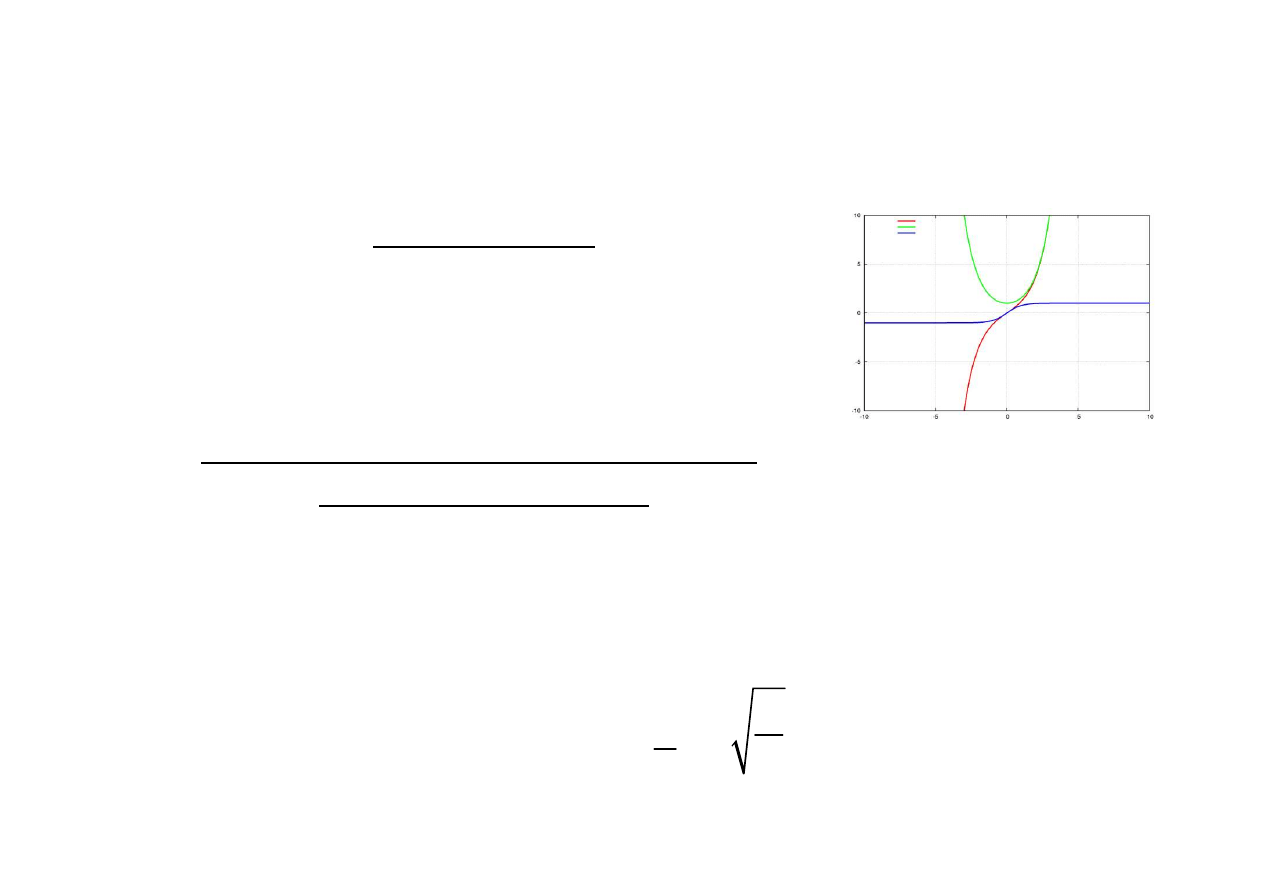
Filtry częstotliwościowe

pasmo tłumienia

Im{A}= sh( a )sin( b ) = 0

a ≠ 0;

sha

≠ 0 to sinb=0 to b=kΠ ( k=±(0,1,2,3,4,5,..)

Re{A}=ch( a) cos( b );

cosb=(±1) to A=±

cha

to A

2

≥1

Charakter impedancji charakterystycznej

w paśmie przepustowym

A

2

-BC=1 i A

2

≤1

to

BC=A

2

-1 ≤ 0 a B i C są urojone

shg

chg

thg

C

B

Z

C

=

Ten warunek jest spełniony gdy B i C mają jednakowe znaki,

wówczas impedancja charakterystyczna jest liczbą rzeczywistą.

W paśmie przepustowym impedancja charakterystyczna jest liczbą rzeczywistą.

Filtry częstotliwościowe

Charakter impedancji charakterystycznej

w paśmie tłumieniowym

A

2

≥1

BC=A

2

-1≥ 0

Ten warunek jest spełniony gdy B i C mają różne znaki.

W paśmie tłumieniowym

impedancja charakterystyczna

ma charakter

albo

indukcyjny

albo

pojemnościowy

.

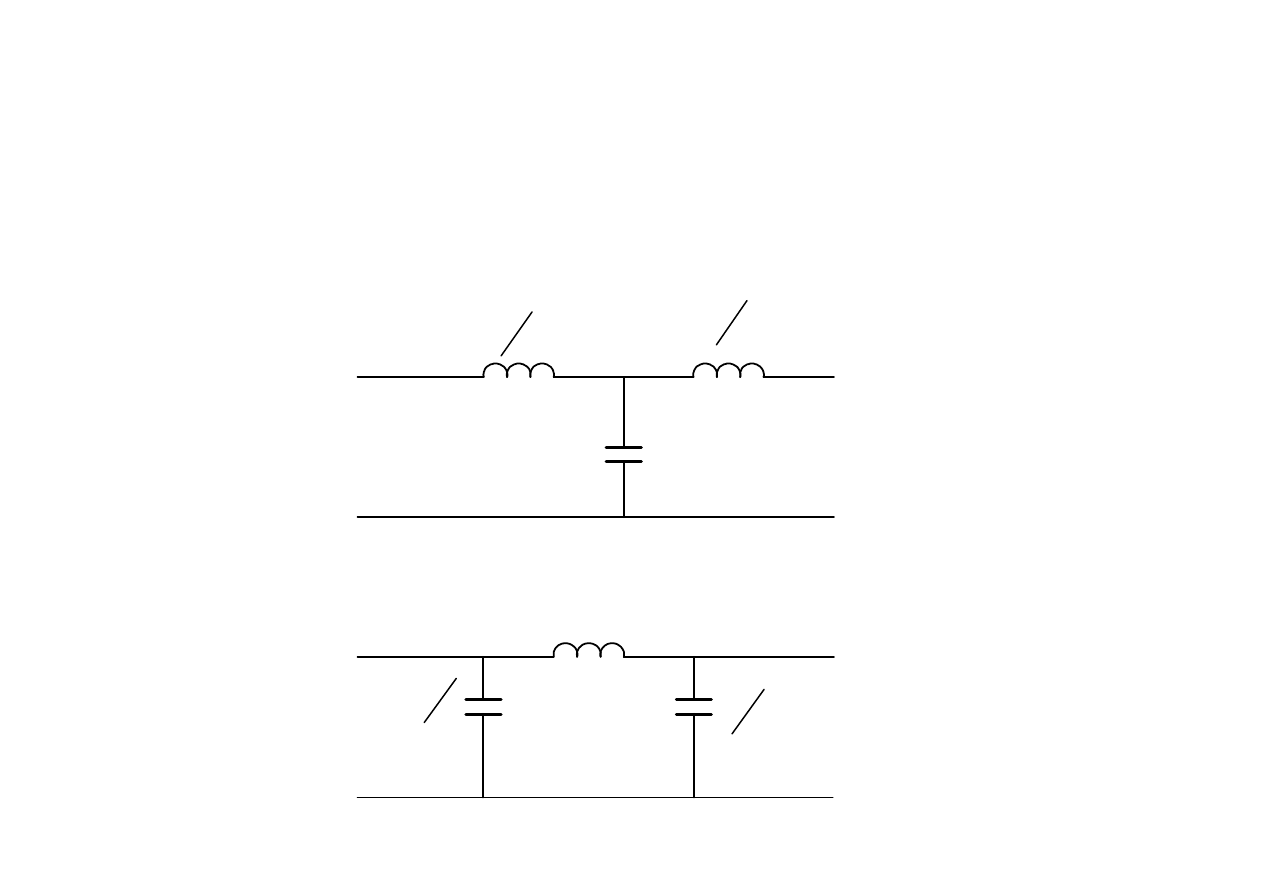
Filtr dolnoprzepustowy

Można zrealizować stosując czwórnik o schemacie

T

lub Π

2

L

2

L

C

2

C

2

C

L

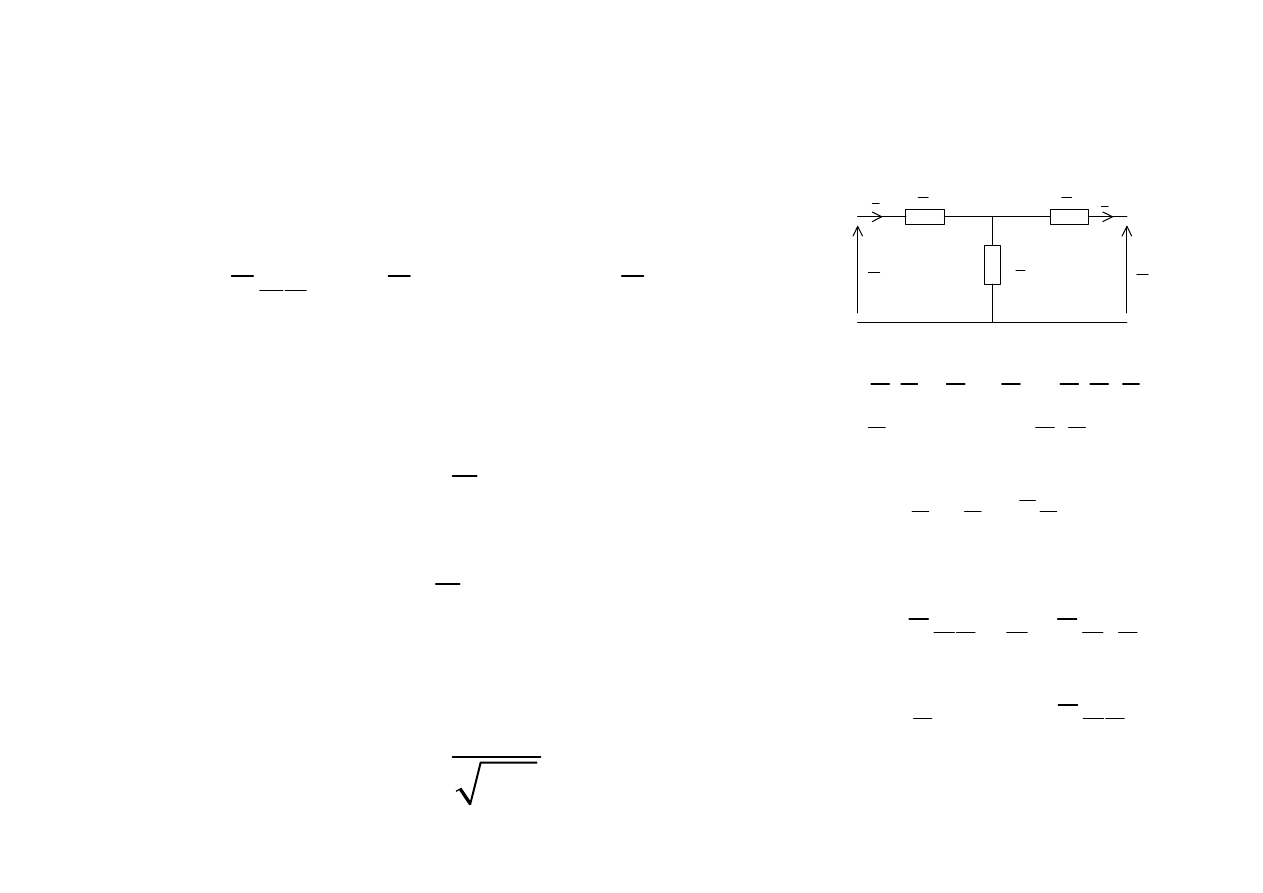
Filtr dolnoprzepustowy

2

1

1

1

1

1

1

2

2

2

A

ZY

j Lj C

LC

ω ω

ω

= +

= +

= −

2

2

2

1

1 1

1

2

1

2

0

2

0

4

2

0

LC

LC

LC

LC

ω

ω

ω

ω

− ≤ −

≤

− ≤ −

≤

≤

≤

≤ ≤

w paśmie przepustowym

a=0 → -1 ≤ A(ω) ≤ 1

1

1

2

1

2

2

1

1

Z Y

Z

Z

Z Z Y

Y

Z Y

+

+

+









+





1

Z

2

Z

Y

1

U

2

U

1

I

2

I

1

2

1

;

2

Z

Z

Z

=

=

2

1

1

1

2

4
1

1

2

ZY

Z

Z Y

Y

ZY





+

+













+









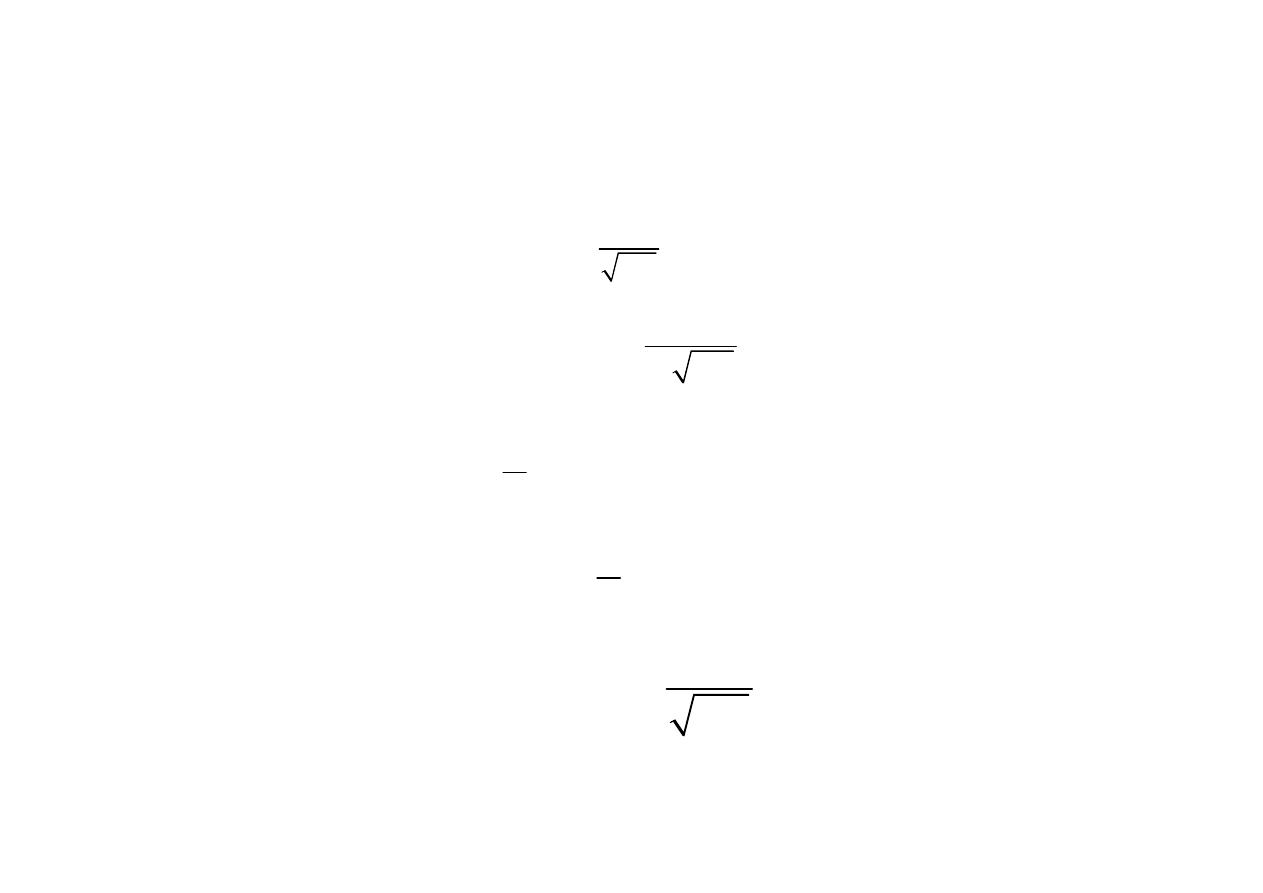
Filtr dolnoprzepustowy

2

g

LC

ω

=

1

g

f

LC

=

Π

2

1

2

1

1

cos

2

1

cos

1

2

A

LC

b

b

LC

ω

ω

−

= −

=





=

−









pulsacja graniczna

częstotliwość graniczna

dla ω=0 → b=0

2

g

b

LC

ω ω

=

=

→ = Π

Współczynnik fazowy

b

w paśmie przepustowym zmienia się od

0 do Π

,

a w paśmie tłumienia ma stałą wartość Π

Filtr dolnoprzepustowy

Współczynnik tłumienia w paśmie tłumieniowym

cos

0

cos

1

A

cha

b

b

A

cha

=

<

= Π →

Π = −

= −

( )

1

1

2

1

2

LC

a

ch

A

ch

ω

−

−





=

−

=

− +









( )

1

2

1

0

g

a

ch

LC

ω ω

−

=

=

→ =

=

dla

w miarę wzrostu pulsacji ( częstotliwości ) współczynnik tłumienia rośnie ( do ∞ )

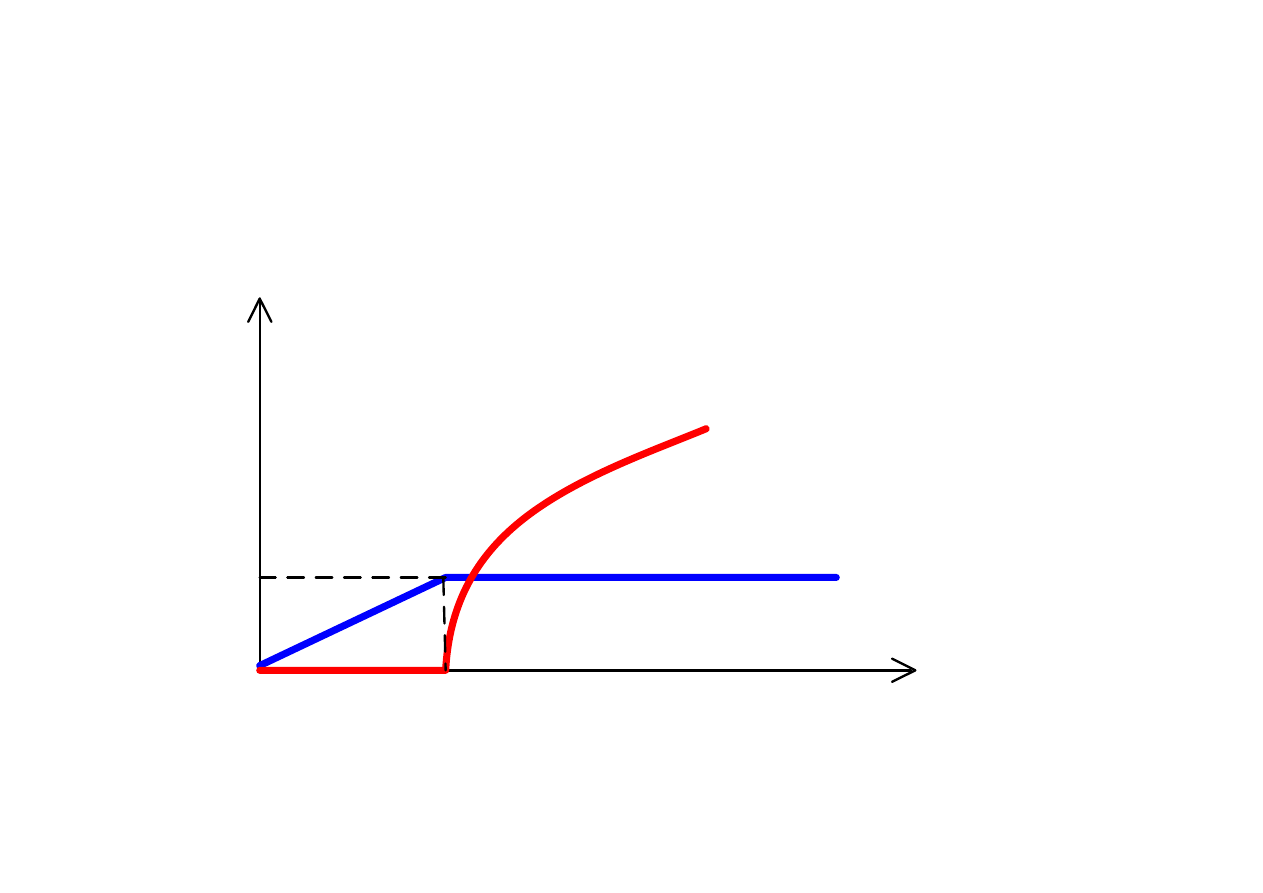
Filtr dolnoprzepustowy

ω

g

ω

Π

a

b

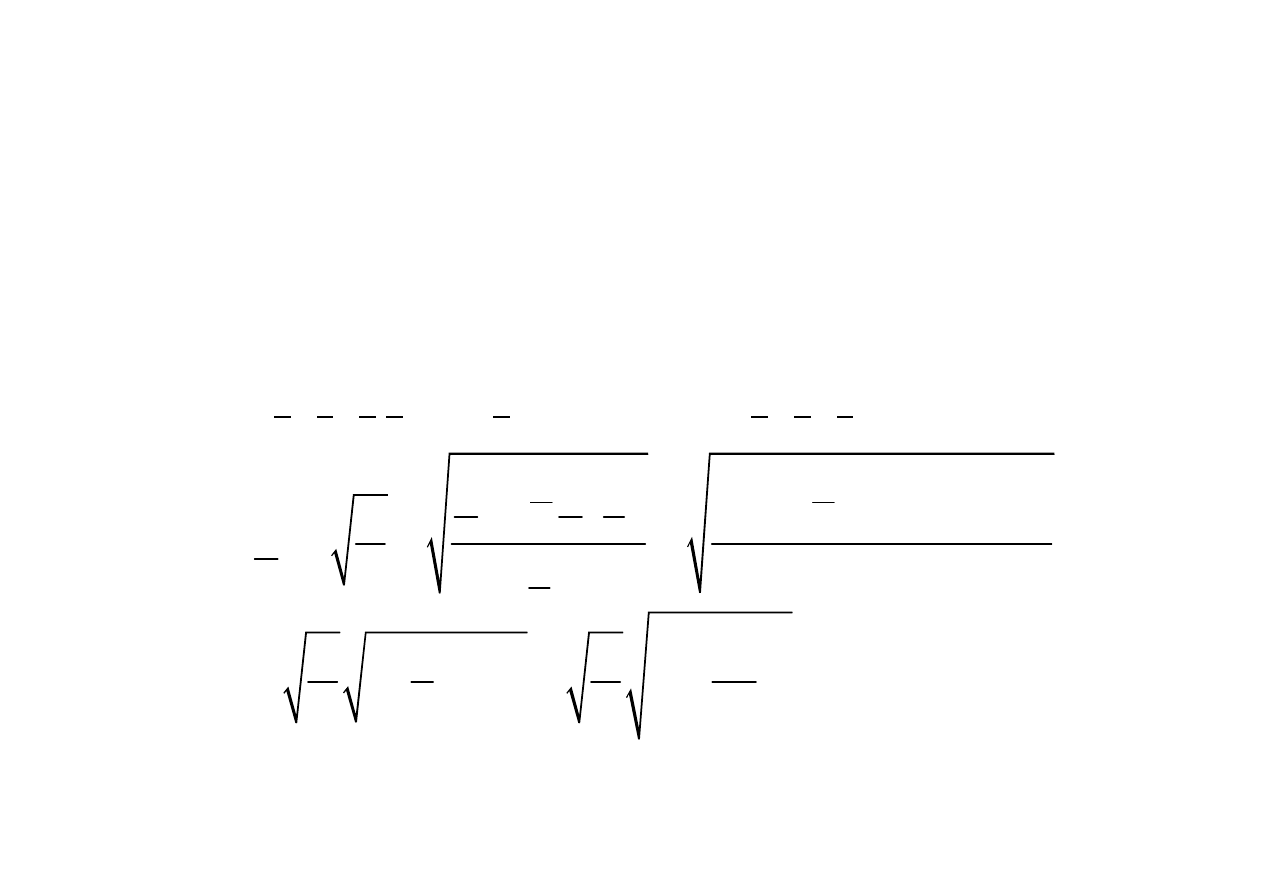
Filtr dolnoprzepustowy

Impedancja charakterystyczna

np. czwórnika typu T

- w paśmie przepustowym –rzeczywista

-

w paśmie tłumieniowym – urojona

B=Z

1

+Z

2

+Z

1

Z

2

Y; C=Y; symetryczny to Z

1

=Z

2

=Z/2

(

) (

)

2

2

2

2

1

1

4

4

1

1

1

4

T

T

T

c

T

g

Z

Z Y

j L

j L

j C

B

Z

C

Y

j C

L

L

LC

C

C

ω

ω

ω

ω

ω

ω

ω

+

+

=

=

=

=





=

−

=

−













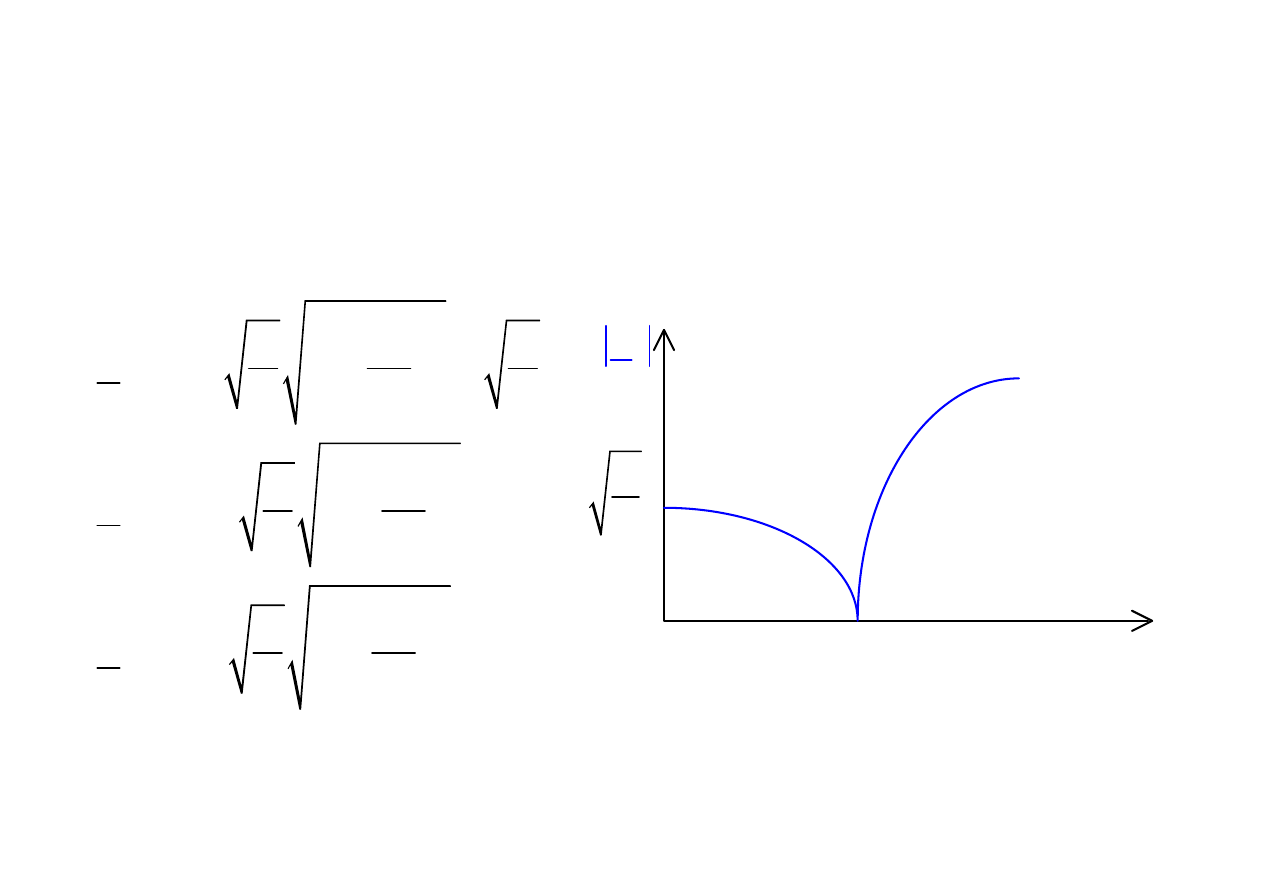
Filtr dolnoprzepustowy

2

0

2

2

lim

1

lim

1

0

lim

1

g

c

g

c

g

c

g

L

L

Z

C

C

L

Z

C

L

Z

C

ω

ω ω

ω

ω

ω

ω

ω

ω

ω

→

→

→∞





=

−

=

















=

−

=

















=

−

= ∞













c

Z

L

C

g

ω

ω

pasmo przepuszczania pasmo tłumienia

char. rzeczywisty char. indukcyjny

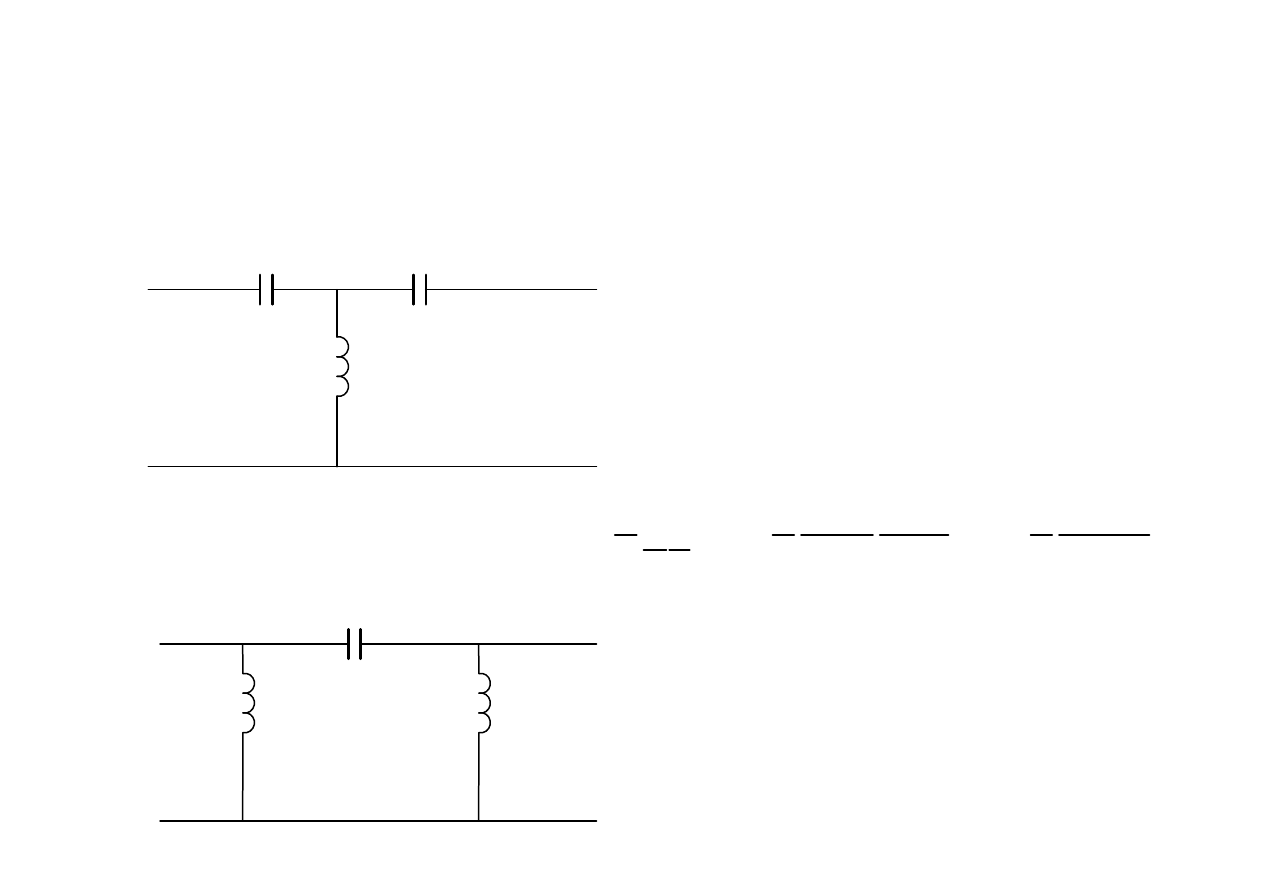
Filtr górnoprzepustowy

2C

2C

L

2L

2L

C

2

1

1

1

1

1

1

1

1

1

2

2

2

A

ZY

j C j L

LC

ω

ω

ω

= +

= +

= −

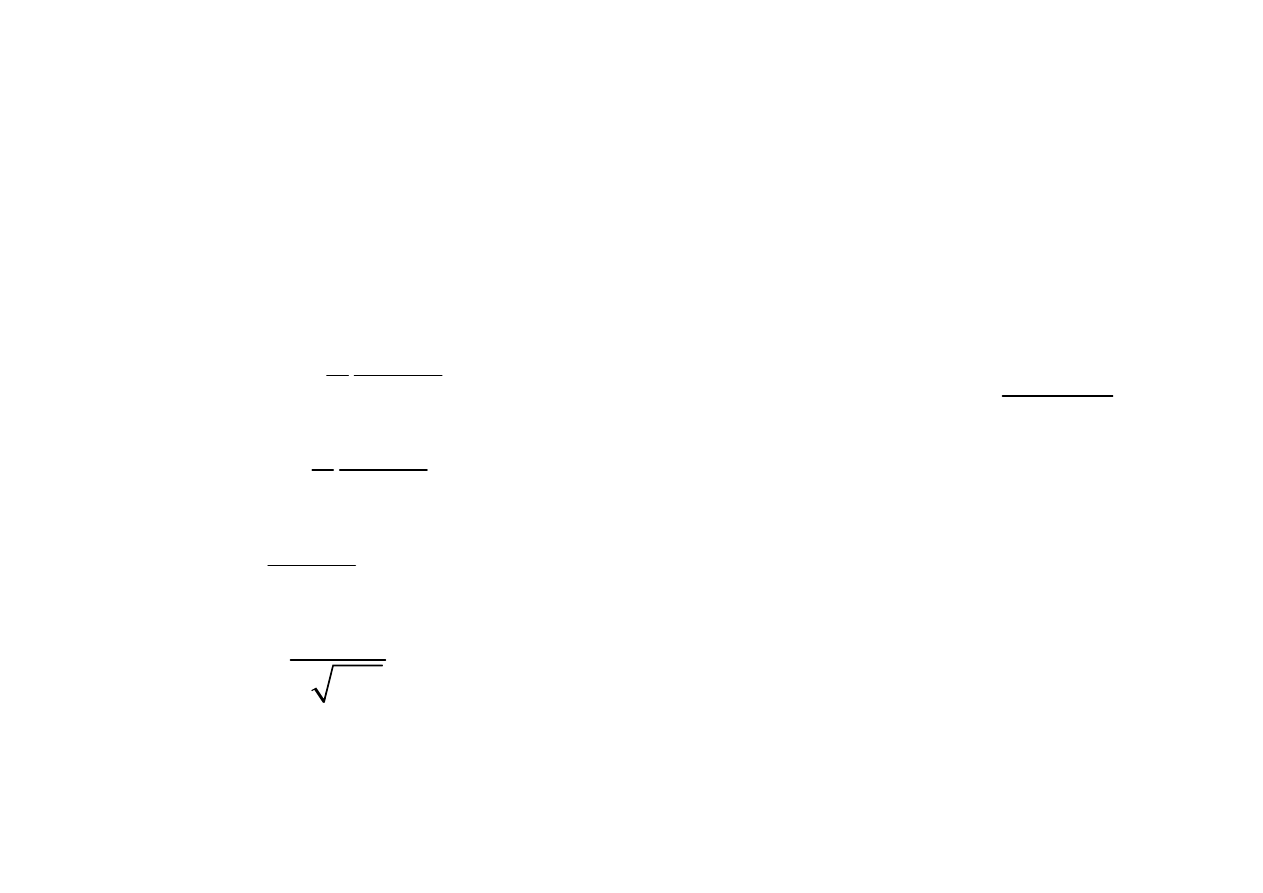
Filtr górnoprzepustowy

w paśmie przepustowym

a=0 → -1≤A(ω)≤1

2

2

2

1

1

1 1

1

2

1

1

2

0

2

1

0

4

1

2

g

LC

LC

LC

LC

ω

ω

ω

ω

ω

− ≤ −

≤

− ≤ −

≤

≤

≤

=

≤ ≤ ∞

1

2

1

cos ;

cos (1

)

2

A

b

b

LC

ω

−

=

=

−

;

0

;

0

;

g

g

b

b

b

ω
ω ω
ω ω

→ ∞

→

>

<

=

= −Π

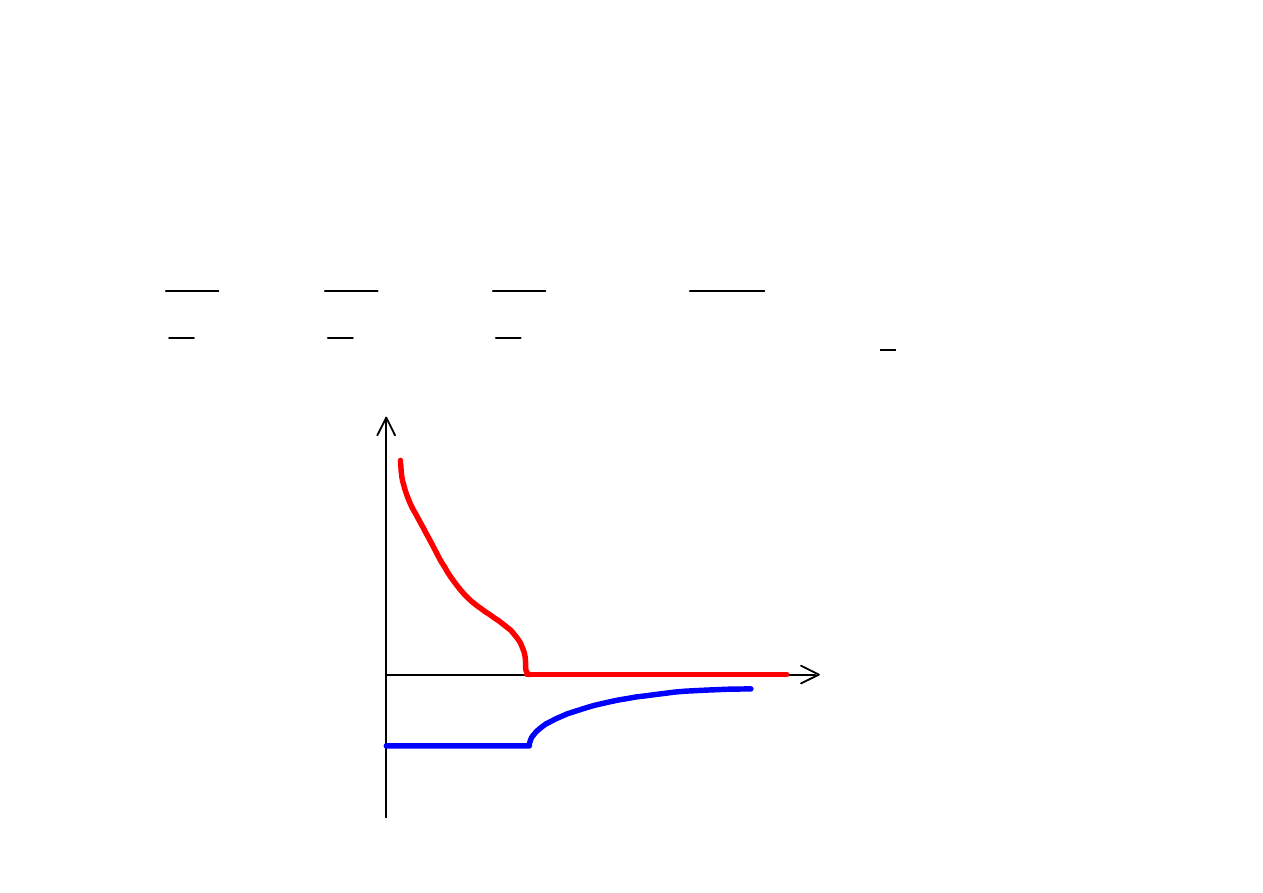
Filtr górnoprzepustowy

1

1

1

1

sin

C

C

C

C

shg

shjb

j

b

Z

Z

Z

j L

ω

=

=

=

=

sinb <0 bo b<0

to

Zc – rzeczywiste

a

b

ω

g

ω

Filtr górnoprzepustowy

w paśmie tłumionym

a≠0 ω<ωg

( )

2

2

2

2

2

1

2

1 2

cos

2

1

2

1

g

g

g

A

cha

cha

a

ch

ω
ω

ω
ω

ω
ω

−

= −

=

−Π

=

−





=

−













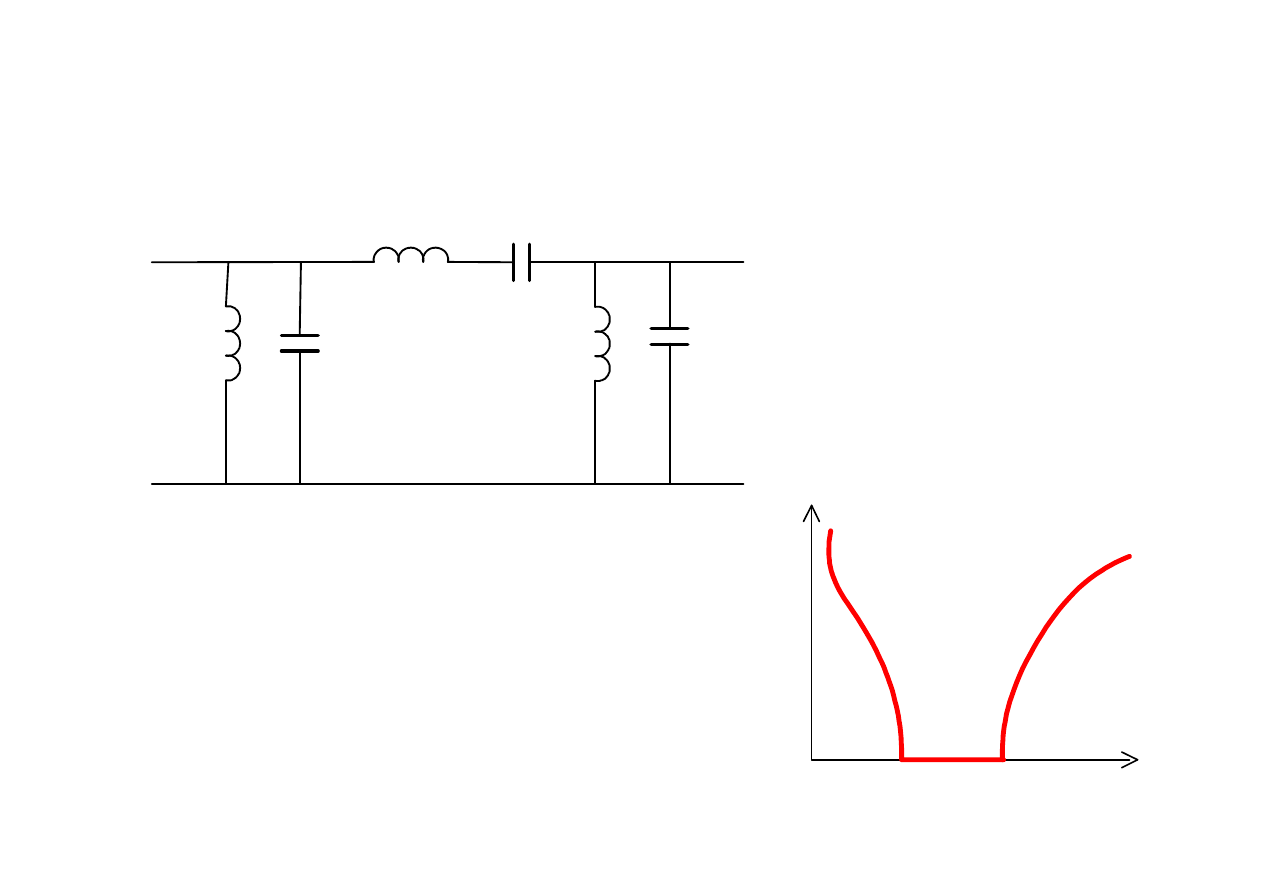
Filtr pasmowy

a

ω

1

ω

2

ω

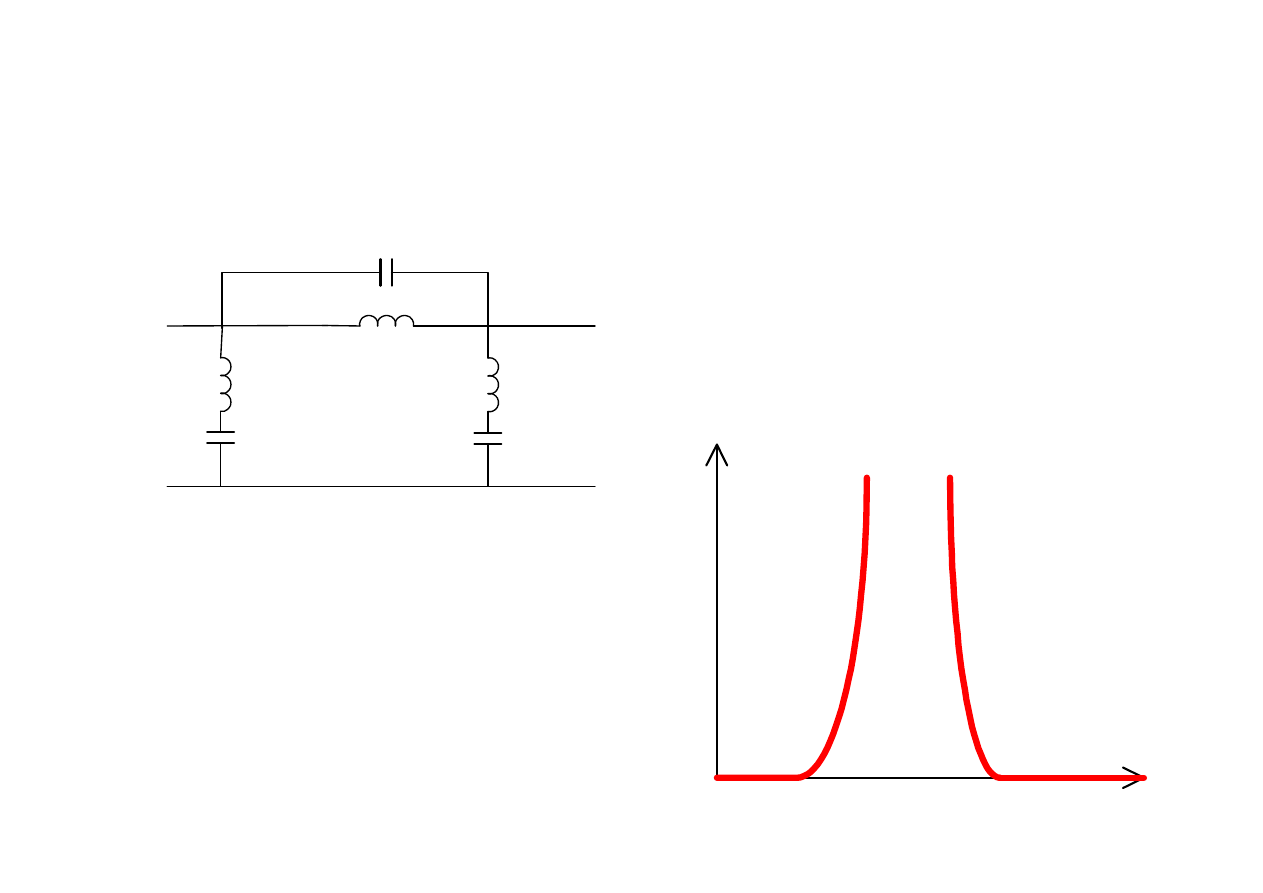
Filtr zaporowy

a

ω

1

ω

2

ω

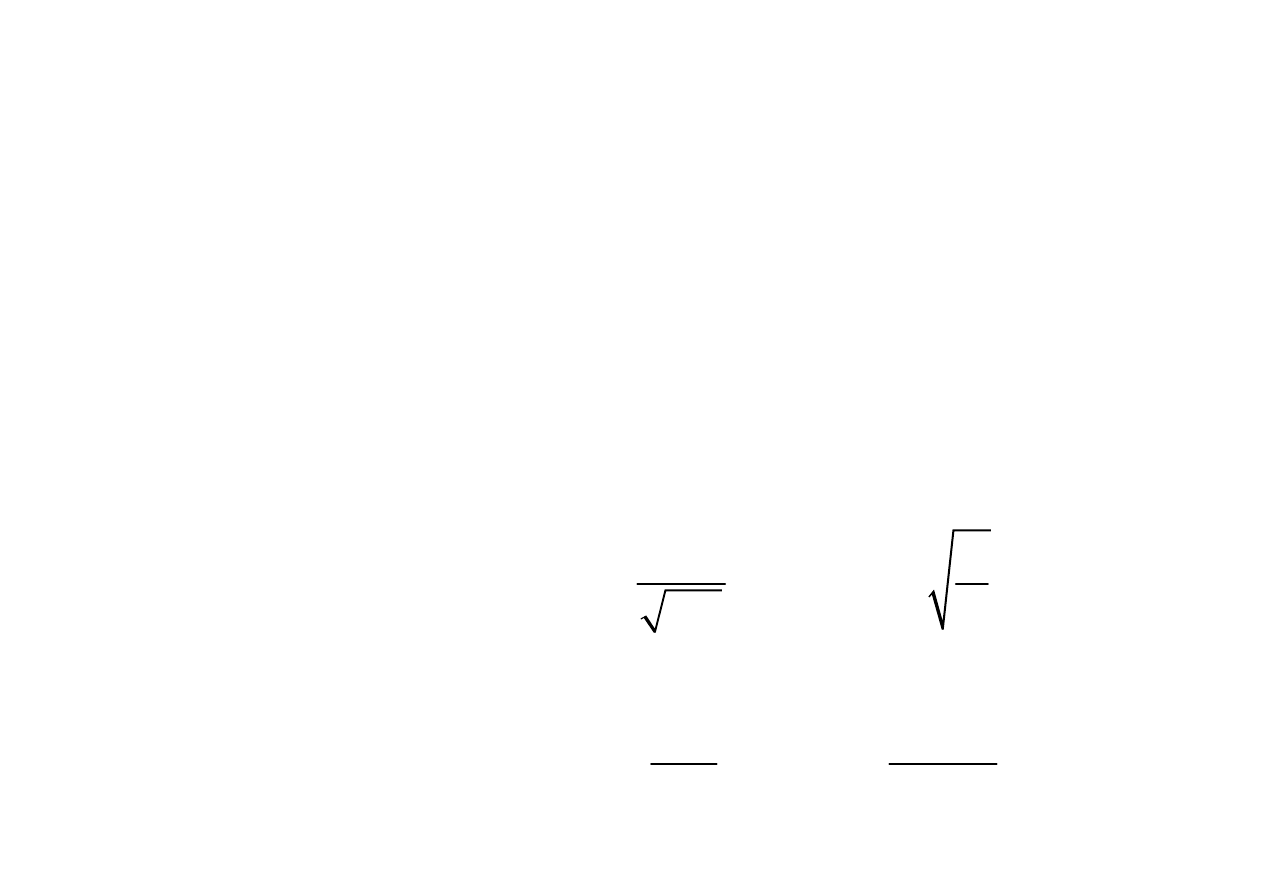
Przykład obliczania filtru

Dane:

f

g

– częstotliwość graniczna →ω

g

Z

cgr

. – impedancja graniczna

Szukamy:

L i C filtru dolnoprzepustowego

2

2

2

g

cgr

cgr

g

g

cgr

L

Z

C

LC

Z

L

C

Z

ω

ω

ω

=

=

=

=

Aktywne filtry częstotliwościowe

Przy projektowaniu filtrów pasywnych największy kłopot sprawiają

rzeczywiste cewki

.

można to wyeliminować stosując elementy aktywne.

Np. element indukcyjny zastępuje się przez żyrator i kondensator.

Wykonuje się filtry aktywne z

- konwertorami ujemno-impedacyjnymi,

- wzmacniaczami operacyjnymi