1
Wstawka matematyczna
1. Rachunek wektorowy
siła F
prędkość v
przyspieszenie a
pęd p
wielko
ści fizyczne
wielko
ści wektorowe
wektor – uporz
ą
dkowana
para punktów (pocz
ą
tek i koniec).
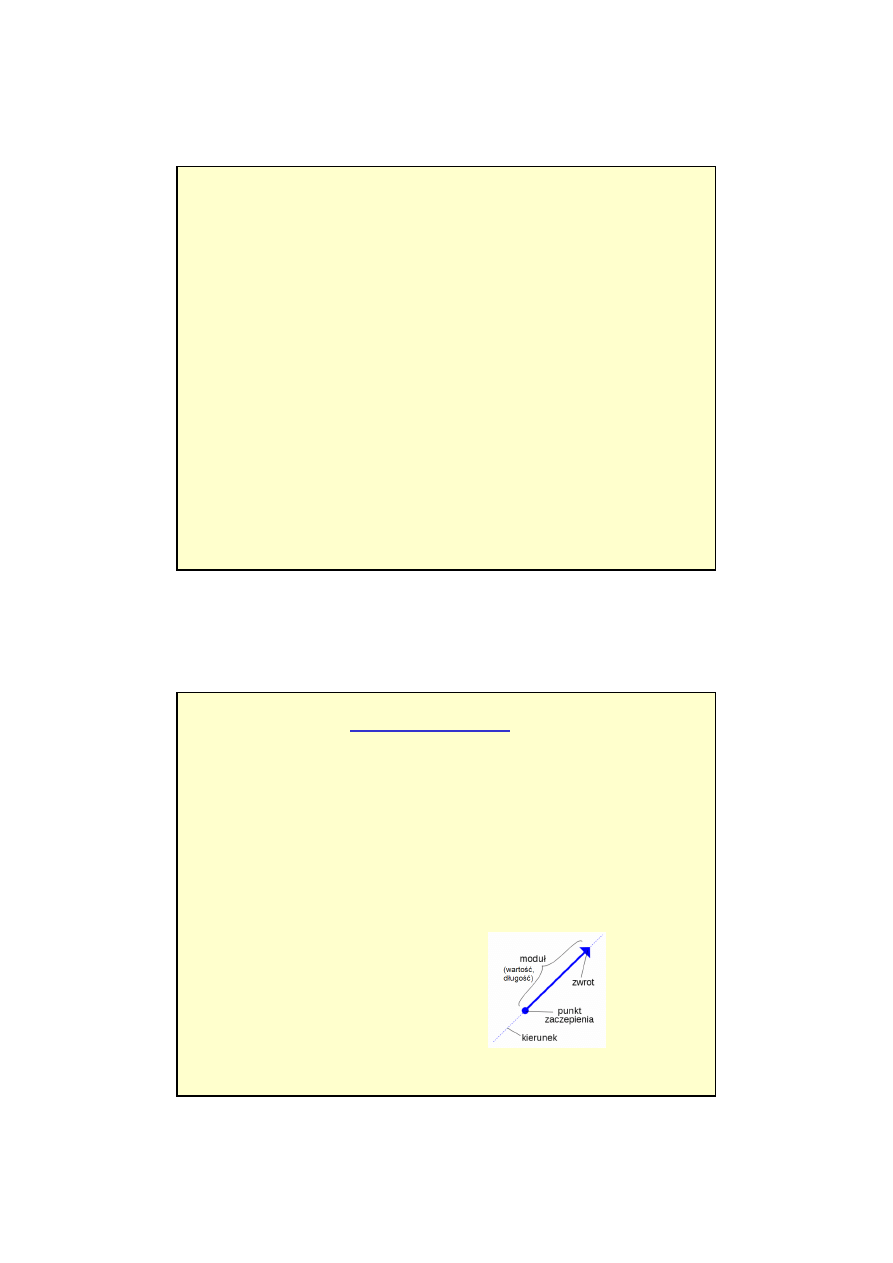
Cechy wektora:
* moduł (warto
ść
, długo
ść
)
* kierunek
* zwrot
* punkt przyło
ż
enia
masa m
czas t
energia E
temperatura T
wielko
ści skalarne
skalary – do okre
ś
lenia
wielko
ś
ci skalarnej wystarczy
jedna liczba
2
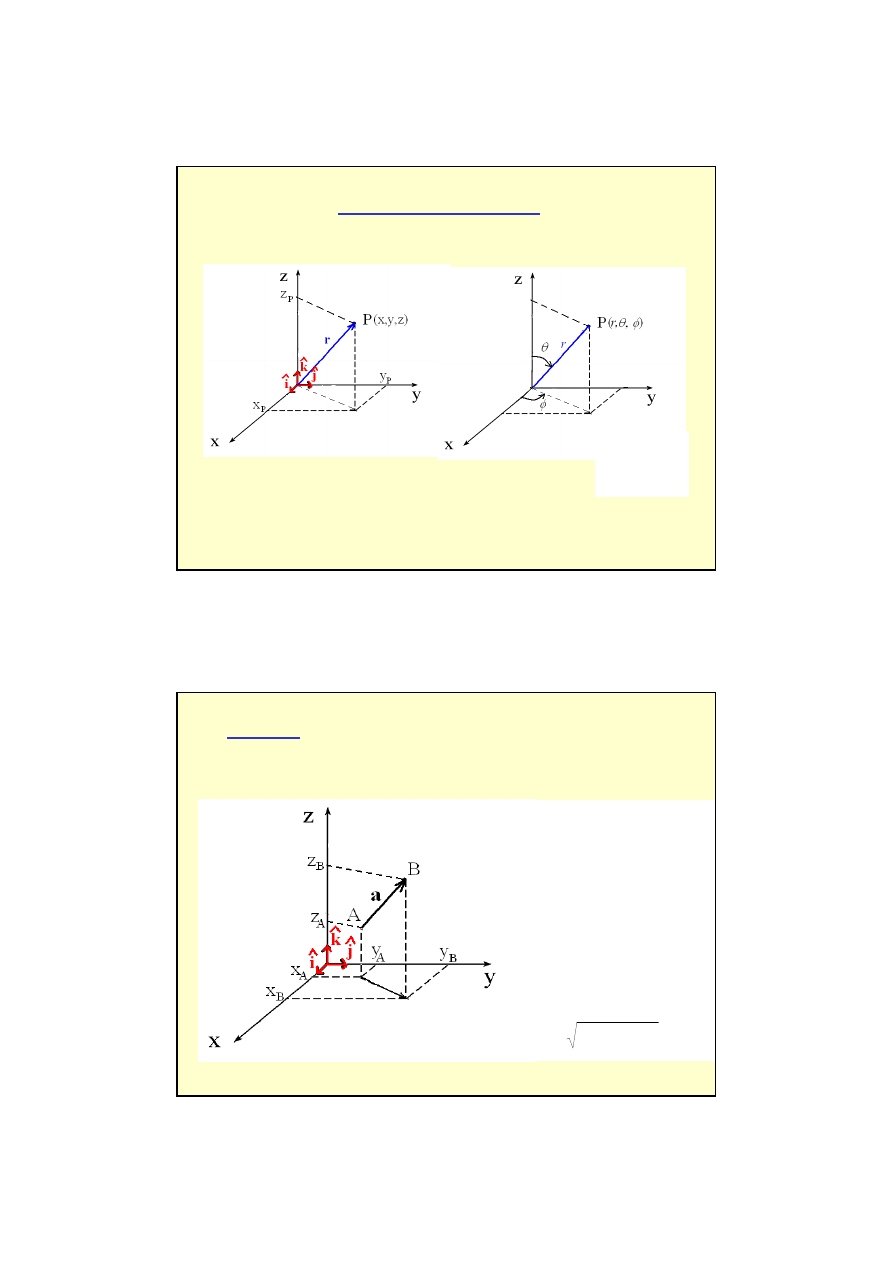
układ kartezja
ński
układ sferyczny
θ
φ
θ
φ
θ
cos
sin
sin
cos
sin
r
z
r
y
r
x
=
=
=
układy współrz
ędnych
- wersor to wektor jednostkowy
iˆ
r - wektor poło
ż
enia
położenie r
prędkość v
przyspieszenie a
pęd p
a
x
=x
B
-x
A
, a
y
=y
B
-y
A
, a
z
=z
B
-z
A
AB = a = [ a
x
, a
y
, a
z
]
wektory
długo
ść
wektora:
a
x
=b
x
, a
y
=b
y
, a
z
=b
z
.
współrz
ę
dne wektorów:
równo
ść
wektorów:
2
2
2
z
y
x
a
a
a
a
+
+
=
b = [ b
x
, b
y
, b
z
]
3
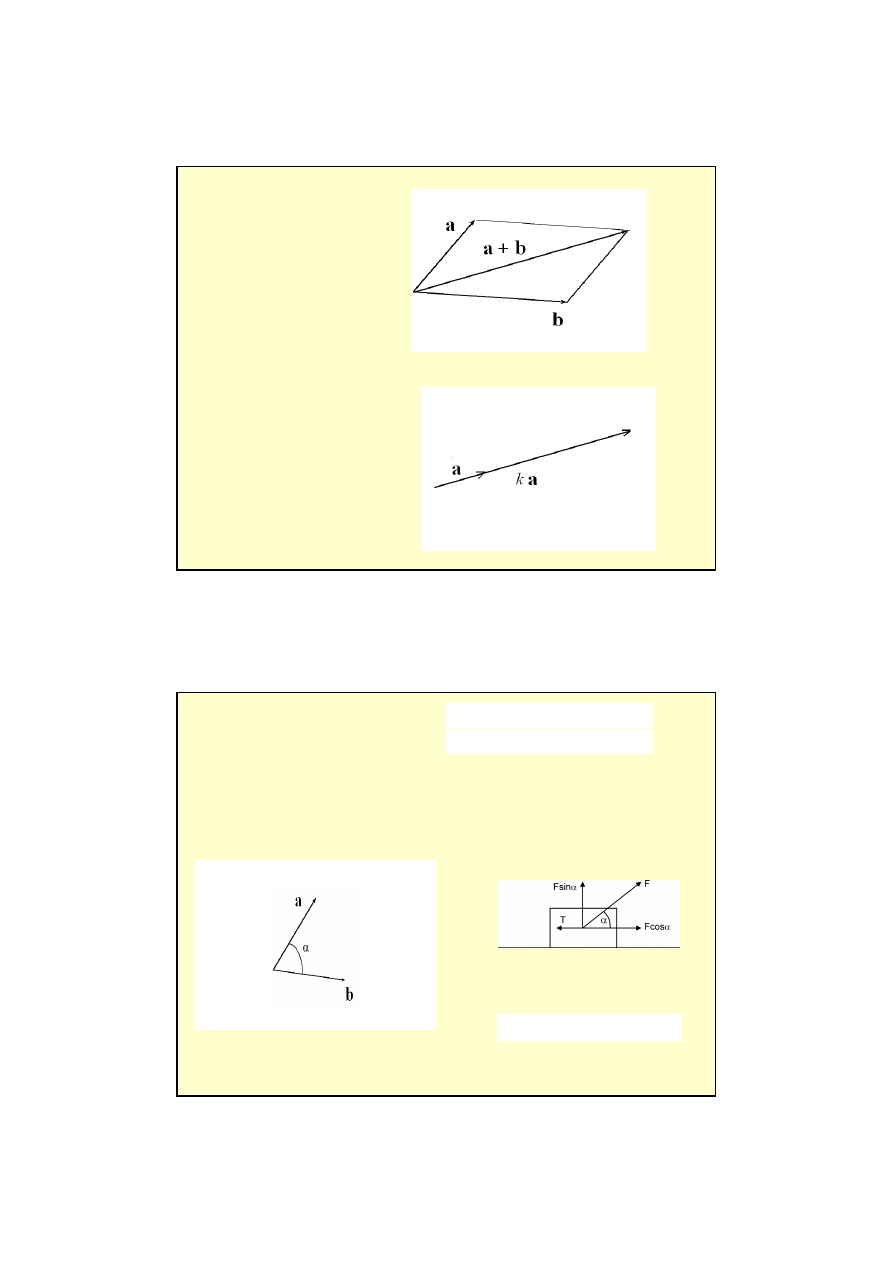
dodawanie wektorów:
mno
ż
enie wektora
przez liczb
ę
:
a + b = c
c
x
=a
x
+b
x
, c
y
=a
y
+b
y
, c
z
=a
z
+b
z
c
x
= k a
x
, c
y
= k a
y
, c
z
= k a
z
c = k a
iloczyn skalarny wektorów:
a·
·
·
·b = a b cos
α
a·
·
·
·b =a
x
b
x
+ a
y
b
y
+ a
z
b
z
a = [ a
x
, a
y
, a
z
]
b= [ b
x
, b
y
, b
z
]
α
cos
Fs
W
=
⋅
=
s
F
przykład:
u
ż
ywaj
ą
c współrz
ę
dnych:
4
k
j
i
a
ˆ
ˆ
ˆ
z
y
x
a
a
a
+
+
=
k
j
i
r
ˆ
ˆ
ˆ
P
P
P
z
y
x
+
+
=
......zapis za pomoca wersorów
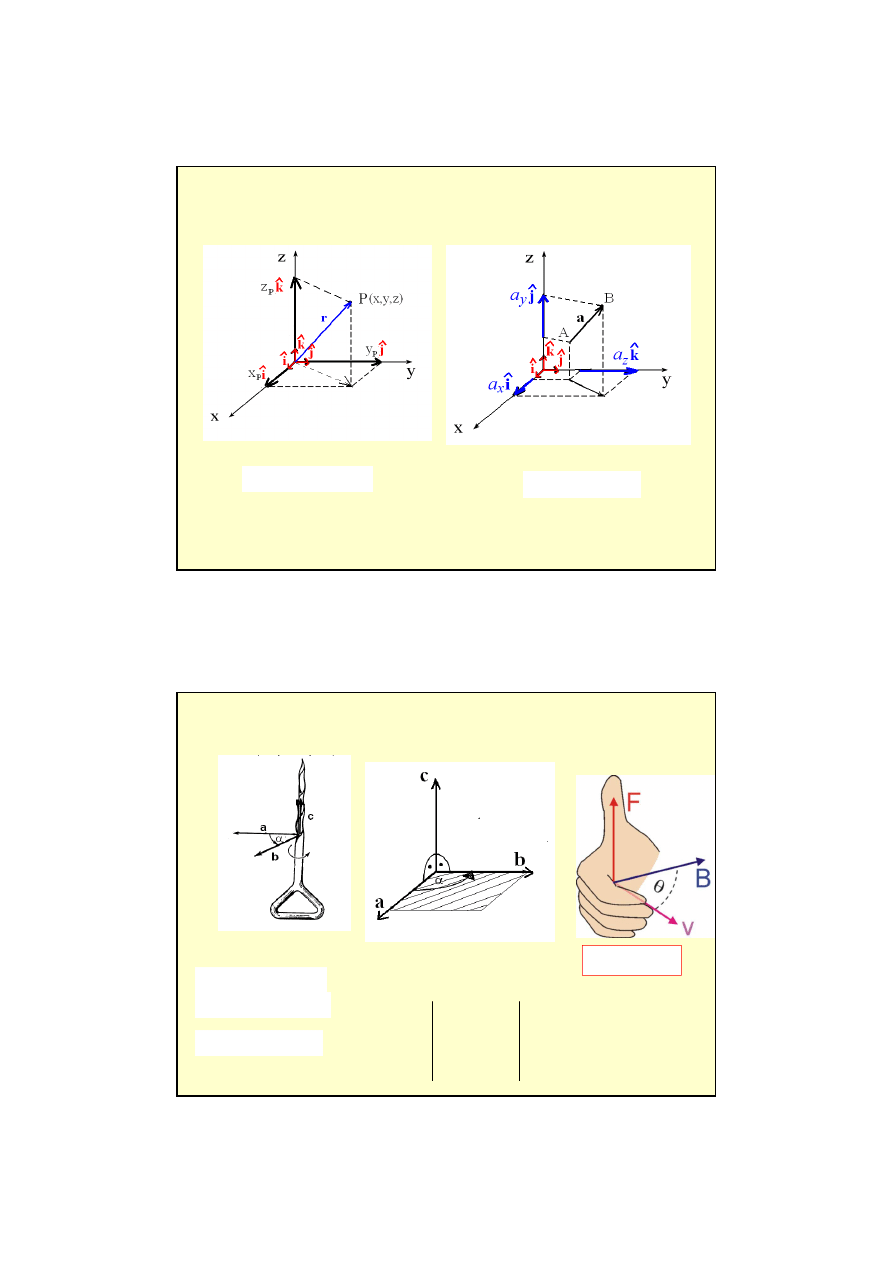
iloczyn wektorowy :
a x
x
x
x b = c
c=a b sin
α
k
j
i
c
ˆ
ˆ
ˆ
z
y
x
c
c
c
+
+
=
z
y
x
z
y
x
b
b
b
a
a
a
k
j
i
c
ˆ
ˆ
ˆ
=
a = [ a
x
, a
y
, a
z
]
b= [ b
x
, b
y
, b
z
]
c= [ c
x
, c
y
, c
z
]
B
v
F
×
=
q
przykład:
-zwrot
- warto
ść
- kierunek
Współrz
ę
dne:
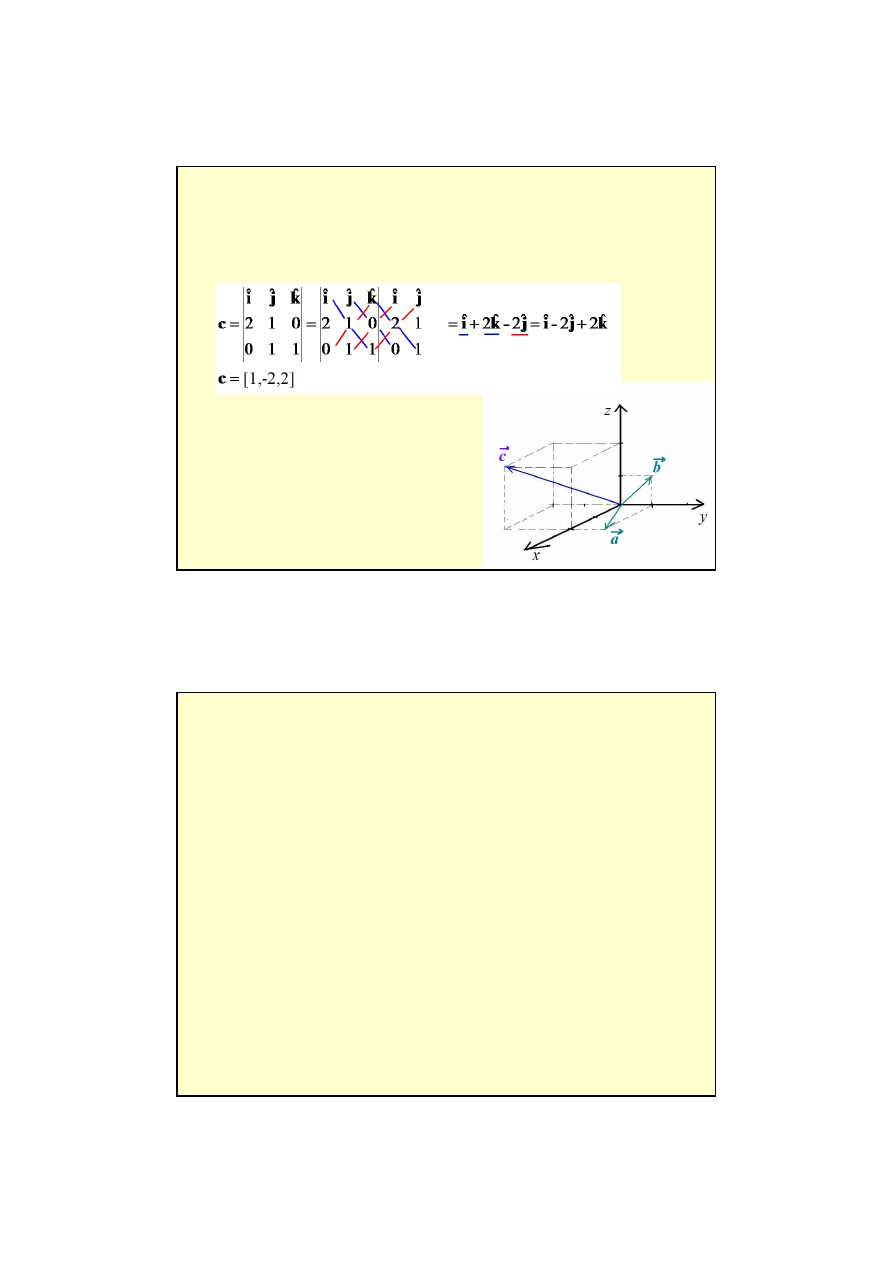
5
c = a x
x
x
x b
ˆ ˆ
[2,1, 0]
2
ˆ
ˆ
[0,1,1]
=
= +
=
= +
a
i
j
b
j k
Przykład iloczynu wektorowego:
Wstawka matematyczna
2. Pochodne
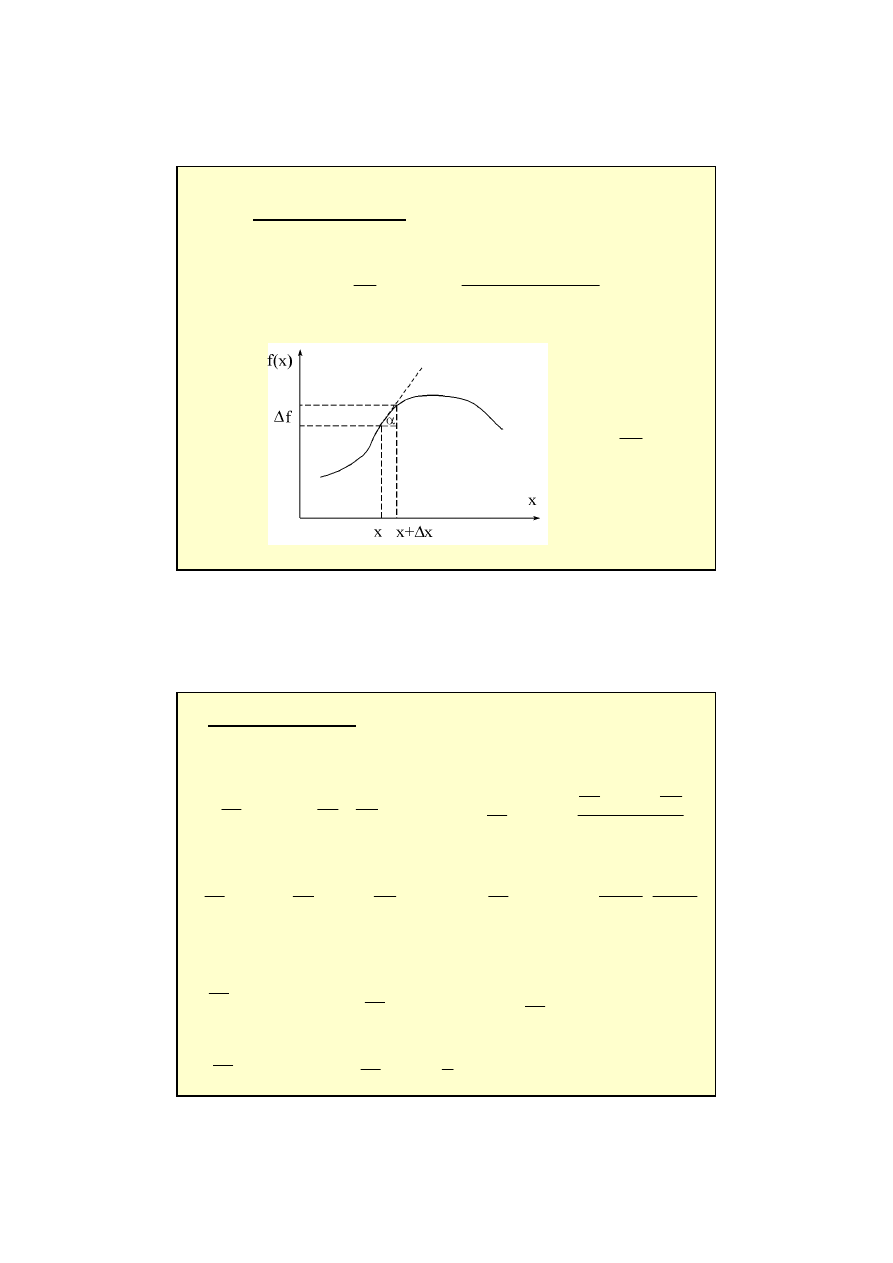
6
x
x
f
x
x
f
dx
df
x
f
x
∆
−
∆
+
=
=
→
∆
)
(
)
(
lim
)
(
'
0
Pochodna funkcji f(x)
α
tg
dx
df
=
Pochodna funkcji
Podstawowe własno
ści pochodnej :
dx
dg
dx
df
g
f
dx
d
+
=
+
)
(
dx
dg
f
g
dx
df
g
f
dx
d
⋅
+
⋅
=
⋅
)
(
2
)
/
(
g
dx
dg
f
g
dx
df
g
f
dx
d
⋅
−
⋅
=
[
]
)
(
:
)
(
)
(
))
(
(
x
g
u
gdzie
dx
x
dg
du
u
df
x
g
f
dx
d
=
⋅
=
Przykłady:
1
)
(
−
=
n
n
nx
x
dx
d
)
0
(
1
)
(ln
>
=
x
x
x
dx
d
x
x
e
e
dx
d
=
)
(
x
x
dx
d
cos
)
(sin
=
x
x
dx
d
sin
)
(cos
−
=
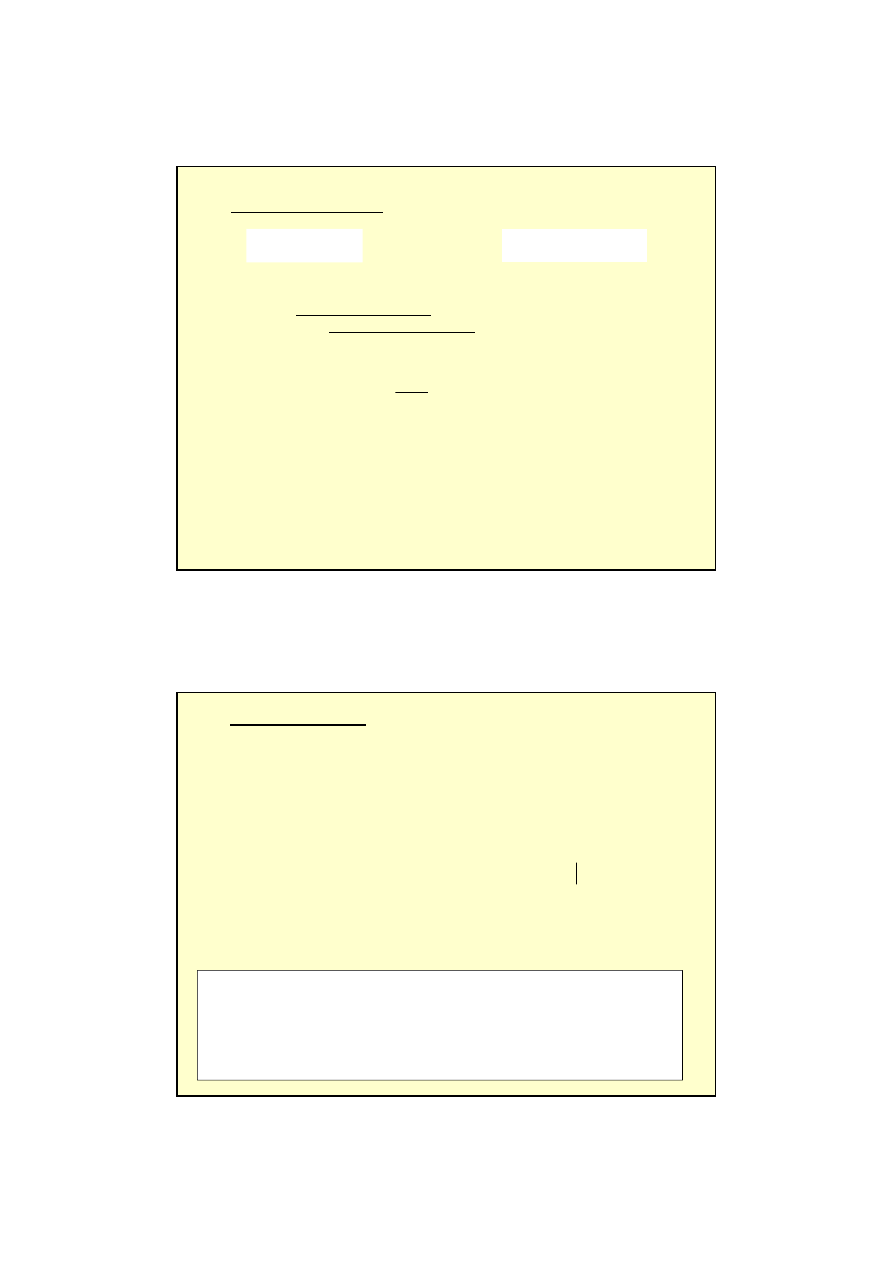
7
Pochodna wektora
Jeśli w przedziale czasu
∆
t przyrost wektora r(t) wynosi
∆
r:
∆
r = r(t+
∆
t) – r(t),
to stosunek:
t
t
t
t
dt
d
t
t
t
t
t
t
∆
−
∆
+
=
→
∆
−
∆
+
=
∆
∆
→
∆
)
(
)
(
lim
)
(
)
(
0
r
r
r
r
r
r
∆
−
∆
+
∆
−
∆
+
∆
−
∆
+
=
→
∆
t
t
z
t
t
z
t
t
y
t
t
y
t
t
x
t
t
x
dt
d
t
)
(
)
(
,
)
(
)
(
,
)
(
)
(
lim
0
r
=
dt
dz
,
dt
dy
,
dt
dx
dt
dr
8
Całka nieoznaczona
∫
=
)
(
)
(
x
f
dx
x
g
Wynik operacji całkowania:
znaleziona funkcja pierwotna f(x) ma taką własność, że po zróżniczkowaniu
jej otrzymujemy funkcję podcałkową g(x):
C
x
f
dx
x
g
+
=
∫
)
(
)
(
ściślej:
[f (x)+C]' = g(x)
Przykłady:
C
x
1
n
1
dx
x
1
n
n
+
+
=
+
∫
∫ e
x
dx = e
x
+ C
∫ (1/x) dx = ln x + C
∫ cos x dx = sin x + C
∫ sin x dx = - cos x + C
Całka oznaczona:
[
] [
]
∫
∫
=
=
+
−
+
=
−
b
a
b
a
dx
x
g
dx
x
g
C
a
f
C
b
f
a
f
b
f
)
(
)
(
)
(
)
(
)
(
)
(
C
x
f
dx
x
g
+
=
∫
)
(
)
(
Niech :
przyrost funkcji pierwotnej na przedziale [a,b]:
nazywamy całką oznaczoną.
)
(
)
(
)
(
a
f
b
f
dx
x
g
b
a
−
=
∫
CZYLI CAŁKA OZNACZONA TO:
C
x
f
dx
x
g
+
=
∫
)
(
)
(
gdzie:
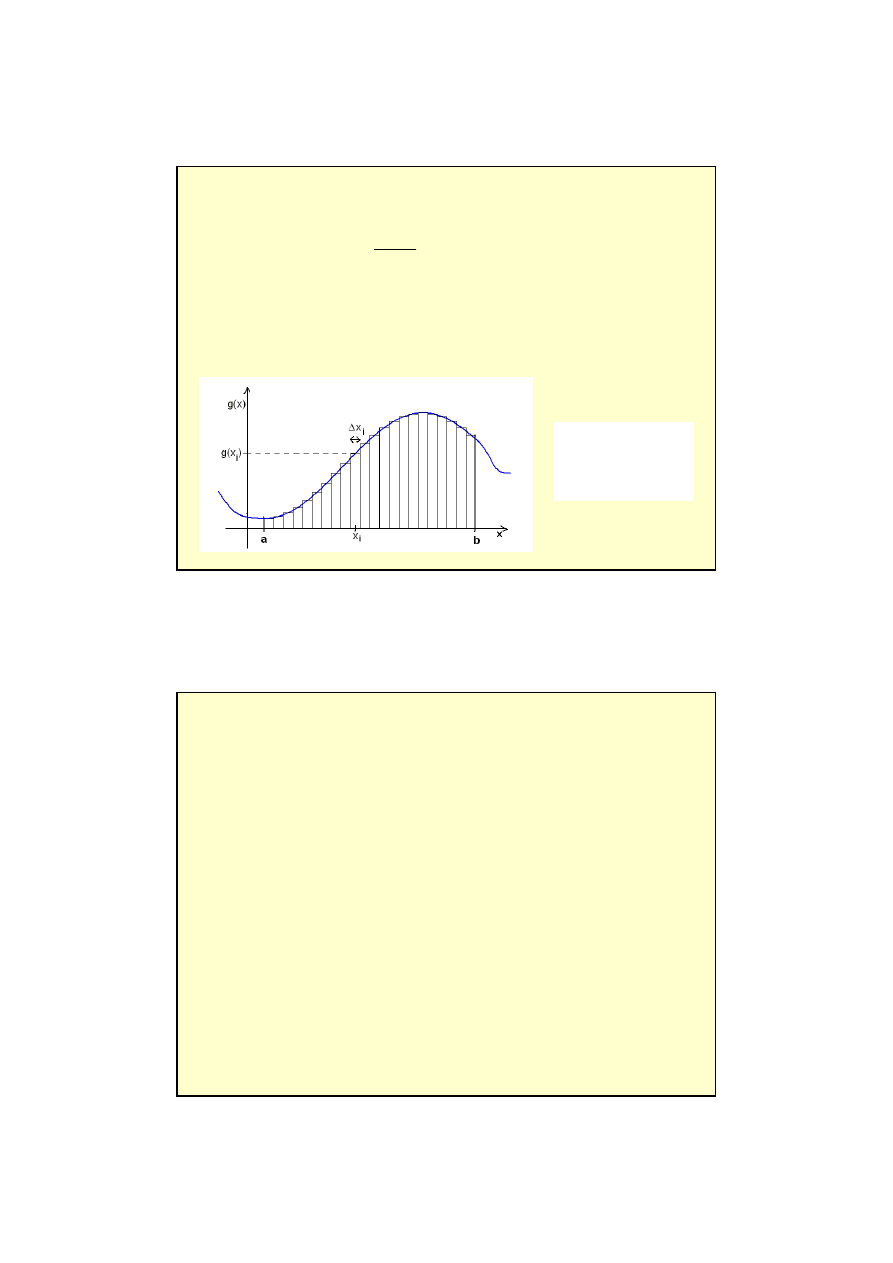
9
S
x
x
g
x
x
f
x
a
f
b
f
dx
x
g
i
N
i
i
i
N
i
i
i
b
a
=
∆
→
∆
=
∆
→
∆
=
−
=
∑
∑
∫
)
(
0
lim
)
(
0
lim
)
(
)
(
)
(
Znaczenie całki oznaczonej:
i
i
i
i
i
x
x
f
x
x
f
x
g
∆
∆
→
∆
=
=
)
(
0
lim
)
(
'
)
(
i
i
i
x
x
g
x
f
∆
=
∆
)
(
)
(
∫
=
b
a
dx
x
g
S
)
(
Kinematyka
(opis ruchu bez analizowania jego przyczyny)
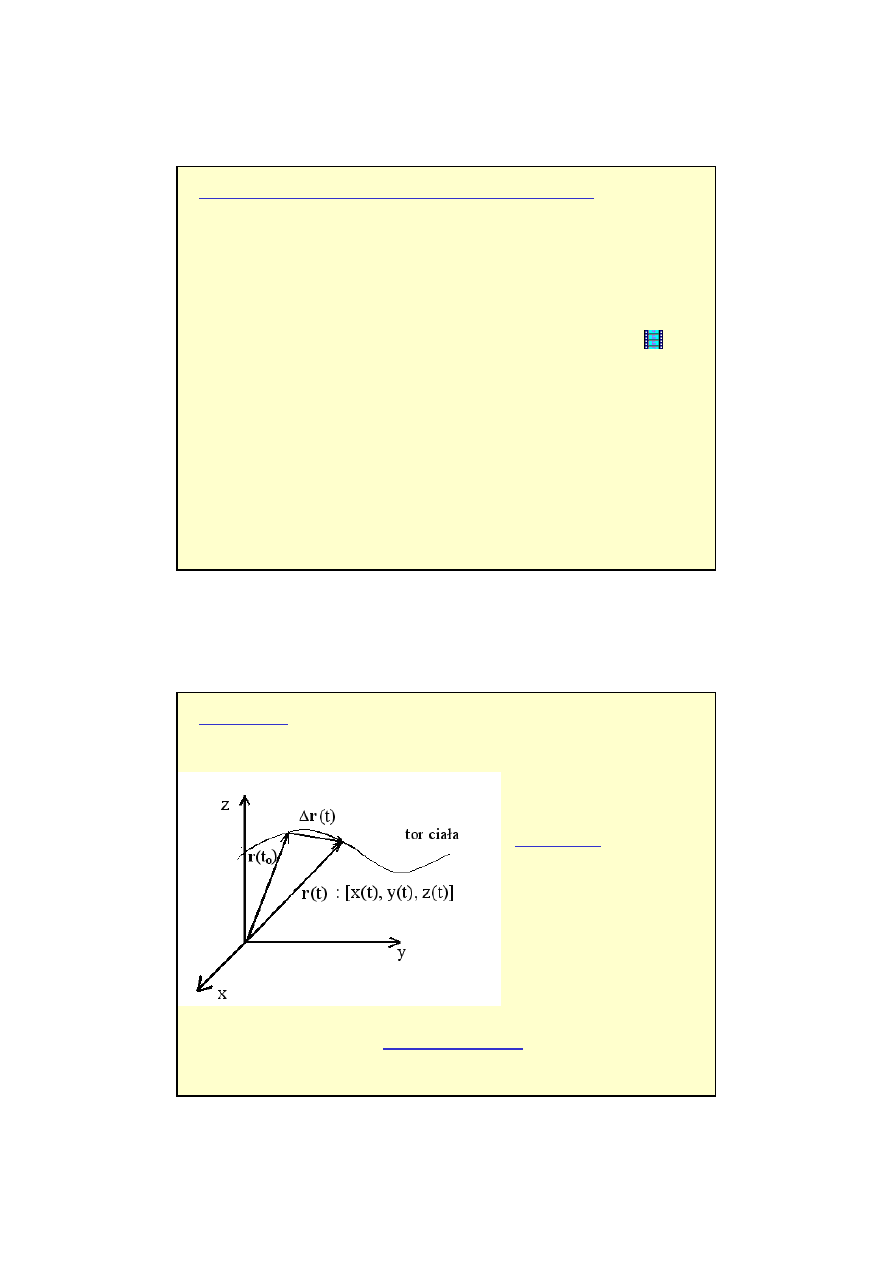
10
Punkty materialne to obiekty obdarzone masą, których rozmiary
(objętość) możemy zaniedbać.
Pod pojęciem ruchu rozumiemy zmiany wzajemnego położenia
jednych ciał względem drugich wraz z upływem czasu.
Ruch odbywa się względem wybranego układu odniesienia.
Kinematyka – opis ruchu bez okre
ś
lania jego przyczyny
)]
(
),
(
),
(
[
t
z
t
y
t
x
=
(t)
r
TOR RUCHU
)]
(
),
(
),
(
[
0
t
z
t
y
t
x
=
)
(t
(t)
(t)
∆
∆
∆
−
=
∆
r
r
r
PRZEMIESZCZENIE
Tor ruchu to krzywa jaką w przestrzeni zakreśla punkt materialny.
POŁO
Ż
ENIE
=
=
=
)
(
)
(
)
(
t
z
z
t
y
y
t
x
x
lub
kinematyczne
równania
ruchu
Układ kartezja
ński
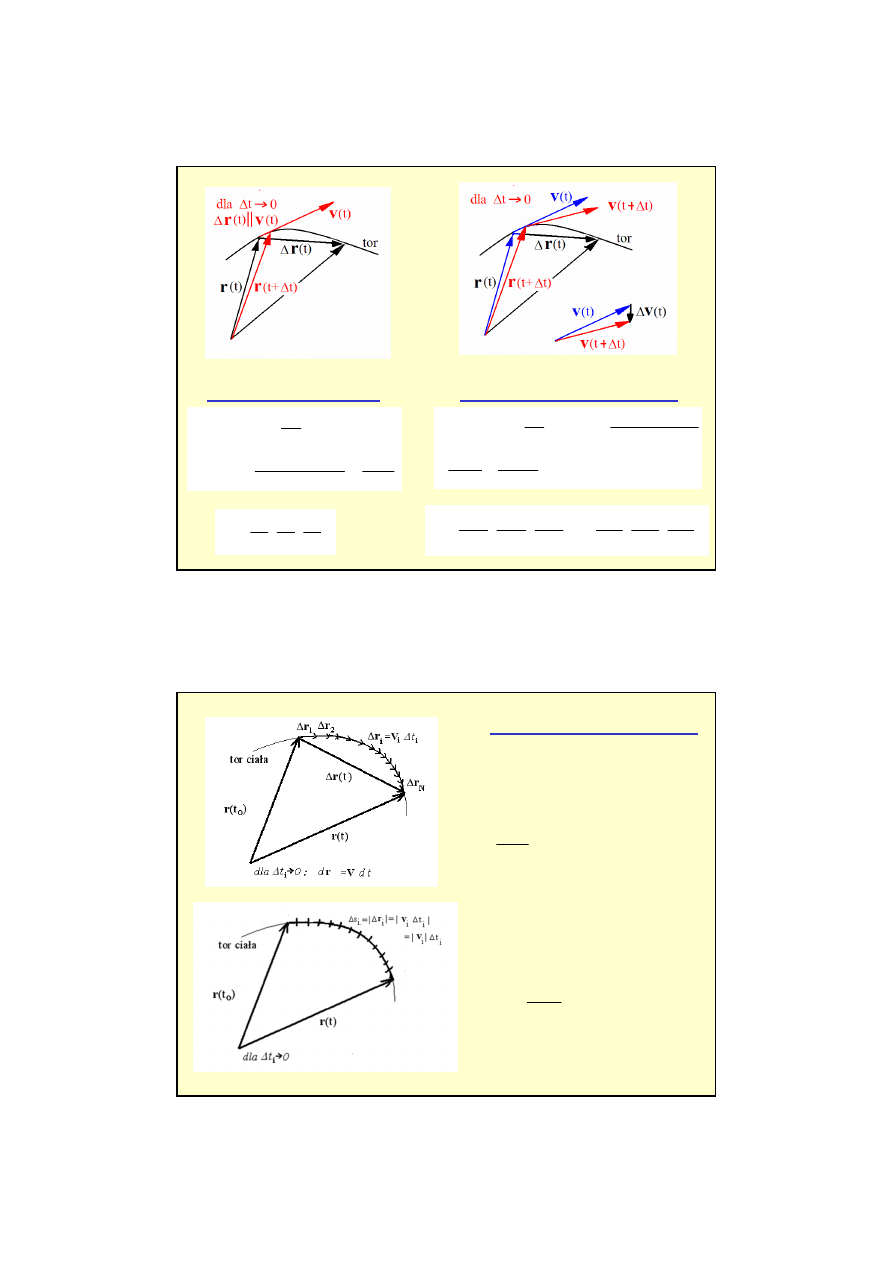
11
PR
Ę
DKO
ŚĆ
CHWILOWA
dt
(t)
d
t
(t)
t)
(t
t
=
(t)
t
t
r
r
r
r
=
∆
−
∆
+
=
=
∆
∆
>
−
∆
>
−
∆
0
0
lim
lim
v
PRZYSPIESZENIE CHWILOWE
2
2
0
0
)
(
)
(
lim
lim
)
(
dt
t
d
dt
t
d
t
(t)
t)
(t
t
t
t
t
r
v
v
v
v
a
=
=
∆
−
∆
+
=
∆
∆
=
>
−
∆
>
−
∆
dt
dz
dt
dy
dt
dx
=
,
,
v
dt
z
d
dt
y
d
dt
x
d
dt
d
dt
d
dt
d
=
=
2
2
2
2
2
2
,
,
,
,
z
y
x
v
v
v
a
PRZEMIESZCZENIE I DROGA
∫
∑
∑
=
∆
=
=
t
t
i
i
i
i
dt
t
t
∆s
t
s
0
)
(
)
(
v
v
i
dt
t
ds
t
)
(
)
(
=
v
Warto
ść
pr
ę
dko
ś
ci
chwilowej
to szybko
ść
(inaczej pr
ę
dko
ść
liniowa)
)
(
|
)
(
|
t
t
v
=
v
∫
∑
∑
=
∆
=
=
t
t
i
i
i
dt
t
t
∆
t
∆
0
)
(
)
(
v
v
r
r
i
i
dt
(t)
d
=
(t)
r
v
12
PR
Ę
DKO
ŚĆ Ś
REDNIA
t
t
t
t
t
t
śr
∆
∆
=
−
−
=
)
(
)
(
)
(
0
0
r
r
r
v
Wektorowa:
t
t
s
t
t
t
s
śr
∆
=
−
=
)
(
)
(
)
(
0
v
Liniowa (szybko
ść
):
|
|
)
(
śr
śr
v
≠
v
Uwaga:
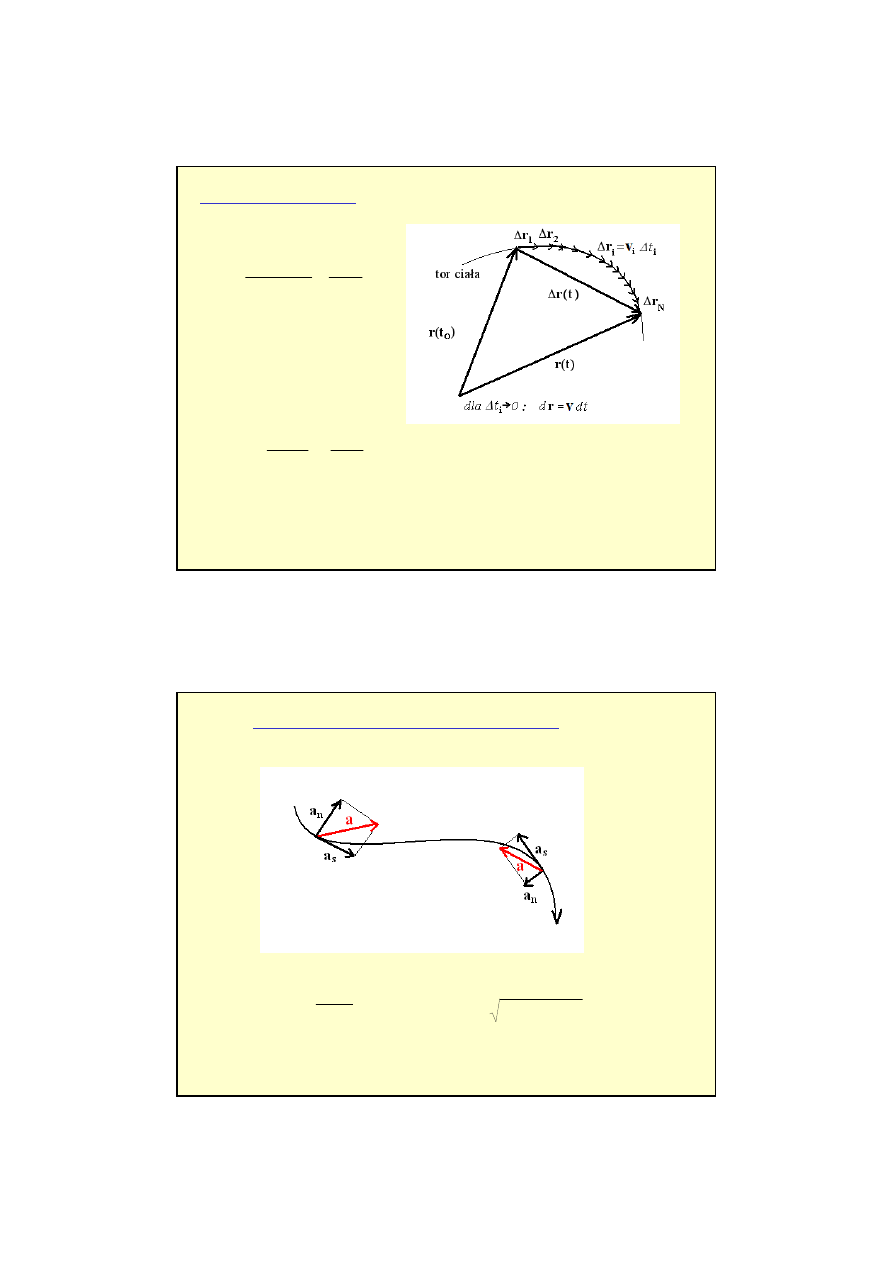
PRZYSPIESZENIE STYCZNE I NORMALNE
dt
t
d
t
a
s
)
(
)
(
v
=
)
(
)
(
)
(
2
2
t
a
t
a
t
a
s
n
−
=
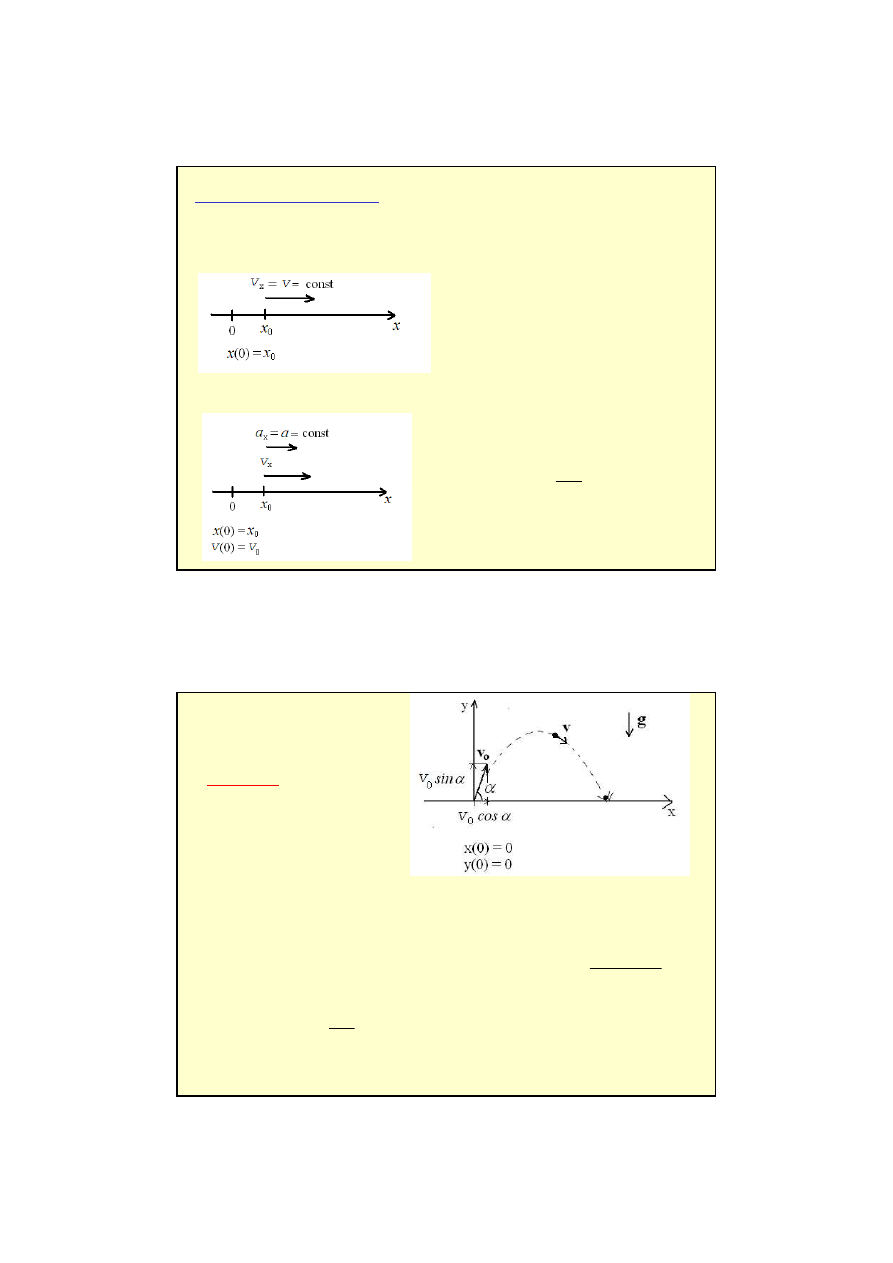
13
PRZYKŁADY RUCHU
Ruch w jednym wymiarze (y=0, z=0):
Ruch jednostajny prostoliniowy
const
x
=
=
v
v
Ruch jednostajnie zmienny prostoliniowy
const
a
a
x
=
=
t
x
x
v
+
=
0
równanie ruchu
t
a
+
=
0
v
v
x
2
2
0
0
at
t
x
x
+
+
=
v
równanie ruchu
UWAGA: v mo
ż
e by
ć
ujemne lub dodatnie
(od tego zale
ż
y, w któr
ą
strone ciało sie porusza)
UWAGA: v
0
,
a
mog
ą
by
ć
ujemne lub dodatnie. Gdy v
0
,
a
maj
ą
:
1) ten sam znak to ruch jest jednostajnie przyspieszony,
2) ró
ż
ne znaki to ruch jest jednostajnie opó
ź
niony.
Ruch w dwóch wymiarach (z=0):
−
=
=
=
=
g
g
a
g
a
y
y
x
x
0
Rzut uko
śny
−
=
=
gt
y
x
α
α
sin
cos
0
0
v
v
v
v
−
=
=
2
)
sin
(
)
cos
(
2
0
0
gt
t
y
t
x
α
α
v
v
równania
ruchu
2
2
0
)
cos
(
2
)
(
x
g
x
tg
y
α
α
v
−
=
równanie toru
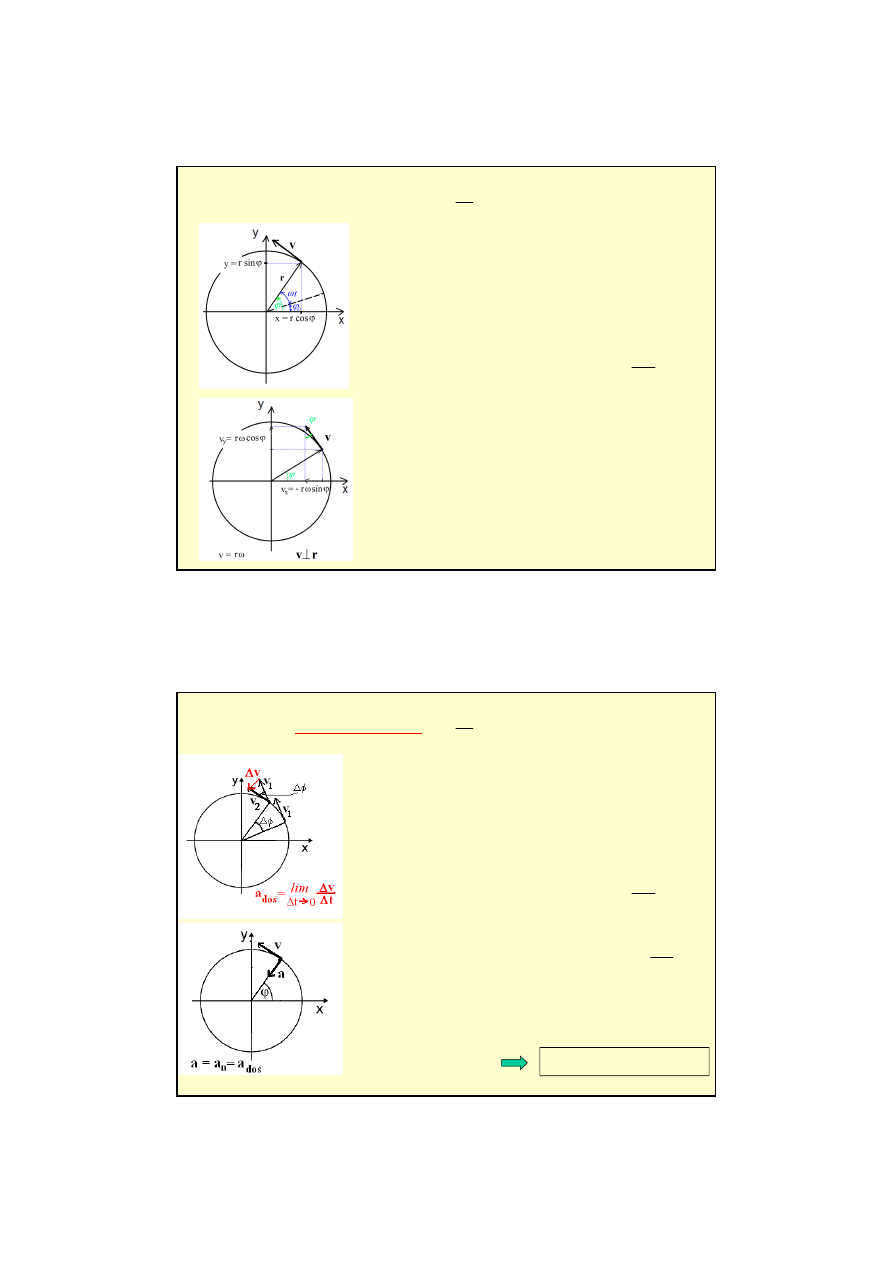
14
Ruch w dwóch wymiarach:
Ruch po okręgu – stała prędkość kątowa:
+
=
=
=
0
)
(
.
)
(
ϕ
ω
ϕ
t
t
const
r
t
r
+
=
+
=
)
sin(
)
(
)
cos(
)
(
0
0
ϕ
ω
ϕ
ω
t
r
t
y
t
r
t
x
+
=
=
+
−
=
=
)
cos(
/
)
sin(
/
0
0
ϕ
ω
ϕ
ω
t
rω
dt
dy
t
rω
dt
dx
y
x
v
v
const
dt
d
=
=
ϕ
ω
równania
ruchu
Układ kartezja
ński:
Układ biegunowy:
const
t
=
∆
∆
= ϕ
ω
Ruch w dwóch wymiarach:
Ruch po okręgu –
stała prędkość kątowa:
0
=
=
dt
d
ω
ε
−
=
+
−
=
=
−
=
+
−
=
=
2
0
2
2
0
2
)
sin(
/
)
cos(
/
yω
t
rω
dt
d
a
xω
t
rω
dt
d
a
y
y
x
x
ϕ
ω
ϕ
ω
v
v
Układ kartezja
ński:
Układ biegunowy:
2
,
0
rω
a
a
a
doś
n
S
=
=
=
2
2
2
[
,
]
xω
yω
ω
= −
−
= −
a
r
lub inaczej:
const
t
=
∆
∆
= ϕ
ω
+
=
=
=
0
)
(
.
)
(
ϕ
ω
ϕ
t
t
const
r
t
r
+
=
+
=
)
sin(
)
(
)
cos(
)
(
0
0
ϕ
ω
ϕ
ω
t
r
t
y
t
r
t
x
+
=
=
+
−
=
=
)
cos(
/
)
sin(
/
0
0
ϕ
ω
ϕ
ω
t
rω
dt
dy
t
rω
dt
dx
y
x
v
v
const
dt
d
=
=
ϕ
ω
równania
ruchu
15
Ruch w dwóch wymiarach:
Ruch po okręgu –
zmienny
=
=
=
r
t
l
t
const
t
r
)
(
)
(
0
oraz
.
)
(
0
ϕ
ϕ
r
t
l
r
t
v
=
=
=
d
d
1
d
d
ϕ
ω
Układ biegunowy:
r
a
t
r
t
s
=
=
=
d
d
1
d
d
v
ω
ε
r
r
a
a
εr
a
doś
n
S
2
2
,
v
=
=
=
=
ω
=
=
=
=
r
rω
a
a
εr
a
doś
n
S
2
2
v
rω
=
v
16
WZGL
Ę
DNO
ŚĆ
RUCHU
(t)
(t)
=
(t)
BA
CB
CA
r
r
r
+
Wzgl
ę
dne poło
ż
enie:
dt
(t)
d
dt
(t)
d
=
dt
(t)
d
BA
CB
CA
r
r
r
+
(t)
(t)
=
(t)
BA
CB
CA
v
v
v
+
Wzgl
ę
dna pr
ę
dko
ść
:
dt
(t)
d
dt
(t)
d
=
dt
(t)
d
BA
CB
CA
v
v
v
+
(t)
(t)
=
(t)
BA
CB
CA
a
a
a
+
Wzgl
ę
dne przyspieszenie:
Wyszukiwarka
Podobne podstrony:
matematyka rozwiazania Nieznany
2013 LATO WAT Matematyka 3 Zada Nieznany (2)
,analiza matematyczna 2, elemen Nieznany (2)
arkusz probny z matematyki 7 id Nieznany (2)
Lamiglowki matematyczne (suma, Nieznany
,analiza matematyczna 2, calki Nieznany (6)
arkusz probny z matematyki 9 id Nieznany (2)
imw w01 wstep system produkcyj Nieznany
gk 01 wstep id 191745 Nieznany
jurlewicz,matematyka ,szeregi f Nieznany
arkusz probny z matematyki 2 id Nieznany (2)
,analiza matematyczna 2, calki Nieznany (2)
arkusz probny z matematyki 5 id Nieznany (2)
,analiza matematyczna 2, calki Nieznany (5)
aue wstep id 72298 Nieznany
19 kwanty wstep 2014id 18308 Nieznany
więcej podobnych podstron