KRATOWNICE
Obliczanie sił w prętach kratownicy z zasady prac wirtualnych
Zadanie 1.
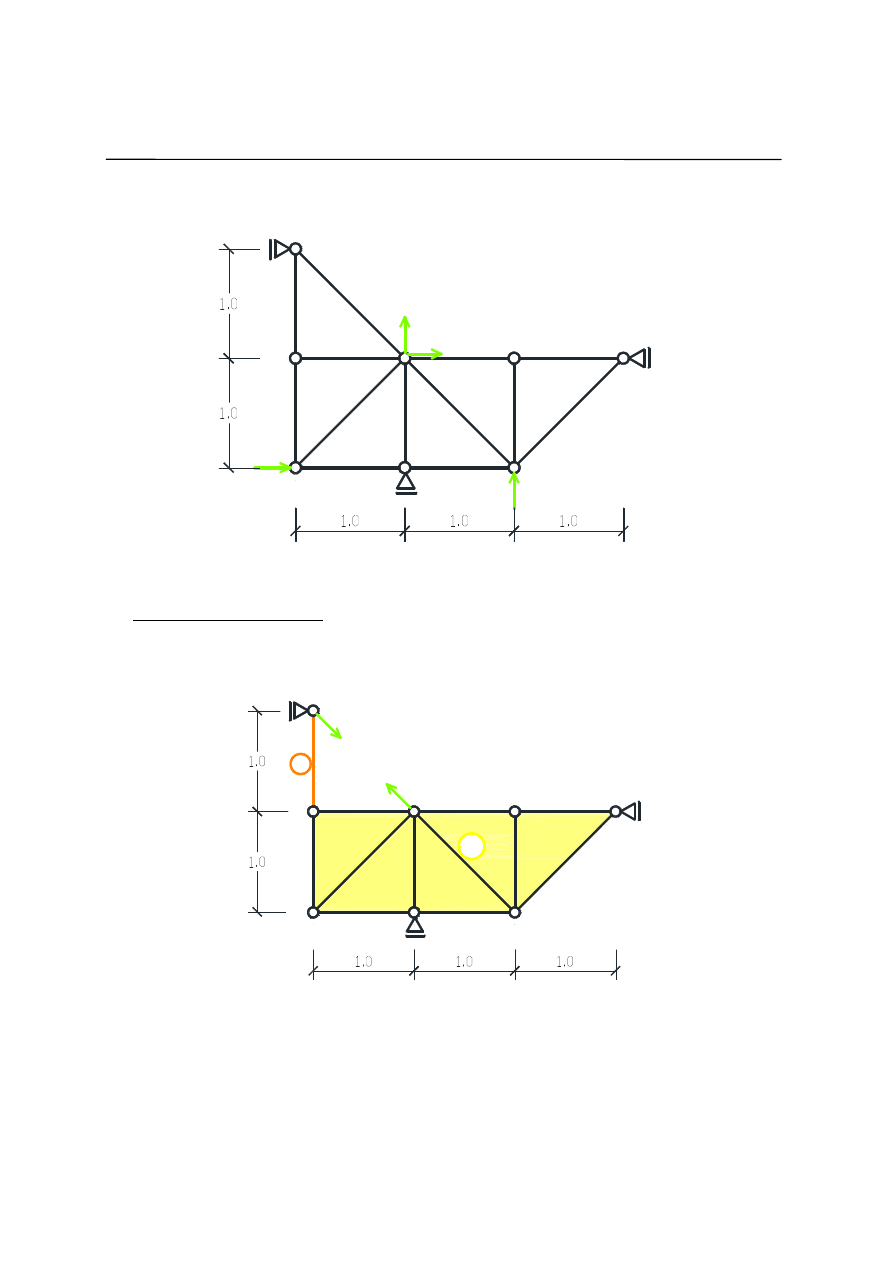
Korzystając z zasady prac wirtualnych wyznacz siłę w pręcie kratownicy nr 2, 4, 9.
4 kN
2 kN
2 kN
4 kN
A
B
C
D
E
F
G
H
1
2
3
6
7
8
9
10
11
12
13
4
5
Rys. 1
1.
Obliczenie siły w pręcie nr 2
Usuwamy pręt nr 2 i jego działanie zastępujemy układem dwóch sił przeciwnych zaczepionych
w węzłach które łączył pręt (węzeł A i C) o kierunku tego pręta (Rys. 2). Po usunięciu pręta powstał
układ złożony z dwóch tarcz połączonych przegubem w punkcie B.
A
B
D
E
F
G
H
I
II
C
N
2
N
2
Rys. 2
Dla powyższego układu należy narysować plan przesunięć wirtualnych. Analizę układu rozpoczynamy
od tarczy nr I. Tarcza ta posiada dwie podpory przegubowo przesuwne, które zezwalają jedynie na
obrót tarczy wokół punktu C. Zakładamy więc, że tarcza może doznać obrotu wokół tego punktu
i przyjmujemy w punkcie C środek chwilowego obrotu tarczy O
I
. Następnie przyjmujemy obrót wokół
punktu O
I
jako zgodny z ruchem wskazówek zegara i rysujemy plan przesunięć wirtualnych tarczy I
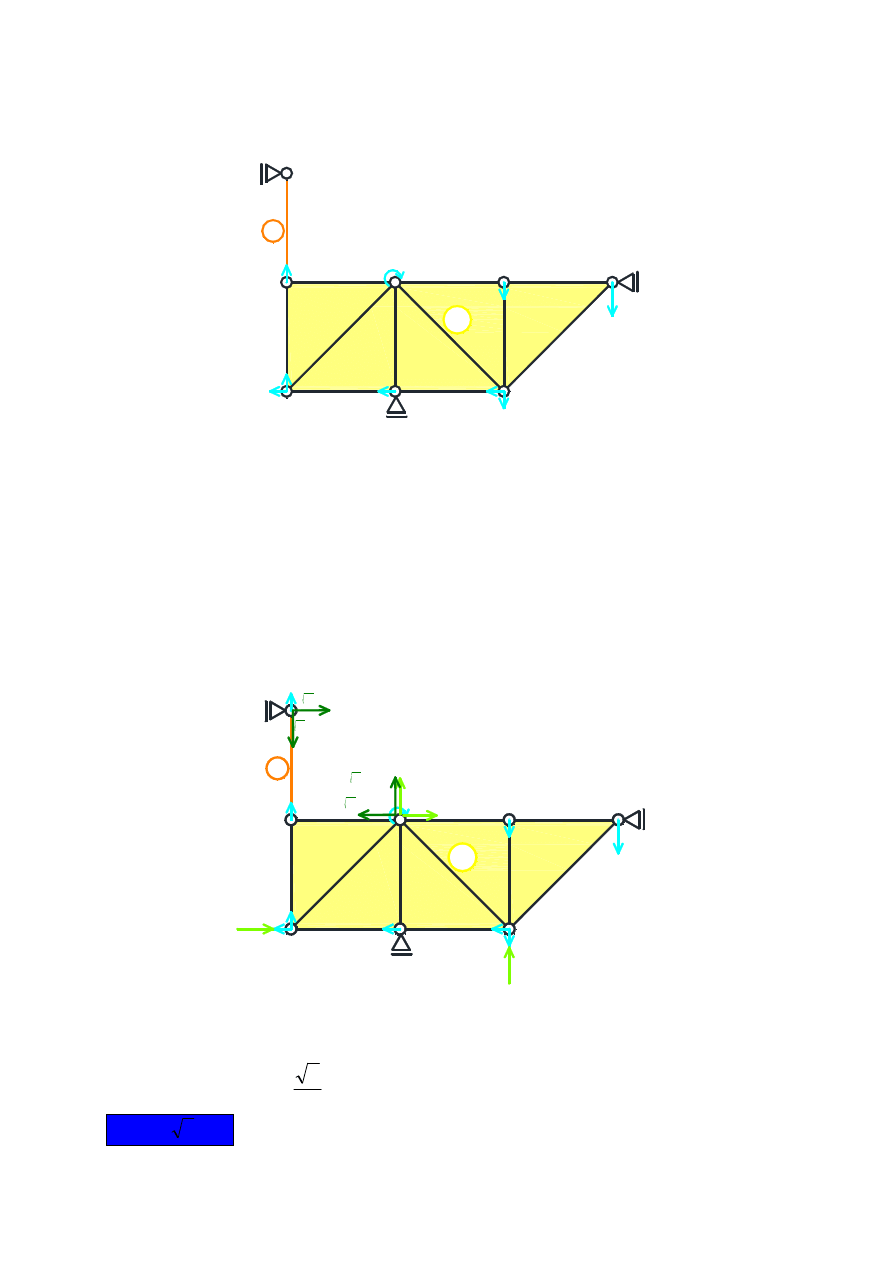
(Rys. 3). Przesunięcia poziome punktów B, C, D, E wynoszą 0δ, podobnie jak przesunięcia pionowe
punktów C i G.
A
B
O
I
D
E
F
G
H
I
II
δ
δ
2δ
δ
δ
δ
δ
δ
Rys. 3
Wyznaczone zostały przesunięcia wirtualne wszystkich punktów tarczy I; niewiadome jest jeszcze
przesunięcie punktu A należącego do tarczy II. Przesunięcie poziome punktu A wynosi 0δ, z uwagi na
przyłożoną w tym punkcie podporę blokującą przesuw poziomy, a przesunięcie pionowe wyznaczamy
z rzutu na kierunek BA (korzystamy z twierdzenia o rzutach):
δ
δ
=
→
=
Ay
By
v
v
Punkty A i B należące do tarczy II mają przesunięcia poziome 0δ, a pionowe 1 δ – tarcza II doznaje
translacji pionowej.
Na rysunku 4 został przedstawiony plan przesunięć wirtualnych całego układu i zaznaczono wszystkie
działające na układ siły:
A
B
O
I
D
E
F
G
H
I
II
δ
δ
2δ
δ
δ
δ
δ
δ
δ
2/2 N
2
4 kN
2 kN
2 kN
4 kN
2/2 N
2
2/2 N
2
2/2 N
2
Rys. 4
Z zasady prac wirtualnych obliczamy siłę N
2
:
δ
δ
δ
δ
∀
=
⋅
−
⋅
−
⋅
−
0
2
2
]
[
2
]
[
2
2
N
kN
kN
]
[
2
4
2
kN
N
−
=
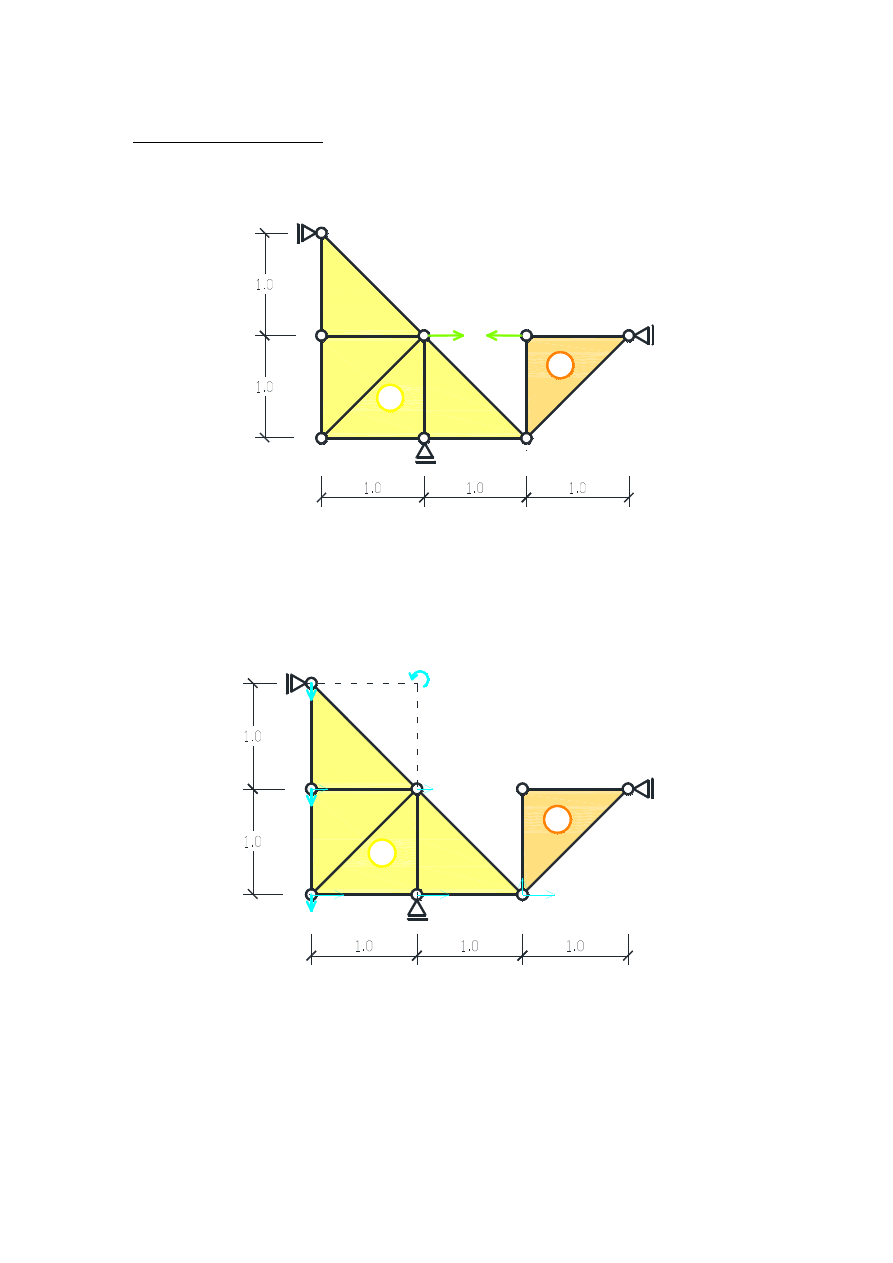
2.
Obliczenie siły w pręcie nr 4
Usuwamy pręt nr 4 i jego działanie zastępujemy układem dwóch sił przeciwnych zaczepionych
w węzłach które łączył pręt (węzeł C i D) o kierunku tego pręta (Rys. 5). Po usunięciu pręta powstał
układ złożony z dwóch tarcz połączonych przegubem w punkcie H.
A
B
D
E
F
G
H
I
II
C
N
4
N
4
Rys. 5
Analizę układu rozpoczynamy od tarczy nr I. Tarcza ta posiada dwie podpory przegubowo przesuwne,
które zezwalają jedynie na obrót tarczy wokół punktu, powstałego na przecięciu się prostych
prostopadłych do dozwolonych przesuwów w punkcie A i G. Zakładamy więc, że tarcza może doznać
obrotu wokół tego punktu i przyjmujemy obrót wokół punktu O
I
jako przeciwny do ruchu wskazówek
zegara. Rysujemy plan przesunięć wirtualnych tarczy I (Rys. 6). Przesunięcie poziome punktu A
wynosi 0δ, podobnie jak przesunięcia pionowe punktów C i G.
A
B
D
E
F
G
H
I
II
C
O
I
δ
δ
δ
2δ
2δ
2δ
δ
δ
δ
Rys. 6
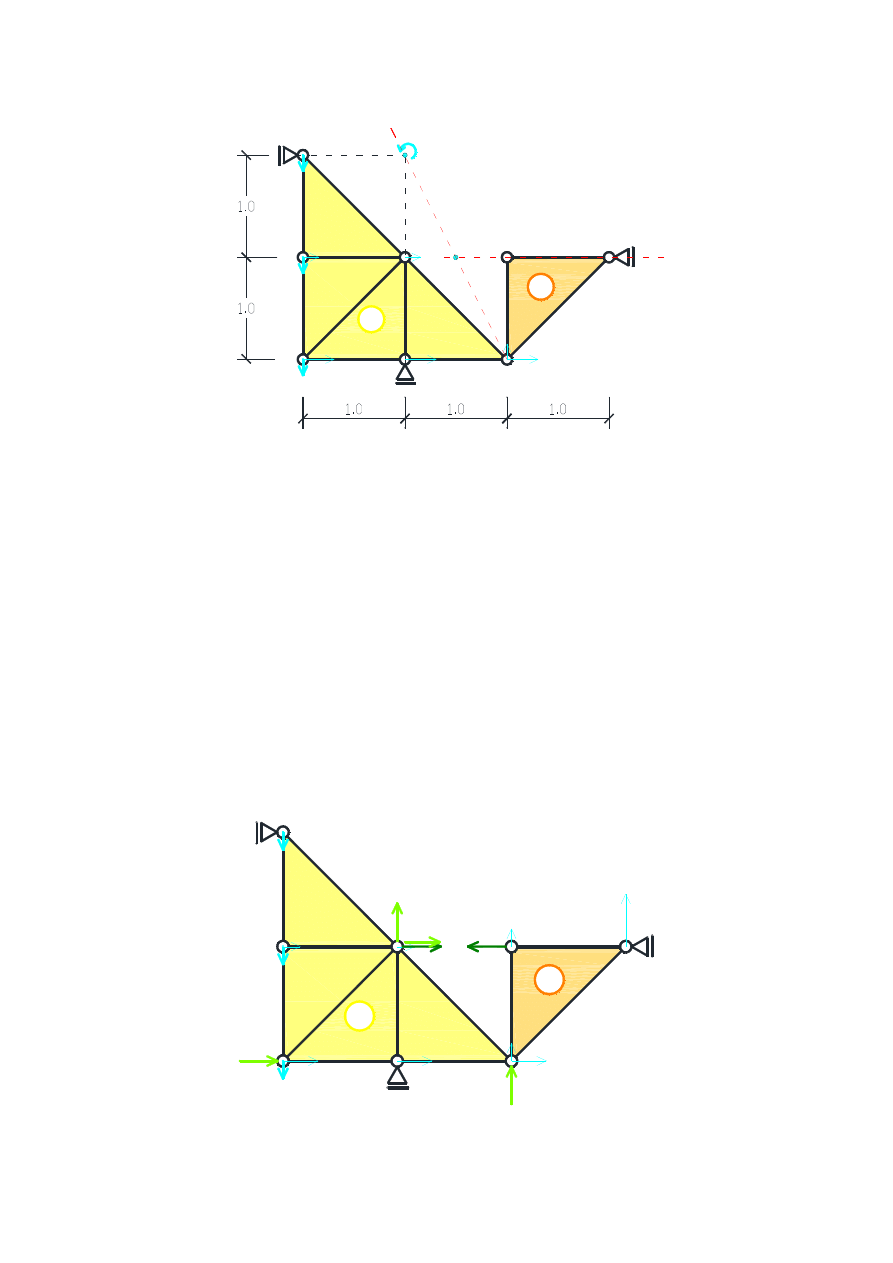
Wyznaczone zostały przesunięcia wirtualne wszystkich punktów tarczy I; niewiadome są jeszcze
przesunięcie punktów należących do tarczy II. Poszukujemy środka chwilowego obrotu tarczy II:
prowadzimy prostą prostopadłą do dozwolonego przesuwu w punkcie E oraz rysujemy prostą łączącą
środek chwilowego obrotu tarczy I (punkt O
I
) i przegub łączący tarcze (punkt H). Na przecięciu się
tych dwóch prostych leży środek chwilowego obrotu tarczy II (rys. 7)
A
B
D
E
F
G
H
I
II
C
O
I
δ
δ
δ
2δ
2δ
2δ
δ
δ
δ
O
II
Rys. 7
Znając środek chwilowego obrotu tarczy II i przesunięcie punktu H należącego do tej tarczy możemy
wyznaczyć przesunięcia pozostałych punktów (rys. 8).
Uwaga:
Można również, bez wyznaczania środka O
II
, określić przesunięcia wirtualne punktów D i E:
•
Przesunięcie poziome punktu E wynosi 0δ (z uwagi na podporę przyłożoną w punkcie E)
•
Przesunięcie pionowe punktu E wyznaczamy z rzutu na kierunek HE:
δ
δ
δ
δ
3
)
1
,
1
(
)
,
0
(
)
1
,
1
(
)
,
2
(
=
→
=
Ey
Ey
v
v
o
o
•
Przesunięcie
poziome
punktu
D
wyznaczamy
z
rzutu
na
kierunek
ED:
δ
δ
0
0
=
→
=
Dx
Ex
v
v
•
Przesunięcie pionowe punktu D wyznaczamy z rzutu na kierunek HD:
δ
δ
=
→
=
Dy
Hy
v
v
Na rysunku 8 został przedstawiony plan przesunięć wirtualnych całego układu i zaznaczono wszystkie
działające na układ siły:
A
B
D
E
F
G
H
I
II
δ
δ
δ
2δ
2δ
2δ
δ
δ
δ
δ
3δ
N
4
N
4
4 kN
2 kN
2 kN
4 kN
Rys. 8
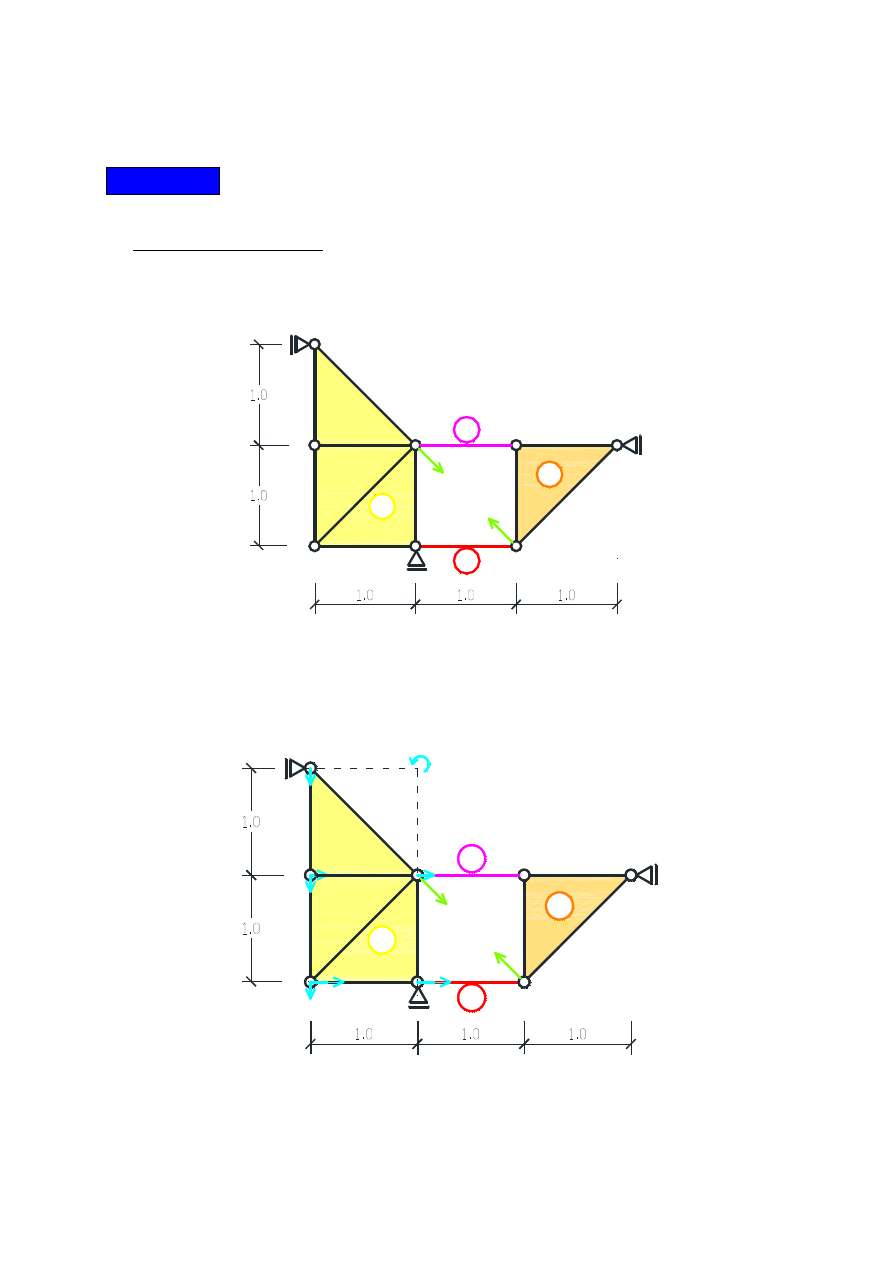
Z zasady prac wirtualnych obliczamy siłę N
4
:
δ
δ
δ
δ
δ
∀
=
⋅
+
⋅
+
⋅
+
⋅
0
]
[
4
]
[
2
2
]
[
2
4
N
kN
kN
kN
]
[
10
4
kN
N
−
=
3.
Obliczenie siły w pręcie nr 9
Usuwamy pręt nr 9 i jego działanie zastępujemy układem dwóch sił przeciwnych zaczepionych
w węzłach które łączył pręt (węzeł C i H) o kierunku tego pręta (Rys. 9). Po usunięciu pręta powstał
układ złożony z czterech tarcz połączonych przegubami w punkcie C, D, G, H.
A
B
D
E
F
G
H
I
II
C
N
9
N
9
III
IV
Rys. 9
Analizę układu rozpoczynamy od tarczy nr I. Tarcza ta posiada dwie podpory przegubowo przesuwne,
które zezwalają jedynie na obrót tarczy wokół punktu, powstałego na przecięciu się prostych
prostopadłych do dozwolonych przesuwów w punkcie A i G. Zakładamy więc, że tarcza może doznać
obrotu wokół tego punktu i przyjmujemy obrót wokół punktu O
I
jako przeciwny do ruchu wskazówek
zegara i dla takiego założenia rysujemy plan przesunięć wirtualnych tarczy I (Rys. 10).
A
B
D
E
F
G
H
I
II
C
N
9
N
9
III
IV
O
I
δ
δ
δ
2δ
2δ
δ
δ
Rys. 10
W kolejnym kroku należy wyznaczyć przesunięcia wirtualne pozostałych punktów układu.
Korzystając z rzutów na prostą CD i DE możemy zapisać:
δ
δ
δ
=
→
=
→
=
Ex
Dx
Cx
v
v
v
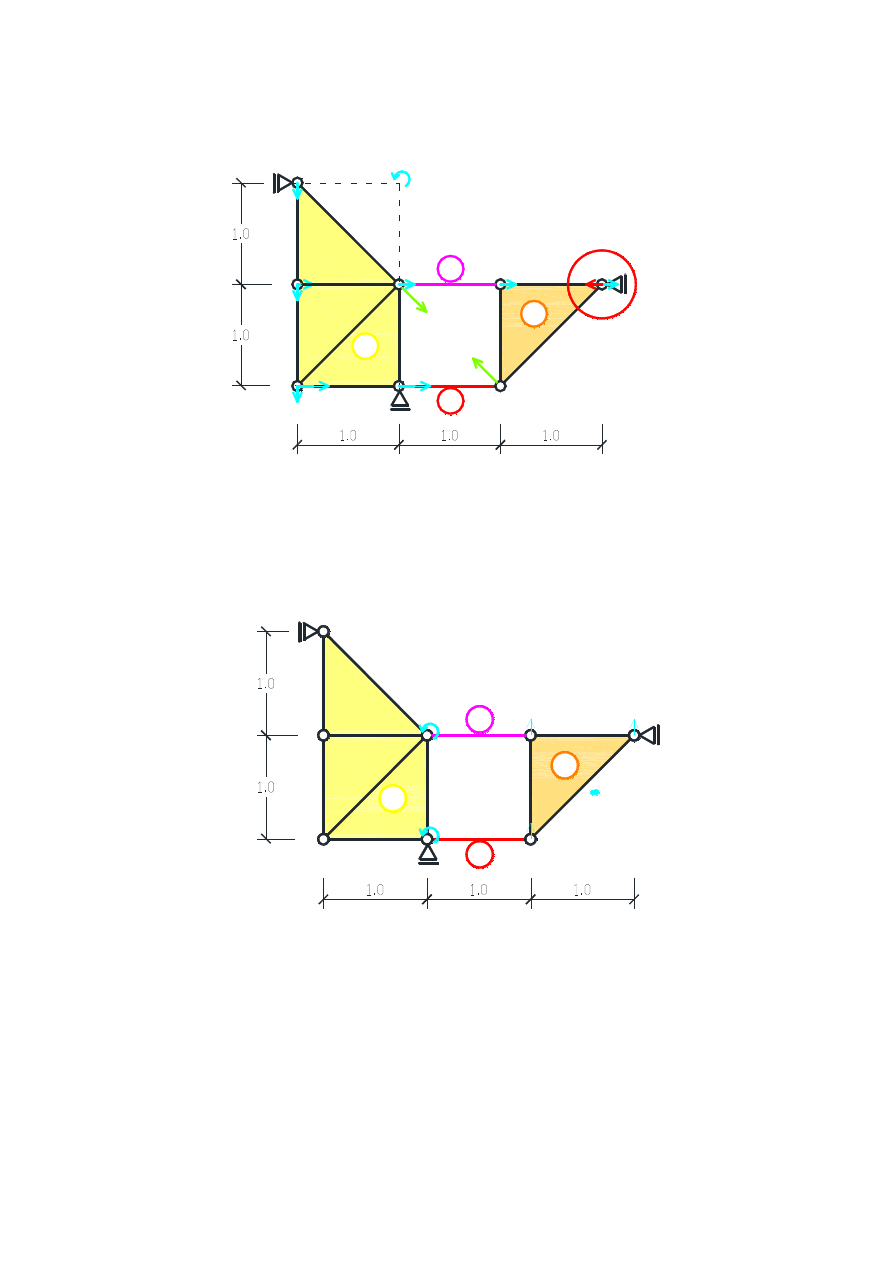
Zauważamy, że dochodzimy do sprzeczności, gdyż w punkcie E przyłożona jest podpora blokująca
przesuw poziomy, stąd wiemy, że przesunięcie poziome punktu E wynosi
δ
0
=
Ex
v
(rys. 11).
A
B
D
E
F
G
H
I
II
C
N
9
N
9
III
IV
O
I
δ
δ
δ
2δ
2δ
δ
δ
δ
δ
0δ
Rys. 11
Oznacza to, iż przyjęte wyjściowe założenie jest błędne. Tarcza I nie doznaje obrotu wokół punktu O
I
,
gdyż ruch ten jest zablokowany przez podporę przesuwną przyłożoną w punkcie E. Skoro tarcza I nie
może obracać się wokół punktu O
I
musi być nieruchoma, gdyż podpory przyłożone do tej tarczy nie
zezwalają na żaden inny ruch (rys. 12).
A
B
D
E
F
H
I
II
III
IV
I-nieruchoma
O
II
O
III
δ
δ
δ
O
IV
C
G
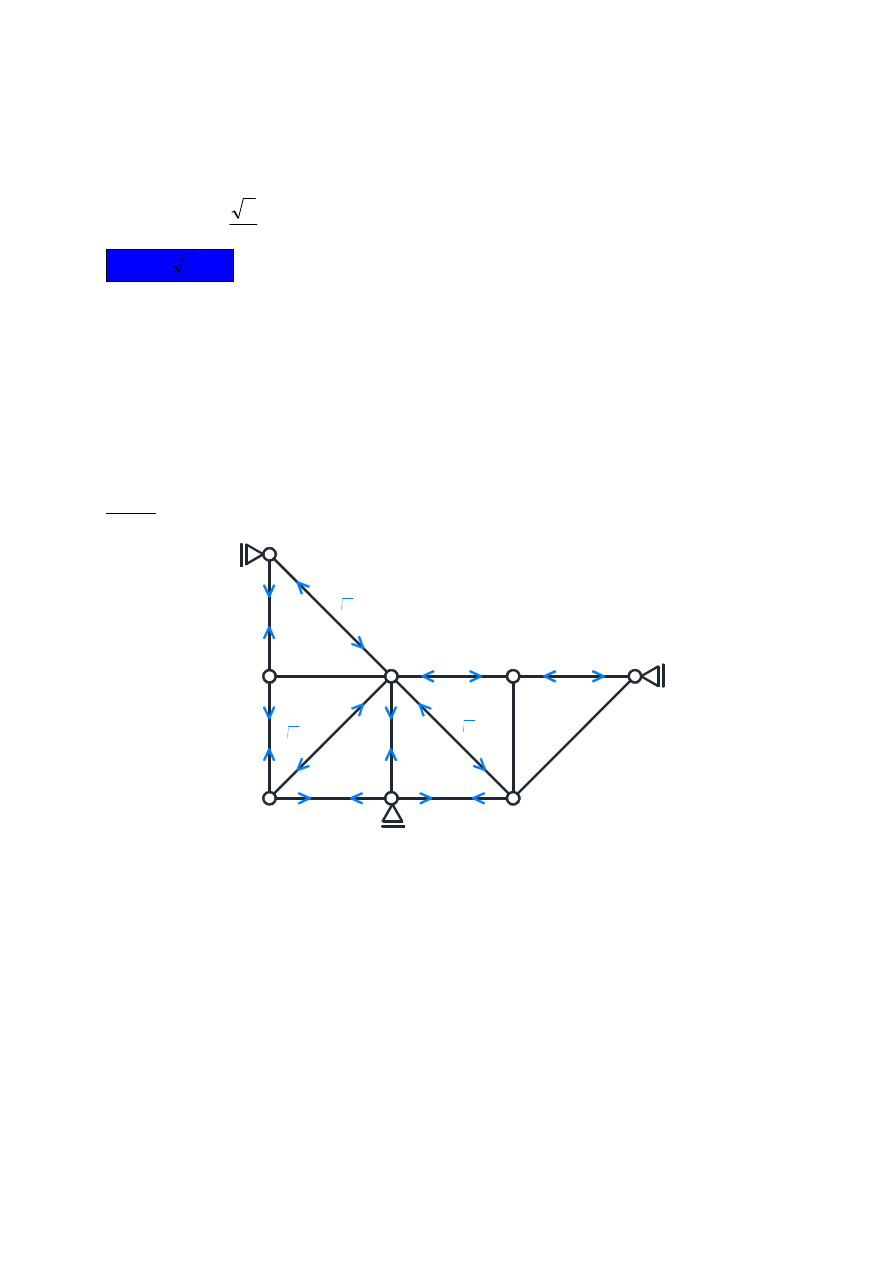
Rys. 12
Rozpoczynamy od początku analizę planu przesunięć wirtualnych układu, tym razem wychodząc od
założenia, że tarcza I pozostaje nieruchoma. Do tarczy III i tarczy IV należy odpowiednio punkt C
i punkt G, czyli punkty nieruchome, wokół których tarcze III i IV mogą się obracać. Przyjmując
wyjściowe przesunięcie wirtualne punktu D:
δ
=
Dy
v
z rzutów wyznaczamy kolejne przesunięcia:
δ
δ
δ
0
0
0
=
→
=
→
=
Ex
Dx
Cx
v
v
v
δ
δ
0
0
=
→
=
Hx
Gx
v
v
δ
δ
=
→
=
Hy
Dy
v
v
Z rzutów na prostą HE wyznaczamy ostatnią niewiadomą:
δ
δ
δ
δ
1
)
1
,
1
(
)
,
0
(
)
1
,
1
(
)
,
0
(
=
→
=
Ey
Ey
v
v
o
o
Ostatecznie z zasady prac wirtualnych obliczamy siłę N
9
:
δ
δ
δ
∀
=
⋅
⋅
+
⋅
0
2
2
]
[
2
9
N
kN
]
[
2
2
9
kN
N
−
=
Zadanie 2.
Wyznacz siły w pozostałych prętach kratownicy korzystając z zasady prac wirtualnych.
Wyniki:
A
B
C
D
E
F
G
H
4
4 2
0
2
2
10
2 2
0
0
10
4 2
4
6
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]
[kN]