CZARNA DZIURA dzia∏ajàca jako komputer mo˝e
wydawaç si´ pomys∏em absurdalnym. Jest to jednak
u˝yteczna koncepcja dla naukowców zajmujàcych si´
kosmologià i podstawami fizyki. JeÊli fizykom uda si´
stworzyç czarne dziury w akceleratorach (niektórzy
uwa˝ajà, ˝e nastàpi to w ciàgu najbli˝szego
dziesi´ciolecia), byç mo˝e b´dà mogli obserwowaç
prowadzone przez nie operacje obliczeniowe.

JEAN-FRANCOIS PODEVIN

C

zym ró˝ni si´ komputer od czarnej dziury? To pytanie, które brzmi jak po-
czàtek kiepskiego dowcipu, jest jednym z najg∏´bszych problemów wspó∏cze-
snej fizyki. Wi´kszoÊç ludzi sàdzi, ˝e komputery to wysoce wyspecjalizowa-

ne urzàdzenia, które mogà mieç postaç op∏ywowych pude∏ek stojàcych na biurku
lub chipów wielkoÊci paznokcia, umieszczanych na przyk∏ad w ekspresach do ka-
wy. Jednak dla fizyka komputerem jest ka˝dy obiekt fizyczny. Kamienie, bomby
atomowe czy galaktyki mogà nie u˝ywaç Linuxa, ale i one rejestrujà oraz przetwa-
rzajà informacj´. Ka˝dy elektron, foton lub inna czàstka elementarna przechowu-
je informacj´, której iloÊç mo˝na wymierzyç w bitach. Za ka˝dym razem, gdy dwie
czàstki oddzia∏ujà ze sobà, bity te ulegajà transformacji. Istnieniu obiektów fizycz-
nych nieod∏àcznie towarzyszy przetwarzanie informacji. Jak mówi John Wheeler,
fizyk z Princeton University: „Byt z bitu” (It from bit).

Odst´pstwem od regu∏y, w myÊl której wszystkie obiekty prowadzà obliczenia, wy-

dawa∏y si´ czarne dziury. Wprowadziç informacj´ do czarnej dziury jest ∏atwo;
jednak zgodnie z ogólnà teorià wzgl´dnoÊci Einsteina jej odzyskanie jest niemo˝-
liwe. Materia wpadajàca do czarnej dziury traci to˝samoÊç, a szczegó∏y jej struk-
tury zostajà zatarte w sposób nieodwracalny. W latach siedemdziesiàtych Stephen
Hawking z University of Cambridge uwzgl´dni∏ efekty mechaniki kwantowej i
stwierdzi∏, ˝e w zmodyfikowanej w ten sposób teorii czarne dziury emitujà pro-
mieniowanie, Êwiecàc niczym ˝arzàcy si´ w´giel. Promieniowanie to ma jednak
charakter losowy i nie niesie ˝adnej informacji. Gdyby do dziury wpad∏ s∏oƒ, mo-

GRUDZIE¡ 2004 ÂWIAT NAUKI

33

Idàc z duchem czasu, naukowcy

zaczynajà traktowaç prawa przyrody

jako programy komputerowe,

a ka˝dy obiekt fizyczny jako komputer

WSZECHÂWIAT

JAKO KOMPUTER

Seth Lloyd i Y. Jack Ng

g∏aby wydostaç si´ z niej iloÊç energii
równowa˝na jego masie spoczynkowej,
ale w postaci takiego galimatiasu, ˝e w
˝aden sposób – nawet czysto teoretycz-
nie – nie da∏oby si´ go odtworzyç.

Poniewa˝ prawa mechaniki kwanto-

wej zachowujà informacj´, jej znikanie
w czarnych dziurach jest powa˝nym
problemem teoretycznym. Dlatego tacy
naukowcy, jak Leonard Susskind ze
Stanford University, John Preskill z Ca-
lifornia Institute of Technology czy Ge-
rard ‘t Hooft z Universiteit Utrecht w
Holandii twierdzà, ˝e promieniowanie
czarnej dziury nie mo˝e mieç charakte-
ru losowego, lecz musi byç przetworzo-
nà formà poch∏oni´tej przez t´ dziur´
materii [patrz: Leonard Susskind „Czar-
ne dziury i paradoks informacji”; Âwiat
Nauki, czerwiec 1997]. Latem tego roku
podobny punkt widzenia przyjà∏ sam
Hawking. Okazuje si´ wi´c, ˝e czarne
dziury tak˝e prowadzà obliczenia.

Obiekty te sà najdziwaczniejszym przy-

k∏adem ogólnej zasady, zgodnie z którà
ca∏y WszechÊwiat odbiera i przetwarza
informacje. Sama zasada wcale nie jest
nowa. W XIX wieku twórcy mechaniki
statystycznej opracowali dziedzin´ ma-
jàcà objaÊniç prawa termodynamiki, któ-
rà póêniej nazwano teorià informacji. Na
pozór termodynamika jest bardzo odleg∏a
od teorii informacji: ta pierwsza powsta-
∏a, aby opisywaç maszyny parowe, druga
zaÊ – by zoptymalizowaç systemy ∏àcz-
noÊci. A jednak entropia – wielkoÊç ter-
modynamiczna ograniczajàca iloÊç u˝y-
tecznej pracy, jakà mo˝e wykonaç
maszyna parowa – jest proporcjonalna
do liczby bitów zmagazynowanych w po-
∏o˝eniach i pr´dkoÊciach czàsteczek, z
których sk∏ada si´ substancja robocza.
Stworzona w XX wieku mechanika kwan-
towa opar∏a to spostrze˝enie na solid-
nych fundamentach iloÊciowych i wpro-
wadzi∏a wa˝nà koncepcj´ informacji

kwantowej. Bity, z których zbudowany
jest WszechÊwiat, to bity kwantowe, czy-
li „qubity”, które pod wzgl´dem w∏asno-
Êci i mo˝liwoÊci sà znacznie ciekawsze i
bogatsze od zwyk∏ych bitów.

Badanie WszechÊwiata za pomocà bi-

tów i bajtów nie zast´puje zwyk∏ej ana-
lizy pos∏ugujàcej si´ konwencjonalnymi
wielkoÊciami takimi jak si∏a czy energia;
dzi´ki tej metodzie poznajemy jednak
nowe i zaskakujàce fakty. Na przyk∏ad
w ramach fizyki statystycznej pozwoli∏a
ona rozwik∏aç znany paradoks demona
Maxwella – urzàdzenia, które na pozór
umo˝liwia∏o wieczny ruch. W ostatnich
latach wraz z innymi fizykami zacz´li-
Êmy stosowaç jà do podstawowych pro-
blemów kosmologii i fizyki, takich jak
istota czarnych dziur, drobnoskalowa
struktura czasoprzestrzeni, natura kos-
micznej ciemnej energii czy ostateczne
prawa przyrody. Powiedzieç o Wszech-
Êwiecie, ˝e jest olbrzymim komputerem,
to za ma∏o – jest on olbrzymim kompu-
terem kwantowym. Fizyk Paola Zizzi z
Universit∫ degli Studi di Padova mówi:
„Byt z qubitu”.

Gdy gigaherc nie wystarcza

ZWIÑZEK FIZYKI Z TEORIÑ INFORMACJI

wyni-

ka z podstawowej maksymy mechaniki
kwantowej: w najdrobniejszej skali na-
tura ma charakter dyskretny (jest nie-
ciàg∏a). Uk∏ad fizyczny mo˝na opisaç za
pomocà skoƒczonej liczby bitów. Ka˝-
da czàstka uk∏adu zachowuje si´ jak
bramka logiczna w komputerze. „OÊ” jej
spinu mo˝e ustawiaç si´ w jednym z
dwóch kierunków, nadajàc w ten spo-
sób wartoÊç bitowi. Mo˝e te˝ szybko
zmieniaç ustawienie, co odpowiada pro-
stej operacji obliczeniowej.

Uk∏ad jest tak˝e dyskretny w czasie.

Zmiana wartoÊci bitu nast´puje nie w
jednej chwili, lecz w skoƒczonym inter-
wale czasowym. Dok∏adnà wartoÊç te-

go interwa∏u podaje twierdzenie Mar-
golusa–Levitina, nazwane tak na czeÊç
pionierów fizyki przetwarzania infor-
macji – Normana Margolusa z Massa-
chusetts Institute of Technology i Lva
Levitina z Boston University. Twierdze-
nie to opiera si´ na zasadzie nieozna-
czonoÊci Heisenberga, która ustala nie-
przekraczalne ograniczenia dok∏adnoÊci
pomiaru wielkoÊci fizycznych, takich
jak po∏o˝enie i p´d czy czas i energia.
Zgodnie z nim interwa∏ t potrzebny do
zmiany wartoÊci bitu zale˝y od iloÊci
energii E zu˝ytej do wykonania tej ope-
racji: im wi´cej energii dostarczymy
uk∏adowi, tym interwa∏ mo˝e byç krót-
szy. Matematycznie mo˝na to zapisaç w
postaci wzoru t

≥ h/4E, w którym h

oznacza sta∏à Plancka (podstawowy pa-
rametr teorii kwantów). Na przyk∏ad pe-
wien typ eksperymentalnego kompute-
ra kwantowego przechowuje bity w
protonach, przekszta∏cajàc je za pomo-
cà pól magnetycznych. Czas trwania
operacji przekszta∏cenia jest równy mi-
nimalnemu czasowi dopuszczalnemu
przez twierdzenie Margolusa–Levitina.

Z twierdzenia Margolusa–Levitina

mo˝na wyciàgnàç wiele wniosków, po-
czynajàc od ograniczeƒ na geometri´
czasoprzestrzeni, a na mo˝liwoÊciach
obliczeniowych ca∏ego WszechÊwiata
koƒczàc. Na rozgrzewk´ ocenimy mo˝-
liwoÊci obliczeniowe jednego kilogra-
ma zwyk∏ej materii umieszczonego w
obj´toÊci jednego litra. Takie urzàdze-
nie b´dziemy dalej nazywaç idealnym
laptopem.

Zasilaczem idealnego laptopa jest sa-

ma materia, która zamienia si´ na ener-
gi´ zgodnie ze s∏awnym wzorem Ein-
steina E = mc

2

. Je˝eli ca∏a ta energia

pos∏u˝y do przekszta∏cania bitów, kom-
puter b´dzie poczàtkowo pracowa∏ w
tempie 10

51

operacji na sekund´; jednak

wraz z wyczerpywaniem si´ energii tem-
po to b´dzie maleç. PojemnoÊç pami´ci
komputera mo˝na obliczyç za pomocà
zasad termodynamiki. JeÊli w obj´toÊci
jednego litra przekszta∏cimy kilogram
materii na energi´, jej temperatura wy-
niesie 10

9

K, entropia zaÊ (która jest pro-

porcjonalna do energii podzielonej przez
temperatur´) b´dzie odpowiadaç 10

31

bitom informacji. Nasz idealny laptop
magazynuje t´ informacj´ w po∏o˝eniach
czàstek elementarnych i w ich ruchach
mikroskopowych. Wykorzystywany jest
ka˝dy bit, na którego istnienie pozwala-
jà prawa termodynamiki.

34

ÂWIAT NAUKI GRUDZIE¡ 2004

n

Przez sam fakt swego istnienia ka˝dy uk∏ad fizyczny magazynuje informacj´. Podlegajàc

dynamicznej ewolucji, przetwarza t´ informacj´. Ca∏y WszechÊwiat prowadzi obliczenia.

n

Je˝eli – jak obecnie podejrzewa wi´kszoÊç fizyków – informacja mo˝e si´ wydostawaç

z czarnych dziur, to tak˝e i one prowadzà obliczenia. PojemnoÊç pami´ci czarnej dziury
jest proporcjonalna do kwadratu tempa obliczeƒ. Mo˝liwoÊç prowadzenia obliczeƒ
przez czarnà dziur´ wynika z kwantowej natury informacji. Gdyby nie efekty kwantowe,
czarne dziury niszczy∏yby wszelkie dane, zamiast je przetwarzaç.

n

Te same prawa fizyki, które ograniczajà moc obliczeniowà komputerów,

okreÊlajà dok∏adnoÊç, z jakà mo˝na mierzyç czasoprzestrzeƒ. Dok∏adnoÊç ta jest
mniejsza, ni˝ do tej pory sàdzono, co powoduje, ˝e „atomy” przestrzeni i czasu
mogà byç wi´ksze, ni˝ si´ spodziewano.

Przeglàd /

Kosmiczne komputery

GRUDZIE¡ 2004 ÂWIAT NAUKI

35

ALFRED T

. KAMAJIAN

OBLICZENIA EKSTREMALNE

CZYM JEST KOMPUTER? Wbrew pozorom to bardzo skomplikowane pytanie. Jakàkolwiek definicj´ byÊmy podali, spe∏nià jà nie tylko
zwyk∏e komputery, ale wszystkie obiekty we WszechÊwiecie. Mimo ˝e na wejÊciu i wyjÊciu takiego „naturalnego komputera” nie poja-
wiajà si´ ˝adne dane majàce praktyczne znaczenie dla cz∏owieka, mo˝e on rozwiàzywaç najprzeró˝niejsze problemy logiczne i mate-
matyczne. Naturalne komputery przechowujà dane w dyskretnych stanach kwantowych takich jak spin czàstek elementarnych, a za-
tem z samej swej istoty sà maszynami cyfrowymi. Ich systemem operacyjnym jest fizyka kwantowa.

WEJÂCIE

Klawiatura i zwiàzana z nià elektronika
kodujà informacj´ w postaci impulsów
elektrycznych.

Urzàdzenie, które zawiera 1 kg goràcej
plazmy w pojemniku o obj´toÊci 1 l, po-
biera dane zakodowane jako po∏o˝enia,
pr´dkoÊci i spiny czàstek.

Ta czarna dziura ma mas´ 1 kg i promieƒ
10

–27

m. Dane i instrukcje sà zakodowa-

ne we wrzucanej do niej materii.

Impulsy oddzia∏ujà ze sobà wewnàtrz urzà-
dzeƒ takich jak tranzystory, które prze-
prowadzajà operacje logiczne (np. NOT).

Czàstki oddzia∏ujà ze sobà. Zderzenia,
które zmieniajà ich stan, mo˝na wyko-
rzystaç do przeprowadzania operacji
logicznych.

Podczas spadku czàstki oddzia∏ujà z sobà
jak w idealnym laptopie, ale wa˝nà rol´
odgrywa tak˝e grawitacja. Nie znamy jesz-
cze praw fizyki rzàdzàcych tym procesem.

Po przetworzeniu impulsy zostajà za-
mienione na zrozumia∏e dla nas sygna-
∏y Êwietlne.

Parametry czàstek opuszczajàcych urzà-
dzenie mo˝na zmierzyç i odpowiednio zin-
terpretowaç. W miar´ wyczerpywania
energii plazmy tempo obliczeƒ maleje.

Czarna dziura emituje promieniowa-
nie Hawkinga. Z najnowszych teorii
wynika, ˝e zakodowane sà w nim wyni-
ki obliczeƒ.

ZWYCZAJNY L

APTOP

CZ¢STOÂå ZEGARA

: 10

9

Hz

n

P

AMI¢å: 10

12

b

IDEALNY

L

APTOP

CZ¢STOÂå ZEGARA

: 10

20

Hz

n

P

AMI¢å: 10

31

b

CZARNA DZIURA

CZ¢STOÂå ZEGARA

: 10

35

Hz

n

P

AMI¢å:

10

16

b

OBLICZENIA

WYJÂCIE

Kiedy czàstki oddzia∏ujà ze sobà, ich

stan ulega zmianie. Proces ten mo˝na
porównaç z programowaniem kompu-
tera w jednym z j´zyków, na przyk∏ad
C albo Java: czàstki odgrywajà rol´
zmiennych, a oddzia∏ywania – operacji
arytmetycznych takich jak dodawanie.
W idealnym laptopie ka˝dy bit mo˝e
ulegaç zmianie 10

20

razy na sekund´,

co odpowiada pr´dkoÊci zegara równej
100 gigagigaherców. W rzeczywistoÊci
uk∏ad dzia∏a zbyt szybko, by móg∏ byç
kontrolowany przez zegar centralny.
Czas, jakiego potrzebuje bit do zmiany
stanu, jest w przybli˝eniu równy czaso-
wi, w jakim sygna∏ jest przekazywany
do sàsiedniego bitu. Tak wi´c idealny
laptop dzia∏a w sposób równoleg∏y: nie
jak pojedynczy procesor, lecz jak ogrom-
ny uk∏ad procesorów, z których ka˝dy
pracuje prawie niezale˝nie od pozosta-
∏ych (szybkoÊç, z jakà procesory komu-
nikujà si´ mi´dzy sobà, jest stosunko-
wo niewielka).

Dla porównania komputer konwen-

cjonalny, który u˝ywa jednego proceso-
ra, operuje na oko∏o 10

12

b i przekszta∏-

ca je w tempie oko∏o 10

9

b/s. Je˝eli

prawo Moore’a* pozostanie w mocy od-
powiednio d∏ugo, nasi potomkowie b´-
dà mogli nabyç idealny laptop w po∏owie
XXIII wieku. (Naturalnie pod warun-
kiem, ˝e in˝ynierowie opracujà przed-
tem metod´ kontrolowania oddzia∏ywaƒ
czàstek w plazmie gor´tszej ni˝ jàdro
S∏oƒca i rozwià˝à problemy zwiàzane
z przechowywaniem komputerów. Trze-
ba te˝ pami´taç, ˝e sterowanie ideal-
nym laptopem i poprawianie b∏´dów w
znacznym stopniu zmniejszy przepusto-
woÊç jego ∏àczy komunikacyjnych).

W pewnym sensie takie urzàdzenie

mo˝na kupiç ju˝ dzisiaj – jeÊli ma si´ od-
powiednie znajomoÊci. Jednokilogramo-
wa porcja materii zamieniona ca∏kowicie
na energi´ to cz´sto u˝ywana definicja
bomby wodorowej o mocy 20 Mt. Wy-
buch termojàdrowy prowadzi do prze-
tworzenia wielkiej iloÊç informacji; na
wejÊciu znajduje si´ poczàtkowa konfigu-
racja bomby, na wyjÊciu zaÊ wyemito-
wane przez nià promieniowanie.

Mniej ni˝ nano

JE

˚ELI KA˚DA PORCJA MATERII

mo˝e byç

komputerem, to otrzymana z niej czar-
na dziura jest – ni mniej, ni wi´cej –
komputerem o najmniejszych mo˝li-
wych rozmiarach. Gdy komputer si´
kurczy, wzrasta si∏a grawitacji, z jakà
dzia∏ajà na siebie jego cz´Êci. W koƒcu
zamienia si´ w czarnà dziur´, której po-
le grawitacyjne jest tak silne, ˝e ˝aden
obiekt materialny nie mo˝e z niego
uciec. Promieƒ czarnej dziury, zwany
promieniem Schwarzschilda, jest wprost
proporcjonalny do jej masy.

Promieƒ czarnej dziury o masie jedne-

go kilograma wynosi oko∏o 10

–27

m. (Dla

porównania, proton ma promieƒ rów-
ny 10

–15

m). Zmniejszenie komputera

nie zmienia zawartej w nim energii, dla-
tego nadal mo˝e on wykonywaç 10

51

operacji na sekund´. Zmianie ulegnie
natomiast pojemnoÊç pami´ci. Gdy gra-
witacja nie ma znaczenia (tzn. gdy roz-

miary komputera sà du˝o wi´ksze od
rozmiarów czarnej dziury o takiej sa-
mej masie), ca∏kowita pojemnoÊç pa-
mi´ci jest proporcjonalna do liczby czà-
stek, a tym samym – do obj´toÊci. Gdy
jednak grawitacja dominuje, czàstki sà
ze sobà powiàzane tak silnie, ˝e ich zdol-
noÊç do przechowywania informacji zo-
staje wydatnie zmniejszona. Ca∏kowita
pojemnoÊç pami´ci czarnej dziury jest
proporcjonalna nie do jej obj´toÊci, lecz
do jej powierzchni. W latach siedem-
dziesiàtych Hawking i Jacob Bekenstein
z Uniwersytetu Hebrajskiego w Jerozo-
limie obliczyli, ˝e jednokilogramowa
czarna dziura mo˝e pomieÊciç 10

15

b,

czyli znacznie mniej ni˝ idealny laptop
przed kompresjà.

Czarna dziura jest za to znacznie szyb-

szym procesorem ni˝ elementy idealne-
go laptopa. Czas, którego potrzebuje,
by przekszta∏ciç bit, wynosi zaledwie
10

–35

s (jest równy czasowi, w jakim

Êwiat∏o pokonuje drog´ równà Êredni-
cy dziury). W odró˝nieniu od idealnego
laptopa, który jest uk∏adem równole-
g∏ym, czarna dziura pracuje jako poje-
dyncza jednostka obliczeniowa.

Jak jednak taka jednostka mo˝e dzia-

∏aç w praktyce? Wprowadzanie danych
wejÊciowych nie nastr´cza wi´kszych
trudnoÊci: trzeba tylko zakodowaç je w
materii lub energii i wrzuciç do czarnej
dziury. Zdolny haker, który nadzoruje
ten proces, powinien daç sobie rad´ z
zaprogramowaniem dziury w taki spo-
sób, by wykonywa∏a ˝àdane obliczenia.
Wszystko, co wrzucamy do dziury, tra-
ci kontakt z resztà WszechÊwiata w
chwili, gdy przekroczy tzw. horyzont
zdarzeƒ – powierzchni´, na której pr´d-
koÊç ucieczki jest równa pr´dkoÊci Êwia-
t∏a. Czàstki wpadajàce pod horyzont od-
dzia∏ujà ze sobà i przez pewien czas
wykonujà obliczenia a˝ do chwili, w któ-
rej docierajà do znajdujàcej si´ w Êrod-
ku dziury osobliwoÊci i tracà to˝samoÊç.
Co si´ z nimi wówczas stanie, zale˝y od
nieznanych obecnie szczegó∏ów kwanto-
wej grawitacji.

Dane wyjÊciowe sà zakodowane w pro-

mieniowaniu Hawkinga. Zgodnie z za-

36

ÂWIAT NAUKI GRUDZIE¡ 2004

ALFRED T

. KAMAJIAN

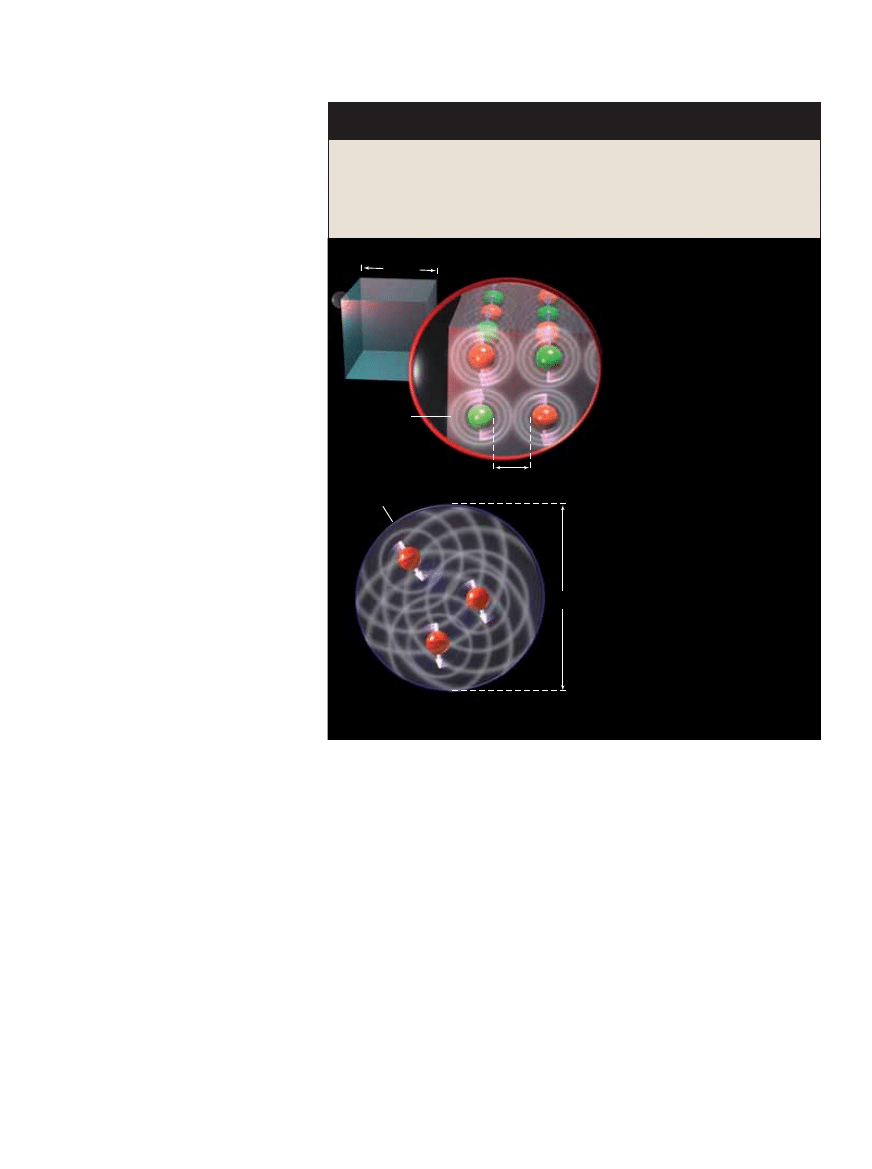
PODSTAWOWA ZASADA obliczeƒ kwan-
towych mówi, ˝e wymagajà one energii.
W spinie protonu zakodowany jest poje-
dynczy bit, którego wartoÊç mo˝na zmie-
niç za pomocà pola magnetycznego. Im
pole jest silniejsze (tzn. im wi´cej zawie-
ra energii), tym krócej trwa zmiana sta-
nu protonu.

Czas

Czas

Silne pole
magnetyczne
(wysoka energia)

S∏abe pole
magnetyczne
(niska energia)

HAKER

, który odpowiednio przygotuje materia∏

wrzucany do czarnej dziury,

MO˚E JÑ ZAPROGRAMOWAå

w taki sposób, by wykonywa∏a ˝àdane obliczenia.

sadà zachowania energii czarna dziura,
która emituje promieniowanie, zmniej-
sza swà mas´. Jednokilogramowy obiekt
ulega unicestwieniu zaledwie w 10

–21

s.

D∏ugoÊç fali, w której promieniowanie
Hawkinga osiàga najwi´ksze nat´˝enie,
jest równa promieniowi dziury. W przy-
padku jednokilogramowego obiektu od-
powiada ona bardzo twardemu promie-
niowaniu gamma. Detektor czàstek mo˝e
je zarejestrowaç i odkodowaç, udost´p-
niajàc nam zawartà w nim informacj´.

Badania, jakie przeprowadzi∏ Haw-

king nad noszàcym jego imi´ promie-
niowaniem, zmieni∏y powszechnie obo-
wiàzujàcy poglàd, ˝e nic nie mo˝e
wydostaç si´ z czarnych dziur [patrz:
Stephen W. Hawking „The Quantum Me-
chanics of Black Holes”; Scientific Ame-
rican, styczeƒ 1977]. Tempo, w jakim
promieniujà czarne dziury, jest odwrot-
nie proporcjonalne do ich rozmiarów.
Z tego powodu wielkie czarne dziury
znajdujàce si´ w centrach galaktyk aku-
mulujà materi´ szybciej, ni˝ tracà ener-
gi´. W przysz∏oÊci eksperymentatorzy
b´dà mogli wytwarzaç w akceleratorach
miniaturowe czarne dziury, które pra-
wie natychmiast eksplodujà, zamienia-
jàc si´ w promieniowanie. Takie dziury
nie b´dà obiektami trwa∏ymi, lecz chwi-
lowymi skupieniami materii, które pro-
wadzà obliczenia z najwi´kszà mo˝liwà
pr´dkoÊcià.

Teleportacja przez horyzont

ZASADNICZÑ KWESTIÑ

jest jednak pytanie,

czy zarejestrowane promieniowanie
Hawkinga rzeczywiÊcie przyniesie nam
zakodowane wyniki obliczeƒ, czy te˝
oka˝e si´ nic nieznaczàcym be∏kotem.
Sprawa pozostaje sporna, ale wi´kszoÊç
fizyków (∏àcznie z samym Hawkingiem)
uwa˝a, ˝e w promieniowaniu zakodo-
wane sà przetworzone informacje, któ-
re dosta∏y si´ do dziury, kiedy powsta-
wa∏a. Oznacza∏oby to, ˝e informacja
mo˝e wydostaç si´ z czarnej dziury, choç
nie mo˝e tego zrobiç materia. Kwestia,
w jaki sposób do tego dochodzi, jest
jednym z najciekawszych problemów
wspó∏czesnej fizyki.

Jeden z mo˝liwych mechanizmów zo-

sta∏ przedstawiony w zesz∏ym roku przez
Gary’ego Horowitza z University of Ca-
lifornia w Santa Barbara i Juana Malda-
cen´ z Institute for Advanced Study w
Princeton w New Jersey. Opiera si´ on
na splàtaniu – efekcie kwantowym, dzi´-
ki któremu w∏asnoÊci co najmniej dwóch

uk∏adów pozostajà ze sobà zwiàzane mi-
mo dzielàcych je wielkich odleg∏oÊci
przestrzennych i czasowych. Splàtanie
umo˝liwia teleportacj´, która niezwy-
kle wiernie przekazuje informacje od
jednej czàstki do drugiej. Wyglàda to
tak, jakby czàstka zosta∏a przes∏ana z
jednego miejsca w drugie z pr´dkoÊcià
si´gajàcà pr´dkoÊci Êwiat∏a.

Teleportacj´ mo˝na przeprowadziç w

laboratorium. Najpierw nale˝y splàtaç
ze sobà dwie czàstki, a nast´pnie doko-
naç wspólnego pomiaru jednej z nich
oraz materii, która zawiera informacj´
przeznaczonà do teleportacji. W nast´p-
stwie pomiaru informacja zostaje wy-
mazana, ale splàtanie powoduje, ˝e po-
jawia si´ ona w zakodowanej formie w
drugiej czàstce. Odleg∏oÊç, jaka dzieli
czàstki, jest bez znaczenia. Informacj´

mo˝na odkodowaç, korzystajàc z klu-
cza, którym sà wyniki pomiaru [patrz:
Anton Zeilinger „Kwantowa teleporta-
cja”; Âwiat Nauki, lipiec 2000].

Podobny mechanizm mo˝e dzia∏aç w

przypadku czarnych dziur. Para splàta-
nych fotonów pojawia si´ tu˝ nad hory-
zontem zdarzeƒ. Jeden z nich odlatuje
na zewnàtrz w postaci obserwowalne-
go promieniowania Hawkinga, drugi
natomiast wpada pod horyzont, gdzie
∏àczy si´ z osobliwoÊcià powsta∏à z ma-
terii, która utworzy∏a czarnà dziur´. Uni-
cestwienie drugiego fotonu spe∏nia rol´
pomiaru, w którego nast´pstwie infor-
macja zawarta w materii wpadajàcej
pod horyzont zostaje przekazana pro-
mieniowaniu Hawkinga.

Aby odkodowaç przekazanà informa-

cj´, nie musimy znaç wyniku tego „po-

GRUDZIE¡ 2004 ÂWIAT NAUKI

37

ALFRED T

. KAMAJIAN

KLASYFIKACJA KOMPUTERÓW

0.1

m

3

× 10

–12

m

Czarna dziura

Sygna∏

1.5

× 10

–27

m

IDEALNY LAPTOP i komputer z czarnej dziury ilustrujà dwie ró˝ne metody zwi´ksza-
nia mocy obliczeniowej. Idealny laptop jest optymalnym komputerem równoleg∏ym, z∏o-
˝onym z olbrzymiej liczby równoczeÊnie pracujàcych procesorów. Czarna dziura to
optymalny komputer jednoprocesorowy, w którym bardzo szybki procesor wykonuje
wszystkie instrukcje po kolei.

Idealny laptop zawiera zbiór
czàstek, które kodujà i przetwarzajà
bity. Ka˝da czàstka mo˝e wykonaç
jednà instrukcj´ w czasie 10

–20

s,

w którym sygna∏ Êwietlny pokonuje
dystans 3

× 10

–12

m (równy

odleg∏oÊci mi´dzy czàstkami).
Przekazywanie danych mi´dzy
oddalonymi od siebie „procesorami”
trwa znacznie d∏u˝ej ni˝ ich
przetwarzanie. Poszczególne grupy
procesorów pracujà prawie
niezale˝nie.

W komputerze z czarnej dziury
tak˝e znajdujà si´ czàstki. Poniewa˝
sà bardzo mocno powiàzane si∏à
grawitacji, mieszczà mniej bitów
ni˝ idealny laptop. Dzi´ki temu na
ka˝dy bit przypada wi´cej energii.
Jedna instrukcja jest wykonywana
w ciàgu 10

–35

s (jest to czas,

w jakim sygna∏ Êwietlny pokonuje
odleg∏oÊç równà Êrednicy dziury).
Przekazywanie danych odbywa si´
z takà samà szybkoÊcià, jak ich
przetwarzanie. Komputer pracuje
jako pojedynczy procesor.

miaru” (co w przypadku teleportacji
przeprowadzanej w laboratorium jest
niezb´dne). Jak wykazali Horowitz i
Maldacena, przy teleportacji przez hory-
zont wynik ten jest ÊciÊle okreÊlony: ze-
wn´trzny obserwator mo˝e go obliczyç,
opierajàc si´ na podstawowych prawach
fizyki i dzi´ki temu odkodowaç infor-
macj´. Wniosek ten – kontrowersyjny,
ale mo˝liwy do przyj´cia – wykracza
poza standardowe sformu∏owanie me-
chaniki kwantowej. Byç mo˝e osobli-
woÊci wewnàtrz czarnych dziur – po-
dobnie jak osobliwoÊç na poczàtku
WszechÊwiata – mogà znajdowaç si´ tyl-

ko w jednym stanie. W czerwcu tego ro-
ku jeden z nas (Lloyd) wykaza∏, ˝e me-
chanizm Horowitza–Maldaceny dzia∏a
niezale˝nie od konkretnej postaci stanu
koƒcowego (pod warunkiem ˝e takowy
istnieje); dla teorii jest wi´c mechani-
zmem bardzo solidnym. Jak si´ jednak
wydaje, prowadzi on do niewielkiej utra-
ty informacji.

Mechanizmy odzyskiwania informa-

cji opracowane przez innych naukow-
ców równie˝ opierajà si´ na dziwacz-
nych efektach kwantowych. W 1996
roku Andrew Strominger i Cumrun Va-
fa z Harvard University wysun´li hipo-

tez´, ˝e czarne dziury sà zbudowane z
wielowymiarowych struktur zwanych
branami, które pojawiajà si´ w teorii
strun. Informacje wpadajàce do czar-
nych dziur sà przechowywane w bra-
nach w postaci fal i mogà zostaç odzy-
skane. W bie˝àcym roku Samir Mathur
z Ohio State University i jego wspó∏pra-
cownicy stworzyli model czarnej dziury
jako plàtaniny strun. Taki „k∏´bek” jest
sk∏adem informacji dostarczanych przez
obiekty wpadajàce do czarnej dziury, a
emitowane przez niego promieniowa-
nie odzwierciedla te informacje. Ostat-
nio Hawking stwierdzi∏, ˝e fluktuacje

38

ÂWIAT NAUKI GRUDZIE¡ 2004

ALFRED T

. KAMAJIAN

Ewolucja teorii czarnych dziur

„OBIEKT tak g´sty, ˝e nawet Êwiat∏o nie mo˝e si´ z niego wydostaç” – choç ta definicja czarnej dziury pojawia si´ cz´sto w gaze-
tach i wyk∏adach z astronomii dla poczàtkujàcych, zapewne nie jest poprawna. Od po∏owy lat siedemdziesiàtych fizycy twierdzà, ˝e
energia wydostaje si´ z czarnych dziur, a obecnie doszli do wniosku, ˝e mo˝e to uczyniç tak˝e informacja (zakodowana w formie,
jakà przybiera energia). Diagramy przedstawiajà czarnà dziur´ widzianà przez hipotetycznego obserwatora, który znajduje si´ poza
czasoprzestrzenià.

W OBRAZIE KLASYCZNYM,
stworzonym na bazie fizyki
przedkwantowej, „granic´ czarnej
dziury” (horyzont zdarzeƒ) mo˝na
przekroczyç tylko raz. Obiekt, który
wpad∏ do czarnej dziury, nie mo˝e si´
ju˝ z niej wydostaç ani przes∏aç
z jej wn´trza ˝adnej informacji.
W Êrodku czarnej dziury znajduje si´
osobliwoÊç, w której materia traci
to˝samoÊç, a informacja ginie.

W MODELU HOROWITZA–MALDACENY
oddalajàca si´ czàstka jest
kwantowomechanicznie splàtana
z czàstkà wpadajàcà do dziury,
która z kolei jest splàtana z materià.
Dzi´ki efektowi splàtania informacja
jest przekazywana z wn´trza czarnej
dziury do jej otoczenia.

MODEL HAWKINGA jest pierwszà
próbà uwzgl´dnienia efektów
kwantowych. Tu˝ nad horyzontem
zdarzeƒ powstajà pary czàstek
wirtualnych (czerwone i niebieskie
kulki). Jedna z czàstek danej pary
wpada do osobliwoÊci razem
z materià, druga natomiast oddala
si´ od czarnej dziury. Spiny
czàstek sà przypadkowe
i nie niosà informacji o wpadajàcej
materii.

Para czàstek wirtualnych

Kwantowa
teleportacja

Materia

Horyzont zdarzeƒ

OsobliwoÊç

kwantowe mogà uniemo˝liwiç powsta-
nie dobrze okreÊlonego horyzontu. ¸a-
wa przysi´g∏ych wcià˝ debatuje nad ty-
mi pomys∏ami.

Cybernetyczna czasoprzestrzeƒ

W

¸AÂCIWOÂCI CZARNYCH DZIUR

sà niero-

zerwalnie zwiàzane z w∏aÊciwoÊciami
czasoprzestrzeni. Je˝eli zatem traktu-
jemy czarnà dziur´ jako komputer, w
taki sam sposób mo˝emy traktowaç cza-
soprzestrzeƒ. Zgodnie z mechanikà
kwantowà czasoprzestrzeƒ – tak jak
wszystkie uk∏ady fizyczne – ma natur´
dyskretnà. Ani odleg∏oÊci, ani odst´pów
czasowych nie mo˝na mierzyç z dowol-
nà dok∏adnoÊcià. W najmniejszej skali
czasoprzestrzeƒ przypomina pian´.
Maksymalna iloÊç informacji, jakà mo-
˝e pomieÊciç dany obszar czasoprze-
strzeni, zale˝y od rozmiarów bitów, któ-
re nie mogà byç mniejsze od „bàbelków”
piany (tzn. podstawowych komórek cza-
soprzestrzeni).

Przez d∏ugi czas fizycy zak∏adali, ˝e

rozmiary podstawowych komórek sà
równe d∏ugoÊci Plancka (l

P

) wynoszà-

cej 10

–35

m. W tej skali wa˝ne stajà si´

zarówno fluktuacje kwantowe, jak i efek-
ty grawitacyjne. Je˝eli to prawda, ko-
mórki sà zbyt ma∏e, byÊmy kiedykolwiek
mogli je zaobserwowaç. Jednak˝e Ng
oraz Hendrik van Dam z University of
North Carolina w Chapel Hill i Frigyes
Károlyházy z Uniwersytetu Loránda
Eötvösa w Budapeszcie wykazali, ˝e nie
majà one uniwersalnych, ustalonych roz-
miarów – obowiàzuje zasada: im wi´k-
szy jest obszar czasoprzestrzeni, tym
wi´ksze sà jego podstawowe komórki.
Z pozoru stwierdzenie to zakrawa na
paradoks: to tak, jakby atomy, z których
sk∏ada si´ s∏oƒ, by∏y wi´ksze od atomów,
z których sk∏ada si´ mysz! Jego wiary-
godnoÊç zwi´ksza jednak fakt, ˝e do
identycznego wniosku doszed∏ niezale˝-
nie Lloyd, korzystajàc z tych samych
praw, które ograniczajà mo˝liwoÊci
komputerów.

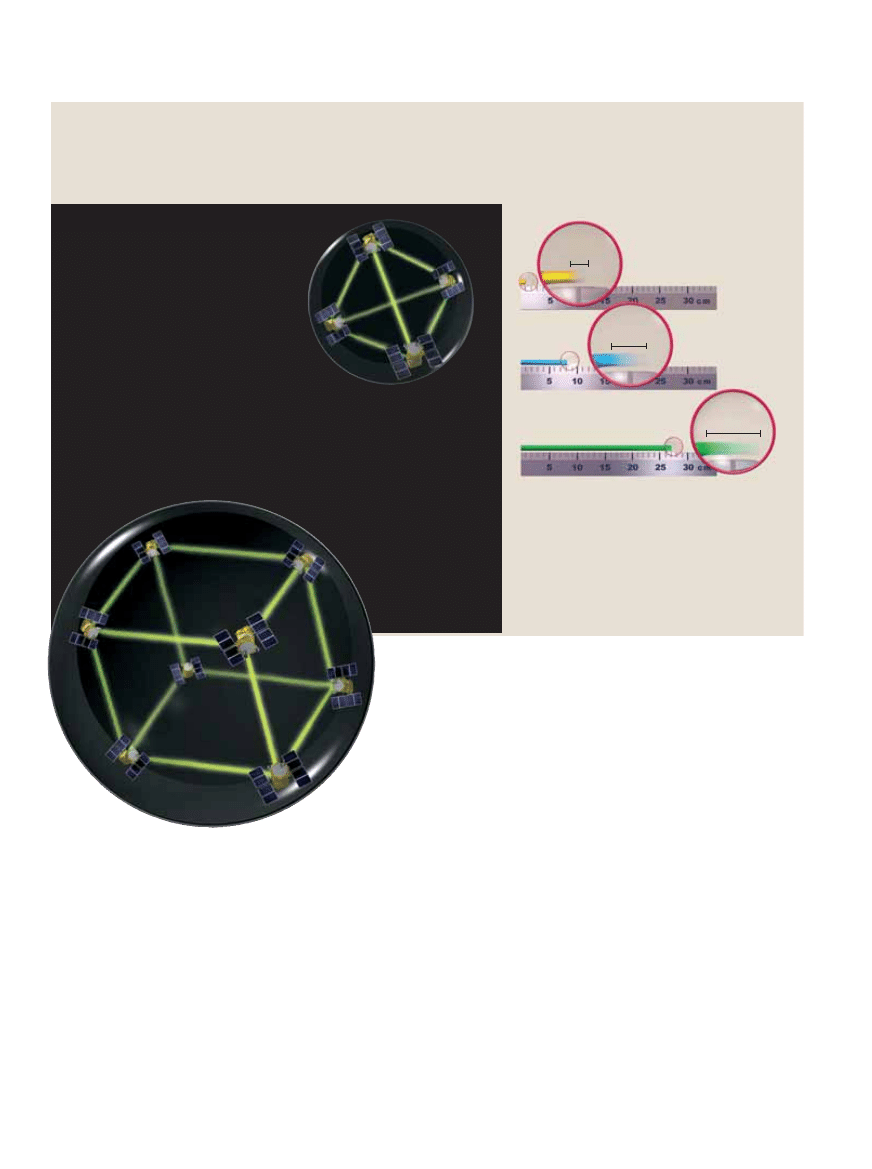
Sporzàdzanie geometrycznej mapy

czasoprzestrzeni jest procesem oblicze-
niowym, w którym transmisja i przetwa-

rzanie informacji s∏u˝y do pomiaru odle-
g∏oÊci. Takà map´ mo˝na wykonaç, roz-
mieszczajàc w badanym obszarze sate-
lity Globalnego Systemu Lokalizacji (GPS
– Global Positioning System). Ka˝dy sa-
telita jest wyposa˝ony w zegar i nadaj-
nik radiowy [ilustracja na nast´pnej stro-
nie]. Aby wyznaczyç odleg∏oÊç, odbiera
sygna∏y innych satelitów, dla ka˝dego z
nich mierzàc interwa∏y czasu mi´dzy wy-
s∏aniem sygna∏u i jego odbiorem. Dok∏ad-
noÊç pomiaru jest odgraniczona – zale˝y
od cz´stoÊci, z jakà tyka zegar. Poniewa˝
tykanie to tak˝e operacja obliczeniowa,
maksymalnà cz´stoÊç okreÊla twierdzenie
Margolusa–Levitina: odst´p czasu mi´-
dzy dwoma tykni´ciami jest odwrotnie
proporcjonalny do energii.

Energia jest tak˝e ograniczona. Gdy-

by satelitom dostarczyç jej zbyt wiele
albo umieÊciç je zbyt blisko siebie, po-
wsta∏aby z nich czarna dziura, co ozna-
cza∏oby koniec pracy nad mapà (dziura
emitowa∏aby promieniowanie Hawkin-
ga o d∏ugoÊci fali porównywalnej z jej
rozmiarami, które by∏oby bezu˝yteczne
dla pomiarów w mniejszej skali). Maksy-
malna ca∏kowita energia zespo∏u sateli-
tów jest proporcjonalna do promienia
badanego obszaru, co oznacza, ˝e roÊnie
wolniej ni˝ jego obj´toÊç. Gdy obszar sta-
je si´ coraz wi´kszy, kartograf musi iÊç na
ust´pstwa – albo zmniejszajàc g´stoÊç
satelitów (czyli rozmieszczajàc je coraz
rzadziej), albo ograniczajàc energi´ do-
st´pnà ka˝demu satelicie (czyli zmniej-
szajàc cz´stotliwoÊç tykania zegarów).
W obu przypadkach maleje dok∏adnoÊç
pomiarów. W czasie potrzebnym do

opracowania mapy obszaru o promie-
niu R ∏àczna liczba tykni´ç wszystkich
satelitów wynosi R

2

/l

P

2

. Je˝eli w tym cza-

sie ka˝dy z nich tyka tylko raz, satelity
muszà byç oddalone od siebie Êrednio o
R

1/3

l

P

2/3

. Co prawda, w pewnym podob-

szarze mo˝na mierzyç mniejsze odleg∏o-
Êci, ale tylko kosztem ograniczenia pre-
cyzji w innym podobszarze. Wniosek ten
jest s∏uszny tak˝e w przypadku rozsze-
rzajàcej si´ przestrzeni.

Najwi´kszà dok∏adnoÊç, z jakà mo˝na

mierzyç odleg∏oÊci, osiàgamy wtedy, gdy
nasz system pomiarowy jest na granicy
przekszta∏cenia si´ w czarnà dziur´. W
mniejszej skali geometria czasoprze-
strzeni przestaje istnieç. Graniczna d∏u-
goÊç, chocia˝ bardzo ma∏a, jest o wiele
wi´ksza od d∏ugoÊci Plancka. W przy-
padku ca∏ego obserwowanego Wszech-
Êwiata minimalna mierzalna d∏ugoÊç
wynosi 10

–15

m. W takiej skali uda si´

byç mo˝e zaobserwowaç ziarnistoÊç
przestrzeni za pomocà precyzyjnych
urzàdzeƒ do pomiaru odleg∏oÊci, na
przyk∏ad przysz∏ych detektorów fal gra-
witacyjnych.

Dla teoretyka wa˝nà konsekwencjà

tego ograniczenia jest mo˝liwoÊç nowe-
go spojrzenia na teori´ czarnych dziur.
Ng wykaza∏, ˝e nieintuicyjna zale˝noÊç
fluktuacji czasoprzestrzennych od pier-
wiastka szeÊciennego odleg∏oÊci pozwa-
la wyprowadziç nowà metodà wzór Be-
kensteina–Hawkinga na pojemnoÊç
pami´ci czarnej dziury. Ponadto z za-
le˝noÊci tej wynika uniwersalne ogra-
niczenie, któremu podlega ka˝dy kom-
puter z czarnej dziury: liczba bitów,

GRUDZIE¡ 2004 ÂWIAT NAUKI

39

SETH LLOYD i Y. JACK NG pracujà na styku dwóch najbardziej ekscytujàcych dziedzin fizy-
ki teoretycznej: kwantowej teorii informacji i kwantowej teorii grawitacji. Lloyd, który jest
profesorem in˝ynierii kwantowej w Massachusetts Institute of Technology, zaprojektowa∏
pierwszy mo˝liwy do zbudowania komputer kwantowy. Obecnie wraz z wieloma zespo∏ami na-
ukowymi zajmuje si´ konstruowaniem i programowaniem komputerów kwantowych oraz sys-
temów ∏àcznoÊci. Ng, profesor fizyki w University of North Carolina w Chapel Hill, bada fun-
damentalnà struktur´ czasoprzestrzeni; opracowa∏ m.in. liczne doÊwiadczenia majàce zg∏´biç
jej kwantowà natur´. Obaj uczeni ubolewajà, ˝e ich praca nie spotyka si´ z uznaniem
najbli˝szych. Kiedy Lloyd opowiada∏ córkom, ˝e wszystko jest zrobione z bitów, jedna z nich
odpar∏a bez ogródek: „Tata, nie masz racji. Wszystko – poza Êwiat∏em – jest zrobione
z atomów”. Natomiast Ng nadszarpnà∏ swój autorytet, poniewa˝ zawsze musi prosiç sy-
nów o pomoc przy komputerze.

O

AUTORACH

MECHANIZM WYP¸YWU INFORMACJI

z czarnej dziury jest jednym z najciekawszych

problemów wspó∏czesnej fizyki.

które mo˝na pomieÊciç w jego pami´-
ci, jest proporcjonalna do kwadratu tem-
pa wykonywania obliczeƒ. Wspó∏czyn-
nik proporcjonalnoÊci, równy Gh/c

5

,

wià˝e informacj´ ze szczególnà teorià
wzgl´dnoÊci (przez pr´dkoÊç Êwiat∏a c),
z ogólnà teorià wzgl´dnoÊci (przez sta-
∏à grawitacji G) i z mechanikà kwanto-
wà (przez sta∏à Plancka h).

Bardzo wa˝ne jest równie˝ to, ˝e

powy˝sze rozwa˝ania prowadzà bez-
poÊrednio do zasady holograficznej,
która mówi, ˝e nasz trójwymiarowy
WszechÊwiat jest w pewien szczególny
sposób dwuwymiarowy. Najwi´ksza

mo˝liwa iloÊç informacji,

jakà mo˝e przechowaç do-

wolny obszar przestrzeni,

jest proporcjonalna nie do

jego obj´toÊci, lecz do jego

powierzchni [patrz: Jacob D.

Bekenstein „Informacja w holo-

graficznym wszechÊwiecie”; Âwiat

Nauki, wrzesieƒ 2003]. Zwykle uwa-

˝a si´, ˝e zasada holograficzna odzwier-
ciedla naszà nieznajomoÊç szczegó∏ów
kwantowej grawitacji, ale – jak si´ oka-
zuje – mo˝na jà tak˝e otrzymaç, wycho-
dzàc z podstawowych ograniczeƒ kwan-
towych na dok∏adnoÊç pomiaru.

Licz´, wi´c jestem

REGU

¸Y MAGAZYNOWANIA

i przetwarzania

informacji, jakim podlegajà komputery
najmniejsze i najbardziej zwarte (bàbel-
ki czasoprzestrzeni i czarne dziury) obo-
wiàzujà tak˝e w przypadku najwi´ksze-
go komputera: ca∏ego WszechÊwiata.
Jego rozmiary mogà byç nieskoƒczone,
ale istnieje on skoƒczony czas – przy-
najmniej w obecnej postaci. Ârednica

jego obserwowalnej cz´Êci wynosi obec-
nie mniej wi´cej kilkadziesiàt miliardów
lat Êwietlnych. Mo˝emy poznaç wyniki
tylko tych obliczeƒ, które zosta∏y wyko-
nane w tym obszarze.

Przeprowadzona powy˝ej analiza ty-

kania zegarów pozwala wyznaczyç licz-
b´ operacji, które WszechÊwiat móg∏
przeprowadziç od momentu swego po-
wstania: wynosi ona 10

123

. Obserwowa-

na g´stoÊç energii kosmicznej (na któ-
rà sk∏ada si´ energia spoczynkowa
materii widzialnej i ciemnej oraz ciem-
na energia odpowiedzialna za przyÊpie-
szenie tempa ekspansji WszechÊwia-
ta) wynosi oko∏o 10

–9

J/m

3

. Ca∏y obser-

wowalny WszechÊwiat zawiera zatem
10

72

J energii i zgodnie z twierdzeniem

Margolusa–Levitina mo˝e wykonywaç
najwy˝ej 10

106

operacji na sekund´. Pra-

cujàc przez ca∏y czas z maksymalnà
pr´dkoÊcià, od chwili powstania móg∏
ich wykonaç nie wi´cej ni˝ 10

123

. Jak

wi´c widzimy, WszechÊwiat przeprowa-
dzi∏ maksymalnà liczb´ operacji, na ja-
kà zezwalajà prawa fizyki.

40

ÂWIAT NAUKI GRUDZIE¡ 2004

ALFRED T

. KAMAJIAN

+

– 1 × 10

–22

cm

+

– 2 × 10

–22

cm

+

– 3 × 10

–22

cm

Geodezja w czasoprzestrzeni

Pomiary odleg∏oÊci i odst´pów czasowych sà rodzajem obliczeƒ; podlegajà wi´c tym samym ograniczeniom, co komputery. Okazuje si´,
˝e mierzenie jest procesem znacznie bardziej skomplikowanym, ni˝ to sobie wyobra˝ano.

ABY SPORZÑDZIå MAP¢ obszaru przestrze-
ni, mo˝na wykorzystaç satelity Globalnego
Systemu Lokalizacji (GPS). Dokonujà one po-
miarów, przesy∏ajàc mi´dzy sobà sygna∏y i
wyznaczajàc momenty ich przybycia. Chcàc
uzyskaç maksymalnà dok∏adnoÊç, trzeba u˝yç
bardzo wielu satelitów. Ich liczba nie mo˝e
byç jednak dowolnie du˝a – jeÊli b´dzie ich
zbyt wiele, zapadnà si´ do czarnej dziury.

Do zmierzenia obszaru o dwukrotnie wi´k-
szych rozmiarach, trzeba u˝yç dwa razy wi´-
cej satelitów. Poniewa˝ obj´toÊç obszaru wzra-
sta oÊmiokrotnie, odleg∏oÊci mi´dzy satelitami
muszà si´ zwi´kszyç. Ka˝dy z nich zajmuje si´
wi´kszym podobszarem, poÊwi´cajàc mniej
uwagi pojedynczym pomiarom. Dok∏adnoÊç
pomiaru maleje.

B¸ÑD POMIARU nie jest zatem sta∏y, lecz zale˝y
od wielkoÊci mierzonego obiektu. Im obiekt ten
jest wi´kszy, tym bardziej rozmyta jest jego struk-
tura. Taki efekt nie wyst´puje w codziennym ˝y-
ciu, w którym b∏àd pomiaru zale˝y tylko od pre-
cyzji podzia∏ki na linijce. Wyglàda na to, ˝e
wybierajàc przedmiot pomiarów, mo˝emy wp∏y-
waç na drobnoskalowà struktur´ czasoprzestrzeni.

s PROMIE¡: 100

km

LICZBA SATELITÓW: 4

ROZSTAW: 90

km

t PROMIE¡: 200

km

LICZBA SATELITÓW: 8

ROZSTAW: 150

km

ZWI¢KSZENIE B¸¢DU: 26%

Ca∏kowità pojemnoÊç pami´ci mate-

rii konwencjonalnej (takiej jak atomy)
lub równowa˝nej jej energii, mo˝na ob-
liczyç, u˝ywajàc standardowych metod
fizyki statystycznej i kosmologii. Okazu-
je si´, ˝e najwi´cej informacji mo˝na
zmagazynowaç w bezmasowych czàst-
kach takich jak fotony. G´stoÊç ich entro-
pii jest proporcjonalna do szeÊcianu tem-
peratury, g´stoÊç energii zaÊ (która
okreÊla liczb´ mo˝liwych do wykonania
operacji) do czwartej pot´gi temperatu-
ry. Ca∏kowita liczba bitów jest równa
liczbie operacji podniesionej do pot´gi

3

/

4

i w przypadku ca∏ego WszechÊwiata

wynosi 10

92

(mo˝e ona nieco wzrosnàç,

jeÊli czàstki majà jakàÊ struktur´ we-
wn´trznà). Bity te mogà przekszta∏caç
si´ szybciej, ni˝ komunikowaç si´ ze so-
bà; dlatego – w odró˝nieniu od czarnej
dziury – zwyk∏a materia jest kompu-
terem równoleg∏ym, podobnie jak
idealny laptop.

Fizycy nie wiedzà, czym jest

ciemna energia, dlatego nie po-
trafià obliczyç iloÊci informa-
cji, jakà mo˝e przechowaç. Z
zasady holograficznej wynika
jednak, ˝e we WszechÊwie-
cie zmieÊci si´ co najwy˝ej
10

123

b – mniej wi´cej tyle,

ile wynosi najwi´ksza mo˝li-
wa liczba operacji. Ta przybli-
˝ona równoÊç nie jest przypad-
kowa. Nasz WszechÊwiat ma
g´stoÊç zbli˝onà do krytycznej.
Gdyby by∏a ona nieznacznie wi´k-
sza, zapad∏by si´ pod wp∏ywem w∏a-
snej grawitacji, tak jak zapada si´ ma-
teria, gdy powstaje z niej czarna dziura.
Z tego w∏aÊnie powodu spe∏nia (lub pra-
wie spe∏nia) warunek maksymalizacji
liczby obliczeƒ. W ka˝dym momencie
maksymalna liczba bitów, jakie mo˝e po-
mieÊciç WszechÊwiat, jest w przybli˝e-
niu równa liczbie operacji, jakie do te-
go momentu mog∏y byç wykonane.

Zwyk∏a materia przeprowadza

ogromnà liczb´ operacji, natomiast
ciemna energia zachowuje si´ zupe∏nie
inaczej. Je˝eli zakodowana jest w niej
maksymalna liczba bitów dopuszczal-

na przez zasad´ holograficznà, wówczas
w ca∏ej historii kosmosu ogromna wi´k-
szoÊç z nich mog∏a ulec przekszta∏ceniu
zaledwie jeden raz. Te niekonwencjo-
nalne bity sà zatem jedynie biernymi ob-
serwatorami obliczeƒ przeprowadza-
nych z o wiele wi´kszà szybkoÊcià przez
znacznie mniej liczne bity konwencjo-
nalne. Czymkolwiek by∏aby ciemna
energia, nie pogrà˝a si´ w obliczeniach.
I wcale nie musi. Dostarczanie Wszech-
Êwiatowi brakujàcej masy i przyÊpiesza-
nie jego ekspansji to zadania niezbyt
skomplikowane numerycznie.

Co oblicza WszechÊwiat? Wyglàda na

to, ˝e nie szuka konkretnej odpowiedzi

na konkretne, choçby bardzo trudne py-
tanie, jak to w klasycznej powieÊci fan-
tastycznonaukowej robi∏ gigantyczny
komputer G∏´boka MyÊl (Douglas Adams
Autostopem przez Galaktyk´; Wydawnic-
two Zysk i S-ka, Poznaƒ 1994). Po pro-
stu oblicza siebie samego. Zaprogramo-
wany przez prawa fizyki, modeluje pola
kwantowe, zwiàzki chemiczne, bakte-
rie, ludzi, gwiazdy i galaktyki. W trakcie
tych operacji tworzy map´ geometrii
swej w∏asnej czasoprzestrzeni z najwi´k-
szà dok∏adnoÊcià, na jakà zezwalajà pra-
wa fizyki. Liczy, czyli jest.

Powy˝sze rozwa˝ania dotyczà zarów-

no zwyk∏ych komputerów, jak i czar-
nych dziur, piany czasoprzestrzennej
oraz problemów kosmologicznych. Tym
samym dajà Êwiadectwo jednoÊci natu-
ry i ods∏aniajà konceptualne zwiàzki

mi´dzy elementami podstaw fizyki.

Co prawda, nie znamy jeszcze pe∏-

nej teorii kwantowej grawitacji,

mo˝emy jednak byç pewni, ˝e

jest ona g∏´boko powiàzana z

informacjà kwantowà. Byt

z qubitu.

n

* Prawo Moore’a g∏osi, ˝e moc ob-
liczeniowa komputerów podwaja si´

co pó∏tora roku.

GRUDZIE¡ 2004 ÂWIAT NAUKI

41

ALFRED T

. KAMAJIAN

Information: The New Language of Science. Hans Christian von Baeyer; Harvard University Press,

2004.

The Black Hole Final State. Gary T. Horowitz i Juan Maldacena; Journal of High Energy Physics,

JHEP02 (2004)008, 2004. Tekst dost´pny na stronie: arXiv.org/abs/hep-th/0310281

Computational Capacity of the Universe. Seth Lloyd; Physical Review Letters, tom 88, nr 23,

artyku∏ 237901Z, 10 VI 2002. Tekst dost´pny na stronie: arXiv.org/abs/quant-ph/0110141

From Computation to Black Holes and Space-Time Foam. Y. Jack Ng; Physical Review Letters,

tom 86, nr 14, s. 2946-2949; 2 IV 2001. Errata, tom 88, nr 13, artyku∏ 139902 (E), 14 III
2002. Tekst dost´pny na stronie: arXiv.org/abs/gr-qc/0006105

Ultimate Physical Limits to Computation. Seth Lloyd; Nature, tom 406, s. 1047-1054; 31 VIII

2000. Tekst dost´pny na stronie: arXiv.org/abs/quant-ph/9908043

JEÂLI CHCESZ WIEDZIEå WI¢CEJ

WSZECHÂWIAT jest komputerem

zbudowanym z dwóch rodzajów

sk∏adników. Materia (czerwony) ma

du˝à dynamik´ i dzia∏a jako szybki kom-

puter równoleg∏y. Ciemna energia (sza-

ry) jest prawie statyczna i dzia∏a jako powol-

ny komputer jednoprocesorowy. Dzia∏ajàc

wspólnie, oba sk∏adniki przeprowadzi∏y maksy-
malnà liczb´ operacji dozwolonà przez prawa fi-
zyki. Computo, ergo sum.

CIEMNA ENERGIA
PR¢DKOÂå: >10

–18

Hz

PAMI¢å: <10

123

b

MATERIA
PR¢DKOÂå: 10

14

Hz

PAMI¢å: 10

92

b

W

szechÊwiat

Od poczàtku swego istnienia WszechÊwiat

przeprowadzi∏

NAJWI¢KSZÑ LICZB¢ OPERACJI

dopuszczalnà przez prawa fizyki.