Arkusz 11: Zginanie z siłami poprzecznymi. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Notatki do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn”

Arkusz

Arkusz

11: Zginanie z siłami poprzecznymi

11: Zginanie z siłami poprzecznymi

1. Zginanie poprzeczne – definicje, pojęcia

Teoria dotycząca zginania – z wykładów, ćwiczeń oraz książek: [1] i [2].

Zginanie z siłami ścinającymi (inaczej: zginanie poprzeczne) jest złożonym stanem mechanicznym – moment zginający
(M

y

lub M

z

lub oba) działa razem z siłami ścinającymi (odpowiednio: F

y

, F

z

).

W celu określenia naprężeń powstających w takim stanie mechanicznym,
przyjmuje się następujące założenia:

•

pręt jest pryzmatyczny,

•

pręt ma przekrój poprzeczny osiowosymetryczny względem osi

prostopadłej do osi zginania (na rys. 1 osią symetrii jest z, natomiast osią
zginania jest y),
•

obciążenie ścinające przyłożone jest na powierzchni pręta symetrycznie

po obu stronach płaszczyzny przechodzącej przez oś pręta x oraz główną
centralną oś bezwładności w kierunku ścinania (na rys. 1 jest to z).

Tensory naprężenia i odkształcenia w zginaniu poprzecznym mają następującą postać:

T

σ

=

[

σ

x

τ

xy

τ

xz

τ

yx

0

0

τ

zx

0

0

]

⇔

związki konstytutywne

T

ε

=

[

σ

x

1

E

τ

xy

2 G

τ

xz

2 G

τ

yx

2 G

σ

x

ν

E

0

τ

zx

2 G

0

σ

x

ν

E

]

Wszystkie wzory określające naprężenia przy zginaniu poprzecznym są wzorami przybliżonymi.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

1

Rysunek 1: Siły poprzeczne powodujące

zginanie pręta pryzmatycznego

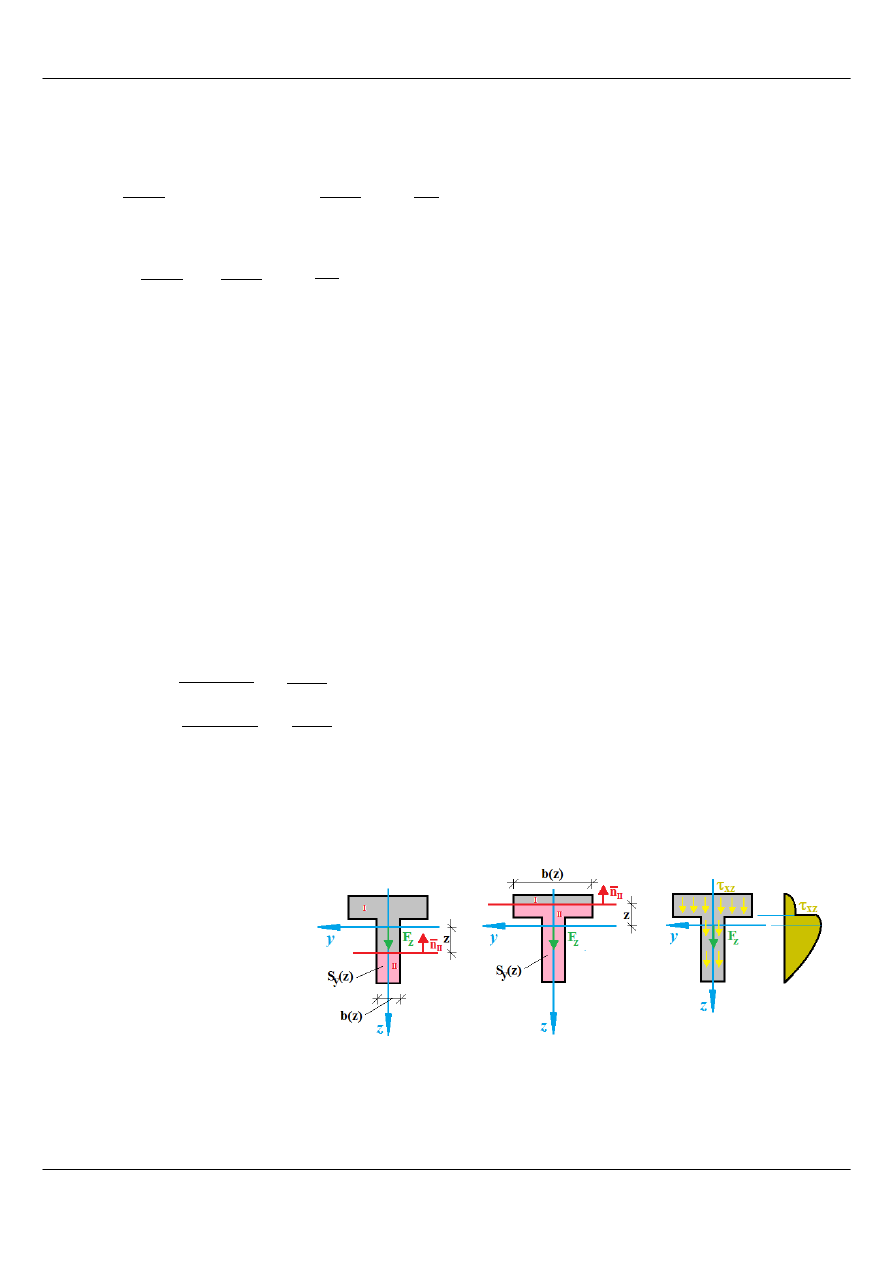
Arkusz 11: Zginanie z siłami poprzecznymi. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

2. Wpływ momentu zginającego (M

y

i/lub M

z

)

Wpływ momentu zginającego na powstające naprężenia normalne jest analogiczny jak w przypadku zginania prostego
lub ukośnego. Załóżmy, że działa jeden moment zginający (M

y

lub M

z

), wówczas:

σ

x

( x , z) =

M

y

(x)

I

y

(x)

⋅z

lub

σ

x

( x , y) =

M

z

( x)

I

z

(x)

⋅ y

[

Nm

m

4

⋅m = Pa

]

.

Jeżeli z kolei zginanie będzie odbywało się w obu płaszczyznach należy przyjąć, że naprężenia normalne powstające w
przekroju są wynikiem superpozycji działania zginania w każdej z płaszczyzn osobno:

σ

x

( x , y , z) =

M

y

(x)

I

y

(x)

⋅z

M

z

( x)

I

z

( x)

⋅ y

[

Nm

m

4

⋅m = Pa

]

.

W każdym z przypadków będzie występowała znana z wcześniejszych zajęć oś obojętna, czyli takie miejsce geometryczne
punktów przekroju, dla których

σ( x , y , z) = 0

.

3. Wpływ siły poprzecznej (F

y

i/lub F

z

)

W pierwszej kolejności omówiony zostanie wpływ siły poprzecznej F

z

, ponieważ występuje ona znacznie częściej w

zadaniach wytrzymałości materiałów niż siła poprzeczna F

y

.

3.a) Siła tnąca F

z

Naprężenia styczne pochodzące od działania siły poprzecznej powstają w dwóch kierunkach, zarówno równolegle do
kierunku działania F

z

, czyli

τ

xz

, jak i w kierunku prostopadłym do kierunku działania tej siły przekrojowej, czyli

τ

xy

.

Niektórzy autorzy przyjmują

τ

xy

≪τ

xz

i z tego powodu pomijają

τ

xy

; w obecnym kursie naprężenia te nie będą

pomijane, ale z racji ich mniejszych wartości, będą przedstawiane i obliczane w drugiej kolejności.

Wzory na naprężenia styczne przy zginaniu:

•

τ

xz

(x , z) =

F

z

(x)⋅S

y

(z)

I

y

⋅b(z)

[

N

⋅m

3

m

4

⋅m

= Pa

]

•

τ

xy

(x , y) =

F

z

(x)⋅S

y

( y)

I

y

⋅h( y)

[

N

⋅m

3

m

4

⋅m

= Pa

]

gdzie: ▪ F

z

(x) jest siłą ścinającą w przekroju o współrzędnej x;

▪ I

y

jest głównym centralnym momentem bezwładności przekroju poprzecznego względem odpowiedniej osi;

▪ S

y

(z,y) jest momentem statycznym odciętej części przekroju;

▪ b(z) bieżącą szerokością przekroju w miejscu przecięcia
▪ h(y) bieżącą wysokością przekroju w miejscu przecięcia.

Rys. 2 jest ilustracją dla pierwszego
wzoru, a także pokazuje rozkład
naprężeń stycznych

τ

xz

(w kierunku

równoległym do działania siły prze-
krojowej F

z

) dla przekroju teowego. Na

rysunku na różowo zaznaczono ob-
szary, pokazując, jak przyjmować
fragmenty figury do obliczania
momentu statycznego względem osi y.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

2

Rysunek 2: Naprężenia styczne

t

xz

i sposób ich obliczania

Arkusz 11: Zginanie z siłami poprzecznymi. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

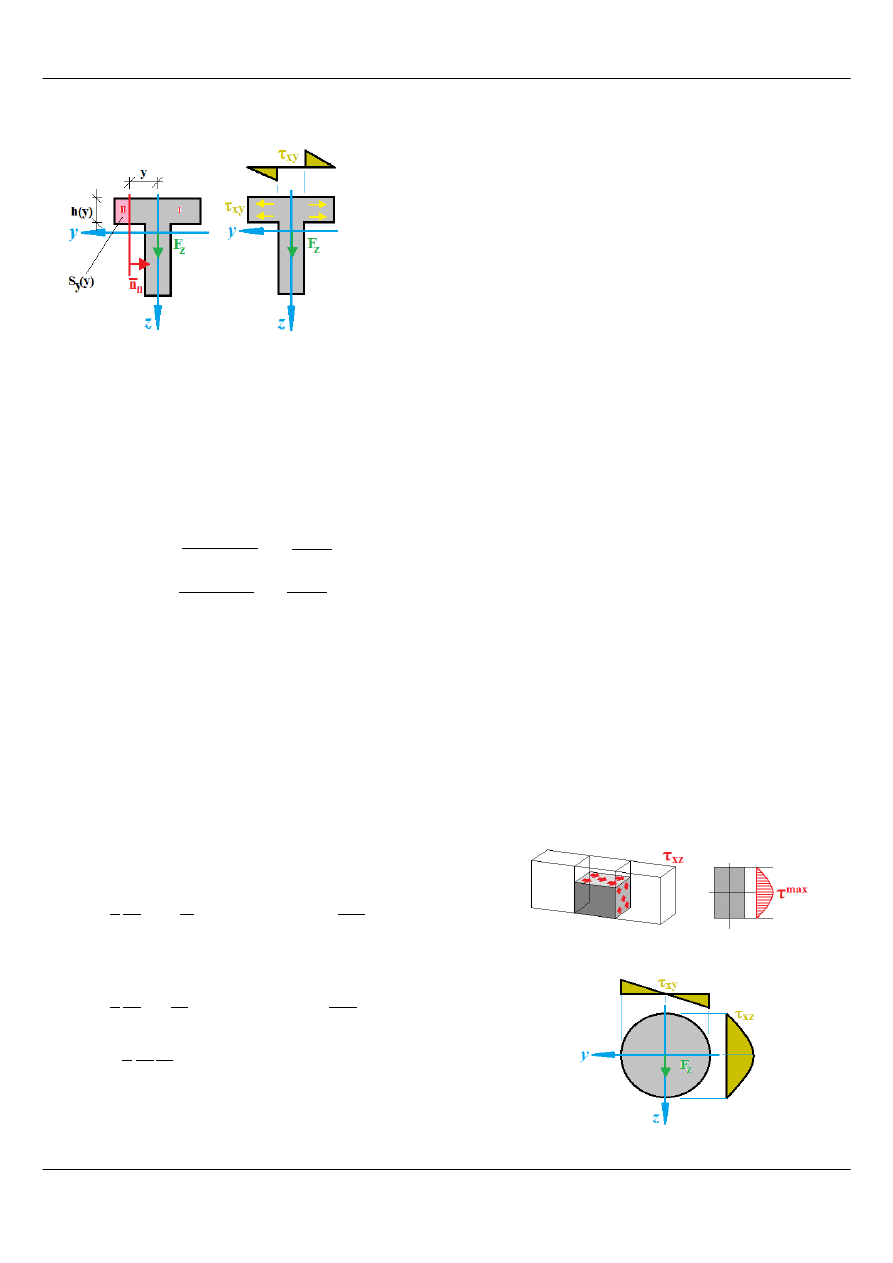
Na rysunku 3 przedstawiono ilustrację dla drugiego wzoru oraz rozkład
naprężeń

τ

xy

. Na różowo zaznaczono przykładowy obszar do

obliczenia momentu statycznego względem osi y.
*Uwaga: Tam, gdzie płaszczyzna podziału przecinałaby oś prostopadłą
do działającego obciążenia ścinającego (czyli tutaj oś y) lub odcięta
część przecinałaby tę oś, otrzymalibyśmy odcięty fragment figury po
obu stronach osi, względem której liczony byłby moment statyczny
(przykładem dla teownika może być przecięcie przez środnik). Byłoby
to zaniżenie momentu statycznego, a zatem zafałszowanie obliczeń
naprężeń stycznych. W takiej sytuacji nie oblicza się dla danego
przecięcia tych naprężeń stycznych. Na rysunku obok jest to obszar
środnika.

3.a) Siła tnąca F

y

Naprężenia styczne pochodzące od działania siły poprzecznej powstają w dwóch kierunkach, zarówno równolegle do
kierunku działania F

y

, czyli

τ

xy

, jak i w kierunku prostopadłym do kierunku działania tej siły przekrojowej, czyli

τ

xz

.

Wzory na naprężenia styczne powstające przy zginaniu konstrukcji siłą tnącą F

y

są analogiczne, jak w poprzednim

przypadku, z uwzględnieniem odpowiednich wynikających ze zmiany osi.

•

τ

xy

(x , y) =

F

y

(x)⋅S

z

( y)

I

z

⋅b( y)

[

N

⋅m

3

m

4

⋅m

= Pa

]

•

τ

xz

(x , z) =

F

y

(x)⋅S

z

(z)

I

z

⋅h( z)

[

N

⋅m

3

m

4

⋅m

= Pa

]

gdzie: ▪ F

y

(x) jest siłą ścinającą w przekroju o współrzędnej x;

▪ I

z

jest głównym centralnym momentem bezwładności przekroju poprzecznego względem odpowiedniej osi;

▪ S

z

(y,z) jest momentem statycznym odciętej części przekroju;

▪ b(y) bieżącą szerokością przekroju w miejscu przecięcia
▪ h(z) bieżącą wysokością przekroju w miejscu przecięcia.

3.c) Wzory Żurawskiego

Ze względu na uproszczenie obliczeń, dla dwóch typowych kształtów przekrojów poprzecznych, prostokąta i koła,
wyprowadzone zostały wzory uproszczone. Przedstawione tutaj wzory dotyczą zginania siłą ścinającą F

z

, wzory dla

zginania siłą działającą w drugim kierunku są analogiczne.

Dla prostokąta:

Dla koła:

We wzorach tych A oznacza całkowitą powierzchnię przekroju
poprzecznego.

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

3

Rysunek 3: Naprężenia styczne

t

xy

i sposób ich obliczania

Rysunek 4: Naprężenia styczne w zginaniu ze ścinaniem

przekroju prostokątnego ([4])

τ

xz

( z) = 3

2

F

z

A

(

1 4

z

2

h

2

)

τ

max

= τ(z=0) =

3 F

z

2 A

τ

xz

( z) = 4

3

F

z

A

(

1

z

2

R

2

)

τ

max

= τ( z =0) =

4 F

z

3 A

τ

xy

(z) =

4
3

F

z

A

yz

R

2

Rysunek 5: Naprężenia styczne w zginaniu ze

ścinaniem przekroju kołowego

Arkusz 11: Zginanie z siłami poprzecznymi. Arkusz przeznaczony do ćwiczeń z przedmiotu „Wytrzymałość elementów maszyn” na II roku dziennych
studiów Wydziału Inżynierii Mechanicznej i Robotyki AGH na kierunku „IMIM” w roku akademickim 2014/2015.

4. Warunek projektowy

Z powyższych wzorów widać, że naprężenia normalne mogą przyjmować wartości ujemne (ściskanie) i dodatnie
(rozciąganie), zależnie od znaku momentu zginającego oraz położenia rozważanego punktu względem kierunku
wysokości przekroju. Stąd, warunek maksymalnych naprężeń musi być rozważany zarówno dla ściskanej, jak i rozciąganej
części przekroju:

•

ściskanie:

| σ

x , c

max

| ⩽ k

g , c

lub

| σ

x , c

max

| ⩽ k

c

lub

| σ

x , c

max

|⩽ k

g

(gdzie c oznacza ściskanie, zaś g oznacza zginanie,

np. k

g,c

– dopuszczalne naprężenia ściskające przy zginaniu);

•

rozciaganie:

σ

x , t

max

⩽ k

g , t

lub

σ

x , t

max

⩽ k

t

lub

σ

x , t

max

⩽ k

g

(gdzie t oznacza rozciąganie, zaś g oznacza zginanie,

np. k

g,t

– dopuszczalne naprężenia rozciągające przy zginaniu).

Oprócz tego należy sprawdzić warunek maksymalnych naprężeń stycznych:

•

|

τ

xy

|

⩽k

g , s

lub

|

τ

xy

|

⩽k

s

(gdzie s oznacza ścinanie, zaś g oznacza zginanie, np. k

g,s

– dopuszczalne naprężenia

ścinające przy zginaniu);

•

|

τ

xz

|

⩽k

g , s

lub

|

τ

xz

|

⩽k

s

.

Warunki podane wyżej są warunkami sprawdzającymi każde naprężenie z osobna, podczas kiedy w rzeczywistości
konstrukcja pracuje w złożonym stanie naprężenia. Należy zatem sprawdzić wspólne działanie naprężeń stycznych oraz
normalnych. Służy temu sprawdzenie nierówności:

σ

red

⩽σ

dop

, gdzie

σ

red

oznaczają naprężenia zredukowane, czyli

pewną funkcję wszystkich naprężeń stycznych i normalnych. Naprężenia zredukowane wyznaczane są wg hipotez
wytężeniowych, o których będzie mowa w dalszej części kursu.

Jest także warunek projektowania związany z użytkowaniem, czyli deformacją zginanej konstrukcji, jednak w czasie
obecnego kursu będzie on rozważany później. Dla pełnej informacji ogólnej podamy tutaj, że warunek ten ma formalną
postać:

f

⩽ f

dop

, gdzie f jest strzałką ugięcia.

5. Podsumowanie

• Rozwiązać przykłady nr: 11.6.3, 11.6.5, 11.6.6 z książki [2] oraz zadanie 8.12 z książki [3].

• Znajomość tensora naprężenia i odkształcenia w zginaniu poprzecznym. Znajomość wzorów na
naprężenia normalne i styczne oraz inżynierskich wzorów Żurawskiego. Znajomość rozkładu naprężeń
stycznych i normalnych w przekroju poprzecznym przy zginaniu z siłami poprzecznymi.
• Umiejętność rozwiązywania zadań dla przypadków zginania poprzecznego – wyznaczanie naprężeń,
wykresy rozkładu naprężeń w przekrojach poprzecznych, znalezienie osi obojętnej, wyznaczanie wymiarów
konstrukcji z warunków projektowych.
• Oś obojętna, definicja, wzory, znaczenie.

6. Literatura

[1] Piechnik S. "Mechanika techniczna ciała stałego", Wydawnictwo PK, Kraków 2007
[2] Bodnar A. „Wytrzymałość materiałów. Podręcznik dla studentów wyższych szkół technicznych”, wydanie drugie

poszerzone i poprawione, Kraków 2004, rozdział 11

[3] Niezgodziński M., Niezgodziński T. "Zadania z wytrzymałości materiałów", Wydawnictwo WNT, Warszawa 2012
[4] dr inż. Paweł Szeptyński, ilustracje

© Copyright: Anna Stręk. Autorem arkusza jest Anna Stręk. Arkusz stanowi przedmiot prawa autorskiego określonego w Ustawie o prawie
autorskim i prawach pokrewnych (Dz. U. 1994 r. Nr 24 poz.83 z późn. zmianami). Autor nie wyraża zgody na inne wykorzystywanie arkusza niż
podane w jego przeznaczeniu.

4