W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

D

RGANIA PRĘTÓW PRYZMATYCZNYCH O CIĄGŁYM ROZKŁADZIE MASY

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

1

Olga Kopacz, Adam Łodygowski, Krzysztof Tymper,

Michał Płotkowiak, Wojciech Pawłowski

Konsultacje naukowe: prof. dr hab. J

ERZY

R

AKOWSKI

Poznań 2002/2003

MECHANIKA BUDOWLI 13

1. DRGANIA POPRZECZNE BELEK

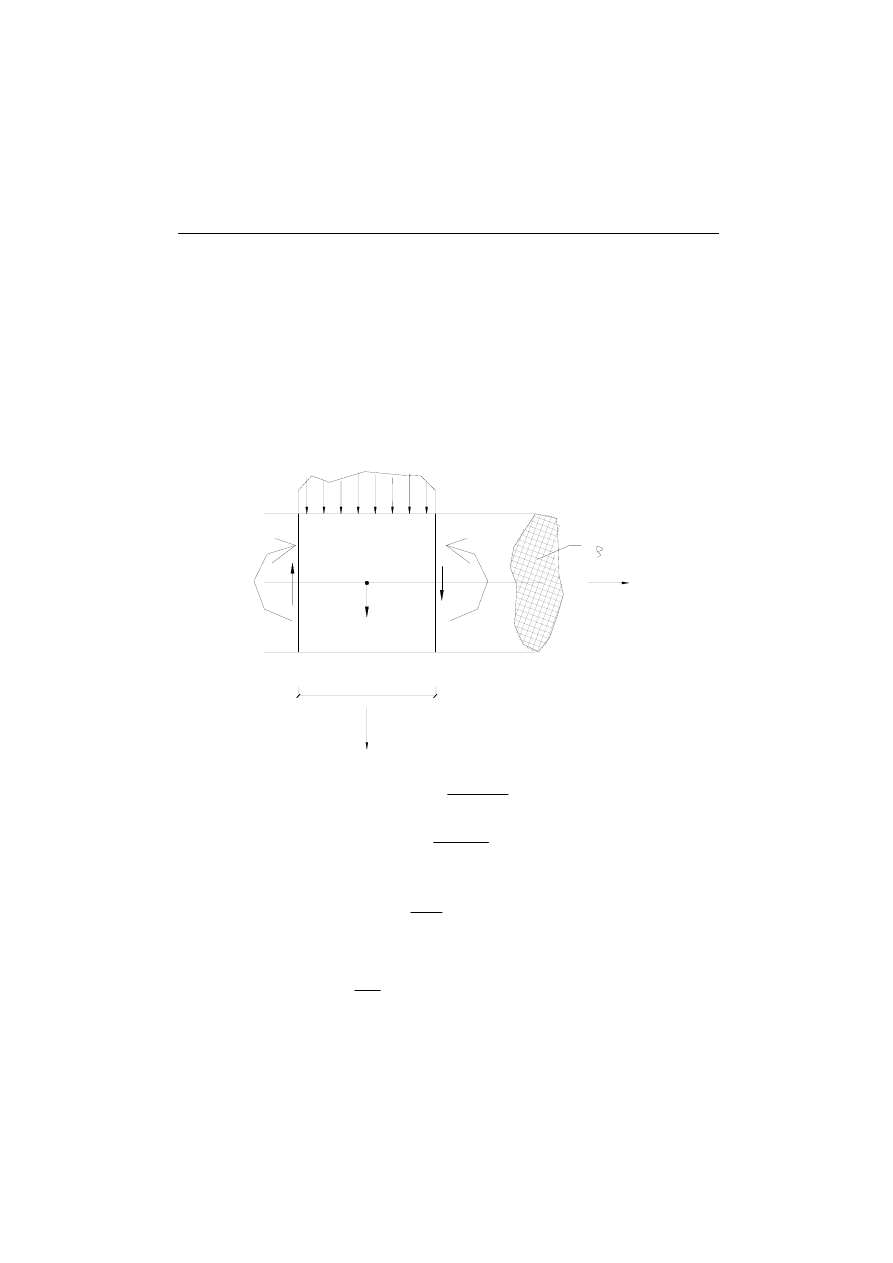
Na nieskończenie mały wycinek belki dx działają siły jak na rys.1

dx

y

r(x,t)

x

A

p(x,t)

(x,t)

T(x,t)

M*(x,t)

T*(x,t)

gęstość (m
właściwa

Rys. 1

( )

( )

( )

( ) ( )

( )

dx

x

t

x

T

t

x

T

t

x

T

dx

x

t

x

M

t

x

M

t

x

M

∂

∂

+

=

∂

∂

+

=

,

,

,

*

,

,

,

*

(13.1)

Gdzie: r - siła oporu (bezwładności)

( )

2

2

2

2

,

t

A

dx

dm

w

dm

t

w

dm

t

x

r

∂

∂

=













⋅

⋅

=

⋅

−

=

∂

∂

⋅

−

=

•

•

•

•

ρ

(13.2)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

D

RGANIA PRĘTÓW PRYZMATYCZNYCH O CIĄGŁYM ROZKŁADZIE MASY

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

2

Można napisać sumę na oś y:

T

x

M

M

x

w

EI

ale

t

w

p

x

T

y

=

∂

∂

−

=

∂

∂

⋅

∂

∂

⋅

=

+

∂

∂

⇒

=

∑

2

2

2

2

0

µ

(13.3)

Po zróżniczkowaniu i przekształceniach otrzymujemy zależność na drgania poprzeczne:

( )

( ) ( )

t

x

p

t

t

x

w

x

t

x

w

EI

,

,

,

2

2

4

4

=

∂

∂

⋅

+

∂

∂

⋅

µ

(13.4)

2. DRGANIA WŁASNE BELEK

Rozpatrujemy drgania własne, w przypadku których siła wymuszająca jest równa 0,
więc zależność (13.4) przyjmuje postać:

( )

( )

0

,

,

2

2

4

4

=

∂

∂

⋅

+

∂

∂

⋅

t

t

x

w

x

t

x

w

EI

µ

(13.5)

Zakładamy rozdzielenie zmiennych

( )

( ) ( )

t

T

x

W

t

x

w

⋅

=

,

(13.6)

Zatem otrzymujemy:

( ) ( )

( ) ( )

0

2

2

4

4

=

⋅

⋅

+

⋅

⋅

x

w

dt

t

T

d

t

T

dx

x

W

d

EI

µ

(13.7)

Po przekształceniach otrzymujemy (pochodne zwyczajne):

( )

( )

( )

( )

2

2

2

4

4

ω

µ

=

⋅

−

=

⋅

t

T

dt

t

T

d

x

w

dx

x

W

d

EI

(13.8)

Wartość wyniku zależności (13.6)

2

ω

musi być stałą a nie funkcją, ponieważ funkcję

przestrzenną przyrównujemy do funkcji czasu.

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

D

RGANIA PRĘTÓW PRYZMATYCZNYCH O CIĄGŁYM ROZKŁADZIE MASY

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

3

Z zapisu (13.8) otrzymujemy zależności (13.9) i (13.10):

( )

( )

0

2

2

2

=

⋅

+

t

T

dt

t

T

d

ω

(13.9)

( )

( )

4

2

2

4

4

1

1

α

µ

ω

µ

ω

=

⋅

⋅

⋅

⋅

−

EI

gdzie

x

W

EI

dx

x

w

d

(13.10)

µ

- gęstość liniowa

Rozwiązanie zależności (13.10):

( )

( )

( )

( )

x

Dch

x

Csh

x

B

x

A

x

W

x

W

x

W

IV

α

α

α

α

α

+

+

+

=

=

−

cos

sin

0

4

(13.11)

Rozwiązanie otrzymujemy korzystając z warunków brzegowych (ponieważ jest to
równanie we współrzędnych przestrzennych):

l

x 0

x l

Rys. 2

Zapisać można następujące warunki brzegowe:

( )

( )

( )

( )

( )

( )

0

''

0

0

)

4

0

0

''

0

0

0

0

)

3

0

)

2

0

0

0

)

1

2

2

0

2

2

=

=

⇒

=

→

=

=

=

⇒

=

→

=

=

→

=

=

→

=

=

=

l

W

dx

W

d

l

M

l

x

W

dx

W

d

M

x

l

W

l

x

W

x

l

x

x

(13.12)

Są to warunki jednorodne, więc bez dodatkowych warunków nie da się rozwiązać.

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

D

RGANIA PRĘTÓW PRYZMATYCZNYCH O CIĄGŁYM ROZKŁADZIE MASY

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

4

[

]

[

]

π

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

α

k

l

l

l

sh

l

wyznacznik

l

Csh

l

A

l

Csh

l

A

D

B

D

B

D

B

l

ch

D

l

sh

C

l

B

l

A

D

B

l

Dch

l

Csh

l

B

l

A

D

C

B

A

=

⇒

=

→

=

⋅

=







=

+

=

+

=

=

→

=

+

−

=

+

=

+

+

+

=

⋅

+

+

⋅

−

+

+

+

=

⋅

+

⋅

+

⋅

+

⋅

0

sin

0

sin

2

0

0

sin

)

4

0

sin

)

2

0

0

0

0

0

cos

sin

)

4

0

1

0

1

0

)

3

cos

sin

)

2

0

1

0

1

0

)

1

2

2

2

2

2

2

(13.13)

Mamy rozwiązanie kiedy

EI

l

k

l

k

µ

ω

π

α

π

α

2

4

4

4

4

=

=

⇒

=

k

- dowolna liczba naturalna

4

4

4

2

k

l

EI

⋅

= π

µ

ω

(13.14)

Dla belki wolnopodpartej:

4

4

4

2

k

l

EI

⋅

⋅

=

π

µ

ω

(13.15)

Gdzie

ω

- częstość kołowa drgań własnych belki wolnopodpartej

Stałe z warunków początkowych

( )

(

)

ϕ

ω +

=

t

a

t

T

sin

(13.16)

Ostatecznie drgania belki wynoszą:

( )

(

)

k

k

k

k

k

t

a

x

t

x

W

ϕ

ω

α

+

⋅

=

sin

sin

,

(13.17)

W

Y K Ł A D Y Z

M

E C H A N I K I

B

U D O W L I

D

RGANIA PRĘTÓW PRYZMATYCZNYCH O CIĄGŁYM ROZKŁADZIE MASY

Politechnika Poznańska® Kopacz,

Łodygowski, Pawłowski, Płotkowiak, Tymper

5

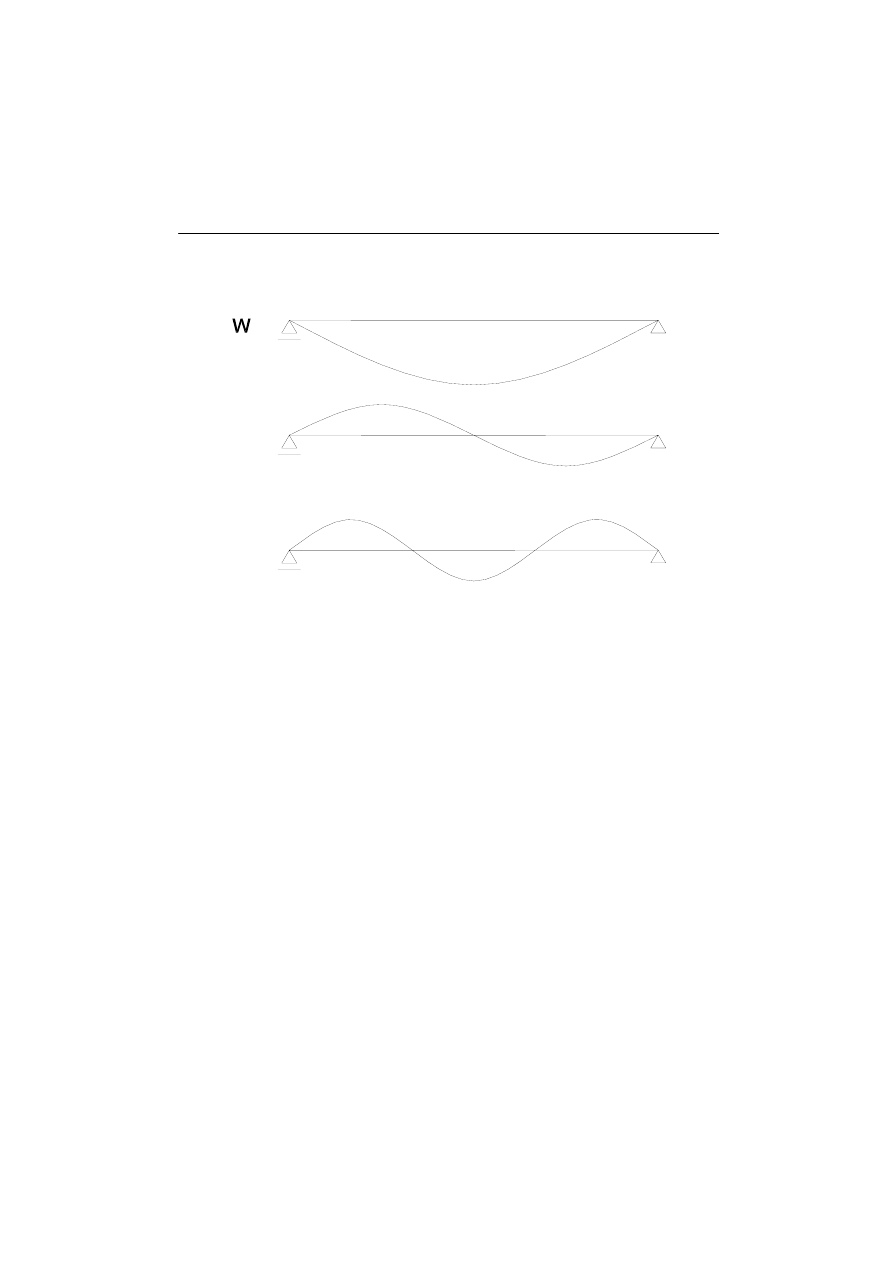
Zależność drgań belki (13.17) obrazuje rys.3

1

w

2

w

3

Rys. 2