Politechnika Opolska

Wydział Elektrotechniki, Automatyki i Informatyki

Instytut Automatyki i Informatyki

Przetworniki i Układy Pomiarowe

Laboratorium

Niezrównoważone układy mostkowe

Opole, 2007

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 2 -

Strona pusta

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 3 -

Niezrównoważone układy mostkowe

1. Cel

ć

wiczenia

Celem

ć

wiczenia jest poznanie wła

ś

ciwo

ś

ci układów mostkowych i zasad doboru jego

elementów.

2. Wprowadzenie teoretyczne

Wiele pomiarów wielko

ś

ci nieelektrycznych sprowadza si

ę

do pomiaru zmian rezystancji

czujnika

np.

elektryczny

pomiar

składu

mieszaniny

gazowej

analizatorem

termokonduktometrycznym, pomiar temperatury termometrem rezystancyjnym, napr

ęż

e

ń

tensometrami itp. Metod

ą

, która umo

ż

liwia uzyskanie najwy

ż

szych dokładno

ś

ci przy pomiarach

zmian rezystancji jest metoda mostkowa. Mostki zrównowa

ż

one zapewniaj

ą

wysok

ą

dokładno

ść

, u

ż

ywane s

ą

jednak prawie wył

ą

cznie w laboratorium poniewa

ż

odczyt wielko

ś

ci

mierzonej jest utrudniony – np. dla okre

ś

lenia temperatury konieczna jest znajomo

ść

charakterystyki

( ) ( )

ϑ

ϑ

f

R

=

, gdzie

( )

ϑ

R

jest rezystancj

ą

sondy termometrycznej w temperaturze

ϑ

, dlatego te

ż

cz

ęś

ciej do tych celów u

ż

ywa si

ę

mostków niezrównowa

ż

onych, w których

sygnałem wyj

ś

ciowym z reguły jest napi

ę

cie nierównowagi powstaj

ą

ce na przek

ą

tnej zerowej.

Sygnał ten mo

ż

e by

ć

wykorzystany bezpo

ś

rednio w mierniku wychyłowym, lub mo

ż

e poprzez

wzmacniacz sterowa

ć

rewersyjnym serwomotorem doprowadzaj

ą

c do stanu równowagi, a

sygnałem wyj

ś

ciowym w tym przypadku jest poło

ż

enie

ś

lizgu potencjometru równowa

żą

cego.

Dla zmniejszenia wpływu czynników zewn

ę

trznych przetwornik wykonany jest zwykle w

układzie ró

ż

nicowym lub porównawczym, tzn. posiada dwa elementy pomiarowy i

porównawczy.

Je

ż

eli rezystancja elementu pomiarowego jest funkcj

ą

szeregu wielko

ś

ci:

(

)

n

p

p

z

z

x

f

R

...,

,

,

1

=

(1)

gdzie x - jest wielko

ś

ci

ą

mierzon

ą

, a

n

z

z

...,

,

1

- s

ą

wielko

ś

ciami wpływaj

ą

cymi (zakłóceniami), to

element porównawczy charakteryzuje zale

ż

no

ść

:

(

)

n

k

k

z

z

x

f

R

...,

,

,

1

=

(2)

Przetwornik ró

ż

nicowy jest tak zbudowany,

ż

e zwi

ę

kszenie wielko

ś

ci mierzonej x

powoduje wzrost rezystancji

p

R , a zmniejszenie rezystancji

k

R , lub odwrotnie. Ogólnie:

x

R

x

R

k

p

∂

∂

−

≈

∂

∂

(3)

W przetworniku porównawczym natomiast:

0

≈

∂

∂

>>

∂

∂

x

R

x

R

k

p

(4)

czyli,

ż

e zmiana wielko

ś

ci mierzonej wpływa głównie na element pomiarowy, natomiast zmiany

rezystancji elementu porównawczego s

ą

znikomo małe (typowym przykładem tak wykonanego

przetwornika jest komora analizatora termokonduktometrycznego). Elementy przetwornika

p

R i

k

R wł

ą

czone s

ą

w układzie mostkowym ró

ż

nicowo w s

ą

siednie gał

ę

zie mostka, spełniaj

ą

c

warunki:

(

)

n

g

z

z

x

f

U

...,

,

,

1

=

(5)

oraz dla

0

X

X

=

,

0

p

p

R

R

=

,

0

k

k

R

R

=

, napi

ę

cie

0

=

g

U

. Wielko

ść

0

x

x

=

nazywamy punktem

zerowym przetwornika.

Celem niniejszego

ć

wiczenia jest dobranie optymalnych warunków pracy przetwornika,

tzn. dobór warto

ś

ci stałych oporników (tj. rezystancji w pozostałych gał

ę

ziach mostka)b

ę

d

ą

cych

parametrami przek

ą

tnej zerowej i przek

ą

tnej zasilania.

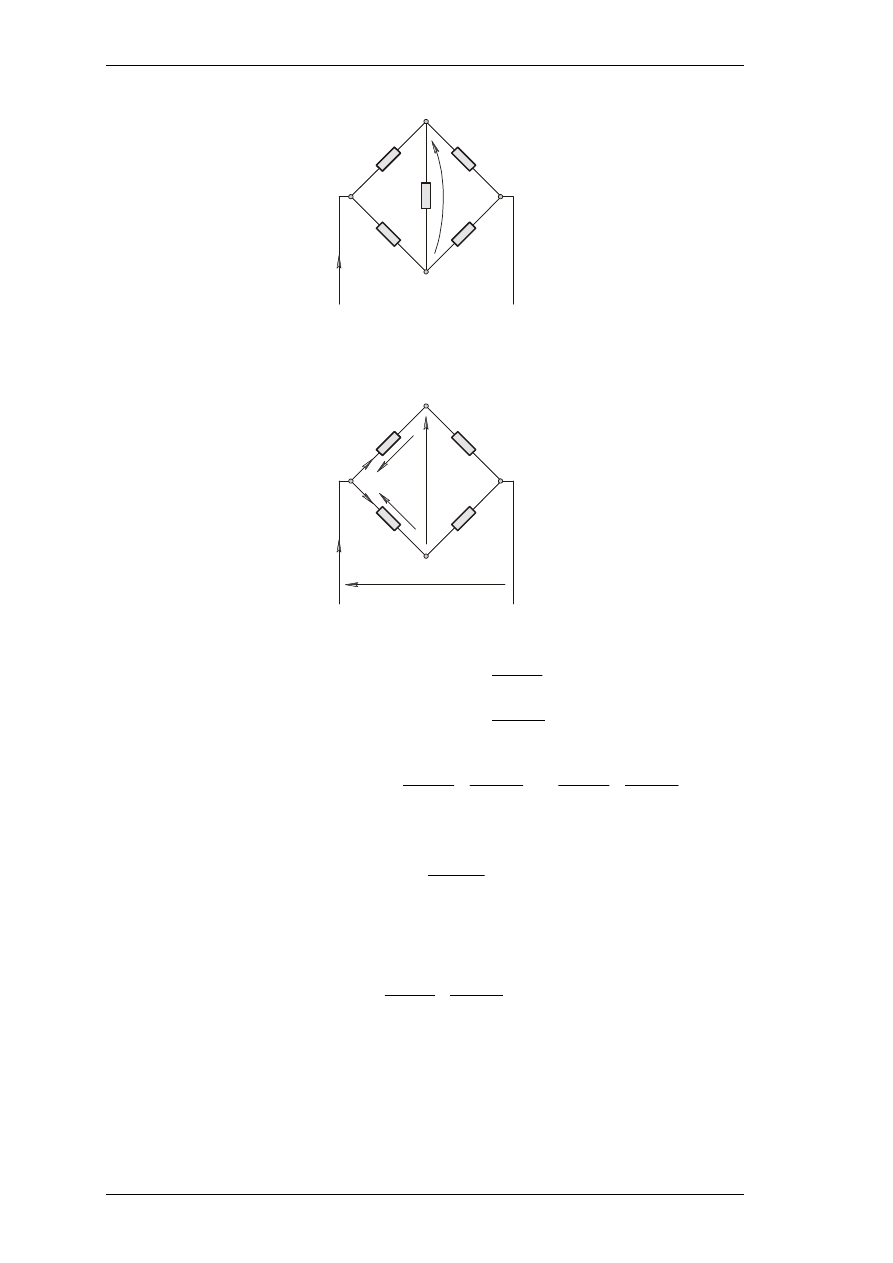
Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 4 -

Model zast

ę

pczy układu mostkowego.

R

3

R

1

R

4

R

2

R

g

U

g

I

m

Rys. 1. Schemat układu mostkowego.

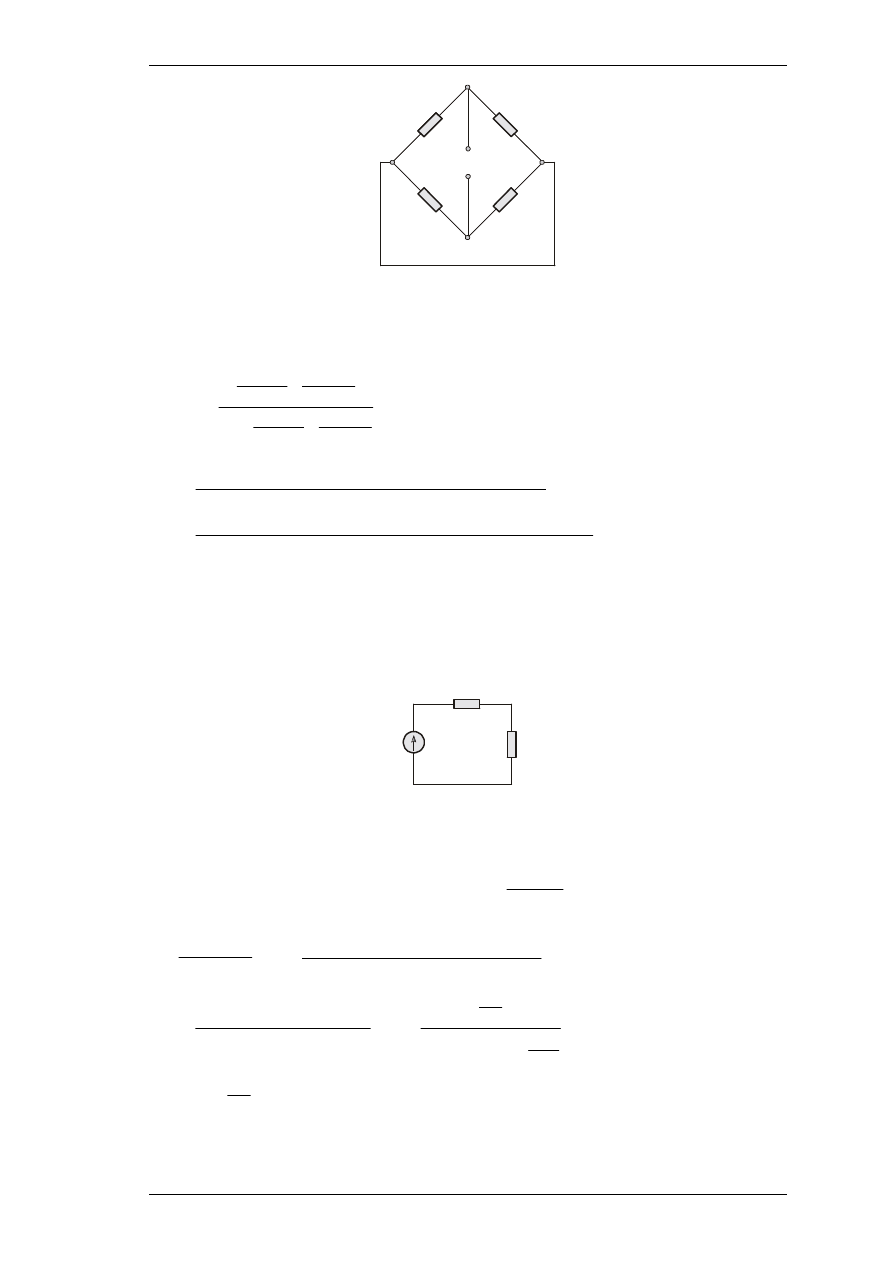
Napi

ę

cie na przek

ą

tnej zerowej mostka, gdy

∞

=

g

R

mo

ż

na obliczy

ć

nast

ę

puj

ą

co:

R

3

R

1

R

4

R

2

U

g

I

m

o o

U

V

b

V

a

I

1

I

2

U

R1

U

R3

Rys. 2. Schemat zast

ę

pczy układu mostkowego.

(

)

U

R

R

I

=

+

2

1

1

2

1

1

R

R

U

I

+

=

(

)

U

R

R

I

=

+

4

3

2

4

3

2

R

R

U

I

+

=













+

−

+

=

+

−

+

=

−

−

+

=

−

=

∞

4

3

3

2

1

1

4

3

3

2

1

1

3

2

1

1

R

R

R

R

R

R

U

R

R

UR

R

R

UR

R

I

U

R

I

U

V

V

U

b

a

g

(6)

Przy obci

ąż

eniu przek

ą

tnej zerowej napi

ę

cie

g

U b

ę

dzie si

ę

zmienia

ć

zgodnie z zale

ż

no

ś

ci

ą

:

m

g

g

g

g

R

R

R

U

U

+

=

∞

(7)

gdzie

m

R jest zast

ę

pcz

ą

oporno

ś

ci

ą

mostka widzian

ą

z zacisków przek

ą

tnej zerowej przy

zało

ż

eniu,

ż

e oporno

ść

wewn

ę

trzna

ź

ródła jest znikomo mała:

4

3

4

3

2

1

2

1

R

R

R

R

R

R

R

R

R

m

+

+

+

=

(8)

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 5 -

R

3

R

1

R

4

R

2

Rys. 3. Schemat układu mostkowego do wyznaczenia oporno

ś

ci zast

ę

pczej

widzianej z zacisków przek

ą

tnej zerowej.

Po podstawieniu uzyskamy:

=

+

+

+

+

+

−

+

=

4

3

4

3

2

1

2

1

4

3

3

2

1

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

UR

U

g

g

g

(9)

(

)

(

)

(

)(

)

(

) (

)

=

+

+

+

+

+

+

+

−

+

=

4

3

2

1

4

3

2

1

4

3

2

1

2

1

3

4

3

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

UR

g

g

(

)(

)

4

3

1

4

3

2

4

2

1

3

2

1

4

3

2

1

3

2

4

1

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

UR

g

g

+

+

+

+

+

+

−

=

2.1. Dobór elementów

2.1.1. Dopasowanie mostka do uzyskania maksimum mocy w mierniku

R

m

R

g

U

g o o

Rys. 4. Schemat zast

ę

pczy układu mostkowego podczas doboru elementów mostka

w celu uzyskania maksimum mocy w mierniku.

g

g

R

I

P

2

=

m

g

g

g

R

R

U

I

+

=

∞

(

)

2

2

m

g

g

g

R

R

R

U

P

+

=

(

)

=

+

+

∆

−

∆

=

g

g

R

R

R

R

R

R

R

R

R

R

UR

4

0

2

4

0

1

2

2

0

4

2

2

2

2

2

g

g

R

R

R

R

R

R

R

UR

0

4

0

2

2

0

2

+

+

∆

−

∆

=

=

∆

−

+

+

∆

=

0

2

4

0

0

2

R

R

R

R

R

R

R

UR

g

g

przyjmuj

ą

c

ε

=

∆

0

R

R

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 6 -

g

g

R

R

R

R

R

UR

2

4

0

2

0

+

+

∆

−

=

ε

=

+

+















∆

−

=

g

g

R

R

R

R

R

UR

2

1

4

2

0

2

0

ε

( )

=

+

+

−

=

g

g

R

R

R

UR

2

1

4

2

0

ε

ε

Pomijaj

ą

c w mianowniku

ε

jako bardzo małe, a zatem

1

1

≈

−

ε

, otrzymujemy wzór na moc w

przek

ą

tnej zerowej:

g

g

g

R

U

P

2

=

(

)

(

)

2

4

0

2

2

2

4

0

2

2

2

2

2

g

g

g

g

g

g

R

R

R

R

U

R

R

R

R

R

U

P

+

+

=

+

+

=

ε

ε

(10)

Ze wzoru (6) wida

ć

,

ż

e dla danych

0

R

,

g

R

i

U najwi

ę

ksz

ą

moc b

ę

dzie dla

0

4

=

R

(najmniejszy

mianownik). Je

ś

li natomiast mostek jest symetryczny wzgl

ę

dem przek

ą

tnej zasilania, tzn.:

R

R

R

∆

+

=

0

1

R

R

R

∆

−

=

0

3

4

2

R

R

=

(

) (

)

(

)

4

2

2

2

m

g

g

m

g

m

g

g

g

R

R

R

R

R

R

R

U

R

P

+

+

−

+

=

∂

∂

∞

MAX

P

P

=

, gdy

0

=

∂

∂

g

R

P

Poniewa

ż

(

)

4

m

g

R

R

+

jest zawsze wi

ę

ksze od zera,

(

) (

)

0

2

2

=

+

−

+

g

m

g

m

g

R

R

R

R

R

0

2

2

2

2

2

2

=

−

−

+

+

m

g

g

m

m

g

g

R

R

R

R

R

R

R

m

g

m

g

R

R

R

R

=

⇒

=

2

2

Obliczaj

ą

c drug

ą

pochodn

ą

mo

ż

na sprawdzi

ć

,

ż

e jest to warunek na maksimum.

0

2

2

<

∂

∂

g

R

P

2.1.2. Dopasowanie biernych gał

ę

zi mostka

R

g

R

3

R

1

R

4

R

2

Rys. 5. Schemat zast

ę

pczy układu mostkowego podczas doboru biernych elementów gał

ę

zi.

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 7 -

Stosuj

ą

c mostek symetryczny wzgl

ę

dem przek

ą

tnej zerowej, tzn.:

4

3

R

R

=

0

2

1

R

R

R

=

=

oraz

R

R

R

∆

+

=

0

1

R

R

R

∆

−

=

0

2

i wprowadzaj

ą

c

ε

=

∆

0

R

R

wzór (9) przybierze posta

ć

:

( )

=

+

+

−

=

g

g

g

R

R

R

UR

U

2

1

4

2

0

ε

ε

(

)(

)

=

+

+

+

+

+

+

−

=

g

g

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

UR

4

3

2

1

4

3

2

4

3

1

4

2

1

3

2

1

3

2

4

1

(

)

(

)

(

)(

)

(

)(

)

(

) (

)

(

)

=

∆

−

+

∆

+

+

∆

+

+

∆

+

+

∆

−

∆

+

+

∆

−

∆

+

∆

−

−

∆

+

=

g

g

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

UR

4

0

0

2

4

0

0

4

0

0

4

0

0

4

0

4

0

2

( )













+

+

+















+

−

=

0

4

4

4

2

0

2

1

2

1

1

R

R

R

R

R

R

R

UR

g

g

g

ε

ε

(12)

Pomijaj

ą

c

ε

w mianowniku jako małe, otrzymamy wyra

ż

enie na moc w przek

ą

tnej zerowej:

2

2

2

2

0

4

4

4

0

2

2

2

1

2

1

M

R

U

R

R

R

R

R

R

R

R

U

P

g

g

g

g

g

ε

ε

=



























+

+

+















+

=

(13)

0

2

2

2

3

2

0

4

2

4

0

=

















+

+

−

−

=

∂

∂

M

R

R

R

R

R

R

R

P

g

g

g

g

ε

(

)

g

g

R

R

R

R

R

2

0

0

2

4

2

=

+

st

ą

d optymalna warto

ść

4

R :

g

g

R

R

R

R

R

+

=

0

0

4

2

(14)

3.

Nieliniowo

ść

skali miernika

Przy zało

ż

eniu,

ż

e oporno

ść

przetwornika jest zale

ż

na liniowo od warto

ś

ci mierzonej,

nieliniowo

ść

skali jak to wynika ze wzoru na

g

U spowodowana jest obecno

ś

ci

ą

ε

w

mianowniku. Oblicza si

ę

j

ą

jako ró

ż

nic

ę

warto

ś

ci

'

g

U

(z pomini

ę

ciem

ε

w mianowniku) i

warto

ś

ci

g

U ze wzoru (5) – podawana jest zwykle jako warto

ść

wzgl

ę

dna.

Przy zało

ż

eniu,

ż

e

2

1

R

R

=

,

4

3

R

R

=

wzgl

ę

dny bł

ą

d liniowo

ś

ci wynosi:

( )

( )

0

0

4

2

4

2

0

4

2

0

4

0

2

1

2

1

2

1

2

'

R

R

R

R

R

R

R

R

R

R

R

R

R

U

U

U

g

g

g

g

g

g

g

u

+

+

≈

+

+

−

+

+

−

−

+

+

=

−

=

ε

ε

ε

ε

ε

ε

σ

Warto

ść

minimaln

ą

osi

ą

gniemy, gdy mianownik d

ąż

y do

∞

, tzn.:

∞

⇒

0

4

R

R

oraz

∞

⇒

0

R

R

g

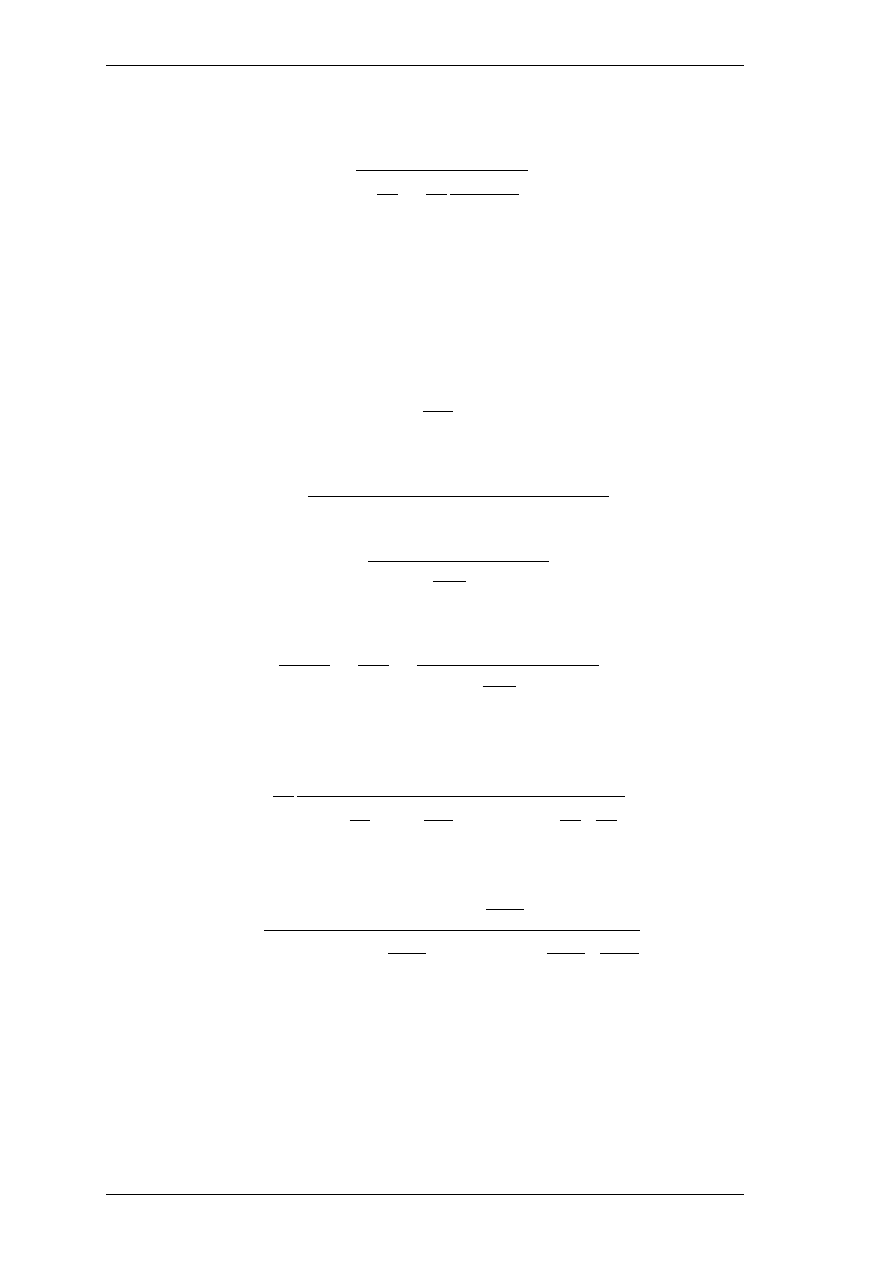
Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 8 -

Dla mostka o symetrii

3

1

R

R

=

oraz

4

2

R

R

=

minimaln

ą

nieliniowo

ść

uzyskuje si

ę

da du

ż

ych

4

R , poniewa

ż

:

(

)















+

+

+

≈

4

4

0

0

0

4

2

2

1

1

R

R

R

R

R

R

R

R

g

g

u

ε

σ

(16)

Je

ż

eli w przetwornikach

R zmienia si

ę

w du

ż

ych granicach, to i bł

ę

dy nieliniowo

ś

ci s

ą

du

ż

e.

4.

Bł

ę

dy dodatkowe

Powstaj

ą

na skutek działania na element pomiarowy i porównawczy wielko

ś

ci zakłócaj

ą

cej

(wpływaj

ą

cej) z np. temperatury otoczenia. Przyjmuj

ą

c,

ż

e przy zmianie wielko

ś

ci

Z o

0

Z

Z

Z

−

=

∆

rezystancja elementów pomiarowego i porównawczego przetwornika zmienia si

ę

równocze

ś

nie o

z

R

∆

0

R

R

z

∆

=

δ

Sygnał wyj

ś

ciowy mostka o symetrii

2

1

R

R

=

,

4

3

R

R

=

pomijaj

ą

c bł

ą

d nieliniowo

ś

ci, wynosi:

(

)

(

)

(

)

δ

δ

δ

ε

+

+

+

+

+

=

1

2

1

2

2

1

2

2

'

4

0

2

4

0

4

2

0

4

0

g

g

g

R

R

R

R

R

R

R

R

R

UR

U

lub po przekształceniu:

(

)













+

+

+

+

+

=

g

g

g

R

R

R

UR

U

2

1

2

1

'

4

0

δ

δ

δ

ε

(17)

Bł

ą

d dodatkowy wynika ze wzoru:

(

)





































+

+

+

+

+

−

+

−

=

−

=

g

g

g

g

z

R

R

R

R

U

U

U

2

1

2

1

1

1

'

4

0

0

δ

δ

δ

δ

δ

σ

(18)

Przy czym

g

U - warto

ść

sygnału w warunkach odniesienia

0

Z

Z

=

dla

0

=

δ

.

Dla symetrii

3

1

R

R

=

i

4

2

R

R

=

(

)

(

)















+

+

+

+

+

+

+

+

=

2

0

2

4

0

4

4

0

4

0

2

1

2

1

2

1

2

1

'

R

R

R

R

R

R

R

R

R

R

U

U

g

g

g

δ

δ

δ

δ

ε

Analogicznie bł

ą

d

z

σ

wynosi:

0

4

4

0

4

0

4

0

4

0

4

0

4

0

2

2

2

2

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

g

g

g

g

g

g

g

z

+

+

+

+

+















+

+

+

+

+

+

−

=

δ

δ

σ

(19)

Powy

ż

sze wzory wskazuj

ą

,

ż

e wielko

ś

ci bł

ę

dów dodatkowych zale

żą

od doboru elementów. Dla

mostków symetrycznych wzgl

ę

dem przek

ą

tnej zerowej bł

ą

d ten maleje ze zmniejszaniem si

ę

4

R i

g

R .

Natomiast dla mostka symetrycznego wzgl

ę

dem przek

ą

tnej zasilania bł

ą

d maleje ze wzrostem

warto

ś

ci

4

R i

g

R a dla

g

R i

4

R

∞

⇒

bł

ą

d dodatkowy maleje do zera.

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 9 -

5.

Wpływ napi

ę

cia zasilania

Warto

ść

napi

ę

cia uzyskiwanego na przek

ą

tnej zerowej jest proporcjonalna do napi

ę

cia

zasilaj

ą

cego.

6.

Nieliniowe elementy mostka

Mostek mo

ż

e zawiera

ć

jako elementy pomiarowe oporniki nieliniowe o charakterystyce:

( )

I

x

f

R

,

=

gdzie x jest wielko

ś

ci

ą

mierzon

ą

, a

I pr

ą

d danego opornika

R . Wszystkie powy

ż

sze wzory s

ą

nadal słuszne, je

ż

eli w miejsce rezystancji wstawi si

ę

rezystancj

ę

dynamiczn

ą

elementu:

I

R

I

R

I

U

R

dyn

∂

∂

+

=

∂

∂

=

Dla elementu liniowego:

R

R

dyn

=

Wymienione powy

ż

ej kryteria doboru elementów mostka s

ą

równie

ż

słuszne dla mostków pr

ą

du

zmiennego, gdzie oczywi

ś

cie zamiast operowa

ć

rezystancjami nale

ż

y wprowadzi

ć

impedancje

elementów.

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 10 -

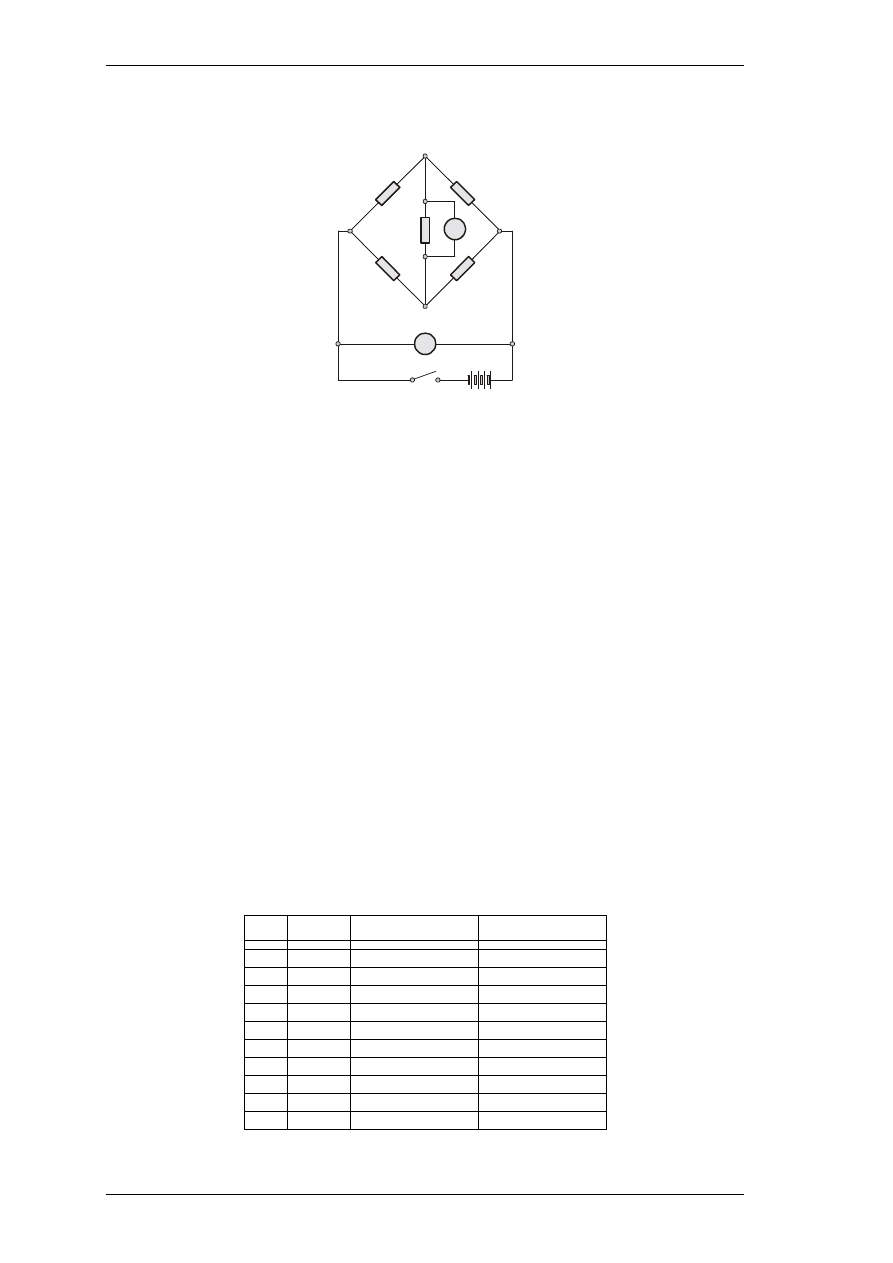
7.

Program

ć

wiczenia

V

V

R

3

R

1

R

4

R

2

R

g

U

ZAS

U

g

Rys. 6. Schemat układu pomiarowego.

Uwaga!
Przedstawiony poni

ż

ej program

ć

wicze

ń

zwi

ą

zany jest z badaniem niezrównowa

ż

onych

układów mostkowych w przypadku symetrii wzgl

ę

dem przek

ą

tnej zasilania. W ramach drugich

zaj

ęć

tego

ć

wiczenia nale

ż

y wyznaczy

ć

wszystkie podane charakterystyki zachowuj

ą

c

odpowiednie zale

ż

no

ś

ci wynikaj

ą

ce z przyj

ę

cia symetrii mostka wzgl

ę

dem przek

ą

tnej zerowej.

7.1. Obliczy

ć

p

R oraz

k

R

(

)

(

)

bZ

X

a

R

R

p

p

+

+

=

1

0

(

)(

)

bZ

X

a

R

R

k

k

+

+

=

1

0

gdzie:

-

X - wielko

ść

mierzona; zakres zmian tej wielko

ś

ci wynosi 0÷100 jednostek. Punkt zerowy

przetwornika odpowiada wielko

ś

ci

0

0

=

=

X

X

.

-

Z - wielko

ść

wpływaj

ą

ca; warto

ść

odniesienia

0

0

=

Z

, zakres zmian wielko

ś

ci

Z wynosi

%

10

±

Z

jednostek wielko

ś

ci

Z .

-

p

a ,

k

a , b i

0

R - wielko

ś

ci stałe.

Dobieramy

k

p

a

a

−

=

, aby otrzyma

ć

przetwornik ró

ż

nicowy.

4

.

0

=

−

=

k

p

a

a

1

.

0

=

b

Ω

=

100

0

R

0

=

Z

Lp.

X

[ ]

Ω

p

R

[ ]

Ω

k

R

1

2

3

4

1

10

2

20

3

30

4

40

5

50

120

80

6

60

7

70

8

80

9

90

10

100

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 11 -

7.2. Wyznaczy

ć

charakterystyk

ę

( )

4

R

f

U

g

=

50

=

X

⇒

Ω

=

=

120

1

R

R

p

oraz

Ω

=

=

80

3

R

R

k

2

4

R

R

=

- symetria wzgl

ę

dem przek

ą

tnej zasilania;

0

=

Z

Ω

=

100

g

R

[ ]

V

U

g

Lp.

2

4

R

R

=

g

U

Lp.

2

4

R

R

=

g

U

Lp.

2

4

R

R

=

g

U

[ ]

Ω

[ ]

V

[ ]

Ω

[ ]

V

[ ]

Ω

[ ]

V

1

2

3

4

5

6

7

8

9

1

10

10

100

19

1000

2

20

11

200

20

2000

3

30

12

300

21

3000

4

40

13

400

22

4000

5

50

14

500

23

5000

6

60

15

600

24

6000

7

70

16

700

25

7000

8

80

17

800

26

8000

9

90

18

900

27

9000

28

10000

Wyznaczy

ć

optymaln

ą

warto

ść

2

4

R

R

=

, dla której

g

U osi

ą

ga maksimum (teoretycznie i

porówna

ć

z pomiarami).

2.a. Wykre

ś

li

ć

charakterystyk

ę

( )

4

R

f

P

g

=

g

g

g

R

U

P

2

=

dla

Ω

=

100

g

R

7.3. Wyznaczy

ć

charakterystyk

ę

( )

X

f

U

g

=

dla

Ω

=

100

g

R

i

∞

=

g

R

oraz

OPT

R

R

R

4

2

4

,

1000

,

100

,

10

Ω

Ω

Ω

=

=

Obliczy

ć

i wykre

ś

li

ć

:

( )

4

R

f

u

=

σ

dla

100

,

80

,

50

,

10

=

X

Ω

=

100

g

R

∞

=

g

R

=

=

2

4

R

R

10

100

1000

OPT

R

4

10

100

1000

OPT

R

4

X

[ ]

V

U

g

[ ]

V

U

g

1

2

3

4

5

6

7

8

9

10

20

30

40

50

60

70

80

90

100

Niezrównowa

ż

one układy mostkowe

Politechnika Opolska

Przetworniki i Układy Pomiarowe

- 12 -

7.4. Wyznaczy

ć

charakterystyk

ę

( )

g

g

R

f

U

=

⇒

=

50

X

Ω

=

=

120

1

R

R

p

oraz

Ω

=

=

80

3

R

R

k

oraz

OPT

R

R

R

4

2

4

=

=

[ ]

V

U

g

Lp.

g

R

g

U

Lp.

g

R

g

U

Lp.

g

R

g

U

[ ]

Ω

[ ]

V

[ ]

Ω

[ ]

V

[ ]

Ω

[ ]

V

1

2

3

4

5

6

7

8

9

1

10

10

100

19

1000

2

20

11

200

20

2000

3

30

12

300

21

3000

4

40

13

400

22

4000

5

50

14

500

23

5000

6

60

15

600

24

6000

7

70

16

700

25

7000

8

80

17

800

26

8000

9

90

18

900

27

9000

28

10000

7.5. Obliczy

ć

(

)

(

)

bZ

X

a

R

R

p

p

+

+

=

1

0

(

)(

)

bZ

X

a

R

R

k

k

+

+

=

1

0

dla

50

=

X

i

(

)

10

...

1

∈

Z

oraz

4

.

0

=

−

=

k

p

a

a

,

1

.

0

=

b

i

Ω

=

100

0

R

50

=

X

Lp.

Z

[ ]

Ω

p

R

[ ]

Ω

k

R

1

2

3

4

1

1

2

2

3

3

4

4

5

5

6

6

7

7

8

8

9

9

10

10

5.a. Wyznaczy

ć

charakterystyk

ę

( )

Z

f

U

g

=

dla

OPT

R

R

R

4

2

4

,

1000

,

100

,

10

Ω

Ω

Ω

=

=

Obliczy

ć

i wykre

ś

li

ć

:

( )

4

R

f

z

=

σ

dla

10

,

8

,

5

,

1

=

Z

Ω

=

100

g

R

=

=

2

4

R

R

10

100

1000

OPT

R

4

Z

[ ]

V

U

g

1

2

3

4

5

1

2

3

4

5

6

7

8

9

10