M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Charakterystyki czasowe

92

Charakterystyką (odpowiedzią) czasową nazywamy przebieg w czasie

odpowiedzi układu (sygnału wejściowego) na określone, standardowe

pobudzenie u(t) podane na wejście układu będącego w stanie równowagi.

Najpopularniejsze charakterystyki:
1. Odpowiedź na skok jednostkowy (odpowiedź skokowa)

2. Odpowiedź na impuls jednostkowy (odpowiedź impulsowa)

UWAGA: pobudzenie impulsowe nie jest realizowane fizycznie!

úû

ù

êë

é

=

î

í

ì

³

<

=

×

=

-

)

(

)

(

0

dla

1

0

dla

0

)

(

)

(

1

s

G

s

a

L

t

h

t

t

t

a

t

u

1

[

]

)

(

)

(

1

)

(

,

0

dla

0

dla

0

)

(

)

(

1

-

s

G

L

t

g

t

t

t

t

t

u

-

¥

¥

=

=

î

í

ì

=

¥

¹

=

=

ò

d

d

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Charakterystyki czasowe

93

Najpopularniejsze charakterystyki:

3. Odpowiedź na pobudzenie rampą

4. Odpowiedź na sygnał sinusoidalny

úû

ù

êë

é

=

î

í

ì

³

×

<

=

×

×

=

-

)

(

)

(

0

dla

0

dla

0

)

(

)

(

2

1

s

G

s

b

L

t

v

t

t

b

t

t

t

b

t

u

1

úû

ù

êë

é

+

=

=

-

)

(

)

(

)

sin(

)

(

2

1

s

G

s

L

t

y

t

A

t

u

w

w

w

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

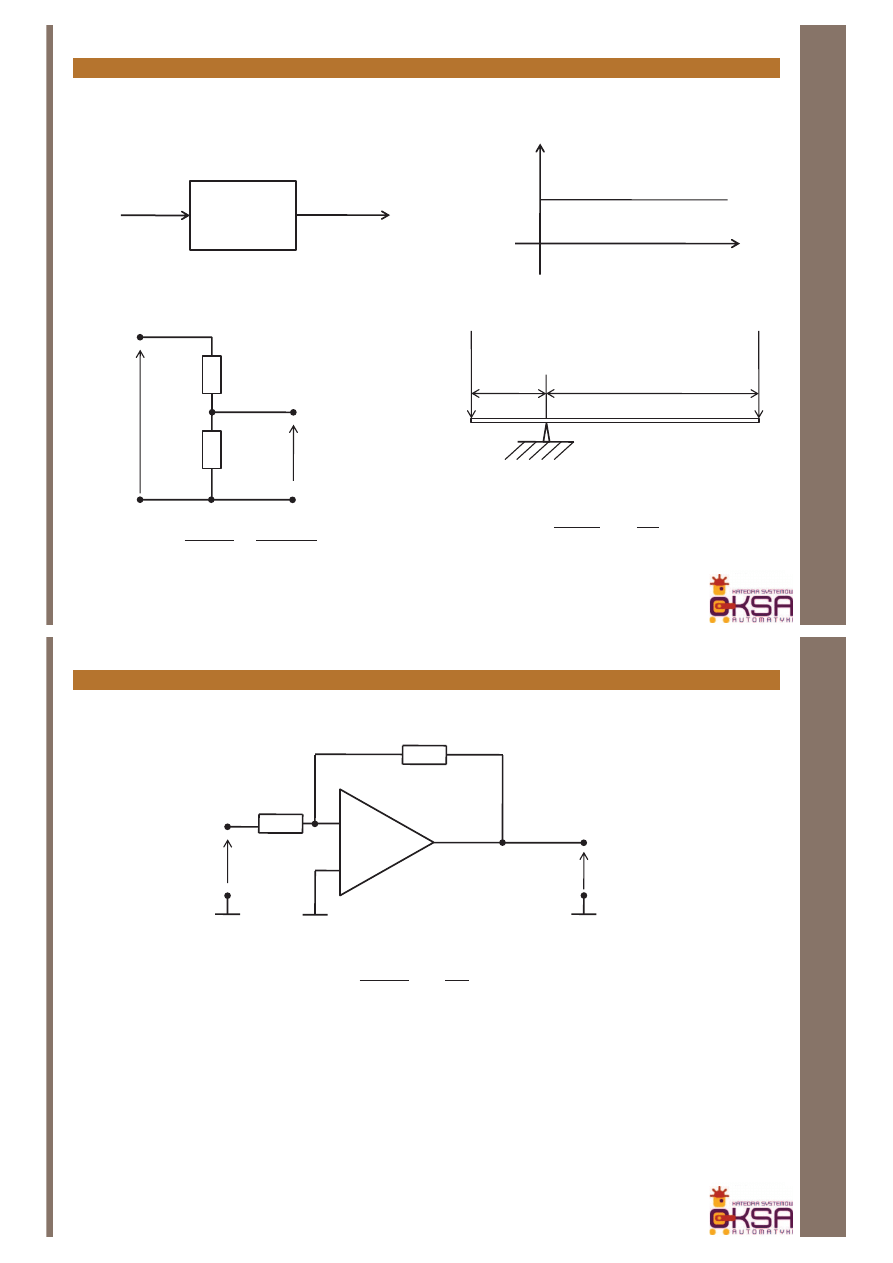
Człony układów regulacji – człon bezinercyjny

94

1. Człon bezinercyjny (wzmacniający)

y(t)

u(t)

)

(

)

(

t

ku

t

y

=

y(t)

t

k

u

1

(t)

u

2

(t)

R

1

R

2

2

1

2

1

2

)

(

)

(

)

(

R

R

R

s

U

s

U

s

G

+

=

=

f

1

(t)

f

2

(t)

L

1

L

2

2

1

1

2

)

(

)

(

)

(

L

L

s

F

s

F

s

G

-

=

=

k

s

G

=

)

(

Inżynieria systemów dynamicznych

G(s)

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon bezinercyjny, przykład

95

R

2

+

_

R

1

u

1

(t)

u

2

(t)

1

2

1

2

)

(

)

(

)

(

R

R

s

U

s

U

s

G

-

=

=

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

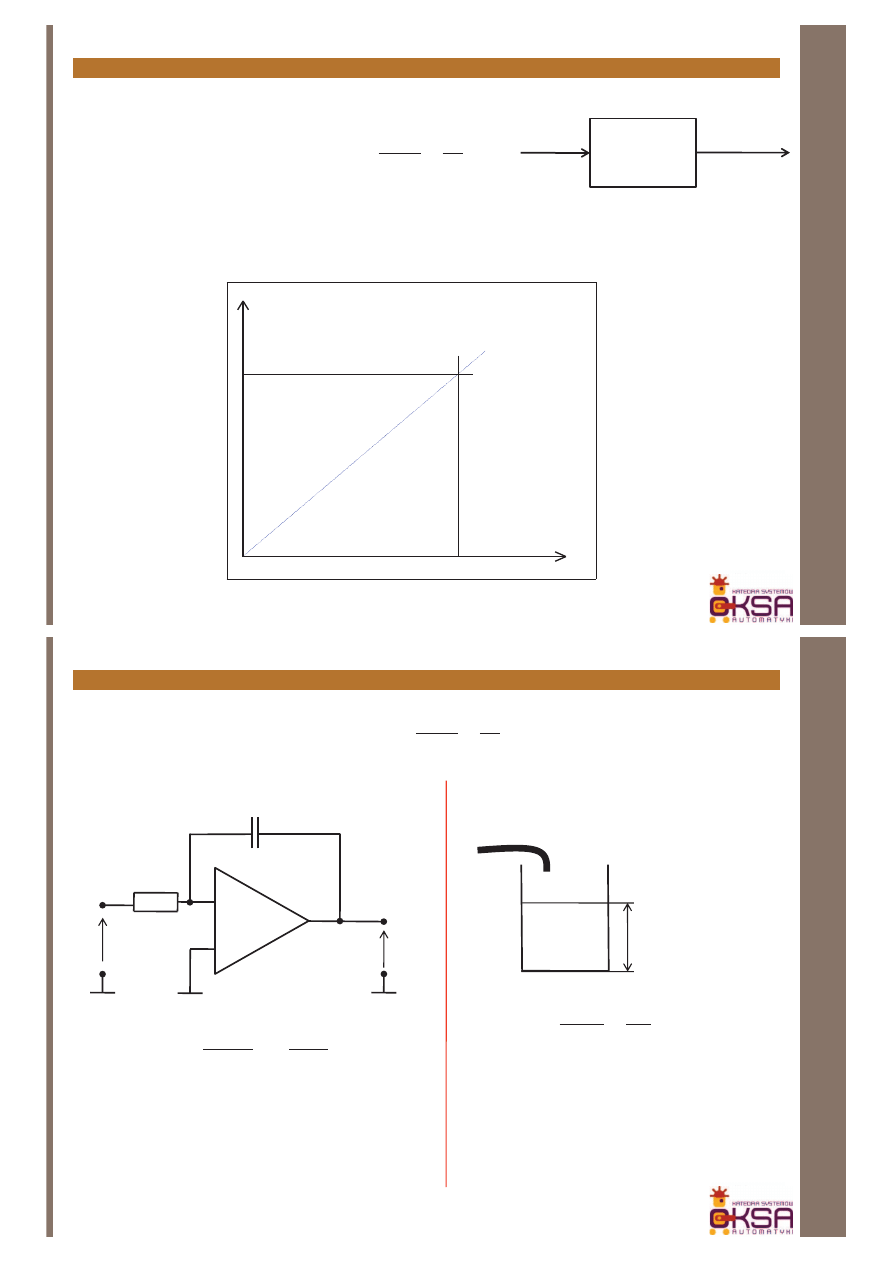
Człony układów regulacji – człon całkujący

96

2. Człon całkujący

y(t)

u(t)

ò

×

=

t

I

u

k

t

y

0

d

)

(

)

(

t

t

Odpowiedź skokowa

s

k

s

U

s

Y

s

G

I

=

=

)

(

)

(

)

(

t

y(t)

k

I

1

)

(

)

(

)

(

)

(

t

t

k

t

y

t

t

u

I

1

1

×

×

=

Þ

=

Inżynieria systemów dynamicznych

G(s)

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon całkujący

97

h(t)

As

s

Q

s

H

s

G

1

)

(

)

(

)

(

=

=

q(t)

q(t)-natężenie przepływu [m

3

/s]

A – powierzchnia dna zbiornika [m

2

]

C

+

_

R

u

1

(t)

u

2

(t)

RCs

s

U

s

U

s

G

1

)

(

)

(

)

(

1

2

-

=

=

s

k

s

U

s

Y

s

G

I

=

=

)

(

)

(

)

(

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

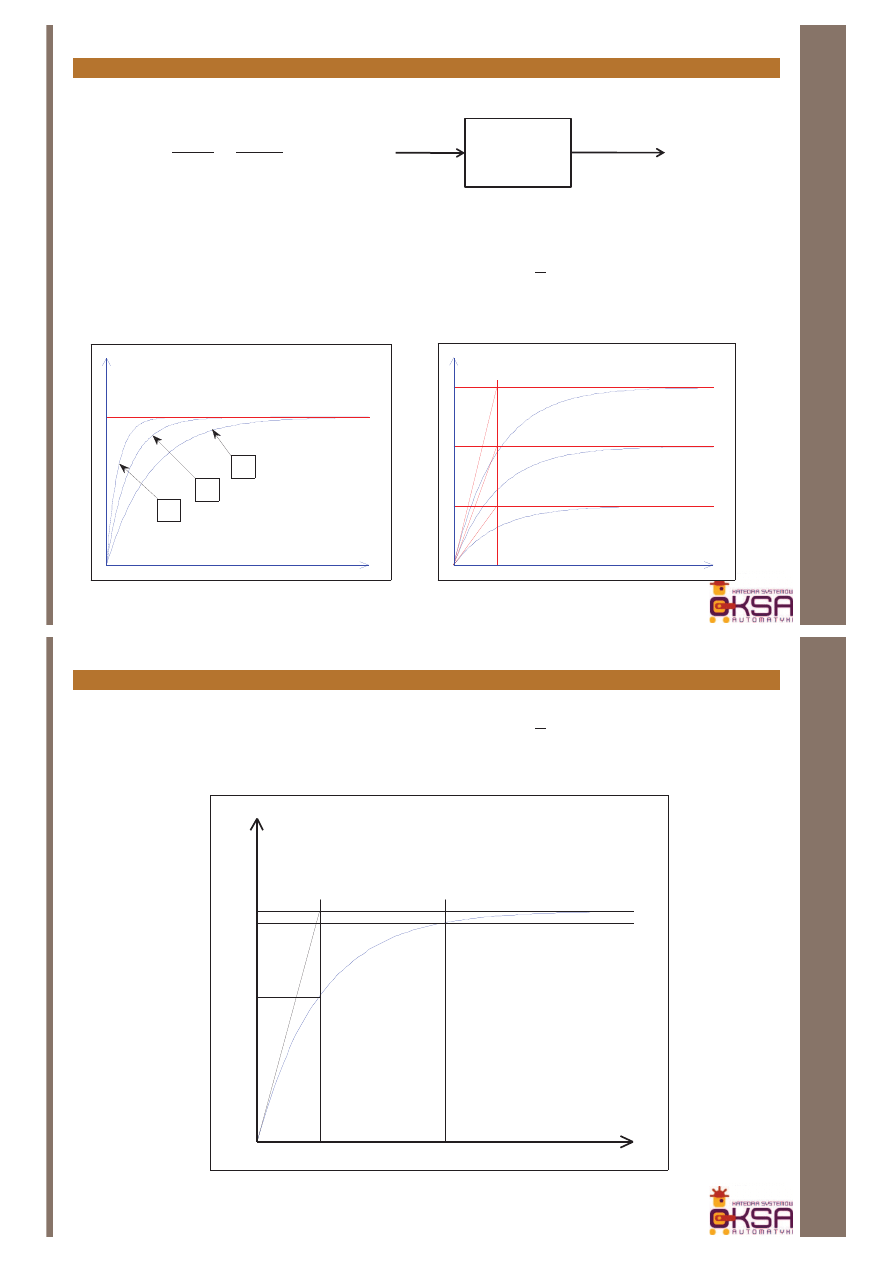
Człony układów regulacji – człon inercyjny I rzędu

98

3. Człon inercyjny I rzędu

y(t)

u(t)

1

)

(

)

(

)

(

+

=

=

Ts

k

s

U

s

Y

s

G

t

y(t)

T

1

T

2

k

T

3

T

1

<T

2

<T

3

t

y(t)

k

1

k

2

k

3

T

k

1

<k

2

<k

3

Odpowiedzi skokowe dla różnych parametrów transmitancji

)

(

1

)

(

)

(

)

(

t

e

k

t

y

t

t

u

T

t

1

1

×

ú

û

ù

ê

ë

é

-

=

Þ

=

-

Inżynieria systemów dynamicznych

G(s)

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon inercyjny I rzędu, parametry odpowiedzi skokowej

99

)

(

1

)

(

)

(

)

(

t

e

k

t

y

t

t

u

T

t

1

1

×

ú

û

ù

ê

ë

é

-

=

Þ

=

-

t

y(t)

0,63k

0,95k

k

T

3T

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

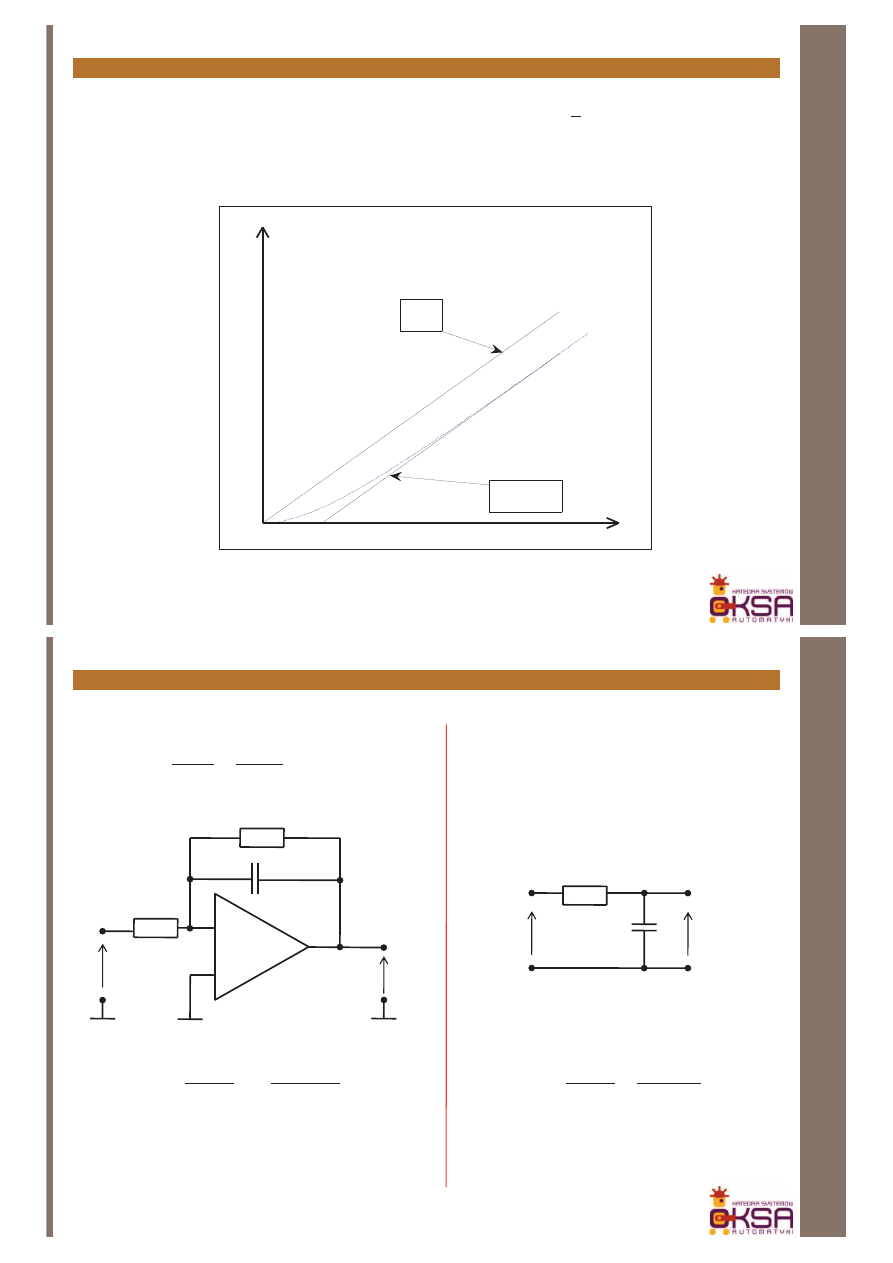
Człony układów regulacji – człon inercyjny I rzędu, parametry odpowiedzi na rampę

100

)

(

)

(

)

(

)

(

t

Te

T

t

k

t

y

t

t

t

u

T

t

1

1

×

ú

û

ù

ê

ë

é

+

-

=

Þ

×

=

-

t

y(t)

T

k(t-T)

kt

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon inercyjny I rzędu, przykłady

101

C

+

_

u

1

(t)

u

2

(t)

1

/

)

(

)

(

)

(

2

1

2

1

2

+

-

=

=

Cs

R

R

R

s

U

s

U

s

G

1

)

(

)

(

)

(

+

=

=

Ts

k

s

U

s

Y

s

G

R

2

R

1

R

u

1

(t)

u

2

(t)

C

1

1

)

(

)

(

)

(

1

2

+

=

=

RCs

s

U

s

U

s

G

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon inercyjny I rzędu

102

h(t)

1

)

(

)

(

)

(

+

=

=

Ts

k

s

Q

s

H

s

G

q(t)

Uwaga: wypływ ze zbiornika laminarny (natężenie przepływu zależy liniowo
od ciśnienia na dnie zbiornika ze współczynnikiem α).

q

2

(t)=αp(t)= αρgh(t)

q

2

(t)

g

A

g

k

ar

ar

=

=

T

,

1

q(t)-natężenie przepływu [m

3

/s]

A – powierzchnia dna zbiornika [m

2

]

p(t) – ciśnienie przy odpływie [Pa]
g – przyśpieszenie ziemskie [m/s

2

]

ρ -gęstość cieczy [kg/m

3

]

Uwaga 2: w przypadku, gdyby w rurze na wylocie zbiornika znajdowała się
kryza (gwałtowne przewężenie) lub zawór, to charakterystyka wypływu
miałaby charakter pierwiastkowy (patrz zbiór zadań)

gdzie:

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon inercyjny I rzędu

103

4. Człon całkujący z inercją

y(t)

u(t)

)

1

(

)

(

)

(

)

(

+

=

=

Ts

s

k

s

U

s

Y

s

G

Odpowiedź skokowa:

)

(

)

(

)

(

)

(

t

Te

T

t

k

t

y

t

t

u

T

t

1

1

×

ú

û

ù

ê

ë

é

+

-

=

Þ

=

-

t

y(t)

T

k(t-T)

kt

Typowy układ: silnik prądu stałego,
gdzie wejściem jest podane napięcia
a wyjściem kąt o jaki obrócił się wał
silnika

Inżynieria systemów dynamicznych

G(s)

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon inercyjny I rzędu

104

5. Człon II rzędu

y(t)

u(t)

2

2

2

2

)

(

)

(

)

(

n

n

n

s

s

k

s

U

s

Y

s

G

w

zw

w

+

+

=

=

Jak pamiętamy, postać odpowiedzi układu zależy od miejsc zerowych wielomianu
mianownika transmitancji, które w omawianym przypadku wynoszą:

(

)

1

1

2

1

4

4

4

2

12

2

2

2

2

2

2

-

±

-

=

Þ

-

=

D

Þ

-

=

-

=

D

z

w

zw

z

w

z

w

w

w

z

n

n

n

n

n

n

s

0

0

>

³

n

w

z

gdzie:

- współczynnik tłumienia
- pulsacja drgań naturalnych

Inżynieria systemów dynamicznych

G(s)

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ dwuinercyjny

105

2

2

2

2

)

(

)

(

)

(

n

n

n

s

s

k

s

U

s

Y

s

G

w

zw

w

+

+

=

=

Przypadek pierwszy: wielomian mianownika ma dwa pierwiastki rzeczywiste ujemne

1

1

2

12

-

±

-

=

Þ

³

z

w

zw

z

n

n

s

12

12

2

1

1

gdzie

,

)

1

)(

1

(

)

(

)

(

)

(

s

T

s

T

s

T

k

s

U

s

Y

s

G

=

+

+

=

=

)

(

1

)

(

)

(

)

(

1

2

2

1

1

2

1

2

t

e

T

T

T

e

T

T

T

k

t

y

t

t

u

T

t

T

t

1

1

×

ú

ú
û

ù

ê

ê
ë

é

-

-

-

+

=

Þ

=

-

-

Inżynieria systemów dynamicznych

t

y(t)

1

z

2

z

3

z

1

1=

z

1

<

z

2

<

z

3

,

w = const

Uwaga: Dla ζ=1 odpowiedź
aperiodyczna krytyczna, najszybsza
możliwa odpowiedź bez
przeregulowań

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ oscylacyjny

106

Przypadek drugi: wielomian mianownika ma dwa pierwiastki zespolone sprzężone

2

12

1

1

0

z

w

zw

z

-

±

-

=

Þ

<

<

n

n

j

s

(

)

)

(

1

sin

1

1

1

)

(

)

(

)

(

2

2

t

e

t

k

t

y

t

t

u

t

n

n

1

1

×

ú

ú
û

ù

ê

ê
ë

é

×

+

-

×

-

-

×

=

Þ

=

-

zw

j

z

w

z

t

y(t)

k

w

1

w

3

w

2

w

1

<

w

2

<

w

3

,

z=const

t

y(t)

k

z

2

z

3

z

1

0<

z

1

<

z

2

<

z

3

<1 ,

w = const

( )

z

j

arccos

=

gdzie:

Inżynieria systemów dynamicznych

t

y(t)

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ oscylacyjny – parametry odpowiedzi skokowej

107

T

n

– czas narastania odpowiedzi

T

d

– czas ustalania (d – najczęściej w procentach)

T

P

– czas maksymalnego przeregulowania

M

P

– maksymalne przeregulowanie

Inżynieria systemów dynamicznych

k

0.9k

0.1k

2dk

T

n

T

P

T

d

M

P

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ oscylacyjny – parametry odpowiedzi skokowej

108

T

n

– czas narastania odpowiedzi

T

d

– czas ustalania (d – najczęściej w procentach)

T

P

– czas maksymalnego przeregulowania

M

P

– maksymalne przeregulowanie

lub w procentach:

Inżynieria systemów dynamicznych

n

n

T

w

8

,

1

=

n

n

T

T

zw

zw

3

,

4

%

5

%

2

=

=

2

1

z

w

p

-

=

n

P

T

÷

÷

ø

ö

ç

ç

è

æ

+

=

-

-

2

1

1

z

zp

e

k

M

P

%

100

%

100

2

1

%

×

=

×

-

=

-

-

z

zp

e

k

k

M

M

P

P

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ oscylacyjny

109

Przypadek trzeci: wielomian mianownika ma dwa pierwiastki urojone sprzężone

n

j

s

w

z

±

=

Þ

=

12

0

( )

[

]

)

(

cos

1

)

(

)

(

)

(

t

t

k

t

y

t

t

u

n

1

1

×

-

×

=

Þ

=

w

Inżynieria systemów dynamicznych

t

y(t)

k

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

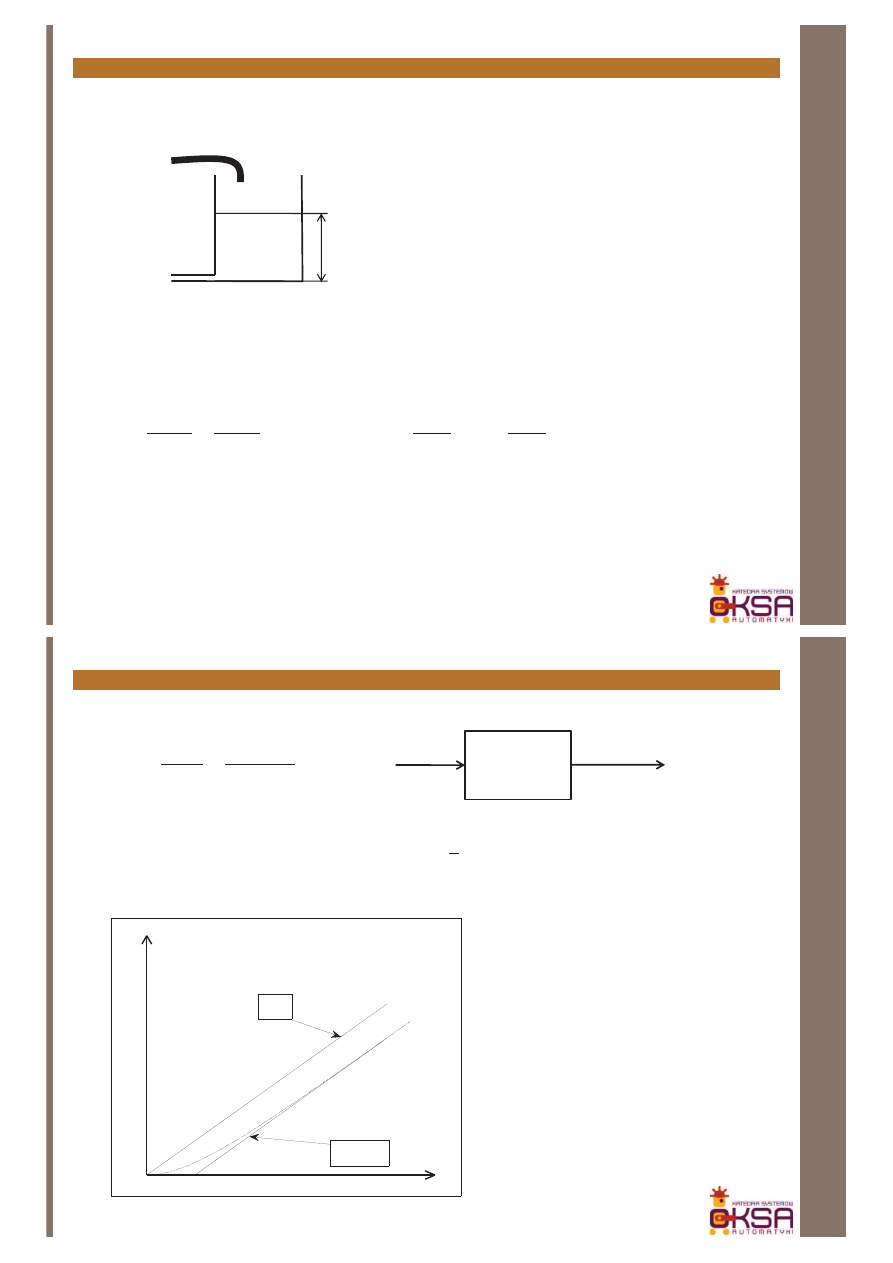
Człony układów regulacji – układ II rzędu, przykłady, układy RLC

110

Układ RLC

R

u

2

(t)

u

1

(t)

L

C

i

L

(t)

)

/(

1

)

/(

1

)

/(

1

)

(

)

(

)

(

2

1

2

LC

s

RC

s

LC

s

U

s

U

s

G

+

+

=

=

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

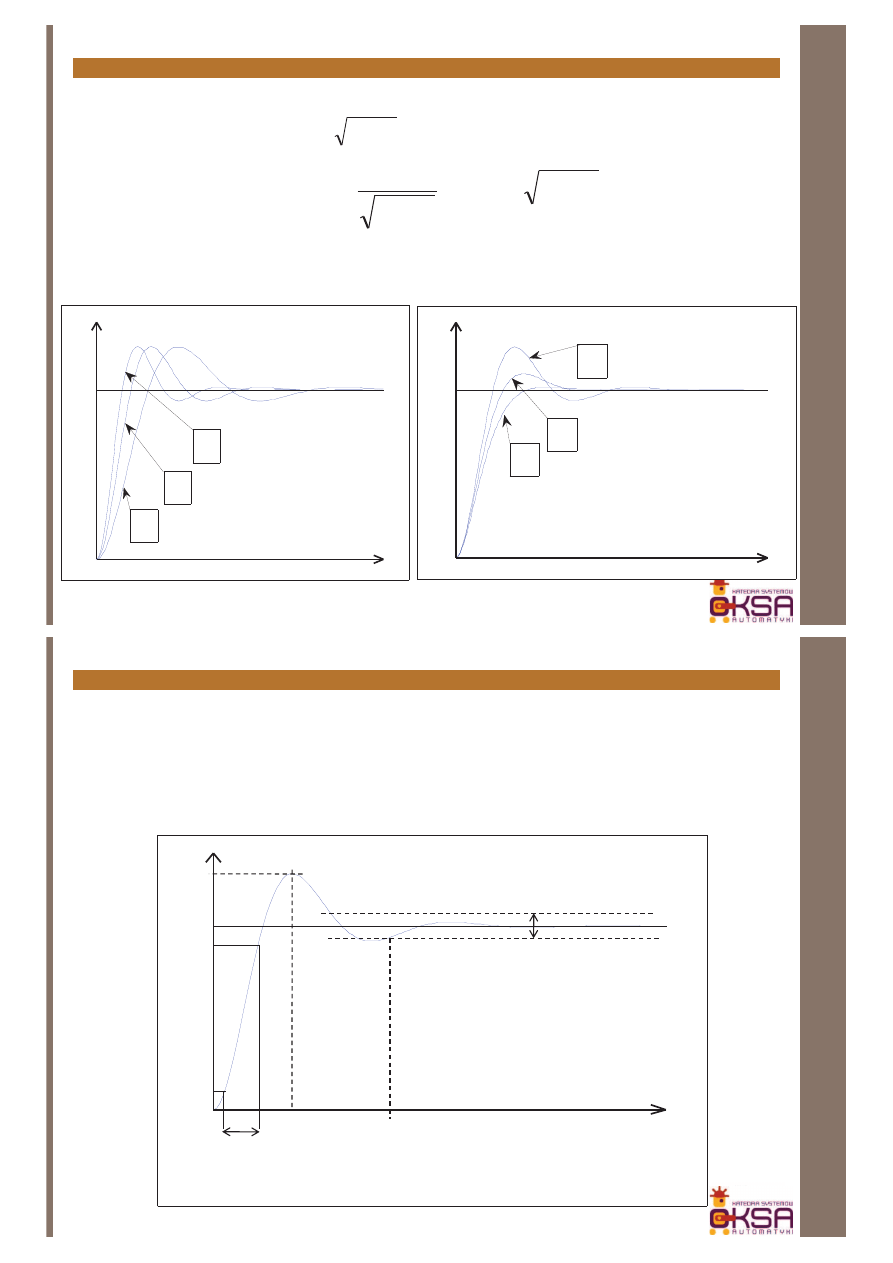
Człony układów regulacji – układ II rzędu, przykłady, układy RLC

111

Układ LC

u

2

(t)

u

1

(t)

L

C

i

L

(t)

)

/(

1

)

/(

1

)

(

)

(

)

(

2

1

2

LC

s

LC

s

U

s

U

s

G

+

=

=

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ II rzędu, przykłady, układy hydrauliczne

112

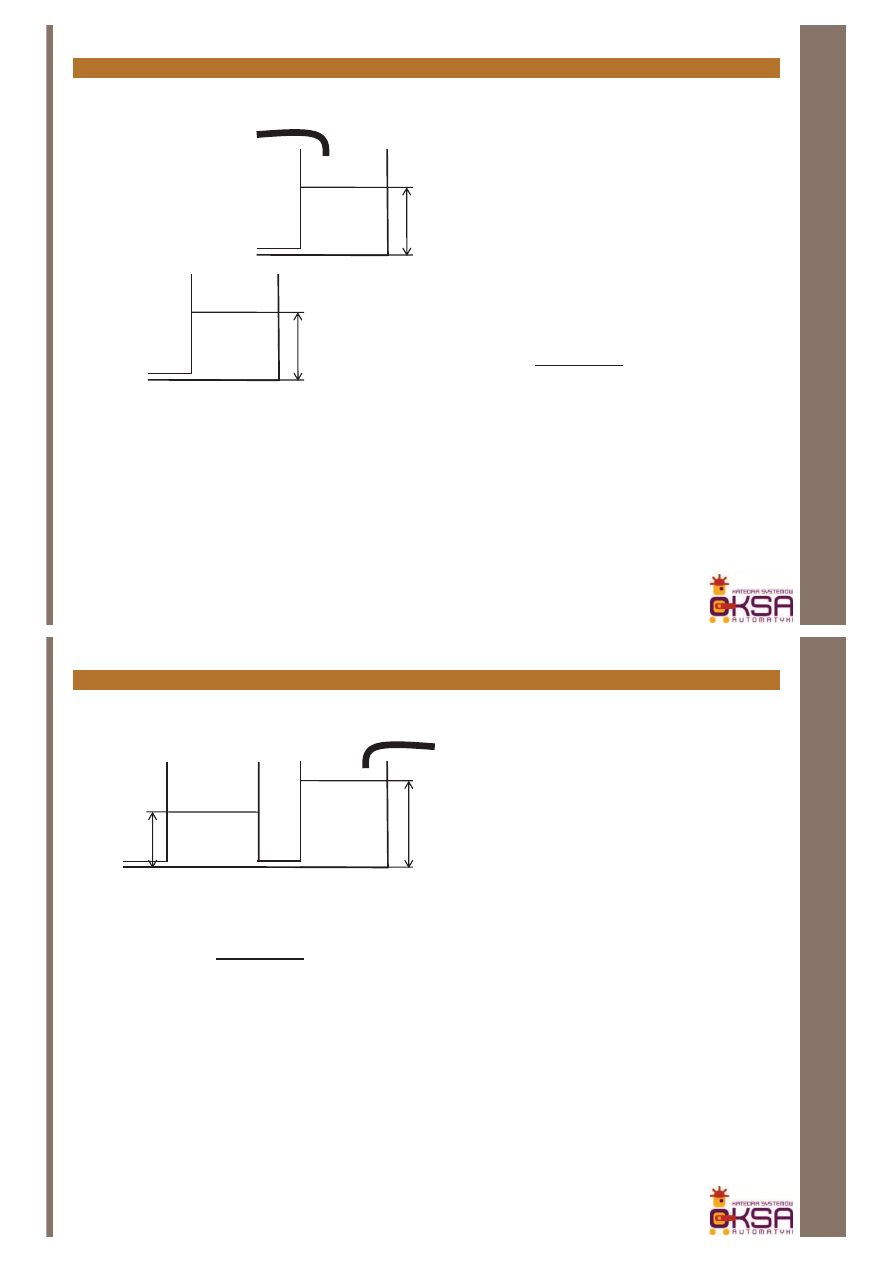
Dwa zbiorniki

h

1

(t)

q

1

(t)

q

2

(t)

h

2

(t)

q

3

(t)

?

)

(

)

(

)

(

1

2

=

=

s

Q

s

H

s

G

Uwaga: wypływ ze zbiornika laminarny (patrz przykład dla członu inercyjnego

I rzędu). Założyć, że gęstość cieczy, powierzchnie den zbiorników oraz
współczynniki

α

i

są znane.

q

i

(t)= αρgh

i-1

(t)

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ II rzędu, przykłady, układy hydrauliczne

113

Dwa zbiorniki

h

1

(t)

q

1

(t)

q

2

(t)

h

2

(t)

q

3

(t)

?

)

(

)

(

)

(

1

2

=

=

s

Q

s

H

s

G

Uwaga: wypływ ze zbiornika laminarny (patrz przykład dla członu inercyjnego

I rzędu). Założyć, że gęstość cieczy, powierzchnie den zbiorników oraz
współczynniki

α

i

są znane.

q

i

(t)= αρgh

i-1

(t)

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – układ II rzędu, przykłady, układy mechaniczne

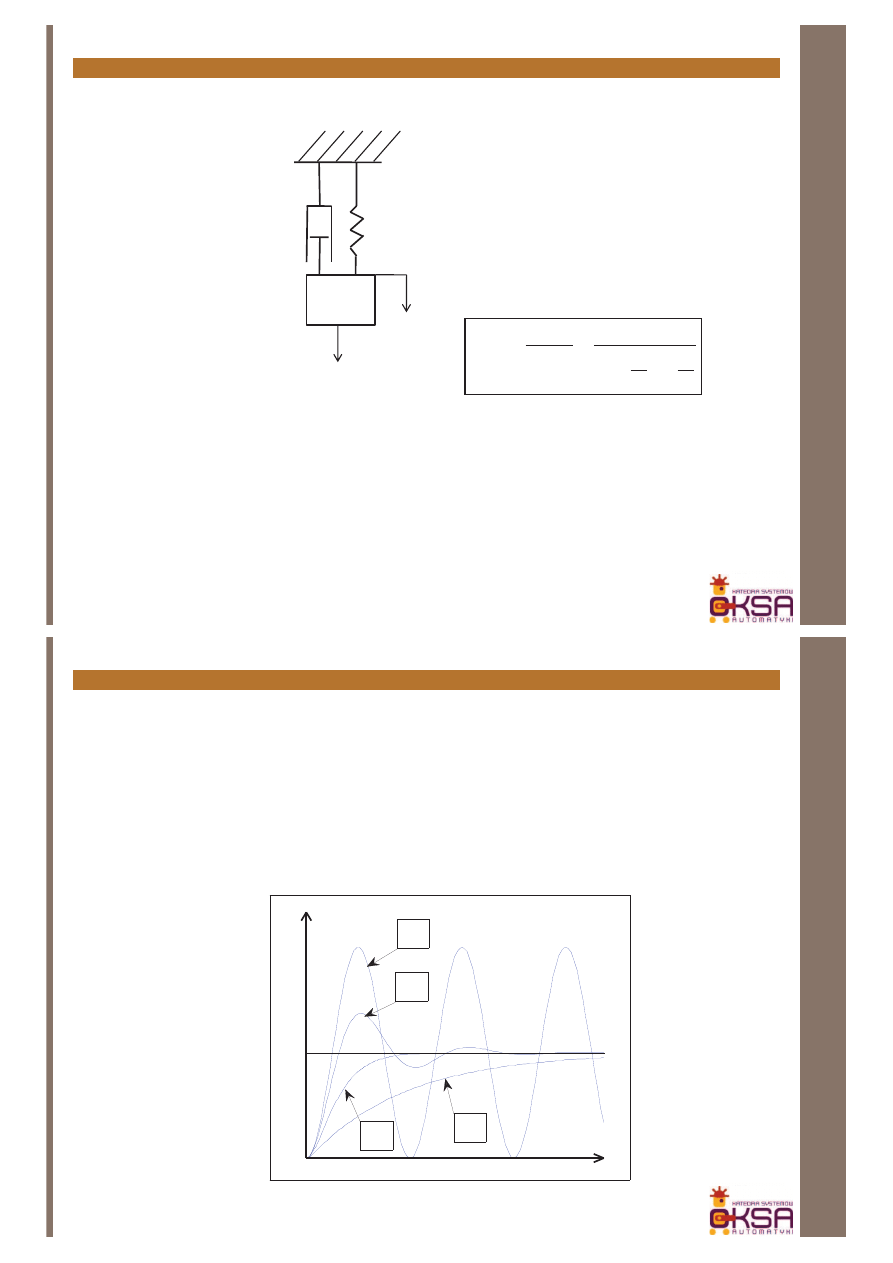
114

Układ mechaniczny

f(t)

b

k

m

1

x

1

(t)

m

k

s

m

b

s

m

s

F

s

X

s

G

+

+

=

=

2

1

/

1

)

(

)

(

)

(

Inżynieria systemów dynamicznych

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

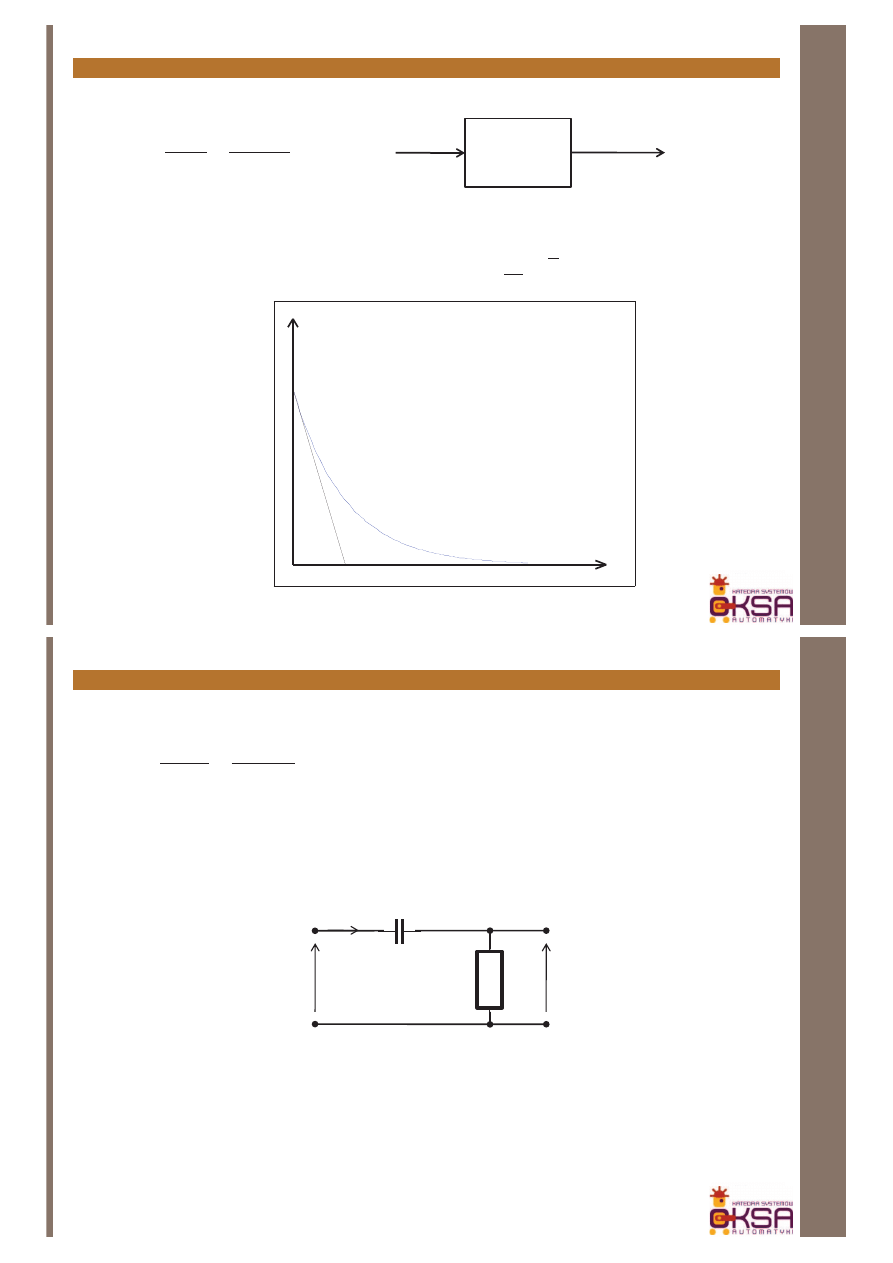
Człony układów regulacji – układ II rzędu - podsumowanie

115

Inżynieria systemów dynamicznych

t

y(t)

k

0<

z<1

z=1

z>1

z=0

Odpowiedzi układu II rzędu
ζ=0 – sinusoida (bieguny urojone sprzężone)
0<ζ<1 – tłumiona sinusoida (bieguny zespolone sprzężone) – odpowiedź niedotłumiona
ζ =1 – odpowiedź aperiodyczna krytyczna (podwójny biegun rzeczywisty)
ζ >1 – odpowiedź aperiodyczna (dwa różne bieguny rzeczywiste) –odpowiedź

przetłumiona

ζ <0 – układ niestabilny – narastające oscylacje

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – rzeczywisty człon różniczkujący

116

6. Rzeczywisty człon różniczkujący

y(t)

u(t)

)

1

(

)

(

)

(

)

(

+

×

=

=

Ts

s

k

s

U

s

Y

s

G

Odpowiedź skokowa:

)

(

)

(

)

(

)

(

t

e

T

k

t

y

t

t

u

T

t

1

1

×

=

Þ

=

-

Inżynieria systemów dynamicznych

t

y(t)

k/T

T

G(s)

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

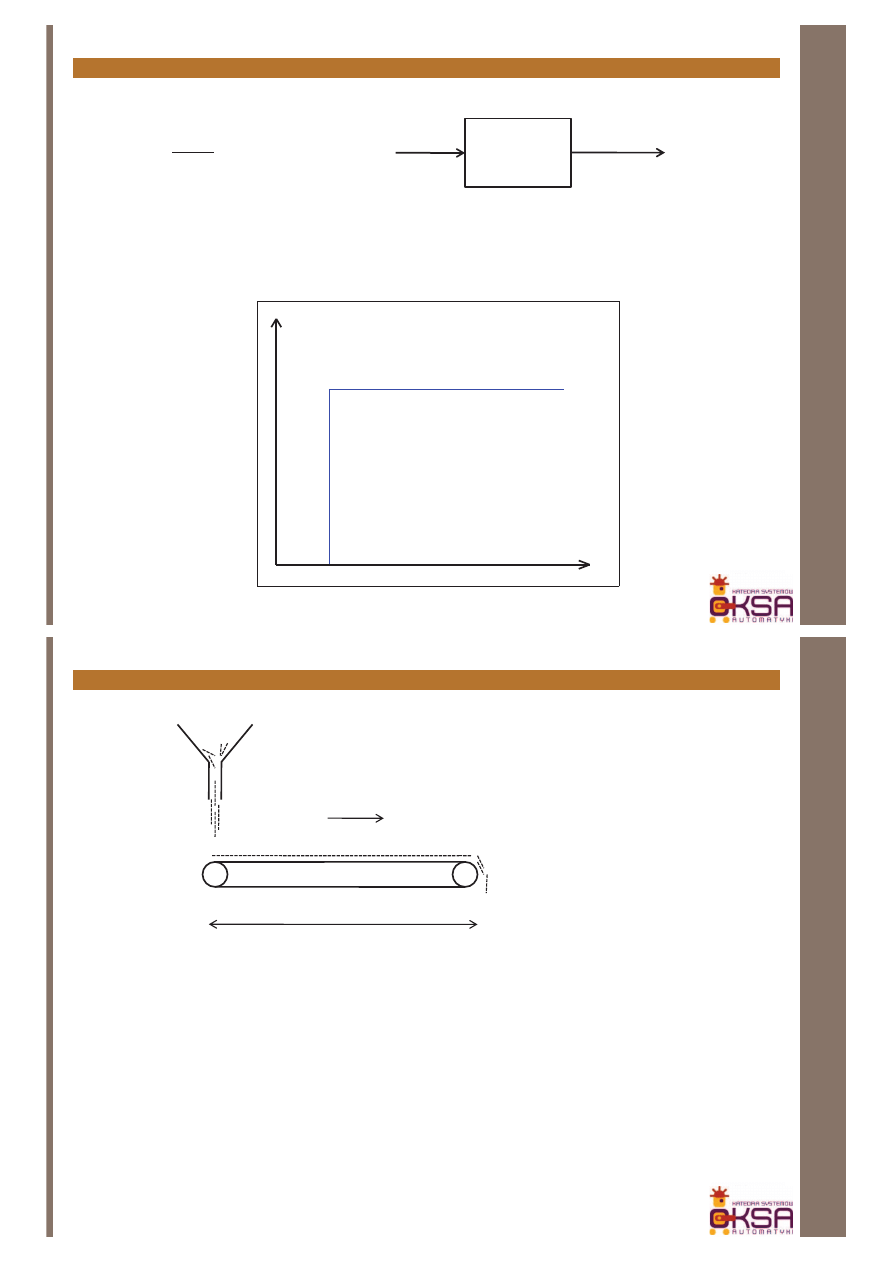
Człony układów regulacji – rzeczywisty człon różniczkujący, przykład RC

117

Przykład: układ RC

1

)

(

)

(

)

(

1

2

+

×

=

=

RCs

s

RC

s

U

s

U

s

G

Inżynieria systemów dynamicznych

R

u

2

(t)

u

1

(t)

C

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon opóźniający

118

7. Człon opóźniający

y(t)

u(t)

s

e

k

s

U

s

Y

s

G

t

-

×

=

=

)

(

)

(

)

(

Odpowiedź skokowa:

)

(

)

(

)

(

)

(

t

-

×

=

Þ

=

t

k

t

y

t

t

u

1

1

Inżynieria systemów dynamicznych

G(s)

)

(

)

(

t

-

×

=

t

u

k

t

y

t

y(t)

k

t

M

E

T

O
D

Y
O
P

IS

U
U

K

Ł

A

D

Ó

W

Człony układów regulacji – człon opóźniający

119

Przykład

Inżynieria systemów dynamicznych

u(t)

y(t)=u(t-τ)

l

v

τ

=l/v

Inne przykłady: rurociąg ciepłej wody, linia długa, kanał wentylacyjny (czyli
wszędzie tam, gdzie transportowane jest medium) stąd

τ

bywa też

nazywane opóźnieniem transportowym