
MESA
A ZAWIERANIE TRANSAKCJI
ZGODNIE Z CYKLAMI
RYNKOWYMI
Wydanie drugie
John F. Ehlers
John Wiley & Sons, Inc.

5
Spis treści
Rozdział 1
Dlaczego na rynku występują cykle
Rozdział 2
Podstawowe pojęcia dotyczące cykli
Rozdział 3
Zasady rządzące cyklami
Rozdział 4
Średnie ruchome
Rozdział 5
Funkcje impetu
Rozdział 6
Pomiar spektrum rynkowego
Rozdział 7
Opis MESA
Rozdział 8
Wskaźnik Sinewave
Rozdział 9
Chwilowa Linia Trendu
Rozdział 10 Dostrajanie standardowych wskaźników
Rozdział 11 Zawieranie transakcji zgodnie z Trybem Cyklu
Rozdział 12 Zyskowne systemy transakcyjne do gry na rynku kcji
Objaśnienia
Informacja
dodatkowa
Skorowidz
rzeczowy

Wstęp
1
Wstęp
Cykle
są wszechobecne. Otaczają nas w każdej skali, od atomu po galaktykę. Cykle są
naturalną odpowiedzią na zaburzenie. Gdy naprężysz gumową tasiemkę pomiędzy palcami,
naciągniesz ją z jednej strony i puścisz, to efektem drgań jest cykliczna oscylacja. Lub też,
jeśli wygniesz wystający poza krawędź biurka koniec linijki i zwolnisz go, linijka także
będzie oscylować. Są to proste przykłady cykli będących efektem zaburzeń.
Z
całą pewnością istnieje aż nadto dużo zaburzeń rynku i mamy wiele powodów
wierzyć, że cykle też tam występują. Oczywiście, cykle rynkowe nie występują przez cały
czas. One przychodzą i odchodzą. Cykle są jednym z kilku mierzalnych parametrów rynku.
Ponieważ cykle są efemeryczne, koniecznością jest ich pomiar za pomocą szybko
reagującego algorytmu, takiego jak Maximum Entropy Spectral Analysis (MESA). Aby
otrzymać wysoko rozdzielcze oszacowanie spektrum, MESA potrzebuje bardzo małą ilość
danych liczbowych. MESA ma swój początek jako środek przetwarzania informacji
sejsmicznych podczas poszukiwań złóż ropy naftowej.
Z teorii wymuszonej drogi przypadkowej, zwanej Spacerem Pijanego, dochodzimy do
konkluzji, że są dwa tryby rynku: Tryb Trendu i Tryb Cyklu. Za pomocą pomiaru cyklu
możemy zidentyfikować tryb rynku. Pomiar za pomocą MESA pozwala także tworzyć
wskaźniki pomagające zawierać transakcje z chirurgiczną precyzją. Rezultatem usuwania
składnika Cyklu Dominującego z ceny, pozostawiając Trend jako resztę, jest Chwilowa Linia
Trendu. Rysując fazę Cyklu Dominującego otrzymamy wskaźnik Sinewave. Jest to wspaniały
wskaźnik trybu cyklu, ponieważ w celu przewidzenia punktów zwrotnych cyklu, fazę można
sztucznie przyśpieszyć. W dodatku, faza nie ma tendencji do przyśpieszania gdy rynek jest w
Trybie Trendu, dzięki czemu unikamy błędnych sygnałów.
Rozdział 1 stanowi przegląd historii cykli i postępu w technice ich pomiaru. Rozdział
2 opisuje rozwiązania problemu Spaceru Pijanego. Te dwa rozwiązania, równanie Dyfuzji i
równanie Telegrafisty, są bezpośrednio związane z Trybem Trendu i Trybem Cyklu rynku.
Rozdział 3 omawia cechy charakterystyczne cykli, tj. częstotliwość, amplitudę i fazę.
Rozdział 4 omawiający średnie ruchome, opisuje nie tylko jak wykonywać gładzenie
ale również, dlaczego nie można uniknąć opóźnienia. Przedstawione są techniki pokazujące
jak chirurgicznie usunąć określone składniki cykliczne i minimalizować opóźnienie. Funkcje
impetu, omówione w Rozdziale 5, w przeciwieństwie do średnich ruchomych, dają
wyprzedzenie fazowe. Wyprzedzenie fazowe może często prowadzić do fałszywych
wniosków, ponieważ wskaźnik może błędnie przewidzieć rzeczywiste zachowanie rynku.
W Rozdziale 6 omówiono metody pomiaru cykli rynkowych oraz porównano je do
innych technik pomiarowych, tak jak szybka transformacja Fouriera (FFT). Omówienie jest
podobne do przedstawionego w książce Rocket Science for Traders i zawiera dodatkowo
tabelą porównawczą. Algorytm MESA opisany jest w Rozdziale 7. Skoro cykl rynkowy jest
mierzalny, to pomierzony Cykl Dominujący może być stosowany do tworzenia nowych,
precyzyjnych technicznie wskaźników. Należą do nich Sinewave Indicator, opisany w
Rozdziale 8 oraz Chwilowa Linia Trendu, opisana w Rozdziale 9. Standardowe wskaźniki są
kombinacją funkcji impetu i średnich ruchomych, a zatem mogą być także ulepszone
dostosowując je do pomierzonego przy pomocy MESA Cyklu Dominującego. Sposoby
ulepszenia wskaźników Commodity Channel Index (CCI), Relative Strength Index (RSI) i
Stochastic, opisane są w Rozdziale 10. Zastosowano tam precyzyjną aplikację algorytmu
MESA, zamiast stosowanego do pomiaru cykli w książce Rocket Science for Traders,
algorytmu Hilbert Discriminator.

Wstęp
2
Stosując pomiar cykli za pomocą MESA, można także utworzyć wysoko efektywny
automatyczny system transakcyjny. Wysoko zyskowny system transakcyjny przedstawiony
jest w Rozdziale 11, który zawiera także szczegółowe omówienie kolejnych etapów tworzenia
takiego systemu, wraz z wynikami testowania i programem komputerowym do zastosowania
na twoim własnym komputerze. W Rozdziale 12 opisane są rynkowe systemy do gry na rynku
akcji, łącznie z programami komputerowymi do zastosowania.
Książka MESA a zawieranie transakcji zgodnie z cyklami rynkowymi obiecuje, że
zapozna ciebie z myśleniem o rynku w kategoriach częstotliwości i dodatkowo w
konwencjonalnej kategorii czasu. Ten nowy sposób myślenia prowadzi nie tylko do wysoko
efektywnych nowych wskaźników, ale może zapewnić ci przenikliwość w ocenie rynku, o
jakiej wcześniej mogłeś tylko marzyć.
JOHN F. EHLERS
Santa Barbara, California
styczeń 2002

Dlaczego na rynku występują cykle
9
Rozdział 1
Dlaczego na rynku występują cykle
Analiza techniczna rynku dlatego jest tak popularna, ponieważ rynek nie zawsze
przynosi korzyść. Dostrzegalne przypadki, które występują w formacjach wykresu, takie jak
podwójne szczyty i fale Elliotta, umożliwiają dokonywanie transakcji na podstawie analizy
technicznej. Cykle są jednym z tych dostrzegalnych przypadków, które występują i są
możliwe do zidentyfikowania przez bezpośredni pomiar. Zidentyfikowanie cykli nie wymaga
dużego doświadczenia czy systemu eksperckiego. Cykle mogą być mierzone bezpośrednio za
pomocą systemu mierzącego odległość pomiędzy kolejnymi dołkami lub za pomocą
specjalnego programu, takiego jak MESA.
Z
faktu,
że istnieją cykle nie wynika, że istnieją one przez cały czas. Cykle przychodzą
i odchodzą. Pozornie, czasem nawet dominują i przyćmiewają istniejące cykle.
Doświadczenie pokazuje, że cykle użyteczne do zawierania transakcji występują tylko przez
15 do 30 procent całego czasu. To w znacznym stopniu zgadza się z poglądem, wyrażonym
przez J. M. Hursta, że „23% całego ruchu ceny ma charakter oscylacyjny i możliwy do
przewidzenia”. Jest to analogiczne do problemu tradera podążającego za trendem, który
stwierdza, że rynek jest w trendzie tylko przez niewielki procent całego czasu.
Rys historyczny
Obserwacje cyklicznie powtarzających się zjawisk naturalnych, od zamierzchłych
czasów obserwowanych przez człowieka, stworzyły podwaliny podstawowych koncepcji
wykorzystywanych w dzisiejszych obliczeniach spektralnych. Na podstawie obserwacji
długości dnia, długości roku, zmian pór roku, faz księżyca oraz ruchów planet i gwiazd,
starożytne cywilizacje były w stanie projektować kalendarze i odmierzać czas. W szóstym
wieku przed naszą erą, Pitagoras odkrył wzajemne relacje pomiędzy wysokością dźwięków
muzycznych wytwarzanych przez napięte struny a liczbami, określającymi długości tych
strun. Wierzył, że istota harmonii związana jest z liczbami. Pitagoras rozszerzył to na ruch
ciał niebieskich, opisując ten ruch jako „muzyka ciał niebieskich”.
Matematyczne podstawy współczesnej analizy spektralnej stworzył Isaac Newton. W
siedemnastym wieku odkrył, że światło słoneczne przechodząc przez pryzmat szklany tworzy
kolorowe widmo. Stwierdził on, że każdy kolor odpowiada określonej długości fali światła
oraz, że białe światło słoneczne zawiera wszystkie długości fal. Jako termin naukowy,
opisujący widmo kolorów, wymyślił słowo spektrum.
W 1738 r. Daniel Bernoulli rozwiązał problem rozkładu fal drgającej struny
muzycznej. Później, w 1822 r. francuski inżynier Jean Baptiste Joseph Fourier rozszerzył to
odkrycie wykazując, że każdą funkcję można przedstawić w postaci ciągu nieskończonego,
składającego się sumowania funkcji sinus i cosinus. Takie matematyczne wyobrażenie, z
powodu harmonicznej relacji wzajemnej pomiędzy funkcjami sinus i cosinus, stało się znane
jako analiza harmoniczna. Na jego cześć, opis ten został nazwany transformacją Fouriera.
Punktem zwrotnym w teorii analizy spektralnej było opublikowanie w 1930 r. przez
Norberta Wienera, klasycznej rozprawy „Generalized Harmonic Analysis”. Wśród jego
zasług była precyzyjna definicja statystyczna autokorelacji i siły gęstości spektralnej dla
stacjonarnych procesów losowych. Użycie transformacji Fouriera, zamiast tradycyjnej analizy

Dlaczego na rynku występują cykle
10
serii Fouriera, umożliwiło Wienerowi zdefiniowanie spektrum widmowego zbioru
częstotliwości.
Pionierem
współczesnej doświadczalnej analizy spektralnej jest John Tukey. W 1949
r. stworzył on podwaliny obliczeń spektralnych, wykorzystując obliczenia korelacji
skończonych sekwencji czasowych. Zawdzięczamy jemu wiele pojęć współczesnych obliczeń
spektralnych (takich jak aliasing, okienkowanie, wybielanie, wygładzanie, gładzenie i
konwersja dziesiętna). W 1965 r., we współpracy z Jimem Cooleyem opisał on efektywny
algorytm obliczeniowy transformacji Fouriera. Jak to przedstawiłem w następnych
rozdziałach, ta szybka transformacja Fouriera (FFT) na nieszczęście nie jest dogodna do
analizy danych rynkowych.
Praca Johna Burga dała pierwszy impuls w obliczeniach spektralnych o dużej
rozdzielczości dla skończonych okresów czasowych. W swojej pracy doktorskiej z 1975 r.
opisał on swoje obliczenia spektralne o wysokiej rozdzielczości i nazwał je formalnie jako
maksymalna entropia. Podejście Burga zostało zastosowane w eksploracji złóż ropy naftowej
i gazu poprzez analizę fal sejsmicznych. Ten sposób podejścia został także zastosowany w
analizie technicznej rynków, ponieważ przeprowadzanie obliczeń spektralnych o wysokiej
rozdzielczości wymaga minimalnej ilości danych liczbowych. Jest to bardzo ważne, ponieważ
krótkoterminowe cykle rynkowe są zazwyczaj zmienne. Inną korzyścią z takiego podejścia
jest to, że metoda ta jest maksymalnie czuła na zakres zaznaczonych danych i nie jest
narażona na zniekształcenie z powodu efektów końcowych ostatnich danych liczbowych.
Wskaźnik MESA jest akronimem słów maximum entropy spectral analysis.
Co to jest cykl?
Definicja słownikowa cyklu jest następująca: „przedział przestrzeni lub czasu, w
którym całkowicie zachodzi jedna runda zjawiska, które powtarza się regularnie w tej samej
sekwencji”. Na rynku, bierzemy pod uwagę klasyczny cykl, istniejący gdy ceny poruszają się
od minimum, wzrastają stopniowo do maksimum w określonej długości czasu i następnie
stopniowo opadają z powrotem do poziomu minimum, w tym samym okresie czasu. Czas
wymagany do wypełnienia cyklu nazywany jest okresem cyklu lub długością cyklu.
Cykle z pewnością występują na rynku. Często mają one uzasadnienie fundamentalne.
Najbardziej oczywiste są zmiany sezonowe cen płodów rolnych (niższe w czasie zbiorów) lub
też, spadek realnych cen w zimie. Analitycy telewizyjni często mówią o stopie inflacji
„regulowanej sezonowo” przez rząd. Ale sezonowość jest szczególnym przypadkiem cyklu,
zawsze wynoszącego 12 miesięcy. Inne fundamentalnie uzasadnione cykle, mogą wynosić na
przykład 18 miesięcy dla hodowli bydła lub miesiąc dla raportu składowanych w chłodni tusz
wieprzowych.
Cykle gospodarcze nie są tak oczywiste, jednak one istnieją. Cykle gospodarcze
zmieniają się wraz ze stopą procentową. Rząd wyznacza cele wzrostu ekonomicznego na
podstawie swoich zdolności do utrzymania inflacji na rozsądnym poziomie. Z powodu zmian
podstawowych stóp procentowych ustalanych przez bank centralny, co powoduje napływ lub
odpływ pieniędzy z gospodarki, wzrost gospodarczy zwiększa się lub zmniejsza.
Zmniejszenie stóp procentowych dodaje odwagi gospodarce, zwiększanie ich powstrzymuje
ją. Nieuchronność kolejności tych procesów powoduje, że widzimy je jako cykle
gospodarcze. Chociaż w praktyce taki cykl może powtórzyć się za taką samą ilość lat,
dokładne powtórzenie okresu nie jest konieczne. Cykl gospodarczy jest ograniczany od góry
przez rząd (zazwyczaj 3 procent), co oznacza wzrost i od dołu (około –1 procent), który
wskazuje na recesję. Rozpiętość cyklu od +3 do –1 procent nazywana jest jego amplitudą.

Dlaczego na rynku występują cykle
11
Składniki rynku
Statystycy i ekonomiści zidentyfikowali cztery ważne cechy charakterystyczne ruchu
ceny. Wszystkie prognozy ceny i analizy zawierają każdy z poniższych elementów:
1. Trend lub tendencja kierunku ruchu w określonym okresie czasu.
2. Współczynnik sezonowości, wzorowany na kalendarzu.
3. Cykl (inny niż sezonowy), istniejący dzięki działaniom rządu, który przycinając przyszły
budżet opóźnia wzrost na początku, powodując spadek gospodarki.
4. Inne dziwne ruchy ceny, często zwane szumem.
Ponieważ obydwa punkty 2 i 3 są cyklami jest jasne, że cykle są ważną i uznaną
częścią wszystkich ruchów cen.
Gdy dokonujesz transakcji na podstawie cykli, głównym problemem jest mierzenie
czasu transakcji. Można wziąć pod uwagę ekstremum 54-letniego cyklu ekonomicznego
Kondratiewa (ale nie bezkrytycznie). Farmerzy bydła mogą preferować 18-miesięczny cykl
hodowlany, podczas gdy farmerzy uprawiający zboże prawdopodobnie zachowają rezerwę,
bazując na rocznych zbiorach. Spekulanci często wykorzystują krótkie (czasem bardzo
krótkie) ruchy cenowe.
Cykliczne zachowania cen są najbardziej popularne w teorii fal Elliota i ostatnich
opracowaniach Ganna. Jednakże, metody te posiadają duży element subiektywności w ich
interpretacji.
Krótkoterminowe cykle mogą istnieć nawet w obrębie zdefiniowanych 4 punktów
„szumu”. Pobieżne spojrzenie na prawie każdy wykres słupkowy pokazuje, w ujęciu
historycznym, że cykle krótkoterminowe przychodzą i odchodzą. Zdolność do wydzielenia i
wykorzystania takich zjawisk rynkowych jak cykle, wiąże się ze świadomością ich istnienia
oraz z dostępem do odpowiednich narzędzi. Metody, które potrafiły to ustalić, nie były
praktycznie stosowane aż do momentu, w którym zaczęto stosować komputery. Teraz te nowe
metody może stosować praktycznie każdy. Założenia tych krótkoterminowych cykli zostały
wyprowadzone z teorii błądzenia losowego i jej rozwinięcia, tak więc zajmując się cyklami w
obrębie 4 punktów, będziesz się czuć bardziej komfortowo.
Błądzenie losowe
Błądzenie rynku jest rezultatem działań dużej ilości graczy, kierujących się odmienną
motywacją zysku, straty, chciwości, strachu i zabawy; jest to skomplikowane w różnych
przedziałach czasowych. Dlatego też, ruch rynku może być analizowany w kategoriach
przypadkowych wartości zmiennych. Jedną z takich analiz jest błądzenie losowe. Wyobraź
sobie atom tlenu w plastikowym pudełku, zawierającym tylko powietrze. Do opisu drogi
atomu wykorzystywana jest teoria ruchów Browna. Zbiór tych ruchów można opisać jako
trójwymiarowe błądzenie losowe. Ponieważ następują po sobie kolejne ruchy przypadkowe,
to należy spodziewać się, że każda pozycja atomu w pudełku jest tak samo prawdopodobna
jak każda inna.
Do opisu ruchu rynku stosowana jest inna forma błądzenia losowego. Forma ta jest
dwuwymiarowym błądzeniem losowym, zwanym „Spacerem Pijanego”. Dwuwymiarowa
struktura jest stosowniejsza do rynku, ponieważ ceny mogą wzrastać lub spadać tylko w
jednym wymiarze. Inny wymiar, czas, może poruszać się tylko do przodu. Jest to podobne do
drogi opisanej za pomocą spaceru pijanego.

Dlaczego na rynku występują cykle
12
Równanie dyfuzji
Spacer Pijanego sformułowano przez uwzględnienie przypadkowego kroku albo w
prawo albo w lewo, na każdy krok do przodu. By zapewnić przypadkowość, decyzja o ruchu
w prawo lub w lewo, podejmowana jest na podstawie uczciwego rzutu monetą. Jeśli
wypadnie orzeł, to wykonywany jest ruch w prawo. Jeśli wypadnie reszka, to wykonywany
jest ruch w lewo. Obrazem tego jest przypadkowa droga, pokazana poniżej. Rys. 1.1
przedstawia generowaną przez komputer drogę, powstałą przy wykorzystaniu reguł Spaceru
Pijanego.
Rysunek 1.1 Droga błądzenia losowego. Kierunek jest zmienną losową.
Dla tego zbioru można napisać równanie różniczkowe, ponieważ jest to rozpiętość
zmian czasu w stosunku do rozpiętości zmian pozycji w dwóch wymiarach.
Dzięki wariacjom, do opisu tych powiązań wykorzystywane są równania różniczkowe.
Na przykład, zmianę odległości w stosunku do czasu, można wyrazić w milach na godzinę.
Prędkość w postaci równania różniczkowego, można napisać jako
V=dx/dt
Równanie to pokazuje, że prędkość to zmiana odległości w stosunku do czasu. Myśl o
d w sensie różnicy. Podobnie, przyśpieszenie jest zmianą prędkości w stosunku do czasu.
Równanie na przyśpieszenie to
a=dV/dt
Dlaczego na rynku występują cykle
13
Ponieważ prędkość jest zmianą odległości w stosunku do czasu, to możemy myśleć o
przyśpieszeniu jak o potędze kwadratowej zmian odległości w stosunku do czasu. Teraz
równanie przyśpieszenia można napisać jako
a=dV/dt=d²x/dt²
Matematycy
używają tych formatów, kiedy piszą równania różniczkowe. Rozwiązując
problem Spaceru Pijaka, równanie różniczkowe brzmi
dP/dt=D*d²P/dx²
gdzie P=pozycja w czasie i przestrzeni
D=stała dyfuzji
To
słynne równanie różniczkowe (przynajmniej wśród matematyków) znane jest jako
równanie dyfuzji. Inaczej mówiąc, to równanie stwierdza, że zmiana położenia w stosunku do
czasu jest proporcjonalna do drugiej potęgi rozpiętości zmian pozycji w stosunku do miejsca
zajmowanego w przestrzeni. Opisuje ono wiele naturalnych zjawisk (np. drogę srebrnej
łyżeczki gdy jest umieszczana w filiżance gorącej kawy). Lepszą analogią do drogi
pokonywanej przez rynek jest smuga dymu ulatniającego się z komina, opisana przez
równanie różniczkowe. Rys. 1.2 pokazuje zbiór 100 kroków generowanych komputerowo,
obrazujących Spacer Pijanego przy pomocy równania dyfuzji. Używając wyobraźni, możesz
postrzegać Rys. 1.2 jako smugę dymu.
Rysunek 1.2 Drogi 100 błądzeń losowych nałożone na siebie. Kierunek jest zmienną losową.
Obraz ten przypomina smugę dymu na łagodnym wietrze. Smuga jest w przybliżeniu
stożkowata, rozszerzająca się w większej odległości od komina. Równanie dyfuzji opisuje
położenie pojedynczej cząstki dymu, a na Rys. 1.2 możesz zobaczyć położenie wszystkich
takich cząstek. Dzięki losowej naturze błądzenia, możesz ustalić najlepszą uśrednioną pozycję

Dlaczego na rynku występują cykle
14
dowolnej cząstki smugi. Oczywiście nie ma tam powikłanych cykli. Wiążąc smugę dymu z
rynkiem, ogólny kierunek może być określony za pomocą uśredniania losowego ceny. Jest to
oczywiście średnia ruchoma. Rozpoznaje ona trend z taką pewnością, jak rozpoznajesz strugę
smugi dymu na wietrze. Gauss, kilka wieków temu udowodnił, że taka średnia jest
najlepszym przybliżeniem oddającym rozkład losowy. Pamiętaj, że dokładność tego
przybliżenia zmniejsza się wraz z odległością smugi dymu od komina. Dlatego też, zdolność
średnich ruchomych do określenia trendu rynku w przyszłości, gwałtownie maleje.
Równanie telegrafisty
Przyjrzyjmy
się ponownie wzorowi matematycznemu problemu Spaceru Pijanego.
Tym razem, rezultat rzutu monetą będzie określał czy następny krok pijanego nastąpi w tym
samym kierunku co poprzedni krok, czy też zmieni kierunek na przeciwny do poprzedniego
kroku. Tworzy to rozkład losowy jego impetu, a nie kierunku. Rys. 1.3 pokazuje generowaną
komputerowo drogę Spaceru Pijanego powstałą przy wykorzystaniu rozkładu losowego
impetu. Matematycy nazywają to Ciągłością Czasową Rozkładu Losowego (Continuous-Time
Random Walk), lub w skrócie CTRW. W tym przypadku, rozkład losowy jest impetem, a nie
jego kierunkiem.
Rysunek 1.3 Droga rozkładu losowego. Zmienna losowa jest impetem.
Przedstawiliśmy funkcję zmian pozycji w czasie. Gdy teraz wyrazimy tę pozycję w
postaci równania różniczkowego, otrzymamy
d²P/dt²+(1/T)*dP/dt=C*d²P/dx²
gdzie T i C są stałymi.
Jest to także znane równanie. Zwane jest ono Równaniem Telegrafisty ponieważ,
oprócz innych rzeczy, opisuje drogę fali elektrycznej w kablu telegraficznym. Pamiętaj, że

Dlaczego na rynku występują cykle
15
struktura Równania Telegrafisty jest identyczna do struktury równania dyfuzji za wyjątkiem
tego, że zawiera dodatkowy człon dla drugiej potęgi zmian pozycji w stosunku do czasu.
Równanie Telegrafisty opisuje także meandrowanie rzeki, zjawisko fizyczne, które możemy
porównać do rynku. Oglądając zdjęcia lotnicze możemy stwierdzić, że wszystkie rzeki na
świecie meandrują. To meandrowanie nie następuje z powodu niejednorodności gleby, ale z
powodu zasady zachowania energii. Można stwierdzić, że jednorodność gleby nie jest tym
czynnikiem, który powoduje meandrowanie rzeki, ponieważ inne cieki wodne, takie jak prądy
oceaniczne, także meandrują mimo, że przebywają w środowisku jednorodnym. Prądy
oceaniczne zachowują się niemal identycznie jak rzeki.
Każdy meander rzeki jest niezależny od innych meandrów, zachowując się losowo.
Jeśli przyjrzymy się meandrom wszystkich rzek, nakładając meandrujące rzeki na siebie, jak
w wielokrotnie naświetlonym zdjęciu, to przypadkowość meandrów staje się oczywista. Zbiór
z nałożonymi na siebie rzekami, będzie prawie taki sam jak przekrój smugi dymu. Rys. 1.4
przedstawia zbiór nałożonych na siebie, 100 kroków Spaceru Pijanego, gdzie zmienną losową
jest impet. Jeśli znajdujemy się w jakimś meandrze, to możemy mieć pewność, że znajdujemy
się w głównym nurcie rzeki. Jednakże, jest to krótkoterminowy związek logiczny i w
dłuższym okresie czasu jest on przypadkowy.
Rysunek 1.4 Drogi 100 błądzeń losowych nałożone na siebie. Zmienną losową jest impet.
Używając analogii można powiedzieć, że meandry rzeki są swoistego rodzaju
cyklami, które istnieją na rynku. Można mierzyć i wykorzystywać takie krótkoterminowe
cykle, jeśli będziemy świadomi tego, że przychodzą one i pozostają przez dłuższy czas.
Można poszerzyć tę analogię do zrozumienia, kiedy występują cykle
krótkoterminowe. Fizyczną przyczyną meandrowania rzeki jest to, że usiłuje ona przedrzeć
się do oceanu, stale rozlewając się. Stałe rozlewanie się wody wynika z zasady zachowania
energii. Jeśli prędkość wody rośnie, to szerokość rzeki zmniejsza się tak, aby przez
poprzeczny przekrój rzeki przepływała taka sama ilość wody w jednostce czasu, jak przy
rzece szerokiej. Szybszy przepływ wymaga większej energii kinetycznej i rzeka próbuje
zwolnić swój bieg, chcąc zmienić kierunek. Jednakże, nie można nagle zmienić kierunku

Dlaczego na rynku występują cykle
16
rzeki, z powodu impetu przepływu. Rezultatem jest meandrowanie. Tak więc, przyczyną
meandrowania jest opór, rozumiany jako energia. Powinniśmy myśleć o rynku w ten sam
sposób. Czas musi posuwać się naprzód, tak jak niewątpliwie rzeka musi wpadać do morza.
Stany wykupienia i wyprzedania wynikają z tego, że rynek próbuje zachować „energię”.
Energia ta pochodzi z emocji strachu i zachłanności wszystkich graczy.
Zasadę zachowania energii możesz przetestować na sobie. Wyobraź sobie pasek
papieru o długości 11 cali i szerokości 1 cala. Jeden koniec paska papieru uchwyć mocno
kciukiem i palcem wskazującym prawej dłoni. W ten sam sposób uchwyć drugi koniec paska
palcami lewej dłoni. Teraz porusz twoimi rękami razem. Taki ruch wkłada pewną energię do
paska papieru, a jego naturalna reakcja może przybrać kilka postaci. Postacie te są
determinowane warunkami granicznymi, które zostały przez ciebie wymuszone. Jeśli
obydwie ręce poruszają się do góry, odpowiedzią jest pojedynczy, skierowany ramionami ku
górze łuk, w przybliżeniu będący falą sinusoidalną. Jeśli obydwie ręce poruszają się do dołu,
odpowiedzią jest łuk skierowany ramionami ku dołowi. Jeśli jedna ręka porusza się do dołu, a
druga ręka porusza się do góry, to odpowiedzią paska papieru na włożoną energię jest w
przybliżeniu pełna fala sinusoidalna. Te cztery stany są naturalną odpowiedzią, wynikającą z
zasady zachowania energii. Możesz wypróbować inne paski papieru, ale efekt będzie zawsze
taki sam i zależny od narzuconych przez ciebie warunków granicznych.
Łącząc te teorie razem możemy stwierdzić, że rynek będzie przypadkowy, gdy
większość graczy będzie zastanawiać się „Czy rynek pójdzie do góry czy do dołu?”. W tym
przypadku, kierunek jest zmienną losową. Jeśli większość graczy będzie się zastanawiać „Czy
trend będzie kontynuowany?”, zmienna losowa jest impetem rynku i będzie występować cykl
krótkoterminowy. Trend zawsze tworzy cykle, ponieważ trend trwa, a gracze nadal będą się
zastanawiać czy trend będzie kontynuowany. Kierowanie się cyklami jest wiarygodną miarą
psychologii rzeszy graczy. Dlatego też, powinniśmy być zadowoleni ze zidentyfikowania
krótkoterminowych cykli, gdy tylko się pojawią.
Wnioski
Argumenty,
że na rynku istnieją cykle, pochodzą nie tylko z rozważań teoretycznych
lub z pomiaru kierunku, ale również mają swoje uzasadnienie w samej naturze zjawisk
fizycznych. Naturalną reakcją na każde zakłócenie fizyczne jest ruch korygujący. Jeśli
szarpniesz strunę gitary, to struna zacznie wibrować cyklicznie, wydając dźwięk.
Analogicznie, mamy wszelkie prawo spodziewać się, że rynek również zareaguje ruchem
cyklicznym na zakłócenia. To przewidywanie wzmocnione jest teorią błądzenia losowego,
która sugeruje, że czasami ceny rynkowe mogą być opisane za pomocą równania dyfuzji, a
czasem za pomocą Równania Telegrafisty.
Wyzwaniem dla graczy technicznych jest rozpoznanie, kiedy występują cykle
krótkoterminowe oraz ich logiczne i konsekwentne wykorzystanie, w celu osiągnięcia zysku.
W
następnych rozdziałach zdefiniuję podstawowe pojęcia dotyczące cykli oraz jak
manipulować nimi, aby nastroić funkcję impetu i funkcję średniej ruchomej, które to funkcje
są składnikami każdego rynkowego wskaźnika technicznego. Cykle podstawowe będą
odpowiadać tradycyjnym formacjom wykresu. Formacje te nabiorą dla ciebie nowego
znaczenia. Być może, ważniejszym będzie omówienie, kiedy wykorzystywać w transakcjach
cykle, a kiedy tego unikać.

Podstawowe pojęcia dotyczące cykli
17
Rozdział 2
Podstawowe pojęcia dotyczące cykli
Jedną z rzeczy, co do której zgadzają się technicy rynkowi jest to, że rynek jest
zmienny. Precyzyjne określenie tych zmian jest tematem nieustannych dyskusji. Każda
technika rynkowa, począwszy od klasycznych formacji wykresu, a skończywszy na falach
Elliotta, konstruuje uproszczony model rynku, opisując go przy pomocy parametrów modelu.
Parametry te są następnie dostosowywane do opisania aktualnego stanu rynku. Na tej
podstawie dokonuje się ekstrapolacji i wysnuwa wnioski o przyszłej aktywności rynku.
Analiza cykli jest jedną z takich technik.
Cykle
są uproszczonym, technicznym modelem rynku. Model ten jest co najmniej tak
złożony jak większość innych modeli, ponieważ kilka cykli może istnieć jednocześnie. Cykle
są często pomieszane z szumem, a wszystkie cykle przypływają i z czasem odpływają.
Podstawowym składnikiem cykli złożonych jest sinusoida. Sinusoida jest naturalnym cyklem
podstawowym, z kilku powodów:
1. Sinusoida jest matematycznie gładzonym kształtem fali, opisującej cykl i harmonię ruchu.
2. Bardziej skomplikowane kształty fal powstają w wyniku sumowania prostych fal
sinusoidalnych.
3. Fale sin i cos są niezależnym parametrem, ustalanym w zaawansowanych analizach,
takich jak transformacja Fouriera.
Tak jak w każdym innym modelu, musimy zdefiniować parametry składników,
stosowanych we wzorze logicznym tego modelu. Parametrami cyklu są częstotliwość, faza i
amplituda.
Częstotliwość
Cykl jest takim procesem, w którym obserwowany punkt powraca do swojego
pierwotnego położenia. Przykładem cyklu jest wahadło zegarowe. Wahadło buja się z taką
regularnością, że było przez wieki wykorzystywane jako wzorzec czasu w zegarach. Tak
więc, pierwszą cechą charakterystyczną cyklu jest częstotliwość. Ruch obrotowy silnika
samochodowego jest cykliczny. Jego częstotliwość jest liczbą obrotów na minutę
wykonywanych przez wał korbowy. Określenie 2000 RPM powinno być zrozumiałe dla
większości kierowców. RPM jest akronimem słów revolutions per minute (obroty na minutę).
Okres takiego cyklu, jak w przykładzie powyżej, wynosi 1/2000 minuty. Tak więc, okres
cyklu jest odwrotnością częstotliwości. Przy omawianiu zagadnień rynkowych, zwykle
będziemy posługiwać się ilością cykli przypadającą na jednostkę czasu, aniżeli terminem
częstotliwość. Na przykład, częstotliwość 10-dniowego cyklu wynosi 0.1 cyklu na dzień.
Pomyśl o korbowodzie silnika samochodowego. Możemy wyobrazić sobie cykl, jako
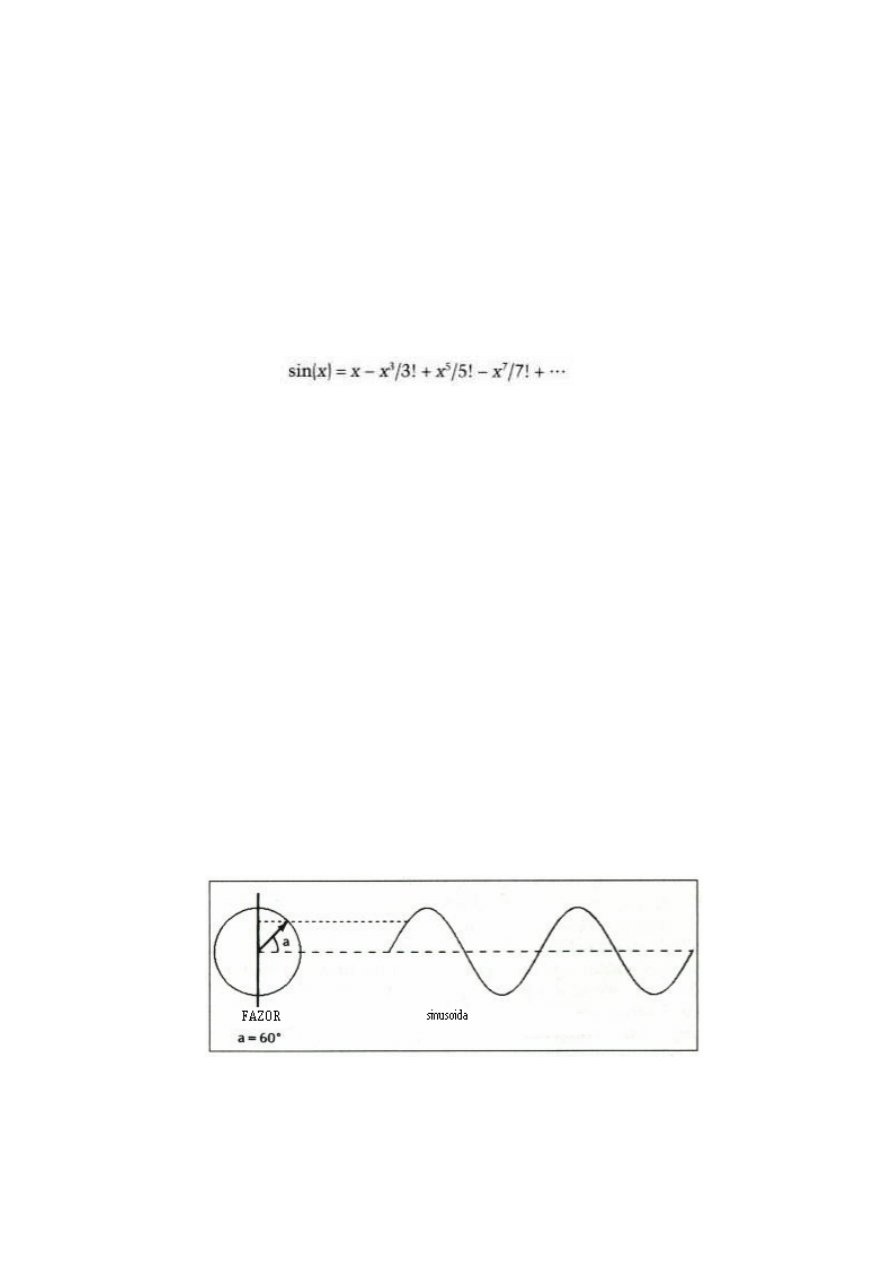
obraz wytwarzany przez obracającą się strzałkę lub wektor, przymocowany do korbowodu.
Taka strzałka nazywana jest fazorem. Cykl wypełni się, gdy koniec fazora wykona całkowity
obrót, powracając do punktu wyjścia. Na podstawie naszej obracającej się strzałki, możemy
utworzyć cykl podstawowy. Wyobraź sobie koniec strzałki rzucającej cień na oś pionową, tak
jak gdyby była ona oświetlona z jednej strony fleszami. Amplituda tego cienia rośnie i maleje
tak jak sinusoida.
Podstawowe pojęcia dotyczące cykli
18
Generatory
prądu zmiennego wytwarzające elektryczność, działają bardzo podobnie
jak nasz fazor. Miedziane kable w wirującym tworniku najpierw poruszają się równolegle do
linii sił pola magnetycznego, a następnie przecinają je wraz z obrotem twornika. Miedziane
kable przecinając pole magnetyczne wytwarzają przepływ prądu elektrycznego. W rezultacie
powstają fale napięcia i prądu mające kształt sinusoid. W Stanach Zjednoczonych
częstotliwość prądu zmiennego jest ujednolicona i wynosi 60 cykli na sekundę.
Częstotliwość jest wyjątkowo regularnym, mierzalnym parametrem cyklu. Prosta
sinusoida może mieć tylko jedną częstotliwość. Sinusoida jest funkcją podstawową, ponieważ
możemy utworzyć złożony kształt fali, dodając sinusoidy o różnych częstotliwościach, fazach
i amplitudach. Sinusoidę można opisać matematycznie za pomocą nieskończonego szeregu
potęgowego jako
gdzie ! oznacza silnię. To jest, 5!=1*2*3*4*5.
Uproszczony opis sinusoidy odpowiadający rozwinięciu szeregu potęgowego jest inną
postacią funkcji podstawowej.
Faza
Dla zrozumienia funkcji średniej ruchomej i funkcji impetu, ważnym jest poznanie
wzajemnych relacji pomiędzy nimi, a fazą cyklu podstawowego. Średnie ruchome powodują
opóźnienie fazowe, a impet powoduje wyprzedzenie fazowe. Pokażemy później jak te
wzajemne relacje zostały połączone w formę użytecznych wskaźników.
Wzajemna relacja pomiędzy fazorem a sinusoidą, pokazana jest na Rys. 2.1. W czasie
zero fazor znajduje się na prawo i amplituda sinusoidy wynosi zero. Fazor obraca się
odwrotnie do wskazówki zegara, więc z upływem czasu sinusoida szybko rośnie, osiągając
dodatnie maksimum. Maksimum zostaje osiągnięte, gdy fazor obróci się o 90 stopni w
stosunku do swojego pierwotnego położenia (tj. pionowo do góry). Po osiągnięciu
maksimum, fazor obraca się dalej do 180 stopni, w stosunku do pierwotnego położenia. Pełny
cykl zostanie wykreślony, gdy fazor powróci do swojego pierwotnego położenia. Dalszy
obrót fazora przeciwnie do ruchu wskazówki zegara, powoduje kreślenie następnych cykli.
Linia przerywana pokazuje wzajemną relację fazora i sinusoidy, gdy kąt fazowy zbliżony jest
do 60 stopni.
Rysunek 2.1 Związek fazora z sinusoidą
Podstawowe pojęcia dotyczące cykli
19
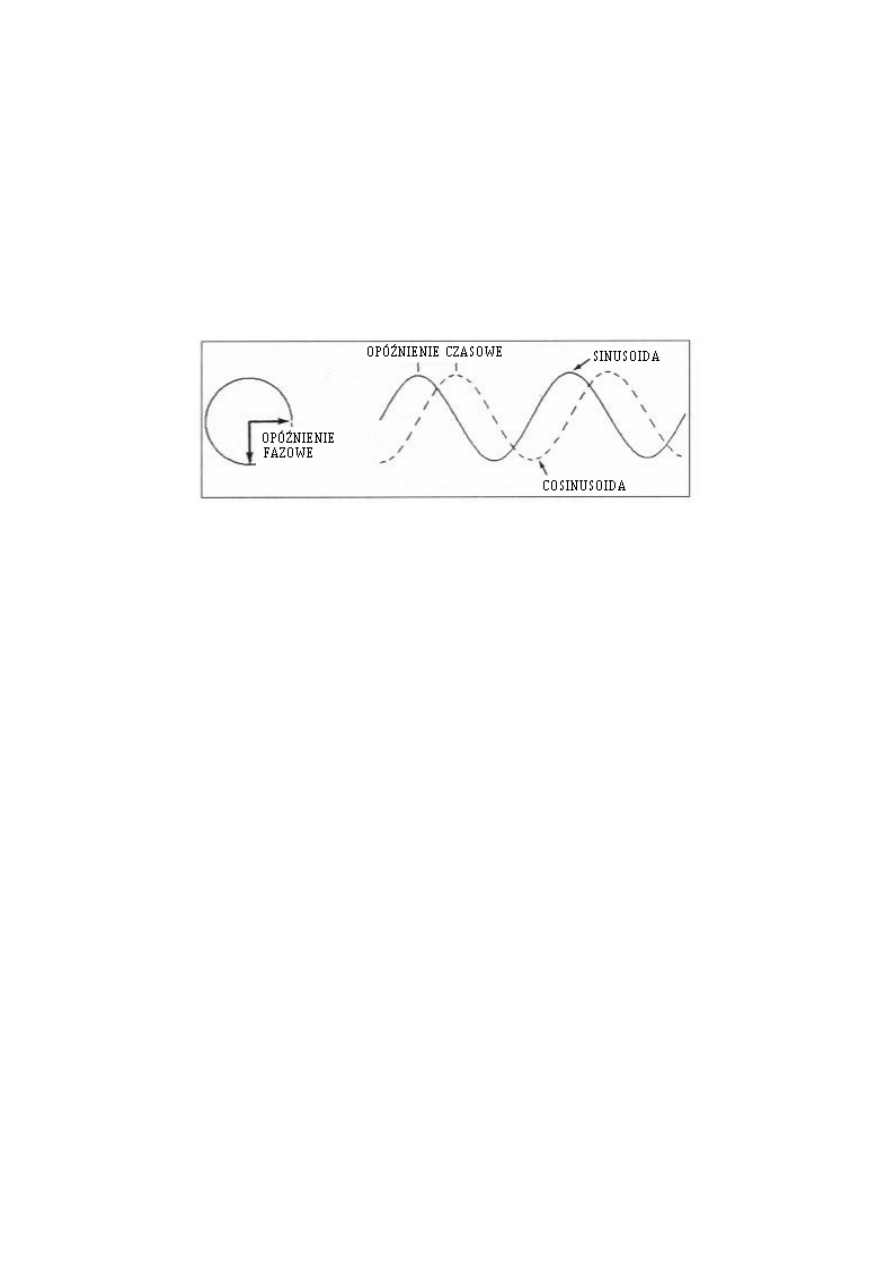
Innym przypadkiem funkcji podstawowej jest cosinusoida. Cosinusoida jest opóźnioną
w fazie o 90 stopni sinusoidą, tak jak to pokazano na Rys. 2.2. Tę cosinusoidę można
utworzyć przez opóźnienie fazora o 90 stopni w stosunku do pierwotnego fazora. Pamiętaj, że
gdy cosinusoida osiąga maksimum, sinusoida ma wartość zero, co odpowiada rozpętości
zmian w tym punkcie. Gdy wartość cosinusoidy zmienia się z ujemnej na dodatnią, to została
osiągnięta maksymalna rozpiętość zmian, która odpowiada maksymalnej amplitudzie
sinusoidy. Sinusoida ma swoją maksymalną ujemną wartość dokładnie wtedy, gdy
cosinusoida przecina zero z dodatniej do ujemnej wartości i jej ujemna rozpiętość zmian jest
maksymalna. Tak więc, Rys. 2.2 pokazuje jakościowo, że rozpiętość zmian ujemnej
cosinusoidy jest taka jak sinusoidy i rozpiętość zmian sinusoidy jest taka jak cosinusoidy.
Rysunek 2.2 Związek fazy z sinusoidą i cosinusoidą
Amplituda
Amplituda jest natężeniem, lub mocą, cyklu. Moc jest niezależna od częstotliwości i
fazy. Moc żarówki w twoim domu wynosi prawdopodobnie 60 watów. Liczba ta pokazuje
moc potrzebną do wytworzenia światła. Moc nie posiada kąta fazowego i jest niezależna od
60-cyklowego napięcia w przewodzie elektrycznym. W rzeczywistości, moc jest
proporcjonalna do kwadratu napięcia, zgodnie z prawem fizycznym zwanym prawem Ohma.
Fazor kwadratu napięcia oznacza, że napięcie jest mnożone przez siebie w tym samym
kierunku, bez względu na kąt fazowy. Tak więc, kąt fazowy nie ma znaczenia dla definicji
mocy.
Warto
odnotować, że moc jest proporcjonalna do kwadratu amplitudy jej fali. Jeśli
jedna fala jest 1.414 (pierwiastek kwadratowy z 2) razy większa od innej fali, to moc tej fali
jest dwukrotnie wyższa.
Moc
może się zmieniać w szerokim zakresie, a często chcemy na wykresie umieścić
sygnały o niskiej amplitudzie wraz z sygnałami o wysokiej amplitudzie. Jednym ze sposobów
aby to uczynić, jest przedstawienie mocy sygnałów w skali logarytmicznej, przez co
otrzymuje się kompresję amplitudy. Załóżmy, że podwójna moc w skali logarytmicznej
wynosi 0.3. Oznacza to, że sygnał o cztery razy większej mocy będzie wynosić w tej skali 0.6,
to jest dwa razy więcej od poprzedniej wartości (0.3). Gdy sygnał mocy jest 10 razy większy,
to w skali logarytmicznej będzie wynosić 1.0.
Moc
jest
często wyrażana w decybelach. Nazwa bel pochodzi od nazwiska Alexander
Graham Bell. Zajmował się on badaniem siły dźwięku, chcąc pomóc głuchym. Bel jest
logarytmem siły dźwięku. Przedrostek decy oznacza jedną dziesięciokrotność. Dlatego,
decybel jest jedną dziesiątą logarytmu siły dźwięku. Siła dźwięku może być większa lub
mniejsza od tej jednostki. Jeśli siła dźwięku jest mniejsza od jedności, znak logarytmu jest
ujemny. Na przykład, siła dźwięku wynosząca 0.5 jest równoważna –3dB, a siła dźwięku
wynosząca 0.01 jest równoważna –20dB. Pierwiastek kwadratowy amplitudy fali jest

Podstawowe pojęcia dotyczące cykli
20
proporcjonalny do mocy, tak więc możemy obliczyć, że –6dB oznacza amplitudę fali, która
wynosi połową amplitudy omawianej fali.
Dobrą praktyką w analizie spektralnej jest porównywanie amplitud wszystkich cyklów
z amplitudą najsilniejszego sygnału. Dlatego, najsilniejszy sygnał ma moc równą zero dB,
ponieważ jest on porównywany ze sobą (logarytm z 1 wynosi 0). Wszystkie inne sygnały
mają moc wyrażoną w decybelach o wartości ujemnej.
Zapamiętaj
• Sinusoida jest gładzoną postacią fali, opisującej cykl i harmonię ruchu.
• Częstotliwość jest pierwszym z parametrów cyklu. Częstotliwość jest odwrotnością
okresu. Okres cyklu mierzony jest od jednego punktu cyklu (na przykład doliny) do tego
samego punktu w następnym, kolejnym cyklu.
• Faza jest drugim parametrem cyklu. W obrębie jednego okresu cyklu faza wynosi 360
stopni. Kąt fazowy odpowiada pozycji w obrębie cyklu.
• Amplituda jest trzecim parametrem cyklu. Po prostu, amplituda jest wielkością fali cyklu.
Amplituda jest często mierzona w decybelach, w skali logarytmicznej.
Zasady rządzące cyklami
21
Rozdział 3
Zasady rządzące cyklami
Tradycyjna ocena wykresów jest techniką analityczną, która jest trudna do
opanowania, z powodu dużej ilości reguł związanych z formacjami wykresu. Wykresy są
trudne do opracowania i często wyglądają jak dzieło artystyczne. Piękno analizy cykli wynika
z tego, że uwzględniając wszystkie te reguły, opisuje ona ruch rynku w sposób jasny i
przejrzysty. Wystarczy zrozumieć, że cykliczność rynku jest rezultatem różnych kombinacji
cykli podstawowych i wszystko staje się jasne.
Wszystkie formacje wykresu rynkowego mogą być opisane przy wykorzystaniu tylko
trzech zasad rządzących cyklami:
1. Zasada proporcjonalności.
2. Zasada superpozycji.
3. Zasada rezonansu.
Zasada proporcjonalności
Zasada proporcjonalności stanowi po prostu, że amplitudy cyklu są proporcjonalne do
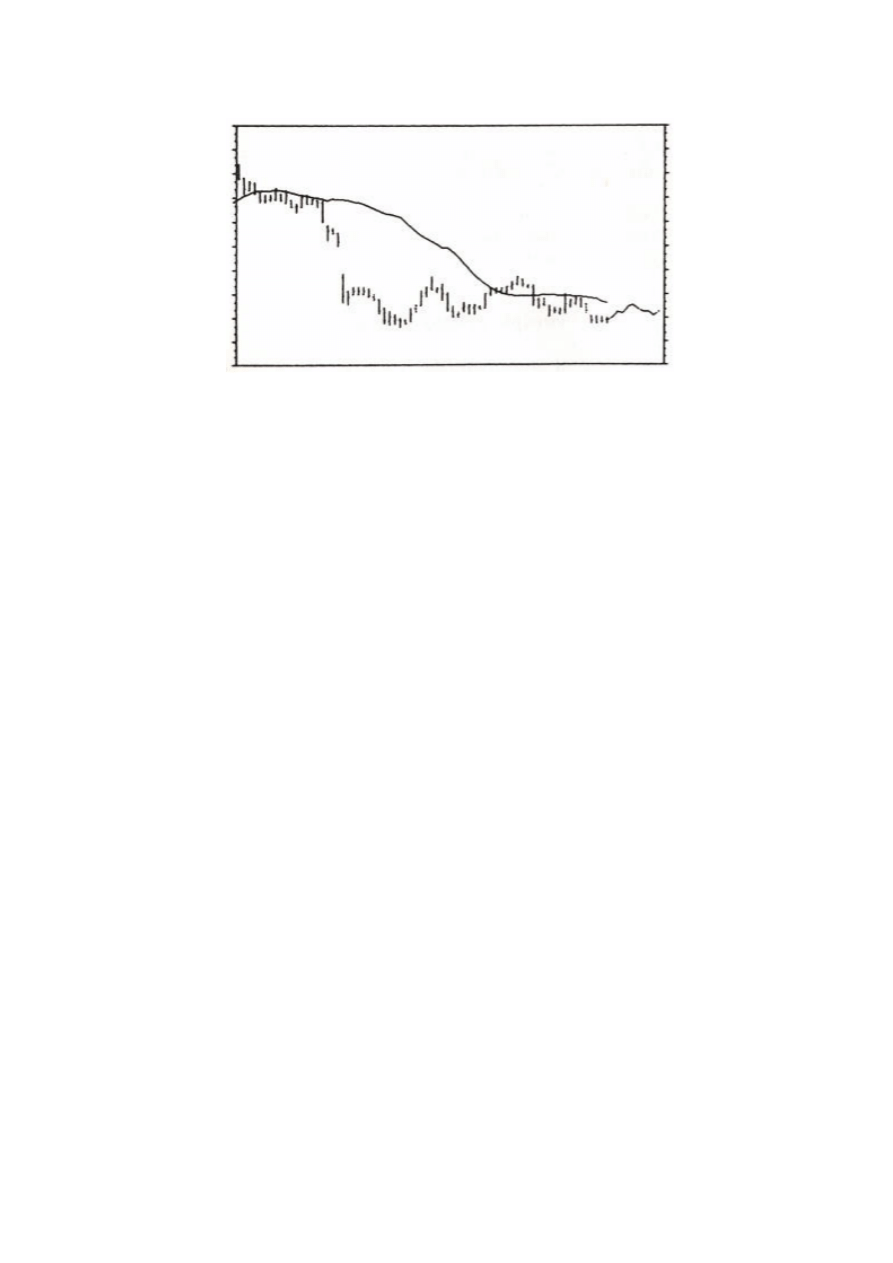
wybranej skali czasu. Rys. 3.1 i Rys. 3.2 przedstawiają wykresy słupkowe tego samego
papieru wartościowego z usuniętą skalą czasu i ceny. Który z nich jest wykresem
tygodniowym, a który wykresem dziennym?
Rysunek 3.1 Wykres tygodniowy czy dzienny?
Z powodu zasady proporcjonalności, nie można na to łatwo odpowiedzieć, posługując
się tylko wizualnym oglądem. Ta zasada ma także zastosowanie jako ważna stała we
współczesnej matematyce fraktalnej.
Zasady rządzące cyklami
22
Rysunek 3.2 Wykres tygodniowy czy dzienny?
Innym sposobem przekonania się o działaniu zasady proporcjonalności jest przyjęcie
założenia, że tak nie jest i następnie przetestowanie wyniku. Załóżmy, że mamy do czynienia
z gwałtownym, powtarzającym się co godzinę rozkołysaniem, które znacznie przekracza
codzienną zmienność. Jeśli prawdą jest, że nie działa zasada proporcjonalności, to wykresy
dzienne miałyby uśrednioną poziomą linię, a dzienne rozpiętości wypełniłyby wykres. Tak
oczywiście nie jest, a więc założenie jest błędne, co potwierdza zasadę proporcjonalności.
Zasada superpozycji
Zasada superpozycji twierdzi, że można zbudować złożony kształt korzystając z
elementów podstawowych. Jeśli kiedyś patrzyłeś na fale wodne, to mogłeś zauważyć, że na
ich kształt wpływają inne fale, pochodzące z różnych źródeł. Na przykład, fale wywoływane
przez płynącą łódź łączą się z falami wywoływanymi przez wiatr.
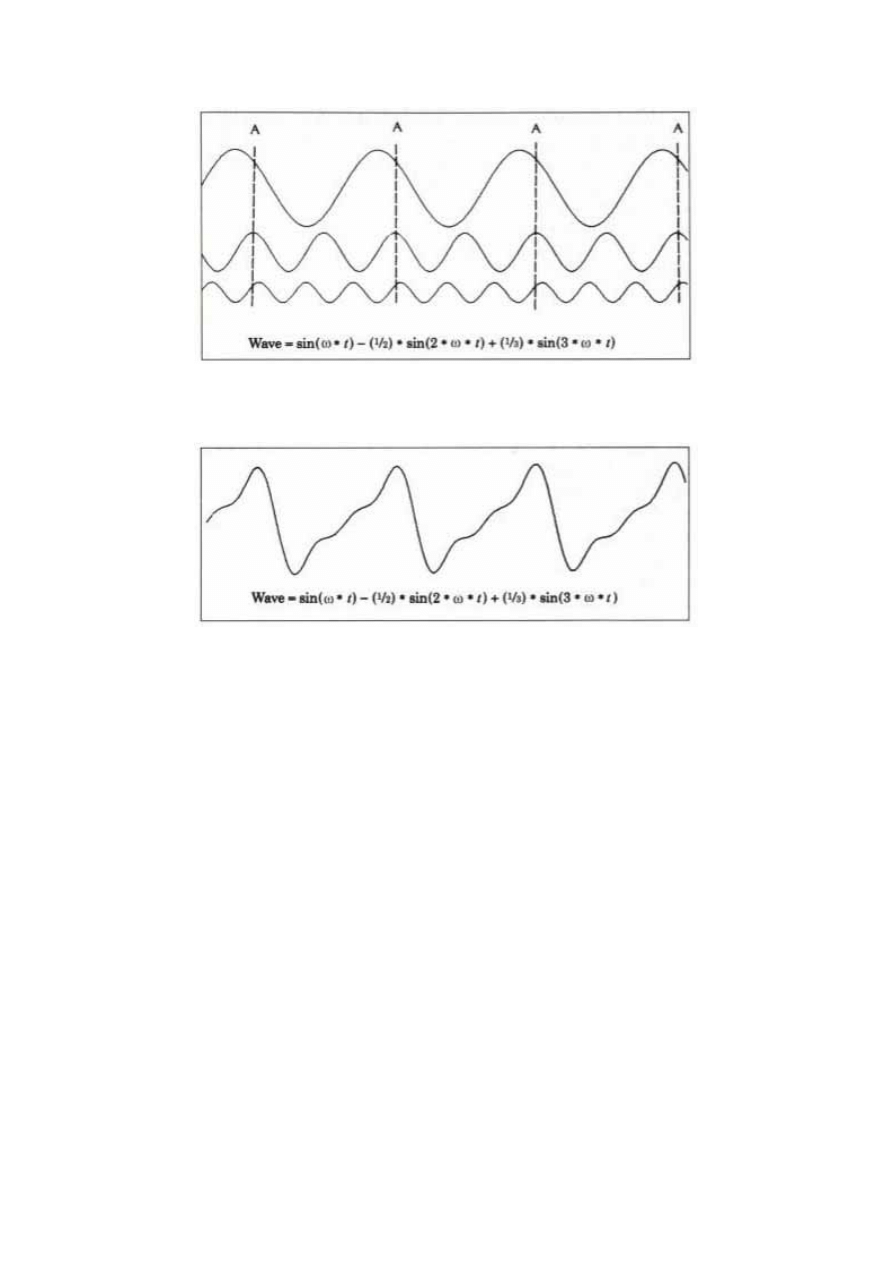
Do utworzenia bardziej złożonych fal możemy wykorzystać cykle podstawowe.
Załóżmy, że rozpoczynamy od sinusoidy, której częstotliwość kątowa wynosi omega i
odejmujemy od niej inną sinusoidę, o częstotliwości dwukrotnie wyższej, ale o amplitudzie o
połowę mniejszej. Następnie dodajemy inną sinusoidę, o częstotliwości trzykrotnie większej i
o amplitudzie trzykrotnie mniejszej, niż pierwsza sinusoida. Rys. 3.3 przedstawia trzy
podstawowe składniki, będące sinusoidami, natomiast Rys. 3.4 pokazuje rezultat końcowy,
będący falą złożoną. Podstawowe fale są prawie w takiej samej fazie w punkcie A, tworząc
maksimum fali złożonej. Fala złożona posiada taką samą częstotliwość jak pierwsza
sinusoida, ponieważ wszystkie składniki są harmonicznie związane ze sobą (ich
częstotliwości są wielokrotnością częstotliwości podstawowej). Złożona fala powtarza swój
cykl, wykonując następny.
Zasady rządzące cyklami
23
Rysunek 3.3 Pojedyncze składniki fali piłokształtnej
Rysunek 3.4 Piłokształtna fala powstała z trzech sinusoid podstawowych
Matematycznym wzorem opisującym złożoną falę, przedstawioną na Rys. 3.4 jest
Fala=sin(ω*t)-(½)*sin(2*ω*t)+(⅓)sin(3*ω*t)
gdzie ω = podstawowa częstotliwość kątowa
T = zmienna czasowa
Możemy kontynuować dodawanie cykli podstawowych, wykorzystując tę sekwencję,
tj. dodając lub odejmując następne składowe harmoniczne o amplitudzie, która jest
odwrotnością jej liczby harmonicznej. Jeśli będziemy powtarzać tę czynność nieskończenie
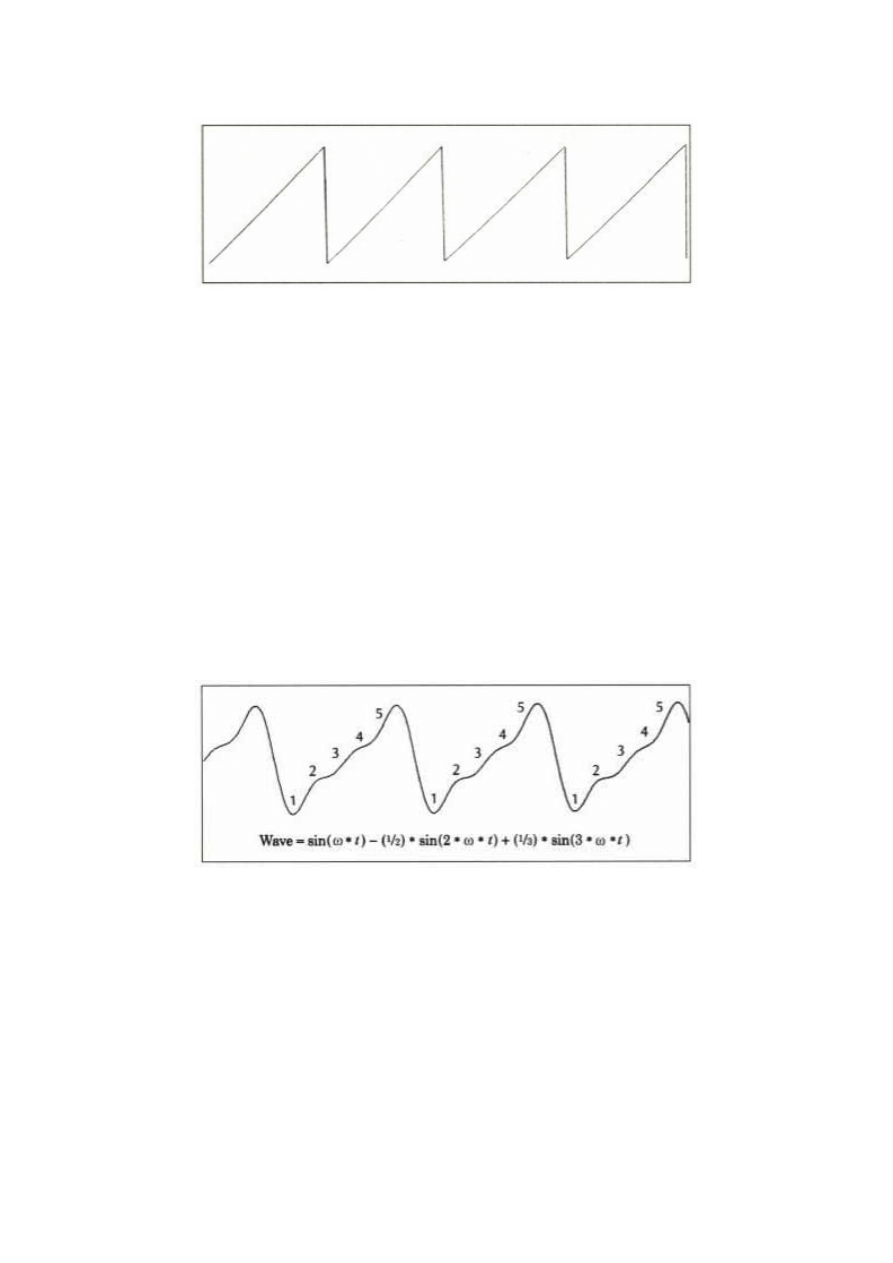
wiele razy, to otrzymamy falę piłokształtną, pokazaną na Rys. 3.5. Taki nieskończony szereg
harmonicznych sinusoid, opisujący złożony kształt fali, zwany jest szeregiem Fouriera. W
przypadku fali piłokształtnej, będzie się ona składać tylko z dwóch prostych linii w jednym
cyklu.
Zasady rządzące cyklami
24
Rysunek 3.5 Doskonała fala piłokształtna (nieskończony szereg Fouriera)
Jest to niezaprzeczalnie łatwa analiza. Równania linii prostych zębów piły są
nieskomplikowane. Do opisania zębów piły za pomocą cykli służy nieskończony szereg
Fouriera. Odwrotnie, każda sinusoida może być opisana jako nieskończony szereg potęgowy,
czyniąc analizę niemożliwą do wykonania. Sedno tkwi w tym, że do analizy musimy zawsze
używać dobrego narzędzia. Jeśli chcemy w przybliżeniu opisać kształt fali za pomocą jej
mierzalnych cykli podstawowych, to cykle są prawidłowym narzędziem do tego.
Cykle podstawowe nie muszą być powiązane harmonicznie. Na przykład, typowe
biorytmy składają się z nałożenia 28, 30 i 32-dniowych sinusoid. Mistycy często
przywiązywali dużą wagę do superpozycji tych trzech nieharmonicznych sinusoid. Ukazujące
się formacje są wyjątkowo rzadkie, ponieważ powtarzają się tylko co około 10 lat. Wynika to
z tego, że najmniejsza liczbą całkowita, przez którą dzielą się bez reszty częstotliwości tych
sinusoid, wynosi około 10 lat (dokładnie 3360 dni).
Odnosząc się do rynku, przykładem fal złożonych jest teoria fal Elliotta, opisująca
rynek za pomocą pięciu fal. Na Rys. 3.6, będącym powtórzeniem Rys. 3.4, oznaczono pięć fal
opisujących rynek, zgodnie z teorią fal Elliotta.
Rysunek 3.6 Fale Elliotta tworzące falę piłokształtną, która powstała w wyniku nałożenia na siebie
trzech pierwszych fal, tworzących szereg Fouriera.
Spoglądając na rynek z tej perspektywy, zwolennicy teorii fal Elliotta mimo wszystko
uwzględniają zasadę proporcjonalności w swoich bardziej złożonych analizach. Ja preferuję
myślenie o rynku tylko w kategoriach mierzalnych cykli podstawowych.
Zasada rezonansu
Czy
patrzyłeś kiedyś na oscylowanie naciągniętej taśmy gumowej po jej szarpnięciu?
Czy obserwowałeś kiedyś linijkę, wystającą jednym końcem poza skraj biurka, po
wprowadzeniu jej w drgania? Są to dwa przykłady rezonansu. Punkty oscylują z
Zasady rządzące cyklami
25
częstotliwością determinowaną przez przyłożoną siłę i warunki graniczne. Maksymalne
wychylenie oscylacji może być opisane jako fala stojąca.
Gdy wrzucisz kamyk do stawu ze spokojną wodą, to wywołasz fale, które będą
rozchodzić się koliście, aż natrafią na jakiś obiekt, np. ścianę, po czym się odbiją. Tak samo
dzieje się z rezonansem. Wyginając linijkę, wkładasz w nią energię. Gdy zwolnisz koniec
linijki, fala zacznie poruszać się wzdłuż linijki, osiągając krawędź biurka. Ponieważ energia
nie może się rozładować, fala odbija się, powracając do punktu wyjścia, co powoduje drgania
końca linijki. Gdy fala powróci do końca linijki, a energia nie ulegnie rozładowaniu,
ponownie następuje ruch powrotny fali w kierunku krawędzi biurka. Zjawisko to będzie
powtarzać się i fala będzie przemieszczać się wzdłuż linijki tam i z powrotem. Poruszające się
tam i z powrotem fale łączą się, tworząc postać fali stojącej, którą możesz zaobserwować jako
maksymalne wychylenie linijki. Z tym samym efektem mamy do czynienia w naprężonej
taśmie gumowej z wyjątkiem tego, że maksymalne wychylenie występuje pośrodku,
ponieważ końce taśmy są przytrzymywane.
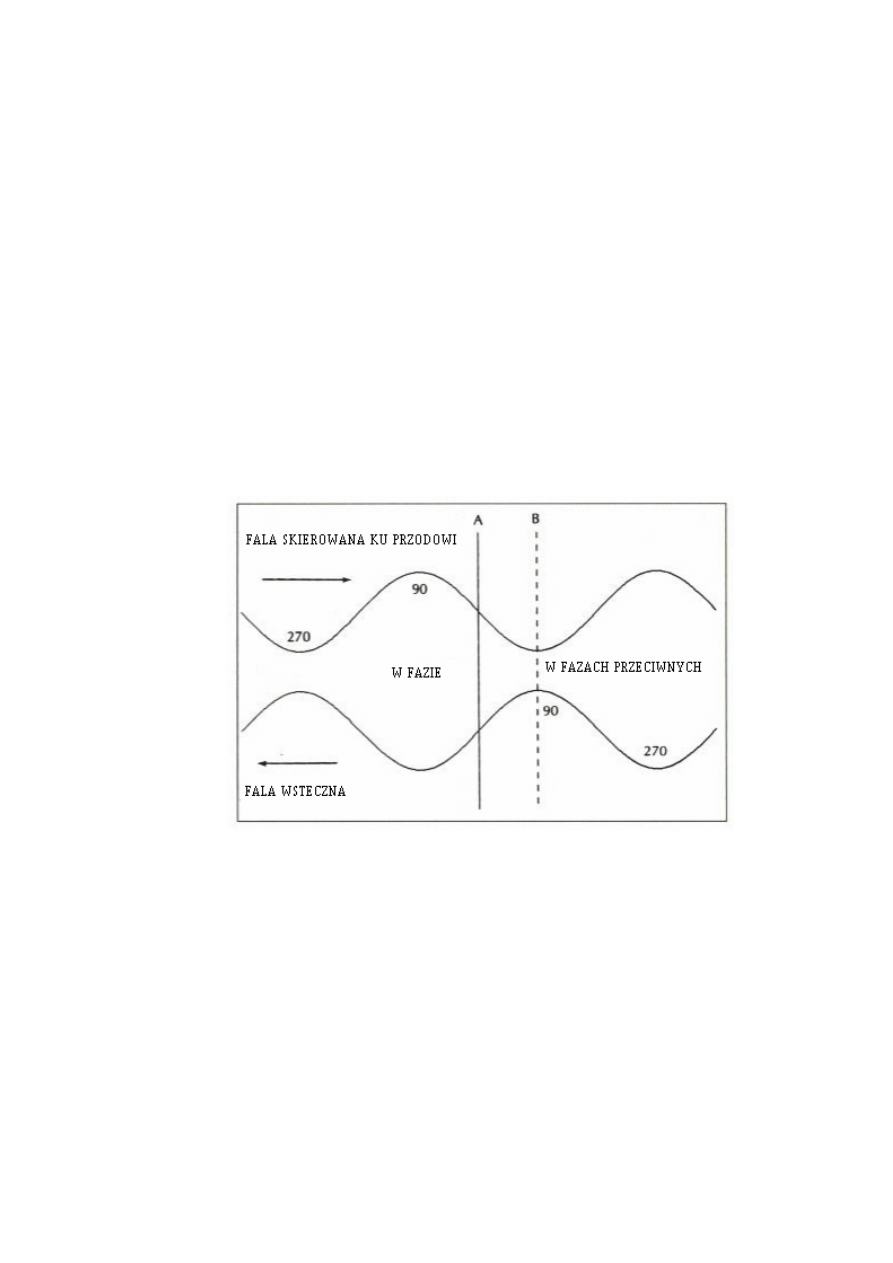
A teraz kilka słów o fali stojącej. Rys. 3.7 pokazuje falę poruszającą się do przodu
oraz falę powrotną. Oczywiście, fale te mają ten sam okres, ponieważ ich częstotliwości są
równe. Jak pokazano, dwie fale są w fazie w punkcie A oraz w fazach przeciwnych w punkcie
B.
Rysunek 3.7 Przemieszczanie się fal
Wyobraź sobie, że wraz upływem czasu, punkt położony na fali poruszającej się do
przodu, z położenia 90 stopni dochodzi do punktu A. Punkt położony przy 90 stopniach, na
fali powrotnej, dochodzi do zaznaczonego punktu A równocześnie z punktem położonym na
fali poruszającej się do przodu, co powoduje, że te dwie fale sumują się ze sobą w punkcie A.
Ponieważ obydwie fale dochodzące do punktu A są w tej samej fazie przez cały czas cyklu,
efekt dodawania jest niezależny od czasu. W dokładnie ten sam sposób fala poruszająca się do
przodu i fala powrotna zawsze są w przeciwnych fazach w punkcie B i te dwie fale znoszą się
wzajemnie niezależnie od czasu.
Tylko z jednego powodu fala stojąca z czasem wygasa. Wynika to z tego, że energia
włożona w linijkę lub w taśmę gumową zostaje stopniowo zamieniana na fale dźwiękowe
oraz jest rozpraszana na pokonywanie sił tarcia między cząsteczkami. Fale stojące
determinowane są przez przyłożoną siłę i narzucone warunki graniczne.
Zasady rządzące cyklami
26
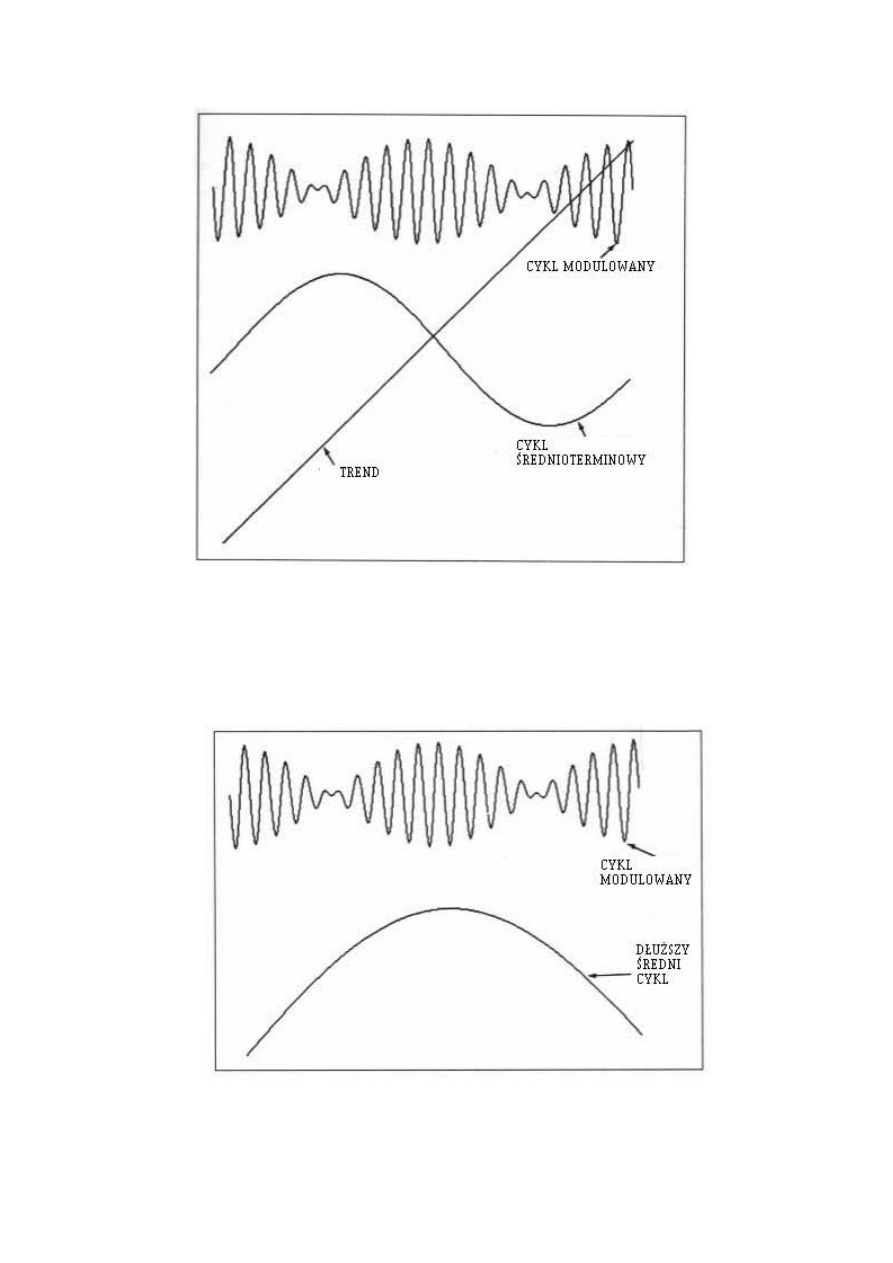
Rys. 3.8 przedstawia pewną falę stojącą, która jest rezultatem działania zasady
rezonansu. Obwiednia tej fali stojącej posiada niższą częstotliwość. Wyższa częstotliwość (w
tym przypadku) porusza się wewnątrz obwiedni tak jak fala, ponieważ nie podlega ona tym
samym warunkom granicznym jak częstotliwość fali stojącej. To jest, jej energia
przekazywana jest dalej lub absorbowana, a nie odbijana. W ten sposób, niższa częstotliwość
fali stojącej moduluje amplitudę wyższej częstotliwości.
Rysunek 3.8 Modulowanie za pomocą fali stojącej o niskiej częstotliwości.
Syntezowanie formacji wykresu
Używając tylko trzech zasad, tj. proporcjonalności, superpozycji i rezonansu, można
syntezować szeroki wachlarz formacji wykresu. Analiza jest odwrotną operacją do syntezy,
tak więc, jeśli zrozumiemy co to jest synteza, to mamy wszelkie dane aby zrozumieć techniki
i procedury analityczne. Podczas gdy synteza jest relatywnie łatwa, to analiza jest bardzo
trudna, ponieważ trzeba uwzględnić szeroki wachlarz powiązanych ze sobą parametrów.
Często przeprowadzamy analizę przyjmując uproszczone założenia i następnie testując je.
Kanały cenowe
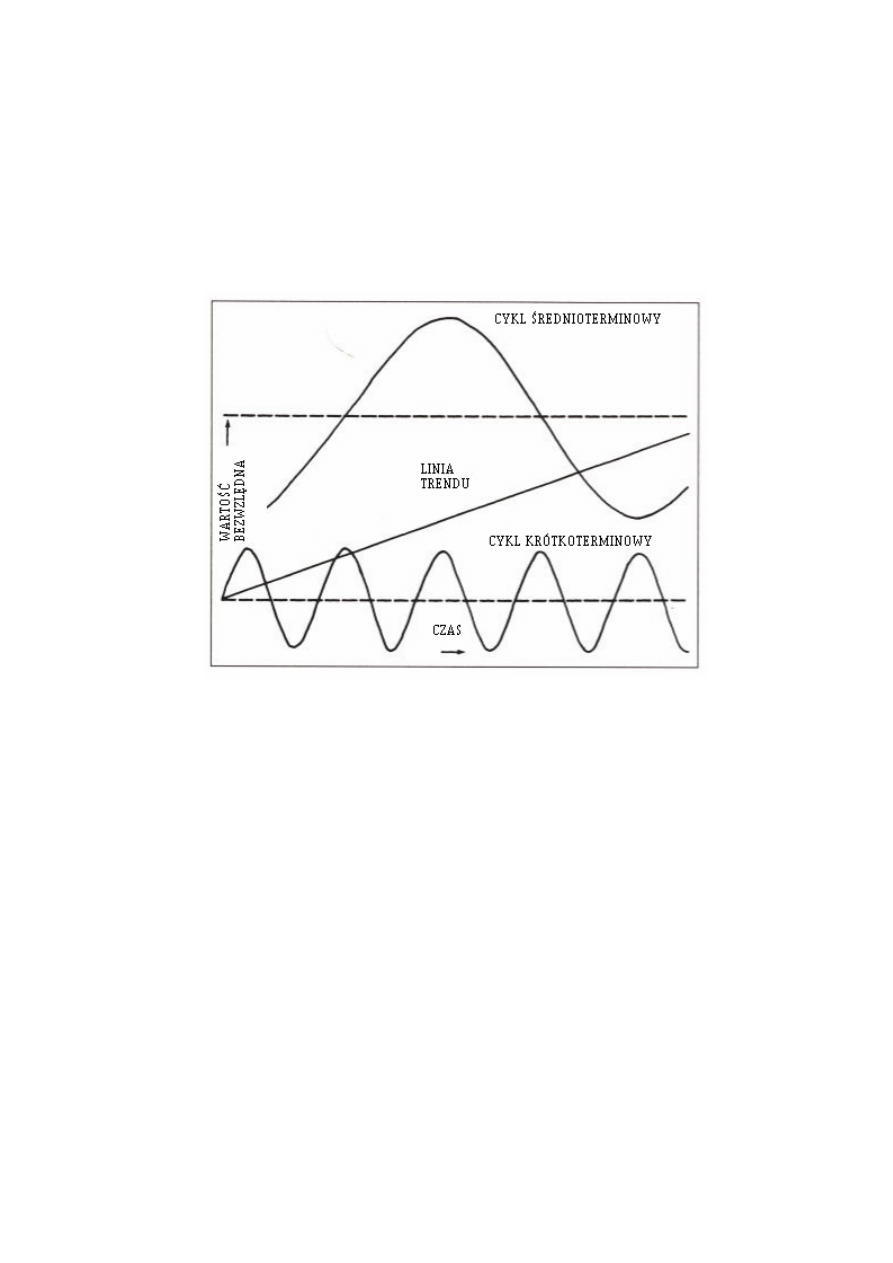
Kanały cenowe syntezuje się przy wykorzystaniu zasady proporcjonalności i zasady
superpozycji. Opieramy się na poniższych trzech składnikach:
1. Trend (część dużej amplitudy długiego cyklu).
2. Średnioterminowy cykl o średniej amplitudzie.
3. Krótkoterminowy cykl o małej amplitudzie.
Gdy zsumujemy te trzy składniki, rezultatem będzie kształt fali pokazanej na Rys. 3.9.
Zasady rządzące cyklami
27
Rysunek 3.9 Zsyntezowany kanał cenowy.
Kanały cenowe to po prostu minima i maksima odchyleń krótkoterminowego cyklu,
połączone z innymi dwoma składnikami cyklicznymi. W tym przypadku „kanał” nie jest linią
prostą, lecz jest zakrzywiony przez cykl średnioterminowy.
Głowa i ramiona
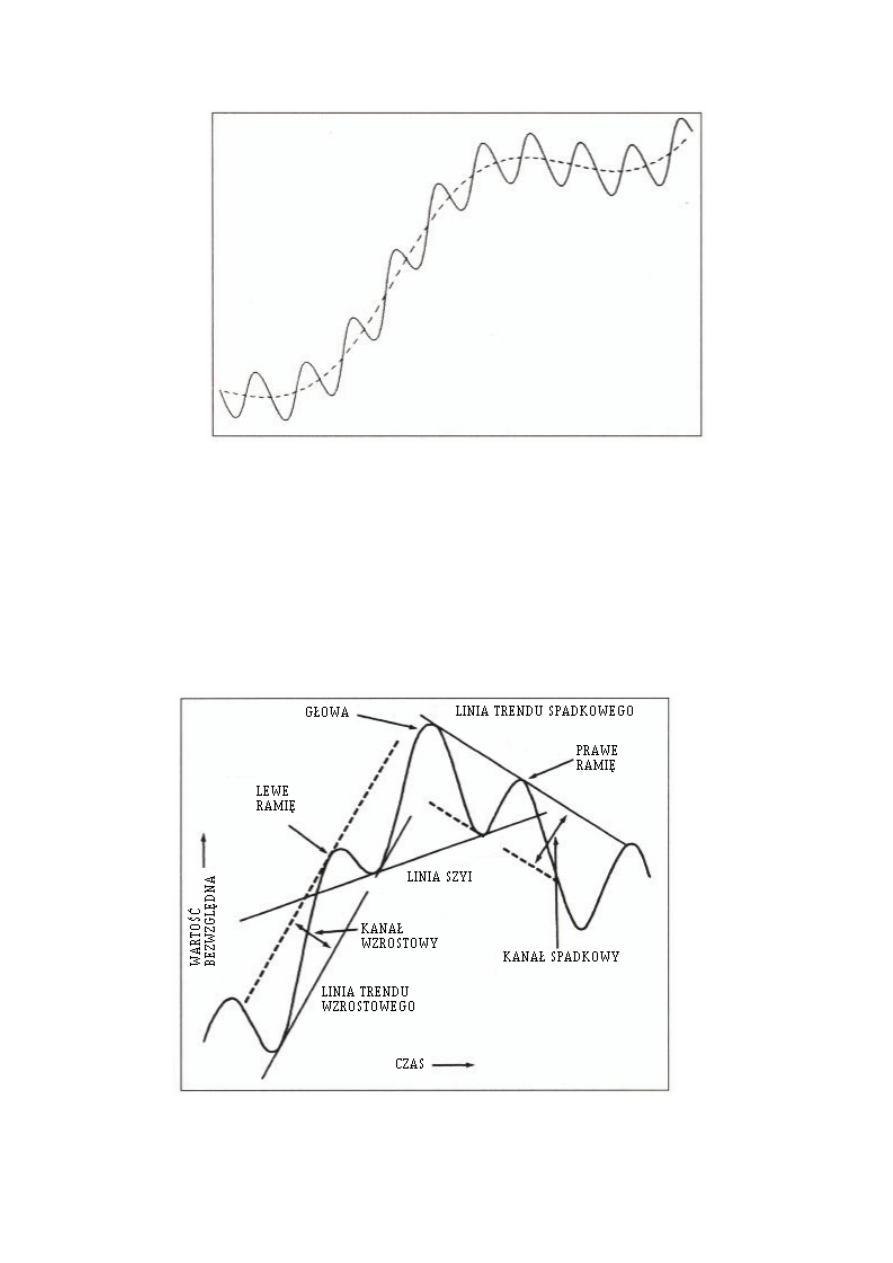
Jedną z formacji cieszących się szczególnym uznaniem jest klasyczna formacja głowy
i ramion, pokazana na Rys. 3.10.
Rysunek 3.10 Formacja głowy i ramion.
Zasady rządzące cyklami
28
Na rysunku pokazano wszystkie elementy wchodzące w skład tej formacji. Typowa
interpretacja powinna obejmować przebicie w dół linii wsparcia, potwierdzająca odwrócenie
trendu, który poprzednio został ustalony na podstawie linii trendu wzrostowego. Chociaż
należy wziąć pod uwagę możliwy ruch powrotny, formacja ta na ogół dobrze określa kierunek
nowego trendu.
Teraz popatrzmy jak można dokonać syntezy tej formacji. Rys. 3.11 pokazuje
podstawowe składniki tego złożonego kształtu fali.
Rysunek 3.11 Składniki cykliczne formacji głowa i ramiona.
Po
prostu,
wykorzystując zasadę superpozycji, dodajemy do siebie linię trendu (część
bardzo długiego cyklu), cykl średnioterminowy i cykl krótkoterminowy o częstotliwości
cztery razy większej, a o amplitudzie o połowę mniejszej. Krótkoterminowy cykl i
średnioterminowy cykl, będąc w tej samej fazie i tworząc jednocześnie szczyty, formują
głowę. Ramiona powstają przez dodawanie do siebie cyklu krótkoterminowego i
średnioterminowego w ich punkcie środkowym.
Znajomość składników cyklicznych czyni analizę łatwiejszą. Trend długoterminowy
można określić bezpośrednio. Trend średnioterminowy i jego punkt przebicia, określa średnią
długość cyklu. Krótkoterminowy cykl, określający najlepszy moment otwarcia pozycji,
ustalany jest na podstawie trendu średnioterminowego. Jest oczywiste, że
prawdopodobieństwo zyskownych transakcji jest największe, jeśli otwierasz pozycję na
podstawie cyklu krótkoterminowego w kierunku zgodnym z cyklem średnioterminowym. Nie
wolno zawierać transakcji, gdy te dwa cykle są przeciwstawne. Jest to wszystko co trzeba
wiedzieć. Nieskomplikowane reguły do nauczenia i zawieranie transakcji zgodnie z
mierzonymi cyklami.
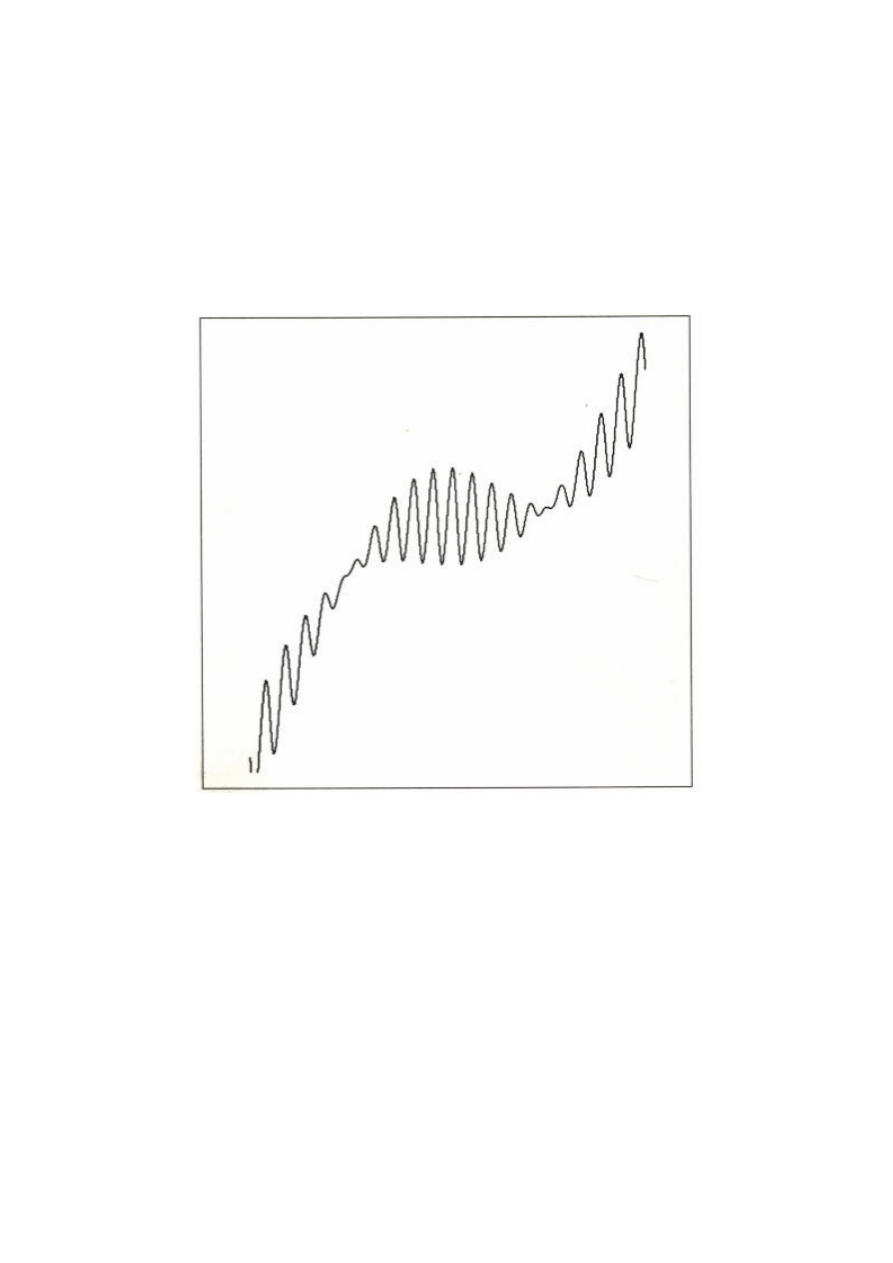
Podwójny szczyt
Co
się stanie z formacją wykresu, przedstawioną na Rys. 3.10, jeśli po prostu
przesuniemy o 120 stopni w lewo, fazę cyklu krótkoterminowego? Przypadek ten pokazuje
Rys. 3.12, gdzie pierwotna faza cyklu krótkoterminowego narysowana jest grubą linią, a
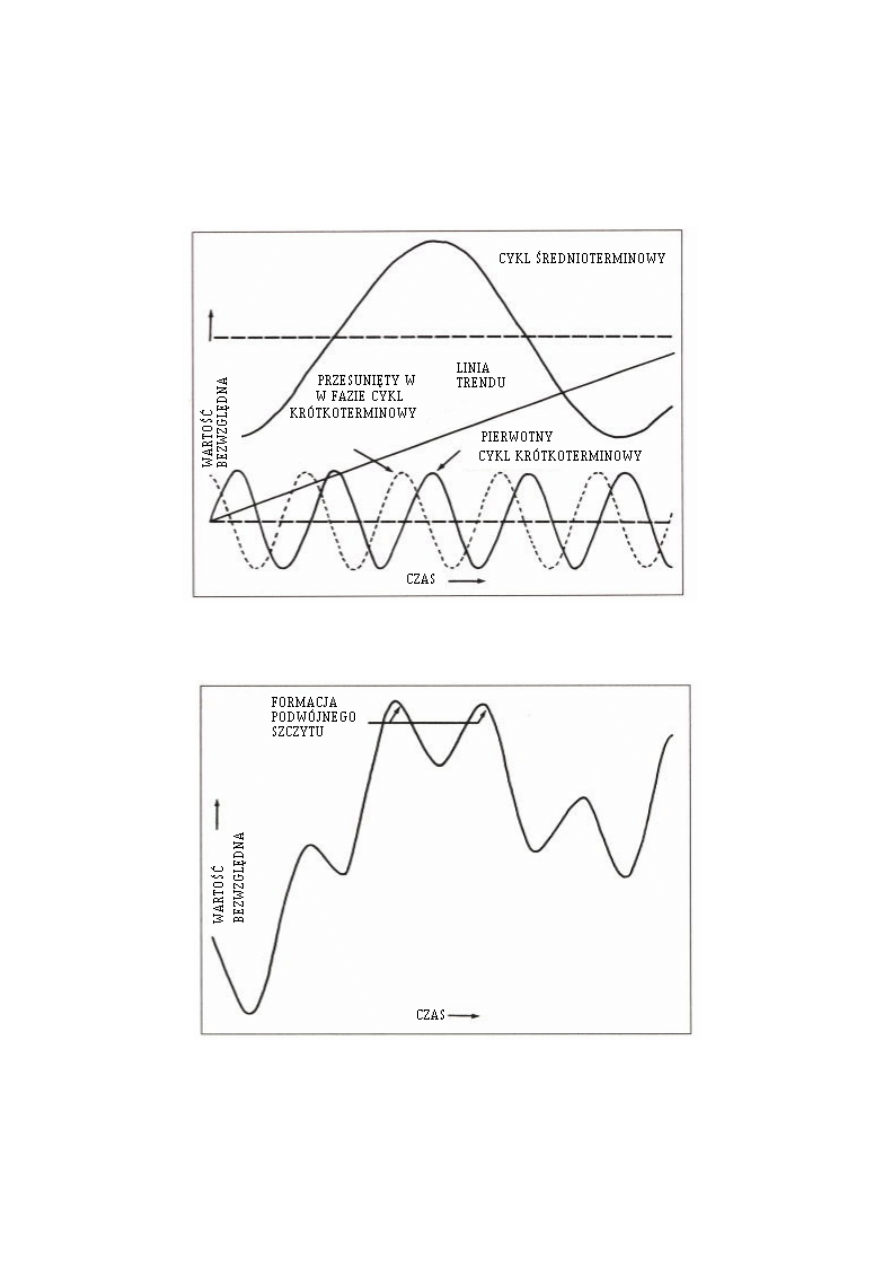
Zasady rządzące cyklami
29
przesunięta faza narysowana jest linią przerywaną. Teraz, odwołując się do zasady
superpozycji, dodajemy szczyty cyklu krótkoterminowego do cyklu średnioterminowego, po
obydwu stronach szczytu średnioterminowego. W efekcie otrzymamy formację podwójnego
szczytu, tak jak na Rys. 3.13.
Rysunek 3.12 Przesunięta faza cyklu krótkoterminowego.
Rysunek 3.13 Formacja podwójnego szczytu.
Wykorzystując analizę cykli i znając podstawowe składniki, nie zmieniamy naszej
strategii inwestycyjnej. Nadal otwieramy pozycję w punkcie zwrotnym cyklu
Zasady rządzące cyklami
30
krótkoterminowego w kierunku zgodnym z kierunkiem cyklu średnioterminowego. Nie
wymaga to żadnych nowych reguł do nauczenia i traktujemy formację podwójnego szczytu
dokładnie tak samo, jak formację głowa i ramiona.
Flagi i chorągiewki
Wszystkie te formacje wykresu charakteryzują się tym, że wstęga górna i wstęga dolna
koperty cenowej nie są równoległe do siebie, tak jak w tradycyjnych kanałach cenowych.
Typowa chorągiewka pokazana jest na Rys. 3.14.
Rysunek 3.14 Chorągiewka kontynuacji.
Typowa interpretacja formacji chorągiewki przyjmuje, że ruch ceny będzie
kontynuowany w tym samym kierunku, co przed uformowaniem chorągiewki. Może to być
prawdą lub nie. Wykorzystując cykle można szybko określić czy ruch ceny będzie
kontynuowany, czy też nastąpi odwrócenie.
Rys. 3.8 pokazuje nierównoległą kopertę cenową, powstałą w wyniku zasady
rezonansu. Jeśli teraz odwołamy się do zasady superpozycji i zasady proporcjonalności, to
możemy utworzyć formację chorągiewki, dodając trend, cykl średnioterminowy i cykl
krótkoterminowy modulowany przez średnią długość cyklu fali stojącej. Używając tych
składników otrzymujemy Rys. 3.15, a typowa interpretacja tej formacji uzyskuje
potwierdzenie i ruch ceny będzie kontynuowany.
Zasady rządzące cyklami
31
Rysunek 3.15 Podstawowe składniki formacji chorągiewki, przesądzające o kontynuowaniu ruchu
cenowego.
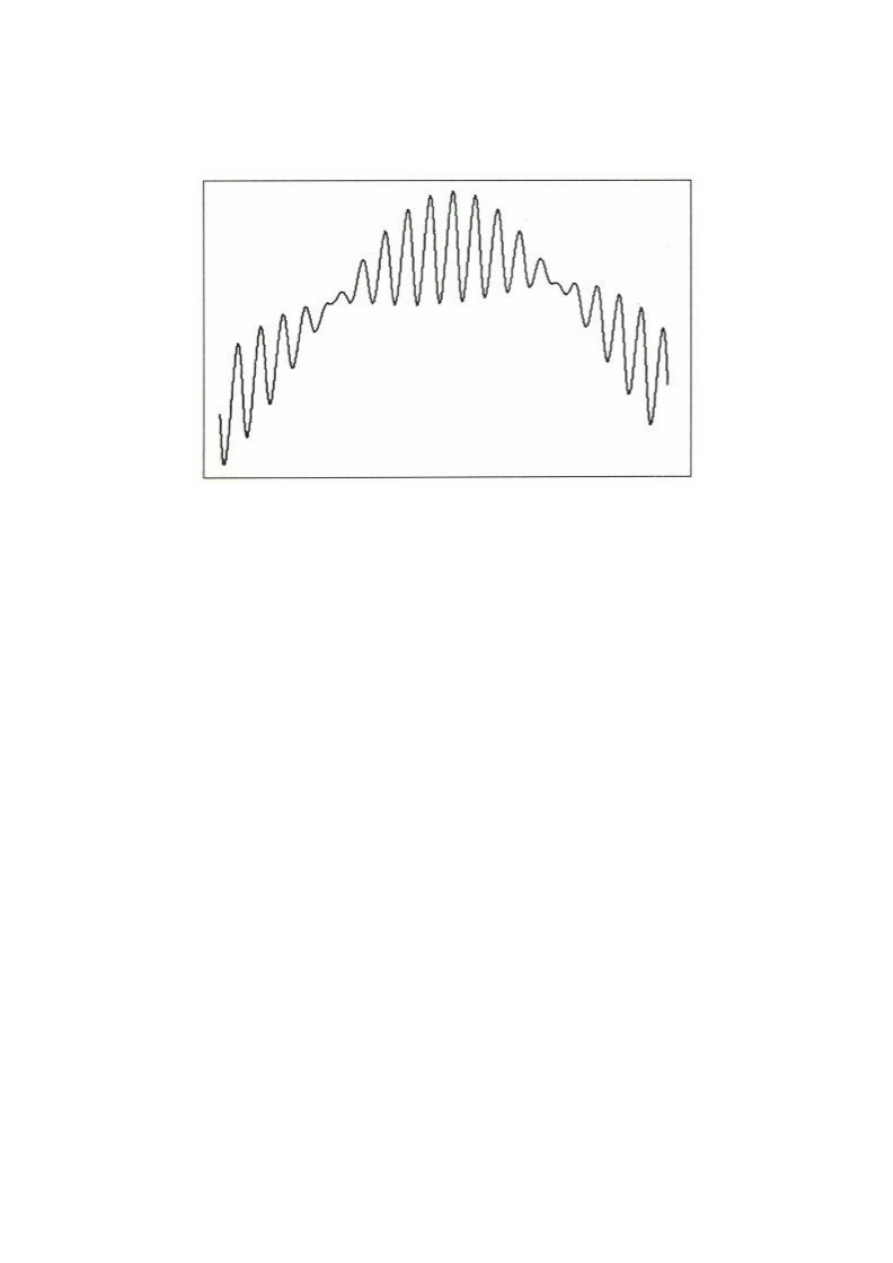
Jednakże, jeśli podwoimy szerokość i amplitudę średnioterminowego cyklu (zasada
proporcjonalności) oraz wyeliminujemy trend, to otrzymamy podstawowe składniki
chorągiewki, tak jak na Rys. 3.16.
Rysunek 3.16 Podstawowe składniki formacji chorągiewki, przesądzające o odwróceniu ceny.
Zasady rządzące cyklami
32
W tym przypadku, cena odwróci się po uformowaniu chorągiewki, ponieważ trend jest
zastąpiony przez mocniejszy cykl. W efekcie otrzymamy kształt, jak na Rys. 3.17.
Rysunek 3.17 Chorągiewka odwrócenia.
Nadal otrzymujemy ten sam kształt chorągiewki, jak na Rys. 3.14, ale odczytując
chorągiewkę pokazaną na Rys. 3.17 jako formację kontynuacji, popełnimy błąd. Jednak, gdy
znamy cykle podstawowe, można łatwo przewidzieć przyszły ruch ceny, pod koniec formacji
chorągiewki.
Informacja dodatkowa
Wzajemne
relacje
pomiędzy formacjami wykresu a cyklami mają tyle różnych
wariantów, że to co zostało przedstawione, może być tylko wprowadzeniem do tego tematu i
zasługuje na oddzielną książkę. Informacje przedstawione w tym rozdziale mają tylko
uświadomić ci, że takie wzajemne relacje istnieją i wykorzystywanie cykli stanowi istotną
pomoc w analizie formacji wykresu. W celu głębszego zapoznania się z tym zagadnieniem,
należy sięgnąć po literaturę uzupełniającą. Polecamy J. M. Hursta.
Zapamiętaj
• Cykl jest podstawą, na której można zbudować wszystkie formacje wykresu.
• Wszystkie formacje wykresu można opisać za pomocą tylko trzech zasad rządzących
cyklami. Są to:
1. Zasada proporcjonalności.
2. Zasada superpozycji.
3. Zasada rezonansu.
• Łatwiej pracować z cyklami podstawowymi, niż uczyć się na pamięć dużej liczby
formacji wykresu.

Średnie ruchome
33
Rozdział 4
Średnie ruchome
Średnie ruchome zwane są wygładzarkami danych liczbowych, ponieważ gładzenie
jest dokładnie tym, co one wyczyniają z kształtami fal. Usuwają one krótkoterminowe
zakrętasy w pierwotnych danych liczbowych. Pracując z cyklami wykorzystujemy zalety
chirurgicznej precyzji średnich ruchomych, a nie ich możliwość ogólnego gładzenia danych.
Krótkoterminowe zakrętasy tworzone są przez składniki o wyższej częstotliwości w fali
złożonej. Są one usuwane, ponieważ średnie ruchome działają jak dolnoprzepustowe filtry.
Dolnoprzepustowy filtr przepuszcza składniki o niskiej częstotliwości nie osłabiając ich,
natomiast blokuje przejście składników o wyższej częstotliwości. Nasza analiza opisuje jak
utworzyć i wykorzystywać w transakcjach filtry dolnoprzepustowe.
Zasadniczo
istnieją dwa rodzaje filtrów dolnoprzepustowych, tj. filtry Finite Impulse
Response (FIR) (Skończone Oddziaływanie Impulsowu) i filtry Infinite Impulse Response
(IIR) (Nieskończone Oddziaływanie Impulsu). Prosta średnia ruchoma (SMA) (Simple
Moving Average) należy do rodziny filtrów FIR. Filtry FIR dlatego tak są nazwane, ponieważ
gdy sygnałem wejściowym będzie krótki szpic, to w wyniku działania tego filtra, sygnał
wyjściowy pojawi się tylko dla ustawionej przepustowości okienka filtra FIR. Tak więc,
odpowiedź filtra na impuls jest skończona w czasie. Filtr IIR wykorzystuje obliczenia
rekursywne do uzyskania sygnału wyjściowego. To jest, aktualny sygnał wyjściowy jest
rezultatem nie tylko aktualnego sygnału wejściowego, ale także rezultatem poprzednio
obliczonych sygnałów wyjściowych. Ponieważ obliczenia są rekursywne, każdy sygnał
wejściowy jest teoretycznie na zawsze obecny w sygnale wyjściowym. Wykładnicza średnia
ruchoma (EMA) (Exponential Moving Average) należy do rodziny filtrów IIR.
Opóźnienie charakterystyczne dla filtrów jest prawdopodobnie największym
zmartwieniem graczy. Jest to znacznie ważniejsze przy przeprowadzaniu transakcji, niż sama
możliwość osiągnięcia gładzenia. Łatwo sprawdzić, że opóźnienie SMA jest w przybliżeniu
równe połowie przepustowości filtra. Ponieważ sygnał wyjściowy reprezentuje wartość bliską
horyzontalnego środka filtra, który ma szerokość N słupków, opóźnienie SMA wynosi
dokładnie (N-1)/2. Inżynierowie nazywają opóźnienie filtra opóźnieniem grupowym.
Rozgraniczają oni opóźnienie grupowe od opóźnienia fazowego. Aby najlepiej zobaczyć
różnice pomiędzy tymi różnymi opóźnieniami, musimy rozważyć prędkość fal. Wyobraźmy
sobie obraz fal oceanicznych zmierzających w stroną lądu, na plażę. Grupowa prędkość to
szybkość, z jaką fale przemieszczają się w kierunku prostopadłym do ruchu fal. Jeśli fale
uderzą w plażę pod jakimś ukośnym kątem, to prędkość fazowa jest szybkością, z jaką szczyt
fali przemieszcza się w dół do plaży. Przykładem filtra, funkcjonującego w rzeczywistym
świecie, jest osłona anteny radiolokatora w samolocie. Osłona anteny radiolokatora jest
przeźroczysta dla częstotliwości radaru, ale jest nieprzeźroczysta dla innych częstotliwości
radiowych. Tak więc, osłona anteny radiolokatora jest rodzajem filtra. Grupowa prędkość nie
może nigdy przekroczyć prędkości światła, ponieważ jest to prędkość przenoszenia energii. Z
drugiej strony, prędkość fazowa może być bardzo duża.
Średnie ruchome
34
Filtry FIR
Wracając do tradycyjnych rodzajów filtrów, rozważmy 2-słupkową SMA. Jasne jest, że
grupowe przesunięcie odpowiada środkowi filtra lub 0.5-słupkowemu przesunięciu.
Przesunięcie fazowe zmienia się liniowo wraz z częstotliwością. Przesunięcie fazowe wynosi
zero dla częstotliwości równej zeru i wzrasta do wartości pi dla kątowej próby częstotliwości.
Częstotliwość kątowa jest 2pi razy większa od rzeczywistej częstotliwości, ponieważ pełny
cykl ma 2pi radianów. Dana rynkowa jest daną próbkowaną, a teoria próby losowej stwierdza,
że musimy mieć co najmniej dwie próbki na cykl. Najwyższa z możliwych częstotliwości
nazywana jest częstotliwością Nyquista. Na przykład, częstotliwość Nyquista wynosi 0.5-
cykla na słupek. Ponieważ zazwyczaj myślimy w kategoriach okresów cykli, a nie jego
odwrotności, to okres Nyquista wynosi 2 słupki na cykl. Rezultaty systemów prób losowych
danych, często przedstawiane są w postaci normalizowanej do częstotliwości Nuquista. Na
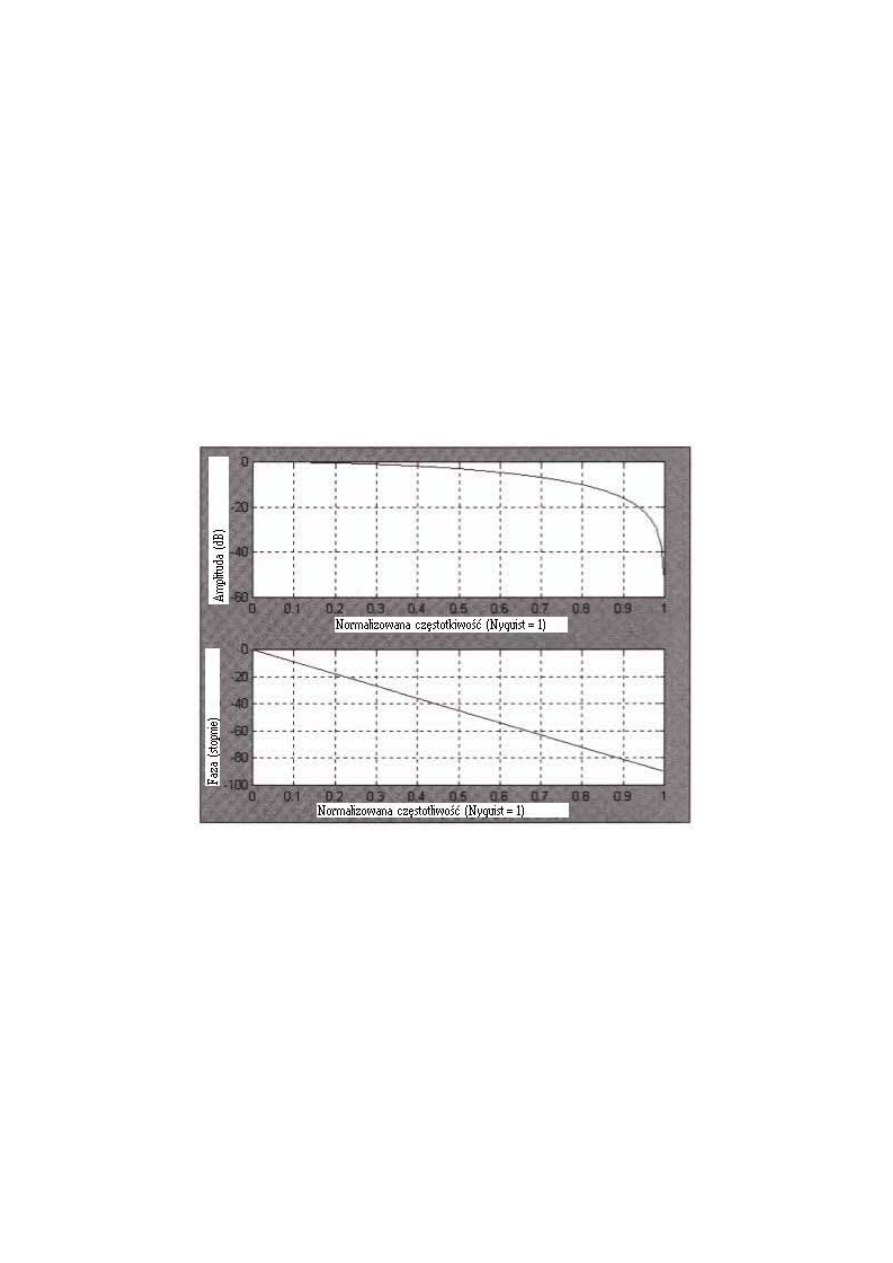
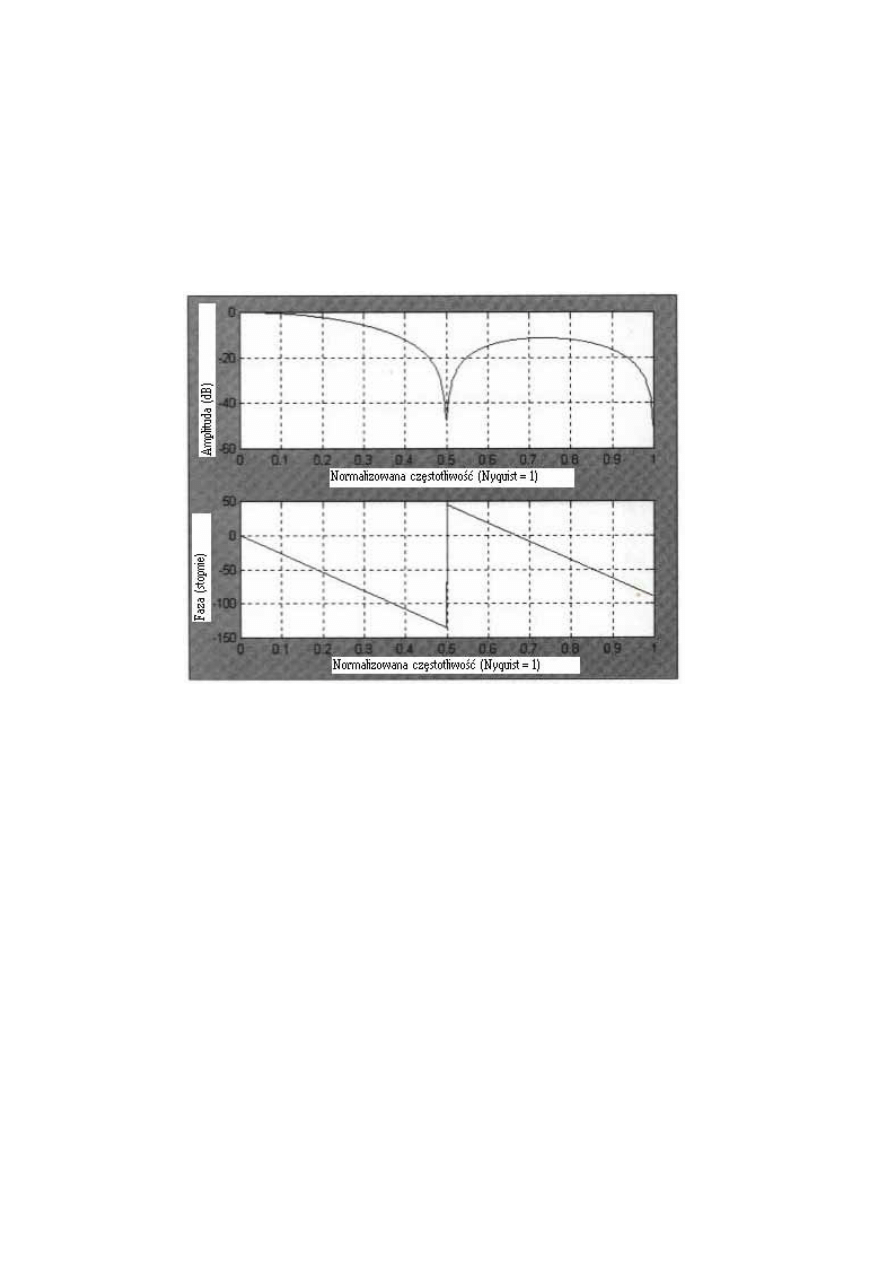
przykład, amplituda i faza danych wyjściowych 2-słupkowej SMA pokazane są na Rys. 4.1.
Amplituda filtra wyjściowego jest wykreślona w decybelach (20*log(amplituda fali)).
Rysunek 4.1 Amplituda i faza odpowiadająca 2-słupkowej SMA.
Rys. 4.1 pokazuje, że 2-słupkowy cykl jest prawie wyeliminowany, ponieważ dwie
próby na cykl średnio dają zero. Wykres fazy pokazuje fazę jako funkcję częstotliwości.
Okres cyklu jest obliczany jako dwa podzielone przez normalizowaną częstotliwość. Dlatego
normalizowana częstotliwość dla 5-słupkowego cyklu wynosi 0.25. Tak więc, 5-słupkowy
cykl doznaje 25-stopniowego opóźnienia fazowego w 2-słupkowej SMA. Podobnie, 3-
słupkowy cykl (normalizowana częstotliwość=0.667) ma 60-stopniowe opóźnienie fazowe.
Definicja opóźnienia grupowego to rozpiętość zmian fazy w stosunku do częstotliwości
kątowej. Rozpiętość zmian fazy 2-słupkowej SMA jest stała dla wszystkich częstotliwości.
Rozpiętość można obliczyć jako fazę, przy częstotliwości Nyquista (1/2*pi), podzieloną przez
kątową częstotliwość Nyquista=2*π*0.5. Przeprowadzając dzielenie zobaczymy, że grupowe
przesunięcie wynosi 0.5 słupka – dokładne opóźnienie wyciągniemy z opóźnienia (N-1)/2
Średnie ruchome
35
obliczonego z szerokości rozważanego filtra. To obliczenie opóźnienia jest bardziej
powszechną definicją opóźnienia, ponieważ ma zastosowanie również do filtrów IIR.
Rys. 4.2 pokazuje, że 2-słupkowy cykl i 4-słupkowy cykl są prawie wyeliminowane w
4-słupkowej SMA. Faza odpowiadająca filtrowi narysowana jest z 90-stopniową przerwą przy
amplitudzie o zerowej wartości, ale rozpiętość zmian fazy jest liniowa, za wyjątkiem
częstotliwości o dokładnie zerowej wartości. Całkowite przesunięcie fazowe wynosi (3*pi)/2
dla częstotliwości kątowej Nyquista wynoszącej pi, w rezultacie czego opóźnienia 1.5 słupka
są obliczane jako rozpiętość zmian fazy. Opóźnienie jest stałe dla wszystkich częstotliwości.
Rysunek 4.2 Amplituda i faza odpowiadająca 4-słupkowej SMA.
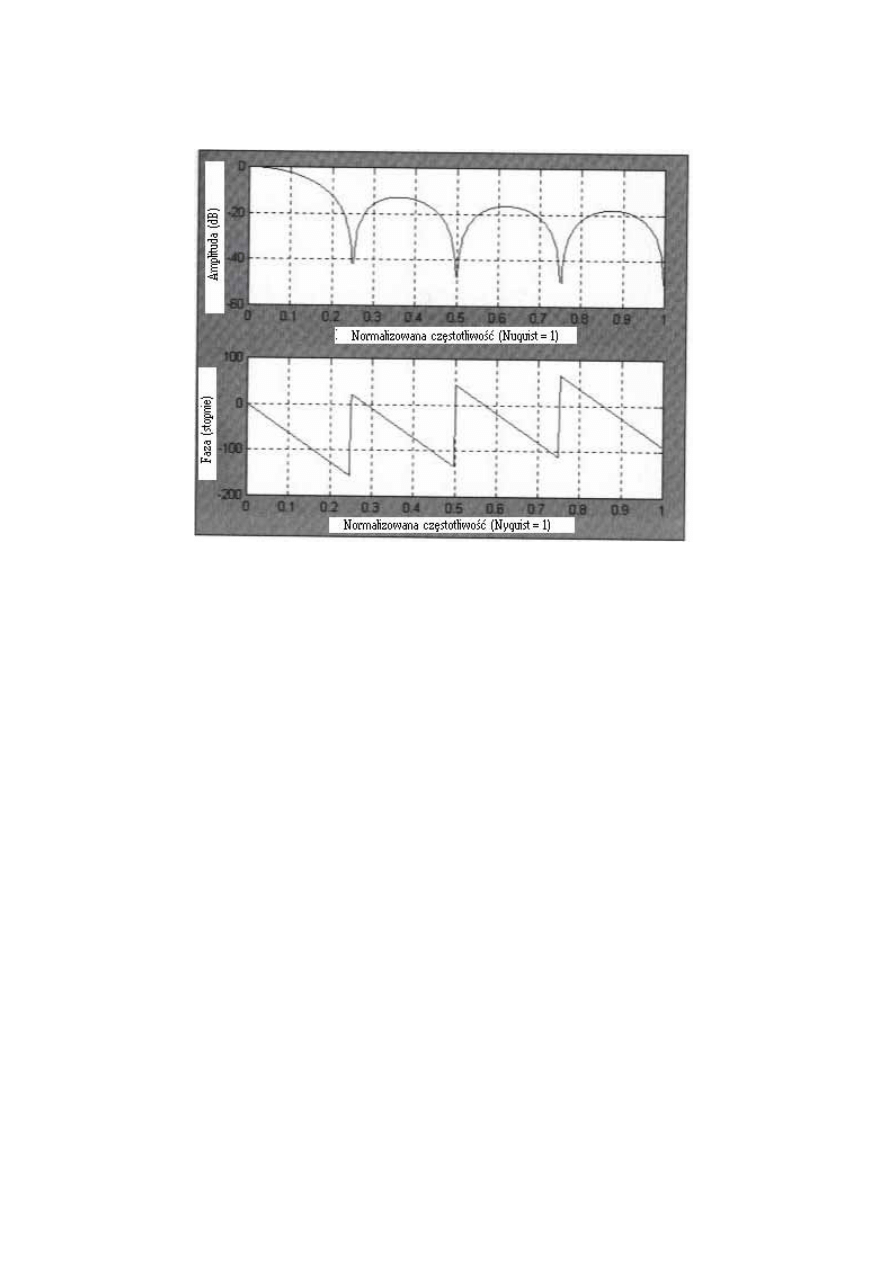
Podwajając ponownie szerokość SMA, zobaczymy opisaną na Rys. 4.3 8-słupkową
SMA. Wszystkie 2-, 8/3-, 4- i 8-słupkowe cykle usuwane są przez filtr, ponieważ każdy
odpowiada wielokrotności liczby całkowitej szerokości filtra. Całkowita liczba okresów cyklu
powoduje, że filtr uśrednia te cykle do zera. Całkowite przesunięcie fazowe przy
częstotliwości Nyquista wynoszącej (7*pi)/2 daje rezultat opóźnienia, chociaż filtr wynosi 3.5
słupków.
Średnie ruchome
36
Nyquista wynoszącej (7*pi)/2 daje rezultat opóźnienia, chociaż filtr wynosi 3.5 słupków.
Rysunek 4.3 Amplituda i faza odpowiadająca 8-słupkowej SMA.
Ważona średnia ruchoma (WMA) (Weighted Moving Average) jest filtrem FIR. Jest
ona podobna do SMA za wyjątkiem tego, że współczynniki filtra są ważone w odwrotnej
proporcji do danych liczbowych w filtrze oraz normalizowane są do sumy współczynników.
W zapisie EasyLanguage, [N] po zmiennej oznacza użycie zmiennej N słupków temu. Tak
więc WMA może napisana być jako
WMA=(4*Cena+3*Cena[1]+2*Cena[2]+Cena[3])/10
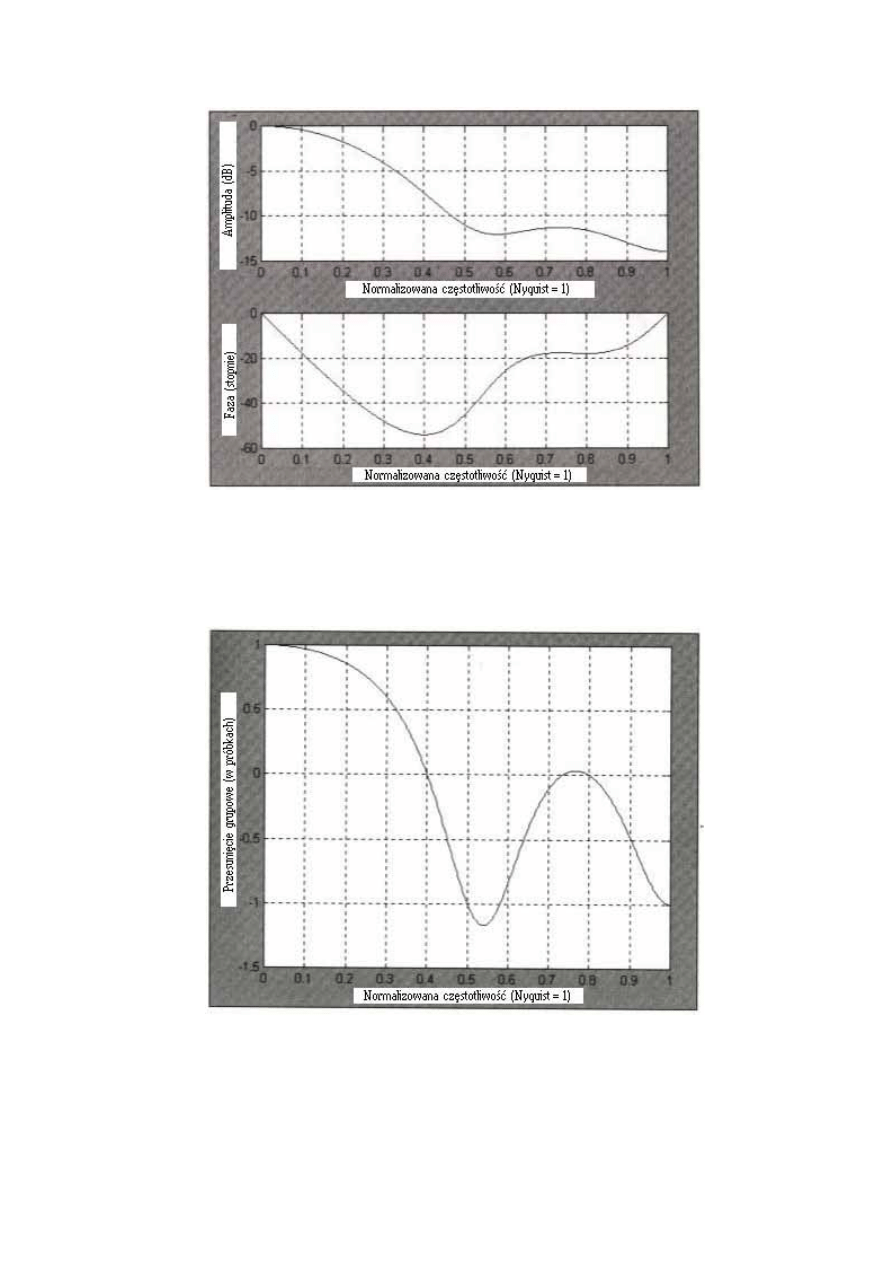
Częstotliwość i faza odpowiadające tej 4-słupkowej WMA pokazane są na Rys. 4.4.
Ponieważ WMA ma asymetrycznie ważone współczynniki, nie ma charakterystycznych
częstotliwości, ponieważ są one wycięte przez filtr.
Średnie ruchome
37
Rysunek 4.4 Amplituda i faza odpowiadająca 4-słupkowej WMA.
Dodatkowo, odpowiadająca faza nie jest liniowa co oznacza, że grupowe przesunięcie
nie jest stałe dla wszystkich częstotliwości. Grupowe przesunięcie 4-słupkowej WMA
pokazane jest na Rys. 4.5.
Rysunek 4.5 Grupowe przesunięcie 4-słupkowej WMA.
Współczynniki WMA tworzą zarys trójkąta w poprzek szerokości filtra. Znaczące
opóźnienie niskiej częstotliwości filtra FIR może być porównane ze „środkiem ciężkości”
figury geometrycznej opisanej za pomocą współczynników filtra. Ponieważ figurą
Średnie ruchome
38
geometryczną współczynników WMA jest trójkąt, opóźnienie niskiej częstotliwości może być
opisane wyrażeniem (N-1)/3, ponieważ jest to środek ciężkości trójkąta. Tak więc, dla 4-
słupkowej WMA, opóźnienie niskiej częstotliwości wynosi dokładnie 1 słupek. Odpowiada to
dokładnie obliczonemu przesunięciu grupowemu niskiej częstotliwości pokazanemu na Rys.
4.5. Opóźnienie dla składników częstotliwości, które były osłabione nie ma nic wspólnego,
ponieważ ich amplituda jest mało porównywalna z ich wejściowymi amplitudami.
Niektóre symetryczne filtry FIR są interesujące dla graczy, ponieważ wycinają
określone składniki częstotliwości, które prawdopodobnie istnieją w danych rynkowych. Na
przykład, 4-słupkowy symetryczny filtr FIR posiada poniższe współczynniki:
FIR=(Cena+2*Cena[1]+2*Cena[2]+Cena[3])/6
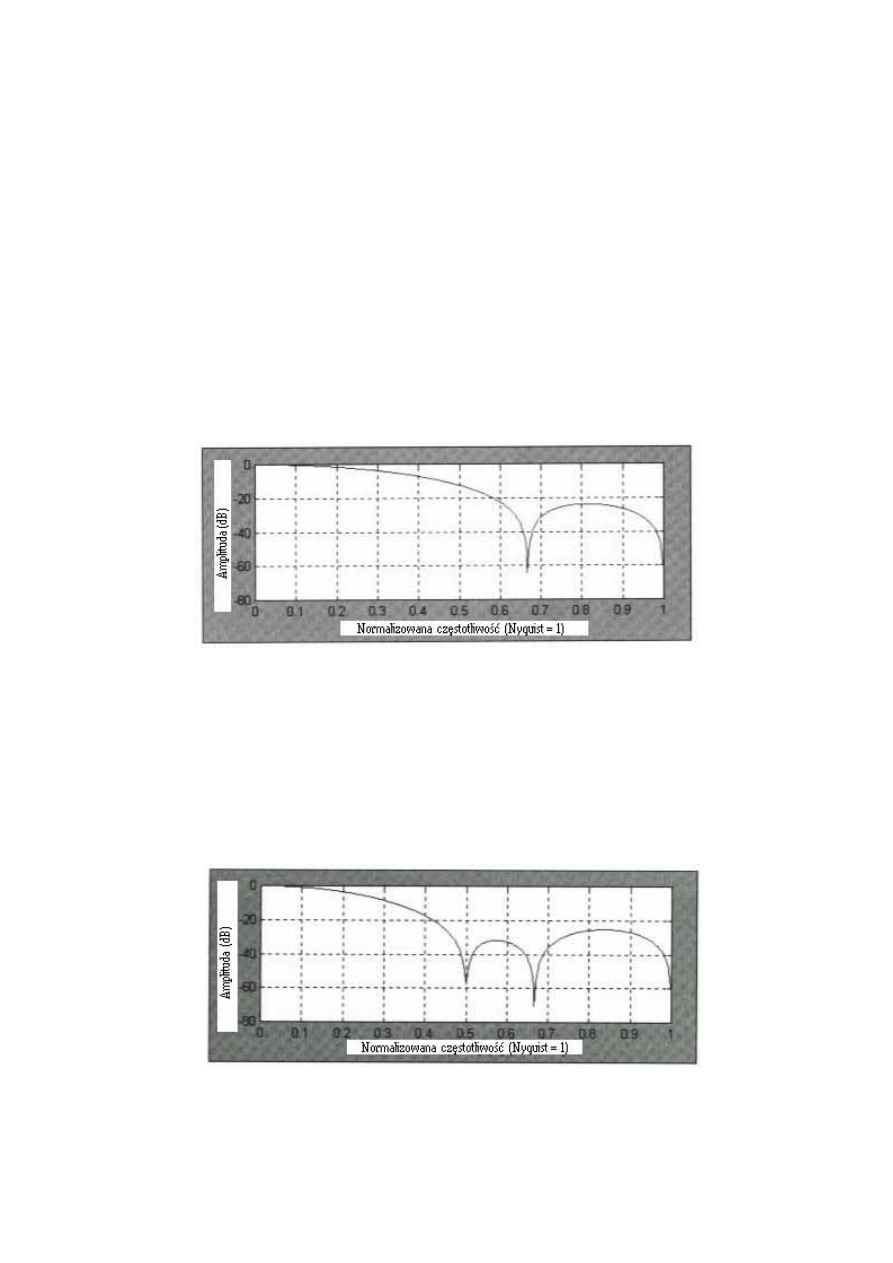
Ten filtr ma częstotliwość odpowiadającą częstotliwości pokazanej na Rys. 4.6. Ten
filtr wycina dokładnie 2- i 3-słupkowe cykle. Ma on opóźnienie 1.5 słupka dla wszystkich
częstotliwości.
Rysunek 4.6 Amplituda odpowiadająca symetrycznemu 4-słupkowemu filtrowi FIR.
Przenosząc to na 6-słupkowy symetryczny filtr FIR, współczynniki będą przedstawiać
się następująco:
FIR=( Cena+2*Cena[1]+3*Cena[2]+3*Cena[3]+2*Cena[4]+Cena[5])/12
Ten filtr posiada częstotliwość odpowiadającą częstotliwości pokazanej na Rys. 4.7.
Ten filtr wycina dokładnie 2-, 3- i 4-słupkowe cykle.
Rysunek 4.7 Amplituda odpowiadająca symetrycznemu 6-słupkowemu filtrowi FIR.

Średnie ruchome
39
Dodatkowo, wycinane okresy mają całkowitą liczbę słupków, filtr trwale osłabia składniki
częstotliwości pomiędzy tymi całkowitymi słupkami cykli. Ma on opóźnienie 2.5 słupka dla
wszystkich częstotliwości.
Filtry IIR
Filtry FIR, które omówiliśmy są nierekursywne. To jest, nie można używać
poprzednich obliczeń do obliczania aktualnej wartości średniej ruchomej. Filtry IIR
zasadniczo różnią się, ponieważ są one rekursywne. Wykładnicze średnie ruchome (EMA) są
najbardziej znane graczom. W EMA obliczenia wykorzystują część aktualnej ceny dodając ją
do innej części obliczonej 1 słupek temu. Pierwsza część, zazwyczaj zwana alfa, może
przybierać wartości pomiędzy zero i jeden. Te dwie części muszą w sumie wynosić jeden, tak
więc druga część musi przybrać wartość jeden minus alfa. Równanie obliczające EMA brzmi:
EMA=α*Cena+(1-α)*EMA[1]
EMA
staje
się średnią ruchomą krocząc od słupka do słupka, od lewej do prawej
strony, przez wszystkie dane liczbowe ceny. Ja zawsze zapisuję EMA w postaci pokazanego
kodu, aby mieć pewność, że suma α i (1-α) daje jeden. Jeśli te dwa składniki nie dają w sumie
jedności, to sygnał wyjściowy filtra jest błędny i może wzrosnąć wystarczająco dużo aby
spowodować zawieszenie pracy komputera.
Termin
wykładnicza opisuje sposób, w jaki EMA przemieszcza odpowiednie rozkłady
danych w amplitudzie w odniesieniu do pojedynczego sygnału wejściowego. Wyobraź sobie
przypadek, w którym ustalone dane liczbowe mają amplitudę 1/alfa dla pierwszego słupka i
amplitudę równą zeru dla każdego innego słupka. Gdy zastosuję EMA do tej danej, to
pierwszym sygnałem wyjściowym z filtra będzie jeden, ponieważ nie było żadnej poprzedniej
wartości EMA. W kolejnych obliczeniach, wartość ceny wynosi zero, a więc następne
obliczenia wymagają bardzo znacznych potęg (1-alfa). Tak więc, wyjściowa amplituda spada
wykładniczo wraz liczbą obliczeń.
Termin alfa jest zwykle odnoszony do długości SMA za pomocą poniższego wzoru:
α=2/(długość+1)
Ja
preferuję myślenie o alfa EMA w kategoriach opóźnienia, ponieważ opóźnienie
bezpośrednio oddziałuje na EMA w moim własnym systemie transakcyjnym. Ponieważ
opóźnienie jest prawie połową długości okienka SMA, to alfa może być obliczone jako:¹
α=1/(Opóźnienie+1)
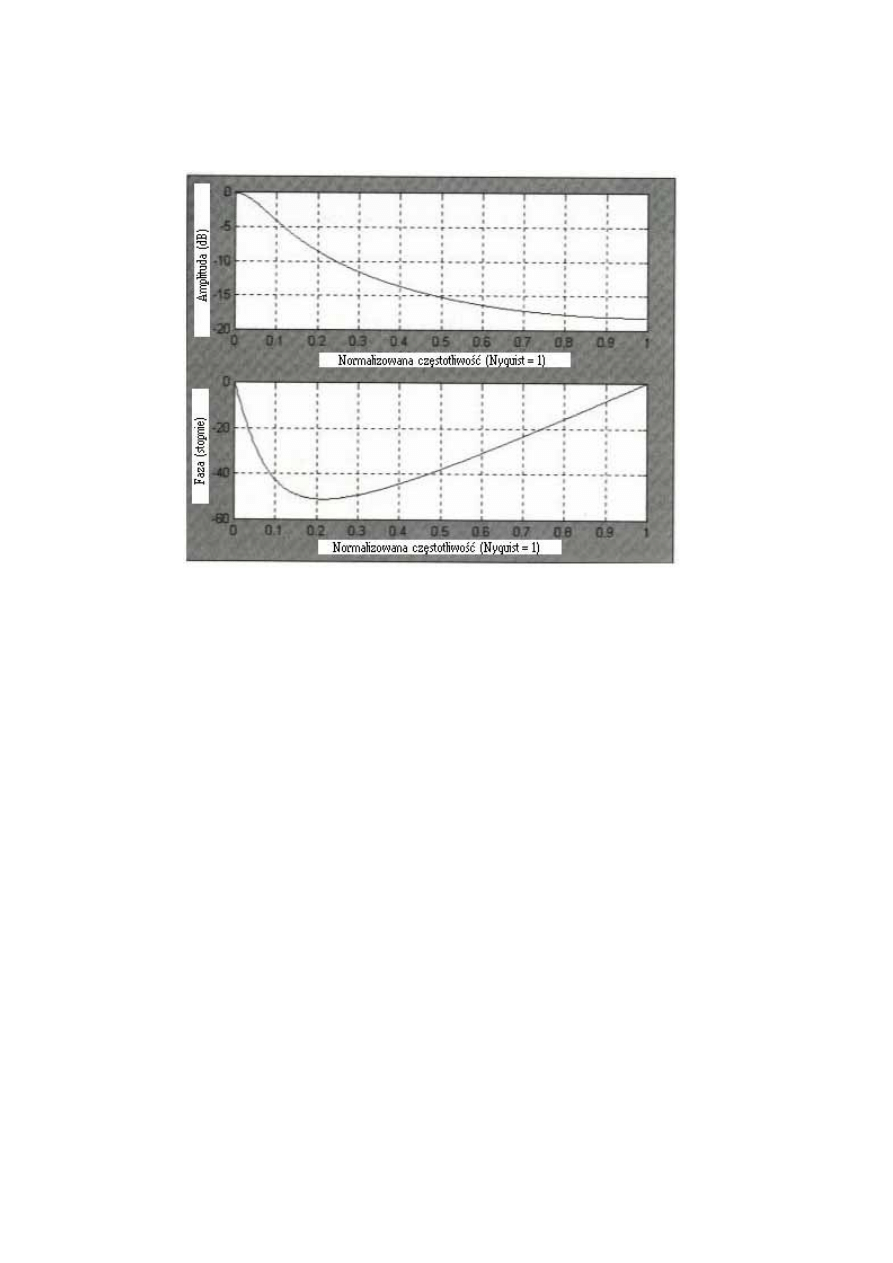
Równoważnikiem alfa w 8-słupkowej SMA jest 0.222. Faza i amplituda
odpowiadająca użytej wartości alfa pokazane są na Rys. 4.8. Można go porównać do
amplitudy i fazy odpowiadającej 8-słupkowej SMA na Rys. 4.3.
_____________
¹John F. Ehlers. Rocket Science for Traders. John Wiley & Sons, New York, 2001, p. 29.
Średnie ruchome
40
Rysunek 4.8 Amplituda i faza odpowiadająca EMA, której α=0.222.
Nie ma ostrych wycięć w odpowiedniej amplitudzie, ponieważ obliczenia rekursywne
wykluczają to. Przesunięcie fazowe jest nieliniowe z powodu tego, że grupowe przesunięcie
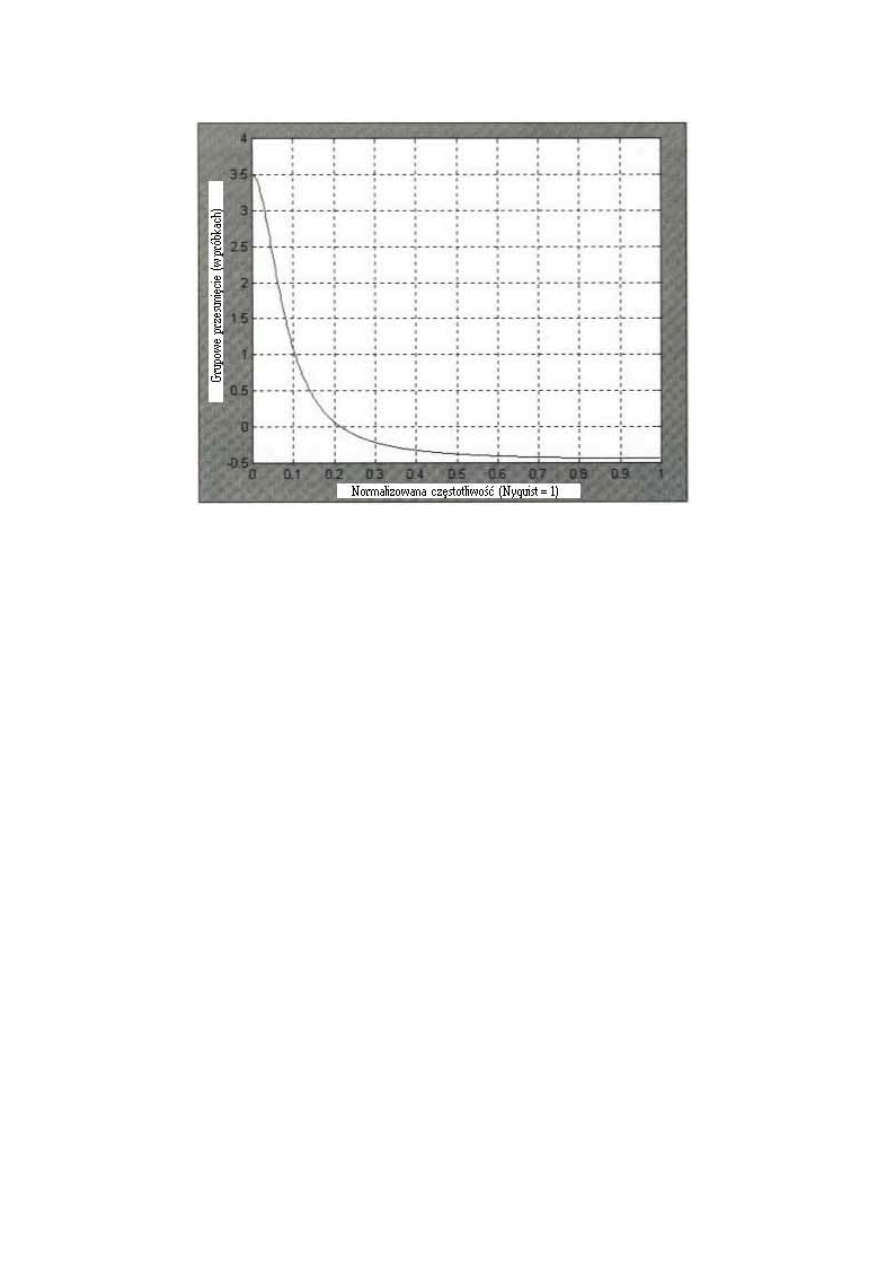
(opóźnienie) nie jest stałe dla wszystkich częstotliwości. Grupowe przesunięcie dla tej EMA
jest przedstawione na Rys. 4.9. Pamiętaj, że opóźnienie niskiej częstotliwości o 3.5 słupka jest
dokładnie takie samo jak opóźnienie równoważnej SMA, ale to opóźnienie spada gwałtownie
wraz ze wzrostem częstotliwości. Spadek opóźnienia wraz ze wzrostem częstotliwości jest
jedną z zasad wykorzystywanych w EMA porównywalnej z SMA.
Średnie ruchome
41
Rysunek 4.9 Grupowe przesunięcie odpowiadające EMA, której α=0.222.
Filtry nieliniowe
Filtry
posiadające idealne charakterystyki zwane są filtrami dopasowanymi. To jest,
ich odpowiedź jest dopasowana do kształtu i prawdopodobieństwa gęstości funkcji kształtów
fal obecnych w jej sygnale wejściowym. Każdy szum, który nie odpowiada spodziewanemu
kształtowi fali jest eliminowany. Oczywiście, jeśli znamy mniej więcej kształty fal
rynkowych nie ma potrzeby ich filtrowania. W dolnoprzepustowych filtrach przyjmujemy
podstawowe założenie, że żądane sygnały mają relatywnie niską częstotliwość, a szum ma
relatywnie wysoką częstotliwość. Tak więc, oddzielamy sygnały od szumu korzystając z ich
charakterystycznych częstotliwości. To założenie nie zawsze jest słuszne.
Wiemy,
że ceny mogą czasem gwałtownie zmieniać się. Te gwałtowne zmiany
oznaczają jakąś krótkotrwale występującą wysoką częstotliwość. Niektóre nieliniowe filtry
zostały zaprojektowane² do przechwycenia tych przypadków i dodatkowo jeszcze do
wyeliminowania szumów o wysokiej częstotliwości. Filtry Kaufman Adaptive Moving
Average (KAMA) i Variable Index Dynamic Average (VIDYA) wykonują to dzięki
przerobieniu alfa w EMA, stosownie do obserwowanej zmienności. Filtr Maximum Entropy
Spectral Analysis (MESA) Adaptive Moving Average (MAMA) przesuwa swoje pasmo
przepustowe stosownie do raptownych ruchów w mierzonej fazie. Filtr Ehlera jest filtrem
FIR, którego współczynniki obliczane są na podstawie ostrych zmian amplitudy w cenie.
Skoro cykle relatywnie powolnie zmieniają parametr w czasie, mierzenie MESA ma
na ogół niewielkie zastosowanie w filtrach nieliniowych. Dlatego, odsyłamy do innych prac,
gdzie są one omówione.
______________
²John F. Ehlers. Rocket Science for Traders. John Wiley & Sons, New York, 2001, Rozdziały 17 i 18.

Średnie ruchome
42
Zapamiętaj
Niezależnie od wzoru, celem średnich ruchomych jest gładzenie wejściowych danych
liczbowych. Ich użycie stanowi kompromis pomiędzy żądanym gładzeniem, a powstałym
opóźnieniem. Poniżej przedstawione są charakterystyki najbardziej popularnych średnich
ruchomych:
SMA
Przesunięcie wynosi (N-1)/2.
Pasmo Przepustowe Okresu wynosi 2*N.
Przesunięcie fazowe jest funkcją liniową szerokości okienka .
Poszczególne okresy ważne dla przeprowadzania transakcji mogą być wycięte za
pomocą symetrycznie ważonych współczynników.
WMA
Przesunięcie wynosi (N-1)/3.
Pasmo Przepustowe Okresu wynosi 2*N.
Daje najlepszy efekt filtrowania dla zadanej wielkości opóźnienia.
EMA
α=1/(Opóźnienie+1).
α=2/(N+1) gdy porównujemy do SMA.
α i (1-α) muszą zawsze dać w sumie jeden.
Pasmo Przepustowe Okresu wynosi -2α/ln(1-α)=4α/(α*(2+α)).
Funkcje impetu
43
Rozdział 5
Funkcje impetu
Faza
odpowiadająca filtrom, stosowana we wskaźnikach technicznych i systemach,
czasami prowadzi do nierealnych wniosków. Średnie ruchome wymagają sumowanych
danych liczbowych i są analogiczne do rachunków całkowych. Impety funkcji wymagają
różnic pomiędzy próbami danych liczbowych i dlatego są analogiczne do rachunku
różniczkowego. Zakładając, że mamy czystą postać fali sinusoidalnej, jej pochodną można
napisać jako:
d[Sin(ωt)]/dt=ωCos(ωt)=ωSin(ωt+90)
Innymi
słowy, rozpiętość zmian czystego cyklu jest dokładnie tym samym cyklem z
90-stopniowym wyprzedzeniem fazowym, pomnożonym przez stałą. Jeśli utworzymy
wyprzedzenie fazowe, to mamy sposób przewidzenia zwrotnego punktu na rynku. Możemy
przedstawić impet w sposób graficzny, tak jak pokazano to na Rys. 5.1, gdzie pokazano impet
czystej sinusoidy.
Rysunek 5.1 Impet wyprzedzający czystą sinusoidę o 90 stopni.
Ponieważ impet jest kierunkiem zmian funkcji, to impet sinusoidy jest maksymalny
przy lewym brzegu rysunku 5.1, gdzie sinusoida przecina zero. Impet maleje wraz ze
wzrostem sinusoidy. Osiąga on zero w punkcie, w którym sinusoida posiada wierzchołek. Kąt
nachylenia sinusoidy w tym punkcie wynosi zero powodując, że impet wynosi zero.
Posuwając się na prawo, kąt nachylenia sinusoidy wzrasta w kierunku ujemnym powodując,
że impet osiąga swoje ujemne maksimum w chwili, gdy sinusoida ponownie przetnie zero.
Impet zaznaczony jest na Rys. 5.1 linią przerywaną. Ta linia przerywana posiada taką
charakterystykę, że osiąga wierzchołek o 90 stopni wcześniej niż sinusoida osiąga swój
wierzchołek i osiąga dno o 90 stopni przed sinusoidą.
Jeśli cena była sinusoidą, to powinniśmy łatwo wyciągnąć wniosek, że impet jest
wskaźnikiem wyprzedzającym. Ale jest to prawdą tylko w przypadku, gdy rynek jest w
Trybie Cyklu. Dlatego też, przed oznaczeniem wskaźnika przydatnego do określenia impetu,

Funkcje impetu
44
najpierw koniecznie należy zidentyfikować tryb rynku. Metody identyfikowania trybu rynku,
omówiono w Rozdziale 11.
Nie jestem w stanie powiedzieć ilu graczy pytało mnie, czy można utworzyć sygnał,
prawidłowo wskazujący przyszły ruch rynku na zaledwie 1 słupek wcześniej. Typowe pytanie
brzmi: ”Czy możesz dokładnie określić impet?”. W większości prostych przypadków impet
jest dokładnie 1-słupkową różnicą ceny. Impet jest jednak zdradliwy, ponieważ może dać
błędny sygnał odwrócenia rynku. Chociaż kusiło to wielu doświadczonych techników,
zaprojektowanie prawidłowego sygnału impetu, tak aby zawsze prawidłowo wskazywał punkt
zwrotny na rynku, jest niemożliwe.
Pierwsze równanie w tym rozdziale pokazuje, że amplituda impetu jest wprost
proporcjonalna do częstotliwości. Amplitudą jest omega (ω), która wynosi 2*π*częstotliwość.
Tego samego zjawiska spodziewamy się na rynku. Jeśli, z jednej strony, weźmiemy prostą
różnicę 2-słupkowego cyklu, który zmienia się pomiędzy +1 i –1, różnica będzie wartością
szczytową, czyli 2. Z drugiej strony, jeśli mamy 50-słupkowy cykl wahający się pomiędzy +1
i –1, to maksimum impetu będzie w przybliżeniu wynosić 2/25=0.08. Nie istnieje impet dla
niezwykle długich cykli, ponieważ zasadniczo nie ma on kierunku zmian, użytecznego dla
transakcji rynkowych. Częstotliwość odpowiadająca prostemu 1-słupkowemu impetowi
pokazana jest na Rys. 5.2.
Rysunek 5.2 Częstotliwość odpowiadająca prostemu impetowi.
Rys. 5.2 pokazuje, że sygnał zerowej częstotliwości jest prawie całkowicie usunięty
przez filtr. Krótsze częstotliwości są usuwane w mniejszym stopniu. Na przykład, sygnał 10-
słupkowego cyklu ma normalizowaną częstotliwość wynoszącą 2/Okres=2/10=0.2 i jest
osłabiony tylko o około 10 dB. Sygnał 4-słupkowego cyklu (2/4=0.5 normalizowanej
częstotliwości) jest osłabiony tylko o około 3 dB. Ponieważ składniki o niskiej częstotliwości
są usuwane a przechodzą składniki o wyższych częstotliwościach, Rys. 5.2 sugeruje, że impet
może być wykorzystywany jako filtr usuwający trend. Jednakże, pasmo przepustowe jest zbyt
wąskie, aby przynosiło praktyczne korzyści. Praktycznie akceptowanym obcięciem
częstotliwości jest punkt połowy mocy lub też inaczej punkt –3 decybelowy. Nawiązując do
tych definicji, tylko cykle o okresie 4-słupkowym lub mniejszym będą przepuszczane przez
filtr. Tworząc szerszy filtr możemy spłaszczyć odpowiedni sygnał. Jednakże, jeśli
poszerzymy filtr, to równocześnie zwiększymy opóźnienie. Podobnie jak w prostej średniej
ruchomej (SMA), opóźnienie N-słupkowego impetu wynosi Opóźnienie=(N-1)/2. A zatem, 1-
słupkowe opóźnienie dla 3-słupkowego impetu wynosi [Opóźnienie=(3-1)/2=2/2=1]. 3-
słupkowy impet obliczany jest z następującego wzoru:
Mo=0.5*Cena-0.5*Cena[2]
Częstotliwość odpowiadająca temu filtrowi pokazana jest na Rys. 5.3.
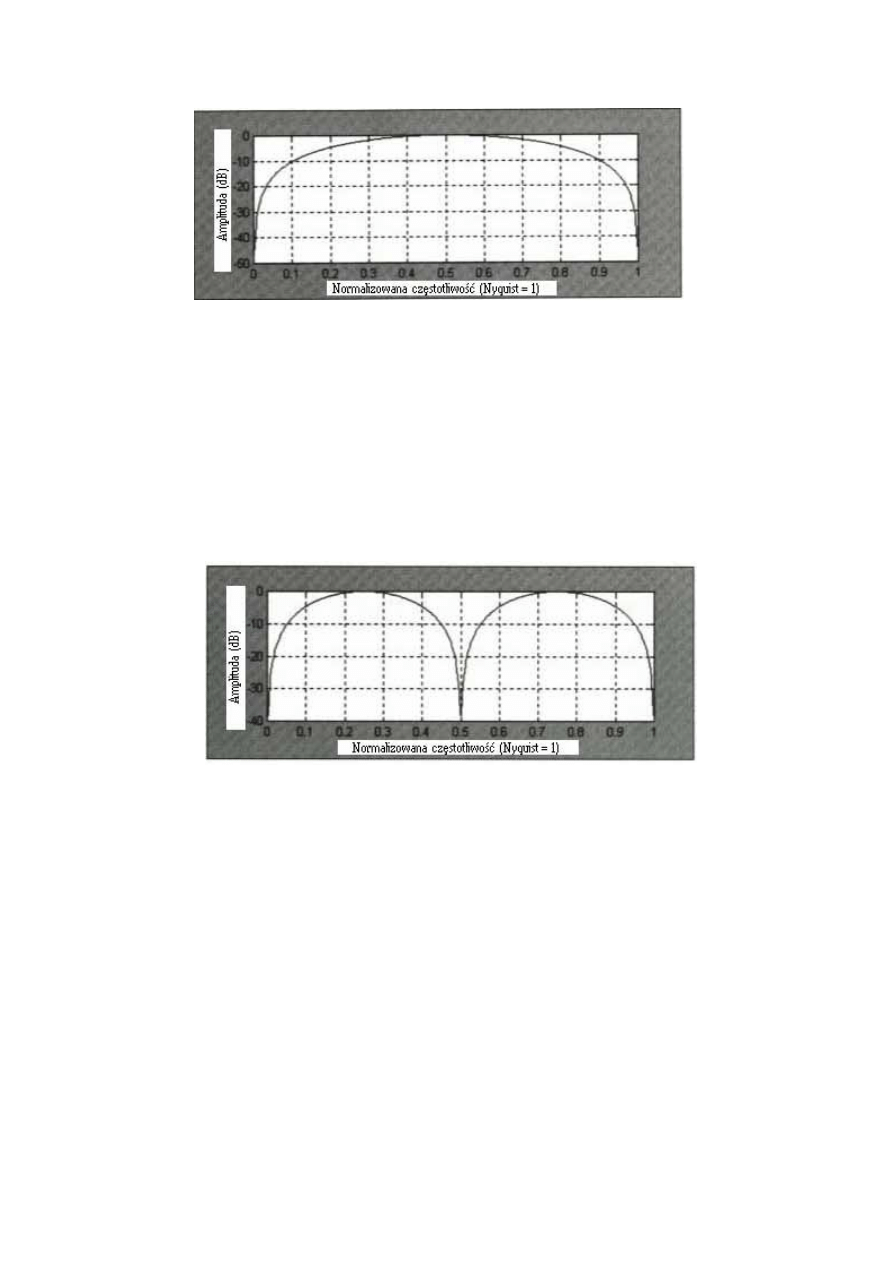
Funkcje impetu
45
Rysunek 5.3 3 słupkowy filtr oddzielający trend powoduje spłaszczenie częstotliwości i usunięcie 2-
słupkowych cykli.
W
przeciwieństwie do prostego impetu filtra na Rys. 5.2, z filtra przedstawionego na
Rys. 5.3 możemy odnieść dwie oczywiste korzyści. Pierwsza korzyść, to częstotliwość
odpowiadająca filtrowi jest bardziej spłaszczona. Na przykład, osłabienie przy
normalizowanej częstotliwości 0.1 (20-słupkowy cykl) wynosi tylko –10 dB zamiast w
przybliżeniu –17 dB, jak na Rys. 5.2. Drugą korzyścią jest to, że 2-słupkowy cykl (o
normalizowanej częstotliwości=1), jest prawie całkowicie wytłumiony. 2-słupkowy filtr jest
zawsze wytłumiony w filtrze impetu jeśli klasa filtra symetrycznego jest nieparzysta.
Jeśli kawałeczek jest dobry, to całość jest znacznie lepsza - być może.
Rysunek 5.4 5-słupkowy impet usuwa 2- i 4-słupkowe składniki cyklu.
Możemy spróbować spłaszczyć odpowiednią częstotliwość, używając 5-słupkowy
impet. Właściwym wzorem jest:
Mo=0.5*Cena-0.5*Cena[4]
Częstotliwość odpowiadająca temu 5-słupkowemu impetowi, pokazana jest na Rys.
5.4. Niestety, wprowadziliśmy inną częstotliwość wycięcia 4-słupkowego cyklu.
Zatrzymajmy się na chwilę i pomyślmy o tym. Widzimy, że to ma sens, ponieważ
odejmowanie danych liczbowych od 4-słupkowego cyklu 4 słupki temu będzie dokładnie
znosić każdy sygnał wejściowy w górnoprzepustowym filtrze.
Wycinanie
częstotliwości przedstawione na Rys. 5.4 może być wyeliminowane przez
utworzenie filtra mającego symetryczne współczynniki. Na przykład, jeśli napiszemy
równanie jako:
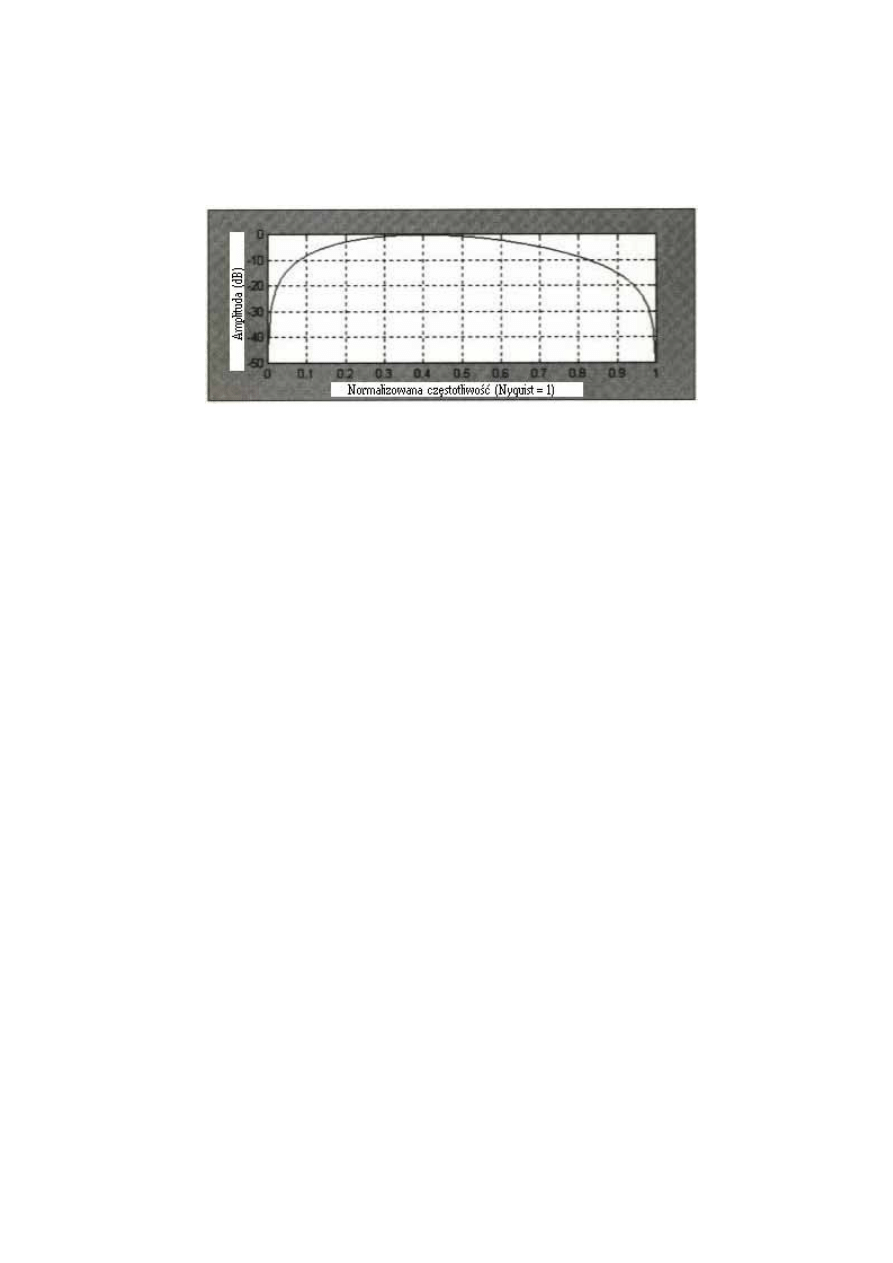
Mo=0.0909*Cena+0.4545*Cena[1]+0-0.4545*Cena[3]-0.0909*Cena[4]
Funkcje impetu
46
Otrzymamy
odpowiednią częstotliwość górnoprzepustową pokazaną na Rysunku 5.5.
Szybko dochodzimy do punktu przewężenia. Na przykład, tłumienie dla 20-słupkowego cyklu
wynosi od –5 dB na Rys. 5.4 do około –8 dB na Rys. 5.5. Dodatkowo, opóźnienie
górnoprzepustowego filtra wynosi 3 słupki.
Rysunek 5.5 Pasmo przepustowe częstotliwości odpowiadające 5-słupkowemu górnoprzepustowemu
filtrowi.
Zaletą 90-stopniowego wyprzedzenia fazowego, dzięki temu zróżnicowaniu, jest
szybki spadek z powodu przesunięcia grupowego. Całkowite opóźnienie fazowe jako funkcję
okresu cyklu, dzięki 3-słupkowemu opóźnieniu, można zapisać jako:
Opóźnienie Fazowe=360*3/Okres-90 stopni
Ustawiając opóźnienie fazowe na zero, możemy przekonać się, że okres krótszego
cyklu nie mającego opóźnienia fazowego, jest okresem 12-słupkowym. Dłuższe cykle będą
mieć wyprzedzenie fazowe. Ponieważ chcemy pracować z okresami cyklu nawet krótszymi
niż 12-słupków, nie ma innego sposobu jak utworzyć zróżnicowany filtr, mający szeroką
przepustowość, ponieważ będzie on wywoływać dodatkowe opóźnienie. W ten sposób
możemy osiągnąć punkt zwrotny tłumienia. Dodatkowe korygowanie amplitudy musi być
realizowane przez pomiar Cyklu Dominującego i następnie zastosowanie go do korygowania
amplitudy. Na szczęście można zmierzyć Cykl Dominujący, a zatem korekcja amplitudy jest
przedsięwzięciem łatwym do wykonania.
Efekt
kompensowania
łatwiej przedstawić na rysunku, wykorzystując dziedzinę czasu
kształtów fal. Rys. 5.6 pokazuje teoretyczne zwężenie kształtu fali, której okres wzrasta od
10-słupkowego cyklu po lewej stronie wykresu, do 45-słupkowego cyklu po prawej stronie
wykresu.
Funkcje impetu
47
Rysunek 5.6 5-słupkowy impet zwężającego się sygnału mającego wzrastający cyklicznie okres.
Wykres utworzony przy pomocy TradeStation 2000i®
Mierzony okres pokazany jest w okienku drugim tego wykresu. 5-słupkowy impet,
którego odpowiednia częstotliwość pokazana jest na Rysunku 5.5, przedstawiony jest w
części 3 Rysunku 5.6. Szczyt amplitudy 10-słupkowego cyklu wynosi około 3.5. Jest to
mniej, niż pełna amplituda wynosząca 5, oryginalnej fali, ale spodziewamy się większego
tłumienia rozpatrywanego Rysunku 5.5. To jest, 10-słupkowy cykl odpowiada
normalizowanej częstotliwości 0.2. Przy tej częstotliwości tłumienie wynosi około 3 dB.
Amplituda dłuższego 40-słupkowego cyklu wynosi około jeden. Tłumienie amplitudy od 5 do
1 wynosi 20*log(0.2)=17 dB. Jest to tyle ile się spodziewamy dla normalizowanej
częstotliwości 0.05 przedstawionej na Rysunku 5.5.
Linię prostą kompensacji można ustalić na podstawie kąta nachylenia tej linii do osi
odciętej, korzystając z dwóch równań z dwiema niewiadomymi. W naszym schemacie
kompensacji chcemy pomnożyć impet przez jeden, gdy okres cyklu wynosi 10 oraz
pomnożyć impet przez 3.5, gdy okres cyklu wynosi 40. Zapisując te równania, otrzymamy:
1=10m+b
3.5=40m+b
Odejmując te równania stronami, otrzymamy:
2.5=30m
Dzieląc obydwie strony tego równania przez 30, otrzymamy wartość kąta nachylenia
m=0.0833. Podstawiając wartość m do pierwszego równania, otrzymamy b=0.167. Tak więc,
nasza amplituda kompensowana impetem, wynosi:
Comp=MO*(0.0833*Cykl Dominujący+0.0167)
Amplituda kompensowana impetem wykreślona jest razem z nieskompensowanym 5-
słupkowym impetem w części 3 Rysunku 5.7.
Funkcje impetu
48
Rysunek 5.7 Amplituda kompensowana impetem dla zawężanego kształtu fali.
Wykres powstał przy pomocy TradeStation 2000i®
Wierzę, że jeśli ma być wykorzystana rzeczywista wartość wskaźnika, to podobne
amplitudy kompensacyjne powinny być używane nie tylko we wskaźnikach impetu, ale
również we wszystkich funkcjach impetu w obrębie wskaźników.
SMA i impet
Interesującym będzie rozpatrzenie impetu SMA. W celu wyjaśnienia tego zagadnienia
załóżmy, że aktualne ceny wynoszą A, B, C, D i E, gdzie A jest ceną ostatnią, a E jest ceną
najstarszą. Przy tym założeniu, 4-słupkowa SMA przedstawia się następująco:
SMA=(A+B+C+D)/4
4-słupkowa SMA jeden słupek temu, wynosi:
SMA[1]=(B+C+D+E)/4
Jeśli utworzymy różnicę tych dwóch średnich ruchomych, otrzymamy:
SMA-SMA[1]=(A-E)/4
Interesującym wnioskiem jest to, że impet 4-słupkowej SMA jest dokładnie taki sam,
jak 4-słupkowy impet w granicach stałego współczynnika uśredniania. Ten wyjątkowy
wniosek można rozciągnąć na każdą szerokość SMA.
Podobnie, SMA czterech impetów prowadzi do tego samego wniosku. Biorąc pod
uwagę te wzajemne relacje, otrzymamy:
[(A-B)+(B-C)+(C-D)+(D-E)]/4=(A-E)/4

Funkcje impetu
49
Wszystko to prowadzi do jednego wniosku: N-słupkowa prosta średnia impetów jest
dokładnie taka sama, jak N-słupkowy impet.
Zapamiętaj
• Impet nie może nigdy wyprzedzić przyszłych wydarzeń.
• Impet jest zawsze słabszy, niż pierwotna funkcja.
• W Trybie Cyklu, impet może tworzyć 90-stopniowe wyprzedzenie fazowe.
• Ulepszanie impetu powoduje szybkie osiągnięcie punktu zwrotnego tłumienia.
• Amplitudę kompensacyjną impetu można ustalić mierząc Cykl Dominujący, a następnie
stosując uzyskany wynik do skorygowania tego okresu cyklu.
• Impet N-słupkowej SMA jest taki sam jak N-słupkowy impet.

Pomiar Spektrum Rynkowego
50
Rozdział 6
Pomiar Spektrum Rynkowego
Wszystkie
główne programy do analizy rynku udostępniają narzędzie o nazwie szybka
transformacja Fouriera. Stosowanie FFT do analizy rynku jest jak cięcie drewna przy pomocy
piły łańcuchowej. Mimo, że piły łańcuchowe są z pewnością efektywne, to jednak nie są one
dobrym narzędziem do tej pracy. W 1986 r. wykorzystując język BASIC dla komputera
Apple II, napisałem jedną z pierwszych FFT, przydatną do przeprowadzania transakcji
giełdowych.¹ Chociaż FFT jest mocnym narzędziem w wielu aplikacjach, do analizy rynku
można wykorzystać lepsze i bardziej precyzyjne narzędzia.
FFT posiada kilka ograniczeń. Jednym z nich jest to, że ustalone przez FFT długości
cyklów, pomnożone przez liczbę całkowitą, muszą dokładnie odpowiadać liczbie danych
liczbowych wziętych do obliczeń. Na przykład, jeśli mamy 64 dane liczbowe, to największa
długość cyklu, który możemy zmierzyć, wynosi 64 słupki. Drugim najdłuższym cyklem jest
cykl 32 słupkowy, bo 64/2=32. Trzecim najdłuższym cyklem jest cykl 16-słupkowy, bo
64/3=21,3. Czwartym najdłuższym cyklem jest cykl 16 słupkowy, bo 64/4=16, i tak dalej.
Tak więc, liczba całkowita powoduje ograniczenie rozkładu możliwych długości cykli.
Tymczasem, rzeczywista długość cyklu może wynosić 14 lub 19 słupków. W powyższym
przykładzie FFT nie dopuszcza takiej możliwości. Innymi słowy, możliwa jest duża
rozbieżność pomiędzy mierzonymi przez FFT długościami cykli, a długościami cykli
występującymi w rzeczywistości na rynku. Dlatego też, taki sposób pomiaru spektrum
rynkowego jest mało przydatny.
Jedynym sposobem zwiększenia przydatności FFT jest zwiększenie ilości danych
liczbowych. Jeśli zwiększymy ilość danych liczbowych do 256, to możliwy rozkład cykli
przedstawia się następująco: 256, 128, 85.3, 64, 51.2, 42.7, 36.6, 32, 28.4, 25.6, 23.3, 21.3,
19.7, 18.3, 17.1, 16, 15.1, 14.2, 13.5, 12.8, itd. Łatwo zauważyć, że w sąsiedztwie 16-
słupkowego cyklu otrzymamy w przybliżeniu rozkład 1-słupkowy, tzn. 18.3, 17.1, 16, 15.1,
14.2 (odstępy między tymi cyklami wynoszą w przybliżeniu 1 słupek). Jednakże, otrzymując
ten rozkład długości cykli, musimy mieć świadomość, że istnieje inna niedogodność. Pomiar
cyklu jest prawidłowy wtedy, gdy dane liczbowe w zbiorze 256 liczb nie zmieniają się. W
naszym przypadku 16-słupkowy cykl musi mieć taką samą amplitudę i fazę przez wszystkie
16 pełnych cykli w zbiorze 256 liczb. Innymi słowy, używając dziennych danych liczbowych,
16-dniowy cykl musi występować przez ponad rok, aby pomiar był prawidłowy. Czy to się
zdarza? Myślę, że nie. Czasami 16-słupkowy cykl występuje przez więcej niż kilka cykli. Jest
on uważnie obserwowany przez każdego gracza na świecie, którzy zniszczą ten cykl,
gremialnie wskakując w niego. Jego potencjalne długoterminowe istnienie jest prawdziwym
powodem jego śmierci. Jedynym sposobem wykonania prawidłowego, wysokorozdzielczego
pomiaru cyklu, jest wybranie takich technik, które wymagają tylko niewielkiej ilości danych
liczbowych. MESA spełnia te wymagania.
___________
¹Perry J. Kaufman. Trading Systems and Methods, trzecia edycja. New York: John Wiley & Sons, 1998, Dodatek
5.
Pomiar Spektrum Rynkowego
51
Nadal
nie
jesteś przekonany? Zademonstrujmy to za pomocą kilku przykładów.
Rysunek 6.1 pokazuje typowe spektrum amplitudy krzywej dzwonowej, przedstawione w
postaci pól o różnych odcieniach szarości. Pomyśl o odcieniach szarości jak o temperaturze.
Kolor biały oznacza ciepło, a kolor czarny oznacza zimno. Kolor biały reprezentujący szczyt,
oznacza prawidłowo zdefiniowany cykl.
Rysunek 6.1 Kolorowa konwersja spektrum amplitudy.
Dolna, szeroka część krzywej dzwonowej mówi nam, że pomiar cyklu w tym punkcie
jest obarczony bardzo dużym błędem. Rysunek 6.2 przedstawia teoretyczną 24-słupkową
sinusoidę, pomierzoną przez FFT dla 64-punktowego zbioru danych.
Rysunek 6.2 64-punktowa FFT teoretycznego 24-słupkowego cyklu.
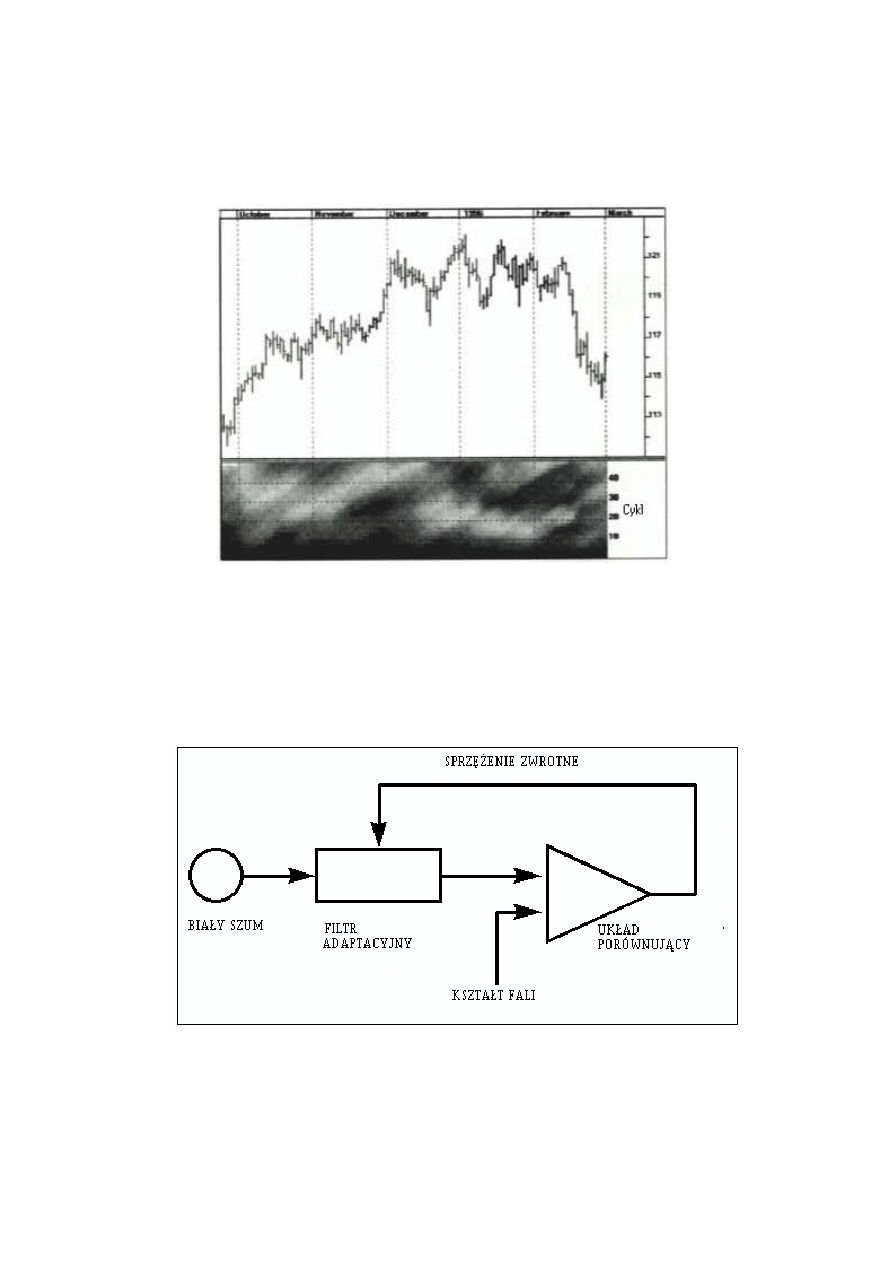
Pomiar Spektrum Rynkowego
52
Ponieważ jest to teoretyczny cykl, bez szumów, pomiar powinien być precyzyjny. Ale
tak nie jest! Spektralny kontur pokazuje, że pomiar jest nieprecyzyjny. Mierzona długość
cyklu może równie łatwo wynosić 15 słupków jak i 30 słupków. Rysunek 6.3 przedstawia 64-
punktowy FFT oparty na rzeczywistych danych rynkowych.
Rysunek 6.3 64-punktowy FFT w marcu 1996 r. dla obligacji.
Tutaj
możemy naocznie przekonać się, że cykl jest ruchomy i niemożliwy do
precyzyjnego ustalenia. Powracając do tych danych później i używając techniki pomiarów
MESA zobaczymy, że system MESA jest znacznie bardziej precyzyjny.
Na Rysunku 6.4 pokazany jest schemat blokowy sposobu pomiaru spektrum za
pomocą MESA.
Rysunek 6.4 Jak MESA mierzy spektrum.
Próba danych liczbowych podawana jest do jednego wejścia układu porównującego.
Próba danych liczbowych może mieć dowolną szerokość – może być nawet mniejsza niż
okres pojedynczego Cyklu Dominującego. Drugim wejściem do układu porównującego płyną
Pomiar Spektrum Rynkowego
53
sygnały z wyjścia filtra cyfrowego. Sygnał, który wprowadzany jest do filtra cyfrowego, jest
białym szumem (zawierający wszystkie częstotliwości i amplitudy). Ten filtr cyfrowy jest
dostrajany przez sygnał wyjściowy układu porównującego aż do chwili, gdy dwa sygnały
wejściowe staną się tak podobne, jak to tylko możliwe. W skrócie, to co musimy zrobić, to
dopasować wzorzec do zakresu czasu.
Gdy raz ustalimy filtr, możemy zrobić z nim kilka rzeczy. Po pierwsze, możemy
połączyć generator podstawy czasu z filtrem wejściowym, aby przedstawić zależność
amplitudy sygnału wyjściowego w postaci zasięgu wstęgi częstotliwości. Tworzy to
spektralną krzywą dzwonową, w przybliżeniu podobną do pokazanej na Rysunku 6.1. To
spektralne przybliżenie w rzeczywistości jest cyklem, zawierającym pierwotne dane liczbowe
w obrębie mierzalnych możliwości filtra cyfrowego. Po drugie, ponieważ filtr cyfrowy oparty
jest na zegarze, możemy nastawić go na przyszłość i przewidzieć przyszłe ceny na podstawie
założenia, że mierzone cykle będą kontynuowane w krótkim czasie.
Pomiar spektrum przy pomocy MESA jest godne uwagi z kilku względów.
Najważniejszym jest, że do pomiaru o wysokiej jakości, wymagana jest tylko niewielka ilość
danych liczbowych. Algorytm MESA jest więc zdolny, z dużym prawdopodobieństwem,
tworzyć pomiar wykorzystując prawie niezmienne dane liczbowe, a takie dane liczbowe są
niezmienne tylko w krótkim okresie czasu. Jak poprzednio wykazano, mierzenie cykli jest
prawidłowe tylko wtedy, gdy dane liczbowe są niezmienne. Po drugie, ponieważ algorytm
MESA wymaga tylko niewielkiej ilości danych, mamy więc możliwość wykorzystania
krótkoterminowego związku logicznego rynku. To jest w pełni logiczne z Równaniem
Telegrafisty rozwiązującym problem Spaceru Pijanego. Oznacza to, że gdy rynek jest w
Trybie Cyklu, mierzone cykle mają możliwość przewidywania przyszłych zachowań rynku.
Po trzecie, tworzone przy pomocy MESA obliczenia spektralne są bardzo przystępne.
Wysoka jakość pomiaru, teoretycznego 24-słupkowego cyklu pokazana jest na Rys. 6.5, gdzie
tylko jeden wartościowy cykl danych wykorzystywany jest w pomiarach.
Rysunek 6.5 Pomiar przy pomocy MESA teoretycznego 24-słupkowego cyklu
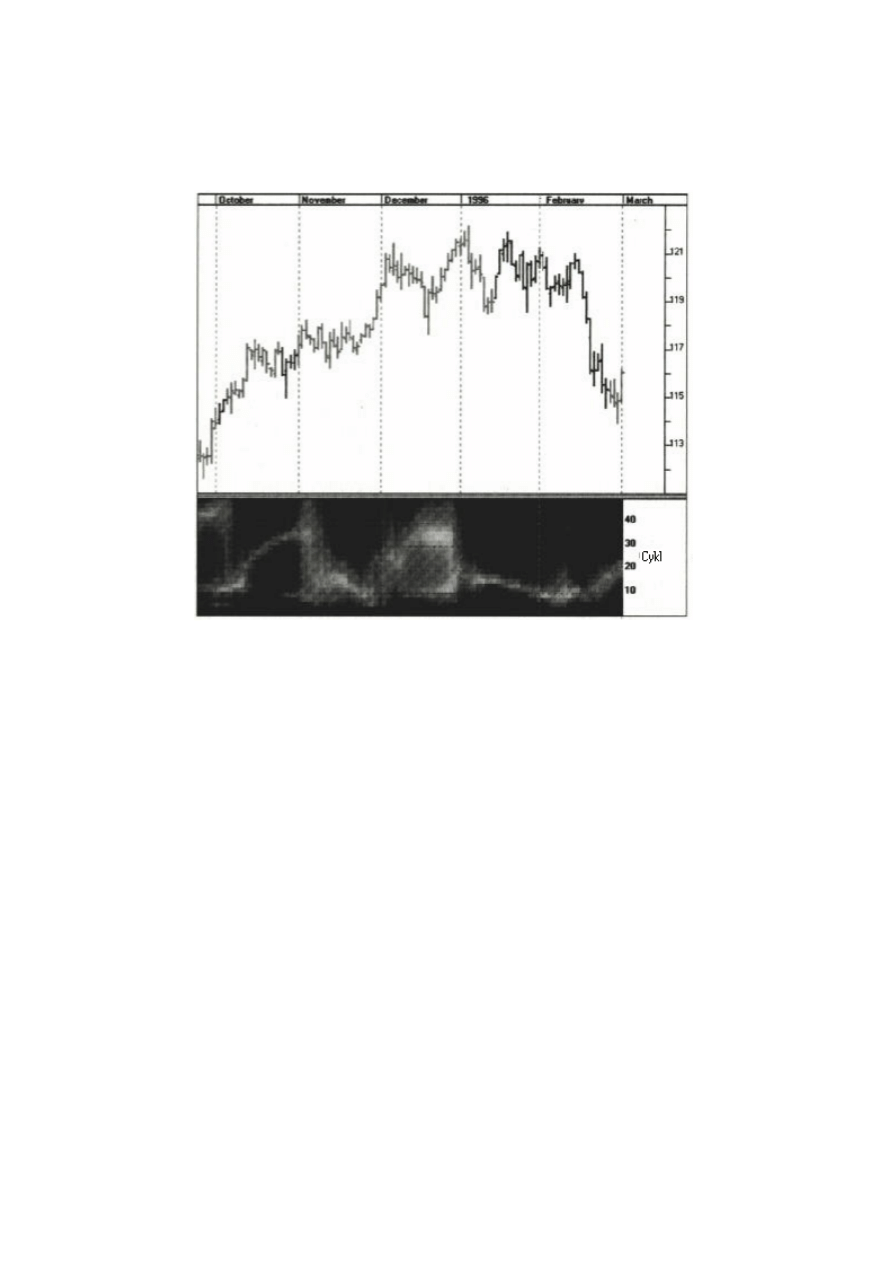
Pomiar Spektrum Rynkowego
54
Tutaj kontur spektralny jest pojedynczą linią oznaczającą, że szczyt tej krzywej
dzwonowej prawidłowo definiuje 24-słupkowy okres. Rysunek 6.6 pokazuje przypływ i
odpływ mierzonych cykli dla obligacji, w marcu 1996 r.
Rysunek 6.6 Spektrum mierzone przez MESA dla obligacji w marcu 1996 r.
Porównując Rysunek 6.3 i Rysunek 6.6 jasno widać istotne różnice pomiędzy MESA a
FFT.
Tabela 6.1 przedstawia różnice pomiędzy pomiarami spektrum za pomocą MESA i
FFT, kolejno je porównując.
Tabela 6.1 Porównanie charakterystyk MESA i FFT
___________________________________________________________________________
Właściwość
FFT
MESA
___________________________________________________________________________
Efekt okienka
Skłębienie okienka spektralnego
Brak efektów okienka, ponieważ
spektralnego
z prawdziwym sygnałem spektrum,
wszystkie opóźnienia są oszacowane
obniża wartość rozwiązania i pozwala
przez funkcję autokorelacji
przenikać błędnym sygnałom przez
okienko
Liniowość
Obliczenia spektralne są liniowe
Obliczenia spektralne nie są liniowe.
spektrum
Relatywna siła amplitud, składnika
częstotliwości, może nie zawsze być
wiarygodna
Szczyt gęstości
Proporcjonalny do P (siła)
Proporcjonalny do (PN)², gdzie N jest
siły
w
klarownej
szerokością danych liczbowych
postaci

Pomiar Spektrum Rynkowego
55
Szerokość
pasma
Proporcjonalna
do
1/N
Proporcjonalna
do
1/(PN)²
w klarownej
postaci
Rozkład dokładności
Proporcjonalny do 1/N
W przybliżeniu proporcjonalny do 1/N²
rozmieszczenia
składników
częstotliwości
Liniowa wykrywalność Spektrum MESA jest zawsze lepsze niż spektrum FFT dla słabych sygnałów,
w spektrum
osadzonych w małej ilości danych liczbowych. Dla większej próby danych
(identyfikacja Cyklu
liczbowych, spektrum MESA jest ulepszone, ponieważ więcej prawidłowych
Dominującego)
wartości funkcji autokorelacji, może być obliczone.
__________________________________________________________________________________________
Zapamiętaj
• Szybka transformacja Fouriera (FFT) nie jest właściwym narzędziem do analizy danych
rynkowych.
• FFT może mierzyć tylko liczbę całkowitych cykli w obrębie obserwowanego okienka.
• Aby otrzymać wysoko przydatne dane, FFT wymaga dużej ilości danych liczbowych.
Jeśli popatrzymy na dane rynkowe w długim okresie czasu, FFT jest bezużyteczna,
ponieważ dane liczbowe nie mogą spełniać wymogu pozostawania relatywnie
niezmiennymi, co jest warunkiem otrzymania prawidłowego pomiaru.
• MESA dopasowuje wzorzec do zakresu czasu. Nieistotne dane liczbowe w krótkim
okienku obserwacyjnym są usuwane.
• Na ogół na rynku występuje w czasie tylko jeden Cykl Dominujący.

Opis MESA
56
Rozdział 7
Opis MESA
Rozdział ten dokładnie opisuje algorytm MESA. Rozdział rozpoczyna się od ogólnych
rozważań na temat dwóch metod obróbki sygnałów cyfrowych, tj. antyaliasing i oddzielanie
trendu. Omówione współczynniki techniczne są następnie stosowane do danych liczbowych,
wykorzystywanych przez MESA oraz do najlepszego ustawienia filtra MESA. Algorytm
MESA jest obszernie omówiony przy pomocy równań i schematów, co jest pomocne w
programowaniu komputera. Jeżeli nie jesteś zainteresowany matematyczną otoczką MESA
lub samodzielnym jego zaprogramowaniem, możesz tylko pobieżnie przejrzeć ten rozdział.
Antyaliasing
Patrząc z perspektywy przetwarzania sygnału, dana liczbowa ceny rynkowej jest próbą
danej. Każdy słupek ceny jest daną liczbową próby. Najbardziej powszechnym rodzajem
próby jest jedna próba na dzień, aczkolwiek rodzaj próby może zmieniać się od pojedynczych
tików cenowych do miesięcznych lub dłuższych. Wskaźnik Nyquista dla tej próby danej –
najkrótszy cykl, który może być rozważany bez antyaliasingu – wynosi 2 słupki na cykl. Jest
to teoretyczna górna granica. W praktyce, przed rozpoczęciem przetwarzania sygnału, krótsze
cykle muszą być wytłumione przez filtrowanie, aby zapobiec wpływowi ich schodkowych
składników na obliczenia.
Inną praktyczną uwagą jest to, że krótsze cykle zmieniają się tak szybko, że obliczenia
nie są stanie uchwycić początkowego lub końcowego punktu cyklicznego ruchu, przed jego
wystąpieniem, w wystarczającym czasie do zawarcia transakcji. Moje doświadczenie mówi,
że najkrótszym cyklem przydatnym do zawierania transakcji, jest cykl 8-słupkowy.
Rozpiętość czasowa od dołka do szczytu, tego 8-słupkowego cyklu, wynosi 4 słupki. Nawet
jeśli spóźnisz się z wejściem tylko o 1 słupek, stracisz około 25 procent ruchu i odpowiednio,
stracisz także około 25 procent ruchu, jeśli spóźnisz się z wyjściem tylko o jeden słupek. W
rezultacie, zyskowność transakcji jest minimalna. Jeśli jesteś spóźniony o 2 słupki, to
najlepiej będzie nie zawierać transakcji.
W rezultacie tych uwag praktycznych, możemy odfiltrować z surowych danych
liczbowych ceny, krótsze cykle i pozostawić zasadniczo niezmienione amplitudy okresów
cykli dłuższych, niż 8 słupków. Najbardziej skutecznym filtrem do wykonania tego jest filtr
eliptyczny. Na Rysunku 7.1 pokazana jest częstotliwość odpowiadająca trzy-słupkowemu
filtrowi eliptycznemu, którego pasmo przepustowe szumu wynosi 0.1 dB oraz pasmo
zaporowe usuwania jest większe niż 30 dB i którego pasmo przepustowe częstotliwości
wynosi 0.22 (w porównaniu do częstotliwości Nyquista). Jak pokazano na rysunku, okresy
cykli dłuższych niż 8 słupków (częstotliwości mniejsze niż 0.25) są przepuszczane bez
tłumienia, podczas gdy 2- i 4-słupkowe cykle są całkowicie wycinane.
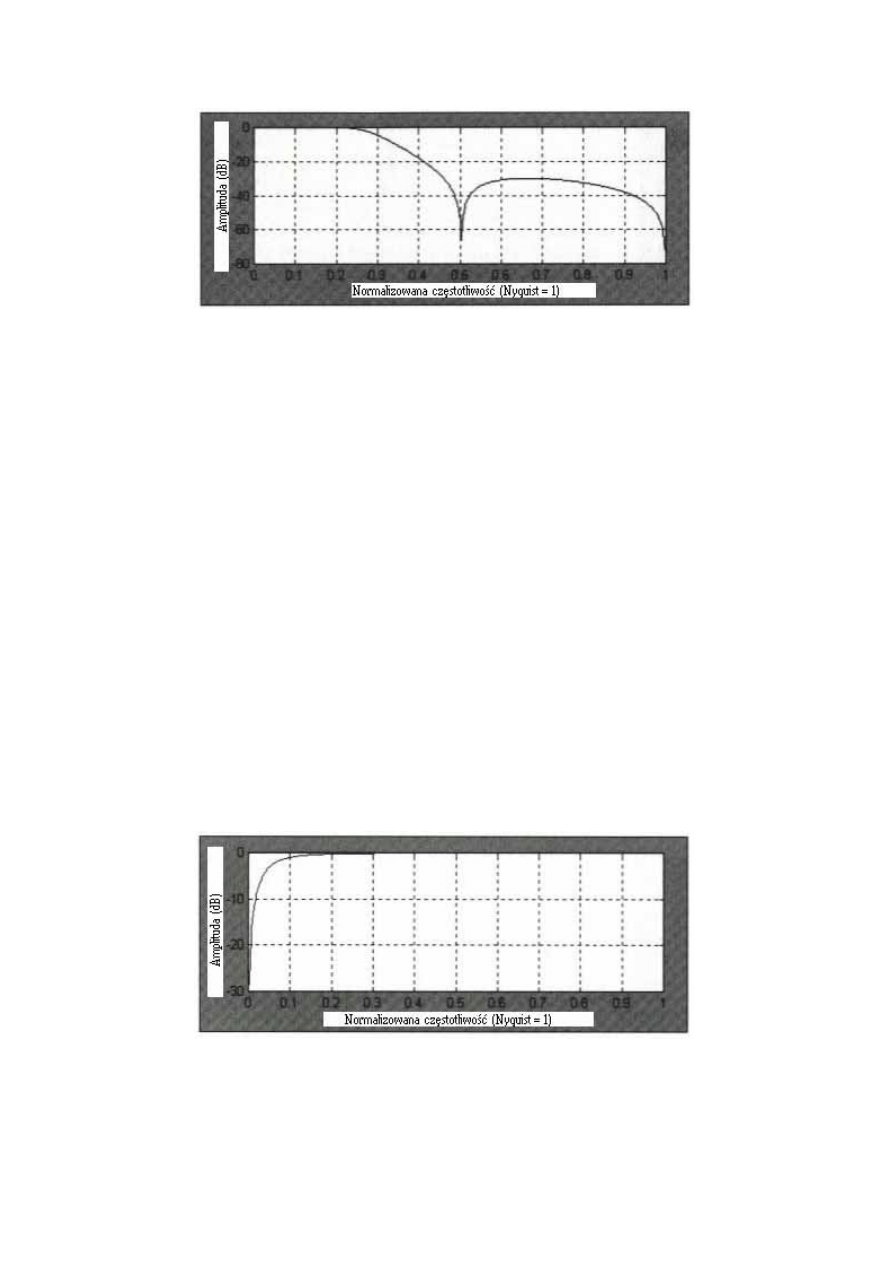
Opis MESA
57
Rysunek 7.1 Częstotliwość odpowiadająca eliptycznemu filtrowi antyaliasingowemu.
W
języku EasyLanguage, zapis Funkcja[N] oznacza wartość tej Funkcji „N” słupków
temu. Używając tego zapisu, równanie eliptycznego filtru przedstawia się następująco:
Filt=0.0774*Cena + 0.0778*Cena[1] + 0.0778*Cena[2] + 0.0774*Cena[3] + 1.4847*Filt[1]
-1.0668*Filt[2] + 0.2698*Filt[3]
Oddzielanie trendu
Teoretyczne cykle wahają się plus minus dookoła średniej zero. Finansowe dane
liczbowe cen nie wynoszą średnio zero i do obliczeń cykli należy je przedtem oddzielić od
trendu. Jeśli nie oddzieliliśmy trendu od danych liczbowych, to powinniśmy umieścić ciężar
usuwania składników o niskiej częstotliwości wyłącznie na algorytmie MESA. Chociaż jest to
możliwe, to jednak nie jest wskazane, ponieważ powoduje błąd obliczeniowy z powodu
wykorzystywania w obliczeniach małych różnic dużych liczb. Oddzielanie trendu zasadniczo
oznacza usuwanie z danych liczbowych składników o bardzo niskiej częstotliwości. Można to
wykonać na kilka sposobów, ale ponieważ interesujemy się zakresem częstotliwości, to
rozsądniejszym jest usunąć składnik o zerowej częstotliwości, używając filtr. Taki filtr
nazywany jest filtrem górnoprzepustowym.
Rozsądny filtr górnoprzepustowy wykorzystywany dla naszych celów oddzielania
trendu z danych liczbowych przed wykonaniem obliczeń MESA, pokazany jest na Rysunku
7.2.
Rysunek 7.2 Częstotliwość odpowiadająca filtrowi górnoprzepustowemu.

Opis MESA
58
Pamiętaj, że częstotliwości większe niż 0.05 (40-słupkowe okresy cykli)
przepuszczane są w zasadzie bez tłumienia. Równanie górnoprzepustowego filtra pokazanego
na Rysunku 7.2, przedstawia się następująco:
Detrend=0.95*Cena-0.95*Cena[1]+0.9*Detrend[1]
Możemy połączyć to z filtrem antyaliasingowym, otrzymując równanie:
Detrend=0.95*Filt-0.95*Filt[1]+0.9*Detrend[1]
A
zatem,
połączone filtrowanie tłumi te składniki, które znajdują się poza
wyznaczonym przedziałem rozpiętości (wyznaczony przedział to cykle od 8-słupków do 40
słupków), podczas gdy składniki w obrębie tego przedziału w zasadzie przepuszczane są bez
tłumienia. Tak przefiltrowane dane liczbowe wykorzystywane są przez algorytm MESA.
Szerokość danych liczbowych
Przewagą stosowania MESA jest możliwość otrzymania spektrum o wysokiej
rozdzielczości przy wykorzystaniu minimalnej ilości danych liczbowych. Prawdą jest także,
że rozdzielczość wzrasta proporcjonalnie do kwadratu liczby wykorzystywanych danych
liczbowych. Rozwiązanie, które przedstawi MESA dla 16-słupkowego cyklu dziennych
danych liczbowych jest w przybliżeniu takie same jak rozwiązanie, które może być otrzymane
wykorzystując FFT i dzienne dane liczbowe z całego roku. Chociaż dla większej ilości
danych liczbowych uzyskiwana jest większa rozdzielczość to prawdopodobieństwo, że te
dane liczbowe w obserwowanym okresie będą pozostawać niezmienne, maleje. Żaden pomiar
nie jest prawidłowy, jeśli dane liczbowe nie są dostatecznie niezmienne. Tak więc, dylemat
polega na wybraniu prawidłowej szerokości danych liczbowych.
Moje
doświadczenie jest takie, że sensowna rozdzielczość może być otrzymana przy
wykorzystaniu tylko jednej szerokości cyklu danych liczbowych. Ponieważ okres cyklu
zmienia się relatywnie wolno, od jednej próby danych liczbowych do następnej próby, to
prostym powtarzalnym rozwiązaniem jest stosowanie poprzednio zmierzonej szerokości
cyklu jako szerokości danych liczbowych stosowanych do aktualnych obliczeń. Minimalizuje
to ukrywanie krótszych cykli i zwiększa dokładność pomiaru dłuższych cykli tak długo, jak
założenie, że okres cyklu zmienia się powoli jest prawdziwe.
Rozmiar filtra
Jedną z szeroko znanych słabości algorytmu MESA jest to, że naraża on na fałszywe
odpowiedzi. Ta fałszywa identyfikacja cykli pochodzi z filtra mającego przesadne ustawienie,
próbujące maksymalizować rozdzielczość. Jeśli istnieje tylko jeden cykl w danych
liczbowych, filtr MESA powinien posiadać tylko dwa słupki w swoim kształcie spektralnym.
Przesadnie ustawiony filtr próbuje dopasować najlepsze rozwiązanie, odpowiadające
parametrom filtra. W takim przypadku, niektóre słupki mogą być błędnie położone, dając
fałszywy sygnał.
Z
mojego
doświadczenia wynika, że błędne sygnały mogą być zredukowane do
akceptowalnego poziomu, jeśli filtr ustawiony jest na 40 procent szerokości danych
liczbowych. Jest to reguła, którą stosuję w moich pracach.
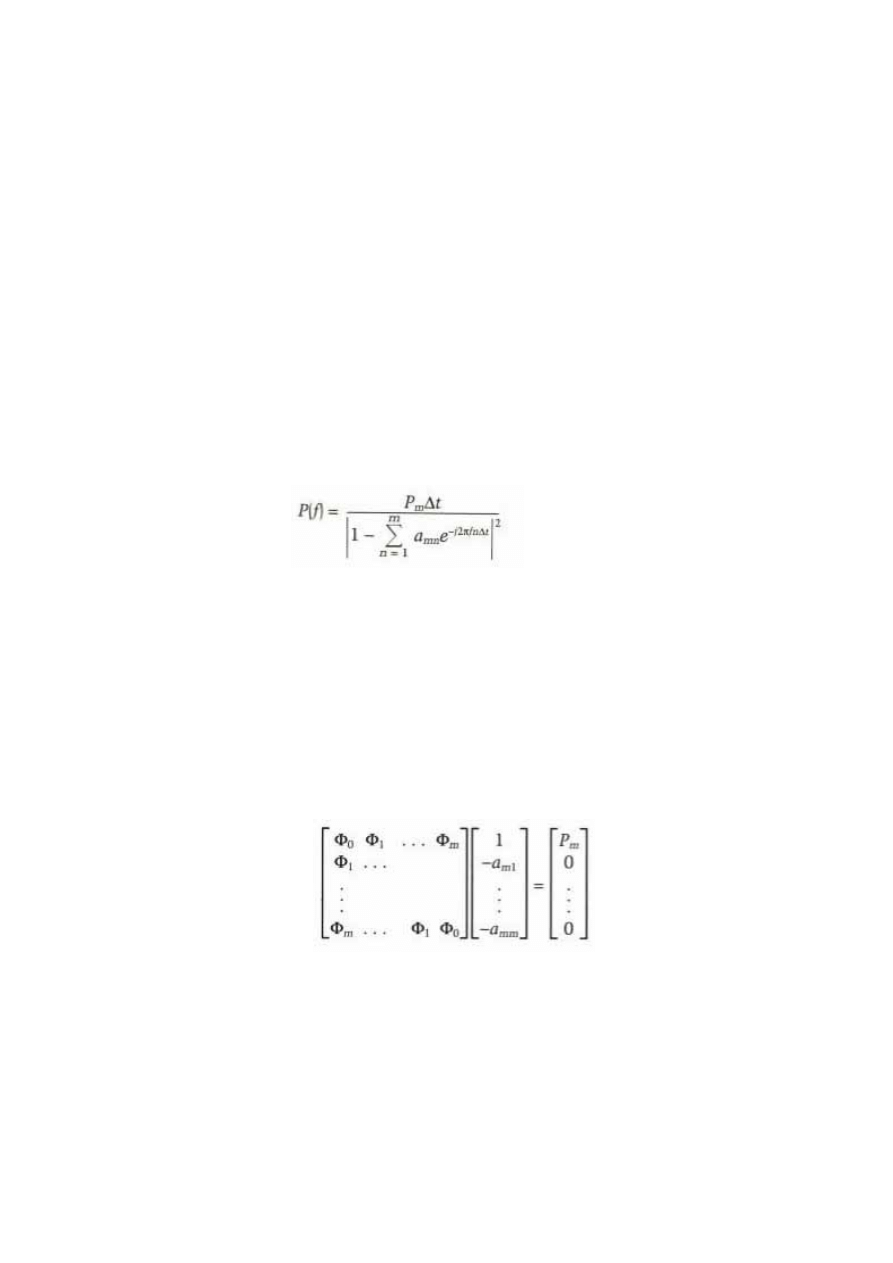
Opis MESA
59
Algorytm MESA
Widmo mocy MESA jest równoważne modelowi najmniejszych kwadratów
wszystkich słupków analizowanych danych liczbowych. Model wszystkich słupków znany
jest jako model autoregresywny. Model wszystkich słupków oznacza, że rozwiązanie zawiera
wielomian tylko w mianowniku rozwiązania, a współczynniki zerowe tego wielomianu są
słupkami rozwiązania. Istnieje podobne rozwiązanie zwane AutoRegressive Moving Average
(ARMA), która dodatkowo uwzględnia zera w liczniku rozwiązania. Z mojego doświadczenia
wynika, że ARMA bardziej naraża na fałszywe sygnały niż MESA, ponieważ zera w liczniku
mogą być prawie takie same jak zera w mianowniku w rezultacie czego, te małe różnice
powodują powstawanie dodatkowych błędnych sygnałów.
Istnieje wiele doskonałych opisów współczesnych analiz spektralnych.
1)2)3)
Chociaż
matematyka i programowanie nie interesuje większości graczy, wielu czytelników
zainteresowanych jest szczegółami dotyczącymi MESA. Pozostała część tego rozdziału
zawiera szczegółowy opis obliczeń spektralnych MESA. Poniższe rozwiązanie opisuje sposób
postępowania Andersena.
4)
Siła spektrum MESA P(f) obliczana jest na podstawie wzoru:
Częstotliwość f jest limitowana przez rozpiętości Nyquista f<(1/2∆t). W danych
rynkowych mamy do czynienia z jedną próbą na słupek. Na przykład, dane liczbowe ceny
mogą być danymi dziennymi. Oznacza to, że najwyższa częstotliwość, jaką możemy
rozważyć, wynosi 0.5 cyklu na słupek lub 2 słupki na cykl. Rozważając niedostatki filtra
antyaliasingowego, najkrótszymi okresami cykli jakie możemy wziąć pod uwagę w
rzeczywistości rynkowej, są cykle o rozpiętości 6 do 8 słupków. Tak więc, jeśli stosujemy
dzienne dane liczbowe, to jest mało prawdopodobne, że możemy realnie zidentyfikować
cykle tygodniowe. Chcąc zidentyfikować takie krótkie cykle, powinniśmy zwiększyć
rozpiętość próby, stosując dane godzinowe.
P
m
i współczynniki a
mn
określane są przez poniższe równanie macierzy:
___________________
1) Modern Spektrum Analysis, wydana przez Donald G. Childers, John Wiley & Sons, New York, 1978.
2) Modern Spektrum Analysis II, wydana przez Stanislaw B. Kesler, John Wiley & Sons, New York, 1986.
3) Digital Spectral Analysis with Applications, S. Lawrence Marple, Jr., Prentice Hall, Engewood Cliffs, NJ,
1987.
4) N. Andersen. „On the calculation of filter coefficients for maximum entropy spectral analysis.” Geophysics,
vol. 39. No. 1, February 1974, pp. 69-72.
Opis MESA
60
Φ
i
jest w autokorelacji z opóźnieniem i, tak więc P
m
jest sygnałem wyjściowym mocy
m+1 dalekiej prognozy błędu filtra (1, -a
m1
,...,-a
mm
). Dla m=0 (zerowe opóźnienie), P
o
jest
obliczane ze wzoru:
Równanie macierzy rozwiązywane jest za pomocą stopniowego wzrostu rozmiaru
macierzy o jeden oraz za pomocą określenia (m+2) niewiadomych jako znane funkcje
autokorelacji. Niewiadome uwzględniają m współczynników filtra, następną wartość funkcji
autokorelacji i błąd mocy. Istnieje tylko (m+1) równań w równaniu macierzy, więc niezbędna
jest dodatkowa zależność. Burg sugeruje, że tą dodatkową zależnością jest minimalizowany
całkowity błąd mocy (suma przyszłych i przeszłych błędów mocy). Na przykład, przyszłe i
przeszłe błędy mocy dla dwupunktowej prognozy filtra (1, a
11
) wynoszą:
Minimalizując e²
f
+e²
b
w stosunku do a
11
, otrzymamy:
Średni sygnał wyjściowy mocy m+1 dalekiej prognozy błędu filtra jest
minimalizowany w stosunku do a
mm
, jako:
Aby
uaktualnić filtr dodając nowy współczynnik, wymagane jest obliczenie starych
współczynników, za pomocą poniższego wzoru:
a
mk
=a
(m-1)k
-a(
m-1)(m-k)
Równanie to jest rezultatem rekursji Levinsona w odniesieniu do równania macierzy.
Uaktualniony błąd mocy wynosi:
P
m
=P
(m-1)*
(1-a
mm
²)

Opis MESA
61
Jeśli ustawimy a
mo
=-1 i a
mk
=0 dla k>m, możemy ponownie napisać przeszłe i przyszłe
równanie mocy, jako:
Podstawiając rekursję Levinsona do tych równań, otrzymamy:
gdzie zdefiniowane serie wynoszą:
Inne
postacie
b
mt
i b’
mt
otrzymywane są przez zmianę wskaźnika k na m-k i
odwrócenie kolejności sumowania. Minimalizując sumę przyszłego błędu mocy i przeszłego
błędu mocy w stosunku do a
mm
, otrzymamy:
Użytecznymi wzorami rekursywnymi dla danych b
mt
i b’
mt
są:
Tak
więc, serie b
mt
i b’
mt
mogą być tworzone z ich poprzednich wartości jako m
zwiększone o 1. Początkowymi wartościami są:
Opis MESA
62
Następnie b
mt
i b’
mt
mogą być obliczone jako m zwiększone od 1 do planowanej
szerokości filtra M.
Rozwiązaniem równania macierzy jest proces samouzgadniania, na podstawie rekursji
od m=1 do M. Rysunek 7.3 pokazuje schemat blokowy dla procedury rekursywnej, tak więc
jeśli zechcesz, możesz obliczyć współczynniki filtra posługując się językiem komputerowym.
Używając języka komputerowego, zmieniono b
mt
na b1 oraz b’
mt
na b2. Tablica danych aa(t)
czasowo przechowuje współczynniki filtra przed ich uaktualnieniem do tablicy danych a(t).
Rysunek 7.3 Proces rekursywny obliczania współczynników filtra MESA.
Możesz zastosować schemat blokowy Rysunku 7.3 do pomiaru, za pomocą MESA,
Cyklu Dominującego. Alternatywnie, możesz zastosować język programowania
EasyLanguage, stosując Dynamic Linked Library (DLL). Ponieważ obliczenia są bardzo
intensywne, zastosowałem DLL do obliczeń MESA, dzięki czemu obliczenia biegną znacznie
szybciej. Kod EasyLanguage na Rysunku 7.4 jest szablonem zwanym DLL i kreśli Cykl
Dominujący. Kod ten jest wykorzystywany jako szablon w innych obliczeniach, w pozostałej
części tej książki. Okienko 1 wprowadzania wartości pozwala dynamicznie ustawiać
szerokość danych. Szerokość okienka może być ustawiona ręcznie do wartości pomiędzy 8 i
50, jeśli nie chcesz uaktywnić elementu, który ustawia szerokość danych liczbowych.

Opis MESA
63
inputs: Price(Close),
Window(1),
RegCode(„LPJDPDTBHB”);
vars: dc(0);
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
int,float,float,float,lpfloat;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
Plot1(dc,”dc”);
Rysunek 7.4 Kod EasyLanguage obliczający MESA DLL i kreślący Cykl Dominujący.
Przybliżenie spektralne MESA obliczane jest ze współczynników filtra, stosownie do
pierwotnego równania.
Ponieważ interesuje nas tylko względne spektrum amplitud, możemy oznaczyć licznik
wartością jednostkową. Kwadraty amplitudy w mianowniku obliczane są mnożąc mianownik
przez jego sprzężenie zespolone. Ja wolę kreślić liniowe spektrum w kategoriach okresów
cykli, ponieważ to jest łatwiejsze do interpretacji przez większość graczy. Dla każdego słupka
serii ceny, spektrum obliczane jest w granicach rozpiętości okresów cykli od minimum
okresu, dzięki filtrowi antyaliasingowemu, do rozsądnego maksimum okresu. Maksimum
okresów większe niż 50 są obarczone poważnym błędem, ponieważ ich wzajemne związki z
fazą są trudne do stwierdzenia w zakresie większych rozpiętości. Fragment kodu do
obliczania spektrum MESA przedstawia Rysunek 7.5. Rzeczywista część sprzężenia
zespolonego w mianowniku wynosi (1+CT), która jest rezultatem definicji Andersena
współczynników filtra, jako –a
mn
.

Opis MESA
64
For Period = 6 To 50
CT
=
0
ST
=
0
For m = 1 To M
CT
=
CT
+
A(m)*Cos(TwoPi*m/Period)
ST
=
ST
+
A(m)*Sin(TwoPi*m/Period)
Next
m
Spectrum(Period)
=
1/((1+CT)*(1+CT)+ST*ST))
Next
Period
Rysunek 7.5 Fragment kodu obliczającego spektrum MESA.
Zapamiętaj
• Równanie doskonałego filtra antyaliasingowego, przedstawia się następująco:
Filt=0.0774*Cena + 0.0778*Cena[1] + 0.0778*Cena[2] + 0.0774*Cena[3] +
1.4847*Filt[1] -1.0668*Filt[2] + 0.2698*Filt[3]
• Równanie filtra usuwającego trend, przedstawia się następująco:
Detrend=0.95*Cena-0.95*Cena[1]+0.9*Detrend[1]
• Dobrą szerokością danych liczbowych, stosowanych do obliczeń MESA, jest poprzednio
obliczony okres cyklu.
• Dobrym ustawieniem filtra MESA jest 40% szerokości danych liczbowych.

Wskaźnik Sinewave
65
Rozdział 8
Wskaźnik Sinewave
Wskaźnik Sinewave jest wyjątkowy w swojej możliwości przewidzenia punktów
zwrotnych cyklu. Jego wyjątkowość polega na tym, że na ogół nie generuje sygnałów, gdy
rynek jest w trybie trendu, co zmniejsza ryzyko zawarcia błędnej transakcji. Dodatkowo,
wskaźnik Sinewave posiada mniej zakłóceń niż pierwotna funkcja ceny, ponieważ wąskie
pasmo filtrowania stosowane jest do pomiaru Cyklu Dominującego a nie do funkcji impetu,
które zawierają więcej zakłóceń. Istnienie wskaźnika Sinewave jest możliwe, ponieważ
dysponujemy pomiarem okresu Cyklu Dominującego.
W Rozdziale 4 wykazaliśmy, że wszystkie średnie ruchome posiadają opóźnienie. W
Rozdziale 5 wykazaliśmy, że funkcje impetu nigdy nie mogą wyprzedzić zmian pierwotnego
kształtu fali. Wszystkie przyczynowe filtry opierają się na kombinacji średnich ruchomych i
funkcji impetu. Tak więc, przyczynowe filtry nigdy nie mogą przewidzieć przyszłych
zdarzeń. Za pomocą wskaźnika Sinewave tworzymy nieprzyczynowy filtr – filtr, który może
przewidzieć zwrotny punkt cykli rynkowych. Przewidywanie punktów zwrotnych cykli jest
główną zaletą wskaźnika Sinewave w porównaniu do innych oscylatorów, takich jak Relative
Strength Index (RSI) i Stochastic, które muszą czekać na potwierdzenie.
Stosując algorytm MESA, możemy mierzyć okres dominującego cyklu rynkowego dla
każdego słupka w serii danych liczbowych. Jednakże, ten pomiar nie powie nam gdzie
znajdujemy się w obrębie cyklu. Aby zlokalizować pozycję cyklu musimy zmierzyć fazę
Cyklu Dominującego. Znając fazę Cyklu Dominującego, możemy zastosować sinus
mierzonej fazy do utworzenia wskaźnika oscylacyjnego. Możemy także kompensować każde
opóźnienie powstałe w wyniku procesu pomiaru fazy. W tym celu możemy łatwo dodać 45
stopni do mierzonej fazy aby utworzyć symulowaną falę wyprzedzającą. Jeśli rynek jest w
Trybie Cyklu, możemy przyśpieszyć fazę zakładając, że mierzony cykl istniejący w
nieodległej przeszłości będzie istnieć w bliskiej przyszłości. Zwiększając fazę o 45 stopni i
biorąc sinus zwiększonego kąta fazowego, otrzymamy oscylator w kształcie fali, który
wyprzedza pierwotną sinusoidę o jedną ósmą cyklu. Jednakże, te dwie sinusoidy przecinają
się o jedną szesnastą cyklu przed szczytem punktu zwrotnego cyklu i przed dołkiem punktu
zwrotnego. Dla 16-słupkowego Cyklu Dominującego daje to idealnie 1 słupek wyprzedzenia
ostrzegawczego bezwzględnego punktu zwrotnego Cyklu Dominującego. Dla 48-słupkowego
cyklu wyprzedzenie wynosi 3 słupki. Dla 8-słupkowego Cyklu Dominującego wyprzedzenie
wynosi teoretycznie tylko 0.5 słupka.
Nasz uproszczony model rynku składa się z Trybu Cyklu i Trybu Trendu. Z pewnością
są dodatkowe składniki, jednakże w tym uproszczonym modelu pomijamy je. Najwyższą
amplitudę cyklu nazywamy Cyklem Dominującym. Opierając się na doświadczeniu
przyjmujemy robocze założenie, że obecny jest pojedynczy Cykl Dominujący. Ale jeśli rynek
zmierza w kierunku czystego trendu, nie istnieje żaden cykl. W takim przypadku dwie fale
sinusoidalne wskaźnika Sinewave nie mogą się przeciąć. Jeśli dwie sinusoidy nie mogą się
przeciąć, wskaźnik Sinewave nie tworzy cyklicznych sygnałów kupna lub sprzedaży. To
unikanie fałszywych sygnałów jest zauważalną przewagą w porównaniu do tradycyjnych
oscylatorów. W praktyce, faza nie znika nagle. Podczas zaniku fazy kształt wskaźnika staje
się zauważalnie różny od typowej fali sinusoidalnej, która powstaje gdy rynek jest cykliczny.
Sinusoidy są poszarpane, nieregularne. Przypadkowe przecięcia linii wskaźnika Sinewave,

Wskaźnik Sinewave
66
gdy rynek jest w Trybie Trendu powstaje z powodu „rozwierania” się kąta fazowego. Ale w
takich przypadkach linie wskaźnika Sinewave nie są sinusoidalne w sąsiedztwie przecięcia.
Dlatego też, te przypadkowe złe sygnały przecięcia są łatwe do zidentyfikowania.
Na podstawie tych obserwacji, faza kształtu fali może być wskaźnikiem dla zawierania
transakcji.
Wskaźnik Sinewave jest częścią pakietu komercyjnego wskaźnika MESA. Kod
EasyLanguage do pomiaru Cyklu Dominującego przedstawiony jest na Rysunku 8.1 i jeśli
zechcesz, możesz wprowadzić własne zmiany w tym wskaźniku.
inputs: Price(Close),
Window(1),
RegCode(„LPJDPDTBHB”);
vars:
dc(0)
SmoothPrice(0),
DCPeriod(0),
RealPart(0),
ImagPart(0),
count(0),
DCPhase(0);
DefineDllFunc: „c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
Int,float,float,float,lpfloat;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,
”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
{Compute Dominant Cycle Phase}
SmoothPrice = (4*Price + 3*Price[1] + 2*Price[2] +
Price[3])/10;
DCPeriod = IntPortion(dc + .5);
RealPart = 0;
ImagPart = 0;
For count = 0 To DCPeriod – 1 begin
RealPart = RealPart + Cosine(360*count/
DCPeriod)*(SmoothPrice[count]);
ImagPart = ImagPart + Sine(360*count /
DCPeriod)*(SmoothPrice[count]);
End;
If AbsValue(RealPart) >0.001 then
DCPhase = Arctangent(ImagPart / RealPart);
Rysunek 8.1 Obliczanie fazy Cyklu Dominującego.

Wskaźnik Sinewave
67
If AbsValue(RealPart) <= 0.001 then
DCPhase
=
90*Sign(ImagPart);
DCPhase = DCPhase + 90;
If RealPart < 0 then DCPhase = DCPhase + 180;
{Compensate for one bar lag of the Weighted
Moving
Average}
If DC <> 0 then DCPhase = DCPhase + 360 / dc;
{Don’t let phase exceed 360 degrees in a cycle}
If DCPhase > 360 then DCPhase = DCPhase – 360;
{Force phase wrap at 315 degrees to avoid full scale
wrap at 0-360 boundary}
If DCPhase > 315 then DCPhase = DCPhase – 360;
Plot1(DCPhase,
„Phase”);
Rysunek 8.1 Ciąg dalszy.
Początkowa część kodu obliczająca Cykl Dominujący (zmienna dc) stosowana jest w
programie komercyjnym MESA dla Tradestation 2000i oraz Tradestation 6.0. Czytelnik może
utworzyć swój własny kod obliczania dc na podstawie opisu, przedstawionego w Rozdziale 7.
Część kodu dotycząca obliczania fazy, rozpoczyna się od linii komentarza w nawiasie.
Pierwszym krokiem jest gładzenie danych liczbowych. Wszystkie składniki posiadające okres
cyklu krótszy niż 6-słupków nie są pożądane i powinny być usunięte przed rozpoczęciem
obliczeń. Ponieważ jesteśmy bardzo wyczuleni na opóźnienie w naszych obliczeniach,
usuwane są one przy pomocy 4-słupkowej ważonej średniej ruchomej (WMA). WMA
wprowadza 1-słupkowe opóźnienie, które zostanie później usunięte przez kompensację
obliczeń. Następnie wygładzona dana liczbowa jest mnożona przez rzeczywisty (cosinus)
składnik Cyklu Dominującego i niezależnie przez urojony (sinus) składnik Cyklu
Dominującego. Wyniki są sumowane dla całego jednego Cyklu Dominującego. Kąt fazowy
obliczany jest jako arctang rozpiętości urojonej części do części rzeczywistej. Faza wzrasta od
lewej do prawej strony wykresu. Niezbędne jest 90 stopniowe przesunięcie, tak więc sinus
kąta fazowego wynosi zero dla wartości fazy wynoszącej zero. Następnie musimy usunąć 1-
słupkowe opóźnienie powstałe w wyniku gładzenia ceny. Wykonujemy to dodając fazę
odpowiadającą 1-słupkowemu opóźnieniu gładzonego Cyklu Dominującego.
W
końcu, faza zakłócająca usuwana jest w tych przypadkach, w których część urojona
jest mniejsza od zera, otrzymując 360 stopniową reprezentację fazy. Normalnie myślimy o
fazie jak o zmieniającej się od zera do 360 stopni i powtarzającej to samo w następnym cyklu.
Jednakże stosujemy powtarzanie cyklu przy 315 stopniach, ponieważ faza ma tendencję do
przyjmowania wartości około zera stopni, gdy rynek jest w trendzie malejącym. Jeśli faza
wynosi około 360 stopni, wahnięcie od dna wykresu do szczytu powinno być mniejsze, niż
rozpiętość ekranu. Nie wpływa to na wskaźnik Sinewave, ale wpływa na wyświetlanie fazy.
Kreśląc sinus mierzonego kąta fazowego, otrzymujemy wskaźnik Sinewave.
Otrzymamy oscylator, który zawsze waha się pomiędzy ograniczeniami –1 i +1.
Wzmacniamy użyteczność tego wskaźnika kreśląc sinus kąta fazowego przesuniętego o 45
stopni. W rezultacie otrzymujemy dwie linie, tak jak na Rysunku 8.2.
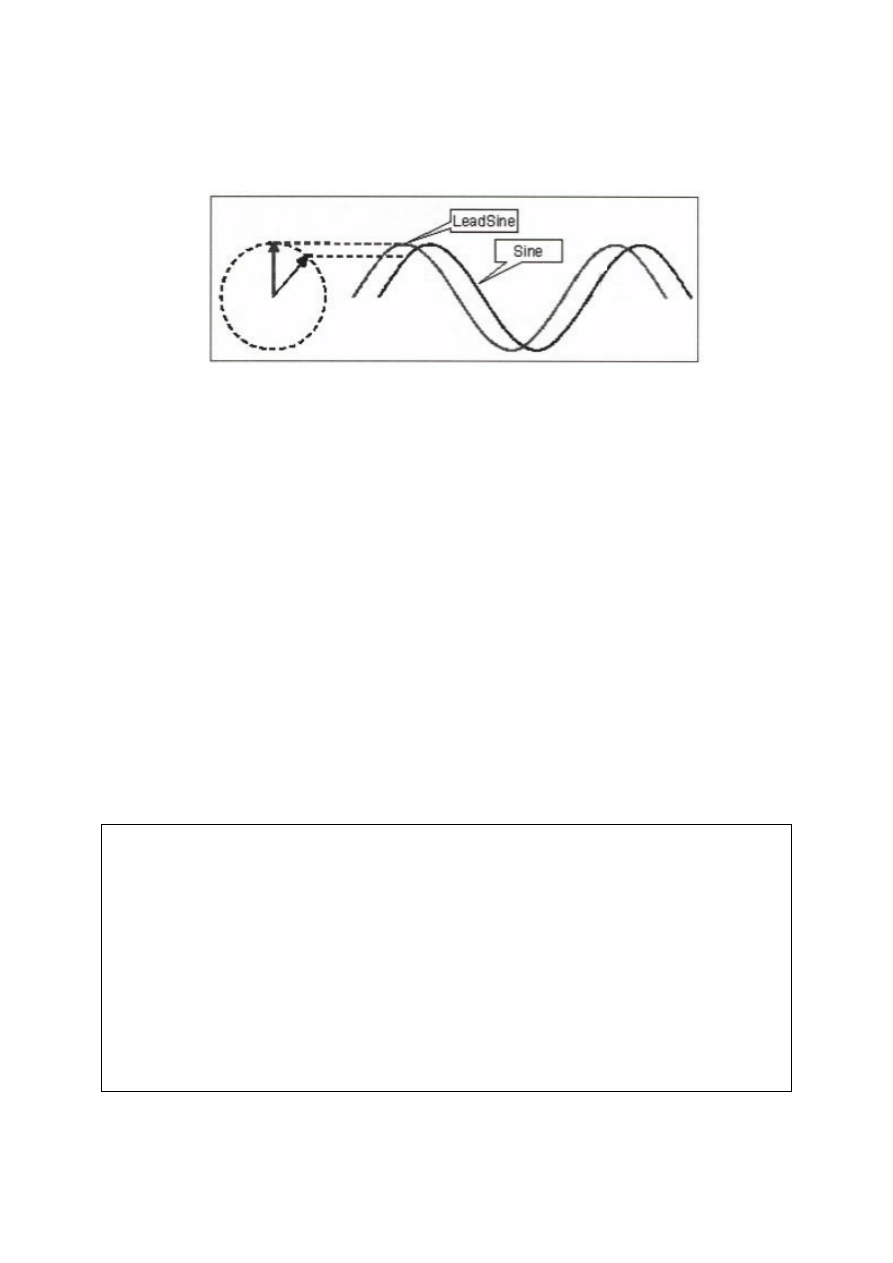
Wskaźnik Sinewave
68
Rysunek 8.2 Fazor i zakres czasu wskaźnika Sinewave.
Dodając 45 stopni bezspornie przesuwamy fazor od 45-stopniowego nachylenia do
pozycji pionowej. To przesunięcie fazy oznacza, że kształt fali LeadSine będzie posiadać
szczyt przed szczytem fali Sine. Linie LeadSine i Sine przecinają się przy 22.5 stopniach, lub
też inaczej mówiąc przy jednej szesnastej cyklu, przed osiągnięciem punktu zwrotnego cyklu.
Jeśli rynek posiada cykl 16-słupkowy, to jest to natychmiastowy sygnał wejścia lub wyjścia.
Jeśli rynek posiada dłuższy cykl, to jest to solidna podstawa do przewidzenia czasu
przeprowadzenia transakcji.
W porównaniu z typowymi oscylatorami, takimi jak Stochastic lub RSI, wskaźnik
Sinewave posiada dwie główne zalety:
• wskaźnik Sinewave antycypuje punkt zwrotny Trybu Cyklu, a nie czeka na potwierdzenie,
• faza nie zmienia się, gdy rynek jest w Trybie Trendu, a zatem, wskaźnik Sinewave ma
tendencję do unikania podawania fałszywych sygnałów, gdy rynek jest w Trybie Trendu.
Dodatkową zaletą jest to, że antycypujący sygnał otrzymywany jest dokładnie do
matematycznie ustalonej fazy. Impet nie jest potrzebny. Tak więc, sygnały wskaźnika
Sinewave nie są bardziej wytłumione niż oryginalny sygnał.
Na Rysunku 8.3 przedstawiono program do obliczania i wyświetlania wskaźnika
Sinewave.
inputs: Price(Close),
Window(1),
RegCode(„LPJDPDTBHB”);
vars:
dc(0)
SmoothPrice(0),
DCPeriod(0),
RealPart(0),
ImagPart(0),
count(0),
DCPhase(0);
Rysunek 8.3 Program w języku EasyLanguage do obliczania wskaźnika Sinewave.

Wskaźnik Sinewave
69
DefineDllFunc: „c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
Int,float,float,float,lpfloat;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,
”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
{Compute Dominant Cycle Phase}
SmoothPrice = (4*Price + 3*Price[1] + 2*Price[2] +
Price[3])/10;
DCPeriod = IntPortion(dc + .5);
RealPart = 0;
ImagPart = 0;
For count = 0 To DCPeriod – 1 begin
RealPart = RealPart + Cosine(360*count/
DCPeriod)*(SmoothPrice[count]);
ImagPart = ImagPart + Sine(360*count /
DCPeriod)*(SmoothPrice[count]);
End;
If AbsValue(RealPart) >0.001 then
DCPhase = Arctangent(ImagPart / RealPart);
If AbsValue(RealPart) <= 0.001 then
DCPhase
=
90*Sign(ImagPart);
DCPhase = DCPhase + 90;
If RealPart < 0 then DCPhase = DCPhase + 180;
{Compensate for one bar lag of the Weighted
Moving
Average}
If DC <> 0 then DCPhase = DCPhase + 360 / dc;
{Don’t let phase exceed 360 degrees in a cycle}
If DCPhase > 360 then DCPhase = DCPhase – 360;
{Force phase wrap at 315 degrees to avoid full scale
wrap at 0-360 boundary}
If DCPhase > 315 then DCPhase = DCPhase – 360;
Plot(Sine(DCPhase),”Sine”);
Plot2(Sine(DCPhase + 45),”LeadSine”);
Rysunek 8.3 Ciąg dalszy.
Wskaźnik Sinewave
70
Program ten jest identyczny do programu obliczającego fazę, przedstawionego na
Rysunku 8.1 za wyjątkiem wyrażenia odnoszącego się do wykresu.
Wskaźniki Faza i Sinewave kreślone są zgodnie z teorią analizy kształtu fali i
rzeczywistymi danymi liczbowymi, co umożliwia zademonstrowanie ich możliwości.
Rysunek 8.4 przedstawia teoretyczny kształt fali sinusoidalnej, której okres wzrasta liniowo
od 10 do 40 słupków.
Rysunek 8.4 Wskaźnik Sinewave zawsze określa punkt zwrotny.
(Wykres utworzono przy pomocy programu TradeStation 2000i®)
Wskaźniki Faza i Sinewave wyświetlane są w dwóch oddzielnych polach. Zauważ jak
rozpiętość zmian fazy zmniejsza się, gdy okres cyklu staje się dłuższy. Linia przerywana jest
typowo oznaczanym punktem ilustrując, że analityczny kształt fali i linia Sine wskaźnika
Sinewave osiągają szczyty jednocześnie, a mierzona faza w tym punkcie wynosi 90 stopni.
LeadSine zawsze przecina linię Sine przed punktem zwrotnym cyklu, dając przyśpieszoną
wskazówkę cyklicznego punktu zwrotnego. Przyśpieszenie wyprzedzenia punktu zwrotnego
zależy od długości cyklu i jest ono mniejsze dla krótszych cykli.
Rzeczywisty scenariusz rynkowy przedstawia Rysunek 8.5. Rynek jest w Trybie
Trendu prawie przez całą pierwszą połowę wykresu, co identyfikowane jest przez brak
kierunku zmian fazy i brak przecięcia się linii wskaźnika Sinewave. Tryb Cyklu rozpoczyna
się, gdy kierunek zmiany fazy jest w przybliżeniu taki sam jak kierunek zmian fazy Cyklu
Dominującego.
Wskaźnik Sinewave
71
Rysunek 8.5 Wskaźnik Sinewave daje dokładne sygnały Trybu Cyklu.
(Wykres utworzono przy pomocy programu TradeStation 2000i®)
Tryb Cyklu kończy się, gdy kierunek zmian fazy staje się ujemny – oczywista
niemożliwość. W czasie Trybu Cyklu okres wskaźnika Sinewave daje trzy sygnały kupna i
dwa sygnały sprzedaży. Wszystkie sygnały są prawidłowe, za wyjątkiem ostatniego, który
prawie zawsze zdarza się, gdy cykl zawodzi.
Zapamiętaj
• Wskaźnik Sinewave jest nieprzyczynowym filtrem przewidującym, opartym na
przesłance, że Cykl Dominujący istniał w niedalekiej przeszłości i będzie trwać dalej w
bliskiej przyszłości.
• Faza posiada stały kierunek zmian, gdy rynek jest w Trybie Cyklu.
• Faza zanika, gdy rynek jest w Trybie Trendu i wtedy może nawet mieć ujemny kierunek
zmian.
• Faza krąży w pobliżu wartości 0 stopni w trendzie malejącym i w pobliżu wartości 180
stopni w trendzie rosnącym.
• Wskaźnik Sinewave składa się z sinusoidy fazy Cyklu Dominującego i z sinusoidy fazy
Cyklu Dominującego przesuniętej o 45 stopni.
• Wskaźnik Sinewave daje sygnały wejścia i wyjścia o jedną szesnastą okresu cyklu
wcześniej niż nastąpi punkt zwrotny.
• Wskaźnik Sinewave rzadko daje błędne sygnały, gdy rynek jest w Trybie Trendu.

Chwilowa Linia Trendu
72
Rozdział 9
Chwilowa Linia Trendu
Być może termin chwilowa jest trochę zarozumiały w zastosowaniu do pojęć
omawianych w tym rozdziale. Niemniej jednak, termin ten do pewnego stopnia jest właściwy,
ponieważ nasza technika umożliwia stałe obliczanie Linii Trendu, za pomocą której możemy
szybko oszacować ruch rynku. Jak dowiedziono w Rozdziale 1, gdzie rozpatrzono problem
Spaceru Pijanego, nasz model rynku składa się z Trybu Trendu i Trybu Cyklu. Bardziej
odpowiednim jest opis rynku za pomocą kombinacji tych dwóch trybów. Dodatkowo, w
Rozdziale 4 wykazaliśmy, że możemy całkowicie wyeliminować składnik Cyklu
Dominującego, przykładając prostą średnią ruchomą (SMA) do okresu cyklu. Jeśli
przyłożymy prostą średnią do okresu Cyklu Dominującego, bazując na słupkach tego cyklu
(ponieważ mamy możliwość ciągłej identyfikacji zmieniającego się Cyklu Dominującego), to
zasadniczo otrzymamy zmienną szerokość średniej ruchomej. Taka średnia ruchoma jest
ważna, ponieważ składnik Cyklu Dominującego jest zawsze usuwany. Wynika z tego, że jeśli
analitycznie złożony kształt fali zawiera tylko składnik trendu i składnik cyklu, usunięcie
składnika cyklu pozostawia nam trend. Oczywiście, nie jest to ściśle dokładne, ponieważ
zawsze są tam obecne składniki inne niż Cykl Dominujący. Nie mniej jednak, rozwiązanie to
jest użyteczne dla przeprowadzania transakcji, ponieważ drugorzędne cykle posiadają
zazwyczaj małe amplitudy.
Ujemną stroną stosowania SMA do długości mierzonego Cyklu Dominującego jest to,
że SMA powoduje nieuniknione opóźnienie (Cykl Dominujący-1)/2. Jeśli Cykl Dominujący
składa się z 21 słupków, to Chwilowa Linia Trendu będzie opóźniona w stosunku do ceny o
10 słupków. Naszym celem jest aby opóźnienie wynosiło prawie zero.
Możemy minimalizować opóźnienie, stosując specjalnie zaprojektowany filtr
wygładzający dający minimalne opóźnienie i następnie stosując filtr wycinający
częstotliwość, do precyzyjnego usunięcia niepożądanych składników częstotliwości. Taka
strategia nie tylko usuwa Cykl Dominujący, ale także wygładza kształt fali ceny, dając lepszą
Chwilową Linię Trendu.
Eliptyczne (lub Cauera) filtry dolnoprzepustowe znane są z tego, że dają niewielkie
opóźnienie dla danej wielkości tłumienia. Jako filtr usuwający składniki o wysokich
częstotliwościach, dobrałem trzypolowy filtr eliptyczny mający 0.8 dB pasmo przepustowe i
30 dB pasmo zaporowe tłumienia. Ustawiając na 0.8 dB pasmo przepustowe dla
częstotliwości normalizowanej 0.22 (9-słupkowy okres cyklu), filtr dokładnie wycina 5-
słupkowy cykl. Dla okresów cykli krótszych niż 5 słupków, ustawiam tłumienie na 30 dB lub
więcej. Częstotliwość odpowiadająca temu filtrowi pokazana jest na Rysunku 9.1.
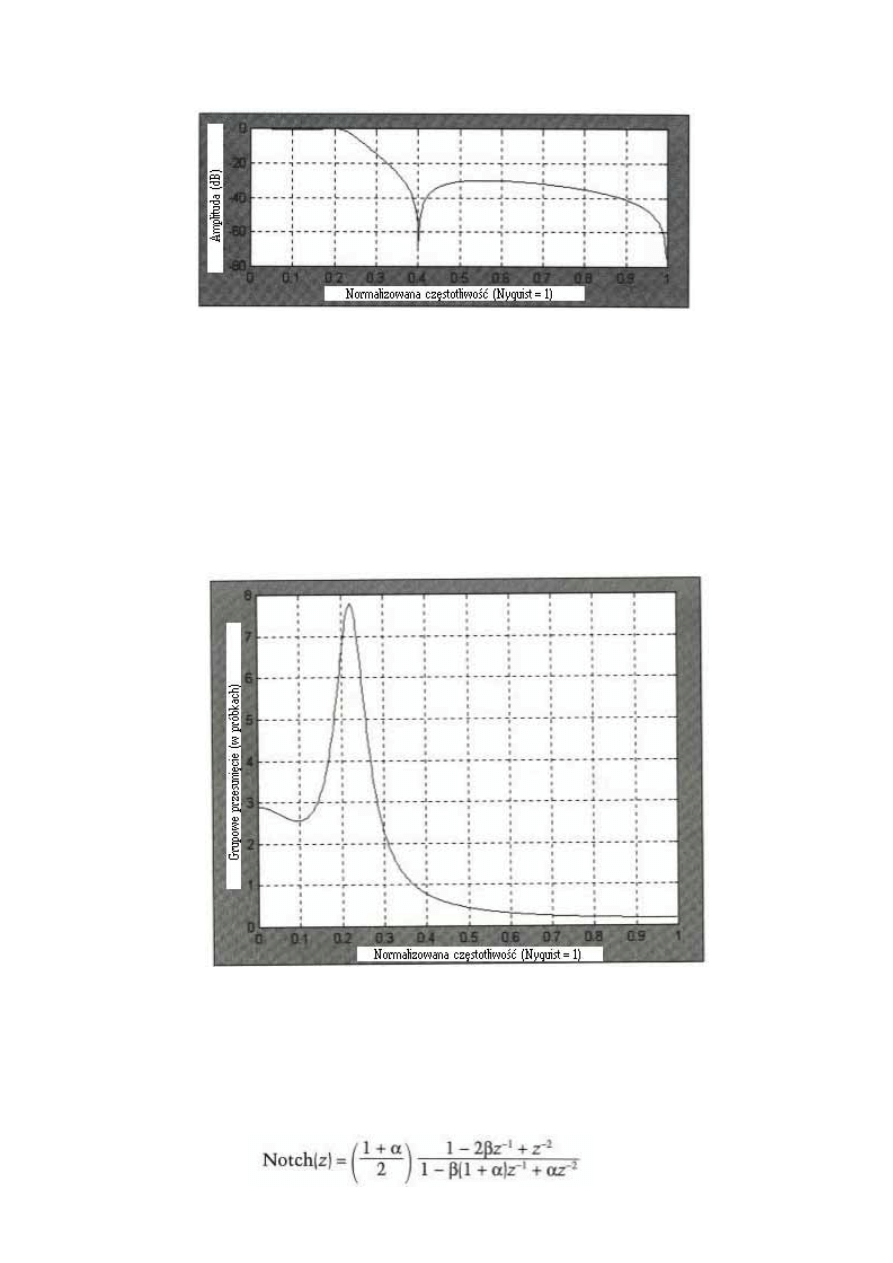
Chwilowa Linia Trendu
73
Rysunek 9.1 Amplituda odpowiadająca 3-słupkowemu filtrowi eliptycznemu.
Równanie tego filtra w języku EasyLanguage przedstawia się następująco:
Filt1=0.0542*Cena+0.021*Cena[1]
+0.021*Cena[2]+0.0542*Cena[3]
+1.9733*Filt1[1]-1.6067*Filt1[2]+0.4831*Filt1[3]
Rysunek 9.2 pokazuje, że opóźnienie niskiej częstotliwości tego filtra eliptycznego
jest mniejsze niż 3 słupki. Jednakże, opóźnienie w sąsiedztwie 10-słupkowego cyklu jest
olbrzymie.
Rysunek 9.2 Przesunięcie grupowe 3-słupkowego filtra eliptycznego.
Jest to nie do zaakceptowania, ponieważ składnik 10-słupkowego cyklu nie jest
wytłumiony. Można to wyeliminować stosując inny filtr.
Równanie
odpowiadające takiemu wycinającemu filtrowi, zwięźle napisane w postaci
transformaty Z, przedstawia się następująco:
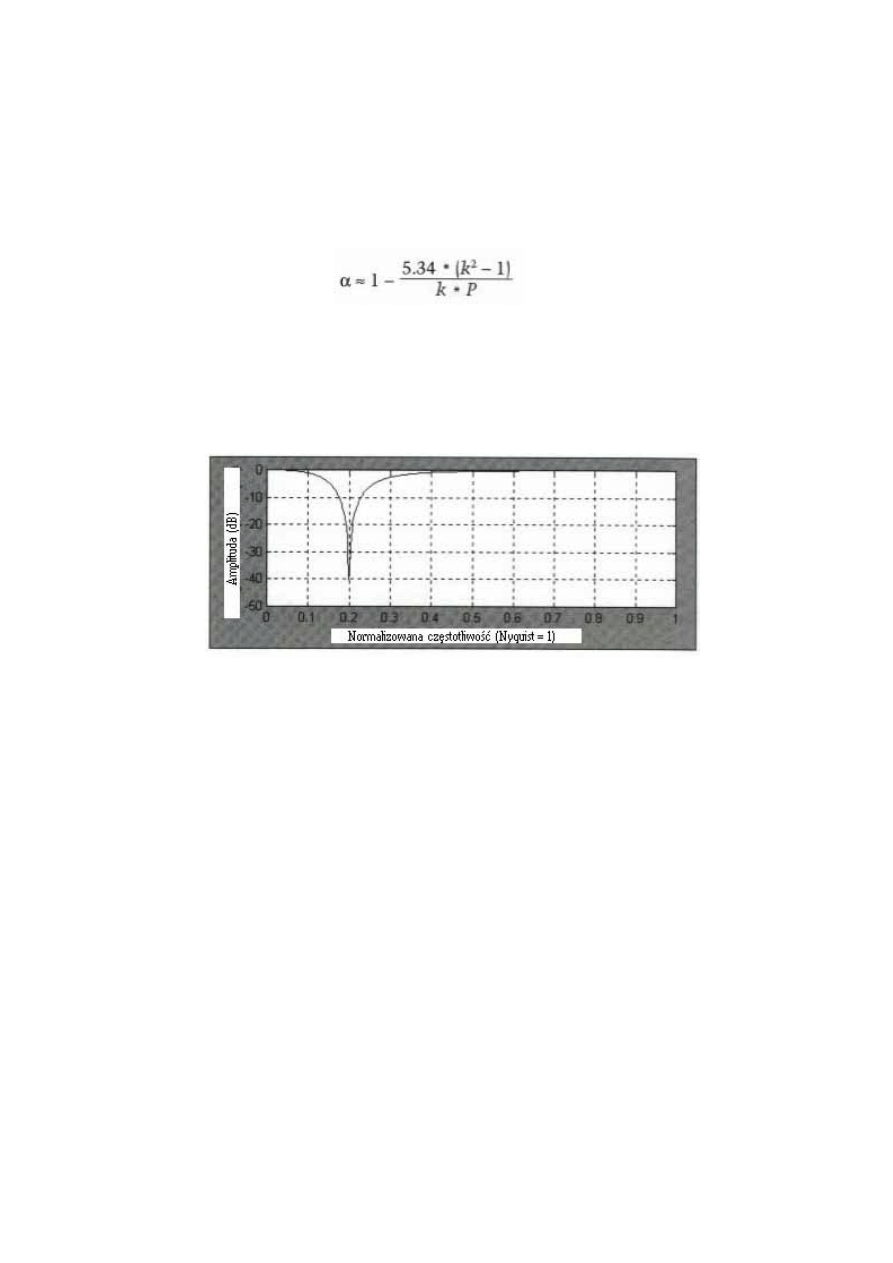
Chwilowa Linia Trendu
74
gdzie β=cos(360/P).
P jest okresem wycinanego cyklu. Wyrażenie alfa w tym równaniu określa szerokość
wycinania. Alfa musi być mniejsze od 1. Wycinanie jest bardzo wąskie, gdy alfa jest bliskie 1
oraz rozszerza się, gdy alfa maleje. Wartość alfa może być obliczona, biorąc pod uwagę
pożądaną szerokość wycinania, z wyrażenia:
gdzie k jest większe o 3 dB częstotliwości w stosunku do wycinanej częstotliwości.
Na
przykład, jeśli chcemy osiągnąć 3 dB punkt, będący o 44% większy niż wycinana
częstotliwość, k=1.44. Podstawiając do równania P=10 otrzymamy w tym przypadku
alfa=0.6. Amplituda odpowiadająca filtrowi wycinającemu, który wycina 10-słupkowy cykl i
posiada α=0.6, pokazana jest na Rysunku 9.3.
Rysunek 9.3 Amplituda odpowiadająca filtrowi wycinającemu 10-słupkowy cykl dla alfa=0.6.
Eliptyczny filtr wycinający usuwa takie składniki częstotliwości, które posiadają duże
przesunięcie grupowe.
Stosując filtr wycinający także jesteśmy narażeni na opóźnienie. Wykres
odpowiadający temu grupowemu przesunięciu, przedstawia Rysunek 9.4.
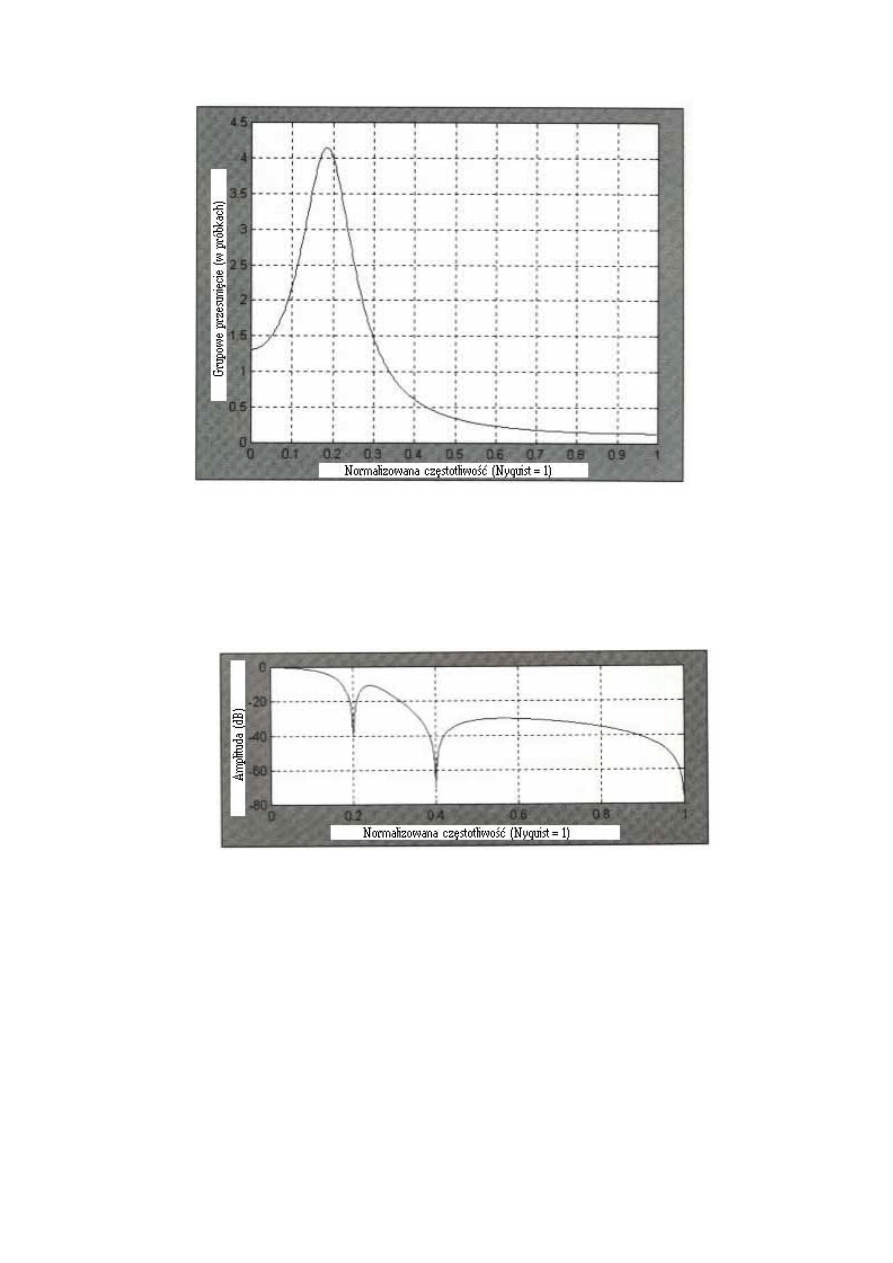
Chwilowa Linia Trendu
75
Rysunek 9.4 Grupowe przesunięcie 10-słupkowego filtra wycinającego dla alfa=0.6.
Wysokie
opóźnienie sygnału wyjściowego składników częstotliwości w pobliżu 10-
słupkowego cyklu nie jest istotne, ponieważ ich amplituda jest mała.
Filtr
złożony, składający się z filtra dolnoprzepustowego i filtra wycinającego, posiada
amplitudę pokazaną na Rysunku 9.5.
Rysunek 9.5 Częstotliwość odpowiadająca filtrowi złożonemu, składającemu się z filtra
dolnoprzepustowego i 10-słupkowego filtra wycinającego.
Rysunek 9.6 pokazuje, że złożone opóźnienie niskiej częstotliwości wynosi tylko 4.2
słupka. Z drugiej strony, większe opóźnienie w pobliżu składnika 10-słupkowego cyklu nie
jest istotne, ponieważ te składniki częstotliwości są małe.
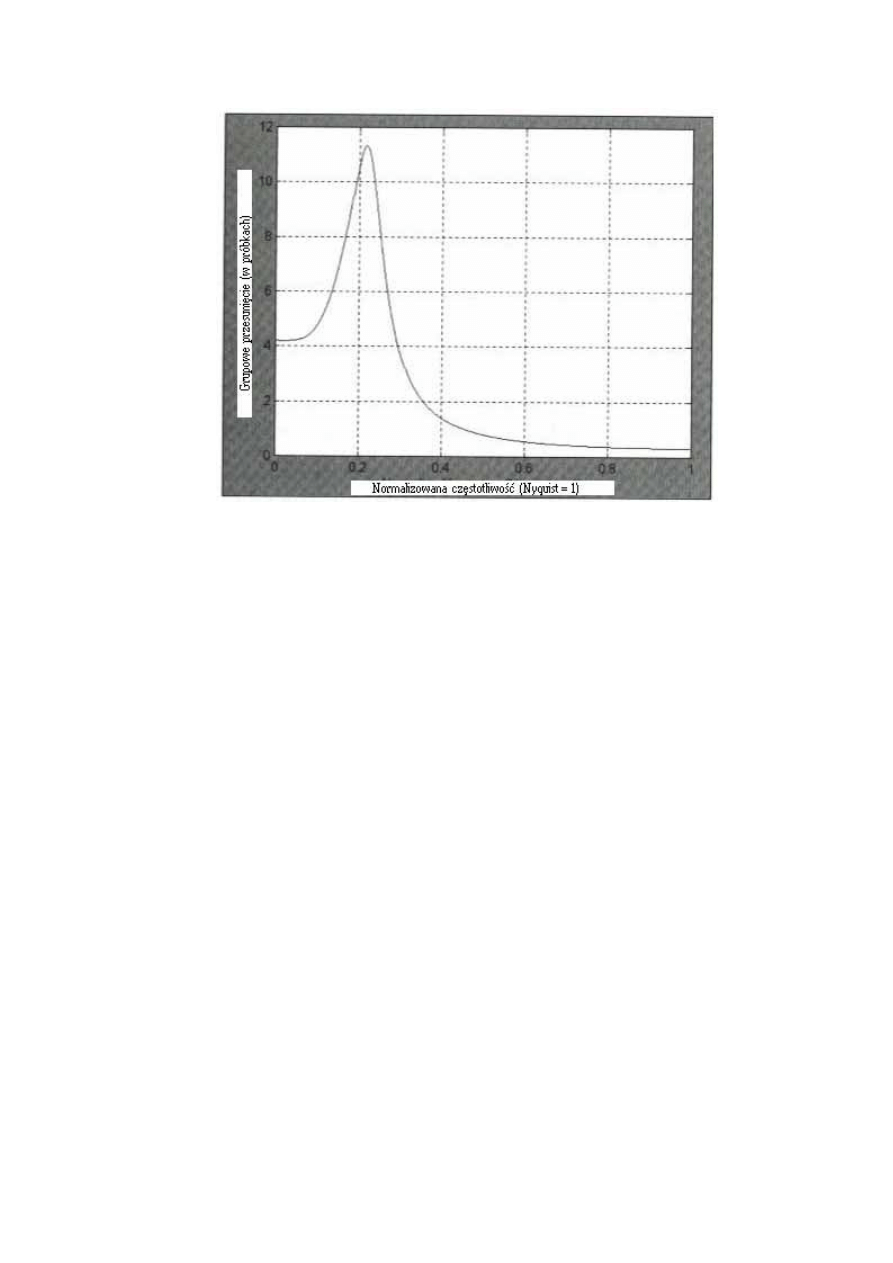
Chwilowa Linia Trendu
76
Rysunek 9.6 Grupowe przesunięcie złożonego filtra składającego się z filtra dolnoprzepustowego i
filtra wycinającego 10-słupkowego.
Następnym krokiem jest dostrojenie innego filtra wycinającego do pomiaru Cyklu
Dominującego. Ja stosuję alfa=0.8 dla takiego filtra, ponieważ rozpiętość wycinania może
stać się nieregularna, gdy dostrajamy się do dłuższych okresów cykli. Jeśli mierzony Cykl
Dominujący ma 21-słupkowy okres, to taki filtr wycinający powoduje opóźnienie niskiej
częstotliwości wynoszące 2.5 słupka. Całkowite opóźnienie jest sumą opóźnień filtra
eliptycznego, 10-słupkowego filtra wycinającego oraz filtra wycinającego Cykl Dominujący.
W przypadku 21-słupkowego Cyklu Dominującego, całkowite opóźnienie wynosi
4.2+2.5=6.7 słupków. Jest to znacząca redukcja opóźnienia w porównaniu do stosowanej 21-
słupkowej SMA do usuwania Cyklu Dominującego. Gdy rynek jest w Trybie Trendu,
mierzony Cykl Dominujący jest często bardzo długi – nawet 40 do 50 słupków. W takich
przypadkach, redukcja opóźnienia realizowana przez filtry wycinające jest rzeczywiście
imponująca. Jeśli alfa=0.8 a Cykl Dominujący wynosi 20 słupków, to roztropnie jest
stosować alfa=0.9 dla Cyklu Dominującego wynoszącego 40 słupków (i przeprowadzać
interpolację liniową pomiędzy 20 i 40 słupkami). Ten sposób dostrajania wycinania
powoduje, że opóźnienie dla 40-słupkowego cyklu wynosi tylko około 4 słupków. To
oznacza, że opóźnienie filtra dla 40-słupkowego Cyklu Dominującego wynosi tylko około 8.2
słupka, zamiast 20-słupkowego opóźnienia, jeśli do usuwania Cyklu Dominującego
stosowana jest 40-słupkowa SMA. Dodatkową korzyścią z takiego podejścia do filtra
wycinającego jest to, że filtr eliptyczny powoduje logiczne gładzenie usuwające wszystkie
składniki o wysokich częstotliwościach obecne w cenie.
My wykorzystamy 4-słupkową Ważoną Średnią Ruchomą (WMA) w połączeniu z
Chwilową Linię Trendu. Wskazówką będzie przecięcie Chwilowej Linii Trendu przez WMA.
Użyteczna do tego jest, posiadająca tylko 1-słupkowe opóźnienie, 4-słupkowa WMA. Jednym
ze sposobów rozpoznania początku trendu jest wsteczne obliczenie liczby słupków od
aktualnego słupka do pierwszego przecięcia WMA i Chwilowej Linii Trendu. Jeśli liczba ta
jest większa od połowy Cyklu Dominującego to wiadomo, że rynek jest w trybie trendu.
Przyczyną tego jest to, że jeśli rynek był w Trybie Cyklu, to możemy spodziewać się, że cena
Chwilowa Linia Trendu
77
będzie przecinać Chwilową Linię Trendu co pół cyklu. Odstępstwo od tej reguły jest jasną
wskazówką Trybu Trendu. Przecinanie co pół cyklu najlepiej sprawdza się w trendzie
bocznym rynku, ponieważ wtedy Chwilowa Linia Trendu jest prawie równoległa do osi X i
jej opóźnienie nie ma wpływu na dokładność sygnału. To prowadzi nas do wniesienia
poprawki do powyższej reguły, a mianowicie, że Tryb Trendu rozpoczyna się, gdy cena
przecięła Chwilową Linię Trendu więcej niż ćwierć cyklu temu i nie sprawia wrażenia, że ma
zamiar powtórnie ją przeciąć. Taka poprawka reguły powoduje, że Tryb Trendu można
określić znacznie wcześniej. Jednakże, jak ze wszystkimi antycypującymi sygnałami, od
czasu do czasu możesz otrzymać błędny sygnał. Tryb Trendu jest zakończony, gdy gładzona
cena przetnie Chwilową Linię Trendu.
Ruch Chwilowej Linii Trendu i zakręty ceny gładzonej, pokazane są na Rysunku 9.7.
Rysunek 9.7 Chwilowa Linia Trendu jasno pokazuje jak zawierać transakcje zgodnie z trendem.
(
wykres utworzono przy pomocy programu TradeStation 2000i®)
Cena
gładzona przecina od dołu Chwilową Linię Trendu w trzecim tygodniu sierpnia.
Mierzony okres Cyklu Dominującego wynosił w tym czasie około 22 słupków. Ponieważ
cena nie próbowała ponownie przeciąć Chwilowej Linii Trendu to stwierdzamy, że trend
zaczął obowiązywać około pięciu dni od dnia przecięcia, tj. od dnia około pierwszego
września. Za wyjątkiem błędnego sygnału w czasie ostatniego tygodnia września, wskaźnik
ten stanowiący parę, dokładnie podążał z trendem aż do połowy grudnia. W tym punkcie
rynek rozpoczął Tryb Cyklu i powinno cyklicznie następować przecinanie się ceny gładzonej
z Chwilową Linią Trendu. Pod koniec lutego ponownie należy stwierdzić Tryb Trendu,
ponieważ cena nie wskazuje na zamiar przecięcia Chwilowej Linii Trendu.
Chwilowa Linia Trendu jest częścią pakietu komercyjnego wskaźników MESA. Kod
w języku EasyLanguage, do pomiaru fazy Cyklu Dominującego, przedstawiony jest na
Rysunku 9.8 i jeśli zechcesz możesz wprowadzić do tego wskaźnika swoje własne zmiany.
Początkowa część kodu obejmująca Cykl Dominujący (zmienna dc) stosowana jest w
komercyjnym programie MESA dla TradeStation2000i lub TradeStation 6.0. Czytelnik może
zastąpić ten kod swoim własnym kodem do pomiaru dc, stosownie do opisu w Rozdziale 7.

Chwilowa Linia Trendu
78
inputs:
Price(Close),
Window(1),
RegCode(„LPJDPDTBHB”);
vars:
dc(0),
DCPeriod(0),
Trendline(0),
SmoothPrice(0);
DefineDllFunc: „c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
Int,float,float,float,lpfloat;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,
”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
{Lowpass Filter is Ellip(3,.8,30,.22)}
Value1 = .0542*Price + .021*Price[1] +
.021*Price[2] + .0542*Price[3] +
1.9733*Value1[1] – 1.6067*Value[2] +
.4831*Value1[3];
{Notch Filter at a 10 bar cycle}
Value2 = .8*(Value1 – 2*Cosine(360/10)*
Value1[1] + Value1[2] +
1.6*Cosine(360/10)*Value2[1]
-
.6*Value2[2];
{Notch Filter the Dominant Cycle}
Trendline = .9*(Value2 – 2*Cosine(360/dc)*
Value2[1]
+Value2[2]
+
1.8*Cosine(360/dc)*Trendline[1]
–
.8*Trendline[2];
SmoothPrice = (4*Price +3*Price[1] +
2*Price[2]
+
Price[3])/10;
Plot1(Trendline,
„Trendline”);
Plot2(SmoothPrice,
„SP”);
Rysunek 9.8 Program w języku EasyLanguage do obliczania Chwilowej Linii Trendu.

Chwilowa Linia Trendu
79
Zapamiętaj
• Chwilowa Linia Trendu tworzona jest przez usunięcie składnika Cyklu Dominującego ze
złożonego kształtu fali. Dokonuje się to za pomocą gładzenia ceny za pomocą filtra
eliptycznego i wycinania składników częstotliwości w pobliżu 10-słupkowego cyklu.
Pomierzone składniki częstotliwości Cyklu Dominującego są także wycinane.
• Trend zaczyna obowiązywać, gdy gładzona cena nie przecięła Chwilowej Linii Trendu w
obrębie ostatniej połowy Cyklu Dominującego.
• Jako szybszy wskaźnik można przyjąć, że początek trendu nastąpił, gdy gładzona cena nie
przecięła Chwilowej Linii Trendu w obrębie ostatniej ćwiartki Cyklu Dominującego i nie
wykazuje ona zamiaru ponownego przecięcia Chwilowej Linii Trendu.
• Trend jest zakończony, gdy cena gładzona przecina Chwilową Linię Trendu.

Dostrajanie standardowych wskaźników
80
Rozdział 10
Dostrajanie standardowych wskaźników
Nie
często się zdarza, gdy zdyszany i wyczerpany kończę seminarium, otrzymuję takie
pytanie jak: „Czy mogę stosować cykle do optymalizacji RSI?”. Moją natychmiastową
reakcję, jak można się domyślić, jest: „Dlaczego ktoś chciałby to zrobić?”. Właśnie
skończyłem pokazywać słuchaczom obliczanie, teoretycznie najbardziej korzystne,
omawianego wskaźnika Sinewave, który miał kilka błędnych sygnałów w Trybie Trendu oraz
skończyłem omawianie Chwilowej Linii Trendu jako narzędzia do zawierania transakcji
zgodnie z Trybem Trendu. Po tym wszystkim jak może być coś lepszego, niż to co
przedstawiłem jako teoretycznie najbardziej korzystne? Czy rzeczywiście istnieje potrzeba
optymalizowania typowych wskaźników? Następnie, po chwili zastanowienia w końcu
uświadomiłem sobie, że pytanie to zaintrygowało mnie od strony analizy technicznej. Nie
jestem skłonny stosować 14-dniowy okres dla RSI tylko dlatego, że tak twierdzi Welles
Wilder. W poszukiwaniu najlepszego sposobu dostosowania się do uwarunkowań rynkowych,
przeprowadziłem wiele badań, których rezultaty zostały chronologicznie przedstawione w tej
książce.
Tak
więc, co jest najlepszym wskaźnikiem? Nie ma prostej odpowiedzi na to pytanie.
Wszystko jest relatywne. Niektóre wskaźniki spisują się na rynku lepiej niż inne. Zależy to
także od preferencji gracza. Stosując kilka wskaźników razem, można odkryć synergię,
niedostępną dla każdego wskaźnika stosowanego oddzielnie.
Istnieje wiele użytecznych wskaźników. Ulepszanie ich, stosownie do aktualnego
stanu rynku, jest zadaniem każdego gracza giełdowego. Jest to także tematem tej książki. W
rozdziale tym dokonałem przeglądu trzech typowych wskaźników: RSI, Stochastic i
Commodity Channel Indicator. Przegląd obejmuje omówienie tych wskaźników z
uwzględnieniem mierzonych okresów cykli. Dodatkowo, możemy oznaczyć szerokość Cyklu
Dominującego. Przy tym podejściu do zagadnienia nie ma potrzeby pomiaru cyklu.
RSI
Welles Wilder zdefiniował RSI, jako¹:
RSI=100-100/(1+RS)
gdzie RS=(zamknięcia po dniach wzrostowych)/(zamknięcia po dniach spadkowych)=CU/CD
RS oznacza Relative Strength. To jest, CU jest sumą różnic cen zamknięcia w
obserwowanym okresie, w którym ta różnica jest dodatnia. Podobnie, CD jest sumą różnic
cen zamknięcia w obserwowanym okresie, w którym ta różnica jest ujemna, ale suma
wyrażona jest jako liczba dodatnia. Gdy zastąpimy CU/CD i uprościmy równanie RSI,
otrzymamy:
_________
¹
J. Welles Wilder, Jr. New Concepts in Technical Trading Systems.
Hunter Publishing, Winston-Salem, NC,1978.

Dostrajanie standardowych wskaźników
81
RSI=100-100/(1+CU/CD)
=100-100CD/(CU+CD)
=(100CU+100CD-100CD)/(CU+CD)
RSI=100CU/(CU+CD)
Innymi
słowy, RSI jest wyrażone w procentach określających stosunek sumy cen
zamknięcia w dniach wzrostowych do sumy wszystkich cen zamknięcia w obserwowanym
okresie. Aby uzyskać maksymalną efektywność, obserwowany okres powinien wynosić
połowę mierzonego cyklu. Jeśli obserwowany okres wynosi połowę Cyklu Dominującego,
wtedy dla czystej fali sinusoidalnej, ceny zamknięcia w dniach wzrostowych są dokładnie
równe wszystkim cenom zamknięcia podczas części cyklu od dołka do szczytu. W tym
przypadku, RSI powinien mieć wartość 100. Podczas innej części cyklu – następnej połowie
cyklu – nie powinno być cen wzrostowych. Podczas tej połowy cyklu, RSI powinien mieć
wartość 0. Jednakże, w zasadzie połowa mierzonego cyklu jest dokładnym odzwierciedleniem
obserwowanego okresu RSI. Na Rysunku 10.1 przedstawiono program w języku
EasyLanguage dla TradeStation 2000i lub TradeStation 6.0 stosujący MESA do obliczania
Cyklu Dominującego.
inputs:
Price(Close),
CycPart(.5),
Window(1),
RegCode(„LPJDPDTBHB);
vars: dc(0),
CU(0),
CD(0),
count(0),
RSI(0);
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
int,float,float,float,lpfloat;
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
CU = 0;
CD = 0;
Rysunek 10.1 Program w języku EasyLanguage do obliczania dostosowanego RSI.

Dostrajanie standardowych wskaźników
82
For count = 0 to IntPortion(CycPart*dc + .5) – 1 begin
If Close[count] – Close[count + 1] > 0 then
CU = CU + (Close[count] – Close[count + 1]);
If Close[count] – Close[count + 1] < 0 then
CD = CD + (Close[count + 1] – Close[count]);
End;
If CU + CD <> 0 then RSI = 100*CU/(CU + CD);
Plot1(RSI,”RSI”);
Rysunek 10.1 Ciąg dalszy.
Następnie ten obliczony okres Cyklu Dominującego wykorzystywany jest jako
podstawa do znalezienia CU i CD oraz do obliczenia RSI. Ponieważ połowa okresu cyklu
może nie być uniwersalną odpowiedzią, dodajemy jako modyfikator sygnał wejściowy
CycPart. Ten sygnał wejściowy pozwala optymalizować obserwowany okres w każdej
szczególnej sytuacji.
Optymalizowany RSI ma tendencję do bycia w fazie z oryginalną daną liczbową ceny.
Sugeruje to sposób zamiany dobrego wskaźnika na jeszcze lepszy. Jeśli odejmiemy 50 od
optymalizowanego RSI to otrzymamy średnio zero i w ten sposób, przy przecięciach zera
przez RSI zmierzamy do statystyki Poissona. Jeśli był taki przypadek, to możemy gładzić
optymalizowane RSI i utworzyć z niego optymalny filtr przewidujący. W ten sposób możemy
antycypować sygnały, a nie czekać na sygnały potwierdzające przecinające linie 30 i 70
procent, tak jak to czyni standardowy wskaźnik. Pozostawię twojej decyzji, która metoda
najlepiej nadaje się do wykorzystania przez ciebie.
Definicja RSI umożliwia stosowanie przybliżonego okresu Cyklu Dominującego, gdy
rynek jest w Trybie Cyklu. Jeśli okres stosowany do obliczania RSI jest dokładnie równy
okresowi Cyklu Dominującego, to ceny zamknięcia w dniach wzrostowych są dokładnie
równe całkowitym cenom zamknięcia gdy pole obserwacyjne okienka umieszczone jest
pomiędzy dnem a szczytem cyklu. W tym przypadku wartość RSI wynosi 100. Jeśli pole
obserwacyjne okienka wynosi dokładnie jedna druga cyklu, to nie ma cen wzrostowych i
wartość RSI wynosi zero. RSI jest czystą sinusoidą, gdy obliczony okres wynosi połowę
Cyklu Dominującego. Pokazuje to Rysunek 10.2.
W tym przypadku RSI wygląda jak sinusoida dokładnie w fazie z cyklem danych
liczbowych rynku i porusza się pomiędzy ograniczeniami 0 i 100.
Jeśli szerokość obliczeniowa jest znacznie krótsza niż połowa okresu cyklu, to ceny
zamknięcia w górę są równe całkowitym cenom zamknięcia tak długo, aż cykl osiągnie swój
szczyt w dodatniej części cyklu. Odpowiednio, ceny zamknięcia w dniach wzrostowych
szybko osiągają zero w ujemnej części cyklu. Jest tak dlatego, że RSI jest ograniczany i
wygląda jak kwadratowa fala gdy jego szerokość obliczeniowa jest znacznie mniejsza niż
połowa okresu Cyklu Dominującego. Ten efekt kwadratowej fali pokazany jest na Rysunku
10.3, gdzie szerokość obliczeniowa wynosi 25 procent Cyklu Dominującego danych
liczbowych fali sinusoidalnej.
Dostrajanie standardowych wskaźników
83
Rysunek 10.2 RSI czystego cyklu wykorzystujący połowę cyklu jako szerokość obliczeniową.
(
Wykres utworzono w oparciu o program TradeStation2000i®)
Rysunek 10.3 RSI, którego szerokość obliczeniowa jest mniejsza, niż połowa Cyklu Dominującego,
jest ograniczony
(Wykres sporządzono w oparciu o program TradeStation2000i®)
Mówiąc inaczej, jeśli szerokość obliczeniowa RSI jest dłuższa niż połowa okresu
Cyklu Dominującego, ceny zamknięcia w dniach wzrostowych nigdy nie będą równe
całkowitym cenom zamknięcia dla cyklu teoretycznego. W tym przypadku, RSI nie może
odchylać się od 0 do 100. Jednakże faza RSI jest opóźniona w stosunku do fazy sinusoidy. Na
przykład, przypadek szerokości obliczeniowej wynoszący 75 procent okresu Cyklu
Dominującego, pokazany jest na Rysunku 10.4.
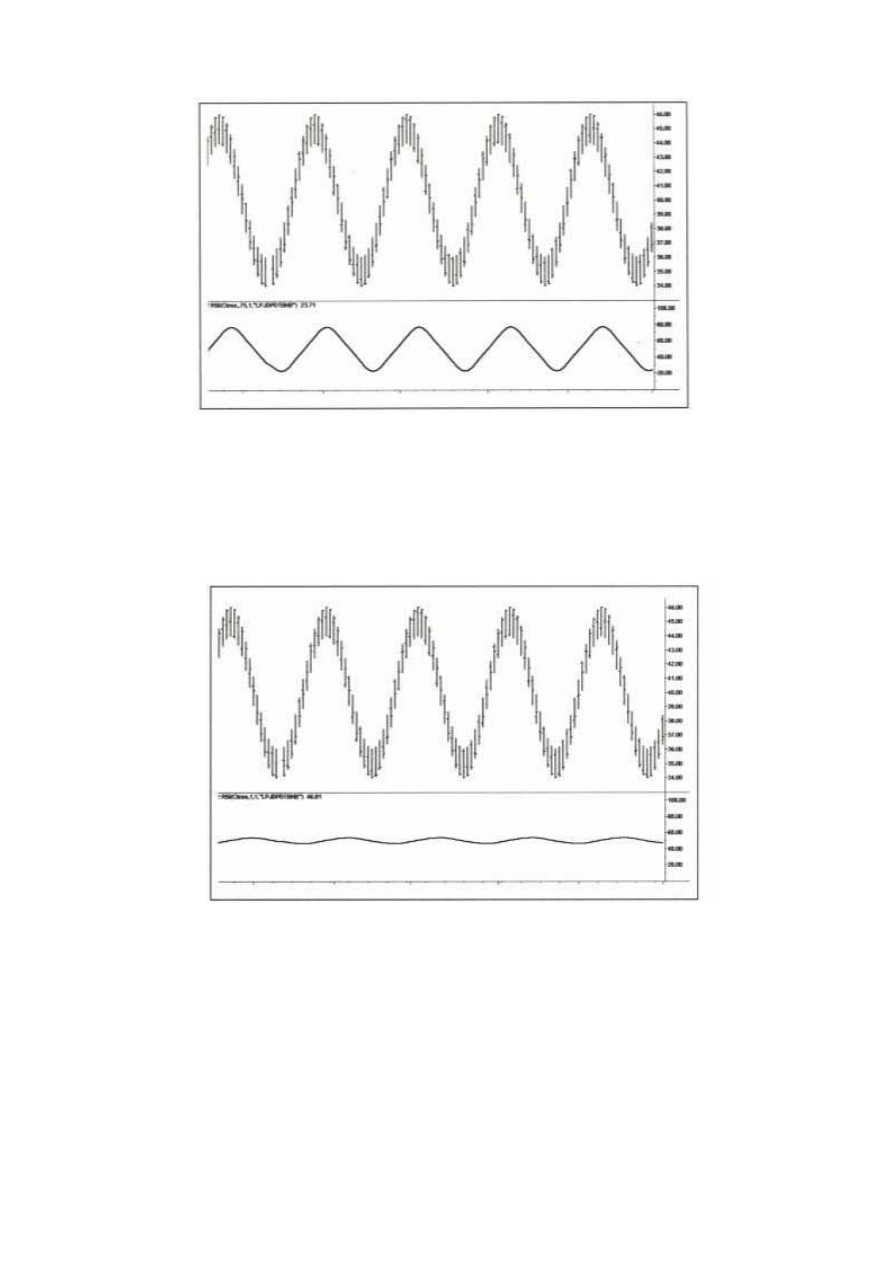
Dostrajanie standardowych wskaźników
84
Rysunek 10.4 RSI, którego szerokość wynosi 75 procent okresu Cyklu Dominującego, posiada
zredukowaną amplitudę i opóźnia się w stosunku do danych liczbowych cyklu.
(Wykres sporządzono w oparciu o program TradeStation2000i®)
Im
dłuższa staje się szerokość obliczeniowa, tym mniejsza rozpiętość RSI. RSI będący
rezultatem zastosowania szerokości obliczeniowej takiej samej jak Cykl Dominujący,
przedstawia Rysunek 10.5.
Rysunek 10.5 RSI, którego szerokość jest równa okresowi Cyklu Dominującego posiada bardzo małą
amplitudę.
(Wykres sporządzono w oparciu o program Tradestation2000i®)
Możemy wykorzystywać te charakterystyki RSI aby przybliżyć okres Cyklu
Dominującego. Zwiększając szerokość obliczeniową i obserwując kiedy RSI przestanie
ograniczać amplitudę oraz nadal będzie w przybliżeniu w fazie z danymi liczbowymi cyklu,
okres Cyklu Dominującego jest w przybliżeniu podwójną szerokością RSI. Jeśli zwiększymy
szerokość RSI zbyt mocno w stosunku do połowy okresu Cyklu Dominującego, RSI przestaje
tworzyć pełne wychylenia i jego faza opóźnia się w stosunku do danych liczbowych cyklu.

Dostrajanie standardowych wskaźników
85
Stochastic
Nazwa
tego
wskaźnika jest myląca, ponieważ nie ma ona absolutnie nic wspólnego ze
statystycznym procesem stochastycznym. Proces stochastyczny jest zdefiniowany jako
przypadkowo określone sekwencje obliczeniowe. Gdy Rick Redmont przesyłał ten wskaźnik
do Tima Slatera, przyszłego prezydenta Compu-Trac, słowo stochastic było naprędce
nabazgrane na marginesie. Tim pomyślał, że była to dobra nazwa i zaczął ją stosować.
Wskaźnik następnie spopularyzował Dr. George Lane.
Stochastic
mierzy
aktualną cenę zamknięcia w stosunku do najmniejszego minimum
(LL) w obserwowanym okresie. Wynik ten jest następnie dzielony przez rozpiętość pomiędzy
najwyższym maksimum a najmniejszym minimum w obserwowanym okresie. Jego równanie
przedstawia się następująco:
Stochastic=(close-LL)/(HH-LL)
Jeśli aktualna cena zamknięcia jest równa największemu maksimum w
obserwowanym okresie, to Stochastic przyjmuje wartość 1. Jeśli aktualna cena zamknięcia
jest równa najmniejszemu minimum w obserwowanym okresie, to Stochastic przyjmuje
wartość zero. Są to granice rozpiętości Stochastica.
Aby
przystosować Stochastic do mierzonego cyklu, należy wziąć połowę tego cyklu,
ponieważ rozpiętość od minimum do maksimum tego wskaźnika osiągana jest co połowę
cyklu w danym okresie. Podobnie jak wcześniej, program w języku EasyLanguage dla
optymalizowania Stochastica (pokazany na Rysunku 10.6), mierzy Cykl Dominujący stosując
pomiar MESA Cyklu Dominującego i następnie stosuje ten okres Cyklu Dominującego jako
podstawę do znalezienia HH i LL oraz obliczenia Stochastica. Ponieważ połowa okresu cyklu
może nie być uniwersalnym rozwiązaniem, dodajemy sygnał wejściowy CycPart jako
modyfikator. Ten sygnał wejściowy pozwala optymalizować obserwowany okres dla każdej
poszczególnej sytuacji.
inputs: Price(Close),
CycPart(.5),
Window(1),
RegCode(„LPJDPDTBHB);
vars: dc(0),
HH(0),
LL(0),
count(0),
Stochastic(0);
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
int,float,float,float,lpfloat;
Rysunek 10.6 Program w języku EasyLanguage dostosowujący Stochastic.

Dostrajanie standardowych wskaźników
86
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
HH = High;
LL = Low;
For count = 0 to IntPortion(CycPart*dc + .5) – 1 begin
If High[count] > HH then HH = High[count];
If Low[count] < LL then LL = Low[count];
End;
If HH – LL <> 0 then Stochastic = (Close – LL)/(HH – LL);
Plot1(Stochastic,”Stoc”);
Rysunek 10.6 Ciąg dalszy.
Optymalizowany Stochastic ma tendencję do bycia w fazie z oryginalną daną liczbową
ceny. Sugeruje to sposób zamiany dobrego wskaźnika na jeszcze lepszy. Jeśli odejmiemy 50
od optymalizowanego Stochastica, to otrzymamy średnio zero i w ten sposób, przy
przecięciach zera przez Stochastic zmierzamy do statystyki Poissona. Jeśli był taki przypadek,
to możemy gładzić optymalizowany Stochastic i utworzyć z niego optymalny filtr
przewidujący. W ten sposób możemy antycypować sygnały, a nie czekać na sygnały
potwierdzające przecinające linie 20 i 80 procent, tak jak to czyni standardowy wskaźnik.
Pozostawię twojej decyzji, która metoda najlepiej nadaje się do wykorzystania przez ciebie.
Commodity Channel Index (CCI)
Commodity Channel Index² oblicza średnią mediany ceny każdego słupka w
obserwowanym okresie. Oblicza on także odchylenie główne (MD) na podstawie tej średniej.
CCI jest przedstawiane jako aktualne odchylenie od średniej ceny normalizowanej do
odchylenia głównego. Na podstawie krzywej rozkładu prawdopodobieństwa Gaussa, 68
procent wszystkich możliwych wyników zawarte jest w obrębie odchylenia standardowego
wynoszącego jeden w porównaniu do odchylenia głównego. CCI jest skalowane, tak więc
wartości powyżej +100 oznaczają, że wynik znajduje się powyżej górnego odchylenia
standardowego wynoszącego jeden w stosunku do odchylenia głównego. Wartości,
znajdujące się poniżej –100 oznaczają, że wynik znajduje się poniżej dolnego odchylenia
standardowego wynoszącego jeden w stosunku do odchylenia głównego.
______________
²
Donald R. Lambert. „Commodity Channel Index” Commodities Magazine, październik 1980, strony 40-41.

Dostrajanie standardowych wskaźników
87
Mnożenie odchylenia głównego (MD), w przedstawionym programie w języku
EasyLanguage przez 0.015, służy do jej normalizowania. Wielu graczy giełdowych stosuje
ten wskaźnik jako sygnał wykupienia/wyprzedania, przyjmując, że gdy wynosi on +100 lub
więcej, to rynek jest wykupiony. Gdy jego wartość jest mniejsza niż –100, to przyjmują, że
rynek jest wyprzedany. Tak więc jest oczywiste, że kanał cenowy kształtowany przez ten
wskaźnik w obserwowanym okresie, jest taki sam jak szerokość cyklu. Ponieważ okres cyklu
może nie być uniwersalnym rozwiązaniem, dodajemy sygnał wejściowy CycPart jako
modyfikator. Ten sygnał wejściowy pozwala optymalizować obserwowany okres dla każdej
poszczególnej sytuacji.
inputs:
Price(Close),
CycPart(.5),
Window(1),
RegCode(„LPJDPDTBHB);
vars: dc(0),
Length(0),
MedianPrice(0),
Avg(0),
MD(0),
count(0),
CCI(0);
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
int,float,float,float,lpfloat;
defineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
Length = IntPortion(CycPart*dc + .5);
MedianPrice = (High + Low + Close)/3;
Avg = 0;
For count = 0 to Length –1 begin
Avg = Avg + MedianPrice[count];
End;
Rysunek 10.7 Program w języku EasyLanguage dostosowujący CCI.

Dostrajanie standardowych wskaźników
88
Avg = Avg / Length;
MD = 0;
For count = 0 to Length – 1 begin
MD = MD + AbsValue(MedianPrice[count] – Avg);
END;
MD = MD / Length;
If MD <> 0 then CCI = (MedianPrice – Avg)/(0.015 * MD);
Plot1(CCI,”CCI”);
Rysunek 10.7 Ciąg dalszy.
Zapamiętaj
• Najbardziej powszechny sposób stosowania wskaźników może być ulepszony zmieniając
ustalone okresy, wykorzystywane do jego obliczania. Można to wykonać za pomocą
pomierzonego okresu Cyklu Dominującego.
• Optymalnym okresem dla RSI jest połowa Cyklu Dominującego.
• Można określić przybliżony okres Cyklu Dominującego zwiększając szerokość RSI, aż do
momentu, w którym RSI przestaje tworzyć pełną rozpiętość. Okres Cyklu Dominującego
wynosi podwójną szerokość RSI. Kontynuując zwiększanie jego szerokości powodujemy
zmniejszanie amplitudy RSI i opóźnienie fazowe.
• Optymalnym okresem dla Stochastica jest połowa Cyklu Dominującego.
• Optymalnym okresem dla CCI jest pełny Cykl Dominujący.

Zawieranie transakcji zgodnie z Trybem Cyklu
89
Rozdział 11
Zawieranie transakcji zgodnie z Trybem
Cyklu
W tym rozdziale przedstawimy całkowicie automatyczny system transakcyjny
Maximum Entropy Spectral Analysis (MESA), oparty na zasadach przedstawionych w
poprzednich rozdziałach. Naszym sposobem podejścia do tego zagadnienia jest ustalenie
okresów dla Trybu Trendu i Trybu Cyklu oraz zawieranie transakcji zgodnie z Trybem Cyklu,
stosując tylko Sinewave Indicator. Kupujemy i sprzedajemy na podstawie przecięcia się tych
dwóch linii, z których składa się ten wskaźnik. System transakcyjny stosujący Tryb Trendu i
Tryb Cyklu łącznie, można rozwinąć i ulepszyć. Zamiarem tego rozdziału jest przedstawienie
niektórych technik ulepszających teoretyczne sygnały Trybu Cyklu w czysto mechanicznym
systemie transakcyjnym zgodnie z którym, przeprowadzane są transakcje na rzeczywistych
rynkach.
Program przedstawiony na Rysunku 11.1 jest kompletnym systemem transakcyjnym
stosującym zasady, ściśle oparte na podstawach teoretycznych. Jest on absolutnie nie do
zastosowania w rzeczywistych sytuacjach transakcyjnych lub dla poszczególnych
indywidualnych papierów wartościowych.
inputs:
Price(Close),
Window(1),
RegCode(„LPJDPDTBHB”);
vars: dc(0),
SmoothPrice(0),
DCPeriod(0),
count(0),
RealPart(0),
ImagPart(0),
DCPhase(0),
DCSine(0),
LeadSine(0),
ITrend(0),
IntPeriod(0),
Trendline(0),
Trend(0),
DaysInTrend(0);
DefineDllFunc: „c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
Rysunek 11.1 Teoretyczny system transakcyjny Trybu Cyklu.

Zawieranie transakcji zgodnie z Trybem Cyklu
90
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
Int,float,float,float,lpfloat;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,
”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
{Compute Dominant Cycle Phase}
SmoothPrice = (4*Price + 3*Price[1] +
2*Price[2] + Price[3]) / 10;
DCPeriod = IntPortion(dc + .5);
RealPart = 0;
ImagPart = 0;
For count = 0 To DCPeriod – 1 begin
RealPart
=
RealPart
+
Cosine(360*count
/
DCPeriod)*
(SmoothPrice[count]);
ImagPart
=
ImagPart
+
Sine(360*count
/
DCPeriod)*
(SmoothPrice[count]);
End;
If AbsValue(RealPart) > 0.001 then
DCPhase = Arctangent(ImagPart / RealPart);
If AbsValue(RealPart) <= 0.001 then
DCPhase
=
90*Sign(ImagPart);
DCPhase = DCPhase + 90;
If RealPart < 0 then DCPhase =
DCPhase
+
180;
{Compensate for one bar lag of the Weighted
Moving Average}
If dc <> 0 then DCPhase = DCPhase + 360 / dc;
{Don’t let phase exceed 360 degrees in a cycle}
If DCPhase > 360 then DCPhase = DCPhase – 360;
{Force phase wrap at 315 degrees to avoid
full scale wrap at 0-360 boundary}
If DCPhase > 315 then DCPhase = DCPhase – 360;
{Compute the Sine and LeadSine Indicators}
DCSine = Sine(DCPhase);
Rysunek 11.1 Ciąg dalszy.

Zawieranie transakcji zgodnie z Trybem Cyklu
91
LeadSine = Sine(DCPhase + 45);
{Compute Trendline as simple average over
the measured Dominant Cycle period}
ITrend = 0;
IntPeriod = IntPortion(dc + .5);
For count = 0 to IntPeriod – 1 begin
ITrend = ITrend + Price[count];
End;
If IntPeriod > 0 then ITrend =
ITrend
/
IntPeriod;
Trendline = (4*ITrend + 3*ITrend[1] +
2*ITrend[2] + ITrend[3]) / 10;
If CurrentBar < 12 then Trendline = Price;
{Assume Trend Mode}
Trend = 1;
{Measure days in trend from last crossing
of the Sinewave Indicator lines}
If LeadSine Crosses Over DCSine or LeadSine Crosses
Under DCSine then begin
DaysInTrend
=
0;
End;
DaysInTrend = DaysInTrend + 1;
If DaysInTrend < .5*dc then Trend = 0;
If AbsValue((SmoothPrice – Trendline)/
Trendline) >= .015 then Trend = 1;
If Trend = 0 then begin
If LeadSine Crosses Over DCSine
then
Buy(„LSine”)
on
Open;
If LeadSine Crosses Under DCSine
then
Sell(„SSine”)
on
Open;
End;
Rysunek 11.1 Teoretyczny system transakcyjny Trybu Cyklu.
Program rozpoczyna się od zdefiniowania funkcji MESA Dynamic Linked Library
(DLL), inicjowania DLL i następnie obliczania Cyklu Dominującego (dc) za pomocą DLL.
Następna część programu mierzy fazę i oblicza Sinewave Indicator dokładnie tak, jak to
zrobiliśmy w Rozdziale 8. Następnie obliczana jest gładzona Chwilowa Linia Trendu
dokładnie tak, jak w Rozdziale 8. Zakładamy, że rynek ma większą skłonność do
przebywania w Trybie Trendu i przyjmujemy Tryb Trendu jako stan domyślny. Następnie
przyjmujemy warunek Trybu Cyklu. Tryb Cyklu na pewno istnieje, gdy LeadSine przecina
DCSine wskaźnika Sinewave Indicator. Ponadto, Tryb Cyklu istnieje przez połowę Cyklu
Dominującego po wystąpieniu tego przypadku. Podążając śladem liczby słupków od czasu
wystąpienia przecięcia i porównując ten czas do połowy Cyklu Dominującego, możemy

Zawieranie transakcji zgodnie z Trybem Cyklu
92
oznaczyć okresy aktywności Trybu Cyklu. Jednakże, bardzo często można zauważyć, że cena
mocno odchyla się od Chwilowej Linii Trendu. W takich przypadkach jest wysoce
nieprawdopodobne, aby cena gładzona (SmoothPrice) przecięła Chwilową Linię Trendu, tak
jak należy spodziewać się tego w Trybie Cyklu. A zatem, ustanawiamy inną arbitralną regułę,
że jeśli SmoothPrice jest większa niż 1.5 procent od Chwilowej Linii Trendu, to rynek jest w
Trybie Trendu. Nasz system jest prosty. Zawieramy transakcje tylko wtedy, gdy rynek jest w
Trybie Cyklu. Kupujemy na otwarciu przy następnym słupku, gdy LeadSine przetnie w górę
DCSine. Sprzedajemy na otwarciu przy następnym słupku, gdy LeadSine przetnie w dół
DCSine. Przedstawaimy także stop zabezpieczający w przypadku, gdy nasze sygnały Trybu
Cyklu są błędne i rynek rozpoczyna Tryb Trendu przeciwko nam. Zajętą pozycję
utrzymujemy aż do momentu, gdy padnie sygnał jej odwrócenia lub osiągnięta została
wartość ustawionego stopu loss.
Jako
przykład, program najpierw zastosowano dla kontraktów futures Treasury Bonds,
ponieważ Treasury Bonds poruszją się cyklicznie w pewnych granicach. To jest, inaczej niż
kontrakty futures S&P i Nasdaq, Treasury Bonds nie mają odchyleń w postaci
długoterminowych trendów. Takiej selekcji dokonano dlatego, ponieważ system zawiera
transakcje, tak długie jak i krótkie, z równomierną częstotliwością, dzięki czemu nie ma
potrzeby dostosowania się do odchyleń systemu. Utworzono kontynuacyjny kontrakt,
począwszy od 9 lipca 1984 r., a skończywszy na 29 września 2000 r., tj. 15.88 lat.
(Kontynuacyjny kontrakt utworzono, wiążąc kolejne kontrakty w jedną całość i regulując
wszystkie ceny w poprzednich kontraktach za pomocą różnicy ceny w stosunku do dodanego
kontraktu. Czynność tę powtarzamy dla każdego nowego poprzedzającego kontraktu).
Dodając 1.000$ jako stop zarządzający, otrzymamy wynik przedstawiony w Tabeli 11.1.
Tabela 11.1 Wyniki początkowe systemu transakcyjnego Trybu Cyklu
__________________________________________________________________________________________
Całkowity
zysk
netto
24,125.00$
Liczba
transakcji
262
% zyskownych transakcji
41.2%
Średni
zysk
na
transakcji
92.08$
Współczynnik
zysku
1.18
Maksymalne osunięcie kapitału
(18,625.00$)
Wynik nie jest szczególnie dobry. Maksymalne osunięcie kapitału jest prawie takie jak
zysk netto, współczynnik zysku (stosunek sumy zysków ze wszystkich transakcji do sumy
strat ze wszystkich transakcji) jest niski. W tym przypadku większe znaczenie ma prowizja
wynosząca 30$ za jedną transakcję, 1 tick poślizgu przy zawieraniu transakcji wynoszący
31.25$ oraz 1 tick poślizgu przy wychodzeniu z rynku. Okaże się wtedy, że nasz średni zysk z
jednej transakcji jest w przybliżeniu równy naszym kosztom transakcyjnym. To jest,
powinniśmy przestać korzystać z takiej pomocy. Można jednak włożyć wysiłek w ulepszenie
rezultatów systemu transakcyjnego.
Pierwszym krokiem w ulepszeniu systemu transakcyjnego jest zrozumienie, że nie
uwzględniliśmy naruszenia teorii. Nasze wejścia na rynek zależą od przecinania się linii
LeadSine i DCSine. Ich wzajemne przecinanie się zależy od mierzonej fazy. Przypuszczalnie
doświadczamy większego opóźnienia niż oznaczyliśmy je teoretycznie. Na przykład,
zawieranie transakcji w następnym dniu na otwarciu, po przecięciu się LeadSine i DCSine,
jest równoznaczne z tym, że dodajemy jeden dzień opóźnienia. Możemy skompensować to
opóźnienie, korygując obliczenie fazy. Konkretyzując, optymalna kompensacja wynosi 3
słupki i taką też kompensację fazy wprowadzamy do programu.

Zawieranie transakcji zgodnie z Trybem Cyklu
93
{Kompensacja opóźnienia czasowego}
If dc <> 0 then DCPhase = DCPhase + 3 * 360 / dc;
Taka kompensacja ulepsza rezultaty systemu transakcyjnego, co przedstawia Tabela
11.2. W szczególności, prawie podwaja zysk netto.
Tabela 11.2 Wyniki systemu transakcyjnego Trybu Cyklu po kompensacji fazy
__________________________________________________________________________________________
Całkowity
zysk
netto
39,625.00$
Liczba
transakcji
334
% zyskownych transakcji
44.3%
Średni
zysk
na
transakcji
118.64$
Współczynnik
zysku
1.25
Maksymalne osunięcie kapitału
(20,406.00$)
Liczba
transakcji
także zwiększyła się, w wyniku czego średni zysk z transakcji wzrósł
tylko nieznacznie. Gdy zbadamy rezultaty bliżej zobaczymy, że transakcje po długiej stronie
rynku miały średni zysk 60$, podczas gdy transakcje po krótkiej stronie rynku miały średnią
stratę 20.375$. Jasne jest, że następnym krokiem ulepszania rezultatów jest spowodowanie
zmniejszenia strat po krótkiej stronie rynku. Zmierzając do końca, wypróbujemy najpierw
filtr, który pozwala na zawieranie krótkich transakcji tylko wtedy, gdy nachylenie Chwilowej
Linii Trendu jest skierowane do dołu. Program taki przedstawia się następująco:
If LeadSine Crosses Under DCSine and Trend < Trend[1] then
Sell(„SSine”) on Open;
Efektem
działanie tego filtra jest nie tylko wzrost zysku netto, ale również
zmniejszenie liczby transakcji, tak więc średni zysk z transakcji wzrasta, co zasługuje na
uwagę, do 245$, tak jak przedstawia to Tabela 11.3.
Tabela 11.3 Wyniki systemu transakcyjnego Trybu Cyklu po zastosowaniu filtra określającego kierunek trendu
__________________________________________________________________________________________
Całkowity
zysk
netto
47,837.00$
Liczba
transakcji
195
% zyskownych transakcji
35.9%
Średni
zysk
na
transakcji
245.83$
Współczynnik
zysku
1.40
Maksymalne osunięcie kapitału
(23,968.00$)
Praktycznie
nie
zmienił się zysk netto z transakcji po długiej stronie rynku, natomiast
strata netto z transakcji po krótkiej stronie rynku zmniejszyła się do 12.375$. Tak więc nadal
mamy problem z wyeliminowaniem straty netto z transakcji po krótkiej stronie rynku.
Zastosujemy
odmienną regułę, polegającą na tym, że zajmujemy krótką pozycję, gdy
pięciodniowa średnia LeadSine jest mniejsza niż pięciodniowa średnia DCSine. Program
uwzględniający tę regułę, przedstawia się następująco:
If LeadSine Crosses Under DCSine and Average(LeadSine,5) <
Average(DCSine,5) then Sell(„SSine”) on Open;

Zawieranie transakcji zgodnie z Trybem Cyklu
94
Bezpośrednim rezultatem tego filtra jest to, że większość transakcji po krótkiej stronie
rynku została wyeliminowana. W rezultacie zysk netto w przybliżeniu podwoił się, tak jak to
przedstawiono w Tabeli 11.4.
Tabela 11.4 Wyniki systemu transakcyjnego Trybu Cyklu po zastosowaniu średniej pięciodniowej do LeadSine
i DCSine
__________________________________________________________________________________________
Całkowity
zysk
netto
92,718.75$
Liczba
transakcji
100
% zyskownych transakcji
36.0%
Średni
zysk
na
transakcji
927.19$
Współczynnik
zysku
2.6
Maksymalne osunięcie kapitału
(15,281.25$)
Nie
tylko
podwoiliśmy zysk netto, ale również zmniejszyliśmy liczbę transakcji
prawie o połowę. Tak więc, średni zysk z transakcji wzrósł do 927$. Współczynnik zysku
(stosunek sumy wszystkich zysków z transakcji do sumy strat ze wszystkich transakcji)
podskoczył do 2.60 – co jest wspaniałym wynikiem, dającym wysokie prawdopodobieństwo
osiągnięcia sukcesu. Wszystkie wyniki raportu ulepszyły się, za wyjątkiem procentu
zyskownych transakcji.
Od
początku ulepszania systemu transakcyjnego nie zmieniliśmy wartości stop loss,
wynoszącego 1.000$. Gdy ustawimy stop loss na poziomie 2.200$ zauważymy, że system jest
znacznie zyskowniejszy. Przedstawia to tabela 11.5.
Tabela 11.5 Wyniki skończonego ulepszania systemu transakcyjnego Trybu Cyklu
__________________________________________________________________________________________
Całkowity
zysk
netto
112,093.75$
Liczba
transakcji
78
% zyskownych transakcji
55.1%
Średni
zysk
na
transakcji
1436.46$
Współczynnik
zysku
2.90
Maksymalne osunięcie kapitału
(17,650.00$)
Zwiększenie wartości stop loss umożliwia uniknięcie kilku stratnych transakcji, z
powodu zbyt szybkiego zamknięcia pozycji. Powoduje to zmniejszenie liczby transakcji, ale
ważniejszą rzeczą jest to, że zwiększył się procent zyskownych transakcji do ponad 50%.
Konsekwentny wzrost krzywej kapitału, przedstawionej na Rysunku 11.2 pokazuje, że system
wywiązywał się dobrze i był on stabilny przez okres 16 lat.
Rozpoczynając od czysto teoretycznych rozważań i wykonując kilka kroków,
doszliśmy do silnego i stabilnego automatycznego systemu transakcyjnego, który konkuruje
lub przewyższa większość dostępnych komercyjnych systemów transakcyjnych. Moim
zdaniem, jasno to dowodzi wartości projektowania systemów transakcyjnych opartych na
modelu teoretycznym.
Zawieranie transakcji zgodnie z Trybem Cyklu
95
Rysunek 11.2 Wzrost krzywej kapitału automatycznego systemu transakcyjnego Trybu Cyklu dla
Treasury Bond przez okres 15.88 lat.
Zapamiętaj
• Stanem domyślnym jest Tryb Trendu.
• Stan Trybu Cyklu trwa przez pół Cyklu Dominującego od momentu przecięcia się linii
wskaźnika LeadSine i DCSine.
• Jako dodatkową regułę przyjmujemy, że stan Trybu Trendu trwa wtedy, gdy SmoothPrice
jest większa o 1.5% od Chwilowej Linii Trendu.
• Opóźnienie można kompensować, modyfikując mierzony kąt fazowy.
• Stratne transakcje można eliminować za pomocą filtra.
• Skuteczność transakcji często można podwyższyć otwierając zlecenie stop loss.

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
96
Rozdział 12
Zyskowne systemy transakcyjne do gry na
rynku akcji
Tradycyjny
pomiar
skuteczności mechanicznych systemów transakcyjnych polega na
porównaniu osiągniętego zysku netto do zysku osiągniętego z prostej strategii kup i trzymaj.
Strategia kup i trzymaj była bardzo trudna do pobicia 1999 r. Obsunięcia kapitału były
minimalne. Nie było praktycznie żadnych kosztów transakcyjnych – rynek szedł prosto do
góry. Jednakże, w 2000 r. Pobicie strategii kup i trzymaj nie stanowiło żadnego problemu. W
rzeczywistości spadek na rynku uwypuklił jedną z największych zalet mechanicznych
systemów transakcyjnych. Tą zaletą jest to, że system transakcyjny dyscyplinuje gracza,
zmuszając go do zamknięcia pozycji przed wystąpieniem spadków.
Zawieranie
transakcji na rynku akcji różni się z kilku powodów od zawierania
transakcji na rynku towarowym. Po pierwsze, aby kupić akcje, inwestor musi podjąć decyzję,
jakie akcje kupować, wykonując proces filtrowania lub bliżej analizując dany papier
wartościowy. Analiza papieru wartościowego polega na sprawdzaniu fundamentów spółki,
takich jak proporcja P/E, zadłużenie, siła sektorowa i tak dalej. Taki ranking można znaleźć w
Investors Business Daily. Gracze mogą wykonać swoje własne przeszukiwania online,
stosując TIP za pomocą Telescan. Niektóre serwisy, takie jak
www.sabrient.com
, do
dokonywania selekcji papierów wartościowych stosują profesjonalną analizę. Z drugiej zaś
strony, gracz na rynkach towarowych łatwo może zdecydować o grze na rynku futures S&P,
Treasury Bonds i tak dalej. Po drugie, gracze zajmujący się akcjami, generalnie zajmują tylko
długą pozycję. Po trzecie, gracze na rynku akcji mają tendencję do mniejszej aktywności i
operują w znacznie dłuższym horyzoncie czasowym. Systemy podążające za trendem
najbardziej odpowiadają ich stylowi zawierania transakcji.
Jednym z najlepszych systemów podążających za trendem jest system wybicia z
kanału cenowego. W tego rodzaju systemie, górne ograniczenie kanału powstaje przez
połączenie cen maksymalnych każdego słupka, a dolne ograniczenie powstaje przez
połączenie cen minimalnych każdego słupka. Kanały te można przesuwać pionowo lub
poziomo w celu maksymalizowania osiągnięć systemu. Przesuwanie poziome można łatwo
wykonać, stosując opóźnienie o N słupków lub też za pomocą gładzenia, stosując średnią
ruchomą i wprowadzając opóźnienie średniej ruchomej do wykreślania tego przesunięcia.
Przesuwanie pionowe zazwyczaj rozszerza kanał i realizowane jest przez dodawanie stałej do
górnego ograniczenia kanału oraz odejmowanie stałej od dolnego ograniczenia kanału.
Powszechnie stosowane jest powiązanie stałej przesunięcia pionowego ze szczytem słupka
ceny. W danym kanale cenowym sygnał kupna występuje wtedy, gdy cena przetnie w górę
górny kanał cenowy, natomiast sygnałem sprzedaży jest przecięcie w dół dolnego kanału
cenowego. Reguły wejścia i wyjścia powinny być odwrócone, gdy stosujemy krótką sprzedaż.
Działanie typowego systemu wybicia z kanału cenowego pokazane jest na Rysunku 12.1.
Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
97
Rysunek 12.1 Działanie typowego systemu wybicia z kanału cenowego.
(Wykres powstał przy pomocy programu TradeStation2000i®)
Gdy gracz czeka na sygnał wejścia, pokazywany jest tylko górny kanał cenowy,
natomiast gdy gracz czeka na sygnał zamknięcia długiej pozycji, pokazywany jest tylko dolny
kanał cenowy.
Rozpoczynając projektowanie naszego systemu, podobnie jak w poprzednich
rozdziałach, stosujemy jako szablon program obliczający Maximum Entropy Spectral
Analysis (MESA) Cyklu Dominującego. Program ten przedstawiony jest na Rysunku 12.2.
inputs:
Price(Close),
CycPart(1),
Window(1),
RegCode(„LPJDPDTBHB”);
vars: dc(0),
alpha(0),
EntChannel(0),
ExitChannel(0);
DefineDllFunc: „c:\mesadll\mesa2kd.dll”,int,”INIT”,int;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,”DomCycle”,
Int,float,float,float,lpfloat;
DefineDllFunc:
„c:\mesadll\mesa2kd.dll”,int,
”MATRIX”,lpstr;
if currentbar = 1 then begin
init(1);
Rysunek 12.2 Program w języku EasyLanguage stosujący MESA w systemie wybicia z kanału
cenowego.

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
98
Matrix(regcode);
end;
DomCycle(Window,Price,H,L,&dc);
Alpha = 2*CycPart/(dc + 1);
EntChannel = alpha*High +
(1
–
alpha)*EntChannel[1];
ExitChannel = alpha*(3*Low – 2*High) +
(1
–
alpha)*ExitChannel[1];
If MarketPosition < 1 then Buy at EntChannel Stop;
If MarketPosition = 1 and ExitChannel >
ExitChannel[1] then ExitLong at
ExitChannel
Stop;
Rysunek 12.2 Program w języku EasyLanguage stosujący MESA w systemie wybicia z kanału
cenowego.
MESA Dynamic Linked Library (DLL) przywołuje obliczany za pomocą MESA Cykl
Dominujący, jako zmienną dc. Zmienna alfa, będąca wykładniczą średnią ruchomą, obliczana
jest przy zastosowaniu dc jako szerokości tej średniej ruchomej. Stosujemy dc ponieważ
wiemy, że ta szerokość usuwa składniki cyklu z ceny. Dodatkowy sygnał, zwany CycPart,
dołączany jest w celu umożliwienia optymalizacji osiągnięć systemu, skalując alfa. Górny
kanał cenowy obliczany jest jako wykładnicza średnia ruchoma cen maksymalnych każdego
słupka ceny. Dolny kanał cenowy obliczany jest jako wykładnicza średnia ruchoma
minimalnych cen każdego słupka minus podwójna rozpiętość pomiędzy ceną maksymalną a
minimalną każdego słupka. Tak zaprojektowany kanał cenowy jest asymetryczny. Kanał
asymetryczny zaprojektowano w celu umożliwienia wejścia na rynek tak szybko jak to
możliwe, gdy cena odwraca się do góry, oraz w celu umożliwienia trzymania pozycji aż do
momentu, gdy ceny pójdą zdecydowanie w dół. System ulepszy się, gdy zastosujemy regułę,
że nachylenie dolnego ograniczenia kanału musi być dodatnie, gdy cena przecina to
ograniczenie. Reguła ta redukuje prawdopodobieństwo wyrzucenia z rynku z powodu
nieprzewidzianych ruchów ceny.
Mając zaprojektowany system, następnym pytaniem jest jak najlepiej testować
wydajność takiego systemu. Przeprowadzenie testowania wymaga danych liczbowych. Im
więcej danych liczbowych tym lepiej. Duża ilość transakcji wymagana jest do upewnienia się,
że system nie jest źle dopasowany do danego rynku lub do danego okresu. Jest powszechną
praktyką tworzenie wstecznie regulowanych wykresów kontynuacyjnych kontraktów dla
towarów. Towary na ogół mają cztery kontrakty rocznie i przechodzimy od jednego kontraktu
do drugiego, gdy poprzedni kontrakt wygasa. Kontynuacyjny kontrakt tworzymy łącząc te
poszczególne kontrakty razem i kompensując wszystkie różnice cen poprzednich kontraktów
na podstawie ceny ostatnio dodanego kontraktu. Czynność ta powtarzana jest za każdym
razem, gdy dodajemy nowy kontrakt. Dane liczbowe akcji podawane są w sposób ciągły i nie
są one regulowane przez tworzenie wykresu kontynuacyjnego uwzględniającego wszystkie
akcje, więc otrzymanie dużej ilości danych liczbowych rynku akcji do testowania jest trudne.

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
99
W celu utworzenia danych liczbowych tak, aby można było przeprowadzić testowanie
rynku akcji stosując tylko pojedynczy zbiór, utworzyliśmy¹ papier wartościowy równoważny
kontraktowi kontynuacyjnemu.
Aby to uczynić, dokonaliśmy selekcji 50 akcji od 2 stycznia 1998 r. do 15 lutego 2001
r. Okres taki wybraliśmy dlatego, by uchwycić rynek byka w 1999 r. i rynek niedźwiedzia w
2001 r. Następnie połączyliśmy razem dane liczbowe cen tych 50 akcji, otrzymując
„rzeczywiste” dane liczbowe w polu liczba otwartych pozycji. Cena każdej akcji była
normalizowana do 100$ na początku danego okresu, w celu uniknięcia zniekształceń z
powodu różnic cenowych. Wykonując to, otrzymaliśmy 150 letni rynek cen akcji, w którym
możemy testować i optymalizować parametry systemu transakcyjnego. Wszystkie otwarte
pozycje zostały zamknięte w dniu 15 lutego 2001 r.
Gdy
testowaliśmy nasz system wybicia z kanału cenowego, którego program
przedstawia Rysunek 12.2, stosując 150 letnie dane liczbowe oraz zawierając transakcje tylko
na jednym papierze wartościowym, otrzymaliśmy wynik, przedstawiony w Tabeli 12.1.
Tabela 12.1 Wynik testu systemu wybicia z kanału cenowego dostosowanego za pomocą MESA
__________________________________________________________________________________________
Całkowity
zysk
netto
3,868.60$
Liczba
transakcji
157
Liczba
transakcji
na
rok
1.05
% zyskownych transakcji
55.4%
Średni
zysk
na
transakcji
24.64$
Współczynnik
zysku
3.19
Maksymalne osunięcie kapitału
(542.38$)
Wyniki
wyglądają ładnie z każdej strony. Stosunek całkowitego zysku do
maksymalnego osunięcia kapitału jest większy niż 7:1. Współczynnik zysku (stosunek sumy
wszystkich zysków do sumy wszystkich strat) jest większy niż 3:1. Więcej niż połowa
transakcji była zyskowna. System zawierał transakcje tylko średnio raz na rok. Biorąc pod
uwagę koszt prowizji wynoszący 0.16$ (na podstawie kosztów 8$ na 100 papierów
wartościowych po każdej stronie transakcji) i poślizgu 1/16 po każdej stronie transakcji,
koszty transakcyjne są mniejsze niż 0.30$ na papier wartościowy. Średni zysk z każdej
transakcji na papierze wartościowym, wynoszący 24,64$, znacznie przekracza koszty
transakcyjne.
Gdy
optymalizowałem współczynnik CycPart, to otrzymałem wartość 0.65. Wyniki
stosowania systemu są spektakularne. Przedstawia je Tabela 12.2.
Tabela 12.2 Wynik testu systemu wybicia z kanału cenowego dostosowanego za pomocą MESA przy
zastosowaniu 0.65 jako optymalizowanego współczynnika CycPart
__________________________________________________________________________________________
Całkowity
zysk
netto
4,153.35$
Liczba
transakcji
116
Liczba
transakcji
na
rok
0.77
% zyskownych transakcji
62.9%
Średni
zysk
na
transakcji
35.80$
Współczynnik
zysku
5.88
Maksymalne osunięcie kapitału
(212.98$)
______________
¹
Zbiór danych liczbowych, który utworzył Mike Barna,
tsda@attglobal.net
.

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
100
Wszystko zmierza w dobrym kierunku. Zysk netto wzrasta, liczba transakcji maleje,
zysk na jednej transakcji wzrasta o 45%.
Gdy
testowałem system transakcyjny podążający za trendem stwierdziłem, że składnik
cyklu ma ograniczone znaczenie. Dlatego też, stosowanie mierzonej długości cyklu przynosi
marginalny zysk w porównaniu z tym samym systemem stosującym stałą szerokość okresów.
Stała szerokość okresów zawierała się w przedziale od 1 do 2 średnio mierzonego okresu
cyklu. W takim przypadku nie ma rzeczywiście potrzeby stosowania złożonego pomiaru
cyklu. Odkryłem, że najlepsze są trzy rodzaje mechanicznych systemów transakcyjnych
podążających za trendem. Są to:
• system wybicia z kanału cenowego,
• system podwójnej średniej ruchomej,
• system konwergencji-dywergencji średniej ruchomej (MACD).
Te trzy systemy zaprojektowałem, przetestowałem i optymalizowałem, stosując te
same dane liczbowe 150 lat, w których testowałem system wybicia z kanału cenowego
dostosowanego za pomocą MESA. Program, dotyczący systemu wybicia z kanału cenowego,
przedstawia Rysunek 12.3.
Inputs:
Price((H+L)/2),
EntryLookBack(28),
ExitLookBack(26),
Vars: count(0),
EntryChannel(0),
ExitChannel(0);
EntryChannel = 0;
for count = 1 to EntryLookBack begin
if EntryChannel < High[count] then
EntryChannel
=
High[count];
end;
ExitChannel = 100000;
for count = 1 to ExitLookBack begin
if ExitChannel > Low[count] then
ExitChannel
=
Low[count];
end;
If MarketPosition = 0 and High >
EntryChannel
then
buy;
If MarketPosition = 1 and Low < ExitChannel
then
ExitLong;
Rysunek 12.3 Program w języku EasyLanguage dla systemu wybicia z kanału cenowego dla rynku
akcji.
Po optymalizacji stwierdziłem, że najlepszy okres do obliczania wejściowego kanału
wynosi 28 słupków. Najlepszy okres dla obliczania wyjściowego kanału wynosił troszeczkę
mniej, 26 słupków. Kanał wejściowy obliczany jest przez znalezienie największego

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
101
maksimum w rozważanym okresie. Kanał wyjściowy obliczany jest przez odnalezienie
najmniejszego minimum w rozważanym okresie. Sygnały transakcyjne są proste. Jeśli
aktualna pozycja jest krótka, sygnał kupna jest wtedy, gdy cena penetruje kanał wejściowy.
Gdy aktualna pozycja jest długa, to sygnał sprzedaży występuje wtedy, gdy cena penetruje
kanał wyjściowy.
W Tabeli 12.3 przedstawiono rezultaty testu systemu transakcyjnego wybicia z kanału
cenowego, przeprowadzonego przy zastosowaniu tych samych danych liczbowych dla 150
lat, co poprzednio.
Tabela 12.3 Wynik testu systemu wybicia z kanału cenowego
__________________________________________________________________________________________
Całkowity
zysk
netto
2,855.00$
Liczba
transakcji
447
Liczba
transakcji
na
rok
2.98
% zyskownych transakcji
45.4%
Średni
zysk
na
transakcji
6.39$
Współczynnik
zysku
1.70
Maksymalne osunięcie kapitału
(460.00$)
W porównaniu do systemu wybicia z kanału cenowego dostosowanego za pomocą
MESA, wzrosła częstotliwość transakcji, częściowo odpowiadająca za obniżenie zysku z
każdej przeprowadzonej transakcji. Maksymalne osunięcie kapitału także wzrosło. Ale
zamiarem tego rozdziału jest przedstawienie kilku systemów transakcyjnych, a nie znalezienie
absolutnie najlepszego, spełniającego wszystkie warunki.
System
przecięcia dwóch średnich ruchomych znany był tak długo jak istnieje analiza
techniczna. Mają one wielki urok, ponieważ gracz może ustalić, że krótsza średnia ruchoma
będzie wiernie podążać za rynkiem, podczas gdy dłuższa średnia ruchoma będzie mniej czuła
na ostatnie ruchy cenowe rynku. Tak więc, dłuższa średnia ruchoma reprezentuje pamięć
rynku. Program w języku EasyLanguage do obliczania systemu transakcyjnego przecięcia się
dwóch średnich ruchomych, przedstawia Rysunek 12.4.
Inputs: Price((H+L)/2),
Period1(11),
Period2(30);
Vars: SMA1(0),
SMA2(0),
EMA1(0);
{compute Simple Moving Averages (SMA)}
SMA1 = Average(Price, Period1);
SMA2 = Average(Price, Period2);
EMA1 = .02*Price + .98*EMA1[1];
Rysunek 12.4 Program w języku EasyLanguage systemu transakcyjnego przecięcia się dwóch
średnich ruchomych.

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
102
If MarketPosition = 0 and EMA1 > EMA1[1] and
SMA1 Crosses Over SMA2 then Buy on Open;
If MarketPosition = 1 and SMA1 Crosses
Under SMA2 then ExitLong on Open;
Rysunek 12.4 Ciąg dalszy.
Alfa 100 słupkowej wykładniczej średniej ruchomej, EMA1, wynosi
alfa=2/(100+1)≈0.02. Aby zapewnić, że długa pozycja będzie otwarta tylko wtedy, gdy trend
jest rosnący, zmuszony jestem przedstawić dodatkową zasadę, a mianowicie, nachylenie 100
słupkowej wykładniczej średniej ruchomej musi być dodatnie, gdy średnie ruchome
przecinają się. Zabezpiecza to przed zajęciem długiej pozycji podczas spadków.
Tabela
12.4
pokazuje,
że system przecięcia się średnich ruchomych, testowany w tym
samym okresie 150 lat, posiada rezultaty możliwe do zaakceptowania. Optymalnym
parametrem dla krótszej średniej ruchomej był okres 11 słupków, natomiast dla dłuższej
średniej ruchomej ten okres wynosi 30 słupków.
Tabela 12.4 Wynik testu systemu przecięcia się dwóch średnich ruchomych
__________________________________________________________________________________________
Całkowity
zysk
netto
2,855.00$
Liczba
transakcji
447
Liczba
transakcji
na
rok
2.98
% zyskownych transakcji
45.4%
Średni
zysk
na
transakcji
6.39$
Współczynnik
zysku
1.86
Maksymalne osunięcie kapitału
(460.00$)
Współczynnik zysku wynosi przyzwoitą wielkość, tj. prawie 2:1. System przecięcia
się średnich ruchomych ma prawie taką samą częstotliwość zawierania transakcji jak system
wybicia z kanału cenowego oraz troszeczkę mniejszy średni zysk na każdej transakcji.
System
MACD
wymyślił Gerald Appel. Nazwa jest akronimem słów: moving average
convergence-divergence (konwergencja-dywergencja średniej ruchomej). Idea zasadza się na
rozpatrywaniu różnicy pomiędzy dwiema średnimi ruchomymi. Różnica ta tworzy kształt fali
pozbawiony trendu, wskazujący sygnał kupna, gdy następuje przebicie od dołu linii zero.
Warunkiem zamknięcia długiej pozycji jest przecięcie linii zero przez gładzony kształt fali,
ponieważ taki warunek zmniejsza ilość błędnych transakcji. Aby upewnić się, że system
otworzy długą pozycję tylko wtedy, gdy trend jest rosnący, ustanowiłem dodatkową regułę, że
nachylenie 40-słupkowej wykładniczej średniej ruchomej (alfa=0.05) musi być dodatnie, gdy
otwierana jest długa pozycja. (Patrz Rysunek 12.5)
Inputs:
Price((H+L)/2),
Period1(8),
Period2(25);
Vars: alpha1(0),
Rysunek 12.5 Program w języku EasyLanguage systemu MACD.

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
103
alpha2(0),
EMA1(0),
EMA2(0),
EMA3(0),
MMACD(0),
Signal(0);
{copmute alphas for Exponential Moving Averages}
alpha1 = 2 / (Period1 + 1);
alpha2 = 2 / (Period2 + 1);
{compute Exponential Moving Averages (EMA)}
EMA1 = alpha1*Price + (1 – alpha1)*EMA1[1];
EMA2 = alpha2*Price + (1 – alpha2)*EMA2[1];
EMA3 = .05*Price + .95*EMA3[1];
MMACD = EMA1 – EMA2;
Signal = .1*MMACD +.9*Signal[1];
If MarketPosition = 0 and EMA3 > EMA3[1]
and MMACD Crosses Over 0 then Buy on Open;
If MarketPosition = 1 and Signal Crosses
Under 0 then ExitLong on Open;
Rysunek 12.5 Ciąg dalszy.
Tabela 12.5 pokazuje, że system MACD daje najwyższy zysk, spośród tych trzech
systemów, a prawdopodobieństwo sukcesu wynosi 2:1 (współczynnik zysku wynosi 2,18).
Można to wytłumaczyć zawieraniem bardziej logicznych transakcji w porównaniu do innych
systemów podążających za trendem. Daje to średni zysk z każdej transakcji wynoszący
10.33$.
Tabela 12.5 Wynik testu systemu MACD
__________________________________________________________________________________________
Całkowity
zysk
netto
4,338.00$
Liczba
transakcji
420
Liczba
transakcji
na
rok
2.80
% zyskownych transakcji
42.4%
Średni
zysk
na
transakcji
10.33$
Współczynnik
zysku
2.18
Maksymalne osunięcie kapitału
(365.00$)
Systemy
podążające za trendem kontrastują z innym typem szeroko znanego systemu,
zwanego systemem wybicia ze zmienności. Program w języku EasyLanguage ujmujący ten
system, przedstawia Rysunek 12.6

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
104
Inputs: EntryFactor(.5),
ExitFactor(1.5),
AveLength(4);
Vars: counter(0),
TR(0),
ATR(0);
If CurrentBar > AveLength then begin
TR = High – Low;
if High – Close[1] > TR then
TR
=
High
–
Close[1];
if Close[1] – Low > TR then
TR
=
Close[1]
–
Low;
ATR
=
0;
For counter = 0 to AveLength – 1
begin
ATR
=
ATR
+
TR[counter];
end;
ATR = ATR / AveLength;
If MarketPosition = 0 then buy at
Close[1]
+
EntryFactor*ATR[1]
stop;
If MarketPosition = 1 then
ExitLong
at
Close[1]
–
ExitFactor*ATR[1]
stop;
end;
Rsunek 12.6 Program w języku EasyLanguage systemu wybicia ze zmienności.
Podstawową ideą jest kupno, gdy cena przekracza poprzednie zamknięcie plus
rzeczywista średnia rozpiętość i zamknięcie długiej pozycji, gdy cena spada poniżej
poprzedniego zamknięcia minus rzeczywista średnia rozpiętość. Punkty wejścia i wyjścia
skalowane są jako części ułamkowe rzeczywistej średniej rozpiętości. Dla wejścia optymalny
współczynnik skalowania wynosi 0.5, a dla wyjścia optymalny współczynnik skalowania
wynosi 1.5. Program rozpoczyna się od obliczenia rzeczywistej rozpiętości (TR). Rzeczywista
rozpiętość to największa wartość z poniższych trzech wartości:
• aktualne maksimum minus aktualne minimum,
• różnica pomiędzy aktualnym maksimum i poprzednim zamknięciem,
• różnica pomiędzy poprzednim zamknięciem i aktualnym minimum.
Rzeczywiste rozpiętości są uśredniane dla tej samej ilości słupków, dzięki czemu
otrzymujemy rzeczywistą średnią rozpiętość (ATR). Ustaliłem, że optymalna ilość słupków
wynosi 4.
System wybicia ze zmienności daje prawie taki sam zysk netto jak systemy podążające
za trendem, ale istotnie wzrasta ilość przeprowadzanych transakcji. System zawiera średnio
około 1.5 transakcji na miesiąc. W rezultacie średni zysk z transakcji zmniejsza się do 1.28$.
Ponieważ koszty transakcyjne wynoszą około 0.3$, system w rzeczywistości przynosi zysk

Zyskowne rynkowe systemy transakcyjne do gry na rynku akcji
105
około 1$ na każdej transakcji. Prawdopodobieństwo sukcesu, który odzwierciedla
współczynnik zysku, jest także mniejsze niż w systemach podążających za trendem. (Patrz
Tabela 12.6)
Tabela 12.6 Wynik testu systemu wybicia ze zmienności
__________________________________________________________________________________________
Całkowity
zysk
netto
3,364.00$
Liczba
transakcji
2630
Liczba
transakcji
na
rok
17.53
% zyskownych transakcji
43.7%
Średni
zysk
na
transakcji
1.28$
Współczynnik
zysku
1.24
Maksymalne osunięcie kapitału
(695.00$)
Zapamiętaj
• Systemy wymagają dużej ilości danych liczbowych aby prawidłowo dobrać parametr.
Można to uczynić tworząc kontrakt kontynuacyjny, w którym normalizowane dane
liczbowe ceny łączone są ze sobą w jedną całość.
• Stosowanie Cyklu Dominującego ustalanego za pomocą MESA nie jest konieczne w
systemach podążających za trendem, ponieważ wpływ Cyklu Dominującego jest
znoszony.
• Systemy transakcyjne podążające za trendem są najlepsze.

Objaśnienia
107
Objaśnienia
aliasing
Fałszywe odtworzenie sygnału będące rezultatem próbkowania poniżej
kryterium próbkowania Nyquista. Przykładem aliasingu są koła dyliżansu, które będąc
w ruchu, sprawiają pozorne wrażenie jakby obracały się do tyłu.
amplituda
Wielkość wychylenia cyklu. Zazwyczaj wyrażana jest jako połowa różnicy
pomiędzy wartością maksymalną a wartością minimalną fankcji cyklu. Amplituda jest
długością fazora cyklu.
Analiza Spektralna Maksymalnej Entropii
Metoda przybliżenia spektralnego, którą
utworzył dr John Parker Burg.
ARMA
Skrót od AutoRegressive Moving Average. Oznacza autoregresywną średnią
ruchomą.
autokorelacja
Funkcja mierząca korelację kształtu fali w czasie z tą samą falą
przebiegającą w opóźnieniu do fali pierwotnej. Na przykład, fala sinusoidalna jest
całkowicie skorelowana z nią samą, przesuniętą o jeden cykl.
bel
Jednostka logarytmicznej miary stosunku energii lub mocy dwóch sygnałów. Nazwa
wprowadzona przez Aleksandra Grahama Bella w jego pracach naukowych na temat
dźwięku.
CCI Skrót od Commodity Channel Index
cena syntetyczna
Funkcja, która jest w fazie z cyklem dominującym dla rzeczywistych
danych liczbowych. Obliczana jest przez odejmowanie prostej średniej ruchomej o
szerokości równej połowie cyklu dominującego od prostej średniej ruchomej o
szerokości równej jednej czwartej cyklu dominującego (lub równoważnych
wykładniczych średnich ruchomych).
CTRW
Skrót od Continuous Time Random Walk. Oznacza kontinuum czasowe
błądzenia losowego.
cykl Ruch, w którym element powraca do punktu pierwotnego po upływie określonego
czasu.
częstotliwość
Prędkość zmian następujących po sobie cykli. Na przykład,
częstotliwością jest 2,000 obrotów na minutę.
dc
Cykl Dominujący.
decy przedrostek oznaczający jedną dziesiątą.
decybel
1 decybel=0.1b.
DLL Skrót od Dynamic Linked Library. Jest to plik, w którym znajduje się skompilowany
kod źródłowy, który może być później wykorzystany w połączeniu z jakąś aplikacją.
drganie
Pochodna lub prędkość zmian impulsu. Może być wizualizowana jako złożenie
dodatniego impulsu i ujemnego impulsu.
dywergencja Występuje wtedy, gdy kierunek zmiany ceny jest przeciwny do kierunku
zmiany wartości jakiegoś wskaźnika. Na przykład, cena wzrasta a impet maleje.
dziesiątkowanie
Literalnie oznacza branie co dziesięć, ale w praktyce zazwyczaj
oznacza branie co dwa. Eksperymentatorzy czasami pamiętają z przeszłości, jak długo
trwało dobieranie odstępów próbkowania w celu otrzymania składników o wysokiej
częstotliwości za pomocą analizy bez aliasingu. Natomiast, aby skrócić czas
obliczania, próbkowanie można usunąć z obliczeń składników niskiej częstotliwości.
EMA Skrót od Exponential Moving Average. Oznacza wykładniczą średnią ruchomą.
energia kinetyczna Energia przypisana masie znajdującej się w ruchu.

Objaśnienia
108
entropia
Miara niedostępnej energii lub nieuporządkowania. Pojęcie stosowane w teorii
termodynamiki i w informatyce. Nazwa pochodzi z języka greckiego i oznacza
przeobrażenie.
faza Określone położenie w obrębie cyklu. Faza jest zazwyczaj wyrażana w kątach w
stosunku do położenia początkowego. Jeden cykl składa się z 360 stopni fazowych.
fazor Wirujący wektor przedstawiający położenie fazy w cyklu.
FFT Skrót od Fast Fourier Transform. Oznacza szybką transformację Fouriera.
filtr dolnoprzepustowy
Filtr, który pozwala na przejście tylko składnikom o niskiej
częstotliwości, blokując składniki o wysokich częstotliwościach. Często stosowany
jako filtr wygładzający.
FIR Skrót od Finite Impulse Response. Oznacza skończone oddziaływanie impulsu.
funkcja liniowa
Funkcja posiadająca stałe nachylenie, rozpoczynające się od jej
początku.
funkcja skokowa
Funkcja mająca nagły brak ciągłości na początku i równomierną
amplitudę wszędzie indziej.
gładzenie
Proces usuwania zmiennych o wysokiej częstotliwości za pomocą filtra
dolnoprzepustowego. Gładzeniu zawsze towarzyszy opóźnienie czasowe.
IIR
Skrót od Infinite Impulse Response. Oznacza nieskończone oddziaływanie impulsu.
impet (mechaniczny)
Właściwość ciała znajdującego się w ruchu, określająca ilość
czasu potrzebną na doprowadzenie go do stanu spoczynku pod wpływem stałej siły
przyłożonej do tego ciała. Na rynku, zazwyczaj oznacza to różnicę pomiędzy cenami
w określonym przedziale czasu.
impuls
Funkcja matematyczna, która istnieje tylko jako funkcja oryginalna. Funkcja
oryginalna posiada nieskończoną wysokość i zerową szerokość, tak więc pole w
obrębie funkcji oryginalnej jest jednostkowe.
KAMA
Skrót od Kaufman Adaptive Moving Average. Oznacza dostosowaną średnią
ruchomą Kaufmana.
konwergencja
Sytuacja, gdy kierunek zmiany ceny jest taki sam jak kierunek zmiany
wartości wskaźnika, na przykład, gdy cena i impet rosną jednocześnie.
maksymalna entropia
Formalizm opisujący optymalną procedurę obliczeniową. Na
przykład, jeśli cała informacja została wydobyta z sygnału, pozostałość jest resztą z
maksymalną entropią. Pozostałość może być testowana dla sprawdzenia, czy
rzeczywiście ma ona maksymalną entropię.
MAMA
Skrót od Mesa Adaptive Moving Average. Oznacza średnią ruchomą
dostosowaną za pomocą Mesa.
MD Odchylenie główne.
MESA
Nazwa programu transakcyjnego opartego na cyklach oraz nazwa firmy,
będącej twórcą tego programu. MESA jest akronimem słów Maximum Entropy
Spectral Analysis. Oznacza to analizę spektralną maksymalnej entropii.
ograniczone próbkowanie Nyquista
Każda funkcja o ograniczonym paśmie, którą
można wiernie odtworzyć na podstawie próbek pobieranych co najmniej dwa razy na
cykl.
okienkowanie
Pobieranie próbki danych liczbowych przedstawiających dłuższy
strumień danych liczbowych. Matematycznie, jest to równoważnik mnożenia danych
liczbowych przez jeden w obrębie szerokości okienka i mnożenie przez zero poza
okienkiem. Efektem okienkowania prostokątnego w transformacji Fouriera sin(X)/X
jest odpowiedź będącą nałożeniem na transformacje Fouriera rzeczywistego sygnału.
okres Szerokość cyklu. Okres jest odwrotnością częstotliwości.
pi
Proporcja wyrażająca stosunek długości okręgu do jego średnicy. Wynosi 3.1415926...

Objaśnienia
109
pierwszy rząd
Termin oznaczający proste przybliżenie. Termin pochodzi od
stosowania tylko pierwszego członu N elementowego rozwinięcia szeregu
potęgowego funkcji jako jej przybliżenie.
pochylenie Prędkość zmian.
prosta średnia ruchoma
Prosta średnia N próbek jest sumą tych próbek, z których każda
ważona jest przez N. Innymi słowy, jest to średnia arytmetyczna N elementów
liczbowych. Taka średnia staje się średnią ruchomą przez równoczesne dodawanie
nowej ważonej próbki i odrzucanie najstarszej ważonej próbki.
rezonans
Stan, w którym oscylowanie jest dopuszczalne tylko dla jednej częstotliwości.
RSI Skrót od słów relative strength index. Oznacza wskaźnik siły względnej.
równanie dyfuzji
równanie różniczkowe opisujące drogę przebytą przez łyżeczkę
umieszczaną w filiżance gorącej kawy lub drogę cząsteczek smugi dymu
opuszczającej komin. Przez analogię, może ono opisywać ruch rynku, pod warunkiem
uwzględnienia Spaceru Pijanego.
Równanie Telegrafisty
Równanie różniczkowe, które opisuje drogę fali w parze drutów
telegraficznych. Przez analogię, opisuje ono rynek w trybie cyklu.
ruchy Browna
Przypadkowe trójwymiarowe ruchy. Można je sobie wyobrazić jako
drogę cząsteczki powietrza w słoiku, w którym panuje próżnia, bez oddziaływań
grawitacyjnych i elektrostatycznych.
sezonowy
Układ, który powtarza się co 12-miesięczny okres.
sin(X)/X
Funkcja matematyczna, w której X wyrażone jest radianach. Jest to
transformacja Fouriera impulsu za pomocą ujednoliconej amplitudy.
SMA Skrót od słów simple moving average. Oznacza prostą średnią ruchomą.
splot metoda obliczania sygnału wyjściowego filtra w dziedzinie czasu stosując jako sygnał
wejściowy kształt fali w dziedzinie czasu i czasowo pofałdowany impuls odpowiedzi
filtra.
syntetyczna cena pozbawiona trendu
Funkcja, która jest w fazie z cyklem
dominującym dla rzeczywistych cen rynkowych. Jest ona obliczana przez
odejmowanie prostej średniej ruchomej o długości równej połowie cyklu
dominującego od prostej średniej ruchomej o długości równej jednej czwartej cyklu
dominującego (lub równoważnych wykładniczych średnich ruchomych).
szereg Fouriera
Teoria, za pomocą której można syntezować każdy, dowolny kształt fali
lub opisywać ją, stosując nieskończoną serię funkcji sinus i cosinus. Każdy element w
tej serii może posiadać niezależną amplitudę i fazę.
szum Wszystkie funkcje, które nie zawierają informacji. Przykładem szumu są zakłócenia w
radiu w postaci pisków. Jedyną informacją jaką zawierają te piski jest to, że radio jest
włączone.
szybka transformacja Fouriera
Metoda obliczania współczynników Fouriera,
sprowadzająca te obliczenia do wzoru N*log(N), gdzie N jest szerokością
próbkowania.
transformacja Fouriera
Asymetryczny proces do opisywania funkcji w zależności od
częstotliwości, dając dziedzinę czasu jako odpowiedź lub opisywanie funkcji w
zależności od czasu, dając częstotliwość jako odpowiedź.
trend Kierunek zmian generalnie liniowy. Na rynku, trendy są często identyfikowane przez
kreślenie linii pomiędzy następującymi po sobie najwyższymi szczytami lub
najniższymi dołkami.

Objaśnienia
110
VIDYA
Skrót od słów Variable Index Dynamic Average. Oznacza zmienny wskaźnik
średniej dynamicznej.
widmo gęstości spektralnej
Funkcja kontynuacyjna opisująca widmo funkcji w
zależności od częstotliwości. Jest to dyskretna w czasie transformacja Fouriera
autokorelacji sekwencji próbkowanej funkcji.
WMA
Skrót od słów Weighted Moving Average. Oznacza ważoną średnią ruchomą.
wskaźnik siły względnej
Normalizowany wskaźnik giełdowy wyrażający stosunek sumy
zdobyczy cenowych z dni, w których cena zamknięcia była wyższa od ceny
zamknięcia w dniu poprzednim do sumy zdobyczy cenowych z dni, w których cena
zamknięcia była wyższa od ceny zamknięcia w dniu poprzednim plus suma strat
cenowych z dni, w których cena zamknięcia była niższa od ceny zamknięcia w
poprzednim dniu, w określonym przedziale czasu.
wskaźnik stochastyczny
Normalizowany wskaźnik, w którym różnica pomiędzy
niedawnym najwyższym maksimum a aktualną ceną zamknięcia jest dzielona przez
różnicę pomiędzy niedawnym najwyższym maksimum a niedawnym najniższym
minimum. Pojęcie niedawny jest przestrzenią czasową wybraną przez technika
analitycznego.
wybielanie wstępne
Usuwanie znanych składników częstotliwości wcześniej
zanalizowanych.
wykładnicza średnia ruchoma
Obliczenia rekursywne średniej ruchomej realizowane
przez dodawanie części aktualnej ceny do dopełnienia tej części poprzednio obliczoną
wartością wykładniczej średniej ruchomej. Czasami nazywana filtrem Infinite Impulse
Response (IIR) (nieskończone oddziaływanie impulsu). Oddziaływanie czasowe na
impuls wejściowy jest wykładniczym rozkładem amplitudy.
wyrażenie pierwotne
Funkcja podstawowa, nie pochodna. Stosowane tutaj fale
sinusoidalne są wyrażeniami pierwotnymi, z których mogą być syntezowane złożone
kształty fal. Patrz szereg Fouriera.
zawężanie
Ważenie współczynnika stosowanego do kształtowania danych liczbowych w
obrębie okna próby. Zawężanie stosowane jest do redukowania echa bocznego
promieniowania anteny takiego jak funkcja sin(X)/X, która jest efektem transformacji
Fouriera okienka prostokątnego.
zmienna losowa
Zmienna, będąca wartością losową spośród dostępnych możliwych
wartości.
zmienna stochastyczna
Wynik doświadczenia mającego wyczerpująco określić
wykluczające się wzajemnie przypadki i określić prawdopodobieństwo ich
występowania, tak nazywana ponieważ branie każdej z możliwych wartości jest
zupełnie przypadkowe.

Skorowidz rzeczowy
113
Skorowidz rzeczowy
A
Akcje:
systemy
transakcyjne,
149-157
transakcje, porównanie z towarami, 143-144
wybieranie,
143-144
Alfa (α), 51-52
filtrów
wycinających, 107-108, 110-111
prostych
średnich ruchomych (SMA), 52
wykładniczych średnich ruchomych (EMA), 51, 52-53, 56, 152
Amplituda, 21-22, 23
impetu,
59
kompensacja,
63-65,67
proporcjonalność do skali czasu, 25-27
Analiza:
harmoniczna,2
przeciwieństwo syntezy, 33
rynku, 1, 3-4, 17, 69-77
spektralna
(patrz Spektralna analiza)
Antyaliasing w MESA, 79-80,91
Autoregresywna średnia ruchoma (ARMA), 84
Autoregresywny model, 83-84
B
Bernoulli, Daniel, 2
Biorytmy, 29
Błądzenie losowe, 6-7, 15. Patrz także Spacer Pijanego
ciągłość czasowa, 10-11
Błędne transakcje, unikanie, 93, 95, 99
Browna ruchy, 6
Burg, John, 3, 85-86
C
Ceny:
analiza
za
pomocą flag/chorągiewek, 39-41
współczynniki w impecie, 5
przewidywanie za pomocą impetu, 58-59
przewidywanie za pomocą MESA, 73
Chorągiewki, 38-41
Chwilowa Linia Trendu, vii, 105-116
i WMA, 111-112
obliczanie,
105-106, 113-115
opóźnienie, 106
oszacowanie trendu, 112-113
Ciągłość czasowa błądzenia losowego (CTRW), 10-11
Commodity Channel Index (CCI), 128-130
obliczanie,
128
optymalny okres, 128, 130
stosowanie,
128
Cooley, Jim, 3
Cosinusoidalne fale, 20-21
Cykle. Patrz także Rynkowe cykle
a fale sinusoidalne, 17-18
amplituda, 5, 21-22, 23
charakterystyka, 1, 4-5, 17-23
częstotliwość, 18-19, 22-23
definicja,
4,
18

Skorowidz rzeczowy
114
Dominujące (Patrz Dominujące Cykle)
faza, 19-21, 23
gospodarcze,
4-5
impetu,
59
jako model rynku, 17
kierunek
zmian,
57
krótkoterminowe, 6, 35, 80, 85
lokalizacja pozycji, 94
okresy, 4, 18, 22-23, 83, 102
parametry,
18
podstawy,
25-41
proporcjonalność, 25-27
rezonans,
30-33
rys historyczny, 2-4,
siła, 21-22
superpozycja,
27-30
średnia szerokość, 35
wykresy odwrotne, 25
zastosowanie w transakcjach, 5-6, 15, 35-41, 80
zawijanie,
98
Cyklu Tryb:
identyfikacja, 135, 141
przewidywanie punktów zwrotnych, 93-94, 99, 104
stosowanie w transakcjach, 131-141
Częstotliwość, 18-19, 22-23
Nyquista,
45
Częstotliwości wycinanie, eliminowanie, 62, 106-109
Częstotliwości odpowiedź, obliczanie, 60-62
D
Dane liczbowe:
oddzielanie trendu, 81-82
próbkowanie,
45
wymagana
ilość do analizy za pomocą FFT, 70, 77
wymagana
ilość do analizy za pomocą MESA, 72, 73-74, 82-83, 92
wymagana
ilość do testowania systemów transakcyjnych, 147-148, 157
Danych liczbowych gładzenie. Patrz Średnie ruchome
Decybele, 22
Dolnoprzepustowe filtry, 43
Dominujący Cykl, 94
a Chwilowa Linia Trendu, 105
obliczanie fazy, 95-98
określenie szerokości, 118
oznaczanie
za
pomocą RSI, 121-124, 130
szerokość w Trybie Trendu, 110
Dopasowane filtry, 54
Dyfuzji równanie, 9-10
E
Ehlera filtr, 55
Eliptyczne filtry, 80, 106-107, 111
Elliotta fal teoria, 29-30
Energia, zasada zachowania, 12-14
F
Fale. Patrz także Sinusoidalne fale
cosinusoidy,
20-21
LeadSine, 98, 102
piłokształtne, 29
przemieszczanie
się, 32-33

Skorowidz rzeczowy
115
stojące, 30-33
syntezowanie z funkcji podstawowych, 27-29
wydzielanie
składników, 105-106
Fali równanie, 2
Faza, 19-21, 23
Cyklu
Dominującego, obliczanie, 95-98
kierunek zmian, 102, 104
usuwanie
niejasności, 98
wpływ na impet, 19, 66
wpływ na średnie ruchome, 19
w Trybie Trendu, 94, 104
Fazory, 18
a
sinusoidy,
19-20
Fazowa prędkość, 44
Fazowe opóźnienie:
EMA,
56
SMA,
55
WMA,
56
Fazowe wyprzedzenie, przewidywanie zachowania rynku, 57, 94
Fazowy kąt, 19-20, 23
obliczanie,
98
Filtry:
antyaliasing,
91
dolnoprzepustowe,
43
dopasowywanie,
54
Ehlera,
55
eliptyczne, 80, 106-107, 111
górnoprzepustowe,
81
impetu,
60
KAMA,
55
krótka
sprzedaż, 138-139
MAMA,
55
nieliniowe,
54-55
nieskończone oddziaływanie impulsu (IIR), 43-44, 51-53
oddzielające trend, 60, 81-82, 92
przyczynowe,
93
skończone oddziaływanie impulsu (Patrz Skończone oddziaływanie impulsu, filtry)
szerokość, przesunięcie, 60
ustawienie w MESA, 73, 83, 92
VIDYA,
55
wycinanie
(Patrz Wycinające filtry)
Flagi, 38-41
Fourier, Jean-Baptiste-Joseph, 2
Fouriera serie, 29
Fouriera transformacja, 2
Fouriera szybkie transformacje (FFT), 3
liczba cykli w polu obserwacyjnym okienka, 69, 76
liczba wymaganych danych liczbowych, 70, 77
pomiar spektrum, 70-72
porównanie z MESA, 76, 82
wady,
69-72
zastosowanie do analizy rynku, 69, 76
Funkcje pierwotne, 18, 19
korzyści, 25, 41
nieharmoniczne,
29
syntezowanie
fal
złożonych, 27-29
G
Gauss, Carl Friedrich, 10
„Generalized Harmonic Analysis”, 3

Skorowidz rzeczowy
116
Gospodarcze cykle, 4-5
Górnoprzepustowe filtry, 81
Głowy i ramion formacja, 34-36
Grupowa prędkość, 44
Grupowe opóźnienie, 44
definicja,
46
H
Harmoniczna analiza, 2
Hurst, j. M., 1
I
Impet, 57-67
amplituda,
59
definicja,
57
efekt relacji wzajemnej z fazą, 19, 66
kompensowanie amplitudy, 63-65, 67
obliczanie,
59-61
przeciwwskazania,
59
przewidywanie cen, 58-59
sinusoidy,
57-58
SMA, 65-66, 67
stosowanie w filtrach, 60
stosowanie w transakcjach, 58-59
Investors Business Daily, 143
K
Kanały, 33
obliczanie,
145-147
Kaufmana dostosowana średnia ruchoma (KAMA), filtr, 55
Kondratiewa cykl ekonomiczny, 5
Krótka sprzedaż, obniżanie strat, 138-139
L
Lane, George, 124
LeadSine fala, 98, 102
M
Maksymalna entropia, 3-4
Maksymalna entropia analizy spektralnej (MESA), vii, 79-92
antyaliasing, 79-80, 91
DLL,
88-89
działanie, 73, 76
i nieliniowe filtry, 55
korzyści, 73-75, 82
maksymalizowanie zysku, 138-140
niedostatki,
83
oddzielanie trendu, 81-82
pomiar spektrum, 72-76, 89-91
porównanie z FFT, 76, 82
projektowanie systemów transakcyjnych, 143-147
przewidywanie cen, 73
przystosowanie
standardowych
wskaźników, 117-130
siła spektrum, 83, 84
stosowany algorytm, 83-91
stosowanie w transakcjach, 131-141
testowanie,
147-149
ustawianie filtrów, 73, 83, 92
wymagana
ilość danych liczbowych, 72, 73-74, 82-83, 92
MESA dostosowana średnia ruchoma (MAMA), filtr, 55

Skorowidz rzeczowy
117
Model wszystkich słupków, 83-84
N
Nasdaq kontrakty futures, 136
Newton, Isaac, 2
Nieliniowe filtry, 54-55
Nierekursywne obliczenia, 51
Nieskończone oddziaływanie impulsu (IIR), filtry, 43-44, 51-53
Nyquista częstotliwość, 45
O
Obligacje, 136
Oddzielające trend filtry, 60, 81-82
równania,
92
Opóźnienie:
a filtry eliptyczne, 107
Chwilowej Linii Trendu, 106
i filtry wycinające, 108-111
minimalizowanie, 98, 137, 141
SMA, 44, 55, 106
szerokość filtra, 60
w filtrach FIR
WMA,
56,
95
P
Piłokształtna fala, 29
Pitagoras, 2
Podwójnego szczytu formacja, 36-38
Prawdziwa rozpiętość (TR), 155-157
średnia, 157
Prąd zmienny, wytwarzanie, 19
Proporcjonalność, 25-27
Prosta średnia ruchoma (SMA), 43-44, 55-56
alfa,
52
impet,
65-66,
67
obliczanie,
44-48
opóźnienie, 44, 55, 106
opóźnienie fazowe, 55
pasmo przepustowe okresu, 55
stosowanie w transakcjach
Przecięcie się dwóch średnich ruchomych systemy, 151-153
wyniki
testu,
153
Przyczynowe filtry, 93
R
Redmont, Rick, 124
Rekursywne obliczenia, 43-44
Relative Strength Indicator (RSI) 93, 118-124
definicja,
118-119
obliczanie,
119-121
obserwowany okres, 119, 130
stosowanie,
121-124
Rezonans, 30-33
Różniczkowe równania, 8-9
Ruchome fale, 32-33
Rynek:
analiza, 1, 3-4, 17, 69-77
cykle jako model, 17
Elliotta fal teoria, 29-30
przewidywanie
stosując wyprzedzenie fazowe, 57, 94

Skorowidz rzeczowy
118
przypadkowość, 6
składniki, 5-6
wiarygodność przewidywań, 10, 74
wykupienia/wyprzedania warunki, 13
Rynkowe cykle, vii-viii, 1
analogia z meandrowaniem rzeki, 12-13
identyfikacja, vii-viii, 1
oddziaływanie na, 4
przewidywanie punktów zwrotnych, 93-94, 99, 104
stosowanie w transakcjach, 5-6, 15, 35-41
Rynkowe tryby:
identyfikacja, 58, 112-113, 115-116, 135-136, 141
zmiany, 94-95, 102-103
Rzeczywista średnia rozpiętość (ATR), 157
Rzeki, meandrowanie 12-13
S
S&P kontrakty futures, 136
Sinewave wskaźnik, vii-viii, 93-104
korzyści, 93, 99
obliczanie,
99-102
Sinusoidy, 17-18, 22
i fale cosinusoidalne, 20-21
i
fazory,
19-20
impet,
57-58
opis
matematyczny,
19
pochodne,
57
Skończone oddziaływanie impulsu (FIR), filtry, 43, 44-51
ocena
opóźnienia, 49
stosowanie w transakcjach, 50-51
Slater, Tim, 124-125
Spacer Pijanego, 6-7
równanie
różniczkowe, 8-9
sformułowanie, 7-14
Spektralna analiza, 2,3
pomiar amplitudy cyklu, 22
rynkowego widma, 69-77
rysowanie
widma,
90
Sporządzanie wykresów:
syntezowanie
formacji,
33-41
trudności, 25
Stochastic, 124-128
definicja,
125-126
optymalny okres, 126, 130
stosowanie,
126-128
Stojące fale, 30-33
Stop loss wartości, 139-140, 141
Stopa procentowa i cykle gospodarcze, 4-5
Superpozycja, 27-30
Synteza przeciwieństwem analizy, 33
Systemy wybicia z kanału cenowego, 144
wyniki
testowania,
150-151
Szum, 5
biały, 73
oddzielanie od sygnału, 54
Ś
Średnich ruchomych konwergencja/dywergencja, (MACD) system, 153-155
wyniki
testów,
155
Średnie ruchome, 43-56

Skorowidz rzeczowy
119
autoregresywna,
84
efekt wzajemnych relacji z fazą, 19
funkcje, 43, 55
porównanie z funkcjami impetu, 57
proste
(Patrz Proste średnie ruchome)
ważone (Patrz Ważone średnie ruchome)
wykładnicze (Patrz Wykładnicze średnie ruchome)
T
Telegrafisty Równanie, 11-12
TIP, 143-144
Towary:
kontrakty,
147
zawieranie
transakcji,
przeciwieństwo akcji, 143-144
Transakcje:
korzyści z systemów mechanicznych, 143
maksymalizacja
zysków, 138-140, 149
porównanie akcji do towarów, 143-144
projektowanie systemów, 143-157
stosowanie cykli, 5-6, 15, 35-41, 80, 131-141
stosowanie EMA, 152, 153
stosowanie filtrów FIR
stosowanie impetu, 58-59
stosowanie
SMA,
56
stosowanie standardowych wskaźników, 117-130
uzgadnianie
czynności w czasie, 136, 150
wzajemne
powiązania, 159-164
Trend, systemy podążające za trendem, 149-155, 157
porównanie z systemami wybicia ze zmienności, 155-157
Trendu Tryb:
identyfikacja, 112, 135-136, 141
faza, 94, 104
szerokość cyklu dominującego, 110
Trendy, 5
identyfikacja, 10, 112, 115-116
systemy
podążające za trendami, 144
związek z cyklami, 14
Tukey, John, 3
V
Variable Index Dynamic Average (VIDYA), filtr, 55
W
Ważone średnie ruchome (WMA):
i Chwilowa Linia Trendu, 111-112
opóźnienie, 56, 95
opóźnienie fazowe, 56
pasmo
przepustowości okresu, 56
przeprowadzanie
obliczeń, 48-50
Wiener, Norbert, 3
Wilder, J. Welles, 118
Wskaźniki, standardowe:
dostosowanie za pomocą MESA, 117-130
wybór,
117-118
Wstecznie regulowane kontynuacyjne kontrakty, 136
dla
towarów,
147
www.sabrient.com
, 144
Wycinające filtry, 106-109
alfa, 107-108, 110-111
opóźnienie, 108-111

Skorowidz rzeczowy
120
równanie,
107
zalety,
111
Wykładnicze średnie ruchome (EMA), 44
alfa, 51, 52-53, 56, 152
korzyści, 53
obliczanie,
51-53
opóźnienie fazowe, 56
pasmo przepustowe okresu, 56
rozkład, 52
stosowanie w transakcjach, 152, 153
Wykupienia/wyprzedania, współczynniki, 13
Z
Zmienność, systemy wybicia ze zmienności, 155-157
wyniki
testowania,
157
Zysk, maksymalizacja, 138-140, 149

Copyright © 2002 by John F. Ehlers. All rights reserved.
Published by John Wiley & Sons, Inc., New York.
Wydano równocześnie w Kanadzie.
Żadna część tej publikacji nie może być kopiowana, przechowywana w bazach danych lub
przekazywana dalej w jakiejkolwiek postaci lub w jakikolwiek sposób, elektroniczny, mechaniczny,
fotokopiowania, nagrania, skanowania lub w inny sposób, z wyjątkiem przypadków określonych w paragrafie
107 lub 108 ustawy o prawie autorskim Stanów Zjednoczonych z 1976 r., bez uprzedniego pisemnego
zezwolenia wydawcy lub bez upoważnienia poprzez wniesienie stosownej opłaty za kopiowanie do Copyright
Clearance Center, 222, Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4744. Prośby do
wydawcy o zezwolenie należy kierować pod następujący adres: Permissions Department, John Wiley & Sons,
Inc., 605 Third Avenue, New York, NY 10158-0012, (212) 850-6011, fax (212) 850-6008, e-mail
PERMREQ@WILEY.COM
.
Zamiarem tej publikacji jest dostarczenie ścisłych i miarodajnych informacji odnoszących się do
omawianego tematu. Wydawca zastrzega sobie, że nie zobowiązuje się do świadczenia profesjonalnej pomocy.
Jeśli wymagana jest profesjonalna porada lub inne wsparcie eksperta, należy zwrócić się o pomoc do
kompetentnej osoby.
Rozdziały 4, 5, 6, 8, 9 i 10 pochodzą, z niewielkimi zmianami, z Rocket Science for Traders, copyright
© 2001 by John F. Ehlers. Przedrukowano za zgodą John Wiley & Sons, Inc.
Dane katalogowe publikacji w Bibliotece Kongresu:
Ehlers, John F., 1933-
MESA and trading market cycles / John F. Ehlers.—2
nd
ed.
p.
cm.—(Wiley
trading)
Łącznie z odnośnikami bibliograficznymi i skorowidzem.
ISBN
0-471-15196-3
(materiał: papier alkaliczny)
1. MESA. 2. Futures-Computer programs. 3. Options (Finance)-Computer programs. 4.
Business cycles-Computer programs. I. Title. II. Series.
HG6024.A3 E43 2001
332.63’2’0285-dc21
2001046617
Wydrukowano w Stanach Zjednoczonych Ameryki
10 9 8 7 6 5 4 3 2 1

111
Informacja dodatkowa
Poszukiwania
są dla mnie nieustającym procesem. Ostatnie wyniki moich poszukiwań
można znaleźć w czasopismach poświęconych analizie technicznej oraz na mojej stronie
internetowej
www.mesasoftware.com
. Moje komercyjne mechaniczne systemy transakcyjne
przedstawione są pod adresem internetowym
www.mesa-systems.com
.
Mój adres:
MESA Software
P.O.Box 1801
Santa Barbara, California 93116
(800) 633-6372
Pomyślnych transakcji!
JOHN
F.
EHLERS

Publikacje wydawnictwa Wiley poświęcone analizie technicznej rynków finansowych:
Beyond Candlesticks / Steve Nison
Beyond Technical Analysis, Second Edition / Tushar Chande
Contrary Opinion / R. Earl Hadady
Cybernetic Trading Strategies / Murray A. Ruggiero, Jr.
Day Trader’s Manual / William F. Eng
Dynamic Option Selection System / Howard L. Simons
Encyclopedia of Chart Patterns / Thomas Bulkowski
Expert Trading Systems / John R. Wolberg
Fibonacci Applications / Robert Fisher
Four Steps to Trading Succes / Clayburg
Fundamental Analysis / Jack Schwager
Genetic Algorithms and Investment Strategies / Richard J. Bauer, Jr.
Hedge Fund Edge / Mark Boucher
Intermarket Technical Analysis / John J. Murphy
Intuitive Trader / Robert Koppel
Investor’s Quotient / Jake Bernstein
Long-Term Secrets to Short-Term Trading / Larry Williams
Managed Trading / Jack Schwager
Mathematics of Money Management / Ralph Vince
McMillan on Options / Lawrence G. McMillan
Neural Network Time Series Forecasting of Financial Markets / E. Michael Azoff
New Market Wizards / Jack Schwager
New Money Management / Ralph Vince
New Options Market, Fourth Edition / Max Ansbacher
New Science of Technical Analysis / Thomas R. DeMark
New Technical Trader / Tushar Chande i Stanley S. Kroll
New Trading Dimensions / Bill Williams
Nonlinear Pricing / Christopher T. May
Option Advisor / Bernie G. Schaeffer
Option Market Making Alan J. Baird
Option Strategies, 2
nd
Edition / Courtney Smith
Options Course / George A. Fontanills
Options Course Workbook / George A. Fontanills
Outperform the Dow / Gunter Meissner, Randall Folsom
Pattern, Price & Time / James A. Hyerczyk
Point and Figure Charting, Second Edition / Thomas J. Dorsey
Schwager on Futures / Jack Schwager
Seasonality / Jake Bernstein
Stock Index Futures & Options / Susan Abbott Gidel
Stock Market Course / George A. Fontanills i Tom Gentile
Stock Market Course Workbook / George A. Fontanills i Tom Gentile
Study Guide for Trading for a Living / Dr Alexander Elder
Study Guide to Accompany Fundamental Analysis / Jack Schwager
Study Guide to Accompany Technical Analysis / Jack Schwager
Technical Analysis / Jack Schwager
Technical Analysis of the Options Markets Richard Hexton
Technical Markets Indicators / Richard J. Bauer, Jr. I Julie R. Dahlquist
Trader Vic II / Victor Sperandeo
Trader’s Tax Solution / Ted Tesser
Trading Applications of Japanese Candlestick Charting / Gary Wagner i Brad Matheny
Trading Chaos / Bill Williams
Trading for a Living / Dr Alexander Elder
Trading Game / Ryan Jones
Trading in the Zone / Ari Kiev, M.D.
Trading Systems & Methods, Third Edition / Perry Kaufman
Trading the Plan / Robert Deel
Trading to Win / Ari Kiev, M.D.
Trading with Crowd Psychology / Carl Gyllenram
Trading with Oscillators / Mark Etzkorn
Trading without Fear / Richard W. Arms, Jr.
Ultimate Trading Guide / John Hill, George Pruitt, Lundy Hill
Document Outline
- strona tytułowa
- Spis treści
- Wstęp
- Rozdział 1
- Rozdział 2
- Rozdział 3
- Rozdział4-1
- Rozdział 4-2
- Rozdział 4-3
- Rozdział 5
- Rozdział 6
- Rozdział 7
- Rozdział 8
- Rozdział 9
- Rozdział 10
- Rozdział 11
- Rozdział 12
- Objaśnienia
- skorowidz rzeczowy
- prawa autorskie
- Informacja dodatkowa
- Publikacje Wileya poświęcone analizie technicznej rynków
Wyszukiwarka
Podobne podstrony:
Opracowanie systemu informatycznego z automatycznym zawieraniem transakcji na rynku walutowym(1)
ubezpieczenia, Praca magisterska, Rynek finansowy jest miejscem na którym dochodzi do zawierania tra
Forex 3 Strategie i systemy transakcyjne Poznaj tajniki rynkow finansowych ktore znaja tylko nielicz
Opracowanie systemu informatycznego z automatycznym zawieraniem transakcji na rynku walutowym
rodzaje struktur rynkowych 2
Transalcje
transakcyjny SQL
Istota gospodarki rynkowej
Struktury rynkowe
6 BERNE ANALIZA TRANSAKCYJNA
Enzymatyczna redukcja związków karbonylowych i zawierających wiązania C=C
Jak kupowac nieruchomosci ponizej ich wartosci rynkowej(1)
C3A4 Transaction in foreign trade Polish ver 2010 10 17
FMP1 Zadania Kursy i transakcje Nieznany
jak kupowac nieruchomosci ponizej ich wartosci rynkowej
2 MECHANIZM RYNKOWY
więcej podobnych podstron