3.

3.

Promieniotwórczość

Promieniotwórczość

Rozpad promieniotwórczy

Rozpad promieniotwórczy



jest

jest procesem

procesem przypadkowym,

przypadkowym, zachodzącym

zachodzącym spontanicznie

spontanicznie –

– nie

nie

można

można przewidzieć,

przewidzieć, kiedy

kiedy określone

określone jądro

jądro ulegnie

ulegnie rozpadowi,

rozpadowi,



można

można go

go opisać

opisać jedynie

jedynie statystycznie

statystycznie..

Prawo rozpadu

Prawo rozpadu

Prawo rozpadu

Prawo rozpadu

Prawo

Prawo rozpadu

rozpadu promieniotwórczego

promieniotwórczego –

–

liczba

liczba jąder

jąder izotopu

izotopu

promieniotwórczego

promieniotwórczego ulegających

ulegających rozpadowi

rozpadowi w

w jednostce

jednostce

czasu,

czasu, jest

jest proporcjonalna

proporcjonalna do

do całkowitej

całkowitej liczby

liczby istniejących

istniejących

atomów

atomów

N

N

zawartych

zawartych w

w rozpatrywanej

rozpatrywanej próbce

próbce..

dt

N

λ

dN









λ

λ,, ss

--1

1

–

–

współczynnik

współczynnik proporcjonalności

proporcjonalności (stała

(stała rozpadu)

rozpadu) –

–

wartość

wartość

charakterystyczna

charakterystyczna dla

dla danego

danego izotopu

izotopu promieniotwórczego,

promieniotwórczego, niezależna

niezależna od

od liczby

liczby

atomów

atomów N

N próbki,

próbki, ani

ani warunków

warunków fizycznych

fizycznych ii chemicznych,

chemicznych, w

w których

których znajduje

znajduje

się

się izotop

izotop..

t

0

e

N

N











→

→

Aktywność

Aktywność

próbki,

próbki,

A

A

–

liczba

przemian

jądrowych

zachodzących

w

jednostce

czasu

(szybkość

rozpadu

promieniotwórczego).

1

1Bq

Bq (Bekerel)

(Bekerel) –

–

jednostka

jednostka aktywności

aktywności ciała

ciała promieniotwórczego

promieniotwórczego..

Bekerel

Bekerel jest

jest to

to aktywność

aktywność ciała

ciała promieniotwórczego,

promieniotwórczego, w

w którym

którym jedna

jedna

samoistna

samoistna przemiana

przemiana jądrowa

jądrowa zachodzi

zachodzi w

w czasie

czasie 1

1s

s..

Jednostką

Jednostką aktywności

aktywności spoza

spoza układu

układu SI

SI jest

jest kiur,

kiur, 1

1 Kiur

Kiur ((1

1 Ci)

Ci) jest

jest

aktywnością

aktywnością preparatu

preparatu promieniotwórczego,

promieniotwórczego, w

w którym

którym liczba

liczba rozpadów

rozpadów

zachodząca

zachodząca w

w 1

1 s

s wynosi

wynosi 3

3,,7

71010

1010,, czyli

czyli 1

1 Ci

Ci =

= 3

3,,7

71010

1010 Bq

Bq..

,, Bq

Bq

N

λ

dt

dN

A









Prawo rozpadu

Prawo rozpadu

Jak widać z zależności

aktywność jest wprost

proporcjonalna do liczby

jąder promieniotwórczych

Prawo rozpadu

Prawo rozpadu

t

λ

0

e

A

A









W

W miarę

miarę trwania

trwania procesu

procesu promieniotwórczego

promieniotwórczego ilość

ilość rozpadów

rozpadów

zmienia

zmienia się

się (zmniejsza

(zmniejsza się

się zgodnie

zgodnie z

z prawem

prawem rozpadu

rozpadu liczba

liczba jąder

jąder

promieniotwórczych)

promieniotwórczych)..

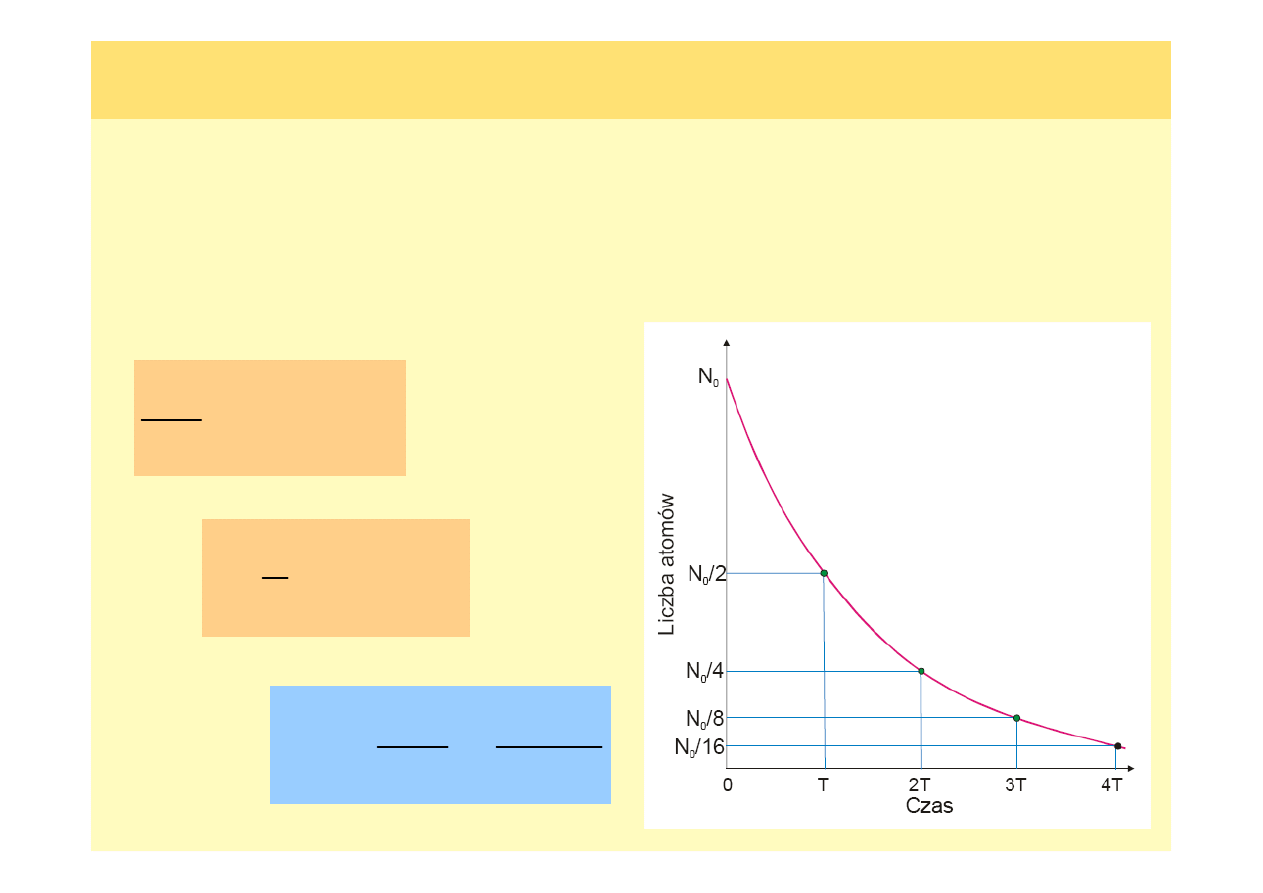
Okres

Okres połowicznego

połowicznego zaniku

zaniku (okres

(okres półrozpadu),

półrozpadu), tt

1

1//2

2

–

–

jest

jest to

to taki

taki

czas

czas tt =

= tt

1

1//2

2

,, po

po upływie

upływie którego

którego aktywność

aktywność próbki

próbki maleje

maleje do

do połowy

połowy

swojej

swojej pierwotnej

pierwotnej wartości

wartości (liczba

(liczba atomów

atomów danego

danego izotopu

izotopu zmniejszy

zmniejszy

się

się o

o połowę)

połowę)..

1/2

t

0

0

e

N

2

N













693

,

0

2

ln

t

1/2





1/2

t

λ

2

1

ln



















Prawo rozpadu

Prawo rozpadu

Przykład

Przykład::

Polon

Polon--210

210 ma

ma okres

okres połowicznego

połowicznego rozpadu

rozpadu równy

równy 140

140 dni

dni.. Jaki

Jaki procent

procent

początkowej

początkowej liczby

liczby jego

jego atomów

atomów pozostanie

pozostanie po

po 100

100 dniach?

dniach?

Z

Z definicji

definicji okresu

okresu połowicznego

połowicznego zaniku

zaniku::

1/2

t

λ

-

0

0

1/2

e

N

2

N

)

N(t









1/2

t

ln2

λ 

2

/

1

1/2

1/2

2

1

2

N

e

N

N(t)

0

t

t

0

ln2

t

t

0

t

t

N































A w konsekwencji:

A w konsekwencji:

→

→

Prawo rozpadu

Prawo rozpadu

gdzie:

gdzie:

N

N

0

0

–

– początkowa liczba

początkowa liczba

N

N

0

0

atomów izotopu,

atomów izotopu,

N(t)

N(t) –

– liczba atomów

liczba atomów

N

N

izotopu po upływie czasu

izotopu po upływie czasu

tt

..

Zatem

Zatem po

po 100

100 dniach

dniach pozostanie

pozostanie jeszcze

jeszcze prawie

prawie

61

61 %

%

początkowej

początkowej ilości

ilości atomów

atomów

izotopu

izotopu..

Jeśli

Jeśli

N

N

0

0

jest

jest początkową

początkową ilością

ilością atomów

atomów izotopu,

izotopu, a

a za

za jednostkę

jednostkę czasu

czasu

tt

przyjmiemy

przyjmiemy 1

1 dzień,

dzień, otrzymamy

otrzymamy::

0

140

100

-

0

N

0,6095

2

N

=

N(100)







Prawo rozpadu

Prawo rozpadu

Przykład

Przykład::

Jaki czas musi upłynąć, by promieniotwórczy stront (90) zredukował liczbę
swoich atomów do 1/16 jej wartości początkowej? Okres połowicznego rozpadu
strontu wynosi 28 lat.





0

t

-

t

-

0

e

N

=

N(t)







gdzie:

N

0

– początkowa liczba

N

N

0

0

atomów izotopu, N

0

= N(t

0

)

N(t) – liczba atomów

N

N

izotopu po upływie czasu

tt

Jeśli t

0

= 0 wówczas:

t

-

0

e

N

=

N(t)







Prawo rozpadu

Prawo rozpadu

Z definicji okresu połowicznego zaniku:

2

N

)

N(t

e

N

0

1/2

t

λ

-

0

1/2









1/2

t

ln2

λ 

1/2

1/2

t

t

0

ln2

t

t

0

2

N

e

N

N(t)















A w konsekwencji:

Zatem, zakładając że jednostką czasu

tt

jest 1 rok:

28

t

0

0

2

N

16

N







lat

112

t 

→

→

→

→

Prawo rozpadu

Prawo rozpadu

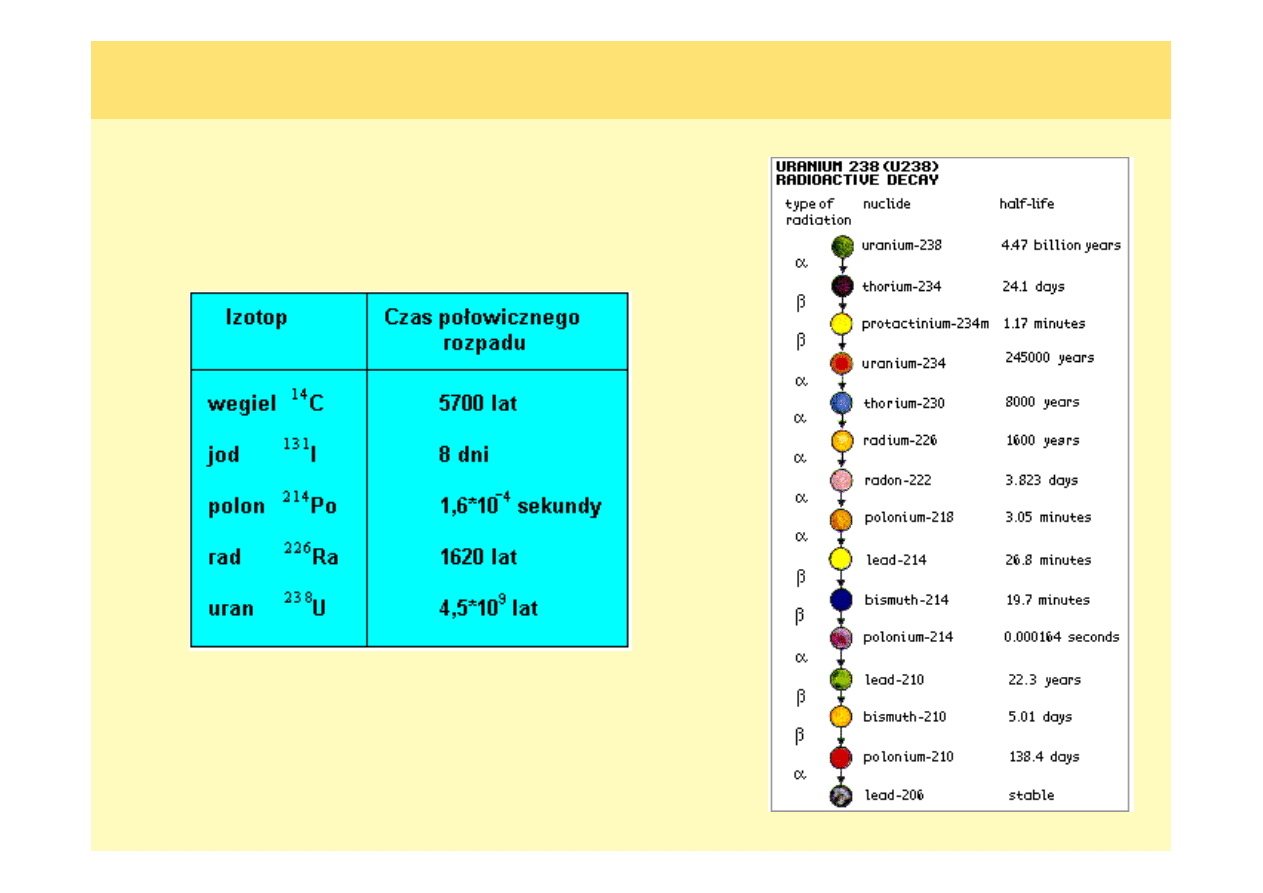
Okres połowicznego zaniku

Okres połowicznego zaniku

wybranych izotopów

wybranych izotopów

Łańcuch promieniotwórczego

Łańcuch promieniotwórczego
rozpadu U

rozpadu U--238

238

→

→

Prawo rozpadu

Prawo rozpadu

Średni

Średni czas

czas życia

życia jądra

jądra izotopu,

izotopu,



–

–

jest

jest to

to suma

suma czasów

czasów

życia

życia wszystkich

wszystkich jąder

jąder promieniotwórczych

promieniotwórczych podzielona

podzielona przez

przez

ich

ich liczbę

liczbę początkową

początkową..

1/2

1

1/2

t

1,443

t

ln2

λ

1

τ

























Prawo rozpadu

Prawo rozpadu

1/2

t

ln2

λ 

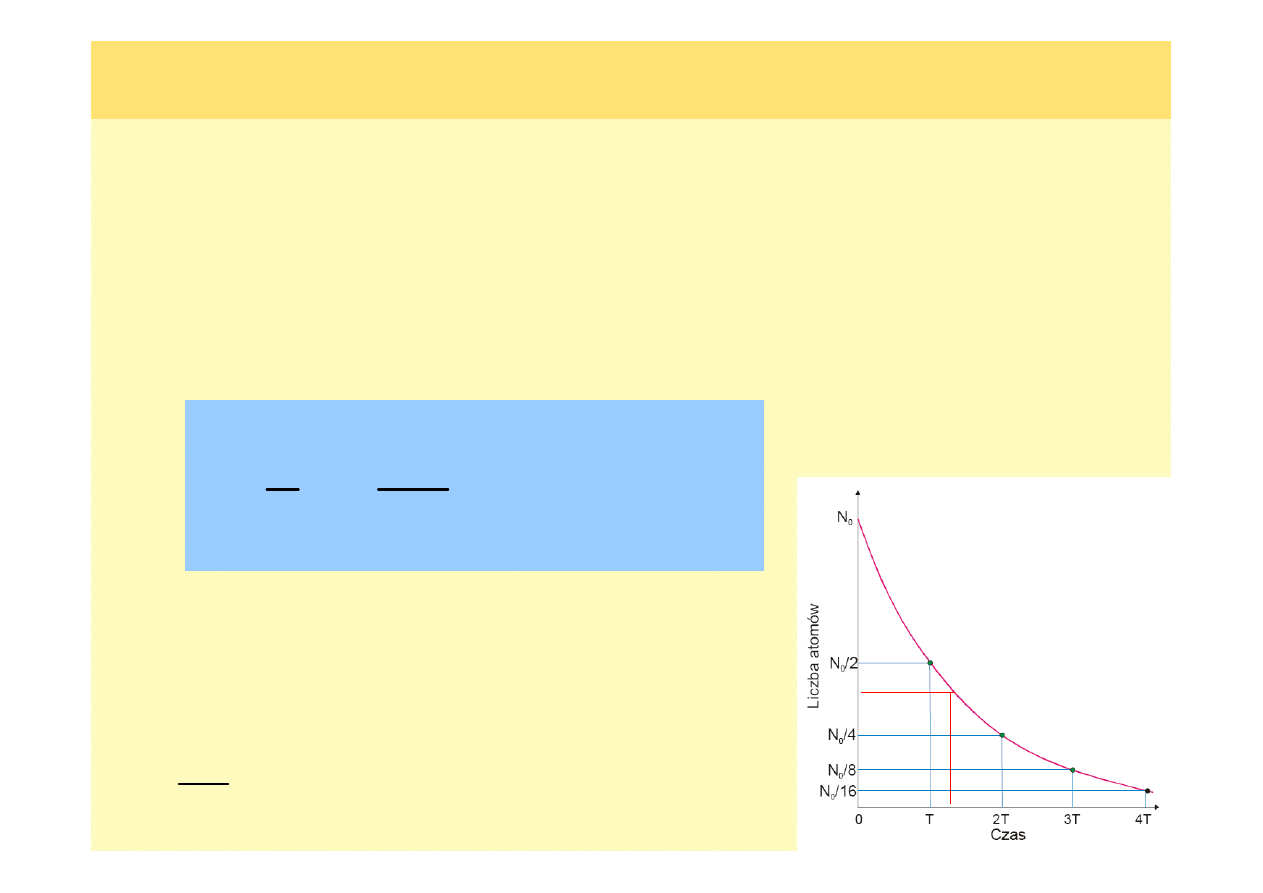
Po upływie czasu



aktywność

próbki spada do 1/e jej

pierwotnej wartości

1/e

1/e



Dla m=10 g radonu t

Dla m=10 g radonu t

1/2

1/2

= 4 dni

= 4 dni

10g 5g 2,5g 1,25g 0,625g

10g 5g 2,5g 1,25g 0,625g

4 dni

4 dni

4 dni

4 dni

1/2

t

-t

0

2

m



 m

Sprawdzenie ze wzoru:

Sprawdzenie ze wzoru: