WPROWADZENIE

DO SZTUCZNEJ INTELIGENCJI

POLITECHNIKA WARSZAWSKA

WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

MEL

MEL

NS 586

Dr in

ż

. Franciszek Dul

© F.A. Dul 2007

21. UCZENIE ZE WZMOCNIENIEM

© F.A. Dul 2007

Uczenie ze wzmocnieniem

W tym rozdziale zobaczymy w jaki
sposób – przy braku nauczyciela –
agent mo

ż

e uczy

ć

si

ę

na podstawie

kar i nagród otrzymywanych za swoje

© F.A. Dul 2007

kar i nagród otrzymywanych za swoje
działania prowadzone w nieznanym

ś

rodowisku.

Jak uczy

ć

si

ę

przy braku wzorców?

Ka

ż

dy rodzaj uczenia wymaga sprz

ęż

enia zwrotnego

informuj

ą

cego agenta o skuteczno

ś

ci nauki.

Uczenie indukcyjne i probabilistyczne wykorzystuje zbiory
wzorców ucz

ą

cych do dostrajania parametrów modeli.

Uczenie ze wzmocnieniem

(uczenie z krytykiem;

reinforcement learning) wykorzystuje

kary

i

nagrody

informuj

ą

ce agenta o poprawno

ś

ci jego działa

ń

.

Celem uczenia ze wzmocnieniem jest wykorzystanie

©

F.A. Dul 2007

Celem uczenia ze wzmocnieniem jest wykorzystanie
obserwowanych nagród i kar do znalezienia optymalnej
strategii działania w danym (nieznanym)

ś

rodowisku.

Uczenie ze wzmocnieniem jest niezast

ą

pione w grach

(np. w szachach), gdzie liczba mo

ż

liwych wzorców jest

tak du

ż

a,

ż

e wyklucza to uczenie indukcyjne.

Uczenie ze wzmocnieniem stanowi jedyn

ą

mo

ż

liwo

ść

uczenia w przypadku gdy

ś

rodowisko jest całkowicie

nieznane - w zadaniach eksploracji.

20.1. Wprowadzenie

• Uczenie pasywne ze wzmocnieniem

• Uczenie aktywne ze wzmocnieniem

• Poszukiwania strategii

•

Zastosowanie – autonomiczne sterowanie

ś

migłowcem

Plan rozdziału

© F.A. Dul 2007

21.2. Uczenie pasywne ze wzmocnieniem

Uczenie pasywne ze wzmocnieniem

polega na nauczeniu

si

ę

u

ż

yteczno

ś

ci stanów

U

π

(s)

przy danej strategii działania

π

(s)

(w stanie

s

agent wykonuje działanie

π

(s)

).

Zakłada si

ę

,

ż

e

ś

rodowisko jest obserwowalne.

W uczeniu pasywnym agent nie zna modelu przej

ś

cia

T(s,a,s’)

i funkcji nagrody

R(s).

Agent wykonuje w

ś

rodowisku zbiór

prób

u

ż

ywaj

ą

c strategii

π

.

Celem tych prób jest nauczenie si

ę

funkcji u

ż

yteczno

ś

ci

U

π

(s)

dla ka

ż

dego stanu

s,

© F.A. Dul 2007

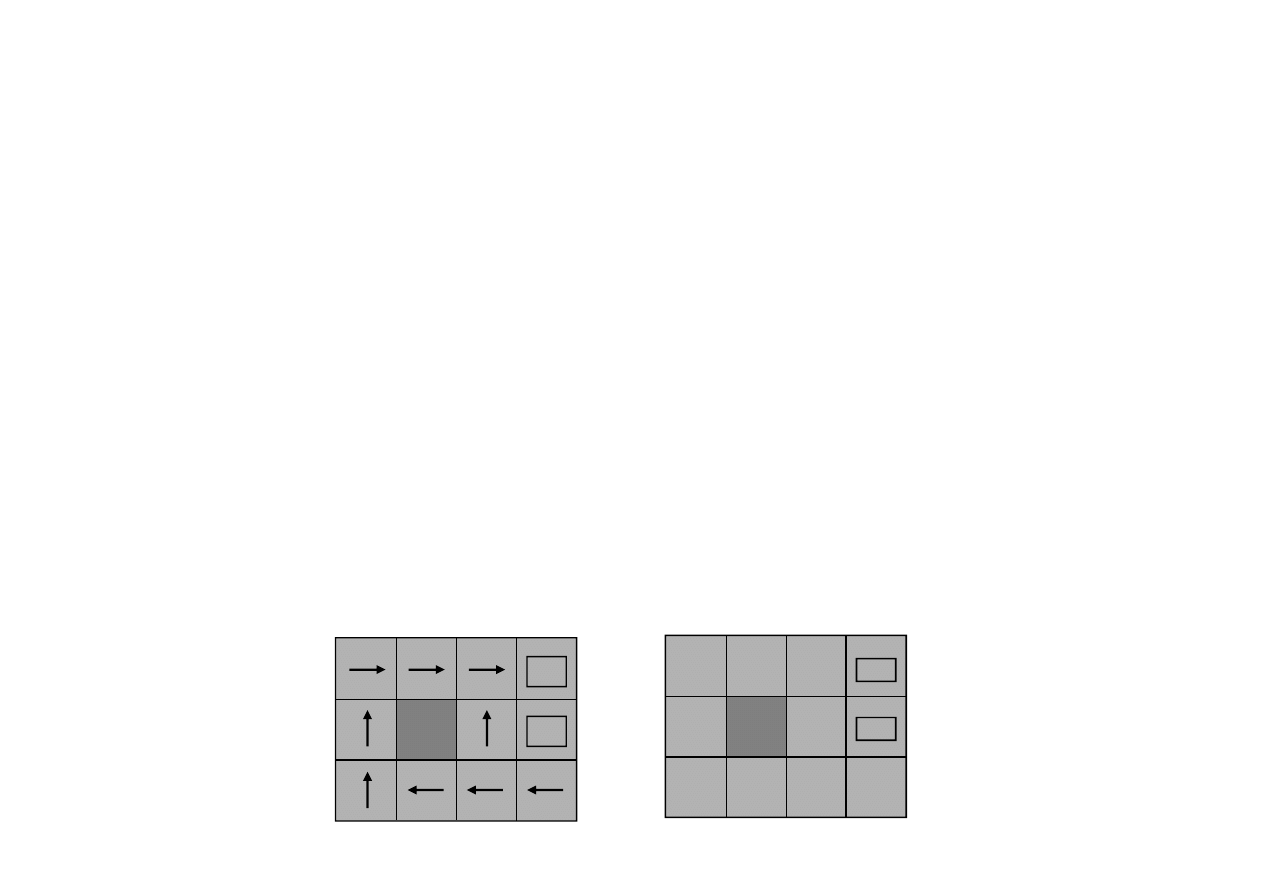
+1

-1

+1

-1

0.705

0.762

0.812 0.868 0.918

0.660

0.611 0.388

0.655

P

RZYKŁAD

Strategia

π

i u

ż

yteczno

ś

ci stanów w

ś

wiecie 4x3.

dla ka

ż

dego stanu

s,













=

=

∑

∞

=

s

s

s

R

E

s

U

t

t

t

0

0

,

|

)

(

)

(

π

γ

π

21.2. Uczenie pasywne ze wzmocnieniem

W adaptacyjnym programowaniu dynamicznym (ADP) agent
uczy si

ę

funkcji przej

ś

cia

T(s,a,s’)

.

Adaptacyjne programowanie dynamiczne

Uczenie metod

ą

adaptacyjnego programowania dynamicznego

Uczenie si

ę

funkcji przej

ś

cia

T(s,a,s’)

i obserwacje funkcji

nagrody

R(s)

pozwalaj

ą

wykorzysta

ć

równanie Bellmana

∑

+

=

'

)

'

(

)

'

),

(

,

(

)

(

)

(

s

s

U

s

s

s

T

s

R

s

U

π

π

π

γ

Umo

ż

liwia to uwzglednienie zale

ż

no

ś

ci mi

ę

dzy u

ż

yteczno

ś

cia-

mi stanów i w efekcie lepsze przybli

ż

enie funkcji u

ż

yteczno

ś

ci.

© F.A. Dul 2007

Uczenie metod

ą

adaptacyjnego programowania dynamicznego

jest łatwe, gdy

ż

odpowiadaj

ą

ce mu równanie Bellmana jest

liniowe (przy stałej strategii nie ma maksymalizacji).

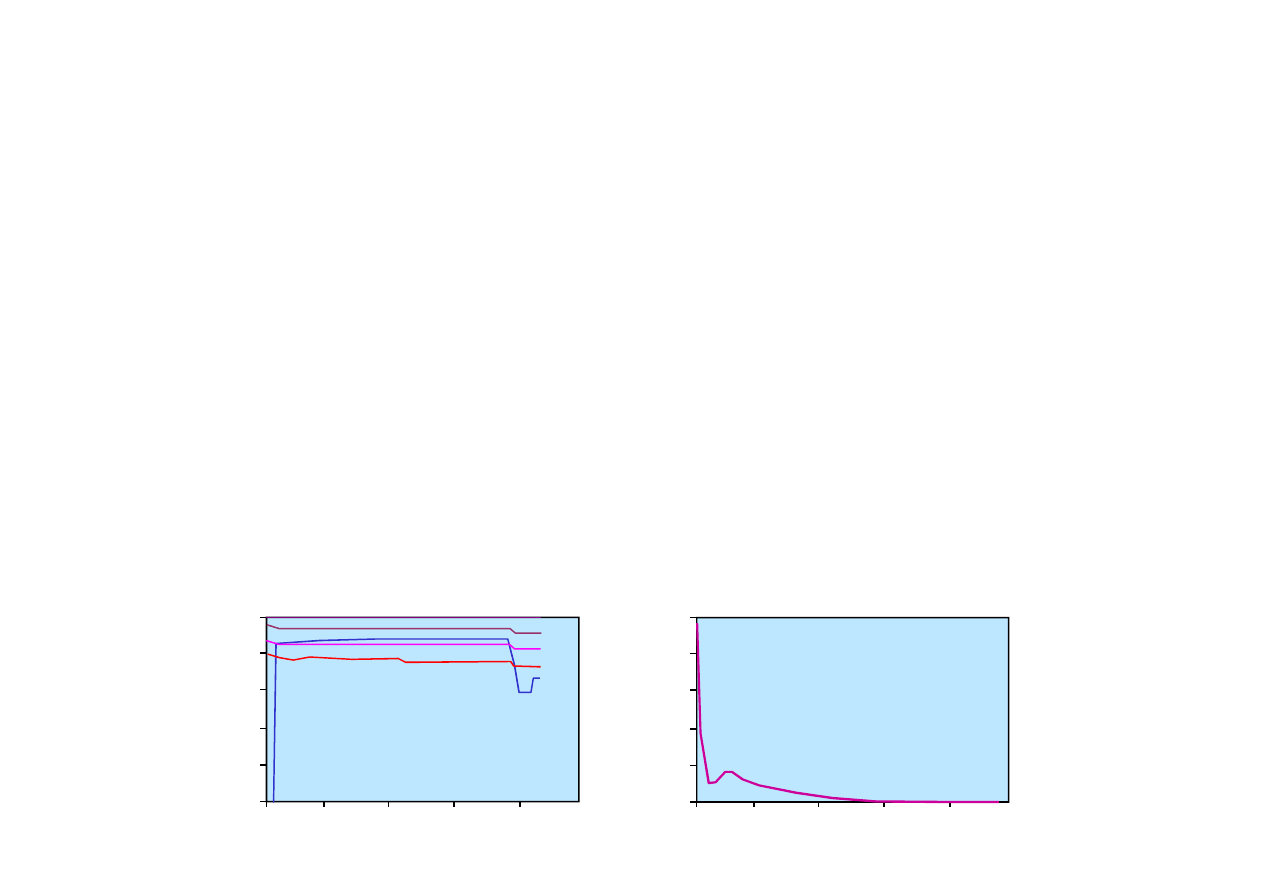
Liczba prób

0.2

0.4

0.6

0.8

1.0

0

20

40

60

80

100

B

ł

ą

d

Wyniki uczenia ADP dla zadania 4x3.

U

ż

y

te

c

z

n

o

ś

c

i

U

π

(s

)

0.2

0.4

0.6

0.8

1.0

0

20

40

60

80

100

Liczba prób

(4,3)

(3,3)
(1,3)

(1,1)
(3,2)

21.3. Uczenie aktywne ze wzmocnieniem

W uczeniu pasywnym strategia działa

ń

agenta jest ustalona.

W

uczeniu aktywnym

agent musi

nauczy

ć

si

ę

kompletnego

modelu

ś

rodowiska ł

ą

cznie z prawdopodobie

ń

stwami efektów

wszystkich działa

ń

.

Wybór działa

ń

optymalnych oraz wyznaczenie funkcji

u

ż

yteczno

ś

ci

U

mog

ą

by

ć

dokonane poprzez rozwi

ą

zanie

Mo

ż

na tego dokona

ć

metodami adaptacyjnego programowania

dynamicznego.

© F.A. Dul 2007

W przypadku iteracji strategii działania optymalne s

ą

otrzymy-

wane bezpo

ś

rednio z równania Bellmana.

u

ż

yteczno

ś

ci

U

mog

ą

by

ć

dokonane poprzez rozwi

ą

zanie

nieliniowego równania Bellmana

∑

+

=

'

)

'

(

)

'

,

,

(

max

)

(

)

(

s

a

s

U

s

a

s

T

s

R

s

U

γ

21.3. Aktywne uczenie ze wzmocnieniem

Eksploracja polega na poznawaniu nieznanego

ś

rodowiska.

Eksploracja

Agent nie posiada modelu

ś

rodowiska; musi si

ę

go nauczy

ć

na podstawie działa

ń

i obserwacji.

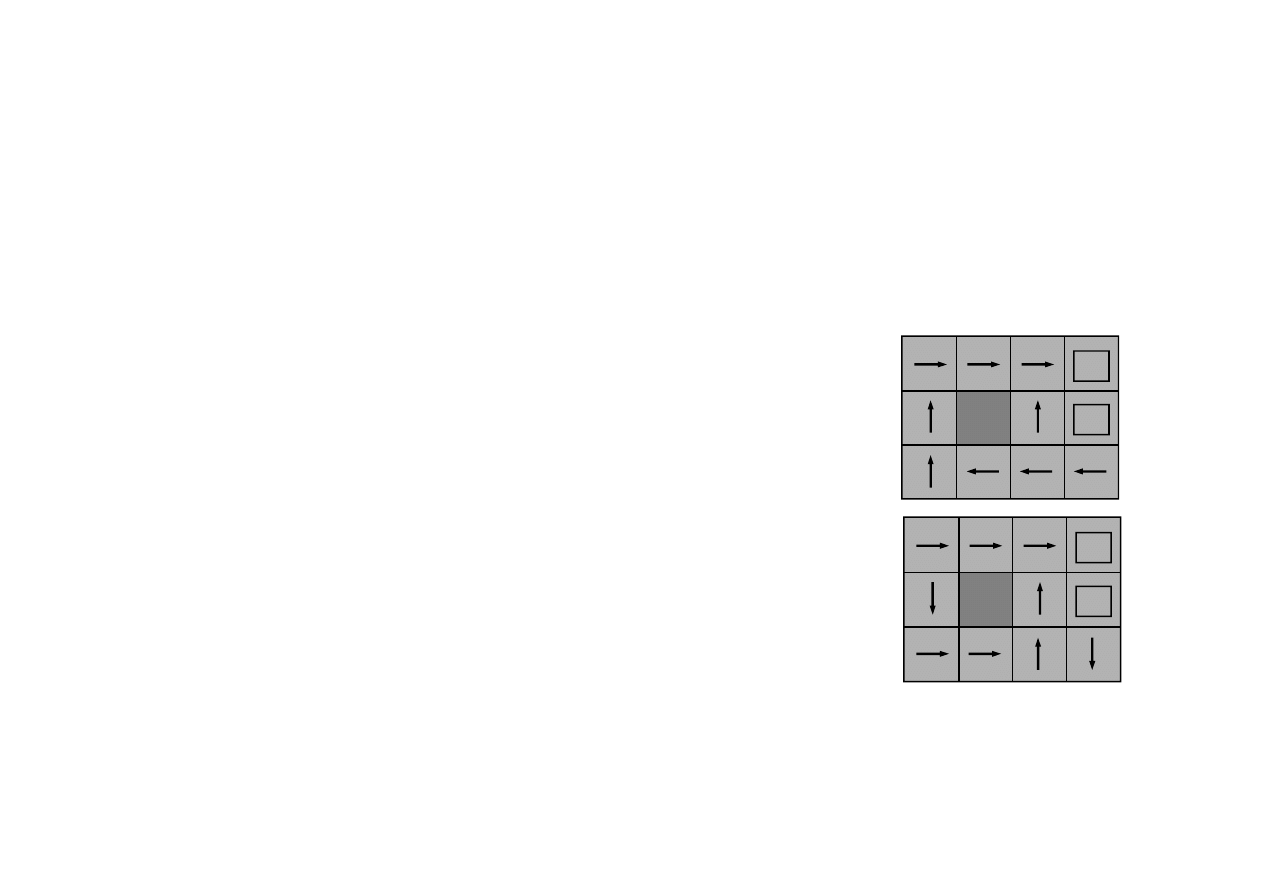
P

RZYKŁAD

Zadanie 4x3. Sekwencja działa

ń

optymalnych (dla modelu

ś

cisłego)...

Strategia wyznaczona na podstawie modelu wyuczonego
mo

ż

e jednak nie by

ć

optymalna.

+1

-1

...oraz wyznaczona na podstawie strategii

© F.A. Dul 2007

+1

-1

Agent nie nauczył si

ę

prawdziwej strategii

optymalnej; nie nauczył si

ę

te

ż

prawdziwych

warto

ś

ci u

ż

yteczno

ś

ci stanów.

...oraz wyznaczona na podstawie strategii
optymalnej dla modelu wyuczonego.

Wyznaczona strategia jest

suboptymalna

.

Agent wyznaczaj

ą

cy strategie suboptymalne nazywany jest

agentem zachłannym

(greedy agent).

Agent zachłanny bardzo rzadko uczy si

ę

strategii optymalnej.

21.3. Aktywne uczenie ze wzmocnieniem

Przyczyn

ą

wyznaczenia strategii suboptymalnych jest

bezkrytyczne uwzgl

ę

dnianie nagród, bez zwracania uwagi

na popraw

ę

jako

ś

ci modelu

ś

rodowiska.

Agent powinien zatem d

ąż

y

ć

do kompromisu pomi

ę

dzy

eksploatacj

ą

ś

rodowiska w celu maksymalizacji nagrody

a

eksploracj

ą

ś

rodowiska w celu poprawienia jako

ś

ci modelu.

Metoda

GLIE

(Greedy in the Limit of Infinite Exploration)

polega na próbowaniu wszystkich działa

ń

we wszystkich

stanach w celu unikni

ę

cia przeoczenia strategii optymalnej.

© F.A. Dul 2007

stanach w celu unikni

ę

cia przeoczenia strategii optymalnej.

Metoda GLIE pozwala agentowi nauczy

ć

si

ę

modelu

prawdziwego, ale odbywa si

ę

to du

ż

ym kosztem.

21.3. Aktywne uczenie ze wzmocnieniem

Uczenie funkcji działania

Agent aktywny który nie korzysta z ustalonej strategii mo

ż

e

u

ż

y

ć

metody czasowo-ró

ż

nicowej (TD),

Alternatywn

ą

wersj

ą

metody czasowo-ró

ż

nicowej jest

Q-uczenie

, które zamiast u

ż

yteczno

ś

ci u

ż

ywa reprezentacji

w postaci warto

ś

ci działania, tzw.

Q-warto

ś

ci

.

Q(a,s)

oznacza warto

ść

wykonania działania

a

dla stanu

s

.

Q-warto

ś

ci zwi

ą

zane s

ą

z u

ż

yteczno

ś

ci

ą

nast

ę

puj

ą

co

)

)

(

)

'

(

)

(

(

)

(

)

(

s

U

s

U

s

R

s

U

s

U

π

π

π

π

γ

α

−

+

+

←

© F.A. Dul 2007

Q-warto

ś

ci zwi

ą

zane s

ą

z u

ż

yteczno

ś

ci

ą

nast

ę

puj

ą

co

)

,

(

max

)

(

s

a

Q

s

U

a

=

Agent czasowo-ró

ż

nicowy ucz

ą

cy si

ę

Q-funkcji nie potrzebuje

modelu

ś

rodowiska ani do uczenia, ani do wyboru działania.

Q-uczenie wymaga znajomo

ś

ci modelu

ś

rodowiska.

∑

+

=

'

'

)

'

,

'

(

max

)

'

,

,

(

)

(

)

,

(

s

a

s

a

Q

s

a

s

T

s

R

s

a

Q

γ

Równanie dla Q-warto

ś

ci ma posta

ć

21.3. Aktywne uczenie ze wzmocnieniem

Równanie metody czasowo-ró

ż

nicowej dla Q-uczenia ma

posta

ć

,

)

)

,

(

)

'

,

'

(

max

)

(

(

)

,

(

)

,

(

'

s

a

Q

s

a

Q

s

R

s

a

Q

s

a

Q

a

−

+

+

=

γ

α

Efektywno

ść

metody TD dla Q-uczenia nie jest zadowalaj

ą

ca.

Metody adaptacyjnego programowania dynamicznego (ADP)
u

ż

ywaj

ą

ce (lub ucz

ą

ce si

ę

) modelu

ś

rodowiska s

ą

zazwyczaj

znacznie wydajniejsze.

Co jest zatem lepsze dla agenta:

© F.A. Dul 2007

Co jest zatem lepsze dla agenta:

Badania AI pokazały,

ż

e podej

ś

cie oparte na wiedzy jest

zazwyczaj lepsze.

Efektywny agent AI powinien zatem posiada

ć

modele

przynajmniej niektórych własno

ś

ci

ś

rodowiska.

uczenie si

ę

modelu i funkcji u

ż

yteczno

ś

ci czy te

ż

uczenie si

ę

funkcji działania bez modelu?

Im bardziej zło

ż

one jest

ś

rodowisko, tym wyra

ź

niej widoczne

s

ą

zalety podej

ś

cia opartego na wiedzy.

21.4. Uogólnienia w uczeniu ze wzmocnieniem

Pierwszym zastosowaniem uczenia ze wzmocnieniem było
opracowanie

programu do gry w warcaby

(1959).

Zastosowania uczenia ze wzmocnieniem - gry

Program wykorzystywał aproksymacj

ę

liniow

ą

z szesnastoma

parametrami; nie wykorzystywał w trakcie uczenia nagród!
Program grał na poziomie dobrych graczy w warcaby.
System TD-Gammon opracowany do

gry w trik-traka

(1992)

ukazuje mo

ż

liwo

ś

ci uczenia ze wzmocnieniem.

Funkcja szacuj

ą

ca była reprezentowana sieci

ą

neuronow

ą

© F.A. Dul 2007

Funkcja szacuj

ą

ca była reprezentowana sieci

ą

neuronow

ą

z jedn

ą

warstw

ą

ukryt

ą

zło

ż

on

ą

z czterdziestu w

ę

złów.

Nagrod

ą

był tylko ko

ń

cowy wynik gry.

Uczenie wykorzystywało metod

ę

TD w wersji parametrycznej.

Uczenie przeprowadzono za pomoc

ą

200,000 prób (obliczenia

trwały dwa tygodnie).
Pó

ź

niejsza wersja programu zawierała 80 w

ę

złów w warstwie

ukrytej i była uczona za pomoc

ą

300,000 prób.

Poziom gry programu TD-Gammon odpowiadał najlepszym
graczom w trik-traka na

ś

wiecie.

21.2. Sformułowanie statystyczne uczenia

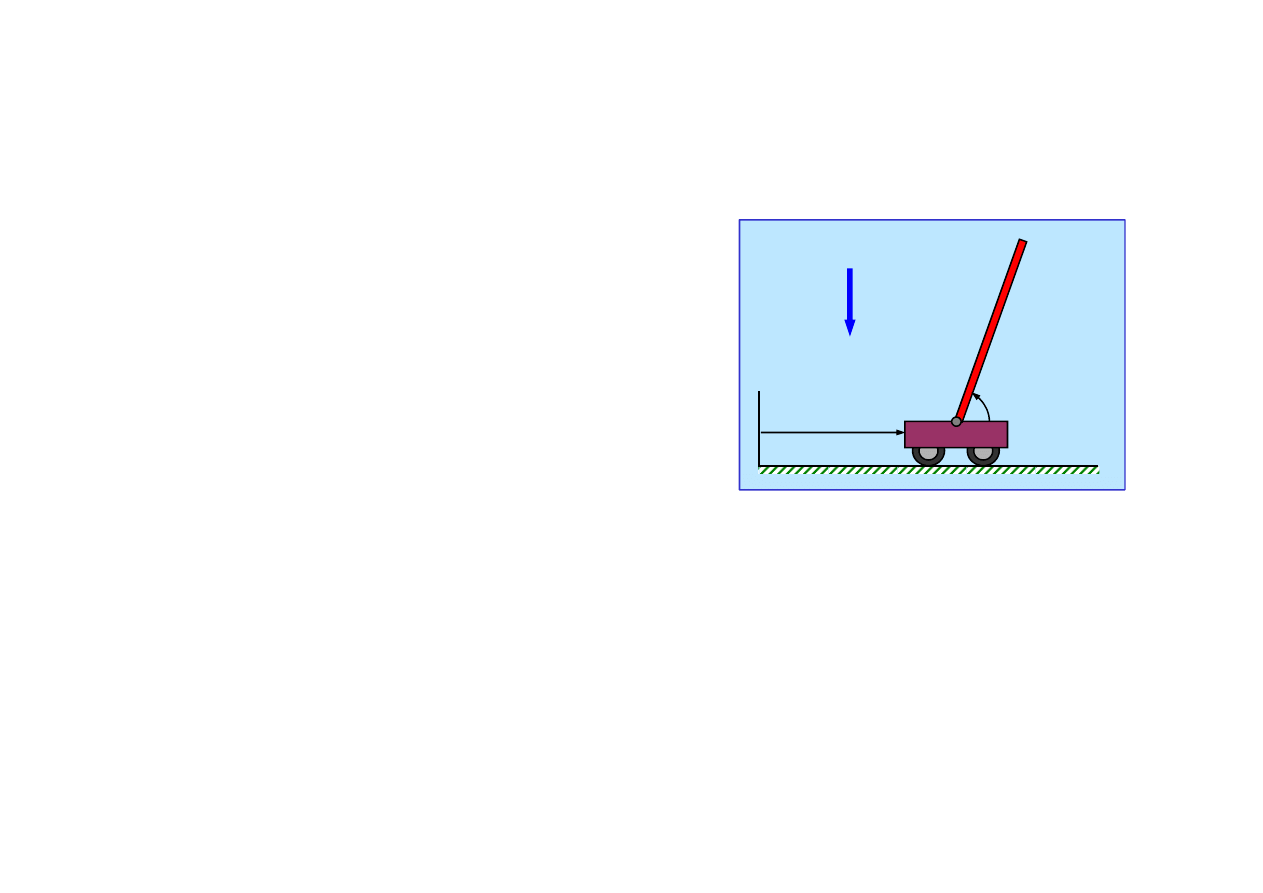
Zastosowania uczenia ze wzmocnieniem - robotyka

Przykładem zastosowania uczenia ze wzmocnieniem
w robotyce jest zadanie sterowania wahadłem odwróconym.
Nale

ż

y tak sterowa

ć

poło

ż

eniem

x

wózka aby utrzyma

ć

wahadło

w poło

ż

eniu pionowym,

θ

~

π

/2

.

g

θ

x

Poło

ż

enie wózka jest ograniczone,

x

∈

[0,L].

Zmienne stanu s

ą

ci

ą

głe.

© F.A. Dul 2007

Zadaniu temu po

ś

wi

ę

cono tysi

ą

ce prac z zakresu teorii

sterowania oraz AI.

Zmienne stanu s

ą

ci

ą

głe.

Sterowanie jest typu bang-bang.

Algorytm B

OXES

(1968) pozwalał wyznaczy

ć

sterowanie

za pomoc

ą

uczenia ze wzmocnieniem ju

ż

po 30 próbach.

Umo

ż

liwiało to sterowanie realnym urz

ą

dzeniem całymi

godzinami.
Obecnie algorytmy oparte na uczeniu ze wzmocnieniem
pozwalaj

ą

wyznacza

ć

sterowanie wahadłem potrójnym.

21.5 Poszukiwania strategii

Uczenie ze wzmocnieniem mo

ż

e by

ć

zastosowane

do poszukiwania strategii działania agenta.

Strategia jako funkcja odwzorowuj

ą

ca stany na działania

mo

ż

e by

ć

reprezentowana w postaci parametrycznej,

np. jako Q-funkcja liniowa wzgl

ę

dem parametrów,

Poszukiwanie strategii jest w ten sposób sprowadzone
do dostrojenia parametrów.

)

,

(

ˆ

max

)

(

s

a

Q

s

a

θ

π

=

© F.A. Dul 2007

do dostrojenia parametrów.

Algorytm P

EGASUS

(2000) wykorzystuje ci

ą

g N liczb losowych

do generowania strategii.

Algorytm P

EGASUS

był u

ż

ywany do wyznaczania efektywnych

strategii w wielu zagadnieniach, np. do

autonomicznego

sterowania

ś

migłowcem

.

Na podstawie artykułów:

„Autonomous helicopter flight via Reinforcement Learning”,

„P

EGASUS:

A policy search method for large MDPs and POMDPs”,

Andrew Y. Ng, Stanford University,

H. Jin Kim, Michael I. Jordan, and Shankar Sastry University of California, Berkeley

(2000). (

www.cs.berkeley.edu

)

Autonomiczne sterowanie

ś

migłowcem jest zadaniem trudnym,

gdy

ż

dynamika ruchu

ś

migłowca jest wyj

ą

tkowo zło

ż

ona.

21.6 Autonomiczne sterowanie

ś

migłowcem -

przykład zastosowania uczenia ze wzmocnieniem

© F.A. Dul 2007

gdy

ż

dynamika ruchu

ś

migłowca jest wyj

ą

tkowo zło

ż

ona.

Ze wzgl

ę

du na niesymetrie zjawisk dynamicznych i aerodyna-

micznych oraz sprz

ęż

enia pomi

ę

dzy poszczególnymi stopniami

swobody ruchu nawet proste manewry wymagaj

ą

precyzyjnego

sterowania.
Metody sztucznej inteligencji pozwoliły opracowa

ć

sterownik

autonomicznie pilotuj

ą

cy

ś

migłowiec w trakcie wykonywania

ró

ż

nych, nawet do

ść

trudnych, manewrów.

Sterownik został opracowany przy u

ż

yciu

algorytmu uczenia

ze wzmocnieniem P

EGASUS

oraz

filtracji Kalmana

.

21.6. Autonomiczne sterowanie

ś

migłowcem

Proces decyzyjny Markowa (MDP) jest opisany poprzez:

Uczenie ze wzmocnieniem: algorytm P

EGASUS

• zbiór stanów

S

,

• stan pocz

ą

tkowy

s

0

∈

S

,

• przestrze

ń

działa

ń

A

,

• prawdopodobie

ń

stwa przej

ś

cia stanów

(s,a)

→

s’ : P

sa

(·)

,

• funkcja nagrody

R(s): S a R

,

• współczynnik dyskonta

γ

< 1

,

• rodzina

Π

Π

Π

Π

strategii

π

: S a A

.

© F.A. Dul 2007

gdzie

s

0

, s

1

, s

2

,... jest trajektori

ą

, czyli ci

ą

giem stanów

odwiedzonych podczas realizacji strategii

π

.

]

|

)

(

)

(

)

(

[

)

(

2

2

1

0

π

γ

γ

π

K

+

+

+

=

s

R

s

R

s

R

E

U

Celem uczenia jest wyznaczenie strategii

π

* o najwi

ę

kszej

u

ż

yteczno

ś

ci,

Uczenie ze wzmocnieniem oparte jest na stochastycznej
funkcji u

ż

yteczno

ś

ci dla strategii

π

• rodzina

Π

Π

Π

Π

strategii

π

: S a A

.

*).

(

)

(

:

π

π

π

U

U

<

Π

∈

∀

21.6. Autonomiczne sterowanie

ś

migłowcem

U

ż

yteczno

ś

ci

U(

π

)

nie mog

ą

by

ć

obliczone bezpo

ś

rednio, ale

mo

ż

na wyznaczy

ć

ich przybli

ż

enia

Ū

(

π

)

metod

ą

Monte Carlo

.

Potrzebny jest do tego

stochastyczny model dynamiki obiektu.

Model taki wykorzystuje rozkład prawdopodobie

ń

stwa stanu

nast

ę

pnego

s’

,

P

sa

(s’),

przy danych: stanie

s

i sterowaniu

a

.

.

)

'

(

:

'

p

s

P

s

p

sa

=

→

Dla danej warto

ś

ci losowej

p

model generuje stan nast

ę

pny

s’

dla którego

P

sa

(s’) = p,

© F.A. Dul 2007

*

1

)

'

(

*,

)

'

(

2

1

p

s

P

p

s

P

sa

sa

−

=

=

Przykład Je

ż

eli dla pary stan-działanie

(s,a)

model mo

ż

e

generowa

ć

dwa stany

s

1

’

i

s

2

’

z prawdopodobie

ń

stwami:

to stan nast

ę

pny

s’

zale

ż

y od warto

ś

ci zmiennej

p

nast

ę

puj

ą

co:

s’= s

1

’

je

ż

eli

p

≤

p* ,

s’= s

2

’

je

ż

eli

p > p* .

Dla danej losowej warto

ś

ci

p

stan nast

ę

pny

s’

wyznaczany jest

deterministycznie

.

21.6. Autonomiczne sterowanie

ś

migłowcem

Model sparametryzowany losowo pozwala uwzgl

ę

dni

ć

zaburzenia stanu lub sterowania spowodowane czynnikami
losowymi (turbulencj

ą

, nierównomierno

ś

ci

ą

pracy silnika, itp.)

).

,

,

(

'

p

a

s

g

s

=

Model stochastyczny mo

ż

na przedstawi

ć

w postaci modelu

deterministycznego

g

sparametryzowanego zmienn

ą

losow

ą

p.

Model dynamiki

g

mo

ż

e by

ć

konstruowany w oparciu o prawa

podstawowe (model przyczynowy) lub te

ż

poprzez

© F.A. Dul 2007

W algorytmie P

EGASUS

sekwencje stanów obliczane s

ą

przy

u

ż

yciu modelu

g

deterministycznie

na podstawie sekwencji

liczb losowych

p

.

Ci

ą

gi liczb losowych na podstawie których oblicza si

ę

sekwencje stanów mog

ą

by

ć

generowane dla ka

ż

dej strategii

π

w sposób

powtarzalny

.

podstawowe (model przyczynowy) lub te

ż

poprzez

identyfikacj

ę

na podstawie pomiarów obiektu rzeczywistego.

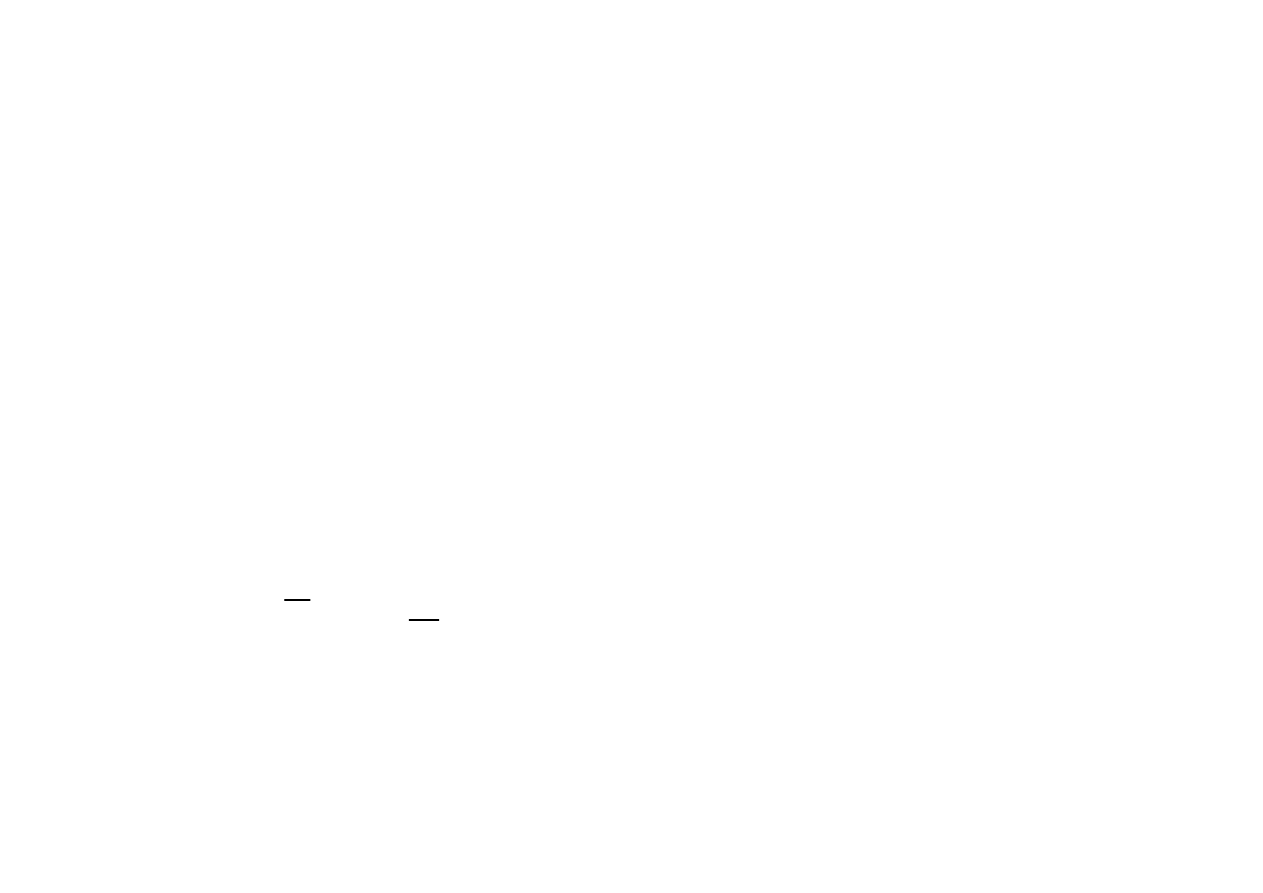
21.6. Autonomiczne sterowanie

ś

migłowcem

Wyznaczenie przybli

ż

onych u

ż

yteczno

ś

ci

Ū

(

π

)

metod

ą

Monte

Carlo przebiega nast

ę

puj

ą

co:

• zakłada si

ę

liczb

ę

kroków czasowych

H

;

• generuje si

ę

ci

ą

g liczb losowych

p

1

, p

2

,..., p

H

;

• dla ka

ż

dej strategii

π ∈ Π

Π

Π

Π

:

– generuje si

ę

losowo

m

stanów pocz

ą

tkowych

s

0

(i)

∈

S

,

czyli tzw. scenariuszy;

– przy u

ż

yciu modelu

g

dla ka

ż

dego stanu pocz

ą

tkowego

s

0

(i)

generuje si

ę

trajektori

ę

s

1

(i)

,

s

2

(i)

, ... ,

s

H

(i)

,

© F.A. Dul 2007

– wyznacza si

ę

przybli

ż

on

ą

u

ż

yteczno

ść

.

1

,...,

0

,

)

),

(

,

(

1

)

(

)

(

)

(

1

−

=

=

+

+

H

k

p

s

s

g

s

k

i

k

i

k

i

k

π

∑

=

+

+

+

+

=

m

i

i

H

H

i

i

i

s

R

s

R

s

R

s

R

m

U

1

)

(

)

(

2

2

)

(

1

)

(

0

)

(

)

(

)

(

)

(

1

)

(

γ

γ

γ

π

K

U

ż

ycie tego samego ci

ą

gu liczb losowych

p

1

, p

2

,..., p

H

dla

wszystkich strategii

π∈Π

Π

Π

Π

i wszystkich scenariuszy zapewnia

porównywalno

ść

i powtarzalno

ść

obliczonych u

ż

yteczno

ś

ci

Ū

(

π

)

.

21.6. Autonomiczne sterowanie

ś

migłowcem

Przy zało

ż

eniu,

ż

e liczba scenariuszy

m

spełnia warunek

Obliczenie zbioru u

ż

yteczno

ś

ci

Ū

(

π

)

dla zbioru sekwencji

stanów pozwala wyznaczy

ć

najlepsz

ą

strategi

ę

π

* jako

0

,

)),

/

1

log(

,

/

1

(

~

>

δ

ε

δ

ε

m

m

.

|

)

(

)

(

|

:

ε

π

π

π

<

−

Π

∈

∀

U

U

przybli

ż

enie funkcji u

ż

yteczno

ś

ci aproksymuje z prawdopodo-

bie

ń

stwem 1-

δ

warto

ść

dokładn

ą

© F.A. Dul 2007

stanów pozwala wyznaczy

ć

najlepsz

ą

strategi

ę

π

* jako

)

(

max

arg

*

π

π

π

U

Π

∈

=

Poniewa

ż

funkcja u

ż

yteczno

ś

ci jest deterministyczna,

to wyznaczenie najlepszej strategii

π

*

mo

ż

e by

ć

przeprowadzone dowoln

ą

metod

ą

poszukiwa

ń

:

metod

ą

najwi

ę

kszego spadku lub metodami gradientowymi.

21.6. Autonomiczne sterowanie

ś

migłowcem

Wyposa

ż

enie

ś

migłowca:

• komputer nawigacyjny,

Do bada

ń

u

ż

yto zdalnie sterowanego modelu

ś

migłowca

Yamaha R-50

• masa 20 kg,
• długo

ść

3.6 m,

•

ś

rednica wirnika 2.8 m,

• warto

ść

70,000 $.

Dane

ś

migłowca:

Ś

migłowiec i jego model

© F.A. Dul 2007

Komputer nawigacyjny wyznaczał estymacj

ę

wektora stanu

na podstawie sygnałów z GPS, INS oraz kompasu cyfrowego
za pomoc

ą

filtru Kalmana

.

• komputer nawigacyjny,
• inercyjny system nawigacji (INS) z trzema akcelerometrami

oraz trzema

ż

yroskopami,

• ró

ż

nicowy system GPS zapewniaj

ą

cy z wyznaczenie poło

ż

enia

z rozdzielczo

ś

ci

ą

2 cm,

• kompas cyfrowy.

Sygnały wej

ś

ciowe z GPS, INS oraz sygnały steruj

ą

ce

były próbkowane z cz

ę

stotliwo

ś

ci

ą

50Hz.

21.6. Autonomiczne sterowanie

ś

migłowcem

Stan

ś

migłowca opisuje dwana

ś

cie zmiennych:

}

,

,

,

,

,

,

,

,

,

,

,

{

ψ

θ

φ

ψ

θ

φ

&

&

&

&

&

&

z

y

x

z

y

x

s

=

Sterowanie

ś

migłowcem opisuj

ą

cztery zmienne:

• x, y, z

- poło

ż

enie,

•

φ

,

θ

,

ψ

- orientacja (k

ą

ty Eulera),

ψ

θ

φ

&

&

&

,

,

•

- pr

ę

dko

ś

ci k

ą

towe.

z

y

x

&

&

&

,

,

•

- pr

ę

dko

ś

ci liniowe,

}

,

,

,

{

a

a

a

a

a

=

© F.A. Dul 2007

• a

1

- pochylenie wirnika,

• a

2

- przechylenie wirnika,

• a

3

- skok wirnika,

• a

4

- skok

ś

migła ogonowego.

}

,

,

,

{

4

3

2

1

a

a

a

a

a

=

Model dynamiki ma posta

ć

niejawn

ą

(„czarna skrzynka”)

...

,

1

,

0

,

12

...,

,

1

,

)

)

(

),

(

(

)

(

)

1

(

=

=

=

−

+

t

k

t

a

t

s

f

t

s

t

s

k

k

k

21.6. Autonomiczne sterowanie

ś

migłowcem

Identyfikacja modelu

Wej

ś

cie

x

modelu tworz

ą

: stan

s

b

zdefiniowany w układzie

zwi

ą

zanym ze

ś

migłowcem,

.

8

,

,

1

,

)

,

0

(

2

K

=

+

=

k

x

y

T

k

k

σ

η

β

Przy opracowaniu sterownika nie u

ż

ywano klasycznego

modelu dynamiki w postaci równa

ń

p

ę

du i kr

ę

tu, lecz

model

typu wej

ś

cie-wyj

ś

cie

z szumem gaussowskim o wariancji

σ

2

,

}

,

,

,

,

,

,

,

{

ψ

θ

φ

θ

φ

&

&

&

&

&

&

b

b

b

b

z

y

x

s

=

© F.A. Dul 2007

.

)

(

)

1

(

t

s

t

s

y

b

k

b

k

k

−

+

=

.

]

,

[

T

b

a

s

x

=

,

}

,

,

,

,

,

,

,

{

ψ

θ

φ

θ

φ

&

&

&

&

&

&

b

b

b

b

z

y

x

s

=

oraz sterowanie

a

w chwili

t

,

Wyj

ś

cia

y

k

tworz

ą

przyrosty zmiennych stanu dla

k=1,...,8,

Wektor współczynników

β

k

jest wyznaczany osobno dla ka

ż

dej

zmiennej stanu na podstawie

m

pomiarów wej

ść

i wyj

ść

modelu

w chwilach

t = 1,...,m.

21.6. Autonomiczne sterowanie

ś

migłowcem

.

y

X

)

X

X

(

1

k

T

T

k

W

W

−

=

β

Współczynniki regresji dla k-tej zmiennej stanu

s

k

s

ą

równe

Do identyfikacji modelu u

ż

yto metody lokalnej regresji liniowej,

któr

ą

zastosowano do ka

ż

dej zmiennej stanu

s

k

, k=1,...,8.

,

X

12

,

2

2

,

2

1

,

2

12

,

1

2

,

1

1

,

1

2

1













=













=

x

x

x

x

x

x

x

x

L

L

.

y

,

2

,

1













=

k

k

y

y

Pomiary wej

ść

i wyj

ść

modelu dynamiki dla

t = 1,...,m

mo

ż

na

zapisa

ć

w postaci macierzowej nast

ę

puj

ą

co

© F.A. Dul 2007

.

)

)

)

(

)

(

exp(

(

1

2

1

i

T

i

x

x

x

x

diag

W

−

Σ

−

−

=

−

Do identyfikacji modelu wykorzystano sze

ś

ciominutowe

rejestracje sterowania i stanu

ś

migłowca sterowanego zdalnie

przez do

ś

wiadczonego pilota.

,

X

12

,

2

,

1

,

12

,

2

2

,

2

1

,

2

2





















=





















=

m

m

m

m

x

x

x

x

x

x

x

x

L

M

O

M

M

L

M

.

y

,

,

2

k





















=

k

m

k

y

y

M

Macierz

W

zdefiniowana jest poprzez zapytanie

x

jako

gdzie

Σ

jest wektorem wag dla poszczególnych pomiarów.

21.6. Autonomiczne sterowanie

ś

migłowcem

Wyniki identyfikacji

Przykład przebiegu zmiennej
stanu

y’(t)

(

——

) oraz jej predykcji

(

——

) wraz z odchyleniem

standardowym bł

ę

du (

- - - -

).

© F.A. Dul 2007

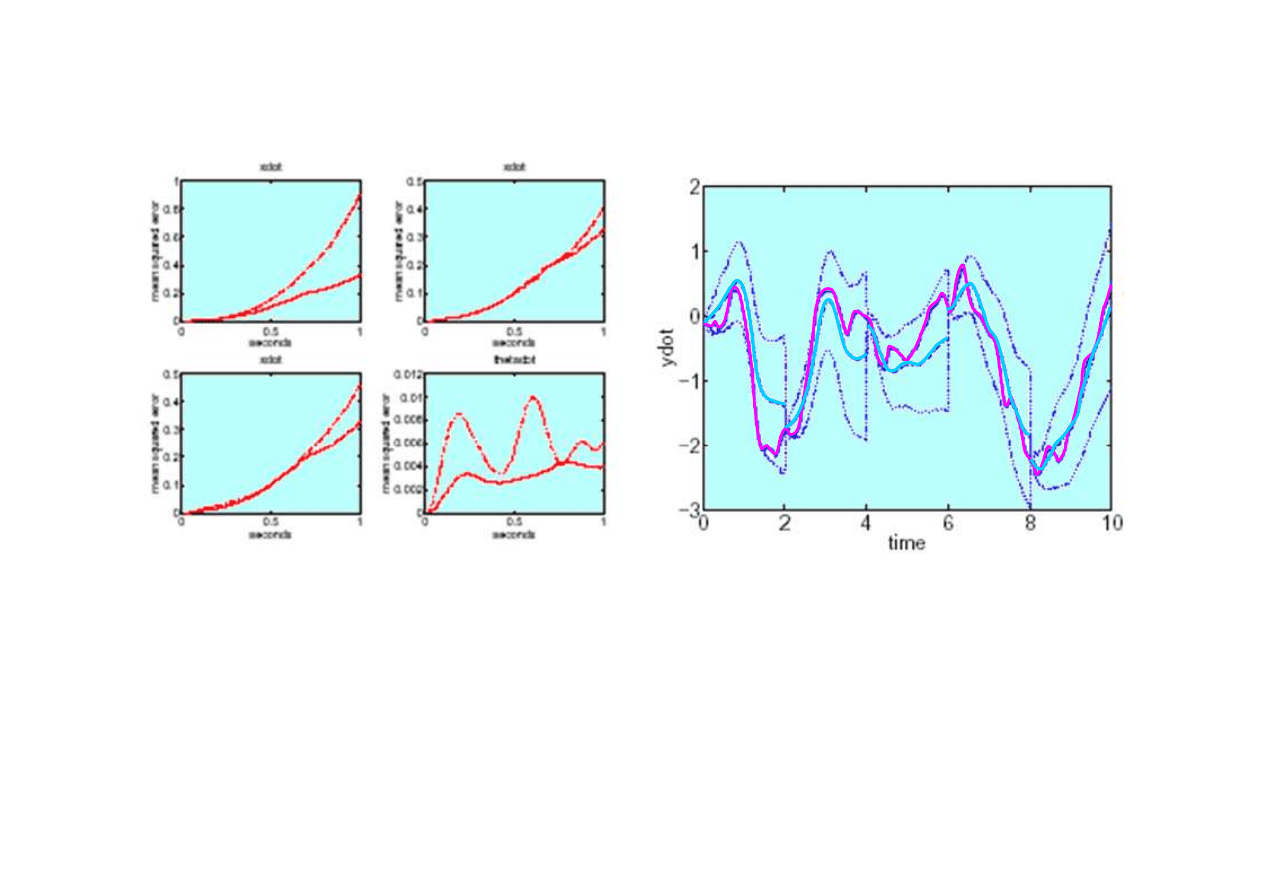
Narastanie bł

ę

dów estymacji w czasie

(a)

x’(t)

bez uwzgl

ę

dnienia

a

1

(b)

x’(t)

bez uwzgl

ę

dnienia szumu,

(c)

x’(t)

dla modelu liniowego,

(d)

θ

’(t)

dla modelu liniowego

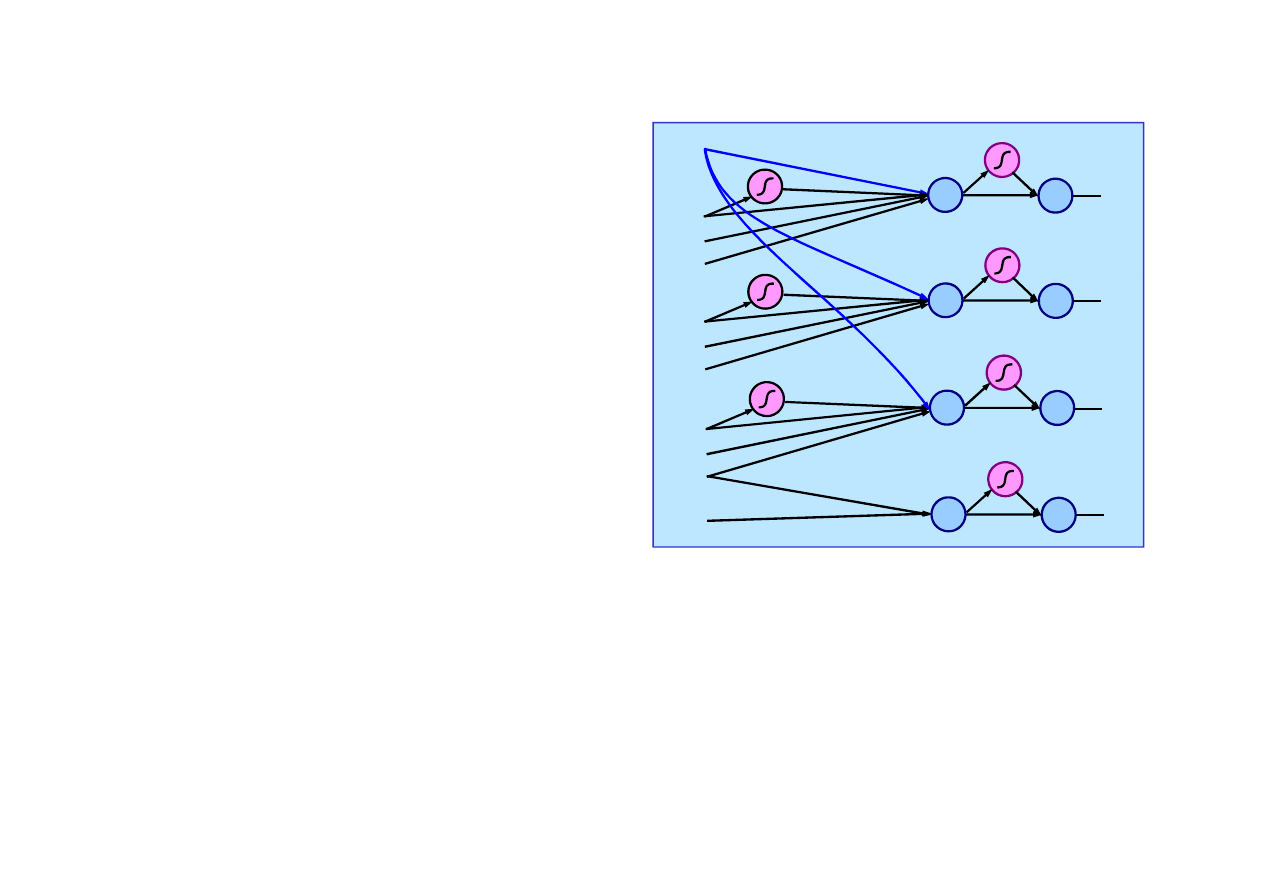
21.6. Autonomiczne sterowanie

ś

migłowcem

Do reprezentacji strategii
sterowania

ś

migłowcem

w zawisie wykorzystano sie

ć

neuronow

ą

acykliczn

ą

.

Struktura sieci została wybrana
tak, aby sterowania były
zwi

ą

zane z odpowiadaj

ą

cym

im zmiennym stanu.

Uczenie lotu w zawisie

+1

ΣΣΣΣ

err

x

a

1

θ

x&

ΣΣΣΣ

ΣΣΣΣ

err

y

a

2

φ

y&

ΣΣΣΣ

ΣΣΣΣ

err

z

a

3

z&

ΣΣΣΣ

© F.A. Dul 2007

θ

6

5

4

3

2

1

1

)

tanh(

w

x

w

err

w

w

err

w

w

t

x

x

+

+

+

+

=

&

1

9

1

8

7

1

)

tanh(

t

w

t

w

w

a

+

=

z&

ψ

&

ΣΣΣΣ

err

ψ

a

4

ΣΣΣΣ

Bł

ę

dy stanu

s

wzgl

ę

dem stanu po

żą

danego

s*

odpowiadaj

ą

-

cego zawisowi s

ą

równe

*

s

s

err

s

−

=

Przykładowo, sterowanie pochyleniem wirnika ma posta

ć

Sie

ć

ma dziesi

ęć

wej

ść

, jedn

ą

warstw

ę

ukryt

ą

, cztery wyj

ś

cia

i 32 współczynniki wagowe

w

i

.

21.6. Autonomiczne sterowanie

ś

migłowcem

Funkcje nagrody dla stanu i sterowania maj

ą

postacie

)

*)

(

*)

(

*)

(

*)

(

(

)

(

2

2

2

2

2

2

2

ψ

ψ

α

α

α

α

α

α

α

ψ

−

+

+

+

+

+

−

+

−

+

−

−

=

&

&

&

&

&

&

&

z

y

x

z

z

y

y

x

x

s

R

z

y

x

z

y

x

)

(

)

(

2

4

2

3

2

2

2

1

4

3

2

1

a

a

a

a

a

R

a

a

a

a

α

α

α

α

+

+

+

−

=

Współczynniki

α

x

,...,

α

a4

zapewniaj

ą

porównywalne wkłady

poszczególnych wyrazów do funkcji nagród.

Do wyznaczania przybli

ż

onych u

ż

yteczno

ś

ci strategii

Ū

(

π

)

zastosowana została metoda P

EGASUS.

© F.A. Dul 2007

zastosowana została metoda P

EGASUS.

Poniewa

ż

strategie

π

s

ą

gładkimi funkcjami wag sieci, to

maksymalizacja

Ū

(

π

)

mo

ż

e by

ć

przeprowadzona metod

ą

najwi

ę

kszego spadku lub metod

ą

gradientow

ą

.

Najkosztowniejsz

ą

cz

ęś

ci

ą

algorytmu

P

EGASUS

jest wyznaczanie sekwencji

stanów

s’

metod

ą

Monte Carlo.

Pierwszy zawis sterowany autonomicznie

⇒

⇒

⇒

⇒

Wyznaczona strategia sterowania
umo

ż

liwiła autonomiczne pilotowanie

ś

migłowcem w zawisie.

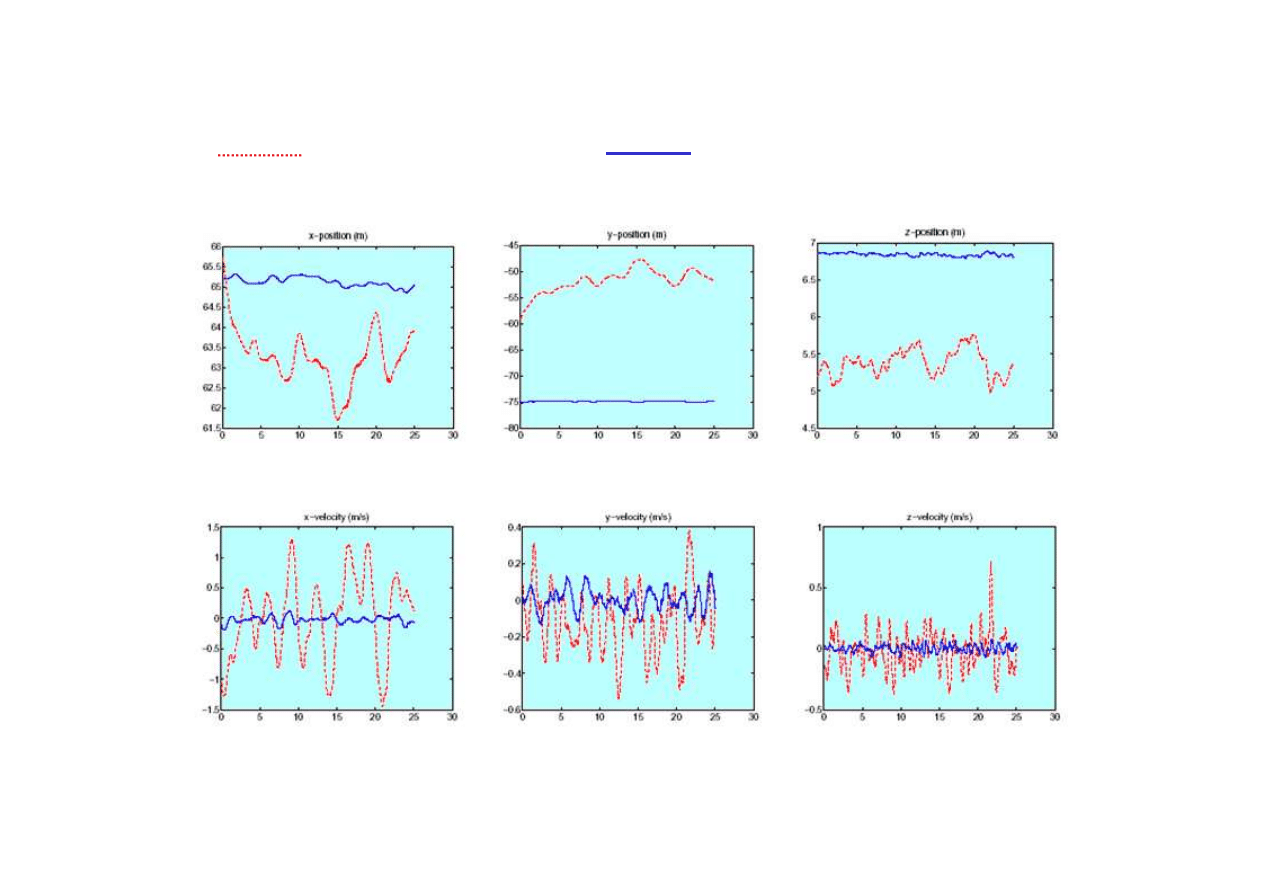
21.6. Autonomiczne sterowanie

ś

migłowcem

Porównanie sterowania

ś

migłowcem w zawisie:

do

ś

wiadczony pilot,

sterownik neuronowy

• bł

ą

d poło

ż

enia (x-x*,y-y*,z-z*)

© F.A. Dul 2007

Nauczony sterownik neuronowy jest w stanie utrzymywa

ć

zawis

ś

migłowca

bardziej precyzyjnie ni

ż

człowiek

.

• bł

ą

d pr

ę

dko

ś

ci (v

x

,v

y

,v

z

)

21.6. Autonomiczne sterowanie

ś

migłowcem

Do reprezentacji strategii
sterowania

ś

migłowcem w

manewrach u

ż

yto sieci

neuronowej stosowanej dla
zawisu, uzupełnionej trzema
poł

ą

czeniami (

→

→

→

→

).

Uczenie manewrów

Strategie sterowania dla
manewrów otrzymuje si

ę

poprzez gładkie przej

ś

cie ze

+1

Σ

err

x

a

1

θ

x&

Σ

Σ

err

y

a

2

φ

y&

Σ

Σ

err

z

a

3

z&

Σ

ψ

&

© F.A. Dul 2007

Metoda P

EGASUS

pozwoliła wyznaczy

ć

strategi

ę

sterowania

ś

migłowcem dla manewrów wykonywanych na zawodach

ś

migłowców sterowanych zdalnie w Klasie III,

odpowiadaj

ą

cej najwy

ż

szemu poziomowi trudno

ś

ci.

poprzez gładkie przej

ś

cie ze

stanu dla zawisu

s*

do stanu

dla manewru

s

p

(t),

Funkcje nagrody dla stanu i sterowania s

ą

zmodyfikowane

pod k

ą

tem uwzgl

ę

dnienia zmiennej trajektorii.

),

(

*

),

(

*

),

(

*

),

(

*

t

t

z

z

t

y

y

t

x

x

p

p

p

p

ψ

ψ

→

→

→

→

ψ

&

Σ

err

ψ

a

4

Σ

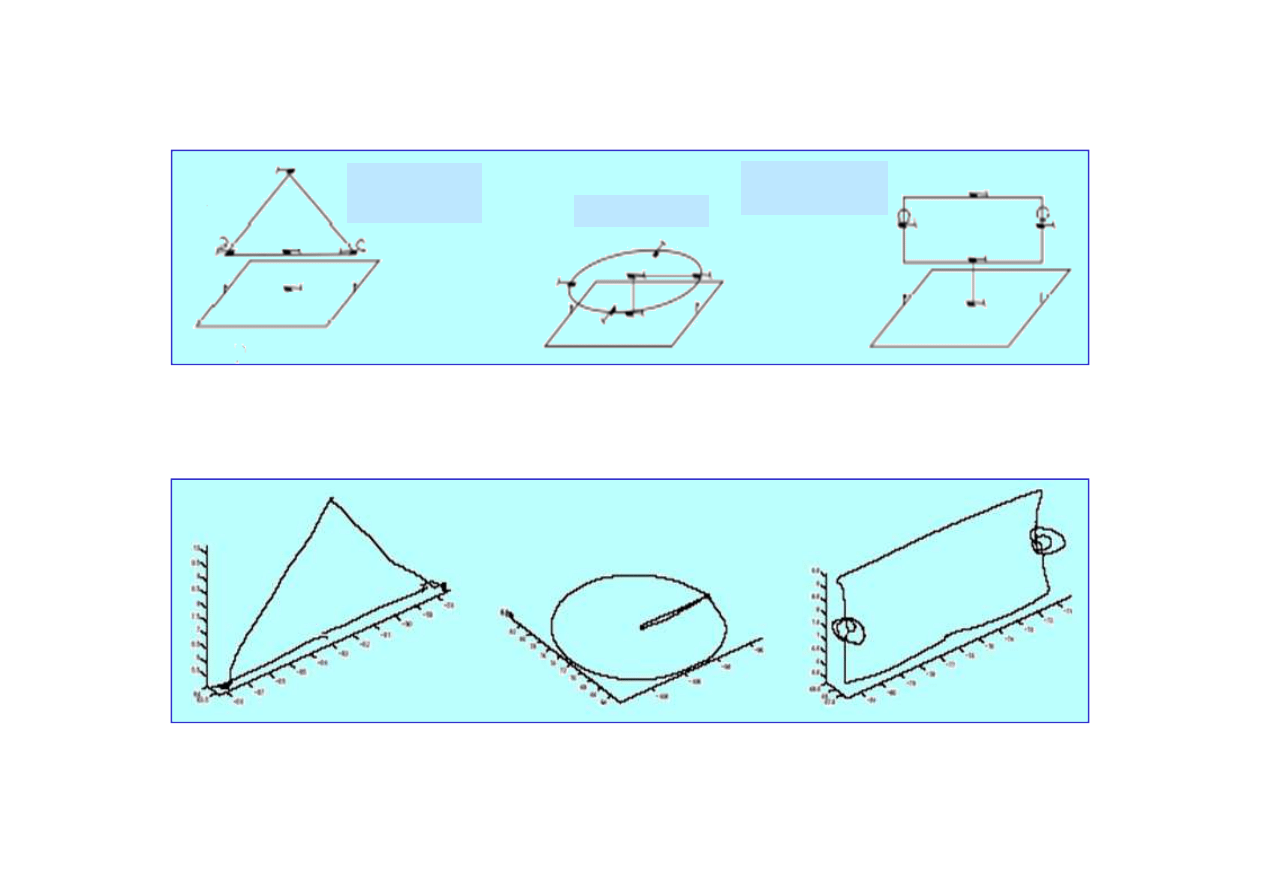
Trójk

ą

t pionowy

z obrotem o 180
stopni

Nos na okr

ę

gu

Prostok

ą

t pionowy

z obrotem o 360
stopni

Manewry

ś

migłowca wykonywane przez pilotów na zawodach

Manewry wykonywane przez

ś

migłowiec sterowany

autonomicznie sterownikiem uczonym algorytmem P

EGASUS.

21.6. Autonomiczne sterowanie

ś

migłowcem

© F.A. Dul 2007

autonomicznie sterownikiem uczonym algorytmem P

EGASUS.

Precyzja manewrów wykonywanych przez

ś

migłowiec

sterowany autonomicznie była zadowalaj

ą

ca.

Manewr „nos na okr

ę

gu”

21.6. Autonomiczne sterowanie

ś

migłowcem

© F.A. Dul 2007

Przedstawione rezultaty ilustruj

ą

potencjalne mo

ż

liwo

ś

ci

algorytmów uczenia ze wzmocnieniem w dziedzinie
bezpilotowych pojazdów autonomicznych (UAV).

Podsumowanie

• Uczenie ze wzmocnieniem polega na budowie modelu

na podstawie nagród i kar otrzymywanych przez agenta.

• Struktura agenta okre

ś

la rodzaj informacji ucz

ą

cej.

• Istniej

ą

trzy typy struktur agenta uczonego ze wzmocnieniem:

– oparta na modelu

ś

rodowiska

T

i funkcji u

ż

yteczno

ś

ci

U

,

– oparta n funkcji działania

Q,

nie wykorzystuj

ą

ca modelu

ś

rodowiska,

– refleksowa, u

ż

ywaj

ą

ca zało

ż

on

ą

strategi

ę

π

.

• Istniej

ą

trzy sposoby uczenia si

ę

u

ż

yteczno

ś

ci przez agenta:

– bezpo

ś

rednia estymacja u

ż

yteczno

ś

ci,

– adaptacyjne programowanie dynamiczne (ADP),

©

F.A. Dul 2007

– adaptacyjne programowanie dynamiczne (ADP),
– ró

ż

nicowa (TD).

• Uczenie z funkcj

ą

działania

Q

nie wymaga modelu

ś

rodowiska,

ale mo

ż

e by

ć

utrudnione w

ś

rodowisku zło

ż

onym.

• Wybór działania w trakcie uczenia wymaga kompromisu

pomi

ę

dzy jego skuteczno

ś

ci

ą

i u

ż

yteczno

ś

ci

ą

w nauce.

• Poszukiwanie strategii polega na bezpo

ś

redniej reprezentacji

strategii i jej ulepszaniu na podstawie oceny skuteczno

ś

ci

działa

ń

.