Schemat własnego ciała i orientacja przestrzenna

Scenariusz zajęć¹

Potrzebne będą następujące rekwizyty: duża kartka białego papieru, cztery piłeczki, miś, kilka kasztanów, trzy klocki, kubek, krzesełko, otwarte pudełko. Ponadto papier, kredki lub mazaki do sporządzania rysunków i pieczątki, takie z dziecięcego zestawu.

Kształtowanie schematu własnego ciała. Różnicowanie i określanie kierunków w przestrzeni

l. Na podłodze leży duża kartka. Prosimy dziecko, aby stanęło na niej. W ten sposób zostało ono wyodrębnione z tła i zajmuje wyraźnie określone miejsce w otoczeniu. Dorosły staje obok dziecka (twarze zwrócone są w tę samą stronę), kładzie dłoń na linii dziecięcego kręgosłupa. Przesuwa w dół, w górę i mówi:

w górę, a teraz w dół. Kucnij, obejmij kolana —jesteś kuleczką. A teraz wyprostuj się, podnieś wysoko ręce, stań na palcach. Wszystko w górę. Popatrz w górę. Opuść ręce, popatrz w dół, kucnij. I znowu: w górę i w dół. Stań prosto. Pokaż kierunek

— w górę. Pokaż kierunek — w dół. Masz 2 piłeczki. Tę rzuć w górę, a tę w dół.

Popatrz przed siebie. To wszystko jest przed tobą (ręce zataczają łuk). Po­wiedz, co widzisz? Masz piłeczkę, rzuć ją do przodu. Co jest z tylu za tobą? (dorosły staje tuż za dzieckiem, dotyka je) Będziesz teraz rzucać pitki w różne strony: w górę, w dół, w przód, w Tył.

2. Dorosły stoi obok dziecka (twarzą zwróconą w tę samą stronę) z prawej strony i mówi: połóż dłoń tam, gdzie bije serce. Serce jest po lewej stronie. Popatrz, moje serce także jest po lewej stronie. To jest twoja lewa strona (dorosły stoi teraz za dzieckiem i przesuwa dłoń wzdłuż lewego boku dziecka). To twoje lewe ramię, lewa ręka, lewy bok, lewa noga. To wszystko jest z lewej strony, tam, gdzie bije serce. Ta strona (przesuwa dłoń po prawej stronie dziecka), to twoja prawa strona. To prawe ramię, prawa ręka... Popatrzmy w stronę lewą. Powiedz, co znajduje się po twojej lewej stronie (łuk ręki wskazujący pole z lewej strony)? Popatrz w stronę prawą. Co znajduje się po prawej stronie (łuk ręki)? Tu są cztery piłeczki. Tę rzuć w prawo, tę w lewo, tę na wprost siebie, tę za siebie.

3. Popatrz pod nogi. Stoisz na kartce. Zrób dwa kroki w prawą stronę. Przesunąłeś się w prawą stronę, w kierunku na prawo. Stań na kartce i zrób dwa kroki w lewo. W którą stronę przesunąłeś się? Znowu stań na kartce i zrób cztery kroki w tył. W którą stronę przesunąłeś się? Ile kroków od kartki białej przesunąłeś się w t y i?

4. Dorosły staje na kartce, dziecko jest obok. Dorosły pyta: gdzie jest moja lewa strona? Moja lewa noga? Pokaż mi moją prawą dłoń. Moje prawe ucho... Daj mi piłeczki i powiedz, w którą stronę mam rzucać (należy tu z całą powagą wykonywać polecenia dziecka). Powiedz mi, ile kroków i w którą stronę mam je zrobić. Wykonując polecenia trzeba ,,pomylić się". W ten sposób sprawdzam, czy dziecko potrafi wyznaczyć kierunki uwzględniając położenie drugiej osoby.

5. Na spacerze można dziecku zaproponować taką zabawę. Dorosły ,,dyk­tuje", w którą stronę i ile kroków ma ono zrobić. Potem dorosły odlicza kroki w różne strony „pod dyktando" dziecka. Następnie można już określać trasę spaceru z uwzględnieniem różnych obiektów, np. pójdziesz prosto przed siebie aż do bramy parku. Potem skręcisz w prawo i pójdziesz wzdłuż płotu... Trzeba taki spacer powtórzyć w mieszkaniu, a potem narysować plan mieszkania i zaznaczyć na nim trasę spaceru.

Bardzo atrakcyjna dla dzieci jest zabawa w odnajdywanie schowanych przedmiotów. Na wspólnie narysowanym planie mieszkania dorosły, a potem dziecko, zaznacza miejsce, gdzie został schowany przedmiot. Kierując się tą informacją trzeba go odnaleźć. Ważne jest, aby dorosły szukając przedmiotu posłużył się ,,głośnym myśleniem" i pokazał dziecku, jak trzeba analizować plan, a potem narysował na nim najkrótszą drogę do poszukiwanego przedmiotu. W trakcie tych czynności dokładnie określa się kierunki: stoję w tym miejscu, twarzą do okna, za mną są drzwi. Muszę iść prosto do tego miejsca, potem skręcić koło stołu w prawo. Po takich doświadczeniach można narysować plan np. osiedla i wyznaczyć na nim drogę do szkoły, do piekarni itp.

6. Przed ćwiczeniami z planem warto przybliżyć dziecku umowy obowiązu­jące przy odczytywaniu płaskich rysunków. Dorosły przypina kartkę papieru np. na drzwiach. Podaje dziecku mazaki, mówi: zaznacz górną krawędź, a po­tem dolną krawędź. Następnie nauczycielka zdejmuje kartkę i kładzie ją na stole przed dzieckiem, i pyta: pokaż górną krawędź, a potem dolną. Dolna jest bliżej ciebie, górna dalej. Spróbujmy ustalić, która krawędź jest lewa, a która

prawa. Połóż dłonie na brzegach kartki. Tam, gdzie lewa — lewy brzeg, tam, gdzie prawa — prawy brzeg. A teraz narysuj wiele kresek od lewej strony do prawej, z góry do dołu, od prawej do lewej i znowu od lewej do prawej itp.

Orientacja w schemacie własnego ciała: prawa-lewa¹

7. Dorosły stoi obok dziecka, patrząc w tę samą stroną. Oboje dotykiem badają i nazywają to, co znajduje się po lewej, a potem po prawej stronie ciała. Dorosły proponuje: żeby nam się nie pomyliło, napiszemy mazakiem na wierzchu swoich lewych dłoni literkę ,,L", a na wierzchu prawych dłoni literkę ,,P". Do prawych dłoni chowamy po jednym kasztanie. Sprawdzamy, czy w prawych dłoniach mamy kasztany (zwraca uwagę na równoległy układ dłoni). Zobacz, jak jest teraz. Dorosły odwraca się twarzą do dziecka i pokazuje, że jego prawa strona jest teraz naprzeciw lewej strony dziecka. W podkreśleniu konsekwencji takiego obrotu pomoże trzymany w prawych dłoniach kasztan, a także podanie lewych, a potem prawych rąk. Trzeba kilka razy powtórzyć to lub podobne ćwiczenie, aby dziecko zdało sobie sprawę z efektu obrotu i umiało określić stronę prawą i lewą nie tylko u siebie, ale i u drugiej osoby także wówczas, gdy jest do niego zwrócona twarzą.

8. Badanie efektów lustrzanego odbicia. Na powierzchni dłoni zaznaczone są literki: L — lewa, P — prawa. Do prawego ucha trzeba przyczepić klips. Teraz można już stanąć przed lustrem. Dorosły stoi obok dziecka i razem badają efekt odbicia. Na kartce dorosły pisze dużymi literami wybrany przez dziecko wyraz. Potem oglądają ten napis odbity w lustrze. Dziecko ogląda także efekt odbicia rozmaitych przedmiotów w lustrze. Celem tych ćwiczeń jest spostrzeżenie, jak lustrzane odbicie zmienia wzajemne położenie obiektów. Efekt ten występuje także przy odbijaniu np, pieczątek. Warto więc na zakończenie tej serii ćwiczeń sporządzić pieczątki z kartofla i odbić kilka. Można zastosować gotowe pieczątki, i

Różnicowanie i określanie położenia przedmiotów

9. Dziecko stoi na białej kartce papieru, dorosły rozkłada wokół kilka przedmiotów i pyta: w którym miejscu znajduje się mis? Czy jest przed tobą, czy po twojej lewej stronie? Dziecko ustala miejsce przedmiotów w stosunku do siebie. Potem dorosły poleca zamknąć na chwilę oczy i przestawia przed­mioty. Dziecko mówi, co się zmieniło i określa miejsce, gdzie teraz znajdują się przedmioty.

10. Dorosły staje na kartce papieru. Dziecko układa przedmioty wokół niego i pyta: co. gdzie się znajduje? Dorosły określa położenie przedmiotów

względem siebie, „myląc się" przy tym. Jeżeli dziecko potrafi skorygo­wać pomyłki, umie określić położenie przedmiotów w stosunku do drugiej osoby.

11. Na białej kartce papieru trzeba ustawić krzesło i wokół niego, pod nim, na nim ułożyć przedmioty. Dziecko ma określić ich położenie w stosunku do krzesła. Dorosły zamyka oczy, a dziecko zmienia układ przedmiotów. Dorosły ustala, co się zmieniło, oczywiście „myląc się", a dziecko czuwa nad poprawnoś­cią. Na koniec oboje siadają obok siebie na krzesełkach, rozglądają się i ustalają, co gdzie się znajduje.

Po tych doświadczeniach można wzbogacić zabawy w trakcie spaceru. Trzeba teraz określić, która strona ulicy jest lewa, a która prawa. Co znajduje się po prawej, a co po jej lewej stronie. Można wyjaśnić niektóre zasady ruchu drogowego.

Rozwijanie dziecięcego liczenia

Scenariusz zajęć¹

Nie sposób tu wymienić wszystkich przedmiotów, na których dziecko uczy się liczyć w codziennych sytuacjach. Dlatego podam tu tylko listę przedmiotów potrzebnych do specjalnie organizowanych ćwiczeń. Należy przygotować:

patyczki, 4 kostki do gry, 12 guzików, bierki, dużo pocztówek, dwa liczydła, metr krawiecki, wiele patyczków (więcej niż tysiąc).

Przykłady wykorzystania typowych sytuacji życiowych do kształtowania dziecięcego liczenia

l. Liczenie przedmiotów. W koszyku są jabłka. Policz, Marysiu, ile ich jest. Jeżeli dziewczynka licząc pomija niektóre, liczy je podwójnie: nie należy jej przerywać liczenia ani też wyjaśniać i korygować. Dorosły powinien powiedzieć:

a może łatwiej będzie policzyć jabłka, jak je wyjmiesz z koszyka i ułożysz w szereg? Zrobimy to razem — dobrze? W trakcie liczenia akcentuje gest wskazywania i wymienia liczebnik przy kolejno liczonych jabłkach. Na koniec pyta: ile jest jabłek. Jeżeli dziecko zaczyna ponownie liczyć i na dodatek pomija niektóre lub liczy podwójnie, oznacza to jedno — dotąd zebrane doświadczenia okazały się niewystarczające dla ukształtowania schematu liczenia oraz dla zrozumienia prawidłowości, których trzeba przestrzegać przy liczeniu. Trzeba więc skłamać je do liczenia dosłownie wszystkiego, co znajduje się w otoczeniu. Na przykład po powrocie z targu dziecko ogląda zakupy. Wyjmuje z torby np. pomidory, liczy je i układa w szereg. Potem wkładając je do koszyka liczy ponownie. Na spacerze zbiera kasztany i liczy je. Ogląda i liczy pocztówki. Dorosły zachęca, pod­powiada liczebniki, liczy razem z dzieckiem, akcentując prawidłowości, lecz nie formułuje ich słownie, nie wyjaśnia „jak trzeba liczyć". Dziecko musi samo zrozumieć, że:

— każdy liczony przedmiot trzeba oznaczyć liczebnikiem (gest wskazywania i wypowiadany liczebnik);

— w trakcie liczenia trzeba dbać o to, aby nie przeskakiwać i nie liczyć podwójnie;

— liczebniki należy wymieniać w ustalonym porządku;

— ostatni z wymienionych liczebników ma specjalne znaczenie, bo określa liczbę policzonych przedmiotów.

2. Wiele doświadczeń logicznych może dziecko zgromadzić w trakcie wspólnego sprzątania. Jurku, ustaw krzesełka do odkurzania i policz je. Ciekawe, czy jak policzysz rozpoczynając z tej strony (dorosły wskazuje przeciwny kierunek liczenia), to także będzie 6 krzesełek? Sprawdź to. Na oknie stoją doniczki z kwiatami. Policz je. A teraz — dorosły zmienił ich układ — policz je znowu. Ciągle jest 8 dlaczego? a przestawiłem je.

Podobne doświadczenia dziecko może zdobyć w trakcie porządkowania biblioteczki, układając zabawki w kąciku itp. Dorosły tak organizuje pracę dziecka, aby miało ono okazję do: a) policzenia ułożonych w szereg przed­miotów, b) liczenia w jednym kierunku, a potem w drugim, c) liczenia przedmiotów po zmianie ich układu, d) liczenia przedmiotów jednorodnych lub niejednorodnych, lecz np. znajdujących się na wspólnym terytorium (np. różne zabawki stojące na półce, wszystkie meble znajdujące się w pokoju). W wyniku takich doświadczeń dziecko powinno samo dojść do wniosku, że:

— wynik liczenia nie jest zależny od tego, czy liczy się „od początku", ,,od końca", trzeba tylko oznaczyć liczebnikami wszystkie przedmioty, nie pominąć żadnego i nie pomylić się przy wymienianiu liczebników;

— można liczyć przedmioty jednorodne i niejednorodne, lecz zawsze trzeba przestrzegać pewnych prawidłowości.

3. Nakrywanie do stołu może być okazją do następnych doświadczeń logicznych. Kasiu, ile osób będzie dzisiaj jadło obiad? Policz i ustaw krzesła tak, aby każdy mógł usiąść przy stole. Może trzeba dostawić jeszcze jedno? Ile potrzebujesz talerzy płytkich? Ile głębokich? Ile deserowych? Ile noży, a ile widelców? Dlaczego wszystkiego musisz mieć 5? Łyżek i łyżeczek także po 5? Sprawdzimy, czy się nie pomyliłaś. Znakomicie...

Podobne doświadczenia może dziecko zgromadzić w trakcie ubierania się przed wyjściem na spacer. Tomku, policz guziki przy płaszczyku, a teraz dziurki. Są 4 guziki i 4 dziurki. Zapnij guziki. Zobacz — widać wyraźnie, że guzików jest tyle, ile dziurek. Pokaż, jak założyłeś buciki, czy prawy jest na prawej nóżce, a lewy... Dwie nóżki i dwa buciki. A teraz rękawiczki...

4. Wspólne sprzątanie szafek w kuchni dostarczy także tego typu doświad­czeń. Wszystko zależy od tego, na ile dorosły potrafi tak zorganizować wspólną pracę, aby dziecko skłonić do liczenia przedmiotów i zastanowienia się, czy jest ich tyle samo, czy jednych jest więcej, a drugich mniej.

Ważne jest aby skłonić dziecko do stosowania dwóch metod: a) ustalenia, czego jest więcej, a czego mniej przez policzenie przedmiotów w obu zbiorach;

b) ułożenia w pary, po jednym elemencie z każdego zbioru. Trzeba, aby dorosły sam stosował obie metody, a nie tylko liczenie. Naj­pierw w sytuacjach, które w naturalny sposób wymuszają łączenie różnych przedmiotów w pary. Czy mamy tyle samo stoików, ile zakrętek? Można po­liczyć i słoiki, i zakrętki, lecz prościej ulożyć w pary: sloik i zakrętka. Czy filiżanek jest tyle, ile spodeczków? Można liczyć, można postawić każdą filiżankę na spodeczku.

Znakomitym źródłem doświadczeń jest sytuacja, w której trzeba porównać dwa zbiory, a w każdym jest mnóstwo elementów. Nie trzeba jednak sugerować dziecku, że ułożenie w pary jest lepszym sposobem rozwiązania tego zadania niż liczenie, przy którym dziecko się myli. Niech samo próbuje, niech się po­myli i zacznie od początku. Potem można sugerować lub samemu pokazać, że ułożenie w pary jest tutaj pewniejsze. Takie żmudne zadania trzeba rozwiązywać razem z dzieckiem i zachęcać do wytrwałości. Każde bowiem zadanie powinno być wykonane do końca i do tego trzeba przyzwyczajać dzieci.

Z moich doświadczeń wynika, że jeżeli dziecko przyswoi sobie obie metody, będzie stosować je równolegle. Porównując liczebność dwóch zbiorów najpierw policzy elementy w obu zbiorach, a potem — już tylko dla sprawdzenia — ustawi w pary. Bywa, że najpierw ustawia w pary, a potem sprawdza wynik przez policzenie elementów w obu zbiorach. Taką staranność w sprawdzaniu zadania trzeba podtrzymać, chwaląc.

5. Codzienne sytuacje dostarczają mnóstwo okazji do intuicyjnego okreś­lania aspektu porządkowego liczby. Dziś są twoje urodziny, Urszulko. Dziś ukończyłaś siedem lat. Rozpoczynasz ósmy rok życia. Za rok będziesz miala osiem lat. Pokaż na palcach, ile lat ukończyłaś. Ile świeczek mam zapalić na urodzinowym torcie dzisiaj, a ile zapalimy za rok? Zastanawiam się, ile świeczek bylo zapalonych w zeszłym roku, gdy miałaś 6 lat.

6. Na spacerze można kontynuować te doświadczenia. Dorosły i dziecko rozmawiają o tym, co widzą. Wyodrębniają obiekty do policzenia, a potem zastanawiają się, ile ich jest — dużo, mało, a może da się je policzyć? Do­rosły wskazuje drzewa rosnące wzdłuż ścieżki i liczy je. Potem mówi: to jest pierwsze drzewo, to drugie, to trzecie — pobiegnij i dotknij czwarte, a teraz dotknij drugie... Policzmy ławki dookoła stawu. Na której siedzi pani z parasolem? Obok której rośnie kasztan? Usiądziemy na piątej lawce — dobrze?

W trakcie spaceru można połączyć ćwiczenia ruchowe z liczeniem. Liczymy kroki, po czwartym kroku podskok. A teraz siedem liczonych kroków i po siódmym wymach rąk itd. Do domu wracają autobusem i liczą przystanki:

pierwszy, drugi... na piątym wysiadamy.

1. Planowanie, ile czego potrzeba. Ze spaceru zostały przyniesione skarby. Trzeba je policzyć. Osobno kasztany, osobno żołędzie, osobno kolorowe liście. Dorosły proponuje: można zrobić konika, o takiego... i rysuje schemat zabawki. Zastanów się, Mirku, ile trzeba przygotować kasztanów na brzuszek? Ile na kopytka? Z czego zrobimy glówkę i szyję? Przygotuj wszystko.

8. Równie bogate doświadczenia dziecko może zgromadzić w kuchni, pomagając przy robieniu makaronu lub pieczeniu ciasta. Dorosły musi

jednak pozwolić dziecku przesypywać, odsypywać, a potem odmierzać miarką i liczyć, ile trzeba .np. łyżek cukru, ile mąki.

Zabawy, gry i zadania specjalne organizowane dla kształtowania dziecięcego liczenia

9. Zabawa: kto ma więcej, ten wygrywa, kto ma mniej, ten przegrywa. Potrzebne będą: 4 kostki do gry. Dorosły proponuje dziecku: zagrajmy, kto wyrzuci więcej, ten wygrywa. Podaje jedną kostkę. Dziecko rzuca, ustala, ile ma oczek. To samo czyni dorosły. Potem porównują wynik... Bywa, że dziecko nie wie jeszcze, że ostatni wymieniony liczebnik określa liczbę kropek. Dlatego po każdym pytaniu: ile masz? ponownie liczy kropki. Ile potrafi określić tylko poprzez czynność liczenia. W takim przypadku można:

a. Zaproponować grę w dwie kostki. Każdy rzuca swoją, a potem porównuje się wynik licząc głośno. Ten ma więcej, kto ma więcej kropek i wymieni więcej liczebników (dłużej liczy).

b. ,,Zanotować" liczbę wyrzuconych kropek na palcach, aby można było potem porównać i określić, czy liczyło się dłużej kropki, czy palce.

Po nabraniu wprawy w grze jedną kostką, można zagrać rzucając dwiema, potem trzema i czterema kostkami. Można także nadal grać jedną kostką, lecz ustalać wygraną i przegraną np. po dwóch, trzech lub pięciu rzutach. Po każ­dym odkładać tyle patyczków, ile zostało wyrzuconych kropek. Na koniec porównać patyczki i ustalić, kto ma więcej. Zastosować i liczenie, i układanie w pary.

10. Po dodaniu jest więcej, a po odjęciu jest mniej. Do wspólnej zabawy potrzeba np. 12 drobnych przedmiotów (guziki, jednakowe klocki, kasztany itd.). Dorosły siada naprzeciw dziecka, kładzie na stole guziki i mówi: głośno je policzymy. Podziel guziki tak, abyś miał tyle samo co ja. Jeżeli dziecko wstrzymuje się od dzielenia, dorosły sam rozdziela guziki: jeden ty, jeden ja, a potem przelicza (głośno) oba zbiory. Następnie formułuje następującą serię zadań;

— policz swoje guziki. Ile masz? Ja mam sześć. Masz sześć, dodam ci dwa, ile masz teraz? Mialam sześć, dodam ci trzy, ile mam? (Dorosły akcen­tuje czynności dodawania i odejmowania, dziecko przelicza przedmioty po każdej zmianie i nie trzeba jeszcze wymagać, by liczyło w pamięci);

— masz osiem, daj mi trzy, ile masz? Miałam cztery, dałeś mi trzy, ile mam?

— mam siedem, oddam ci pięć, ile mam? Miałeś pięć, dodałam ci pięć, ile masz?

Można takich zadań układać więcej, aż dziecko będzie z łatwością wy­znaczało wynik dodawania i odejmowania. Potem można zwiększyć liczbę przedmiotów, na których dokonuje się manipulacji. Na koniec warto zabawę tę wzbogacić i zasłonić (czyni to dorosły) wynik manipulacji. Wymusi się wówczas liczenie „w pamięci". Jeżeli jednak dziecko nie potrafi tego uczynić, trzeba odsłonić np. guziki, aby mogło je policzyć.

11. Gra w bierki. Przepisy są znane i nie muszę ich tu podawać. Warto jednak pamiętać, że w tej grze dziecko nie tylko liczy zebrane bierki, lecz w sytuacji napięcia musi skupić się i wykonać precyzyjną czynność — zebrać ze stosu bierkę tak, aby nie poruszyć następnych. Właśnie dlatego trzeba grać w bierki bodaj na każdych zajęciach w pierwszym okresie zajęć korekcyjno-wyrównawczych. Dla podniesienia walorów kształcących należy zmieniać instrukcję i w kolejnej rozgrywce nadać inną wartość bierkom. Żeby ułatwić zapamiętanie, a potem porównanie zdobytych punktów, należy używać dwóch liczydeł. Na jednym dziecko ,,odnotowuje" swoje wygrane punkty, na drugim czyni to dorosły. Potem wystarczy policzyć, ile kto ma, porównać liczydła i stwierdzić, kto wy­grał i o ile ma więcej.

12. Podobne walory kształcące ma gra, którą dorośli znają ze swego dzieciństwa. Jest ona i dzisiaj bardzo atrakcyjna dla dzieci, chociaż realizują ją w nieco zmienionej konwencji. Potrzebny będzie stos pocztówek, najlepiej tych, które otrzymuje się z okazji różnych uroczystości i świąt. Trzeba wy­brać 5 sztywnych pocztówek i na stosie pozostałych zbudować domek z kart. Potem przemiennie wyjmuje się po kilka, np. po trzy, tak, aby nie zburzyć domku. Gra kończy się w chwili katastrofy — zburzenia domku. Potem trzeba policzyć pocztówki i już wiadomo, kto wygrał. Dla większej atrakcyjności i intensywniejszego treningu w liczeniu proponuję wprowadzenie takiej in­nowacji — na odwrocie pocztówek zapisuje się wartość np. l, 2, 3 i więcej punktów. Po zakończeniu gry liczy się te punkty. Można tu także posłużyć się liczydłem lub patyczkami, zwłaszcza gdy dziecko jest na poziomie dodawania i odejmowania konkretnych obiektów.

13. Liczenie przedmiotów — zarys systemu pozycyjnego. Trzeba przygo­tować dużą liczbę patyczków (więcej niż sto, a potem tysiąc). Może to być także fasola lub groch. Zadaniem dziecka jest policzyć wszystkie patyczki i powiązać po 10, po 100 i po 1000. W przypadku fasoli należy przygotować odpowiednie pudełka lub woreczki. Jest to żmudne zadanie i dlatego dorośli muszą uczestniczyć w tym ,,wielkim liczeniu". Ważne jest, aby dziecko samo policzyło wszystkie patyczki. Zrozumie wówczas, jakim świetnym wy­nalazkiem jest organizowanie liczenia po 10. Po takim doświadczeniu układ pozycyjny jawi się jako wielkie ułatwienie, a nie „coś trudnego, co trzeba za­pamiętać".

14. Metr krawiecki jako winda. To także ulubiona zabawa moich dzieci. Dziecko ogląda taśmę metrową i liczy (wskazując kolejne pola) do 150.1 znowu ważne jest doświadczenie żmudnego liczenia, aby przyjąć układ pozycyjny jako ułatwienie. Przykładowo, można zaproponować następującą zabawę. Rozciąg­nąć taśmę metrową i umówić się z dzieckiem, że jest to winda w domu, który ma 150 pięter. Przygotować małą klamerkę. To jest winda. Gra polega na przemiennym pełnieniu funkcji windziarza i pasażera, który pragnie się za­trzymać na przykład na 75 piętrze, a potem jeszcze podnieść się o 10 pięter wyżej lub zjechać o 26 pięter niżej. Można także zatrzymać się na piętrach nr 10, 20, 30, 40 itd., albo na tych, które oznaczone są liczbami 5, 15, 25, 35, 45, 50 itd.

Konwencje - układanie przepisów gier i respektowanie ich w rozgrywkach

Scenariusz zajęć

Trzeba przygotować do każdej gry potrzebne rekwizyty, a więc arkusze papieru, mazaki, kilka kostek do gry, a także figurki zwierzaków (mogą być ulepione z modeliny i potem utwardzone). Konieczne są także pionki i dwa małe klocki do rysowania segmentów (chodniczka), wszak muszą być jed­nakowej długości.

l. Gra w węża. Na stole znajduje się arkusz papieru do pakowania, mazaki, dwa klocki, dwie kostki do gry i dwa żetony. Dorosły proponuje dziecku grę, a potem zamaszystym ruchem rysuje węża i razem z dzieckiem odmierzają segmenty od ogona do głowy (rys. 29).

Rys. 29. Gra w węża

1+6=7

Pionki układa się „przy ogonie", a gra polega na ściganiu się, kto wcześniej dotrze do głowy. Tę prościutką instrukcję podaje dziecku dorosły w trakcie rysowania planszy. Potem —już w czasie gry — musi pokazać, że bardzo mu zależy, aby być pierwszym. Trzeba jednak tak rzucać kostką, aby ten pierwszy raz dziecko odniosło sukces. Potem może już być różnie.

Po kilku rozgrywkach można wzbogacić przepisy. Na przykład można grać dwiema kostkami, aby wyścig nabrał rumieńców, a dziecko miało okazję do szybkiego obliczenia sumy. Można wprowadzić preferencje — jeżeli zostanie wyrzucona jedynka, gracz dolicza sobie 6 punktów i posuwa się o siedem segmentów do przodu. W podobny sposób można wyróżnić dwójkę, trójkę itp. Żeby łatwiej zapamiętać, na planszy można zapisać np. l + 6 ==7.

2. Gra-opowiadanie „wyścigi zajęcy do pola kapusty". Na stole leży arkusz papieru, mazaki, kostki do gry i figurki zwierzaków: 2 zające, lis. Dorosły rysuje układającą się w serpentyny drogę. Razem z dzieckiem odmierzają jej segmenty (chodniczek) klockiem. Na początku drogi ustawione są zające,

a na końcu trzeba narysować dwie kapusty. Potem ustalić pułapki — na przy­kład lisią norę. Trzeba ją narysować i postawić lisa oraz umówić się z dzieckiem, że jeżeli na tym polu (zakreskowanym) stanie zając, „to trudno, będzie z niego śniadanie dla lisa". Obok narysować obejście, jeżeli zając jest uważny, może obejść łukiem lisią norę i nic mu się nie stanie. Lisią norę można także przeskoczyć, jeżeli liczba wyrzuconych oczek jest 5. Za kolejnym zakrętem drogi płynie rzeka i mostek jest zerwany. Zając może przeskoczyć z rozpędu, jeżeli jednak wypada mu skoczyć do wody, może się utopić i lepiej wybrać drogę okrężną z kładką. Po kolejnym zakręcie jest dobrze ukryta ścieżka i moż­na — jeżeli się uważa — znacznie skrócić drogę do pola kapusty i wygrać. Taką grę przedstawiłam na rysunku 30.

Po kilku rozgrywkach można grać używając kilku kostek. Teraz dziecko musi nie tylko przewidywać pułapki i ułatwienia, lecz także decydować, czy chce rzucać jedną, czy np. dwiema kostkami i szybko obliczyć kolejne sumy.

3. Wyścigi dwóch misiów do dzbanka miodu. Potrzebne będą figurki zwie­rzaków, arkusz papieru, kilka kostek i mazaki. Na arkuszu rysuje się krętą ścieżkę i dzieli się ją na segmenty, a na jej końcu dzbanek z miodem. Teraz można pomyśleć o przygodach. Moje dzieci zaplanowały następujące pułapki:

a) lisią norę, w której mieszka lis-mądrala i miś, który zatrzyma się przed norą, musi do niego zajść na rozmowę i traci jedną kolejkę rzutów, b) łąkę pełną kwiatów, a miś, który zatrzyma się obok niej, musi je powąchać i traci aż dwa rzuty kostką, c) rzekę pełną wody i miś musi przeskoczyć ją z rozbiegu lub poszukać kładki. Oprócz pułapek dzieci zaplanowały: a) dobrze ukrytą ścieżkę pozwalającą mocno skrócić drogę do dzbanka miodu, b) wiewiórkę-spryciarę, która potrafi wskazać znacznie krótszą drogę, jeżeli miś stanie pod jej drzewem.

4. Zima i sanki. To gra-opowiadanie, którą dzieci ułożyły w zimie. Potrzebny jest arkusz papieru, kostki do gry, pionki i mazaki. Na arkuszu trzeba narysować góry i doliny. Potem wykreślić trasę i zaznaczyć na niej segmenty. Po nich trzeba się wdrapywać mozolnie w górę, a potem szybko zjechać na dół. W trakcie ,,wdrapywania się" od liczby wyrzuconych oczek trzeba było odjąć np. 2, a w trakcie jazdy w dół do każdego rzutu należało dodać np. 3. Można było także skorzystać z kolejki linowej, jeżeli pionek zatrzymał się obok stacji takiej kolejki.

5. Gra w trzy kostki. Potrzebny będzie arkusz papieru, mazaki, 2 pionki i 3 kostki, np. białe i jedna czarna. I znowu trzeba narysować drogę np. skręconą w spiralę i wyznaczyć chodniczek. Potem odliczyć cztery pola do końca i tu będzie start. Na końcu zaznaczyć metę. Gra to ściganie się według ustalonych reguł: rzuca się 3 kostkami razem. To, co łącznie wyrzuca się na białych kostkach, oznacza ruch do przodu, a to, co jest na kostce czarnej — cofa pionek do tyłu. Taka gra jest pełna niespodzianek i dlatego bardzo interesująca. Nie trzeba jednak mówić dziecku, że czasami nie warto pracowicie dodawać kroki „do przodu", a potem odliczać kroki „do tyłu". Szczególnie, gdy na jednej kostce białej jest np. 5 i na czarnej także 5. Niech dziecko samo odkryje ułatwienia. Jeżeli tego nie czyni, można ,,pomóc" mu i zastosować strzałki dla oznaczenia skoków pionka. Będzie to już inny wariant gry.

6. Gra „wyścigi na osi liczbowej". Jest to także gra w trzy kostki. Trzeba przygotować wąski i długi pasek papieru, dwa pionki, mazaki i 3 kostki (dwie białe i jedną czarną). Narysować należy strzałkę skierowaną w prawo i od­mierzyć na niej (klockiem) segmenty. Wskazując dziecku fragment osi mówimy:

gramy odtąd, dotąd. Tu jest start, a tu meta. Każdy skok pionka zaznaczyć trzeba strzałką. Ja będę rysować twoje skoki, a ty moje. Zaczynamy. Rzucaj 3 kostkami. Na rysunku 31 przedstawiam taką grę.

W innej grze oś może być „zwinięta w spiralę". Strzałki ,,do przodu" można rysować czerwonym kolorem, a „do tyłu" niebieskim kolorem, ł znowu nie trzeba wyręczać dziecka w odkrywaniu ułatwień. To dziecko ma spostrzegać prawidłowości i formułować wnioski. Dorosły odgrywa tu rolę inspirującą i wspomagającą — nie może ,,myśleć za dziecko".

7. Gra pełna pułapek. Na arkuszu papieru narysować krętą drogę. Okreś­lić miejsce startu i metę. Niektóre płytki chodniczka oznaczyć jako pułapki,

a obok napisać np. —8. Oznacza to, że jeżeli pionek stanie w tym miejscu, trzeba cofnąć się o 8 płytek. Można także ,,grafem" oznaczyć ruch cofania się. Takich pułapek powinno być więcej przy końcu drogi. Należy je jednak wyrównać premiami, a więc zakreślić kolorem wybranej płytki i obok zapi­sać np. +6, a potem strzałką zaznaczyć skok „do przodu". Taką grę przedstawiłam na rysunku 32.

To niezwykle atrakcyjna gra. Posiada także sporo walorów kształcących Można bowiem każdą czynność „pokazać" za pomocą ,,grafu". W sposób naturalny można także składać czynności i łączyć daną czynność z przeciwną a wszystko ma wyrazistą reprezentację graficzną.

8. Zgadnij, o jakiej liczbie myślę. Jest to gra innego typu i zaczerpnęłam je z „Family math" (J.K.. Stenmark, V. Thompson, R. Cossey 1986). Warto je zrealizować, bo jest znakomitym ćwiczeniem w zakresie kształtowania pojęcie liczby. Trzeba przygotować chodniczek liczbowy — przedstawiłam go m rysunku 33 — i 20 kartoników o wymiarach jednej płytki chodniczka.

Rys. 33. Chodniczek liczbowy do gry: :zgadnij o jakiej liczbie myślę

Grę zaczyna dziecko — ma wybrać sobie liczbę, jedną z tych, które znajduj;

się na chodniczku. Dorosły ma zgadnąć, jaka to liczba, pyta więc: wybrałeś 8 Dziecko w zależności od sytuacji odpowiada: za dużo, za mało, tak — to jes liczba 8. W przypadku, gdy powiedziało: za dużo, dorosły zakrywa kartonikiem liczbę 8 i wszystkie większe. Potem pyta: wybrałeś liczbę 5? Dziecko odpowiada: za mało. Dorosły zasłania liczbę 5, a także wszystkie mniejsze i pyta: wybrałeś liczbę 7? Tak — odpowiada dziecko. W następnej kolejności dorosły wybiera liczbę z chodniczka, a dziecko stara się ją odgadnąć

Po pewnej wprawie chodniczek może być zastąpiony taśmą krawiecką, a do precyzyjnego określania przedziału, gdzie znajduje się zgadywana liczba, można użyć dwóch spinaczy lub małych klamerek.

Zrozumienie, że liczba elementów w zbiorze jest stała mimo zmiany jej układu

Scenariusz zajęć

Oprócz przedmiotów, które znajdują się w domu i mogą być wykorzystane do ćwiczeń wtopionych w różne sytuacje życiowe, należy przygotować: sporo patyczków, żetonów, woreczek guzików, woreczek kasztanów lub żołędzi, krążki, pionki i zwykłe klocki.

1. Wykorzystanie codziennych sytuacji

Trzeba nakryć do obiadu. Tomek ustala, ile osób będzie jadło obiad, dla każdej ustawia krzesełko (para). Przy każdym krzesełku stawia talerz płytki (para). Na nim kładzie talerz głęboki (para). Potem łyżki, widelce, noże i łyżeczki itd. Na koniec dziecko przeliczy, czy wszystkiego jest np. po pięć, bo tyle osób będzie jadło obiad.

Jest jesień, pora wekowania. Dziecko pomaga i wybiera słoiki, a potem kompletuje wieczka. Może policzyć osobno słoje, a potem wieczka. Może nałożyć wieczko na każdy słoik.

Na targu mama kupiła jabłka. Dziecko pomaga jej sprawdzać, czy starczy dla każdego po jednym jabłku. Czy jabłek jest tyle samo, ile osób (para: jabłko — człowiek).

Mama przygotowuje deser, a dziecko ustala: ile trzeba umyć miseczek i napełnić galaretką. Miseczek musi być tyle, ile osób (para: człowiek — mi­seczka).

Jest wiosna i mama postanowiła przesadzić kwiatki. Dziecko ustala: ile potrzeba doniczek, ile jest i ile należy kupić. Może narysować kwiatki i doniczki. Potem zastanawia się, ile trzeba podstawek, aby pod każdą doniczką była podstawka.

W takich i podobnych sytuacjach należy skłonić dziecko, aby stosowało dwie metody dla określenia: jest tyle samo, tu jest więcej (ustawianie w pary i liczenie przedmiotów najpierw w jednym zbiorze, a potem w drugim).

2. Zadania

Tworzenie par przez nakładanie. Przygotować w jednym pudełku krążki, a w drugim np. pionki do gry. Jednych i drugich powinno być sporo, aby można się było pomylić przy liczeniu. Dziecko ma sprawdzić, czy krążków jest tyle samo, co pionków. Jeżeli mozolnie liczy, trzeba zasugerować układanie par. Po prostu nałożyć na krążek pionek i powiedzieć: spróbuj tak —potem policzysz, jak pokazałam na rysunku 60.

Rys. 60. Sprawdzenie: czego jest więcej?

Łączenie przedmiotów w pary za pomocą kresek lub strzałek. Potrzebna będzie kartka papieru, mazak lub kredka i pieczątki. Dorosły odbija (za pomocą

pieczątek) lub rysuje kilkanaście gwiazdek i trochę mniej baloników. Zada­niem dziecka jest ustalenie tego, czy gwiazdek i baloników jest tyle samo. Ponieważ przy liczeniu dziecko myli się (przeskakuje lub liczy podwójnie), samo dochodzi do wniosku — ewentualnie przy odrobinie sugestii — że lepiej jest połączyć w pary gwiazdki i baloniki (rys. 61).

Rys. 61. Sprawdzenie: czego jest więcej?

Zwykle po takim ustaleniu równoliczności dzieci odczuwają potrzebę sprawdzenia i liczą elementy w obu zbiorach. Nie należy przeszkadzać, lecz nagradzać za skrupulatność.

Zakreślanie pętelką par. Narysować w rzędzie kilkanaście piłeczek, a w dru­gim rzędzie nieco więcej pałek. Układ nie powinien sugerować odpowiedniości jeden do jednego. Dziecko ma zbadać, czy więcej jest piłeczek czy pałek. Może połączyć w pary — piłeczkę i pałkę — za pomocą pętli (rys. 62) lub zwykłej kreski. Na koniec niech dziecko policzy piłeczki i pałki.

Rys. 62. Sprawdzenie: czego jest więcej?

Rozsuwanie przedmiotów i układanie ich w pary. W pudełku są np. guziki czerwone i guziki niebieskie. Jest ich sporo. Dziecko ma określić, czy guzików czerwonych jest tyle samo, co niebieskich. Zwykle czyni to w sposób przed­stawiony na rysunku 63. Potem liczy, już tylko dla sprawdzenia, czy się nie pomyliło.

Ustalanie, czy po zmianie układu przedmiotów nadal jest ich tyle samo. Przygotować sporo klocków np. trójkątnych i tyle samo klocków prostokątnych. Dziecko ustala, czy jednych i drugich jest tyle samo. Może to zrobić w dowolny sposób. Dorosły wsypuje klocki trójkątne do pudełka — zmiana układu, przemieszczenie — i pyta: czy nadal tych klocków jest tyle samo, co tych? Jeżeli dziecko ponownie chce ustalić równoliczność, oznacza to, że trzeba podobnych ćwiczeń przeprowadzić więcej. W każdym przypadku dziecko ustala, ile jest przedmiotów w jednym zbiorze lub ustala równoliczność dwóch

Rys. 63. Sprawdzenie: czego jest więcej?

zbiorów. Potem następuje zmiana układu tych przedmiotów w jednym ze zbiorów i pojawia się pytanie: czy nadal jest tyle samo?

Wymiana jeden do jednego. Potrzebne będą zwykłe klocki, takie do budowa­nia, oraz żetony-monety. Dorosły proponuje zabawę „w kupowanie klocków". Na początku dziecko odgrywa rolę kupującego, a dorosły rolę sprzedawcy. Dziecko otrzymuje żetony-pieniądze wraz z informacją, że za jeden pieniądz może kupić jeden klocek. W trakcie następnych zabaw trzeba zmienić cenę klocków - taka przecena. Teraz za mały klocek trzeba dać jedną monetę, a za duży dwie monety. Można także inaczej różnicować cenę i brać pod uwagę kolor lub kształt klocków. Ważne jest także, aby dziecko pełniło rolę i sprzedawcy, i kupującego, a także ustalało cenę klocków. Bywa, że dzieci chcą rozbudować tę zabawę i kupują klocki na konkretną budowę. Każdą taką inicjatywę należy pochwalić i nagrodzić. Niezależnie od tego, jaki kształt przyjmie zabawa, musi w niej wystąpić wymiana jeden do jednego (lub jeden do dwóch, lub więcej) i słowne określenie takiej wymiany.

Po kilku takich ćwiczeniach trzeba realizować zabawę w kupowanie i sprze­dawanie w znacznie trudniejszej wersji. Za różne przedmioty trzeba ,,zapłacić" określoną liczbę żetonów. Tyle za to, a tyle za tamto.

Oprócz zabaw w sklep, dziecko powinno radzić sobie w prawdziwym sklepie przy prostych zakupach. Niestety, sporo moich dzieci jeszcze pod koniec kla­sy I nie potrafiło np. kupić kilku bułek. W jaki sposób miały rozumieć sens zadań z podręcznika do matematyki, w których jest mowa o kupowaniu? Są to bardzo ważne doświadczenia. Dlatego należy zadbać o to, aby dziecko je zgromadziło. Najpierw proste zakupy, takie z odliczoną kwotą, którą trzeba zapłacić. Niech dziecko zrozumie samą ideę wymiany i stosowane przy tym umowy (cena, wartość, pieniądze, wymiana). Polem należy sporo rozmawiać na temat cen i obliczonej kwoty, którą należy zapłacić. Jednocześnie niech dziecko ma okazję do poznania pieniędzy: odczytywania wartości, rozmieniania na drobniejsze itp. Można także przemyśleć problem ,,kieszonkowego". Nic tak nie uczy oszczędnego gospodarowania, jak własne pieniądze, które można wydać w różny sposób.

Wiele ciekawych gier i zabaw przedstawiłam w książce Jak nauczyć dzieci sztuki konstruowania gier? str. 69-74, 91-96. Natomiast w książce Dziecięca matematyka opisałam ćwiczenia przydatne do rozwijania umiejętności usta­lonej równoliczności, rozdziały 6.3 i 6.4. tak, aby nie przeciąć narysowanych już linii (jest to także dobre ćwiczenie na koordynację wzrokowo-ruchową). Potem można się umówić inaczej, że każda następna jest większa o dwa. Można jeszcze inaczej.

Miara i sens mierzenia. Problem stałości długości przy obserwowanych przekształceniach

Scenariusz zajęć

Do tej serii ćwiczeń potrzebne będą przedmioty znajdujące się w każdym domu, a więc kawałki sznurka, resztki kabla (druty w osłonkach plastykowych dające się łatwo odginać), wstążki użyte kiedyś do zdobienia kwiatków, paski z cienkiej folii, paski z grubszego papieru, 16 jednakowych patyczków. A ponadto: nożyczki, krawiecka taśma do mierzenia, metr stolarski (składana miarka stolarska), taśma miernicza i kilka szkolnych linijek, zestaw klocków „liczby w kolorach".

l. Wykorzystanie zwykłych sytuacji życiowych dla przybliżenia dziecku sensu mierzenia.

Zacząć trzeba od prostego eksperymentu. Dorosły wskazuje dziecku dwa różne krzesła z oparciem (powinny niewiele różnić się wysokością, a jedno od drugiego ma być oddalone o 4 kroki) i mówi: jak myślisz, czy te krzesła są tej samej wysokości? Jeżeli dziecko poprzestaje na ocenie „na oko", dorosły mówi: chcę wiedzieć dokładnie. Może umiesz je jakoś porównać? Jeżeli dziecko rozumie potrzebę bardziej precyzyjnego porównania, to zechce coś zrobić. Może krzesła przybliżyć, może także wymyślić inny sposób. To, jak dziecko poradzi sobie z tym problemem, będzie dla dorosłego wskazówką dotyczącą sposobu formułowania poleceń i takiego aranżowania sytuacji, aby dostarczyły mu doświadczeń logicznych na miarę strefy najbliższego rozwoju.

Zapewne w każdym domu jest zwyczaj oznaczania na framudze drzwi kolejnych pomiarów wzrostu dziecka. Podczas zapisywania kolejnego pomiaru może mieć miejsce taka, na przykład, rozmowa. Jeszcze wiosną — mówi mama — byłeś taki. O tu zaznaczyłam twój wzrost. A teraz jesteś wyższy. Popatrz, taki jesteś wysoki. Tyle urosłeś od wiosny.

Dorosły spaceruje z dzieckiem i razem zastanawiają się, czy te dwa drzewa są tej samej wysokości? Czy to jest wyższe niż dziecko? Dziecko znalazło zgrabny kijek, przyda się do mierzenia. Można teraz sprawdzić, czy ta ławka i ta ławka są tej samej długości?

Mama kupiła materiał na ściereczki. Chce ustalić, na ile ściereczek wystar­czy tkaniny. Zaprasza dziecko do pomocy. Wspólnie określają długość jednej ściereczki i przygotowują miarę — kawałek sznurka, pasek papieru itp. Potem sprawdzają, ile takich miarek mieści się w długości kupionej tkaniny.

Trzeba wysłać paczkę do cioci. Jest opakowana w papier. Tata zwraca się do dziecka o pomoc. Razem zastanawiają się, ile trzeba odciąć sznurka z kłębka, aby starczyło na solidne obwiązanie paczki. Ruchem ręki określają, gdzie trzeba przewiązać paczkę, a potem przymierzają sznurek.

2. Zadania przybliżające sens przekształceń w zakresie długości

Dorosły przygotowuje dwa paski folii i dwa paski grubszego papieru (długości około 25 cm, szerokości 2 cm każdy), dwa kawałki drutu (długości około 22 cm każdy) i dwa kawałki wstążki lub sznurka (długości około 30 cm każdy). Dziecko ogląda przygotowane przedmioty i segreguje je. Dorosły wyjaśnia: to wszystko jest nam potrzebne do eksperymentowania.

Porównywanie. Trzeba jeszcze raz obejrzeć przedmioty. Porównać je w pa­rach i przyciąć nożyczkami tak, aby na pewno w każdej parze przedmioty te były tej samej długości.

Przekształcanie pasków folii. Dorosły zwraca się do dziecka: najpierw zbadamy, co stanie się z folią. Czy te dwa paski są tej samej długości? Zwiń ten pasek w rulonik i połóż go nad prostym kawałkiem (rys. 66).

Rys. 66. Porównywanie długości dwóch pasków folii

Co zauważyłeś? Czy teraz te dwa kawałki są nada! tej samej długości? Jak myślisz?... Możesz to sprawdzić — rozwiń folię. Jeżeli dziecko powiedziało, że teraz prosty kawałek jest dłuższy — nie trzeba pouczać, poprawiać, protesto­wać. Ono po prostu kieruje się innym kryterium. Wskazówka dorosłego — możesz rozwinąć i sprawdzić — zupełnie wystarczy, aby obudzić ciekawość, skłonić dziecko do refleksji.

Przekształcanie pasków papieru. Dziecko jeszcze raz porównuje paski papieru — przycina je, bo muszą być dokładnie tej samej długości. Z jednego paska sporządza harmonijkę, a potem kładzie ją tuż nad prostym paskiem papieru (rys. 67).

Rys. 67. Porównywanie długości dwóch pasków papieru

Dorosły pyta, podobnie jak w poprzednim zadaniu: czy teraz ten paseczek i ten (wskazuje na harmonijkę) jest tej samej długości? Uważnie wysłuchuje dziecięcych wyjaśnień. Jeżeli dziecko jest przekonane, że po takim przekształ­ceniu ulega zmianie długość, dorosły skłania je do odwrócenia przekształcenia. Rozprostuj, proszę, i porównaj... teraz złóż pasek w harmonijkę... Co zauważyłeś? W przypadku, gdy mimo takich doświadczeń dziecko nadal twierdzi, że po złożeniu paska w harmonijkę, ten założony pasek jest krótszy — nie trzeba twierdzić, że jest inaczej. Widocznie miało zbyt mało doświadczeń dla prowadze­nia wniosków o odwracalnym sensie takich przekształceń.

Przekształcanie kawałków drutu. Zadanie to ma podobną konstrukcję do poprzednich. Dziecko porównuje druty i przycina. Potem z jednego formułuje np. kółko. Kładzie je nad prostym kawałkiem i zastanawia się, czy są nadal tej samej długości (rys. 68).

Rys. 68. Porównywanie długości drutów Rys. 69. Porównywanie długości sznurków

Dziecko ogląda druty i zastanawia się: czy są tej samej długości. Może wyprostować drut, porównać ich długości i ponownie formować.

Zadanie ze sznurkiem. Dziecko przycina dwa jednakowe kawałki sznurka. Z jednego wiąże kokardę. Drugi leży obok. Porównuje i wyjaśnia: czy nadal są tej samej długości? Jeżeli chcesz możesz rozwiązać kokardę, porównać kawałki sznurka (rys. 69).

Zadanie z patyczkami. Trzeba wybrać 8, a potem jeszcze 8 patyczków o jednakowej długości. Dorosły razem z dzieckiem układa 8 patyczków w jeden szereg, a z pozostałych układa drugi szereg. Porównują patyczkowe szeregi i ustalają, że są tej samej długości. Następnie zmieniają układ 8 patyczków, jak na rysunku 70.

Rys. 70. Porównywanie długości szeregów patyczków

Potem pojawia się pytanie: czy te dwa szeregi patyczków są tej samej długości. Dziecko może zmieniać układ patyczków, liczyć je itp.

3. Zadania przybliżające dziecku sens pomiaru długości

Na podwórku dorosły zwraca się do dziecka: jak myślisz, jakiej długości jest ten plot? Można zmierzyć krokami. Zrobimy tak: ja policzę kroki, a potem ty policzysz swoje i sprawdzisz, czy się nie pomyliłam. Okazuje się, że liczba ,,dorosłych kroków" jest znacznie mniejsza niż ,,dziecięcych kroków". Za­stanawiają się, dlaczego tak jest? Dziecko proponuje (przy odrobinie sugestii dorosłego), żeby porównać długość kroków. Pojawia się potrzeba zastosowania bardziej obiektywnej miary. Dorosły pokazuje dziecku składaną miarkę stolars­ką (l metr) i proponuje zmierzyć płot taką miarką. Na koniec rozmawiają o tym, w jaki sposób ekspedientka odmierza w sklepie tasiemkę.

Warto także pokazać dziecku, że własne ciało może być doskonałym narzędziem pomiaru. Szerokością dłoni — trzeba je tylko zmierzyć — można zmierzyć np. długość stołu przykładając je kolejno do siebie. Długość kroków i mierzenie krokami. Długość stopy i mierzenie stopami tak, jak to czynią zwykle ogrodnicy ustalając długość grządek.

Mierzenie klocków ,,liczby w kolorach". Dziecko już potrafi mierzyć klocki, posługując się białym klockiem. Dorosły i dziecko wybierają 4 klocki brązowe (klocek 8). Potem sprawdzają, ile klocków białych mieści się w brązowym klocku, ile klocków różowych, a ile czerwonych. Podobnie analizują klocki zielone (jest to klocek 6 i trzeba określić, ile mieści się w nim klocków białych, różowych i niebieskich), granatowe (klocek 9 zmierzyć trzeba klockami białymi i niebieskimi), a także wszystkie pozostałe.

Po takim wprowadzeniu można metrową miarą mierzyć np. sznurek z kłębka, długość dywanu, ściany w pokoju. W trakcie takich pomiarów pojawi się potrzeba zastosowania jednostek mniejszych. Trzeba wówczas pokazać dziecku kilka innych narzędzi do mierzenia: metr krawiecki, metr stolarski, taśmę mierniczą — taką zwiniętą w rolkę, linijkę szkolną. Niech dziecko obejrzy i ustali, co jest wspólne i czym się różnią. Teraz dopiero można zapoznać go z umowami, które funkcjonują w świecie dorosłych dla zapewnienia precyzyjnego i jednoznacznego pomiaru długości.

Problem stałości wielkości ciągłych: masa-tworzywa-płyny

Scenariusz zajęć

Oprócz przedmiotów znajdujących się w domu, potrzebna będzie masa solna;

lub plastelina i kolekcja naczyń: dwie wysokie szklanki, dwie szerokie szklanki (mogą to być także dwie duże butelki i dwie małe od wody mineralnej), dzbanek i 6 szklanek, miś, lalka i inne zabawki.

Sytuacje życiowe

Już w poprzednich scenariuszach podałam przykłady, jak bardzo kształcące są zwykłe zajęcia w kuchni, jeżeli dorosły zechce tylko podkreślić sens wykonywanych czynności i zwrócić dziecku uwagę na uzyskane efekty. A po ten skłania je do słownego formułowania swoich przemyśleń. Przygotowywanie posiłków i pieczenie ciasta to sytuacje znakomicie nadające się do badanie przekształceń zmieniających wygląd cieczy i masy (tworzywa). Można także zdobyć tu doświadczenia dotyczące ustalania dobrych proporcji, a także przewidywania efektu końcowego procesu zmian. Oto kilka przykładów takich ćwiczeń poznawczych.

Mama przygotowuje domowy makaron. Zaprasza dziecko do wspólne pracy. Razem czytają stosowny przepis i przygotowują produkty. Mama zagniata ciasto, dziecko na początku obserwuje, a potem próbuje samo zagnieść kawałek. Ma okazję obserwować i powodować rozmaite odkształcenia. Widz następny typ zmiany — efekt rozwałkowania, a potem zwinięcia ciasta w rulon i cienkiego krajania. Wystarczy zwrócić dziecięcą uwagę na to, że kawałek ciast.;

zmienia kształt i wydaje się, że jest go po jednej zmianie mało, a po drugie znacznie więcej. Podobne doświadczenia zgromadzi dziecko w trakcie współ niego pieczenia faworków, pączków itp.

Trzeba przegotować mleko na śniadanie. Każdy wypija jedną szklankę Dorosły zwraca się do dziecka: przygotuj 4 szklanki, a tu w butelce jest mleko. nie wiem, czy starczy? Przelej mleko do szklanek... O, starczyli) — w tej butelce mieści się tyle mleka, ile w tych czterech szklankach. Warto zapamiętać Przelej mleko do rondla... Popatrz, wygląda, że jest go mniej. Czy naprawdę przelałeś mleko z czterech szklanek?

Podobne doświadczenia dziecko zgromadzi, jeżeli pozwolimy mu rozdzielić kompot tak, aby było sprawiedliwie, „po równo". Gdy będzie przygotowywało herbatę dla domowników, wkładało budyń do miseczek itp.

Zabawy i zadania

Zabawa „w piekarza". Piekarz otrzymuje zamówienie, aby z jednakowych kawałków ciasta upiec bułeczki, bagietkę, chleb i placek. Dziecko i dorosły formułują z ciasta (masa solna, plastelina) jednakowe kule. Dokładnie spraw­dzają: czy w każdej kuli jest tyle samo ciasta. Potem dziecko bierze dwie kule, jedną przekształca w bagietkę. Porównuje kulę i bagietkę i zastanawia się: czy w kuli i bagietce jest tyle samo ciasta. Potem bierze następne dwie kule i porównuje, czy są takie same i jedną przekształca w chleb. Następnie porównuje: czy kula i chleb są zrobione z tej samej ilości ciasta. I znowu dwie kule — po porównaniu, jedną zmienia w placek. Ogląda placek oraz kulę, a potem zastanawia się, czy kula i placek to tyle samo ciasta. Na koniec porównuje dwie kule i z jednej robi bułeczki.

Na stole leżą obok siebie kule i to, co dziecko z nich uformowało (rys. 71). Trzeba sprawdzić, czy zamówienie zostało należycie zrealizowane. Dorosły ma wątpliwości — to placek wydaje mu się większy, to chleb zbyt maty. Dziecko argumentuje i wyjaśnia. Można także przeformować np. placek w kulę, aby w ten sposób upewnić się.

Rys. 71. Porównywanie kuł całych i przeformowanych na różne sposoby

Dorosły proponuje: będziemy czarować mleko. Przygotowuje naczynia:

2 duże butelki do mleka, 2 mniejsze butelki i 6 szklanek (mogą to być także 2 wysokie szklanki, 2 szklanki niskie o szerokim dnie i 6 »literatek«). Do dzban­ka wlewa wodę i zabarwiają kilkoma kroplami mleka lub atramentu. A potem zwraca się do dziecka: do tych dwóch butelek (wskazuje mniejsze butelki, mogą to być także szklanki z szerokim dnem) nalej mleka, aby było po równo... Przelej mleko z jednej butelki do tej (wskazuje dużą butelkę). Porównaj mleko w obu butelkach (rys. 72).

Jeżeli dziecko mówi, że teraz jest więcej w jednej z butelek, dorosły sugeruje:

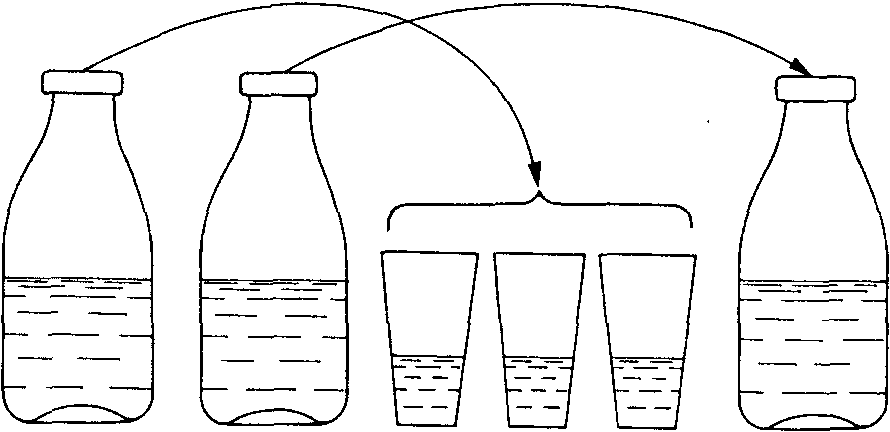
Rys. 72. Porównywanie ilości mleka

może przelejesz z powrotem? Potem poleca przelać mleko z drugiej małej butelki do dużej. Teraz jest tyle samo mleka w obu dużych butelkach. Można więc zbadać skutki następnej zmiany. Dziecko przelewa mleko z butelki do 3 szklanek tak. aby w każdej było trochę mleka. I znowu pojawia się problem:

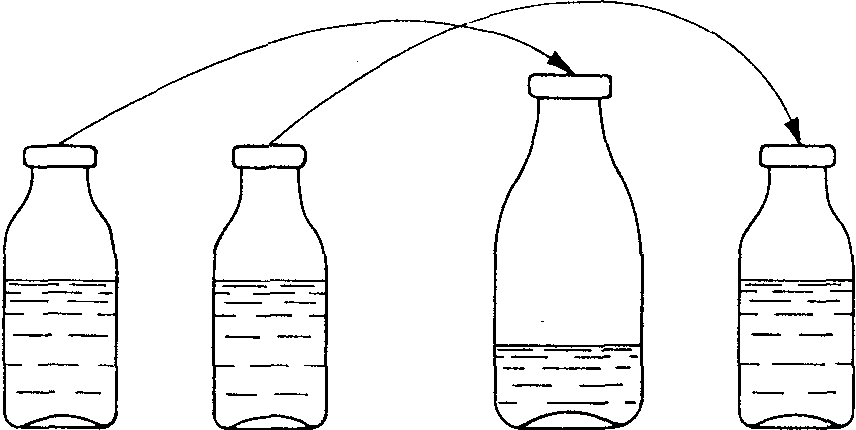
czy tu i tu jest tyle samo mleka? (rys. 73).

Na koniec tej serii eksperymentów dziecko przelewa mleko z drugiej butelk do trzech następnych szklanek i znowu porównuje. Jeżeli dziecko nie jest znudzone doświadczeniami, można powtórzyć całą serię.

Po jakimś czasie należy zorganizować podobną serię ćwiczeń. Przygotować kolekcję naczyń (3 lub 4 pary) o kontrastowym kształcie. Wlać mleko do jedne pary naczyń tak, aby było „po równo". Potem przelewać z jednego naczynia dc innego z innej pary. Porównywać i znowu sprowadzić do równości przelewając z drugiego naczynia do tego drugiego z drugiej pary itd. W trakcie takie! eksperymentów dziecko musi mieć możliwość porównywania naczyń i przelewa' nią w innej kolejności, niż to przewidział dorosły.

Przyjęcie u misia. Dla dzieci młodszych, tych w klasie zerowej, możne organizować taką zabawę. Dorosły zaczyna opowiadać: Miś postanowi/ za prosić na swoje urodziny kotkę Panterkę i jej dwoje kociąt, lalkę Małgorzatkę i je przyjaciela Kubusia... Kogo by jeszcze zaprosić? Zastanawia się miś... Zwykłe dzieci podejmują wątek i wyliczają następnych uczestników przyjęcia. Zastanawiają się nad potrawami i napojami, a kiedy jadłospis jest gotowy — razem z dorosłym przygotowują .potrawy... Jest to okazja do dzielenia całości na określoną liczbę części, formowania »różności« z jednakowych kawałków, przelewania płynu do małych naczyń, przyporządkowania ,,jeden do jednego" w trakcie nakrywania do stołu itp.

Tego rodzaju zabawy znajdują się w repertuarze każdego dziecka. Udział dorosłego nada zabawie szczególnie atrakcyjną formę. A co najważniejsze, umiejętnie postawione pytania spowodują, że dziecko skupi swą uwagę na następujących czynnościach: dzielenie i mieszczenie, przekształcanie i przy­wracanie poprzedniego kształtu, przyporządkowywanie na różne sposoby i liczenie. Określi je słownie i zastanowi się nad uzyskanymi efektami. Nie bez znaczenia jest także to, że te intelektualne czynności będą wtulone ciepłymi emocjami«.

Różnicowanie zmian zachodzących w czasie. Wprowadzenie do pomiaru czasu

Scenariusz zajęć

Potrzebne będą paski z papieru do pakowania, kartki z bloku i kredki lub mazaki do rysowania, makieta-zegar z ruchomymi wskazówkami (zegar-zabawka), budzik, kilka typów kalendarzy, historyjki obrazkowe (można je wycinać z dziecięcych czasopism).

Czas i kalendarz

Trzeba przygotować paski papieru do pakowania o szerokości 30 cm. Każdy podzielić na 7 pól. W każdym należy wpisać u góry nazwę dnia tygodnia. Najlepiej pismem drukowanym, aby dziecku było łatwo przeczytać lub zapamię­tać obraz graficzny nazwy dnia. Na pustych polach dziecko przypnie obrazki-rysunki. W poniedziałek dziecko narysuje to, co w tym dniu było ważne, na przykład karmienie kaczek, i rysunek ten przypnie w okienku — poniedziałek. We wtorek narysuje to, co kupiło w sklepie, a rysunek umieści w okienku — wtorek. Jednocześnie określi: to miało miejsce dzisiaj, a to było wczoraj. W środę narysuje swoją przygodę z psem i przypnie rysunek w okienku — środa. Można także dla zapamiętania narysować kino, bo w piątek postanowiono, że dziecko zobaczy film. W trakcie wykonywania każdego rysunku jest miejsce na wielce kształcące rozmowy o tym: co było wczoraj, przedwczoraj, co miało miejsce dzisiaj i co będzie np. za dwa dni (rys. 74).

Rys. 74. Ustalanie zdarzeń w czasie

Taki kalendarz zdarzeń trzeba prowadzić systematycznie przez kilka tygo­dni. Jest to znakomite źródło doświadczeń logicznych. Przy tej okazji dziecko zapamięta łatwo nazwy i kolejność dni w tygodniu.

Rodzice planują wyjazd do babci. Jest poniedziałek, a wyjadą w sobotę. Tata i dziecko przeglądają ścienny kalendarz i ustalają, ile czasu upłynie. Liczą dni, a potem zastanawiają się, co to oznacza. Dzień — rano wstaje słońce, a pod koniec dnia — zachodzi. Potem jest noc. Jedna kartka w kalendarzu (kartka w kalendarzu „do wyrywania") to jeden dzień i jedna noc. Jedna doba.

Warto przyzwyczaić dziecko do tego, że kalendarze mogą mieć różne formy. Dorosły zastanawiając się, za ile dni będzie miało miejsce określone wydarzenie, pokazuje dziecku inny kalendarz. Można także wspólnie z dzieckiem wykonać kalendarz podobny do tarczy zegarowej (rys. 75).

Taka forma kalendarza sugeruje cykliczność, a więc to, że zawsze po sobocie będzie niedziela, a po niedzieli — poniedziałek itd.

Po takim wprowadzeniu można już razem z dzieckiem planować urlop i zastanawiać się, ile czasu upłynie do wyjazdu. Ustalać, za ile dni, tygodni, miesięcy odbędą się różne ważne wydarzenia, np. urodziny babci, mamy, taty, za ile tygodni święty Mikołaj przyniesie prezenty itp.

Rys. 75. Kalendarz w formie tarczy

Badanie, ile czasu trwają różne czynności

Dorosły zastanawia się, jak długo trwa np. jedzenie śniadania. Proponuje:

można to zmierzyć na zegarze. Zrobimy tak. Ten zegar (budzik) wskazuje czas. Przesuwa/asie wskazówki. Na tym zegarze (zegar-zabawka) ustawimy wskazówki dokładnie tak, jak na prawdziwym zegarze. Potem będzie można zobaczyć, o ile przesunęły się wskazówki po zakończeniu śniadania. Od tej chwili mierzymy czas... Już skończyłeś. Zobaczymy, co się zmieniło w układzie wskazówek?... Dziecko porównuje tarcze zegarowe i określa, że wskazówka przesunęła się odtąd— dotąd. Dorosły mówi: co to znaczy, że śniadanie trwało 15 minut. Odtąd — dotąd to 15 minut... W podobny sposób trzeba ustalać, ile trwa kąpiel, sprzątanie w kąciku zabawek, film dla dzieci itp. W tego typu sytuacjach dziecko uchwyci, co w tarczy zegarowej jest najważniejsze (przesunięcie wskazówek o tyle), a co stanowi element ozdobny. Intuicyjnie rozumie sens pomiaru. Powoli uczy się odczytywać informacje przedstawione na tarczy zegarowej. Wszystko to jest silnie skojarzone z przepływem czasu, z tym, co działo się, co się dzieje i co będzie się dziać.

Po takich doświadczeniach można przejść do ćwiczeń w rozpoznawaniu czasu na zegarze. A potem do prostych obliczeń i rozwiązywania zadań. Kształcące jest uświadomienie dziecku rytmicznej organizacji czasu. Jak to zrobić, opisałam w rozdziale 4 książki Dziecięca matematyka.

---