E GRUSZCZYK KORCZYŃSKA DZIECI ZE SPECYFICZNYMI TRUDNOŚCIAMI W UCZENIU SIĘ MATEMATYKI(streszczenie)

E. Gruszczyk-Korczy ska „Dzieci ze specyficznymi trudno ciami w

uczniu si matematyki”

ROZDZIA I

Trudno ci dzielimy na:

Trudno ci zwyk e - pojawiaj ce si w nauce matematyki w sposób
naturalny
Trudno ci specyficzne, z którymi dziecko poradzi sobie nie mo e.

dzieci cych dramatów

ównym sposobem uczenia si matematyki jest rozwi zywanie zada .

Jest to ród o do wiadcze logicznych i matematycznych. Mo na
powiedzie ; e bez rozwi zywania zada nie ma uczenia si matematyki.
Rozwi zanie ka dego zadania, nawet atwego, jest równoznaczne z
pokonaniem trudno ci. Dlatego pokonywanie trudno ci stanowi integraln
cz

procesu uczenia si matematyki. Nie jest wi c le, je eli dziecko

ucz c, si matematyki napotyka na trudno ci, lecz niezmiernie wa ne jest,
aby potrafi o je w miar samodzielnie pokona . Je eli tak si dzieje — s to
trudno ci zwyczajne i takie prze ywaj wszystkie dzieci w trakcie uczenia
si matematyki.

Jest jednak w szkole spora grupa dzieci, które mimo wysi ku nie potrafi

poradzi sobie nawet z atwymi zadaniami. Nie rozumiej ich
matematycznego sensu i nie dostrzegaj zale no ci pomi dzy liczbami.
Bywa, e nie potrafi wytrzyma napi , które zawsze towarzysz
rozwi zywaniu zada z powodu swej niskiej odporno ci emocjonalnej.
Narysowanie grafu, tabelki, a nawet czytelne zapisanie dzia ania mo e by
zbyt trudne, je eli dziecko ma obni on sprawno manualn . W takich
przypadkach trzeba mówi o specyficznych trudno ciach w uczeniu si
matematyki.

Dzieci, które doznaj takich trudno ci, potrzebuj fachowej pomocy ze

strony doros ych. Je eli jej nie otrzymuj w por , wówczas pojawiaj si
niepowodzenia i blokady w uczeniu si matematyki. Towarzysz temu silne
napi cia emocjonalne, które odbijaj si niekorzystnie na rozwoju

osobowo ci tych dzieci. Znika motywacja do nauki i pojawia si niech do
wszystkiego, co wi e si z matematyk . Towarzyszy temu utrata wiary we

asne mo liwo ci poznawcze i wykonawcze. Obawa przed nieuchronnym

niepowodzeniem ka e tym dzieciom wycofywa si z zada wymagaj cych
wysi ku intelektualnego. Pog bia si ich nerwowo oraz zmniejsza si i tak
ju niska odporno

emocjonalna. Wszystko to sprawia, e nast puje

zwolnienie rozwoju umys owego tej, niestety, licznej grupy dzieci.

Z bada wynika, e zdecydowana wi kszo dzieci doznaj cych

specyficznych trudno ci w uczeniu si

matematyki rozpoczyna nauk w

szkole bez nale ytej dojrza

ci do uczenia si matematyki. Charakteryzuje

si nieco wolniejszym rozwojem tych procesów psychicznych, które s
zaanga owane w nabywanie poj i umiej tno ci matematycznych.
Najcz ciej s to opó nienia niewielkie, si gaj ce kilku miesi cy. Jednak w
czasie rozpoczynania nauki w szkole dzieci te reprezentuj

mniejsz

podatno i wra liwo w zakresie uczenia si matematyki. Je eli nie
rozumuj jeszcze na poziomie operacji konkretnych, to nie potrafi
zrozumie ani wyja nie nauczyciela, ani sensu zada matematycznych,
gdy te s utrzymane w konwencji operacyjnej.

Sytuacj pogarsza silna motywacja, któr przejawiaj wszyscy

pierwszoklasi ci. Nie chc zawie oczekiwa rodziców i pragn zaskarbi
wzgl dy swojej nauczycielki. Pracuj wi c na granicy swych mo liwo ci.
Jednak mimo tych stara efekty bywaj ró ne. Na dodatek doro li nie
rozumiej c przyczyn s sk onni uwa

, e przyczyn jest lenistwo lub z a

wola dziecka. Zmuszaj je do nadmiernego wysi ku, a nie udzielaj
nale ytej pomocy. Dziecko musi wi c samo jako sobie poradzi . Uczy si
szybko zachowa obronnych. Wstrzymuje si od odpowiedzi, a potem
powtarza, co powiedzia y inne dzieci. Opanowuje na pami schematy
czynno ci, nie próbuj c nawet zrozumie ich sensu. Wymusza daleko id
pomoc przy odrabianiu zadania lub odpisuje gotowy wynik. Takie i
podobne zachowania pomagaj unikn represji, lecz w konsekwencji
obracaj si przeciw dziecku. Powoduj bowiem blokady w uczeniu si
matematyki ze wszystkimi ich konsekwencjami.

Przyczyny nadmiernych trudno ci – wska niki dojrza

ci:

wiadomo , w jaki sposób nale y liczy przedmioty. Niepowodze w

uczeniu si matematyki doznaj dzieci, które nie potrafi rozró ni
biednego liczenia od poprawnego, a tak e nie umiej dodawa i
odejmowa na palcach do 10. Podstaw dzieci cego liczenia s intuicje

matematyczne, które dziecko przyswaja sobie ju na poziomie
przedoperacyjnym, a wi c w wieku przedszkolnym. Wszelkie
nieprawid owo ci w przyswajaniu tych intuicji mog by przyczyn
nadmiernych trudno ci w zakresie uczenia si matematyki.

2. Odpowiedni poziom operacyjnego rozumowania. Je eli w czasie

rozpoczynania nauki w klasie I dzieci nie osi gn y jeszcze w swoim
rozumowaniu operacji konkretnych (w zakresie koniecznym dla,
zrozumienia poj cia liczby naturalnej), to natrafiaj na ogromne
trudno ci w uczeniu si matematyki ju w pierwszych tygodniach nauki
w szkole. Tym samym opó nienia w operacyjnym rozumowaniu w
stosunku do czasu rozpoczynania nauki w szkole s przyczyn
specyficznych trudno ci w uczeniu si matematyki.

3. Zdolno do funkcjonowania na poziomie symbolicznym i ikonicznym

bez potrzeby odwo ania si do poziomu enaktywnego, do poziomu
dzia

praktycznych. Szkolne nauczanie preferuje s owo i obraz.

Rzadko dziecko ma okazj sprawdzi w realnym dzia aniu to, co zosta o
powiedziane, zapisane lub pokazane w formie graficznej. Dlatego
warunkiem powodzenia w uczeniu si matematyki jest zdolno do
swobodnego przechodzenia z jednego poziomu reprezentacji na drugi,
przy du ej dojrza

ci funkcjonowania na poziomie symboli i

przedstawie graficznych.

4. Stosunkowo wysoki poziom odporno ci emocjonalnej na sytuacje

trudne. Dzieci ma o odporne nie wytrzymuj napi , które zawsze
towarzysz rozwi zywaniu nawet atwych zada matematycznych. Nie

bowiem zdolne do racjonalnego zachowania podczas pokonywania

trudno ci. Obni ony poziom odporno ci emocjonalnej jest wi c
przyczyn niepowodze w uczeniu si matematyki.

5. Nale yta sprawno manualna, precyzja spostrzegania i koordynacja

wzrokowo-mchowa. Je eli dziecko nie potrafi wykona prostych
rysunków i konstrukcji z klocków, ani wyszuka potrzebnej strony w
swym podr czniku, to mo e mie powa ne k opoty na lekcjach. Nie
mo e skupi si nale ycie na problemach matematycznych, a to ma
wysoce niekorzystny wp yw na zakres do wiadcze matematycznych i
logicznych, które dziecko mo e zgromadzi na lekcji.

Z tego opisu g ównych wska ników dojrza

ci wynika, e pokrywaj

si one z zakresem przyczyn nadmiernych trudno ci w uczeniu si

matematyku. Mog si one pog bia w wyniku nieprawid owego nauczania
lub z ych warunków, w jakich odbywa si kszta cenie, np. zbyt liczne klasy,
lekcje na 3 zmian . Nieprawid owo ci procesu nauczania odbijaj si
najsilniej na tych dzieciach, którym i tak trudno sprosta wymaganiom.

Teoria interioryzacji – przy pomocy odpowiednio zorganizowanego

uczenia mo na korzystnie wp yn na przebieg rozwoju dzieci – wspomóc
to co zbyt wolno si rozwija, wyciszy l ki i uprzedzenia, ukszta towa
zdolno do racjonalnego zachowania si i zwi kszy odporno
emocjonaln , a potem rekonstruowa system wiadomo ci i umiej tno ci
matematycznych.

Szans na sukces daje przestrzeganie zasady:
Stawiania zada i wymaga na miar strefy najbli szego rozwoju
dziecka;
Pe nej opieki i wspó pracy z doros ymi zajmuj cymi si dzieckiem na co
dzie ;
Akceptacji dziecka i dobrego z nim kontaktu.
Konstruowanie programów – opracowuje si je dla ka dego dziecka

osobno, stosownie do jego potrzeb i mo liwo ci rozwojowych.

Zaj cia powinny by realizowane w diadzie: terapeuta-dziecko.

Dlatego wszystko, co si na nich dziej, przybiera form dialogu mi dzy
doros ym i dzieckiem. W ten sposób mo na w miar precyzyjnie sterowa
mechanizmem interioryzacji, wykorzystywa modelowanie i
na ladownictwo oraz wzmacnia i utrwala po

dane zachowania. Istot

dialogu pomi dzy doros ym a dzieckiem jest naprzemienne uk adanie i
rozwi zywanie zada . Pozwala to tak organizowa proces uczenia si , aby
zmie ci go w strefie najbli szego rozwoju. Mo na wykorzysta elementy
metod czynno ciowych, co jest szczególnie cenne przy rekonstruowaniu
systemu wiadomo ci i umiej tno ci matematycznych dziecka.

Najtrudniej doros ym kszta towa u dzieci dojrza

do ucznia si

matematyki, gdy problem ten niezwykle rzadko jest omawiany w literaturze
metodycznej. Kszta towanie takiej dojrza

ci to wspomaganie rozwoju i

korygowanie zaburze rozwojowych w zakresie sfery intelektualnej,
emocjonalnej i sprawno ciowej. Jest to wi c usuwanie przyczyn
nadmiernych trudno ci w uczeniu si matematyki.

ROZDZIA II

DOJRZA

DO UCZNIA SI MATEMATYKI

Problem wra liwo ci i podatno ci w zakresie uczenia si matematyki na

sposób szkolny.

Niepowodze w uczniu si matematyki doznaj dzieci, które

rozpoczynaj nauk w szkole bez dojrza

ci koniecznej do ucznia si

matematyki w warunkach klasowo-lekcyjnych.

Dojrza

do ucznia si matematyki zawiera si w zakresie poj cia

dojrza

szkolna. Dojrza

szkoln mo na ujmowa :

Statycznie, jako moment równowagi pomi dzy wymaganiami szko y,
a mo liwo ciami rozwojowymi dziecka
Dynamicznie, jako d ugotrwa y proces przemian psychicznych i
fizycznych, który prowadzi do przystosowania si dziecka do
szkolnego systemu nauczania.

Popularny jest jednak statyczny sposób okre lania dojrza

ci szkolnej

i wówczas podkre la si , e jest to taki poziom rozwoju umys owego,
spo eczno-moralnego oraz fizycznego, który umo liwia dziecku
przystosowanie si do wymaga szko y i zapewnia uzyskanie powodzenia w
nauce szkolnej.

Przy wyznaczaniu dojrza

ci do ucznia si matematyki bierze si

pod uwag poziom rozwoju tych procesów psychicznych, które dziecko
anga uje w trakcie nabywania wiadomo ci i umiej tno ci matematycznych
w szkole oraz wymagania stawiane mu na lekcjach. Mówi si o dojrza

do ucznia si matematyki na sposób szkolny albo w warunkach szkolnych.

Tre ci i metody nauczania matematyki maj wp yw na to, co sk ada

si na dojrza

do ucznia si matematyki w warunkach szkolnych. Wraz

ze zmian programu pocz tkowego nauczania matematyki i zastosowania
nowych metod zmieni si zakres tego, co dzieci musz reprezentowa , aby
obecnie sprosta wymaganiom.

Od samego pocz tku szkolnej edukacji, dziecko musi by zdolne

do rozumowania operacyjnego na poziomie konkretnym w 2 zakresach:

1. Uznawanie sta

ci ilo ci nieci

ych przy obserwowanych

zmianach. Oznacza to wnioskowanie o sta

ci liczby elementów w

porównywanych zbiorach niezale nie od tego, w jakiej konfiguracji
si znajduj i w jaki sposób s przemieszczane. Dziecko musi umie
skupi si jednocze nie na dwóch zbiorach i koncentrowa si na
liczbie elementów, pomijaj c ich wielko , kolor i u

enie.

Porównuj c liczebno zbiorów powinno pos ugiwa si biegle

dwoma metodami: liczeniem przedmiotów w obu zbiorach i
przyporz dkowaniem kolejnym elementom jednego zbioru po
jednym elemencie ze zbioru drugiego ( czenie w pary). Wa ne jest,
aby potrafi o ujmowa obserwowane zmiany w uk adzie elementów
jako odwracalne i nie potrzebowa o ci gle przelicza ich. Takie
kompetencje s dziecku potrzebne dla zrozumienia aspektu
kardynalnego liczby naturalnej.

2. Porz dkowanie elementów zbioru, aby utworzy konsekwentn

seri . Dziecko musi umie ujmowa ka dy kolejny np. patyczek jako
najmniejszy w nieuporz dkowanym zbiorze i u

go jako

najwi kszy w tworzonej serii. Taki sposób post powania oznacza, e
potrafi przegrupowa porz dkowane elementy w wyobra ni i ustali
miejsce ka dego z nich w tworzonej serii. Dlatego umie szeregowa
„po kolei" przedmioty ró ni ce si wielko ci , grubo ci ,
nasyceniem koloru. Potrafi ustali miejsce ka dego przedmiotu w
tworzonej serii i okre li , e ten jest pierwszy, ten drugi, ten trzeci.
Taki sposób rozumowania jest baz dla kszta towania w umys ach
dzieci aspektu porz dkowego liczby naturalnej. Jest w nim równie
zawarta intuicja innego poj cia.

Dla kszta towania poj cia miary wielko ci ci

ych dziecko musi

rozumowa operacyjnie na poziomie konkretnym w zakresie przestrzeni
i czasie.

Z chwil rozpocz cia nauki w szkole wymaga si od dziecka, aby

potrafi o funkcjonowa na poziomie reprezentacji ikonicznych i
symbolicznych. Dziecko musi rozumie sens kodowania i dekodowania
informacji za pomoc umownych symboli. Najprostsze zapisane dzia anie
jest syntez symboliczn (np. 3+2=5; 6-4=2). Liczby i czynno dodawania i
odejmowania s przedstawione w ustalonym systemie znaków.

Jednym z wa nych wska ników dojrza

ci do ucznia si matematyki w

warunkach szkolnych jest zdolno do funkcjonowania na poziomie
symbolicznym i ikonicznym bez konieczno ci odwo ywania si do
praktycznych dzia

Nauka matematyki w szkole nie jest pierwsz form edukacji

matematycznej. Wcze niej doro li ucz dzieci wa nych umiej tno ci:

Wyodr bnia przedmiotów do policzenia i liczenia ich w
okre lony sposób;
Ustalania, gdzie jest wi cej, a gdzie mniej poprzez policzenie
przedmiotów;
Okre lenie wyniku dodawania i odejmowania

Jest to dzieci ce liczenie – podstaw s pewne intuicje matematyczne

dost pne dzieciom na poziomie wyobra

przedoperacyjnych, np.

wi kszo dzieci przedszkolnych potrafi ustali wynik dodawania i

odejmowania tylko wówczas, gdy widz przedmioty i mog je policzy
dotykaj c lub wskazuj c ka dy.

Sama umiej tno liczenia przedmiotów nie wystarcza dzieciom, aby

sprosta wymaganiom stawianym im na lekcjach matematyki, chocia jest to
wa ny wska nik dojrza

ci do ucznia si matematyki w szkole.

Wa nymi wska nikami dojrza

ci do ucznia si matematyki jest

pozytywne nastawienie dzieci do samodzielnego rozwi zywania zada i
odporno emocjonalna na pokonywanie trudno ci typu intelektualnego.

Dzieci rozpoczynaj ce nauk w szkole musz reprezentowa

stosunkowo wysoki poziom zdolno ci do syntezowania oraz integrowania
czynno ci poznawczych i motorycznych.

Dla efektywnego uczenia si matematyki w warunkach szkolnych

dziecko musi umie znosi przykre podniecenia i napi cia. Musi by
odporne emocjonalnie, tak aby mimo nastaj cych napi potrafi o rozwi za
zadanie.

Kodowanie i dekodowanie w nauczaniu matematyki odbywa si od

samego pocz tku na wysokim poziomie uogólnienia i wymaga operacyjnego
rozumowania na poziomie konkretnym.

Dzieci s dojrza e do uczenia si matematyki w szkole wówczas, gdy

chc si uczy matematyki i potrafi zrozumie sens zale no ci
matematycznych omawianych na lekcjach i z atwo ci wytrzymuj
napi cia, które towarzysz rozwi zywaniu zada matematycznych.

Wska niki spo ecznego przystosowania si dzieci do obowi zków

szkolnych:

1. zdolno do radzenia sobie w prostych sytuacjach
2. umiej tno zachowania si w grupie doros ych lub rówie ników w

sposób dostosowany do przyj tych norm i obyczajów

3. samodzielno
4. wykonywanie polece skierowanych bezpo rednio do dziecka i do

ca ej grupy

5. zdolno do podporz dkowania si wymaganiom zwi zanym z

uczniem si w grupie rówie niczej

Zakres dojrza

ci do ucznia si matematyki w warunkach

szkolnych:
1)

Dzieci ce liczenie:
Sprawne liczenie i rozró nianie b dnego liczenia od poprawnego;
Umiej tno wyznaczania wyniku dodawania i odejmowania w
zakresie 10 „w pami ci” lub na palcach.

Operacyjne rozumowanie na poziomie konkretnym w zakresie:
Uznawania sta

ci ilo ci nieci

ych (zdolno do wnioskowania o

równoliczno ci mimo obserwowanych zmian w uk adzie elementów
porównywanych zbiorów)

Wyznaczanie konsekwentnych serii (zdolno do ujmowania
ka dego z porz dkowych elementów jako mniejszego od
nieuporz dkowanych i jednocze nie jako najwi kszego w zbiorze
liczb ju uporz dkowanych).

3) Zdolno do odrywania si od konkretów i pos ugiwanie si

reprezentacjami symbolicznymi w zakresie:

Poj liczbowych (aspekt j zykowo-symboliczny)
Dzia

arytmetycznych (formu a arytmetyczna i jej przekszta cenia)

Schematu graficznego (grafy strza kowe, drzewka, tabele i inne
uproszczone rysunki)

Dojrza

emocjonalna wyra aj ca si w:

Pozytywnym nastawieniu do samodzielnego rozwi zywania zada
Odporno emocjonalna na sytuacje trudne intelektualnie (zdolno
do kierowania swym zachowaniem w sposób racjonalny mimo
prze ywanych napi )

Zdolno ci do syntetyzowania oraz zintegrowania funkcji

percepcyjno-motorycznych, która wyra a si w sprawnym
odwzorowywaniu z

onych kszta tów, rysowaniu i konstruowaniu.

ROZDZIA III

DZIECI CE LICZENIE PODSTAW UCZENIA SI

MATEMATYKI W SZKOLE

INTUICJE MATEMATYCZNE DOST PNE DZIECIOM

PRZEDSZKOLNYM.

Dzieci ce liczenie jest to efekt edukacji matematycznej, o która troszcz

si rodzice, zanim dziecko rozpocznie nauk w szko . Znacz cy jest wp yw

rodowiska, poniewa dziecko widzi, jak doro li licz przedmioty, pos uguj

si kalendarzem, kupuj lub sprzedaj itd. W rezultacie wi kszo dzieci,
jeszcze przed pój ciem do szko y, potrafi:

policzy przedmioty i okre li , ile ich jest:
ustali wynik dodawania i odejmowania, je eli mog policzy
przedmioty lub pomóc sobie liczeniem na palcach.

Podstaw dzieci cego liczenia wg R. Gelman s pewne intuicje

matematyczne dost pne dzieciom bardzo wcze nie, ju na pocz tku okresu
wyobra

przedoperacyjnych. Liczenie i prosie rachunki s przyswajane

podobnie jak mowa ojczysta. Analogicznie do rozwoju mowy i w zakresie
liczenia dzieci posiadaj zdolno wychwytywania prawid owo ci. Ma e
dzieci potrafi poj sens liczenia i okre li wynik dodawania oraz
odejmowania. S zdolne opanowa te umiej tno ci zanim poznaj wi kszy
zakres liczebników i nim osi gn poziom operacyjnego rozumowania w
zakresie potrzebnym do przyswojenia poj cia liczby naturalnej.

R. Gelman ustali a, e ju 3-latek rozumie i potrafi stosowa :

zasad „jeden do jednego”: liczenie oznacza dla niego dotykanie

lub wskazywanie przedmiotów i nazywanie ich liczebnikami;

zasad „sta

ci porz dku”: licz c przedmioty wypowiada kolejne

liczebniki, dlatego mo e policzy nie tylko przedmioty u

one liniowo,

lecz tak e je eli s zgrupowane, bo porz dkuje je tak, jak liczebniki;

zasad „kardynalno ci”: ostatni z wypowiadanych liczebników ma

specjalne znaczenie, bo okre la liczb przedmiotów w zbiorze.

Przed 5 rokiem ycia, wg R. Gelman dzieci potrafi stosowa w

trakcie liczenia zasady:

zasad „abstrakcji": wcze niej liczy y przedmioty jednorodne, a w

przypadku liczenia przedmiotów ró norodnych dzieli y je na grupy i
liczy y oddzielnie „te, a potem te". Teraz potrafi ju policzy przedmioty
razem, nie bacz c na ró nice jako ciowe, abstrahuj c od tych ró nic;

zasad „niezale no ci porz dkowej": chc c okre li liczebno

zbioru, dziecko liczy przedmioty „od pocz tku", lecz je eli wskaza
pi ciolatkowi ostatni przedmiot i okre li „ten jest pierwszy", potrafi
policzy w przeciwnym kierunku. Dziecko wie bowiem, e liczebno
zbioru nie zale y od kolejno ci przeliczania jego elementów.

R. Gelman twierdzi, e przed 5 rokiem ycia dziecko potrafi ustali , w

którym zbiorze jest wi cej elementów. Wie, e w wyniku dodawania
zwi ksza si liczba liczonych przedmiotów, a w wyniku odejmowania ulega
zmniejszeniu. Umie okre li wynik dodawania i odejmowania je eli mo e
manipulowa przedmiotami i policzy je.

Przy liczeniu dziecko najpierw oddziela przedmioty „do policzenia” od

pozosta ych – ogarnia je wzrokiem lub gestem. Potem skupia si tylko na
jednym z porównywanych zbiorów i ka dy element oznacza liczebnikiem.
Z rytmu liczenia wywodzi poczucie „tyle jest”, a ostatni wypowiadany
liczebnik nazywa to poczucie. Teraz dziecko przenosi uwag na drugi zbiór i
liczy elementy. Na koniec porównuje ostatnie liczebniki i ustala, czy w obu
zbiorach jest tyle samo elementów.

W przypadku, gdy dziecko stosuje metod uk adania w pary musi umie

skupi uwag jednocze nie na dwóch zbiorach. Zna sposób uk adania w
pary, stosowa go konsekwentnie (przyporz dkowa ka demu elementowi
jednego zbioru po jednym elemencie z drugiego zbioru).

Umiej tno ci dodawania i odejmowania s najsilniej wiczone. Doro li

uwa aj je bowiem za wa ny warunek nale ytego przygotowania dzieci do
szko y. Tak e w klasie zerowej i na pocz tku klasy pierwszej sporo uwagi
po wi ca si kszta towaniu tych umiej tno ci.

ROZWÓJ DZIECI CEGO LICZENIA

Liczenie nie jest czym , Co dziecko mo e opanowa w krótkim czasie.

Umiej tno ta kszta tuje si kilka lat i mo na tu wyró ni co najmniej dwie
fazy, nim stanie si integraln cz ci szkolnego nauczania matematyki.
Efekty tego procesu, wyznaczone s czynnikami:
1)

Wcze nie rozwijaj

si u dzieci zdolno ci do nadawania

znaczenia prostym sytuacjom spo ecznym i rozumienia intencji
doros ych ( atwo wychwytywania prawid owo ci w tym wszystkim, co
dzieje si pomi dzy doros ym a dzieckiem). Zdolno ta przejawia si w

eniu do okre lania i porz dkowania tego, co znajduje si w otoczeniu.

W zakresie tej zdolno ci; istniej spore ró nice indywidualne. Dlatego

jedne dzieci potrafi sobie wcze niej przyswoi prawid owo ci b

podstaw liczenia i szybciej opanowuj schemat czynno ci liczeni.

Wp ywem doros ych, którzy przybli aj dzieciom proste intuicje

matematyczne, ucz c je liczenia, sposobów ustalania gdzie jest wi cej, a
gdzie mniej, a tak e wyznaczania wyniku dodawania i odejmowania.
Taka edukacja zaczyna si wcze nie i towarzyszy nauce mowy. Potem
prowadzona jest równolegle do tego czego uczy si dziecko w
przedszkolu i stanowi cz

przygotowania dziecka do szko y.

Ró nice indywidualne w opanowaniu liczenia s spowodowane
wi ksza lub mniejsz zdolno ci do wychwytywania
prawid owo ci oraz tym, w jaki sposób doro li przybli ali dziecku
sens intuicji matematycznych, ucz c je liczenia.

Gest wskazywania - w ko cu 1 roku ycia, przez 2, 3 i 4 rok ycia.

Dziecko skupia uwag na jakim przedmiocie i stara si przekaza
doros emu, e to w

nie go interesuje. Wyci ga r

w ge cie wskazywania

i dopomina si , aby doros y bra udzia w tym akcie poznania i oznaczy ten
obiekt s owem-nazw . Zdaniem S. Szumana gest wskazywania wyst puje w
zachowaniu dziecka z ogromna natarczywo ci i przy ka dej okazji. Jest to
sposób wyró niania przedmiotu ze wszystkich pozosta ych, które w danym
momencie nie s dla dziecka istotne. Ten spontaniczny gest pe ni niezwykle
wa

rol w kszta towaniu si mowy. Jest to tak e pocz tek liczenia.

Doro li okre laj s owem-etykietk wskazywany przez dziecko obiekt, a

tak e sami wskazuj i nazywaj inne obiekty. W ten sposób kieruj na nie
uwag dziecka. Je eli w otoczeniu znajduje si wi cej podobnych obiektów,
wskazuj je kolejno (gest, dotyk) i mówi , np: jab ko i to jab ko, a nast pnie
jedno jab ko (gest), drugie jab ko (gest) lub: jeden (gest wskazuj cy jab ko),
dwa (gest) itd.

Wszystkie dzieci w tym przedziale wiekowym (1-4) d

y do

wyodr bnienia przedmiotów „do policzenia". Wa ny by dla nich uk ad
przedmiotów (rz dem — rytmiczne liczenie by o atwiejsze, bo zosta o
poniek d wymuszone rytmem np. kasztanów, gdy przedmioty by y
skupione, zadanie okaza o si znacznie trudniejsze, dzieci spostrzega y je
jako jedn ca

i pytanie „ile" traci o sens). Dzieci stara y si dotyka

liczone przedmioty, wypowiadaj c s owa: do liczenia. Nie zawsze
wiedzia y, e wa na jest kolejno liczebników, wypowiada y je w ró nym
porz dku, powtarzaj c niektóre.

Taki schemat liczenia doskonali si w trakcie nast pnych lat, w

przedszkolu, a potem w szkole. W trakcie przyporz dkowania dziecko ma
okazj do kszta towania poczucia „Jest tyle”. Sprzyja temu powtarzaj cy
si rytm liczenia i czas wykonywania tej czynno ci. Im d

ej trwa o

liczenie tym wi cej by o do policzenia. Ostatni z wypowiadanych
liczebników zaczyna odgrywa specjaln rol - okre la poczucie „Jest tego
tyle” i nazywa to poczucie. Na pocz tku kszta towania si schematu liczenia
dzieci nie nadaj znaczenia ostatniemu z wypowiedzianych liczebników.
Je eli je spyta tu po policzeniu: ile jest?, zaczynaj ponownie liczy , bo
,,ile" odnosi si najpierw do powtarzanych czynno ci. W tym czasie nie
przywi zuj wagi do tego, w jakiej kolejno ci wymieniaj liczebniki.
Wskazuj c przedmioty mówi : jeden, dwa, trzy, pi , osiem. Zapytane: ile
jest odpowiadaj : osiem. Jednak s owo to odnosi si do tylu dotkni , ile
by o przedmiotów. Gdy skojarz brzmienie liczebników z poczuciem ,,tyle"
wywodz cym si z rytmu liczenia, zaczynaj dba o nale yt kolejno
wypowiadanych liczebników.

Kolejna wa na umiej tno to wyznaczanie wyniku dodawania i

odejmowania. Mo na tu tak e wyró ni 2 fazy:

Pocz tek pierwszej zaczyna si gdy dziecko zaczyna si

interesowa zmian wywo an dodawaniem lub odejmowaniem i d

do okre lenia „jak jest teraz", po obserwowanej zmianie. Zbiega si to z
faz kszta towania si schematu liczenia przedmiotów. Dlatego dziecko
stwierdzaj c obecno przedmiotów po zmianie typu doda i odj , stara
si dotkn ka dy z osobna przedmiot oraz oznaczy go s owem-
liczebnikiem. Wa na jest czynno dotykania i oznaczania, a nie wynik.
Dzieci zapytane: ile jest razem, ponownie stara y si je wszystkie
dotkn . Faza ta trwa przeci tnie do 5 roku ycia.

Druga faza zaczyna si gdy dziecko spostrzega, e dodawanie to

czenie, a odejmowanie to odbieranie. Rozumie, e s to zmiany

specyficzne, maj ce wp yw na liczb przedmiotów: w wyniku
dodawania zwi ksza, a w wyniku odejmowania zmniejsza si ich liczba.
Obok czynno ci liczenia znaczenia nabiera liczba przedmiotów, to czy
jest ich teraz wi cej, czy mniej. Dziecko d

y do tego, aby po ka dej

zmianie typu doda lub odj , dok adnie policzy przedmioty i jest
zainteresowane wynikiem. Na pocz tku tej fazy dziecko potrafi ustali
wynik tylko wówczas, gdy widzi przedmioty, na których dokonano
manipulacji i mo e je wskazuj c policzy . Trwa to mniej wi cej do 7

roku ycia. Trzeba wiele do wiadcze , aby dziecko potrafi o oderwa
sens dodawania i odejmowania od konkretnej sytuacji i ustali wynik na
poziomie symbolicznym. Nim tak si stanie, dziecko przechodzi zwykle
przez okres liczenia na palcach - okres symulowania dodawania i
odejmowania ró nych przedmiotów na zbiorze zast pczym. Czynno
zginania i prostowania palców reprezentuje dodawanie i odejmowanie
przedmiotów, o których jest mowa, a wynik mo na ustali metod
przeliczenia palców.

LICZENIE NA PALCACH. OGRANICZENIA POZNAWCZE

CHARAKTERYZUJ CE DZIECI CE LICZENIE

Zakres umiej tno ci sk adaj cych si na dzieci ce liczenie nie wystarcza

dzieciom dla sprostania wymaganiom stawianym im na lekcjach
matematyki. Ma to miejsce wtedy, gdy dziecko nie rozumuje jeszcze na
poziomie operacji konkretnych.

Przyczyn s

ograniczenia poznawcze charakteryzuj ce dzieci ce

liczenie:

silny zwi zek czynno ci liczenia z konkretnymi obiektami „do
policzenia"
ustalanie wyniku dodawania i odejmowania na podstawie
manipulowania obiektami
potrzeba wielokrotnego przeliczania rozpatrywanego zbioru po
ka dej obserwowanej zmianie uk adu elementów.

Liczenie dotyczy konkretnych obiektów, a poczucie liczebno ci wynika

z czasu trwania wskazywania i oznaczania ich liczebnikami. Pod koniec
okresu kszta towania si schematu, czynno ci dodawania i odejmowania
odnosz si tylko do obiektów, które dziecko mo e wskaza i policzy .
Zadanie komplikuje si gdy ma ono ustali wynik, a nie widzi obiektów, na
których dokonano manipulacji. Nie widzi bowiem sensu w liczeniu czego ,
co jest nieobecne.

Pierwsz prób symulowania jest liczenie na palcach. Dziecko zast puje

nieobecne obiekty palcami jeden do jednego, a zmiany typu doda lub odj
przedstawia za pomoc prostowania lub zginania palców. Wynik dodawania
i odejmowania, ustala licz c wyprostowane palce. Z chwil opanowania
liczenia na palcach rozszerzaj si znacznie mo liwo ci poznawcze dziecka -
mo e ustala wynik dodawania i odejmowania bez potrzeby badania
konkretnej sytuacji, pos uguj c si zbiorem zast pczym.

Liczenie na palcach pozwala dziecku przek ada sens zada

sformu owanych na wy szym poziomie abstrakcji na bardziej konkretny
poziom. Zadania sformu owane s ownie np.

Ile jest piec doda cztery?
lub przedstawione w postaci formu y arytmetycznej:
5+4=?
Zadania te, s sformu owane na poziomie poj liczbowych i stanowi

swojego rodzaju syntezy symboliczne. Rozwi zanie ich wymaga od dziecka
rozumowania na poziomie wyobra

poj ciowych, bo wówczas umie

wyliczy „w pami ci". Gdy dziecko nie reprezentuje takiego poziomu
rozwoju mo e pos

si w

nie liczeniem na palcach. Pokazuje pierwsz

liczb na wyprostowanych palcach, a potem prostuje (przy dodawaniu) lub
zgina (przy odejmowaniu) odpowiedni liczb palców. Nast pnie przelicza
efekt tej manipulacji - wyprostowane palce, a ostatni z wymienianych
liczebników jest rozwi zaniem zadania. Jednak zakres liczenia na palcach
jest ograniczony do 10. Je eli dziecko musi rozwi zywa zadania
wykraczaj ce poza liczb palców, próbuje sobie jako poradzi . Np. Marysia
rozwi zuje zadanie:

12-4=?
Po

a na stole d onie. Rozsun a szeroko palce i policzy a je. Potem

a obok dwa o ówki. Nast pnie policzy a palce i o ówki razem.

Odliczy a „od ko ca" cztery i policzy a reszt . Na koniec o wiadczy a: jest
osiem.

ROZDZIA IV

ROZWÓJ OPERACYJNEGO ROZUMOWANIA I JEGO NACZENIE

W UCZNIU SI MATEMATYKI

Operacyjne rozumowanie to sposób funkcjonowania intelektualnego,

który kszta tuje si i dojrzewa zgodnie z rytmem rozwojowym cz owieka. W
kolejnych okresach i stadiach rozwojowych zmienia si sposób w jaki
cz owiek ujmuje i porz dkuje oraz wyja nia rzeczywisto . Zmiany te maj
charakter progresywny i przebiegaj od form prostych, silnie powi zanych
ze spostrzeganiem i wykonywanymi czynno ciami, do form coraz bardziej
precyzyjnych, zrealizowanych w umy le, a wi c abstrakcyjnych i
hipotetycznych.

Wska niki wyznaczaj ce zakres operacyjnego rozumowania na

poziomie konkretnym:
1. Operacyjne rozumowanie w obr bie ustalania sta

ci ilo ci

nieci

ych. Warunkiem koniecznym dla zrozumienia aspektu

kardynalnego liczby naturalnej jest zdolno do wyprowadzania
wniosku, e liczba elementów nie zmienia si mimo obserwowanych
przemieszcze tych elementów, a tak e zdolno do operacyjnego
ustalania równoliczno ci zbiorów. Jest to tak e podstawa rozumienia i
opanowania czterech dzia

arytmetycznych oraz uchwycenia sensu

matematycznego zada tekstowych.

2. Operacyjne porz dkowanie elementów w zbiorze przy wyznaczaniu

konsekwentnych serii. Ten zakres rozumowania jest podstawa
rozumienia relacji porz dkuj cej i jej w asno ci, a potem aspektu
porz dkowego i miarowego liczby naturalnej. Umo liwia dzieciom
wydobycie sensu matematycznego z wielu zada tekstowych.

3. Operacyjne rozumowanie w zakresie ustalania sta

ci masy

(tworzywa). Dla kszta towania poj cia miary i umiej tno ci mierzenia
jest potrzebne wnioskowanie: jest tyle samo, mimo e zmiany
przekszta caj ce sugeruj , i teraz: jest wi cej lub mniej. Ten sposób
rozumowania pozwala dzieciom zrozumie zale no ci zawarte w
zadaniach tekstowych dotycz cych pomiaru masy lub tworzywa.

4. Operacyjne rozumowanie w zakresie ustalania sta

ci d ugo ci przy

obserwowanych przekszta ceniach. Postawa dla kszta towania poj
geometrycznych oraz opanowywania umiej tno ci mierzenia d ugo ci.
Umo liwia dzieciom rozumienie zada tekstowych dotycz cych pomiaru

ugo ci.

5. Operacyjne rozumowanie w zakresie ustalania sta ej obj to ci

cieczy, przy transformacjach zmieniaj cych jej wygl d. Jest to
konieczne dla rozumienia pomiaru pojemno ci. Umo liwia dzieciom
rozumienie zada tekstowych, w których wyst puj jednostki
pojemno ci.
Wi kszo zaburze w uczeniu si matematyki jest spowodowana tym,

e dzieci nie rozumuj operacyjnie, a musz uczy si matematyki na sposób

szkolny, który wymaga takiego rozumowania. Wa na jest kolejno :

pierwsze dwa wska niki operacyjnego rozumowania s dzieciom
bezwzgl dnie potrzebne dla uczenia si matematyki ju pod koniec klasy
zerowej i na pocz tku klasy pierwszej;
nast pne wska niki operacyjnego rozumowania s konieczne dla
sprostania wymaganiom stawianym dzieciom pod koniec klasy
pierwszej;
na pocz tku klasy drugiej dzieci powinny ju rozumowa operacyjnie, co
najmniej w zakresie wszystkich wymienionych wska ników.
Je eli tak nie jest pojawiaj si nadmierne trudno ci w zakresie uczenia

si matematyki. Kszta tuj si mechanizmy obronne, które powoduj , e
dziecko unika rozwi zywania zada wymagaj cych wysi ku intelektualnego.
Nast puje zwolnienie tempa rozwoju umys owego i nie ma w

ciwie szans,

by dalszy rozwój operacyjnego rozumowania przebiega prawid owo.
Oznacza to, e pozosta e wska niki operacyjnego rozumowania pojawiaj
si znacznie pó niej. Wa ne jest, aby ka de dziecko, pod koniec klasy
zerowej i najpó niej na pocz tku klasy pierwszej, rozumia o ju operacyjnie
w co najmniej dwóch pierwszych wska nikach.
1. niski poziom operacyjnego rozumowania, poziom przedoperacyjny
2.

redni poziom operacyjnego rozumowani, poziom przej ciowy

3. wysoki poziom operacyjnego rozumowania, poziom operacji

konkretnych

Za pomoc pomiaru mo liwo ci intelektualnych Skal inteligencji D.

Wechslera nie mo na jednoznacznie okre li przyczyn niepowodze w
uczniu si matematyki u dzieci z klas pocz tkowych.

Klasyczne testy inteligencji nie wyja niaj , dlaczego dziecko ma

nadmierne trudno ci w uczniu si matematyki.

Doro li i nauczyciele, nie maj elementarnej wiedzy o tym, jak

bardzo ró ni si ich rozumowanie od dzieci cego my lenia. Dlatego:

a) Zmuszaj dzieci do rozwi zywania zada nie bacz c, czy s one im

dost pne. Poniewa zadania te wydaj si doros ym atwe, niemo no
rozwi zywania ich przez dziecko interpretuj jako przejaw zlej woli lub
lenistwa. Dlatego zamiast przybli

dziecku tre zadania, s sk onni

kara je za to, e rozwi zywanie zadania nie przebiega nale ycie.

b) Narzucaj dzieciom swój doros y sposób rozumowania - przejaw logiki

operacyjnej na poziomie konkretnym lub formalnym. Nie dostrzegaj , e
takie my lenie jest dziecku jeszcze obce i niezgodne z jego sposobem
ujmowania rzeczywisto ci. Je eli dziecko ujawnia swój punkt widzenia,
jest karcone lub wy miewane.

c) Przekazuj dzieciom polecenia, a tak e wyja niaj im problemy za

pomoc s ów i zwrotów, których one nic znaj lub inaczej rozumiej .
Dzieci nie potrafi nawet wyrazi s owami, czego nie pojmuj , gdy nie

w stanie powtórzy nawet tego, co mówi doros y, a có dopiero

podj dyskusj i okre li swe w tpliwo ci.

Pod wp ywem tych nacisków dzieci rezygnuj z w asnego
rozumowania i zast puj go podanym wzorem. Ucz si na pami
schematów i stosuj je niezale nie od tego, czy jest to potrzebne, czy
nie. Staj si ma o samodzielne i wycofuj si z zada wymagaj cych
wysi ku intelektualnego. Boj si cokolwiek powiedzie , aby si nie

mieszy . Trac krytycyzm i uzale niaj si od innych. Ucz si

bezradno ci zamiast samodzielnego rozwi zywani problemów.

ROZDZIA V

ZDOLNO

DO SWOBODNEGO POS UGIWANIA SI

REPREZENTACJAMI IKONICZNYMI I SYMBOLICZNYMI

PODSTAW UCZENIA SI MATEMATYKI W WARUNKACH

SZKOLNYCH

J.S. Bruner d

c do okre lania natury rozwoju intelektualnego, mocno

akcentowa rol reprezentacji (zbiór regu , w kategoriach których jednostka
tworzy pojecie sta

ci zdarze , z jakimi si zetkn a. Reprezentacja wiata

lub fragmentu do wiadczenia ma nast puj ce cechy:

a) jest selektywna ze wzgl du na cel,
b) tworzy si na trzech omawianych tu poziomach,
c) uczenie si kolejnych reprezentacji polega na indukowaniu bardziej

ogólnych regu dla tworzenia ekonomicznych reprezentacji)

Twierdzi , e w miar rozwoju dzieci ucz si sposobów reprezentacji

powtarzaj cych si w ich otoczeniu prawid owo ci, a potem czenia ich z
przesz

ci i przysz

ci .

Wyró nia 3 systemy reprezentacji:

Enaktywna - ubieg e zdarzenia mog by reprezentowane w formie

schematów dzia ania;

Ikoniczna - zdarzenia dane cz owiekowi w do wiadczeniu mog by

reprezentowane w postaci syntetycznych obrazów;

Symboliczna - reprezentowanie sensu zdarze za pomoc s ów lub

innych symboli
Dziecko rozpoczynaj ce nauk w szkole musi by zdolne do tworzenia

reprezentacji na trzech poziomach: enaktywnym, ikonicznym,
symbolicznym. Musi umie swobodnie przechodzi z jednego poziomu
reprezentacji na drugi. Oznacza to zdolno do ustalania relacji pomi dzy
swym dzia aniem, obrazowym przedstawieniem rzeczy i zdarze oraz
symbolicznym ich reprezentowaniem.

Sukcesy w nauce zale od atwo ci przechodzenia z jednego poziomu

reprezentacji na drugi, do integrowania do wiadcze na poziomie
reprezentacji symbolicznych. Takie kompetencje s konieczne dla
rozpocz cia nauki czytania i pisania, a tak e do uczenia si matematyki na
sposób szkolny. Dziecko musi si nauczy kodowania i dekodowania
informacji oraz zrozumie sens tak ujmowanych poj i umie si nimi
pos ugiwa .

W matematyce, ju na pocz tku nauczania szkolnego, dziecko musi

umie zapisa proste dzia ania w postaci formu y arytmetycznej, a potem tak
zakodowane zadanie sprawnie wyliczy .

To co dziecko zapisuje w formie najprostszego dzia ania, jest syntez

symboli nowo poznawanych poj . Podobnie jest w przypadku reprezentacji
graficznych — „grafy'' s tak e form symbolicznego zapisu
zarysowuj cych si dopiero w umy le dziecka poj . Szkolny sposób
nauczania matematyki, od pierwszych dni pobytu w szkole, wymaga od
dziecka pokonania dwóch nak adaj cych si obszarów trudno ci:

opanowania techniki kodowania i dekodowania w ci le okre lonym

systemie znaków: cyfry, znaki dzia

, schematy graficzne,

przyswojenia abstrakcyjnych poj , zapisywania ich i pos ugiwania

si nimi w rozmaitych sytuacjach.
Aby temu sprosta , dziecko musi by zdolne nie tylko funkcjonowa na

poziomie reprezentacji symbolicznych, ikonicznych i enaktywnych, lecz
musi z atwo ci przechodzi z jednego poziomu na drugi.

PRZYK AD:
Zadnie wymaga przej cia z poziomu reprezentacji ikonicznych na

poziom reprezentacji symbolicznych/

6-2=…

6-…=…

Dziecko musi si wykaza zdolno ci do przechodzenia z jednego

poziomu reprezentacji na drugi.

Tatu z Zosi s w parku. Zosia znalaz a 4 kasztany i w

a je do

koszyka. Tatu do

jeszcze 2 kasztany. Ile kasztanów jest w koszyku –

pyta tatu ?

Je eli dziecko mo e manipulowa kasztanami, a potem je policzy ,

rozwi zuje zadanie na poziomie reprezentacji enaktywnych. Gdy jednak
wi zanie ma sformu owa ustnie, a potem je zapisa , b dzie to
równoznaczne z przej ciem na poziom reprezentacji symbolicznych. Obie
formy przedstawienia zadania:

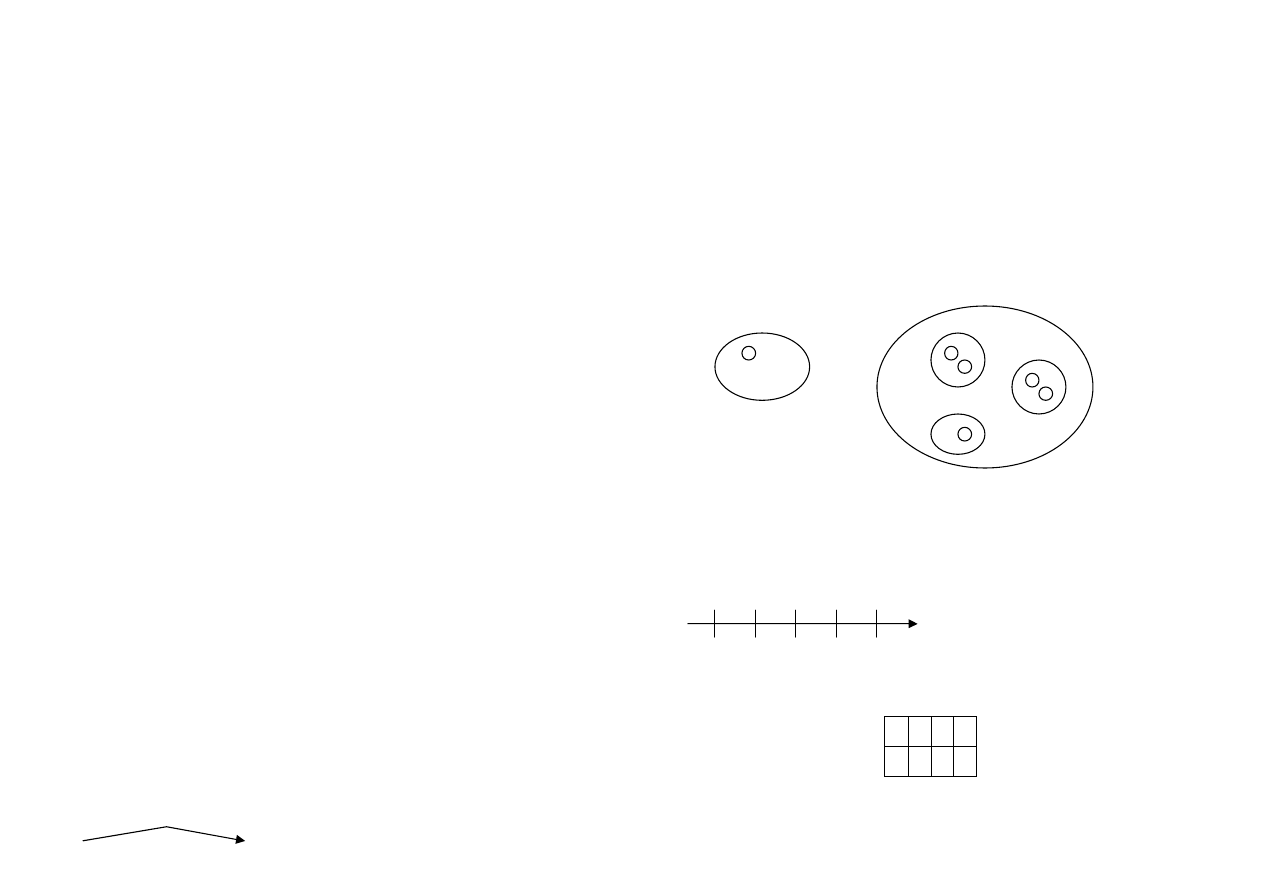
Pi doda trzy równa si osiem
5+3=8
Dydaktycy matematyki twierdz , e schematy graficzne to etap po redni

pomi dzy my leniem konkretnym, a my leniem abstrakcyjnym.
Reprezentacje graficzne s pewnym uogólnieniem konkretnej sytuacji i
krokiem naprzód w kierunku formalnej matematyzacji.

Reprezentacje s przydatne, gdy sytuacja opisana werbalnie (np. zadanie

tekstowe) oka e si zbyt trudna dla dziecka: rysowanie schematu b dzie
wówczas pogl dowym przedstawieniem tej sytuacji. Ju sama czynno
rysowania schematu stanowi upogladowienie sytuacji, u atwia dziecku
rozumowanie i mo e zast pi wykonanie analogicznych czynno ci na
prawdziwych przedmiotach.

W praktyce szkolnej sporo dzieci ma k opoty w pos ugiwaniu si

„grafami". Nawet te dzieci, które radz sobie z matematyk , niewiedz
cz sto, po co ka e si im „narysowa graf do zadania". Unikaj
rozwi zywania zada „na grafie" i wol najpierw upora si z zadaniem
licz c „w pami ci", a potem „dla wi tego spokoju" rysuj „graf. Cz
dzieci w ogóle nie rozumie umownego j zyka „grafów" i dlatego rysuje w
swoich zeszytach co , w czym trudno dopatrzy si jakiegokolwiek sensu.
W niektórych przypadkach dzieci wr cz odmawiaj narysowania ,,grafu",
twierdz c e nie potrafi .

Dlaczego reprezentacje graficzne trac sens kszta

cy i staj si

zb dne?

ówn przyczyna s b dy metodyczne. Nauczyciel nie rozumie idei

stosowania reprezentacji graficznych w edukacji matematycznej. Czuj c si
zobowi zany do ich stosowania, podaje dzieciom do zapami tania gotowe
schematy graficzne, a potem wymaga, aby si nimi pos ugiwa y.

Zestaw schematów graficznych które znajduj si w repertuarze

dzieci z klasy I:
1)

Takie strza ki lub kreski przedstawiaj czynno

czenia w pary

wybranych obiektów, a wi c przyporz dkowanie. Mog one
reprezentowa czynno dodawania, odejmowania, a potem mno enia i
dzielenia. W takich przypadkach nad strza

2 elementy

zapisuje si odpowiedni znak i licz , aby by o wiadomo, ile trzeba doda
lub odj , aby uzyska wielko okre lon przez drug liczb w parze.

„to z tym”

Takie p tle to symbol oddzielania wybranych obiektów od innych.

Jest to tak e sposób grupowania na wspólnym terytorium obiektów w
jaki sposób podobnych. W rodku i obok p tli mog by realistycznie
narysowane obiekty lub ich symbole – kropki – i wówczas mo na je
oznaczy literkami lub cyframi. Jest to schemat graficzny zbioru i jego
elementów. Dla wyodr bnienia cz ci z ca

ci wewn trz du ej p tli

rysuje si jedn , dwie lub wi cej ma ych p tli. Jet to obraz bioru i jego
podzbiorów.

Taka strza ka z zaznaczonymi w równych odst pach punktami i

zapisanymi obok cyframi to schemat osi liczbowej. Mo na na niej
interpretowa aspekty liczby naturalnej. Zwykle o liczbowa jest
ukazana w po

eniu poziomym, ze strza

skierowan w prawo. Mo e

by jednak u

ona zupe nie dowolnie.

Pierwsze tabelki s zamieszczane w podr czniku dzieci cym przy

monograficznym opracowaniu liczb, aby dzieci mog y zapisa w nich
wynik dodawania oraz odejmowania.

+ 2 3 4
4

Taki schemat graficzny jest nazywany „drzewkiem” – s

y do

przedstawiania klasyfikacji. W arytmetyce stosuje si go do ukazania

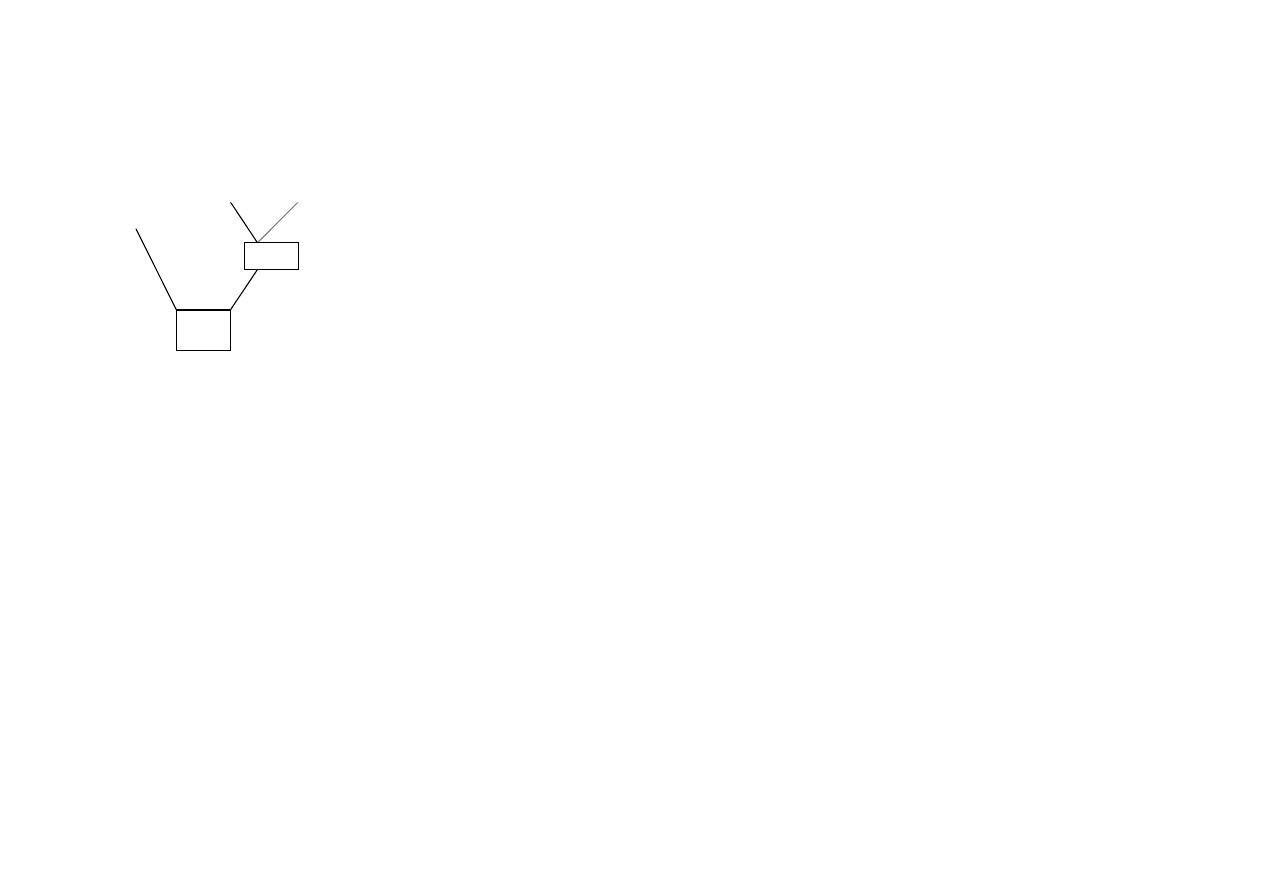
kolejno ci dzia

. Na takim schemacie dzieci poznaj kolejno dzia

i maj zrozumie sens stosowania nawiasów

W czasie, gdy dzieci zapoznaj si z tymi schematami graficznymi,

musz opanowa sposób zapisywania cyfr oznaczaj cych liczby pierwszej
dziesi tki i sprawnie pos ugiwa si znakami +,-,=,<,> przy zapisywaniu
dzia

ROZDZIA VI

DOJRZA

EMOCJONALNA I JEJ ZNACZENIE W UCZNIU

SI MATEMATYKI

Rozwi zywanie zada umo liwia:

Opanowanie podstawowych poj matematycznych;
Kszta towanie umiej tno ci pos ugiwania si metodami

matematycznymi w sytuacjach yciowych;

Rozwijanie postawy intelektualnej wyra aj cej si w twórczym,

logicznym i krytycznym my leniu, samodzielnym pokonywaniu
trudno ci i matematycznym analizowaniu zjawisk.

Efekty kszta cenia s zale ne od nastawienia dzieci do zada i sposobu

funkcjonowania podczas ich rozwi zywania.

Dla dzieci, które mia y nadmierne trudno ci w uczniu si matematyki,

zadania zmienia y swój sens. Zamiast stanowi sytuacj trudn
intelektualnie, rozwi zywanie zada stawa o si sytuacj niezno
emocjonalnie, przed któr nale y si broni .

Zadania tekstowe sprawiaj dzieciom najwi cej k opotów — s to

gotowe zadania zawarte w dzieci cym podr czniku lub zeszycie wicze .
Mog by to zadania formu owane przez nauczyciela lub uczniów na
lekcjach matematyki. Zadanie sk ada si z historyjki typu problemowego,
bliskiej dzieciom, bo powi zanej tematycznie z ich do wiadczeniami. Ka da
taka historyjka zawiera wielko ci dane, niewiadom oraz warunek
okre laj cy zwi zki pomi dzy wielko ciami okre lone w formie s ownej.
Ka de zadanie ma pytanie ko cowe dotycz ce warto ci poszukiwanej.

Jakie czynno ci poznawcze sk adaj si na rozwi zanie zadania?

Na pocz tku dziecko musi si zapozna z tre ci zadania i zrozumie sens
historyjki. Potem dokona analizy i u wiadomi sobie, co jest wielko ci
dan , co poszukiwan , jakie s zale no ci pomi dzy nimi, a tak e czego
dotyczy pytanie ko cowe. Nast pnie musi to wszystko prze

na j zyk

matematyki. Jest to matematyzacja sytuacji yciowej przedstawionej w
zadaniu. W ten sposób dziecko ustala matematyczn struktur zadania i
znajduje schemat rozwi zania. Mo e nim by np. dzia anie, uk ad równa .
Teraz wystarczy obliczy wynik, ustali odpowied na pytanie ko cowe i
zadanie jest rozwi zane.

W ka dym zadaniu, je eli ma ono mie sens kszta

cy, wyst puje

okre lona trudno . Pokonanie jej jest równoznaczne z rozwi zaniem
zadania. W zadaniach z

onych mo e wyst powa kilka trudno ci, które

trzeba kolejno i metodycznie pokonywa , aby znale ostateczne
rozwi zanie. Odczucie trudno ci ma wyra nie indywidualny charakter. To
samo zadanie dla jednych osób jest sytuacj , któr mo na automatycznie i
bez wysi ku rozwi za . Dla innych zadanie to mo e by barier nie do
pokonania. W odczuciu stopnia trudno ci zadania decyduj ce znaczenie ma
zakres indywidualnych do wiadcze . Odczuwalny stopie trudno ci zadania
zale y tak e od tego w jakich warunkach dziecko musi to zadanie
rozwi zywa . Na trudno tkwi

w zadaniu mog si nak ada dodatkowe

utrudnienia.

Dzieci rozwi zuj zadania w klasie w gronie rówie ników. Wyst puje

tutaj mo liwo skorzystania z pomocy kolegów, realne jest odpisanie
gotowego wyniku. Jednocze nie dziecko mo e porówna wynik swej pracy
z tym, co osi gn li inni. Jest to doskona a okazja do kszta towania
samooceny. Jednak w przypadku nadmiernych trudno ci mo e to by

ród o

nieustannych frustracji, które mog powodowa stopniow utrat wiary we

asne mo liwo ci. Dziecko widzi wyra nie, e to, co jemu sprawia tyle

opotów, inni osi gaj z atwo ci . Takich obci

nie ma, gdy dziecko

rozwi zuje zadanie w domu, musi jednak polega na w asnych si ach.
Doro li rzadko potrafi mu pomóc: albo zadanie wydaje si im zbyt atwe i
zwracanie si do nich o pomoc interpretuj jako ,,wymigiwanie si ", albo po
prostu sami nie potrafi zadania poprawnie rozwi za .

Dzieci mog rozwi zywa zadania samodzielnie, wywo ane do

tablicy. Wówczas na trudno zawart w zadaniu nak adaj si dodatkowe
utrudnienia:

obawa przed o mieszeniem, bo rówie nicy obserwuj jego

poczynania,

wiadomo , e je eli otrzyma z ocen , to w domu spotkaj go

dalsze nieprzyjemno ci.

Gdy dziecko ma rozwi za zadanie stoj c „w awce"- zadania s

prostsze, lecz nauczyciel wymaga krótkiej i szybkiej odpowiedzi. Nie ma tu
czasu na zastanowienie si , a to rodzi obaw , e si nie zd y lub nie uda si
poda dok adnie takiej odpowiedzi, jakiej oczekuje nauczyciel. Oznacza to
mo e niezadowolenie osoby znacz cej, bo taka osob jest nauczyciel,
wyra one odpowiednia mina i krótkim: siadaj – le!. Najcz ciej dziecko nie
wie, dlaczego „ le", a wiadomo pora ki wzmaga jeszcze to e wiadkami
takiego wydarzenia s rówie nicy.

Gdy

nauczyciel wymaga samodzielnej pracy i postanowi

przypilnowa , aby dzieci samodzielnie rozwi zywa y zadania (kartkówki
lub klasówki). Dziecko jest tutaj zdane na w asne si y i nie mo e stawia

pyta ani prosi o dodatkowe wyja nienia. Rozwi zywanie zada odbywa
si w aurze napi cia i strachu. Wiadomo, e wynik pracy b dzie oceniany.
Na trudno zawart w zadaniu nak adaj si tutaj utrudnienia spowodowane
napi ciami, które maj negatywny wp yw na jako wykonania.

To samo zadanie ma inny stopie trudno ci w zale no ci od tego,

czy dziecko rozwi zuje je w awce, przy tablicy czy te w domu zdane
na w asne si y. Na trudno typu intelektualnego zawart w ka dym
zadaniu matematycznym nak adaj si dodatkowe utrudnienia
wynikaj ce .z warunków, w jakich dziecko ma to zadanie rozwi za .
Czynniki funkcjonowania dzieci podczas rozwi zywania zada

matematycznych:
1.

Tre zadania i sposób zapoznania si z zadaniem.

Percepcja zadania zale y od tego, czy dziecko musi je samo przeczyta z
podr cznika, czy zadanie przedstawi nauczyciel, czy te sformu uje je
inne dziecko. Na poziomie klas pocz tkowych dzieci s wdro one do
uwa nego s uchania wówczas, gdy mówi osoba znacz ca. Je eli mówi
inne dziecko, wydaje si im, e to nie jest takie wa ne. Najtrudniej
dzieciom zrozumie tre zadania wówczas, gdy maj je przeczyta .
Wynika to ze s abej techniki czytania. Mozol c si nad przeczytaniem
kolejnych wyrazów trac sens ca

ci. Dla dzieci z klasy I istotne jest

tak e, czy zadanie jest ilustrowane. Pomaga to wyobrazi sobie sytuacj ,
o której mowa jest w zadaniu, a potem symulowa j np. na palcach.

Spo eczne warunki rozwi zywania. Zadanie mo e by

rozwi zywane samodzielnie, zespo owo lub zbiorowo z ca klas . Du
rol odgrywa to, czy dziecko mo e skorzysta z pomocy kolegów, a
tak e efekt oceny spo ecznej towarzysz cy sukcesowi lub pora ce.
Formy nacisku stosowane przez nauczyciela z jednej strony pomagaj
dziecku skupi uwag na zadaniu, lecz z drugiej stanowi dodatkowy
element frustracyjny.

Cechy osobowo ci rozwi zuj cego: stan motywacji,

dojrza

emocjonalna wyra aj ca si w zdolno ci do kierowania swym

zachowaniem mimo doznawanych napi , nastawienie do pokonywania
trudno ci, system nawyków sk adaj cy si na rozumne zachowanie
wówczas, gdy trzeba pokona trudno , poziom wiadomo ci i
umiej tno ci matematycznych potrzebnych do rozwi zania danego
zadania.
Pokonywanie trudno ci jest integraln cz ci ucznia si

matematyki. Dzieci z niepowodzeniami w uczniu si matematyki maj :
1.

tendencj do przed

ania cz ci organizacyjnej lekcji: dzieci zbyt

ugo przygotowuj przybory, grzebi w tornistrze, oci gaj si z

wyj ciem zeszytów, za atwiaj wa ne sprawy rozmawiaj c z
rówie nikami, spó niaj si na lekcje, a potem d ugo usprawiedliwiaj

spó nienie; w ten sposób d

do odwleczenia chwili, gdy b

musia y

zaj si zadaniami lub wykaza si wiadomo ciami i umiej tno ciami
matematycznymi.

Zupe ny brak zrozumienia sensu zada matematycznych

Kierowanie aktywno ci na obron przed konieczno ci

rozwi zywania zada

Dzieci te nie uczestnicz w procesie ucznia si matematyki,

mimo e by y obecne na lekcjach i stwarza y pozory podporz dkowania
wymaganiom nauczyciela. Zamiast gromadzi do wiadczenia logiczne i
matematyczne dzieci te popada y w stany frustracyjne i uczy y si , jak
unika rozwi zywania zada .

Dla dzieci ogromne wa ne s komunikaty emocjonalne

towarzysz ce rozmowie. Wa niejsze jest to jak si mówi, mniej to, co si
mówi.
Podczas podejmowanych prób rozwi zywania zadania u wszystkich

dzieci obserwuje si :
1)

Gwa towne narastanie napi cia i emocji ujemnych –

dzieci opuszczaj g ówk i kul si , nie panuj nad mimik , zaciskaj

ce i nawet nie patrz w stron zadania. Demonstruj bezradno , a

potem usi uj zaj si czym innym.

Siln regresj zachowa - wielokrotnie i

nieskutecznie powtarzaj czynno ci, wymuszaj pomoc, a potem
na laduj pokazane czynno ci, mozolnie przepisuj lub przerysowuj
tre zadania. Czyni to nawet wówczas, gdy nie trzeba przepisywa ,
tylko rozwi zywa . Zapisuj co podobnego do formu y zadania z
przypadkowo dobranych liczb, a potem nieskutecznie próbuj wylicza
lub odgadywa wynik.

enie do mo liwie szybkiego przerwania

konieczno ci zajmowania si zadaniem.
Wg M. Tyszkowej sytuacje zwane trudnymi (sytuacja trudna to taki

uk ad zada , warunków dzia ania i mo liwo ci dzia aj cego podmiotu, w
jakim naruszona zosta a równowaga pomi dzy tymi elementami w stopniu
wymagaj cym nowej koordynacji, co wywo uje przeci enie systemu
regulacji i emocje ujemne; w konsekwencji trwania tego stanu pojawiaj si
zmiany w zachowaniu jednostki, m.in. reorganizacja lub dezorganizacja,
ukierunkowanej na cel czynno ci) charakteryzuj si w

ciwo ciami:

zawieraj czynniki wywo uj ce zak ócenia w ukierunkowanej na cel

aktywno ci jednostki w zakresie zaspokojenia potrzeb, realizacji d

wykonywania zada itp.

posiadaj czynniki zagra aj ce zaspokojeniu potrzeby realizacji

lub warto ci cenionej przez jednostk ,

wywo uj u jednostki przykre prze ycia emocjonalne i powoduj

stany silnego napi cia emocjonalnego, które s reakcj na przeci enia
psychiczne.
Zmiany zachodz ce w zachowaniu si cz owieka w sytuacji trudnej s

spowodowane podwy szeniem poziomu aktywacji emocjonalnej i

onymi procesami odzwierciedlenia sytuacji trudnej. W genezie zmian w

zachowaniu cz owieka w sytuacji trudnej istotn rol odgrywaj zarówno
podwy szenie poziomu aktywacji emocjonalnej i inne bardziej z

one

procesy odzwierciedlania tych sytuacji, które s okre lane jako prze ycie
trudno ci.

W sytuacjach trudnych wiele odbieranych sygna ów ma dla

cz owieka znaczenie niekorzystne i wywo uje emocje ujemne. One to

nie odgrywaj rol detektora trudno ci i czynnika inicjuj cego

zmiany aktywno ci. Zmiany te mog i w dwóch kierunkach:
a)

W kierunku inicjowania aktywno ci kompensacyjno-korekcyjnych, i

w tym przypadku jednostka utrzymuje si w zadaniowej strukturze
sytuacji, a wzburzone przez trudno ci emocje negatywne nie wytr caj
jej z tego sposobu funkcjonowania.

W kierunku usztywnienia si w prze ywaniu trudno ci i zwi zanych z

tym emocji ujemnych, ich wzrostu i stopniowej dezorganizacji
zachowania, co jest spowodowane os abieniem percepcji sytuacji
zadaniowej i koncentrowaniem si na stymulacyjnym aspekcie trudno ci.
Tyszkowa ujmuje odporno emocjonaln trojako:

w jej aspekcie behawioralnym, tj. jako odporno na

destruktywne zachowania si mimo spostrzegania trudno ci i
doznawania silnych emocji ujemnych,

jako odporno emocjonaln , czyli zdolno jednostki do

kontrolowania w asnych procesów emocjonalnych i znoszenia emocji
ujemnych.

jako zdolno jednostki do sterowania w asnymi procesami

odzwierciedlenia — percepcyjnego, intelektualnego i emocjonalnego —
sytuacji w asnej aktywno ci i koncentrowania si na jej warto ci
informacyjnej, istotnej z punktu widzenia celu czynno ci.

Odporno emocjonalna jest wa nym sk adnikiem zdolno ci

cz owieka do samokontroli i samosterowania zachowaniem.
Wyznacznikami takiej odporno ci, wg Tyszkowej s :
1.

Samoorientacja i elementarna cho by zdolno do

introspekcji, a tak e samopoznania. Wi e si z tym konieczno
przyswojenia poj niezb dnych do wyodr bnienia, w

ciwego

rozpoznania i nazywania w asnych dozna . Mo liwo nazwania

asnych prze

uczuciowych pozwala je ujmowa w kategoriach

poznawczych, a przez to nada im bardziej zobiektywizowany charakter.

Kontrola w asnych prze

i zachowa . Polega to na

regulowaniu ich zgodnie z okre lonymi przez jednostk standardami
spo ecznymi. Jednostka musi sobie u wiadomi w asne prze ycia czy
zachowania, porównuj c je z akceptowanym wzorem. Potem podj
wysi ek upodobnienia w asnych prze

do owych wzorów b

powstrzymania si od pewnych zachowa je eli uzna je za niezgodne z
przyj tymi standardami.

Kontrola w asnego post powania i prze

, tak e

emocjonalnych, dokonuje si u cz owieka na drodze wytwarzania
wewn trznych programów aktywno ci, w których powstawaniu i
realizacji podstawow rol odgrywa mowa wewn trzna. Procesy mowy
wewn trznej ingeruj w tok wykonywanych dzia

, dokonuj ci

reorientacji w sytuacji i rekonstrualizacji pola aktywno ci. Dzi ki temu
mowa wewn trzna czyni jednostk w pewnym stopniu niezale

oddzia ywania zewn trznych czynników sytuacyjnych.
Charakterystyczn cecha zachowania si dzieci nieodpornych

psychicznie na sytuacje trudne jest to, e cz sto zmieniaj cel zachowania.
Zamiast d

do rozwi zania zadania i pokonania trudno ci, staraj si ze

wszystkich swych si ochroni siebie przed zagro eniem i czyni to nawet
przy zadaniach o stosunkowo niskim stopniu trudno ci. Dla tych dzieci
trudno zawarta w zadaniu oznacza zagro enie, kieruj wi c sw
aktywno na obron przed zadaniem. W ten sposób tworz si nawyki
obronnego reagowania na pojawiaj ce si trudno ci. Wszystko to razem
powoduje specyficzne nastawienie si tych dzieci do zada nawet o
niewielkim stopniu trudno ci. Reaguj wi c obronnie na odleg e sygna y
zbli aj cej si sytuacji trudnej — jest to antycypacja niebezpiecze stwa.

Konieczno rozwi zywania zada stanowi sytuacj frustracyjn

zapowiadaj

ca y zespó stresorów:

nasilenie napi cia i emocji ujemnych nie wyrównanych adnymi

prze yciami przyjemnymi,

dostarczenie kolejnego dowodu poczucia ni szej warto ci, gdy to,

czego one nie potrafi poj , inne dzieci wykonuj z atwo ci ,

rozmaite zagro enia cz ce si z faktem, e nauczyciel mo e

zauwa

, e nie potrafi sprosta wymaganiom i postawi ocen

niedostateczn , a w najlepszym przypadku zgani w obecno ci
rówie ników.
Dlatego has o rozwi zywanie zada matematycznych jest tu sygna em

zagro enia. Dzieci doskonale zdaj sobie spraw z tego, „co b dzie dalej" i
próbuj za wszelk cen unikn niebezpiecze stwa. Dlatego przed

wst pn lekcji, guzdraj si , uciekaj w chorob . Zd

y ju nauczy

si , e takie zachowania s korzystne. Zauwa

y, i nauczycielka, widz c

zbola min , zwykle rezygnuje z odpytywania i podobnie czyni, gdy
dziecko nie zd

o roz

przyborów. Op aca si tak e zwleka z

zapisywaniem danych, a potem szybko odpisa wynik. Mo na w ten sposób
ukry swe intencje. Dobrze jest okazywa bezradno , bo inne dzieci
pomog .

Takie wykorzystywanie spo ecznych warunków pracy na lekcji

powoduje, e nadmierne trudno ci w uczeniu si matematyki s zbyt pó no
wykrywane. Zwykle ma to miejsce pod koniec którego semestru, gdy
nauczycielka postanowi przeprowadzi klasówk lub gruntowniej pyta przy
tablicy. Wówczas okazuje si , e dziecko nie potrafi rozwi zywa
najprostszych zada , a zaleg

ci w nauce si gaj kilku semestrów.

Co si dzieje, je eli dziecku nic uda si unikn

konieczno ci

rozwi zania zadania? Na pocz tku próbuje zrozumie tre zadania.
Przekracza to jednak jego mo liwo ci (przyczyn jest zwykle niski poziom
operacyjnego rozumowania lub enuj ce braki w wiadomo ciach i
umiej tno ciach matematycznych). Dlatego ka de zadanie jawi si dziecku
jako ogromnie trudne i tym silniej odczuwa sw beznadziejn sytuacj . Ta
informacja emocjonalna wyznacza ramy dalszego zachowania. Dziecko
podejmuje chaotyczne próby wyj cia z tej zagra aj cej sytuacji: d y do
przepisania zadania, aby pokaza , e co robi, odwzorowuje to, co wykona y
inne dzieci, wymusza pomoc od innych. Takie zachowania podnosz poziom
emocji ujemnych i prowadz do fali dezorganizacji. Nast puje jeszcze
wi ksze nasilenie reakcji obronnych. Dziecko robi wszystko, eby przerwa

niezno

sytuacj . Obserwowa mo na charakterystyczne zaw

enie

pola percepcji. A wszelkie próby wyja niania, t umaczenia lub
podpowiadania mu s nieskuteczne. Dziecko jest bowiem skupione na
swych emocjach, na tym, aby wytrzyma napi cie. Próby pomagania s
odbierane jako dodatkowe sygna y zagro enia i wzmagaj tylko nat

enie

reakcji obronnych. Dziecko staje si ” lepe i g uche” na wszelkie

umaczenia, a to oznacza definitywne przerwanie czynno ci zwi zanych z

rozwi zaniem zadania matematycznego.

Wystarczy, e taka, pe na napi sytuacja powtórzy si kilka razy a ju

si ukszta towa specyficzne nastawienia do zada matematycznych.

Wszystko, co wi e si z takimi zadaniami, zostaje skojarzone z
zagro eniem. Na zasadzie antycypacji niebezpiecze stwa dziecko zaczyna
reagowa obronnie na zapowied : trzeba rozwi zywa zadanie, gdy
przewiduje, co to b dzie dalej. Wzrost napi cia pojawia si znacznie
wcze niej, jeszcze zanim zajmie si zdaniem. Dlatego dzieci, którym le
wiedzie si w zakresie matematyki, przed pój ciem do szko y, skar si na
ból np. brzucha, nie chc je

niadania, z wielk niech ci id do szko y.

One boj si tego, co nast pi.

W zwi zku ze specyficzn rol zada matematycznych najwa niejsze

jest to, aby dzieci posiada y stosunkowo wysoki poziom odporno ci
emocjonalnej a sytuacje trudne. Jest to warunek ucznia si matematyki.

U dzieci, które nie radzi y sobie z zadaniami matematycznymi stwierdza

si s abo ukszta towan organizacj rozumnego zachowania (proste formy
wymiany my li i elementarna troska o skuteczno swego dzia ania, dzieci
te nie maj wyrobionego nawyku s uchania, nie troszcz si tak e aby druga
osoba mog a zrozumie ich wypowiedzi).

Wewn trzstarowno – rzadko które dziecko potrafi skupi si na

wykonywanej czynno ci przez d

szy czas i ma potrzeb doko czy

zacz

prac . Wi kszo porzuca rozpocz

czynno , gdy tylko co

innego pojawia si w otoczeniu.

Niska odporno ci emocjonalna charakteryzowa y si dzieci z

zaburzeniami nerwicowymi: nadmierna reaktywno lub zaburzenia
równowagi procesów nerwowych — zespól nadpobudliwo ci lub
zahamowania. Nadmierna ruchliwo

dzieci nadpobudliwych nie pozwala

im prawid owo scala aktywno ci intelektualnej i ruchowej. Rozproszenie
uwagi nie sprzyja zrozumieniu polece nauczyciela. Przeszkadza w
wys uchaniu do ko ca wyja nie i w uwa nym czytaniu zadania. Dlatego
dzieci te z wielkim trudem chwytaj sens nawet prostego zadania
matematycznego. Pochopno i pobie no my lenia przeszkadza im w
trafnym uj ciu zale no ci. Nadmierna ekspansja ruchowa przeszkadza na
lekcji innym dzieciom i dokucza nauczycielowi. Dzieci te s wi c cz sto
karcone i upominane, a to podwy sza i tak ju podniesiony poziom napi cia.

Sytuacja dzieci z przejawami zahamowania psychoruchowego. Za

wolno wykonuj one polecenia i reaguj poznawczo. Na wszystko
potrzebuj wi cej czasu i nie potrafi nad

z wykonaniem

poszczególnych czynno ci. S upominane, przynaglane. Nienad

anie za

tempem pracy na lekcji powoduje pi trzenie si wymaga : jeszcze nie
upora y si z zapisem danych, a ju wymaga si od nich wyniku, jeszcze nie
zapisa y rozwi zania, a ju trzeba rozwi zywa nast pne zadanie.

ROZDZIA VII

INTEGRACJA CZYNNO CI PERCEPCYJNO-MOTORYCZNYCH A

UCZNIE SI MATEMATYKI W SZKOLE

Czynno ci organizacyjne - przygotowanie potrzebnych przyborów,

odszukanie w ksi ce lub zeszycie wicze zadania, zapisanie czego .
Dzieci musza je wykona tak aby nie zak óca toku lekcji, szybko i
sprawnie. Poniewa nagromadzenie tych czynno ci wyst puje we wst pnej
fazie lekcji, ju od samego pocz tku gorzej wiedzie si tym dzieciom które
nie potrafi scali swej aktywno ci ruchowej, emocjonalnej oraz
intelektualnej. Czyni wiele zamieszania swa niezgrabno ci : str caj
przedmioty, szukaj czego w po piechu, ha asuj , kr

si . Wyd

czas przebaczony na wykonanie czynno ci organizacyjnych. S upominane i
karcone, a to podnosi poziom napi cia oraz obni a i tak ju mniejsze
mo liwo ci tych dzieci.

Dzieci te nie potrafi nad

z wykonaniem polece , s pod ci

presj pi trz cych si wymaga .

Grupy czynno ci organizacyjnych:

Dziecko musi przeczyta tre zadania. Jest tu wymagana

umiej tno czytania ze zrozumieniem. Sporo dzieci nie potrafi
przeczyta zadania na tyle p ynnie, aby zorientowa si w tre ci.
Wysi ek w

ony w czytanie jest zbyt wielki, a zrozumienie sensu

czytanych zda — adne. W przypadku, gdy zadanie wypowiada
nauczyciel lub wybrane dziecko, trzeba z uwag s ucha i dokonywa
analizy tre ci. Jest to trudne zw aszcza dla dzieci nadpobudliwych i tych,
które nie maj ukszta towanego nawyku skupiania wiadomo ci na
czym , co jest nakazane i nic wi e si bezpo rednio z ich aktualnymi
zainteresowaniami.

Analizuj c tre zadania dziecko musi umie wyszuka dane i

znale zale no ci pomi dzy nimi. Pomaga w tym uproszczony rysunek
lub symulacja na przedmiotach zast pczych. Musi sprawnie u
patyczki lub etony „do liczenia", albo rozpi gumki na geopianie.

Ustalaj c zale no ci zawarte w zadaniu dzieci rysuj odpowiedni

graf, wykre laj i czytelnie wype niaj tabelki, kre

drzewka. Na

koniec zapisuj odpowied . Wszystko to musz wykona sprawnie i na
wymaganym przez nauczyciela poziomie estetycznym.

Dobre efekty w uczeniu si matematyki w warunkach szkolnych s w

du ej mierze zale ne od tego, na ile dziecko jest zdolne do integrowania
czynno ci percepcyjnych i motorycznych. Przyczyn niepowodze w

uczeniu si matematyki mog by zaburzenia zdolno ci do syntetyzowania i
koordynowania funkcji percepcyjnych z funkcjami motorycznymi,
reakcjami ruchowymi.

Percepcja i motoryka s jednak ze sob

ci le sprz

one i dlatego

trzeba je rozpatrywa

cznie, jako ca

funkcjonaln .

Dzieci nabywaj znaczenie mniej do wiadcze logicznych i

matematycznych. Koncentruj c si nadmiernie na czynno ciach
technicznych gubi ich sens intelektualny. Narysowanie grafu staje si dla
nich celem, a nie rodkiem wspomagaj cym rozumowanie. Samo zapisanie
czego podobnego do formu y dzia ania tak absorbuje dziecko, e nie ma
ono ju si y na wyliczenie zadania. Nast puje odwrócenie sensu
wykonywanych czynno ci, to co pe ni rol pomocnicz , zaczyna by celem.

Zaburzenia zdolno ci do efektywnego czenia i koordynowania

funkcji percepcyjnych i motorycznych maj po redni, lecz znacz cy wp yw
na efekty ucznia si matematyki na poziomie klas pocz tkowych.

ROZDZIA VIII

PODSTAWY DIAGNOY DZIA ALNO CI MATEMATYCZNEJ

Diagnoza wg S. Ziemskiego to rozpoznanie jakiego stanu rzeczy i

jego tendencji rozwojowych w oparciu o znajomo ogólnych
prawid owo ci; okre la si podmiot diagnozy, jej cele ogólne i szczegó owe.
Podaje si informacje o wykorzystywanych metodach i warunkach, w jakich
by y stosowana.

Je eli wyst puj nadmierne trudno ci lub niepowodzenia w uczeniu si

matematyki, diagnoz trzeba przeprowadzi dla precyzyjnego okre lenia
dzia

naprawczych. W przypadku ponadprzeci tnych osi gni w

matematyce nale y okre li poziom uzdolnie specjalnych, a potem dobra
bardziej intensywne metody kszta cenia bez szkody dla harmonijnego
rozwoju dziecka.

Poj cie edukacja matematyczna obejmuje swym zakresem to, czego

dziecko uczy si w szkole, co opanowa o wcze niej, przed pój ciem do
szko y. Wa ne s do wiadczenia logiczne i matematyczne zgromadzone
poza lekcjami, w trakcie rozwi zywania rozmaitych problemów yciowych,
pod wp ywem doros ych, starszego rodze stwa, lektur, itp.

Doro li rozpoczynaj edukacj matematyczn dzieci od nauki liczenia.

Pod ich kierunkiem dzieci ucz si liczy rozmaite przedmioty, ustala , „ile
jest”, porównywa dwa zbiory i okre la , „czy jest wi cej, mniej, tyle
samo”. Ustalaj wynik odejmowania i dodawania. Gdy zaczynaj
ucz szcza do przedszkola w proces edukacji matematycznej w cza si
kolejny doros y – nauczycielka, która realizuje program kszta towania poj
matematycznych. Na edukacje matematyczn sk adaj si wówczas:

Do wiadczenia logiczne i matematyczne gromadzone na zaj ciach w
przedszkolu oraz
Dzia alno matematyczna, któr dziecko realizuje w domu lub np.
na spacerze, rozwi zuj c przy pomocy rodziców rozmaite zadania

yciowe.

Z chwil rozpoczynania nauki w szkole zaczynaj dominowa szkolne

formy dzia alno ci matematycznej, to czego dziecko uczy si na lekcjach,
pod kierunkiem nauczyciela i w trakcie odrabiania zada domowych.

Gdy edukacja matematyczna zosta a w jaki sposób zaburzona i

dziecko ma nadmierne trudno ci w uczniu si matematyki – trudno ci
nie pojawiaj si u dzieci nagle, jest to d ugotrwa y proces, który ma swój
pocz tek, mo na w nim wyró ni kilka faz i ko czy si wszystko
niepowodzeniami, proces ten s ugo pozostaje w ukryciu.

Dla okre lenia intelektualnych przyczyn nadmiernych trudno ci w

uczniu si matematyki stosuje si popularne skale inteligencji, dzieci
uzyskuj w badaniach niskie wyniki, bo nie wykonuj wielu prób z tych
testów. Obni ony w badaniach testowych wynik mo e wi c by skutkiem
mechanizmów obronnych i nie musi wiadczy o gorszych mo liwo ciach
intelektualnych dziecka.

W obecnym zakresie bada uwzgl dnia si tylko 2 wska niki

dojrza

ci do ucznia si matematyki:

1. Zdolno do syntezowania oraz integrowania funkcji percepcyjno-

motorycznych; bada si g ównie poziom rozwoju sprawno ci manualnej
i percepcji wzrokowej

2. umiej tno liczenia przedmiotów, doliczanie i odliczanie, a tak e ustala,

czy w porównywanych zbiorach jest tyle samo przedmiotów.

Badania dojrza

ci szkolnej nie uwzgl dniaj odporno ci

emocjonalnej dziecka na sytuacje trudne intelektualnie.

Sporo dzieci rozpoczyna nauk w klasie I bez koniecznej dla ucznia

si matematyki dojrza

ci psychicznej. Fakt ten umyka uwadze

nauczycieli, rodziców pedagogów i psychologów pracuj cych w poradniach.
Jest to g ówna przyczyna nadmiernych trudno ci, a potem niepowodze w
uczniu si matematyki.

Niepowodze w uczniu si matematyki doznaj tak e dzieci, które

rozpocz y nauk w szkole z nale yt dojrza

ci . Wynika to z

niekorzystnych wydarze :
1.

sza choroba dziecka powoduje, e musi ono opu ci kilkana cie dni

nauki. Doro li nie zawsze potrafi pomóc dziecku w nadrobieniu
zaleg

ci. Pojawiaj si luki w systemie wiadomo ci i umiej tno ci.

Dziecko mo e mie nadmierne trudno ci w opanowaniu nast pnych
bardziej z

onych tre ci.

2. zmian miejsca zamieszkania, gdy dziecko musi przej do innej szko y,

pod opiek innego nauczyciela. Koszty adaptacji do nowych warunków
mog by zbyt wielkie i dziecko nie potrafi uczestniczy w lekcjach
matematyki w nale yty sposób.

U dzieci wychowywanych w niekorzystnych warunkach, gdzie

doro li nie zadaj sobie trudu interesowania si ich szkolnymi losami. Dzieci
te przychodz do szko y brudne, zaniedbane, nie maj odrobionych zada
ani potrzebnych przyborów. Sprawiaj od pocz tku wiele k opotów swym
nauczycielom i s nieakceptowane przez rówie ników. Do wiadczenia
gromadzone na lekcjach nie wystarczaj do opanowania wymaganych poj
i umiej tno ci.

Mimo ró nych przyczyn, które powoduj , e dziecko po raz pierwszy

doznaje nadmiernych trudno ci w uczniu si matematyki, proces narastania
niepowodze u wszystkich dzieci jest podobny. Podobne s tak e
konsekwencje. U wszystkich dzieci stwierdza si reakcje obronne przed
samodzielnym rozwi zywaniem zada wymagaj cych od nich wysi ku
intelektualnego. A tak e:

przecenianie stopnia trudno ci zada typu szkolnego, l kowe
wycofywanie si i rezygnacja z rozwi zywania;
ma odporno emocjonaln na sytuacje trudne i poddawanie si fali
frustracji przy niewielkim stopniu trudno ci zadania;

abo ukszta towane nawyki kierowania swym zachowaniem w

racjonalny sposób;
ograniczenia w zakresie funkcjonowania na poziomie symbolicznym i
przechodzenia z jednego poziomu reprezentacji na inny;
obni ony poziom operacyjnego rozumowania w sensie Piageta;
niski poziom opanowania technik szkolnych, wiadomo ci i umiej tno ci
matematycznych zdobywanych w szkole.

W.J. Paluchowski - „diagnostyka jako nauka stosowana s

y terapii.

Ogólnie rzecz bior c, diagnoza polega na tym, aby zebra dane o
zachowaniu jednostki lub efektach tych zachowa , dane te zinterpretowa i
wyprowadzi wnioski, by na tej podstawie podj odpowiednie
profesjonalne dzia ania. Diagnoza s

y wi c przygotowaniu specyficznej

terapii i powinna by oceniana wedle tego, w jakim stopniu pomaga w
wyborze i stosowaniu terapii”.

ROZDZIA IX

ZADANIA BADAWCZE, KTÓRE WARTO REALIZOWA W

RAMACH DZIA ALNO CI MATEMATYCZNEJ DZIECI

Badania diagnostyczne trzeba rozpocz

od opisu

funkcjonowania dziecka w szkolnych formach dzia alno ci
matematycznej. Podstaw jest obserwacja zachowania dziecka na
lekcjach matematyki w sytuacji gdy:
a)

powinno rozwi za samodzielnie zadanie, siedz c w awce,

jest wywo ane do tablicy i nauczyciel ka e mu rozwi zywa

zadanie, a rówie nicy obserwuj jego poczynania,

dzieci rozwi zuj zadania wspólnie.

Analiza poziomu wiadomo ci i umiej tno ci matematycznych

dziecka. Nale y ustali , co dziecko wie i umie oraz oceni , w jakim
stopniu jest to zgodne z wymaganiami obowi zuj cymi na lekcjach
matematyki. Najlepiej zastosowa „metod cofania si ”. Na pocz tku
dziecko otrzymuje do rozwi zania zadania ze sprawdzianu
obowi zuj cego w klasie, do której ucz szcza, potem kolejne
sprawdziany dla klas ni szych. Tak nale y czyni , a dziecko otrzyma
ocen dostateczn . W ten sposób mo na ustali rzeczywisty poziom
wiadomo ci i umiej tno ci matematycznych i okre li ró nic w
stosunku do wymaga . Dla zbadania faktycznego poziomu wiadomo ci i
umiej tno ci matematycznych dzieci z klas I-III opracowano specjaln
metod diagnozowania.

Okre lenie poziomu rozwoju procesów psychicznych, które s

zaanga owane w nauk matematyki.
a)

Jaki jest poziom czynno ci nadawczych, odbiorczych i

wykonawczych (wspó praca oka i r ki)

Jaki jest poziom rozwoju umys owego dziecka?

W przypadku dzieci rozpoczynaj cych nauk w szkole wa nej jest aby

wykazywa y si operacyjnym rozumowaniem w zakresie:

Sta

ci ilo ci nieci

ych (dziecko nie ma

tpliwo ci, e w obu porównywanych zbiorach jest tyle samo

elementów mimo obserwowanych zmian w ich uk adzie:
eksperyment diagnostyczny z kolorowymi kr kami);

Wyznaczanie konsekwentnych serii (dziecko potrafi

ujmowa ka dy patyczek jako najmniejszy w zbiorze patyczków
nieuporz dkowanych i jako najwi kszy w tworzonej serii:
eksperyment diagnostyczny z patyczkami o ró nej d ugo ci).

Dziecko pod koniec klasy I i na pocz tku klasy II powinno si
wykazywa operacyjnym rozumowanie w zakresie:

Ustalania sta

ci ilo ci masy (dziecko jest przekonane, e mimo

obserwowanych przekszta ce nie zmienia si ilo np. plasteliny
w porównywanych kszta tach: eksperyment z kulkami
plasteliny);
Ustalania sta

ci d ugo ci (dziecko jest przekonane, e mimo

obserwowanych zmian w kszta cie d ugo ci dwóch
porównywanych kawa ków drutu nie ulega zmianie: eksperyment
z dwoma kawa kami drutu);
Ustalania sta ej obj to ci p ynów (dziecko jest przekonane, e
zmiany w wygl dzie przelanej np. wody nie maj wp ywu na jej
obj to : eksperyment z przelewaniem wody).

Jak dziecko zachowuje si w sytuacji trudnej, która wymaga

od niego wysi ku intelektualnego?

Kolejne zdanie diagnostyczne ma na celu okre lenie efektu

edukacji matematycznej, przedszkolnej. Pytania badawcze:
a)

Czy dziecko potrafi odró ni prawid owe liczenie od

dnego? W jakim stopniu dziecko rozumie, e:

Licz c przedmioty nale y je wskazywa i wypowiada kolejne
liczebniki (przyporz dkowanie gestu wskazywania i liczebnika
kolejnym licznym obiektom),
Licz c, trzeba obra kierunek (mo e by za ka dym razem inny),
a potem liczy tak, aby nie przeskakiwa ani nie liczy
podwójnie (liczone obiekty musz by tak uporz dkowane jak
liczebniki),
Ostatni z wypowiadanych liczebników ma specjalne znaczenie i
okre la licz elementów w rozpatrywanym zbiorze.

Na jakim poziomie dziecko opanowa o czynno dodawania i

odejmowania?

W jaki sposób dziecko ustala, w którym zbiorze jest wi cej

elementów.

Wyja nienie genezy stwierdzonych nieprawid owo ci w uczniu

si matematyki i funkcjonowania dziecka. Podstaw b dzie
psychologiczny yciorys dziecka oraz analiza warunków yciowych, w
których ono yje.
Psychologiczny yciorys dziecka to historia jego rozwoju od pocz cia,
przez urodzenie, dzieci stwo, a do chwili obecnej. ród em informacji
jest wywiad rodzicami, g ównie matk lub osob sprawuj

opiek nad

dzieckiem, oraz dane z ksi eczki zdrowia. Za najwa niejsze trzeba
uzna informacje dotycz ce przebiegu rozwoju psychoruchowego, stanu
zdrowia i przebytych chorób. Wa ne jest kto i w jakim zakresie
sprawowa opiek nad dzieckiem i jak ten problem przedstawia si
obecnie. Do yciorysu psychologicznego trzeba w czy informacje o
pobycie dziecka w przedszkolu, w klasie zerowej i w szkole.
Analiza warunków, w których dziecko yje. Jest to istotne dla ustalenia
genezy zaburze i dla opracowania programu dzia

naprawczych oraz

pozyskania sojuszników w gronie osób dziecku najbli szych.
Najwa niejsze jest ustalenie tego, jak otocznie sprzyja prawid owemu
rozwojowi i jak pomaga dziecku w sprostaniu wymaganiom szkolnym.

M. Tyszkowa „Prze ywanie emocji ujemnych jest nieod cznym

sk adnikiem ludzkiego dzia ania. Odgrywaj one te niejednokrotnie

pozytywn w wysokim stopniu, a zawsze wa

rol w psychicznej

regulacji zachowania”.

ROZDZIA X

INTERPERETACJA WYNIKÓW BADA

DIAGNOZA NA U YTEK ZAJ

KOREKCYJNO-

WYCHOWAWCZYCH

Diagnoza zachowania - podstawa s informacje o funkcjonowaniu

dziecka wtedy, gdy musi pos

si wiadomo ciami i umiej tno ci

matematycznymi przy rozwi zywaniu rozmaitych zada .
Dzieci z klasy zerowej, gdy przypuszcza si , e nie osi gn y dojrza

do uczenia si matematyki w warunkach szkolnych, trzeba razem zebra ;
a) efekty obserwacji poczynionych w przedszkolu lub w klasie zerowej:

efekt analizy zachowania badanego dziecka wówczas, gdy mia o
rozwi za samodzielnie lub w grupie rówie niczej, zadanie
wymagaj ce wysi ku intelektualnego,

b) wyniki uzyskane w trzech eksperymentach diagnostycznych:

rozró nianie prawid owego liczenia od b dnego,
dodawanie i odejmowanie przy zas oni tych kasztanach,
preferowany sposób ustalania, w którym z porównywanych

zbiorów jest wi cej elementów.

Teraz trzeba przyst pi do analizy i ustali , w jakim stopniu dziecko

jest podatne na nauczanie matematyki na sposób szkolny, i czy poziom
przyswojonych intuicji matematycznych jest wystarczaj cy dla sprostania
wymaganiom, które zostan mu postawione w szkole, na lekcjach
matematyki

Dzieci z klasy I. W przypadku, gdy niepowodzenia zosta y wykryte pod
koniec klasy I, trzeba zebra razem wyniki dotycz ce:

a) funkcjonowania dziecka na lekcjach matematyki oraz informacje

uzyskane w trakcie rozmowy z nauczycielk i rodzicami,

b) pomiaru faktycznego poziomu wiadomo ci i umiej tno ci

matematycznych opanowanych przez dziecko (poziom klasy
zerowej i klasy I),

c) zachowania dziecka w eksperymentach diagnostycznych:

dodawanie i odejmowanie i preferowany sposób ustalania, w
którym zbiorze jest wi cej elementów. Je eli dziecko w tych
eksperymentach funkcjonuje na poziomie niskim lub najni szym,
wówczas mo na dodatkowo przeprowadzi eksperyment
dotycz cy rozró niania prawid owego liczenia od biednego,
chocia jest on zbyt atwy dla siedmiolatków;

d) zaburze w zachowaniu dziecka w trakcie bada : repertuar

zachowa obronnych, k opoty z kierowaniem swym
zachowaniem podczas pokonywania trudno ci, sposoby
reagowania na napi cia itp.

Dzieci z klasy II lub III – przy analizie wyników bada dotycz cych:

a) funkcjonowania dziecka w szkolnych formach dzia alno ci

matematycznych (szczególn uwag zwróci na zachowania
obronne, te stosowane w klasie, na lekcjach matematyki),

b) poziomu wiadomo ci i umiej tno ci matematycznych faktycznie

opanowanych przez dziecko w stosunku do wymaga
obowi zuj cych w klasie, do której ono ucz szcza,

c) zachowania dziecka w trakcie rozwi zywania zada w

warunkach eksperymentalnych (sposób reagowania na silne
napi cia, pojawianie si blokad emocjonalnych, reakcje
obronne).

Diagnoza procesów regulacji – trzeba zebra informacje z bada

dotycz cych procesów psychicznych, które s zaanga owane w uczenie
si matematyki w warunkach szkolnych. Przyczyn niepowodze mo e
bowiem by :
a) nieprawid owa integracja czynno ci percepcyjnych i motorycznych:

komplikacje wi

ce si z zaburzeniami dynamiki procesów

nerwowych obni aj ce efekty zcalania dzia ania i spostrzegania, w
tym gorsza sprawno manualna oraz niski poziom analizy i syntezy
wzrokowej;

b) zbyt niski poziom rozwoju operacyjnego rozumowania w stosunku

do zakresu poj i umiej tno ci matematycznych, które dzieci
powinny sobie przyswoi ;

aba odporno emocjonalna i obni ona zdolno do kierowania

swym zachowaniem w sytuacjach trudnych, wymagaj cych wysi ku
intelektualnego;

d) nieadekwatna samoocena, zw aszcza w zakresie mo liwo ci

poznawczych i wykonawczych;

e) zaburzenia motywacji.

Diagnoza genetyczna - formowanie hipotez o tym, co le y u

podstaw i czym s spowodowane zaburzenia. Ten zakres diagnozy jest
niezwykle wa ny dla wytyczenia ogólnej strategii dzia

naprawczych.

Jest to jednak trudne, gdy wiedza o ród ach zaburze ma ci gle
charakter wst pnych hipotez. Zaburzenia mog by bowiem
spowodowane:

a) Mikrouszkodzeniami

lub dysfunkcjami o rodkowego uk adu

nerwowego i wed ug tej hipotezy przyczyn jest defekt, uszkodzenie,
wadliwa struktura,

b) niedostatecznym wiczeniem danej funkcji w okresie sensytywnym,

a wi c przyczyna zaburze mo e by tak e zubo enie do wiadcze
w dotychczasowym yciu dziecka

W zale no ci od przyj cia jednej z tych dwóch hipotez cele, zakres i
metody oddzia ywania korekcyjnego powinny by odmienne. W
przypadku, gdy uzna si , e deficyt rozwojowy w zakresie danej funkcji
zosta

spowodowany mikrouszkodzcniami, wówczas post powanie

korekcyjne powinno by nastawione na kompensacj stwierdzonych
braków. W takim post powaniu trzeba oprze si na dobrze rozwini tych
u danego dziecka funkcjach czy zdolno ciach. Dlatego w diagnozie
nale y zadba nie tylko o ustalenie braków, lecz trzeba uwzgl dni tak e
dobrze, rozwini te strony osobowo ci dziecka.
Gdy przyjmuje si , e stwierdzony w diagnozie deficyt rozwojowy jest
wynikiem braku wiczenia, wówczas post powanie korekcyjne powinno
by nastawione na intensywny trening tej funkcji. Teza ta nawi zuje do
koncepcji okresów sensytywnych

Zak ada si , e w yciu cz owieka

istniej okresy, w których uczenie si pewnych zachowa przynosi
znakomite rezultaty. S to okresy najwi kszej gotowo ci rozwojowej dla
kszta towania zdolno ci, które warunkuj te zachowania. Gdy mija ten
sensytywny okres, wra liwo na oddzia ywanie bod ców danej
kategorii s abnie i nabywanie do wiadcze jest mniej efektywne. Przy
niesprzyjaj cych warunkach rodowiskowo-wychowawczych
przypadaj cych na okresy sensytywne, dziecko mo e nie mie
mo liwo ci dla wykorzystania swych potencjalnych mo liwo ci.
Nast puje zwolnienie tempa rozwoju w zakresie tej funkcji, której okres
sensytywny w tym czasie mija.

Prognoza – podejmowanie dzia

zmieniaj cych na lepsze losy

badanego dziecka. Dla niektórych dzieci najlepiej rozwa

mo liwo

odroczenia i zaproponowa podj cie nauki w szkole o rok pó niej. W ten
sposób maja one osi gn konieczn do uczenia si szkolnego dojrza
intelektualn i emocjonaln . Je eli jednak opó nienia s powa niejsze,
zwykle powtórzenie klasy zerowej mo e nie wystarczy i trzeba
zatroszczy si o zorganizowanie specjalnych zaj wspomagaj cych
rozwój dziecka.

Takie zaj cia powinny by prowadzone wg specjalnego programu
dostosowanego do potrzeb i mo liwo ci konkretnego dziecka. Podstaw
dla opracowania takiego programu s mi dzy innymi wnioski z bada
diagnostycznych. Taki program to zbiór konkretnych celów, które b
realizowane w trakcie zaj z dzieckiem.