1

Uczenie ze wzmocnieniem

Literatura:

• Paweł Cichosz, Systemy uczące się,

Wydawnictwa Naukowo-Techniczne, Warszawa
2000, str. 712-792.

• Richard Sutton, Andrew G. Barto,

Reinforcement Learning: An Introduction,
MIT Press, Cambridge, MA, 1998.

http://www.cs.ualberta.ca/~sutton/book/the-book.html

• Stuart J.Russel, Peter Norvig, Artificial

Intelligence, Prentice-Hall, London, 2003, str.
598-645.

2

Plan wykładu

• Wieloetapowe procesy decyzyjne - typy procesów i

środowisk

• Programowanie dynamiczne a metoda Monte Carlo
• Uczenie ze wzmocnieniem – podstawowy algorytm
• Eksploatacja a eksploracja
• Metody przyśpieszania zbieżności - ślady

aktywności

• Aproksymacja funkcji wartości stanów
• Metody kodowania stanów
• Agregacja stanów

3

Środowisko

Cechy środowiska w sztucznych systemach uczących się:

• przydziela nagrody i wyznacza bieżący stan

• jest niezależne od ucznia, czyli oznacza wszystko to, na co

uczeń nie ma wpływu

Typy środowisk:

• stacjonarne / niestacjonarne (zmienne w czasie)

• deterministyczne / niedeterministyczne - taka sama akcja

może spowodować przejście do różnych stanów, a przy
przejściu do takiego samego stanu można uzyskać różne
nagrody z tym, że wartości oczekiwane nagród i
prawdopodobieństwa przejść są stałe

• niedeterministyczne o znanym / nieznanym modelu

• o parametrach ciągłych / dyskretnych

• o pełnej informacji o stanie (własność Markowa) / o

niepełnej informacji o stanie

4

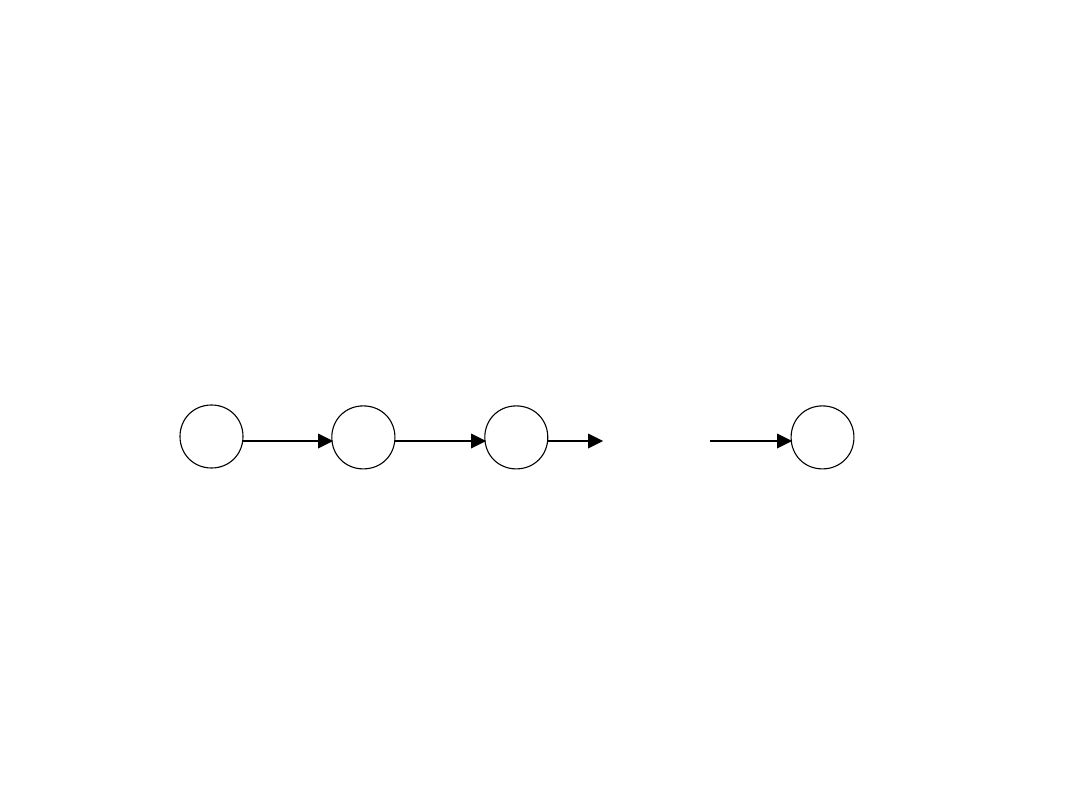
Wieloetapowe procesy decyzyjne

• Procesy polegające na wielokrotnej interakcji ucznia

(agenta) ze środowiskiem. W wyniku podjęcia jednej
z możliwych akcji a

t

w danym stanie s

t

, środowisko

przechodzi do nowego stanu s

t+1

i zwraca nagrodę

r

t+1

• Celem uczenia jest maksymalizacja nagród

uzyskanych w ciągu całego procesu, niezależnie od
stanu początkowego

• Wniosek: należy szukać optymalnej strategii (policy)

zachowania ucznia (wyboru odpowiedniej akcji w
każdym ze stanów)

s

t

s

t+1

s

t+2

s

t+k

...

a

t,

r

t+1

a

t+1,

r

t+2

a

t+k-1,

r

t+k

5

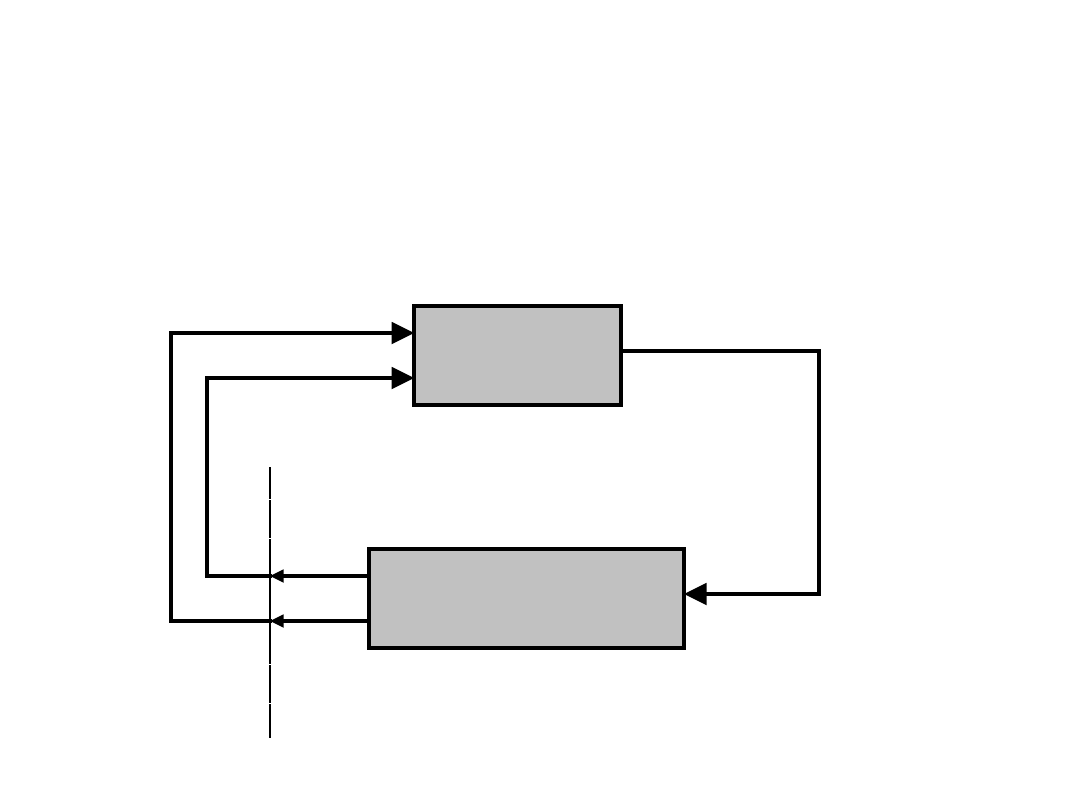
Ogólny schemat uczenia się w

interakcji ze środowiskiem

UCZEŃ

ŚRODOWISKO

akcja a

t

s

t

r

t+

1

r

t

s

t+1

6

Typy procesów

• Ze względu na środowisko: deterministyczne /

niedeterministyczne, stacjonarne / niestacjonarne

• Ze względu na informacje o stanie: spełniające

własność Markowa / niespełniające własności
Markowa

• Ze względu na ogólną liczbę stanów środowiska: o

skończonej liczbie stanów / o nieskończonej liczbie
stanów

• Ze względu na typ przestrzeni stanów: ciągłe

(nieprzeliczalne)/ dyskretne

• Ze względu na umiejscowienie nagród: tylko w

stanach końcowych (terminalnych) / tylko w stanach
pośrednich / w stanach końcowych oraz pośrednich

• Ze względu na liczbę etapów procesu: nieskończone /

epizodyczne (kończące się po pewnej liczbie kroków)

7

Metody szukania optymalnej

strategii

• Programowanie dynamiczne

• Metoda Monte Carlo

• Metoda różnic czasowych (TD)

8

Zadanie optymalizacji w procesach

epizodycznych

]

...

[

1

3

2

2

1

0

1









































n

t

n

t

t

t

n

k

k

t

k

r

r

r

r

E

r

E









Maksymalizacja:

gdzie r

t

- nagroda w kroku t,



- współczynnik

dyskontowania,
0



1, reguluje ważność krótko i

długoterminowych nagród.

Zastosowanie współczynnika dyskontowania
wynika z pewnych praktycznych spostrzeżeń:
nagrody warto zdobywać jak najszybciej (zadania
do-sukcesu), kary jak najdłużej odwlekać
(zadania do-porażki)

9

Dobór współczynnika

dyskontowania w zależności od

wartości nagród

,

2

1

1

0

1

1

0

2

1

1

1

0

2

1

r

r

r

r

r

r

r

n

n

t

n

t

n

t

n

t

n

t

n

t

















































Niech r

2

oznacza wartość nagrody w stanie końcowym, r

1

-

wartość nagrody w pozostałych stanach

Zadania do-sukcesu:

1

2

r

r 

2

1

1

r

r







stąd:

10

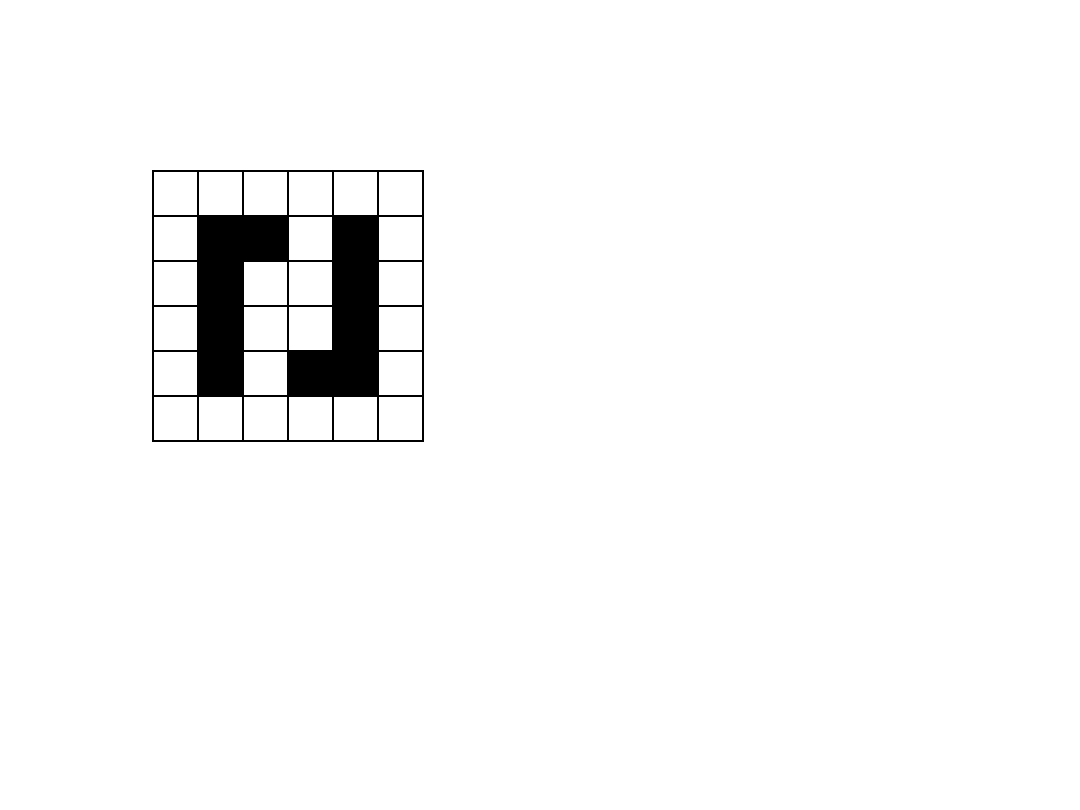
Przykład GRID-6

0.5

1































h

pozostalyc

dla

0

)

5

,

5

(

'

dla

5

.

0

)

5

,

0

(

'

dla

1

e

niedostepn

pole

w

prowadzi

nie

akcja

gdy

1

)}

5

,

5

(

),...,

1

,

0

(

),

0

,

0

{(

},

,

,

,

{

s

s

R

P

S

A

ij

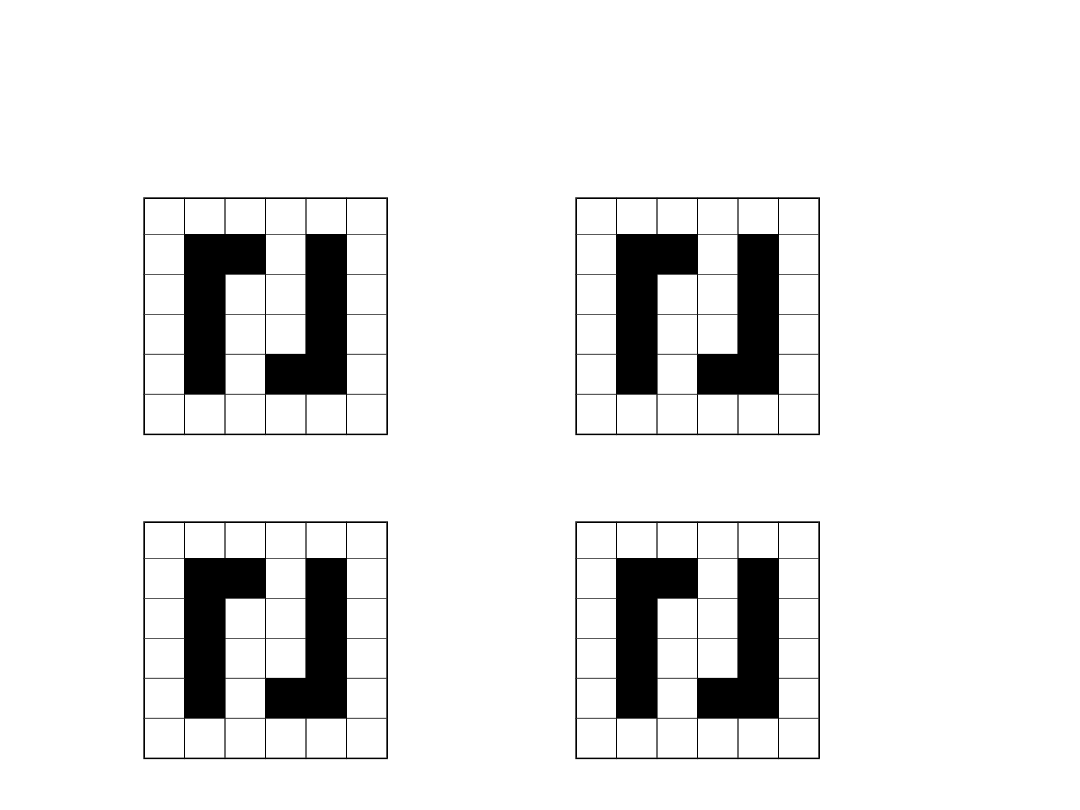
11

Przykład GRID-6 – przykładowe

strategie

     








 





 









     

     








 





 









     

     








 





 









     

     








 





 









     



1



3



4



2

12

Funkcje wartości

























n

k

t

k

t

k

s

s

r

E

s

V

0

1

|

)

(







Funkcja wartości stanu s

t

przy strategii



:



























n

k

t

t

k

t

k

a

a

s

s

r

E

a

s

Q

0

1

,

|

)

,

(







Funkcja wartości pary [stan,akcja]: (s

t

, a

t

) przy strategii



:

))

(

,

(

)

(

s

s

Q

s

V









Przy danej strategii



dla każdego stanu s zachodzi równanie:

13

Porównanie funkcji V oraz Q

• Użycie funkcji wartości stanu V(s) wymaga

każdorazowej symulacji wykonania jednego
kroku naprzód w celu znalezienia akcji
optymalnej

• Użycie funkcji Q(s,a) wymaga stosowania

większych tablic lub bardziej złożonych
aproksymatorów funkcji

14

Strategia optymalna

Strategia

’ jest lepsza od strategii  jeśli dla każdego s:

oraz istnieje takie s, że zachodzi:

Strategia jest optymalna, gdy nie ma od niej lepszej.

Zachłanna metoda wyboru akcji:

Zachłanna metoda wyboru akcji względem optymalnej funkcji
wartości lub funkcji wartości akcji jest realizacją strategii
optymalnej

)

(

)

(

'

s

V

s

V







)

(

)

(

'

s

V

s

V







)

,

(

max

arg

)

(

))

'

(

(

max

arg

)

(

'

'

'

a

s

Q

s

s

V

R

P

s

a

s

a

ss

a

ss

a















a

ss

P

'

- prawdopodobieństwo przejścia od
stanu s do s’ przy wykonaniu akcji a
- średnia nagroda przy przejściu od s do
s’ dzięki a

a

ss

R

'

15

Proces decyzyjny Markowa

Proces decyzyjny Markowa można zdefiniować

jako czwórkę (S, A,



,



):

• S - skończony zbiór stanów

• A - skończony zbiór akcji





(s,a) - funkcja wzmocnienia - zmienna

losowa o wartościach rzeczywistych
oznaczająca nagrodę po wykonaniu akcji a
w stanie s





(s,a) - funkcja przejść stanów - zmienna

losowa o wartościach ze zbioru S
oznaczająca następny stan po wykonaniu
akcji a w stanie s

W ogólności w każdym kroku t nagroda r

t+1

jest realizacją zmiennej losowej



(s

t

,a

t

) a

stan s

t+1

jest realizacją zmiennej losowej



(s

t

,a

t

)

16

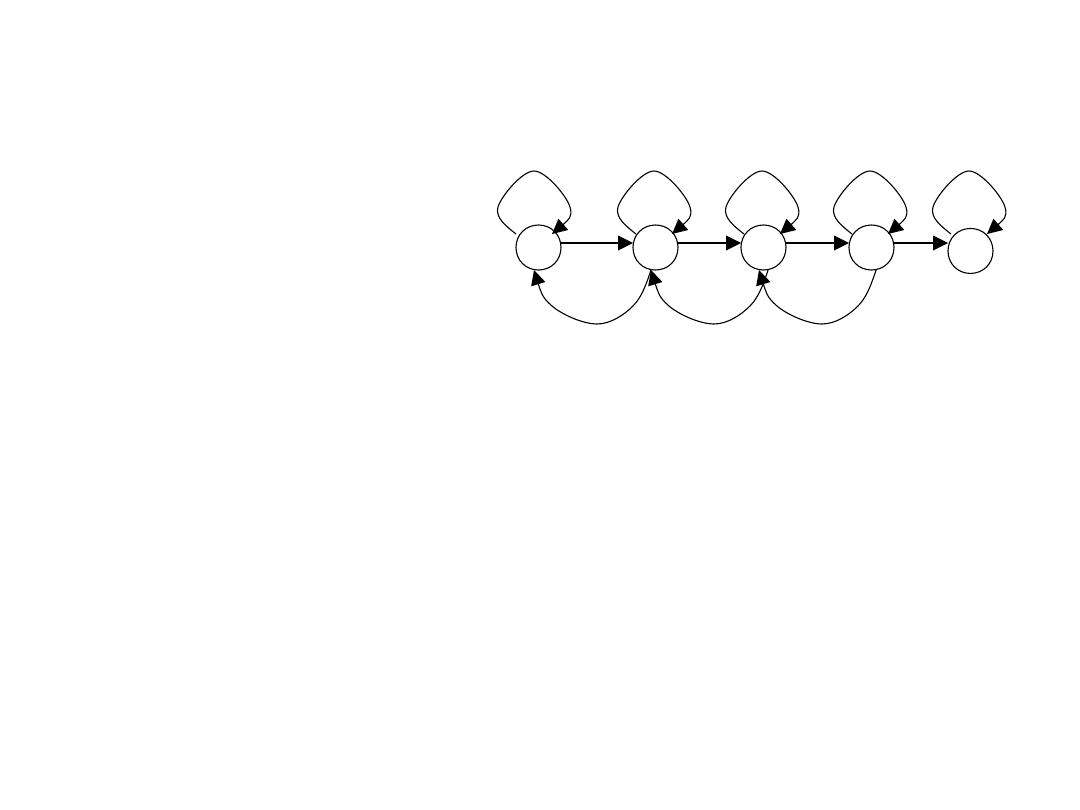
Przykład GRAF-5

S = {1,2,3,4,5}, A={0,1}































































































5

lub

1

dla

0

1

,

5

1

dla

1

.

0

0

,

5

1

dla

4

.

0

)

(

5

dla

1

1

,

1

dla

2

.

0

0

,

1

dla

8

.

0

1

,

5

1

dla

1

.

0

0

,

5

1

dla

4

.

0

)

(

5

dla

0

1

,

5

dla

8

.

0

0

,

5

dla

2

.

0

)

(

1

,

,

1

,

s

s

a

s

a

s

a

P

s

a

s

a

s

a

s

a

s

a

P

s

a

s

a

s

a

P

s

s

s

s

s

s





















h

pozostalyc

dla

0

1

,

4

dla

8

.

0

0

,

4

dla

2

.

0

)

,

(

a

s

a

s

a

s

R

1

2

3

4

5

Nagroda za akcję a w stanie s:

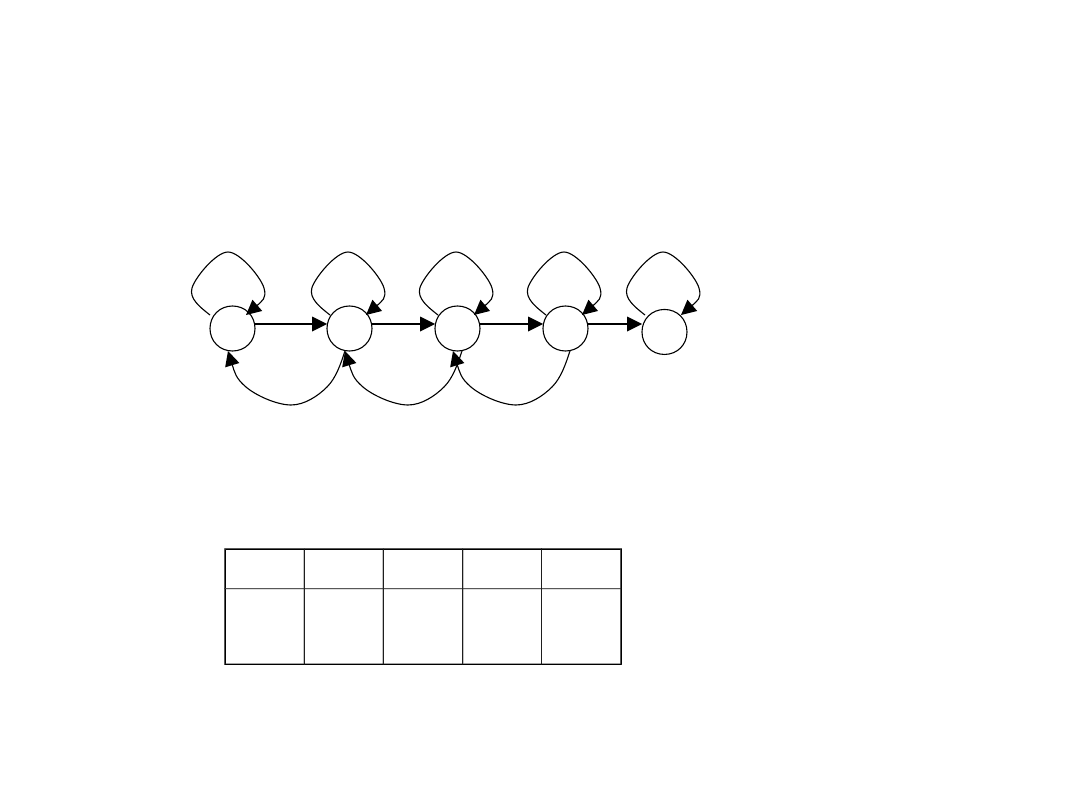
17

Przykład GRAF-5

Optymalne wartości stanów dla



= 0.9

1

2

3

4

5

V(1) V(2) V(3) V(4) V(5)

0.29

9

0.52

7

0.76

8

0.94

5

0

18

Uczenie ze wzmocnieniem - ogólny

algorytm

Zainicjuj Q(s,a) lub V(s)
Repeat (dla kolejnych epizodów):
Zainicjuj s
Repeat (dla kolejnych kroków epizodu):
obserwuj aktualny stan s

t

;

wybierz akcję a

t

do wykonania w stanie s

t

;

wykonaj akcję a

t

;

obserwuj wzmocnienie r

t+1

i następny stan s

t+1

;

ucz się na podstawie doświadczenia
(s

t

,a

t

,r

t+1

,s

t+1

,a

t+1

);

until s jest stanem końcowym
until spełniony warunek końca

19

Prawdopodobieństwo przejścia ze stanu s do s’
po wykonaniu akcji a, oraz średnia wartość
nagrody związanej z tym zdarzeniem:

}

'

,

,

|

{

}

,

|'

Pr{

1

1

'

1

'

s

s

a

a

s

s

r

E

R

a

a

s

s

s

s

P

t

t

t

t

a

ss

t

t

t

a

ss























)]

'

(

[

)

(

)

(

'

'

)

(

'

s

V

R

P

s

V

s

ss

s

s

ss

















Równania równowagi Bellmana dla reprezentacji [stan]
oraz [stan,akcja] i strategii



, (



(s) - akcja w stanie s

zgodna ze strategią



):

))]

'

(

,'

(

[

)

,

(

'

'

'

s

s

Q

R

P

a

s

Q

a

ss

s

a

ss















Programowanie dynamiczne

Model
środowisk
a

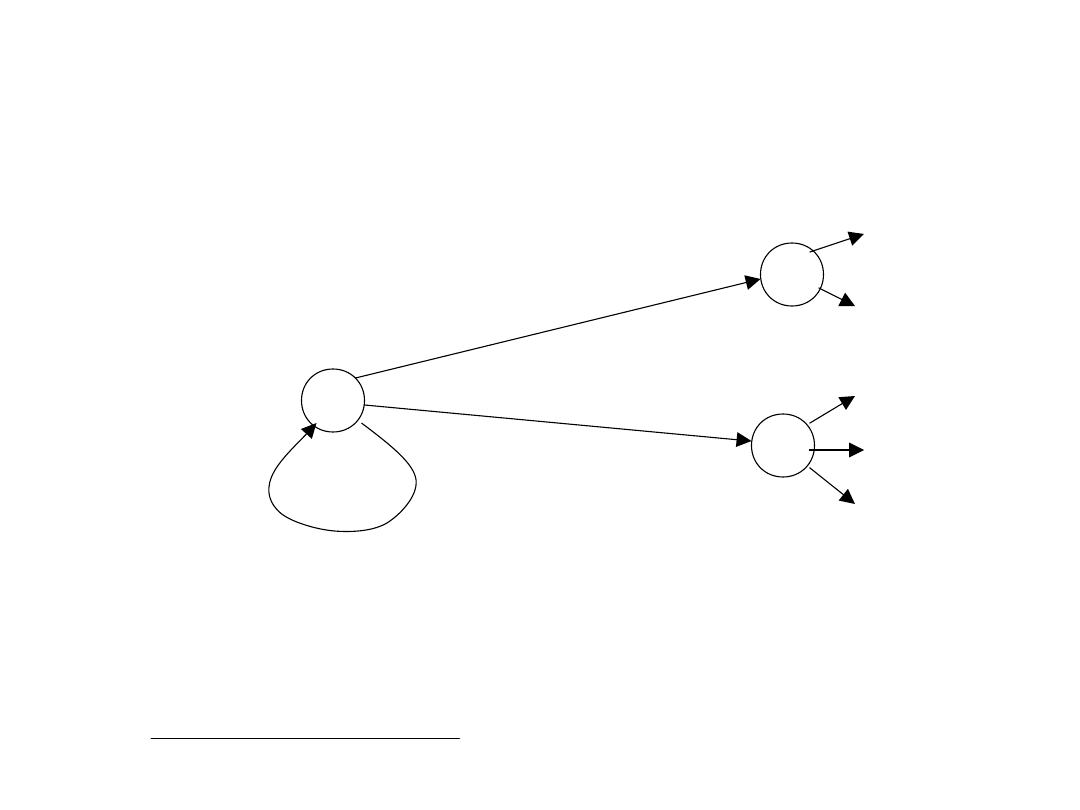
20

Przykładowy graf przejść ze stanu s=s

1

do s’ {s

1

,

s

2

, s

3

}, po wykonaniu akcji a:

)]

'

(

[

)

(

)

(

'

'

)

(

'

s

V

R

P

s

V

s

ss

s

s

ss

















Programowanie dynamiczne

s

2

s

1

s

3

1

,

2

.

0





R

P

1

,

7

.

0





R

P

5

.

0

,

1

.

0





R

P

))

(

5

.

0

(

1

.

0

))

(

1

(

7

.

0

))

(

1

(

2

.

0

)

(

1

3

2

1

s

V

s

V

s

V

s

V

























1

.

0

1

)

(

7

.

0

)

(

2

.

0

95

.

0

)

(

3

2

1









s

V

s

V

s

V

stąd:

21

Wyprowadzenie równania równowagi dla
funkcji wartości stanu s:

Programowanie dynamiczne

)]

'

(

[

]

'

|

[

|

|

)

(

)

(

'

'

)

(

'

0

1

2

)

(

'

'

)

(

'

0

2

1

0

1

s

V

R

P

s

s

r

E

R

P

s

s

r

r

E

s

s

r

E

s

V

s

ss

s

s

ss

k

t

k

t

k

s

ss

s

s

ss

k

t

k

t

k

t

k

t

k

t

k



































































































































22

)]

'

(

[

max

)

(

*

'

'

'

*

s

V

R

P

s

V

a

ss

s

a

ss

a









Równania optymalności Bellmana dla reprezentacji [stan] oraz [stan,akcja]:

)]

'

,'

(

max

[

)

,

(

*

'

'

'

'

*

a

s

Q

R

P

a

s

Q

a

a

ss

s

a

ss









Programowanie dynamiczne

)

,

(

),

(

*

*

a

s

Q

s

V

- wartości odpowiadające strategii
optymalnej

23

Metody wyznaczania optymalnej strategii:

• Rozwiązanie układu równań o |S| (lub |SA| w

przypadku reprezentacji [stan,akcja])
niewiadomych

• Iteracja strategii - naprzemienne obliczanie

przybliżonych wartości V



(s) dla wszystkich

stanów przy danej (początkowo losowej) strategii
 oraz wyznaczanie lepszej strategii ’ dla V



(s)

do momentu, gdy w kolejnych dwóch iteracjach
strategia

 pozostanie niezmienna

• Iteracja wartości - obliczanie V(s) stosując

zachłanną metodę wyboru akcji do momentu, gdy
wartości V(s) przestaną się zmieniać

Programowanie dynamiczne

24

Iteracja strategii dla reprezentacji

[stan]

)]

'

(

~

[

)

(

~

)

(

'

'

)

(

'

s

V

R

P

s

V

s

ss

s

s

ss

















powtarzaj dla wszystkich s:

mając dane:

, P



, R



aż nastąpi w kroku k















)

(

~

)

(

~

max

1

s

V

s

V

k

k

S

s







'

'

'

))

'

(

~

(

max

arg

)

(

'

s

a

ss

a

ss

a

s

V

R

P

s







obliczanie funkcji wartości stanu dla strategii



:

dla wszystkich s:

wyznaczanie nowej strategii



’:

*

2

1

~

~

~

2

1

V

V

V

k

























25

Iteracja wartości dla reprezentacji

[stan]

)]

'

(

~

[

max

)

(

~

'

'

'

s

V

R

P

s

V

a

ss

s

a

ss

a









powtarzaj dla wszystkich s:

mając dane: P



, R



aż nastąpi w kroku k











)

(

~

)

(

~

max

1

s

V

s

V

k

k

S

s

26

Programowanie dynamiczne - wady i

zalety

Wady:

• konieczność znajomości modelu środowiska

(prawdopodobieństw przejść pomiędzy stanami
dla wszystkich możliwych akcji i oczekiwanych
wartości nagród)

• duża złożoność obliczeniowa (brak

ukierunkowania przy obliczeniach - nakład
obliczeń nie zależy od wartości stanu)

Zalety:

• pewność znalezienia rozwiązania w przypadku

metody dokładnej oraz zbieżność metod
iteracyjnych

27

Metody Monte Carlo

Obliczanie funkcji wartości stanów lub par [stan,
akcja] dla pewnej strategii



metodą uśredniania

nagród z wielu epizodów.

,

)

(

~

1

0

1

,

L

r

s

V

L

e

n

k

k

t

e

k

e



 











gdzie L - liczba epizodów

Wyznaczanie strategii optymalnej: np. metodą
iteracji strategii

lub metodą iteracji wartości

*

2

1

~

~

~

2

1

V

V

V

k

























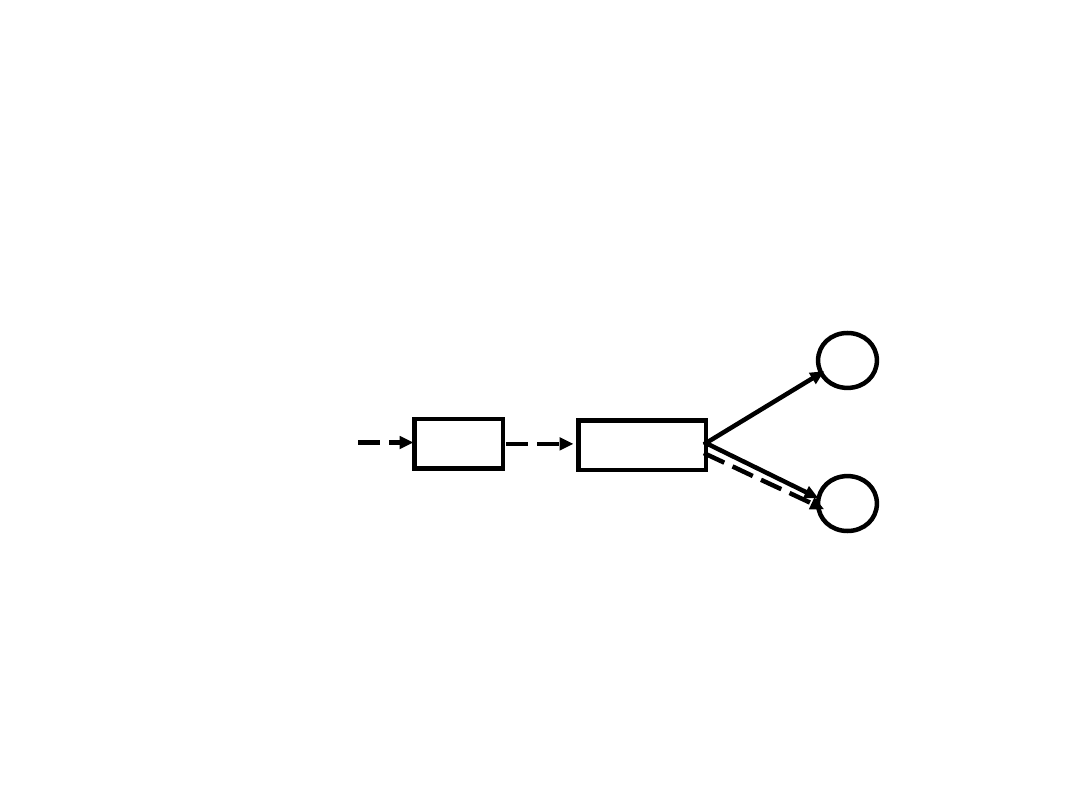
28

Metody Monte Carlo - wady i zalety

V = ?

V = -0.8

-1

1

p =

0.

9

p =

0.1

nowy stan

Wady:

• Powolna zbieżność - obliczenie funkcji

wartości nowego stanu bez
uwzględnienia wartości stanów
następujących po danym (bootstraping)

Zalety:

• Pewna zbieżność do funkcji wartości

V(s) dla ustalonej strategii przy
odpowiedniej eksploracji

• Nie jest wymagana znajomość modelu

środowiska

29

Metoda różnic czasowych – TD(0)

)]

(

)

(

[

)

(

)

(

1

1

t

t

t

t

t

s

V

s

V

r

s

V

s

V

















)]

,

(

)

,

(

[

)

,

(

)

,

(

1

1

1

t

t

t

t

t

t

t

t

t

a

s

Q

a

s

Q

r

a

s

Q

a

s

Q



















Aktualizacja wartości stanu - ogólna postać:

)

(

1

1









t

t

t

s

V

r

I



)]

(

[

)

(

)

(

t

t

t

t

s

V

I

s

V

s

V









Całkowity dochód uzyskany po wyjściu ze stanu s

t

:

Reprezentacja [stan,akcja]:

)

,

(

1

1

1











t

t

t

t

a

s

Q

r

I



30

Metoda różnic czasowych – TD(0)

Metody uczenia:

• Q-learning (off-policy)

• SARSA (on-policy)

• Actor-Critic (on-policy) (dodatkowy

system wartościowania strategii
przyjętej do uczenia (strategia
działania + eksploracja)

Zalety metod TD:

• nie jest wymagany model środowiska

• możliwość uczenia w czasie rzeczywistym

(online-learning)

• zastosowanie w przypadku niestacjonarnego

środowiska

• duża uniwersalność zastosowań

• dobra zbieżność

31

Algorytm Q-learning

Algorytm Q-learning z aktualizacją wartości par
[stan,akcja] niezależną od aktualnej strategii wyboru
akcji (off-policy)

Zainicjuj Q(s,a)
Repeat (dla kolejnych epizodów):
Zainicjuj s
Repeat (dla kolejnych kroków epizodu):
Wykonaj akcję a w stanie s zgodnie z wybraną
strategią(np. ε-zachłanną względem Q(s,a))

until s jest stanem końcowym
until spełniony warunek końca

]

)

,

(

)

'

,'

(

max

[

)

,

(

)

,

(

'

a

s

Q

a

s

Q

r

a

s

Q

a

s

Q

a













;'

s

s

32

Algorytm SARSA

Algorytm SARSA z aktualizacją wartości par
[stan,akcja] zgodnie z aktualną strategią np.



-

zachłanną (on-policy)

Zainicjuj Q(s,a)
Repeat (dla kolejnych epizodów):
Zainicjuj s
Wykonaj akcję a w stanie s zgodnie ze strategią
opartą na Q (np. ε-zachłanną)
Repeat (dla kolejnych kroków epizodu):
Wykonaj akcję a’ w stanie s’ zgodnie ze strategią
wyboru akcji (np.



-zachłanną względem Q(s’,a’))

until s jest stanem końcowym
until spełniony warunek końca

]

)

,

(

)

'

,'

(

[

)

,

(

)

,

(

a

s

Q

a

s

Q

r

a

s

Q

a

s

Q













;'

;'

a

a

s

s





33

• strategia optymalizująca zyski (eksploatacja)
• strategia uczenia (eksploatacja +

eksploracja):

• bieżące zyski nie mają znaczenia w

trakcie uczenia lub mają (np. w
problemie k-rękiego bandyty)

• optymalizacja zysków przy nieznanej

początkowo strategii optymalnej pozwala
na ukierunkowanie poszukiwań

• optymalizacja procesu uczenia dzięki

sprawdzeniu wielu potencjalnie dobrych
akcji w wielu potencjalnie dobrych
stanach

Typy strategii

34

Przykłady strategii wyboru akcji w

trakcie uczenia:

• maksimum
• losowa




-zachłanna

• softmax

Eksploatacja i eksploracja

Strategia



-zachłanna :

• z prawdopodobieństwem



wybierz akcję losowo

• z prawdopodobieństwem 1-



wybierz akcję:

Strategia softmax - wybór akcji zgodnie z rozkładem

Bolzmanna (prawdopodobieństwo wylosowania
akcji proporcjonalne do jej funkcji wartości):

)

,

(

max

arg

a

s

Q

a

a

































)

(

)

,

(

exp

)

,

(

exp

)

(

s

A

b

T

b

s

Q

T

a

s

Q

a

P

35

Warunki zbieżności:
• tablicowa reprezentacja funkcji Q
• stosowanie ciągu zmiennych

współczynników α

• dostateczna eksploracja

Q-learning - zbieżność





















1

2

1

1

1

i

i

i

i





36

Różnica pomiędzy algorytmami

SARSA i

Q-learning - przykład

SARSA – zabezpieczenie przed niedeterminizmem
strategii użytej do uczenia np.



-zachłannej

S

KLIF

K

Droga bezpieczna

Droga
optymalna Q-
learning

Nauka chodzenia po krawędzi klifu (od S do K): za każdy krok
odbierany jest 1 pkt, za wejście w przepaść odbieranych jest
1000 pkt.

Pytanie: Która droga zostanie wybrana w przypadku

-

zachłannej

strategii uczenia przez system uczony algorytmem

SARSA?

37

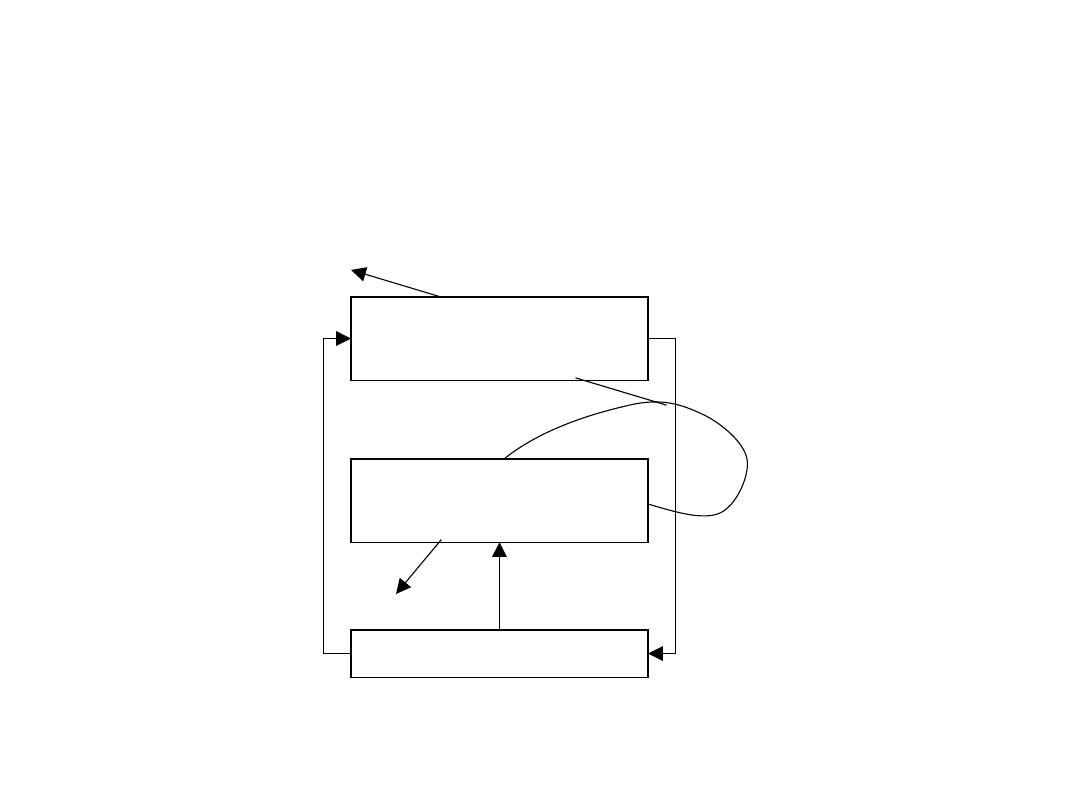
Metoda Actor-Critic - schemat

Schemat ogólny:

Funkcja strategii



(s,a) (actor)

Funkcja wartości

V(s) (critic)

Środowisko

akcja

stan

nagroda

błąd TD - 

)

(

)

'

(

s

V

s

V

r











38

Algorytm Actor-Critic

Algorytm Actor-Critic z funkcją wartości stanów V(s) i
dodatkową funkcją wyboru akcji

Zainicjuj V(s),



(s,a)

Repeat (dla kolejnych epizodów):
Zainicjuj s
Repeat (dla kolejnych kroków epizodu):
Wykonaj akcję a w stanie s zgodnie ze strategią
wyboru akcji (np.



-zachłanną względem



(s,a))

until s jest stanem końcowym
until spełniony warunek końca

'

)

,

(

)

,

(

)

(

)

(

)]

(

)

'

(

[

s

s

a

s

a

s

s

V

s

V

s

V

s

V

r





























39

Metoda Actor-Critic - zaleta

Zaleta:

• W stosunku do standardowego algorytmu z

reprezentacją stanów (V(s)) wymaga małego nakładu
obliczeniowego przy wyborze akcji

40

Przybliżenie TD(0)

)]

(

)

(

[

)

(

)

(

1

1

t

t

t

t

t

s

V

s

V

r

s

V

s

V

















)

(

1

1









t

t

t

s

V

r

I



Wartość stanu w danym epizodzie jest
modyfikowana tylko na podstawie wartości
następnego stanu i nagrody:

s

t

s

t+1

r > 0

41

Inne przybliżenia

)

(

)

(

)

(

2

1

)

(

2

2

2

1

)

2

(

1

1

)

1

(

n

t

n

t

t

n

t

t

t

t

t

t

t

t

s

V

r

r

I

s

V

r

r

I

s

V

r

I

















































Można wyznaczyć sumę ważoną przybliżeń
przyjmując, że im przybliżenie dalsze, tym mniej
istotne:

)

(

1

1

)

1

(

i

t

n

i

i

t

I

I

















42

Ślady aktywności TD() -

wyprowadzenie

)]

(

[

)

1

(

)]

(

[

)

1

(

)]

(

[

)

1

(

)

(

)

(

)

(

1

)],

(

[

)

(

)

(

1

1

3

2

2

1

2

2

2

1

1

1

1

0

'





































































n

t

n

t

t

t

n

t

t

t

t

t

t

t

t

t

t

t

t

t

s

V

r

r

r

s

V

r

r

s

V

r

s

V

s

V

I

s

V

s

V

I

s

V

s

V







































)]

(

)

(

[

)

(

)]

(

)

(

[

)

(

)]

(

)

(

[

)

(

)

(

)

(

1

1

1

1

2

2

2

1

1

1

1

0





















































n

t

n

t

n

t

n

t

t

t

t

t

t

t

t

s

V

s

V

r

s

V

s

V

r

s

V

s

V

r

s

V

s

V

























Sumując elementy w kolumnach i uwzględniając:
otrzymujemy:

,

1

)

1

(

1

1



 















n

n

i

i





43

Ślady aktywności TD() -

wyprowadzenie















































































































1

1

1

1

2

2

1

1

1

0

1

1

1

2

2

2

1

1

1

1

0

)

(

)]

(

)

(

[

)

(

)]

(

)

(

[

)

(

)]

(

)

(

[

)

(

)]

(

)

(

[

)

(

)]

(

)

(

[

)

(

)]

(

)

(

[

)

(

)

(

)

(

)

(

1

T

t

k

k

t

k

n

t

n

t

n

t

n

t

t

t

t

t

t

n

t

n

t

n

t

n

t

t

t

t

t

t

t

t

t

t

s

V

s

V

r

s

V

s

V

r

s

V

s

V

r

s

V

s

V

r

s

V

s

V

r

s

V

s

V

r

s

V

s

V

I

s

V













































)

(

)

(

1

1

t

t

t

t

s

V

s

V

r















gdzie

Przesuwamy ostatnią
kolumnę w dół. Wstawiamy
-V(s

t

) do pierwszego wiersza

45

Ślady aktywności - algorytm

Zainicjuj V(s)
Repeat (dla kolejnych epizodów):
Zainicjuj s, e(s)=0 dla wszystkich s
Repeat (dla kolejnych kroków epizodu):
Wykonaj akcję a w stanie s zgodnie z



,

obserwuj nagrodę r i następny stan s’

for all states s

x

:

end for

until s jest stanem końcowym
until spełniony warunek końca

)

(

)

'

(

s

V

s

V

r











1

)

(

)

(



 s

e

s

e

'

s

s

)

(

)

(

)

(

)

(

)

(

x

x

x

x

x

s

e

s

e

s

e

s

V

s

V











46

Ślady aktywności TD() - zalety

• Przyspieszenie uczenia dzięki

równoległemu przypisywaniu zasług
wszystkim stanom lub akcjom, które
poprzedzają otrzymanie nagrody

• Połączenie zalet metod Monte Carlo i TD(0)

przez odpowiedni wybór współczynnika
świeżości



• Znaczne przyspieszenie uczenia w

przypadku nagród znacznie oddalonych

47

Agregacja, kodowanie,

aproksymacja

Agregacja stanów – przekształcenie wektorów

z pierwotnej przestrzeni stanów s = [s

1

,

s

2

,..., s

N

] (np. układu figur na szachownicy)

do przestrzeni cech istotnych dla
określenia wartości stanu:
z wykorzystaniem wiedzy o
problemie

)]

(

),...,

2

(

),

1

(

[

)

(

M

s

s

s

s

s



















Kodowanie stanów – transformacja stanów do

nowej przestrzeni cech, lecz bez
wykorzystania wiedzy o problemie

Aproksymacja funkcji wartości –

przedstawienie funkcji wartości stanów
lub par [stan,akcja] w postaci modelu
parametrycznego funkcji (struktury) o
odpowiednio dobranych (nauczonych)
wartościach parametrów

))

(

),...,

2

(

),

1

(

(

n

t

t

t

t













48

Aproksymatory funkcji

Przykłady:

• Aproksymator liniowy
• Wielomiany stopnia > 1
• Sztuczne sieci neuronowe (SNN)
• Sieci o podstawie radialnej (Radial Basis

Functions – RBF)

• Systemy rozmyte

Zalety:
• Oszczędność miejsca przy dużych zbiorach

stanów lub par [stan,akcja]

• Możliwość uogólniania wiedzy dla stanów

pośrednich

• Brak dyskretyzacji w przypadku

rzeczywistoliczbowej reprezentacji stanów lub
akcji

49

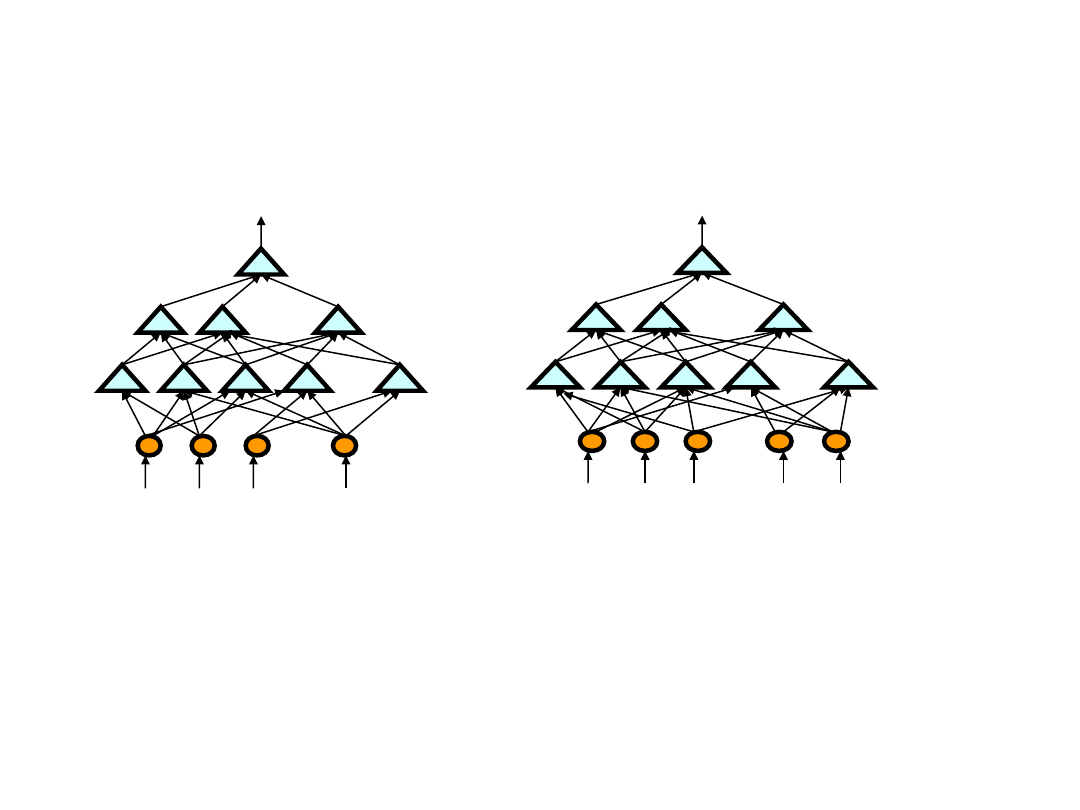
• zamiast pełnej informacji o stanie w postaci wektora s,

można wykorzystać stan uogólniony w postaci wektora cech

• Wektorowi parametrów modelu odpowiada wektor wag sieci
• Gradient funkcji wartości oblicza się metodą propagacji

wstecznej błędu

Aproksymator SSN

...

...

Q(s,a)

s

1

s

2

s

3

s

N

a

...

...

...

s

1

s

2

s

3

s

N

V(s)

...

)]

(

),...,

2

(

),

1

(

[

M

s

s

s

s













50

Aproksymatory funkcji - definicje

))

(

),...,

2

(

),

1

(

(

n

t

t

t

t













Wektor parametrów:

Kryterium optymalizacji:





,

)

(

)

(

)

(

2









S

s

t

s

V

s

V

MSE







V



(s) – poszukiwana wartość stanu s dla strategii



V(s) – aktualna wartość stanu s

)

,

(

)

,

(

a

s

F

a

s

Q







)

(

)

(

s

F

s

V







Wartości stanów lub par [stan,akcja]
reprezentowane są za pomocą funkcji zależnej
od parametrów



(i):

51

Gradientowa metoda aproksymacji

funkcji wartości stanów









)

(

)

(

)

(

)

(

)

(

2

1

2

1

t

t

t

t

t

t

t

t

s

V

s

V

s

V

s

V

s

V

t

t















































Przyjmując przybliżenie:

)

(

)

(

1

1









t

t

t

s

V

r

s

V





Otrzymujemy algorytm aktualizacji wartości stanu:

(następny slajd)





























)

(

)

(

,

,

)

2

(

)

(

,

)

1

(

)

(

)

(

gradient

gdzie

n

f

f

f

f

t

t

t

t

t

t

t

t



































parametry funkcji
wartości modyfikowane
są w kierunku
maksymalnego spadku
funkcji błędu

52

Gradientowa metoda aproksymacji

funkcji wartości stanów - TD()

Zainicjuj
Repeat (dla kolejnych epizodów):
Zainicjuj s,
Repeat (dla kolejnych kroków epizodu):
Wybierz i wykonaj akcję a w stanie s zgodnie z

przyjętą strategią

until s jest stanem końcowym
until spełniony warunek końca

)

(

)

'

(

s

V

s

V

r











)

(s

V

e

e

















'

s

s

e















]

0

,...,

0

,

0

[



e

)

(

)

,

(

)

(

s

F

s

F

s

V













53

Metody wyznaczania kierunku

modyfikacji wektora parametrów

funkcji wartości

• Metoda spadku gradientu funkcji błędu
• Metoda Newtona
• Metody quasi-Newtonowskie
• Metoda gradientów sprzężonych
• Metoda Levenberga-Marquardta

54

Metody kodowania stanów w

aproksymacji funkcji wartości

Metody kodowania (obliczania cech):

• Kodowanie metodą pokryć (CMAC, tile coding)

• Kodowanie przybliżone (coarse coding)

• Kodowanie przybliżone rozproszone - np. metodą Kanervy

55

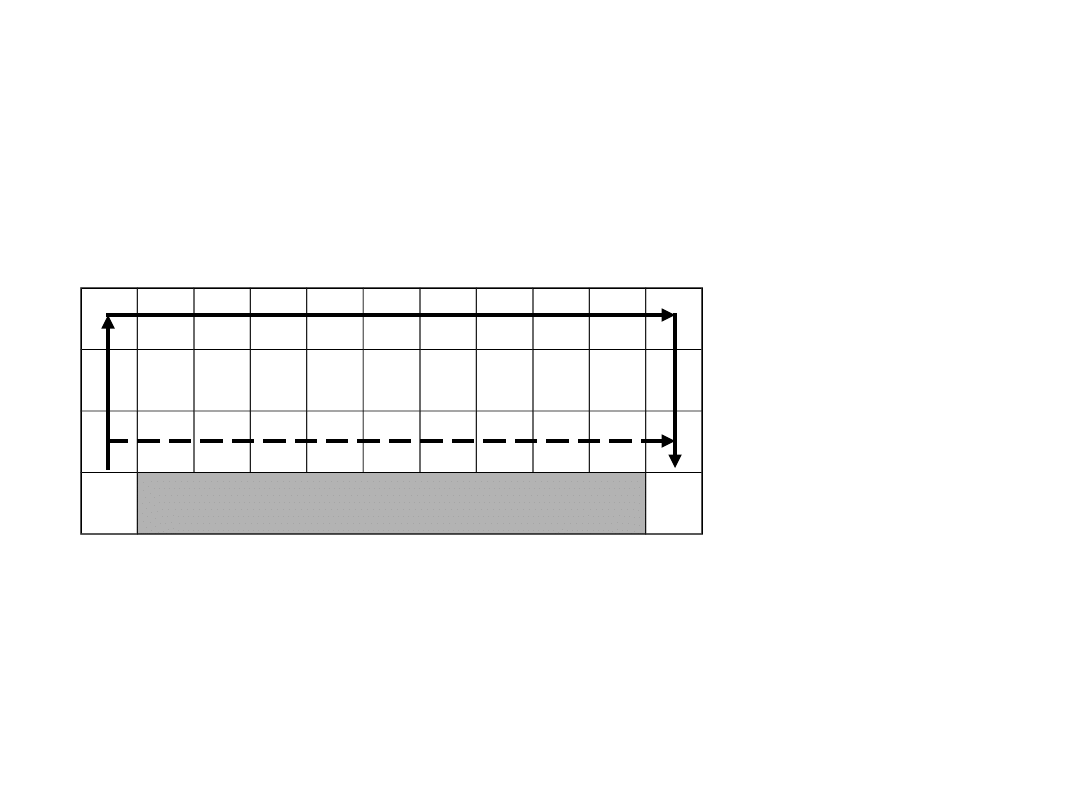
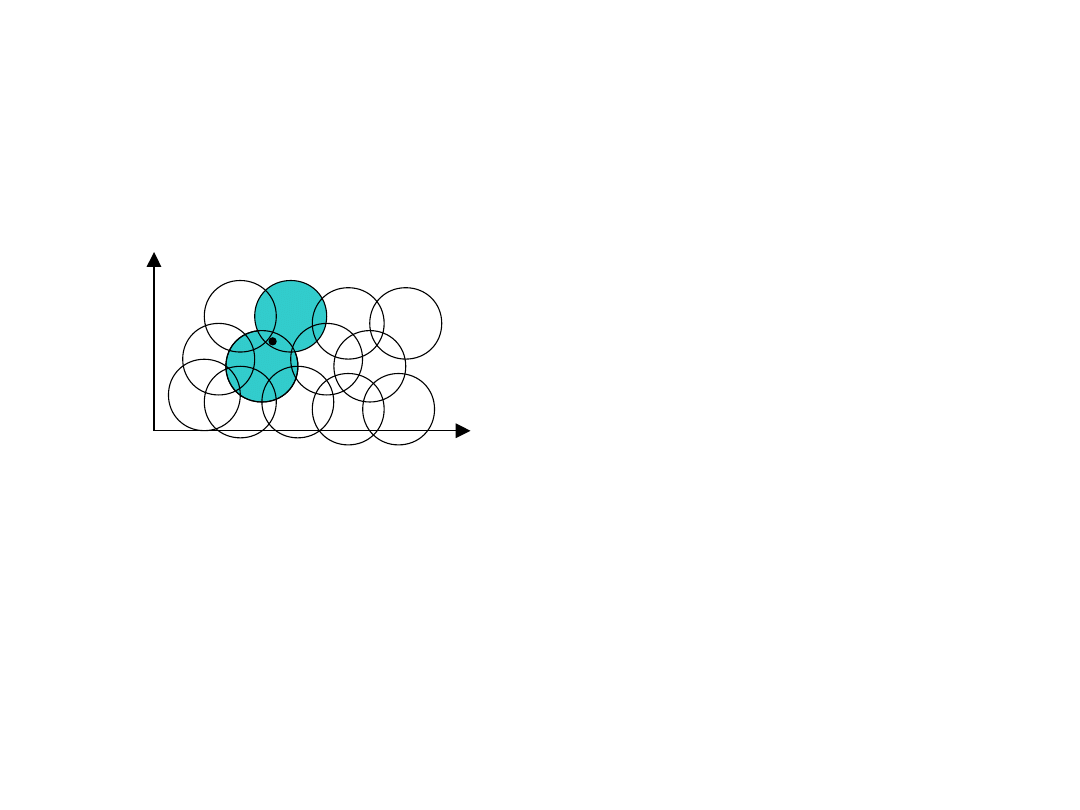
Kodowanie przybliżone

Przykładowe zastosowanie: aproksymator liniowy z wykorzystaniem zbioru cech:









n

i

s

s

T

i

i

s

V

1

)

(

)

(

)

(













s





- wektor cech stanu

Kodowanie przybliżone dla 2-wymiarowej przestrzeni stanów -
każde pole jest związane z jedną cechą binarną, równą 1 jeśli
stan znajduje się wewnątrz pola:

x

y

Licząc po kolejnych
wierszach od lewej do
prawej wektor cech:

]

0

,

0

,

0

,

0

,

0

,

0

,

0

,

1

,

0

,

0

,

0

,

1

,

0

[



s





gradient funkcji wartości:

)]

(

),...,

2

(

),

1

(

[

)

(

M

s

V

s

s

s

s





















56

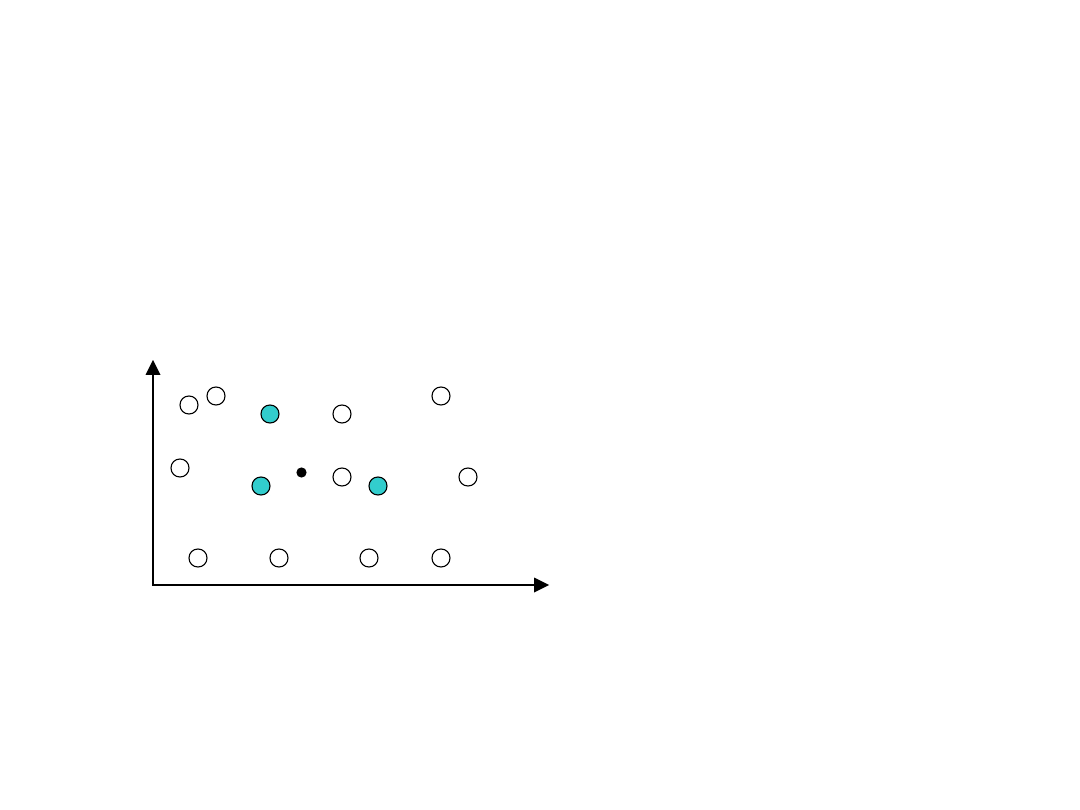
Kodowanie przybliżone, rozproszone

(kodowanie Kanervy)

Kodowanie przybliżone dla przykładowej 2-wymiarowej
przestrzeni stanów - każdy prototyp stanu jest związany z
jedną cechą binarną, równą 1 jeśli spełnione jest kryterium
odległości (w przypadku kodowania Kanervy jest to odległość
Hamminga):

x

y

Licząc po kolejnych
wierszach od lewej do
prawej nowy wektor
cech:

]

0

,

0

,

0

,

0

,

0

,

1

,

0

,

1

,

0

,

0

,

0

,

1

,

0

,

0

[



s





Prototypowe stany lub pary [stan, akcja] są początkowo
wybierane losowo. Dodatkowo, w bardziej zaawansowanych
metodach mogą być przemieszczane w celu większego ich
skupienia w ważniejszych obszarach przestrzeni stanów