Akademia Górniczo- Hutnicza

Im. Stanisława Staszica w Krakowie

BADANIE TURBIN WODNYCH

Część 1. Badanie akcyjnej turbiny wodnej – turbina Peltona

Część 2. Badanie reakcyjnej turbiny wodnej – turbina Francisa

Prowadzący:

mgr inż. Tomasz Siwek

[e-mail]

1. Wprowadzenie

1.1. Zasady wykorzystania energii wodnej

Ruch wody rzeki jest wywołany pochyleniem jej koryta, w wyniku czego siły

ciężkości wody powodują jej przepływ. W warunkach naturalnych część energii ruchu

wody (energii cieku) jest zużywana na tarcie o koryto, rozmywanie brzegów,

przenoszenie rumowiska, pokonywanie oporów przy zmianie kierunku przepływu itp.;

pozostała część jest przy swobodnym przepływie rzeki tracona. Energia cieku może

być w znacznym stopniu wykorzystana przez zmniejszenie oporów przepływu i

zmniejszenie jego prędkości, przy jednoczesnym odpowiednim spiętrzeniu rzeki.

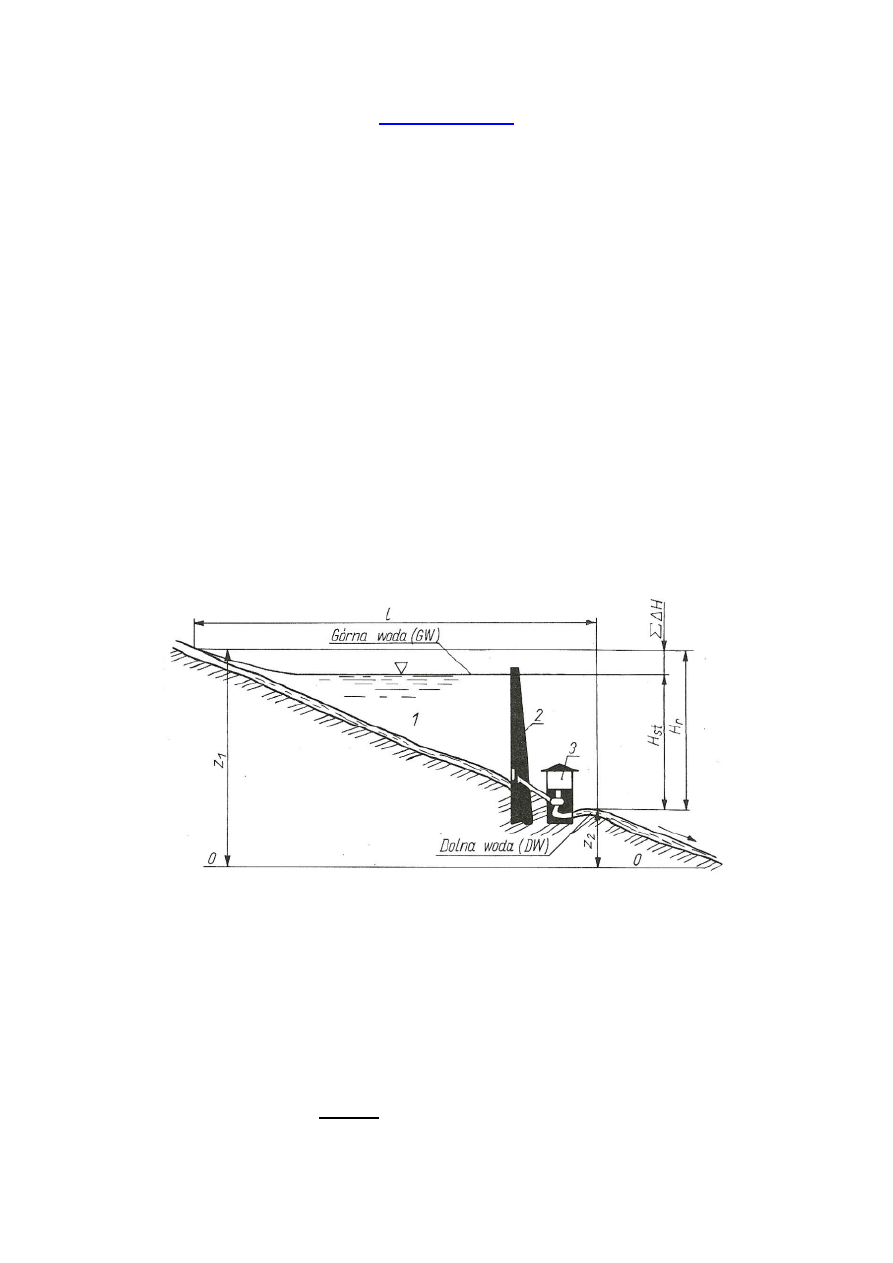
Jeżeli na pewnym odcinku rzeki l (rys.1.) jej spad wynosi:

𝐻

𝑟

= 𝑧

1

− 𝑧

2

gdzie z

1

oraz z

2

—

wzniesienia początku i końca odcinka rzeki w metrach, to przy

swobodnym przepływie spad ten będzie miarą straconej energii cieku. Po
przegrodzeniu

rzeki w końcu rozpatrywanego odcinka zaporą 2 poziom rzeki przed

zaporą podnosi się prawie do korony zapory. Spad statyczny H

st

elektrowni 3 (spad

brutto) jest różnicą poziomów górnej i dolnej wody i może być wykorzystany do
uruchomienia turbiny wodnej. Straty spadu

� ∆𝐻 = 𝐻

𝑟

− 𝐻

𝑠𝑡

Rys.1. Schemat energetycznego wykorzystania rzeki 1 — zbiornik, 2 — budowla

piętrząca, 3 — elektrownia

wynikają z konieczności utrzymania ruchu wody i pokonania oporów przepływu w

zbiorniku i przewodach doprowadzających wodę do elektrowni. Energia zawarta w
spadzie H

s t

została uzyskana dzięki zmniejszeniu prędkości i strat w przepływie

przed zaporą, wskutek powiększenia się koryta w głąb i wszerz. Spad
wykorzystywany w turbinach elektrowni nazywamy

spadem użytecznym (spad

netto),

uwzględniający różnice prędkości strumienia na wlocie i wylocie turbiny oraz

straty

∆h

występujące w trakcie przepływu przez budowle i urządzenia elektrowni:

𝐻

𝑢

= 𝐻

𝑠𝑡

+

𝑣

1

2

− 𝑣

2

2

2𝑔 − � ∆ℎ 𝑙𝑢𝑏 𝐻

𝑢

= 𝑝

𝑐𝑔

− 𝑝

𝑐𝑑

Spadek użyteczny możemy wyrazić również przez różnicę ciśnień całkowitych w

króćcu wlotowym p

cg

i wylotowym turbiny p

cd

.

Zadaniem elektrowni wodnej

jest zamiana energii potencjalnej spiętrzonej wody na

energię mechaniczną (w turbinie wodnej), a następnie na energię elektryczną (w

prądnicy). Moc cieku (moc hydrauliczna) P

hyd

,

która teoretycznie mogłaby być

zamieniona na energię elektryczną, równa się

𝑃

ℎ𝑦𝑑

= 𝜌𝑔𝑄𝐻

𝑢

gdzie: Q —

strumień objętości (natężenie przepływu objętości) wody, tj.

przełyk

elektrowni

(przełyk turbiny).

Moc elektrowni wodnej P,

wykorzystującej rozpatrywany odcinek rzeki, jest

mniejsza od P

hyd

wskutek różnego typu strat występujących w procesie przetwa-

rzania energii i wynosi:

𝑃 = 𝜂

𝑒

𝑃

ℎ𝑦𝑑

gdzie

η

e

—

sprawność elektrowni, równa iloczynowi sprawności poszczególnych

urządzeń: turbiny η

t

,

prądnicy η

g

i transformatora

η

tr,

czyli

𝜂

𝑒

= 𝜂

𝑡

𝜂

𝑔

𝜂

𝑡𝑟

Wartości poszczególnych sprawności wynoszą przeciętnie: η

t

= 0,88÷0,93;

η

g

= 0,95÷0,98;

η

tr

= 0,97÷0,995.

Wyższe wartości odnoszą się do maszyn dużej mocy.

Sprawność elektrowni zawiera się więc w granicach η

e

= 0,84 ÷ 0,875; we

wstępnych obliczeniach przyjmuje się na ogół η

e

= 0,85.

M

oc elektrowni jest zależna od spadu i przełyku. Spad elektrowni zależy od

war

unków topograficznych doliny rzeki oraz rozwiązania stopnia wodnego i decyduje

o charakterze elektrowni. Przełyk elektrowni ma zasadniczy wpływ na wymiary turbin

i budynku elektrowni oraz na wielkość budowli hydrotechnicznych doprowadzających

wodę do elektrowni. Dobór tej wielkości jest uzależniony od zakresu przepływów
wody w rzece, sposobu zagospodarowania rzeki oraz od charakteru pracy
elektrowni.

Ilość wody w rzekach zmienia się w ciągu roku, jak również w okresach

dłuższych. Intensywność wahań stanu wody w rzekach zależy od wielu czynników,

jak: źródło zasilania rzeki (jezioro, lodowiec, woda gruntowa), charakter terenu

(równina, góry), charakter gruntu dorzecza (piaszczysty, gliniasty, skalisty), ilość

opadów w ciągu roku itp. Na podstawie wieloletnich obserwacji można przewidzieć

stany wody w rzekach, zwane stanami przepływu. Przy określaniu zasobów

energetycznych rzeki oznacza się tzw. przepływy 50% i 95%. Przepływem 50% (lub

95%) nazywa się taki przepływ, który trwa 50% (lub 95%) rozpatrywanego czasu

obserwacyjnego. Wartości te są uwzględniane przy wyborze przepływu

obliczeniowego (przełyku).

Wybór maksymalnego przepływu spowodowałby w okresie małych

przepływów niepełne zasilanie turbin i uniemożliwił ich pracę; przyjęcie minimalnego

przepływu pociągnęłoby za sobą konieczność upuszczenia przez zaporę nadmiaru

wody w okresie zwiększonych przepływów i tym samym nieekonomiczną pracę

elektrowni. Przy wyborze przełyku trzeba też kierować się możliwościami przejęcia
przez zbiornik wód powodziowych.

Nie mni

ej złożone jest zagadnienie doboru spadu. Z punktu widzenia

energetyki korzystny jest spad jak największy. Jednakże im wyższy jest przewidziany

spad, tym większa powinna być wysokość zapory spiętrzającej, a tym samym

większe obszary przed zaporą będą zalane wodą. Wysokie spiętrzenie wody

wymaga też wzmocnienia wałów ochronnych, zabezpieczających sąsiadujące

obiekty. Jak więc widać, nadmierne zwiększenie spadu może okazać się

nieekonomiczne. Ostatecznego doboru przełyku i spadu dokonuje się na podstawie
gruntownej analizy ekonomicznej szeregu wariantów.

Elektrownie wodne mogą być budowane jako pojedyncze obiekty,

wykorzystujące tylko pewien odcinek rzeki, lub jako szereg wzajemnie powiązanych

elektrowni, wykorzystujących całą rzekę lub jej części i nazywany kaskadą rzeki.

Kaskadowe wykorzystanie rzeki ma szereg istotnych zalet, łagodząc wymienione

wyżej trudności.

1.2. Rodzaje elektrowni wodnych

a.

W zależności od spadu w warunkach polskich rozróżniamy elektrownie

niskiego spadu H < 15 m, średniego spadu 15 < H < 50 m i wysokiego spadu
H > 50 m.

b.

W zależności od czasu pracy w ciągu roku w układzie elektroenergetycznym

elektrownie wodne dzieli się na podstawowe, podszczytowe i szczytowe.

c.

Sposób rozwiązania hydrotechnicznego pozwala wyróżnić elektrownie przy-
jazowe (przyzaporowe) oraz elektrownie derywacyjne.

W przyzaporowej elektrowni wodnej (rys. 2

) całe urządzenie jest umieszczone

w jednej budowli, bezpośrednio w korycie rzeki. Sama elektrownia może stanowić

przedłużenie zapory przegradzającej rzekę i wtedy spełnia dodatkowo funkcję

zapory, może być również wzniesiona przy zaporze od strony dolnej wody 9 i wtedy
budynek elektrowni nie przenosi naporu wody górnej 3. Budynek elektrowni 1 wznosi

się przy zaporze od strony dolnej wody. Wodę do turbiny 6 doprowadza się przez

zabezpieczone kratami otwory w zaporze 2, zamykane zasuwą 4, oraz przez kanał

dopływowy 5. Z turbiny woda przechodzi do koryta rzeki przez rurę ssawną 8.

Rys.2. Schemat elektrowni wo

dnej przyzaporowej przepływowej

1 — budynek elektrowni, 2 — zapora, 3 — górna woda, 4 — zasuwa, 5 —

kanał dopływowy,

6 — turbina, 7 —

prądnica, 8 — rura ssawna, 9 — dolna woda, 10 — transformator

Bezpośrednio sprzężona z turbiną prądnica 7 zamienia energię mechaniczną

z turbiny na energię elektryczną, odprowadzaną do sieci przez transformator 10.

W elektrowni derywacyjnej (rys.

3) zapora 3 spiętrza wodę 1 i przez ujęcie 4

odprowadza ją do kanału derywacyjnego 6 o łagodnym spadku. Na końcu kanału

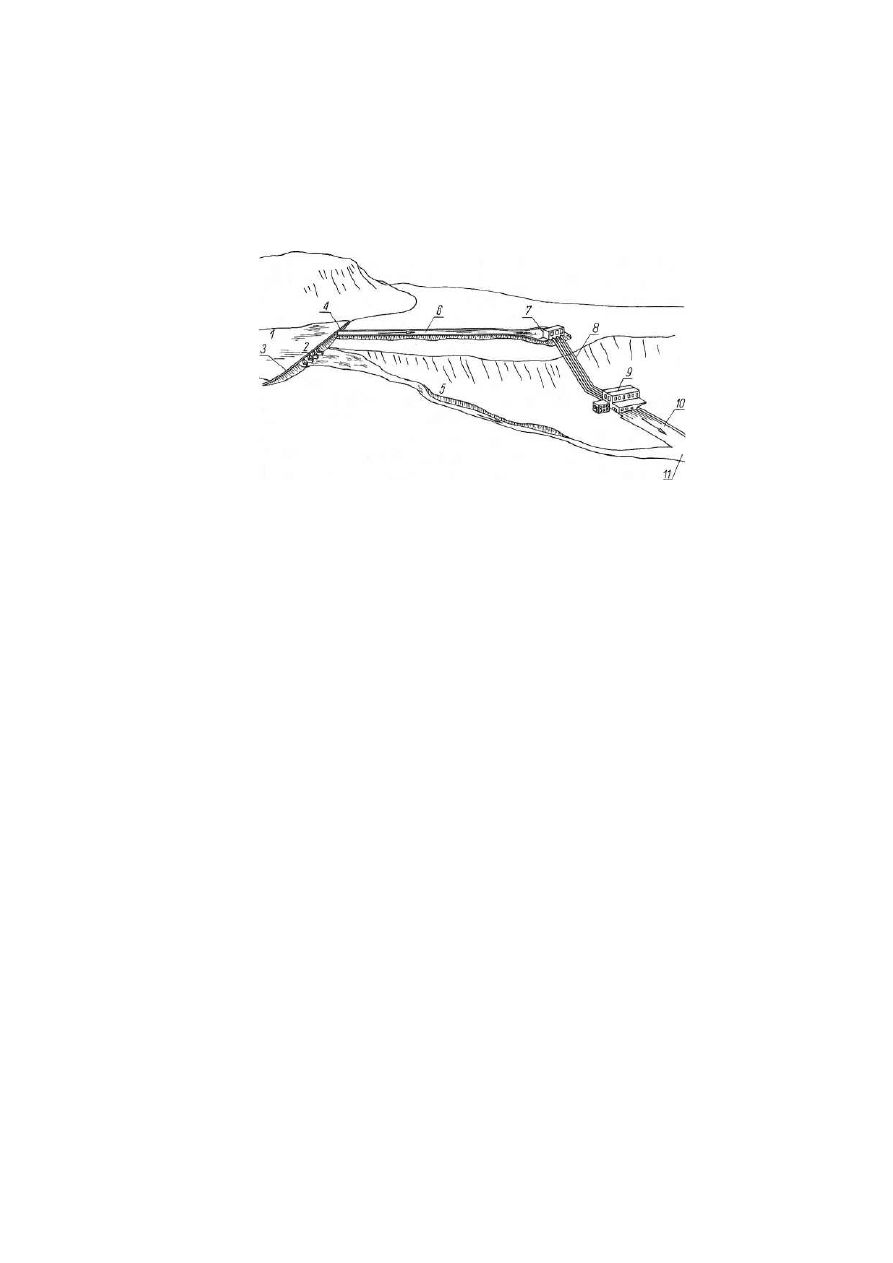
tworzy się zbiornik 7 górnej wody, która rurociągami ciśnieniowymi 8 jest
doprowadzana do turbin umieszczonych w budynkach elektrowni 9,

a następnie

kanałem odpływowym 10 do naturalnego koryta rzeki 11. Przepływ starym korytem 5

na odcinku między zaporą i budynkiem elektrowni ma miejsce w przypadku
upuszczenia wody przez przelewo

wą część zapory 2 z pominięciem turbin.

Elektrownie derywacyjne są zwykle budowane na rzekach górskich.

Rys.3. Elektrownia wodna derywacyjna

1 — górna woda, 2 — przelew zapory, 3 — zapora, 4 —

ujęcie, 5 — stare koryto, 6

—

kanał derywacyjny, 7 — zbiornik górnej wody, 8 — rurociągi ciśnieniowe, 9 —•

elektrownia, 10 —

kanał odpływowy, 11 — naturalne koryto rzeki

d.

W zależności od sposobu wykorzystania zasobów wodnych elektrownie

można podzielić na przepływowe i zbiornikowe. Elektrownie przepływowe są

przeznaczone do pracy ciągłej (podstawowej. Elektrownie zbiornikowe pracują

głównie jako szczytowe. W okresie poza szczytami obciążenia woda jest tu

gromadzona w zbiorniku górnym przez naturalny napływ lub pompowanie
(elektrownie szczytowo-pompowe) i wyko

rzystywana w szczycie obciążenia.

e.

Istnieją też możliwości wykorzystania energii wód morskich przejawiającej się

w wahaniach poziomu wody, w procesie falowania, w prądach morskich; w

strefach tropikalnych dodatkowe źródło energii może stanowić różnica
tempe

ratury górnych i dolnych warstw morza. W tej dziedzinie istnieją

rozwiązania francuskie w postaci elektrowni pływów morskich u brzegów
Atlantyku. Elektrownia Rence

jest zainstalowana w zaporach odgradzających

zatokę od morza, a jej turbiny są dostosowane do pracy przy obu kierunkach

przepływu, tj. zarówno podczas przypływu, jak i odpływu morza. Morze

Bałtyckie wykazuje bardzo słabe ruchy poziomu wywołane pływami, nie

stanowi więc istotnego zasobnika energetycznego.

Z

asoby energetyczne rzek polskich są niewielkie, a warunki do budowy

elektrowni wodnych —

niekorzystne, w dodatku tam, gdzie przepływ wody jest duży,

np. w średniej i dolnej Wiśle, nie ma warunków do spiętrzania wody i przeciwnie —

na Podkarpaciu są warunki do uzyskania większych spadów, ale przepływy są słabe
i nieregularne.

Istotne moce osiągane są tylko w elektrowniach szczytowo

pompowych, których zasadniczą rolą jest regulacja systemu elektro-energetycznego.

Do największych krajowych elektrowni wodnych należą: Elektrownia Wodna

Żarnowiec (szczytowo-pompowa) — 716 MW, Elektrownia Porąbka-Żar (szczytowo-
pompowa) — 500 MW,

Włocławek (przepływowa) o mocy 160 MW, Solina

(przepływowo-szczytowo-pompowa) — 136 MW, Dychów — 80 MW, Elektrownia
Czorsztyn-Niedzica-

Sromowce Wyżne (przepływowo-szczytowo-pompowa) — 100

MW,

Żydowo (szczytowo-pompowa) —150 MW,. Dla porównania — moc wielkich

elektrowni wodnych na rzekach syberyjskich w Rosji wynosi 5000 MW —Krasnojarsk
na Jeniseju, 4500 MW — Brack na Angarze.

Poza turbinami i prądnicami, stanowiącymi zasadnicze wyposażenie

elektrowni

, jest jeszcze wiele innych urządzeń koniecznych do ich prawidłowej pracy.

Dla podwyższenia napięcia wytwarzanego prądu, niezbędnego do przesyłu na

dalsze odległości, instalowane są transformatory, zwykle w otwartej (odkrytej)

rozdzielni. Wyposażenie pomocnicze obejmuje: zamknięcia na doprowadzeniach i
odprowadzeniach wody (zasuwy lub zawory, zastawki remontowe); kraty i

urządzenia do ich oczyszczania instalowane na wlocie do kanału dopływowego jako
zabezpi

eczenie przed dostaniem się większych zanieczyszczeń, urządzenia

dźwigowe do obsługi maszyn i zasuw, instalację sprężonego powietrza i olejową,

urządzenia kontrolno-pomiarowe oraz do regulacji i sterowania.

1.3. Turbiny wodne

Określenie turbozespół wodny obejmuje całość urządzenia służącego do prze-

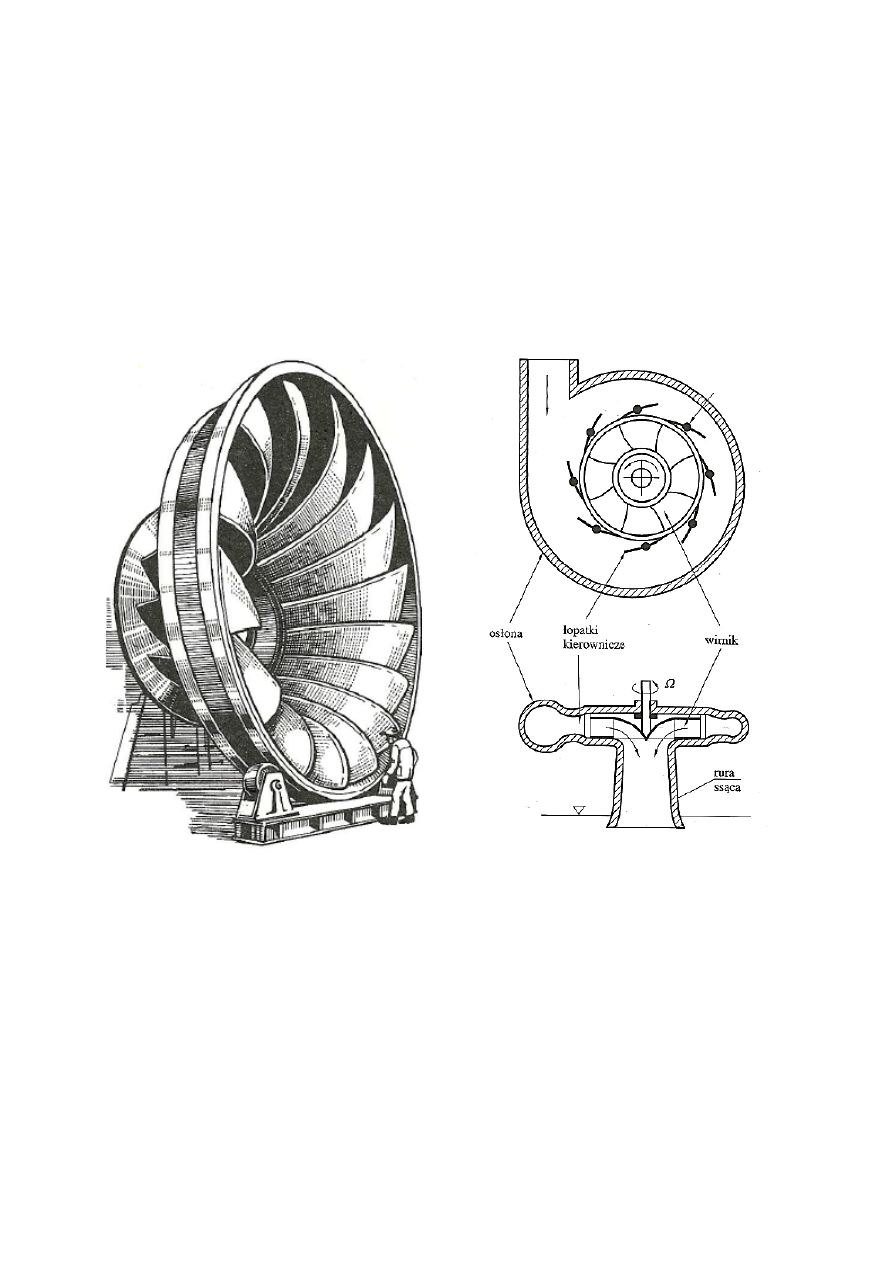
miany energii wody na energię elektryczną. Przedstawiony na rys.4 turbozespół

wodny składa się z dwóch zasadniczych maszyn: turbiny wodnej i bezpośrednio

sprzęgniętej z nią prądnicy (generatora). Przy małych mocach możliwy jest napęd

prądnicy za pośrednictwem przekładni, zwykle zębatej.

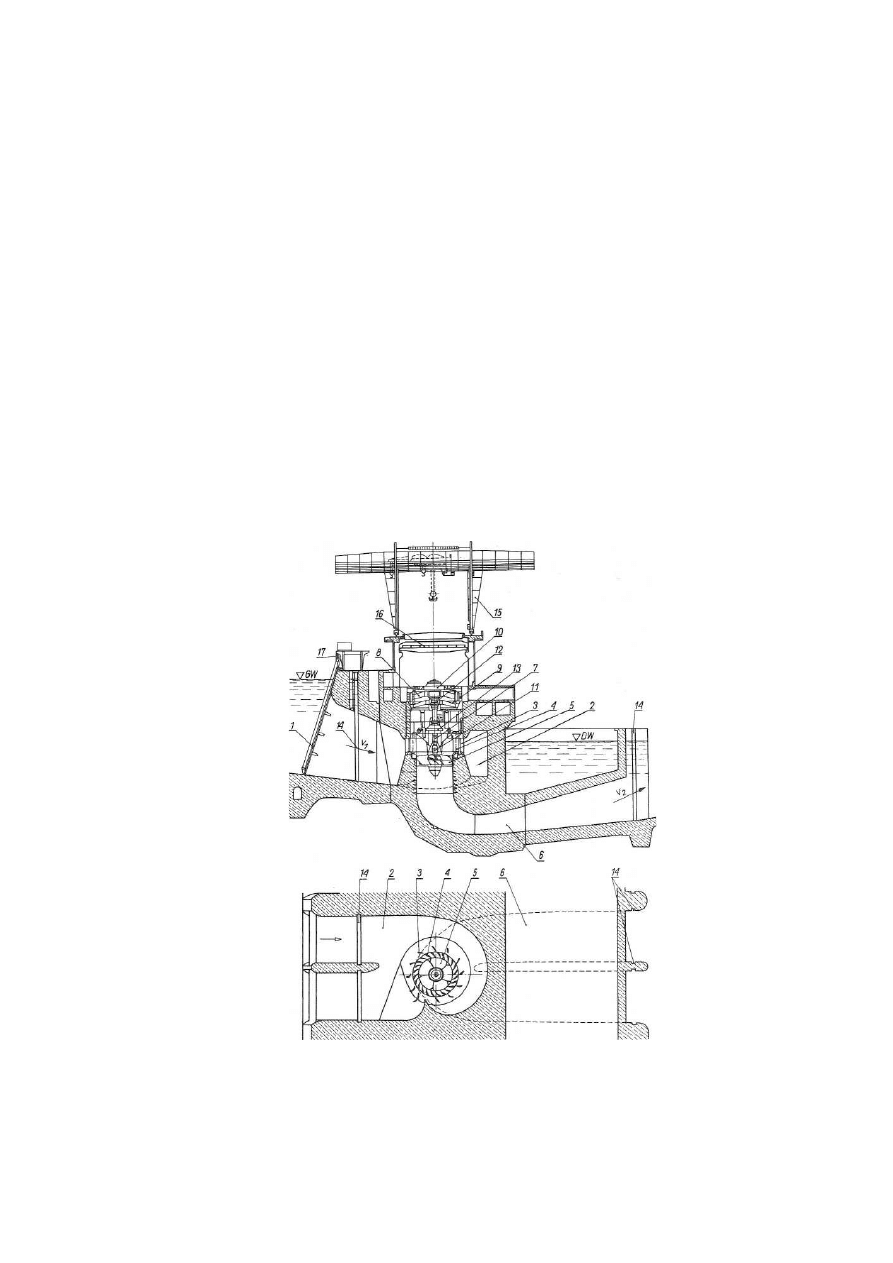
Rys.4.

Turbozespół elektrowni wodnej niskospadowej przepływowej z turbiną Kapłana [4]

1 — kraty wlotowe, 2 — spirala jako komora wlotowa, 3 —

łopatki wsporcze, 4 — aparat

kierowniczy z łopatkami kierowniczymi, 5 — wirnik, 6 — rura ssawna, 7 — wał, 8 — wirnik

generatora, 9 — stojan generatora, 10 — wzbudnica, 11 —

łożysko prowadzące dolne, 12 —

łożysko prowadzące górne, 13 — łożysko wzdłużne (oporowe), 14 — wnęki na zastawki

remontowe, 15 —

główna suwnica montażowa, 16 — suwnice pomocnicze, 17 — maszyna

do czyszczenia krat

Turbina wodna (typu Kaplana) przedstawiona na rys

.4 składa się z

następujących zespołów: właściwej maszyny, stanowiącej konstrukcję mechaniczną,

spirali doprowadzającej wodę do turbiny, rury ssawnej odprowadzającej wodę z

wirnika turbiny oraz układu regulacji. Istnieją też rozwiązania turbin wodnych bez
spirali lub rury ssawnej, w których doprowadzenie i odprowadzenie wody z wirnika

odbywa się w odmienny sposób.

Generator z rys.

4 składa się z następujących zespołów: stojana i wirnika,

ułożyskowania części wirujących, układu wzbudzenia i układu chłodzenia.

W turbozespole woda dopływa przez kraty wlotowe 1, a następnie przechodzi

przez spiralę 2, łopatki wsporcze 3 do aparatu kierowniczego 4 z ruchomymi

łopatkami kierowniczymi, służącymi do regulacji przełyku turbiny. Z kierownicy woda

wpływa do wirnika turbiny 5, przekazując mu swoją energię, i wypływa przez rurę

ssawną 6. Wirnik turbiny przekazuje z kolei energię mechaniczną poprzez wał

turbozespołu 7 na wirnik prądnicy 8. Wirnik turbiny, wał, wirnik prądnicy oraz

ewentualnie osadzony nad nim wirnik wzbudnicy 10, stanowią część wirującą

turbozespołu. Wał turbiny jest ułożyskowany bezpośrednio przy wirniku w łożysku 11

turbiny, stanowiącym dolne łożysko prowadzące. Górne łożysko poprzeczne —

łożysko prądnicy 12 —jest umieszczone pod lub nad prądnicą; niekiedy istnieją dwa

prowadzące łożyska prądnicy umieszczone z obu stron jej wirnika. Napór osiowy,
wyn

ikający z ciężaru części wirującej i naporu hydraulicznego na wirnik turbiny, jest

przejmowany przez łożysko wzdłużne 13, zwane łożyskiem oporowym. Łożysko to

może znajdować się nad prądnicą lub tuż pod nią i wtedy jest często umieszczone
na konstrukcji opartej na pokrywie turbiny.

1.3.1. Parametry pracy turbin wodnych

a)

Moc użyteczna (efektywna) turbiny P

u

– moc mechaniczna na wale turbiny,

możliwa do wykorzystania do produkcji energii elektrycznej, odebrana od

mocy cieku za pomocą organu roboczego (wirnika).

𝑃

𝑢

= 𝑀𝜔

Gdzie: M - moment na wale ,

ω - prędkość kątowa.

b)

Sprawność całkowita turbiny η

t

–

stosunek mocy użytecznej do mocy

hydraulicznej cieku zdefiniowanej w punkcie 1.1.:

𝜂

𝑡

=

𝑃

𝑢

𝑃

ℎ𝑦𝑑

Sprawność całkowita turbiny uwzględnia straty:

•

objętościowe (wolumetryczne), η

v

–

związana z nieszczelnościami i

przepływami ubocznymi,

• hydrauliczne

η

h

–

obejmujące straty energii płynu na skutek zjawisk

przepływowych (straty tarcia, mieszania, oderwania itp.),

• mechaniczne

η

m

–

straty w łożyskach i przekładniach.

Możemy więc wyrazić sprawność całkowitą iloczynem:

𝜂

𝑡

= 𝜂

𝑣

𝜂

ℎ

𝜂

𝑚

c)

Przełyk turbiny Q – odpowiada objętościowemu natężeniu przepływu przez

turbinę i jest równy iloczynowi prędkości w króćcu dolotowym (górnym) i polu

przekroju króćca dolotowego turbiny (odpowiednio dla przewodu

odpływowego/dolnego):

𝑄 = 𝐴

𝑔

𝑣

𝑔

= 𝐴

𝑑

𝑣

𝑑

d)

Prędkość obrotowa n przy współpracy z generatorem synchronicznym –

wynika z prędkości obrotowej generatora synchronicznego i przy

bezpośrednim sprzęgnięciu turbiny z prądnicą o liczbie par biegunów p (przy

częstotliwości sieci 50Hz) wynosi:

𝑛 =

3000

𝑝 𝑜𝑏𝑟/𝑚𝑖𝑛

W przypadku

zastosowania przekładni należy tu jeszcze uwzględnić jej

przełożenie. Prędkość obrotowa jest w trakcie pracy turbin wodnych w

elektrowniach wpiętych do krajowego systemu energetycznego stała.

e)

Wyróżnik szybkobieżności n

sp

jest to wskaźnik porównawczy, wprowadzony

dla porównywania i ułatwienia właściwego doboru różnych typów wirników

turbin wodnych do różnych spadów i mocy, określony jako:

𝑛

𝑠𝑝

= 1,17

𝑛�𝑃

𝑢

�𝐻

𝑠𝑡

5

4

Gdzie:

n – w [obr/min], P

u

– w [kW], H

st

– w [m]

1.3.2. Rodzaje turbin wodnych

Obecnie są stosowane następujące systemy turbin wodnych, nazywane od nazwisk

konstruktorów (podano też orientacyjne zakresy spadów i wyróżników

szybkobieżności):

Rodzaj turbiny

Wysokość spadu H [m] Wyróżnik szybkobieżności n

sp

Peltona

300-2000

2-35

Francisa

25-500

50-450

Deriaza

13-300

250-500

Kaplana

3-80

300-1000

Rys.5.

Kształty wirników turbin wodnych różnych systemów, zależnie od wyróżnika

szybkobieżności: a, b) turbiny Peltona, c, d, e) turbiny Francisa, f, g) turbiny Kaplana

W ramach systemu turbiny występują różne typy, charakteryzujące się wyróżnikiem

szybkobieżności lub też układem turbozespołu. Turbiny poszczególnych systemów

nazywa się szybkobieżnymi, średniobieżnymi i wolnobieżnymi, zależnie od

względnej wartości n

sp

w stosunku do wartości granicznych dla tego systemu turbin.

Kształty wirników turbin różnych systemów w zależności od wyróżnika
sz

ybkobieżności pokazano na rys. 5. Średnice wirników turbin wodnych mogą być

znaczne, dochodzące do kilkunastu metrów, a osiągane moce do kilkuset MW.

a) Turbina Peltona

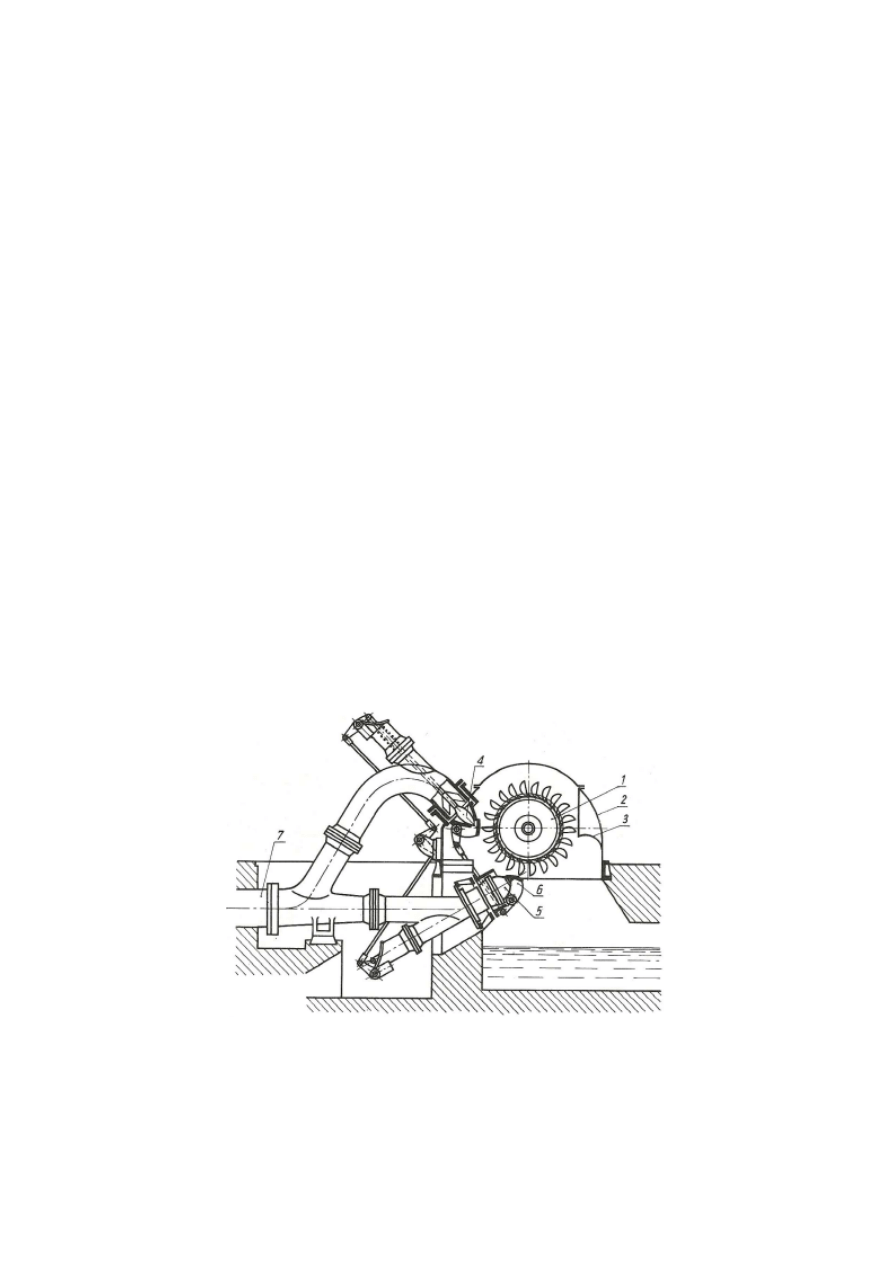
Turbiny Peltona są stosowane na największe spady. Dwudyszową turbinę Peltona
przedstawiono na rys. 6. Woda jest tu doprowadzana do wirnika 1 dwiema dyszami
5,

odgrywającymi rolę wieńca kierowniczego turbiny. Strumień wody wypływający z

każdej z dysz uderza w łopatki wirnika w kształcie czarek (rys.5 a i b). Czarki są

ukształtowane w ten sposób, że rozdzielają strumień na dwie części i jednocześnie

odchylają go w kierunku przeciwnym do kierunku prędkości obwodowej prawie o
180°

(w praktyce około 165°). Dzięki temu energia kinetyczna strugi jest

przekazywana wirnikowi. Turbina może mieć jedną lub szereg dysz (w przykładzie

dwie). Po spłynięciu z czarki woda opada grawitacyjnie w komorze wirnika i jest

odprowadzana do wody dolnej. Strumień objętości wody, a więc i moc turbiny,

można regulować w sposób ciągły, przesuwając osiowo iglicę 4, co zmienia przekrój

wylotowy dyszy z możliwością całkowitego jej zamknięcia. Odchylacz strumienia 6

umożliwia szybkie przerwanie działania strumienia wody na wirnik przez odchylenie

go od wirnika. Turbina Peltona jest rzadkim obecnie przykładem turbiny czysto

akcyjnej, w której zwiększenie prędkości czynnika ma miejsce tylko w wieńcu

kierowniczym, natomiast w wirniku następuje zmiana krętu wyłącznie przez

odchylenie strumienia. Pozostałe systemy turbin wodnych dotyczą turbin
reakcyjnych.

Rys. 6. Dwudyszowa turbina Peltona

1— wirnik, 2 — obudowa wirnika, 3 — zbieracz wody, 4 — iglica, J — dysza, 6 — odchylacz

strumienia, 7 —

rurociąg zasilający

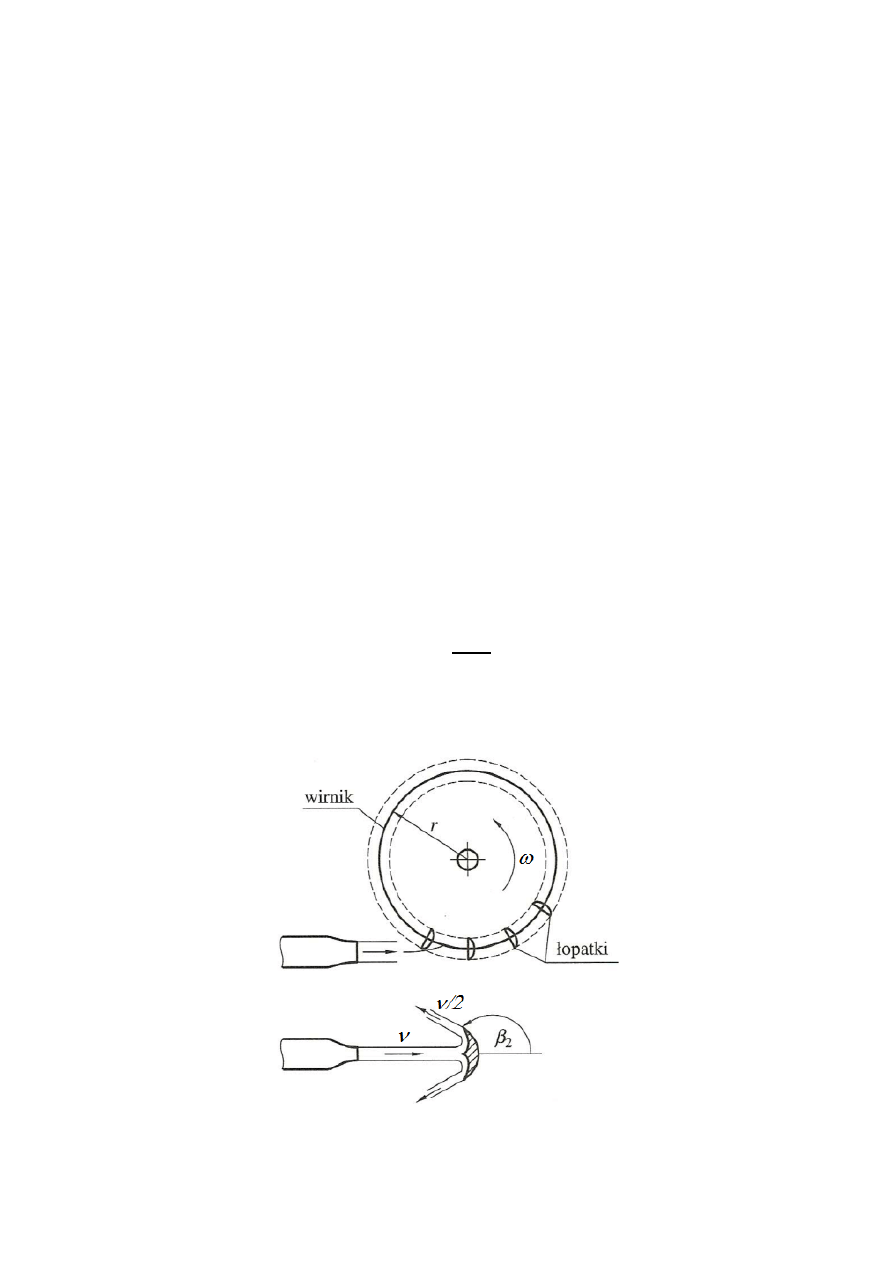
Teoretyczna analiza osiągów turbiny Peltona

Turbina Peltona

należy do grupy maszyn przepływowych oopierających swoją

zasadę działania o zmianę krętu czynnika roboczego. Struga rozpędzona w dyszy

opływa łopatki specjalnie oprofilowane i zamocowane na obwodzie koła. Na

łopatkach struga rozdziela się na dwie, które odwracają swój bieg o kąt β

2

~165°.

Dzięki temu struga wytraca prawie całą energię kinetyczną i grawitacyjnie spływa do

kanału. Reakcja dynamiczna strugi wytwarza moment obrotowy na wale obliczany z

zasady zachowania krętu:

� 𝑀𝑑𝜏

2

1

= � 𝑑𝐾

2

1

Analizując sytuację przedstawioną na rysunku 7, po prostych podstawieniach i

przekształceniach matematycznych dostajemy ostateczny wzór na moment
teoretyczny na wale:

𝑀 = 𝜌𝑄𝑟(𝑣 − 𝑢)(1 − 𝑐𝑜𝑠𝛽

2

)

Moc teoretyczna wynosi:

𝑁 = 𝑀𝜔

Gdzie: v —

prędkość bezwzględna strugi na wylocie z dyszy, u=ωr — prędkość

obwodowa na promieniu r;

ω

jest prędkością kątową wirnika. Maksimum mocy

występuje, gdy u = v/2. Prędkość bezwzględna zależy od rozporządzalnej różnicy
poziomów H (wzór Torricellego):

𝑣 = 𝜑�2𝑔𝐻

Gdzie: Współczynnik kontrakcji φ=0,92 - 0,98.

Rys.7.

Zasada działania turbiny Peltona

b) Turbina Francisa

W turbinie reakcyjnej Francisa (rys.8.a.)

struga wody wypływa z łopatek

kierowniczych, gdzie uzyskuje znaczny kręt względem osi obrotu, i wpływa do

kanałów międzyłopatkowych na obwodzie wirnika (rys. 8.b.). W obrębie wirnika kręt

(i prędkość styczna) ulega redukcji, co ma swój równoważnik dynamiczny w
momencie obrotowym i

w mocy, przekazywanej do generatora. Wypływ z wirnika

odbywa się promieniowo i przy nadciśnieniu. Dopiero w rurze ssawnej ciśnienie
wzrasta do atmosferycznego, kosztem energii kinetycznej.

a)

b)

Rys. 8. Turbina Fracisa a) widok wirnika turbiny, b) schemat ideowy

Zaletom turbin Fracisa ( i jej modyfikacji tj. turbiny Derioza) jest jej odwracalne
działanie, co determinuje ich przeznaczenie do elektrowni szczytowo-pompowych. W

szczycie energetycznym pracują jako turbiny - oddając moc do systemu

elektroenergetycznego, a poza szczytem pracują jako pompy obciążając system.,
celem jego regulacji.

Teoretyczna analiza osiągów turbiny Fracisa

Na rysunku 9 przedstawiono analizę kinematyki przepływu wody przez turbinę

Fracisa. Turbina ta należy do maszyn przepływowych krętnych, więc o przyroście

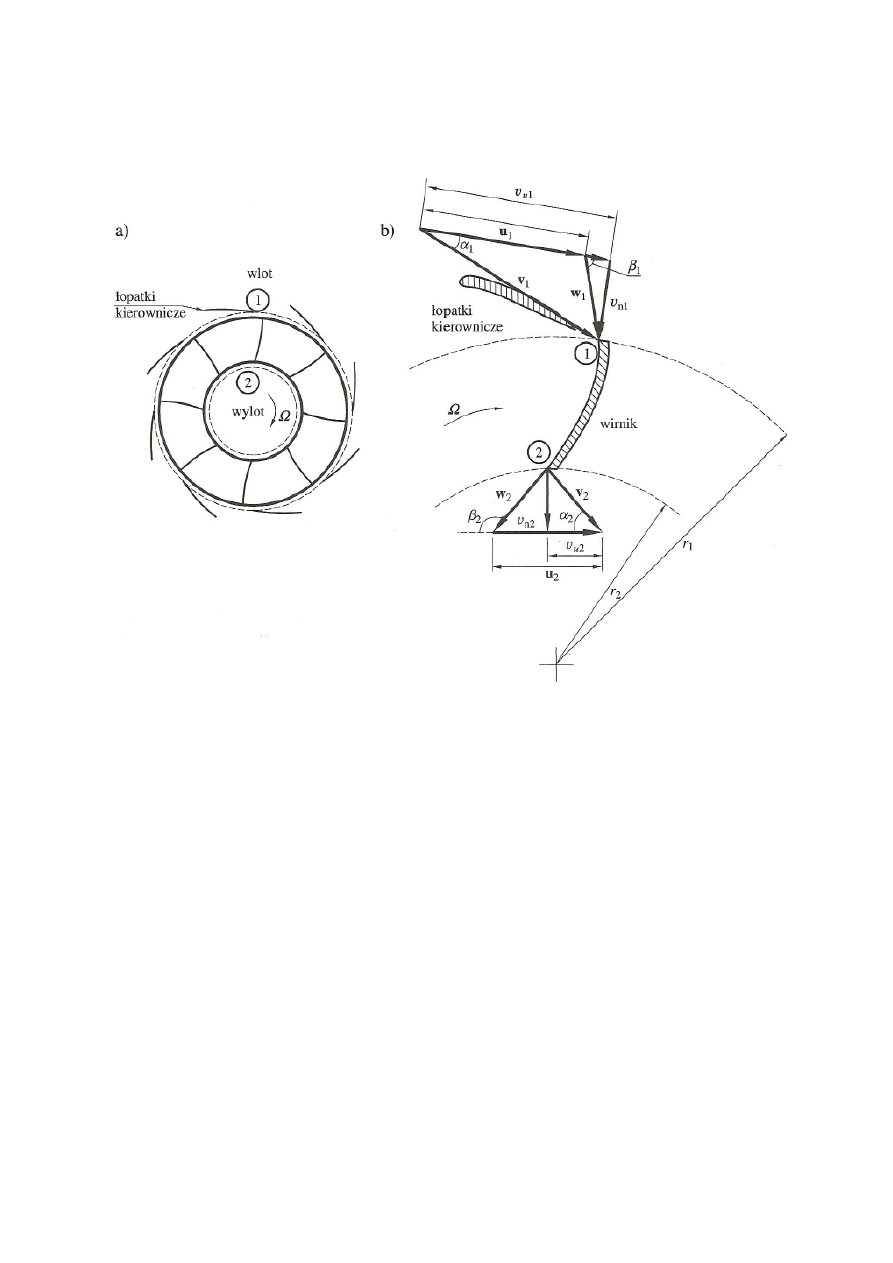
energii na wale maszyny decyduje zmiana

krętu czynnika w wirniku i kierownicach

maszyny.

Rys. 9.

Analiza przepływu przez turbinę Fracisa a)schemat ideowy kierownic i wirnika, b)

kinematyka przepływu

Zgodnie z zasadą zachowania krętu możemy zapisać zależność na moment

generowany przez płyn na wale wirnika:

� 𝑀𝑑𝜏

2

1

= � 𝑑𝐾

2

1

i podzieleniu przez

Δt otrzymujemy:

𝑀 = 𝐾̇

1

− 𝐾̇

2

= 𝑚̇ ∙ 𝑣

1

∙ 𝑙

1

− 𝑚̇ ∙ 𝑣

2

∙ 𝑙

2

= 𝑚̇ ∙ (𝑣

1

∙ 𝑙

1

− 𝑣

2

∙ 𝑙

2

)

gdzie:

𝑀 - moment obrotowy,

𝐾̇

2

-

strumień krętu czynnika u wylotu,

𝐾̇

1

-

strumień krętu czynnika u wlotu,

𝑚̇ - strumień masy,

𝑣

2

, 𝑣

1

-

prędkość gazu u wylotu i wlotu wirnika,

𝑙

2,

𝑙

1

-

odległość prędkości od osi wirnika (normalna do kierunku działania

prędkości).

Z relacji

trygonometrycznych przedstawionych na rysunku 9 wynikają następujące

zależności:

𝑙

2

= 𝑟

2

∙ 𝑐𝑜𝑠 𝛼

2

, 𝑙

1

= 𝑟

1

∙ 𝑐𝑜𝑠 𝛼

1

Po podstawienia do równania na moment otrzymujemy:

𝑀 = 𝑚̇ ∙ (𝑣

1

∙ 𝑟

1

∙ 𝑐𝑜𝑠 𝛼

1

− 𝑣

2

∙ 𝑟

2

∙ 𝑐𝑜𝑠 𝛼

2

) .

Z trójkątów prędkości na wlocie i wylocie do wirnika wynika, że:

𝑣

2𝑢

= 𝑣

2

∙ 𝑐𝑜𝑠𝛼

2

, 𝑣

1𝑢

= 𝑣

1

∙ 𝑐𝑜𝑠 𝛼

1

i dalej:

𝑀 = 𝑚̇ ∙ (𝑣

1𝑢

∙ 𝑟

1

−𝑣

2𝑢

∙ 𝑟

2

) .

Chcąc przejść na wymiar mocy mnożymy obydwie strony równania przez prędkość
obrotową ω:

𝑁

𝑢𝑡∞

= 𝑀 ∙ 𝜔 = 𝑚̇ ∙ 𝜔(𝑣

1𝑢

∙ 𝑟

1

−𝑣

2𝑢

∙ 𝑟

2

) = 𝑚̇ ∙ (𝑣

1𝑢

∙ 𝑢

1

− 𝑣

2𝑢

∙ 𝑢

2

),

bowiem

𝑢

2

= 𝑟

2

∙ 𝜔, 𝑢

1

= 𝑟

1

∙ 𝜔

Moc

dostarczoną na wał turbiny wyrazić możemy iloczynem strumienia masy i pracy

jednostkowej:

𝑁

𝑢𝑡∞

= 𝑚̇ ∙ 𝑙

𝑢𝑡∞

,

z czego wynika, że praca jednostkowa jest rówan:

𝑙

𝑢𝑡∞

= 𝑣

1𝑢

∙ 𝑢

1

− 𝑣

2𝑢

∙ 𝑢

2

Jest to pierwsza, podstawowa postać równania maszyn przepływowych, zwana

również równaniem Eulera. Poszczególne indeksy mówią, że jest to jednostkowa
praca użyteczna, teoretyczna dla nieskończonej liczby łopatek. W wirniku
rzeczywistym występuje skończona ilość łopatek. Fakt ten uwzględnia się za pomocą
sprawności hydraulicznej (przepływowej) turbiny:

𝜂

ℎ

=

𝑁

𝑢𝑡∞

𝜌𝑔𝑄𝐻

𝑇

Gdzie:

𝐻

𝑇

–

spadek wysokości ciśnienia hydraulicznego w turbinie (kierownice +

wirnik) .

P

rzenalizujmy wpływ ustawienia kierownic na prędkość obrotową wirnika przy

zmiennym przełyku turbiny:

Na wlocie prędkość bezwzględna ma składową styczną do kierunku obwodowego
𝑣

1𝑢

i normalną (promieniową ) 𝑣

1𝑛

. Wektor prędkości bezwzględnej odchylony jest od

kierunku obwodowego zgodnie z kątem ustawienia kierownic tj. kątem 𝛼

1

, zatem:

𝑣

1𝑢

= 𝑣

1𝑛

𝑐𝑡𝑔 ∝

1

Z trójkąt prędkości wynika, że:

𝑣

1𝑢

= 𝑢

1

+ 𝑣

1𝑛

𝑐𝑡𝑔𝛽

1

.

Prędkość promieniową możemy wyrazić przez przepustowość (przełyk) Q oraz pole
przekroju wlotowego wirnika:

𝑣

1𝑛

=

𝑄

2𝜋𝑟

1

𝑏

1

Ostatecznie:

𝑣

1𝑛

𝑐𝑡𝑔 ∝

1

= 𝑢

1

+ 𝑣

1𝑛

𝑐𝑡𝑔𝛽

1

𝑐𝑡𝑔 ∝

1

=

𝑢

1

𝑣

1𝑛

+ 𝑐𝑡𝑔𝛽

1

𝑐𝑡𝑔 ∝

1

=

𝜔𝑟

1

𝑣

1𝑛

+ 𝑐𝑡𝑔𝛽

1

𝑐𝑡𝑔 ∝

1

=

𝜔2𝜋𝑟

1

2

𝑏

1

𝑄

+ 𝑐𝑡𝑔𝛽

1

∝

1

= 𝑎𝑟𝑐𝑐𝑡𝑔 �

𝜔2𝜋𝑟

1

2

𝑏

1

𝑄

+ 𝑐𝑡𝑔𝛽

1

�

Ostatni wyrażenie jest algorytmem regulacji kąta ustawienia łopatek przy zmiennym

przełyku turbiny. Daje możliwość kontroli prędkości obrotowej wału turbiny, poprzez

zmianę krętu czynnika wlotowego. W przypadku pracy turbiny w systemie
elektroenergetyc

znym. Utrzymanie stałej prędkości obrotowej wału turbiny jest

konieczne do synchronizacji generatora z siecią.

2. Instrukcja – Turbina Peltona

2.1.

Cel ćwiczenia

Celem ćwiczenia jest zbadanie podstawowych wielkości charakteryzujących

pracę turbiny Peltona oraz ich związków z osiągami turbiny.

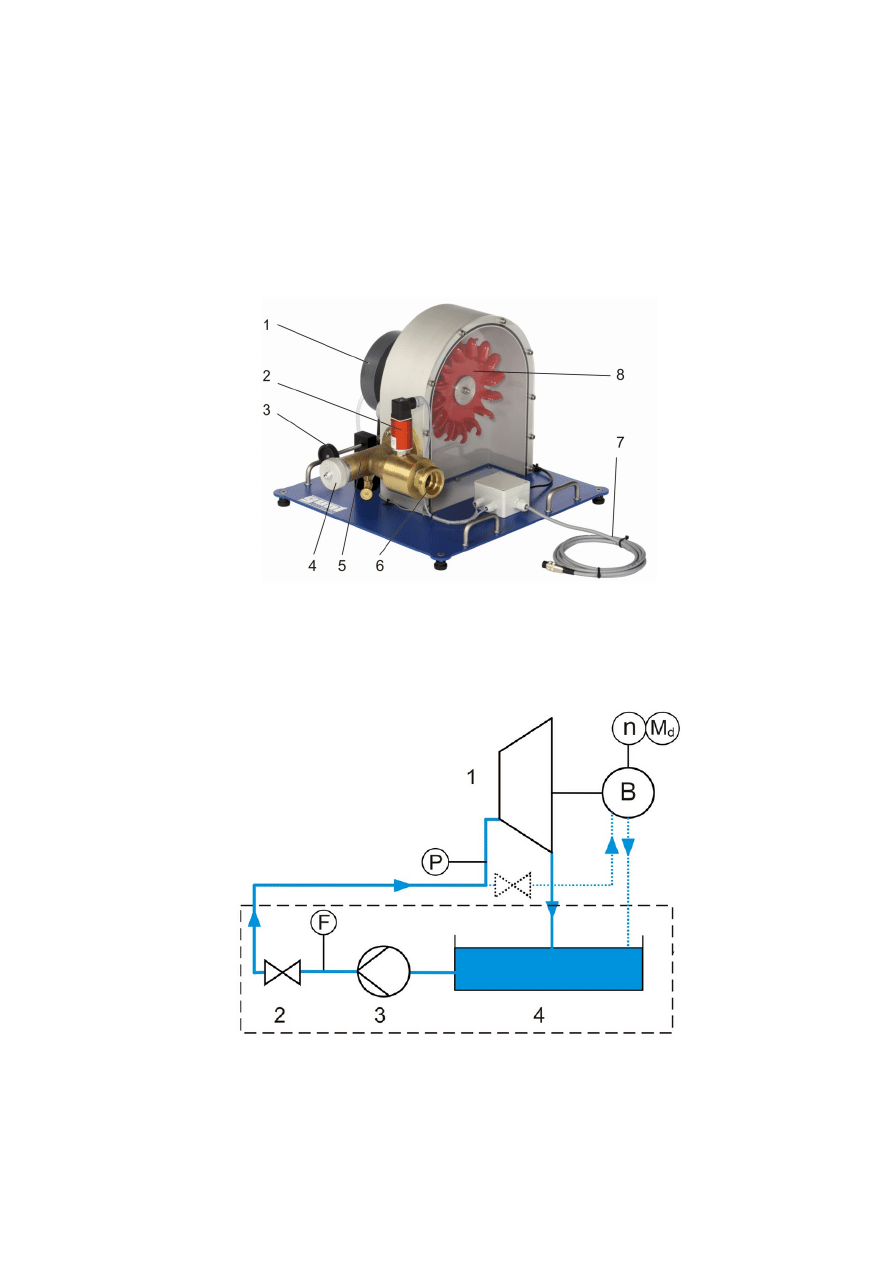
2.2.

Obiekt badań i schemat stanowiska pomiarowego

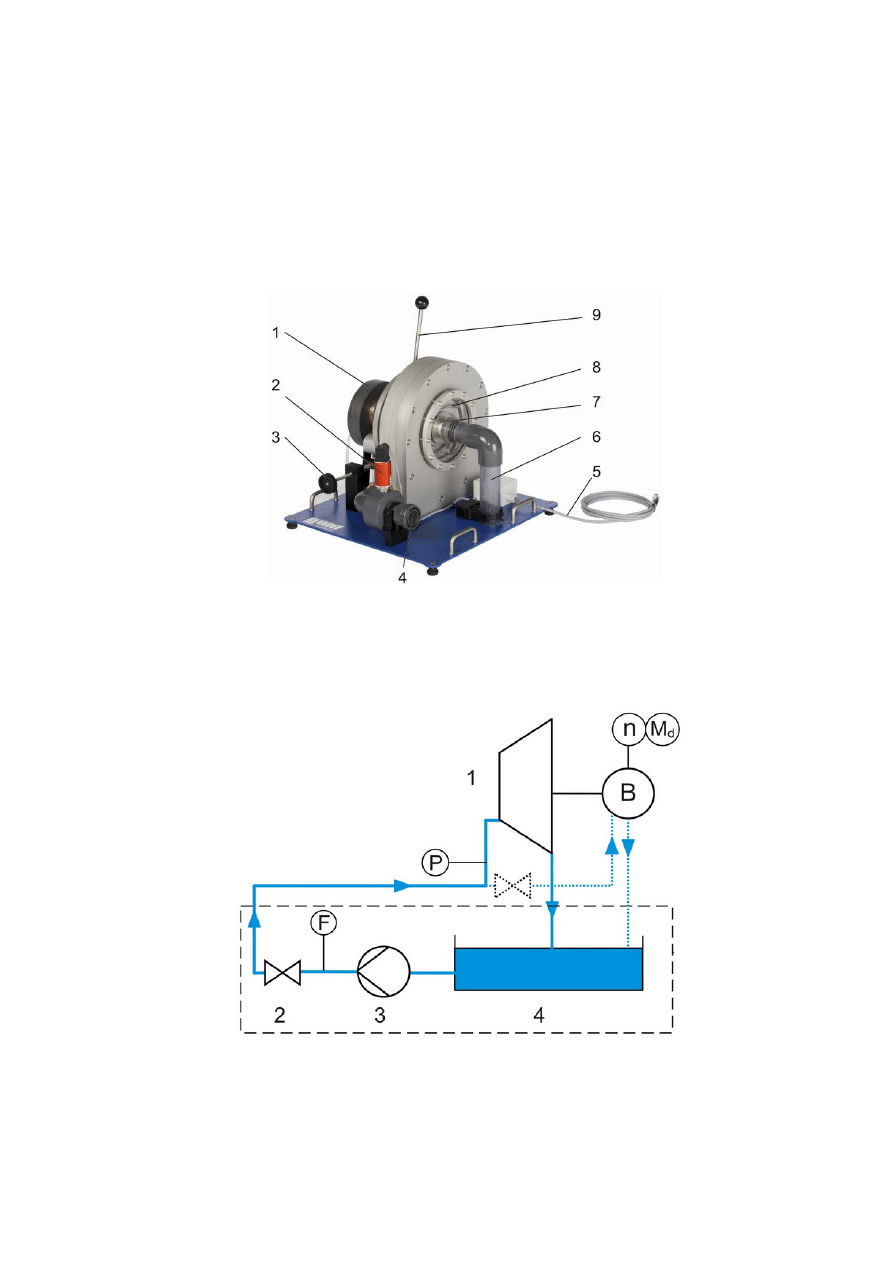
Rys.8. Turbina Peltona zamontowana w Laboratorium KMCiP (1-

koło pasowe, 2 -

czujnik ciśnienia hydrostatycznego wody, 3-ręczna regulacja obciążenia

(opcjonalnie), 4-regulacja

przymknięcia dyszy natryskowej, 5-dysza, 6-króciec

przyłączeniowy, 7-przewód sygnału z przetwornika ciśnienia.

Rys.9. Schemat ideowy stanowiska (1-turbina, 2 –zawór regulacyjno-

odcinający, 3-

pompa wytwarzająca wysokość dyspozycyjną, 4-zbiornik wody, B-układ hamujący (n-

pomiar obrotów, M

d

-pomiar momentu na wale , F - pomiar temperatury wody, P-

pomiar ciśnienia hydrostatycznego wody.

2.3.

Przebieg ćwiczenia – pomiary

2.3.1. Wyznaczanie kompletu charakterystyk wymiarowych turbiny Peltona

Zadaniem jest wyznaczenie charakterystyk turbiny Peltona

jako zależności

mocy użytecznej, sprawności całkowitej, momentu, przełyku i mocy hydraulicznej od

obrotów turbiny. Należy wyznaczyć pięć charakterystyk dla różnych ustawień dyszy
natryskowej (dane ustawienie odpowiada wybranemu spadowi hydrostatycznemu).

Ustaw. Dyszy / Spad

[m]

………….

Nr

pomiaru

Przełyk

𝑄 [𝑙

⁄ 𝑚𝑖𝑛]

Moment

na wale

[Nm]

Moc

użyteczna

𝑃

𝑢

[𝑊]

Moc

hydrauliczna

𝑃

ℎ𝑦𝑑

[𝑊]

Sprawność

całkowita

𝜂

𝑡

Obroty

n

[1/min]

1.

………….

………….

………….

………….

………….

2.

………….

………….

………….

………….

………….

…

2.4. Opracowanie wyników

Grupa ćwiczeniowa dostaje wyniki w formie danych cyfrowych celem

zaimportowania do programu umożliwiającego ich dalszą obróbkę np. MS Excel,
Matlab.

Opracowanie graficzne powinno zawierać:

a. Porównanie na jednym wykresie wyników pomiarów z punktu 2.3.1.

ujętych w formie charakterystyk celem pokazania wpływu zmiany

wysokości dyspozycyjnej na ich kształt i przebieg.

o

Wykres 1:

𝜂

𝑡

= 𝑓(𝑛 ) dla wszystkich badanych spadów,

o

Wykres 2:

𝑀, 𝑃

ℎ𝑦𝑑

, 𝑃

𝑢

= 𝑓(𝑛 ) dla wszystkich badanych spadów

b.

Wykreślenie na jednym wykresie zależności maksymalnej możliwej

sprawności całkowitej i maksymalnej możliwej mocy użytecznej od

wysokości dyspozycyjnej (spadu) tj. 𝑃

𝑢𝑚𝑎𝑥

, 𝜂

𝑡𝑚𝑎𝑥

= 𝑓(𝐻 ). Wielkości te

ustalić na podstawie charakterystyk z punktu 2.4.a.

c.

Wykreślenie na jednym wykresie zależności maksymalnej możliwej

sprawności całkowitej i maksymalnej możliwej mocy użytecznej od

wyróżnika szybkobieżności turbiny tj. 𝑃

𝑢𝑚𝑎𝑥

, 𝜂

𝑡𝑚𝑎𝑥

= 𝑓(𝑛

𝑠𝑝

) (definicja

wyróżnika w punkcie 1.3.e – pamiętać o odpowiednim przeliczeniu

jednostek do wyróżnika). Wielkości te ustalić na podstawie
charakterystyk z punktu 2.4.a.

2.5. Sprawozdanie

Sprawozdanie wykonane odręcznie bądź komputerowo w grupach 3 osobowych,

powinno zawierać:

•

Tabelę informacyjną (zgodnie z załącznikiem do instrukcji),

•

Cel ćwiczenia,

• Schemat stanowiska pomiarowego,

• Opracowanie wyników pomiarów zgodnie z wytycznymi punktem 2.4,

•

Wnioski wynikające z przeprowadzonego ćwiczenia (interpretacja wykresów
z

punktu 2.4, własne uwagi i spostrzeżenia)

3. Instrukcja – Turbina Francisa

3.1.

Cel ćwiczenia

Celem ćwiczenia jest zbadanie podstawowych wielkości charakteryzujących

pracę turbiny Francisa oraz ich związków z osiągami turbiny.

3.2.

Obiekt badań i schemat stanowiska pomiarowego

Rys.8. Turbina Francisa zamontowana w Laboratorium KMCiP (1-

koło pasowe, 2 -

czujnik ciśnienia hydrostatycznego wody, 3-ręczna regulacja obciążenia

(opcjonalnie), 4-

króciec przyłączeniowy, 5-przewód sygnału z przetwornika ciśnienia,

6-przewód wylotowy, 7-wirnik turbiny, 8-kierownice, 9-

regulacja kąta ustawienia

kierownic.

Rys.9. Schemat ideowy stanowiska (1-turbina, 2 –zawór regulacyjno-

odcinający, 3-

pompa wytwarzająca wysokość dyspozycyjną, 4-zbiornik wody, B-układ hamujący (n-

pomiar obrotów, M

d

-pomiar momentu na wale , F - pomiar temperatury wody, P-

pomiar ciśnienia hydrostatycznego wody.

3.3.

Przebieg ćwiczenia – pomiary

3.3.1. Wyznaczanie kompletu charakterystyk wymiarowych turbiny Francisa

Zadaniem jest wyznaczenie charakterystyk turbiny Francisa

jako zależności

mocy użytecznej, sprawności całkowitej, momentu, przełyku i mocy hydraulicznej od

obrotów turbiny. Należy wyznaczyć komplet charakterystyk przepływowych dla

różnych ustawień kąta kierownic.

Ustawienie

kierownic

………….

Nr

pomiaru

Przełyk

𝑄 [𝑙

⁄ 𝑚𝑖𝑛]

Moment

na wale

[Nm]

Moc

użyteczna

𝑃

𝑢

[𝑊]

Moc

hydrauliczna

𝑃

ℎ𝑦𝑑

[𝑊]

Sprawność

całkowita

𝜂

𝑡

Obroty

n

[1/min]

1.

…………. …………. ………….

………….

………….

………….

2.

…………. …………. ………….

………….

………….

………….

…

3.3.2. Wyznaczenie krzywej regulacji turbiny Francisa

Zadaniem jest wyznaczeniem zależności mocy użytecznej, sprawności

całkowitej, momentu, przełyku i mocy hydraulicznej od kąta ustawienia kierownic

turbiny Francisa dla dwóch różnych prędkości obrotowych wirnika.

Prędkość obrotowa

[1/min]

………….

Nr

pomiaru

Przełyk

𝑄 [𝑙

⁄ 𝑚𝑖𝑛]

Moment

na wale

[Nm]

Moc

użyteczna

𝑃

𝑢

[𝑊]

Moc

hydrauliczna

𝑃

ℎ𝑦𝑑

[𝑊]

Sprawność

całkowita

𝜂

𝑡

Ustawienie

kierownic

α [-]

1.

…………. …………. …………. ………….

………….

………….

2.

…………. …………. …………. ………….

………….

………….

…

3.4. Opracowanie wyników

Opracowanie graficzne powinno zawierać:

a) Porównanie na jednym wykresie wyników pomiarów z punktu 3.3.1.

ujętych w formie charakterystyk celem pokazania wpływu zmiany kąta
ustawienia kierownic na ich

kształt i przebieg.

• Wykres 1: 𝜂

𝑡

= 𝑓(𝑛 ) dla wszystkich badanych ustawień,

• Wykres 2: 𝑀, 𝑃

ℎ𝑦𝑑

, 𝑃

𝑢

= 𝑓(𝑛 ) dla wszystkich badanych ustawień,

• Wykres 3: 𝐻

𝑢

= 𝑓(𝑛 ) dla wszystkich badanych ustawień,

b) Porównanie na jednym wykresie wyników pomiarów z punktu 3.3.2.

ujętych w formie charakterystyk celem pokazania wpływu prędkości

obrotowej wirnika na ich kształt i przebieg.

a. Wykres 1:

𝜂

𝑡

= 𝑓(𝛼 ) dla wszystkich badanych prędkości

wirnika,

b. Wykres 2:

𝑀, 𝑃

ℎ𝑦𝑑

, 𝑃

𝑢

= 𝑓(𝛼 ) dla wszystkich badanych prędkości

wirnika,

3.5. Sprawozdanie

Sprawozdanie wykonane odręcznie bądź komputerowo w grupach 3 osobowych,

powinno zawierać:

•

Tabelę informacyjną (zgodnie z załącznikiem do instrukcji),

•

Cel ćwiczenia,

• Schemat stanowiska pomiarowego,

• Opracowanie wyników pomiarów zgodnie z wytycznymi punktem 3.4,

•

Wnioski wynikające z przeprowadzonego ćwiczenia (interpretacja wykresów
z punktu 3

.4, własne uwagi i spostrzeżenia)