Monika Cichoń

PLAN PRACY

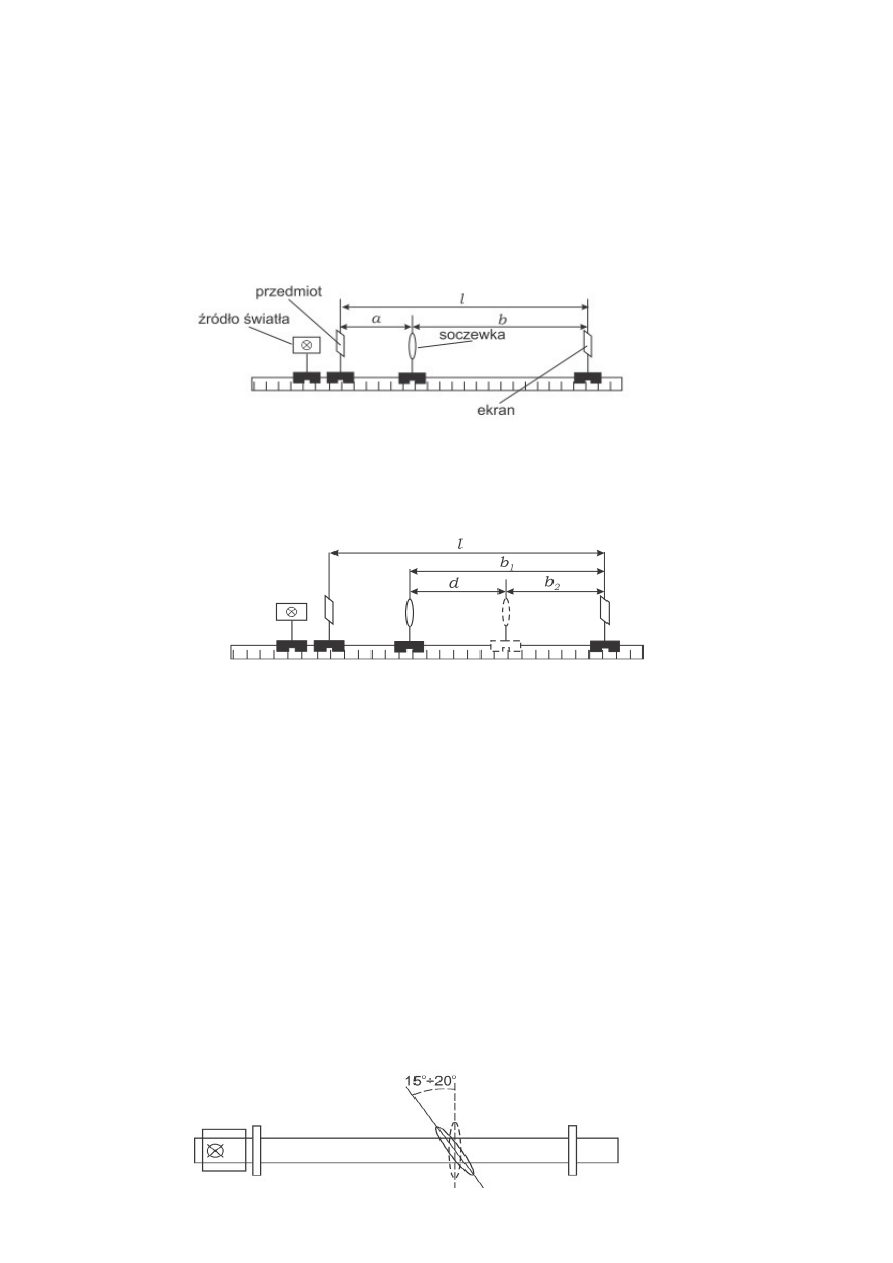
1. Wyznaczyć ogniskową soczewki skupiającej za pomocą metody wykorzystującej równania soczewki

•

zmierzyć odległość między przedmiotem a ekranem

•

wielokrotnie odczytać położenie soczewki, dla którego obserwuje się ostry powiększony obraz

•

powtórzyć pomiar obracając soczewkę o 180

0

•

wykonać analogiczne pomiary dla innych odległości przedmiotu od ekranu

2. Wyznaczyć ogniskową dla tej samej soczewki metodą Bessela

•

zmierzyć odległość między przedmiotem a ekranem

•

wielokrotnie odczytać położenie soczewki, dla którego obserwuje się ostry powiększony obraz
(pomniejszony i powiększony)

•

wykonać analogiczne pomiary dla innych odległości przedmiotu od ekranu

3. Wyznaczyć ogniskową soczewki rozpraszającej

•

zmierzyć ogniskową układu dwóch soczewek – soczewki rozpraszającej i skupiającej o znanej ogniskowej
(układ daje rzeczywisty obraz przedmiotu) za pomocą metody Bessela

4.Badanie aberracji sferycznej

•

zamontować na soczewce przesłony do badania aberracji sferycznej

•

wyznaczyć metoda Bessela ogniskową dla promieni przyosiowych, pośrednich i brzegowych

5.Badanie aberracji chromatycznej

•

wyznaczyć ogniskową soczewki metodą Bessela dla światła czerwonego, niebieskiego i zielonego
umieszczając odpowiedni filtr pomiędzy źródłem światła a przedmiotem

6. Badanie astygmatyzmu

•

soczewkę umieścić na statywie zaopatrzonym w podziałkę kątową

•

odnaleźć położenie soczewki, w którym na ekranie obserwowanym jest ostry powiększony obraz
przedmiotu a płaszczyzna główna soczewki jest prostopadła do wiązki światła

•

obrócić soczewkę o 15-20

0

, tak aby w obrazie przedmiotu widoczne były tylko linie poziome lub pionowe

•

odczytać wielokrotnie położenie soczewki dla obu wymienionych przypadków

Monika Cichoń

WSTĘP TEORETYCZNY

1.Soczewka

Soczewka jest to przedmiot optyczny zbudowany z przezroczystego materiału, ograniczony z dwóch stron
powierzchniami sferycznymi. Soczewki dzielimy na:

−

skupiające

−

rozpraszające

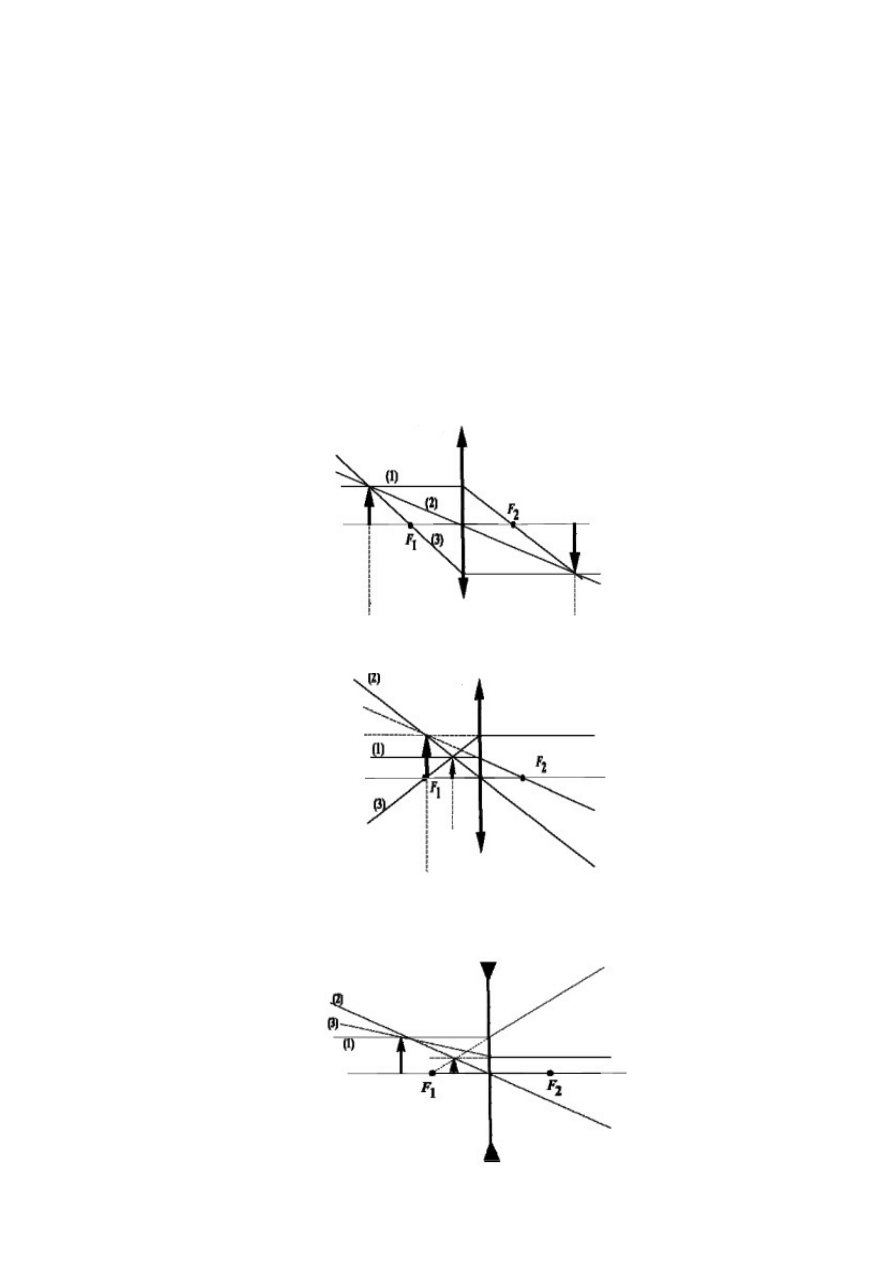
2.Obrazy powstające w soczewce

Rodzaj obrazu powstającego w soczewce soczewce zależy od rodzaju soczewki oraz odległości w jakiej jest
ustawiony przedmiot w stosunku do głównej osi optycznej soczewki.

•

Obraz powstający w soczewce skupiającej jeżeli przedmiot leży w odległości >f i <2f od głównej osi
optycznej soczewki

obraz jest:
- rzeczywisty
- powiększony
- odwrócony

•

Obraz powstający w soczewce skupiającej jeżeli przedmiot leży w odległości <2f od głównej osi
optycznej soczewki

obraz jest:
- prosty
- pozorny
- powiększony

•

Obraz powstający w soczewce rozpraszającej jeżeli przedmiot leży w odległości > f od głównej osi
optycznej soczewki

obraz jest:

- prosty
- pozorny
- pomniejszony

Monika Cichoń

3. Ogniskowa soczewki

Jeżeli do soczewki dociera wiązka promieni równoległych to promienie bliskie osi optycznej soczewki padające na
nią pod kątem prostym przechodzą przez jeden wspólny punkt F. Punkt ten nazywamy ogniskiem soczewki, a jego
odległość f od płaszczyzny środkowej soczewki nazywamy ogniskową soczewki.
Soczewki skupiające posiadają ognisko rzeczywiste a rozpraszające ognisko pozorne powstające w miejscu
przecięcia się przedłużeń promieni załamanych.

4. Metody wyznaczania ogniskowej soczewki

Istnieją dwie metody wyznaczania ogniskowej soczewki:

•

w oparciu o równanie soczewki – jest to metoda oparta na zależności odległości przedmiotu od soczewki
– a i odległości obrazu od soczewki – b od ogniskowej f. Zależność tą przedstawia wzór:

1
a



1
b

=

1

f

•

metodą Bessela – jest to metoda, w której szukamy dwóch ostrych obrazów przedmiotu – powiększonego
(b

1

) i pomniejszonego (b

2

). Odległości między ekranem a soczewką, przy których obserwowany jest ostry

obraz można wyznaczyć z równania:

1

l −b



l

b

=

1

f

l - ustalona odległość między przedmiotem

a ekranem

Metoda Bessela jest uznawana za lepszą metodę pomiarową, ponieważ wykorzystuje ona pomiary względne, nie
wymagające znajomości dokładnego położenia płaszczyzn głównych soczewki.

5. Wady soczewek

Do wad soczewek zaliczamy:

•

aberrację sferyczną – występuje w przypadku, gdy wiązka światła padająca na soczewkę jest zbyt
szeroka. Promienie przyosiowe załamują się wtedy inaczej niż promienie brzegowe. W efekcie zamiast
pojedynczego punktu, w którym skupiają się wszystkie promienie wzdłuż osi pojawia się rozmyty obszar.
Miarą tego zjawiska jest różnica ogniskowych promieni przyosiowych i brzegowych.

•

aberracja chromatyczna – wywołana jest przez zjawisko dyspersji światła polegającego na zależności
współczynnika załamania światła n od długości fali. W efekcie światło różnej barwy, a więc o różnej
długości fali załamuje się pod różnym kątem.

•

astygmatyzm – wada spowodowana zróżnicowaniem warunków geometrycznych powierzchni soczewki.
Obraz powstający po przejściu wiązki promieni przez taką soczewkę jest rozmyty i nieostry.

Monika Cichoń

OPIS DOŚWIADCZENIA

1.Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie ogniskowych soczewek skupiających i rozpraszających za pomocą dwóch
metod: w oparciu o równanie soczewki i metodą Bessla oraz badanie wad soczewek: aberracji sferycznej i
chromatycznej, astygmatyzmu. W doświadczeniu wyznaczane będą także niepewności jakimi obarczone są
mierzone wielkości.

2. Układ doświadczalny

W trakcie badań wykorzystywano następujące przyrządy:

–

ława optyczna

–

źródło światła

–

soczewka skupiająca: +8 D

–

soczewka rozpraszająca: -2 D

–

ekran

–

przedmiot: litera na matówce, kratka na matówce

–

filtry optyczne: czerwony, niebieski, zielony

OPRACOWANIE WYNIKÓW

1. Wyznaczanie ogniskowej soczewki skupiającej – metoda równania soczewki

Wyniki pomiarów zebrano w tabeli

położenie

przedmiotu x [cm]

położenie ekranu y

[cm]

położenie soczewki s

1

-

obraz ostry, powiększony

[cm]

położenie soczewki s

2

–

po odwróceniu o 180

0

[cm]

18.9

82.5

35.8

38.2

35.9

38.4

35.4

38.3

35.6

38.1

35.7

38.5

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 82.5 – 18.9 = 63.6 [cm]

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

35.8 35.935.435.635.7

5

= 35.68 [cm]

s

2

=

38.238.4 38.338.138.5

5

= 38.30 [cm]

Monika Cichoń

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

1

dla 5

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.776

s

s

1

=

2.776



0.01440.00160.07840.00640.0004

20

= 0.1967 ~ 0.20 [cm]

s

s

2

=

2.776



0.010.0100.040.04

20

= 0.1955 ~ 0.20 [cm]

s

1

= 35. 68 ± 0.20 [cm]

s

2

= 38.30 ± 0.20 [cm]

Wyznaczono geometryczny środek soczewki

s=

35.6838.30

2

= 36.99 [cm]

Δs=

1
2

0.20

1
2

0.20 = 0.20 [cm]

s = 36.99 ± 0.20 [cm]

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 36.99 – 18.90 = 18.09 [cm]
b = y – s
b = 82.5 – 36.99 = 45.51 [cm]

-

niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm

-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = Δb = 0.1 + 0.1 + 0.6 = 0.8[cm]

1 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Korzystając z równania soczewki wyznaczamy ogniskową:

f =

18.09⋅45.51

18.0945.51

= 12.94 [cm]

Obliczamy błąd wyznaczania ogniskowej soczewki:

Δf =

45.1

2



45.5118.09 

2

⋅

0.8

18.09

2



45.5118.09

2

⋅

0.8

= 0.47 [cm]

Ogniskowa wynosi zatem:

f = 12.94 ± 0.47 [cm] = (12.94 ± 0.47) 10

-2

[m]

2.

Wyznaczanie ogniskowej soczewki skupiającej – metoda Bessela

Wyniki pomiarów zebrano w tabeli

położenie przedmiotu

x [cm]

położenie ekranu y

[cm]

położenie soczewki s

1

-

obraz powiększony

[cm]

położenie soczewki s

2

–

obraz pomniejszony

[cm]

18.9

82.5

38.7

64.8

38.2

65.2

38.5

64.9

38.1

65.0

38.3

65.1

38.6

64.7

38.1

65.1

38.4

65.3

38.2

65.1

38.3

65.0

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

38.738.238.538.138.338.638.138.4 38.238.3

10

= 38.34 [cm]

s

2

=

64.865.2 64.965.065.164.765.165.365.165.0

10

= 65.02 [cm]

Monika Cichoń

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

2

dla 10

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.262

s

s

1

=

2.262



0.12960.01960.02560.05760.00160.06760.05760.00360.01960.0016

90

=

= 0.1478 ~ 0.15 [cm]

s

s

2

=

2.262



0.04840.03240.01440.00040.00640.10240.00640.07840.00640.0004

90

=

0.1297 ~ 0.13 [cm]

s

1

= 38.34 ± 0.15 [cm]

s

2

= 65.02 ± 0.13 [cm]

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 38.34 – 18.90 = 19.44 [cm]
b = y – s
b = 65.02 – 36.99 = 28.03 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = 0.1 + 0.1 + 0.45 = 0.65[cm]
Δb = 0.1 + 0.1 + 0.39 = 0.59[cm]

błąd całkowity =

1
2 ( Δa + Δb) =

1
2 (0.65 + 0.59) = 0.62 [cm]

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 82.5 – 18.9 = 63.6 [cm]

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 65.02 - 38.34 = 26.68 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.18 + 0.16 = 0.34

2 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Obliczono ogniskową soczewki ze wzoru:

f =



l

2

−

d

2



4l

f =



63.6

2

−

26.68

2



4⋅63.6

= 13.10 [cm]

Obliczono błąd wyznaczenia ogniskowej:

Δf =

∣

1
4



26.68

2

4⋅63.6

2

∣⋅

0.2∣

26.68

2⋅63.6

∣⋅

0.34

= 0.1301 ~ 0.13 [cm]

f = 13.10 ± 0.13 [cm] = (13.10 ± 0.13) 10

-2

[m]

3. Wyznaczanie ogniskowej soczewki rozpraszającej – metoda Bessela

W celu wyznaczenia ogniskowej soczewki rozpraszającej zbudowano układ złożony z soczewki skupiającej i
rozpraszającej.

Wyniki pomiarów zebrano w tabeli

położenie

przedmiotu x [cm]

położenie ekranu y

[cm]

położenie soczewki s

1

-

obraz powiększony

[cm]

położenie soczewki s

2

–

obraz pomniejszony

[cm]

18.9

98.2

41.5

71.6

41.6

71.9

42.3

72.3

41.8

72.0

42.2

71.8

41.9

72.0

41.6

71.7

42.0

71.8

41.7

72.1

42.2

72.5

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

41.541.642.341.842.241.941.642.041.742.2

10

= 41.88 [cm]

s

2

=

71.671.972.372.071.872.071.771.872.172.5

10

= 71.97 [cm]

Monika Cichoń

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

3

dla 10

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.262

s

s

1

=

2.262



0.14440.07840.17640.00640.10240.00040.07840.01440.03240.1024

90

=

= 0.2046 ~ 0.20 [cm]

s

s

2

=

2.262



0.13690.00490.10890.00090.02890.00090.07290.02890.01690.2809

90

=

0.1968 ~ 0.20[cm]

s

1

= 41.88 ± 0.20 [cm]

s

2

= 71.97 ± 0.20 [cm]

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0.1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0.1cm

Obliczamy średnią odległość przedmiotu i ekranu od układu soczewek korzystając ze wzorów:

a = s – x
a = 41.88 – 18.90 = 22.98 [cm]
b = s – y
b = 98.20 – 71.97 = 26.23 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od układu soczewk:

Δa = Δb = 0.1+ 0.1 + 0.20 = 0.40[cm]

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 98.2 – 18.9 = 79.3 [cm]

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 71.97 - 41.88 = 30.09 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.25 + 0.24 = 0.49

3 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Obliczono ogniskową układu soczewek ze wzoru:

f =



l

2

−

d

2



4l

f =



79.3

2

−

30.09

2



4⋅79.3

= 16.97 [cm]

Obliczono błąd wyznaczenia ogniskowej układu soczewek:

Δf =

∣

1
4



30.09

2

4⋅79.3

2

∣⋅

0.2∣

30.09

2⋅79.3

∣⋅

0.49

= 0.1717 ~ 0.17 [cm]

f = 16.97 ± 0.17 [cm]

Obliczono ogniskową soczewki rozpraszającej:

f

rozp

=

f

ukł

⋅

f

skup

f

skup

−

f

ukł

f

rozp

=

16.97⋅13.10

13.10−16.97

= - 57.44 [cm]

Obliczono błąd pomiaru:

Δf

rozp

=

∣

∂

f

rozp

∂

f

skup

∣⋅

f

skup

∣

∂

f

rozp

∂

f

ukł

∣⋅

f

ukł

Δf

rozp

=

∣

−

f

ukł



2



f

skup

−

f

ukl



2

∣⋅

f

skup

∣



f

skup



2



f

skup

−

f

ukl



2

∣⋅

f

ukł

Δf

rozp

=

∣

−

16.97

2



13.10−16.97

2

∣⋅

0.13∣



13.10

2



13.10−16.97

2

∣⋅

0.17

= 0.5518 ~ 0.55 [cm]

f

rozpr

= - 57.44 ± 0.55 [cm] = (- 57.44 ± 0.55) 10

-2

[m]

Monika Cichoń

4. Badanie aberracji sferycznej

Wyniki pomiarów zebrano w tabeli

położenie

przedmiotu

x

[cm]

położenie

ekranu

y

[cm]

położenie soczewki dla

promieni przyosiowych

[cm]

położenie soczewki dla

promieni pośrednich

[cm]

położenie soczewki dla

promieni brzeżnych

[cm]

obraz

powiększony

s

1

obraz

pomniejszony

s

2

obraz

powiększony

s

1

obraz

pomniejszony

s

2

obraz

powiększony

s

1

obraz

pomniejszony

s

2

18.7

107.3

49.5

78.9

46.7

79.7

42.3

82.3

49.3

79.0

47.2

79.6

42.6

81.9

49.5

79.2

47.3

79.8

42.2

82.1

49.6

78.6

46.9

79.2

42.5

81.8

49.2

78.8

47.0

79.4

42.4

82.0

49.7

78.9

47.1

79.4

42.2

82.2

•

Wyznaczanie ogniskowej soczewki dla promieni przyosiowych

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

49.549.349.549.649.249.7

6

= 49.46 [cm]

s

2

=

78.979.079.278.678.878.9

6

= 78.9 [cm]

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

4

dla 6

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.571

s

s

1

=

2.571



0.00160.02560.00160.01960.06760.0576

50

= 0.1515 = 0.15 [cm]

s

s

2

=

2.571



00.010.090.090.010

50

= 0.1626 ~ 0.16 [cm]

s

1

= 49.46 ± 0.15 [cm]

s

2

= 78.9 ± 0.16 [cm]

4 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 49.46 – 18.70 = 30.76 [cm]
b = y – s
b = 107.30 - 78.90 = 28.40 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = 0.1 + 0.1 + 0.45 = 0.65[cm]
Δb = 0.1 + 0.1 + 0.48 = 0.69[cm]

błąd całkowity =

1
2 ( Δa + Δb) =

1
2 (0.65 + 0.69) = 0.67 [cm]

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 107.30 – 18.70 = 88.60 [cm]

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 78.9 – 49.46 = 26.68 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.16 + 0.15 = 0.31

Obliczono ogniskową soczewki ze wzoru:

f =



l

2

−

d

2



4l

f =



88.60

2

−

26.68

2



4⋅88.60

= 20.14 [cm]

Obliczono błąd wyznaczenia ogniskowej:

Δf =

∣

1
4



26.68

2

4⋅88.60

2

∣⋅

0.2∣

26.68

2⋅88.60

∣⋅

0.31

= 0.1012 ~ 0.10 [cm]

f = 20.14 ± 0.10 [cm] = (20.14 ± 0.10) 10

-2

[m]

Monika Cichoń

•

Wyznaczanie ogniskowej soczewki dla promieni pośrednich

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

46.747.247.346.947.047.1

6

= 47.03 [cm]

s

2

=

79.779.679.879.279.479.4

6

= 79.52 [cm]

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

5

dla 6

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.571

s

s

1

=

2.571



0.10890.02890.07290.01690.00090.0049

50

= 0.1757 = 0.18 [cm]

s

s

2

=

2.571



0.03240.00640.07840.10240.01440.0144

50

= 0.1812 ~ 0.18 [cm]

s

1

= 47.03 ± 0.18 [cm]

s

2

= 79.52 ± 0.18 [cm]

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 47.03 – 18.70 = 28.33 [cm]
b = y – s
b = 107.30 – 79.52 = 27.78 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = Δb = 0.1 + 0.1 + 0.54 = 0.74[cm]

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 107.30 – 18.70 = 88.60 [cm]

5 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 79.52 – 47.03 = 32.49 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.18 + 0.18 = 0.36

Obliczono ogniskową soczewki ze wzoru:

f =



l

2

−

d

2



4l

f =



88.60

2

−

32.49

2



4⋅88.60

= 19.17 [cm]

Obliczono błąd wyznaczenia ogniskowej:

Δf =

∣

1
4



32.49

2

4⋅88.60

2

∣⋅

0.2∣

32.49

2⋅88.60

∣⋅

0.36

= 0.1227 ~ 0.12[cm]

f = 19.17 ± 0.12 [cm] = (19.17 ± 0.12) 10

-2

[m]

•

Wyznaczanie ogniskowej soczewki dla promieni brzeżnych

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

42.342.642.242.542.442.2

6

= 42.37 [cm]

s

2

=

82.381.982.181.882.082.2

6

= 82.05 [cm]

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

6

dla 6

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.571

6 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

s

s

1

=

2.571



0.00490.05290.02890.00090.0289

50

= 0.1241 = 0.12 [cm]

s

s

2

=

2.571



0.06250.02250.00250.06250.00250.0225

50

= 0.1521 ~ 0.15 [cm]

s

1

= 42.37 ± 0.12 [cm]

s

2

= 82.05 ± 0.15 [cm]

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 42.37 – 18.70 = 23.67 [cm]
b = y – s
b = 107.30 – 82.05 = 25.25 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = 0.1 + 0.1 + 0.36 = 0.56 [cm]
Δb = 0.1 + 0.1 + 0.45 = 0.65[cm]

błąd całkowity =

1
2 ( Δa + Δb) =

1
2 (0.56 + 0.65) = 0.605 ~ 0.60 [cm]

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 107.30 – 18.70 = 88.60 [cm]

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 82.05 – 42.37 = 39.68 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.12 + 0.15 = 0.27 [cm]

Obliczono ogniskową soczewki ze wzoru:

f =



l

2

−

d

2



4l

f =



88.60

2

−

39.68

2



4⋅88.60

= 17.71 [cm]

Monika Cichoń

Obliczono błąd wyznaczenia ogniskowej:

Δf =

∣

1
4



39.68

2

4⋅88.60

2

∣⋅

0.2∣

39.68

2⋅88.60

∣⋅

0.27

= 0.1205 ~ 0.12[cm]

f = 17.71 ± 0.12 [cm] = ( 17.71 ± 0.12) 10

-2

[m]

Miarą podłużnej aberracji sferycznej jest różnica pomiędzy ogniskowymi promieni przyosiowych i brzeżnych:

A

sf

= 20.14 – 17.71 = 2.43 [cm]

Obliczono błąd pomiaru aberracji sferycznej:

ΔA

sf

= Δf

przyosiowych

+ Δf

brzeżnych

ΔA

sf

= 0.10 + 0.12 = 0.24 [cm]

A

sf

= 2.43 ± 0.24 [cm] = (2.43 ± 0.24) 10

-2

[m]

5. Badanie aberracji chromatycznej

Wyniki pomiarów zebrano w tabeli

położenie

przedmiotu x

[cm]

położenie

ekranu

y

[cm]

położenie soczewki dla

filtru niebieskiego

[cm]

położenie soczewki dla

filtru czerwonego

[cm]

położenie soczewki dla

filtru zielonego

[cm]

obraz

powiększony

s

1

obraz

pomniejszonys

2

obraz

powiększony

s

1

obraz

pomniejszony

s

2

obraz

powiększonys

1

obraz

pomniejszony

s

2

24.1

94.5

42.3

78.1

42.4

78.5

42.4

78.5

42.3

78.3

42.0

78.2

42.5

78.7

42.1

78.4

42.3

78.4

42.4

78.6

42.4

78.6

42.1

78.3

42.2

78.3

42.1

78.3

42.5

78.6

42.3

78.4

42.4

78.7

42.1

78.4

42.1

78.2

•

Wyznaczanie ogniskowej soczewki dla filtru niebieskiego

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

42.342.642.142.442.142.4

6

= 42.27 [cm]

s

2

=

78.178.378.478.678.378.7

6

= 78.4 [cm]

Monika Cichoń

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

7

dla 6

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.571

s

s

1

=

2.571



0.00090.00090.02890.01690.02890.0169

50

= 0.1111 = 0.11[cm]

s

s

2

=

2.571



0.090.0100.040.010.09

50

= 0.1781 ~ 0.18 [cm]

s

1

= 42.27 ± 0.11 [cm]

s

2

= 78.4 ± 0.18 [cm]

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 42.27 – 24.1 = 18.17 [cm]
b = y – s
b = 94.50 – 78.40 = 16.1 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = 0.1 + 0.1 + 0.33 = 0.53 [cm]
Δb = 0.1 + 0.1 + 0.54 = 0.74[cm]

błąd całkowity =

1
2 ( Δa + Δb) =

1
2 (0.53 + 0.74) = 0.635 ~ 0.64 [cm]

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 94.50 – 24.10 = 70.40 [cm]

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 78.40 – 42.27 = 36.13 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.11 + 0.18 = 0.29 [cm]

7 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Obliczono ogniskową soczewki ze wzoru:

f =



l

2

−

d

2



4l

f =



70.40

2

−

36.13

2



4⋅70.40

= 12.96 [cm]

Obliczono błąd wyznaczenia ogniskowej:

Δf =

∣

1
4



36.13

2

4⋅70.40

2

∣⋅

0.2∣

36.13

2⋅70.40

∣⋅

0.29

= 0.1376 ~ 0.14[cm]

f = 12.96 ± 0.14 [cm] = (12.96 ± 0.14) 10

-2

[m]

•

Wyznaczanie ogniskowej soczewki dla filtru czerwonego

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

42.442.042.342.142.542.1

6

= 42.23 [cm]

s

2

=

78.578.278.478.378.678.4

6

= 78.4 [cm]

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

8

dla 6

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.571

s

s

1

=

2.571



0.02890.05290.00490.01690.07290.0169

50

= 0.1772 = 0.18[cm]

s

s

2

=

2.571



0.010.0400.010.040

50

= 0.1016 ~ 0.10 [cm]

s

1

= 42.23 ± 0.18 [cm]

s

2

= 78.4 ± 0.10 [cm]

8 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 42.23 – 24.10 = 18.13 [cm]
b = y – s
b = 94.50 – 78.40 = 16.1 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = 0.1 + 0.1 + 0.54 = 0.74 [cm]
Δb = 0.1 + 0.1 + 0.30 = 0.50[cm]

błąd całkowity =

1
2

( Δa + Δb) =

1
2

(0.74 + 0.50) = 0.62 [cm]

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 94.50 – 24.10 = 70.40 [cm]

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 78.40 – 42.23 = 36.17 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.18 + 0.10 = 0.28 [cm]

Obliczono ogniskową soczewki ze wzoru:

f =



l

2

−

d

2



4l

f =



70.40

2

−

36.17

2



4⋅70.40

= 12.95 [cm]

Obliczono błąd wyznaczenia ogniskowej:

Δf =

∣

1
4



36.17

2

4⋅70.40

2

∣⋅

0.2∣

36.17

2⋅70.40

∣⋅

0.28

= 0.1351 ~ 0.14[cm]

f = 12.95 ± 0.14 [cm] = (12.95 ± 0.14) 10

-2

[m]

Monika Cichoń

•

Wyznaczanie ogniskowej soczewki dla filtru zielonego

Obliczono średnie położenie soczewek s

1

i s

2

s

1

=

42.442.542.442.242.342.1

6

= 42.32 [cm]

s

2

=

82.381.982.181.882.082.2

6

= 78.45 [cm]

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

9

dla 6

pomiarów (dla α=0,95 i n=5) wynoszący k = 2.571

s

s

1

=

2.571



0.00640.03240.00640.01440.00040.0484

50

= 0.1197 = 0.12 [cm]

s

s

2

=

2.571



0.00250.06250.02250.00250.00250.0625

50

= 0.1324 ~ 0.13 [cm]

s

1

= 42.32 ± 0.12 [cm]

s

2

= 78.45 ± 0.13 [cm]

Obliczono:
-niepewność wyznaczania położeń przedmiotu x i ekranu y: ∆x = ∆y = 0,1cm
-niepewność wyznaczania położeń soczewki to niepewność systematyczna: ∆s

syst.

= 0,1cm

Obliczamy średnią odległość przedmiotu i ekranu od soczewek korzystając ze wzorów:

a = s – x
a = 42.32 – 24.1 = 18.22 [cm]
b = y – s
b = 94.50 – 78.45 = 16.05 [cm]

Obliczamy błąd pomiaru odległości przedmiotu i ekranu od soczewki:

Δa = 0.1 + 0.1 + 0.36 = 0.56 [cm]
Δb = 0.1 + 0.1 + 0.39 = 0.59[cm]

błąd całkowity =

1
2

( Δa + Δb) =

1
2

(0.39 + 0.59) = 0.49 [cm]

9 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

Obliczono l - odległość przedmiotu od ekranu

l = y - x
l = 94.50 – 24.10 = 70.40 [cm]

Obliczono d – odległość między położeniami soczewek:

d = s

2

– s

1

d = 78.45 – 42.32 = 36.13 [cm]

Obliczono błąd obu tych odległości:

Δl = Δy + Δx
Δl = 0.1 + 0.1 = 0.2 [cm]

Δd = Δs

2

+ Δs

1

Δd = 0.12 + 0.13 = 0.25 [cm]

Obliczono ogniskową soczewki ze wzoru:

f =



l

2

−

d

2



4l

f =



70.40

2

−

36.13

2



4⋅70.40

= 12.96 [cm]

Obliczono błąd wyznaczenia ogniskowej:

Δf =

∣

1
4



36.13

2

4⋅70.40

2

∣⋅

0.2∣

36.13

2⋅70.40

∣⋅

0.29

= 0.1376 ~ 0.14[cm]

f = 12.96 ± 0.14 [cm] = (12.96 ± 0.14) 10

-2

[m]

Obliczono aberrację chromatyczną:

A

ch

= f

czerwony

– f

niebieski

A

ch

= 12.96 – 12.95 = 0.01 [cm]

Obliczono błąd wyznaczania aberracji chromatycznej

ΔA

ch

= Δf

czerwony

+ Δ

fniebieski

ΔA

ch

= 0.14 – 0.14 = 0 [cm]

A

ch

=

0.01 ± 0 [cm] = (0.01 ± 0) 10

-2

[m]

Monika Cichoń

6. Badanie astygmatyzmu

Wyniki zebrano w tabeli:

obraz ostry [cm]

37.6

36.4

linie poziome s

1

[cm]

45.2

44.5

linie pionowe s

2

[cm]

34.8

33.4

Obliczono średnie położenia soczewki s

1

i s

2

:

s

1

=

45.244.5

2

= 44.85 [cm]

s

2

=

34.833.4

2

= 34.10 [cm]

Obliczono odchylenie standardowe średniej. Uwzględniono współczynnik Studenta odczytany z tablic

10

dla 2

pomiarów (dla α=0,95 i n=5) wynoszący k = 12.706

s

s

1

=

12.706



0.122501225

2

= 4.4471~ 4.45 [cm]

s

s

2

=

12.706



0.490.49

2

= 8.8942 ~ 8.89 [cm]

Obliczono różnicę średnich położeń soczewki:

Δs = s

1

– s

2

Δs = 44.85 – 34.10 = 10.75 [cm]

Obliczono błąd wyznaczenia różnicy średnich położeń soczewki:

Δs

s

= s

1

+ s

2

Δs

s

= 4.45 + 8.89 = 13.34

Pełen astygmatyzm:

Astygmatyzm = 10.75 ± 13.34 [cm] = (10.75 ± 13.34) 10

-2

[m]

10 A. Łomnicki „Wprowadzenie do statystyki dla przyrodników” , PWN, Warszawa 2003

Monika Cichoń

DYSKUSJA WYNIKÓW

1. Zaobserwowano,ze dokładniejszą metodą wyznaczania ogniskowej soczewki jest metoda Bessela, ponieważ
metoda oparta na równaniu soczewki obarczona jest większym błędem

•

metoda równania soczewki: f = (12.94 ± 0.47) 10

-2

[m]

•

metoda Bessela : f = (13.10 ± 0.13) 10

-2

[m]

2. Moc soczewek otrzymanych do badania wynosiła odpowiednio:

•

soczewka rozpraszająca: - 2 D

•

soczewka skupiająca: +8 D

co w przeliczeniu na ogniskową daje

•

soczewka rozpraszająca: - 50 [cm]

•

soczewka skupiająca: 12.5 [cm]

Wyniki otrzymane w doświadczeniu są więc bardzo zbliżone do wartości teoretycznych.

3. W doświadczeniu zaobserwowano aberrację sferyczną: A

sf

= (2.43 ± 0.24) 10

-2

[m]

4. W doświadczeniu nie zaobserwowano aberracji chromatycznej: A

ch

= (0.01 ± 0) 10

-2

[m]

Mogło to być spowodowane użyciem w doświadczeniu soczewki cienkiej zamiast grubej Ponieważ aberracja
chromatyczna związana jest ze zjawiskiem dyspersji można ją obserwować tylko na soczewkach grubych.

5. W doświadczeniu badano także astygmatyzm. Otrzymane wartości: (10.75 ± 13.34) 10

-2

[m]

nie są jednak miarodajne ze względu na zbyt małą ilość pomiarów.