
1

2
1. Kinematyka punktu materialnego
1.1. Pojęcia podstawowe
W mechanice punktem materialnym nazywa się obiekt fizyczny, którego rozmiary są
małe w porównaniu z przemieszczeniem, jakiego on doznaje w czasie ruchu. Przyjęcie
takiego pojęcia pozwala zastąpić badane ciało w ruchu punktem materialnym i zaniedbać
strukturę wewnętrzną ciała, która jest nieistotna z punktu widzenia badania samego ruchu.
Ruchem mechanicznym nazywamy zmianę położenia jednego ciała względem innego.
To inne ciało lub zespół ciał materialnych nazywamy układem odniesienia. Jeżeli dane ciało
nie zmienia położenia względem układu odniesienia, to mówimy, że jest ono w spoczynku
względem tego układu odniesienia. Wybór układu odniesienia jest podstawowym
i koniecznym warunkiem opisu ruchu ciała lub jego spoczynku. W różnych jednak sytuacjach
układ odniesienia możemy wybrać dowolnie. Doświadczenie uczy nas, że zarówno ruch jak
i spoczynek są pojęciami względnymi. To, co względem jednego układu odniesienia jest
spoczynkiem, względem innego układu odniesienia może być ruchem jednostajnym lub
zmiennym. Nie ma zatem ruchu lub spoczynku absolutnego. Jest tylko ruch i spoczynek
względny, odniesiony do konkretnego układu odniesienia.
Przy opisie ruchu lub spoczynku ciała materialnego, traktowanego dalej jako punkt
materialny poruszający się względem wybranego układu odniesienia, wprowadzamy układ
współrzędnych. Układ współrzędnych wiążemy z układem odniesienia. Układem
współrzędnych może być między innymi układ kartezjański jednowymiarowy,
dwuwymiarowy lub trójwymiarowy.
1.2. Położenie punktu materialnego w przestrzeni
Weźmy układ współrzędnych związany z pewnym ciałem traktowanym jako punkt
materialny O, tak jak na rysunku.
P ( x , y , z )
O
z
z
y
y
x
r
x
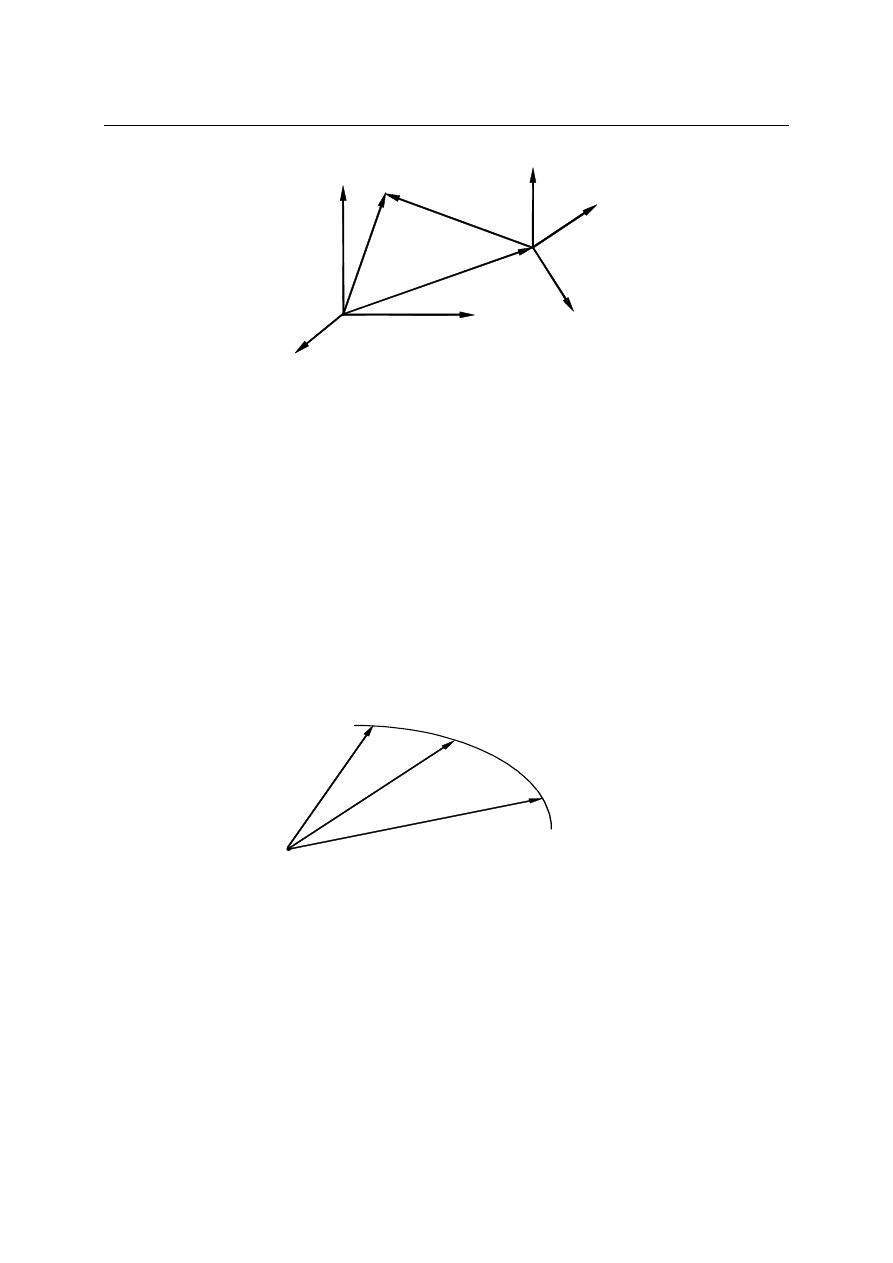
Położenie obserwowanego punktu materialnego, np. P w takim układzie odniesienia,
możemy określić przy pomocy wektora położenia r, jak na rysunku. Wektor ten możemy
rozkładać na różne składowe, np. składowe w różnych układach współrzędnych.
W
układzie kartezjańskim wektor położenia można zapisać równaniem:
z
x
x
eˆ
z
eˆ
y
eˆ
x
r
+
+
=
r
,

3
gdzie e
x
, e
y
i e
z
są wektorami jednostkowymi i stanowią bazę układu kartezjańskiego.
Przedstawiając położenie punktu w przestrzeni przy pomocy trzech składowych zakładamy,
że przestrzeń jest trójwymiarowa. Jest to założenie o charakterze fizycznym, które odrzuca
ogólna teoria względności.
1.3. Odległość między dwoma punktami
Położenie dwóch punktów materialnych w przestrzeni może być określone w danym
układzie przez dwa wektory położenia
r
r
r i r
1
2
, zaś w innym układzie odniesienia, np. O'
przez
, co pokazano na załączonym rysunku.
'
r
i
'
r
2
1
r
r
r
1
’
O’
r
2
r
1,2
y’
x’
z’
z
2
1
y
x
r
2
’
O
r
1
⎪⎩
⎪
⎨
⎧
+
+
=
+
+
=
⎪⎩
⎪
⎨
⎧
+
+
=
+
+
=
,
eˆ
'
z
eˆ
'
y
eˆ
'
x
'
r
,
eˆ
'
z
eˆ
'
y
eˆ
'
x
'
r
,
eˆ
z
eˆ
y
eˆ
x
r
,
eˆ
z
eˆ
y
eˆ
x
r
'
z
2
'
y
2
'
x
2
2
'
z
1
'
y
1
'
x
1
1
z
2
y
2
x
2
2
z
1
y
1
x
1
1
r
r
r
r
⎪⎩
⎪
⎨
⎧
−
+
−
+
−
=
=
−
−
+
−
+
−
=
=
−
.
)
z
z
(
)
y
y
(
)
x
x
(
r
r
r
,
eˆ
)
z
z
(
eˆ
)
y
y
(
eˆ
)
x
x
(
r
r
r
2
1
2
2
1
2
2
1
2
12
1
2
z
1
2
y
1
2
x
1
2
12
1
2
r
r
r
r
r
r
⎪⎩
⎪
⎨
⎧
−
+
−
+
−
=
=
−
−
+
−
+
−
=
=
−
.
)
'
z
'
z
(
)
'
y
'
y
(
)
'
x
'
x
(
'
r
'
r
'
r
,
eˆ
)
'
z
'
z
(
eˆ
)
'
y
'
y
(
eˆ
)
'
x
'
x
(
'
r
'
r
'
r
2
1
2
2
1
2
2
1
2
12
1
2
'
z
1
2
'
y
1
2
'
x
1
2
12
1
2
r
r
r
r
r
r
Przestrzeń, w której odległość między dwoma dowolnymi punktami o współrzędnych
(x
1
, y
1
, z
1
) i (x
2
, y
2
, z
2
) dana jest przez związek:
2
1
2
2
1
2
2
1
2
12
)
z
z
(
)
y
y
(
)
x
x
(
r
−
+
−
+
−
=
r
nazywa się euklidesową.
Zwróćmy uwagę, że w obydwu układach długość wektora jest niezmiennikiem:
.
r
r
12
12
′
= r
r
Z tego ostatniego związku wynika, że rzuty wektora r
12
na osie układu O', i rzuty
wektora na osie układu O, są ze sobą związane przekształceniami ortogonalnymi, które
otrzymuje się mnożąc kolejno przez wektory jednostkowe e
x’
, e
y’
, e
z’
następujące równanie:
,
eˆ
z
eˆ
y
eˆ
x
eˆ
z
eˆ
y
eˆ
x
z
y
x
z
y
x
′
′
′
′
∆
+
′
∆
+
′
∆
=
∆
+
∆
+
∆
a następnie rozwiązując je względem odpowiednich składowych. Przekształcenia te
(transformacje) mają postać:
⎪
⎩
⎪
⎨
⎧
∆
+
∆
+
∆
=
⋅
∆
+
⋅
∆
+
⋅
∆
=
′
∆
∆
+
∆
+
∆
=
⋅
∆
+
⋅
∆
+
⋅
∆
=
′
∆
∆
+
∆
+
∆
=
⋅
∆
+
⋅
∆
+
⋅
∆
=
′
∆
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
′
,
z
a
y
a
x
a
)
eˆ
eˆ
(
z
)
eˆ
eˆ
(
y
)
eˆ
eˆ
(
x
z
,
z
a
y
a
x
a
)
eˆ
eˆ
(
z
)
eˆ
eˆ
(
y
)
eˆ
eˆ
(
x
y
,
z
a
y
a
x
a
)
eˆ
eˆ
(
z
)
eˆ
eˆ
(
y
)
e
eˆ
(
x
x
z
z
y
z
x
z
z
z
z
y
z
x
z
y
y
y
x
y
y
z
y
y
y
x
z
x
y
x
x
x
x
z
x
y
x
x
gdzie
itd.
∆
∆
x x
x
x
x
x
=
−
′ = ′ − ′
2
1
2
1
,
,
4
Z
powyższego spostrzeżenia wynika bardzo ważny wniosek odnośnie położenia
punktu w dwu różnych układach odniesienia.
r
o
r’
r
O’
O
Z rysunku widać, że:
,
r
r
r
0
′
+
=
r
r
r
tj. wektor położenia w układzie nieprimowanym wyraża się przez wektor położenia
w układzie primowanym i wektor położenia początku układu primowanego względem
nieprimowanego. Oczywiście, to stwierdzenie jest prawdziwe tylko w mechanice klasycznej.
Odnośnie czasu postuluje się w mechanice klasycznej istnienie zegarów, których okres
nie ulega zmianie przy dowolnym ruchu. Założenie to jest równoważne twierdzeniu, że
wielkość przedziału czasowego między dwoma dowolnymi zdarzeniami, jest taka sama
w różnych poruszających się w dowolny sposób układach odniesienia:
12
12
t
t
′
=
.
Mamy zatem dwa podstawowe założenia mechaniki klasycznej:
1° przestrzeń jest przestrzenią euklidesową,
2° czas biegnie jednakowo we wszystkich układach odniesienia.
1.4. Ruch punktu materialnego
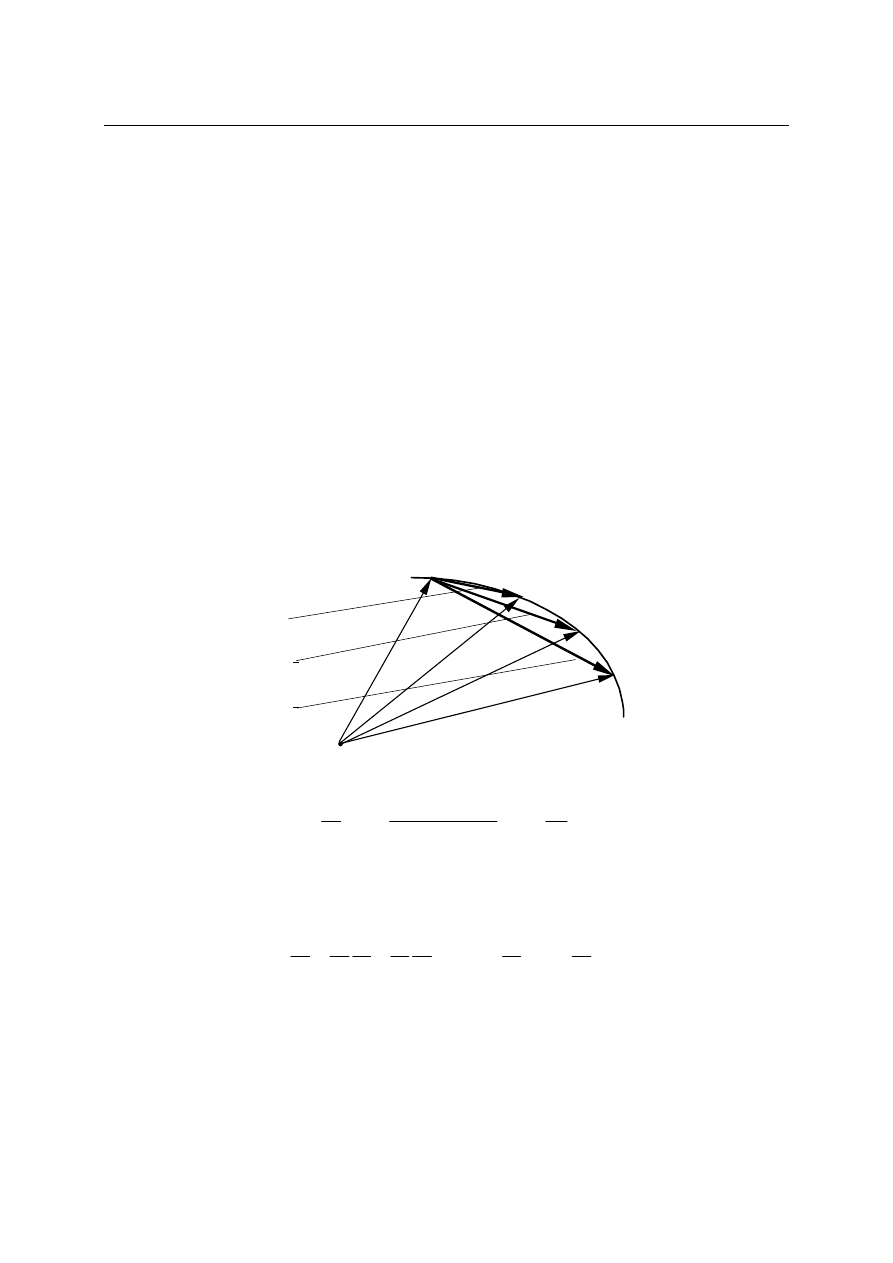
Jeżeli punkt materialny przemieszcza się w wybranym układzie odniesienia jak na
rysunku,
r(t)
r(t+
∆ t+ ∆ t’)
r(t+
∆ t)
O
to jego wektor położenia zależy od czasu:
r r
r
r t
= ( ).
Równanie wektorowe, wyrażające czasową zależność wektora wodzącego od czasu,
jest równaniem parametrycznym ruchu. Parametrem tego równania jest czas.
Miejsce geometryczne punktów, jakie wyznacza koniec wektora wodzącego w czasie,
nazywa się hodografem wektora położenia lub torem poruszającego się punktu materialnego.
W
układzie kartezjańskim nieruchomym równanie:
,
eˆ
)
t
(
z
eˆ
)
t
(
y
eˆ
)
t
(
x
)
t
(
r
r
z
y
x
+
+
=
= r
r
jest równoważne trzem równaniom skalarnym:
⎪
⎩
⎪
⎨
⎧
=
=
=
).
t
(
z
z
),
t
(
y
y
),
t
(
x
x
5
Są to równania parametryczne ruchu punktu materialnego w układzie kartezjańskim.
Eliminując parametr czasu z tych równań otrzymujemy równania uwikłane toru.
Wyznaczamy czas z pierwszego równania układu: t = t(x) i podstawiając do pozostałych
równań układu, otrzymujemy:
⎩
⎨
⎧
=
=
).
x
(
z
z
),
x
(
y
y
Gdy ruch odbywa się w płaszczyźnie, to zawsze możemy tak wybrać układ
współrzędnych, aby ruch odbywał się w płaszczyźnie (x, y). Wtedy wektor wodzący punktu
jest dany przez równanie:
,
eˆ
)
t
(
y
eˆ
)
t
(
x
r
y
x
+
=
r
a układ równań parametrycznych redukuje się do dwóch:
⎩
⎨
⎧
=
=
).
t
(
y
y
),
t
(
x
x
Wyznaczając z pierwszego równania czas i wstawiając do drugiego, otrzymujemy
równanie toru ruchu płaskiego:
y y x
= ( ).
1.5. Prędkość punktu materialnego
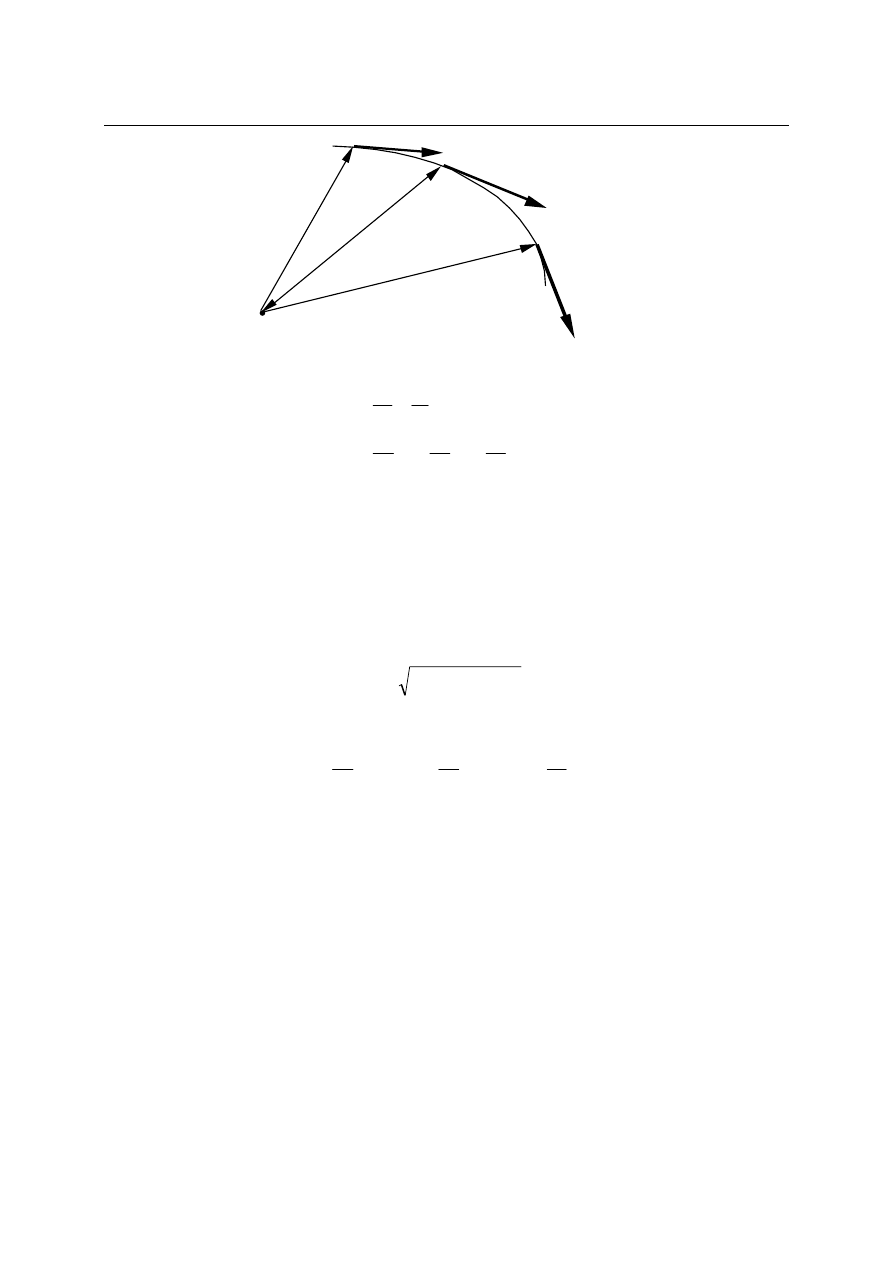
Niech punkt materialny porusza się po torze jak to przedstawia rysunek:
r(t)
r(t+2∆t)
r(t+3∆t)
r(t+∆t)
O
∆r=r(t+3∆t)-r(t)
∆r=r(t+2∆t)-r(t)
∆r=r(t+∆t)-r(t)
Prędkością poruszającego się punktu materialnego nazywamy pochodną wektora
wodzącego po czasie:
r
t
r
lim
t
)
t
(
r
)
t
t
(
r
lim
dt
r
d
v
0
t
0
t
&r
r
r
r
r
r
=
∆
∆
=
∆
−
∆
+
=
=
→
∆
→
∆
.
Z
powyższej definicji wynika, że wektor prędkości jest wektorem stycznym do toru.
Gdy
∆
t dąży do zera, to kierunek wektora
∆r
dąży do stycznej. Taki jest również kierunek
i zwrot wektora prędkości.
Możemy to równanie zapisać analitycznie następująco:
,
eˆ
ds
r
d
,
v
dt
ds
,
eˆ
v
ds
r
d
dt
ds
dt
ds
ds
r
d
dt
r
d
v
S
S
≡
=
=
=
=
=
r
r
r
r
r
gdzie s jest drogą mierzoną wzdłuż toru. Pochodna drogi po czasie jest wartością prędkości
(długością wektora prędkości), a pochodna wektora wodzącego po drodze definiuje wektor
jednostkowy styczny do toru. Mamy więc zdefiniowany wektor prędkości w każdym punkcie
toru. Wektory te pokazano na kolejnym rysunku.
6
v(t)
v(t+2
∆t)
r(t)
r(t+
∆t)
r(t+2
∆t)
v(t+
∆t)
O
W
układzie współrzędnych kartezjańskich możemy rozłożyć wektor prędkości na
składowe:
[
]
.
eˆ
z
eˆ
y
eˆ
x
eˆ
dt
dz
eˆ
dt
dy
eˆ
dt
dx
eˆ
z
eˆ
y
eˆ
x
dt
d
dt
r
d
v
z
y
x
z
x
x
z
y
x
&
&
&
r
r
+
+
=
+
+
=
+
+
=
=
To równanie wektorowe jest równoważne trzem równaniom skalarnym:
⎪
⎩
⎪
⎨
⎧
=
=
=
=
=
=
).
t
(
v
z
v
),
t
(
v
y
v
),
t
(
v
x
v
z
z
y
y
x
x
&
&
&
Są to równania parametryczne hodografu wektora prędkości, przy czym wartość prędkości
dana jest przez związek:
2
z
2
y
2
x
v
v
v
v
+
+
=
a składowe wektora prędkości wzdłuż osi układu kartezjańskiego są dane przez operacje
różniczkowania składowych wektora położenia po czasie:
.
z
dt
dz
v
,
y
dt
dy
v
,
x
dt
dx
v
z
y
x
&
&
&
≡
=
≡
=
≡
=
1.6. Przyspieszenie
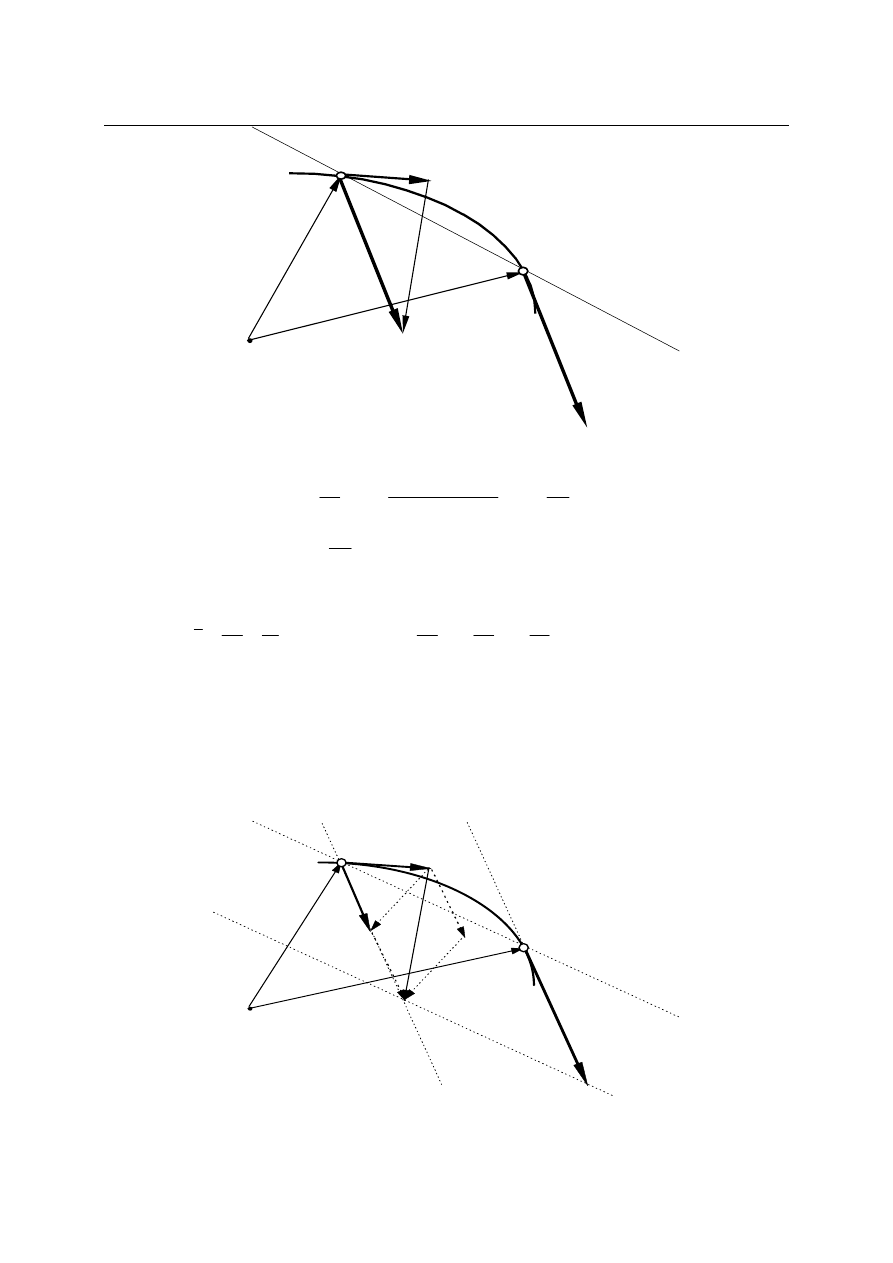
Niech punkt materialny porusza się po torze jak na rysunku i niech wektor prędkości
w dwóch chwilach czasu odległych o
∆t wynosi v(t) i v(t+∆t). Wektory te pokazano wraz
z odpowiednią konstrukcją na tym samym rysunku.
7
v(t)
∆v(t)
r(t)
r(t+∆t)
v(t+∆t)
v(t+∆t)
O
Przyspieszeniem nazywamy pochodną prędkości po czasie:
.
v
t
v
lim
t
)
t
(
v
)
t
t
(
v
lim
dt
v
d
a
0
t
0
t
&r
r
r
r
r
r
=
∆
∆
=
∆
−
∆
+
=
=
→
∆
→
∆
Gdy
∆t dąży do zera, to iloraz
t
v
∆
∆r
dąży do wektora
ar
.
Podobnie jak dla wektora prędkości, w układzie kartezjańskim mamy dla
przyspieszenia następujące związki:
[
]
.
eˆ
z
eˆ
y
eˆ
x
eˆ
dt
z
d
eˆ
dt
y
d
eˆ
dt
x
d
eˆ
z
eˆ
y
eˆ
x
dt
d
dt
v
d
a
z
y
x
z
y
x
z
y
x
&&
&&
&&
&
&
&
&
&
&
r
+
+
=
+
+
=
+
+
=
=
⎪
⎩
⎪
⎨
⎧
=
=
=
=
=
=
=
=
=
).
t
(
a
)
t
(
v
z
a
)
t
(
a
)
t
(
v
y
a
),
t
(
a
)
t
(
v
x
a
z
z
z
y
y
y
x
x
x
&
&&
&
&&
&
&&
1.7. Rozkład przyspieszenia na składowe: styczną i normalną
Rozważmy następującą konstrukcję wektorów prędkości rozważanych w poprzednim
punkcie:
v(t)
v(t)
∆v
n
∆v
s
∆v(t)
r(t)
r(t+∆t)
v(t+∆t)
O
Z przedstawionego rysunku widać, że wektor przyrostu prędkości
∆v można rozłożyć
na składowe:
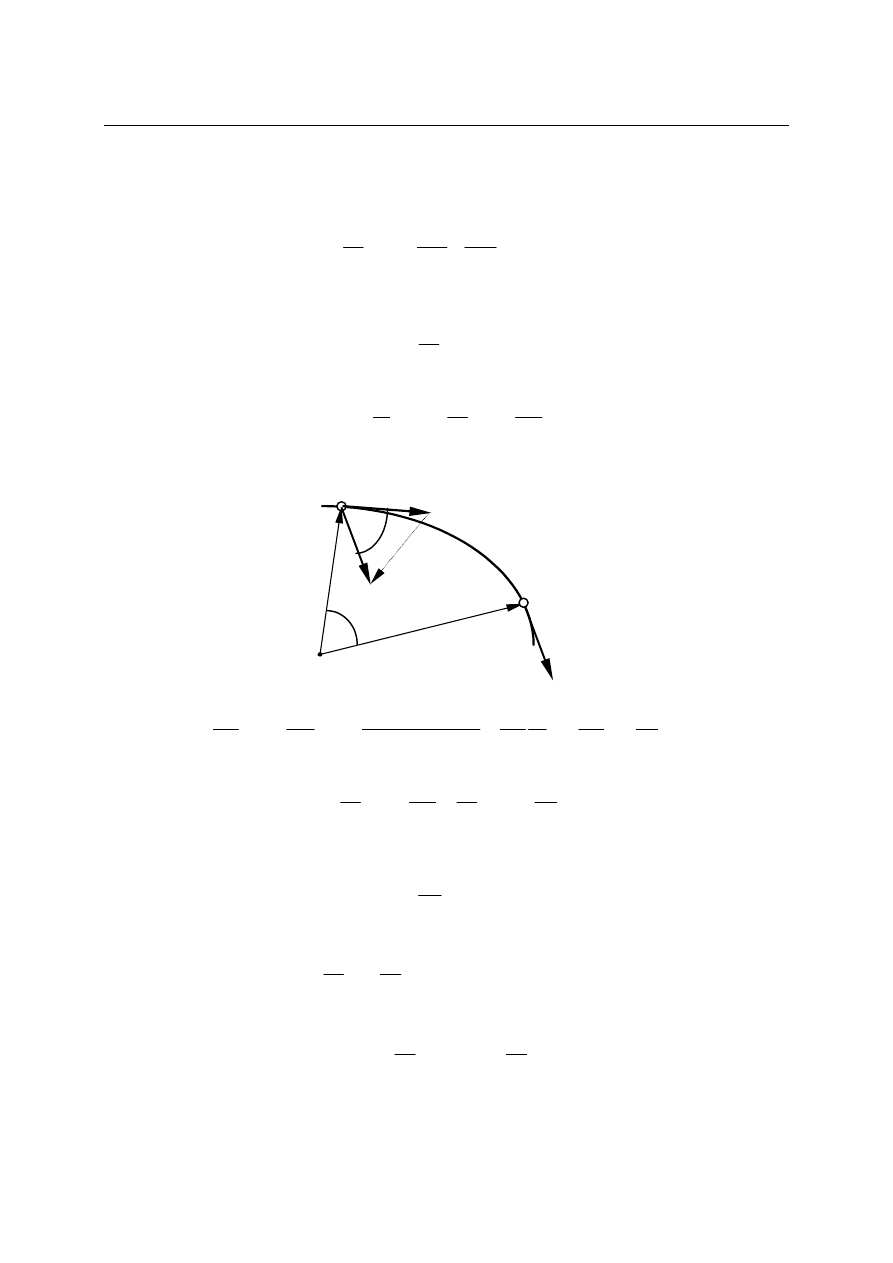
8
n
s
v
v
v
r
r
r
∆
+
∆
=
∆
,
przy czym
∆v
s
jest wektorem związanym ze zmianą wartości wektora prędkości, zaś
∆v
n
wiąże się ze zmianą kierunku wektora prędkości. Mamy zatem następujący rozkład wektora
przyspieszenia:
.
a
a
t
v
t
v
lim
dt
v
d
a
n
s
n
s
0
t
r
r
r
r
r
r
+
=
⎥⎦
⎤
⎢⎣
⎡
∆
∆
+
∆
∆
=
=
→
∆
Ten sam rozkład wektora przyspieszenia na składowe styczną i normalną można
otrzymać również analitycznie. Wiemy już, że
.
eˆ
v
v
i
dt
v
d
a
s
=
=
r
r
r
Mamy zatem:
( )
dt
eˆ
d
v
eˆ
dt
dv
eˆ
v
dt
d
a
s
s
s
+
=
=
r
.
Z drugiej strony z definicji wektora jednostkowego stycznego do toru konstruujemy
rysunek:
e
s
(t+
∆t)
e
s
(t+
∆t)
e
s
(t)
∆e
s
r(t)
r(t+
∆t)
O
∆ϕ
∆
s
∆ϕ
Przy pomocy tego rysunku i definicji pochodnej mamy:
.
eˆ
ds
d
v
ds
eˆ
d
v
dt
ds
ds
eˆ
d
t
)
t
(
eˆ
)
t
t
(
eˆ
lim
t
eˆ
lim
dt
eˆ
d
n
s
s
s
s
0
t
s
0
t
s
ϕ
=
=
=
∆
−
∆
+
=
∆
∆
=
→
∆
→
∆
Podstawiając wynik do wyrażenia na przyspieszenie, otrzymujemy:
ra dv
dt
e
v
de
dt
dv
dt
e
v
d
ds
e
s
s
s
n
=
+
=
+
$
$
$
$ .
2
ϕ
Ponieważ pochodna drogi po kącie, pod jakim ta droga jest widziana z początku
układu odniesienia, jest równa promieniowi krzywizny:
ds
d
ϕ
ρ
= ,
to wzór na rozkład przyspieszenia przyjmuje postać:
r
r
r
a
dv
dt
e
v
e
a
a
a e
a e
s
n
s
n
s s
=
+
=
+
=
+
$
$
$
2
ρ
n n
$
,
przy czym wartości składowych przyspieszeń stycznego i normalnego wynoszą odpowiednio:
.
v
a
,
dt
dv
a
2
n
s
ρ
=
=
Niezależnie od wyboru układu współrzędnych, ruch opisany jest więc przez wektor prędkości
i przyspieszenia:

9
.
dt
r
d
eˆ
a
eˆ
a
a
,
dt
r
d
eˆ
v
v
2
2
n
n
s
s
s
r
r
r
r
=
+
=
=
=
1.8. Podstawowe zagadnienie kinematyki
Mając zdefiniowane wektory prędkości i przyspieszenia możemy teraz sformułować
podstawowe zagadnienie kinematyki w następujący sposób:
Dane są parametryczne równania ruchu i warunki początkowe, znaleźć ruch punktu
materialnego.
Przez dane warunki początkowe rozumiemy, że dane są: wektor położenia i wektor
prędkości punktu materialnego w chwili początkowej. Znaleźć ruch punktu, znaczy określić
zależność wektora wodzącego i prędkości od czasu. Stąd łatwo wyznaczyć pozostałe
parametry ruchu. Te dwa wektory, tj. wektor położenia i wektor prędkości dla danej chwili
czasu, wyznaczają w kinematyce jednoznacznie stan poruszającego się punktu materialnego.
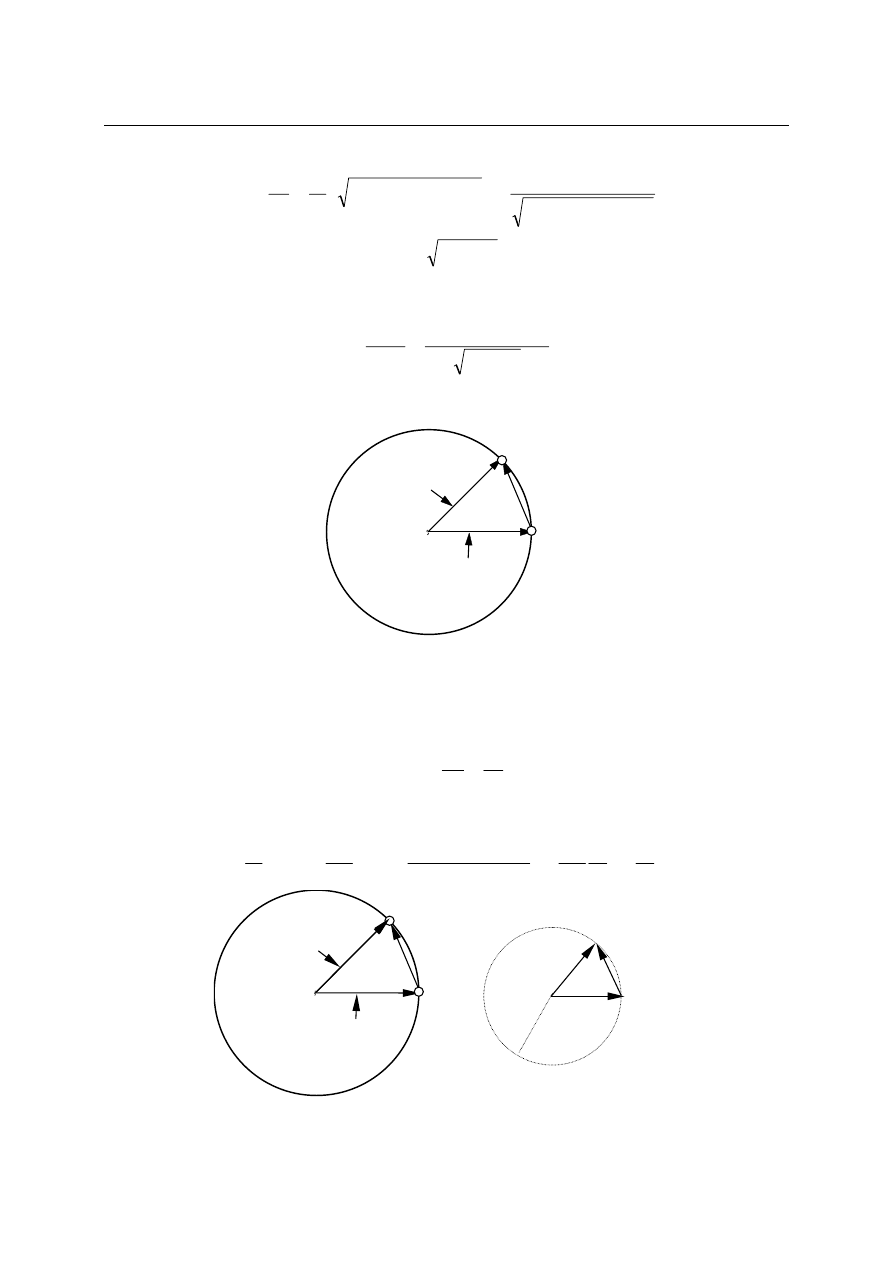
Przykład.
Rzut ukośny punktu materialnego w układzie kartezjańskim.
90-α
y
x
g
v
ox
v
ox
v
ox
v
oy
v
o
Równania parametryczne dla tego ruchu są następujące:
⎪⎩
⎪
⎨
⎧
−
=
=
2
y
0
x
0
gt
2
1
t
v
y
,
t
v
x
Wyliczając czas z pierwszego z równań, mamy: t = x/v
0x
; podstawienie tego czasu do
drugiego z równań daje równanie toru:
2
x
0
2
x
0
y
0
v
2
gx
x
v
v
y
−
=
.
Różniczkując równania parametryczne po czasie otrzymujemy składowe prędkości
w kierunku osi x i y:
⎩
⎨
⎧
−
=
=
=
=
.
gt
v
y
)
t
(
v
,
v
x
)
t
(
v
y
0
y
x
0
x
&
&
Wartość prędkości w dowolnej chwili t wyznaczamy zatem ze związku:
.
)
gt
v
(
v
v
2
y
0
2
x
0
−
+
=
Dalej
różniczkowanie równań parametrycznych prędkości daje składowe
przyspieszenia:
.
g
a
g
y
v
)
t
(
a
,
0
x
v
)
t
(
a
y
y
x
x
=
⇒
⎩
⎨
⎧
−
=
=
=
=
=
=
&&
&
&&
&
10
Znając wartość prędkości oraz całkowite przyspieszenie, znajdujemy składowe
styczną i normalną przyspieszenia:
(
)
.
)
gt
v
(
v
gt
v
g
.
)
gt
v
(
v
dt
d
dt
dv
a
2
y
0
2
x
0
y
0
2
y
0
2
x
0
s
−
+
−
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
+
=
=
2
s
2
n
a
g
a
−
=
.
Ze wzoru na przyspieszenie dośrodkowe możemy znaleźć promień krzywizny toru
w dowolnej chwili czasu:
.
a
g
)
gt
v
(
v
)
t
(
a
)
t
(
v
2
s
2
2
y
0
2
x
0
n
2
−
−
+
=
=
ρ
1.9. Ruch punktu po okręgu
Niech punkt materialny porusza się po okręgu o promieniu r.
∆r
r(t+∆t)
∆ϕ
0
r(t)
W czasie ruchu wektor wodzący poruszającego się punktu będzie zmieniał swój kierunek jak
na rysunku.
Przyrost wektora wodzącego jest dany przez różnicę:
).
t
(
r
)
t
t
(
r
r
r
r
r
−
∆
+
=
∆
Prędkość, jako wektor zgodnie z ogólną definicją, jest równa:
.
dt
r
d
t
r
lim
v
0
t
r
r
r
=
∆
∆
=
→
∆
Ponieważ długość wektora wodzącego w tym ruchu jest taka sama, to możemy
zapisać:
( )
.
eˆ
dt
ds
r
dt
ds
ds
eˆ
d
r
t
)
t
(
eˆ
)
t
t
(
eˆ
lim
r
dt
eˆ
d
r
eˆ
r
dt
d
v
s
r
r
r
0
t
r
r
=
=
∆
−
∆
+
=
=
=
→
∆
r
s=2
π
∆s=|∆e
r
|
∆e
r
∆r
r(t+∆t)
∆ϕ
∆ϕ
0
e
r
(t+∆t
)
|e
r
|=1
e
r
(t)
r(t)
0
S=2
πr

11
Ostatni wiersz ostatniego równania wynika z rysunku, na którym przedstawiono
hodograf radialnego wektora jednostkowego . We wzorach tych ds oznacza drogę na okręgu
hodografu wektora jednostkowego radialnego. Droga ta jest równa:
r
eˆ
.
d
1
ds
ϕ
⋅
=
Zatem ostatecznie wektor prędkości można zapisać w postaci:
.
dt
d
;
eˆ
r
eˆ
dt
d
r
eˆ
dt
ds
r
v
s
s
s
ϕ
=
ω
ω
=
ϕ
=
=
r
Uogólniając ten wzór do postaci wektorowej korzystamy z rysunku:
r(t+
∆t)
r(t)
∆r
∆ϕ
∆ϕ
∆ϕ
Zdefiniowany
wektor
∆ϕ, prostopadły do płaszczyzny ruchu i o długości równej
kątowi
∆ϕ jaki wektor wodzący zakreśli w czasie ∆t, dany jest równaniem wektorowym:
.
r
r
r
r
r
×
ϕ
∆
=
∆
Tworząc iloraz różnicowy:
,
r
t
t
r
r
r
r
×
∆
ϕ
∆
=
∆
∆
w granicy mamy:
.
r
v
r
r
r
×
ω
=
Równanie to definiuje nam wektor prędkości kątowej.
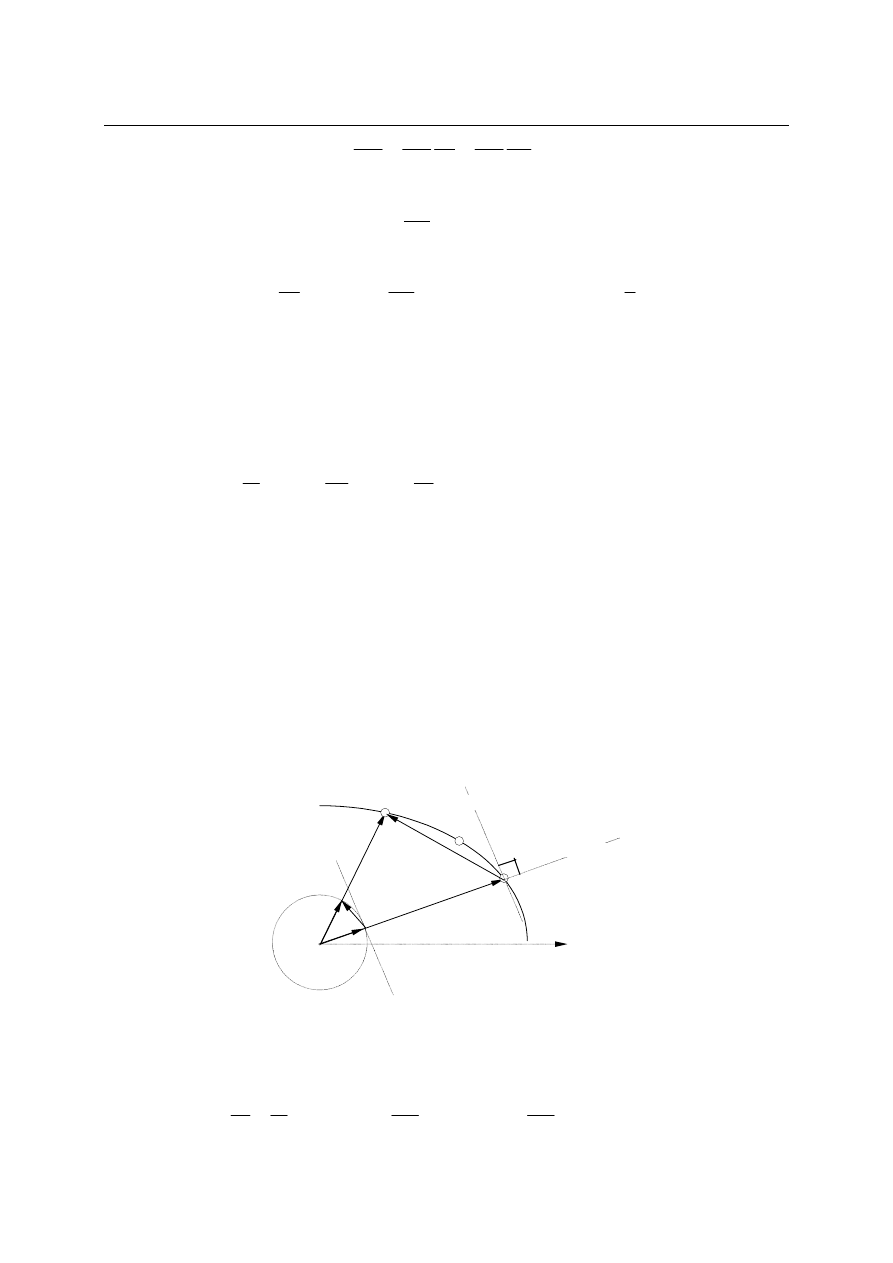
1.10. Przyspieszenie w ruchu po okręgu
Korzystając, z wyprowadzonego w poprzednim punkcie wzoru na wektor prędkości
w ruchu obrotowym, mamy związek:
.
eˆ
r
v
s
ω
=
r
Różniczkując po czasie to równanie otrzymujemy przyspieszenie:
.
dt
eˆ
d
r
eˆ
r
dt
v
d
a
s
s
ω
+
ω
=
=
&
r
r
Aby zróżniczkować wektor e
s
po czasie, skorzystamy z hodografu tego wektora. z rysunku
widać, że hodografem wektora jednostkowego stycznego do toru jest okrąg o promieniu
jednostkowym. Tworząc iloraz różnicowy:
0
0
r(t)
r(t+∆t)
e
s
(t+
∆t)
v(t+∆t)
∆s=∆ϕ
e
s
(t)
∆e
s
v(t)
∆ϕ
e
s
(t)
12
,
t
s
eˆ
t
s
s
eˆ
t
eˆ
s
s
s
∆
ϕ
∆
∆
∆
=
∆
∆
∆
∆
=
∆
∆
w granicy otrzymujemy:
.
eˆ
dt
eˆ
d
r
s
ω
−
=
Podstawiając ten związek do wzoru na przyspieszenie, mamy:
.
r
r
eˆ
;
eˆ
r
eˆ
r
dt
eˆ
d
r
eˆ
r
dt
v
d
a
n
n
2
s
s
s
r
&
r
r
−
=
ω
+
ε
=
ω
+
ω
=
=
Otrzymaliśmy zatem rozkład wektora przyspieszenia na składowe: styczną i normalną.
Dla przyspieszenia w ruchu po okręgu mamy zatem następujące wzory:
⎩
⎨
⎧
ω
=
ϕ
=
ε
=
+
=
.
r
a
r
r
a
;
eˆ
a
eˆ
a
a
2
n
s
n
n
s
s
&&
r
Z drugiej strony, korzystając ze wzoru wektorowego definiującego wektor prędkości
kątowej, mamy:
(
)
).
r
(
r
v
r
dt
r
d
r
dt
d
r
dt
d
a
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
×
ω
×
ω
+
×
ε
=
×
ω
+
×
ε
=
×
ω
+
×
ω
=
×
ω
=
Rozkładając wektor r na składowe r
⊥
i r
||
do wektora prędkości kątowej, podwójny
iloczyn wektorowy po prawej stronie ostatniego równania daje się jeszcze zapisać w postaci:
2
2
||
r
r
)
r
(
)
r
(
)]
r
r
(
[
)
r
(
ω
−
=
ω
−
ω
ω
=
×
ω
×
ω
=
+
×
ω
×
ω
=
×
ω
×
ω
⊥
⊥
⊥
⊥
⊥
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
.
Stąd rozkład przyspieszenia na składowe styczną i normalną w ruchu punktu po okręgu
przyjmuje następującą postać:
.
eˆ
r
r
a
,
r
a
;
a
a
r
r
a
n
2
2
n
s
n
s
2
ω
=
ω
−
=
×
ε
=
+
=
ω
−
×
ε
=
r
r
r
r
r
r
r
r
r
r
r
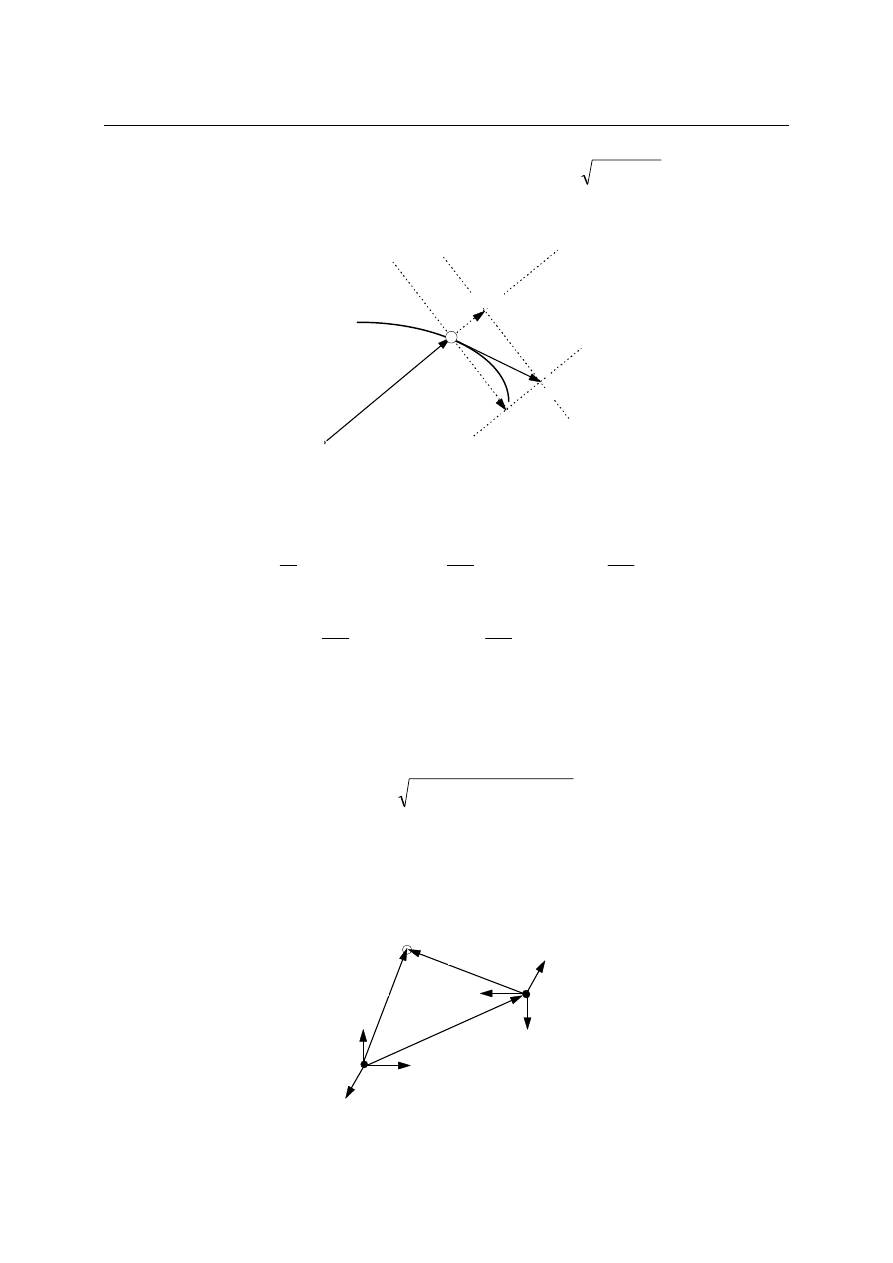
1.11. Składowa radialna i transwersalna w ruchu na płaszczyźnie
Składowa radialna i transwersalna prędkości
Dla ruchu na płaszczyźnie wygodnie jest wybrać układ współrzędnych biegunowych
(r,
ϕ).
x
e
r
(t+∆t)
∆r
∆e
r
∆ϕ
r(t)
e
r
(t)
r(t+∆t)
radialny
transwersalny
transwersalny
Definiując wektor radialny e
r
, dla wektora położenia mamy równanie:
.
eˆ
r
r
r
=
r
Gdy punkt materialny porusza się, to r i e
r
zależą od czasu. Dlatego też wektor prędkości jest
równy:
( )
.
eˆ
eˆ
,
eˆ
dt
eˆ
d
,
eˆ
r
eˆ
r
dt
eˆ
d
r
eˆ
r
eˆ
r
dt
d
dt
r
d
v
r
t
t
r
t
r
r
r
r
⊥
ϕ
=
ϕ
+
=
+
=
=
=
&
&
&
&
r
r
13
Mamy zatem podstawowe wzory dla wektora prędkości:
.
r
r
v
,
r
v
,
r
v
;
eˆ
r
eˆ
r
v
v
v
2
2
2
t
r
t
r
t
r
ϕ
+
=
⎩
⎨
⎧
ϕ
=
=
ϕ
+
=
+
=
&
&
&
r
&
&
&
r
r
r
Rozkład wektora prędkości na składowe radialną i transwersalną przedstawia kolejny
rysunek.
O
v
t
(t
)
v
r
(t)
r(t)
v(t)
Składowa radialna i transwersalna przyspieszenia
Przyspieszenie w ruchu punktu materialnego na płaszczyźnie otrzymamy z definicji tej
wielkości. Mamy:
(
)
.
dt
eˆ
d
r
eˆ
r
eˆ
r
dt
eˆ
d
r
eˆ
r
eˆ
r
eˆ
r
dt
d
a
t
t
t
r
r
t
r
ϕ
+
ϕ
+
ϕ
+
+
=
ϕ
+
=
&
&&
&
&
&
&&
&
&
r
Ponieważ
r
t
t
r
eˆ
dt
eˆ
d
i
eˆ
dt
eˆ
d
ϕ
−
=
ϕ
=
&
&
,
stąd dla przyspieszenia dostajemy:
(
)
(
)
.
eˆ
a
eˆ
a
eˆ
r
r
2
eˆ
r
r
eˆ
r
eˆ
r
eˆ
r
eˆ
r
eˆ
r
a
t
t
r
r
t
r
2
r
2
t
t
t
r
+
=
ϕ
+
ϕ
+
ϕ
−
=
ϕ
−
ϕ
+
ϕ
+
ϕ
+
=
&&
&
&
&
&&
&
&&
&
&
&
&
&&
r
Mamy zatem wzory na składowe radialną i transwersalną przyspieszenia:
(
)
(
)
.
a
a
;
r
r
2
r
r
a
,
`
r
r
2
a
,
r
r
a
t
r
2
2
2
t
2
r
r
r
&&
&
&
&
&&
&&
&
&
&
&&
⊥
ϕ
+
ϕ
+
ϕ
−
=
⎩
⎨
⎧
ϕ
+
ϕ
=
ϕ
−
=
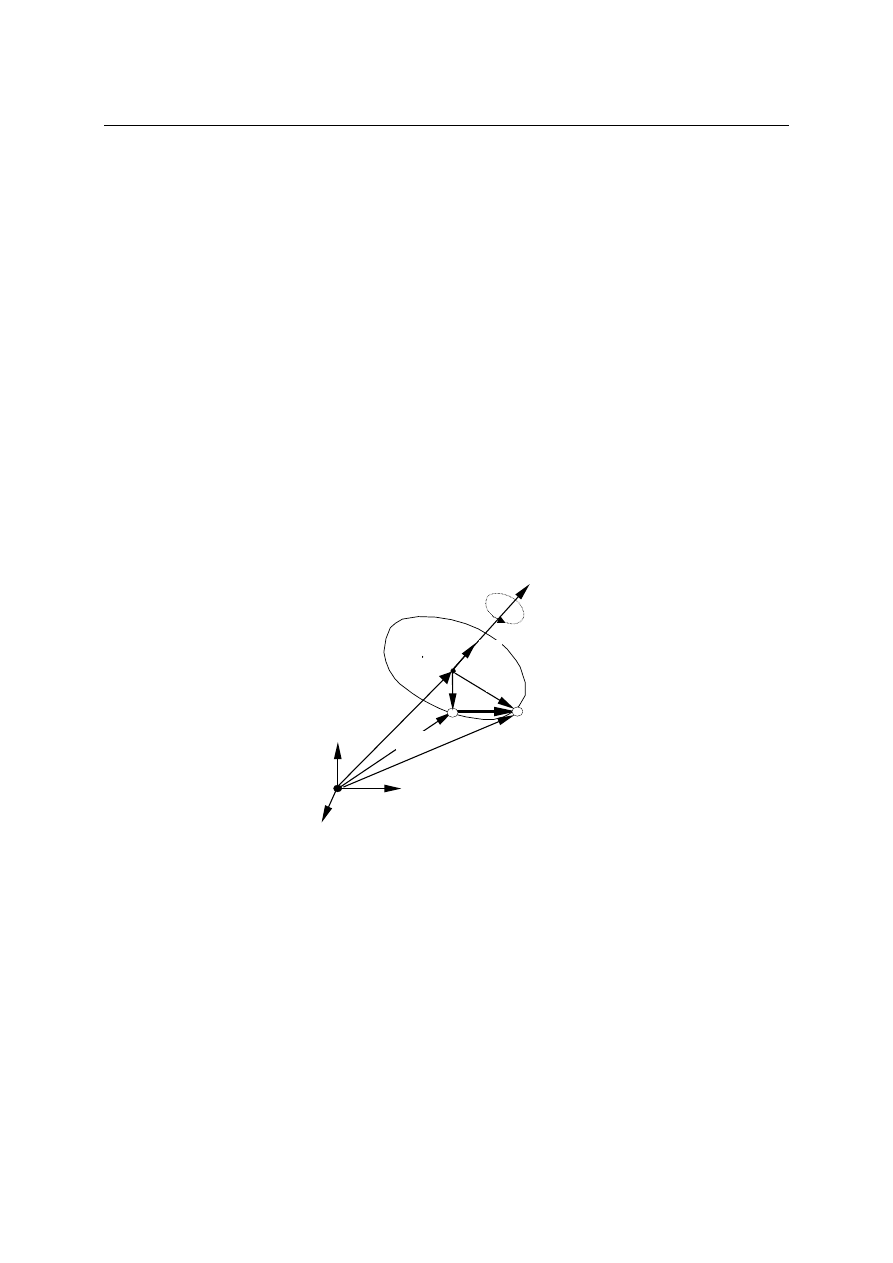
1.12. Prędkość i przyspieszenie w ruchu względnym
Rozważmy dwa układy odniesienia o i O' jak na rysunku i punkt materialny P
poruszający się względem tych układów. Niech układ odniesienia o spoczywa, a układ O'
porusza się.
r
0
r’
O
O’
P
r
Z rysunku widać przede wszystkim, że:
'.
r
r
r
0
r
r
r
+
=
14
Jeżeli punkt P porusza się, to
).
t
(
'
r
)
t
(
r
)
t
(
r
0
r
r
r
+
=
Chcemy
wiedzieć, jak wyrażają się prędkość i przyspieszenie w jednym układzie,
przez te wielkości w drugim układzie. Aby takie związki znaleźć, musimy najpierw znaleźć
transformację wiążącą przesunięcie infinitezymalne punktu P mierzone w układzie O,
z infinitezymalnym przesunięciem mierzonym w poruszającym się układzie O’. Niech układ
O’ porusza się wskutek translacji i obrotu.
Każde przesunięcie w przestrzeni można złożyć z translacji i obrotów. Oznaczmy
przez (dr)
tr
przesunięcie infinitezymalne układu związane z translacją tego układu, a przez
(dr)
rot
przesunięcie związane z obrotem układu wokół pewnej osi obrotu. Wtedy przesunięcie
punktu materialnego, zmierzone w układzie spoczywającym, możemy zapisać w postaci:
rot
tr
)
r
(d
)
r
(d
'
r
d
r
d
r
r
r
r
+
+
=
.
Translacja charakteryzuje się tym, że wszystkie punkty układu przesuwają się w tym
samym kierunku i o tę samą wielkość. Przesunięcie nie zależy zatem od punktu przestrzeni.
Cechą charakterystyczną obrotów jest istnienie osi obrotu. Gdy układ O' obraca się
względem pewnej osi obrotu, to dowolny punkt leżący względem początku tego układu
w położeniu opisanym przez r’, porusza się po pewnym okręgu leżącym w płaszczyźnie
prostopadłej do osi obrotu. Środek tego okręgu leży na osi obrotu. Dla takiego ruchu wektor
r’, opisujący ruch punktu materialnego P w tym układzie, pozwala obliczyć drogę jaką przy
tym obrocie zatacza punkt materialny P. Mianowicie, niech układ obraca się z prędkością
ω,
tak jak to przedstawia rysunek.
r’(t+∆t)
ω
r
0
’
r’(t)
d
ϕ
O’
d
(dr’)
rot
Długość łuku, jaką przebędzie punkt po okręgu w czasie dt, jest równa:
.
d
d
)
r
d
(
i
d
d
ds
rot
r
r
r
×
ϕ
=
ϕ
⋅
=
Ponieważ jednak z rysunku widać, że
,
'
r
'
r
d
0
r
r
r
−
=
to podstawiając ostatni związek do poprzedniego mamy:
,'
r
d
)
'
r
'
r
(
d
d
d
)
r
d
(
0
rot
r
r
r
r
r
r
r
r
×
ϕ
=
−
×
ϕ
=
×
ϕ
=
gdzie skorzystano z faktu, że wektory d
ϕ i r
0
’ są współliniowe.
Mamy
więc równanie wyrażające zależność infinitezymalnie małego przesunięcia
związanego z obrotem od wektora położenia punktu w obracającym się układzie:
'
r
d
)
r
d
(
rot
r
r
r
×
ϕ
=
Pełne przesunięcie poruszającego się punktu mierzone w układzie spoczywającym
wyniesie zatem:
'.
r
d
)
r
d
(
'
r
d
r
d
tr
r
r
r
r
r
×
ϕ
+
+
=

15
Jeżeli ten wzór zastosować do ruchu początku układu O' (translacja), to wtedy
w czasie infinitezymalnie małym, przesunięcie poruszającego się punktu materialnego można
zapisać w postaci:
'
r
d
r
d
'
r
d
r
d
0
r
r
r
r
r
×
ϕ
+
+
=
Stąd prędkość poruszającego się punktu materialnego w układzie nieruchomym wyraża się
wzorem:
,'
r
dt
d
dt
dr
dt
'
r
d
dt
r
d
v
0
r
r
r
r
r
×
ϕ
+
+
=
=
lub inaczej:
.
v
dt
r
d
v
;'
r
v
'
v
v
0
0
tr
tr
r
r
r
r
r
r
r
r
=
=
×
ω
+
+
=
Oznaczając przez
v
u
prędkość unoszenia, zdefiniowaną wzorem:
,'
r
v
v
tr
u
r
r
r
r
×
ω
+
=
możemy wzór na prędkość punktu materialnego mierzoną względem układu o zapisać jak
następuje:
.
v
'
v
v
u
r
r
r
+
=
Prędkość tę interpretujemy jako prędkość unoszenia, bo punkt który spoczywa
w układzie O' (
v’ = 0) ma prędkość v
0,
tj. prędkość z jaką układ O' porusza się na skutek
translacji i prędkości obrotu z jaką unosi dany punkt.
Zwróćmy jeszcze uwagę, że
ω i v
tr
są dla wszystkich punktów układu O' takie same.
Sens fizyczny wektora
ω znamy z poprzedniego wykładu, mianowicie:
ω
ϕ
=
ω
eˆ
dt
d
r
,
gdzie
e
ω
jest wektorem jednostkowym skierowanym wzdłuż osi obrotu (chwilowej)
'
v
r
eˆ
eˆ
dt
d
r
r
r
×
=
ω
=
ϕ
=
ω
ω
ω
.
1.13. Transformacja pochodnej dowolnego wektora po czasie
Wyżej wyznaczyliśmy wektor prędkości korzystając z własności translacji i obrotu.
Spróbujmy teraz znaleźć wyrażenie na pochodną dowolnego wektora po czasie.
Weźmy dowolny wektor
r, którego początek i koniec są opisane w dwu układach, tak
jak na rysunku:
r
1
’
r
2
’
r
2
r
1
r
O’
O
Mamy z rysunku związek:
'
r
'
r
r
r
r
1
2
1
2
r
r
r
r
r
−
=
−
=
.
Dla pochodnych wektora
r
1
i
r
2
mamy związki:

16
⎪
⎪
⎩
⎪⎪
⎨
⎧
×
ω
+
+
=
×
ω
+
+
=
'.
r
v
dt
'
r
'
d
dt
r
d
,'
r
v
dt
'
r
'
d
dt
r
d
2
tr
2
2
1
tr
1
1
r
r
r
r
r
r
r
r
r
r
Odejmując stronami pierwsze równanie od drugiego mamy:
(
)
d r
r
dt
d r
r
dt
r
r
r
r
r r
r
r r
2
1
2
1
2
1
−
=
−
+ ×
−
'( '
')
( '
').
ω
Czyli
dr
dt
d r
dt
r
r
r
r r
=
+ ×
'
ω
.
Skorzystaliśmy z tego, że prędkość translacji w obu układach jest taka sama.
Stosując ten wzór do wektora
r’, który opisuje poruszający się punkt w układzie
poruszającym się, mamy:
'.
r
dt
'
r
'
d
dt
'
r
d
r
r
r
r
×
ω
+
=
W szczególności jeżeli z punktem O' zwiążemy układ kartezjański o wersorach
e
x,
e
y
,
e
z
, to
w układzie primowanym
.
0
dt
eˆ
'
d
,
0
dt
eˆ
'
d
,
0
dt
eˆ
'
d
'
z
'
y
'
x
=
=
=
Wtedy transformacje pochodnych wersorów jednostkowych są dane przez związki:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
×
ω
=
×
ω
+
=
×
ω
=
×
ω
+
=
×
ω
=
×
ω
+
=
.
eˆ
eˆ
dt
eˆ
'
d
dt
eˆ
d
,
eˆ
eˆ
dt
eˆ
'
d
dt
eˆ
d
,
eˆ
eˆ
dt
eˆ
'
d
dt
eˆ
d
'
z
'
z
'
z
z
'
y
'
y
'
y
y
'
x
'
x
'
x
x
r
r
r
r
r
r
Mając wzór na pochodną po czasie wektora
r’, tj. wzór
'
r
'
v
'
r
dt
'
r
'
d
dt
'
r
d
r
r
r
r
r
r
r
×
ω
+
=
×
ω
+
=
możemy znaleźć przyspieszenie różniczkując po czasie wektor prędkości:
'.
r
v
'
v
v
tr
r
r
r
r
r
×
ω
+
+
=
Mamy:
'.
v
2
)
'
r
(
'
r
a
'
a
'
r
dt
'
r
'
d
r
dt
d
dt
v
d
'
v
dt
'
v
'
d
dt
'
r
d
'
r
dt
d
dt
v
d
dt
'
v
d
dt
v
d
tr
tr
tr
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
×
ω
+
×
ω
×
ω
+
×
ε
+
+
=
⎥⎦
⎤
⎢⎣
⎡
×
ω
+
×
ω
+
×
ω
+
+
⎥⎦
⎤
⎢⎣
⎡
×
ω
+
=
×
ω
+
×
ω
+
+
=
Tak
więc przyspieszenie poruszającego się punktu w układzie nieprimowanym można
zapisać następująco:
,
u
a
'
a
a
r
r
r
+
=
gdzie przyspieszenie unoszenia jest równe:

17
,
a
a
a
rot
tr
u
r
r
r
+
=
przy czym przyspieszenie związane z ruchem obrotowym jest dane przez związek:
'.
v
2
)
'
r
(
'
r
a
rot
r
r
r
r
r
r
r
r
×
ω
+
×
ω
×
ω
+
×
ε
=
Gdy
układ obraca się ze stałą prędkością kątową
ω = const, to dω/dt = ε = 0 i wzory
na prędkość oraz przyspieszenie przyjmują postać:
⎩
⎨
⎧
×
ω
+
×
ω
×
ω
+
+
=
×
ω
+
+
=
'.
v
2
)
'
r
(
a
'
a
a
,'
r
v
'
v
v
tr
tr
r
r
r
r
r
r
r
r
r
r
r
r
r
Tak wyraża się prędkość i przyspieszenie w układzie nieruchomym, przez odpowiednie
wielkości mierzone w układzie poruszającym się ze stałą prędkością kątową
ω i prędkością
translacji v
tr
układu O' względem układu O.
W szczególnym przypadku, gdy układ doznaje tylko translacji, tzn. prędkość
unoszenia wynosi:
,
dt
r
d
v
v
0
tr
0
r
r
r
=
=
to
⎩
⎨
⎧
+
=
+
=
.
a
'
a
a
,
v
'
v
v
tr
tr
r
r
r
r
r
r
Jeżeli dodatkowo założymy, że translacja odbywa się ze stałą prędkością v
tr
=const, to
a
tr
= 0, bo d
v
tr
/dt = 0. Wtedy pełny komplet związków transformacyjnych nazywa się
transformacjami Galileusza. Transformacje te mają postać:
⎪
⎩
⎪
⎨
⎧
=
+
=
=
+
=
'.
a
a
,
v
'
v
v
,
t
t
,
r
'
r
r
0
0
r
r
r
r
r
r
r
r
Układy poruszające się względem siebie ze stałą prędkością (po prostych),
v
0
=
const,
nazywają się układami inercjalnymi. Transformacje Galileusza są zatem transformacjami
wielkości kinematycznych między układami inercjalnymi.
W ogólnym przypadku związki te są dane przez formuły:
⎪
⎩
⎪
⎨
⎧
×
ω
+
×
ω
×
ω
+
×
ε
+
+
=
×
ω
+
+
=
=
+
=
'.
v
2
)
'
r
(
'
r
a
'
a
a
,'
r
v
'
v
v
,'
t
t
,
r
'
r
r
tr
tr
tr
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
2. Dynamika punktu materialnego
2.1. Pierwsza zasada dynamiki
Obserwacja zjawisk przyrody, a także doświadczenia życia codziennego uczą, że ciała
materialne mają zdolność oddziaływania między sobą. Obecność oddziaływania między
dwoma ciałami poznajemy po tym, że stan jednego ciała zmienia się w wyniku obecności
w jego otoczeniu drugiego ciała. Przykładem może być ruch punktu materialnego w pobliżu
Ziemi, jak to widać na rysunku.

18
g
y
x
v
0
Gdyby Ziemia nie działała na punkt materialny wyrzucony z prędkością
v
0
, punkt materialny
poruszałby się ruchem jednostajnym po linii prostej. Tymczasem jak wiemy z kinematyki
ruch ten odbywa się po paraboli. Takich przykładów można podać znacznie więcej.
Do tego, by opisać zachowanie się punktu materialnego oddziaływującego z innymi
ciałami, trzeba przede wszystkim zdać sobie sprawę z tego, jak zachowuje się punkt
materialny, na który nic nie działa. Kłopot polega na tym, że w warunkach ziemskich,
w których dokonujemy naszych doświadczeń, wszystkie ciała poddane są oddziaływaniu
Ziemi, tj. są przez Ziemię przyciągane. To przyciąganie można częściowo wyeliminować,
umieszczając badane ciało na poziomym stole. Ciało położone na takim stole, zachowuje się
tak, jak gdyby nie było przyciągane przez Ziemię. w istocie rzeczy jest inaczej, bowiem
wystarczy usunąć stół, żeby się przekonać, że Ziemia działa przez cały czas na to ciało. Pod
wpływem tego oddziaływania stół ulega odkształceniu, ale sprężystość stołu równoważy siłę
przyciągania.
Jak zachowuje się zatem ciało pozostawione na twardym stole?
Doświadczenie pokazuje, że ciało spoczywa. Można by stąd wysunąć wniosek, że
ciało na które nic nie działa pozostaje w spoczynku. Jest to jednak wniosek błędny. Jeżeli
bowiem zakłócimy stan spoczynku ciała na stole zauważymy, że ciało to po przebyciu pewnej
drogi po stole zatrzyma się. Przebyta droga zależeć będzie od gładkości powierzchni stołu.
Stwierdzamy więc, że ruch ciała po stole nie jest ruchem ciała, na które nic nie działa. Działa
bowiem powierzchnia stołu powodując ruch hamujący ciała.
Aby
stwierdzić jak zachowuje się ciało, na które nie działa powierzchnia stołu,
musimy wyeliminować chropowatość powierzchni. Całkowicie tarcia nie da się
wyeliminować. Można je znacznie jednak zmniejszyć. w takim przypadku ciało, wprawione
w ruch z prędkością
v, będzie się z tą prędkością poruszać ruchem prostoliniowym. Ruch ten
nie w każdym jednak układzie odniesienia będzie ruchem jednostajnym. Ruch będzie
prostoliniowym względem stołu, ale np. względem Słońca będzie krzywoliniowym, a zatem
przyśpieszonym.
Wnioskujemy
zatem,
że nie w każdym układzie odniesienia ruch ciała, na które nic nie
działa, jest ruchem jednostajnym.
Układ, w którym punkt materialny, na który nic nie działa, porusza się ruchem
jednostajnym lub spoczywa, nazywa się układem inercjalnym odniesienia.
Pytamy, czy taki układ istnieje?
Odpowiedź na tak postawione pytanie daje nam pierwsza zasada dynamiki:
Istnieje taki układ odniesienia, w którym punkt materialny, na który nic nie
działa, spoczywa lub porusza się ruchem jednostajnym.
Zasada ta jest postulatem istnienia układu inercjalnego, nie podaje ona jednak,
z jakimi ciałami należy taki układ wiązać. Ani układ związany z Ziemią ani też ze Słońcem,
czy tzw. gwiazdami stałymi, nie jest układem inercjalnym dokładnie. w praktyce pomijamy
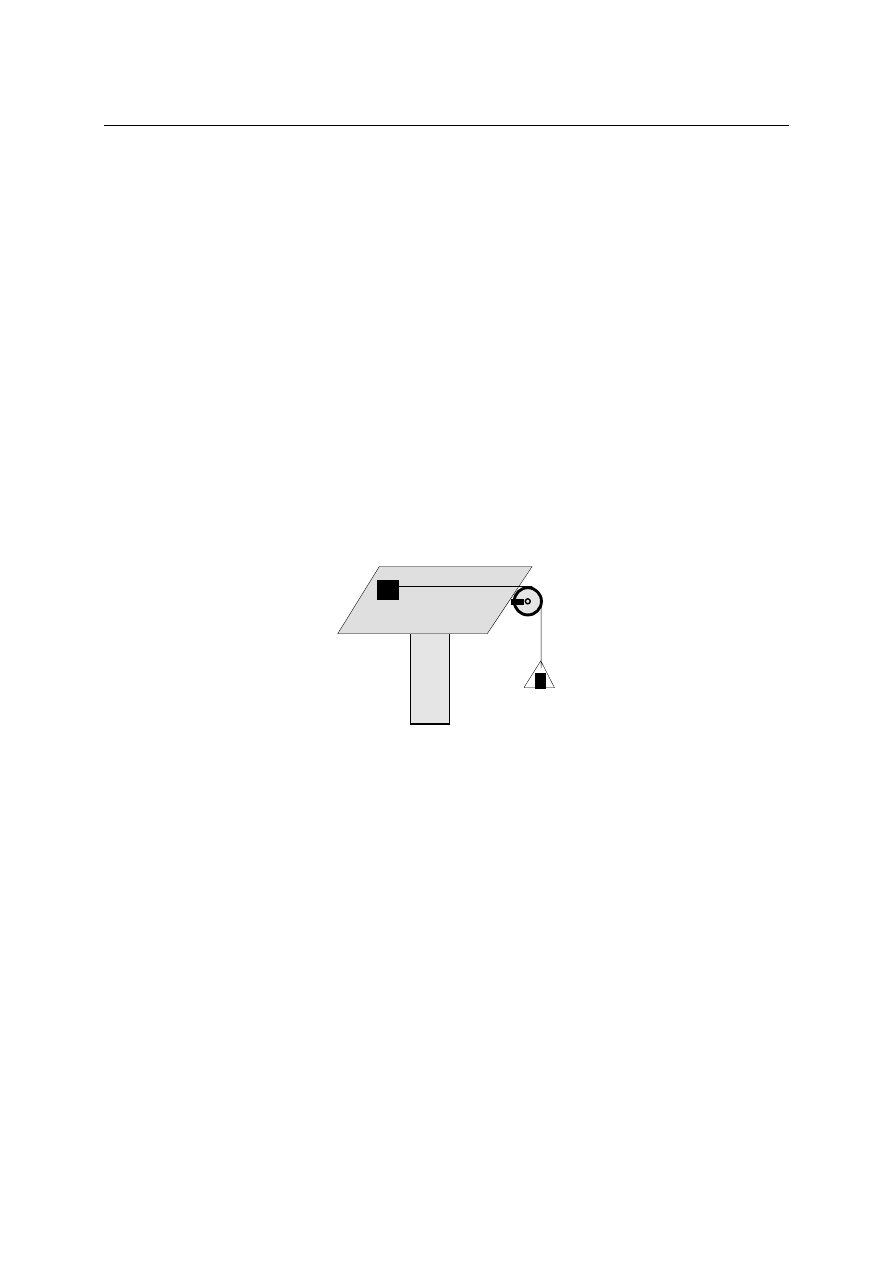
19
jednak niewielkie odchylenie tych układów od inercjalnego układu, traktując te układy jako
w przybliżeniu inercjalne.
Problem znalezienia układu inercjalnego w mechanice jest więc problemem otwartym.
Stąd zasada ta nie jest prawem doświadczalnym, lecz tylko postulatem.
2.2. Druga zasada dynamiki
Wiemy
już jak zachowuje się punkt materialny, na który nic nie działa. w układzie
inercjalnym taki punkt pozostaje w spoczynku lub porusza się ruchem jednostajnym. Jeżeli
zatem wyobrazimy sobie inny punkt materialny, który porusza się w układzie inercjalnym
ruchem innym niż ruch jednostajny, to takie odchylenie od ruchu jednostajnego jest miarą
faktu, że na ten punkt działają inne ciała. Za miarę tego oddziaływania można przyjąć
przyspieszenie punktu materialnego, ponieważ ono jest odstępstwem tego ruchu od ruchu
jednostajnego.
Dalej,
doświadczenie uczy nas, że oddziaływanie między ciałami zależy od odległości
między nimi. Chcąc zatem zbadać, jak porusza się punkt materialny, gdy na niego działa inny
punkt materialny musimy w czasie eksperymentu utrzymywać stałą odległość między nimi.
Stałość oddziaływania między ciałami (punktami materialnymi) można uzyskać umieszczając
badany punkt materialny M na stole doskonale gładkim i działać nań przyrządem
przyspieszającym, zwanym akceleratorem. Akcelerator tego typu przedstawiono na rysunku.
.
A
,......,
A
,
A
:
A
,
M
,.....,
M
,
M
:
M
k
2
1
n
2
1
A
M
Obserwując ruch punktu na stole można mierzyć przyspieszenie tego punktu.
Ponieważ druga zasada dynamiki jest prawem doświadczalnym wprowadzimy ją na
podstawie odpowiedniego eksperymentu. Załóżmy, że dysponujemy n punktami materialnymi
M i k akceleratorami A.
Działając kolejno pierwszym akceleratorem A
1
na kolejne punkty materialne
mierzymy odpowiednie przyspieszenia:
.
a
,........
a
,
a
,
a
:
A
)
1
(
n
)
1
(
3
)
1
(
2
)
1
(
1
1
r
r
r
r
Doświadczenie to pokazuje, że wszystkie przyspieszenia mają ten sam kierunek i zwrot.
Można zatem wybrać n dodatnich liczb:
,
m
,.......
m
,
m
,
m
)
1
(
n
)
1
(
3
)
1
(
2
)
1
(
1
takich by spełniały równania:
.
a
m
........
a
m
a
m
a
m
:
A
)
1
(
n
)
1
(
n
)
1
(
3
)
1
(
3
)
1
(
2
)
1
(
2
)
1
(
1
)
1
(
1
1
r
r
r
r
⋅
=
=
⋅
=
⋅
=
⋅
Liczby
są określone z dokładnością do stałego czynnika.
Układ równań nie zmieni się, jeżeli pomnożymy każdą z liczb
przez dowolny czynnik.
,
m
,.......
m
,
m
,
m
)
1
(
n
)
1
(
3
)
1
(
2
)
1
(
1
,
m
,.......
m
,
m
,
m
)
1
(
n
)
1
(
3
)
1
(
2
)
1
(
1
Powtórzmy eksperyment z drugim akceleratorem A2. Działając akceleratorem A
2
na
kolejne punkty i mierząc przyspieszenia tych punktów mamy:

20
.
a
,........
a
,
a
,
a
:
A
)
2
(
n
)
2
(
3
)
2
(
2
)
2
(
1
2
r
r
r
r
Wybieramy
nowe
liczby
takie by spełnione były
równania:
,
m
,.......
m
,
m
,
m
)
2
(
n
)
2
(
3
)
2
(
2
)
2
(
1
.
a
m
........
a
m
a
m
a
m
:
A
)
2
(
n
)
2
(
n
)
2
(
3
)
2
(
3
)
2
(
2
)
2
(
2
)
2
(
1
)
2
(
1
2
r
r
r
r
⋅
=
=
⋅
=
⋅
=
⋅
Tak samo postępujemy z kolejnymi akceleratorami aż do k-tego.
Dla k-tego akceleratora mamy:
.
a
,........
a
,
a
,
a
:
A
)
k
(
n
)
k
(
3
)
k
(
2
)
k
(
1
k
r
r
r
r
,
m
,.......
m
,
m
,
m
)
k
(
n
)
k
(
3
)
k
(
2
)
k
(
1
.
a
m
......
a
m
a
m
a
m
:
A
)
k
(
n
)
k
(
n
)
k
(
3
)
k
(
3
)
k
(
2
)
k
(
2
)
k
(
1
)
k
(
1
k
r
r
r
r
⋅
=
=
⋅
=
⋅
=
⋅
Zestawiając komplet równań wiążących wszystkie wyniki pomiarów i wybranych liczb
mamy:
.
a
m
........
a
m
a
m
a
m
:
A
)
1
(
n
)
1
(
n
)
1
(
3
)
1
(
3
)
1
(
2
)
1
(
2
)
1
(
1
)
1
(
1
1
r
r
r
r
⋅
=
⋅
=
⋅
=
⋅
.
a
m
........
a
m
a
m
a
m
:
A
)
2
(
n
)
2
(
n
)
2
(
3
)
2
(
3
)
2
(
2
)
2
(
2
)
2
(
1
)
2
(
1
2
r
r
r
r
⋅
=
⋅
=
⋅
=
⋅
......................................................................................
......................................................................................
.
a
m
........
a
m
a
m
a
m
:
A
)
k
(
n
)
k
(
n
)
k
(
3
)
k
(
3
)
k
(
2
)
k
(
2
)
k
(
1
)
k
(
1
k
r
r
r
r
⋅
=
⋅
=
⋅
=
⋅
Podkreślmy w tym miejscu, że wszystkie liczby
dla
dowolnego i = 1, 2, ...., k dobrane są z dokładnością do stałego czynnika. Możemy zatem
ustalić ten czynnik tak, aby było spełnione równanie:
,
m
,.......
m
,
m
,
m
)
i
(
n
)
i
(
3
)
i(
2
)
i
(
1
,
m
m
.......
m
m
m
1
)
k
(
1
)
3
(
1
)
2
(
1
)
1
(
1
=
=
=
=
=
tzn. tak, aby liczby te nie zależały od akceleratora.
Wypisana seria równań charakteryzuje w pewien sposób punkt materialny M
1
i pociąga za sobą następną serię równości charakteryzujących punkt M
2
:
.
m
m
.......
m
m
m
2
)
k
(
2
)
3
(
2
)
2
(
2
)
1
(
2
=
=
=
=
=
Te równania wymagają, aby były spełnione również równości:
,
m
m
.......
m
m
m
3
)
k
(
3
)
3
(
3
)
2
(
3
)
1
(
3
=
=
=
=
=
i tak postępowanie można przedłużyć aż do n-tego punktu M
n
, dla którego otrzymujemy:
.
m
m
.......
m
m
m
n
)
k
(
n
)
3
(
n
)
2
(
n
)
1
(
n
=
=
=
=
=
Przy takim wyborze liczb m, nasz układ równań wiążących te liczby z wynikami pomiarów
przyspieszeń, przyjmuje postać:
.
a
m
........
a
m
a
m
a
m
:
A
)
1
(
n
n
)
1
(
3
3
)
1
(
2
2
)
1
(
1
1
1
r
r
r
r
⋅
=
⋅
=
⋅
=
⋅
.
a
m
........
a
m
a
m
a
m
:
A
)
2
(
n
n
)
2
(
3
3
)
2
(
2
2
)
2
(
1
1
2
r
r
r
r
⋅
=
⋅
=
⋅
=
⋅
......................................................................................
......................................................................................
.
a
m
........
a
m
a
m
a
m
:
A
)
k
(
n
n
)
k
(
3
3
)
k
(
2
2
)
k
(
1
1
k
r
r
r
r
⋅
=
⋅
=
⋅
=
⋅
Mamy w tych równaniach sytuację, w której liczby mi (i = 1, 2,..., n) nie zależą od
akceleratora, są takie same dla różnych akceleratorów, charakteryzują natomiast punkty
materialne. z kolei iloczyn m
i
a
i
(j)
dla ustalonego j nie zależy od punktu, charakteryzuje zatem
j-ty akcelerator. Możemy każdy wiersz równań przyrównać do stałej wielkości

21
charakteryzującej oddziaływanie danego akceleratora. Wielkość tę nazywać będziemy siłą.
Równania przyjmują postać:
.
F
a
m
........
a
m
a
m
a
m
:
A
1
)
1
(
n
n
)
1
(
3
3
)
1
(
2
2
)
1
(
1
1
1
r
r
r
r
r
=
⋅
=
⋅
=
⋅
=
⋅
.
F
a
m
........
a
m
a
m
a
m
:
A
2
)
2
(
n
n
)
2
(
3
3
)
2
(
2
2
)
2
(
1
1
2
r
r
r
r
r
=
⋅
=
⋅
=
⋅
=
⋅
......................................................................................
......................................................................................
.
F
a
m
........
a
m
a
m
a
m
:
A
k
)
k
(
n
n
)
k
(
3
3
)
k
(
2
2
)
k
(
1
1
k
r
r
r
r
r
=
⋅
=
⋅
=
⋅
=
⋅
Miarą oddziaływania danego akceleratora na dowolny punkt materialny jest iloczyn
przyspieszenia, jakie ten akcelerator nadaje danemu punktowi i pewnej wielkości skalarnej m
charakteryzującej ten punkt. Ten iloczyn, jako wielkość wektorowa, zwany jest siłą. w ten
sposób II zasadę dynamiki możemy zapisać równaniem:
.
F
a
m
r
r =
⋅
Przy zadanym akceleratorze przyspieszenie punktu materialnego jest zależne od liczby
m właściwej temu punktowi.
Punkty o dużych wartościach m poruszają się pod wpływem danej siły z mniejszym
przyspieszeniem niż punkty o mniejszych wartościach m. Wielkość m charakteryzuje więc
podatność ciała (punktu materialnego) na ruch. Wielkość tą nazywa się masą bezwładną ciała.
Jeżeli dwa punkty materialne o masach odpowiednio m1 i m2 połączyć ze sobą, tak by
stanowiły jeden punkt, to będzie się on poruszał pod wpływem danej siły jak punkt o masie m
= m1+m2. Masa bezwładna jest więc miarą ilości materii związanej z punktem.
Drugą zasadę dynamiki można również zapisać w postaci
,
m
F
a
r
r =
co czytamy: przyspieszenie punktu materialnego w jego ruchu pod wpływem siły jest
proporcjonalne do tej siły i odwrotnie proporcjonalne do masy bezwładności punktu. Zasada
ta definiuje równocześnie dwie wielkości fizyczne siłę i masę bezwładną.
2.3. Zasada niezależności działania sił
Ze
związku:
,
F
a
m
r
r =
⋅
wynika, że siła jest wektorem. Poddając punkt materialny o masie m kolejno działaniu sił:
F
1
,
F
2
,....,
F
n
i mierząc przyspieszenia
a
1
,
a
2
,.....,
a
n,
jakie każda z sił nadaje temu punktowi
materialnemu, II zasada dynamiki pozwala nam napisać następujące równania ruchu:
.
F
a
m
........,
,
F
a
m
,
F
a
m
n
n
2
2
1
1
r
r
r
r
r
r
=
⋅
=
⋅
=
⋅
Jeżeli teraz na ten punkt podziałamy równocześnie wszystkimi siłami, tj. wypadkową
siłą:
n
2
1
F
F
F
F
r
K
r
r
r
+
+
+
=
,
to równanie ruchu będzie miało postać dokładnie taką samą, jak dla jednej siły:
,
F
a
m
r
r =
⋅
przy czym teraz przyspieszenie jest równe sumie wektorowej przyspieszeń, jakie punkt
materialny uzyskał pod wpływem działania każdej siły oddzielnie, tj.
n
2
1
a
a
a
a
r
K
r
r
r
+
+
+
=
.
Twierdzenie to jest nazywane zasadą niezależności działania sił i może być sformułowane
następująco:

22
Jeżeli na punkt materialny działa kilka sił, to punkt ten porusza się z przyspieszeniem
równym sumie przyspieszeń jakie uzyskuje on pod wpływem poszczególnych sił działających
niezależnie.
2.4. Pomiar masy bezwładnej
Jeżeli mamy dwa punkty materialne o masach m
1
i m
2
, to działając kolejno tą samą
siłą na te punkty, możemy mierzyć przyspieszenia
a
1
i
a
2
. Wtedy na mocy drugiej zasady
dynamiki mamy równania:
⎪⎩
⎪
⎨
⎧
=
⋅
=
⋅
,
F
a
m
,
F
a
m
2
2
1
1
r
r
r
r
które redukują się do jednego:
.
a
m
a
m
1
1
2
2
r
r
⋅
=
⋅
Ponieważ przyspieszenia mają te same kierunki, to z tego równania można wyrazić
masę bezwładną m
2
przez masę bezwładną m
1
:
.
m
a
a
m
1
2
1
2
=
Mierząc przyspieszenia dwóch ciał, pochodzące od działania tej samej siły i wybierając masę
bezwładną jednego z ciał za masę jednostkową, możemy wyznaczyć masę drugiego według
powyższego wzoru.
Za
masę jednostkową przyjęto masę walca o wysokości 33 mm i takiej samej średnicy,
wykonanego z platyny i irydu. Tę masę jednostkową nazwano kilogramem.
Mając metodę pomiaru masy bezwładnej i jednostkę tej wielkości, można mierzyć
również siłę na podstawie równania:
.
a
m
F
r
r
=
Mierząc zatem masę i przyspieszenie, jakie ta siła nadaje danej masie, mamy metodę
pomiaru siły. Jednostką siły jest niuton (N). Jest to siła, która działając na masę jednego
kilograma nadaje jej przyspieszenie jednego metra na sekundę do kwadratu:
[ ] [ ] [ ]
.
s
m
kg
N
a
m
F
2
⋅
=
⇒
⋅
=
2.5. Trzecia zasada dynamiki
Jeżeli ciało a działa na ciało B siłą F
AB
, to ciało B działa na ciało a z siłą F
BA
równą co do wartości sile F
AB
, lecz przeciwnie skierowaną.
Trzy zasady dynamiki stanowią podstawę tzw. mechaniki niutonowskiej. Zasad tych
nie da się rozdzielić. Pierwsza zasada ustala układ inercjalny, druga stanowi równanie ruchu,
a trzecia wskazuje siły działające na dany punkt materialny pochodzące od innych ciał
(traktowanych jak punkty materialne).
2.6. Podstawowe zagadnienia dynamiki
Podstawowe zagadnienia dynamiki dla punktu materialnego formułuje się
następująco.
Dane są siły działające na punkt materialny i warunki początkowe, tj. położenie
i prędkość w chwili początkowej, znaleźć ruch punktu materialnego.

23
3. Pole grawitacyjne
3.1. Oddziaływanie grawitacyjne
Wiemy,
że aby opisać ruch punktu materialnego należy wyznaczyć siłę działającą na
dany punkt materialny. Ponieważ siły występujące w przyrodzie zależą od rodzaju
oddziaływania, któremu poddany został punkt materialny, dlatego też, badanie charakteru
oddziaływań jest głównym zadaniem fizyki. Siły z jakimi spotykamy się w podstawowym
zagadnieniu dynamiki zależą od położenia, prędkości i czasu, tj. mogą być ogólnie zapisane
przy pomocy funkcji:
)
t
,
v
,
r
(
F
F
r
r
r
r
=
.
Oddziaływanie grawitacyjne jest przykładem oddziaływania, które zależy tylko od
współrzędnych przestrzennych. Nie zależy natomiast ani od prędkości, ani od czasu.
Siła z jaką przyciągają się dwa punkty materialne jest wprost proporcjonalna do
iloczynu mas grawitacyjnych tych punktów, ma kierunek prostej łączącej punkty i jest
odwrotnie proporcjonalna do kwadratu odległości między nimi. Na rysunku niżej pokazano
siłę, jaką działa punkt materialny o masie grawitacyjnej
µ
2
,
umieszczony w początku układu
współrzędnych, na punkt o masie grawitacyjnej
µ
2
, znajdujący się w położeniu wyznaczonym
przez wektor
r.
r
F
µ
2
µ
1
Siła ta jest równa:
r
r
k
F
3
2
1
r
r
µ
µ
−
=
.
Ciało o większej masie grawitacyjnej ma większą podatność na oddziaływanie
grawitacyjne i odwrotnie, ciało o mniejszej masie grawitacyjnej oddziaływuje słabiej
z innymi ciałami. Masa grawitacyjna jest więc miarą podatności ciała na oddziaływanie
grawitacyjne.
Porównując oddziaływania między różnymi punktami materialnymi, o różnych
masach grawitacyjnych stwierdzamy, że stosunek sił grawitacyjnych jest równy stosunkowi
mas grawitacyjnych. Oznaczając siłę z jaką
µ
1
działa na
µ
2
przez:
r
r
k
F
3
2
1
2
r
r
µ
µ
−
=
,
zaś siłę oddziaływania
µ
1
na
µ
3
dla tej samej odległości przez:
r
r
k
F
3
3
1
3
r
r
µ
µ
−
=
,
otrzymujemy stosunek sił grawitacyjnych, którego miarą jest stosunek mas grawitacyjnych
punktów, na które działa ustalony punkt o masie
µ
1
24
3
2
2
3
1
2
2
1
3
2
r
k
r
k
F
F
µ
µ
=
µ
µ
µ
µ
=
.
Mamy więc metodę pomiaru mas grawitacyjnych.
Z drugiej strony doświadczenie uczy, że masa grawitacyjna jest proporcjonalna do
masy bezwładnej punktu materialnego. Niezbitym dowodem tego twierdzenia jest fakt, że
ciała w pobliżu Ziemi poruszają się z tym samym przyspieszeniem g = 9,81m/s
2
.
Równanie ruchu punktu materialnego o masie bezwładnej m i masie grawitacyjnej
µ
pod wpływem siły grawitacyjnej Ziemi, której masę grawitacyjną oznaczymy przez
µ
Z
,
można zapisać w postaci:
,
r
k
ma
2
Z
µ
µ
−
=
przy czym a = g. Dzieląc to równanie przez stałą wartość przyspieszenia, możemy to
równanie zapisać jako związek masy bezwładnej i masy grawitacyjnej danego punktu:
.
g
r
k
const
,
const
m
2
Z
µ
=
µ
⋅
=
Wybierając const = 1 otrzymujemy równość masy grawitacyjnej i masy bezwładnej:
.
m
µ
=
Możemy zatem mierzyć masę grawitacyjną w tych samych jednostkach co masę
bezwładną i nie rozróżniać tych dwóch wielkości fizycznych, choć są to różne wielkości
charakteryzujące ciało.
Prawo powszechnego ciążenia możemy teraz zapisać w postaci:
,
r
r
mM
G
F
3
r
r
−
=
gdzie G jest stałą grawitacyjną o wymiarze:
[ ] [ ]
[ ]
[ ]
2
2
2
2
kg
m
N
m
r
F
G
⋅
=
=
.
Wartość stałej grawitacji jest równa:
2
2
11
kg
Nm
10
67
,
6
G
−
⋅
=
.
Jest to siła z jaką przyciągają się dwa punkty materialne o masach jednego kilograma każdy,
umieszczone w odległości jednego metra od siebie.
3.2. Pole siły grawitacji i energia potencjalna
Rozważmy dokładniej oddziaływanie dwóch punktów materialnych o masach m i M
rozmieszczonych w przestrzeni, tak jak na rysunku:
F
m
r-r’
r
r’
m
M
O
Siła grawitacyjna działająca na punkt o masie m jest równa:

25
).
'
r
r
(
'
r
r
Mm
G
F
3
m
r
r
r
r
−
−
−
=
Siła ta bierze się stąd, że w punkcie wyznaczonym przez wektor
r’, znajduje się ciało o masie
M, które przyciąga (działa) ciało o masie m. Zamiast mówić, że ciało M działa grawitacyjnie
na ciało m, możemy mówić, że ciało M wytwarza wokół siebie pole grawitacyjne.
Rozumiemy przez to, że obecność ciała M zmienia przestrzeń wokół tego ciała w ten sposób,
że w każdym punkcie tej przestrzeni na umieszczony punkt, działa siła grawitacji określona
wzorem podanym wyżej. Siła ta jest w każdym punkcie inna i zależy od masy m, na którą
działa. Dla ustalonej masy m, którą dalej będziemy nazywać masą próbną, bo służy ona do
stwierdzenia, czy w danym punkcie przestrzeni istnieje pole, siła ta zależy tylko od masy
wytwarzającej pole i punktu przestrzeni, w którym pole mierzymy.
Doświadczenie uczy nas, że jeżeli w przestrzeni otaczającej masę M umieścić masę
próbną (sondę), to w dowolnym punkcie na sondę będzie działać siła. Siła ta jest określona
prawem powszechnego ciążenia i jest różna w różnych punktach przestrzeni. Mówimy, że
w przestrzeni otaczającej masę M jest określone pole wektorowe siły grawitacyjnej. Dalej
możemy opuścić indeks m przy definicji siły, rozumiejąc, że w każdym punkcie pola działa
siła na umieszczony w tym punkcie przestrzeni ten sam punkt materialny o masie m.
Będziemy zatem prawo powszechnego ciążenia pisać w postaci:
).
'
r
r
(
'
r
r
Mm
G
F
3
r
r
r
r
−
−
−
=
Równanie to określa pole siły grawitacyjnej wokół masy M, którą nazywać będziemy
źródłem tego pola, a punkt położenia tego źródła nazywać będziemy centrum pola.
Zwróćmy uwagę, że
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
∇
=
−
−
−
'
r
r
1
'
r
r
'
r
r
3
r
r
r
r
r
r
,
gdzie
dz
d
eˆ
dy
d
eˆ
dx
d
eˆ
z
y
x
+
+
=
∇
jest operatorem różniczkowania zwanym operatorem Nabla.
Rzeczywiście, mamy:
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
∇
r
1
dz
d
eˆ
r
1
d
d
eˆ
r
1
dx
d
eˆ
r
1
z
y
x
dz
dr
r
1
dr
d
eˆ
dy
dr
r
1
dr
d
eˆ
dx
dr
r
1
dr
d
eˆ
z
y
x
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
=
.
r
r
r
2
z
2
eˆ
r
2
y
2
eˆ
r
2
x
2
eˆ
r
1
dz
dr
eˆ
dy
dr
eˆ
dx
dr
eˆ
r
1
z
y
x
2
z
y
x
2
r
−
=
⎥⎦
⎤
⎢⎣
⎡
+
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
+
−
=
Wykorzystując ten związek, równanie na siłę pola grawitacyjnego, możemy zapisać
w postaci:
.
'
r
r
GMm
'
r
r
1
GMm
F
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−∇
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
∇
=
r
r
r
r
r
Definiując energię potencjalną U masy m w polu siły grawitacyjnej równaniem:

26
.
'
r
r
GMm
U
r
r −
−
=
mamy związek:
.
U
F
−∇
=
r
Siła grawitacyjna daje się zatem przedstawić w postaci ujemnego gradientu energii
potencjalnej. Taką siłę nazywa się potencjalną. Jeżeli energia potencjalna siły potencjalnej nie
zależy od czasu, to siłę nazywa się zachowawczą. Ponieważ energia potencjalna U dla pola
grawitacyjnego nie zależy od czasu, to siła grawitacji jest siłą zachowawczą.
3.3. Natężenie i potencjał pola grawitacyjnego
Zwróćmy uwagę, że w każdym punkcie pola siły grawitacyjnej, siła zależy od masy
umieszczonej w danym punkcie pola. Siła ta niejednoznacznie charakteryzuje własność pola
w danym punkcie. Dlatego też definiujemy w każdym punkcie pola grawitacyjnego nowy
wektor
g, zwany natężeniem pola grawitacyjnego:
.
m
F
g
r
r =
Mamy
więc nowe pole wektorowe wektora natężenia pola grawitacyjnego.
Wstawiając do tego wzoru wyrażenie na siłę grawitacyjną otrzymujemy jawną postać
wektora natężenia:
).
'
r
r
(
'
r
r
GM
g
3
r
r
r
r
−
−
−
=
Ze wzoru tego widać teraz, że wektor ten jednoznacznie opisuje pole grawitacyjne,
ponieważ zależy tylko od wektora położenia punktu w przestrzeni
r, położenia źródła pola r’
i masy wytwarzającej pole grawitacyjne M.
Ponieważ wiemy już, że
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
∇
=
−
−
−
'
r
r
1
'
r
r
'
r
r
3
r
r
r
r
r
r
,
to wektor natężenia może być przedstawiony w postaci gradientu pewnej funkcji skalarnej
ϕ.
Mianowicie:
),
r
(
'
r
r
GM
)
'
r
r
(
'
r
r
GM
g
3
ϕ
−∇
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−∇
=
−
−
−
=
r
r
r
r
r
r
gdzie funkcja skalarna
ϕ zwana potencjałem pola grawitacyjnego jest zdefiniowana
równaniem:
.
'
r
r
GM
)
r
(
r
r −
−
=
ϕ
Jest to druga z wielkości fizycznych, jednoznacznie charakteryzujących pole
grawitacyjne. Potencjał pola grawitacyjnego zależy, podobnie jak wektor natężenia pola,
tylko od położenia punktu względem źródła pola i masy wytwarzającej to pole. Wielkości te
związane są równaniem:
.
grad
g
ϕ
−∇
=
ϕ
−
=
r
Na podstawie tego związku stwierdzamy, że pole wektora natężenia pola
grawitacyjnego, podobnie jak pole wektora siły grawitacyjnej, jest polem potencjalnym.
Dalej, ponieważ potencjał
ϕ nie zależy od czasu, to również pole wektora natężenia pola
grawitacyjnego jest polem zachowawczym.
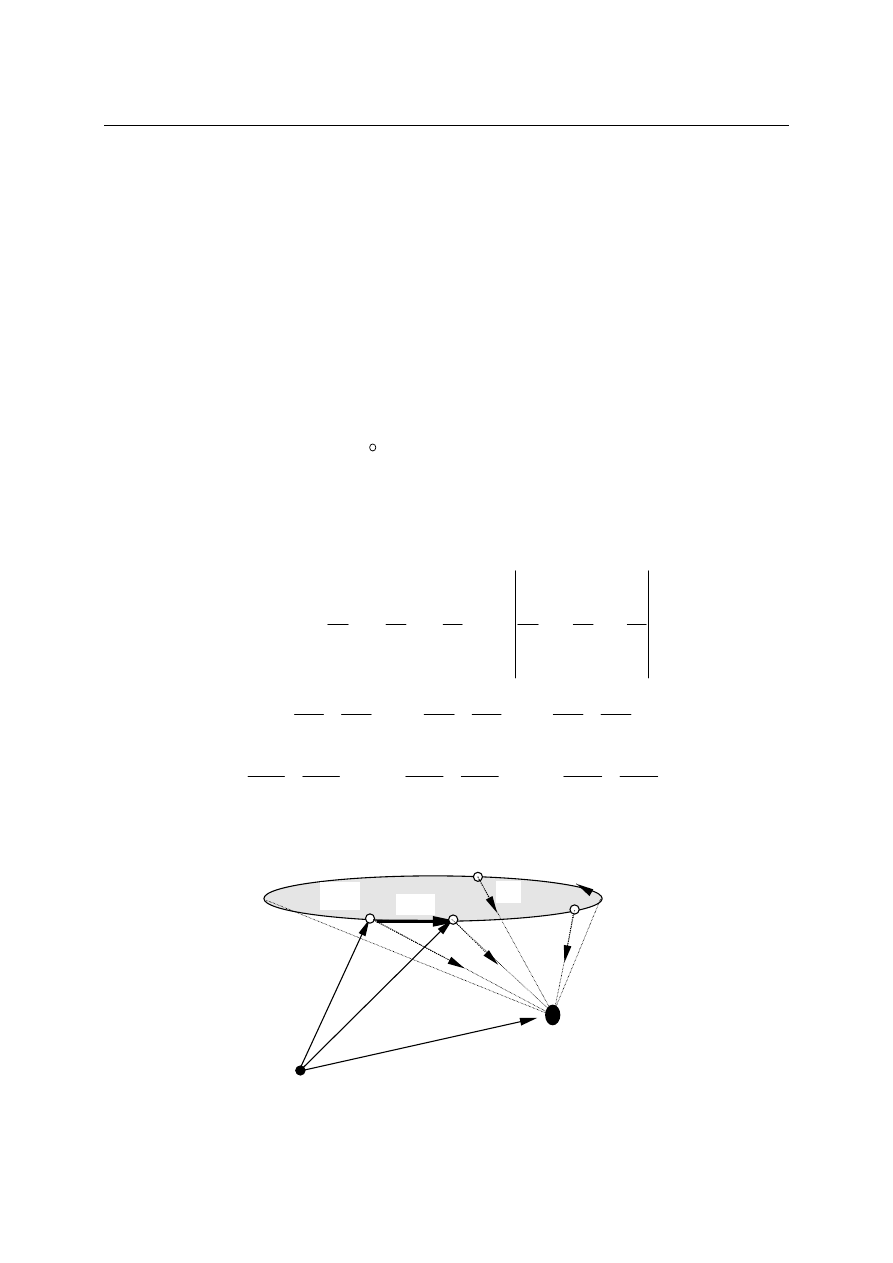
27
3.4. Sens fizyczny wprowadzonych wielkości
Stwierdziliśmy, że w przypadku pola grawitacyjnego, zarówno pole wektora siły
grawitacyjnej, jak i pole wektora natężenia pola grawitacyjnego, dają się przedstawić
w postaci gradientów funkcji skalarnych mających sens fizyczny energii potencjalnej
i potencjału. Porównując równanie
,
U
F
z
g
−∇
=
ϕ
−∇
=
r
r
widzimy, że energia potencjalna punktu materialnego i potencjał pola grawitacyjnego
w wybranym punkcie pola, są ze sobą związane relacją:
.
m
U
ϕ
=
Dalej z definicji wektora natężenia pola grawitacyjnego mamy:
.
g
m
F
r
r
=
Aby wyjaśnić sens fizyczny potencjalnego charakteru pól: siły grawitacyjnej i natężenia pola
grawitacyjnego, wykorzystamy znane w matematyce twierdzenie Stokesa:
∫
∫
⋅
×
∇
=
S
d
)
A
(
r
d
A
r
r
r
r
.
Dla naszych potrzeb wystarczy wiedzieć, że całkę po krzywej zamkniętej z dowolnego
wektora
A, można zamienić na całkę po powierzchni ograniczonej tą krzywą z iloczynu
wektorowego
∇×A. Weźmy najpierw pole wektora natężenia pola grawitacyjnego g.
Pokażemy, że wektor
∇×g jest równy zero. Mamy:
z
y
x
z
y
x
z
y
x
g
g
g
dz
d
dy
d
dx
d
eˆ
eˆ
eˆ
g
dz
d
eˆ
dy
d
eˆ
dx
d
eˆ
g
=
×
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
×
∇
r
r
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
+
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
dy
dg
dx
dg
eˆ
dx
dg
dz
dg
eˆ
dz
dg
dy
dg
eˆ
x
y
z
z
x
y
y
z
x
.
0
dydx
d
dxdy
d
eˆ
dxdz
d
dzdx
d
eˆ
dzdy
d
dydz
d
eˆ
2
2
z
2
2
y
2
2
x
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
ϕ
+
ϕ
−
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
ϕ
+
ϕ
−
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
ϕ
+
ϕ
−
=
Weźmy teraz pewną skierowaną krzywą zamkniętą
l w polu grawitacyjnym masy M,
jak na rysunku. Krzywa ta obejmuje powierzchnię S. z faktu, że krzywa brana jest w polu
wektora
g, wynika, że w każdym punkcie krzywej jest określony wektor natężenia pola g.
O
M
g
g
g
r+dr
r
dr
l
S
r’
Zapiszmy teraz całkę z natężenia pola g po przedstawionej na rysunku krzywej
zamkniętej. Mamy:

28
.
0
g
bo
,
0
S
d
g
r
d
g
=
×
∇
=
×
∇
=
∫
∫
r
r
r
r
r
Widzimy więc, że dzięki temu, iż g dało się przedstawić w postaci gradientu z potencjału (z
pola skalarnego), to znika wektor
∇ × =
rg 0
, a to pociąga za sobą, równość:
.
0
r
d
g
∫
=
r
r
Sens fizyczny tej ostatniej relacji jest bardzo prosty, wystarczy pomnożyć to równanie przez
m, wtedy mamy:
.
0
r
d
F
r
d
g
m
∫
∫
=
=
r
r
r
r
Wyrażenie podcałkowe stanowi teraz pracę elementarną przesunięcia masy m na drodze dr.
Dochodzimy więc do stwierdzenia, iż praca przeniesienia ciała o masie m po drodze
zamkniętej w polu grawitacyjnym jest równa zero. Jest to właśnie sens fizyczny
zachowawczego charakteru pola. Pola grawitacyjne, zarówno siły grawitacyjnej, jak
i natężenia pola są zachowawczymi, bo praca przeniesienia dowolnego ciała w tych polach po
dowolnej drodze zamkniętej jest równa zero.
Skoro praca po dowolnej krzywej zamkniętej jest równa zero, to praca nie zależy od
drogi po której porusza się ciało, co ilustruje rysunek:
dr
D
C
B
A
Praca przeniesienia ciała z a do B nie zależy od tego, czy ciało jest przenoszone po
drodze ACB, czy też po drodze ADB. Praca ta jest równa:
[
]
.
)
r
(
)
r
(
m
)
r
(
U
)
r
(
U
dU
r
Ud
r
d
F
W
B
A
B
A
B
A
B
A
B
A
AB
ϕ
−
ϕ
=
−
=
−
=
∇
−
=
=
∫
∫
∫
r
r
r
Praca
zależy tylko od wyboru punktu początkowego i końcowego i dodatkowo wyraża
się przez iloczyn różnicy potencjałów w początkowym i końcowym punkcie, oraz masy
przenoszonego ciała.
Jeżeli zapiszemy to ostatnie wyrażenie w jawnej postaci, to przyjmie ono formę:
.
r
1
r
1
GMm
r
d
F
W
B
A
B
A
AB
⎥
⎦
⎤
⎢
⎣
⎡
−
=
=
∫
r
r
Gdy r
A
=
∝, to potencjał w punkcie a jest równy zeru. Wtedy:
.
r
GMm
U
B
B
−
=
Energia potencjalna ciała o masie m w punkcie r pola jest więc pracą siły zewnętrznej,
jaką trzeba wykonać, aby przenieść ciało z nieskończoności do danego punktu.
3.5.
Twierdzenie Gaussa dla pola grawitacyjnego
Zanim
sformułujemy i udowodnimy prawo Gaussa dla pola grawitacyjnego,
uogólnimy najpierw prawo powszechnego ciążenia na przypadek układu
punktów materialnych wytwarzających pole grawitacyjne.
Układ N punktów materialnych zdefiniowano na rysunku.

29
O
r
r
N
r
1
r-r
i
F
i
m
N
m
1
m
j
m
4
m
2
m
i
r
i
Mamy tutaj N punktów materialnych skupionych w pewnym obszarze. Każdy z nich
ma określone położenie w układzie odniesienia przez wektor położenia
r
i
(i = 1, 2, ..., N), a masy punktów są m
i
. Interesuje nas wypadkowy wektor pola siły
grawitacyjnej (lub natężenia pola) w punkcie r.
Wiemy
już, że z zasady niezależności wynika, iż skutek działania kilku sił jest
równoważny skutkowi wywołanemu jedną siłą, równą wypadkowej wszystkich sił. Dlatego
też, wypadkowa siła działająca na punkt materialny o masie m w punkcie r, pochodząca od
wszystkich pól wywołanych masami m
i
układu, jest równa:
,
F
F
N
1
i
i
∑
=
=
r
r
gdzie
).
r
r
(
r
r
m
Gm
F
i
3
i
i
i
r
r
r
r
−
−
−
=
Gdy w pewnym obszarze mamy bardzo dużą liczbę punktów materialnych, to możemy
zdefiniować gęstość masy
ρ w punkcie r tego obszaru równaniem:
.
dV
dM
)
r
(
=
ρ
Wtedy siła grawitacji pochodząca od elementu dV = d
3
r’ zlokalizowanego wokół punktu r’,
gdzie gęstość masy jest
ρ(r’), może być zapisana w postaci:
'.
r
d
'
r
r
)
'
r
r
)(
'
r
(
Gm
)
'
r
r
(
'
r
r
GmdM
F
d
3
3
3
r
r
r
r
r
r
r
r
−
−
ρ
−
=
−
−
−
=
Całkowitą siłę grawitacji otrzymamy całkując to równanie po całym obszarze,
w którym jest rozłożona masa. Mamy więc ogólne wyrażenie na siłę grawitacji masy M
rozłożonej w pewnej objętości V z gęstością
ρ:
'.
r
d
'
r
r
)
'
r
r
)(
'
r
(
mG
F
3
V
3
⎮
⌡
⌠
−
−
ρ
−
=
r
r
r
r
r
Jest to ogólne prawo grawitacji. Podobne wyrażenie otrzymamy dla natężenia pola
grawitacyjnego. Wykorzystując definicję tej wielkości, mamy:
'.
r
d
'
r
r
)
'
r
r
)(
'
r
(
G
g
3
V
3
⎮
⌡
⌠
−
−
ρ
−
=
r
r
r
r
r
Ponieważ obydwa pola są potencjalne, to przedstawiając te wektory w postaci
gradientu energii potencjalnej i potencjału, otrzymujemy uogólnione wyrażenia na energię
potencjalną i potencjał pola wytworzonego przez dowolny rozkład masy:
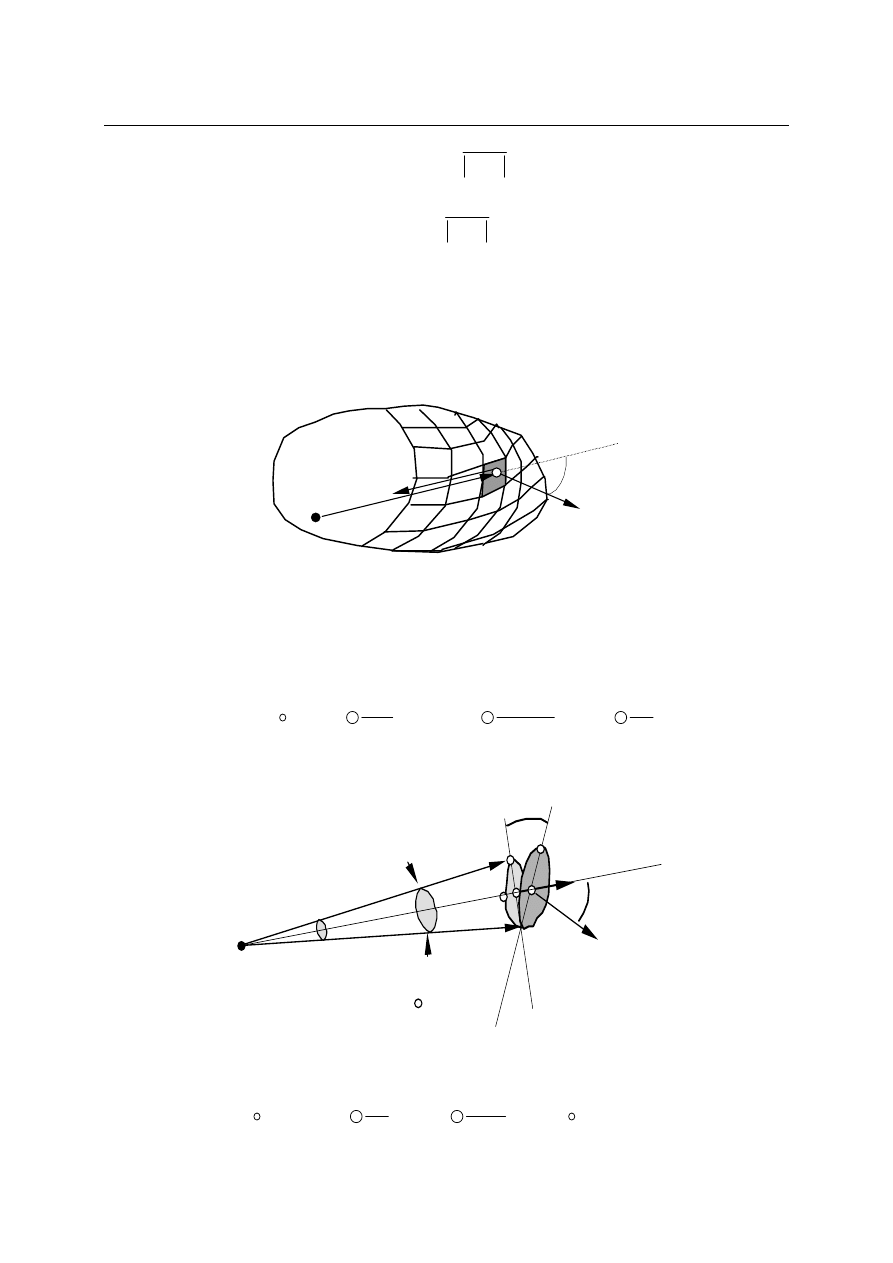
30
'.
r
d
'
r
r
)
'
r
(
G
)
r
(
,'
r
d
'
r
r
)
'
r
(
mG
)
r
(
U
3
V
3
V
⎮
⌡
⌠
−
ρ
−
=
ϕ
⎮
⌡
⌠
−
ρ
−
=
r
r
r
r
r
r
r
r
Weźmy teraz dowolną powierzchnię zamkniętą S, wewnątrz której znajduje się masa
M (dla uproszczenia punktowa) wytwarzająca pole grawitacyjne. w dowolnym punkcie tej
powierzchni natężenie tego pola zależy od odległości punktu do centrum pola. Podzielmy
powierzchnię zamkniętą na infinitezymalnie małe powierzchnie i skupmy uwagę na
elemencie skierowanym tej powierzchni dS, pokazanym na rysunku. Wektor n oznacza
normalną zewnętrzną do powierzchni w punkcie r, a dS jest wielkością zaznaczonego
elementu powierzchni.
θ
ndS
g
r
M
S
Obliczymy teraz strumień wektora natężenia g przez tę powierzchnię zamkniętą.
Ponieważ strumieniem dowolnego wektora przez powierzchnię elementarną nazywamy
iloczyn skalarny tego wektora przez powierzchnię elementarną skierowaną, to w naszym
przypadku elementarny strumień wektora g przez powierzchnię dS jest równy:
.
S
d
g
d
g
r
r
=
Φ
Pełny strumień przez powierzchnię zamkniętą jest więc całką:
,
r
'
dS
GM
r
cos
dS
GM
S
d
r
r
GM
S
d
g
2
2
3
B
⎮
⌡
⌠
−
=
⎮
⌡
⌠
⎮
⌡
⌠
θ
−
=
−
=
=
Φ
∫
r
r
r
r
gdzie dS’ jest rzutem elementu dS na powierzchnię kuli o promieniu r, co pokazano
konstrukcyjnie na rysunku:
r
dΩ
dΩ
θ
n
θ
O
n’
r
dS’
dS
Ponieważ powierzchnia dS’ jest równa r
2
d
Ω, gdzie dΩ jest kątem bryłowym pod jakim widać
tę powierzchnię z punktu O, to całkowanie po powierzchni zamkniętej sprowadza się do
elementarnego całkowania po kącie bryłowym:
∫
∫
π
−
=
Ω
−
⎮
⌡
⌠
=
Ω
−
⎮
⌡
⌠
=
−
=
=
Φ
GM
4
d
GM
r
d
r
GM
r
'
dS
GM
S
d
g
2
2
2
g
r
r
.

31
W przypadku, gdy masa M nie jest punktowa, lecz jest rozłożona z gęstością
ρ
w pewnej objętości, zawartej w rozważanej powierzchni zamkniętej, to po prawej stronie
ostatniego równania należy M zastąpić masą zawartą w zamkniętej powierzchni i daną całką
∫
ρ
=
'.
r
d
)
'
r
(
M
3
r
Wtedy strumień natężenia pola przez dowolną powierzchnię zamkniętą można zapisać
równaniem:
∫
∫
ρ
π
−
=
=
Φ
V
3
g
'.
r
d
)
'
r
(
G
4
S
d
g
r
r
r
Całkowanie w ostatniej całce dotyczy obszaru V zawartego wewnątrz powierzchni
zamkniętej, przez którą liczymy strumień natężenia pola. Równanie to wyraża treść prawa
Gaussa dla pola grawitacyjnego. Podkreślmy w tym miejscu, że jeżeli wewnątrz nie ma
obszaru z rozkładem masy wytwarzającym pole grawitacyjnej, tj. wewnątrz rozważanej
powierzchni zamkniętej nie ma masy, to całkowity strumień natężenia pola grawitacyjnego
jest równy zeru.
4. Zasady zachowania dla punktu materialnego
4.1. Energia kinetyczna, praca i moc
Wychodzimy z równania ruchu dla punktu materialnego, na który działa wypadkowa
siła F. Oznaczając masę rozważanego punktu materialnego przez m, a jego prędkość przez v,
równanie ruchu ma postać:
.
F
F
;
F
dt
v
d
m
i
i
∑
=
=
r
r
r
r
Mnożąc to równanie przez infinitezymalnie małe przesunięcie tego punktu
drr
, mamy:
.
r
d
F
r
d
dt
v
d
m
r
r
r
r
=
Prawa strona tego równania definiuje nam pracę elementarną dW siły F na
przesunięciu dr:
).
r
d
,
F
cos(
Fdr
r
d
F
=
dW
r
r
r
r
=
Lewą stronę równania ruchu przekształcimy jak następuje (rozszerzenie pochodnej):
.
mv
2
1
d
v
d
v
m
dr
dr
v
d
v
m
r
d
dt
dr
dr
v
d
m
2
⎟
⎠
⎞
⎜
⎝
⎛
=
=
=
⋅
r
r
r
r
r
r
Definiując energię kinetyczną T jako połowę iloczynu masy i kwadratu prędkości:
,
2
mv
=
T
2
równanie ruchu sprowadza się do postaci:
.
dW
dT
lub
r
d
F
2
mv
d
2
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
r
r
Widzimy
więc, że lewa strona równania Newtona pomnożona przez wektor
przesunięcia elementarnego dr, stanowi różniczkę zupełną energii kinetycznej.

32
Mamy
więc ważny wniosek dla dowolnej siły: „zmiana energii kinetycznej jest równa
wykonanej pracy”
r
d
F
dT
r
r
=
.
Wychodząc z definicji pracy elementarnej:
,
r
d
F
dW
r
r
=
wykonanej w czasie dt i definicji mocy:
,
dt
dW
P
=
mamy dla siły niezależnej od czasu wyrażenia:
v
F
dt
r
d
F
dt
dW
P
r
r
r
r
=
=
=
.
4.2. Zasada zachowania pędu
Wychodzimy z II zasady dynamiki zapisanej w postaci:
.
F
dt
p
d
r
r
=
Jest to najogólniejsza definicja siły. Stąd mamy równanie:
.
dt
F
p
d
r
r =
Zmiana pędu jest równa popędowi siły (Fdt).
Dalej, gdy na układ m nie działa siła lub wypadkowa wszystkich sił działających na
punkt materialny jest równa zeru,
, to
∑
= 0
F
i
0ˆ
p
d
=
r
.
Całkując to równanie obustronnie, mamy:
const
=
p
p
0
r
r =
.
Zatem zasadę zachowania pędu możemy sformułować następująco: jeżeli na punkt materialny
nie działa żadna siła lub siły wzajemnie się równoważą, to w układzie inercjalnym pęd punktu
materialnego jest stały w czasie. Ponieważ pęd jest wielkością wektorową, to mamy trzy stałe
ruchu zwane całkami pierwszymi (
const
p
,
p
,
p
z
y
x
=
).
4.3. Zasada zachowania energii dla punktu materialnego
Wychodzimy z równania ruchu w postaci.
F
dt
v
d
m
=
r
.
Mnożąc skalarnie obie strony tego równania przez wektor infinitezymalnie małego
przesunięcia dr, mamy równanie ruchu w formie:
,
r
d
F
r
d
dt
v
d
m
r
r
r
r
=
które jak już wiemy, sprowadza się do postaci:
r
d
F
dT
r
r
=
.
Równanie to będzie dla nas punktem wyjścia do dyskusji zasady zachowania energii.
W przyrodzie występują różne rodzaje oddziaływań. z każdym z nich związany jest
pewien rodzaj siły. Wszystkie te siły charakteryzują się różną zależnością od położenia r,
prędkości v i czasu t. Dowolną z takich sił można zapisać przy pomocy równania:
).
t
,
v
,
r
(
F
F
r
r
r
r
=

33
Rozważymy cztery rodzaje sił, które najczęściej spotykamy przy opisie oddziaływań
występujących w przyrodzie.
Jeżeli siłę daje się przedstawić w postaci gradientu pewnej funkcji skalarnej niezależnej od
czasu:
)
r
(
U
=
F
−∇
r
,
to taką siłę nazywa się siłą potencjalną i zachowawczą. w przypadku, gdy siła daje się
przedstawić w postaci gradientu funkcji skalarnej, ale zależnej od czasu, to siłę nazywa się
siłą potencjalną niezachowawczą. Dla tego typu sił mamy związek:
)).
t
,
r
(
U
=
F
r
r
−∇
Przykładem sił zależnych od prędkości są siły żyroskopowe, to jest siły, które
działając na punkt materialny powodują jego ruch w kierunku prostopadłym do działającej
siły. Przykładem takiej siły jest dobrze znana siła Lorentza:
B
v
q
F
g
r
r
r
×
=
.
Czwarty rodzaj sił, to siły dyssypatywne zdefiniowane następującą zależnością siły od
prędkości:
v
k
F
d
r
r
−
=
.
Przykładem tego typu sił są siły oporu stawiane poruszającym się ciałom w ośrodkach
lepkich, np. siła Stokesa:
,
rv
6
F
πη
−
=
gdzie
η jest współczynnikiem lepkości, r charakteryzuje wymiar liniowy ciała (promień
poruszającej się kulki), a v jest prędkością.
Siły zachowawcze
Wiemy,
że siła jest zachowawcza, gdy daje się zapisać jako
U
F
−∇
=
. Mamy zatem
dla zmiany energii kinetycznej poruszającego się punktu równanie:
(
)
,
dz
eˆ
dy
eˆ
dx
eˆ
z
)
r
(
U
eˆ
y
)
r
(
U
eˆ
x
)
r
(
U
eˆ
r
d
)
r
(
U
dT
z
y
x
z
y
x
+
+
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
−
=
−∇
=
r
r
r
r
r
które po wymnożeniu przyjmuje postać:
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
−
=
dz
z
U
dy
y
U
dx
x
U
dT
dU
dr
r
U
dz
z
r
dy
y
r
dx
x
r
r
U
−
=
∂
∂
−
=
⎥⎦
⎤
⎢⎣
⎡
∂
∂
+
∂
∂
+
∂
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−
=
lub krótko:
dU
dT
−
=
.
Różniczka zupełna energii kinetycznej jest równa ujemnej różniczce zupełnej energii
potencjalnej.
Całkując to równanie mamy:
∫
∫
−
=
dU
dT
,
co w jawnej postaci można zapisać wzorem:
∫
∫
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
r
r
2
v
v
0
0
)
r
(
dU
2
mv
d
r
.

34
Po scałkowaniu mamy równość:
)
r
(
U
)
r
(
U
2
mv
2
mv
0
2
0
2
+
−
=
−
.
Dalej, porządkując otrzymujemy związek:
const
)
r
(
U
2
mv
)
r
(
U
2
mv
2
0
2
0
=
+
=
+
r
.
Sumę energii kinetycznej i potencjalnej (
T U
+
) nazywa się energią mechaniczną i oznacza
się literką E. Zatem energia mechaniczna
U
T
E
+
=
jest dla siły zachowawczej całką ruchu, tzn. jest wielkością stałą. Jest to treść zasady
zachowania energii. Zasadę tę można również wypowiedzieć następująco: jeżeli na punkt
materialny działa siła zachowawcza, to całkowita energia mechaniczna pozostaje stała
w czasie. Ponieważ energia jest wielkością skalarną, to zasada zachowania energii dostarcza
nam jedną stałą ruchu, tj. energię całkowitą.
Siły potencjalne niezachowawcze
Weźmy siłę zależną od czasu, dającą się przedstawić w postaci gradientu funkcji
skalarnej U:
( )
t
,
r
U
F
r
r
−∇
=
.
Jeżeli zatem na punkt materialny będzie działać taka siła, to zmiana energii
kinetycznej punktu materialnego w infinitezymalnie krótkim czasie będzie równa:
( )
r
d
t
,
r
U
r
d
F
dT
r
r
r
r
−∇
=
=
,
przy czym energia potencjalna U, jest teraz funkcją dwóch zmiennych
( )
t
,
rr
.
Dla energii potencjalnej U, jako funkcji dwóch zmiennych, różniczka zupełna jest
równa:
( )
dt
t
U
r
Ud
t
,
r
dU
∂
∂
+
∇
=
r
r
,
gdzie operator Nabla oznacza różniczkowanie po składowych wektora r i mnożenie przez
odpowiednie wersory wybranego układu współrzędnych.
Wyznaczając z ostatniego równania pierwszy wyraz stojący po prawej stronie, mamy:
dt
t
U
dU
r
Ud
∂
∂
−
=
∇
r
.
Wstawiając to wyrażenie do równania na różniczkę energii kinetycznej, otrzymujemy
związek:
.
dt
t
U
dU
dT
∂
∂
+
−
=
Przeniesienie różniczki zupełnej energii potencjalnej na lewą stronę równania i połączenie jej
z różniczką energii kinetycznej, prowadzi do wyrażenia na różniczkę energii mechanicznej:
(
)
.
dt
t
U
U
T
d
∂
∂
=
+
To ostatnie równanie określa dodatkowo szybkość zmiany energii całkowitej:
( )
t
U
E
dt
d
∂
∂
=
.

35
Szybkość zmiany energii mechanicznej punktu materialnego, poruszającego się wskutek
działania siły niezachowawczej (ale potencjalnej), jest równa pochodnej cząstkowej energii
potencjalnej tej siły po czasie.
Całkując ostatnie równanie stronami, mamy:
∫
∂
∂
=
−
dt
t
U
E
E
0
.
Widzimy, że energia mechaniczna nie jest zachowana (energia całkowita nie jest stała), stąd
nazwa „siła niezachowawcza”.
Siły żyroskopowe
Siły żyroskopowe, to siły proporcjonalne do prędkości, przy czym spełniające
dodatkowo warunek wzajemnej prostopadłości:
v
F
r
r
⊥
.
Rozważmy zatem bilans energii dla punktu materialnego poddanego działaniu jednej z takich
sił, np. siły Lorentza:
.
B
v
q
F
g
r
r
r
×
=
w tym przypadku szybkość zmiany energii kinetycznej punktu może być wyrażona
równaniem:
( )
( )
( )
.
v
C
0
v
C
q
v
B
v
q
dt
r
d
B
v
q
dt
dT
r
r
r
r
r
r
r
r
r
r
⊥
=
⋅
=
×
=
×
=
Widzimy więc, że działanie sił żyroskopowych na punkt materialny nie zmienia jego energii
kinetycznej (T = const). Energia kinetyczna w takim ruchu jest stałą ruchu (całką). Całkowita
energia jednak zmienia się (nie jest zachowana).
Siły dyssypatywne
Siły dyssypatywne zdefiniowaliśmy jako proporcjonalne i współliniowe do prędkości:
.
v
k
F
d
r
r
−
=
Równanie ruchu punktu materialnego pod działaniem takiej siły, pomnożone przez
wektor prędkości, ma postać:
v
F
v
dt
v
d
m
d
r
r
r
r
=
.
Lewa strona tego równania przedstawia szybkość zmiany energii kinetycznej a prawa
strona jest mocą siły dyssypacji. Mamy więc równanie bilansu energii:
.
d
dt
T
kv
= − r
2
Szybkość zmiany energii kinetycznej punktu materialnego, związanej z działaniem siły
dyssypatywnej, jest równa mocy dyssypacji ze znakiem minus.
Jeżeli na punkt materialny działają różne rodzaje sił omówione wyżej, to ogólne
równanie ruchu punktu materialnego może być zapisane w postaci:
( )
m
dv
dt
F
r t
F
F
pot
g
d
r
r
r
r
r
=
+
,
+
,
a szybkość zmiany energii kinetycznej pod wpływem tych sił określa równanie:
dT
dt
dU
dt
U
t
F v
d
= −
+
+
∂
∂
r r
.
Porządkując to równanie, po wprowadzeniu do niego energii mechanicznej E=T+U,
otrzymujemy równanie bilansu energii mechanicznej (całkowitej):

36
.
v
F
t
U
dt
dE
d
r
r
+
∂
∂
=
Równanie to mówi, że szybkość zmiany energii mechanicznej punktu materialnego pod
działaniem sił niezachowawczych, żyroskopowych i dyssypatywnych jest równa sumie:
pochodnej cząstkowej po czasie z energii potencjalnej siły niezachowawczej i mocy
dyssypacji.
Zasada zachowania momentu pędu
Niech punkt materialny porusza się pod wpływem pewnej siły po okręgu leżącym
w płaszczyźnie poziomej, jak na rysunku.
v
L
L
z
x
y
r
r
Z rysunku widać, że jeżeli wektor wodzący r kończący się w dowolnym punkcie toru,
przesunąć do wspólnego punktu przyłożenia z wektorem prędkości w tym punkcie toru, to
przy pomocy tych dwóch wektorów możemy zdefiniować trzeci wektor, zwany momentem
pędu L punktu materialnego o masie m w ruchu krzywoliniowym.
Moment pędu definiujemy więc jako iloczyn wektorowy wektora położenia i wektora pędu:
r r r
L r p
e
e
e
x
y
z
p
p
p
x
y
z
x
y
z
= × =
$
$
$
.
Wykonując wskazane działania algebraiczne znajdujemy wyrażenie na składowe tego
wektora:
(
)
(
)
(
)
r
L e yp
zp
e zp
xp
e xp
yp
e L
e L
e L
x
z
y
y
x
z
z
y
x
x
x
y
y
z
z
=
−
+
−
+
−
==
+
+
$
$
$
$
$
.
$
Zatem składowe wektora momentu pędu dane są przez:
(
)
(
)
(
)
.
yp
xp
L
,
xp
zp
L
,
zp
yp
L
,
p
r
=
L
x
y
z
z
x
y
y
z
x
−
=
−
=
−
=
× r
r
r
Aby
wprowadzić zasadę zachowania momentu pędu, wychodzimy jak zawsze
w mechanice newtonowskiej, z równania ruchu (tj. z drugiej zasady dynamiki Newtona):
m
dv
dt
F
r
r
=
,
gdzie F oznacza siłę powodującą ruch punktu materialnego.
Teraz
mnożymy obie strony tego równania wektorowo przez wektor r z prawej strony
(
rr ×
) i otrzymujemy:
m r
dv
dt
r
F
r
r
r r
×
⎛
⎝⎜
⎞
⎠⎟ = × .

37
Po prawej stronie, w ten sposób otrzymanego równania, stoi moment M siły F
zdefiniowany również iloczynem wektorowym:
r
r r
M
r
F
= × .
Dalej, lewą stronę równania ruchu przekształćmy jak następuje:
(
)
d
dt
r
v
v v r
dv
dt
r
dv
dt
r r
r r r
r
r
r
×
= × + ×
= ×
.
Mamy
więc równanie:
(
)
m
d
dt
r
v
M
r r
r
×
= ,
które po uwzględnieniu definicji momentu pędu przyjmuje postać następującą:
.
M
dt
L
d
r
r
=
Jest to równanie ruchu obrotowego punktu pod wpływem momentu siły M.
Z równania tego widać, że dla M = 0,
dL
dt
,
r
= $0
co oznacza, że
r
L
= const.
Mamy
więc zasadę zachowania momentu pędu, która mówi, że w układzie
inercjalnym, gdy na punkt materialny nie działa żaden moment siły, to moment pędu jest stały
(jest zachowany w czasie). Ponieważ moment pędu jest wektorem, to mamy trzy dodatkowe
stałe ruchu L
x
, L
y
i L
z
(całki ruchu).
5. Drgania harmoniczne
5.1. Oscylator harmoniczny prosty
Ruch
odbywający się pod wpływem siły:
r
F
kre
r
= − $
,
zależnej tylko od modułu
rr
= r jest ruchem harmonicznym punktu materialnego, przy czym r
jest odległością punktu od centrum siły harmonicznej. Jeżeli ruch odbywa się w jednym
wymiarze, np. w kierunku osi x, to ruch jest ruchem harmonicznym prostym. Dla oscylatora
harmonicznego prostego siła dana jest równaniem:
F
kx
= −
.
Sformułujmy zatem następujące podstawowe zagadnienie dynamiki. Dane jest
równanie ruchu oscylatora harmonicznego prostego:
m
d x
dt
kx
2
2
= −
i warunki początkowe:
x
x
x
( )
& ( )
0
0
0
0
=
=
i v
.
Znaleźć ruch tego oscylatora, tj. określić funkcję
r r
r
r t
= ( )
.
Aby
rozwiązać to zagadnienie przekształcimy nieco nasze równanie. Zapisując je
najpierw w postaci:

38
,
0
x
m
k
dt
x
d
2
2
=
+
oznaczymy współczynnik występujący przy szukanej funkcji x = x(t) przez
ω
0
2
:
k
m
= ω
0
2
.
Wtedy równanie, które mamy rozwiązać przyjmuje postać:
&&x
x
+
=
ω
0
2
0
.
Funkcja poszukiwana x(t) musi więc mieć taką postać, aby po dwukrotnym
zróżniczkowaniu po czasie, była równa sobie z dokładnością do ujemnego stałego czynnika.
Może to być zarówno funkcja sinus, cosinus lub funkcja wykładnicza.
Aby
znaleźć ogólne rozwiązanie tego równania, wybierzmy funkcję wykładniczą
z dowolną stałą
α w wykładniku i obliczmy pierwszą i drugą pochodną tej funkcji:
x e
e
e
t
t
=
⇒
=
⇒
=
α
α
α
α
x
x
&
&&
2
t
α
.
Podstawiając funkcję x i jej drugą pochodną do równania, otrzymujemy równanie
algebraiczne, z którego można wyznaczyć wprowadzoną stałą
α. Takie równanie nazywa się
równaniem charakterystycznym. w naszym przypadku ma ono postać:
α
ω
2
0
2
0
+
=
.
Jego
rozwiązaniem są dwa pierwiastki:
α
ω
1 2
0
,
= ±i
.
Rozwiązaniem ogólnym naszego równania jest liniowa kombinacja funkcji wykładniczych:
x Ae
Be
i
t
i
t
=
+
−
ω
ω
0
0
.
Posługując się wzorem Eulera dla liczb zespolonych funkcję spełniającą nasze
równania możemy przekształcić do jednej z następujących postaci:
[
] [
]
).
t
cos(
C
sin
t
sin
C
cos
t
cos
C
t
sin
b
t
cos
a
t
sin
)
B
A
(
i
t
cos
)
B
A
(
t
sin
i
t
cos
B
t
sin
i
t
cos
A
Be
Ae
x
x
0
x
0
x
0
x
0
x
0
x
0
0
0
0
t
i
t
i
0
ϕ
+
ω
=
ϕ
ω
−
ϕ
ω
=
ω
+
ω
=
ω
−
+
ω
+
=
ω
−
ω
+
ω
+
ω
=
+
=
ω
ω
Podkreślmy w tym miejscu, że rozwiązywane równanie różniczkowe jest równaniem
drugiego rzędu i każda z powyższych postaci rozwiązań, zawiera dwie stałe dowolne. Stałe te
wyznaczamy z warunków początkowych. Dla interpretacji stałych pojawiających się w tej
funkcji weźmy równanie:
x C
t
x
x
=
+
cos(
).
ω
ϕ
0
Sens fizyczny stałych jest następujący. z faktu, że maksymalne wartości funkcji
cosinus są dane przez:
cos(
)|
,
max
ω
ϕ
0
1
t
x
+
= ±
wynika, iż x
max
= C
x
. Oznacza to, że stała C
x
jest największym wychyleniem z położenia
równowagi w kierunku dodatnim lub ujemnym. Wielkość C
x
jest więc amplitudą drgań
harmonicznych.
Drugą stałą
ϕ
x
, pojawiającą się jako parametr rozwiązania interpretujemy jako
przesunięcie fazowe zależne od stanu oscylatora w chwili t = 0. Mamy bowiem dla t = 0:
x
( )
cos
arccos
( )
0
0
=
⇒
=
⎛
⎝⎜
⎞
⎠⎟
C
x
x
x
x
Cx
ϕ
ϕ
,
a więc przesunięcie fazowe
ϕ
x
jest jednoznacznie określone przez wychylenie w chwili
początkowej i amplitudę ruchu harmonicznego.

39
Następnie wyjaśnimy sens fizyczny wielkości wprowadzonej do równania ruchu
i oznaczonej przez
ω
0
. Nietrudno sprawdzić, że wymiar tej wielkości jest:
[ ]
[ ]
[ ]
ω
0
2
2
1
=
=
=
k
m
N m
kg
s
/
.
Wielkość
ω
0
ma więc wymiar sekundy do potęgi minus pierwszej.
Jeżeli argument funkcji x = x(t) = C
x
cos(
ω
0
t+
ϕ
x
) zmienimy, dokonując translacji czasu
o wielkość (2
π/ω
0
), to funkcja x(t) będzie miała tę samą wartość, mianowicie:
[
]
(
)
x t
C
t
C
t
x t
x
x
x
x
+
⎛
⎝
⎜
⎞
⎠
⎟ =
+
+
=
+
=
2
2
0
0
0
π
ω
ω
π ϕ
ω
ϕ
cos
cos
( ).
Oznacza to, że przesunięcie czasowe ma sens okresu drgań. Mamy zatem:
T
2
2
0
π
ω
π
=
⇒
=
T
m
k
.
Tak
więc,
ω
0
ma sens fizyczny częstości kątowej i to uzasadnia wprowadzoną
definicję jej kwadratu jako stosunek współczynnika sztywności k do masy oscylatora
harmonicznego m.
5.2. Oscylator harmoniczny trójwymiarowy izotropowy
Dla oscylatora harmonicznego trójwymiarowego siła harmoniczna dana jest przez
związek:
r
r
F
kr
= −
Jeżeli współczynnik proporcjonalności w tym równaniu nie zależy od kierunku, tzn.
jest taki sam dla kierunku osi x, y i z, to mówimy, że oscylator harmoniczny jest izotropowy.
Równanie ruchu dla takiego oscylatora jest równaniem wektorowym:
mr
kr
r
r
&& = −
i może być zapisane w postaci układu trzech równań skalarnych następująco:
mr
r
r
r
&& +
=
ω
0
2
0
⇒
&&
,
&&
,
&&
,
x
x
y
y
z
z
+
=
+
=
+
=
⎧
⎨
⎪
⎩
⎪
ω
ω
ω
0
2
0
2
0
2
0
0
0
gdzie podobnie, jak w przypadku oscylatora harmonicznego prostego, wprowadzono częstość
kołową zdefiniowaną wzorem:
ω
0
2
=
k
m
.
Mamy zatem trzy równania, każde stanowi równanie oscylatora harmonicznego
prostego, dla trzech wzajemnie ortogonalnych kierunków osi układu kartezjańskiego. Ich
rozwiązaniami są funkcje:
x a
t b
t C
t
y a
t b
t C
t
z a
t b
t C
t
x
x
x
y
y
y
z
z
z
=
x
y
z
+
=
+
=
+
=
+
=
+
=
+
cos
sin
cos(
),
cos
sin
cos(
),
cos
sin
cos(
).
ω
ω
ω
ϕ
ω
ω
ω
ω
ω
ω
0
0
0
0
0
0
0
0
0
ϕ
ϕ
Pełne rozwiązanie dla oscylatora trójwymiarowego może być zatem zapisane
w postaci wektorowej:
r r
r
r a
t b
t
=
+
cos
sin
ω
ω
0
0
.
Widać z tego równania, że ruch jest ruchem płaskim i odbywa się w płaszczyźnie
wyznaczonej przez wektory
r
r
a
b
i
.
40
Wprowadzając dla tego oscylatora warunki początkowe
r
r
r
r
r
v
( )
( )
,
0
0
0
=
0
=
i
możemy wyznaczyć stałe wektory a i b:
.
v
=
b
b
)
0
(
v
,
a
)
0
(
r
o
0
0
ω
⇒
ω
=
=
r
r
r
r
r
r
Zatem fizyczne rozwiązanie tj. z nałożonymi warunkami początkowymi przyjmuje postać:
r r
r
r
r
v
t
=
0
0
0
cos
t +
0
ω
ω
ω
sin
.
Ponieważ stwierdziliśmy, że ruch jest płaski, to za płaszczyznę ruchu wybieramy
płaszczyznę (x, y) kartezjańskiego układu współrzędnych. Składowe wektora położenia
w tym nowym układzie współrzędnych są określone przez równania parametryczne:
x r
t
v
t C
t
y r
t
v
t C
t
x
x
x
x
y
y
y
y
=
+
=
+
=
+
=
+
⎧
⎨
⎪⎪
⎩
⎪
⎪
0
0
0
0
0
0
0
0
0
0
0
0
cos
sin
cos(
),
cos
sin
cos(
).
ω
ω
ω
ω
ω
ω
ω
ω
ϕ
ϕ
Jeżeli wyrazimy przesunięcie fazowe dla ruchu punktu w kierunku osi y przez
odpowiednie przesunięcie fazowe związane z ruchem w kierunku osi x
następująco:
ϕ
ϕ
δ
y
x
=
+
, wtedy ostatni układ równań przyjmuje postać:
⎪
⎪
⎩
⎪⎪
⎨
⎧
δ
ϕ
+
ω
−
δ
ϕ
+
ω
=
ϕ
+
ω
=
.
sin
)
t
sin(
cos
)
t
cos(
C
y
),
t
cos(
C
x
x
0
x
0
y
x
0
x
Podnosząc te równania stronami do kwadratu i dodając stronami mamy:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
ϕ
+
ω
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
δ
ϕ
+
ω
−
δ
ϕ
+
ω
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
,
t
sin
cos
t
cos
C
y
sin
1
),
t
(
cos
C
x
x
0
2
2
x
0
y
2
x
0
2
2
x
)
(
)
(
.
sin
cos
C
C
xy
2
cos
C
x
C
y
sin
C
x
2
y
x
2
2
x
2
y
2
2
2
x
2
δ
=
δ
−
δ
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
δ
Wykorzystując jedynkę trygonometryczną otrzymujemy równanie toru:
x
C
y
C
xy
C C
x
y
x
y
2
2
2
2
2
2
+
−
=
cos
sin
δ
δ
.
Jest to ruch po elipsie, bo wartości współrzędnych x i y są ograniczone:
).
t
cos(
C
y
),
t
cos(
C
x
y
y
x
x
ϕ
+
ω
=
ϕ
+
ω
=
5.3. Oscylator harmoniczny anizotropowy
W przypadku, gdy stałe siłowe dla siły harmonicznej są zależne od kierunku, to siła
harmoniczna dla oscylatora harmonicznego ma postać:
r
F
k xe
k ye
k ze
x
x
y
y
z
z
= −
+
+
(
$
$
)
$
,

41
a oscylator nazywa się anizotropowym.
Równania ruchu w tym przypadku dla kierunków osi x, y, z są następujące:
&&
,
,
&&
,
&&
,
.
,
x
x
k
m
y
y
k
m
z
z
k
m
x
x
x
y
y
y
z
z
z
+
=
=
+
=
=
+
=
=
⎧
⎨
⎪
⎪⎪
⎩
⎪
⎪
⎪
ω
ω
ω
ω
ω
ω
2
2
2
2
2
2
0
0
0
Te trzy równania można też zapisać przy pomocy jednego równania
.
3
,
2
,
1
i
gdzie
,
0
x
x
i
2
i
i
=
=
ω
+
&&
Rozwiązanie tego typu równania jest nam już znane z poprzednich wywodów i ma postać:
(
)
x
a
t b
t
C
t
i
i
i
i
i
i
i
i
=
+
=
+
cos
sin
cos
ω
ω
ω
ϕ
.
Aby ten ruch był periodyczny, tj. aby odbywał się po krzywej zamkniętej, jest
koniecznym, aby istniał okres T tego ruchu. To oznacza, że muszą równocześnie być
spełnione równania:
(
)
[
]
(
)
.
3
,
2
,
1
i
,
t
cos
T
t
cos
)
t
(
z
)
T
t
(
z
)
t
(
y
)
T
t
(
y
)
t
(
x
)
T
t
(
x
i
i
i
i
=
ϕ
+
ω
=
ϕ
+
+
ω
⇒
⎪⎩
⎪
⎨
⎧
=
+
=
+
=
+
Czyli
...
,
2
,
1
n
n
2
T
i
i
i
=
π
=
ω
.
Stąd, aby ruch był periodyczny, okres drgań musi spełniać relację:
T
n
i
i
= 2π
ω
.
5.4. Ruch harmoniczny
tłumiony
Jest to ruch pod wpływem siły harmonicznej,
F
kx
= −
i siły tłumiącej,
. Ta
ostatnia jest siłą oporu ośrodka, przy czym siła oporu jest przeciwnie skierowana do ruchu.
F
k
1
= − &x
1
x
Podstawowe zagadnienia dynamiki dla oscylatora harmonicznego tłumionego
formułujemy następująco:
Dana jest siła
F
kx k
= −
−
1
&
, działająca na punkt materialny o masie m i warunki
początkowe:
znaleźć ruch punktu materialnego.
,
v
)
0
(
v
,
x
)
0
(
x
0
0
=
=
Zagadnienie to sprowadza się do rozwiązania równania ruchu:
m
d x
dt
kx k x
2
2
1
= −
−
&
.
Po podzieleniu ostatniego równania przez m i uporządkowaniu mamy do rozwiązania
równanie:
&&
&
x
x
x
+
+
=
2
0
0
2
β
ω
,
gdzie wprowadzono oznaczenia:
ω
β
0
2
1
2
=
=
k
m
k
m
i
.
Równanie to jest jednorodnym równaniem różniczkowym, liniowym, II-go rzędu,
o stałych współczynnikach. Szukamy zatem równania charakterystycznego. Niech:
x t
e
( )
= α t
.

42
Różniczkując tę funkcję dwukrotnie i wstawiając do równania, otrzymujemy równanie
charakterystyczne:
(
)
α
βα ω
β
ω
2
0
2
2
0
2
2
0
4
+
+
=
=
−
,
∆
.
Zatem pierwiastkami tego równania są:
γ
±
β
−
=
ω
−
β
±
β
−
=
α
2
0
2
2
,
1
.
Mamy dwa przypadki:
i = 0.
γ
γ
≠ 0
1. Dla
rozwiązaniem jest funkcja:
0
≠
γ
[
]
x t
e
Ae
Be
t
t
( )
=
+
−
−
β
γ
γ
t
.
Jej pochodna po czasie jest równa:
(
)
[
]
t
t
t
e
B
e
)
(
A
e
)
t
(
x
γ
−
γ
β
−
γ
+
β
−
γ
+
β
−
=
&
.
Nakładając na te dwa ostatnie równania warunki początkowe
,
mamy:
0
0
v
)
0
(
v
,
x
)
0
(
x
=
=
(
) (
)
⎩
⎨
⎧
β
+
γ
−
β
−
γ
=
+
=
.
B
A
v
,
B
A
x
0
0
Rozwiązując te równania względem stałych a i B znajdujemy te stałe całkowania:
A
x
v
x
B
x
v
x
=
+
+
=
−
+
0
0
0
0
2
2
2
2
0
0
β
γ
β
γ
Ostatecznie
więc rozwiązanie fizyczne dla przypadku
γ ≠ 0
ma jawną postać:
x t
e
x
v
x
e
x
v
x
e
t
t
t
( )
;
=
+
+
⎛
⎝
⎜
⎞
⎠
⎟
+
−
+
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
≠
−
−
β
γ
γ
β
γ
β
γ
γ
0
0
0
0
0
0
2
2
2
2
0
.
2. w drugim przypadku:
i
γ = 0
β
−
=
α
2
,
1
.
Rozwiązaniem jest liniowa funkcja czasu pomnożona przez funkcję wykładniczą:
x t
e
A Bt
t
( )
(
).
=
+
−β
Jej pochodna po czasie jest równa:
[
]
& ( )
.
x t
e
B
A
Bt
t
=
−
−
−β
β
β
Dla
stałych a i B otrzymujemy następujące równania:
x
A
v
x
A x
B v
x
0
0
0
0
0
0
=
= −
+
⇒
=
=
+
⎧
⎨
⎩
,
,
.
,
β
β
β
Pełne rozwiązanie naszego równania dla tego przypadku przyjmuje postać:
(
)
[
]
x t
e
x
v
x t
t
( )
=
+
+
−β
β
0
0
0
;
γ = 0
.
Dalej zajmiemy się rozwiązaniem dla
γ ≠ 0
, które ma postać:
x t
e
x
v
x
e
x
v
x
e
t
t
t
( )
=
+
+
⎛
⎝
⎜
⎞
⎠
⎟
+
−
+
⎛
⎝
⎜
⎞
⎠
⎟
⎡
⎣
⎢
⎤
⎦
⎥
−
−
β
γ
γ
β
γ
β
γ
0
0
0
0
0
0
2
2
2
2
Przypadek ten rozbijemy na dwa:
γ >
i
0
γ < 0
.
Gdy
γ >
, to rozwiązanie możemy zapisać w postaci:
0

43
(
)
(
)
x t
e
x
e
e
v
x
e
e
t
t
t
( )
=
+
+
+
−
⎡
⎣
⎢
⎤
⎦
⎥
−
−
−
β
γ
γ
γ
γ
β
γ
0
0
0
2
2
t
t
,
ale
(
)
(
)
= cosh( t) i
t
t
1
2
1
2
e
e
e
e
t
t
t
γ
γ
γ
γ
γ
γ
+
−
−
−
sinh( )
=
.
Stąd:
x t
e
x
t
v
x
t
( )
cosh
sinh
=
+
+
⎡
⎣
⎢
⎤
⎦
⎥
−β
γ
β
γ
γ
t
0
0
0
;
.
γ > 0
Natomiast,
gdy
γ <
, to wielkość
γ można przedstawić w postaci:
0
(
)
γ
β
ω
ω
β
=
−
= −
−
=
2
0
2
0
2
2
i
γ
,
gdzie
(
)
γ
ω
β
=
−
0
2
2
0
>
.
Wtedy rozwiązanie naszego równania przyjmuje postać
(
)
(
)
.
t
sin
x
v
t
cos
x
e
=
e
e
i
2
x
v
e
e
2
x
e
)
t
(
x
0
0
0
t
t
i
t
i
0
0
t
i
t
i
0
t
⎥⎦
⎤
⎢⎣
⎡
γ
γ
β
+
+
γ
⎥⎦
⎤
⎢⎣
⎡
−
γ
β
+
+
+
=
β
−
γ
−
γ
γ
−
γ
β
−
Definiując nowe stałe przy pomocy związków:
A
x
v
x
A
=
+
= −
0
0
0
cos
sin
ϕ
β
γ
ϕ
i
,
x(t) może być zapisane w formie:
(
)
x t
e
A
t
( )
cos
=
+
−β
γ
ϕ
t
.
Z dwóch przedostatnich równań można wyliczyć przesunięcie fazowe:
tg
v
x
x
ϕ
β
γ
= −
+
⇒
0
0
0
ϕ
β
ω
β
=
−
−
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
arctg
x
v
x
0
0
0
0
2
2
,
i amplitudę A:
(
)
A
x
v
x
=
+
+
−
⎡
⎣
⎢
⎢
⎤
⎦
⎥
⎥
0
2
0
0
2
0
2
2
1
2
β
ω
β
.
Otrzymane w ten sposób pełne rozwiązanie dla tego przypadku jest:
(
)
x e
x
v
x
t
=
+
−
−
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
⎛
⎝
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
+
−β
β
ω
β
ω
ϕ
t
0
2
0
0
0
2
2
2
1
2
cos
,
przy czym częstość kołowa jest równa:
ω
ω
β
=
−
0
2
2
.
Wielkość

44
e
x
v
x
−
+
−
−
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
β
β
ω
β
t
0
2
0
0
2
2
2
1
2
,
spełnia rolę amplitudy.
Podsumowując, wypiszemy razem otrzymane rezultaty:
(
)
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎨
⎧
<
γ
β
−
ω
−
β
ϕ
β
−
ω
=
ω
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
β
−
ω
β
+
+
=
ϕ
+
ω
=
.
0
,
x
v
x
arctg
=
,
,
x
v
x
A
);
t
cos(
A
)
t
(
x
2
2
0
0
0
0
2
2
0
2
1
2
2
0
2
0
0
2
0
(
)
[
]
0.
=
,
x
v
x
e
)
t
(
x
0
0
0
t
γ
β
+
+
=
β
−
( ) (
)
( )
.
0
=
,
t
sinh
x
v
t
cosh
x
e
)
t
(
x
2
0
2
0
0
0
t
>
ω
−
β
γ
⎥⎦
⎤
⎢⎣
⎡
γ
γ
β
+
+
γ
=
β
−
Wielkość
będącą stosunkiem kolejnych wychyleń dla drgań
periodycznych (gdy
γ < 0) jest równa:
x t x t T
( ) / (
)
+
(
)
(
)
e
A
t
e
A
t
e
−
−
−
+
+
+
=
=
β
β β
β
ω
ϕ
ω
ϕ
δ
t
t
T
T
cos
cos
.
Wielkość tę nazywa się logarytmicznym współczynnikiem tłumienia.
Widać, że
.
2
=
T
;
T
ln
T
ln
2
2
0
β
−
ω
π
δ
=
β
⇒
β
=
δ
Stąd można wyznaczyć współczynnik k
1
siły tłumiącej
(
)
F
k x
= −
1
&
.
6. Siły centralne
Wśród sił występujących w przyrodzie szczególne znaczenie mają siły centralne
(środkowe). Siłę nazywamy centralną, jeżeli jej moduł (wartość) zależy tylko od odległości
punktu materialnego, na który działa siła, od pewnego stałego punktu zwanego centrum siły,
a kierunek siły leży na prostej łączącej centrum z punktem materialnym.

45
m
r
e
r
C
Każdą siłę centralną można zatem zapisać w postaci:
r
r
F F r
r
r
= ( )
$
= F(r)e .
r
Przykłady siły centralnej:
a) siła grawitacji:
F r
GMm
r
( )
= −
2
;
b) siła kulombowska:
F r
r
( )
= ±
1
4
2
πε
;
c) siła harmoniczna:
F r
kr
( )
= −
.
6.1. Własności siły centralnej
Praca elementarna siły centralnej dana jest przez iloczyn wartości siły i wartości
przesunięcia dr:
dW Fdr
F r
r
r
dr
F r dr
=
=
=
r r
r
r
( )
( )
.
Ponieważ siła centralna daje się przedstawić w postaci gradientu energii potencjalnej:
F r
r
r
U r
( )
( )
r
= −∇
,
to
.
r
r
r
U
r
r
U
z
r
eˆ
y
r
eˆ
x
r
eˆ
r
U
z
)
r
(
U
eˆ
y
)
r
(
U
eˆ
x
)
r
(
U
eˆ
r
r
)
r
(
F
z
y
x
z
y
x
r
r
∂
∂
−
=
∇
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
∂
∂
−
=
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
−
=
Stąd też mamy proste związki dla wartości siły centralnej i energii potencjalnej:
F r
U
r
( )
= −
∂
∂
.
Mnożąc to równanie przez dr (skalarnie), mamy:
F r dr
U
r
dr
dU
( )
= −
= −
∂
∂
.
Całkując ostatnie równanie stronami po drodze zamkniętej, otrzymujemy:
r r
Fdr
dU
=
=
∫
∫
0.
Całka z pracy elementarnej po drodze zamkniętej dla siły centralnej jest równa zero. To
oznacza, że każda siła centralna jest zachowawcza..
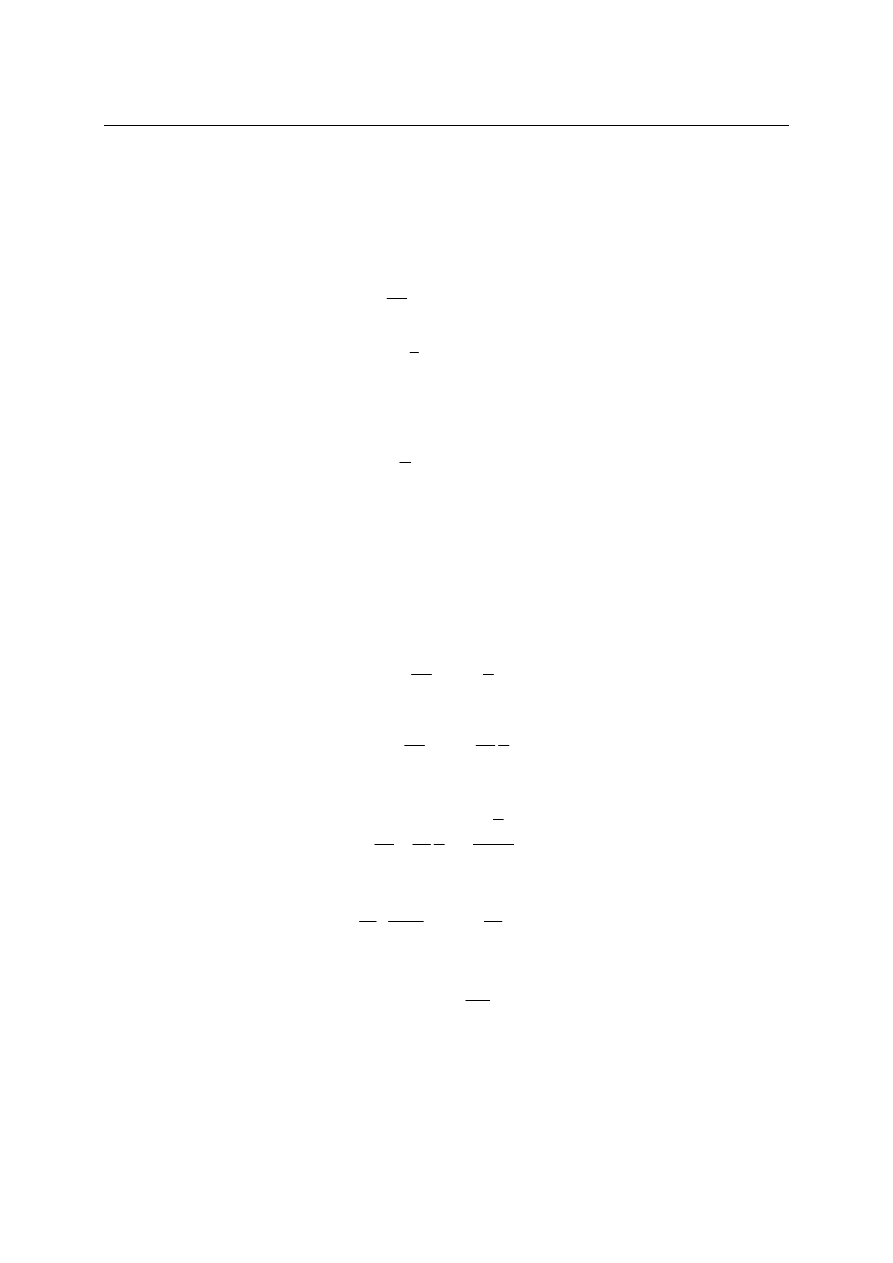
46
6.2. Zasada zachowania energii dla siły centralnej
Algorytm wyprowadzenia zasady zachowania energii dla siły centralnej jest
szczególnym przypadkiem ogólnego algorytmu dla siły zachowawczej, który już znamy. Ze
względu jednak na znaczenie sił centralnych zastosujemy go tutaj w celu otrzymania szeregu
istotnych związków wyrażających własności tych sił.
Wychodząc z równania ruchu dla siły centralnej i mnożąc je przez wektor
elementarnego przesunięcia punktu wywołanego tą siłą, mamy:
m
dv
dt
dr
U r
r
r
r
= −∇ ( )dr
,
następnie, po skorzystaniu z definicji wektora prędkości, otrzymujemy równanie:
mvdv
U r
r
r
= −∇ ( )dr
.
Lewa strona tego równania jest infinitezymalnie małą zmianą energii kinetycznej,
a prawa strona przedstawia odpowiednią nieskończenie małą zmianę energii potencjalnej
punktu materialnego poddanego działaniu rozważanej siły:
d
1
2
mv
dU
r
2
⎛
⎝⎜
⎞
⎠⎟ = −
.
Po wprowadzeniu do tego równania całkowitej energii mechanicznej T+U, mamy
zasadę zachowania energii dla siły centralnej
(
)
d T U
const
+
=
,
energia całkowita jest więc zachowana.
Ten sam wynik można otrzymać bez korzystania na początku z własności
przedstawienia siły centralnej w postaci gradientu energii potencjalnej. w tym przypadku
z równania ruchu:
( )
m
dv
dt
F r
r
r
r
r
=
,
i po pomnożeniu obu stron równania przez prędkość otrzymujemy równość:
( )
mv
dv
dt
F r
dr
dt
r
r
r
r
r r
=
.
Ponieważ:
dr
dt
dr
dt
r
r
r
d
r
r
dt
r
r
r
=
+
⎛
⎝⎜
⎞
⎠⎟
,
to poprzednie równanie przekształca się do postaci
d
dt
mv
F r
dr
dt
2
2
0
⎛
⎝
⎜
⎞
⎠
⎟ =
+
( )
.
Wykorzystując w tym miejscu jedną z własności siły centralnej:
F( )
r
dU
dr
= −
,
otrzymujemy poprzedni rezultat:
T U const
+ =
.
6.3. Zasada zachowania momentu pędu
W celu wyprowadzenia zasady zachowania momentu pędu, dla punktu materialnego
poddanego działaniu siły centralnej, wychodzimy z równania ruchu:
47
m
dv
dt
F F r
r
r
r
r
r
= = ( )
.
Mnożąc to równanie wektorowo przez wektor wodzący punktu materialnego (r
×),
mamy:
r
r
r r
r
dp
dt
F r
r
r
r
×
=
×
=
( )
0
.
Ponieważ lewa strona może być zapisana jako pochodna z momentu pędu
(
)
r
r r
r r r
r
r
dp
dt
d
dt
r
p
v p r
dp
dt
×
=
×
= × + ×
,
to otrzymujemy ostatecznie równania:
(
)
d
dt
r
p
L r
p
r r
r r r
×
=
⇒
= × =
0
const
,
wyrażające zasadę zachowania momentu pędu dla siły centralnej.
6.4. Dynamika punktu w polu siły centralnej
Pokażemy, że dla dowolnego ruchu centralnego pod wpływem siły centralnej zależnej
odwrotnie proporcjonalnie od r:
r
F
r
e
r
= −
χ
2
$
,
oprócz całki energii i momentu pędu, istnieje dodatkowa wektorowa wielkość
r
r r
C v L
e
r
= × − χ$
,
która pozostaje stała w czasie ruchu.
W tym celu skorzystamy z równań:
m
dv
dt
r
e
v r
v e
de
dt
r
r
r
r
r r
= −
= =
+
χ
2
$
&
$
$
.
i
r
r
Przekształcając wyrażenie na moment pędu, mamy:
⎥⎦
⎤
⎢⎣
⎡
×
+
×
=
⎟
⎠
⎞
⎜
⎝
⎛
+
×
=
×
=
dt
eˆ
d
r
eˆ
v
eˆ
eˆ
mr
dt
eˆ
d
r
eˆ
v
m
r
v
m
r
L
r
r
r
r
r
r
r
r
r
r
r
r
(
)
=
×
=
×
mr e
r
de
dt
I e
e
r
r
r
r
2
$
$
$&
.
Mnożąc, zapisane wyżej, równanie ruchu wektorowo przez wektor momentu pędu:
m
dv
dt
L
r
e
r
r
r
r
× = −
×
χ
2
$ L,
a następnie po prawej stronie podstawiając otrzymane wyżej wyrażenie na moment pędu:
(
)
r
L mr e
e
r
r
=
×
2
$
$&
,
po wykonaniu algebraicznych działań, dochodzimy do równania:
(
)
(
)
[
]
m
d
dt
v L
m
r
r e
e
e
r
r
r
r r
×
= −
×
×
χ
2
2
$
$
$&
.
Prawa strona tego równania może być jeszcze uproszczona. Mianowicie,
wykorzystanie znanego wzoru na podwójny iloczyn wektorowy:
)
b
a
(
c
)
c
a
(
b
)
c
b
(
a
r
r
r
r
r
r
r
⋅
−
⋅
=
×
×
,
upraszcza nasze równanie do postaci:

48
(
)
[
]
(
)
(
)
[
]
.
dt
eˆ
d
m
eˆ
eˆ
eˆ
eˆ
eˆ
e
m
eˆ
eˆ
eˆ
r
r
m
r
r
r
r
r
r
r
r
r
r
2
2
χ
+
=
⋅
−
⋅
χ
−
=
×
×
χ
−
&
&
&
Dochodzimy
więc do równania różniczkowego:
(
)
,
dt
eˆ
d
m
L
v
dt
d
m
r
χ
+
=
×
r
r
które staje się, po przeniesieniu prawej strony na lewą i połączeniu obu pochodnych,
równaniem jednorodnym:
(
)
d
dt
v L
e
r
r r
× −
=
χ$
0
.
Jego
rozwiązaniem jest rzeczywiście wektor C, który jest całką ruchu:
r
r r
C v L
e
r
= × − ×$ .
Dla
siły grawitacji stała
χ =
i stąd łatwo znaleźć równanie toru poruszającego
się punktu w polu siły grawitacyjnej. Mamy bowiem wyprowadzony związek:
+GMm
r
eˆ
C
L
v
χ
+
=
×
r
r
r
oraz wyrażenie na kwadrat momentu pędu, który można przedstawić jak następuje:
(
)
(
)
(
)
(
)
L
L L L r
mv
mL r
v
mv L r
mr v L
2
= ⋅ =
×
=
×
=
×
=
×
r r
r r
r
r r r
r r r
r r r
,
gdzie wykorzystano własności iloczynu mieszanego. Dalej, w ostatnim wyrażeniu po prawej
stronie, w miejsce iloczynu wektorowego prędkości i momentu pędu, podstawiamy wyrażenie
z całki ruchu C. Mamy więc:
(
)
(
)
(
)
mr C
e
mr e C
mr
C
m r
C
r
r
r r
r
+
=
+
=
+
=
+
⎛
⎝
⎜
⎞
⎠
⎟
χ
χ
χ
ϕ
χ
χ
ϕ
$
$
cos
cos
1
,
gdzie
( )
Cˆ
,
eˆ
cos
cos
r
=
ϕ
.
W ten sposób otrzymujemy równanie:
L
m r
C
2
1
=
+
⎛
⎝
⎜
⎞
⎠
⎟
χ
χ
ϕ
cos
.
Dzieląc to równanie przez m i
χ oraz definiując parametry:
p
L
m
=
2
χ
i
ε
χ
=
C
,
dostajemy równanie toru:
.
cos
1
p
r
ϕ
ε
+
=
Widzimy,
że ruch punktu materialnego w polu siły centralnej, takiej jak siła
grawitacji, odbywa się po elipsie. Równanie elipsy, zapisane wyżej, będzie jeszcze otrzymane
z całki energii dla dowolnego ruchu centralnego.
6.5. Ruch punktu materialnego w polu dowolnej siły centralnej
Wychodzimy z II zasady dynamiki zapisując równanie ruchu dla punktu materialnego
w polu dowolnej siły centralnej. Równanie to ma postać:
m
dv
dt
F r
r
r
r
r
= ( )
.
Mnożąc to równanie przez wektor e
r
otrzymujemy równanie skalarne:

49
ma
F r
r
= ( )
,
gdzie a
r
jest przyspieszeniem radialnym i dane jest znanym z kinematyki wzorem:
a
r r
r
= −
&&
&ϕ
2
.
Równanie ruchu punktu materialnego w polu siły centralnej przyjmuje więc postać:
(
)
m r r
F r
&&
&
( )
−
=
ϕ
2
.
Wiemy
już, że dla siły centralnej jest spełniona zasada zachowania momentu pędu.
Oznacza to, że istnieje stała wartość momentu pędu:
L mr
=
2
&ϕ
i ruch jest płaski. Stąd możemy wyliczyć wielkości występujące w przyspieszeniu radialnym:
&ϕ =
L
mr
2
i
r
L
m r
&ϕ
2
2
2 3
=
.
Aby wyliczyć drugą pochodną promienia wodzącego po czasie, która stoi w przyspieszeniu
radialnym, liczymy najpierw pierwszą pochodną następująco:
&
&
r =
d
dt
r
dr
d
d
dt
dr
d
L
mr
dr
d
=
⋅
=
=
ϕ
ϕ
ϕ
ϕ
ϕ
2
.
Ponieważ:
d
d
r
r
dr
d
ϕ
ϕ
1
1
2
⎛
⎝⎜
⎞
⎠⎟
= −
,
to pochodna po czasie wartości wektora położenia (prędkość radialna) przyjmuje następującą
postać:
&r
L
m
d
d
r
= −
⎛
⎝⎜
⎞
⎠⎟
ϕ
1
,
v
L
m
d
d
r
r
= −
⎛
⎝⎜
⎞
⎠⎟
ϕ
1
.
Liczymy dalej drugą pochodną
&&r
. Mamy:
&&
&
&
.
r
dr
dt
dr
d
d
dt
L
mr
d
d
L
m
d
d
r
L
m r
d
d
r
=
=
⋅
=
−
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝⎜
⎞
⎠⎟
⎡
⎣
⎢
⎤
⎦
⎥ = −
⎛
⎝⎜
⎞
⎠⎟
ϕ
ϕ
ϕ
ϕ
ϕ
2
2
2 2
2
2
1
1
Podstawiając te wyniki do równania ruchu, otrzymujemy wyrażenie na wartość siły
centralnej F(r) w funkcji wartości wektora wodzącego:
(
)
F r
m r r
m
L
m r
d
d
r
L
m r
L
mr
d
d
r
r
( )
&&
&
.
=
−
=
−
⎛
⎝⎜
⎞
⎠⎟ −
⎡
⎣
⎢
⎤
⎦
⎥ = −
⎛
⎝⎜
⎞
⎠⎟ +
⎡
⎣
⎢
⎤
⎦
⎥
ϕ
ϕ
ϕ
2
2
2 2
2
2
2
2 3
2
2
2
2
1
1
1
Otrzymane
równanie:
F(r) =
−
⎛
⎝⎜
⎞
⎠⎟
+
⎡
⎣
⎢
⎤
⎦
⎥
L
mr
d
d
r
r
2
2
2
2
1
1
ϕ
,
znane jest jako równanie Bineta.
6.6. Całka energii dla siły potencjalnej
Wiemy
już, że jeżeli siła zależy tylko od wartości promienia r punktu materialnego od
centrum siły, to dla ruchu punktu materialnego w polu takiej siły istnieje całka energii E
i całka momentu pędu L. Ruch odbywający się pod wpływem takiej siły jest płaski.
Można wobec tego wyrazić prędkość, jako sumę składowej radialnej i transwersalnej
w ruchu płaskim:
rv re r e
r
t
=
+
&$
& $ ,
ϕ
stąd kwadrat prędkości jest dany wyrażeniem

50
v
r
r
2
2
2
2
=
+
&
& .
ϕ
Ponieważ wartość momentu pędu L jest również całką ruchu, daną przez wyrażenie:
L mr
=
2
& ,
ϕ
to stąd:
.
mr
L
2
=
ϕ&
Dalej
prędkość radialna w tym ruchu równa się:
&
.
r
dr
d
d
dt
L
mr
dr
d
L
m
d
r
d
=
⋅
=
= −
⎛
⎝⎜
⎞
⎠⎟
ϕ
ϕ
ϕ
ϕ
2
1
Wstawiając otrzymane wyrażenia do wzoru na kwadrat prędkości, mamy:
v
L
m
d
r
d
r
L
m r
L
m
d
r
d
r
2
2
2
2
2
2
2 4
2
2
2
2
1
1
1
=
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
+
=
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
+
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
ϕ
ϕ
.
Zatem
energię kinetyczną punktu materialnego w polu siły centralnej można
przedstawić kolejnymi wzorami:
(
)
T
m
v
m
r
r
L
m
d
r
d
r
=
=
+
=
⎛
⎝⎜
⎞
⎠⎟
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
+
⎡
⎣
⎢
⎢
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎥
⎥
2
2
2
1
1
2
2
2
2
2
2
2
&
&ϕ
ϕ
.
Jeżeli energię potencjalną punktu oznaczyć przez U(r), to całka energii czyli całkowita
energia punktu materialnego w polu siły centralnej, przyjmie jedną z postaci:
6.7. Całkowanie równań ruchu przy pomocy całek pierwszych
Ostatnie równanie dla całki energii siły centralnej można zapisać w postaci:
(
)
.
r
1
d
r
1
d
)
r
(
U
E
L
m
2
2
2
2
+
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
ϕ
⎟
⎠
⎞
⎜
⎝
⎛
=
−
Rozwiązując to równanie względem
( )
d
d
r
1
ϕ
, otrzymujemy równanie różniczkowe
o rozdzielonych zmiennych:
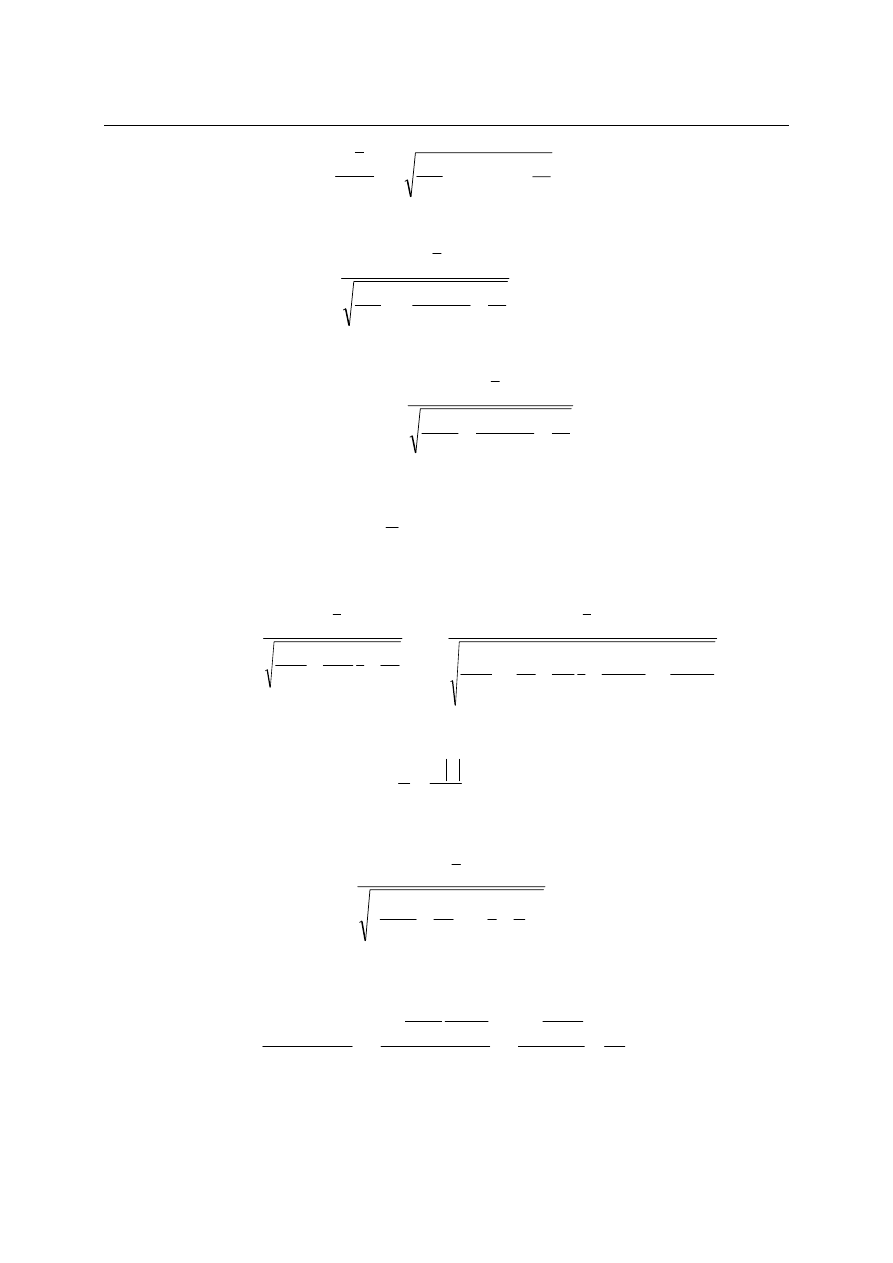
51
[
]
2
2
r
1
)
r
(
U
E
L
m
2
d
r
1
d
−
−
±
=
ϕ
⎟
⎠
⎞
⎜
⎝
⎛
.
Rozdzielamy więc zmienne i otrzymujemy:
.
d
r
1
L
)
r
(
mU
2
E
L
m
2
r
1
d
2
2
2
ϕ
=
−
−
⎟
⎠
⎞
⎜
⎝
⎛
±
Całkując to równanie mamy:
.
r
1
L
)
r
(
mU
2
L
mE
2
r
1
d
2
2
2
0
⎮
⎮
⎮
⎮
⌡
⌠
−
−
⎟
⎠
⎞
⎜
⎝
⎛
±
=
ϕ
−
ϕ
Jest to całkowa postać krzywej stożkowej.
Ograniczając się dalej do potencjałów postaci:
U r
r
( )
= ±
χ
,
(
)
⎩
⎨
⎧
πε
=
χ
=
χ
,
4
/
1
,
GMm
mamy:
⎮
⎮
⎮
⎮
⎮
⌡
⌠
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
±
=
⎮
⎮
⎮
⎮
⌡
⌠
⎟
⎠
⎞
⎜
⎝
⎛
±
=
ϕ
−
ϕ
χ
+
χ
+
±
−
−
χ
−
4
L
2
2
m
4
L
2
2
m
r
1
2
L
m
2
2
r
1
2
L
mE
2
r
1
d
2
r
1
r
1
2
L
m
2
2
L
mE
2
r
1
d
0
,
gdzie uzupełniono wyrażenie pod pierwiastkiem do kwadratu sumy dwóch wyrażeń.
Wprowadzając dalej oznaczenie:
0
L
m
p
1
2
>
χ
=
,
całkę po prawej stronie równania całkowego można przekształcić do postaci:
⎮
⎮
⎮
⎮
⌡
⌠
⎟
⎠
⎞
⎜
⎝
⎛ ±
−
⎟
⎠
⎞
⎜
⎝
⎛
+
⎟
⎠
⎞
⎜
⎝
⎛
2
2
2
p
1
r
1
p
1
L
mE
2
r
1
d
.
Wyrażenie pod pierwiastkiem przyjmie prostą formę, gdy sprowadzimy je do
wspólnego mianownika i zdefiniujemy dodatkowy parametr
ε, następująco:
.
p
p
m
EL
2
1
p
m
L
L
mE
2
1
p
L
L
mEp
2
2
2
2
2
2
2
2
2
4
2
2
2
2
2
ε
=
χ
+
=
⎟⎟
⎟
⎟
⎟
⎠
⎞
⎜⎜
⎜
⎜
⎜
⎝
⎛
χ
+
=
+
Mamy
więc równanie

52
.
p
1
r
1
p
r
1
d
2
2
2
0
⎮
⎮
⎮
⎮
⌡
⌠
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
±
−
ε
⎟
⎠
⎞
⎜
⎝
⎛
−
=
ϕ
−
ϕ
Korzystamy dalej z tego, że
d
1
1
1
r
p
d
r
±
⎛
⎝
⎜
⎞
⎠
⎟ =
⎛
⎝⎜
⎞
⎠⎟
,
otrzymujemy do wyliczenia całkę:
⎮
⎮
⎮
⎮
⎮
⌡
⌠
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
±
−
ε
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
±
−
=
ϕ
−
ϕ
2
2
2
0
p
1
r
1
p
p
1
r
1
d
.
Zamieniając zmienną całkowania:
1
1
r
p
x
± =
,
dostajemy całkę:
.
x
p
1
p
dx
2
2
2
2
2
0
⎮
⎮
⎮
⌡
⌠
ε
−
ε
−
=
ϕ
−
ϕ
Dodatkowa zamiana zmiennej x na z:
px
z
ε
= ,
prowadzi do całki elementarnej:
⎥
⎦
⎤
⎢
⎣
⎡
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
±
ε
=
=
⎮
⌡
⌠
−
−
=
⎮
⎮
⌡
⌠
−
ε
ε
−
=
ϕ
−
ϕ
p
1
r
1
p
arccos
z
arccos
z
1
dz
z
1
dz
p
p
1
2
2
0
.
Rozwiązując to równanie względem 1/r, otrzymujemy:
(
)
(
)
p
os
c
1
cos
p
p
1
r
1
0
0
ϕ
−
ϕ
ε
+
±
=
ϕ
−
ϕ
ε
+
= m
.
Tak
więc ogólne równanie toru dla ruchu punktu materialnego w polu dowolnej siły
centralnej przyjmuje postać:
(
)
0
os
c
1
p
r
ϕ
−
ϕ
ε
+
±
=
,
gdzie znak plus dotyczy oddziaływania przyciągającego (
0
>
χ
) a minus dotyczy
oddziaływania odpychającego (
).
0
<
χ
Jest to równanie: hiperboli, gdy
ε >1, paraboli, gdy ε =1, elipsy, gdy ε < 1 i okręgu,
gdy
ε = 0.

53
Przykład
. Oscylator harmoniczny (prosty)
Całka energii dla oscylatora harmonicznego prostego ma postać:
E
mx
kx
=
+
1
2
1
2
2
2
&
.
Stąd na prędkość mamy równanie różniczkowe:
&x
E
m
k
m
x
=
−
2
2
.
Jest to równanie różniczkowe pierwszego rzędu względem czasu o rozdzielonych
zmiennych i może być zapisane również w postaci:
dx
dt
E
m
k
E
x
=
−
2
1
2
2
.
Rozdzielamy zmienne, otrzymując
dx
k
E
x
E
m
dt
1
2
2
2
−
=
.
Całkujemy stronami i otrzymujemy:
t t
m
E
dx
k
E
x
−
=
−
⌠
⌡
⎮
⎮
0
2
2
1
2
.
Zmieniając zmienne:
,
dz
k
E
2
dx
z
x
E
2
k
=
⇒
=
otrzymujemy rezultat całkowania:
t t
m
k
dz
z
m
k
m
k
k
E
x
−
=
−
⌠
⌡
⎮
=
=
0
2
1
2
arcsin
arcsin
z
.
Mamy zatem równanie:
(
)
sin
m
k
t t
k
E
x
−
=
0
2
,
z którego ostatecznie wyznaczamy zależność wychylenia, jako funkcję czasu:
(
)
.
t
,
k
m
;
t
sin
k
E
2
)
t
(
x
0
ω
−
=
ϕ
=
ω
ϕ
+
ω
=
Ponieważ,
2
2
2
A
m
2
1
E
i
m
E
2
k
E
2
ω
=
ω
=
(A jest amplitudą),
to otrzymujemy również wyrażenie na amplitudę wyrażoną przez energię, masę oscylatora
i jego częstość:
2
2
E
m
A .
ω
=
W ten sposób z całki energii dla oscylatora znajdujemy zależność wychylenia od
czasu:
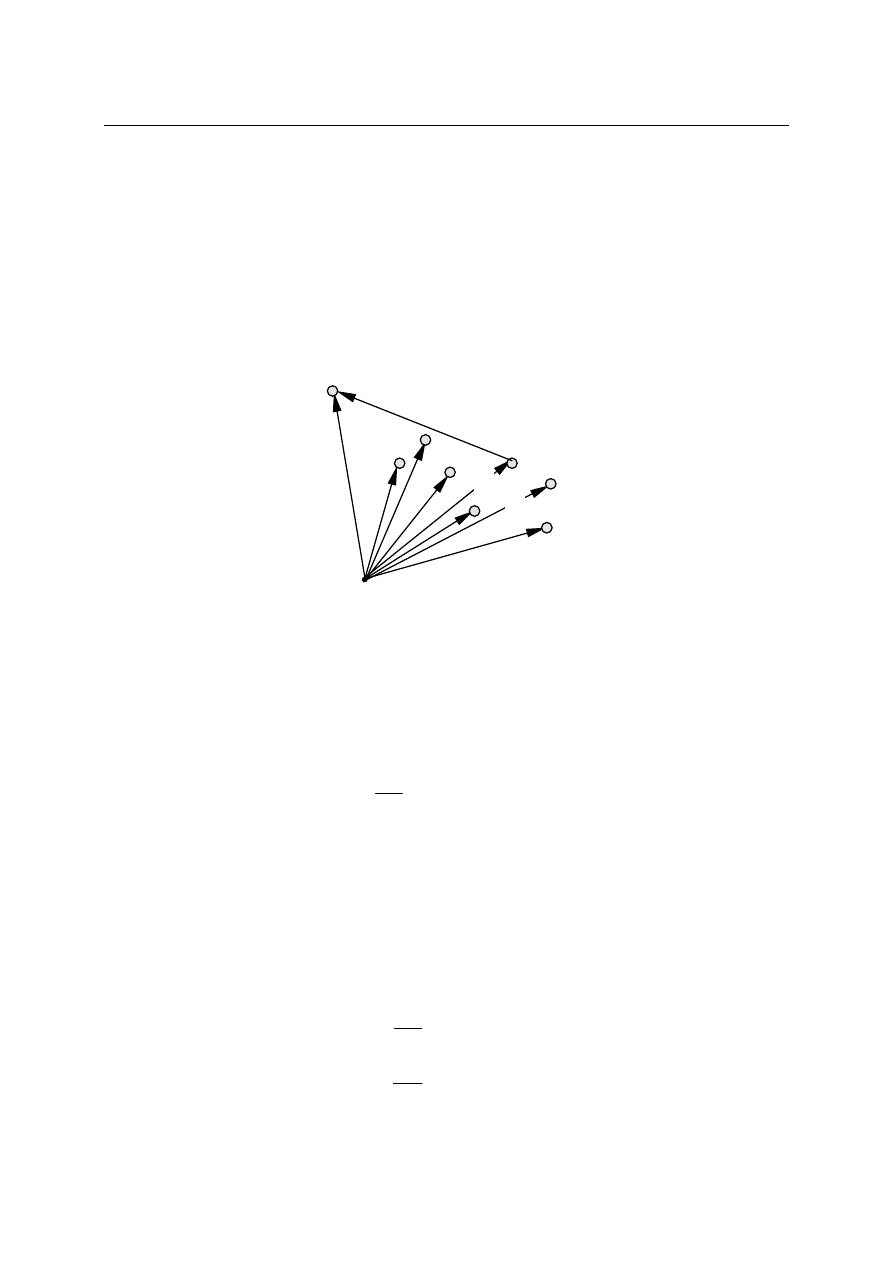
54
(
)
x t
A
t
( )
sin
=
+
ω
ϕ
.
7. Dynamika układu punktów materialnych
W dotychczasowych rozważaniach mówiliśmy o ruchu jednego punktu materialnego
poddanego działaniu różnego rodzaju sił. w mechanice często mamy do czynienia nie
z jednym punktem, lecz z układem punktów materialnych. Układ punktów w danej chwili jest
zadany (zdefiniowany), jeżeli znamy masy i położenia punktów w układzie, tj. mamy zadane
N wektorów położenia, jak na rysunku.
O
m
4
m
N
m
j
m
i
m
3
m
2
r-r
i
r
1
m
1
r
N
r
m
r
i
r
j
Punkty materialne mogą między sobą oddziaływać. Siły oddziaływania między
punktami należącymi do układu nazywają się siłami wewnętrznymi. Siły (oddziaływania)
pochodzące od ciał nie należących do układu nazywamy siłami zewnętrznymi.
Układ izolowany, to taki układ mechaniczny, na który nie działają siły zewnętrzne.
Weźmy układ N punktów materialnych o masach m
i
(i = 1, ..., N), położonych
w punktach o wektorach wodzących rr
i
. Niech na poszczególne punkty materialne działają
siły zewnętrzne, tak np. na i-ty punkt niech działa siła zewnętrzna
oi
F
r
. w układzie inercjalnym
druga zasada dynamiki dla i-tego punktu przyjmie postać:
m
dv
dt
F
F
i
oi
ij
j
i
F
r
r
r
=
+
=
∑
r
,
gdzie przez
oznacza siłę wewnętrzną z jaką j-ty punkt materialny działa
na i-ty punkt. Widzimy więc, że w przypadku układu punktów materialnych pełna siła
działająca na i-ty punkt składa się z siły zewnętrznej
r
F
ij
r
F
oi
i sił wewnętrznych pochodzących od
pozostałych punktów
(
)
r
F
ii
= 0 .
Zgodnie z trzecią zasadą dynamiki F
F
ij
ji
= − , to znaczy siły wewnętrzne są parami
równe i przeciwnie skierowane. Ruch układu N punktów materialnych jest zatem opisany
przez następujący układ równań:
,
F
F
dt
v
d
m
j
j
1
01
1
1
∑
+
=
r
r
r
,
F
F
dt
v
d
m
j
j
2
02
2
2
∑
+
=
r
r
r
.................................
.................................

55
∑
+
=
j
Nj
N
0
N
N
.
F
F
dt
v
d
m
r
r
r
Dodając te równania stronami, mamy równanie opisujące cały układ:
.
F
F
dt
r
d
m
lub
F
F
dt
v
d
m
i
j
ij
i
i
0
2
i
2
N
1
i
i
i
j
ij
i
i
0
i
N
1
i
i
∑∑
∑
∑
∑∑
∑
∑
+
=
+
=
=
=
r
r
r
r
r
r
Zdefiniujmy
środek masy układu N punktów materialnych jako punkt o wektorze
wodzącym
r
R
s
:
r
r
r
R
m r
m
M
m r
s
i i
i
i
i
i i
i
=
=
∑
∑
∑
1
,
gdzie M jest masą całego układu równą:
M
m
i
i
=
∑
.
Różniczkując równanie definiujące środek masy układu N punktów dwukrotnie po
czasie, mamy kolejno:
dR
dt
v
M
m r
M
m v
s
s
i i
i
i
i
i
r
r
r
=
=
=
∑
∑
1
1
&
r
d R
dt
a
M
m r
M
m a
s
s
i i
i
i i
i
2
2
1
1
r
r
r
=
=
=
∑
∑
&&
.
r
Oznaczając wypadkową siłę zewnętrzną działającą na cały układ przez , mamy:
0
F
r
.
0
F
oraz
F
F
i
j
ij
i
i
0
0
=
=
∑∑
∑
r
r
r
Równanie ruchu, dla układu N punktów materialnych, przyjmie więc postać:
M
d R
dt
F
s
2
2
0
r
r
=
.
Równanie to określa ruch środka masy układu. Środek masy porusza się tak jak punkt
materialny o masie
pod wpływem wypadkowej sił zewnętrznych:
M
m
i
i
=
∑
r
r
F
F
i
i
0
0
=
∑
.
Siły wewnętrzne nie zmieniają więc stanu ruchu środka masy układu.
Równanie:
r
r
R
M
m r
s
i
i
i
=
∑
1
,
jak każde równanie wektorowe, jest równoważne układowi równań skalarnych:
X
M
m x
Y
M
m y
Z
M
m z
s
i
i
i
s
i
i
i
s
i
i
i
=
=
=
⎧
⎨
⎪
⎪
⎪
⎩
⎪
⎪
⎪
∑
∑
∑
1
1
1
,
,
.
56
7.1. Zasada zachowania pędu układu punktów materialnych
Wychodzimy z równań ruchu dla układu N punktów materialnych:
.
N
,...,
1
i
;
F
F
dt
p
d
j
ij
oi
i
=
+
=
∑
r
r
r
Sumując stronami po wszystkich punktach materialnych układu, mamy:
∑∑
∑
∑
+
=
=
=
i
j
ij
n
1
i
oi
n
1
i
i
F
F
dt
p
d
r
r
r
.
Włączając sumowanie pod znak pochodnej dochodzimy do równania:
(
)
d
dt
p
F
i
r
r
∑
=
0
,
przy czym:
r
r
r
F
F
ij
j
i
oi
i
∑
∑
F
∑
=
=
0
0
,
.
Definiując pęd układu wzorem:
p
=
∑
rp
i
i
,
otrzymujemy równanie ruchu układu dowolnej liczby punktów:
d
dt
p F
r r
=
0
.
Jeżeli układ ten jest odosobnionym, to
r
r
F
dp
dt
0
0
= 0 i wtedy
= $. To oznacza, że jest
spełniona zasada zachowania pędu dla układu punktów materialnych:
rp = const.
Siły wewnętrzne nie zmieniają pędu układu.
7.2. Zasada zachowania momentu pędu układu punktów
Weźmy pod uwagę równania ruchu dla układu N punktów materialnych:
.
N
,...,
1
i
,
F
F
dt
p
d
j
ij
i
0
i
=
+
=
∑
r
r
r
Pomnóżmy wektorowo i-te równanie (dla i-tego punktu) przez wektor wodzący rr
i
z lewej strony
( )
rr
i
× .
Mamy wtedy:
r
r
r
r
r
r
r
dp
dt
r
F
r
F
N
i
i
i
i
i
ij
j
×
= ×
+
×
=
∑
0
1
; i
,..., .
Dodajemy teraz wszystkie równania do siebie i otrzymujemy:
r
r
r
r
r
r
r
dp
dt
r
F
r
F
i
i
i
i
i
i
i
i
j
i
×
=
×
+
×
∑
∑
∑
∑
0
j
.
Zauważamy, że:
1
0
i
i
0
i
M
F
r
r
r
r
=
×
, jest momentem siły zewnętrznej względem początku układu odniesienia.
(
)
.
F
||
r
r
;
0
F
r
r
2
1
F
r
2
1
F
r
2
1
F
r
2
ij
j
i
ij
ij
j
i
ji
ji
j
ij
ij
i
i
j
ij
i
0
r
r
r
r
r
r
r
r
r
r
r
r
−
=
×
−
=
×
+
×
=
×
∑
∑
∑
∑∑
57
3
0
(
)
;
r
r
r
r
r
r
r
dp
dt
d
dt
r
p
r
p
i
i
i
i
i
i
×
=
×
×
=
&
.
0
Biorąc pod uwagę powyższe związki możemy równanie ruchu zapisać w postaci:
(
)
∑
∑
=
×
i
i
i
i
i
M
p
r
dt
d
r
r
r
lub korzystając z definicji momentu pędu dla i-tego punktu:
r
r
r
L
r
p
i
i
= ×
i
,
otrzymujemy związek:
dL
dt
M
i
i
i
i
r
r
∑
∑
=
.
Dalej
definiując moment pędu układu:
r
r
L
L
i
i
=
∑
i moment sił zewnętrznych:
r
r
M
M
i
i
0
=
∑
,
dochodzimy do równania ruchu układu punktów materialnych, które wiąże moment pędu
układu i moment sił zewnętrznych:
dL
dt
M
r
r
=
0
.
Równanie to mówi nam, że pochodna momentu pędu układu jest równa
wypadkowemu momentowi sił zewnętrznych. Gdy moment sił zewnętrznych
r
r
M
dL
dt
= 0,
$
to
= 0 i wtedy moment pędu układu jest stały.
7.3. Zasada zachowania energii układu punktów materialnych
Wychodzimy z równań ruchu zapisanych w postaci
.
N
,...,
1
i
;
F
F
dt
v
d
m
j
ij
i
0
i
i
=
+
=
∑
r
r
r
Mnożąc skalarnie to równanie przez wektor prędkości i-tego punktu, mamy:
,.
N
,...,
1
i
;
F
v
F
v
dt
v
d
v
m
j
ij
i
i
0
i
i
i
i
=
+
=
∑
r
r
r
r
r
r
lub
d
dt
m v
F
dr
dt
F
dr
dt
i
i
i
i
ij
j
i
2
0
2
⎛
⎝
⎜
⎞
⎠
⎟ =
+
∑
r
r
r r
.
Sumując teraz po wszystkich punktach materialnych i definiując energię kinetyczną
układu wzorem:
T
T
mv
i
i
i
i
=
=
∑
∑
r
2
,
otrzymujemy równanie ruchu w postaci:
d
dt
T
F
dr
dt
F
dr
dt
i
i
ij
ij
i
( )
.
=
+
∑
∑
r
r
r
r
0
Dla uproszczenia założymy teraz, że siły wewnętrzne są potencjalne, tzn.
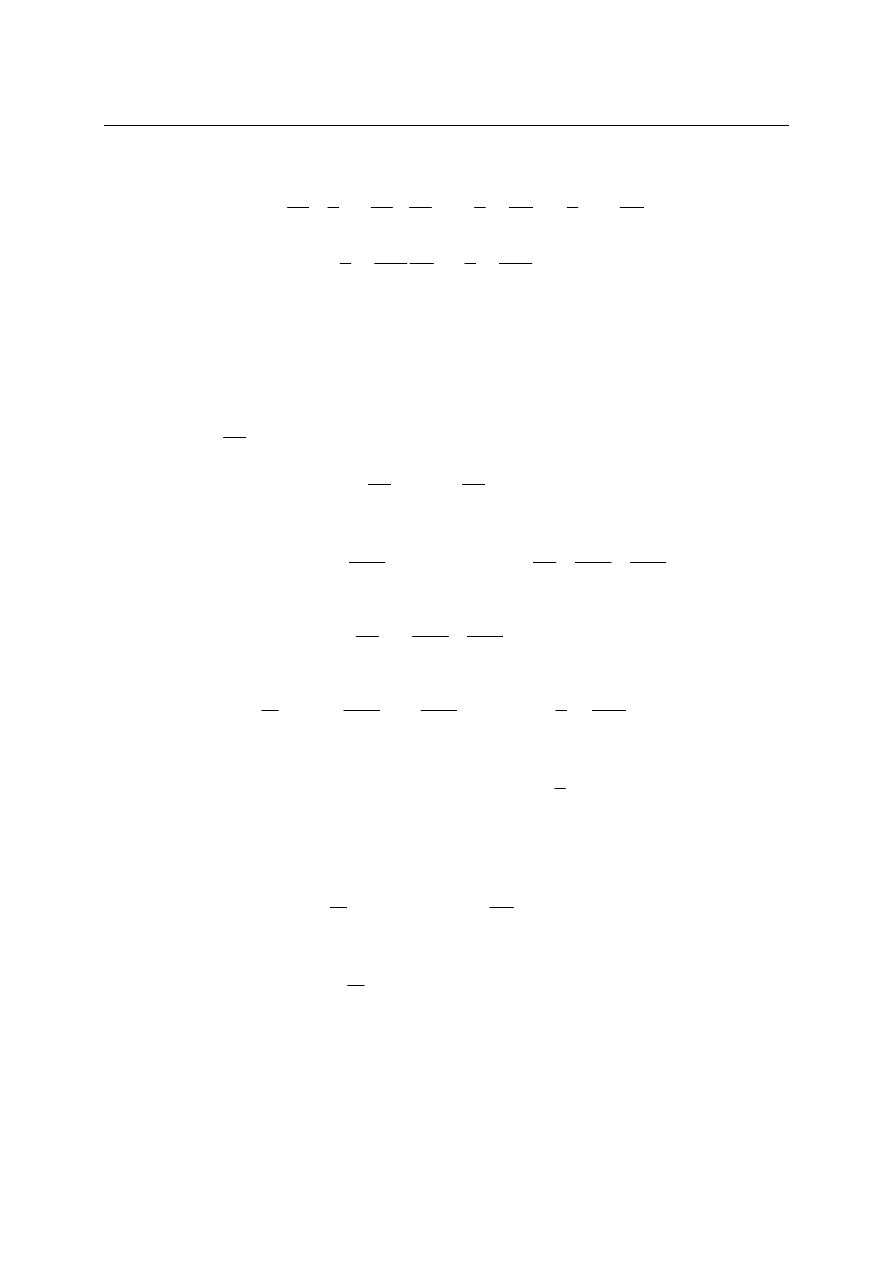
58
r
F
U
ij
ij
ij
= −∇
.
Wtedy podwójną sumę po prawej stronie równania ruchu przekształcimy następująco:
.
dt
dU
2
1
dt
dr
r
U
2
1
dt
dr
F
2
1
F
dt
r
d
2
1
F
dt
r
d
dt
r
d
2
1
dt
r
d
F
ij
ij
ij
ij
ij
ij
ij
ij
ij
ij
ij
ij
ij
ij
j
i
i
ij
ij
∑
∑
∑
∑
∑
∑
−
=
∂
∂
−
=
=
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
r
r
r
r
r
r
r
Założymy również, że siły zewnętrzne
r
F
oi
(i = 1, 2, ..., N) są potencjalne:
( )
r
r
F
U r
oi
i
( )
,
1
= −∇
t
.
Dodatkowo niech na układ działają zewnętrzne siły dyssypatywne:
r
r
F
k
oi
d
i
i
( )
= − v
,
wtedy człon
r
r
F
dr
dt
oi
i
, może być zapisany w postaci:
r
r
r
r
F
dr
dt
U
dr
dt
k v
oi
i
oi
i
i
i
= −∇
−
2
,
gdzie
można obliczyć z różniczki zupełnej
. Mianowicie:
∇U
oi
U
oi
dU
U dr
U
t
dt
U
dr
dt
dU
dt
U
t
oi
oi
i
oi
oi
i
oi
= ∇
+
⇒
∇
=
−
r
oi
r
∂
∂
∂
∂
,
.
Wtedy:
r
r
F
dr
dt
dU
dt
U
t
k v
oi
i
oi
oi
i
i
= −
+
−
∂
∂
2
.
Równanie ruchu w takim przypadku dla układu punktów przyjmuje postać:
d
dt
T
dU
dt
U
t
k v
dU
dt
oi
i
oi
i
i
i
i
ij
ij
= −
+
−
−
∑
∑
∑
∑
∂
∂
2
1
2
.
Definiując wielkości:
,
U
U
2
1
P
v
k
),
t
(
U
U
wew
ij
ij
dys
i
2
i
i
0
i
oi
=
=
=
∑
∑
∑
,
gdzie U
0
(t) jest energią potencjalną sił zewnętrznych, P
dys
oznacza moc dyssypacji układu,
a U
wew
stoi jako energia potencjalna sił wewnętrznych układu, mamy ostatecznie równanie
bilansu energii układu:
(
)
d
dt
T U
U
U
t
P
wew
dys
+
+
=
−
0
∂
∂
.
Gdy
siły zewnętrzne nie zależą od czasu:
U t
U
0
( )
,
0
=
wtedy
(
)
d
dt
T U
U
P
wew
dys
+
+
= −
0
.
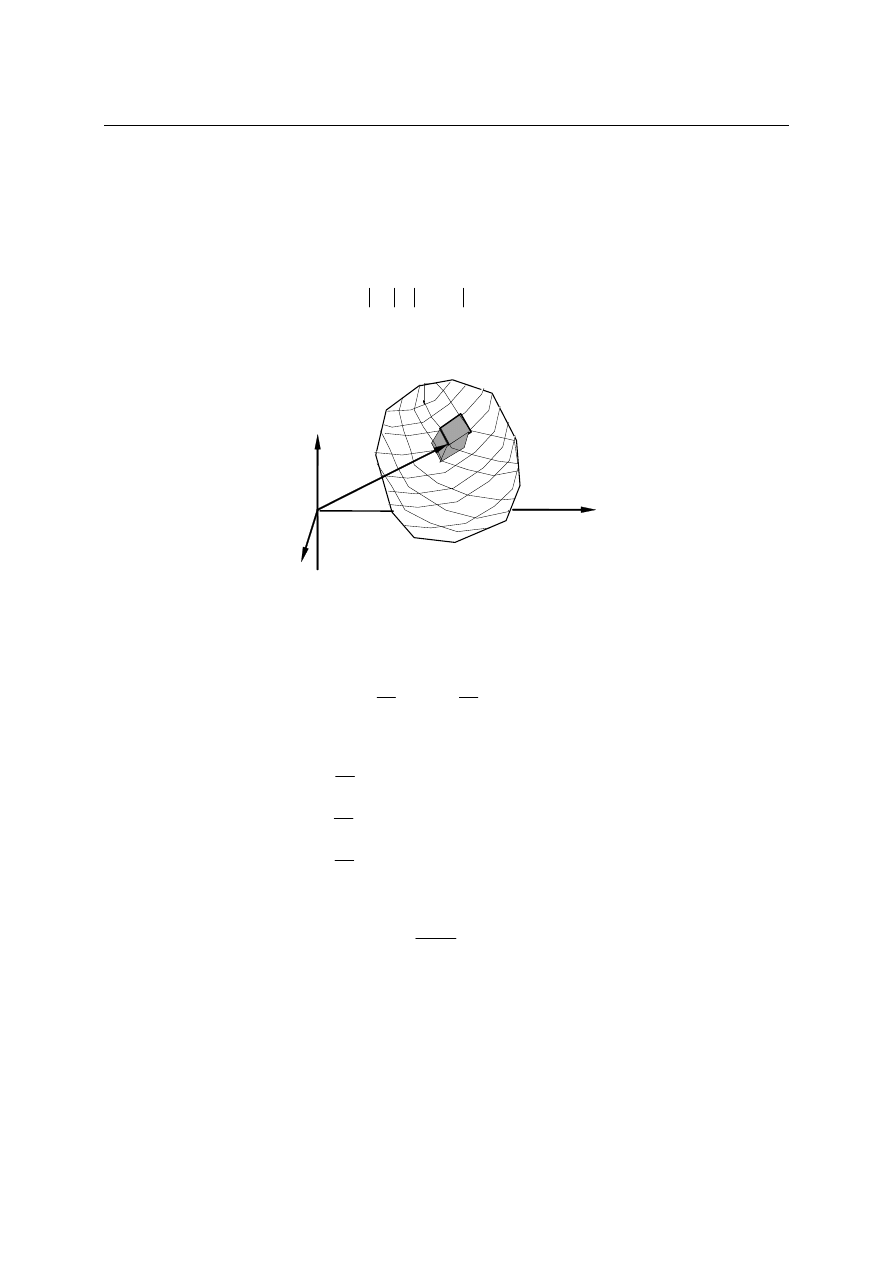
59
8. Dynamika bryły sztywnej
8.1. Środek masy i równanie ruchu środka masy
Bryłą sztywną nazywa się bryłę (ciało), w którym odległość między dowolnymi
punktami a i B jest stała:
.
const
r
r
r
B
A
AB
=
−
=
r
r
r
Jeżeli weźmiemy układ N punktów materialnych, przy czym N będzie duże
i odległości między punktami będą stałe, to w bryle sztywnej odpowiada to podziałowi na
nieskończenie wiele części.
r
O
Oznaczając masę i-tego elementu przez dm, a jego położenie w układzie odniesienia
o przez rr , możemy napisać, że masa bryły
( )
∫
M
dm
r d
=
=
∫
ρ
r
r
3
.
Środek masy tej bryły będzie określony równaniem:
.
r
d
)
r
(
r
M
1
dm
r
M
1
R
v
3
s
∫
∫
ρ
=
=
r
r
r
r
Równanie to jest równoważne trzem równaniom skalarnym na składowe środka masy:
X
M
xdm
Y
M
ydm
Z
M
zdm
r
x y z
s
s
s
=
=
=
⎧
⎨
⎪
⎪⎪
⎩
⎪
⎪
⎪
=
∫
∫
∫
1
1
1
,
,
,
( , , ).
r
Ruch
środka masy bryły opisany jest więc równaniem:
,
F
dt
R
d
M
0
2
s
2
r
=
w którym M jest masą bryły sztywnej, a
0
F
r
siłą zewnętrzną działającą na całą bryłę i jest dana
przez związek:
r
r
F
dF
0
0
=
∫
,
przy czym dF
r
0
jest siłą zewnętrzną działającą na element dm.
8.2. Moment pędu bryły sztywnej
Jeżeli na układ działają momenty sił zewnętrznych, to ruch będzie ruchem obrotowym
względem pewnej osi.
60
ω
dm’
dm
O
r
⊥
r
⊥
‘
r
r’
Zauważmy, że różne elementy bryły leżą w różnej odległości od osi obrotu i będą
poruszały się z różnymi prędkościami liniowymi, natomiast prędkość kątowa r
ω będzie dla
wszystkich punktów (elementów) stała.
Możemy wyrazić prędkość liniową elementu dm przez prędkość kątową r
ω według
wzoru:
(
)
.
r
r
r
v
||
r
r
r
r
r
r
×
ω
=
×
×
ω
=
⊥
Wobec
powyższego, moment pędu układu
(
)
r
r r
L
dm r
v
=
×
∫
, można przedstawić
w postaci:
(
)
r
r
r r
L
dmr
r
=
×
×
∫
ω
.
Jest to moment pędu bryły względem osi obrotu przechodzącej przez początek układu
odniesienia.
Jest to wzór ogólny i można go zapisać jeszcze inaczej. Wyrazimy w tym celu
wektory położenia i prędkości kątowej przez ich składowe:
(
)
r
r
r
x y z
x
y
z
=
=
( , , )
,
,
i
ω
ω ω ω
,
wtedy
( )
(
)
[
]
(
)
[
(
)(
]
(
)
(
)
(
)
(
)
(
)
(
)
.
eˆ
z
r
zy
zx
dm
eˆ
xz
y
r
yx
dm
eˆ
xz
xy
x
r
dm
z
y
x
eˆ
z
eˆ
y
eˆ
x
r
eˆ
eˆ
eˆ
dm
r
r
r
dm
L
z
2
2
z
y
x
y
z
2
2
y
x
x
z
y
2
2
x
z
y
x
z
y
x
2
z
z
y
y
x
x
2
−
ω
+
ω
−
ω
−
⋅
+
ω
−
−
ω
+
ω
−
⋅
+
ω
−
ω
−
−
ω
⋅
=
ω
+
ω
+
ω
+
+
−
ω
+
ω
+
ω
=
⋅
ω
−
ω
=
∫
∫
∫
∫
∫
)
r
r
r
r
r
r
Stąd dla składowych momentu pędu otrzymujemy wyrażenia:
(
)
[
]
(
)
[
]
(
)
[
]
.
z
r
zy
zx
dm
L
,
yz
y
r
yx
dm
L
,
xz
xy
x
r
dm
L
2
2
z
y
x
z
z
2
2
y
x
y
z
y
2
2
x
x
−
ω
+
ω
−
ω
−
=
ω
−
−
ω
+
ω
−
=
ω
−
ω
−
−
ω
=
∫
∫
∫

61
8.3. Macierz bezwładności
Definiujemy
wielkości typu:
(
)
(
)
(
)
,
I
x
r
dm
,
I
y
r
dm
,
I
x
r
dm
zz
2
2
yy
2
2
xx
2
2
=
−
=
−
=
−
∫
∫
∫
oraz typu:
(
)
−
=
∫
dm xy I
I
I
I
I
I
xy
xz
yx
yz
zx
zy
;
,
,
,
,
.
Przy pomocy tych wielkości składowe momentu pędu przyjmują formę:
L
I
I
x
x xx
y xy
z
I
xz
=
+
+
ω
ω
ω
,
L
y
x yx
y yy
z
I
I
yz
I
=
+
+
ω
ω
ω
,
L
z
x zx
y zy
z z
I
I
z
I
=
+
+
ω
ω
ω
.
Zapisując wektory
r r
L i
ω w postaci macierzy jednokolumnowych:
r
r
L
L
L
L
x
y
z
x
y
z
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
,
ω
ω
ω
ω
,
oraz definiując macierz bezwładności:
I
I
I
I
I
I
I
I
I
I
xx
xy
xz
yx
yy
yz
zx
zy
zz
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
.
Łatwo zauważyć, że
r
L przy pomocy wyprowadzonych związków można zapisać
w postaci iloczynu macierzy bezwładności i macierzy prędkości kątowej:
r
r
L
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
xx
xy
xz
yx
yy
yz
zx
zy
zz
x
y
z
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
ω
ω
ω
ω
ω
ω
ω
11
12
13
21
22
23
31
32
33
1
2
3
.
Układ współrzędnych można zawsze tak dobrać, aby wszystkie elementy
niediagonalne (momenty dewiacji) były równe 0 (patrz diagonalizacja macierzy), tj. by
wielkości typu:
I
I
I
I
I
I
xy
xz
yz
yx
zx
zy
=
=
=
=
=
= 0
.
Taki układ osi x, y, z nazywamy osiami głównymi. w układzie osi głównych macierz
bezwładności ma postać diagonalną:
I
I
I
I
I
I
I
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
=
⎡
⎣
⎢
⎢
⎢
⎤
⎦
⎥
⎥
⎥
11
22
33
1
2
3
0
0
0
0
0
0
0
0
0
0
0
0
.
Wielkość:
(
)
I
dm r
x
I
dm r
11
2
2
1
1
2
=
−
=
=
∫
∫
,
gdzie rr
1
jest odległością elementu dm od osi obrotu 1.
Analogicznie:

62
(
)
(
)
I
dm r
y
I
dm r
I
dm r
z
I
dm r
22
2
2
2
2
2
33
2
2
3
3
2
=
−
=
=
=
−
=
=
∫
∫
∫
∫
,
.
Wielkości
I I
noszą nazwę głównych momentów bezwładności względem
trzech odpowiednich osi głównych.
I
1
2
3
, ,
Document Outline
- Kinematyka punktu materialnego
- Pojęcia podstawowe
- Położenie punktu materialnego w przestrzeni
- Odległość między dwoma punktami
- Ruch punktu materialnego
- Prędkość punktu materialnego
- Przyspieszenie
- Rozkład przyspieszenia na składowe: styczną i normalną
- Podstawowe zagadnienie kinematyki
- Ruch punktu po okręgu
- Przyspieszenie w ruchu po okręgu
- Składowa radialna i transwersalna w ruchu na płaszczyźnie
- Prędkość i przyspieszenie w ruchu względnym
- Transformacja pochodnej dowolnego wektora po czasie
- Dynamika punktu materialnego
- Pole grawitacyjne
- Zasady zachowania dla punktu materialnego
- Drgania harmoniczne
- Siły centralne
- Dynamika układu punktów materialnych
- Dynamika bryły sztywnej
Wyszukiwarka
Podobne podstrony:
mechanika plynow wyklad sciaga Nieznany
Mechanika budowli wyklad 1 1 id Nieznany
mechanika 3 id 290735 Nieznany
manual mechanika 2 2 id 279133 Nieznany
Badania operacyjne wyklad 2 id Nieznany
historia gospodarcza wyklady id Nieznany
m010p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
mechanizmy komunikacji chemiczn Nieznany
Chemia ogolna wyklady 5 6 2012 Nieznany
Inzynieria wyklad wprowadzajacy Nieznany
Pedagogika ogolna wyklady 2013 Nieznany
Ocena zgodnosci wyklad 4 akredy Nieznany
09 wykladid 8098 Nieznany
Mechanika wykład II semestr
Materialoznawstwo Wyklad6 Diese Nieznany
Derma dermatologia wyklad8 id 6 Nieznany
Audyt 2012 zaoczne wyklad 4 id Nieznany (2)
Mechanisms 1 S id 291610 Nieznany
więcej podobnych podstron