
str. 2
Spis treści
Prawdopodobieństwo bezawaryjnej pracy między uszkodzeniami P(t) ...................... 4
Wzory do wyznaczenia wskaźników niezawodności na podstawie danych z
Prawdopodobieństwo bezawaryjnej pracy między uszkodzeniami P(t) ...................... 6
Wyznaczenie estymatorów wskaźników niezawodności ......................................... 6

str. 3
1. Cel i zakres pracy
Wyznaczenie wskaźników niezawodności zbiornika wodociągowego na
podstawie danych z eksploatacji.
2. Dane wykorzystane w ćwiczeniu
t
io
[h]: 2, 4, 8, 10, 16, 7, 2, 5, 20, 5, 4, 13, 6, 9, 20, 12, 5, 11, 2, 3, 5, 6, 9
t
pi
[h]: 16010, 14010, 13040, 15390, 66210, 14290, 32505, 21610, 11700, 71903,
22330, 42400, 34950, 52190, 13720, 238910, 41000, 2991, 1990, 44910, 22201,
3382, 3890
t=
8 lat
3. Definicje wskaźników niezawodności
a) Średni czas odnowy To
Parametr ten jest wartością oczekiwaną zmiennej losowej T’
o
określającej czas
odnowy obiektu. Wskaźnik ten opisuje wzór:
0
)
(
)
'
(
dt
t
tfo
o
T
E
To
gdzie: f
o
(t) jest gęstością czasu odnowy
b) Średni czas bezawaryjnej pracy Tp
Parametr ten jest wartością oczekiwaną zmiennej losowej T
pi
, określającej czas
pracy obiektu między dwoma kolejnymi uszkodzeniami. Wskaźnik ten opisuje się
wzorem:
dt
t
fp
t
p
T
E
Tp
)
(
)
'
(
0
gdzie: f
p
(t) – jest gęstością czasu pracy
c) Parametr strumienia uszkodzeń
Wskaźnik ten określa prawdopodobieństwo uszkodzenia obiektu w przedziale
czasu (t, t+
t) niezależnie od tego czy w momencie t obiekt był sprawny czy też nie.
Parametr strumienia odnowy jest więc pochodną funkcji odnowy E[v(t)] co
można zapisać następująco:
t
t
t
t
Q
dt
t
n
dE
t
t
)
,
(
lim
)
(
)
(
0
gdzie:
Q(t,t+
t) – średnia liczba uszkodzeń w przedziale czasu
t.

str. 4
d) Wskaźnik gotowości Kg
Przy założeniu, że czas pracy T
p
i czas odnowy T
o
mają rozkłady wykładnicze,
stacjonarny wskaźnik gotowości będzie miał postać:
K
g
= µ/(µ+ω)
e) Prawdopodobieństwo bezawaryjnej pracy między uszkodzeniami P(t)
Wskaźnik ten definiuje się jako prawdopodobieństwo tego, że w przedziale
czasu (0,t) między kolejnymi uszkodzeniami, licząc od momentu uruchomienia po
uszkodzeniu, obiekt nie uszkodzi się. Jednocześnie przyjmuje się założenie, że na
początku rozpatrywanego przedziału czasu tj. t=0 obiekt był sprawny tzn. P(0) =1.
Stąd prawdopodobieństwo pracy można zapisać w postaci wzoru:
P(0,t) = P(0)*P(t) = P(t)
gdzie: P(0,t) – prawdopodobieństwo tego, że obiekt nie uszkodzi się w przedziale
czasu (0,t) i w momencie t=0 był sprawny.
W przyjętym dwustanowym modelu niezawodności: sprawność-niesprawność
nie uszkodzenia się obiektu w rozpatrywanym przedziale czasu (0,t) oznacza, że czas
pracy nie będzie krótszy od dowolnego zadanego czasu tj:
P(t)=P(0,t)=P(Tp’>t)
gdzie:
Tp – zmienna losowa opisująca czas pracy obiektu
Prawdopodobieństwo bezawaryjnej pracy wyraża się wzorem:
P(t)=exp(-
t)
gdzie:
- parametr strumienia uszkodzeń
Dopełnienie do jedności prawdopodobieństwa bezawaryjnej pracy jest (w modelu
dwustronnym) prawdopodobieństwa uszkodzeń tj.:
F(t)=1-P(t)=1-exp(-
t)
Jest to postać prawdopodobieństwa przy założeniu, że proces odnowy jest stacjonarny
i bez następstw i pojedynczy.
f) Prawdopodobieństwo odnowy Po(t)
Wskaźnik ten określa prawdopodobieństwo zdarzenia, polegającego na tym, że
w przedziale czasu (0,t) usuwanie uszkodzenia będzie zakończone:
t
o
o
o
d
f
t
T
P
t
P
0
)
(
)
(
)
(
gdzie:
T’
o
– czas odnowy
f
o
(t) - gęstość czasu odnowy
W przypadku gdy czas odnowy ma rozkład wykładniczy, prawdopodobieństwo
odnowy przyjmuje postać:
P
o
(t) = 1 – exp (-µt)

str. 5
w którym µ jest intensywnością odnowy (wartość stała). Z powyższego wzoru wynika,
że:
1/µ = T
o
4. Wzory do wyznaczenia wskaźników niezawodności na podstawie danych z
eksploatacji
a) Średni czas odnowy To
Wartość czasu odnowy można oszacować na podstawie danych z eksploatacji
korzystając ze wzoru:
no
toi
no
o
T
1
1
*
gdzie: n
o
– liczba odnów(uszkodzeń),
t
oi
– czas trwania i-tej odnowy
b) Średni czas bezawaryjnej pracy Tp
Wartość czasu pracy można oszacować na podstawie danych z eksploatacji
korzystając ze wzoru:
np
i
tpi
np
p
T
1
)
(
1
*
gdzie: n
p
– liczba czasów pracy
t
pi
– czas trwania i-tego czasu pracy
c) Parametr strumienia uszkodzeń
Na podstawie danych z eksploatacji parametr strumienia uszkodzeń można
oszacować według wzoru:
t
N
t
t
t
n
t
)
,
(
)
(
*
gdzie:
n(t,t+
t) – liczba uszkodzeń w przedziale czasu
t
t – przedział czasu na jaki podzielono okres badań (obserwacji)
N- liczba badanych obiektów
d) Wskaźnik gotowości Kg
Stacjonarną wartość wskaźnika gotowości można oszacować na podstawie
danych z eksploatacji korzystając ze wzoru:
K
g
= T
*
p
/(T
*
p
+ T
*
o
)
gdzie:
T
*
p
, T
*
o
– średni czas odpowiednio pracy i odnowy
Można również wskaźnik ten oszacować ze wzoru:
K
g
= t
p
/(t
p
+ t
o
)

str. 6
w którym:
t
p
– sumaryczny czas pracy (sprawności) w badanym okresie
t
o
– sumaryczny czas odnów (niesprawności) w badanym okresie
e) Prawdopodobieństwo bezawaryjnej pracy między uszkodzeniami P(t)
Prawdopodobieństwo pracy sieci można oszacować empirycznie, tj. na postawie
danych zebranych z eksploatacji na podstawie wzoru:
P*(t)=1-n(t)/Np.
gdzie:
n(t) – liczba zdarzeń polegających na tym że zarejestrowana wartość czasu pracy tpi
jest mniejsza od założonej wartości czasu t
Np. – liczba wszystkich zarejestrowanych wartości czasu
f) Prawdopodobieństwo odnowy Po(t)
Wartość prawdopodobieństwa odnowy P*(t) można oszacować na podstawie
danych z eksploatacji wg wzoru:
P*(t) = [n(t)]/n
gdzie: n(t) – liczba zdarzeń polegających na tym, że czas usuwania niesprawności
(odnowy) jest mniejszy lub co najwyżej równy czasowi t
n – liczba wartości wszystkich wartości czasów odnowy rozpatrywanych
obiektów
5. Wyznaczenie estymatorów wskaźników niezawodności
Dane czasów pracy z eksploatacji podzielono na 8 klas co 10000h. Natomiast
dane czasów odnów z eksploatacji podzielono na 6 klas co 4h. Poniżej przedstawiono
tabele wraz z szeregiem obliczeń pozwalających na wyznaczenie wskaźników
niezawodności.
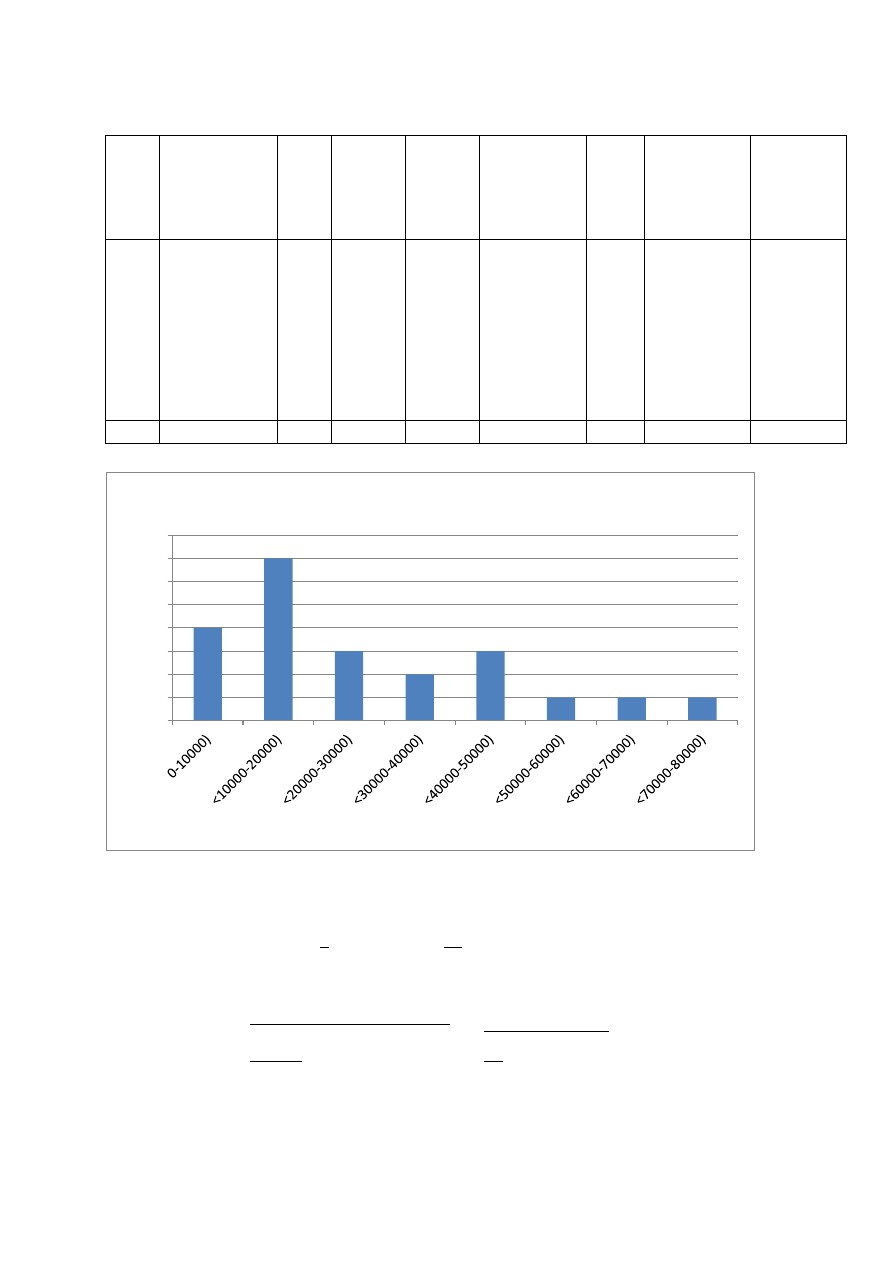
str. 7
Zestawienie obliczeń dla wartości czasów pracy
Lp.
Granice
przedziału Δt[h]
Liczeb
ność
przedz
iału ni
Środek
przedziału
tśri
ni*tśr
ni(tśri-t*)^2
Gestoś
ć
empiry
czna
pi=ni/n
Częstość
skumulowana
(dystrybuanta
empiryczna)
F(t)=F(Tp<t)=S
pi
Empiryczna
funkcja
nieawodności
P*i(t)=P(Tp>
=t)=1-Spi
1
0-10000)
4
5000
20000
1984297521
0,18
0,18
0,82
2
<10000-20000)
7
15000
105000
1054338843
0,32
0,50
0,50
3
<20000-30000)
3
25000
75000
15495867,77
0,14
0,64
0,36
4
<30000-40000)
2
35000
70000
119421487,6
0,09
0,73
0,27
5
<40000-50000)
3
45000
135000
942768595
0,14
0,86
0,14
6
<50000-60000)
1
55000
55000
768801652,9
0,05
0,91
0,09
7
<60000-70000)
1
65000
65000
1423347107
0,05
0,95
0,05
8
<70000-80000)
1
75000
75000
2277892562
0,05
1,00
0,00
suma
22
600000
8586363636
1
Średni czas pracy między uszkodzeniami t* oszacowano na podstawie podanego wcześniej
wzoru:
∑
Odchylenie standardowe:
√
∑
√
Współczynnik zmienności:
0
1
2
3
4
5
6
7
8
n
t[h]
Rozkład czasu pracy
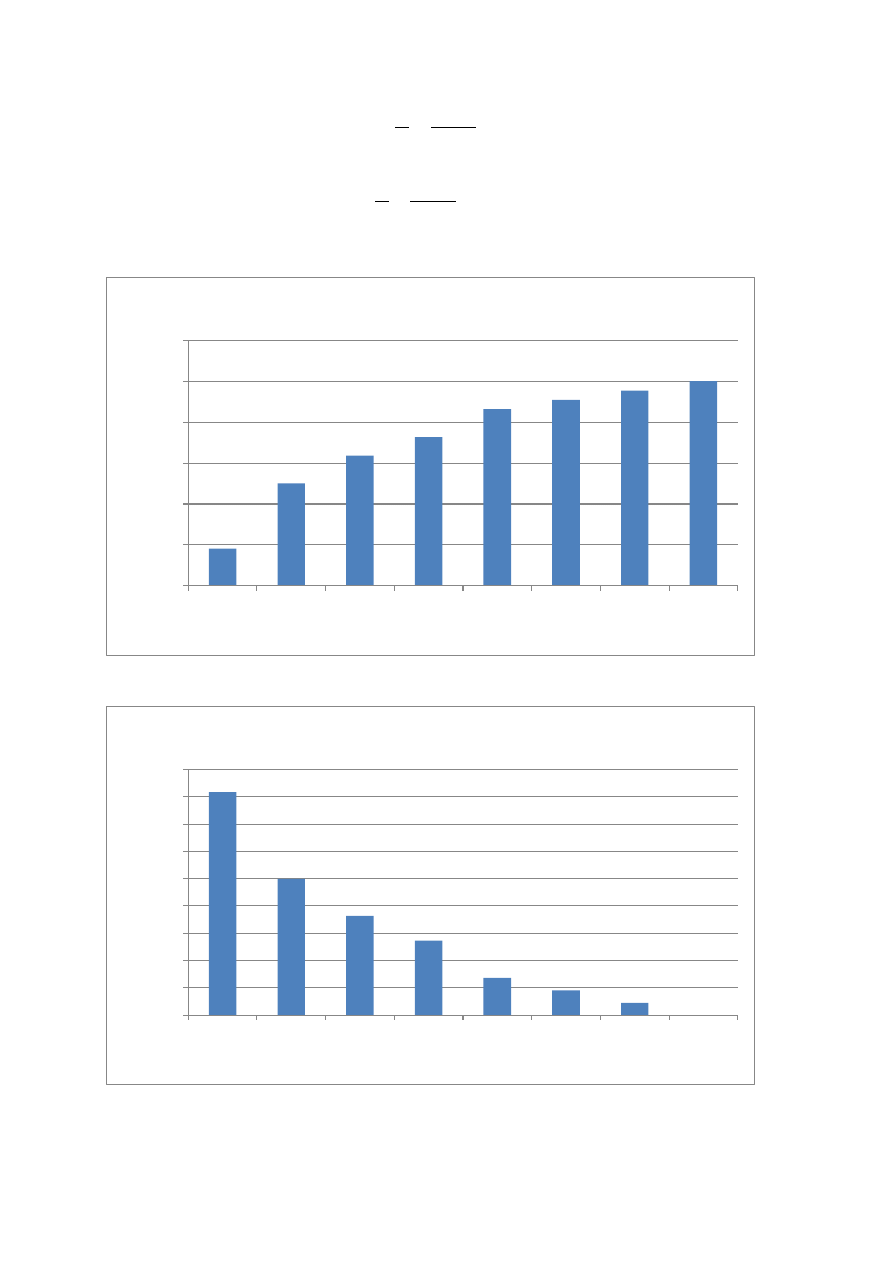
str. 8
Parametr strumienia uszkodzeń:
0,00
0,20
0,40
0,60
0,80
1,00
1,20
10000
20000
30000
40000
50000
60000
70000
80000
P(T≤
t)
Granica przedziału ∆t[h]
Dystrybuanta empiryczna czasu pracy
0,00
0,10
0,20
0,30
0,40
0,50
0,60
0,70
0,80
0,90
10000
20000
30000
40000
50000
60000
70000
80000
P(T≤
t)
Granica przedziału ∆t[h]
Empiryczna funkcja niezawodności
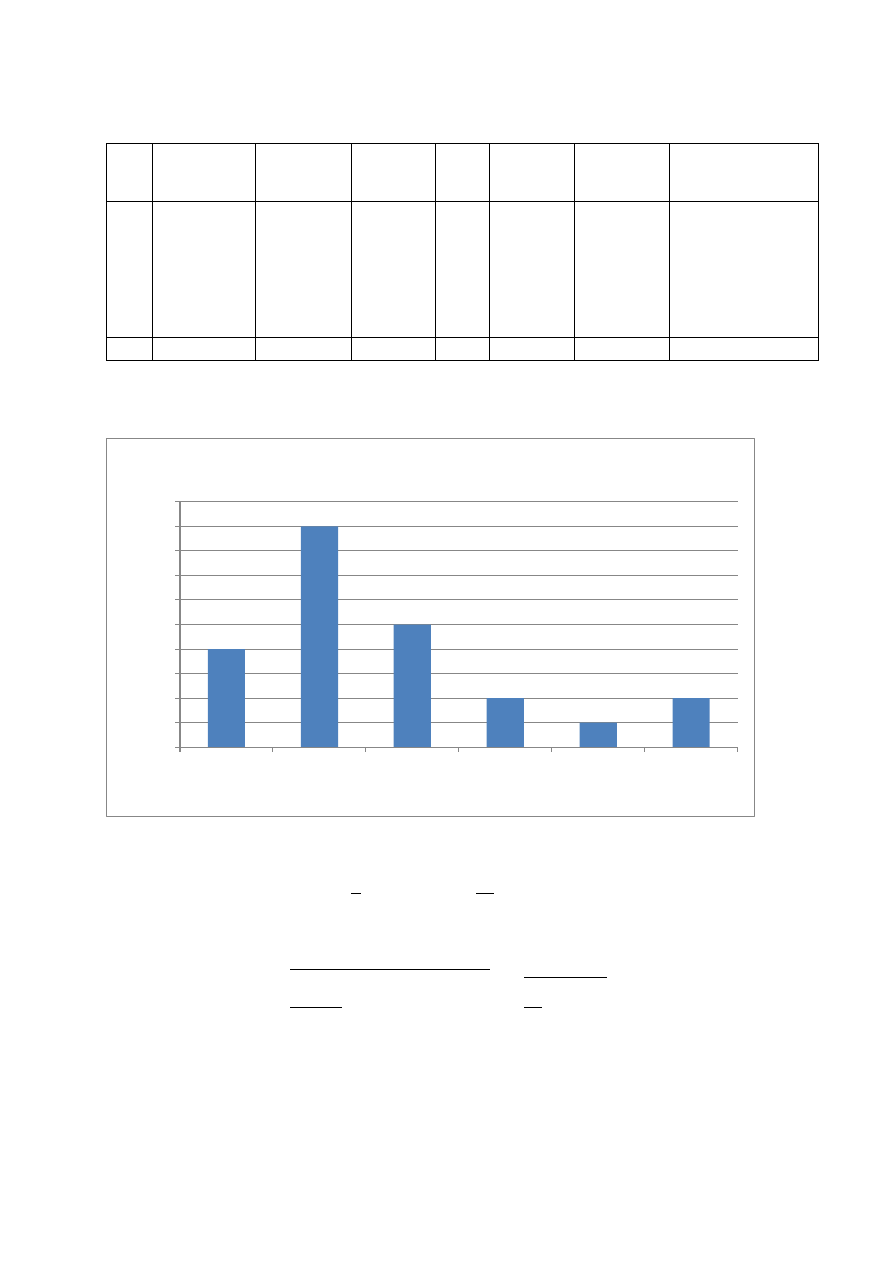
str. 9
Zestawienie obliczeń dla wartości czasów odnów
Lp.
Granice
przedziału
Δt[h]
Liczebność
przedziału ni
Środek
przedziału
tśri
ni*tśr ni(tśri-t*)^2
Gestość
empiryczna
pi=ni/n
Prawdopodobieństwo
odnowy P(t)=P(Tp<t)
1
0-4)
4
2
8
184,02
0,17
0,17
2
<4-8)
9
6
54
69,69
0,39
0,57
3
<8-12)
5
10
50
7,41
0,22
0,78
4
<12-16)
2
14
28
54,44
0,09
0,87
5
<16-20)
1
18
18
84,96
0,04
0,91
6
<20-24)
2
22
44
349,40
0,09
1,00
suma
23
202
749,92
Średni czas odnowy t* oszacowano na podstawie podanego wcześniej wzoru:
∑
Odchylenie standardowe:
√
∑
√
0
1
2
3
4
5
6
7
8
9
10
0-4)
<4-8)
<8-12)
<12-16)
<16-20)
<20-24)
n
t[h]
Rozkład czasu odnowy
str. 10
Wskaźnik gotowości:
(
)
6. Uwagi końcowe
Przeprowadzone w projekcie obliczenia zapoznają ze sposobem przeprowadzania analizy
niezawodności obiektów inżynierskich na podstawie danych z eksploatacji. Dokładność takiej
analizy rośnie wraz z ilością zarejestrowanych cykli pracy urządzenia. Dla opisywanego
zbiornika wodociągowego dostępne były 23 wartości czasów pracy oraz odnowy. Ponieważ
jedna wartość czasu pracy (238910) znacząco odstaje od pozostałych zachodzi
prawdopodobieństwo, że jest to błąd gruby dlatego też wartość została pominięta w
obliczeniach. Ilość pomiarów przekraczała 20 dlatego dane zostały ustawione w szeregu
rozdzielczym i podzielone na klasy – 8 (co 10000h) w przypadku czasów pracy oraz 6 (co 4h)
odnośnie czasów odnów.
W projekcie objaśniono a następnie wyliczono wartości wskaźników:
- średniego czasu odnowy
- średniego czasu bezawaryjnej pracy
- jednostkowego parametru strumienia uszkodzeń
- wskaźnika gotowości
Sporządzono wykresy empiryczne dla prawdopodobieństwa czasu bezawaryjnej pracy oraz
prawdopodobieństwa odnowy, które są graficznym przedstawieniem prawdopodobieństwa
wystąpienia awarii oraz czasu w jakim może być usunięta.
Na podstawie uzyskanych wyników możemy wnioskować, że badany zbiornik wodociągowy
jest urządzeniem mało awaryjnym, a czas w którym są usuwane nie jest długi.
0,00
0,20
0,40
0,60
0,80
1,00
1,20
0-4)
<4-8)
<8-12)
<12-16)
<16-20)
<20-24)
Prawdopodobieństwo odnowy
Wyszukiwarka
Podobne podstrony:
Niezawodnosc systemow
Przyklad zadan z ETN(1), WAT, V SEM, niezawodnosc systemow
systemy bezp wprowadzenie
pytania do obiektów prostych, WAT, V SEM, niezawodnosc systemow
Funkcja niezawodności, Przedmioty, Niezawodność systemów
zawodność obiektu tech złożonego, Przedmioty, Niezawodność systemów
spis literatury, WAT, V SEM, niezawodnosc systemow
Niezawodność systemów sieci i urządzeń elektroenergetycznych
Niezawodnosc systemow
Niezawodność systemów pomiarowych
Wskaźniki niezawodnościowe systemów elektroenergetycznych
Poprawa jakości i niezawodności systemó zasilania w energię elektryczną kluczem do wzrostu przychod
143. Środki SB - Polska w systemach zbiorowego bezp., STUDIA EDB, Obrona narodowa i terytorialna
Niezawodność i?zpieczeństwo systemów inż
pytania systemy, WNOŻCiK wieczorowe, semestr V, systemy zapew bezp żyw
Niezawodność i bezpieczeństwo systemów mechatronicznych Praca domowa nr 1
podnoszenie niezawodności i wydajności systemów produkcyjnych
więcej podobnych podstron