1

OCENA BEZPIECZE

Ń

STWA KONSTRUKCJI STATKU

PRZY POMOCY MODELU RYZYKA

Jan Jankowski, Polski Rejestr Statków

PODSUMOWANIE

W pracy dokonano oceny poziomu bezpieczeństwa przy pomocy prawdopodobieństwa
uszkodzenia konstrukcji, wykorzystując do tego celu model ryzyka zawierający przewidywalne
scenariusze uszkodzenia konstrukcji oraz zdarzenia w poszczególnych scenariuszach. Opisane są
one przy pomocy modeli matematycznych.

Statystyki uszkodzeń spowodowanych podstawowymi zdarzeniami ujętymi w drzewie uszkodzeń,
zostały opracowane na podstawie symulacji ruchu statków na fali nieregularnej. Modele
deterministyczne, umożliwiające symulacje ruchu statku na fali są zasadnicze w analizie ryzyka
uszkodzenia konstrukcji statku i jego zatonięcia.

Przedstawione w pracy obliczenia prawdopodobieństwa uszkodzenia i zatonięcia masowca dają
podstawę do dyskusji i dalszego rozwoju tego modelu ryzyka.

1. WPROWADZENIE

Drzewo uszkodzeń jest graficznym modelem równoległych i szeregowych kombinacji uszkodzeń,
które mają wpływ na wystąpienie wcześniej zdefiniowanego niepożądanego zdarzenia [1].
Opisuje ono logiczne relacje zdarzeń podstawowych, które „prowadzą” do wystąpienia zdarzenia
terminalnego (niepożądanego). Zdarzeniem terminalnym SL w analizie bezpieczeństwa
konstrukcji statku jest jego zatonięcie.

W przypadku masowca z pojedynczą burtą, następujące scenariusze mogą prowadzić do
wystąpienia zdarzenia terminalnego:

•

utrata wytrzymałości belki kadłuba (HS),

•

uszkodzenie burty, a następnie zapadniecie się kolejnych grodzi spowodowane zalaniem
ładowni (D

i

B

i

, i=1,2,3,4 są numerami ładowni),

•

zapadniecie pokrywy luku w ładowni nr 1, spowodowane zalewaniem pokładu, a następnie
zapadniecie się kolejnych grodzi na skutek zalania ładowni (C

1

B).

W konstruowaniu drzewa uszkodzeń założono, że uszkodzenie pokrywy luku nad ładownią nr 1
lub uszkodzenie burty w obrębie ładowni nr 4,3,2, i 1 prowadzi do zalania ładowni, zapadnięcia
się grodzi pomiędzy zalaną i nie zalaną ładownią, zalanie kolejnych ładowni i zapadniecie się
kolejnych grodzi, co prowadzi do zatonięcia statku.

Analizowany masowiec typu Panamax ma siedem ładowni. Ładownia nr 5 jest ładownią
balastową i uszkodzenie w obrębie ładowni nie prowadzi do zatonięcia statku, gdyż jej grodzie
wytrzymują zalanie ładowni wodą zaburtową. Statystyki uszkodzeń wskazują, że ładownie nr 6 i 7
nie ulegają uszkodzeniu i dlatego nie zostały włączone do drzewa uszkodzeń.

W niniejszej pracy nie przeprowadzono analiz wytrzymałości zmęczeniowej burty, gdyż analizy te
wymagają odpowiedniego opracowania i są przedmiotem badań. Natomiast wykonano analizę

2

wytrzymałości granicznej pokrywy, obciążonej wodą na pokładzie, tylko dla ładowni nr 1, gdyż
obciążenie to na pozostałych pokrywach nie jest znaczące i może być pominięte.

Drzewo uszkodzeń jest modelem jakościowym, które jednak może być wykorzystane do
dokonania ocen ilościowych. Podstawową teorią w analizie drzewa uszkodzeń jest teoria
prawdopodobieństwa, ponieważ umożliwia ona analizę losowo występujących zdarzeń i ich ocenę
ilościową.

2. UPROSZCZONY MODEL RYZYKA KONSTRUKCJI MASOWCA

Falowanie morza, odpowiedzi statku na falę oraz operowanie statkiem mają charakter losowy i
dlatego deterministyczne i probabilistyczne modele wymagają najpierw opracowania i następnie
zastosowania w celu ilościowej oceny poszczególnych zdarzeń prowadzących do uszkodzenia
konstrukcji statku. Drzewo uszkodzeń zawierające podstawowe zdarzenia opisane przy pomocy
matematycznych modeli nazywa się modelem ryzyka wystąpienie niepożądanego zdarzenia. W
rozważanym przypadku jest to utrata wytrzymałości konstrukcji statku prowadząca do jego
zatonięcia. Model ryzyka umożliwia identyfikacje ryzyka (prawdopodobieństwo) utraty funkcji
statku i porównania jego wartości z poziomem ryzyka uważanego za kryterium.

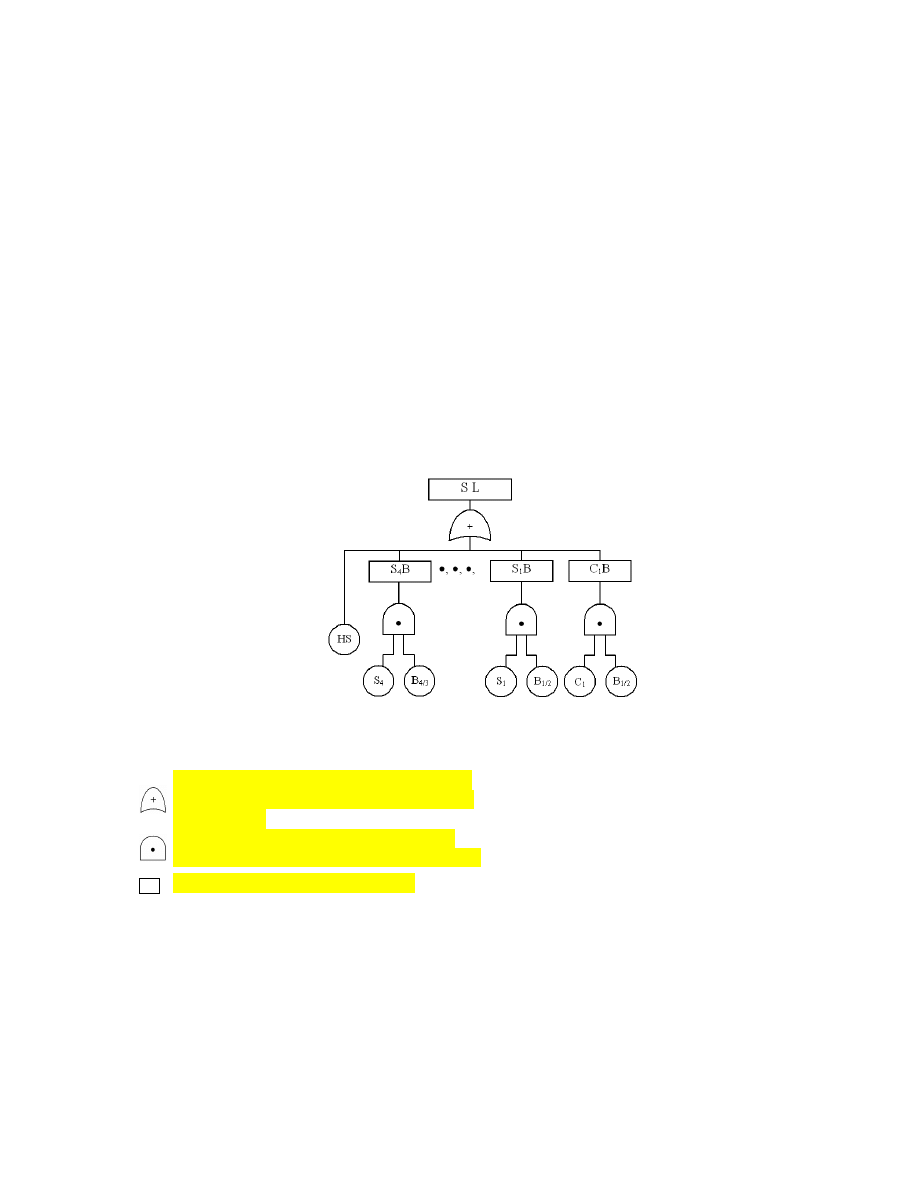
Uproszczony model ryzyka zdarzenia terminalnego SL (zatoniecie statku z powodu uszkodzenia
konstrukcji) przedstawiono na rys. 1.

Rys. 1. Uproszczony model ryzyka uszkodzeń konstrukcji masowca

bramka “lub” efekt wyjściowy w przypadku
wystąpienia przynajmniej jednego zdarzenia
wejściowego,

bramka “i” efekt wyjściowy w przypadku
wystąpienia wszystkich zdarzeń wejściowych,

zdarzenie pośrednie lub terminalne.

Scenariusze S

i

B, i=1,...,4 zawierają następujące podstawowe zdarzenia: S

i

, i=1,...,4, jest

uszkodzeniem konstrukcji burty w obrębie ładowni nr 1,2,3 i 4 spowodowane utratą
wytrzymałości wręgów obciążonych załadowaniem statku i działaniem fali; B

i/i-1

, i=4,3,2 i B

1/2

jest utratą wytrzymałości grodzi falistych pomiędzy ładownią nr i-1 oraz i, natomiast scenariusz
C

1

B zawiera: zdarzenie C

1

, które jest utratą wytrzymałości pokrywy nad ładownią nr 1 na skutek

obciążenia ją wodą wdzierająca się na pokład statku, a B

1/2

jest zdarzeniem opisanym powyżej.

3

3. MODELE PROBABILISTYCZNE

3.1. Prawdopodobie

ń

stwo zatoni

ę

cia masowca spowodowane uszkodzeniem

konstrukcji

Uwzględniając założenia wprowadzone przy budowie drzewa uszkodzeń, prawdopodobieństwa
zatonięcia statku na skutek uszkodzenia konstrukcji określone jest następującą sumą
prawdopodobieństw

.

)

(

)

(

)

(

Pr

)

(

4

1

1

∑

=

+

+

=

i

i

B

S

Pr

B

C

Pr

HS

SL

Pr

(1)

Zmiennie losowe reprezentujące poszczególne zdarzenia występujące we wzorze (1) mają
następujące znaczenie:

•

dla wytrzymałości belki kadłuba HS

(

)

W

S

U

H

M

M

M

M

+

−

=

,

(2)

gdzie M

U

jest momentem granicznym belki kadłuba (po przekroczeniu którego belka kadłuba

ulegnie uszkodzeniu), M

W

jest momentem gnącym generowanym przez falę, a M

S

jest

momentem generowanym różnicami w rozkładzie ładunku i wyporu na wodzie spokojnej;

•

dla wytrzymałości pokrywy luku C

1

∑

∑

∑

−

=

LC

Y

C

,

(3)

gdzie Σ

Y

jest granicą plastyczności materiału, z którego wykonana jest pokrywa, a Σ

LC

, jest

naprężeniem wywołanym wodą na pokładzie;

•

dla wytrzymałości grodzi falistej B

i/i-1

, i=2,3,4

L

U

B

F

F

F

−

=

,

(4)

gdzie F

U

jest siłą graniczną po przekroczeniu której gródź się zapada, a F

L

jest siłą

generowaną przez poruszającą się wodę w zalanej ładowni;

•

dla wytrzymałości wręgów S

i

, i=1,2,3,4

∑

∑

∑

−

=

LF

FY

F

.

(5)

gdzie Σ

FY

jest granicą plastyczności materiału, z którego wykonane są wręgi, a F

LF

jest

naprężeniem wywołanym ciśnieniem hydrodynamicznym oraz rozłożeniem ładunku wewnątrz
kadłuba statku.

Stopień bezpieczeństwa konstrukcji zależy od marginesu pomiędzy rzeczywistą wartością efektu
obciążenia, a tym co konstrukcja jest w stanie przenieść w sensie granicznym (wzory (2) do (5)).
Marginesy M

H

, Σ

C

, F

B

, Σ

F

nazywają się „funkcjami stanów granicznych”. Konstrukcja ulega

uszkodzeniu, gdy stan graniczny jest mniejszy od zera.

W przypadku wytrzymałości belki kadłuba uszkodzenie wystąpi, gdy graniczny moment gnący
M

U

, jaki jest w stanie przenieść belka kadłuba, będzie mniejszy od sumy momentów gnących

generowanych przez wodę spokojną i falę. Podobna sytuacja jest w przypadku grodzi falistej. Jej

4

uszkodzenie nastąpi, gdy siła F

L

spowodowana poruszającą się wodą w zalanej ładowni i

działającą na gródź, przekroczy silę graniczną F

U

, jaką ta gródź jest w stanie przenieść. Założono,

że burta utraci integralność gdy naprężenie Σ

LF

w płaskowniku wręgu przekroczy granicę

plastyczności materiału Σ

FY

. Po tym nastąpi utrata stateczności tego wręgu. Natomiast w

przypadku pokrywy luku założono, że utraci ona integralność, gdy wytrzymałość graniczna
ściskanego poszycia pokrywy lub jej usztywnień zostanie przekroczona przez efekt działania
wody zalewającej pokład. W wyniku utraty integralności burty lub pokrywy luku zostają zalane
ładownie, co z kolei prowadzi do nadmiernego obciążenia grodzi, jej zapadnięcia, zalania
kolejnych ładowni i w konsekwencji utraty pływalności statku.

Rozważane efekty działania obciążenia M

S

, M

W

, Σ

LC,

F

L,

Σ

LF

i wartości graniczne możliwości

przenoszenia obciążeń przez konstrukcje statku M

U

, Σ

U,

F

U,

Σ

Y

są zmiennymi losowymi, wiec

odpowiadające im „funkcje stanów granicznych” M

H

, Σ

C,

F

U,

Σ

F

są również zmiennymi losowymi.

Biorąc pod uwagę zmienne losowe reprezentujące funkcje stanów granicznych (wzory (2) do (5)),
prawdopodobieństwo

uszkodzenia

poszczególnych

konstrukcji

statku

określane

jest

następującymi wzorami:

Prawdopodobieństwo utraty wytrzymałości belki kadłuba nastąpi, gdy:

,

)dm

f(m

)

P(M

Pr(HS)

H

H

H

∫

∞

−

=

<

=

0

0

(6)

gdzie f jest funkcją gęstości prawdopodobieństwa zmiennej losowej M

H

. Prawdopodobieństwo, że

wystąpi ciąg zdarzeń C

1

i B

1/2

(rys. 1) jest równe:

Pr(C

1

B)= Pr(B

1/2

(C

1

)Pr(C

1

),

gdzie

( )

(

)

∫

∑

∞

−

=

<

=

0

1

0

C

C

C

)dσ

g(σ

P

C

Pr

,

(7)

(

) (

)

.

)df

|C

(f

g

|C

F

P

|C

B

Pr

B

B

B

B

/

∫

∞

−

=

<

=

0

1

1

1

2

1

0

(8)

Prawdopodobieństwo, że wystąpi ciąg zdarzeń S

i

i B

i/i-1

, i=2,3,4, lub S

i

i B

1/2

jest równe:

( ) (

) ( )

,

,

,

i

,

S

Pr

|S

B

P

B

S

Pr

i

i

i/i

i

4

3

2

0

1

=

<

=

−

(9)

(dla S

1

B podobnie), gdzie

( )

(

)

( )

,

dσ

σ

h

P

S

Pr

F

F

i

Fi

i

∫

∑

∞

−

=

<

=

0

0

(10)

i

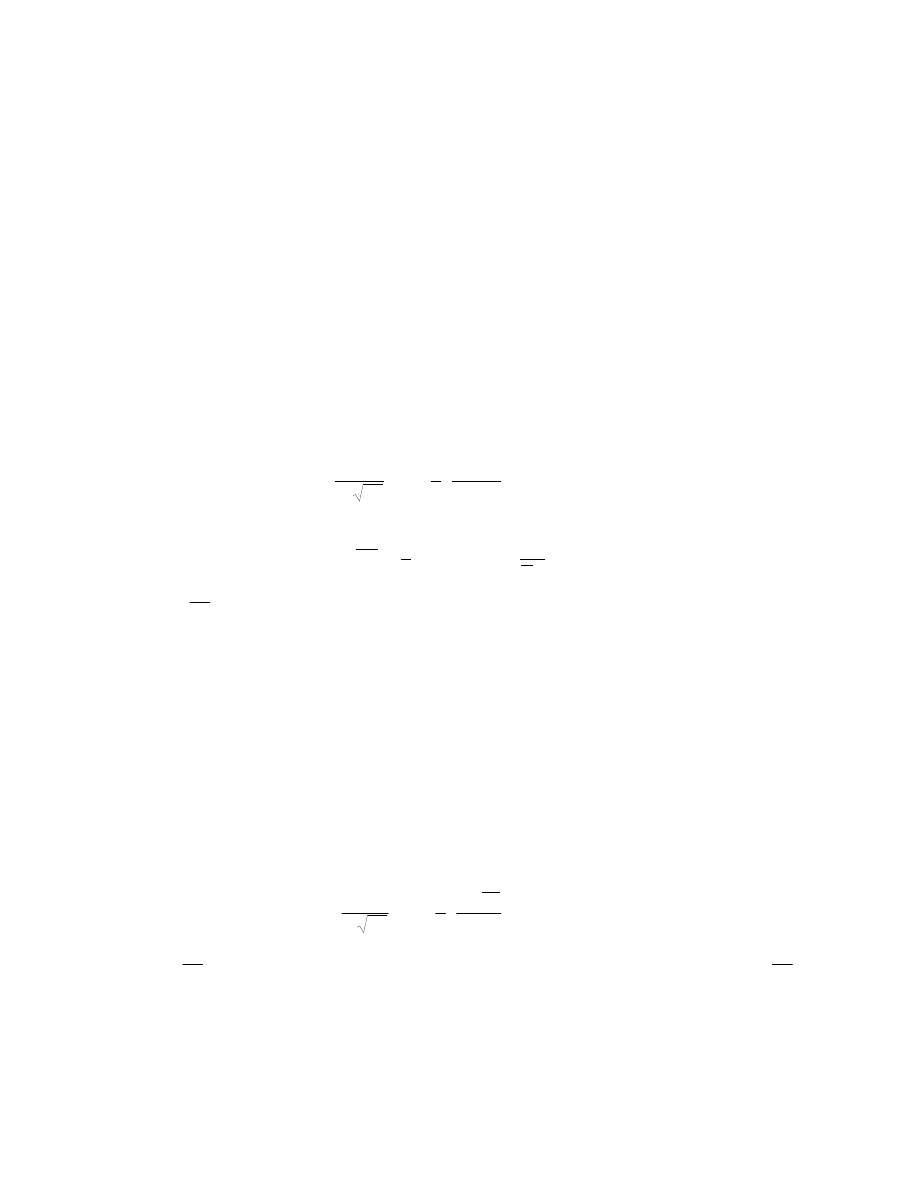
5

(

)

(

)

4

3

2

0

0

1

1

,

,

i

,

)df

|σ

(f

g

|S

F

P

|S

B

Pr

B

F

B

B

i

Bi/i

i

i/i

i

i

=

=

<

=

∫

∞

−

−

−

(11)

Funkcje gęstości prawdopodobieństwa f, g, g

B

, h

i

i h

Bi,

sa funkcjami, które zależą od zmiennych

losowych, które z kolei są sumami lub różnicami innych zmiennych losowych (wzory (2) do (5))
mających swoje funkcje gęstości. Funkcje f, g, g

B

, h

i

i h

Bi,

otrzymuje się w wyniku kompozycji

rozkładów składowych. Dokonuje się to przy pomocy splotów. Przykładowo kompozycję
rozkładów zmiennych losowych M

S

(moment gnący na wodzie spokojnej) i M

W

(moment gnący na

fali), odpowiadającą ich sumie, określona jest następującym splotem:

∫

∞

∞

−

−

=

.

)dm

m

(m

)f

(m

f

h(m)

s

s

w

s

s

(12)

3.2. Rozkłady probabilistyczne u

ż

ywane w modelu ryzyka konstrukcji masowca

Rozkłady statystyczne nośności granicznej konstrukcji aproksymuje się zazwyczaj przy pomocy
rozkładu logarytmiczno-normalnego. Przykładowo, dla momentu granicznego M

U

ma ona

następującą postać:

,

x

,

ζ

λ

x

π

ζ

(x)

f

x

u

∞

≤

≤



























−

−

=

0

ln

2

1

exp

2

1

2

(13)

gdzie

,

1

ln

2

1

ln

2

2

2

2

















+

=

−

=

U

u

U

m

S

, ζ

ζ

)

m

(

λ

gdzie

S

m

jest wartością średnią momentu granicznego M

U

a S

U

jest jego odchyleniem

standardowym. Rozkład ten opisuje również mechaniczne własności stali.

Równanie na temat losowego charakteru gnącego momentu przedstawione są w artykule [2].
Jednak statystyczny rozkład M

S

dla masowców jest inny niż sugerowane w tym artykule. Dlatego

w niniejszej pracy założono, że na masowcach:

•

występują typowe stany ich załadowania (stan jednorodny, naprzemienny i balastowy) i ich
prawdopodobieństwa występowania są określone,

•

każdy typowy stan załadowania ma charakter losowy – spowodowane jest to różnicami w
rozkładzie ładunku i jego masie w kolejnych rejsach,

•

moment gnący na wodzie spokojnej, odpowiadający typowemu stanowi załadowania, ma
rozkład normalny N (m

S

, S

S

), z następującą funkcją gęstości:

,

x

-

,

s

m

x

π

s

(x)

f

s

s

s

l

∞

≤

≤

∞



























−

−

=

2

1

exp

2

1

2

(14)

gdzie

S

m

jest wartością średnią, a S

S

jest odchyleniem standardowym. Założono, że S

S

=0.08

S

m

.

Symulacja ruchu statku na fali i odpowiedź jego konstrukcji na działanie fali umożliwia określenie
jego maksimów i minimów w każdym cyklu, co z kolei umożliwia określenie numerycznej funkcji
gęstości prawdopodobieństwa rozważanej odpowiedzi konstrukcji statku na falę (np. gnący
moment falowy M

W

), traktowanej jako zmienna losowa. Tak określony numeryczny rozkład

6

prawdopodobieństwa zmiennej losowej reprezentującej odpowiedź statku na falę aproksymowano
rozkładem Weibulla:

,

ε

ε

η

x

F(x)

ξ



























−

−

−

−

=

exp

1

(15)

z funkcją gęstości prawdopodobieństwa:

exp

1

,

ε

η

ε

x

ε

η

ε

x

ε

η

ζ

f(x)

ξ

ζ



























−

−

−













−

−

−

=

−

(16)

gdzie parametry

ξ

η

, i

ε

są parametrami rozkładu Weibulla.

4. MODELE DETERMINISTYCZNE

4.1. Symulacja ruchu statku na fali regularnej

Symulacja ruchu statku na fali dokonuje się w wyniku numerycznego rozwiązania nieliniowych
równań ruchu (17). Równania te przedstawione są w [3].

W stosowanym modelu założono, że siła hydrodynamiczna działająca na statek i definiujące
równania jego ruchu, można traktować jako sumę sił Froude’a-Kryłowa, siły dyfrakcyjnej i
radiacyjnej.

Siłę Froude’a-Kryłowa otrzymuje się całkując ciśnienie w niezakłóconej fali nieregularnej na
zwilżonej powierzchni statku w danej chwili kroku czasowego.

Siły dyfrakcyjne określono jako superpozycję sił dyfrakcyjnych, wygenerowanych przez
harmoniczne komponenty rozważanej fali nieregularnej (przyjęto, że fala nieregularna jest
superpozycją odpowiedniej liczby fal harmonicznych). Założono, że statek powodujący dyfrakcję
jest w jego średnim położeniu. Takie podejście jest możliwe przy założeniu, że zjawisko dyfrakcji
może być opisane przy pomocy liniowego hydrodynamicznego zagadnienia różniczkowego.
Upraszcza ono znacznie obliczenia, gdyż ich uciążliwą część wykonuje się przed symulacją,
a w trakcie symulacji wykorzystuje się gotowe rozwiązania.

Siły radiacyjne są sumą masy towarzyszącej wody dla nieskończonej częstości i tak zwanej
funkcji pamięci w postaci splotu. Funkcja pamięci uwzględnia zakłócenie wody spowodowane
przez poruszający się na fali statek i oddziałujące na ten statek w danej chwili [4].

Równanie ruchu statku na fali nieregularnej zapisano w nieinercjalnym układzie odniesienia, który
zaczepiony jest w środku mas Q. W tym układzie przyjmują one następującą postać [3]:

),

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

G,

1

)

(

F

)

(

F

)

(

F

)

(

F

)

(

F

)]

(

V

)

(

)

(

.

V

[

t

QA

t

QT

t

QR

t

QD

t

QW

t

t

t

mD

t

A

t

T

t

R

t

D

t

W

t

Q

t

t

Q

m

M

M

M

M

M

L

Ω

L

+

+

+

+

=

×

+

•

−

+

+

+

+

+

=

×

+

Ω

)

(

))

(

),

(

),

(

(

),

(

)

(

)

(

V

)

(

R

1

t

D

t

t

t

t

t

t

t

T

UQ

Q

UQ

Ω

R

Ω

−

Ω

•

•

•

•

=

×

−

=

ψ

θ

ϕ

(17)

gdzie m jest masą statku, V

Q

jest prędkością środka masy statku, Ω jest jego prędkością kątową,

R

UQ

jest wektorem położenia środka masy statku, (φ, θ, ψ) są kątami Eulera reprezentującymi

7

kołysania, kiwania i myszkowanie statku, F

W

, F

D

i F

R

są odpowiednio siłami Froude’a-Kryłowa,

dyfrakcyjnymi i radiacyjnymi, M

QW

, M

QD

i M

QR

są momentami powyżej wymienionych sił,

G = (0,0,- g), a g jest przyspieszeniem ziemskim, F

A

i M

QA

są dodatkowymi siłami takimi, jak siły

tłumienia czy generowanymi przez ster, a D jest macierzą obrotu.

Sposoby rozwiązania trójwymiarowych hydrodynamicznych problemów, w wyniku których
otrzymuje się siły określające równania ruchu (17), przedstawiono w [3]. Natomiast nieliniowe
równanie ruchu (17) rozwiazano przy pomocy metod przedstawionych w [5].

4.2. Symulacja odpowiedzi konstrukcji statku na fal

ę

nieregularn

ą

Kilka wybranych parametrów odpowiedzi statku na falę, jako funkcję czasu i wzniosu fali
przedstawia rys. 2. Obliczono je dla fali zdefiniowanej znaczącą wysokości fali H

S

=10m oraz

średnim okresem przekroczeń miejsc zerowych T

O

=8s, w położeniu statku czołem do fali.

2000.00

2020.00

2040.00

2060.00

2080.00

2100.00

sloshing force acting on the bullehead, kN

0.00

1000.00

2000.00

2000.00

2020.00

2040.00

2060.00

2080.00

2100.00

wave elevation, m

-10.00

0.00

10.00

2000.00

2020.00

2040.00

2060.00

2080.00

2100.00

still water + wave bending moment at midship, kNm

-4 10

7

0.00

4 10

7

2000.00

2020.00

2040.00

2060.00

2080.00

2100.00

stresses in frame (in point denoted in Fig. 5), MPa

-250.00

-200.00

-150.00

Rys. 2. Symulacja odpowiedzi statku na działanie fali: M

S

+ M

W

– pionowy moment gnący na

śródokręciu,

∑

F

- naprężenie we wręgu burtowym w ładowni nr 4, F

L

– siła generowana

na grodzi przez wodę w zalanej ładowni i działająca prostopadle do grodzi oraz
ζ - wznios fali.

Metodę obliczenia momentu granicznego, jaki jest w stanie przenieść belka kadłuba,
przedstawiono w [6]. Moment falowy, generowany w dowolnym przekroju belki kadłuba,
obliczono jako wynik działania zewnętrznego ciśnienia, wzbudzonego na zwilżonej powierzchni
statku przez ruch falowy, i siły inercyjne masy działające na części kadłuba i ładunku od rufy do
rozważanego przekroju.

Wręgi burtowe na statku, dla którego przeprowadzono analizę ryzyka, są teownikami z
węzłówkami na końcu. Węzłówki są integralną częścią wręgu (rys. 3). Założono, że graniczna
wytrzymałość wręgu jest osiągnięta, gdy naprężenie

∑

F

w płaskowniku czołowym w jego dolnej

części przekroczy granicę plastyczności

∑

FY

. Takie podejście w ocenie nośności wręgów jest

zalecane w [7]. Na masowcach największe naprężenia generowane są we wręgach w punkcie,

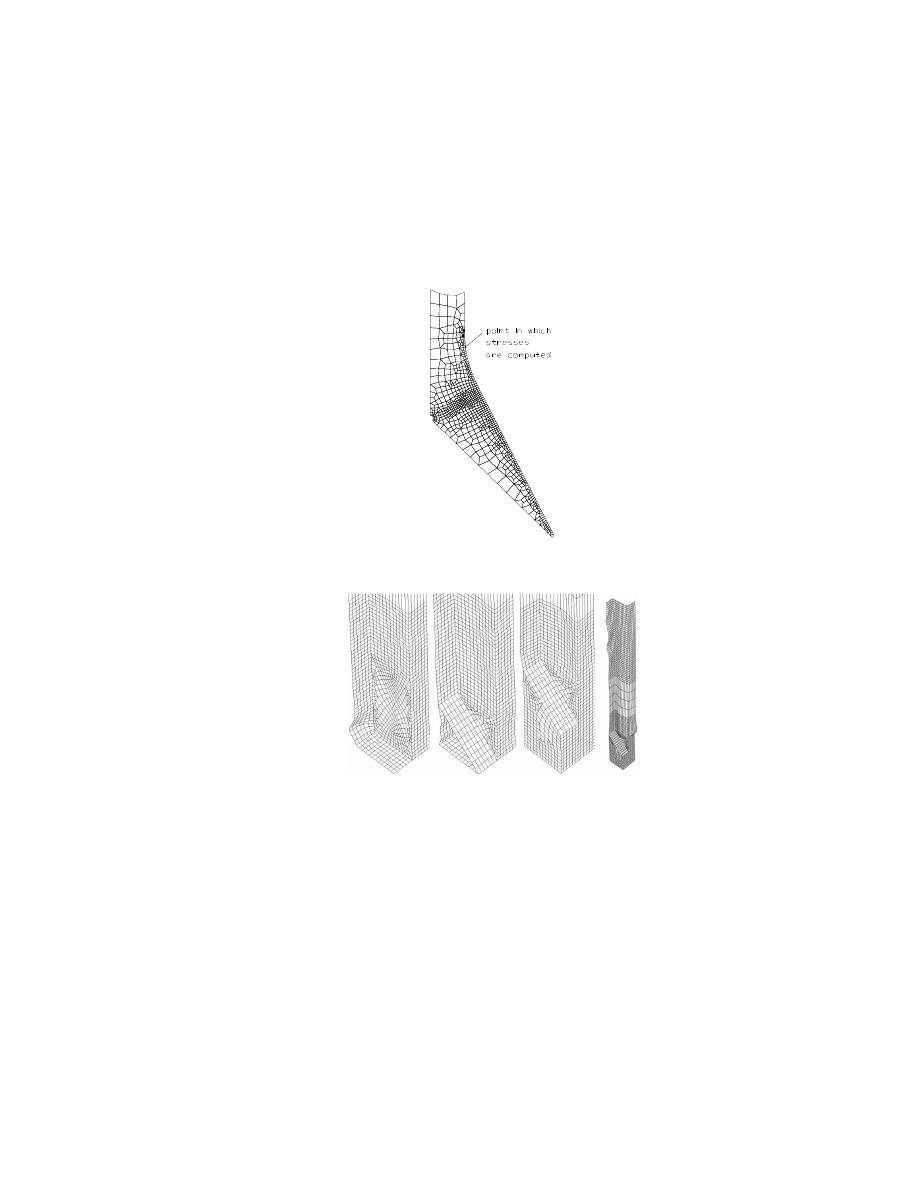
8

gdzie część pryzmatyczna przechodzi w węzłówkę (rys. 3) i dlatego tylko w tej części wręgu
dokonano symulacji naprężeń.

Wartości naprężeń we wręgach obliczano stosując oryginalną koncepcję współczynników wpływu
ciśnienia. Wartości tych współczynników obliczono oddzielnie (przed symulacją ruchu statku na
fali) stosując metodę elementów skończonych do części kadłuba składającego się z trzech
ładowni. Wartości ciśnienia zewnętrznego w wybranych punktach poszycia kadłuba (na aktualnie
zwilżonej powierzchni kadłuba statku) oraz ciśnienia generowanego przez ładunek w wybranych
punktach dna wewnętrznego, obliczano w czasie symulacji ruchu statku na fali i mnożono je przez
współczynniki wpływu, co w wyniku dawało naprężenia we wręgach. Założono, że tak obliczone
ciśnienia zmieniają się liniowo pomiędzy wybranymi punktami poszycia statku.

Rys. 3.

Punkt wręgu, w którym występują największe naprężenia

Rys. 4.

Uszkodzona gródź falista

Założono, że gródź falista utraci integralność i że zalanie kolejnych ładowni nastąpi, gdy
pojedyncza fala grodzi utraci, na skutek działania wody w zalanej ładowni, swa nośność
graniczną. Nośność tę obliczono stosując nieliniowe analizy przy pomocy metody elementów
skończonych (rys. 4). Obliczoną siłę F

U

,

reprezentującą nośność graniczną fali grodzi, użyto jako

kryterium wytrzymałości grodzi, na którą działa poruszająca się w zalanej ładowni woda [8].
Przykład wyników obliczeń przedstawiono na rys. 2.

Pokrywa luku nad ładownią nr 1 ma postać dwóch paneli, kontaktujących się ze sobą w
płaszczyźnie wręgu. Przyjęto, że panele nie oddziaływają na siebie i, że są swobodnie podparte.
Założono, że utrata nośności granicznej pokrywy luku pod obciążeniem wody na pokładzie
nastąpi, gdy wystąpi jeden z poniższych warunków [9]:

a) zostanie przekroczona nośność graniczna ściskanego poszycia pokrywy w pobliżu krawędzi

pokrywy w płaszczyźnie symetrii statku,

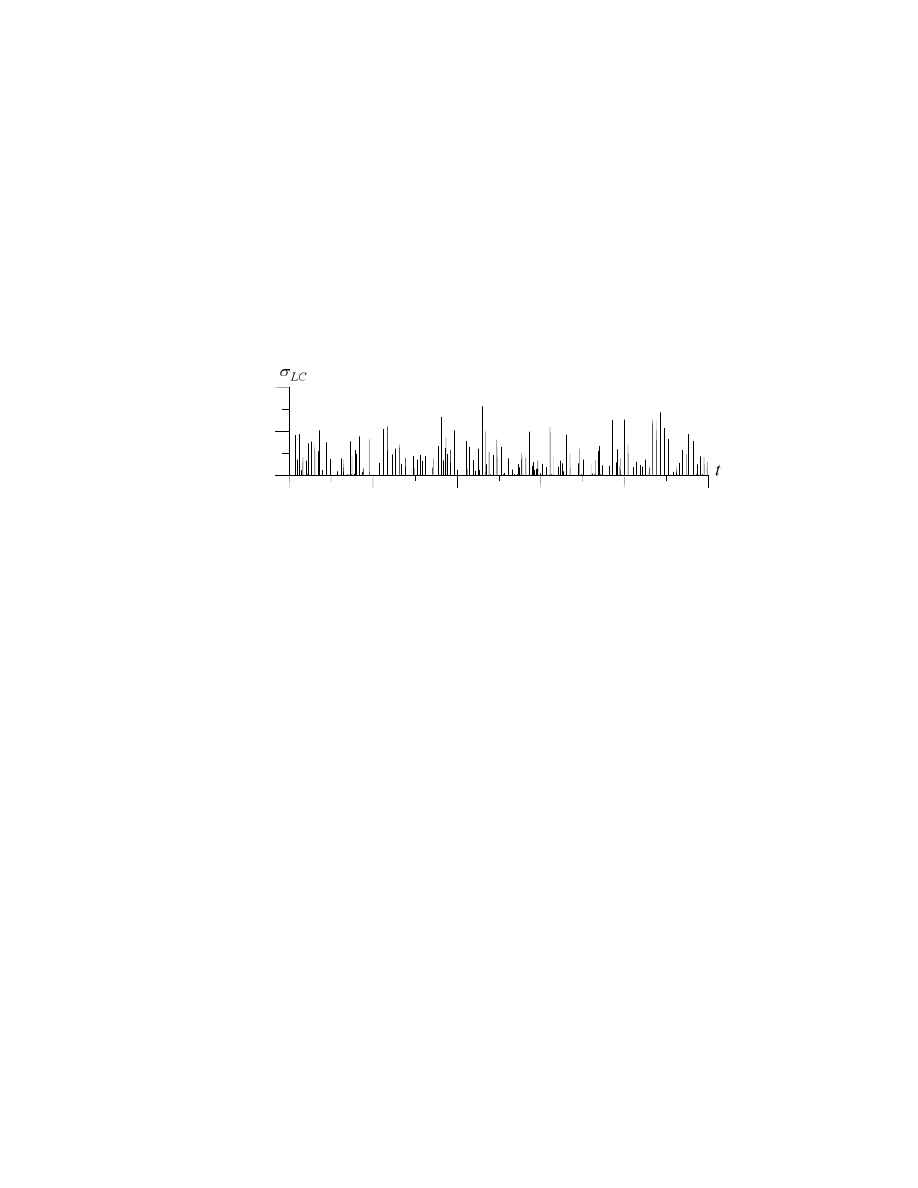
9

b) całkowite naprężenia w usztywnieniach poszycia pokrywy, wynikające ze zginania pokrywy i

lokalnego zginania tych usztywnień, podpartych przez wiązary pokrywy, osiągnie granicę
plastyczności.

W obliczeniach wykorzystano parametryczne wzory określające nośność graniczną płyt [6].
Nośność graniczną pokrywy luku dwóch, powyżej wymienionych form, określono stosując
nieliniowe analizy przy pomocy metody elementów skończonych [8].

Naprężenia, które mogą spowodować utratę nośności pokrywy wyznaczono podczas symulacji
ruchu statku na fali z uwzględnieniem wody wdzierającej się na pokład przy zastosowaniu analizy
w zakresie liniowym oraz metody elementów skończonych.

W tym celu wykorzystano koncepcje współczynników wpływu ciśnienia generowanego na
pokrywie przez wodę na pokładzie podobną do zastosowanej do wyznaczenia naprężeń we
wręgach. Przykład obliczeń przedstawiono na rys.5

0

2000

4000

6000

8000

10000

stresses in hatch cover during the green seas
occurance, MPa

0

100

200

Rys. 5.

Naprężenia w pokrywie luku wywołane wodą na pokładzie

5. OBLICZENIA PRAWDOPODOBIE

Ń

STWA ZATONI

Ę

CIA STATKU

SPOWODOWANEGO USZKODZENIEM JEGO KONSTRUKCJI

5.1. Parametry rozkładów probabilistycznych

W ocenie bezpieczeństwa konstrukcji występują wiele elementów niepewnych [7]. Dotyczą one,
między innymi:

•

własności materiału takich jak jego granicy plastyczności, wytrzymałości zmęczeniowej,
wytrzymałość w miejscu występowania karbów, efektów spawania;

•

analiz wytrzymałościowych konstrukcji, w których z konieczności przyjmuje się założenia
upraszczające, aproksymujące i idealizację przy sformułowaniu matematycznych modeli
opisujących fizyczne środowisko;

•

jakość budowy statku;

•

efektów, eksploatacji statku (np. trwałe deformacje konstrukcji) itp.

Na podstawie dużej liczby badań rozciągania próbek stali, z której produkuje się statki ustalono,
że rozkład logarytmiczno-normalny granicy plastyczności materiału posiada odchylenie
standardowe równe 0.1 wartości średniej. Aby uwzględnić powyżej wspomniane niepewności
założono, że odchylenie standardowe zmiennej losowej reprezentującej wytrzymałość graniczną
konstrukcji statku jest równe 0.15 jej średniej wartości, co zgadza się z wartością zaproponowaną
w [2]. Parametry rozkładu logarytmiczno-normalnego dla zmiennych losowych użytych w
analizach przedstawiono w Tablicy 1.

10

Tablica 1.

Parametry rozkładu logarytmiczno-normalnego

Wartość średnia

Zmienna losowa

Konstrukcja po

budowie

Konstrukcja

skorodowana

M

U sag

[KNm]

4580000

0.9

M

U hog

[KNm]

5450000

0.8

∑

FY

,

[MPa]

265

1

F

U

, hold 4, [KN]

1863

0.9

F

U

, hold 1, [KN]

1896

0.9

∑

Y

,

[MPa]

265

1

W przypadku pokrywy luku i wręgów, korozję uwzględniono poprzez redukcję ich wskaźników
przekroju, zgodnie z doświadczeniem instytucji klasyfikacyjnych. Założono również, że udział
konstrukcji nieskorodowanej i skorodowanej w prawdopodobieństwie jej uszkodzenia wynosi
odpowiednio 60% i 40%.

Z informacji o stateczności statku wyselekcjonowano następujące stany załadowania dla
rozważanego masowca:

•

jednorodny stan załadowania:

s

m =706840 kNm − w rejonie śródokręcia, w stanie ugięcia

statku;

•

naprzemienny stan załadowania:

s

m =1227490 kNm

− w rejonie śródokręcia, w stanie

przegięcia;

•

balastowym:

s

m

= 1364600 − w rejonie śródokręcia, w stanie przegięcia,

gdzie

s

m

jest średnią momentu gnącego M

S

. Rozkład momentu gnącego M

S

jest rozkładem

normalnym N(

s

m , S

S

).

Założono, że poszczególne stany załadowania wystąpią z następującymi

prawdopodobieństwami: 1

o

jednorodny, p

1

=0.4; 2

o

naprzemienny p

2

=0.3; 3

o

balastowy, p

3

=0.3.

Rozkłady probabilistyczne zmiennych losowych, reprezentujących rozważane odpowiedzi
konstrukcji statku na falę zostały określone przy pomocy symulacji i ruchu statku na fali. Razem z
symulacją ruchu statku na fali wyznaczono: falowy moment gnący M

w

, siłę wody działającą na

gródź F

2

, naprężenia w dolnej części wręgu Σ

F

i naprężenie w pokrywie luku Σ

L

, jako funkcję

czasu (rys. 2; 5). Ich wartości ekstremalne w każdym cyklu były identyfikowane i użyte do
budowy funkcji schodkowych, które z kolei aproksymowano rozkładem Weibulla, stosując
metodę najmniejszych kwadratów. Rozkłady te użyto do obliczenia prawdopodobieństwa
uszkodzenia konstrukcji statku.

5.2. Prawdopodobie

ń

stwo uszkodzenia konstrukcji statku – ilo

ś

ciowa ocena utraty

statku.

Prawdopodobieństwo utraty statku z powodu uszkodzenia konstrukcji obliczono zgodnie ze
wzorami (1), (6), (7), (8), (9), (10) i (11). Kompozycję rozkładu zrobiono zgodnie ze wzorem (12).
Przykłady tych kompozycji przedstawiono na rys. 6 i 7.

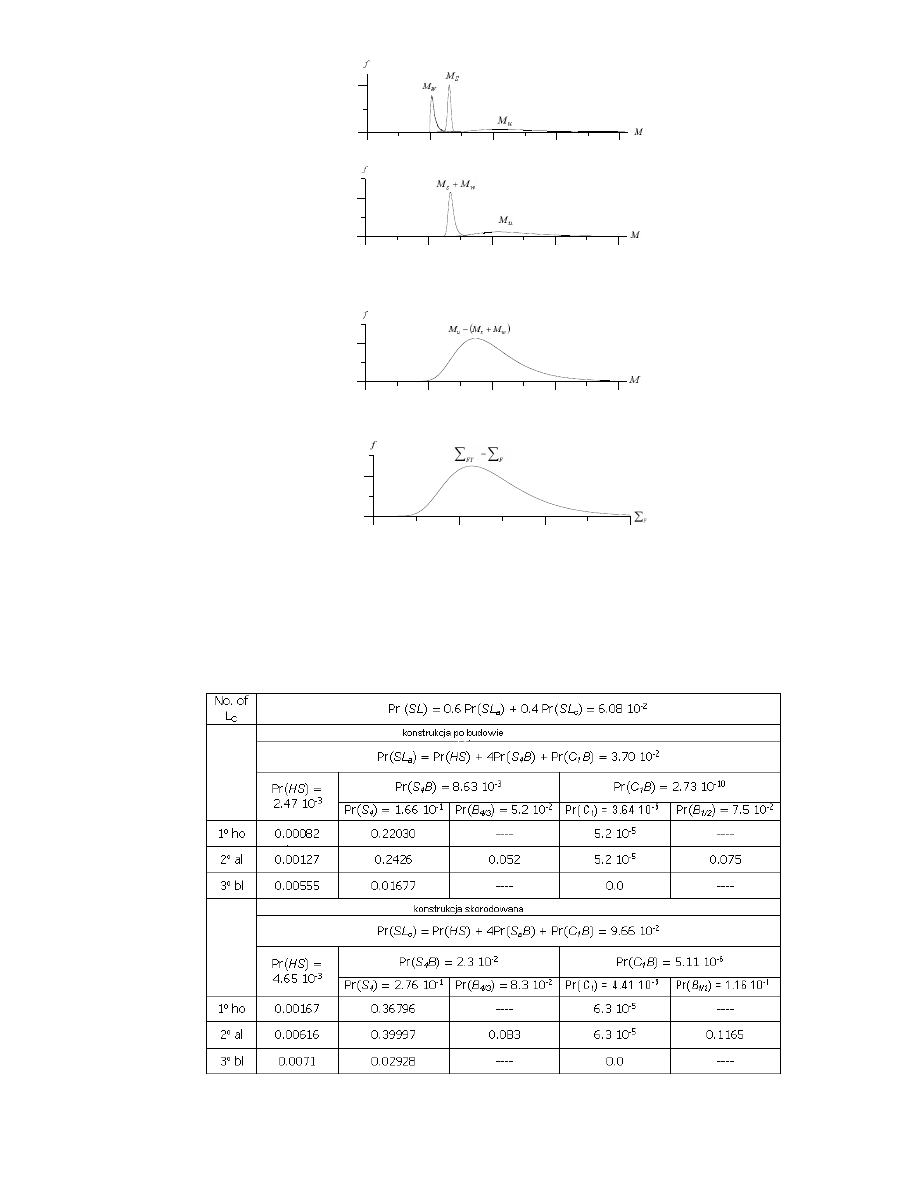
11

-4.0E+6

0.0E+0

4.0E+6

8.0E+6

1.2E+7

0.0E+0

4.0E-6

-4.0E+6

0.0E+0

4.0E+6

8.0E+6

1.2E+7

0.0E+0

2.0E-6

-4.0E+6

0.0E+0

4.0E+6

8.0E+6

1.2E+7

0.0E+0

2.0E-7

Rys 6.

Prawdopodobieństwo rozkładu wytrzymałości belki kadłuba

-200.00

0.00

200.00

400.00

0.0E+0

4.0E-3

Rys 7.

Prawdopodobieństwo rozkładu wytrzymałości wręgu (w obrębie ładowni nr 4)

Wyniki poszczególnych etapów obliczeń prawdopodobieństwa zatonięcia statku SL,
przeprowadzone zgodnie z drzewem uszkodzeń (rys. 1), przedstawiono w tablicy 2. Wzięto pod
uwagę prawdopodobieństwa wystąpienia poszczególnych stanów załadowania oraz wpływ korozji
konstrukcji na te prawdopodobieństwa.

Tablica 2.

Prawdopodobieństwo zatonięcia statku z powodu uszkodzenia konstrukcji

12

Z powodu bardzo długo trwających symulacji określono prawdopodobieństwo następujących
scenariuszy i zdarzeń: H

S

, S

4

, B

4/2

oraz C

1

i założono, że scenariusze S

i

B, i

=3,2 i 1, mają te same

prawdopodobieństwa, co S

4

B

. Założenie to dało:

P

r

(SL) =P

r

(H

S

)+ P

r

(C

1

B

)+ 4P

r

(S

4

B

)

(18)

6. WNIOSKI

Drzewo uszkodzeń umożliwiło wzięcie pod uwagę różne możliwe scenariusze zatonięcia statku z
powodu uszkodzenia konstrukcji – te znane ze statystyk uszkodzeń i te, które można przewidzieć.

W analizie drzewa uszkodzeń narzędziem jest rachunek prawdopodobieństwa, lecz aby określić
rozkłady prawdopodobieństwa zmiennych losowych reprezentujących różne uszkodzenia,
podstawowe zdarzenia muszą być opisane przy pomocy matematycznych modeli i symulowane
przy pomocy programów komputerowych, opracowanych na podstawie tych modeli. W tym
sensie drzewo uszkodzeń łączy teorię procesów stochastycznych, mechanikę fal morskich,
mechanikę konstrukcji i tworzy model ryzyka. Taki model oparty na drzewie uszkodzeń
zazwyczaj charakteryzują się dużym skomplikowaniem.

Przedstawiony model ryzyka wymaga dalszego rozwoju. Jednak zaprezentowany, względnie
prosty, model ryzyka zatonięcia statku z powodu uszkodzenia konstrukcji pokazał, że:

•

najsłabszymi elementami konstrukcyjnymi są wręgi burtowe zainstalowane pomiędzy
sztywnymi zbiornikami,

•

najbardziej prawdopodobnym scenariuszem zatonięcia statku jest utrata integralności burty, a
następnie zapadnięcie się grodzi falistej na skutek działania wody w zalanej ładowni i
progresywne zalewanie kolejnych ładowni, prowadzące do zatonięcia statku.

Zastosowanie przedstawionego modelu ryzyka pokazało również, że jest on dobrym narzędziem
do pomiaru bezpieczeństwa konstrukcji statku.

LITERATURA

[1]

Vesely W.E, Golberg F.F., Roberts N.H., Haasl D.F., Fault tree handbook, US Nuclear
Regulatory Commission, 1981

[2]

Guedes Soares C., Toixoira A.P., Structural reliability of two bulk carriers designs, Marine
Structures 13, 2000

[3]

Jankowski J., Ship facing waves, Technical Report No. 52, Polish Register of Shipping,
2006, (in Polish)

[4]

Cummins W.E., The impulse response function and ship motions, Schiffstechnik, Vol. 9,
No.47, 1962

[5]

Ralston A., First course in numerical analysis, PWN, Warsaw, 1975

[6]

Konieczny L., Dębek P., Development of probabilistic method of ship structural safety
assessment

, Technical Report No. RK 2006/T-054/E, Ship Design and Research Centre S.A.,

Gdańsk, 2006

[7]

Hughes O.F., Ship structural design, A Rationally-Based, Computer-Aided, Optimization
Approach

, The Society of Naval Architects and Marine Engineers, New Jersey 1988

[8]

Warmowska M., Determination of the liquid motion in ship tank including non-linear
phenomena

(in Polish) , Doctor thesis, Gdańsk University of Technology, Gdańsk 2006 (in

Polish)

[9]

Tetsuya Yao, Atsushi Magaino, Toshiro Koiwa, Shugo Sato, Collapse strength of hatch
cover of bulk carrier subjected to lateral pressure load

, Marine Structures 16, 2003.