1

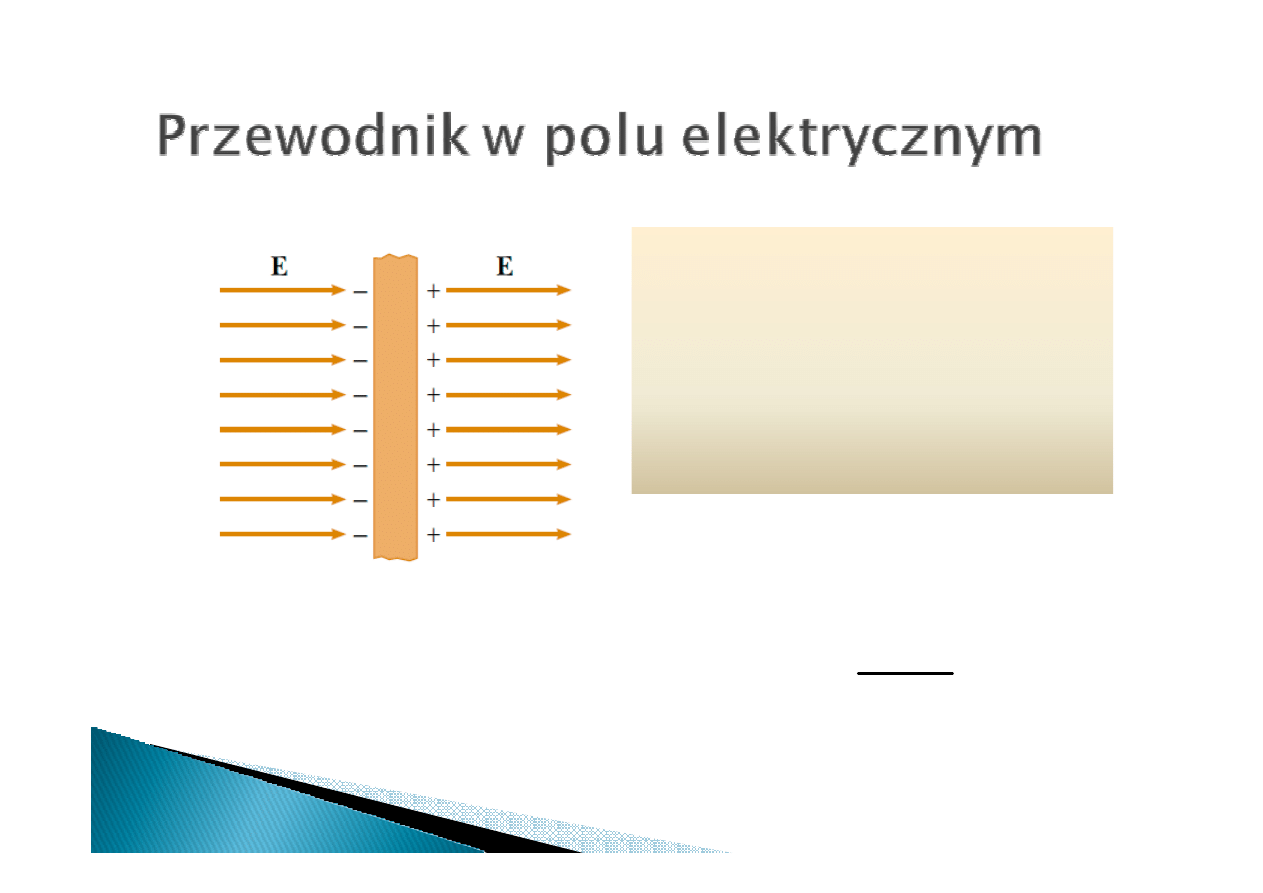
W stanie równowagi
elektrostatycznej (nośniki
ładunku są w spoczynku)
wewnątrz przewodnika
natężenie pola E wynosi zero

zero

zero

zero.

Cały ładunek jest zgromadzony
na powierzchni

na powierzchni

na powierzchni

na powierzchni przewodnika.

Tuż przy powierzchni przewodnika
natężnie pola jest takie jak w sąsedztwie
nieskończenie dużej płaszczyzny:

0

2

ε

σ

=

E

2

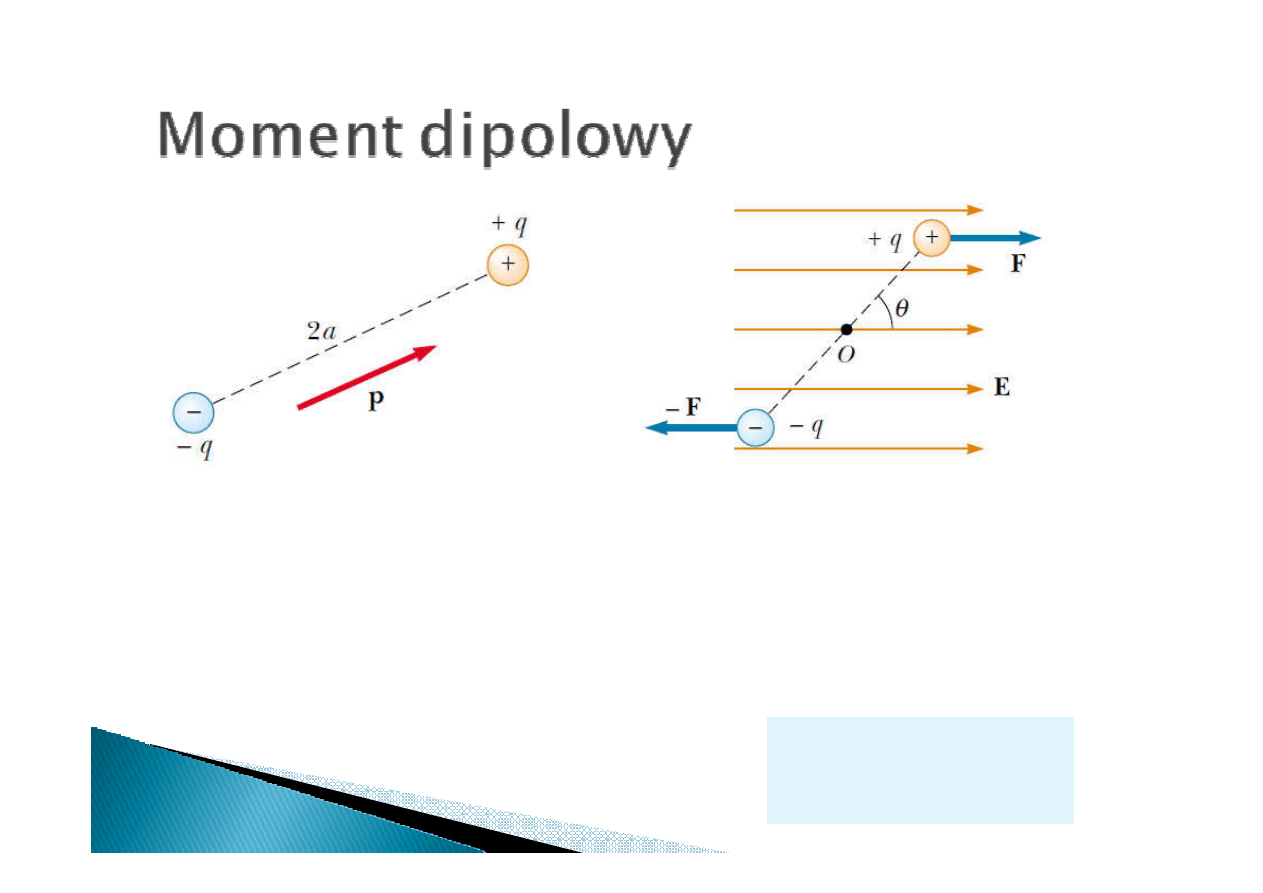
Momentem dipolowym ładunków
+

q

i –

q

oddalonych o 2

a

(dipola)

nazwamy wektor skierowany od
–

q

do +

q

i o wartości:

a

q

p

2

=

Na dipol umieszczony w
zewnętrznym polu o natężeniu E
działa moment siły

τ

.

θ

τ

sin

2Fa

=

Eq

F

=

θ

τ

sin

2a

Eq

=

E

p

τ

×

=

3

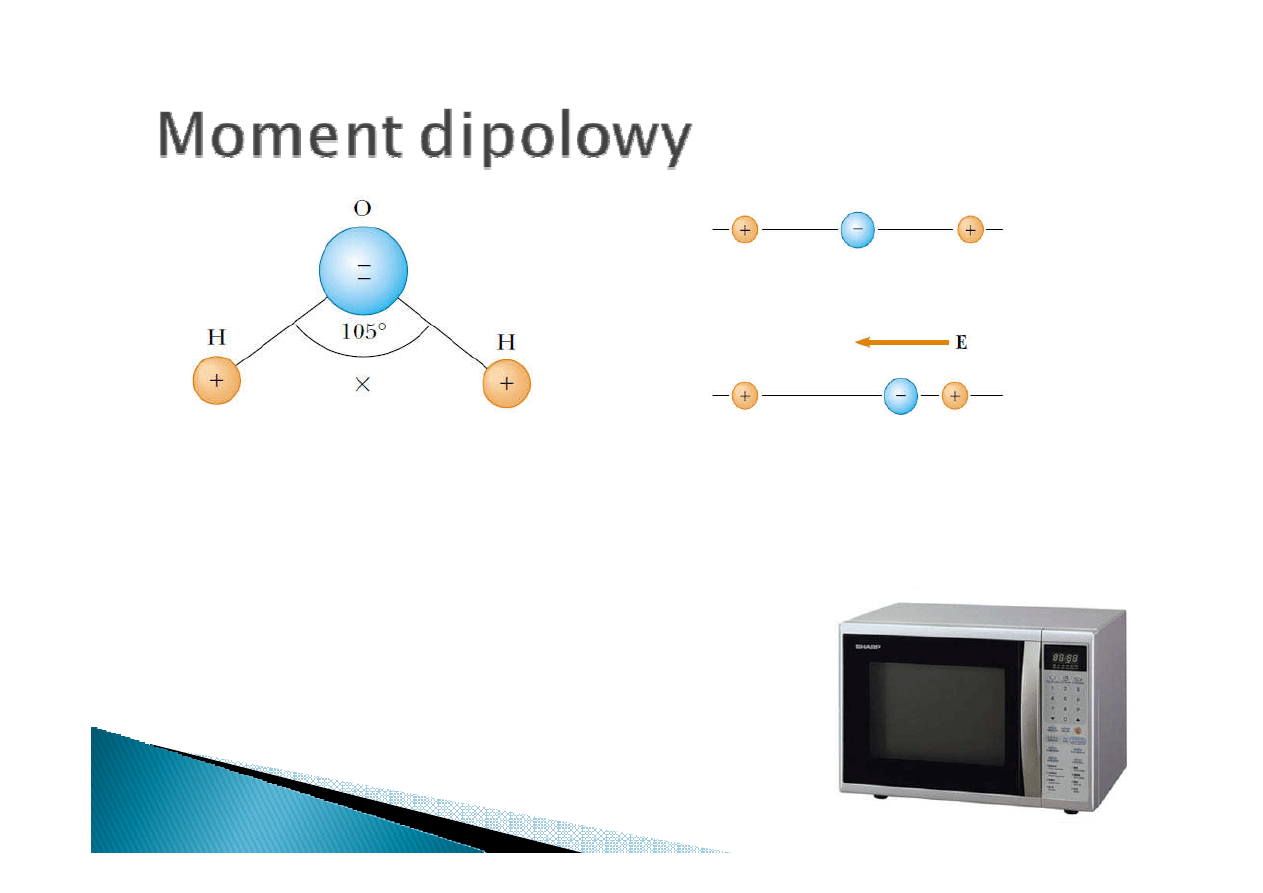
Cząsteczki które posiadają
moment dipolowy nazywamy
polarnymi

polarnymi

polarnymi

polarnymi. Przykładem takiej
substancji jest woda.

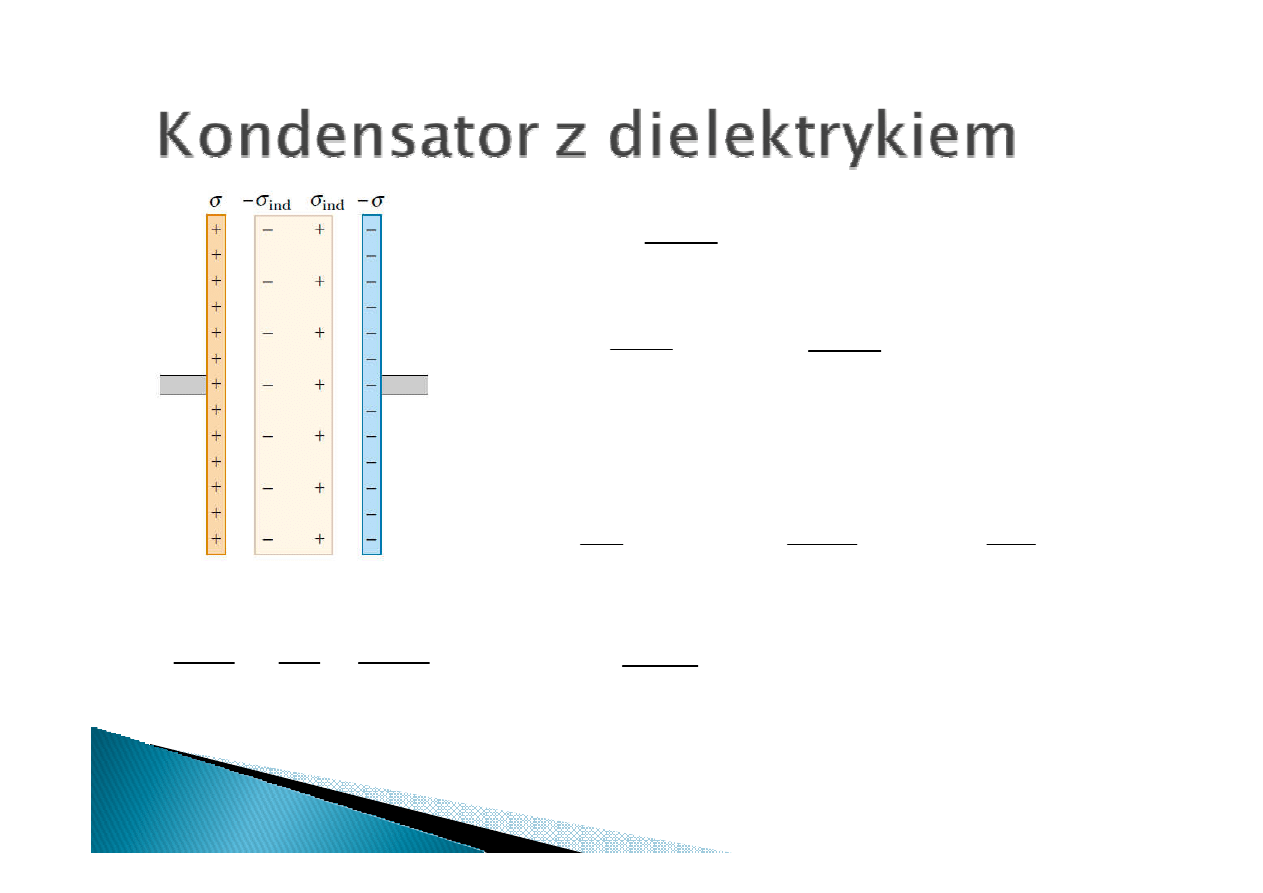
Polaryzacja indukowana
zewnętrznym polem E w
cząsteczce symetrycznej

W kuchence mikrofalowej zmienne pole
elektryczne wprawia w drgania cząsteczki
polarne, które absorbują energię pola. Drgania
cząsteczek powodują wzrost energii wewnętrznej
i tym samym wzrost temperatury.

4

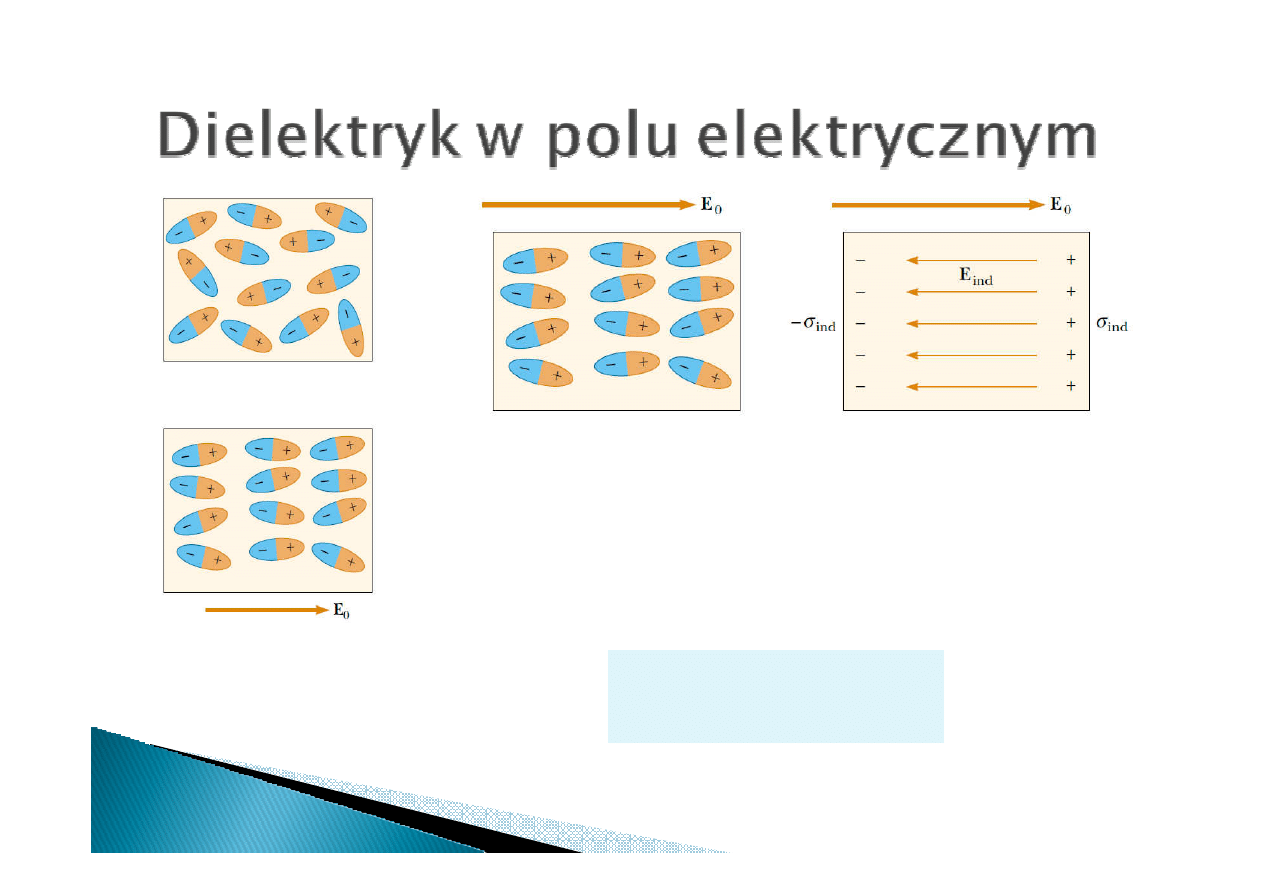
Zewnętrzne pole
elektryczne E

0

porządkuje momenty
dipolowe w dielektryku

Uporządkowanie momentów dipolowych powoduje
powstanie ładunku indukowanego

ładunku indukowanego

ładunku indukowanego

ładunku indukowanego na powierzchni

dielektryka. Ładunek indukowany wytwarza pole E

ind

wewnątrz dielektryka. Wypadkowe natężnie pola
wewnątrz dielektryka wynosi:

ind

E

E

E

−

=

0

5

ε

0

V

V

∆

=

∆

ε

- stała dielektryczna

∆

V

0

– różnica potencjałów

między okładkami bez
dieleketryka

V

Q

C

∆

=

0

0

V

Q

C

∆

=

ε

0

C

C

=

Ed

V

=

∆

0

0

0

ε

σ

=

E

0

ε

σ

ind

ind

E

=

ε

0

E

E

=

0

0

0

ε

σ

ε

σ

εε

σ

ind

−

=

σ

ε

ε

σ













−

=

1

ind

Ponieważ

ε

>1,

σ

ind

<

σ

.

Gęstość ładunku
indukowanego jest mniejsza

mniejsza

mniejsza

mniejsza

niż gęstość ładunku na
okładkach kondensatora.

6

r

ev

e

T

e

I

π

π

ω

2

2

=

=

=

evr

r

r

ev

IA

2

1

2

2

=













=

=

π

π

µ

L

m

ev

e













=

2

µ

vr

m

L

e

=

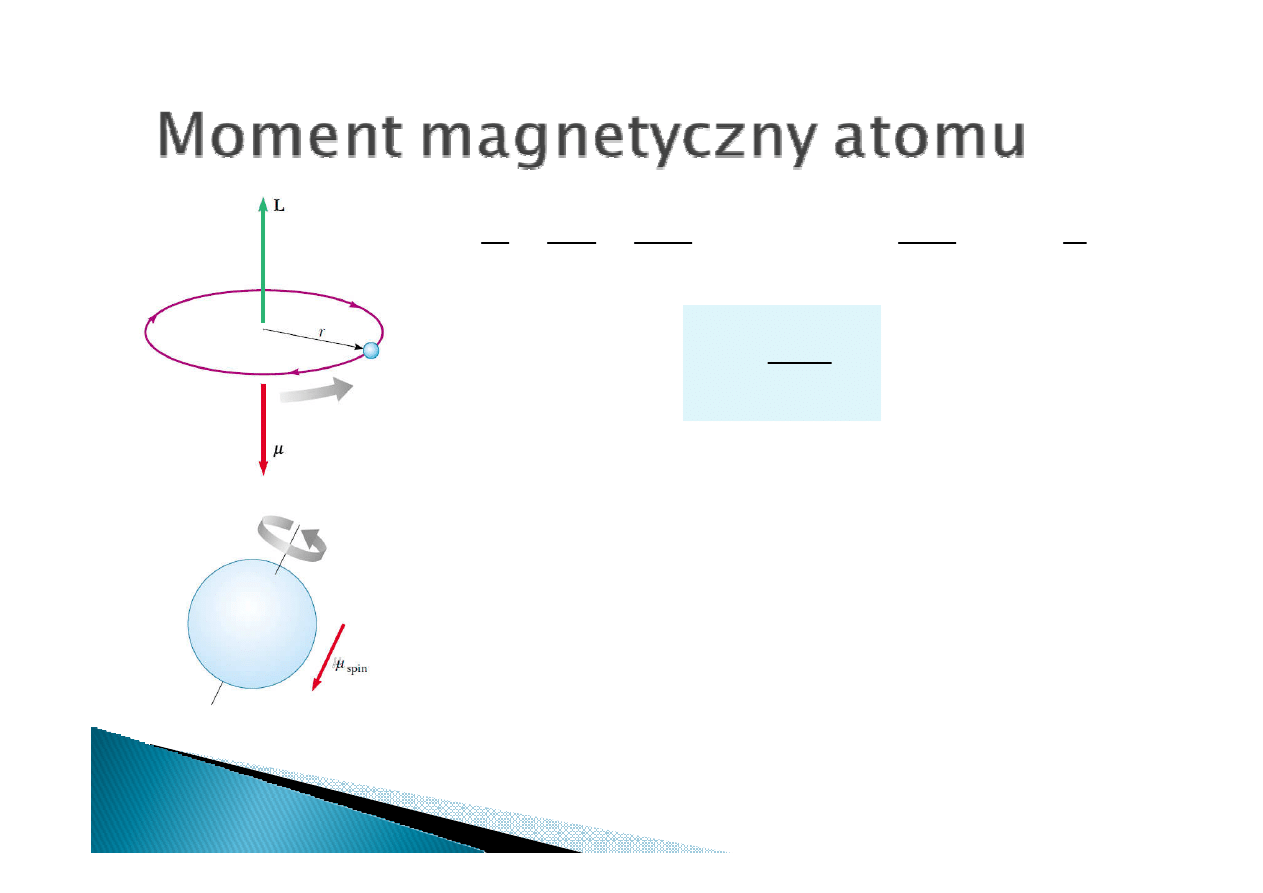
Orbitalny

Orbitalny

Orbitalny

Orbitalny moment magnetyczny elektronu krążącego
wokół jądra jest proporcjonalny do jego momentu pędu.
Oprócz orbitalnego momentu magnetycznego elektron w
atomie posiada spinowy

spinowy

spinowy

spinowy (wewnętrzny) moment

magnetyczny. Momenty orbitalny i spinowy elektronu
dodają się wektorowo.
Moment magnetyczny atomu jest sumą wektorową

Moment magnetyczny atomu jest sumą wektorową

Moment magnetyczny atomu jest sumą wektorową

Moment magnetyczny atomu jest sumą wektorową
momentów magnetycznych (spinowych i orbitalnych)

momentów magnetycznych (spinowych i orbitalnych)

momentów magnetycznych (spinowych i orbitalnych)

momentów magnetycznych (spinowych i orbitalnych)
w szystkich elektronów. Suma ta może wynosić zero lub

w szystkich elektronów. Suma ta może wynosić zero lub

w szystkich elektronów. Suma ta może wynosić zero lub

w szystkich elektronów. Suma ta może wynosić zero lub
być różna od zera.

być różna od zera.

być różna od zera.

być różna od zera.

Moment orbitalny

Moment spinowy

7

Wektorem namagnesowania M

Wektorem namagnesowania M

Wektorem namagnesowania M

Wektorem namagnesowania M (magnetyzacją

magnetyzacją

magnetyzacją

magnetyzacją) ośrodka nazywamy

moment magnetyczny przypadający na jednostkę objętości

m

B

B

B

+

=

0

Indukcja magnetyczna wewnątrz materiału jest sumą
indukcji pola zewnętrznego B

0

i indukcji związanej z

namagnesowaniem materiału B

m

M

B

0

µ

=

m

M

B

B

0

0

µ

+

=

(

)

M

H

B

0

+

=

µ

Natężenie

Natężenie

Natężenie

Natężenie pola magnetycznego H

pola magnetycznego H

pola magnetycznego H

pola magnetycznego H wewnątrz ośrodka jest

niezależne

niezależne

niezależne

niezależne od własności magnetycznych tego ośrodka

M

B

B

H

0

0

0

−

=

=

µ

µ

8

•

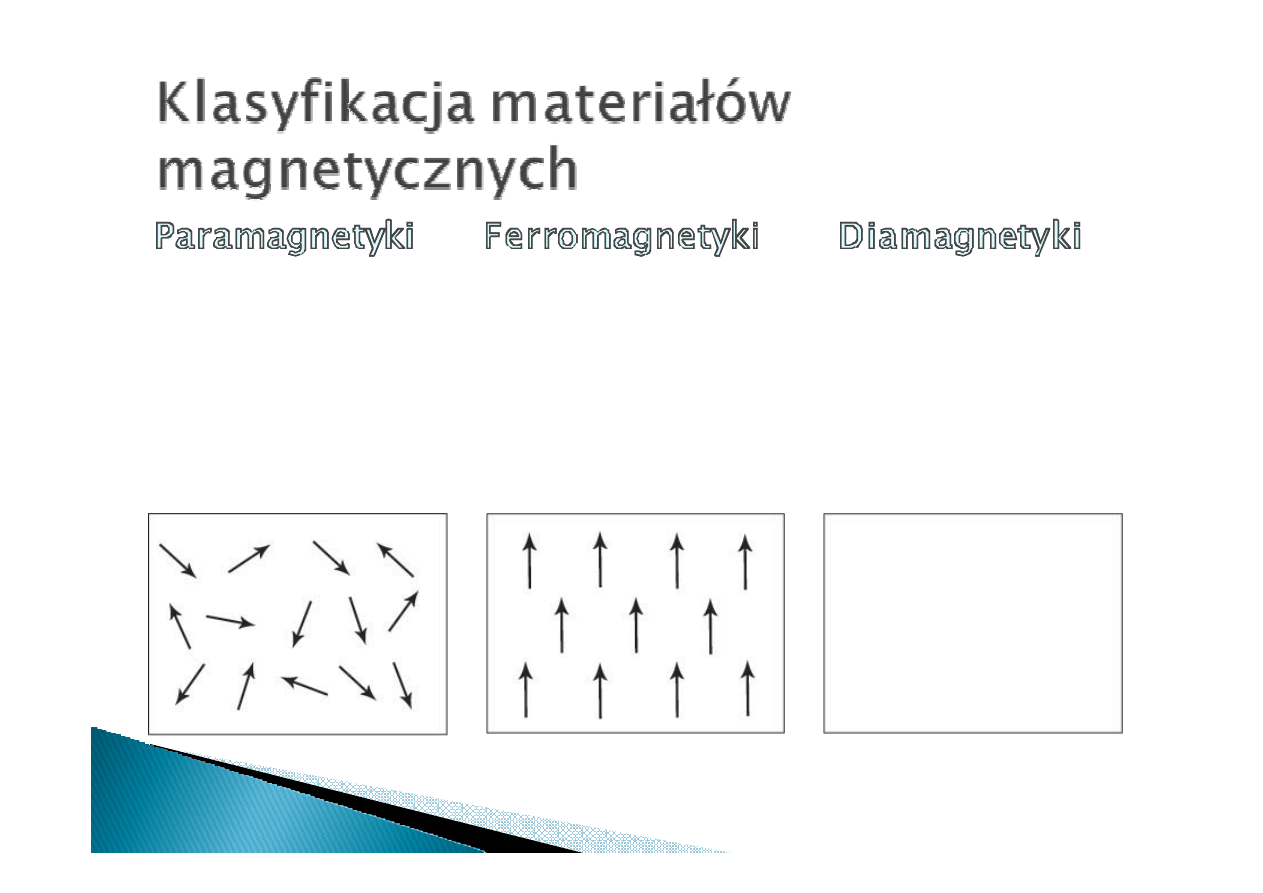
Atomy paramagnetyka
posiadają nie zerowy moment

nie zerowy moment

nie zerowy moment

nie zerowy moment

ma gnetyczny

ma gnetyczny

ma gnetyczny

ma gnetyczny

•

Momenty magnetyczne są
ułożone cha otycznie

cha otycznie

cha otycznie

cha otycznie

•

Przy braku pola zewnętrznego,
próbka paramagnetyka nie

nie

nie

nie

p osiada wypadkowego

p osiada wypadkowego

p osiada wypadkowego

p osiada wypadkowego
mome ntu magnetycznego

mome ntu magnetycznego

mome ntu magnetycznego

mome ntu magnetycznego

•

Paramagnetyk jest wcią gany

wcią gany

wcią gany

wcią gany w

obszar pola magnetycznego

•

Atomy diamagnetyka
posiadają ze rowy

ze rowy

ze rowy

ze rowy moment

magnetyczny

•

Przy braku pola
zewnętrznego, próbka
diamagnetyka nie p osiada

nie p osiada

nie p osiada

nie p osiada

wyp adkowego momentu

wyp adkowego momentu

wyp adkowego momentu

wyp adkowego momentu
ma gnetycznego

ma gnetycznego

ma gnetycznego

ma gnetycznego

•

Diamagnetyk jest wyp ychany

wyp ychany

wyp ychany

wyp ychany

z pola magnetycznego

•

Atomy ferromagnetyka posiadają
nie zerowy

nie zerowy

nie zerowy

nie zerowy moment magnetyczny

•

Momenty magnetyczne są ułożone
w tym sa mym kierunku

w tym sa mym kierunku

w tym sa mym kierunku

w tym sa mym kierunku

•

Przy braku pola zewnętrznego,
próbka ferromagnetyka p osiada

p osiada

p osiada

p osiada

wyp adkowy moment magnetyczny

wyp adkowy moment magnetyczny

wyp adkowy moment magnetyczny

wyp adkowy moment magnetyczny

9

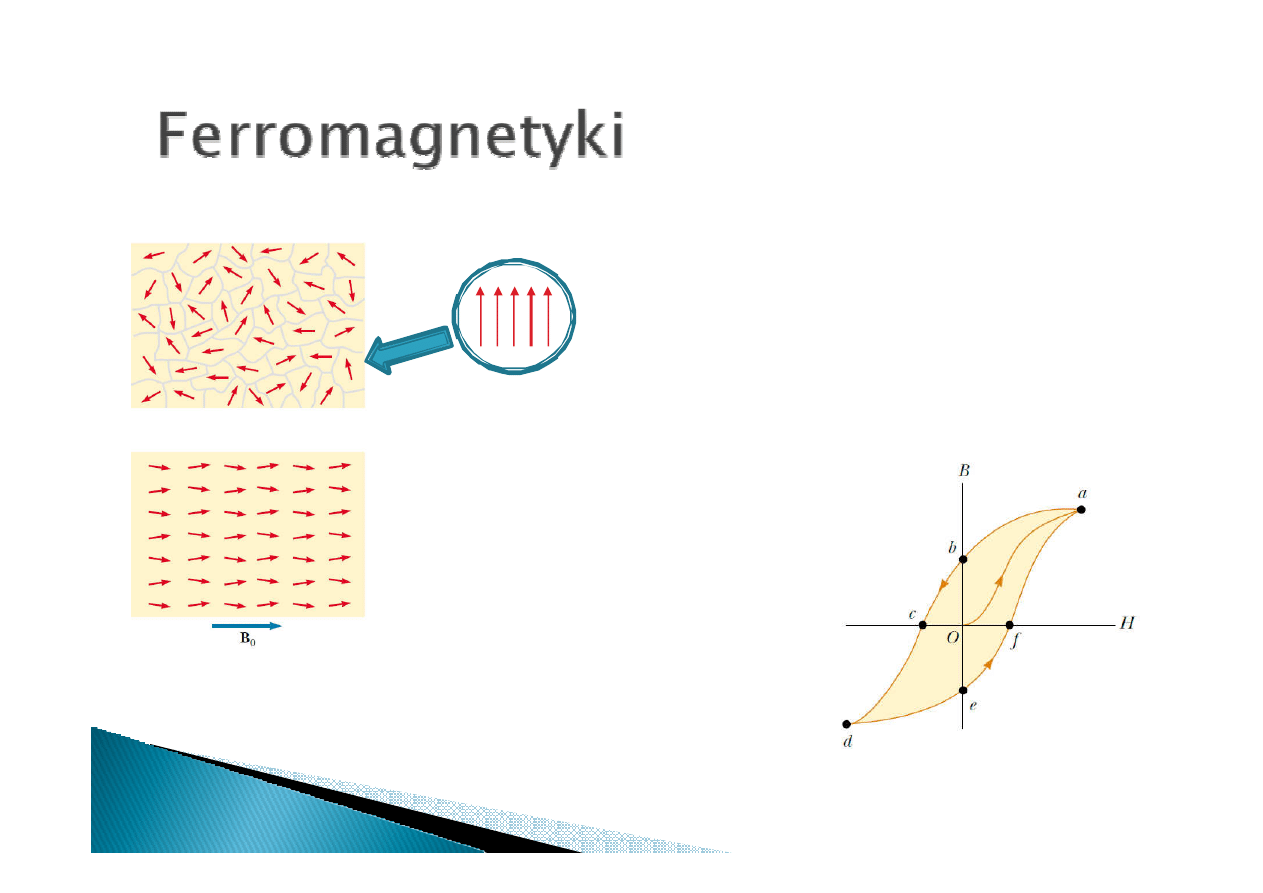
Uporządkowanie
momentów magnetycznych
atomów ferromagnetyka

Strutura domenowa ferromagnetyka

Porządkowanie momentów
magnetycznych przez pole
zewnętrzne

W ferromagnetyku momenty
magnetyczne atomów układają się
równolegle bez obecności pola
zewnętrznego. Ferromagnetyki składają
się z domen

domen

domen

domen magnetycznych.

Uporządkowanie momentów w obrębie
jednej domeny jest takie samo.
Domeny dzielą ściany domenowe

ściany domenowe

ściany domenowe

ściany domenowe

Zewnętrzne pole magnetyczne
przesuwa ściany domenowe i
obraca same domeny. Wpływ pola
zewnętrznego na strukturę
domenową obrazuje pę tla

pę tla

pę tla

pę tla

histerezy magnetycznej.

histerezy magnetycznej.

histerezy magnetycznej.

histerezy magnetycznej.
Przykłady ferromagnetyków:
żelazo, kobalt, nikiel

Pętla histerezy ferromagnetyka

10

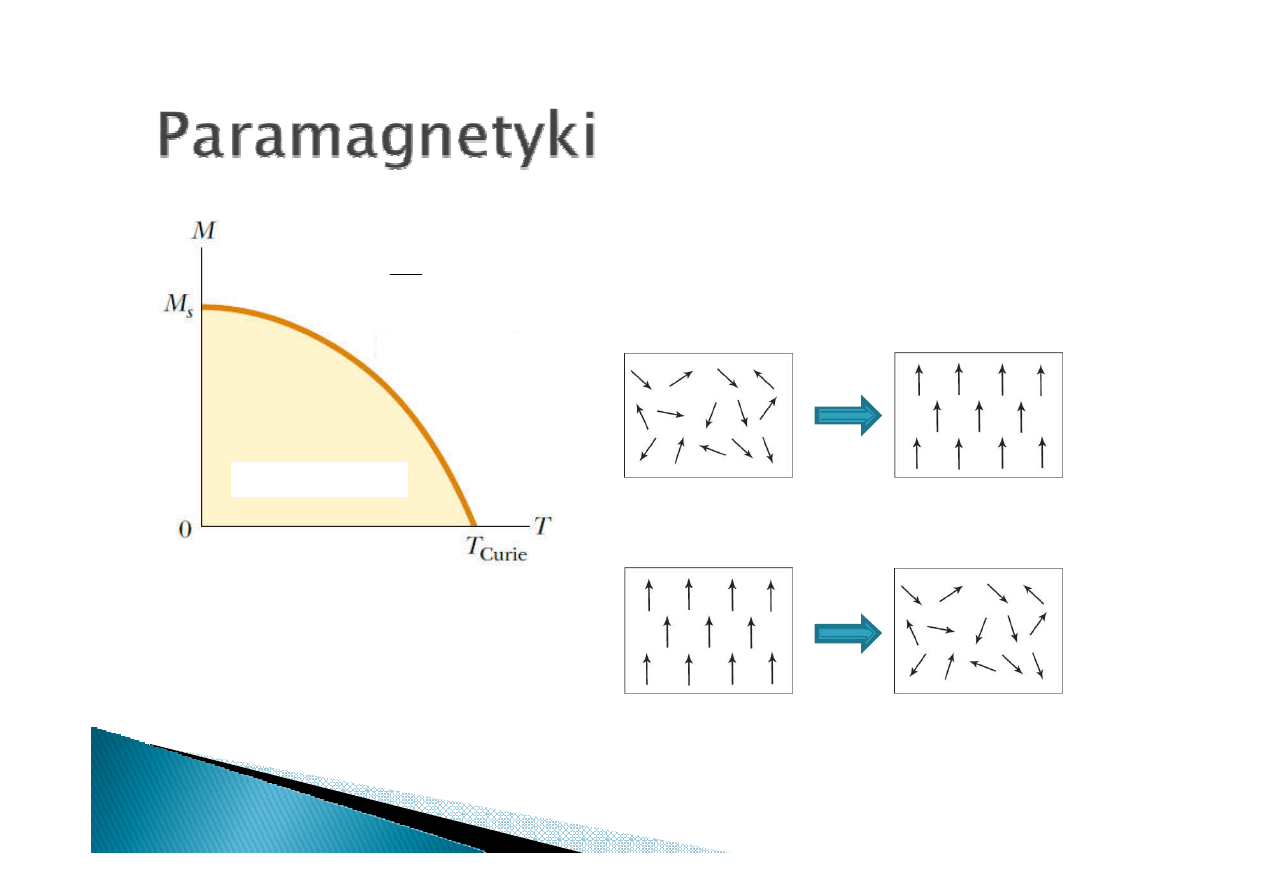
paramagnetyk

ferromagnetyk

W obecności zewnętrznego pola magnetycznego
chaotycznie zorientowane momenty
magentyczne atomów paramagnetyka ustawiają
się zgodnie z kierunkiem pola i paramagnetyk
jest wciągany w obszar pola.

Zależność magnetyzacji od temperatury
dla ferromagnetyka. W temperaturze Curie

temperaturze Curie

temperaturze Curie

temperaturze Curie

uporządkowanie ferromagnetyczne zostaje
zniszczenie. Następuje przejście
ferromagnetyk-paramagnetyk.

Wpływ zewnętrznego pola magnetycznego na
uporządkowanie momentów w paramagnetyku

Wpływ temperatury na uporządkowanie momentów
w ferromagentyku

T

M

1

∝

11

Paramagnetykami są min. tlen cząsteczkowy,
aluminium, platyna, sód

Magnes lewitujący nad nadprzewodnikiem –

idealnym diamagnetykiem

Zewnętrzne pole magnetyczne powoduje zmianę ruchu orbitalnego elektronów
wokół jądra i w efekcie powstanie indukowanego momentu magnetycznego

indukowanego momentu magnetycznego

indukowanego momentu magnetycznego

indukowanego momentu magnetycznego.

Zgodnie z regułą Lenza moment ten jest skierowany przeciwnie

przeciwnie

przeciwnie

przeciwnie do pola

zewnętrznego. W efekcie diamagnetyk jest w ypychany

w ypychany

w ypychany

w ypychany z pola magnetycznego.

12

Diamagnetyzm występuje we
w szystkich

w szystkich

w szystkich

w szystkich substancjach, jednak w
niektórych efekt diamagnetyczny jest
zdominowany przez efekt para- lub
ferromagnetyczny.
Przykładami diamagnetyków są:
woda, węgiel, miedź, rtęć, srebro

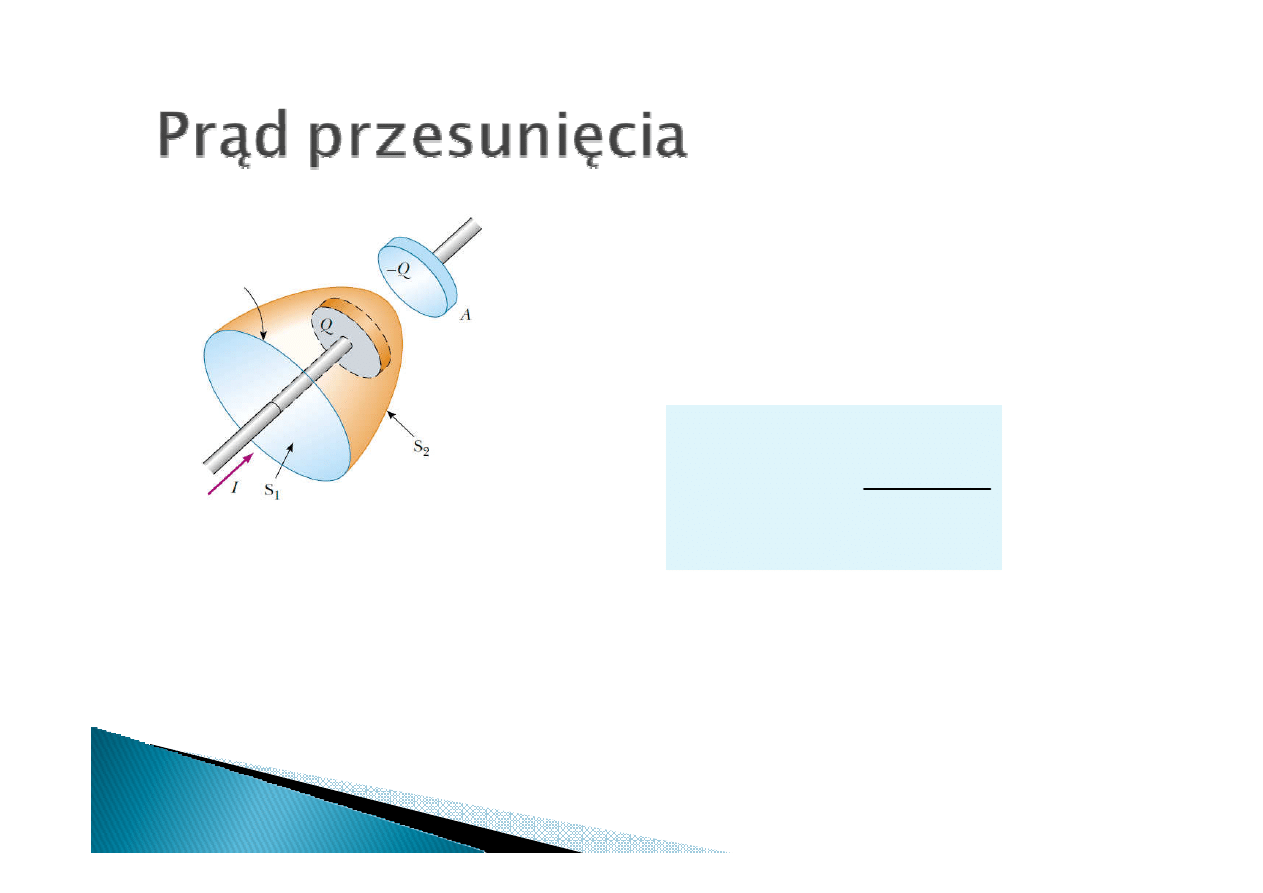
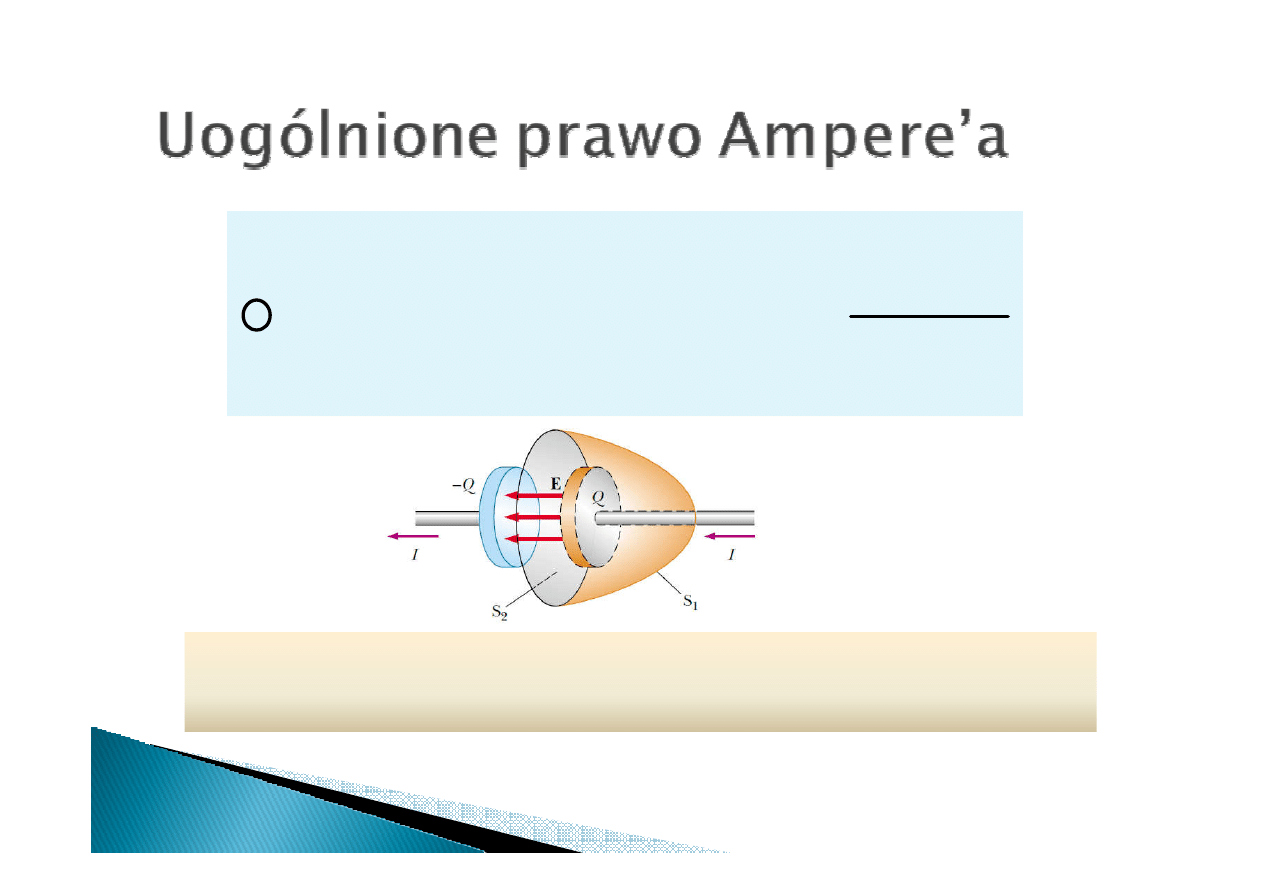
Kontur całkowania

Kontur całkowania zamyka powierzchnie S

1

i S

2

. Prąd przepływający przez powierzchnię

S

1

wynosi

I

, prąd przez powierzcnię S

2

wynosi 0.

0.

0.

0.

Prąd między okładkami jest nieciągły.

Prawo Ampere’a głosi, że całka po konturze z
B

B

B

B‧ds

s

s

s wynosi

µ

0

I

gdzie

I

jest prądem

przepływającym przez dow olną

dow olną

dow olną

dow olną powierzchnię

ograniczoną konturem całkowania.

Prąd przesunięcia

Prąd przesunięcia

Prąd przesunięcia

Prąd przesunięcia definiujemy jako:

dt

d

I

E

p

Φ

≡

0

ε

∫

⋅

=

Φ

A

E

E

d

Prąd przesunięcia można traktować jako
kontynuację prądu przewodzenia

kontynuację prądu przewodzenia

kontynuację prądu przewodzenia

kontynuację prądu przewodzenia płynącego
przez przewodnik

13

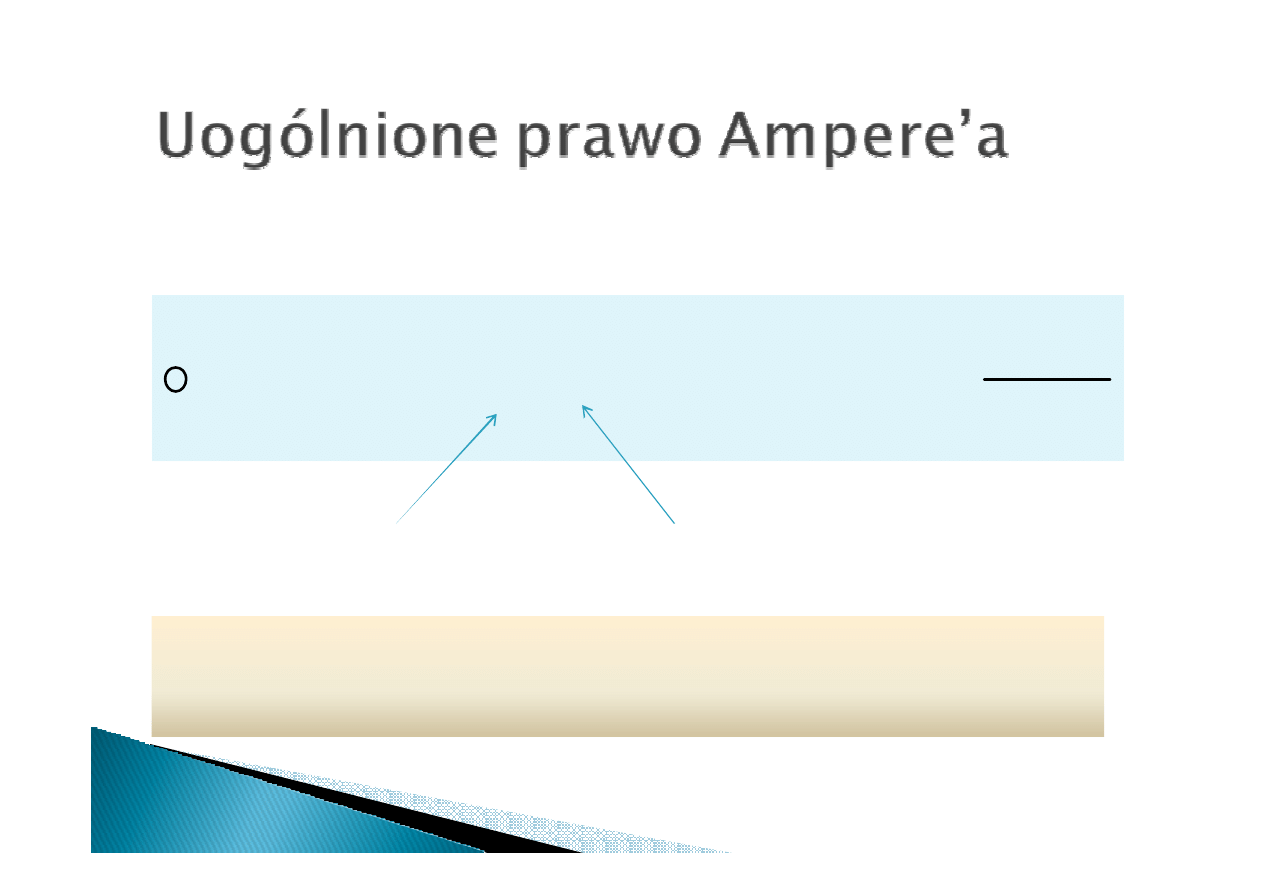
Uogólnione prawo Ampere’a (prawo Maxwella-Ampere’a) to prawo
Ampere’a uzupełnione o prąd przesunięcia.

(

)

dt

d

I

I

I

d

E

p

Φ

+

=

+

=

⋅

∫

0

0

0

0

ε

µ

µ

µ

s

B

Prąd przewodznia

(płynący przez

przewodnik)

Prąd przesunięcia

Prawo Ampere’a obowiązuje tylko dla stałego w czasie pola E.

Prawo Ampere’a obowiązuje tylko dla stałego w czasie pola E.

Prawo Ampere’a obowiązuje tylko dla stałego w czasie pola E.

Prawo Ampere’a obowiązuje tylko dla stałego w czasie pola E.
Uogólnione prawo Ampere’a obowiązuje zarówno dla stałego w

Uogólnione prawo Ampere’a obowiązuje zarówno dla stałego w

Uogólnione prawo Ampere’a obowiązuje zarówno dla stałego w

Uogólnione prawo Ampere’a obowiązuje zarówno dla stałego w
czasie, jaki i zmiennego pola E.

czasie, jaki i zmiennego pola E.

czasie, jaki i zmiennego pola E.

czasie, jaki i zmiennego pola E.

14

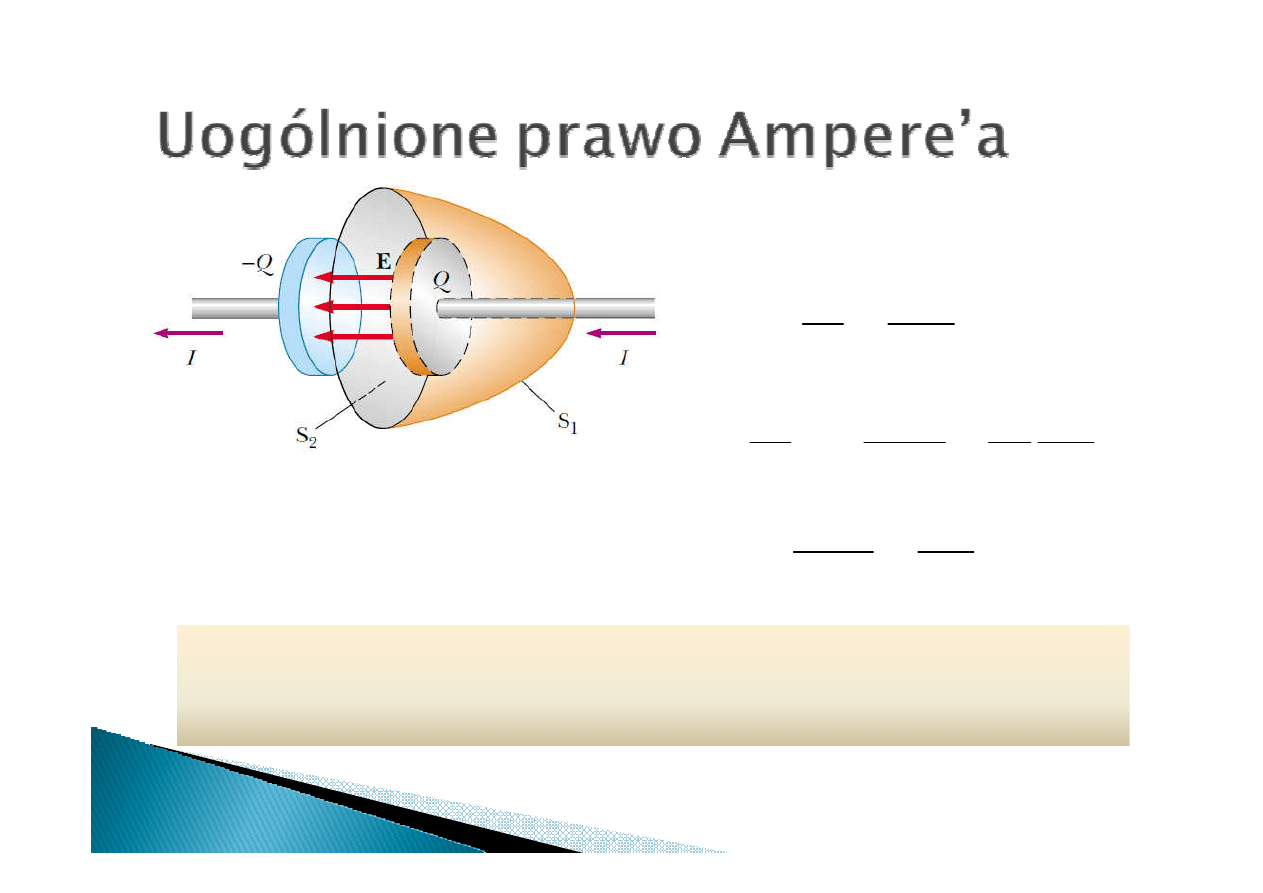
Ciągłość prądu wymaga aby prąd
przewodzenia I=dQ/dt (przez
powierzchnię S

1

) był równy prądowi

przesunięcia I

p

=

ε

0

d

Φ

E

/dt (przez

powierzchnię S

2

)

EA

=

Φ

E

A

Q

E

0

0

ε

ε

σ

=

=

0

ε

Q

=

Φ

E

dt

dQ

dt

d

0

1

ε

=

Φ

E

I

dt

dQ

dt

d

I

p

=

=

Φ

=

E

0

ε

Prąd przesunięcia powoduje powstanie pola B na konturze
obejmującym powierzchnię S

2

. Pole magnetyczne może

Pole magnetyczne może

Pole magnetyczne może

Pole magnetyczne może

wytwarzać prąd przewodzenia oraz zmienne pole E

wytwarzać prąd przewodzenia oraz zmienne pole E

wytwarzać prąd przewodzenia oraz zmienne pole E

wytwarzać prąd przewodzenia oraz zmienne pole E

15

Jam es Clark Maxwell

Jam es Clark Maxwell

Jam es Clark Maxwell

Jam es Clark Maxwell

( 1831

( 1831

( 1831

( 1831-

-

-

-1879)

1879)

1879)

1879)

Równania Maxwella są podstawowymi równaniami
elektrodynamiki, czyli działu fizyki zajmującego się
własnościami i oddziaływaniami obiektów
obdarzonych ładunkiem.
Równania opisują własności pól elektrycznego i
magnetycznego oraz zależności między tymi polami.

(

)

B

v

E

F

×

+

=

q

q

Oddziaływanie ładunku z polami E i B opisuje
równanie na siłę Lorntza:

Cztery równania Maxwella wraz z równaniem na siłę Lorentza
opisują wszystkie

wszystkie

wszystkie

wszystkie zjawiska w elektrodynamice !

16

∫

=

⋅

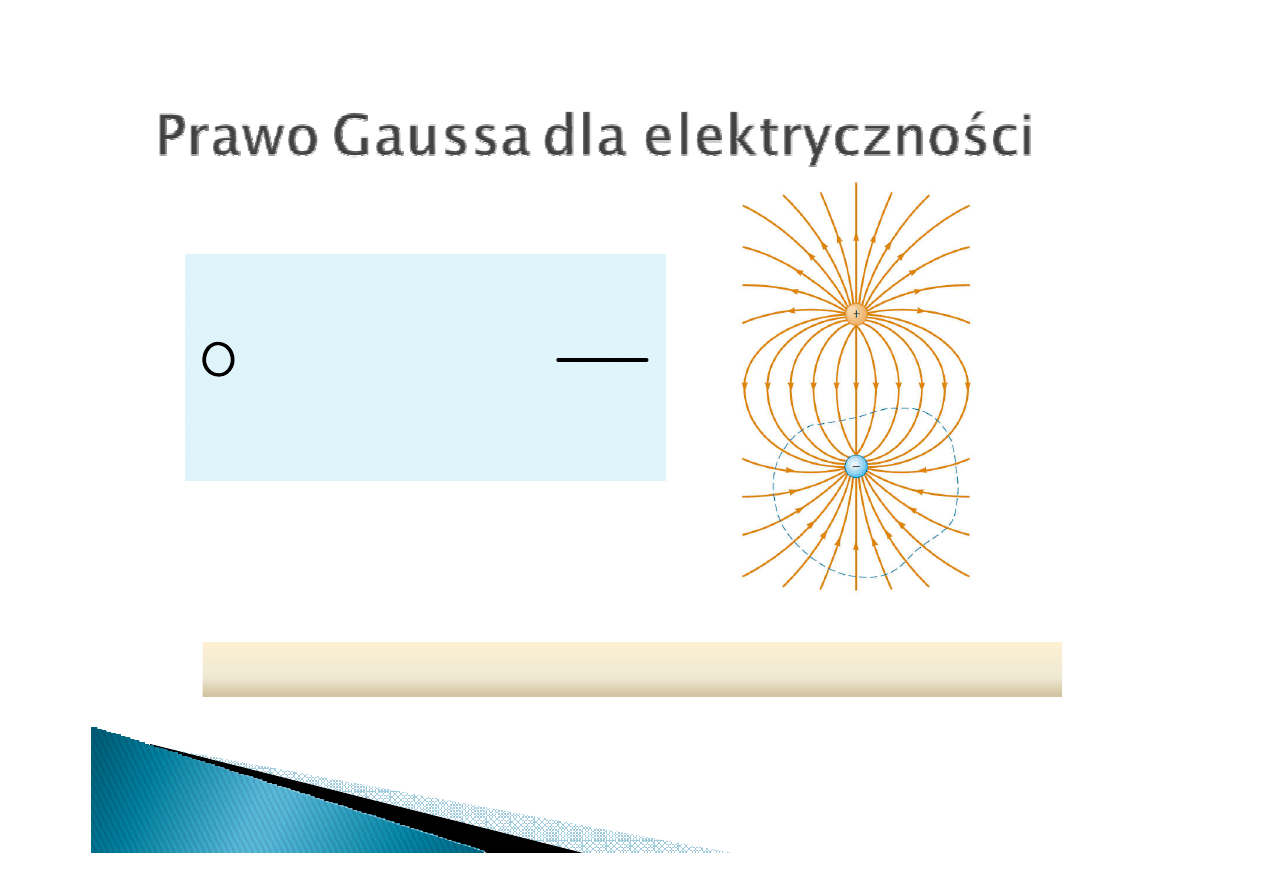
0

ε

Q

dA

E

Źródłem pola elektrycznego są ładunki.

17

∫

=

⋅

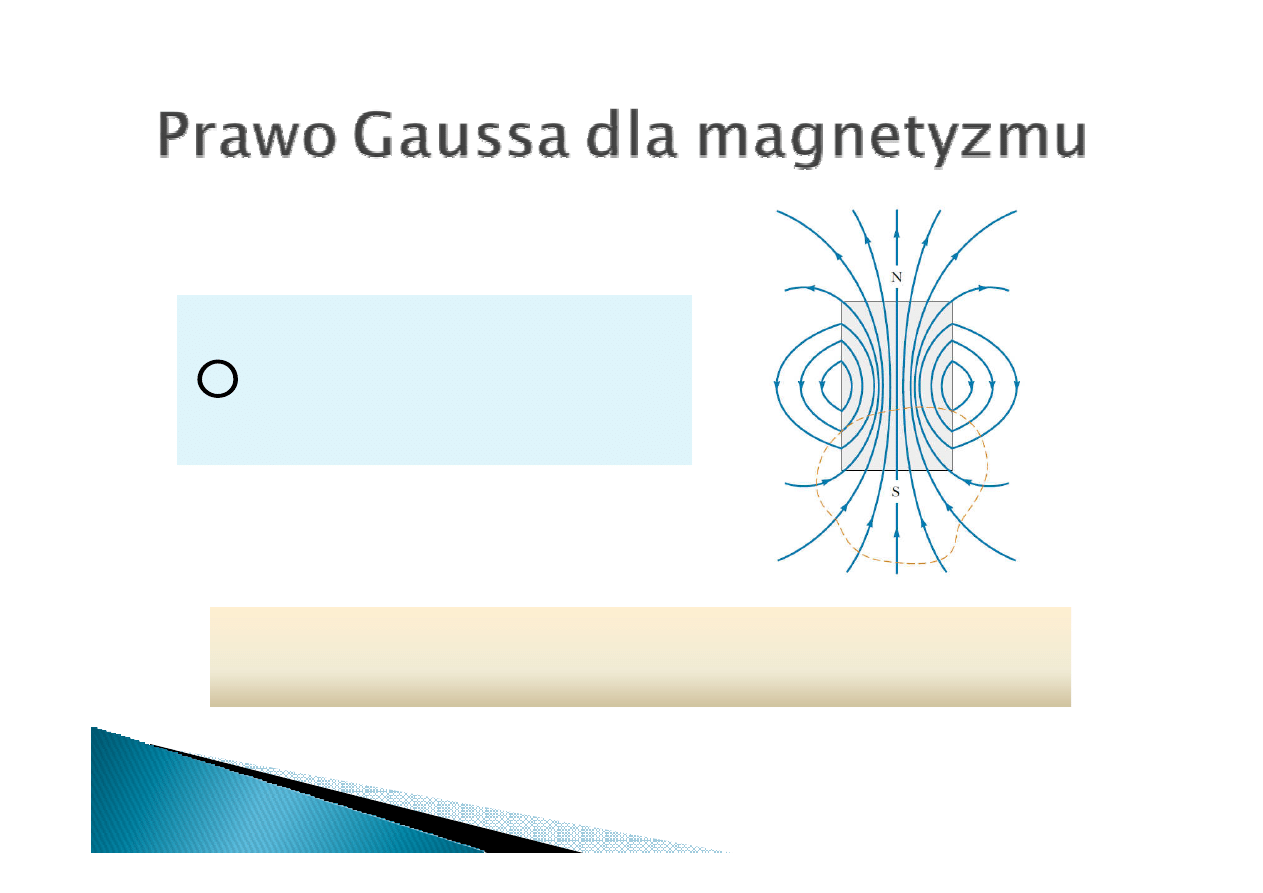
0

A

B d

Pole magnetyczne jest bezźródłowe.

Linie pola magnetycznego są zamknięte

18

∫

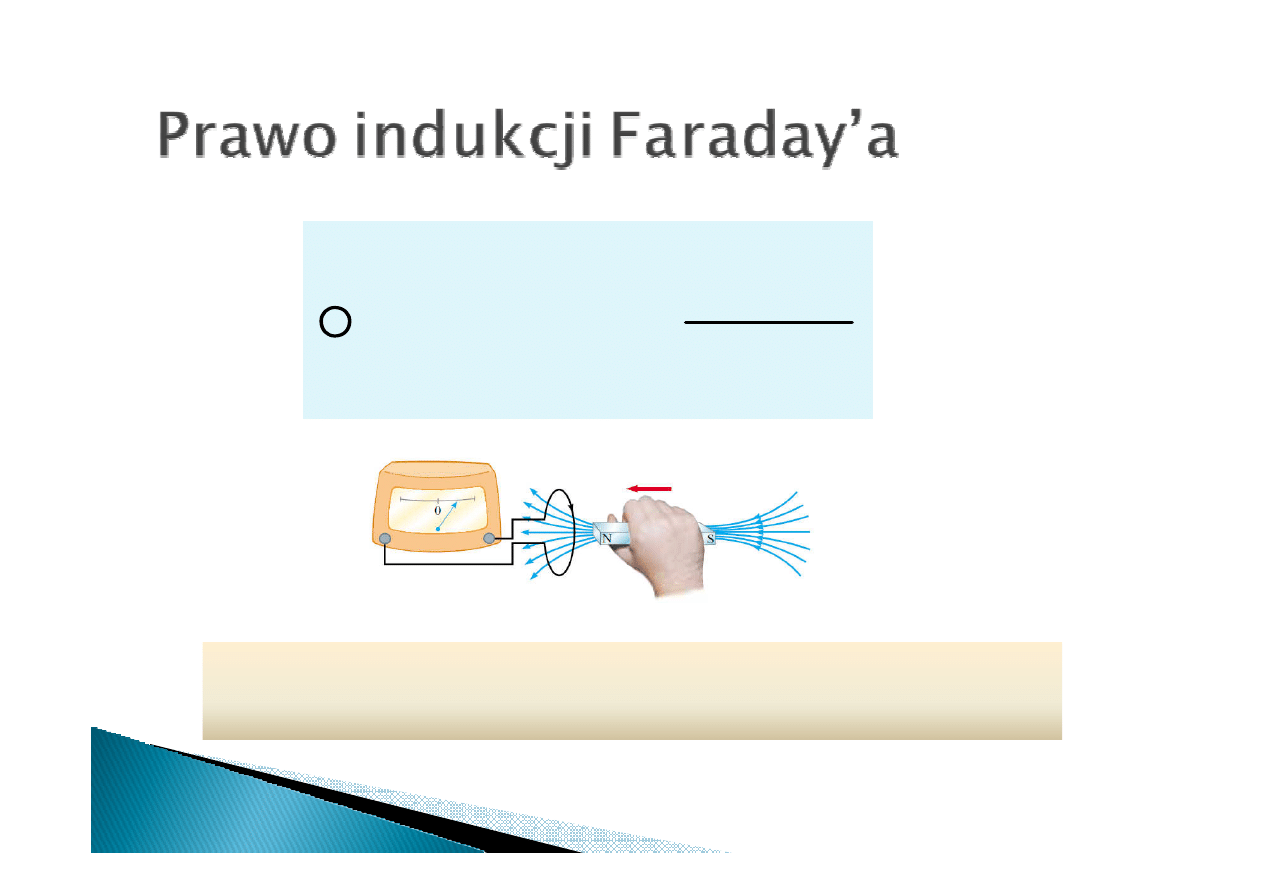
Φ

−

=

⋅

dt

d

d

B

s

E

Zmienne w czasie pole magnetyczne wytwarza

pole elektryczne

19

dt

d

I

d

E

Φ

+

=

⋅

∫

0

0

0

ε

µ

µ

s

B

Pole magnetyczne może wytwarzać przepływający

prąd oraz zmienne pole elektryczne

20

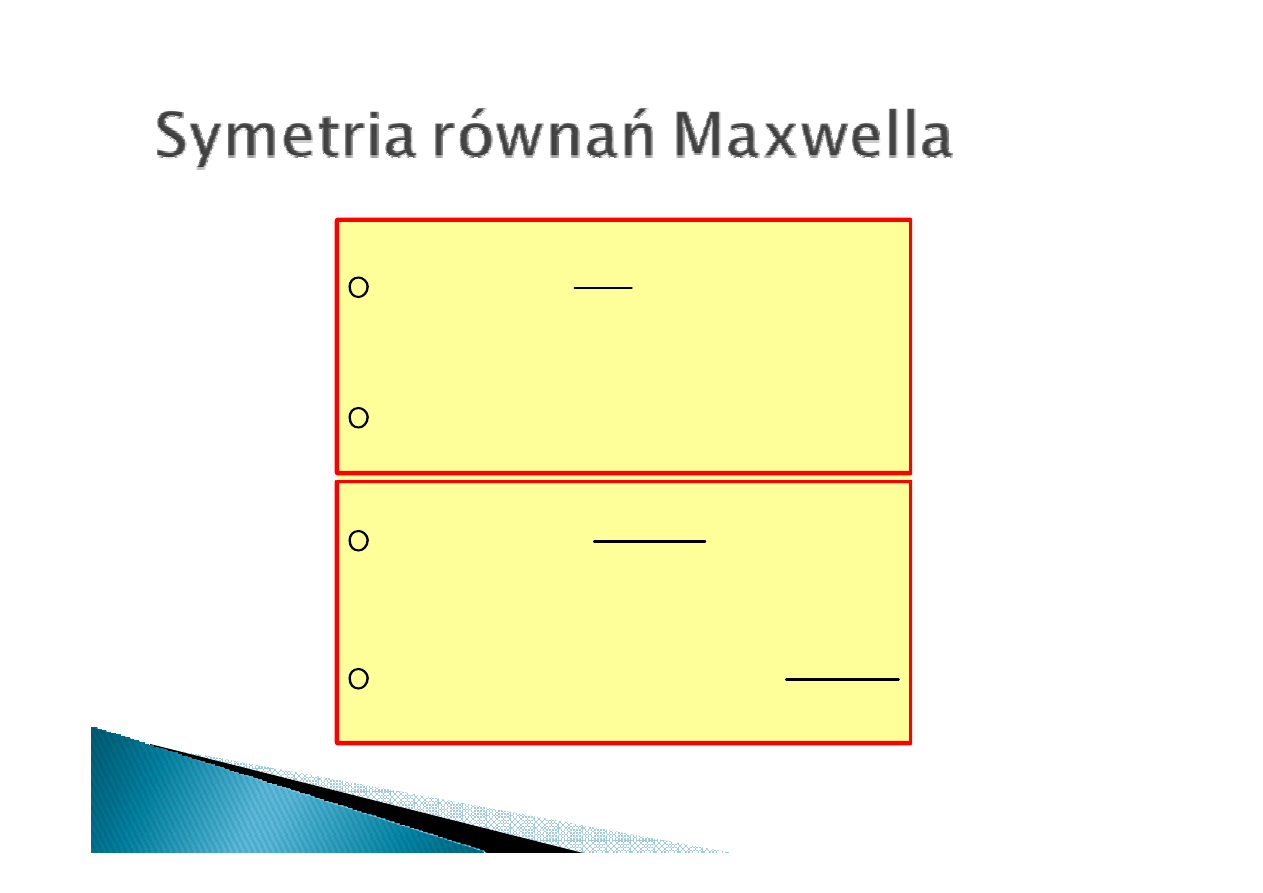
dt

d

I

d

dt

d

d

d

Q

d

E

B

Φ

+

=

⋅

Φ

−

=

⋅

=

⋅

=

⋅

∫

∫

∫

∫

0

0

0

0

0

ε

µ

µ

ε

s

B

s

E

A

B

A

E

21