K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

IV.

TEORIA (MODEL) BOHRA ATOMU (1913)

Bohr zastanawiał się, jak wyjaśnić strukturę widm liniowych.

Elektron musi krążyć, aby zrównoważyć siłę Coulomba (przyciągającą). Skoro krąży to 
doznaje przyspieszenia i promieniuje, a wówczas traci energię.

IV.1. WIDMA PROMIENIOWANIA ATOMÓW

Rys. IV.1. Schemat spektrometru optycznego. Wiązka światła pada na pryzmat i zostaje rozszczepiona.

Rys.IV.2. Z Rys.IV.1. – na kliszy uzyskamy taki obraz padającej wiązki. Jest to widmo liniowe.

Rodzaje widm – podział:

I.  według (ze względu na) długość fali λ
a) widma optyczne 

– powstają w wyniku zmiany energii elektronów zewnętrznych

– 1 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

(100Å ≤ λ ≤ daleka podczerwień)
– widma widzialne (VIS):

4000Å ≤ λ ≤ 8000Å

– widma podczerwone (IR):

    λ ≥ 8000Å

– widma nadfioletowe (UV): 

    λ ≤ 4000Å

b) widma rtg (rentgenowskie)

– powstają w wyniku zmiany energii elektronów wewnętrznych (najbliższych jądra 
atomowego)

II. według struktury linii

a) widma liniowe  | |  |  ||  |  ||   |  : atomy (jony) swobodne
b) widma pasmowe ||| ||||  ||| |||| – gdy linie są zgrupowane bardzo gęsto obok 

siebie: drobiny (jony drobin) np. CO

2

, NH

3

, CH

4

,...

c) widma ciągłe – są charakterystyczne dla materii skondensowanej: ciała stałe 

(metale), ciecze i gazy w wysokich ciśnieniach. Nie da się jednoznacznie 
przypisać konkretnej substancji.

a) i b) są charakterystyczne dla danej substancji – określają ją w sposób jednoznaczny 

Dwie linie blisko siebie w widmie – dublet (np. widmo sodu).

III. ze względu na sposób obserwacji

a) widma emisyjne – obserwujemy promieniowanie wysyłane 
b) widma absorbcyjne – powstają gdy widmo ciągłe przepuścimy przez daną 

substancję (np. gaz), różnica widma ciągłego i liniowego. Na podstawie 
analizy linii widmowych możemy stwierdzić przez jakie pierwiastki widmo 
zostało przepuszczone

– 2 –

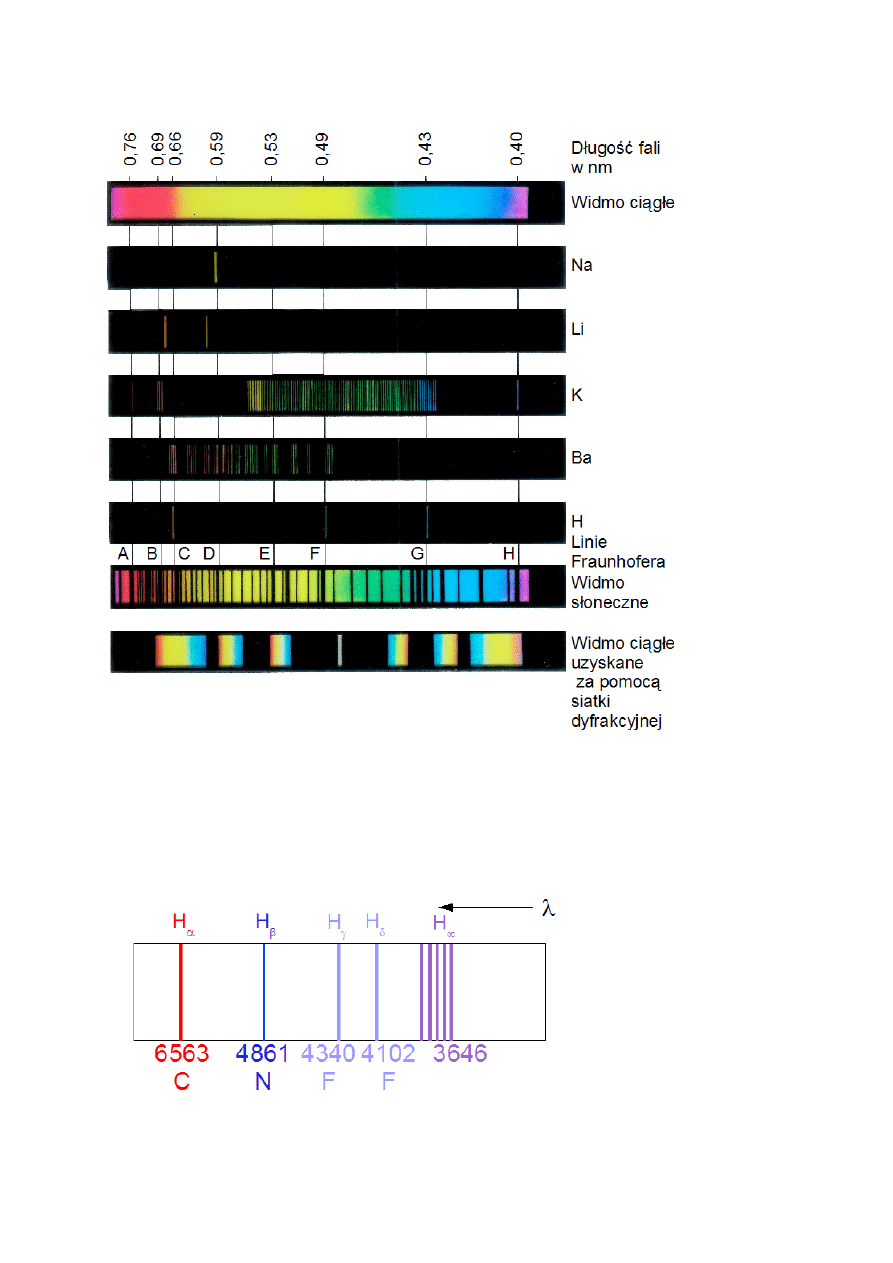
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

Rys.IV.3. Przykłady widm.

IV.2. WIDMO ATOMU WODORU (DOŚWIADCZENIE)

Rys.IV.4. Widmo atomu wodoru – przedstawienie graficzne ilustrujące serię Balmera.

– 3 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

Balmer zaproponował wzór dzięki któremu możemy znaleźć położenie każdej z linii 
widmowych atomu wodoru.



n

=

B

⋅n

2

n

2

−4

,

 n = 3,4,5,....

     (IV.2.1)

λ

3

 = 

λ

α

 

= 6563 [Å]

H

∞

 – granica serii Balmera ( λ =3646Å)

Każda seria kończy się pewną linią graniczną.
W serii Balmera wykryto 10 linii.

Rydberg   wprowadził   pewną   modyfikację   z   której   wynika,   że   wygodniej   położenie   linii 
opisywać przez tzw. liczbę falową k, którą wyrażają zależności (IV.2.2a) lub (IV.2.2b):

k

=

1



   (IV.2.2a)

lub                    

k

=

2





   (IV.2.2b)

k

n

=R

H



1

2

2

−

1

n

2



,

n = 3,4,5,...

     (IV.2.3)

gdzie:
stała Rydberga – R

H

 = 109677,58 cm

-1

Znanych jest 6 serii linii widmowych, których linie opisuje uogólniony wzór Rydberga:

k

= R

∞

Z

2



1

n

1

2

−

1

n

2

2



     (IV.2.4)

n

2

 = n

1

+1, n

1

 = const dla danej serii i 1 ≤ n

1 

≤ 6

  

– 4 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

SERIA

ROK

n

1 

ZAKRES

Lymana 

Balmera

Paschena

1906
1885
1908

1
2
3

UV

VIS+UV

IR

przed teorią 

Bohra

Bracketta

Pfunda

Humpkreysa

1922
1924
1952

4
5
6

po teorii Bohra

IR
IR
IR

Tabela IV.2. Serie widmowe atomu wodoru.

Model Bohra przewidział istnienie dalszych serii w podczerwieni zanim zostały praktycznie 
wykryte.
Teoria Bohra wyprowadzona dla atomu z jednym elektronem – atomy wodoropodobne.

IV.3. TERMY I ZASADA KOMBINACJI RYDBERGA – RITZA (1908)

k

=



R

H

n

1

2

−

R

H

n

2

2



k

=T

1

−T

1

, T

1

=

R

H

n

1

2

, T

2

=

R

H

n

2

2

T

n

=

df

R

H

n

2

     (IV.3.1)

Wzór   (IV.3.1)   –   pojęcie   termu,   którego   matematyczna   postać   jest   inna   dla   każdego 
pierwiastka.

Położenie dla dowolnego widma (linii) możemy przedstawić jako różnicę dwóch termów:

k

n

=T

n

'

−T

n1

'

Wzory termów dla atomów innych niż wodór, mają inną postać.

Zasada kombinacji Rydberga – Ritza

Liczby falowe dowolnych linii spektralnych mogą być wyrażone jako różnice odpowiednich 
termów. Termy te poprzez kombinacje z innymi termami mogą służyć do obliczania liczb 

– 5 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

falowych innych linii tego samego widma.

Podsumowanie:

Widma atomowe nie są ciągłe – są liniowe, a więc skwantowane!

IV.4. POSTULATY BOHRA

Teoria Bohra oparta jest na następujących postulatach:

I. Elektron   porusza   się   po   orbicie   kołowej   i   podlega   prawom   fizyki   klasycznej 

(równowaga zapewniona przez prawo Coulomba i II zasadę dynamiki Newtona). 
Siła   przyciągająca   między   ładunkiem   a   jądrem   jest   równoważona   przez   siłę 
odśrodkową.

II. Zamiast   nieskończonej   liczby   orbit   ,   które   dozwolone   są   z   punktu   widzenia 

mechaniki   klasycznej,   elektron   może   poruszać   się   tylko   po   takich   orbitach,   dla 
których orbitalny moment pędu L spełnia warunek:

L

= n⋅ħ

, n = 1,2,3,...

ħ

=

df

h

2



     (IV.4.1)

L

=∣L∣

 – kręt orbitalny

L = r×p , 

p = m⋅v

Jest to tzw. postulat kwantowy.

III. Całkowita energia na danej orbicie stacjonarnej jest stała:

E=const

A zatem Bohr przyjął, że elektron nie traci energii!

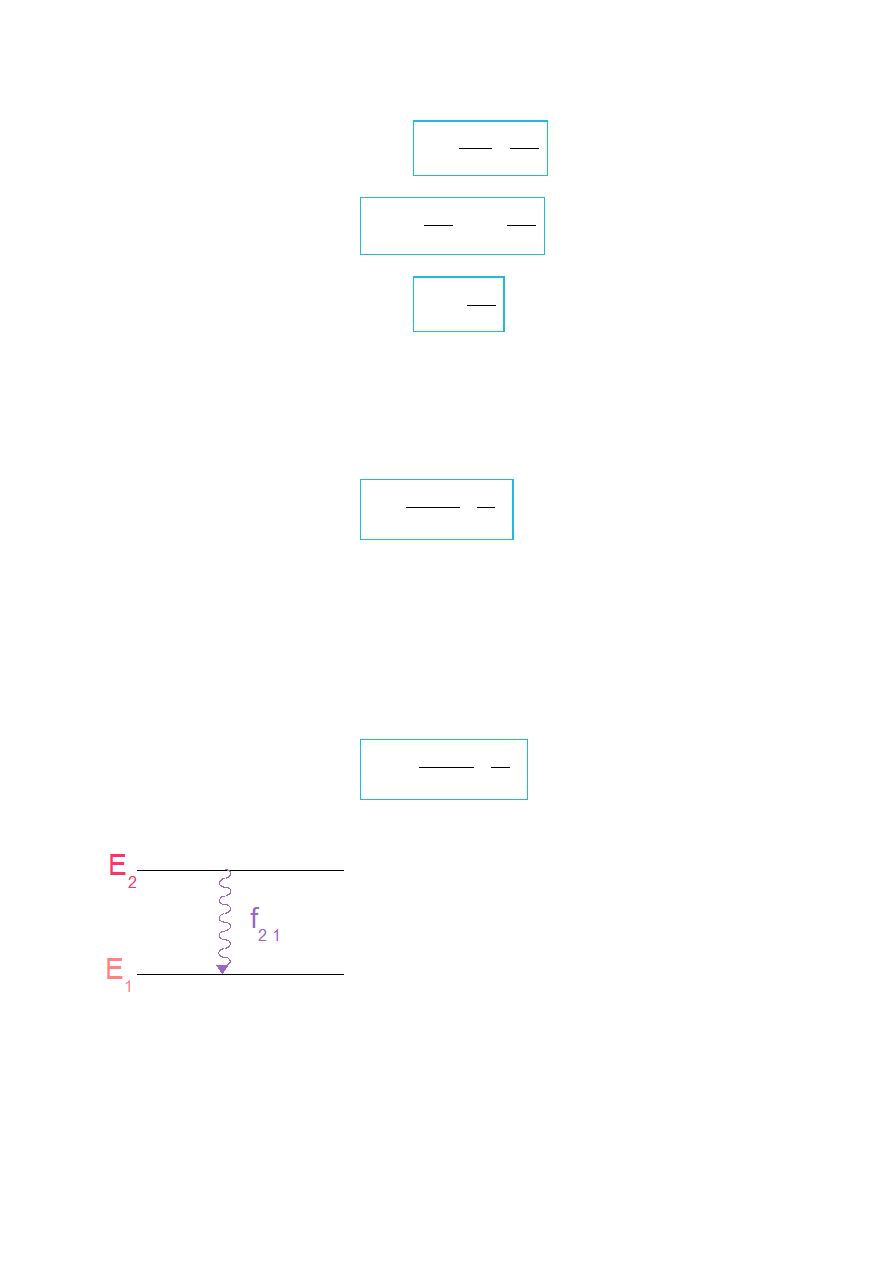
IV. Przy przejsciu elektronu z jednej orbity na drugą atom wysyła promieniowanie.

E

2

→ E

1

 < E

2 

– 6 –

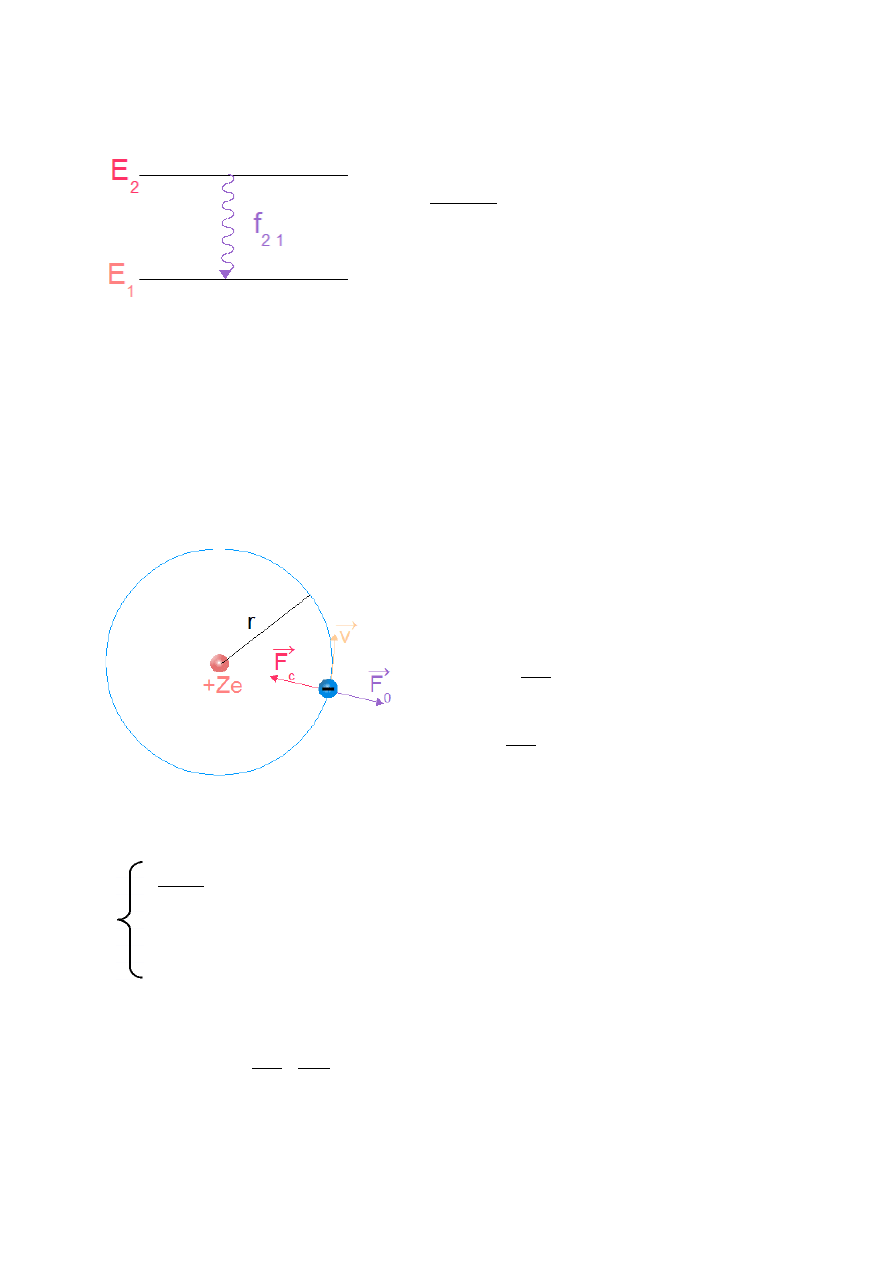
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

f

21

=

E

2

− E

1



h

 – częstość wyemitowanego 

promieniowania

Rys.IV.5. Promieniowanie emitowane przy przejściu elektronu z orbity wyższej na niższą.

Postulat analogiczny do postulatu Einsteina!
Bazując na tych postulatach można wyprowadzić wzór Rydberga.

IV.5. WYPROWADZENIE WZORU RYDBERGA.

F

e

=F

o

F

c

=k

'

Ze

2 

r

2

F

o

=

mv

2

r

Rys. IV.6. Elektron krążący po orbicie wokół jądra atomu.

 

1

4



0

układ (SI)

k'= 
 

1

           układ (Gaussa)

założenie: k'=1

Ze

2 

r

2 

=

mv

2 

r

, z czego i ze wzoru (IV.5.3) wynika, że

– 7 –

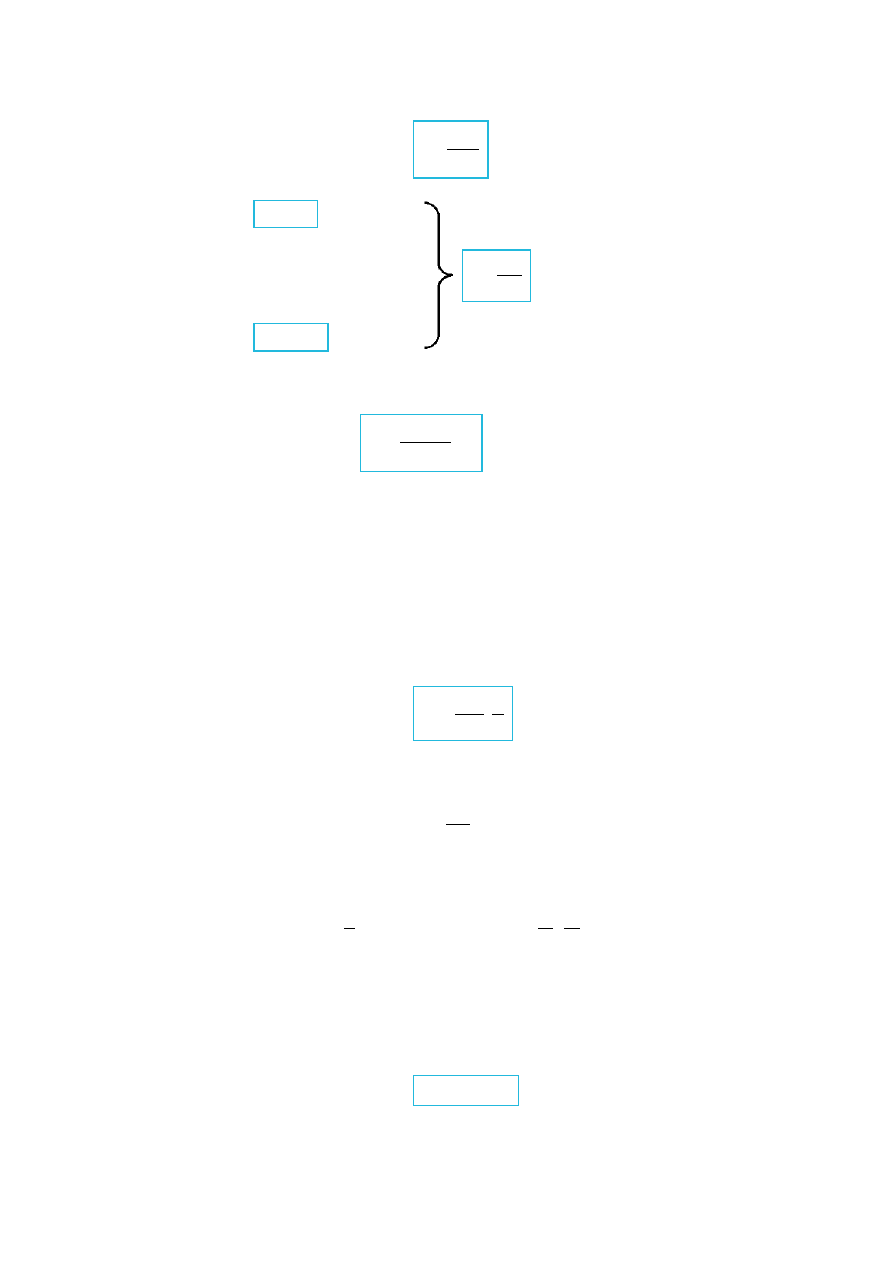
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

r

=

Ze

2

mv

2

     (IV.5.4)

L

=nħ

       (IV.5.1)

v

=

nħ

mr

         (IV.5.3)

L

=mvr

    (IV.5.2)

A zatem:

r

n

=

ħ

2

Ze

2

⋅m

⋅n

2

n = 1,2,3,

     (IV.5.5)

r

1

:r

2

: r

3

:...

=1: 4 :9:...

z wzoru (IV.5.5) możemy wyliczyć promień wodoru na pierwszej orbicie (w stanie 
podstawowym) – promień Bohra:

r

1

=5,3 ⋅10

−9 

cm

Z (IV.5.3) i (IV.5.5) wynika, że prędkość na n-tej orbicie wynosi:

v

n

=

Ze

2

ħ

⋅

1

n

     (IV.5.6)

Z wzoru (IV.5.6) możemy wyliczyć, że:

v

1

=2 ⋅10

8 

cm

s

< 1% c

A zatem jak widać, nie ma efektu relatywistycznego.

v

k

~

1
n

, czyli 

v

1 

:v

2 

: v

3 

=1 :

1 
2 

:

1 

3

Jak wynika z powyższych obliczeń, największą prędkość uzyskuje elektron na 1 orbicie. 

Całkowita energia elektronu jest sumą energii kinetycznej E

k

 i potencjalnej E

p

:

E

=E

k

E

p

     (IV.5.7)

– 8 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

E

k

=

mv

2

2

=

Ze

2

2r

     (IV.5.8)

E

p

=

∫

Ze

2

r

2

dr

=−

Ze

2

r

     (IV.5.9)

E

=−

Ze

2

2r

   (IV.5.10)

Z zależności (IV.5.7) – (IV.5.10) wynika, że:

E

=−E

k

Czyli, że energia całkowita elektronu jest ujemna, a więc elektron jest związany. 

E

n

=−

Z

2

e

4

2ħ

2

⋅



1

n

2



   (IV.5.11)

E

n

 – całkowita energia elektronu na n–tej orbicie.

Z   zależności   (IV.5.11)   można   obliczyć  

E

1

=−13,6 eV

  ,   stąd   wynika,   że   najsilniej 

związany jest elektron na pierwszej powłoce.

E

1

=−13,6 eV

 – taką energię trzeba dostarczyć ,aby oderwać elektron z 1 orbity

(zjonizować atom wodoru w stanie podstawowym).

E

n

=−

me

4

Z

2

2ħ

2

⋅



1

n

2



   (IV.5.12)

Rys.IV.7. Przejście między stanami E

2

 – E

1

.

– 9 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

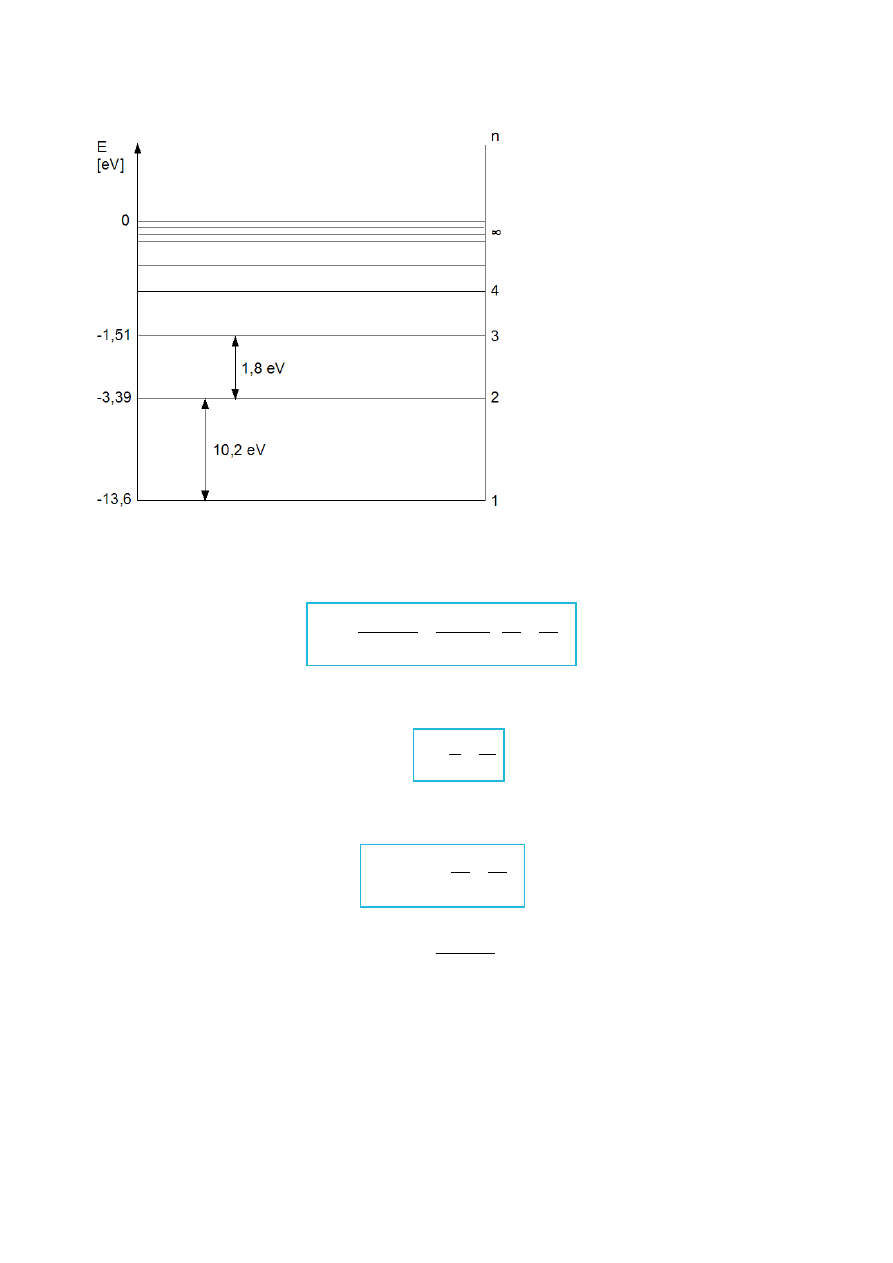
Rys.IV.8. Drabina poziomów energetycznych.

Znając energię dowolnego poziomu energetycznego, możemy wyznaczyć częstość f:

f

21

=

E

2

−E

1

h

=

me

4

Z

2

4

 ħ

3



1

n

1

2

−

1

n

2

2



   (IV.5.13)

Wprowadzamy liczbę falową k daną wzorem (IV.2.2a):

k

=

1

λ

=

f

c

   (IV.5.14)

Po podstawieniu częstości danej wzorem (IV.5.13) do wzoru (IV.5.14) otrzymujemy:

k

= R

∞

Z

2



1

n

1

2

−

1

n

2

2



   (IV.5.15)

R

∞

=

df

me

4

4

 ℏ

3

c

Po wstawieniu wartości liczbowych można wyliczyć, że:

R

∞

=109737,3128 cm

−1

Wzór   (IV.5.15)   określa   położenie   dowolnej   linii.   Dla   Z=1   jest   on   zgodny   ze   wzorem 
Rytberga.

– 10 –

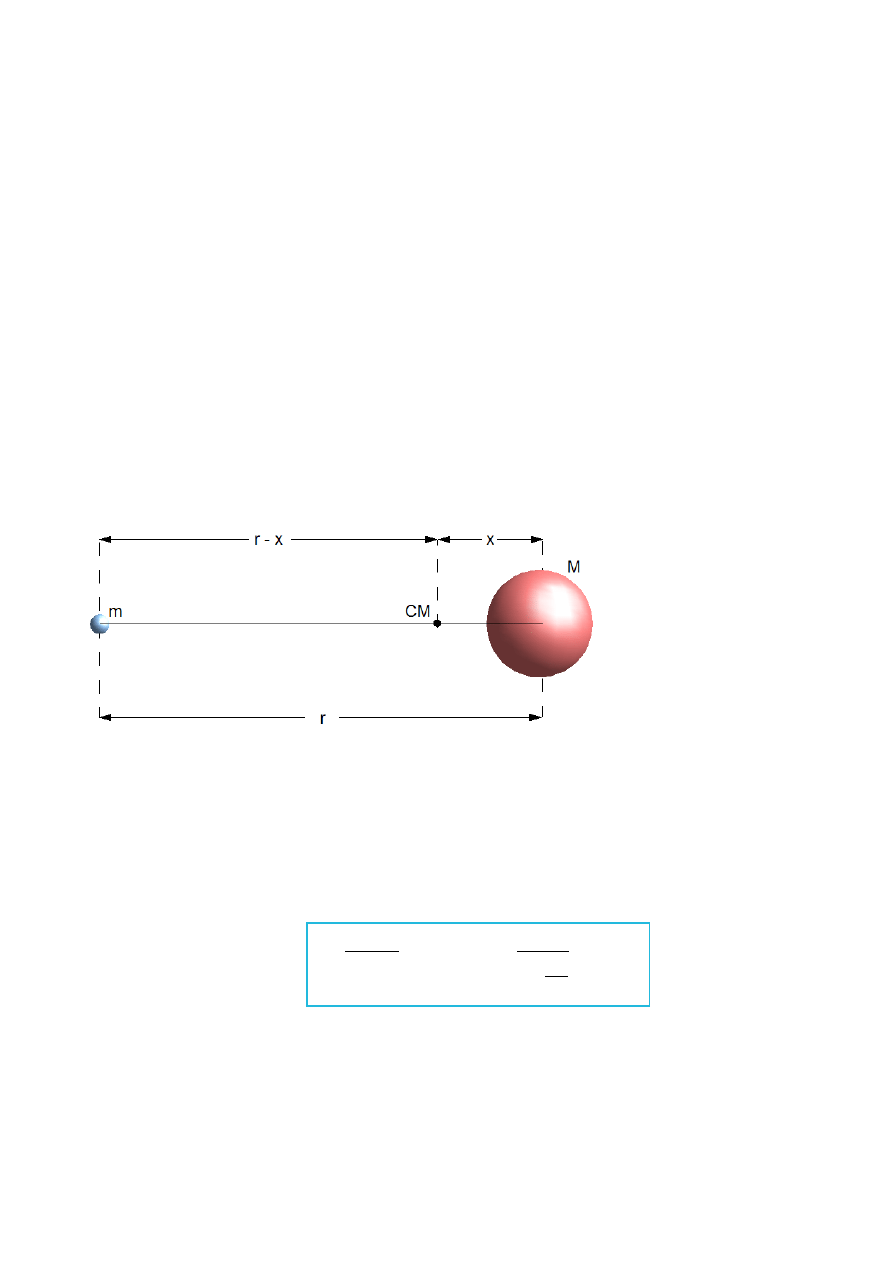
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

R

H

=109677,58 cm

−1

R

∞

≃R

H

± 0,05%

Teoria Bohra jest w stanie wyjaśnić położenie linii w tych wszystkich 6 seriach widmowych 
wodoru. Potwierdziła bardzo dokładnie położenie linii widmowych w znanych 3 seriach 
oraz   przewidziała   istnienie   3   kolejnych.   Każda   seria   odpowiada   przejściu   elektronu   z 
dowolnej powłoki n

2 

= (n

1

 + n) na powłokę n

1

.

IV.6. POPRAWKA NA SKOŃCZONĄ MASĘ JĄDRA, M≠ ∞

W rzeczywistości, w atomie wodoropodobnym, oba ciała jądro i elektron poruszają się 
wokół środka masy CM.

Rys.IV.9. Schematyczne przedstawienie środka masy w układzie jądro – elektron (nie w skali). Masa jądra 
atomowego M jest skończona i wynosi niecałe 200 m

e

, im lżejsze jądro atomowe tym większe przesunięcie 

środka ciężkości CM w stronę elektronu. M – masa elektronu, r – odległość elektronu od jądra atomowego, x 
– odległość środka ciężkości atomu od środka jądra atomowego.

Można   pokazać,   że   kręt   elektronu   w   takim   przypadku   (tzn.   gdy   masa   elektronu   jest 
skończona) wynosi:

L

= mM

m

M

⋅r

2

⋅=



mr

2



1

1



m

M



mr

2



     (IV.6.1)

A zatem  możemy stosować wszystkie wyprowadzone wcześniej wzory, tyle ze za masę 
wstawiamy tzw. masę zredukowaną μ.

– 11 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

=

df

mM

m

M

     (IV.6.2)

Uwzględniając to, że jądro ma skończoną masę, wzór Rydberga ma poniższą postać:

k

= R

M

Z

2



1

n

1

2

−

1

n

2

2



     (IV.6.3)

R

M

=

e

4

4

e ℏ

3

     (IV.6.4)

R

M

 – stała Rytberga dla atomów ze skończoną wartością masy jądra.

IV.7. DOŚWIADCZENIE FRANCKA- HERTZA (1914)

Eksperymentalne potwierdzenie punktu IV.6.

Doświadczenie Francka – Hertza dotyczy zderzania się elektronów z dowolnymi atomami 
metali (np. rtęci).
Jeżeli poszczególne poziomy energetyczne w atomie są skwantowane, to poziomy całego 
atomu powinny być skwantowane (suma).

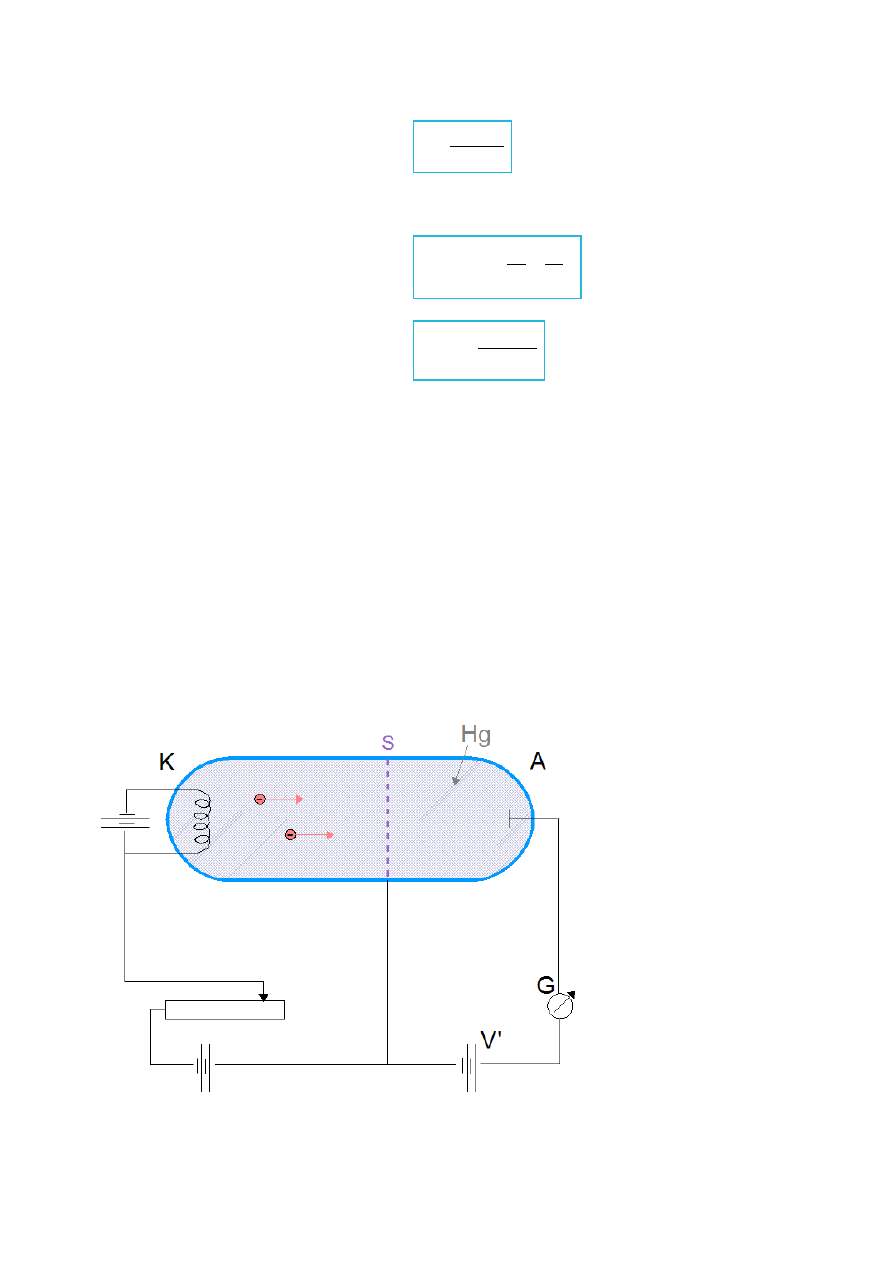
Rys.IV.10. Ilustracja doświadczenia Francka – Hertza. Bańka została wypełniona atomami Hg. S – siatka 
(aby elektrony z katody K mogły przelecieć do anody A) służąca jako dodatkowa elektroda. Pomiędzy siatką 

– 12 –

K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

S a anodą A – potencjał hamujący V'.

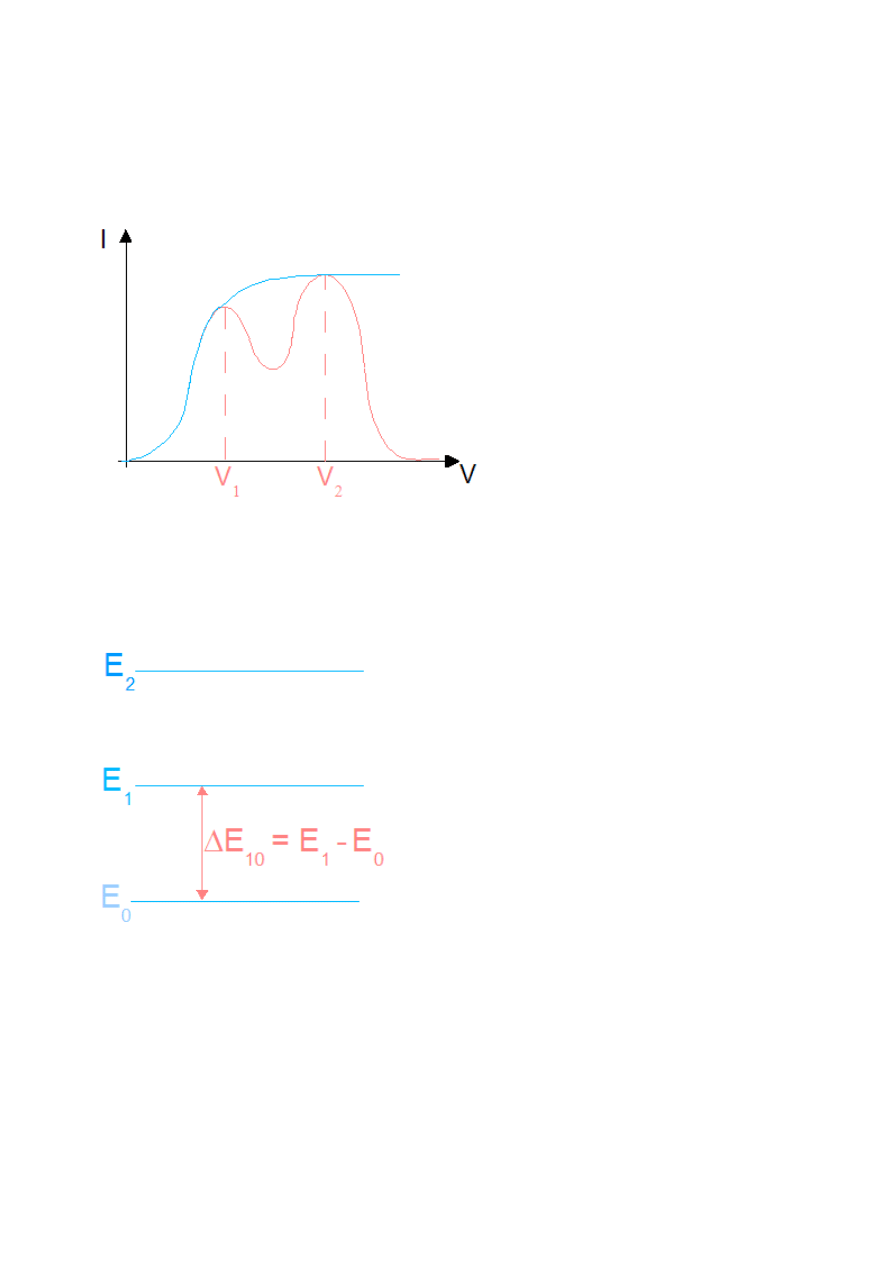
Rys.IV.11. Wykres niebieski – jeżeli stany atomów są skwantowane możliwe jest tylko pokazanie 
odpowiedniej dawki energii (ukazuje jak zmieniałoby się natężenie gdyby w bańce była próżnia i elektrony 
nie zderzały się z atomami Hg, lub też gdyby te zderzenia były sprężyste). Wykres czerwony – ilustruje 
rzeczywisty przebieg zależności (przy zderzeniach niesprężystych część energii jest przekazywana przez 
elektrony atomom rtęci.)

E

k

≠ ∆ E

10

E

k

=eV

∆ E

k

= ∆ E

10

eV

1

=∆ E

10

 

eV

2

=∆ E

20

V

1

=4,9 eV

Rys.IV.12. Schemat poziomów energetycznych układu skwantowanego. 

–

W charakterystyce i – V obserwujemy skoki (piki) związane ze wzbudzeniem atomów 
Hg do coraz wyższych potencjałów energetycznych

–

doświadczenie   pokazuje   w   sposób   jakościowy   oraz   ilościowy   (można   wyliczyć),   że 
atom jest układem skwantowanym 

Przy napięciu V

1

 wzbudzenie do E

1

, przy V

2

 wzbudzenie do E

2.

– 13 –

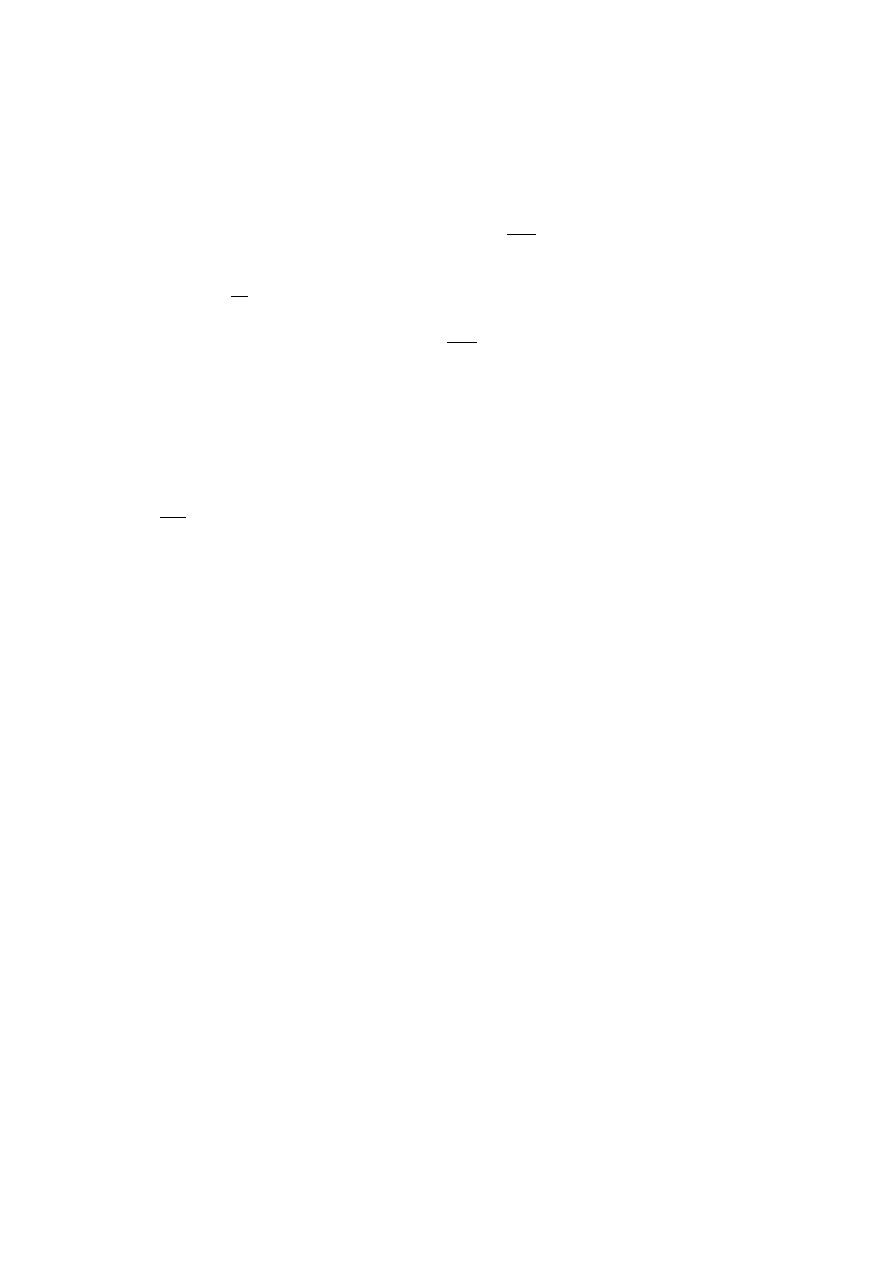
K.Czopek, M.Zazulak – Notatki w internecie. Wstęp do fizyki atomowej i kwantowej. 

Jeżeli znamy napięcie pierwszego piku 

V

1

=4,9 eV  ,

to możemy obliczyć częstość f

1

:

eV

1

=hf

1

→  f

1

=

eV

1

h

A ponieważ  f

1

=

c



1

, to możemy obliczyć długość fali 

λ

1

:



1

=

hc

eV

1

Z teorii dostajemy 



1

=2530 Å UV 

Z doświadczenia Francka – Hertza 



1

FH

=2537 Å

A zatem

∆





≈0,3%

Doświadczenie to potwierdza słuszność teorii Bohra.

– 14 –