METALE i PÓŁPRZEWODNIKI

O właściwościach elektrycznych metali decydują

zdelokalizowane elektrony walencyjne s i p,
a

w

przypadku

metali przejściowych

(tj.

pierwiastków rodzin bloku d) również elektrony d.
W bardzo niskich temperaturach, zwykle rzędu
kilku

K,

niektóre

metale

osiągają

stan

nadprzewodnictwa, gdyż ich oporność elektryczna
skokowo maleje praktycznie do zera. Zachowanie się
i właściwości fizyczne metali oraz innych ciał stałych
o

strukturze

krystalicznej

można

wyjaśnić

posługując się modelem pasmowym ciała stałego.

Stan

kwantowo-mechaniczny

elektronów

walencyjnych atomów w krystalicznej fazie stałej
różni się zasadniczo w porównaniu z ich stanem
w swobodnych izolowanych atomach. W izolowanym
atomie orbitalom s, p i d odpowiadają określone
poziomy energii. Jeśli pewna liczba atomów, np.
dwa, trzy, .... , N, zbliży się do siebie na odległości
porównywalne z ich wymiarami, to w wyniku dwu-,
trzy-, ..... , N-krotnego rozszczepienia poziomów
energetycznych odpowiednich orbitali pojawiają się
pasma energetyczne o określonej szerokości (rys. 1).

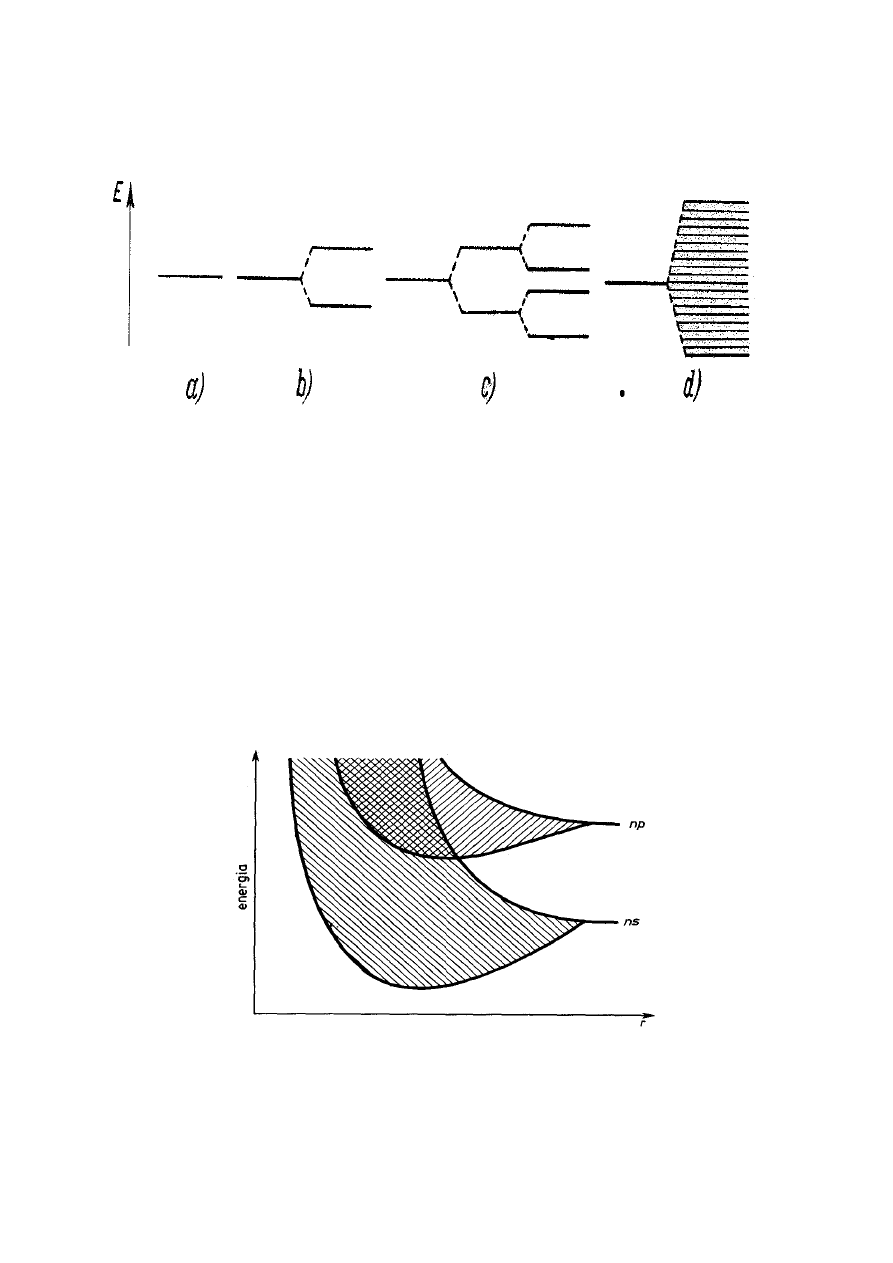
Rys. 1. Rozszczepienie poziomów energetycznych

a) poziom energetyczny nie rozszczepiony,

b) poziom rozszczepiony w przypadku dwu atomów,

c) poziom rozszczepiony w przypadku czterech atomów,

d)

to samo dla N atomów

W przypadku metali pasma energetyczne orbitali

ns i np w znacznym stopniu nakładają się na siebie
tak, jak to pokazano na rys. 2.

Rys. 2. Nakładanie się rozszczepionych poziomów energetycznych

orbitali ns i np

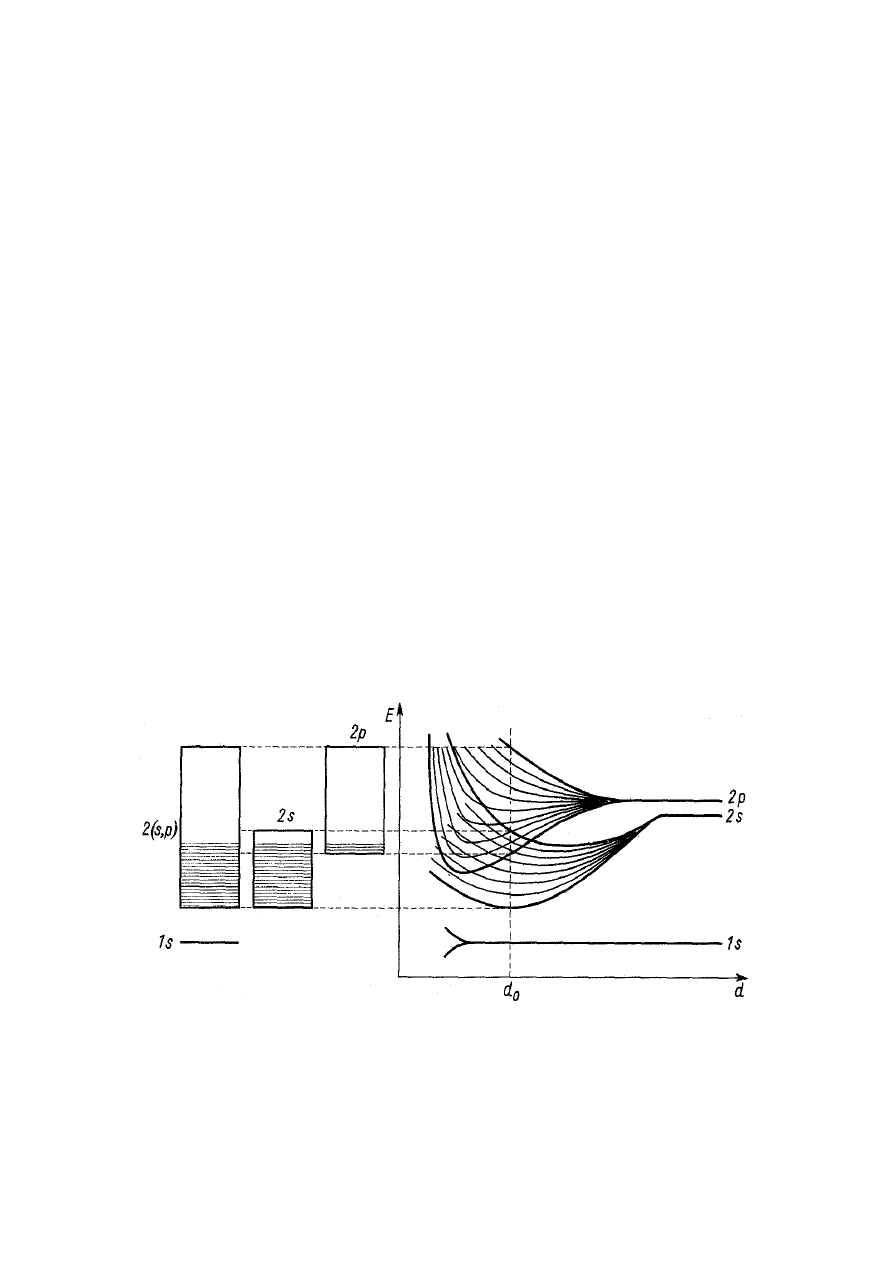
Poziomy o najniższej energii obsadzone przez

elektrony walencyjne N atomów metalu tworzą
pasmo podstawowe (walencyjne), natomiast łatwo
dostępne dla elektronów walencyjnych poziomy
energetyczne w obszarze nakładania się obydwu
pasm tworzą pasmo przewodnictwa.

W taki właśnie sposób nakładają się na siebie

pasma energetyczne 2s i 2p berylu, którego
swobodne izolowane atomy mają wypełniony orbital
2s

2

(rys. 3). Dzięki temu elektrony walencyjne

atomów berylu mają udostępnione poziomy
energetyczne nieco wyżej położonego pasma 2p
i w ten sposób stają się swobodnymi elektronami
przewodnictwa.

Rys. 3. Nakładanie się pasm 2s i 2p berylu

W podobny sposób nakładają się na siebie poziomy
energetyczne rozszczepionych orbitali ns i (n-1)d
tworząc pasmo podstawowe (walencyjne) i pasmo
przewodnictwa u metali przejściowych.

U

innych

substancji

krystalicznych

rozszczepione poziomy energetyczne orbitali ns i np
lub ns i (n-1)d nie nakładają się na siebie, ponieważ
odpowiednie pasma oddziela odstęp energetyczny
zwany pasmem wzbronionym.

Jeśli pasmo wzbronione jest dostatecznie wąskie,

to energia termiczna elektronów wystarcza do
przeskoku z pasma podstawowego do pustego pasma
przewodnictwa.

Liczba

tak

promowanych

elektronów przewodnictwa wzrasta ze wzrostem
temperatury.

Taką

zależność

temperaturową

przewodnictwa wykazują półprzewodniki samoistne,
np. german i krzem.

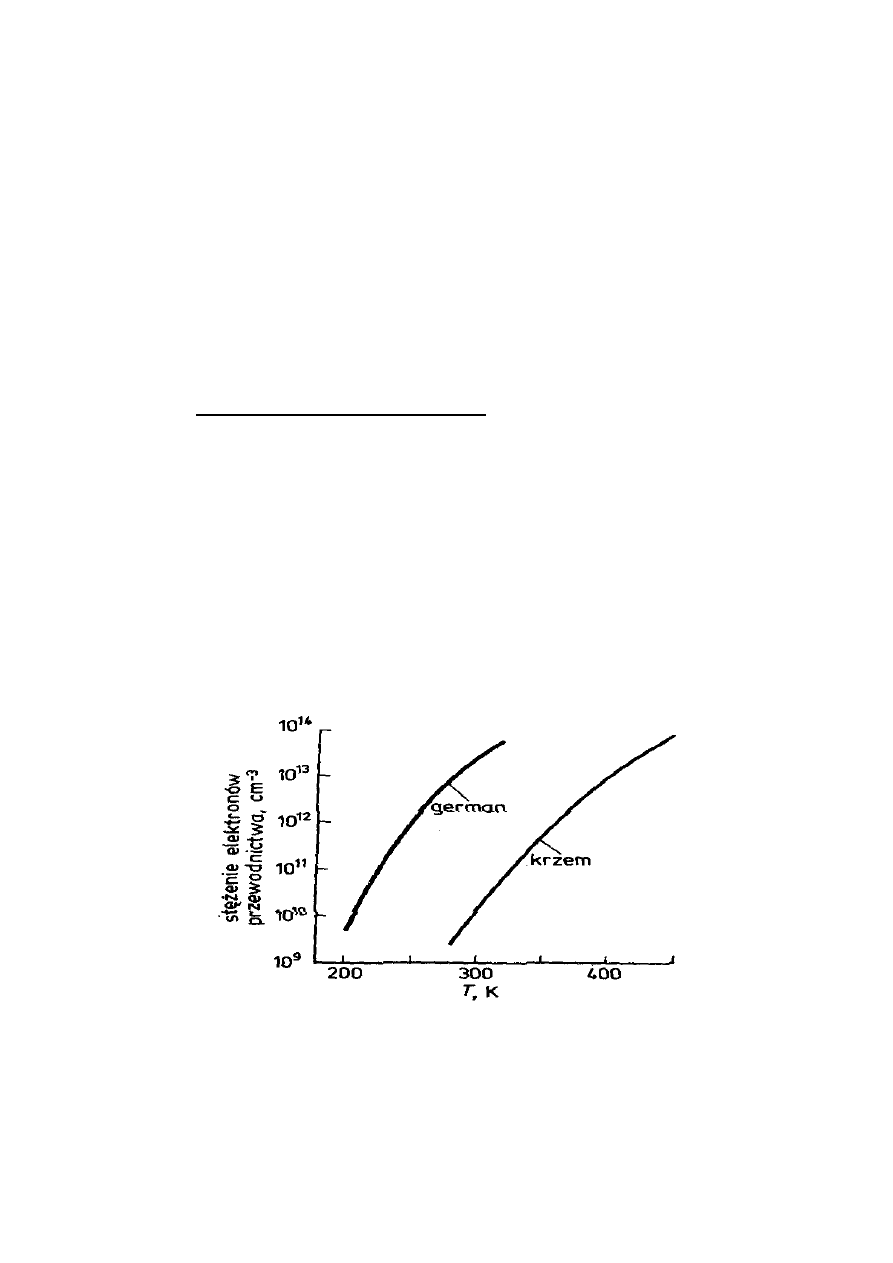
Rys. 4. Zależność stężenia elektronów przewodnictwa od

temperatury dla krzemu i germanu

Gdy pasmo wzbronione jest bardzo szerokie,

wówczas

przeskok

elektronów

z

pasma

podstawowego

do

pasma

przewodnictwa jest

praktycznie niemożliwy, ponieważ wymagałoby to
bardzo dużego nakładu energii. Z tego powodu
substancja

krystaliczna

jako

dielektryk

nie

przewodzi prądu elektrycznego.

Różnice

między

metalami,

dielektrykami

(izolatorami) i półprzewodnikami można jakościowo
przedstawić w sposób pokazany na rys. 5.

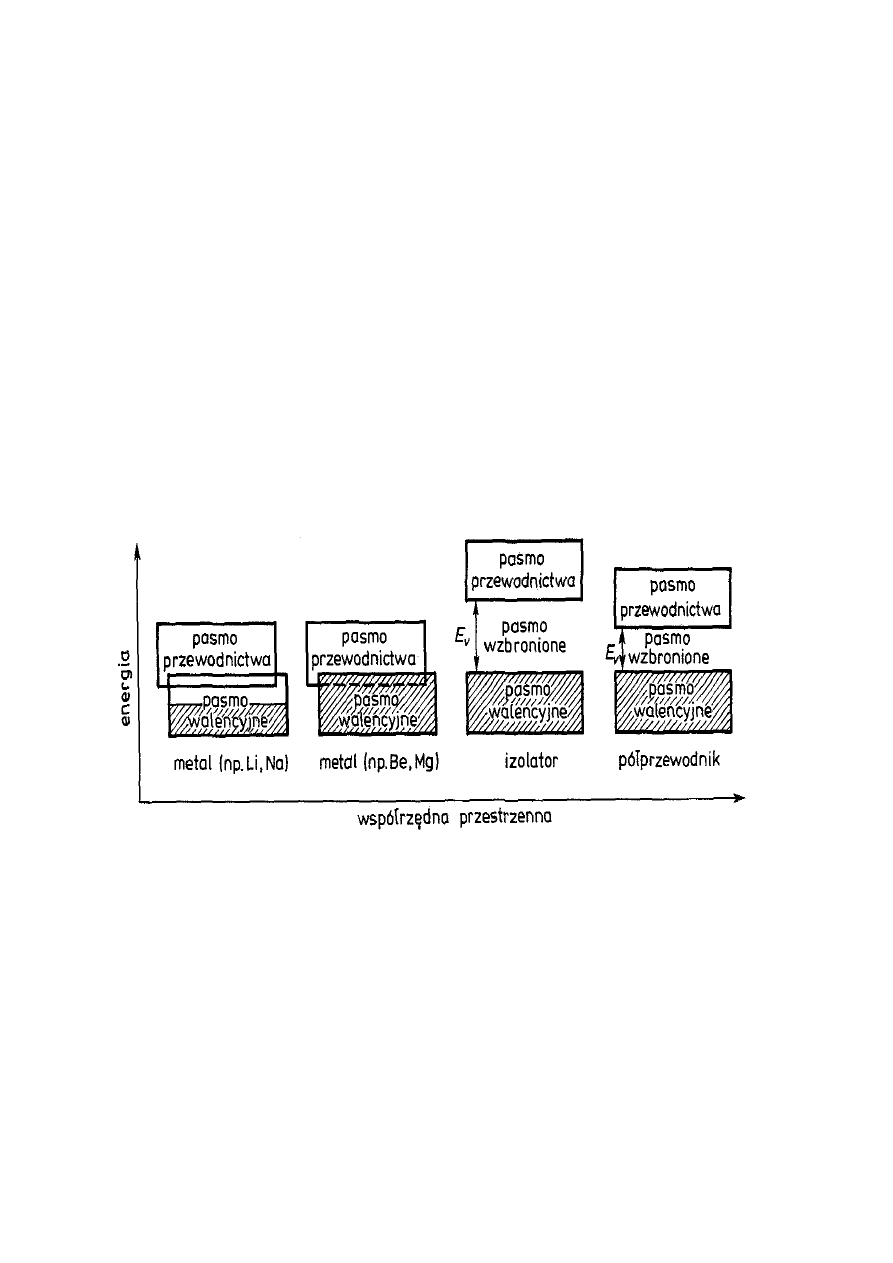
Rys. 5. Układ pasm podstawowego (walencyjnego) i pasma

przewodnictwa u metali oraz rozdzielenie tych pasm pasmem

wzbronionym w dielektrykach (izolatorach) i półprzewodnikach

samoistnych

Zasadnicza

różnica

między

metalem

a

półprzewodnikiem

polega

na

tym,

że

w półprzewodniku liczba elektronów przewodnictwa
zależy od temperatury (rys. 5), natomiast w metalu
pozostaje praktycznie stała. Półprzewodniki mają
ujemny współczynnik temperaturowy oporności
elektrycznej. W temperaturze 0 K półprzewodniki
stają się izolatorami, natomiast metale wykazują
najmniejszą oporność elektryczną.

Rys. 6. Stężenie elektronów przewodnictwa u metali, metaloidów

i półprzewodników samoistnych w temperaturze pokojowej

Dodatkowa różnica polega na tym, że najlepsze

przewodnictwo mają metale w stanie czystym,
natomiast

różne

domieszki

zwiększają

przewodnictwo półprzewodników.

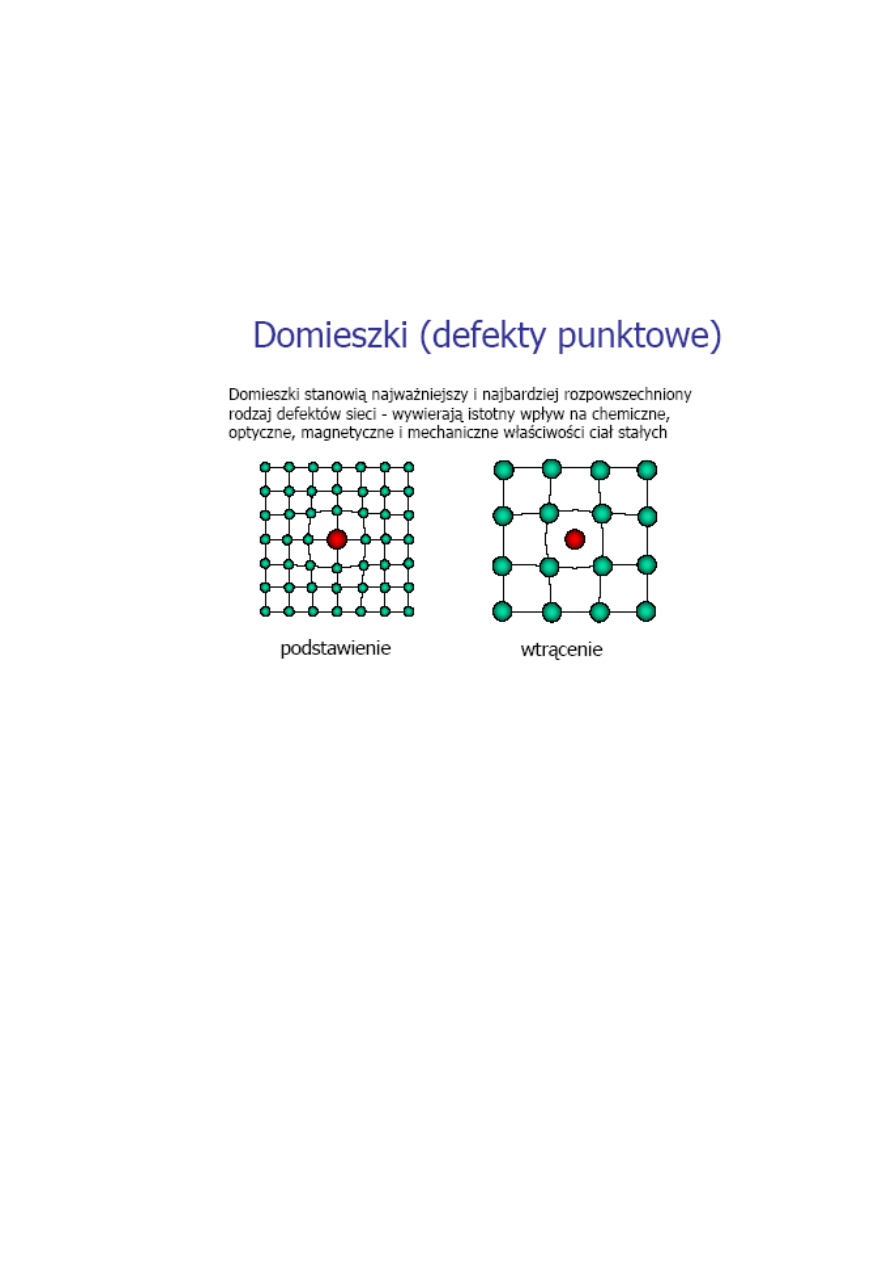
Rys. 7. Typy defektów sieci spowodowane domieszkowaniem

Jeżeli

do

macierzystego

półprzewodnika,

wprowadzi się domieszkę, której atomy mają więcej
elektronów walencyjnych od atomów macierzystych,
wówczas domieszka działa jak donor elektronów,
łatwo oddawanych do pasma przewodnictwa.
Uzyskuje się w ten sposób półprzewodnik typu n,
zwany także półprzewodnikiem nadmiarowym.
Przykładem półprzewodnika typu n jest german
domieszkowany arsenem

Jeżeli

do

półprzewodnika

wprowadzimy

domieszkę, której atomy mają mniej elektronów

walencyjnych od atomów macierzystych, to
domieszka będzie działać jako akceptor elektronów
pochodzących z pasma podstawowego, w którym
pojawią się wolne poziomy energetyczne, tzw.
dziury elektronowe, przewodzące prąd elektryczny
w przeciwnym kierunku niż elektrony. Uzyskuje się
w ten sposób półprzewodnik typu p, określany
również mianem półprzewodnika niedomiarowego.
Przykładem takiego półprzewodnika jest german
domieszkowany indem.

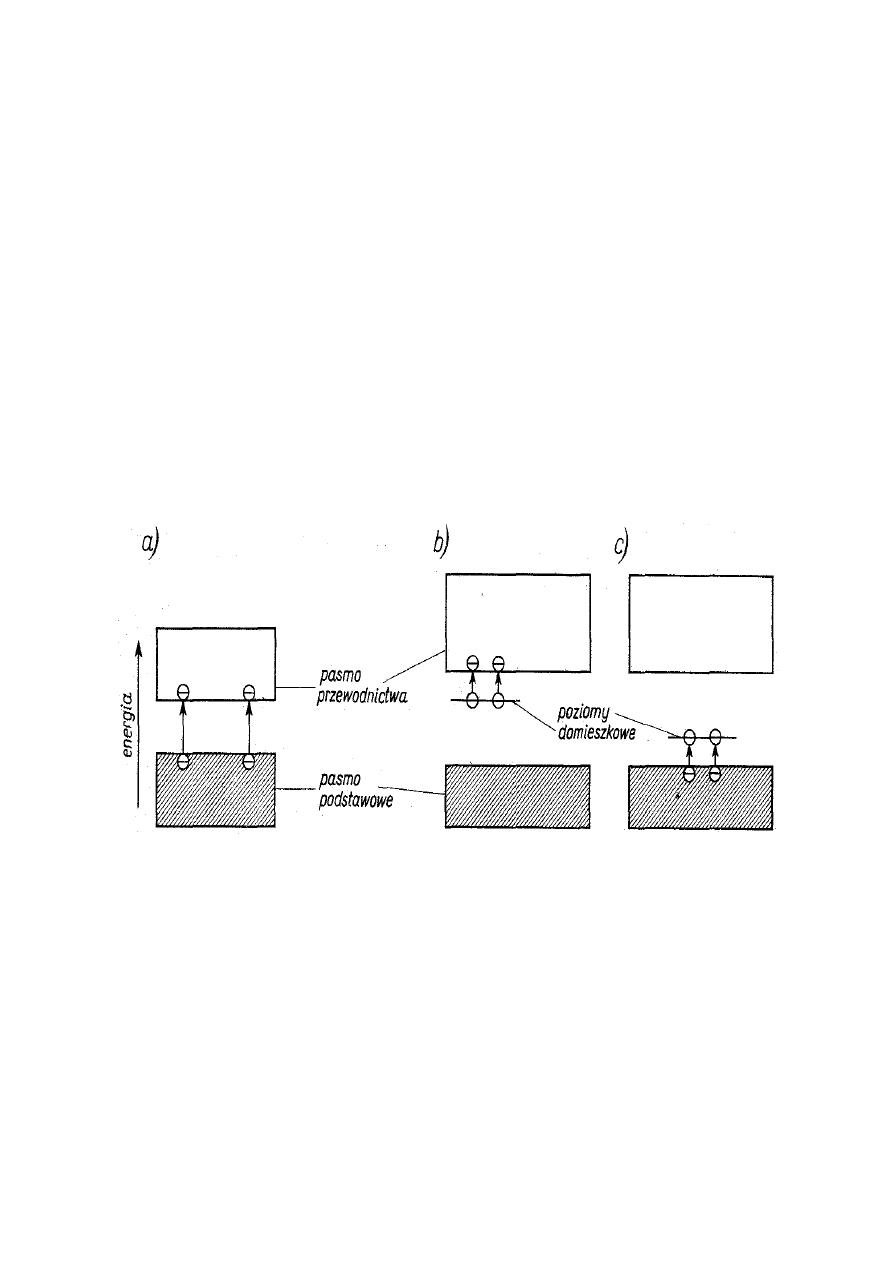
Rys. 8. Układ pasm w półprzewodnikach

a) półprzewodnik samoistny, b) półprzewodnik

domieszkowy typu n, c) półprzewodnik domieszkowy typu p

W

kryształach

omówionych

dotychczas

półprzewodników istotną rolę odgrywa wiązanie
kowalencyjne.

Właściwości

półprzewodnikowe

wykazują

również

liczne

związki

chemiczne

o charakterze jonowym, które formalnie powinny być
dielektrykami (izolatorami). Przyczyną wystąpienia
półprzewodnictwa u tych związków są bardzo
niewielkie odchylenia od idealnej stechiometrii oraz
wynikające stąd defekty struktury krystalicznej.

Substancje wykazujące nawet bardzo niewielkie

odstępstwa od stechiometrii nazywamy bertolidami.

Związki z nadmiarem jonów metalu, np. ZnO,

CdO, CdS, SnO

2

, TiO

2

, Ag

2

S, wykazują defekt Frenkla,

tzn. nadmiarowe jony metalu muszą znaleźć się w
przestrzeniach międzywęzłowych, ponieważ wszystkie
węzły sieci kryształu są już obsadzone. Nadmiarowy
dodatni ładunek kationów jest kompensowany przez
równoważną ilość mobilnych elektronów, co w
konsekwencji

powoduje, że rozważane związki

zachowują się jak półprzewodniki nadmiarowe.

Związki z niedomiarem jonów metalu, np. Cu

2

O,

SnS, FeO, CoO, NiO, wykazują defekt Schottky’ego,
tzn. niektóre węzły w sieci kryształu są puste.
Przewodnictwo tej grupy związków ma charakter
„dziurowy” i w rezultacie są one półprzewodnikami
niedomiarowymi.

Zaistnienie

takiego

rodzaju

przewodnictwa jest uwarunkowane zdolnością metalu
do tworzenia kationów na dwóch różnych stopniach
utlenienia, np. Cu

+

i Cu

2+

, Sn

2+

i Sn

4+

, Fe

2+

i Fe

3+

, Co

2+

Co

3+

, Ni

2+

i Ni

3+

, itp.

Tlenek cynku może wykazywać nieznaczny

niedobór jonów tlenkowych O

2–

, lub co jest

jednoznaczne, pewien nadmiar jonów metalu,

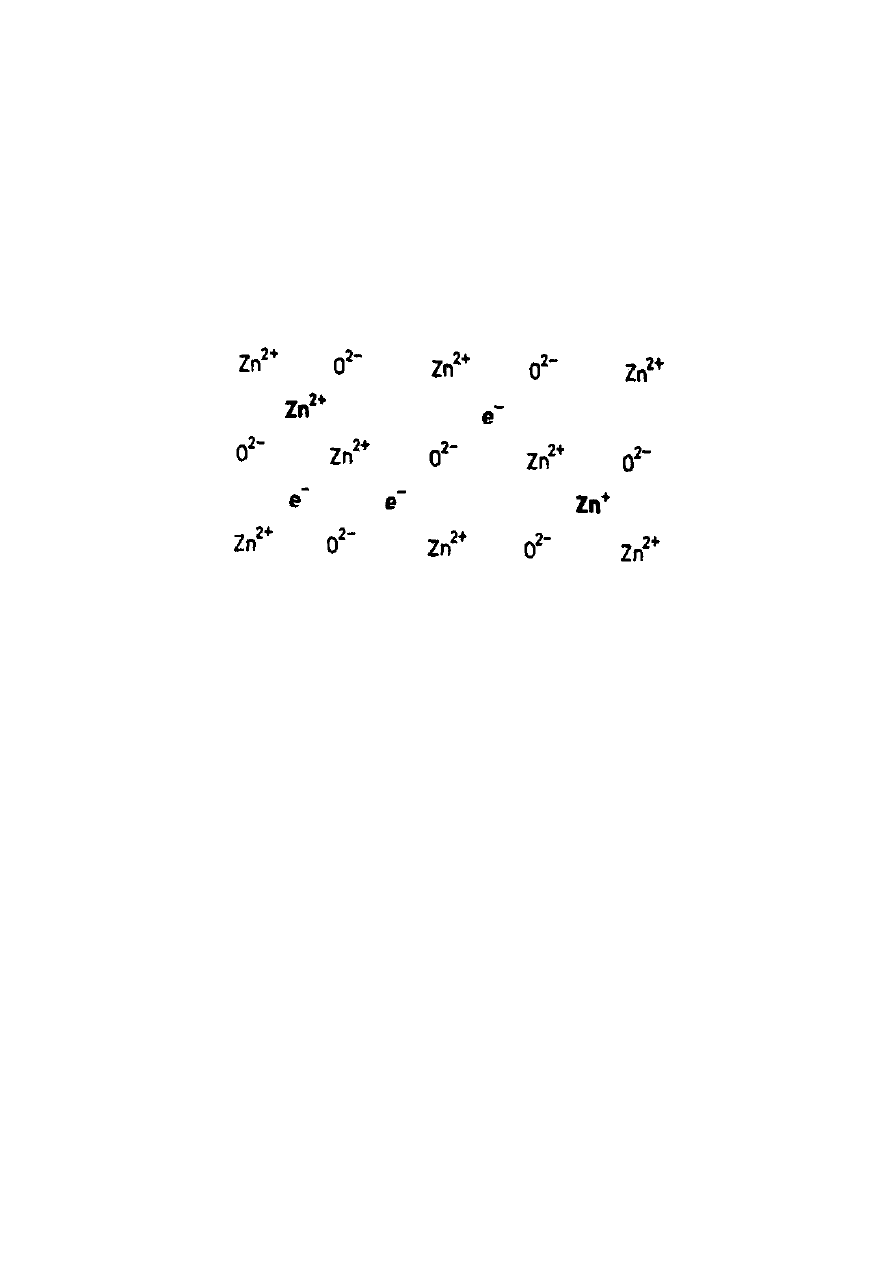
w wyniku czego jego skład nie odpowiada formule
ZnO, ale np. Zn

1,00

O

0,99

. Z tego powodu nadmiarowe

kationy cynku muszą się znaleźć w przestrzeniach
międzywęzłowych, a wraz z nimi równoważna liczba
elektronów, co wynika z warunku elektroobojętności
kryształu.

Rys. 9. Dwuwymiarowy model defektów sieciowych dla tlenku

cynku

W zewnętrznym polu elektrycznym elektrony
znajdujące się w przestrzeniach międzywęzłowych
kryształu tlenku cynku są mobilne, dlatego tlenek
ten jest półprzewodnikiem typu n.

Komórka

elementarna

stechiometrycznego

tlenku miedzi(I), Cu

2

O, krystalizującego w układzie

regularnym (rys. 10) zawiera cztery atomy miedzi
i dwa atomy tlenu.

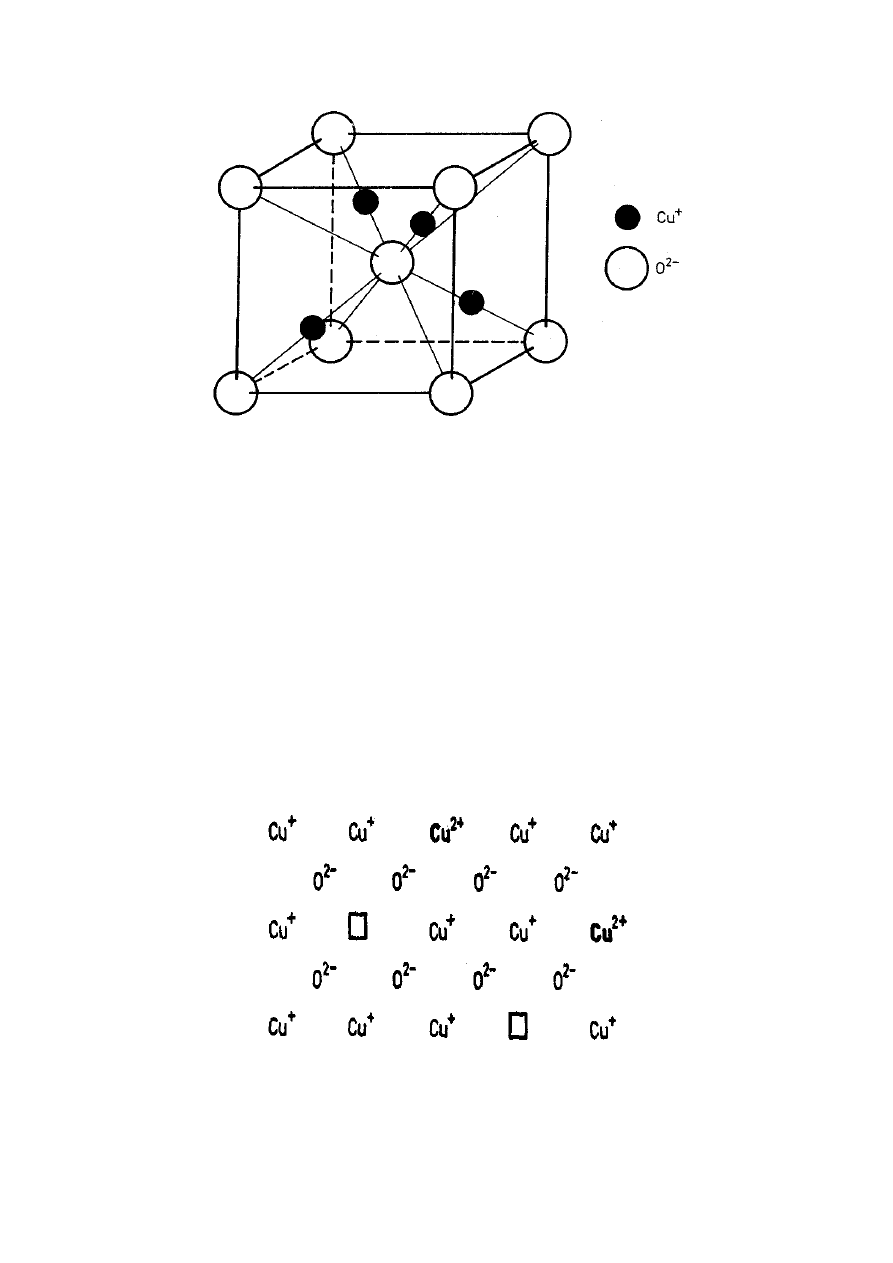
Rys. 9. Komórka elementarna Cu

2

O

Okazuje się jednak, że tlenek miedzi(I) może
wykazywać nieznaczny niedobór atomów metalu
i z tego powodu nie odpowiada idealnej stechiometrii
Cu

2

O. Gdy aktualny skład tlenku miedzi(I)

odpowiada formule Cu

1,99

O

1,00

, to na każdy tysiąc

jonów tlenkowych O

2–

przypada 1980 kationów Cu

+

oraz 10 kationów Cu

2+

, a 10 miejsc obsadzanych

w idealnej sieci krystalicznej przez kationy pozostaje
puste.

□

puste, nie obsadzone miejsce w sieci

Rys. 11. Dwuwymiarowy model defektów sieciowych u tlenku

miedzi(I)

Tlenek miedzi(I) jest półprzewodnikiem typu p,
ponieważ kationy Cu

2+

zachowują się jak dziura

elektronowa, która w wyniku przeskoku elektronu
z sąsiedniego kationu Cu

+

przenoszona jest

w przeciwnym kierunku:

Cu

+

+ Cu

2+

→ Cu

2+

+ Cu+

└─e─┘
W zewnętrznym polu elektrycznym proces ten się
powtarza i dziura elektronowa przemieszcza się
w kierunku przeciwnym do ruchu elektronów.