G.6. Linie geodezyjne

Przez dany punkt P powierzchni L można poprowadzić nieskończenie wiele krzywych.

Styczne do tych krzywych w punkcie P tworzą płaszczyznę styczną (ściśle styczną) do po-

wierzchni L w punkcie P.

Definicja

Płaszczyzną styczną do powierzchni w jej punkcie P nazywamy płaszczyznę, w której leżą

styczne w tym punkcie do każdej krzywej leżącej na tej powierzchni i przechodzącej przez

ten punkt.

Definicja

Prostą normalną do powierzchni w punkcie P nazywamy prostą przechodzącą przez ten

punkt i prostopadłą do płaszczyzny stycznej do tej powierzchni w tym punkcie.

Definicja

Linią geodezyjną (geodetyką lub ortodromą) nazywamy krzywą zawartą w danej powierzch-

ni o tej własności, że w każdym jej punkcie normalna główna do tej krzywej jest jednocześnie

normalną do powierzchni w tym punkcie.

Twierdzenie

a) Linia geodezyjna zawiera najkrótszą drogę pomiędzy dowolnymi dostatecznie bliskimi

swoimi punktami.

b) Na płaszczyźnie, linia geodezyjna jest prostą.

c) Linia geodezyjna łącząca dwa punkty sfery (powierzchni kuli) jest łukiem okręgu wielkie-

go koła, które jest wyznaczone przez te punkty i środek sfery.

Definicja

Figurą geodezyjną na danej powierzchniach (np. płaszczyźnie, kuli, elipsoidzie) nazywamy

figurę zawartą w tej powierzchni, której brzegiem (bokami) są odcinki linii geodezyjnych.

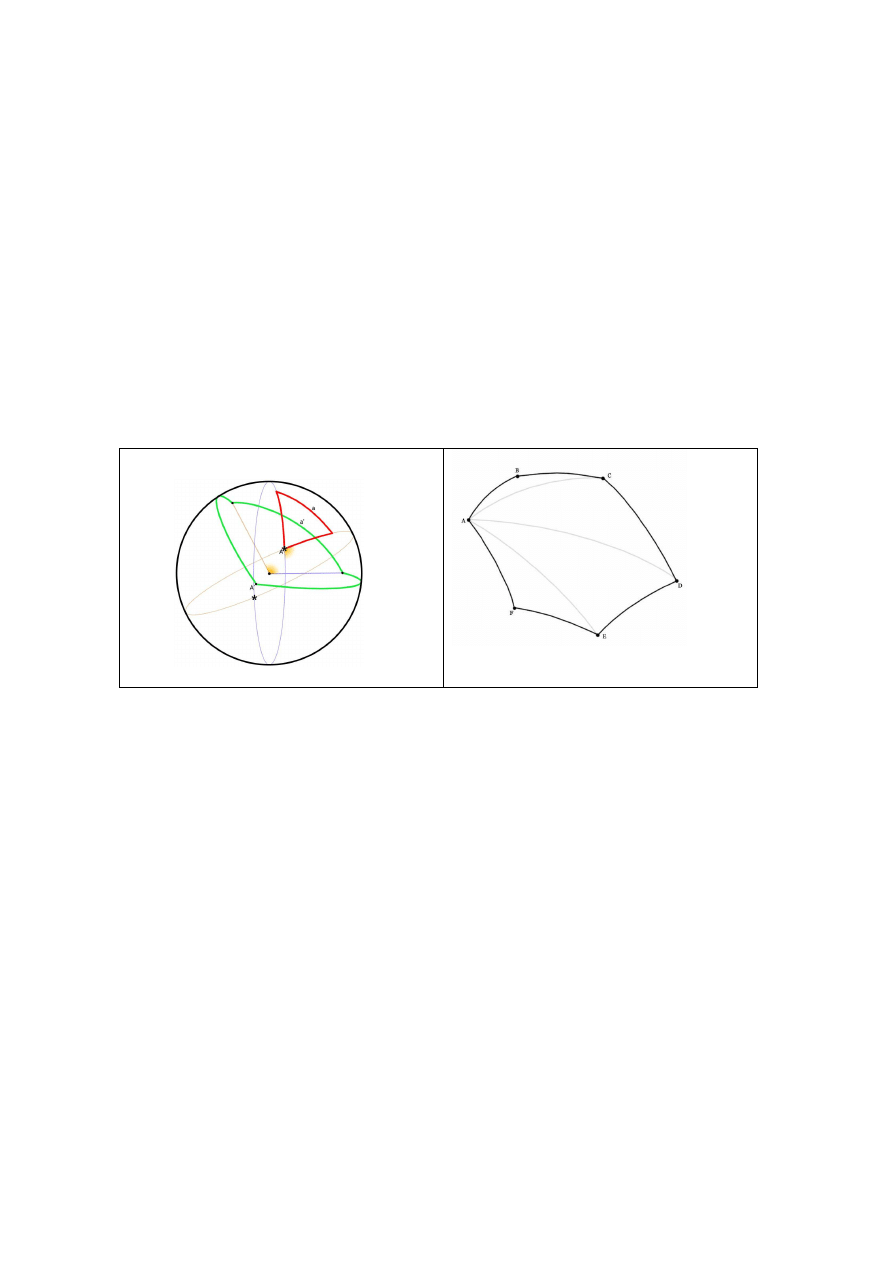
Rysunek a) przedstawia dwa trójkąty geodezyjne na sferze (brzeg jednego zaznaczono

kolorem zielonym, drugiego - czerwonym), zaś rysunek b) przedstawia sześciobok geodezyj-

ny na sferze.

a)

b)

Twierdzenie

Rozważmy n – kąt na sferze (n – kąt sferyczny). Pole n – kąta sferycznego jest równe

S = r

2

[

Σ

k – (n-2)

π

], gdzie r jest promieniem sfery,

Σ

k sumą miar kątów wewnętrznych tego

n – kąta.

Definicja

Niech Z będzie niepustym zbiorem. Każdej parze elementów zbioru Z przyporządkujmy licz-

bę rzeczywistą nieujemną, zwaną odległością (metryką) tych punktów.

Zbiór Z z tak określoną metryką nazywamy przestrzenią metryczną.

Przykład 1.

W zbiorze punktów płaszczyzny z układem współrzędnych Oxy określamy odległość punk-

tów A = (a

1

, a

2

) , B = (b

1

, b

2

) wzorem: |AB| =

2

2

2

2

1

1

)

(

)

(

b

a

b

a

−

+

−

. Płaszczyzna z tak

określoną odległością jest przestrzenia metryczną.

Definicja

Niezmiennikiem przekształcenia nazywamy własność (relację), która nie zmienia się w tym

przekształceniu. Inaczej ta własność przysługuje zarówno danemu zbiorowi jak i jego obra-

zowi w tym przekształceniu.

Przykład 2.

a) Niech p będzie daną płaszczyzną oraz a prostą leżącą na tej płaszczyźnie. Przekształcamy

płaszczyznę p przez symetrię względem prostej a. Wiemy, że symetria osiowa nie zmienia

pola figury, czyli figura i jej obraz w symetrii osiowej mają to samo pole.

Zatem pole figury jest niezmiennikiem symetrii osiowej.

b) Rzutujemy prostopadle przestrzeń trójwymiarową z układem współrzędnych Oxyz na

płaszczyznę Oxy. Pole figury nie jest niezmiennikiem rzutu prostopadłego, ponieważ rzu-

tując prostopadle kwadrat (np. ustawiony prostopadle względem płaszczyzny Oxy ) mo-

ż

emy otrzymać odcinek. A więc figurę o innym polu niż kwadrat.

Definicja

Funkcję F : X

→

Y, czyli F(X) = Y, przekształcającą przestrzeń metryczną X na przestrzeń

metryczną Y nazywamy homeomorfizmem, gdy F jest funkcją ciągłą, różnowartościową

oraz funkcja F

-1

do niej odwrotna jest też ciągła.

Definicja

Niech F będzie homeomorficznym odwzorowaniem powierzchni S

1

(oryginał) na powierzch-

nię S

2

(obraz), czyli F(S

1

) = S

2

.

W odwzorowaniu F obrazem wieloboku geodezyjnego na ogół nie jest figura geodezyjna, lecz

wielobok krzywoliniowy, którego boki są odcinkami pewnych krzywych nie będących liniami

geodezyjnymi.

Definicja

Odwzorowania homeomorficzne, w których obrazami linii geodezyjnych są linie geodezyjne,

nazywamy odwzorowaniami geodezyjnymi.

Definicja

Odpowiednikiem redukcyjnym w danym odwzorowaniu geodezyjnym figury geodezyjnej

G

1

zdefiniowanej na powierzchni oryginału nazywamy figurę geodezyjną G

2

będącą jej obra-

zem na powierzchni obrazu.

Odpowiednik redukcyjny jest zbudowany z odcinków linii geodezyjnych właściwych

powierzchni obrazu, łączących odpowiedniki obrazowe wierzchołków figury oryginału.

Deformacje (zmiany, różnice) zachodzące pomiędzy odpowiadającymi sobie parame-

trami metrycznymi figury geodezyjnej zlokalizowanej na powierzchni oryginału i odpowied-

nika redukcyjnego tej figury na powierzchni obrazu, nazywamy redukcjami odwzorowaw-

czymi geodezyjnymi.

Redukcje odwzorowawcze geodezyjne mogą dotyczyć długości boków, kątów we-

wnętrznych lub azymutów boków, a także pól figur geodezyjnych.

W geodezji i w kartografii formułuje się do rozwiązania dwa zadania, w których należy

uwzględnić redukcje odwzorowawcze.

Zadanie 1

Na elipsoidzie obrotowej spłaszczonej dany jest punkt P

1

, azymut A

1

linii geodezyjnej w

punkcie P

1

oraz długość

∆

s łuku linii geodezyjnej łączącej punkty P

1

i P

2

. Poszukujemy re-

dukcji odwzorowawczych w tzw. aspekcie prostym.

Obliczenie redukcji odwzorowawczych w tym przypadku sprowadza się do wyznacze-

nia azymutu linii geodezyjnej w punkcie P

2

oraz współrzędnych punktu P

2

. W tym celu wy-

starczy wyznaczyć współrzędne P

2

wprost na tej elipsoidzie. Następnie wyznaczyć współ-

rzędne prostokątne na płaszczyźnie obrazów P’

1

i P’

2

punktów P

1

i P

2

kątów pomiędzy od-

cinkiem P’

1

P’

2

i obrazami południków w punktach P’

1

i P’

2

, a także długości odcinka P’

1

P’

2

.

Zadanie 2

W płaszczyźnie obrazu odwzorowania dane są punkty P’

1

i P’

2

. Poszukujemy redukcji od-

wzorowawczych w tzw. aspekcie odwrotnym.

Obliczenie redukcji odwzorowawczych w tym przypadku polega na przejściu od współ-

rzędnych prostokątnych x, y punktów P’

1

i P’

2

w płaszczyźnie obrazu do współrzędnych geo-

dezyjnych powierzchni oryginału.

Zadania do samodzielnego rozwiązywania

Zadanie 1.

Napisz równanie sfery o środku S i promieniu r, gdy:

a) S=(0, 0, 0) i r = 2, b) S=(1, 2, -3) i r = 5, c) S=(-1, -3, -2) i r = 4.

Zadanie 2.

Napisz równanie okręgu wielkiego sfery o środku S i promieniu r, zawartego w płasz-

czyźnie p, gdy:

a) S=(0, 0, 0) i r = 2, p: z = 0; b) S=(0, 0, 0) i r = 3, p: x = 0;

c) S=(0, 0, 0) i r = 1, p: x + y = 0; d) S=(0, 0, 0) i r = 5, p: z +2 y = 0.

Zadanie 3.

Napisz równanie okręgu wielkiego sfery o środku S i promieniu r, zawartego w płasz-

czyźnie p, gdy:

a) S=(-1, -3, -2) i r = 4, p: z = 0; b) S=(-1, -3, -2) i r = 3, p: x = 0;

c) S=(-1, -3, -2) i r = 1, p: x + y = 0.

Zadanie 4.

Napisz równanie okręgu wielkiego sfery o środku S i promieniu r, przechodzącego

przez punkty A, B, gdy:

a) S=(1, 2, -3) i r = 5, A=(-1, 0, 2), B=(2, 1, 0) ;

b) S=(1, 2, -3) i r = 3, A=(-1, 0, -2), B=(0, -1, 0).

Zadanie 5.

Wyznacz miarę łukową kąta każdego dwukąta sfery o środku S i promieniu r, wyzna-

czonego przez okręgi O

1

i O

2

, gdy:

S=(1, 2, -3) i r = 3, A=(-1, 0, -2), B=(0, -1, 0), A, B

∈

O

1

,

C=( 0, 0, 0) D=( 1, 0, 0 ), C, D

∈

O

2

.