Wyrównanie odporne na błędy grube

Wpływ danych na modele prostej regresji

1. Źródła błędów.

● Pomyłki w odczycie (również dotyczy instrumentów elektronicznych

– RL)

● Zła numeracja – np.. włączenie obserwacji pikiety do wyrównania

dla sieci modularnych.

● Przekłamania w transmisji – rzadkość bo lepsze algorytmy

wykorzystują sumy kontrolne – trywialny przykład dla transmisji
przez RS 232 to bit parzystości czyli

● Bitem parzystości nazywamy bit kontrolny, który przyjmuje

wartość 1, gdy liczba jedynek w przesyłanej wiadomości jest
nieparzysta lub 0, gdy odwrotnie. Innymi słowy – bit parzystości
sprawia, że wiadomość ma zawsze parzystą liczbę jedynek.

● W tym wariancie bit parzystości możemy obliczyć wykonując sumę

modulo dwa na wszystkich bitach wiadomości.

● Mniej trywialne to sumy kontrolne MD5 – ciąg znaków w ciąg 128

bitowy

● Zaburzenia środowiska pomiarowego (zwłaszcza gdy chwilowe ale

znaczące) – różniczka wzoru Barrella Searsa. - przykład...

2. Przedział dla losowych poprawek

● Zakładamy symetrię
● Ustalamy przedział dopuszczany dla poprawek
● P{(v<a)v(v>a)}=1-γ
● Granice przedziału wiążemy z dokładnością pomiary (vide ISO),

oraz przyjętym poziomem prawdopodobieństwa

● Warunek: szczegółowe założenia o modelu probabilistycznym….

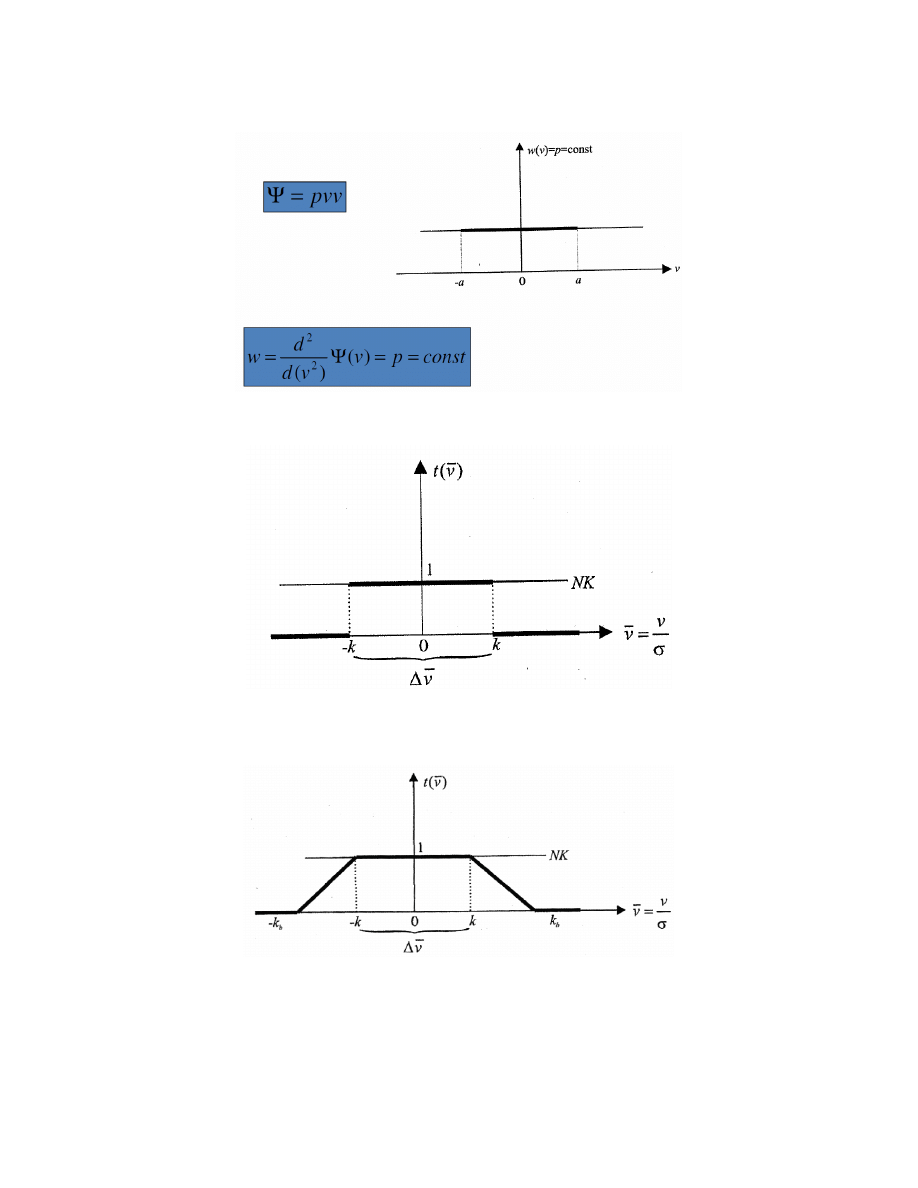
3. Dlaczego NIE MNK [LSF]? (Rys. Wiśniewski, 2005)

A. Inne funkcje tłumienia: Hubera (radykalna) (Rys. Wiśniewski, 2005)

B. Inne funkcje tłumienia: Hampela (Rys. Wiśniewski, 2005)

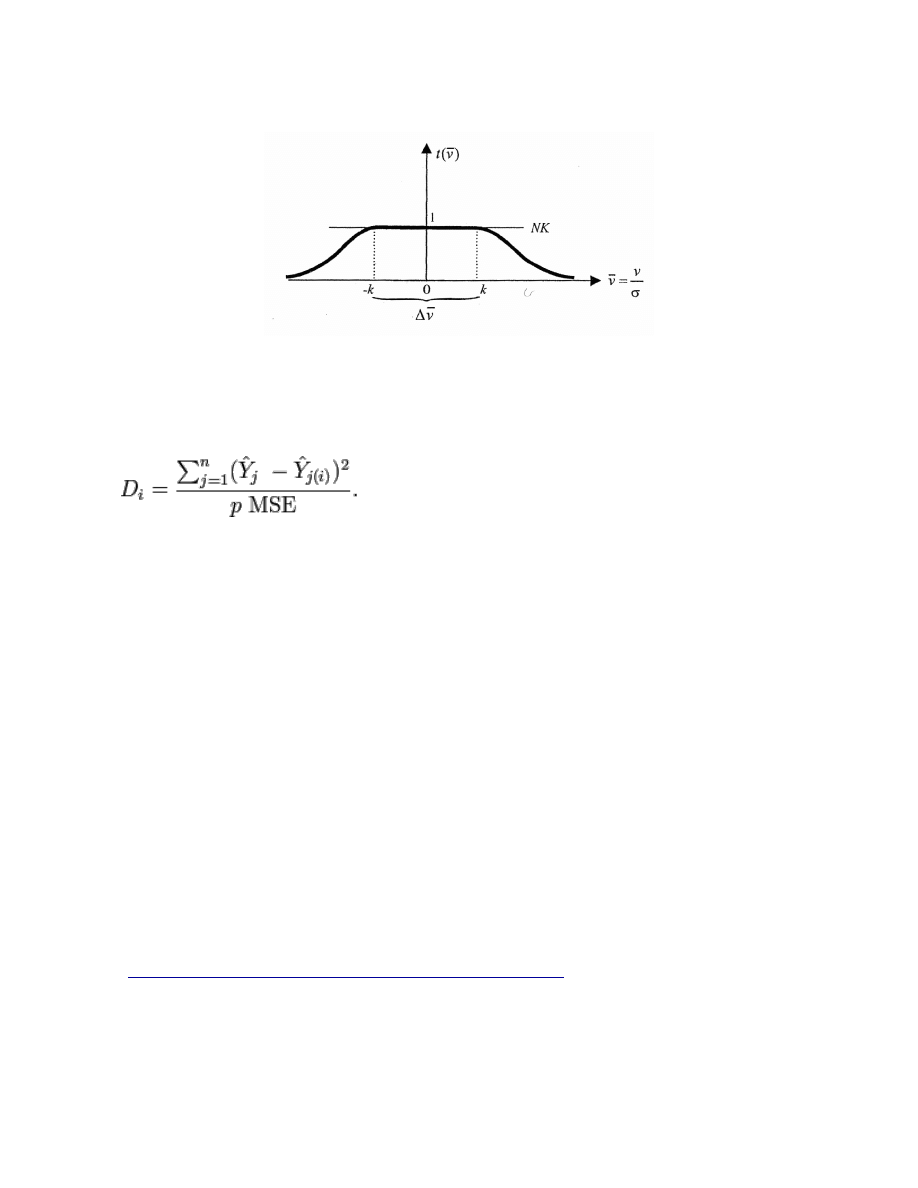
C. Inne funkcje tłumienia: Duńska (Rys. Wiśniewski, 2005)

4. Które dane są warte naszej uwagi w przypadku prostej regresji?

Odległość Cooka pomaga oszacować wpływ poszczególnych danych, na
wyniki analizy regresji metodą najmniejszych kwadratów.

Gdzie:

- odległość Cook'a

D

i

- predykcja z pełnego modelu dla j-tej obserwacji

Y

i

(i) - predykcja dla j-tej obserwacji z modelu gdzie j-ta

Y

j

obserwacja była pominięta
MSE - (mean square error) Błąd średnio kwadratowy modelu regresji
MSE(0^)=E[(0^-0)^2]
p - liczba parametrów modelu

Di > 1 lub di>4/n (n-liczba obserwacji)=> obserwacja "ciekawa"

Podczas analizy danych odległość Cooka można wykorzystać aby wskazać:
A) Dane, które są szczególnie warte sprawdzenia (jeżeli chodzi o ich
ew. poprawność),
B) Miejsca, gdzie byłoby dobrze, aby móc otrzymać więcej (punktów)
danych.

Źródło:

Influential Observations in Linear Regression R. Dennis Cook

{

http://www.jstor.org/stable/2286747?seq=1 }

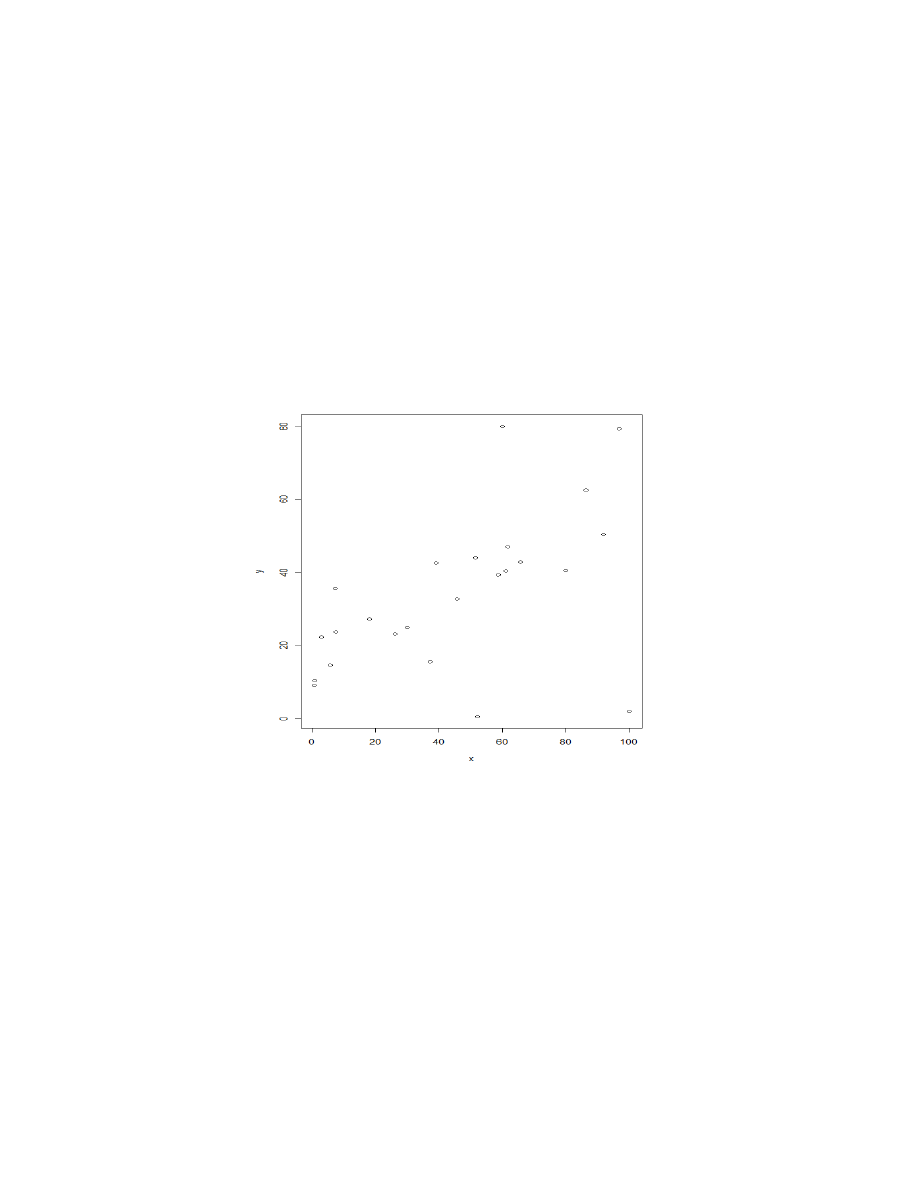
Pliki wejściowe: Mx.txt, My.txt (wydruk danych na końcu konspektu na
wszelki wypadek)

1. Wczytujemy dane, tworzymy ramkę ds3.
File/Change Dir...

x=scan(file="Mx.txt")
y=scan(file="My.txt")

2. Wyplot danych

plot (y~x)

3. Model regresji liniowej

ds3=data.frame(x=x,y=y)
m.lm=lm(y~x,data=ds3)

// regresja liniowa

summary(m.lm)

// podsumowanie modelu (zapisać a oraz x)

Call:
lm(formula = y ~ x, data = ds)
Residuals:
Min 1Q Median 3Q Max
-50.714 -5.302 1.078 7.682 41.116
Coefficients:
Estimate Std. Error t value Pr(>|t|)

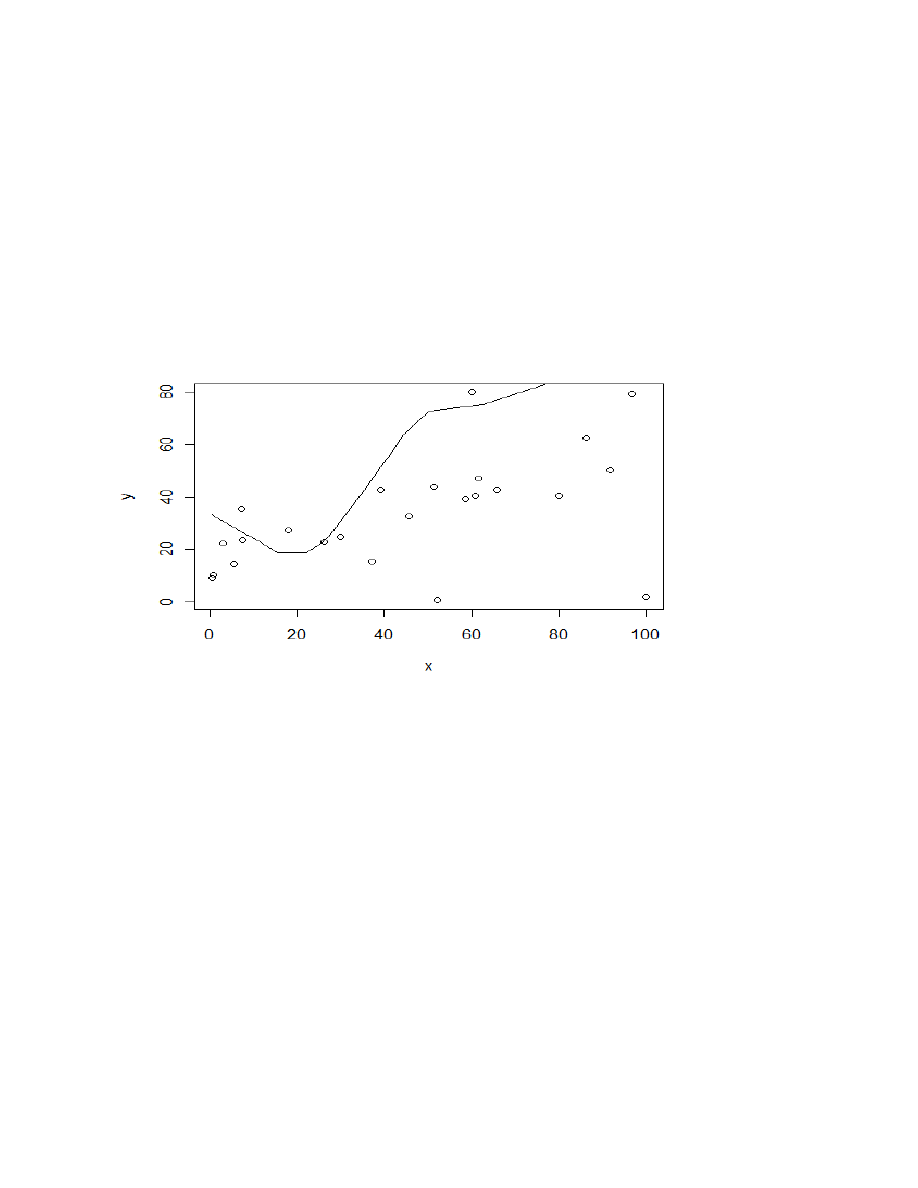
(Intercept) 18.1406 6.6035 2.747 0.01176 *
x 0.3457 0.1198 2.886 0.00859 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 18.46 on 22 degrees of freedom
Multiple R-squared: 0.2746,

Adjusted R-squared: 0.2416

F-statistic: 8.326 on 1 and 22 DF, p-value: 0.008586

layout(1)
plot(x~y)
lines(lowess(y,x)) // locally-weighted polynomial regression

op=par(mfrow=c(2,2),pty="s")//definicja wydruku 2x2
plot(m.lm)

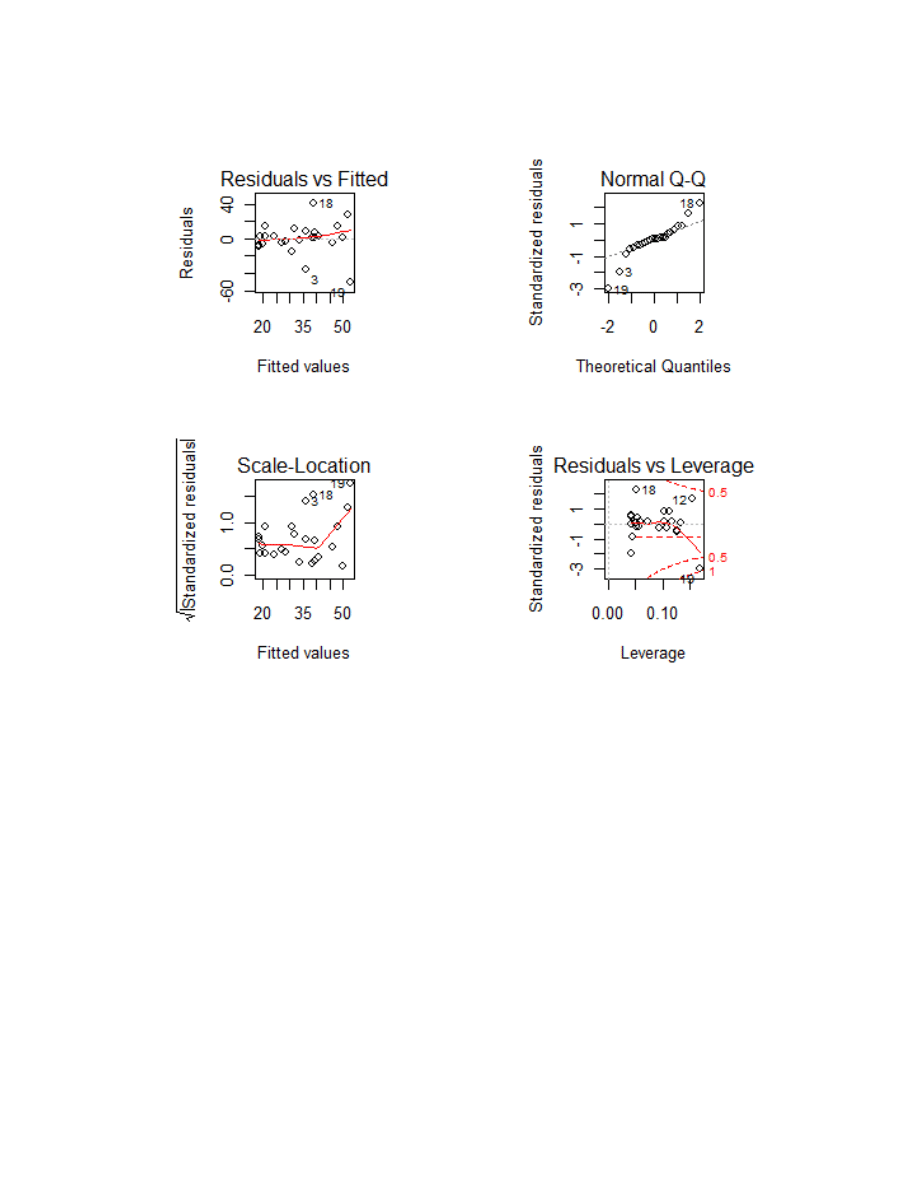
library(MASS)
d1=cooks.distance(m.lm)//obliczmy odległości cooka
r=stdres(m.lm)//obliczamy warości zestandaryzowanych reszt
a=cbind(ds3,d1,r)
a[d1>4/24,]

x y d1 r
12 96.67613 79.40566 0.2428324 1.639264
19 100.00000 2.00000 0.9158652 -3.012530

rabs=abs(r) // wartości bezwzględne reszt zestandaryzowanych
a=cbind(ds3, d1, r, rabs) // scalamy informację
asorted=a[order(-rabs), ] //sortujemy malejąco
asorted[1:10,] // listujemy 10 pierwszych

x y d1 r rabs
19 100.0000000 2.0000000 0.915865158 -3.0125301 3.0125301
18 60.0000000 80.0000000 0.139978076 2.2867363 2.2867363

3 52.0505557 0.5434521 0.088662280 -1.9720859 1.9720859
12 96.6761269 79.4056646 0.242832421 1.6392644 1.6392644
8 37.2332223 15.5271050 0.017112466 -0.8583942 0.8583942
9 7.2942088 35.5748647 0.041513194 0.8529058 0.8529058
4 86.3099961 62.5757242 0.044751591 0.8395604 0.8395604
10 39.1836418 42.5974663 0.008251017 0.6043665 0.6043665
14 0.6359537 9.0659875 0.020838509 -0.5385943 0.5385943
16 0.8701528 10.4350800 0.015323760 -0.4637177 0.4637177

library(car)
influencePlot(lm(y~x), main="InfluencePlot",sub="Promień kółka jest
proporcjonalny do odległości Cooka")

influence.measures(lm(y~x))

Influence measures of

lm(formula = y ~ x) :

dfb.1_ dfb.x dffit cov.r cook.d hat inf
1 0.063432 -0.050892 0.0635 1.239 2.11e-03 0.1167
2 0.021039 -0.068941 -0.0930 1.200 4.51e-03 0.0926
3 -0.174303 -0.095644 -0.4534 0.778 8.87e-02 0.0436
4 -0.090640 0.235845 0.2971 1.159 4.48e-02 0.1127
5 -0.004102 0.009410 0.0114 1.266 6.76e-05 0.1329
6 0.012329 0.045030 0.0975 1.140 4.94e-03 0.0530
7 0.037669 0.017924 0.0936 1.126 4.54e-03 0.0433
8 -0.138996 0.045511 -0.1839 1.073 1.71e-02 0.0444
9 0.285270 -0.220512 0.2863 1.143 4.15e-02 0.1024
10 0.090629 -0.024039 0.1266 1.109 8.25e-03 0.0432
11 0.055650 -0.042926 0.0559 1.219 1.63e-03 0.1017
12 -0.292888 0.619953 0.7267 0.999 2.43e-01 0.1531
13 0.042350 -0.028576 0.0437 1.181 1.00e-03 0.0727
14 -0.200779 0.164143 -0.2008 1.222 2.08e-02 0.1256
15 -0.107720 0.084549 -0.1079 1.219 6.07e-03 0.1078
16 -0.171874 0.140269 -0.1719 1.230 1.53e-02 0.1247
17 0.000833 0.014927 0.0274 1.165 3.92e-04 0.0593
18 0.099496 0.251240 0.5921 0.672 1.40e-01 0.0508 *
19 0.738421 -1.495924 -1.7252 0.455 9.16e-01 0.1679 *
20 -0.050289 0.028550 -0.0550 1.158 1.58e-03 0.0570
21 0.002272 0.004340 0.0111 1.154 6.47e-05 0.0492
22 -0.039110 0.019669 -0.0448 1.153 1.05e-03 0.0516
23 0.002317 0.007122 0.0160 1.157 1.34e-04 0.0520
24 -0.006997 -0.000135 -0.0125 1.145 8.13e-05 0.0417

outlier.test(m)

4. Regresja linowa z "ręcznym" usunięciem danych
m.lm2=lm(y~x,subset=-c(3,18,19))
summary(l.m2)
plot(m.lm2)
d1.2=cooks.distance(m.lm2)//obliczmy odległości cooka
r2=stdres(m.lm)//obliczamy warości zlinearyzowanych reszt
s=seq(1,24,by=1)
s=s[-c(3,18,19)]
a2=cbind(s,d1.2,r2)
a2[d1.2>4/21,]
rabs2=abs(r2) // wartości bezwzględne reszt zestandaryzowanych
a2=cbind(s, d1.2, r2, rabs) // scalamy informację
asorted2=a2[order(-rabs2), ] //sortujemy malejąco
asorted2[1:10,] // listujemy 10 pierwszych

5. Regresja z modelem Hubera

library(MASS)
m.hub=rlm(y~x)
summary(m.hub)
plot(m.hub)
plot(m.hub$w, ylab="Wagi Hubera")
a=cbind(ds3, d1, r, m1.huber$w)
asorted=a[order(m1.huber$w),]
asasorted[1:10,]

6. Regresja z modelem Bisquare
m.bi=rlm(y~x,method='MM')
m.bi
plot(m.bi$w, ylab="Wagi Bis",type="p",lwd=10)

Mx.txt

3.0711495

80.0157624
52.0505557
86.3099961
91.7997094
61.6446204
51.4024111
37.2332223

7.2942088

39.1836418

7.5142277

96.6761269
18.1192078

0.6359537
5.6490005
0.8701528

65.7154647

60

100

26.1871036
58.6032036
29.8974961
60.9082682
45.6065505

My.txt

22.2998127
40.5770039

0.5434521

62.5757242
50.3886458
46.9980806
44.0056351

15.527105

35.5748647
42.5974663
23.7082553
79.4056646
27.2431878

9.0659875

14.5665301

10.43508
42.85773

80

2

23.09355

39.3016

24.94875
40.45413
32.80328