1

Podstawy estymacji: poj

Podstawy estymacji: poj

ę

ę

cie i podstawowe w

cie i podstawowe w

ł

ł

asno

asno

ś

ś

ci

ci

estymator

estymator

ó

ó

w (1)

w (1)

CZYM JEST ESTYMATOR ORAZ PROCES ESTYMACJI?

CZYM JEST ESTYMATOR ORAZ PROCES ESTYMACJI?

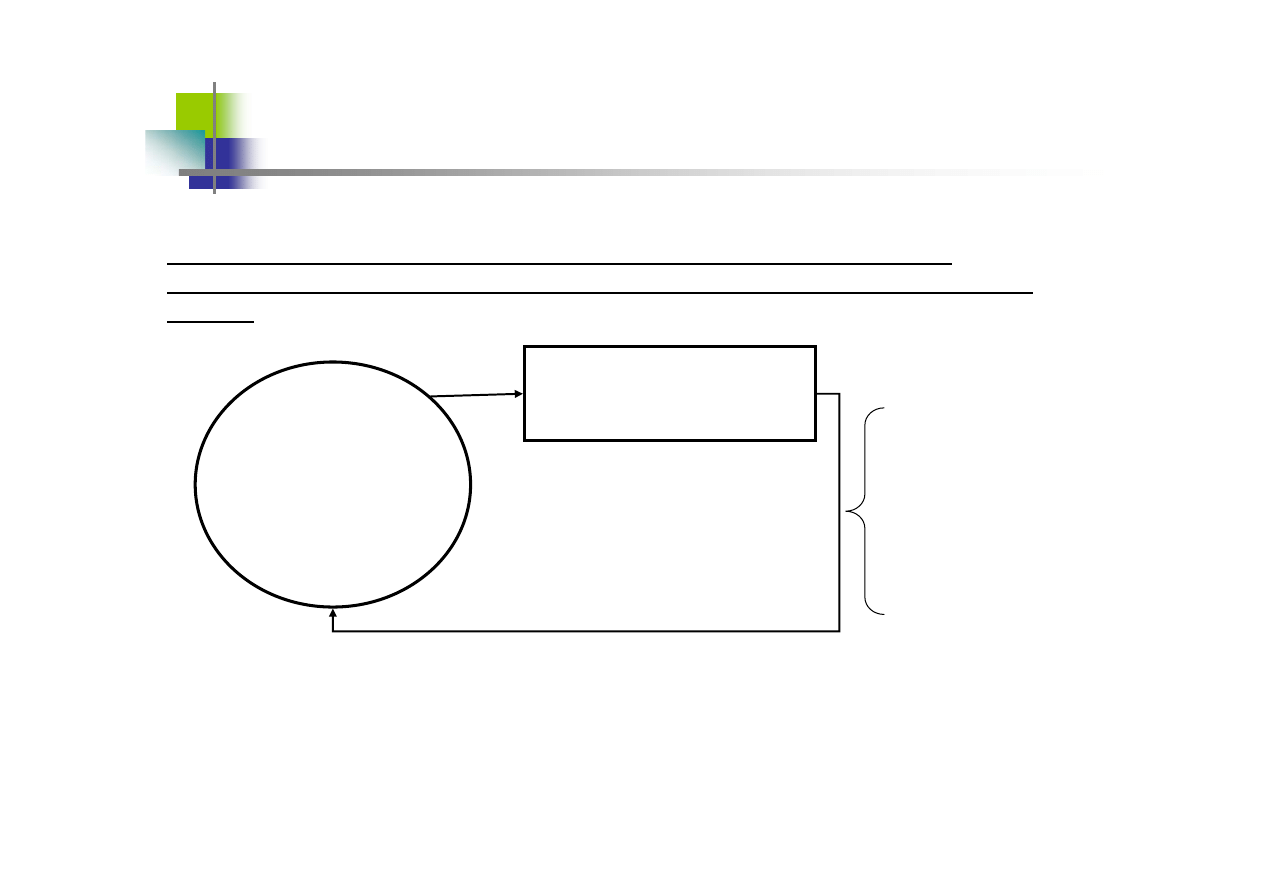
Chcemy

wnioskować na

podstawie próby o

charakterystykach

populacyjnych

Estymatorem będzie statystyka z próby która posłuży nam do estymacji (czyli

wnioskowania) o nieznanych charakterystykach populacyjnych.

nie znamy charakterystyk
np.: średniej ani częstości

Populacja

Próba losowa

znamy statystyki z próby
np.: średnią albo częstość

Estymacja jest zbiorem metod szacowania wartości pewnych nieznanych
parametrów cechy statystycznej (bądź jej postaci funkcyjnej) na podstawie próby
losowej.

2

JAKIE RODZAJE ESTYMACJI I ESTYMATOR

JAKIE RODZAJE ESTYMACJI I ESTYMATOR

Ó

Ó

W MO

W MO

Ż

Ż

EMY WYR

EMY WYR

Ó

Ó

Ż

Ż

NI

NI

Ć

Ć

?

?

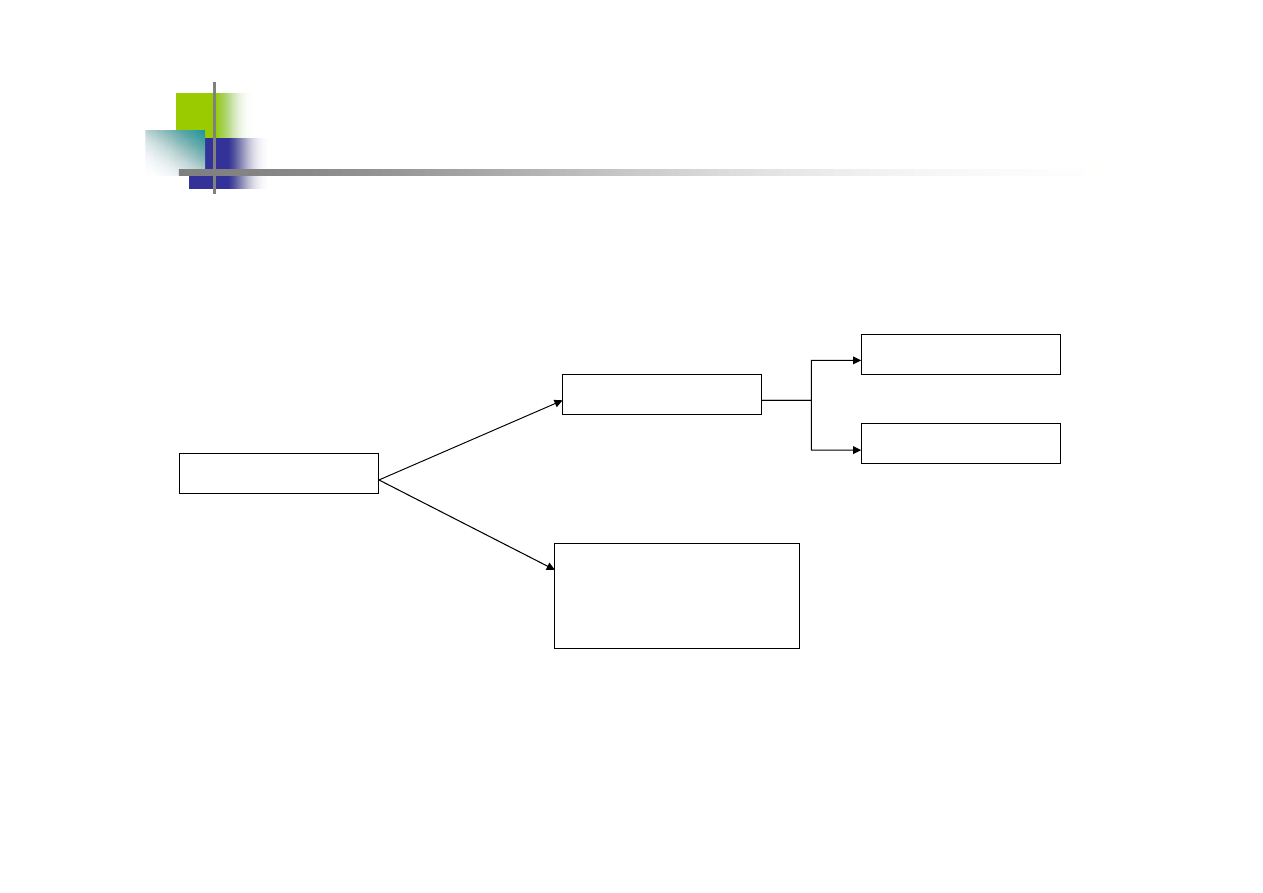
Estymacja

Parametryczna

Nieparametryczna

Dotyczy rozkładu

zmiennej

punktowa

przedziałowa

Podstawy estymacji: poj

Podstawy estymacji: poj

ę

ę

cie i podstawowe w

cie i podstawowe w

ł

ł

asno

asno

ś

ś

ci

ci

estymator

estymator

ó

ó

w (2)

w (2)

My zajmiemy się jedynie estymacją punktową oraz

przedziałową średniej oraz częstości

3

Θ – szacowany parametr populacyjny

T

n

– estymator

t

n

– ocena parametru Θ za pomocą estymatora T

n

Ponieważ szacunku dokonujemy na podstawie próby losowej istnieje możliwość
popełnienia błędu. Jest to różnica między estymatorem a wartością parametru:

d

n

T

=

Θ

−

Konkretna wartość jaką przyjmuje estymator (a więc wartość statystyki z próby) dla
danej próby losowej nazywamy oceną parametru (t

n

).

Taka ocena parametru jest więc punktowym oszacowaniem nieznanego parametru
populacyjnego.

Podstawy estymacji: poj

Podstawy estymacji: poj

ę

ę

cie i podstawowe w

cie i podstawowe w

ł

ł

asno

asno

ś

ś

ci

ci

estymator

estymator

ó

ó

w (3)

w (3)

PODSTAWOWE OZNACZENIA

PODSTAWOWE OZNACZENIA

4

Nieznany parametr Θ

Wybieramy estymator T

n

realizacją w próbie losowej jest

t

n

Ocena (

t

n

) parametru Θ za pomocą estymatora T

n

pochodzi z próby losowej:

stąd estymator jest zmienną losową → patrz: rozkłady statystyk z próby

d

n

T

=

Θ

−

Możemy
popełnić błąd

Na podstawie oceny - t

n

- dokonujemy estymacji punktowej lub przedziałowej

Podstawy estymacji: poj

Podstawy estymacji: poj

ę

ę

cie i podstawowe w

cie i podstawowe w

ł

ł

asno

asno

ś

ś

ci

ci

estymator

estymator

ó

ó

w (4)

w (4)

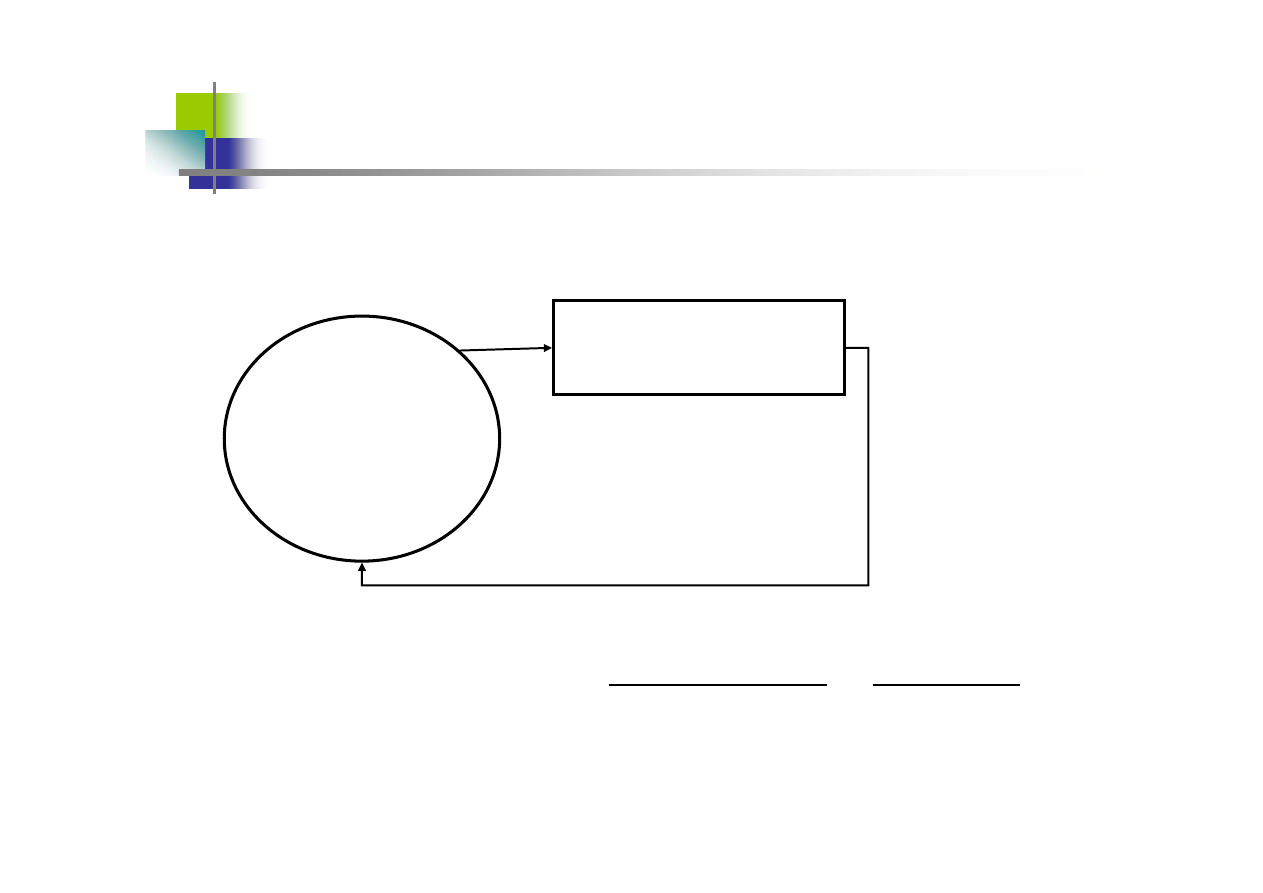
nie znamy charakterystyk
np.: średniej ani częstości

Populacja

Próba losowa

znamy statystyki z próby
np.: średnią albo częstość

5

JAKI ESTYMATOR B

JAKI ESTYMATOR B

Ę

Ę

DZIE

DZIE

„

„

DOBRYM

DOBRYM

”

”

ESTYMATOREM?

ESTYMATOREM?

W

W

Ł

Ł

ASNO

ASNO

Ś

Ś

CI ESTYMATOR

CI ESTYMATOR

Ó

Ó

W.

W.

Bior

Bior

ą

ą

c pod uwag

c pod uwag

ę

ę

te kryteria najlepszymi punktowymi estymatorami

te kryteria najlepszymi punktowymi estymatorami

ś

ś

redniej i cz

redniej i cz

ę

ę

sto

sto

ś

ś

ci populacyjnej b

ci populacyjnej b

ę

ę

d

d

ą

ą

ś

ś

rednia i cz

rednia i cz

ę

ę

sto

sto

ść

ść

z pr

z pr

ó

ó

by.

by.

Jakość estymatora punktowego możemy również ocenić za pomocą:

• Odchylenia standardowego estymatora D(T

n

) – jest to średni błąd szacunku

• Błędu względnego estymatora określanego jako

n

n

n

T

T

D

T

V

)

(

)

(

^

^

=

Obciążenie estymatora:

estymator jest nieobciążony jeśli zachodzi

: E(Tn)=Θ

Efektywność estymatora:

Z dwóch estymatorów efektywniejszy jest ten którego

wariancja jest mniejsza. Mniejsze prawdopodobieństwo uzyskania w próbie
losowej wartości bardzo odbiegających od parametru Θ

Zgodność estymatora:

estymator jest zgodny jeśli zachodzi:

(

)

1

lim

=

<

Θ

−

∞

→

ε

n

n

T

P

Podstawy estymacji: poj

Podstawy estymacji: poj

ę

ę

cie i podstawowe w

cie i podstawowe w

ł

ł

asno

asno

ś

ś

ci

ci

estymator

estymator

ó

ó

w (4)

w (4)

6

Zagadnienie estymacji przedzia

Zagadnienie estymacji przedzia

ł

ł

owej

owej

ś

ś

redniej i

redniej i

cz

cz

ę

ę

sto

sto

ś

ś

ci

ci

¾

Punktowa ocena parametru za pomocą estymatora może być obciążona błędem lub
całkowicie nietrafna: wynika to z losowości próby oraz z faktu że w przypadku cech
ciągłych prawdopodobieństwo, że estymator przyjmie wartość szacowanego
parametru jest równe zero.

¾

Dlatego też stosujemy tzw. estymację przedziałową,

→

konstrukcja przedziału

liczbowego (tzw. przedziału ufności), który z założonym prawdopodobieństwem
pokrywa wartość szacowanego parametru.

¾

W przypadku estymacji punktowej otrzymujemy jedną liczbę a w przypadku
estymacji przedziałowej otrzymujemy przedział liczbowy.

¾

Dzięki estymacji przedziałowej możemy ocenić jak często uznanie za wartość
parametru konkretnej liczby z proponowanego przedziału jest oszacowaniem
prawidłowym.

¾

Częstość oszacowań prawidłowych zwana jest współczynnikiem ufności i
oznaczana jako 1-α. Podkreśla to, że zależy nam na jak największej liczbie
oszacowań prawidłowych i na małej liczbie oszacowań nieprawidłowych (α).
Zazwyczaj α to mała liczba np.: 0,05 lub 0,01.

7

Jak konstruujemy przedzia

Jak konstruujemy przedzia

ł

ł

ufno

ufno

ś

ś

ci?

ci?

Zaczynamy od oceny punktowej parametru czyli T

n

Znając błąd standardowy estymatora oraz zakładając że jego rozkład
jest normalny oraz że jest on nieobciążony, to wówczas 68% wartość jakie
może on przyjmować należy do przedziału:

Czyli z prawdopodobieństwem 0,68 otrzymujemy takie oceny parametru
które należą do tego przedziału. Przedział ten będzie miał krańce o
wartościach:

Ponieważ punktowa ocena parametru jak i jego błąd standardowy pochodzą z
realizacji próby losowej za każdym razem możemy otrzymać inną wartość
krańca przedziału jednak zawsze przedziały te będą zawierały oszacowany
parametr Θ

)

(

ˆ

n

T

D

>

−

Θ

−

Θ

<

)

(

ˆ

;

)

(

ˆ

n

n

T

D

T

D

>

+

−

<

)

(

ˆ

;

)

(

ˆ

n

n

n

n

T

D

t

T

D

t

8

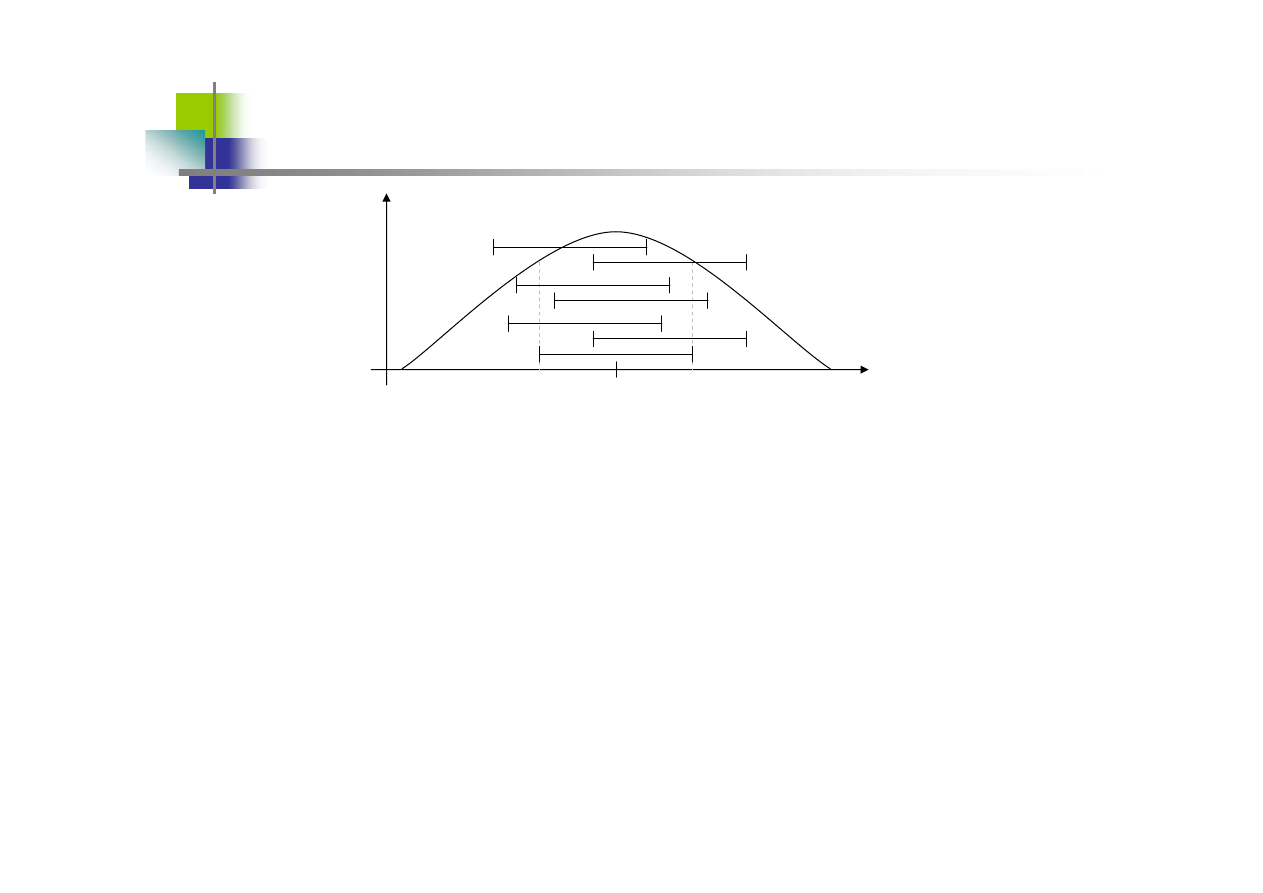
f(t

n

)

t

n

D(T

n

)-Θ E(T

n

)=Θ D(T

n

)+Θ

Dysponując jedynie tymi przedziałami nie możemy jednoznacznie wskazać gdzie
znajduje się szacowany parametr. Możemy jedynie powiedzieć, że szacowany
parametr będzie zawierał się w przedziale z określonym prawdopodobieństwem

(

)

68

,

0

)

(

ˆ

)

(

ˆ

=

+

<

Θ

<

−

n

n

n

n

T

D

t

T

D

t

P

Można powiedzieć że 68 na 100 skonstruowanych przedziałów będzie zawierało
szacowany parametr. Jednocześnie częstość błędnych oszacowań wynosi 0,32.

Chcielibyśmy mieć więcej oszacowań prawidłowych. Możemy to zrobić zwiększając
rozpiętość przedziału do dwukrotnego lub trzykrotnego błędu średniego. Ogólnie
możemy zwiększyć tę rozpiętość do u

α

-krotnego błędu średniego

Jak konstruujemy przedzia

Jak konstruujemy przedzia

ł

ł

ufno

ufno

ś

ś

ci? (2)

ci? (2)

9

Wtedy: rośnie częstość oszacowań prawidłowych oznaczana przez 1-α natomiast
zacznie maleć częstość oszacowań nieprawidłowych oznaczona jako α.

Jeśli estymator ma rozkład normalny to związek poziomu ufności ze zmienną
losową U opisującą krotność odchylenia standardowego estymatora jaką należy
brać pod uwagę konstruując przedział jest następujący:

(

)

α

α

−

=

≤

1

U

P

Gdy → P=0,68

1

≤

U

Gdy → P=0,95

2

≤

U

Gdy → P=0,99

3

≤

U

>

+

−

<

)

(

;

)

(

^

n

^

n

n

n

T

D

t

T

D

t

>

+

−

<

)

(

2

;

)

(

2

^

n

^

n

n

n

T

D

t

T

D

t

>

+

−

<

)

(

3

;

)

(

3

^

n

^

n

n

n

T

D

t

T

D

t

Jak konstruujemy przedzia

Jak konstruujemy przedzia

ł

ł

ufno

ufno

ś

ś

ci? (3)

ci? (3)

10

α

α

α

−

=













∗

+

<

Θ

<

∗

−

1

)

(

)

(

n

n

n

n

T

D

u

t

T

D

u

t

P

Ogólnie konstrukcję przedziału ufności możemy zapisać następująco:

Krańce przedziału są losowe gdyż zmienia się wartość oceny punktowej
parametru. Jednak zawsze, z prawdopodobieństwem 1-α, pokryje on szukaną
wartość parametru.

Przy ustalonej liczebności próby, przyjęte prawdopodobieństwo 1-α rozstrzyga o
tym jaka będzie rozpiętość przedziału.

Im większa częstość poprawnych oszacowań tym większa wymagana krotność
błędu standardowego i szerszy przedział.

Zależność między precyzją a pewnością oszacowania

→

wysoka wiarygodność

ufność nie sprzyja precyzji oszacowania.

Jak konstruujemy przedzia

Jak konstruujemy przedzia

ł

ł

ufno

ufno

ś

ś

ci? (4)

ci? (4)

11

Jak konstruujemy przedzia

Jak konstruujemy przedzia

ł

ł

ufno

ufno

ś

ś

ci? (5)

ci? (5)

12

Dok

Dok

ł

ł

adno

adno

ść

ść

estymacji; zagadnienie minimalnej

estymacji; zagadnienie minimalnej

liczebno

liczebno

ś

ś

ci pr

ci pr

ó

ó

by.

by.

)

(

n

T

D

u

d

∗

=

α

Problem precyzji oszacowania sprowadza się do wyboru między długością
przedziału a częstością trafnych oszacowań:

szerszy przedział

→

większa częstości trafnych oszacowań

→

mała precyzja

wąski przedział

→

niższa częstość trafnych oszacowań

→

większa precyzja

Szerokość

przedziału możemy modyfikować

przez zmiany w wartości

prawdopodobieństwa 1-α

→

to rozwiązanie nas nie interesuje!

Możemy także „manipulować” wielkością próby w celu osiągnięcia założonej
precyzji oszacowania. Precyzja jest mierzona jest za pomocą tzw. błędu
maksymalnego czyli połowy długości przedziału. Błąd ten oznaczany jest jako d:

13

2

2

4

1
d

u

n

α

=

Gdy nie ma przewidywań co do
wartości p za p* przyjmujemy 0,5

Stąd możemy postawić pytanie: Jaka powinna być minimalna liczba obserwacji w
próbie niezbędna do przeprowadzenia wnioskowania o wymaganej precyzji i ustalonej
ufności 1-α?

2

2

2

1

)

(

d

X

D

u

n

α

=

Dla szacowania

średniej

Dla szacowania

częstości

2

2

)

1

(

d

p

p

u

n

∗

∗

−

=

α

Gdy przewidujemy p na
podstawie p*

Dok

Dok

ł

ł

adno

adno

ść

ść

estymacji; zagadnienie minimalnej

estymacji; zagadnienie minimalnej

liczebno

liczebno

ś

ś

ci pr

ci pr

ó

ó

by. (2)

by. (2)

14

Typowe zadania

Typowe zadania

1. Z przygotowanej do sprzedaży partii skrzynek z jabłkami w pewnej hurtowni

wybrano losowo 200 skrzynek jabłek i 146 z nich zakwalifikowano jako I
gatunek. Oszacować punktowo frakcji jabłek I gatunku w całej partii. Wyznaczyć
przedział ufności dla frakcji jabłek I gatunku. Przyjąć 1 -

α = 0,90.

3. Jak liczna powinna być próba by oszacować odsetek pracowników,

awansujących trzykrotnie w karierze zawodowej z maksymalnym błędem 2% ?
Jeśli badanie pilotażowe wskazuje iż spodziewana wielkość kształtuje się w
granicach 15%?

2. Wiadomo, że w przedsiębiorstwie X średni czas losowo wybranych 100 rozmów

międzymiastowych wynosił 10 min. i charakteryzował się zmiennością 40%,
należy ocenić przedziałowo średni czas trwania tej rozmowy. Przyjąć 1-

α = 0,95.