Wszelkie prawa do zada

ń

, plików  i instrukcji s

ą

 zastrze

ż

one, nikt poza prowadz

ą

cymi zaj

ę

cia i studentami IA na AGH 

nie ma prawa ich wykorzystywa

ć

.  A tych co maj

ą

 takie prawa, prosz

ę

, aby nie umieszczali ich w innym miejscu w sieci.  

 

 INTERPOLACJA

to poszukiwanie

wartości pomiędzy więzami

Interpolacja jest zagadnieniem polegającym na znalezieniu funkcji, która na tyle dobrze 

przybliżałaby inną, nieznaną, aby możliwe było wykorzystanie jej  do obliczenia wartości f (x) dla 

dowolnego x

i

 nie będącego X.  

yi=interp1(X,Y,xi,method) interpoluje wartości funkcji w punktach xi

 

X - wektor wartości X danych pomiarowych  
Y - wektor wartości y=f(X) danych pomiarowych  
xi - zwiększona ilość wartości X ( wielkość wektora X < wartości wektora xi)  
yi - wartości interpolowane Y dla punktów xi daną metodą  
method - metoda interpolacji  
method = 'nearest' – metoda przybliżania wartości punktów przy pomocy wartości  
najbliższego punktu  
method = 'linear' - metoda przybliżania wartości punktów przy pomocy linii utworzonej 
pomiędzy dwoma poszczególnymi punktami  
method = 'spline' - metoda przybliżania wartości punktów przy pomocy wielomianu 3-go stopnia 
pomiędzy punktami  
method = 'pchip' or 'cubic' - metoda przybliżania wartości punktów przy pomocy wielomianu 3-
go stopnia Hermita

 

 

Zad 1. Dla następujących 

danych X=0:1:10; Y=sin(X) oraz xi=0:0.25:10  w jednym oknie  

i na 4 wykresach proszę narysować (za pomocą czerwonej *) wartości pomiaru i wynik interpolacji  

( za pomocą ciągłej linii).  

W tytule proszę podać metodę interpolacji.

 

 

 

0

1

2

3

4

5

6

7

8

9

10

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

metoda:nearest

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Spline 

yi = spline(X,Y,xi) 

w wywołaniu mamy  

wektor węzłów (muszą być uporządkowane rosnąco), wektor wartości funkcji interpolowanej  

w węzłach oraz wektor wartości zmiennej niezależnej, dla których ma być obliczona funkcja 

interpolująca.  

wynikiem jest 

wektor, którego kolejnymi współrzędnymi są wartości funkcji interpolującej 

w wyspecyfikowanych punktach. W przypadku funkcji spline jest to funkcja 

sklejana sześcienna. 

  

pchip- interpolacja wielomianowa Hermite’a 

yi = pchip(X,Y,xi) 

 

Zad 2. Proszę wyliczyć 5 wartości z krokiem co 1 dla dowolnej funkcji wykładniczej, logarytmicznej  

i dla dowolnego wielomianu. Proszę dla każdej funkcji osobno porównać na wykresie interpolację za 

pomocą funkcji 

spline

 

interp1(….’spline’) i pchip. Proszę dołożyć legendę. 

 

 
 
Funkcje interp2, interpn 
to funkcje interpolujące w 2 wymiarach. 

Zad 3. Za pomocą wcześniej poznanych metod interpolacji (

nearest

 itp.) wykorzystując funkcje 

interpolujące w dwóch wymiarach proszę przeprowadzić interpolację obrazka, który składa się  
z wylosowanych wartości pixeli. 

Prosz

ę

 sobie przypomnie

ć

 co oznaczaj

ą

 poszczególne 

polecenia i prosz

ę

 narysowa

ć

 poni

ż

sze obrazy w przestrzeni 3D. 

 

 
figure(2)

 

 
subplot(2,2,1)

 

S=(3*rand(20,20));

 

imshow(S)

 

colormap 

jet(16)

 

 
 
xi=1:0.1:20;

 

yi=1:0.1:20;

 

[X Y]=meshgrid(xi,yi);

 

S1=interp2(S,X,Y,

'spline'

);

 

subplot 

222

 

imshow(S1)

 

colormap 

jet(16) 

itp…

 

 

 

 

Zad 3A – dodatkowe – jak będziecie mieli czas to proszę do niego wrócić. Proszę interpolować 

dowolnie wybraną przez Państwa funkcję z=f(x,y).  

  

 

aproksymacja wielomianami

 

Aproksymacja to dopasowanie/przybliżenie/ zastępowanie  jednych wielkości drugimi.  

p=polyfit(x,y,r); - to aproksymacja za pomocą wielomianu 
 x, y – serie danych,  
r – zadany stopień, wielomianu przybliżającego 

 

przypomnienie z pierwszych zajęć – funkcja polyval oblicza wartość wielomianu o współczynnikach 

zawartych  w wektorze p ( wektor p uzyskujemy z polyfit) w punktach zawartych w wektorze xi . 

yi = polyval(p,xi);  

Niech poszukiwana jest krzywa opisana równaniem F(x) dla zadanej liczby punktów ( x

i

 , y

i 

). 

Aproksymacja stosowana jest wówczas, gdy ilość zadanych punktów m jest mniejsza od ilości 

nieznanych współczynników n krzywej F(x). Zwykle nie można przeprowadzić krzywej przez wszystkie 

punkty. Poszukiwana jest wówczas najbliższa krzywa w sensie minimum kwadratu błędu:

 

Zad 4. Na jednym wykresie proszę za pomocą wielomianów  o stopniu 0,1,2 ,3,4,5 przybliżyć 

następujące dane X=1:5 y=sin(X). 

 

aproksymacja za pomocą narzędzia
cftool

Zad 5. Proszę aproksymować X=1:5 Y=cos(X) za pomocą narzędzia cftool.  

Uwaga! Zmienne X i Y muszą być w pamięci komputera/ w przestrzeni Matlab’a. 

1.

 

Wstawiamy dane do Data 

 

 

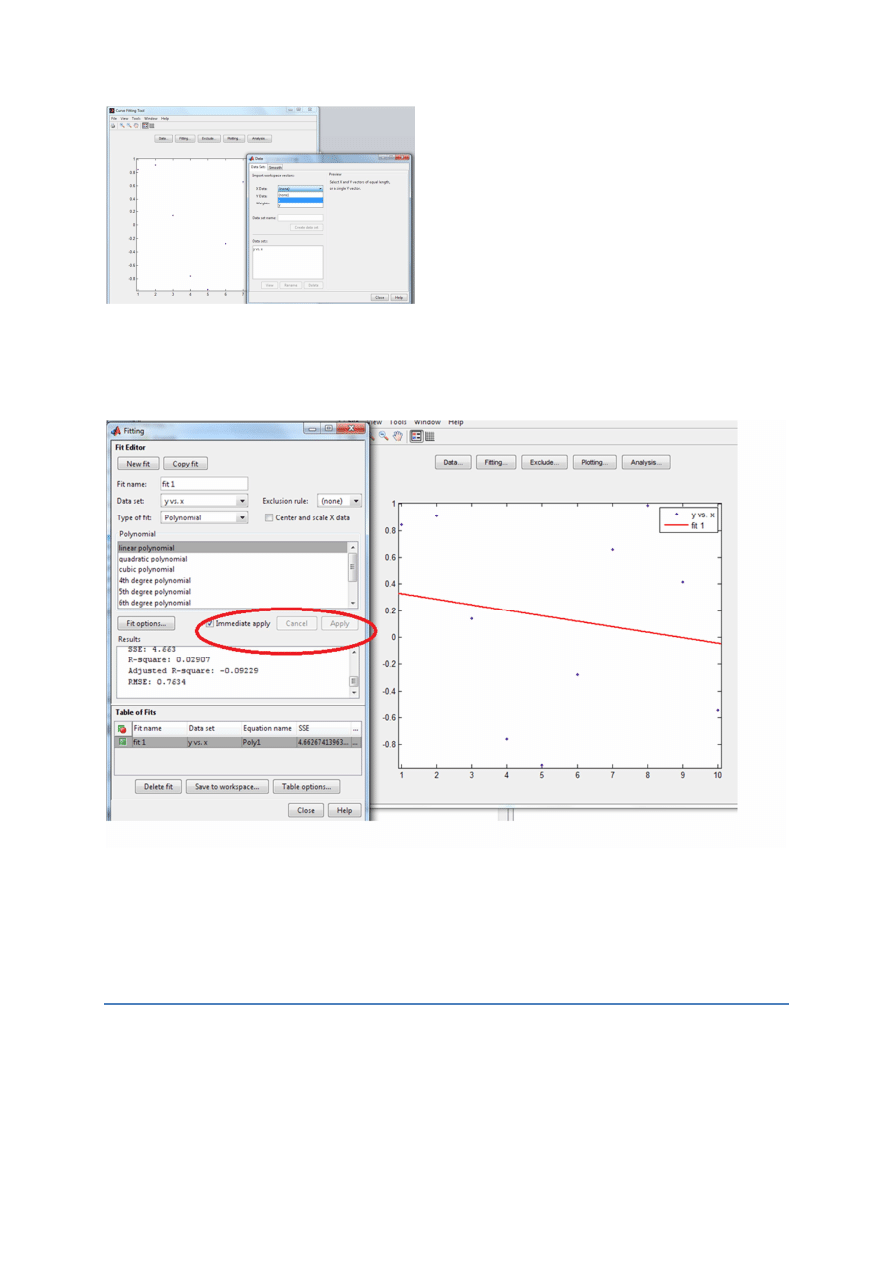
2.

 

Wykorzystując przycisk Fiting poszukujemy funkcji aproksymującej. Wartości współczynników 

wpisane są do okna Result. 

 

3.

 

Zmieniając 

type of fit 

proszę poszukać funkcji, która najlepiej aproksymuje naszą funkcję. 

aproksymacja za pomocą polecenia fit

f=fit(x,y, method) 

zad 6. Niech x=1:5 a  dla y proszę wylosować 5 liczb całkowitych o średniej 4  i odchyleniu 

standardowym 3. 

Proszę wyświetlić wartości jakie zwraca funkcja fit dla 3 dowolnych metod aproksymacji 

wymienionych na stronie: 

http://www.mathworks.com/help/curvefit/list-of-library-models-for-curve-and-surface-fitting.html

 

np. 

f=fit(x,y,’exp1’) itp 

Proszę za pomocą wyliczonych przez funkcję fit wartości narysować wykresy funkcji otrzymanych  

z aproksymacji.  

Wskazówka: 

 dla    General model Exp1: 

       f(x) = a*exp(b*x) % wzór fukcji aproksymującej 

     Coefficients (with 95% confidence bounds): 

       a =       2.593  (-8.487, 13.67) %aby użyć tej wartości należy napisać: f.a 

       b =     -0.9712  (-4.394, 2.452) %aby użyć tej wartości należy napisać: f.b 

jeśli chcemy narysować aproksymowany y to musimy go wyliczyć: 

y_aprosymowany=f.a*exp(f.b*x); 

 

EKSTRAPOLACJA to poszukiwanie
wartości poza zakresem więzów

Ekstrapolacja korzysta z poleceń interpolacji i aproksymacji.  

zad 6. Cd proszę za pomocą interpolacji wielomianem i aproksymacji wybranymi wcześniej funkcjami 

wyliczyć 3  kroki do tyłu ( dla x=-2,-1,0) i trzy kroki do przodu ( dla x=6,7,8). Wyniki proszę przedstawić 

na kolejnym wykresie.