Interpolacja - aproksymacja

Ewa Skubalska-
Rafajłowicz
Wrocław 2009

Interpolacja

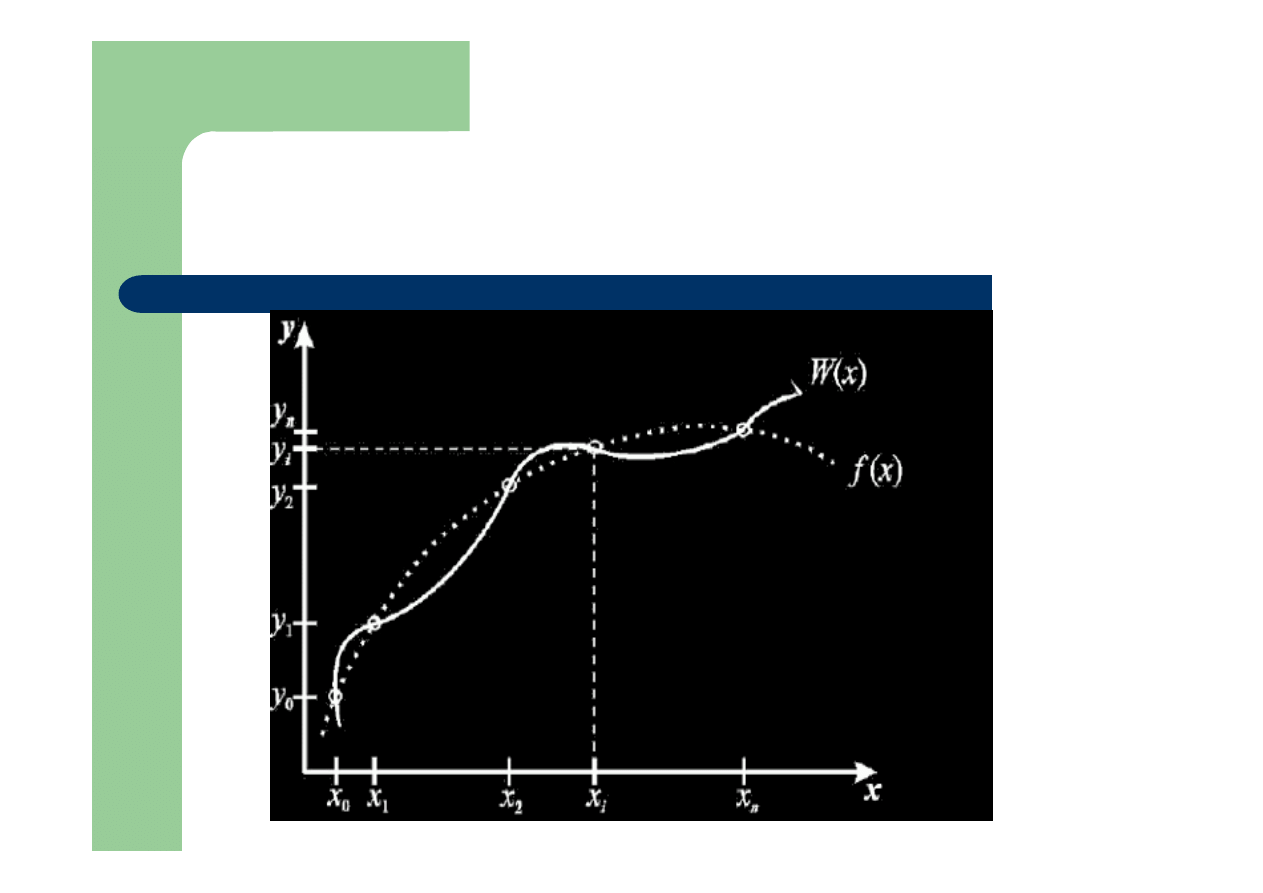
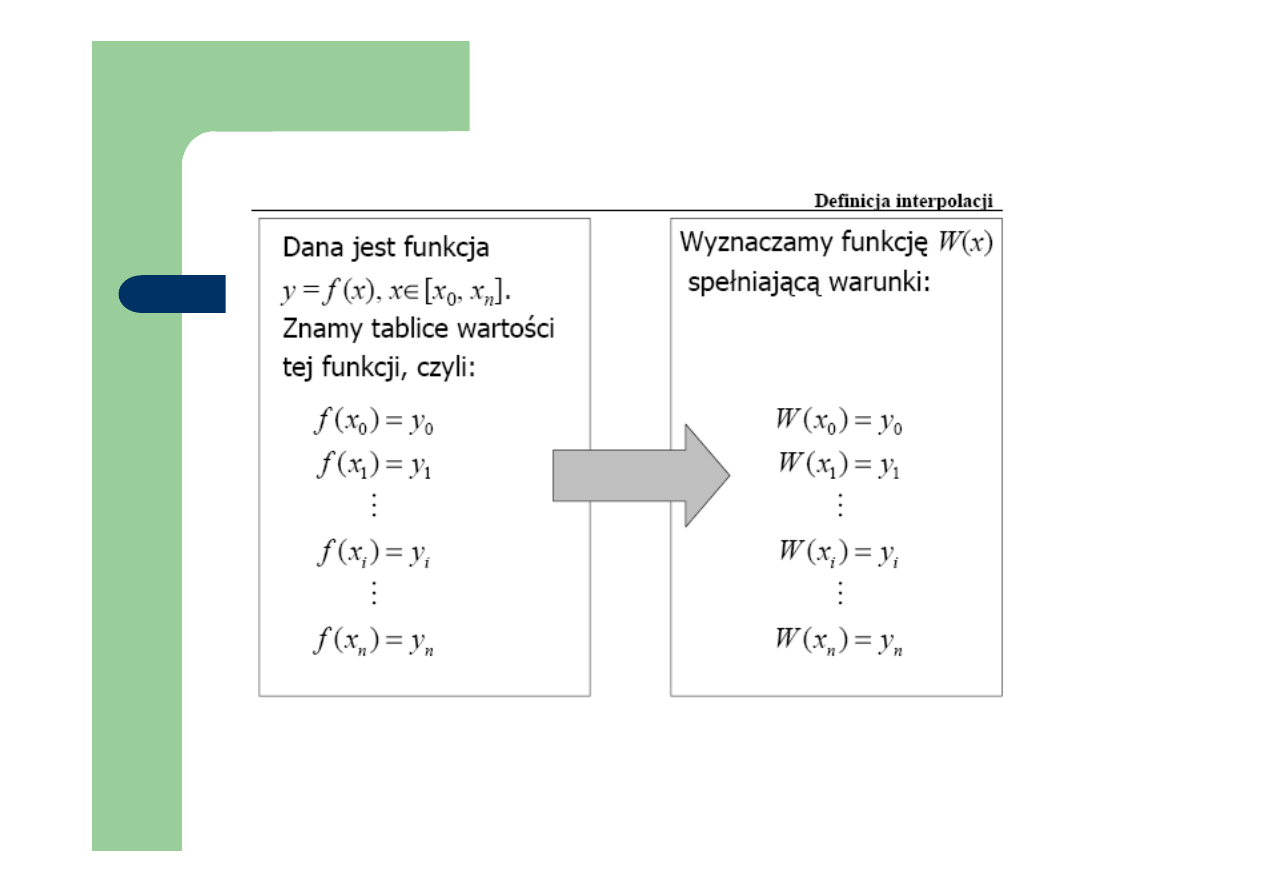
Interpolacja:

™zachowuje bowiem  wartości w wybranych punktach 

(zwanych węzłami) pomiędzy funkcją, którą chcemy przybliżyć

(interpolowaną), a funkcją przybliżającą (interpolującą) 

™Zazwyczaj zależy nam dodatkowo, aby w punktach które nie są
węzłami przybliżenie było również jak najlepsze. Jako funkcje 
interpolujące najczęściej wykorzystuje się wielomiany algebraiczne, 
trygonometryczne lub funkcje wymierne. 

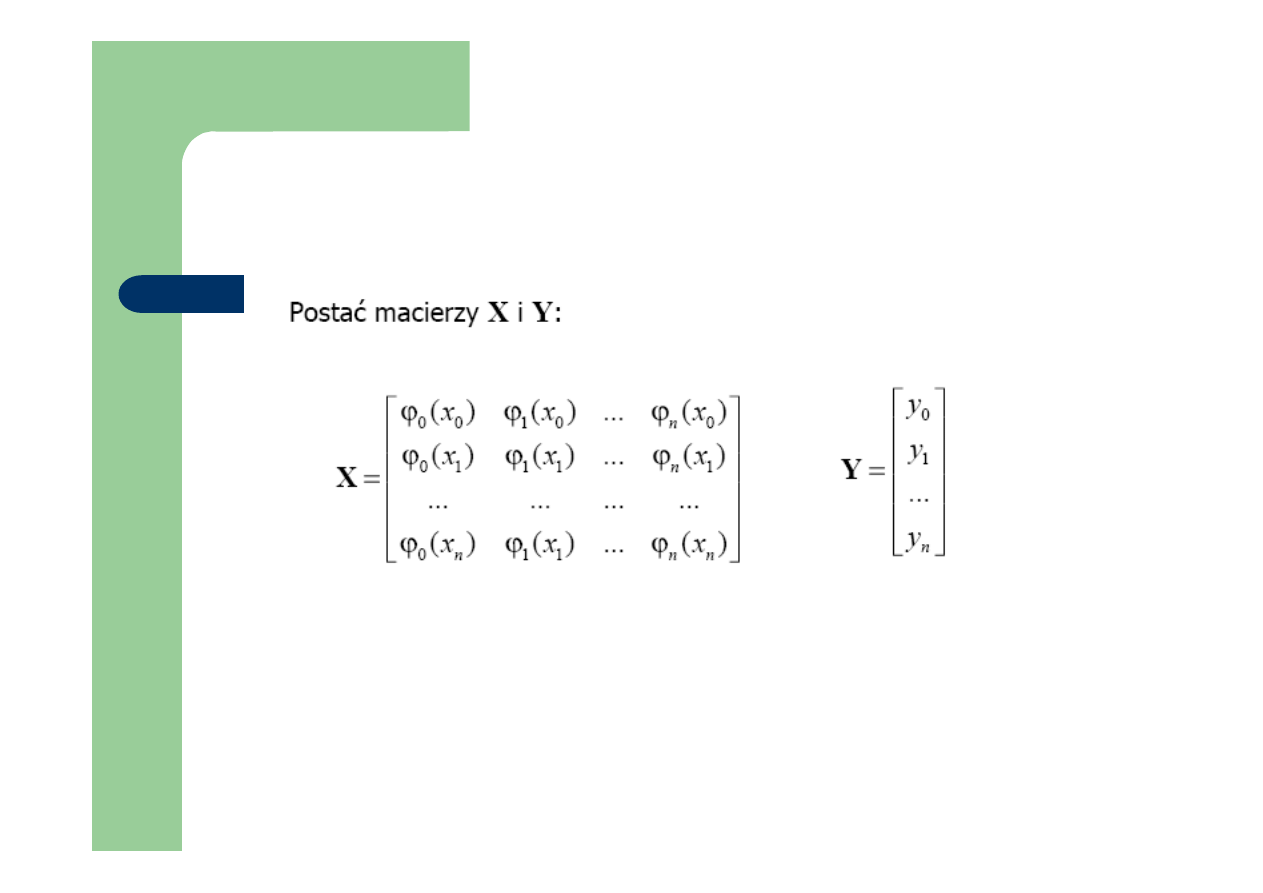
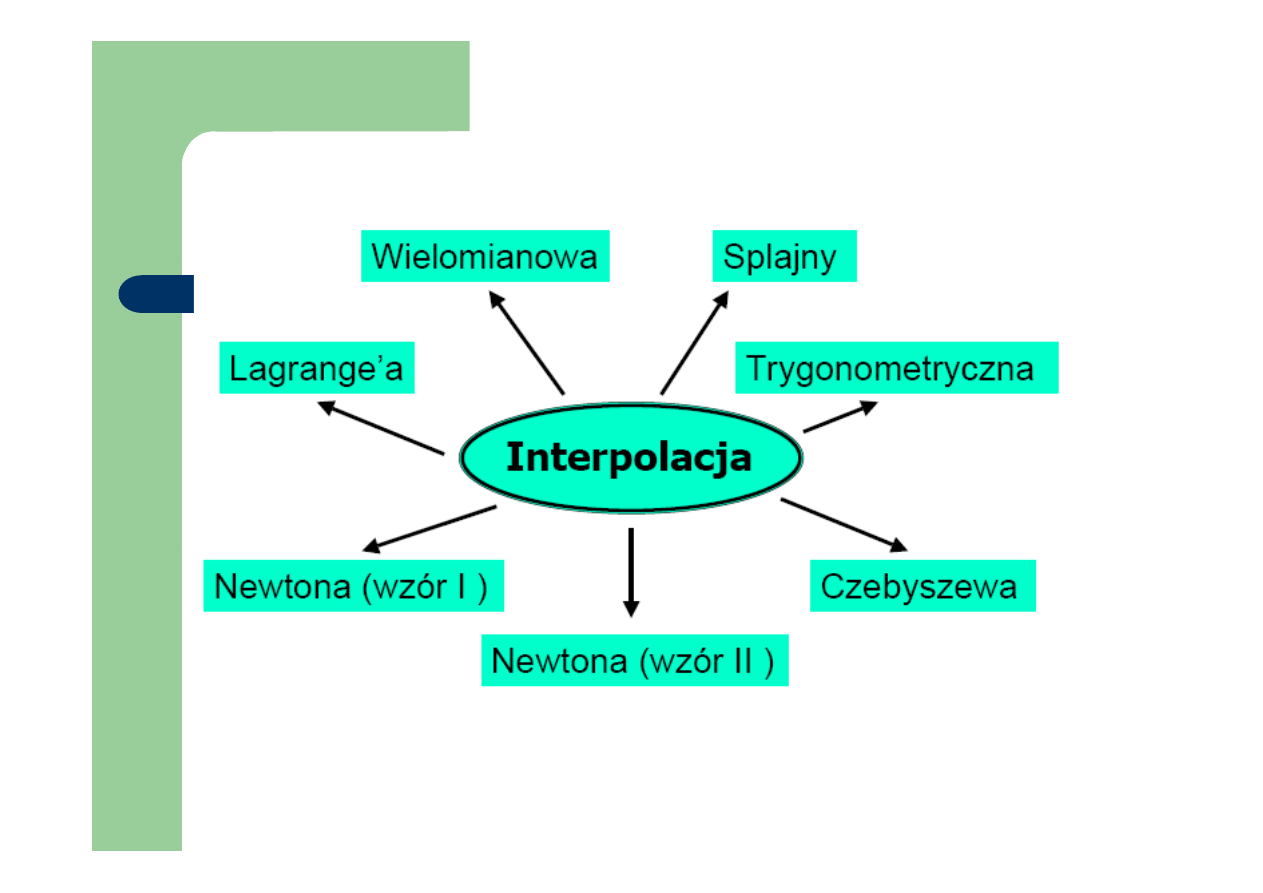
Interpolacja wielomianowa

Interpolacja

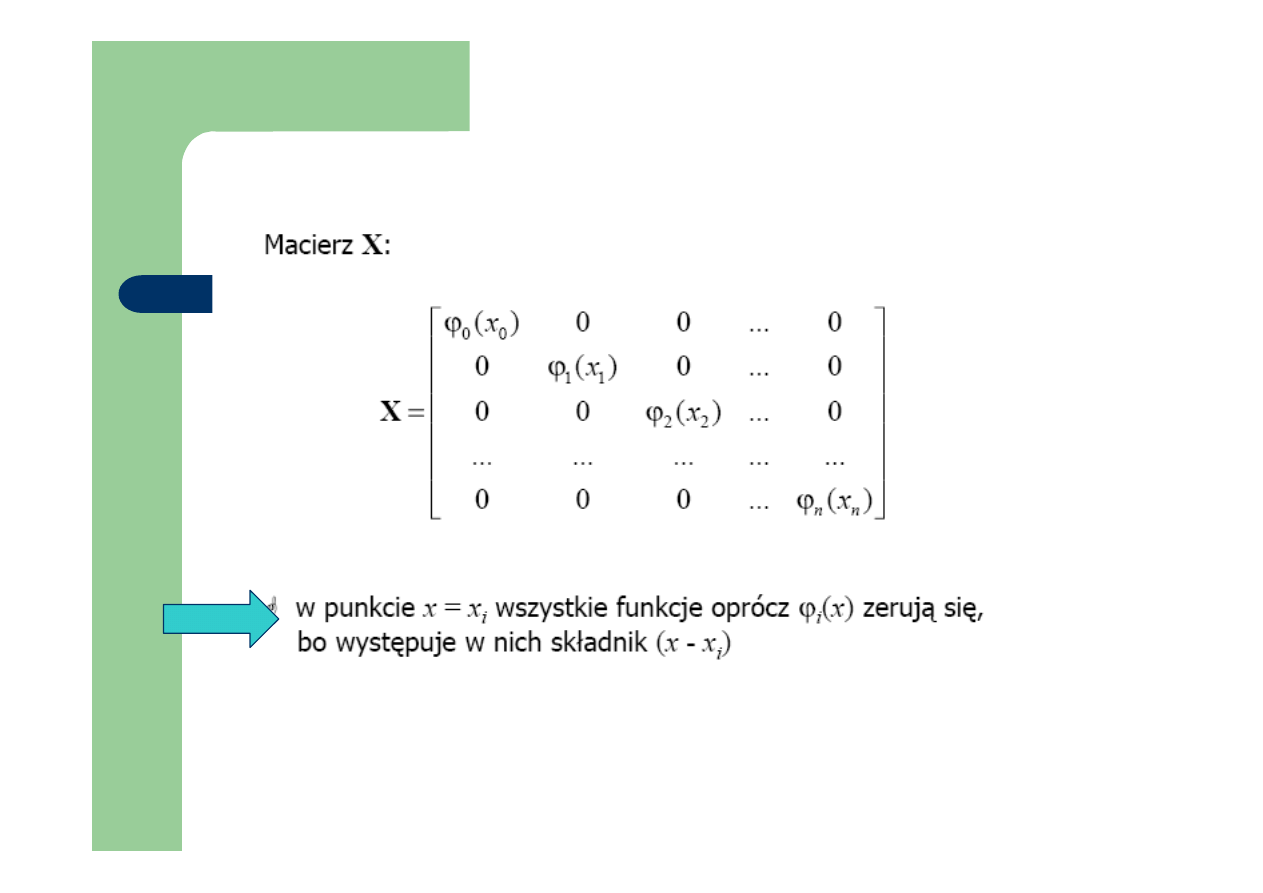
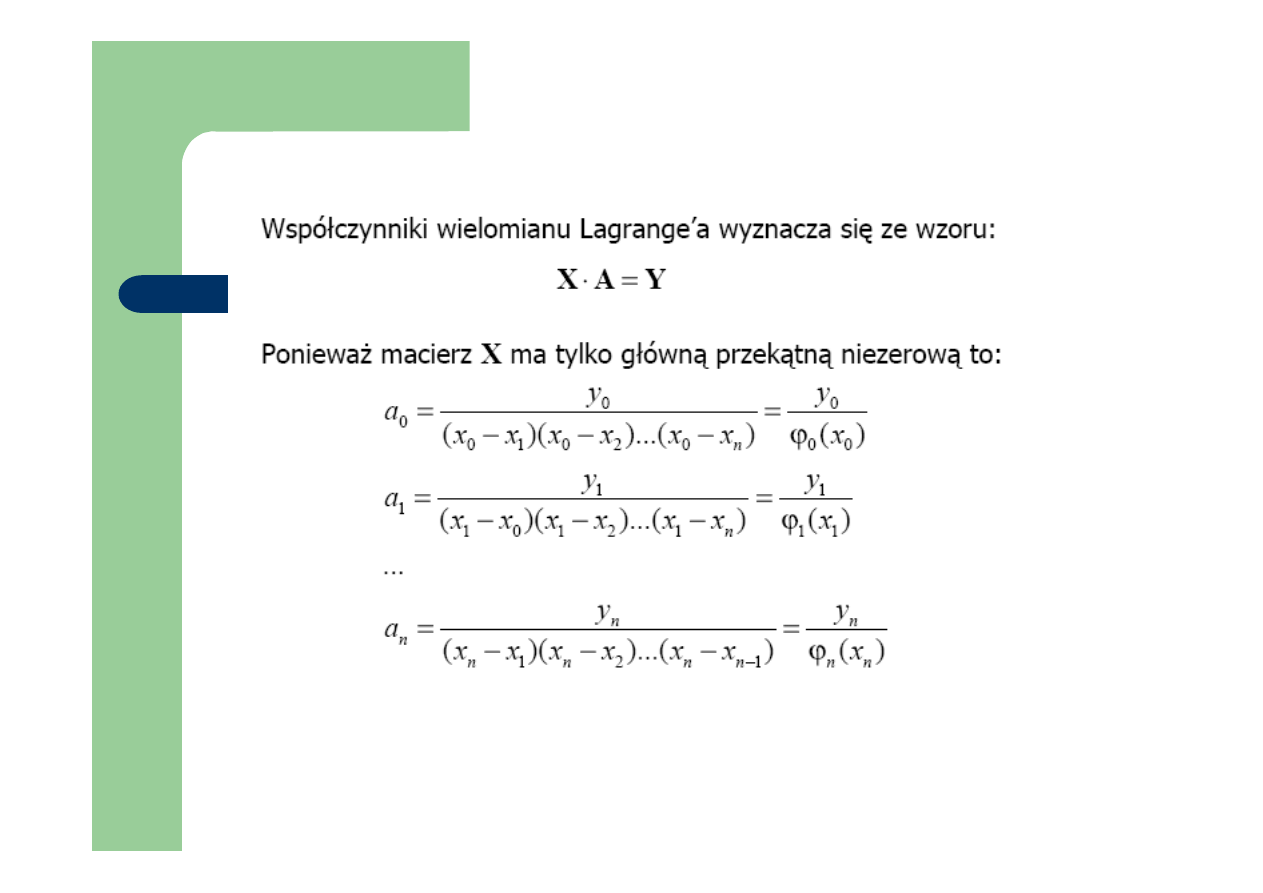
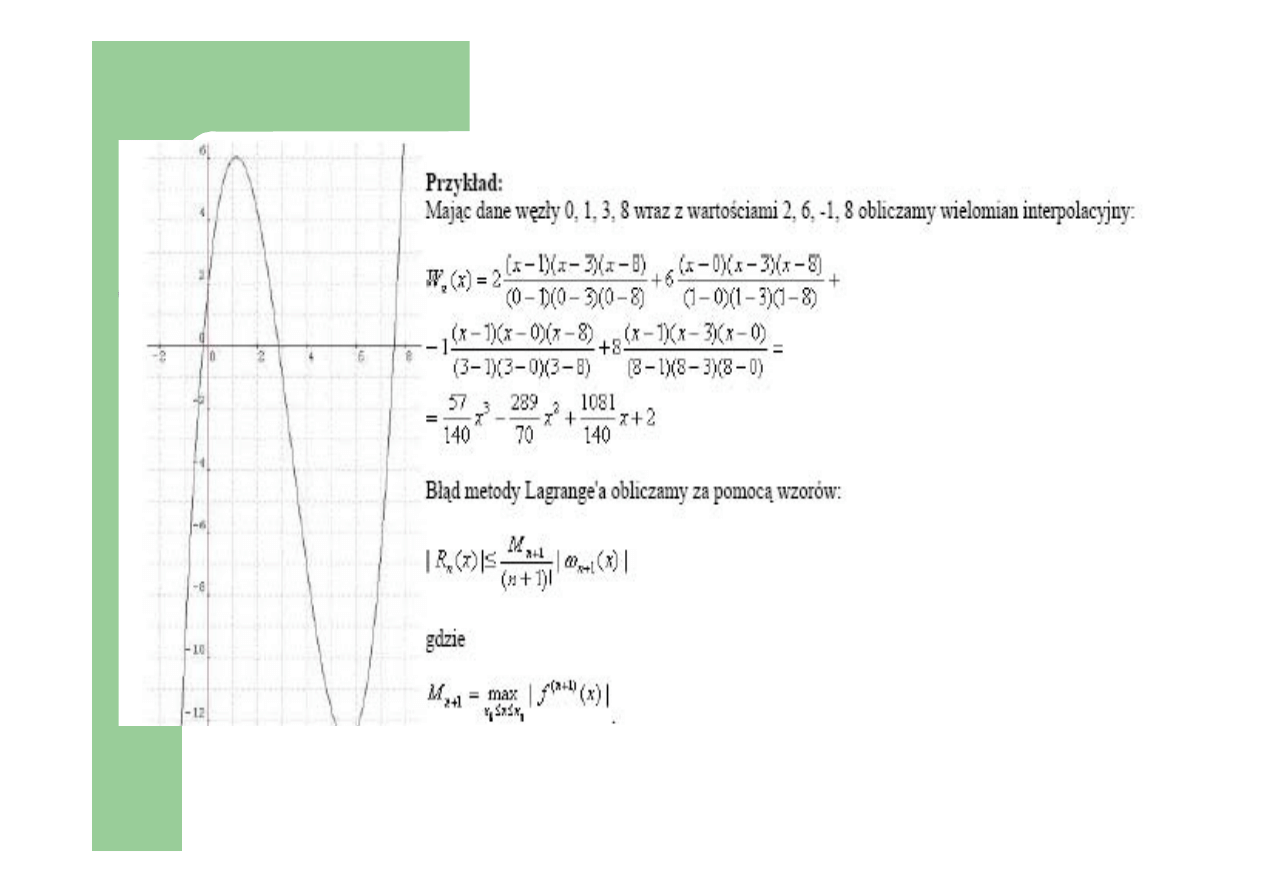
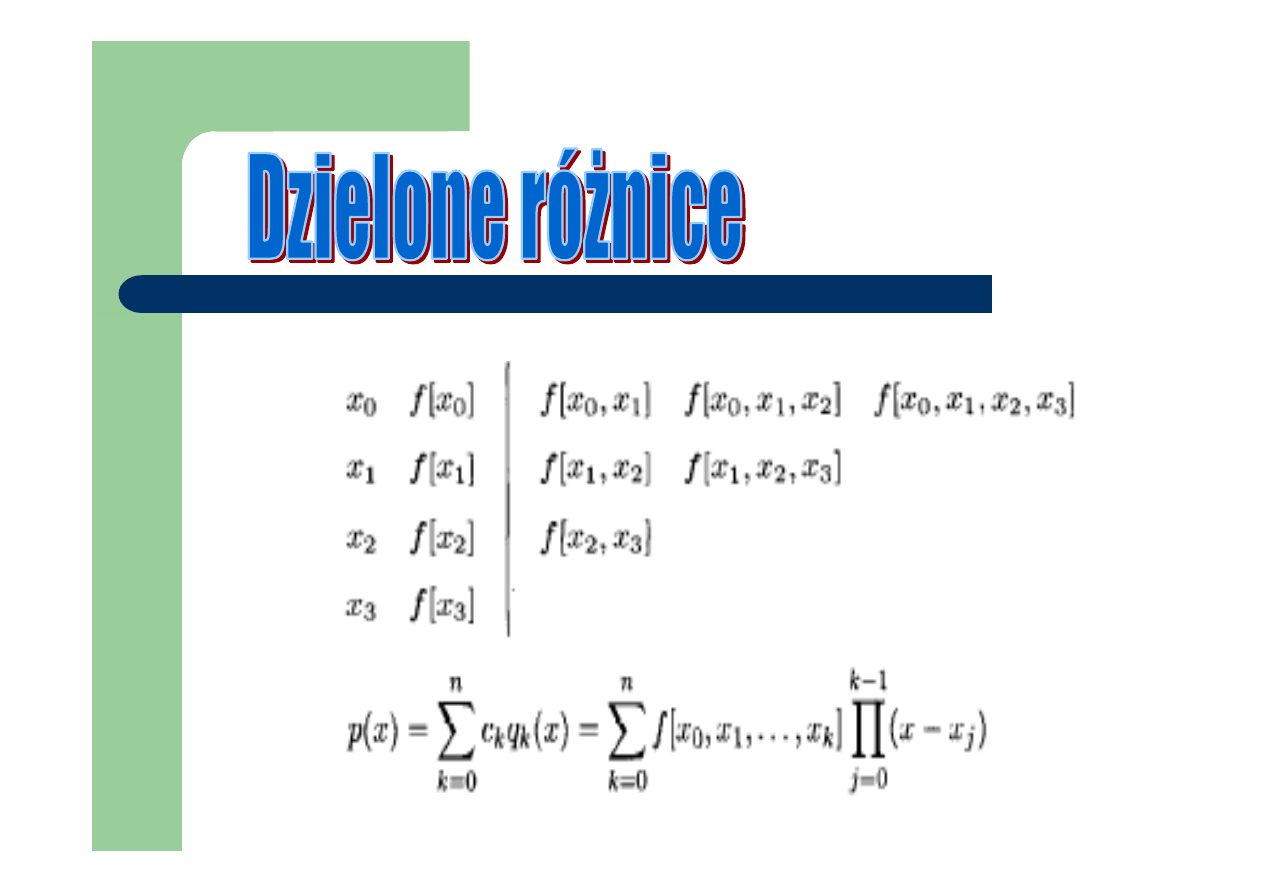
Argumenty równoodległe

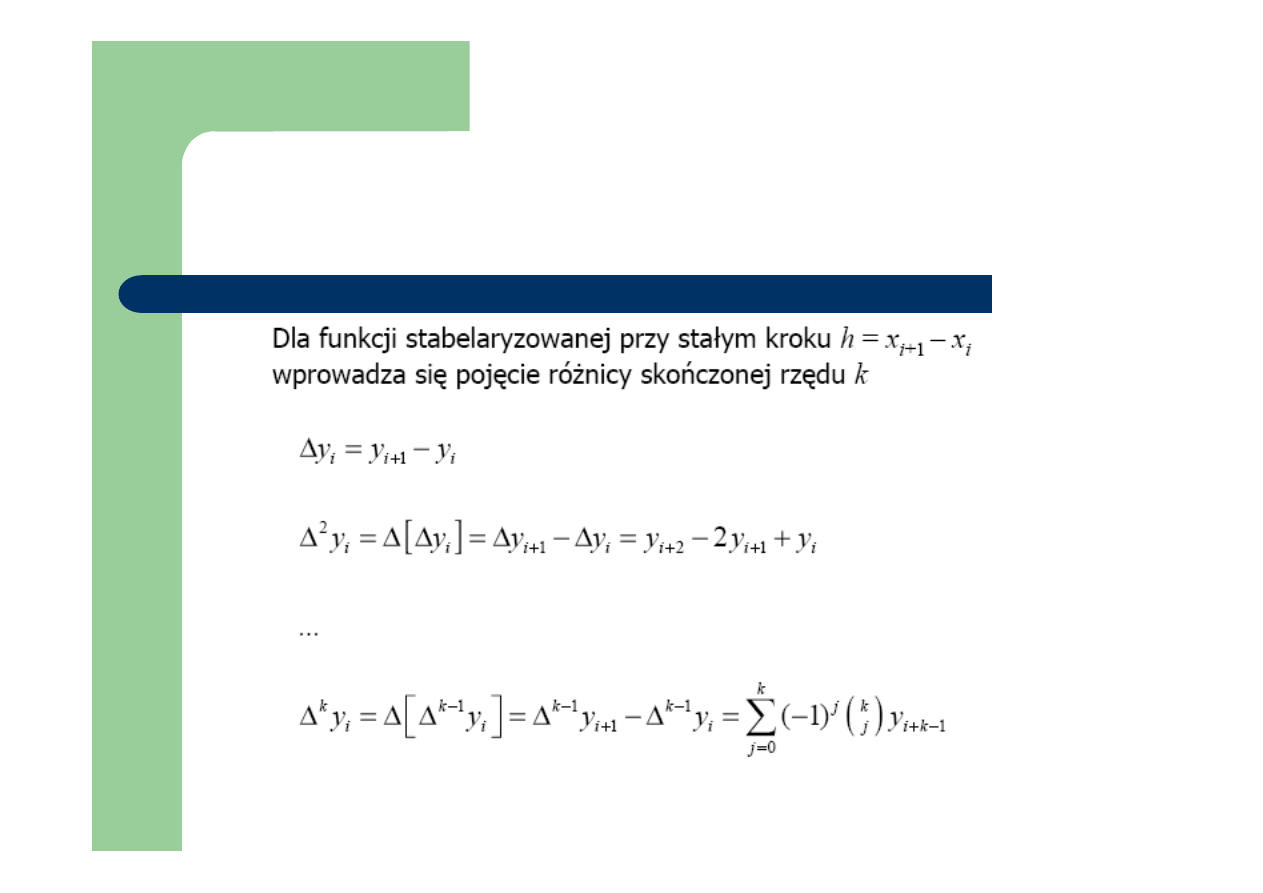
Różnice skończone

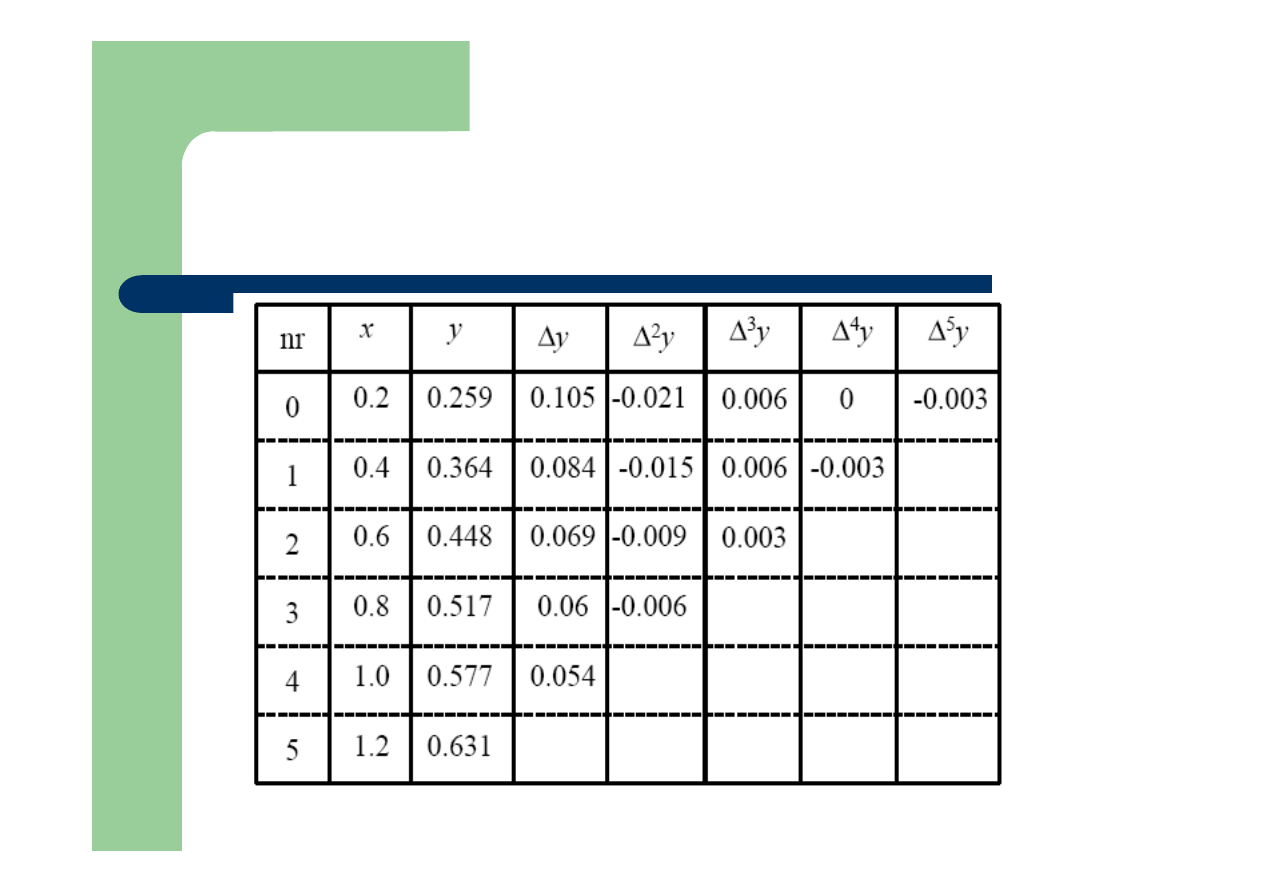
Przykład:

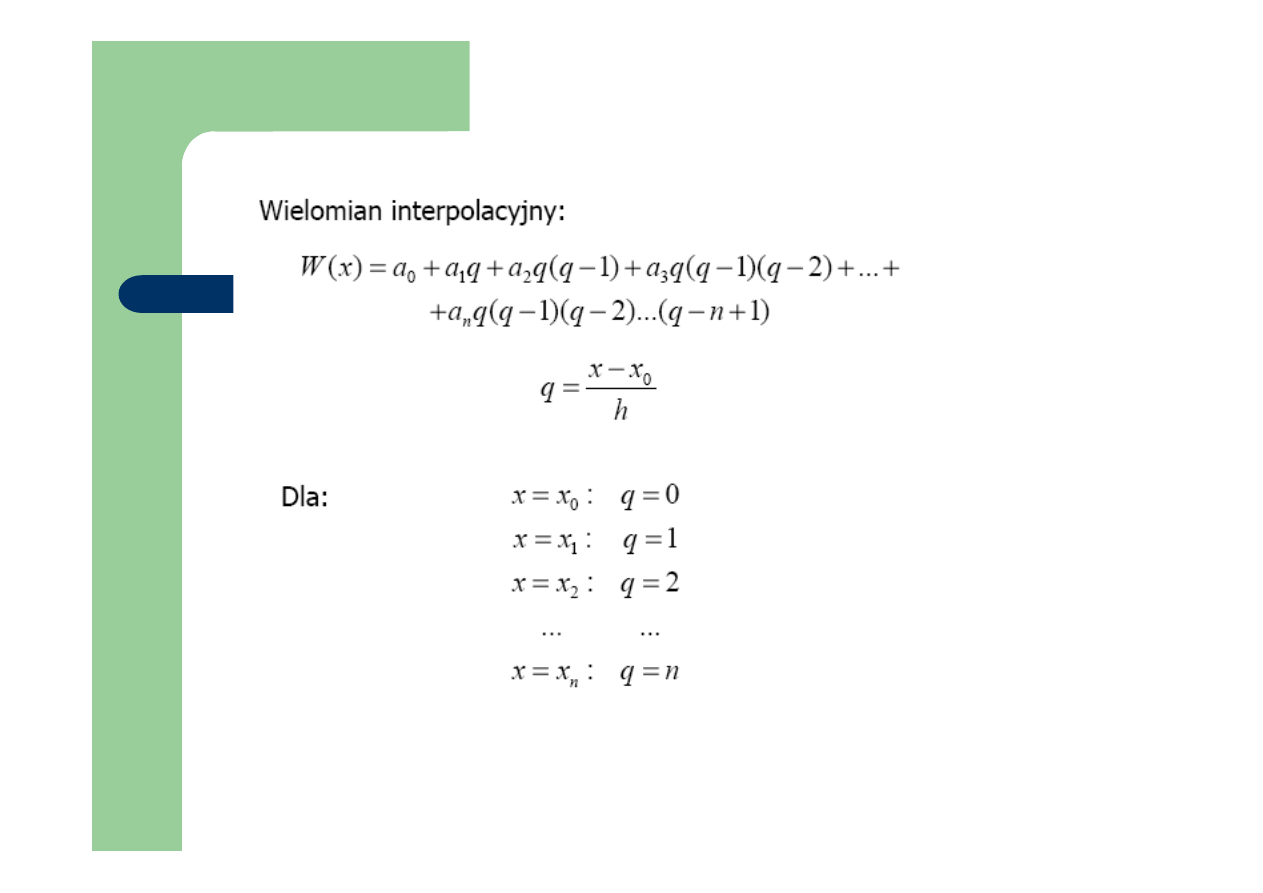
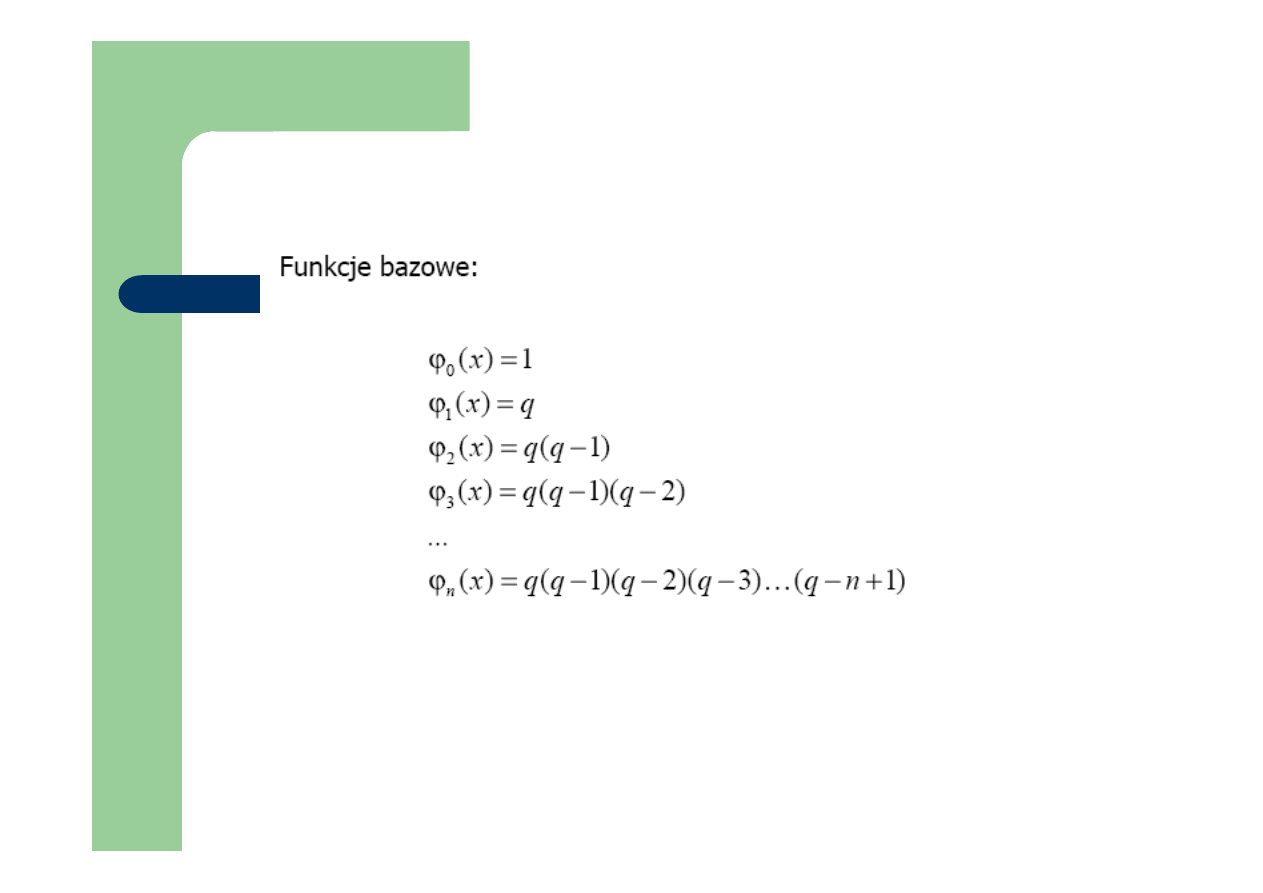
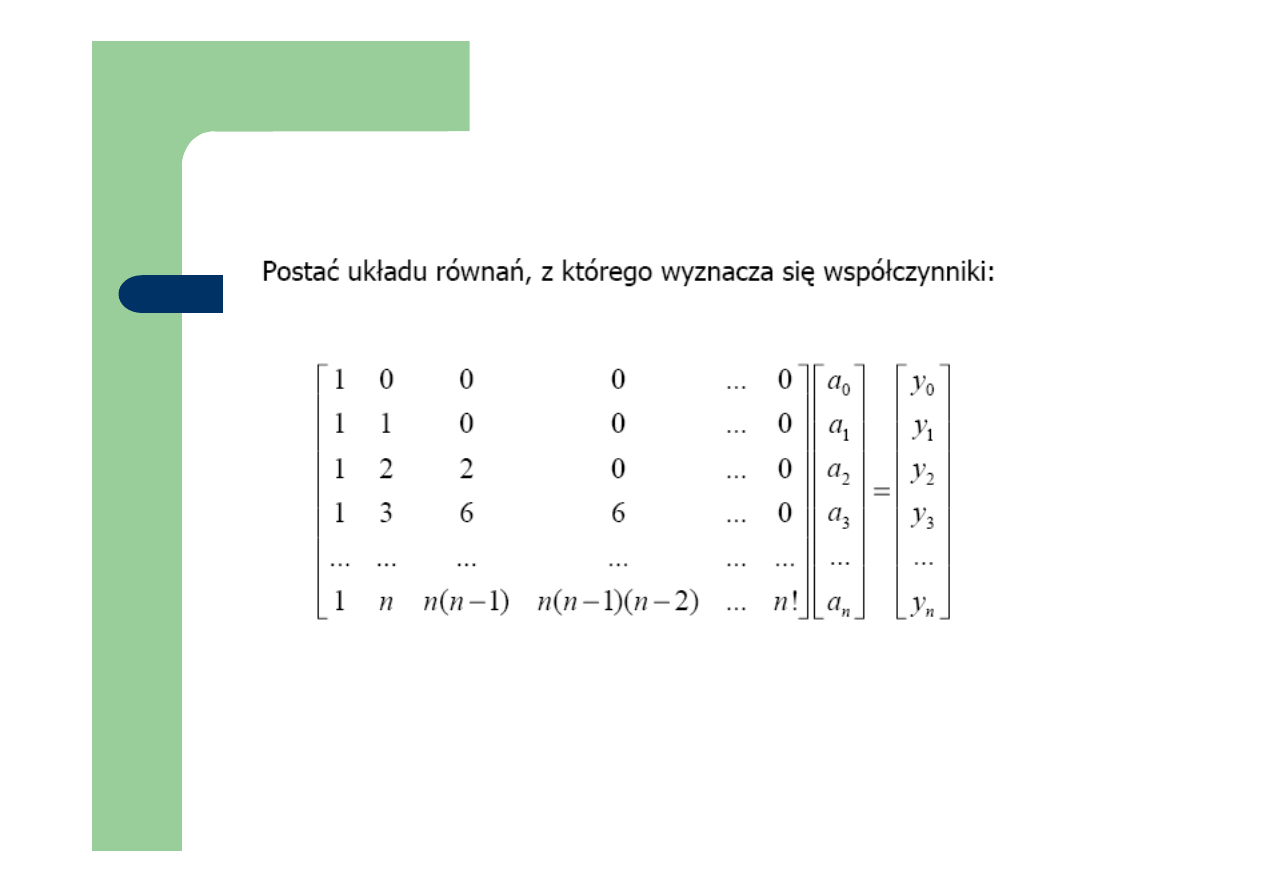
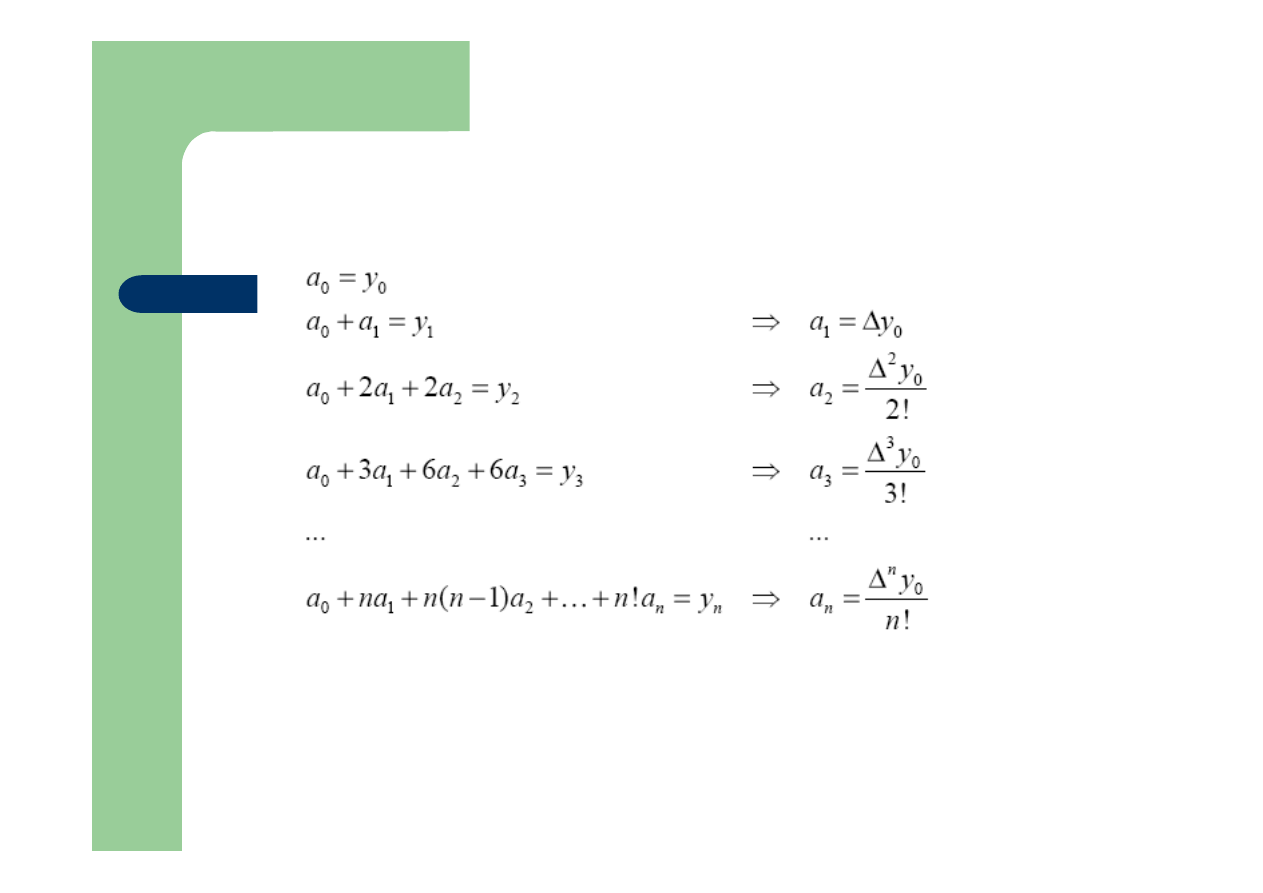
Interpolacja wstecz-wzór Newtona

Przykład:

Baza Czebyszewa

Przykład:

Interpolacja trygonometryczna

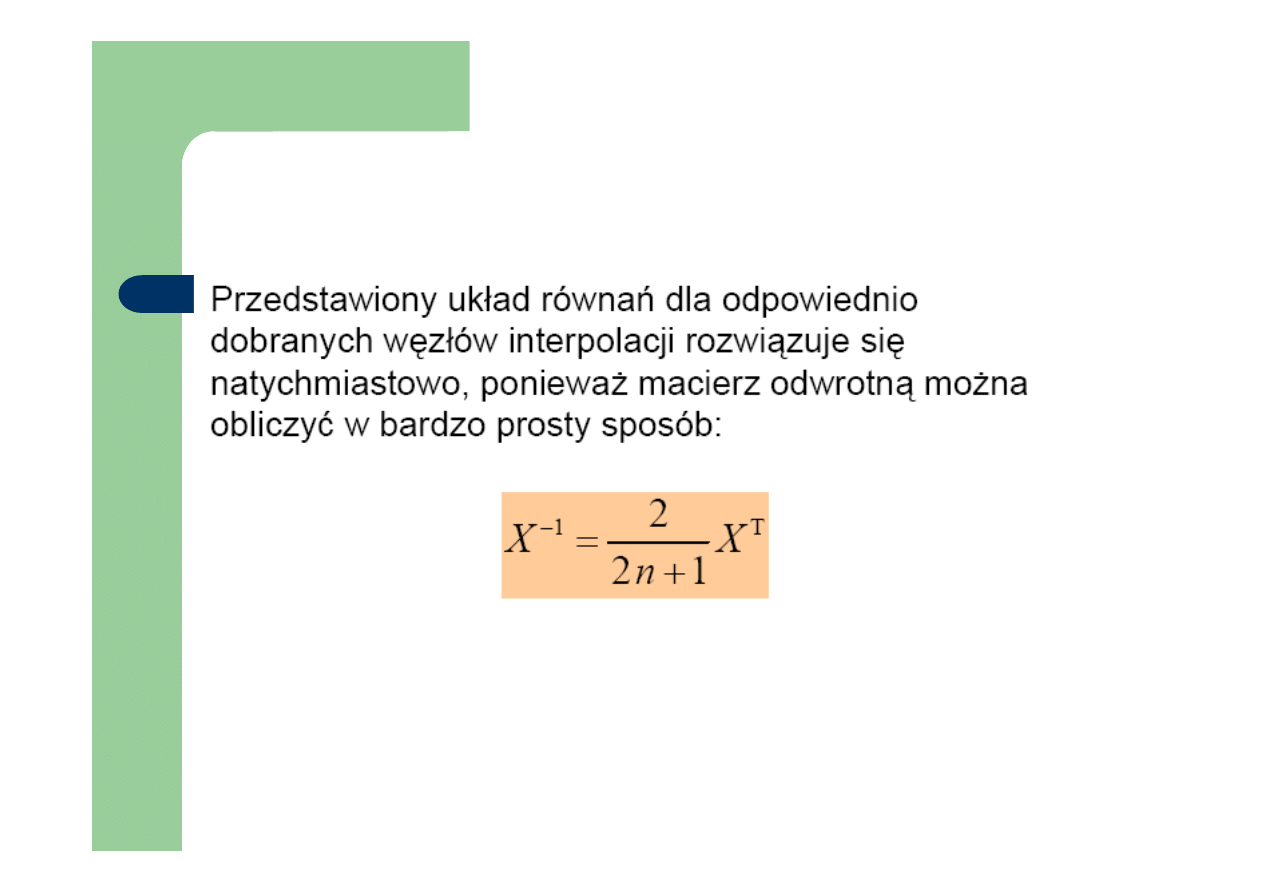
Inne ważne wielomiany:

z

Hermite`a

z

Laguerre`a

z

Bernsteina

z

Legendre`a

Zastosowania interpolacji:

Interpolacja zdecydowanie nie należy do tej części matematyki z którą
spotykamy się na co dzień, jednak stanowi ona nieocenione narzędzie. 
Oto najpopularniejsze zastosowania interpolacji:

•zastępowanie skomplikowanego wzoru funkcji prostszym (np. 
wielomianem)
•obliczanie wartości stablicowanej funkcji w punkcie różnym od 
danych (szczególnie przydatne w przypadku tablic matematycznych, 
pozwala to także na zmniejszenie rozmiaru tablic)
•rozwiązywanie równań f(x)=0

(interpolacja odwrotna)

•wiele innych metod numerycznych opiera się na metodach 
interpolacyjnych, np. różniczkowanie i całkowanie numeryczne

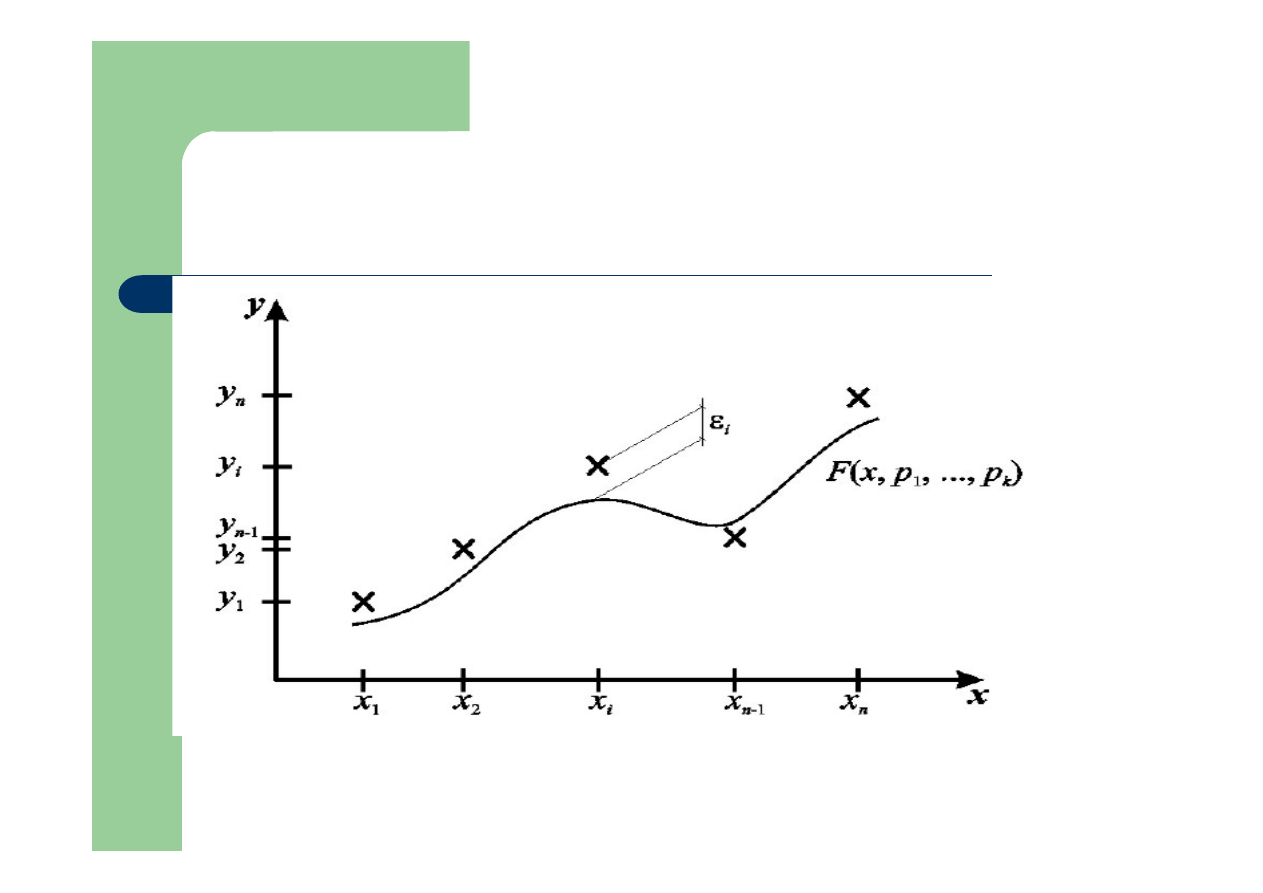
Aproksymacja

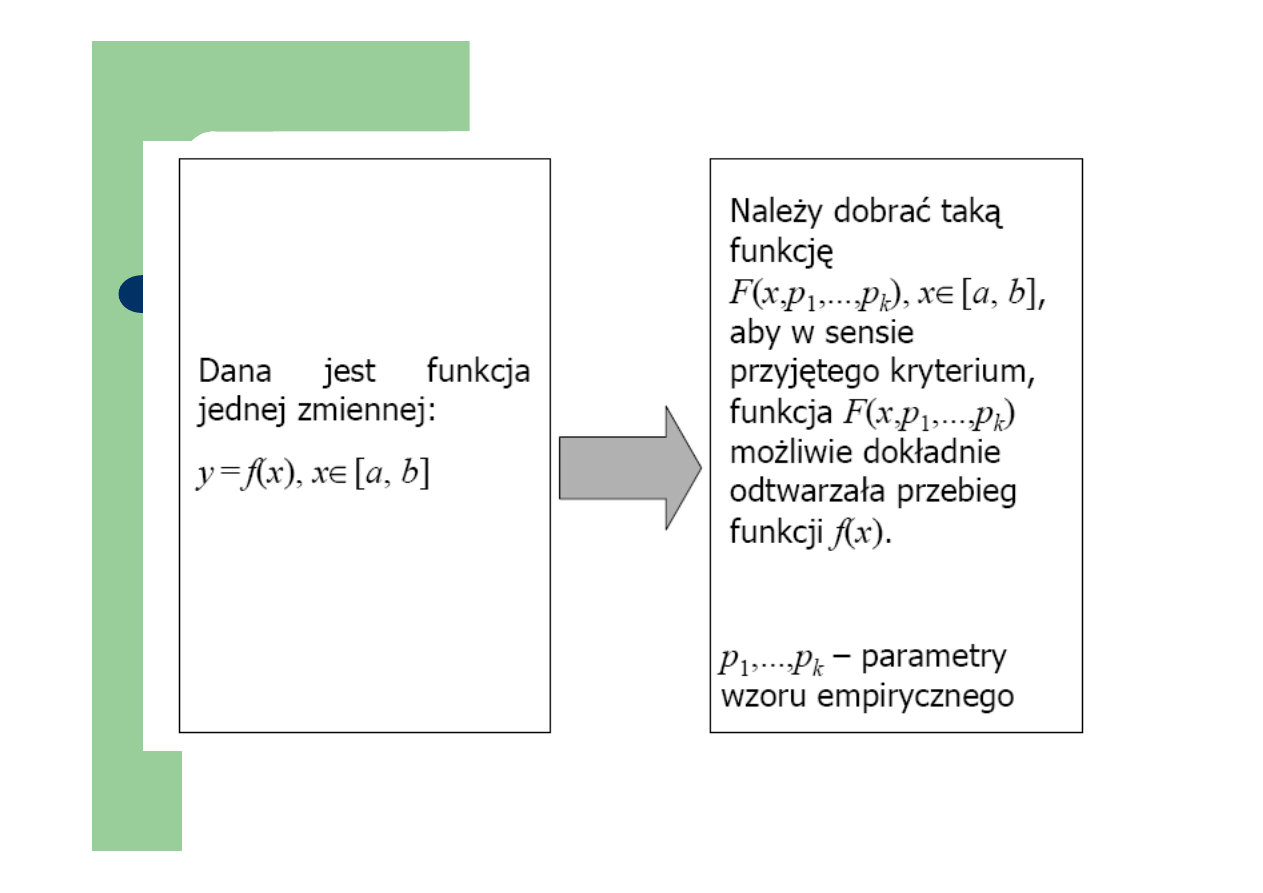
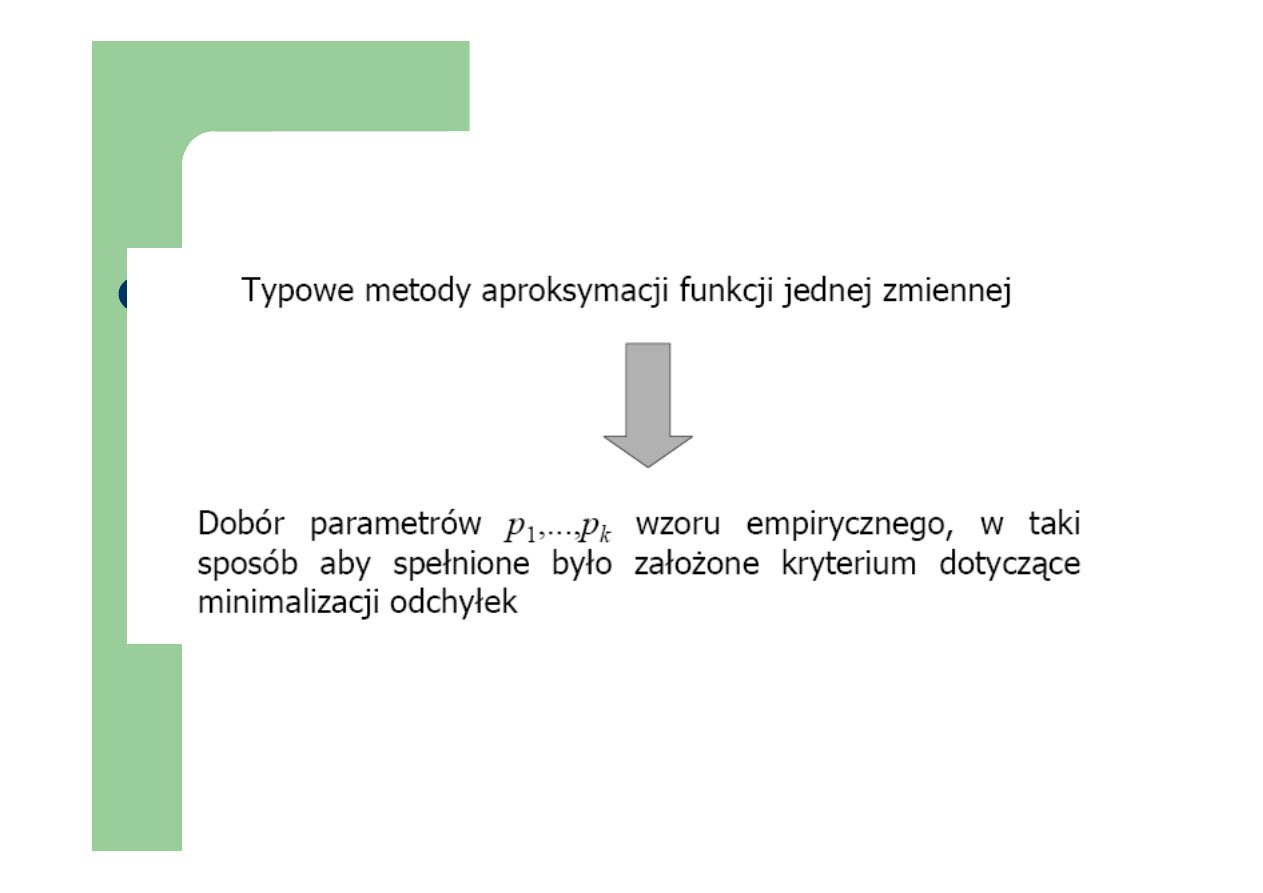
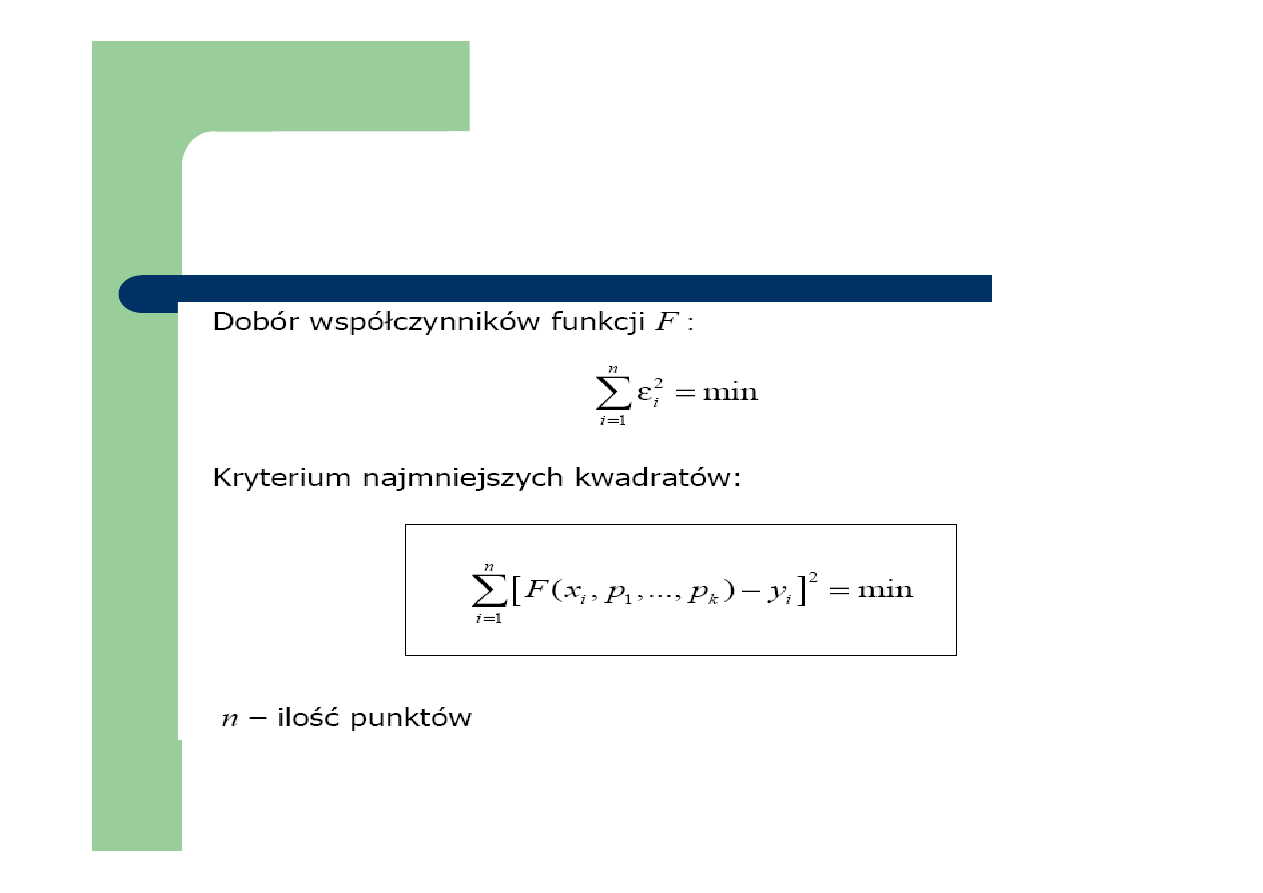
Metoda najmniejszych kwadratów

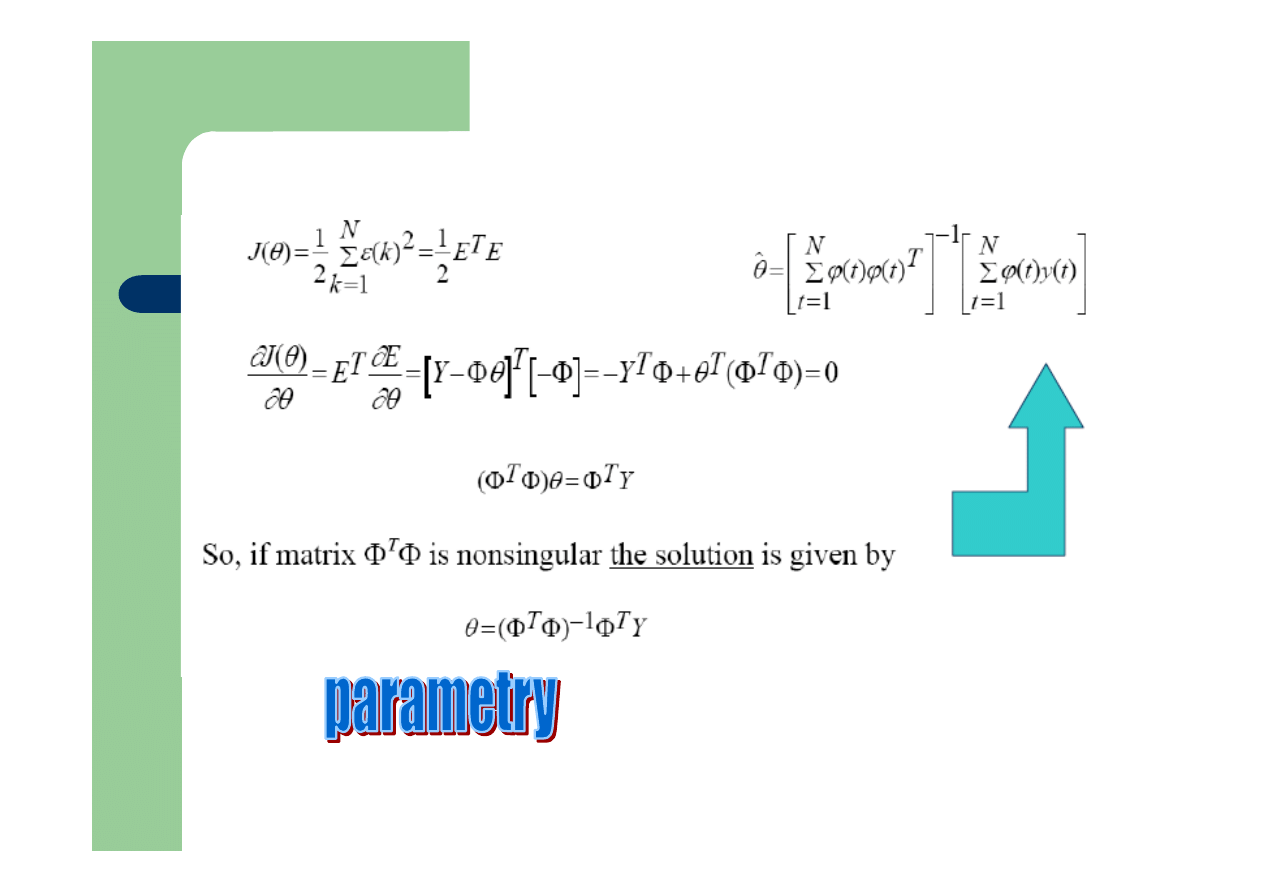
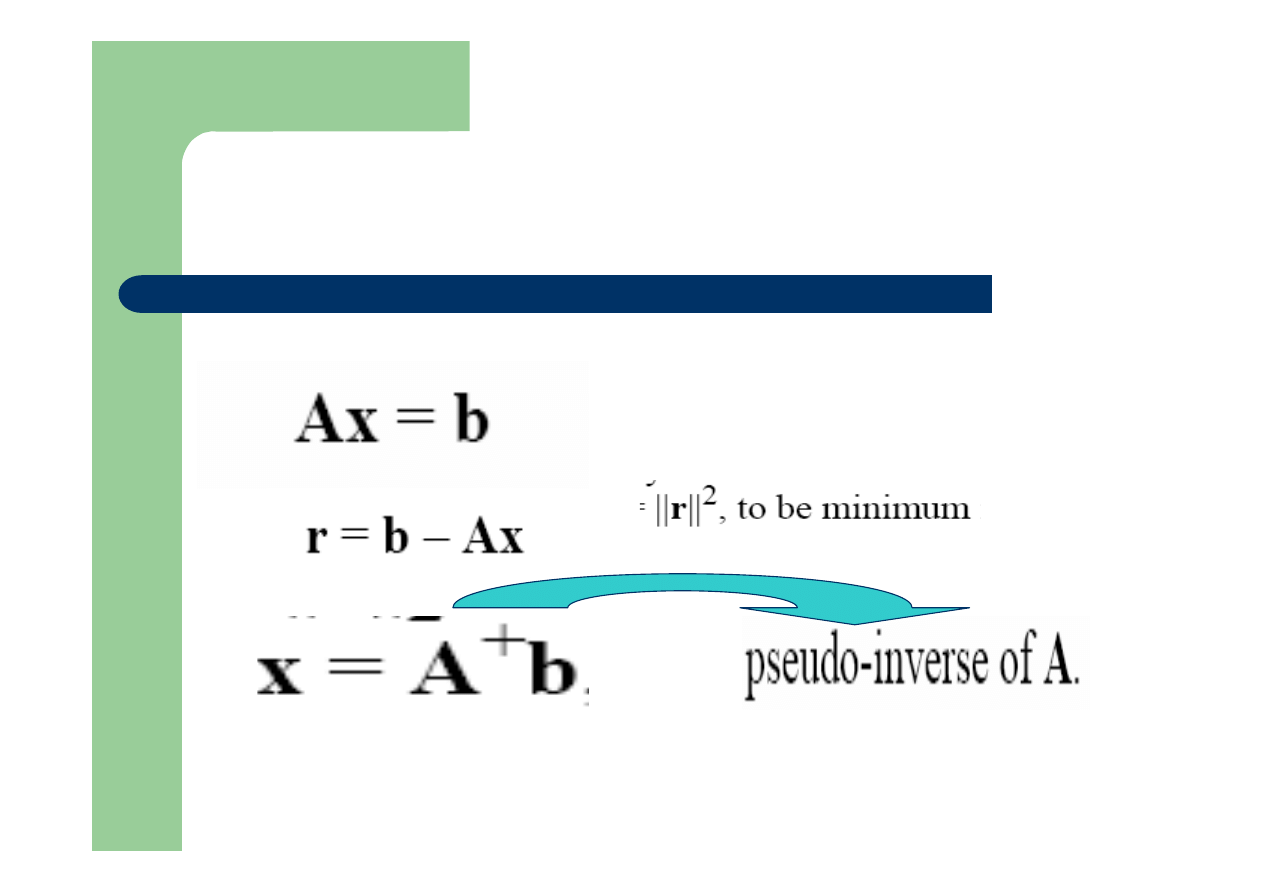
Liniowe najmniejsze kwadraty

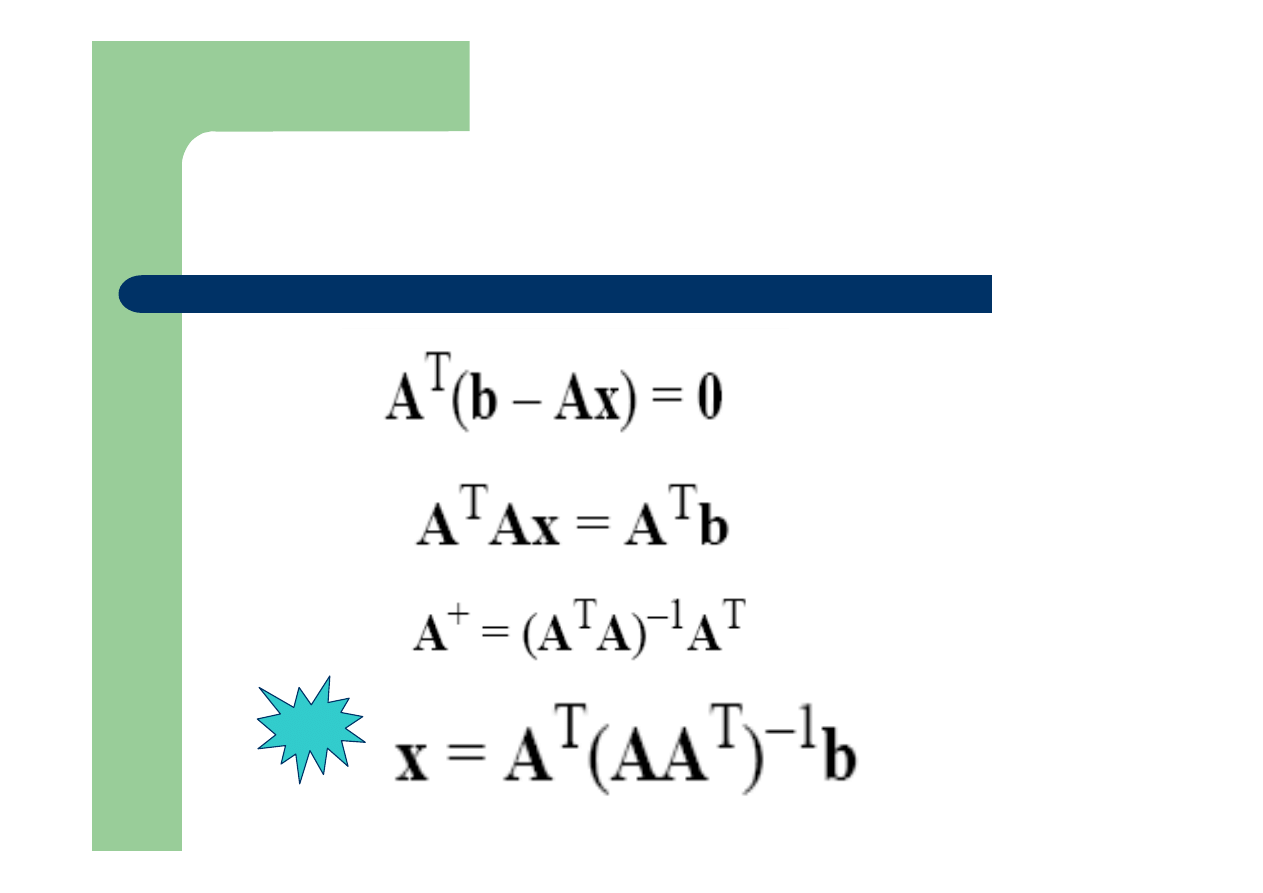
Warunek konieczny i dostateczny

minimum