Aproksymacja i interpolacja

PWSZ, Elbląg 2002

Elbąg, PWSZ 2002r.

2

Aproksymacja

Aproksymacja jest to przybli

ż

anie, zast

ę

powanie jednych wielko

ś

ci

drugimi.

Aproksymacja

mo

ż

e

dotyczy

ć

dowolnych

wielko

ś

ci

matematycznych – liczb, funkcji, krzywych, obszarów, wektorów, macierzy.
Zast

ę

powanie danej wielko

ś

ci inn

ą

obarczone jest pewnym bł

ę

dem.

Oszacowanie wielko

ś

ci bł

ę

du pozwala na ocen

ę

, czy dane przybli

ż

enie

jest zadawalaj

ą

ce, czy te

ż

nie.

Niech poszukiwana jest krzywa

dla zadanej liczby

punktów:

jest opisana równaniem:

Aproksymacja stosowana jest wówczas, gdy ilo

ść

zadanych punktów m

jest mniejsza od ilo

ś

ci nieznanych współczynników n krzywej F(x).

Zwykle nie mo

ż

na przeprowadzi

ć

krzywej przez wszystkie punkty.

Poszukiwana jest wówczas najbli

ż

sza krzywa w sensie minimum

kwadratu bł

ę

du.

)

(x

F

y

=

)

,

(

i

i

y

x

)

(

...

)

(

)

(

)

(

2

2

1

1

x

f

c

x

f

c

x

f

c

x

F

n

n

+

+

+

=

Elbąg, PWSZ 2002r.

3

Regresja liniowa

Najbardziej

podstawow

ą

i

najprostsz

ą

metod

ą

aproksymacji

ś

redniokwadratowej jest aproksymacja funkcj

ą

liniow

ą

czyli regresja

liniowa. Wówczas:

Pozostałe funkcje:

Dla kolejnych punktów otrzymujemy:

1

)

(

,

)

(

2

1

=

=

x

f

x

x

f

1

)

(

=

x

f

j

























=



















































=

+

=

+

=

+

m

m

m

m

n

y

y

y

c

c

x

x

x

y

c

x

c

y

c

x

c

y

c

x

c

Μ

Μ

Μ

2

1

2

1

2

1

2

2

2

2

1

1

2

1

1

1

1

1

lub

Elbąg, PWSZ 2002r.

4

Regresja liniowa

co mo

ż

na zapisa

ć

w postaci macierzowej Ac=y. Równanie to dla m>n nie

ma dokładnego rozwi

ą

zania, st

ą

d:

gdzie: r – wektor pionowych odległo

ś

ci pomi

ę

dzy poszukiwan

ą

krzyw

ą

a

zadanymi punktami. Szukane jest takie rozwi

ą

zanie, dla którego:

lub macierzowo

osi

ą

ga minimum.

St

ą

d:

Ac

y

r

−

=

∑

=

m

i

i

r

1

2

r

r

T

(

) (

)

Ac

A

c

Ac

y

y

y

Ac

A

c

y

A

c

Ac

y

y

y

Ac

y

Ac

y

r

r

T

T

T

T

T

T

T

T

T

T

T

T

+

−

=

+

−

−

=

−

−

=

2

Elbąg, PWSZ 2002r.

5

Regresja liniowa

Iloczyn ten osi

ą

gnie minimum je

ś

li:

st

ą

d:

Powy

ż

sze równanie nazywane jest równaniem aproksymacji.

( )

0

0

=

+

−

→

=

Ac

A

y

A

r

r

dc

d

T

T

T

( )

y

A

c

A

A

T

T

=

Elbąg, PWSZ 2002r.

6

Regresja liniowa

Przykład 1:

Wyznaczenie prostej aproksymuj

ą

cej punkty o współrz

ę

dnych (1,1), (2,2),

(4,2), (5,3):

x=[1 2 4 5]; y=[1 2 2 3];

x=x'; y=y';

A=[x ones(size(x))];

c=(A'*A)\(A'*y)

ya=c(1)*x+c(2)

plot(x,y,'o',x,ya,'-')

grid on

xlabel('x')

ylabel('y=F(x)')

1

1.5

2

2.5

3

3.5

4

4.5

5

1

1.2

1.4

1.6

1.8

2

2.2

2.4

2.6

2.8

3

x

y

=

F

(x

)

Elbąg, PWSZ 2002r.

7

Regresja liniowa

W programie MATLAB dzielenie lewostronne jest równoznaczne operacji:

y=A\y=(A’*A)\(A’*y)

Je

ż

eli macierz A

ma wymiar m x n, gdzie m>n program MATLAB

rozwi

ą

zuje zagadnienie regresji liniowej (znajduje współczynniki linii

prostej).

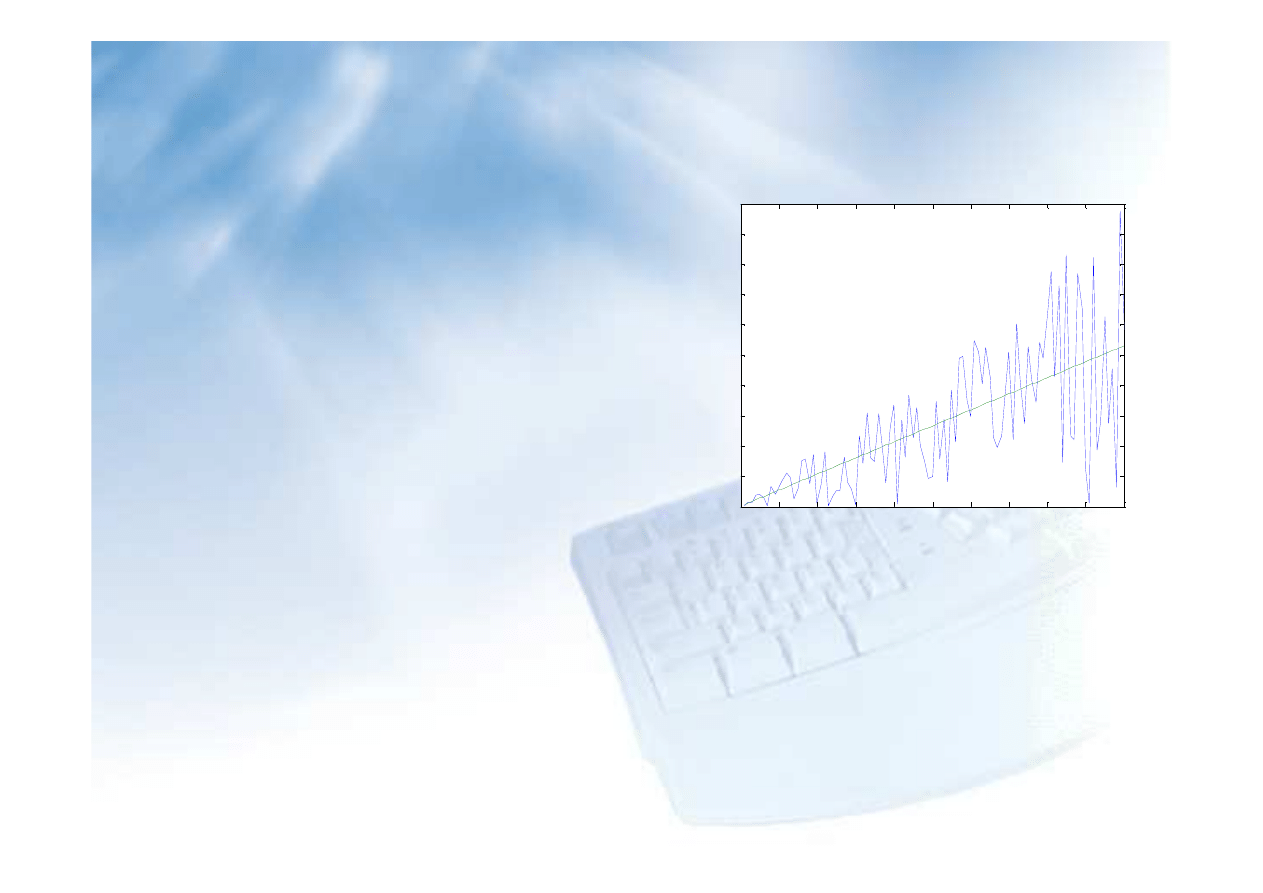
Przykład 2:

Przedstawione poni

ż

ej polecenia realizuj

ą

aproksymacj

ę

funkcj

ą

liniow

ą

.

Wygenerowane dane umieszczono w wektorach kolumnowych

x

i

y

. Przy

generowaniu danych u

ż

yto funkcj

ę

r

and

generuj

ą

ca liczby pseudolosowe

o rozkładzie normalnym o zadanej warto

ś

ci

ś

redniej i wariancji. Dane

generowane s

ą

w p

ę

tli, w ka

ż

dym jej kroku zwi

ę

ksza si

ę ś

redni

ą

generowanych liczb.

Elbąg, PWSZ 2002r.

8

Regresja liniowa

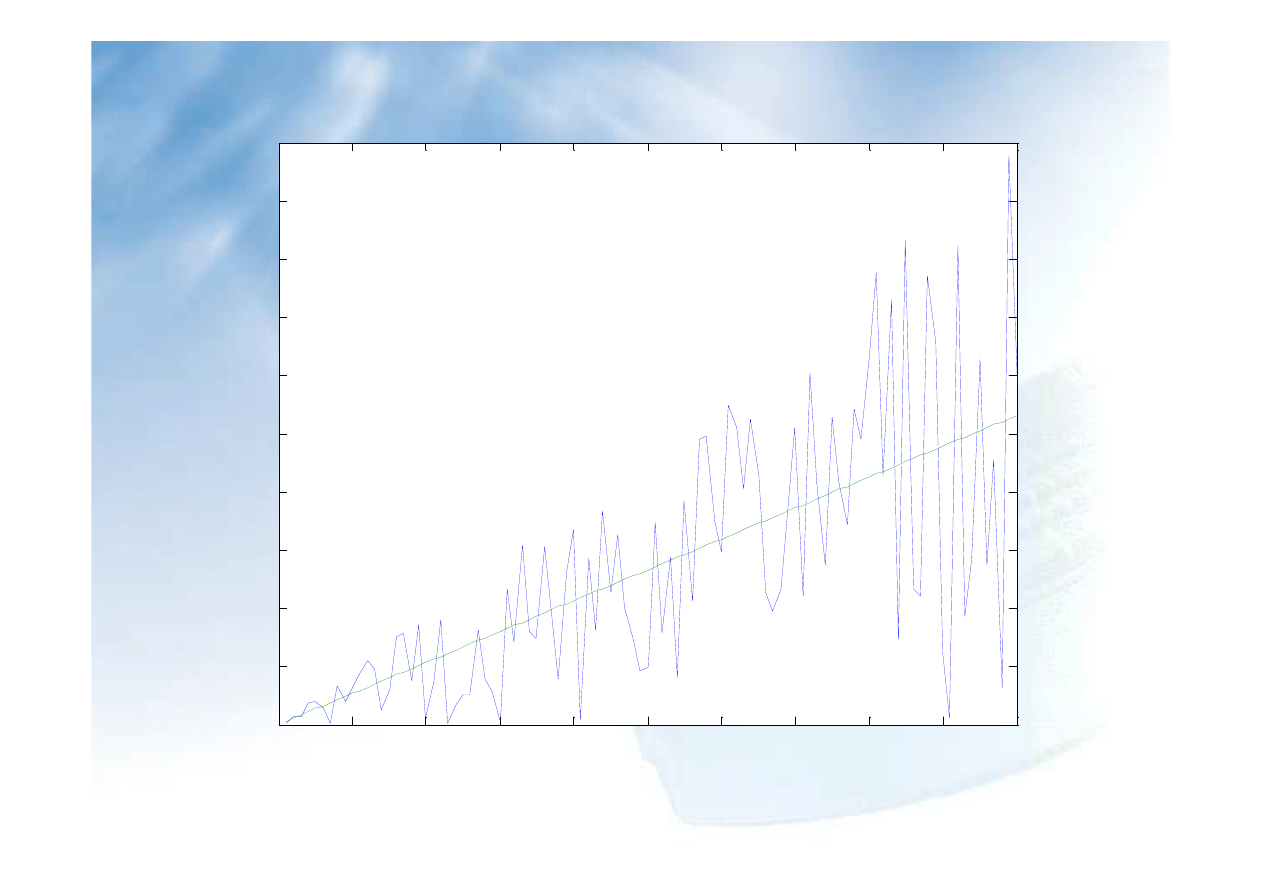
%% Przygotowanie danych do obliczen

clear

x=[0.1:0.1:10]';

[m,n]=size(x);

for i=1:m

y(i,1)=i*0.1*rand(1,1);

end

plot(x,y,'.');

%% poszukiwanie funkcji y=ax

%% najlepiej w sensie sumy kwadratów

%% przyblizajace te dane

a=x\y;

plot(x,y,x,a*x);

0

1

2

3

4

5

6

7

8

9

10

0

1

2

3

4

5

6

7

8

9

10

Elbąg, PWSZ 2002r.

9

Regresja liniowa

0

1

2

3

4

5

6

7

8

9

10

0

1

2

3

4

5

6

7

8

9

10

Elbąg, PWSZ 2002r.

10

Aproksymacja

Równanie aproksymacji:

jest prawdziwe dla dowolnej funkcji aproksymacji:

gdzie: - nieznane współczynniki,

-

funkcje

bazowe,

za

ś

macierze A, c i y:

( )

y

A

c

A

A

T

T

=

)

(

...

)

(

)

(

)

(

2

2

1

1

x

f

c

x

f

c

x

f

c

x

F

n

n

+

+

+

=

j

c

( )

x

f

j

( )

( )

( )

( )

( )

( )

( )

( )

( )

























=

























=

























=

m

n

m

n

m

m

n

n

y

y

y

y

c

c

c

c

x

f

x

f

x

f

x

f

x

f

x

f

x

f

x

f

x

f

A

Μ

Μ

Κ

Μ

Κ

Κ

2

1

2

1

2

1

2

2

2

2

1

1

1

2

1

1

,

,

Elbąg, PWSZ 2002r.

11

Aproksymacja

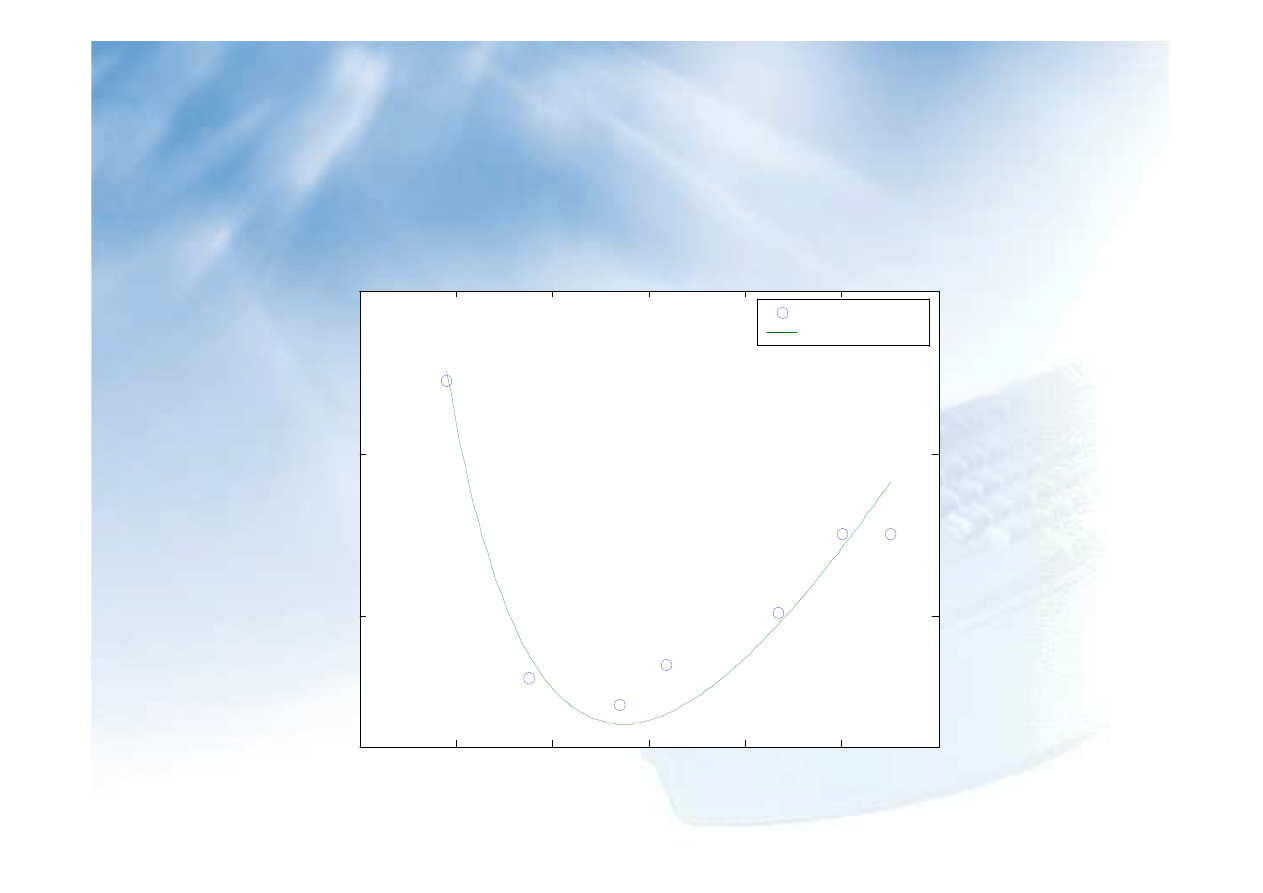
Przykład 3:
Dla zadanego zbioru punktów poszukiwana jest funkcja aproksymuj

ą

ca:

x=[0.955 1.380 1.854 2.093 2.674 3.006 3.255]';

y=[5.722 4.812 4.727 4.850 5.011 5.253 5.253]';

A=[1./x x]; %przygotowanie macierzy A

c=(A'*A)\(A'*y)

%funkcja linspace generuje wektor

%wierszowy o elementach równoodleglych

%w zadanym zakresie

xa=linspace(min(x),max(x),100);

xa=xa';

Aa=[1./xa xa];

ya=Aa*c;

x

c

x

c

y

2

1

+

=

Elbąg, PWSZ 2002r.

12

Aproksymacja

plot(x,y,'o',xa,ya,'-');

xlabel('x'); ylabel('y=F(x)');

legend('dane','aproksymacja')

0.5

1

1.5

2

2.5

3

3.5

5

5.5

6

x

y

=

F

(x

)

dane
aproksymacja

Elbąg, PWSZ 2002r.

13

Aproksymacja wielomianem

Aproksymacja funkcj

ą

liniow

ą

mo

ż

e okaza

ć

si

ę

nie wystarczaj

ą

ca

wówczas, gdy mi

ę

dzy danymi wyst

ę

puje bardziej zło

ż

ona zale

ż

no

ść

.

Stosuje si

ę

wówczas zazwyczaj aproksymacj

ę

wielomianem:

któr

ą

w programie MATLAB mo

ż

na zrealizowa

ć

przy pomocy funkcji

polyfit

:

a=polyfit(x,y,r)

dla danych wektorów

x

i

y

wyznaczaj

ą

cej współczynniki wielomianu

stopnia

r

przybli

ż

aj

ą

cego najlepiej w sensie

ś

redniokwadratowym

zale

ż

no

ść

mi

ę

dzy seri

ą

danych

x

a

y

.

( )

0

1

1

1

...

a

x

a

x

a

x

a

x

W

r

r

r

r

+

+

+

+

=

−

−

Elbąg, PWSZ 2002r.

14

Aproksymacja wielomianem

Przykład 4:
Przedstawione poni

ż

ej polecenia generuj

ą

dane losowe, a nast

ę

pnie

przybli

ż

aj

ą

zale

ż

no

ść

pomi

ę

dzy nimi wielomianami stopni od 1 do 10:

clear

close all

x=[0.1:0.1:10]';

[m,n]=size(x);

for i=1:m

y(i,1)=(sin(0.05*i)+2*cos(0.08*i))*rand(1,1);

end

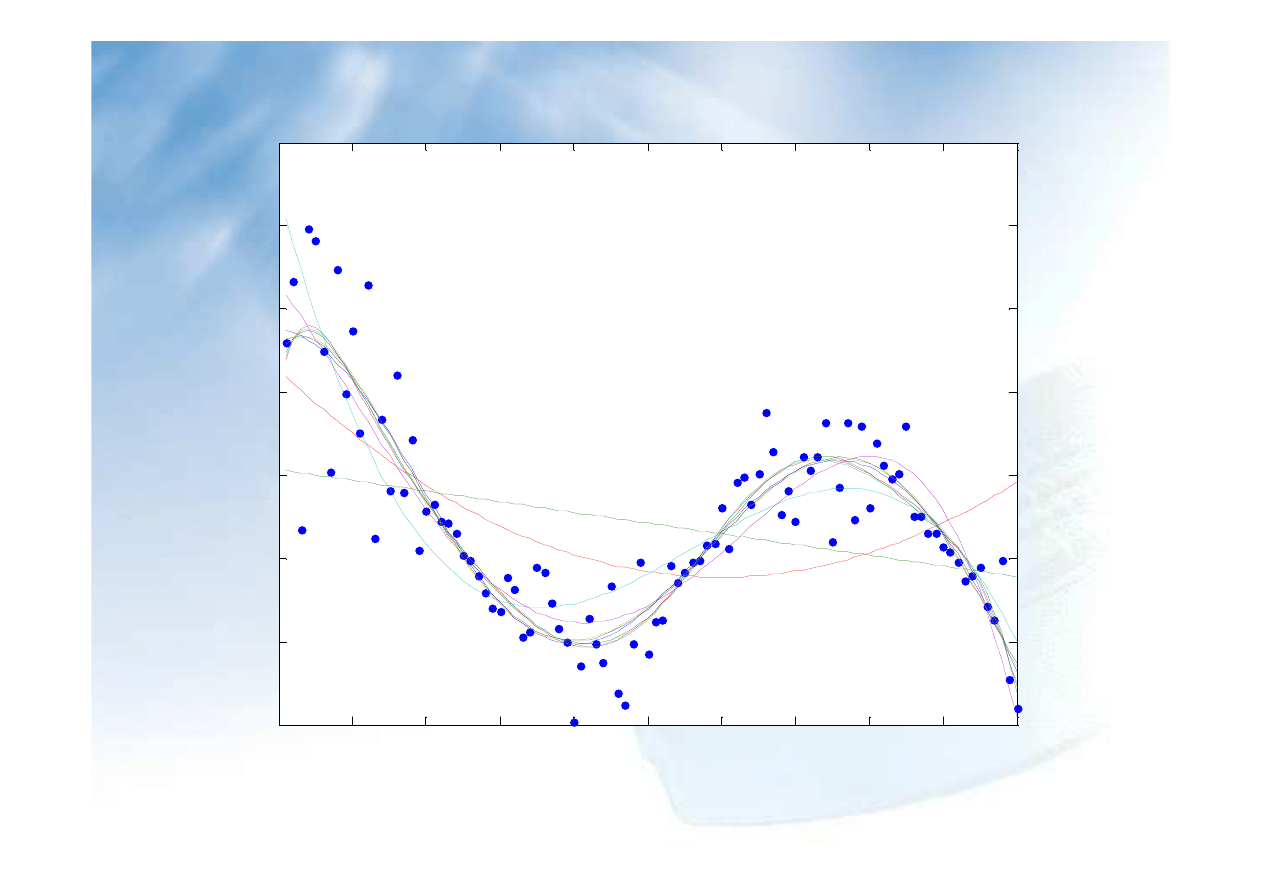
d=1

for N=1:d:10

figure(N)

a=polyfit(x,y,N);

ya(:,N/d)=polyval(a,x);

plot(x,y,'.',x,ya);

end

Elbąg, PWSZ 2002r.

15

Aproksymacja wielomianem

0

1

2

3

4

5

6

7

8

9

10

-1

-0.5

0

0.5

1

1.5

2

2.5

Elbąg, PWSZ 2002r.

16

Interpolacja

Interpolacja polega na poszukiwaniu funkcji pomi

ę

dzy znanymi punktami

(podobnie jak aproksymacja). W odró

ż

nieniu jednak od aproksymacji

funkcja ta przechodzi przez te punkty. Je

ż

eli poszukiwana jest funkcja

poza zakresem zadanych punktów mamy do czynienia z ekstrapolacj

ą

.

Wybrane metody interpolacji:

1) interpolacja wielomianem:

2) interpolacja wielomianem Lagrange’a:

3) interpolacja wielomianem Newtona:

( )

n

n

n

n

n

c

x

c

x

c

x

c

x

P

+

+

+

+

=

−

−

−

−

1

2

2

1

1

1

Κ

( )

( )

( )

( )

( )

∏

≠

=

−

−

−

=

+

+

+

=

n

j

k

k

k

j

k

j

n

n

n

x

x

x

x

x

L

gdzie

x

L

y

x

L

y

x

L

y

x

P

,

1

2

2

1

1

1

,

Κ

( )

(

) (

)(

)

(

)(

) (

)

n

n

n

x

x

x

x

x

x

c

x

c

x

x

c

x

x

c

c

x

P

−

−

−

+

+

−

−

+

−

+

=

−

Λ

Κ

2

1

2

1

3

1

2

1

1

Elbąg, PWSZ 2002r.

17

Interpolacja

Elbąg, PWSZ 2002r.

18

Interpolacja

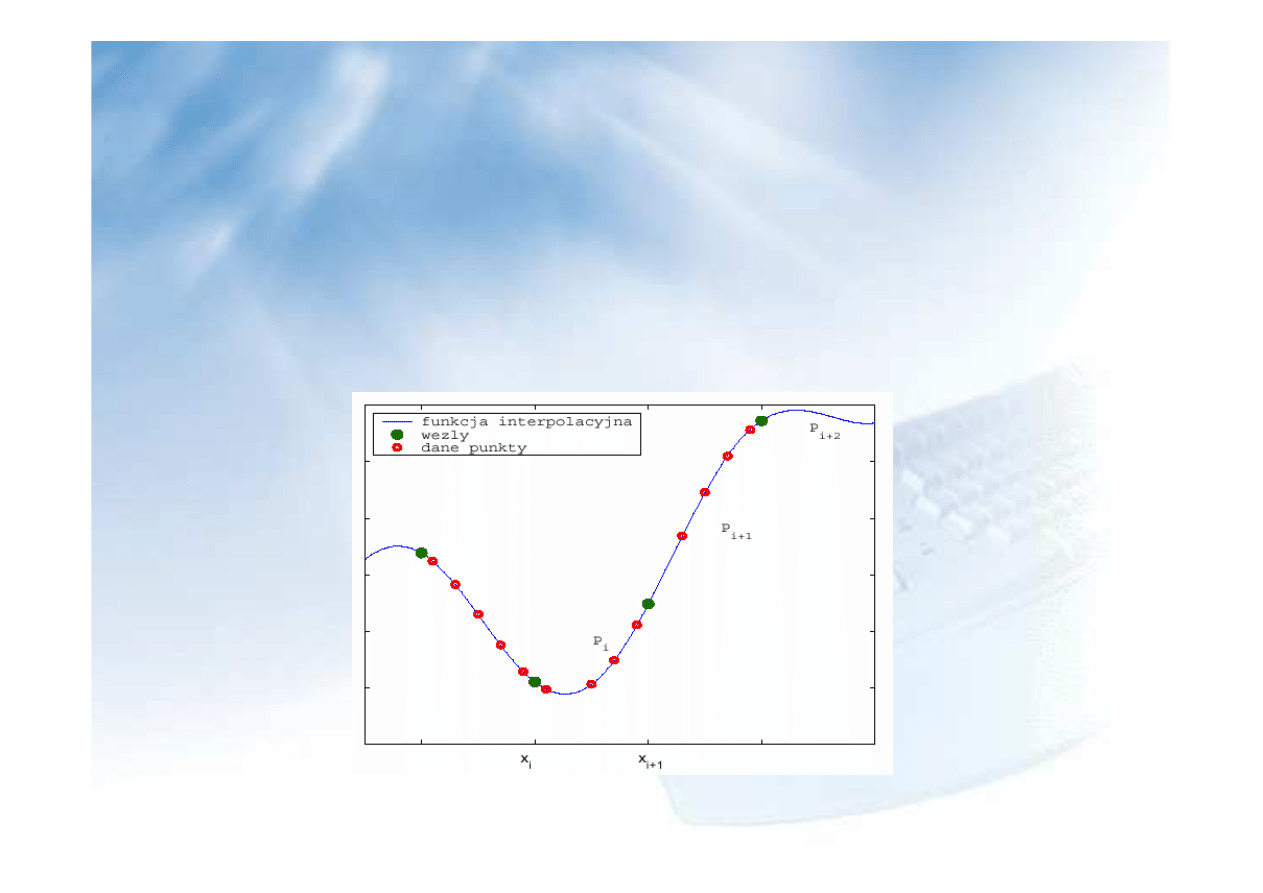
Interpolacja wielomianami sklejanymi

W interpolacji wielomianami sklejanymi zamiast stosowania jednego
wielomianu dla wszystkich danych punktów stosowane jest wiele
wielomianów niskiego poziomu dla danego przedziału danych:

Punkty ł

ą

czenia wielomianów nazywamy w

ę

złami. We

w

ę

złach sprawdzane s

ą

warunki ci

ą

gło

ś

ci (np. ci

ą

gło

ść

pochodnych).

( )

x

P

i

1

+

≤

≤

i

i

x

x

x

Elbąg, PWSZ 2002r.

19

Interpolacja

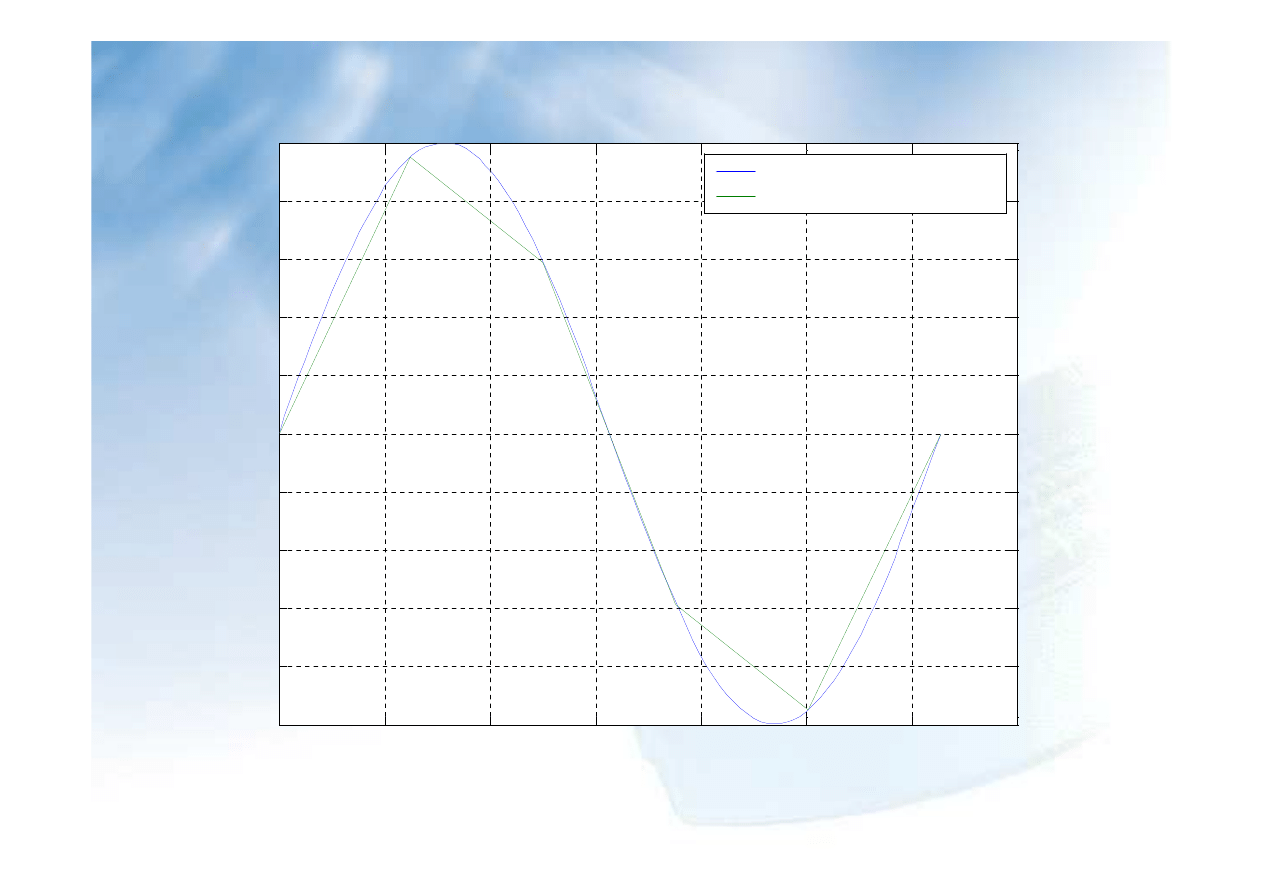
Interpolacja kawałkami liniowa

Przykład 5:

x1=linspace(0,2*pi,100);

x2=linspace(0,2*pi,6);

plot(x1,sin(x1),x2,sin(x2))

grid on

xlabel('x')

ylabel('plot(x,sin(x)')

legend('x=linspace(0,2*pi,100)',...

'x=linspace(0,2*pi,6)')

0

1

2

3

4

5

6

7

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

x

p

lo

t(

x

,s

in

(x

)

x=linspace(0,2*pi,100)
x=linspace(0,2*pi,6)

Elbąg, PWSZ 2002r.

20

Interpolacja

0

1

2

3

4

5

6

7

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

x

p

lo

t(

x

,s

in

(x

)

x=linspace(0,2*pi,100)
x=linspace(0,2*pi,6)

Elbąg, PWSZ 2002r.

21

Interpolacja

Interpolacja kawałkami sze

ś

cienna – Hermite’a

gdzie:

s

ą

poszukiwanymi współczynnikami, dla których s

ą

spełnione we w

ę

złach nast

ę

puj

ą

ce warunki:

1) ci

ą

gło

ś

ci:

2) znane s

ą

warto

ś

ci pierwszej pochodnej i jej ci

ą

gło

ść

:

Interpolacja kawałkami sze

ś

cienna – splajny

Metoda ta w odró

ż

nieniu od interpolacji Hermite’a nie wymaga znajomo

ś

ci

pochodnych we wszystkich punktach w

ę

złowych, musz

ą

by

ć

jednak

spełnione nast

ę

puj

ą

ce warunki:

( )

(

) (

)

(

)

3

2

i

i

i

i

i

i

i

i

x

x

d

x

x

c

x

x

b

a

x

P

−

+

−

+

−

+

=

i

i

i

i

d

c

b

a

,

,

,

( ) ( )

i

i

i

i

x

P

x

P

=

−

1

( )

( )

i

i

i

i

x

P

x

P

′

=

′

−

1

Elbąg, PWSZ 2002r.

22

Interpolacja

1) ci

ą

gło

ść

drugiej pochodnej:

2) pierwsze pochodne (nachylenia krzywej) musz

ą

by

ć

znane na ko

ń

cach

przedziału

- ustalone nachylenie:

- naturalne nachylenie:

- nachylenie nieznane:

( )

( )

i

i

i

i

x

P

x

P

′′

=

′′

−

1

( )

( )

n

n

x

P

x

P

′

′

,

1

1

( )

( )

,

2

,

1

1

1

st

x

P

st

x

P

n

n

=

′

=

′

( )

( )

,

0

1

1

=

′′

=

′′

n

n

x

P

x

P

( )

( )

( )

( )

2

2

2

1

2

2

2

1

x

P

x

P

i

x

P

x

P

′′′

=

′′′

′′′

=

′′′

Elbąg, PWSZ 2002r.

23

Interpolacja

Program MATLAB realizuje interpolacj

ę

za pomoc

ą

nast

ę

puj

ą

cych metod:

1) interpolacja kawałkami liniowa i sze

ś

cienna,

2) interpolacja za pomoc

ą

funkcji sklejanych.

Funkcja

interp1

:

yi=interp1(x, y, x1, ‘metoda’)

Funkcja

interp1

umo

ż

liwia wykonanie interpolacji funkcji jednej zmiennej

w punktach okre

ś

lonych wektorem

xi

. W

ę

zły interpolacji okre

ś

lone s

ą

parametrami

x

i

y

. Parametr

‘metoda’

umo

ż

liwia wybór metody

interpolacji:
1)

‘linear’

– interpolacja funkcj

ą

łaman

ą

(kawałkami liniowa),

2)

‘spline’

– interpolacja funkcjami sklejanymi trzeciego stopnia,

3)

‘cubic’

– interpolacja wielomianami trzeciego stopnia (kawałkami

sze

ś

cienna),

Elbąg, PWSZ 2002r.

24

Interpolacja

Elementy wektora

x

musz

ą

tworzy

ć

ci

ą

g rosn

ą

cy, dodatkowo w przypadku

interpolacji wielomianami trzeciego stopnia przyrosty warto

ś

ci elementów

wektora

x

musz

ą

by

ć

sobie równe.

Przykład 6:

Interpolacja ró

ż

nymi metodami:

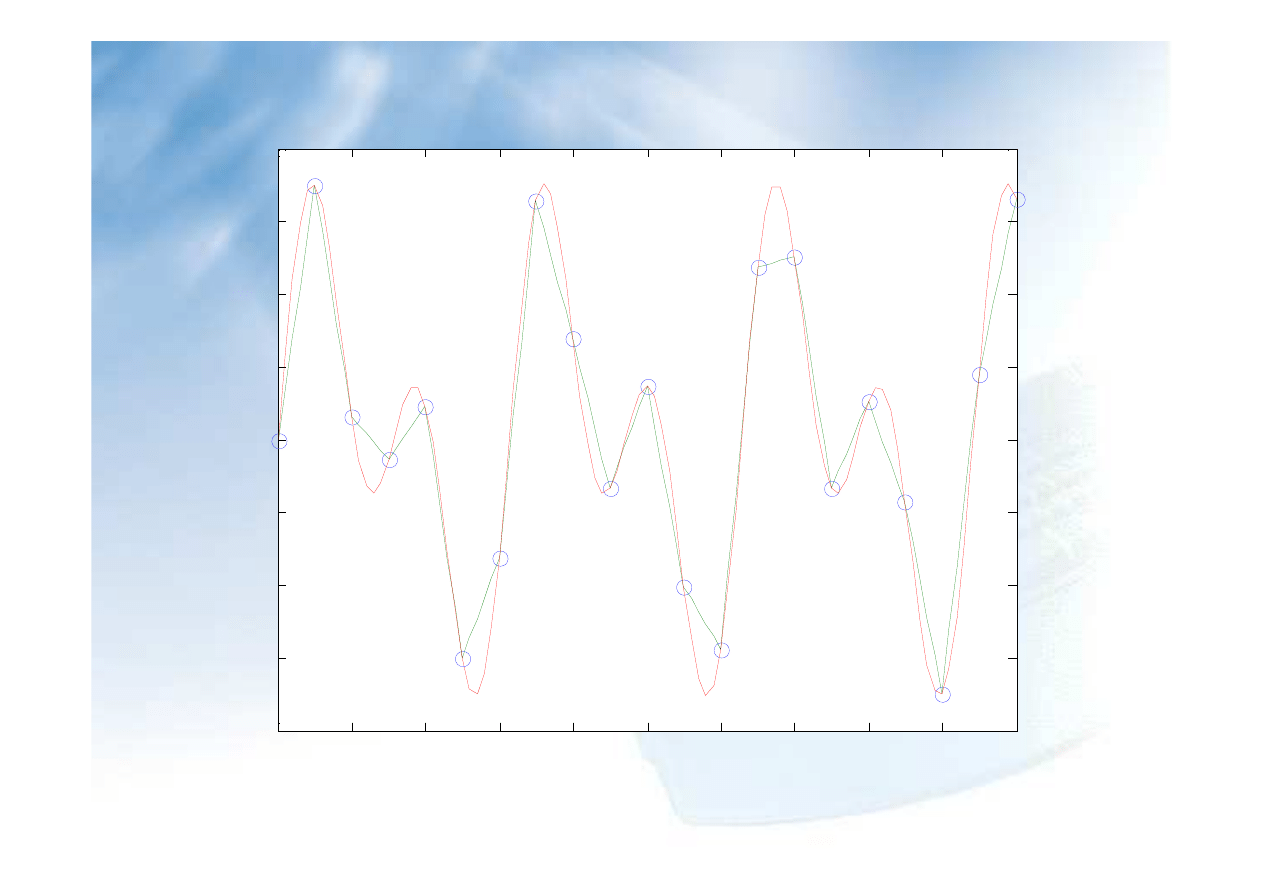
x=0:20; y=sin(x)+sin(2*x);

xi=0:0.2:20;

yi=interp1(x,y,xi,'linear');

plot(x,y,'o',xi,yi,xi,sin(xi)+sin(2*xi));

xlabel('x');

ylabel('y');

title('Interpolacja kawalkami liniowa')

Elbąg, PWSZ 2002r.

25

Interpolacja

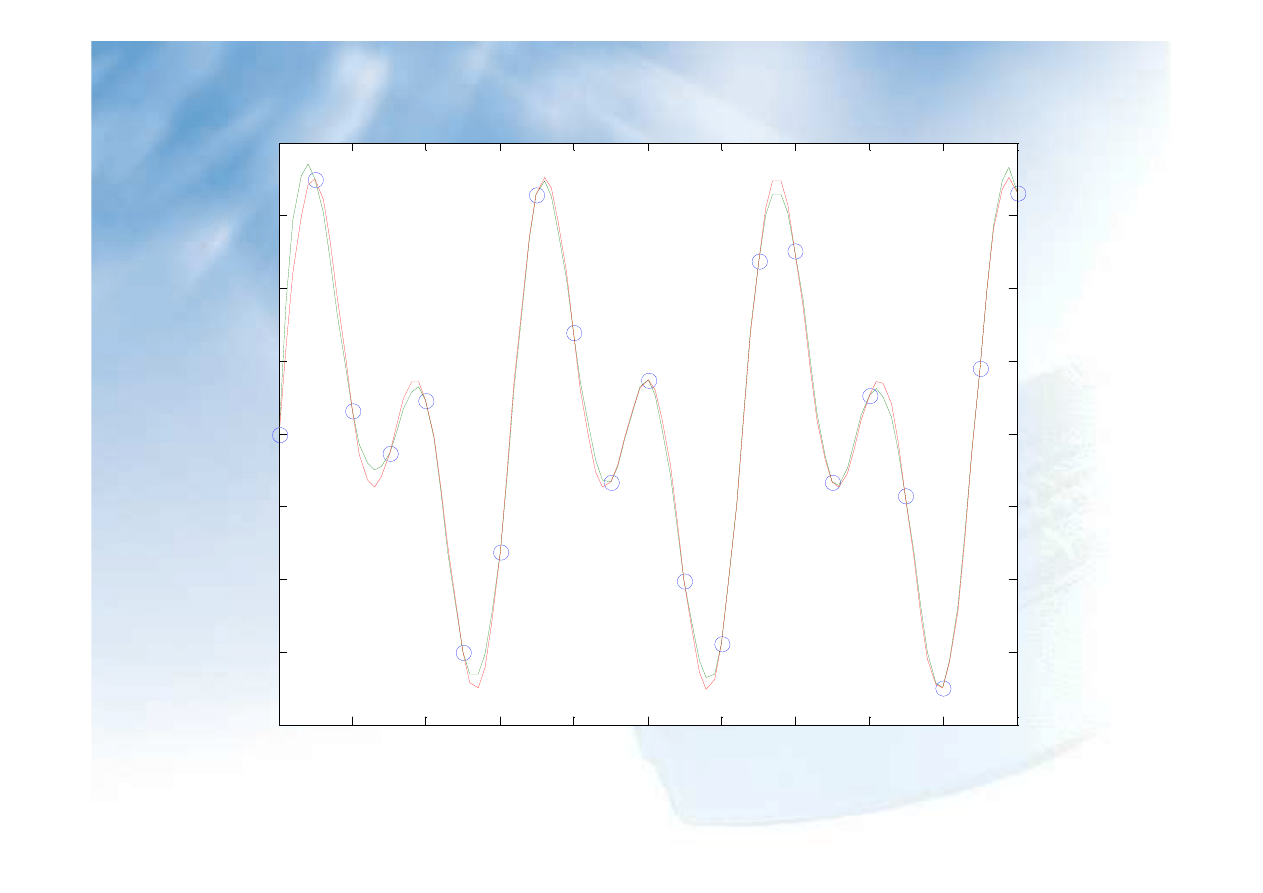
figure(2)

yi=interp1(x,y,xi,'cubic');

plot(x,y,'o',xi,yi,xi,sin(xi)+sin(2*xi));

xlabel('x');

ylabel('y');

title('Interpolacja kawalkami szescienna')

figure(3)

yi=interp1(x,y,xi,'spline');

plot(x,y,'o',xi,yi,xi,sin(xi)+sin(2*xi));

xlabel('x');

ylabel('y');

title('Interpolacja funkcjami sklejanymi')

Elbąg, PWSZ 2002r.

26

Interpolacja

0

2

4

6

8

10

12

14

16

18

20

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

x

y

Interpolacja kawalkami liniowa

Elbąg, PWSZ 2002r.

27

Interpolacja

0

2

4

6

8

10

12

14

16

18

20

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

x

y

Interpolacja kawalkami szescienna

Elbąg, PWSZ 2002r.

28

Interpolacja

0

2

4

6

8

10

12

14

16

18

20

-2

-1.5

-1

-0.5

0

0.5

1

1.5

2

x

y

Interpolacja funkcjami sklejanymi

Dzi

ę

kuj

ę

za uwag

ę