1

Aproksymacja funkcji

2

Aproksymacja oznacza przybli

ż

anie.

Funkcja aproksymuj

ą

ca powinna by

ć

okre

ś

lona na tym samym zbiorze

argumentów, co funkcja aproksymowana.

W matematyce aproksymacja oznacza zast

ę

powanie obiektów innymi

obiektami, z reguły o prostszej strukturze.

Wykonanie aproksymacji wymaga okre

ś

lenia:

- funkcji aproksymowanej – zwykle funkcja dyskretna,

- zbioru funkcji, z których wybieramy funkcj

ę

aproksymuj

ą

c

ą

,

- kryterium oceny jako

ść

aproksymacji.

3

Kryterium okre

ś

laj

ą

ce jako

ść

aproksymacji

Jest to warunek osi

ą

gni

ę

cia warto

ś

ci minimalnej przez funkcj

ę

bł

ę

du, która jest

zale

ż

na od funkcji aproksymowanej i aproksymuj

ą

cej.

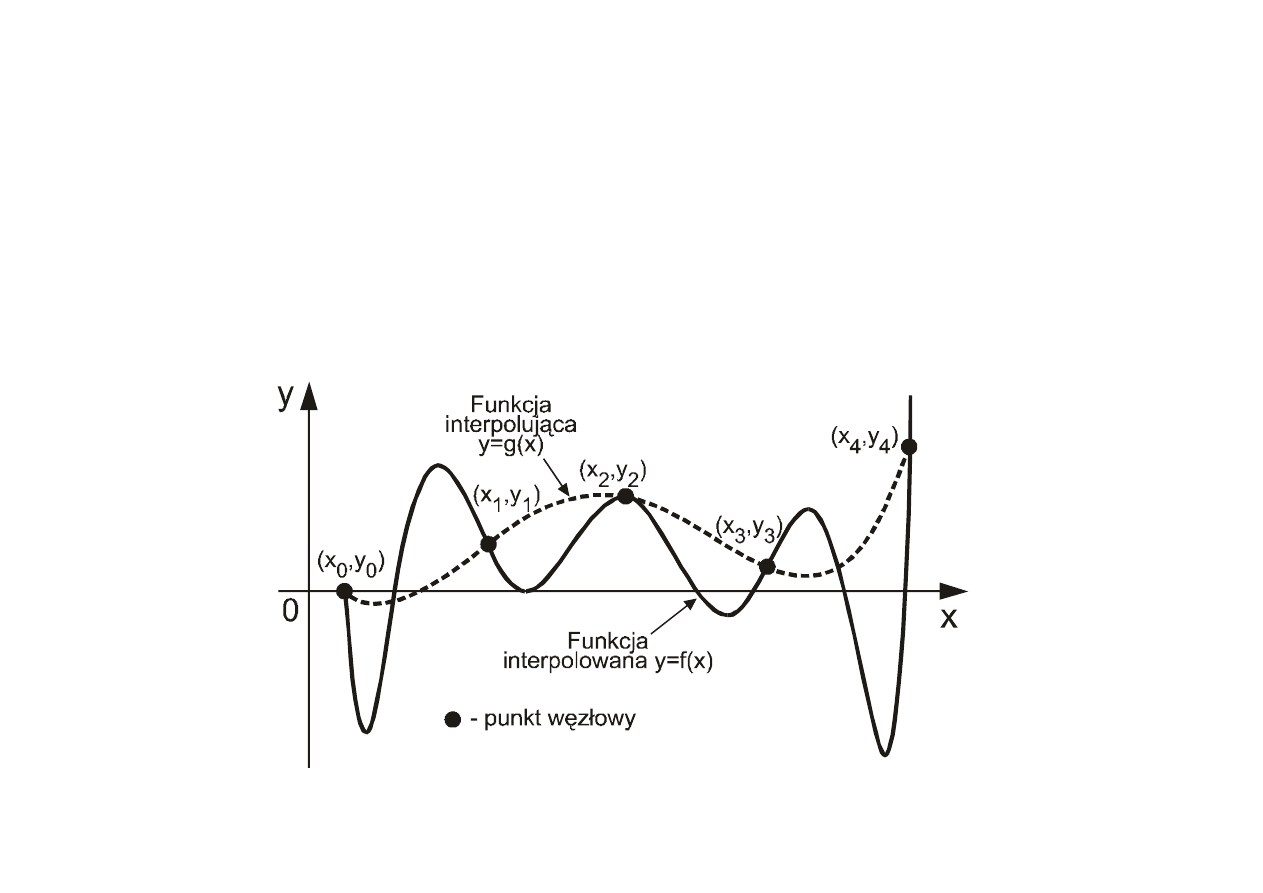
Interpolacja jest szczególnym przypadkiem aproksymacji.

Interpolacja

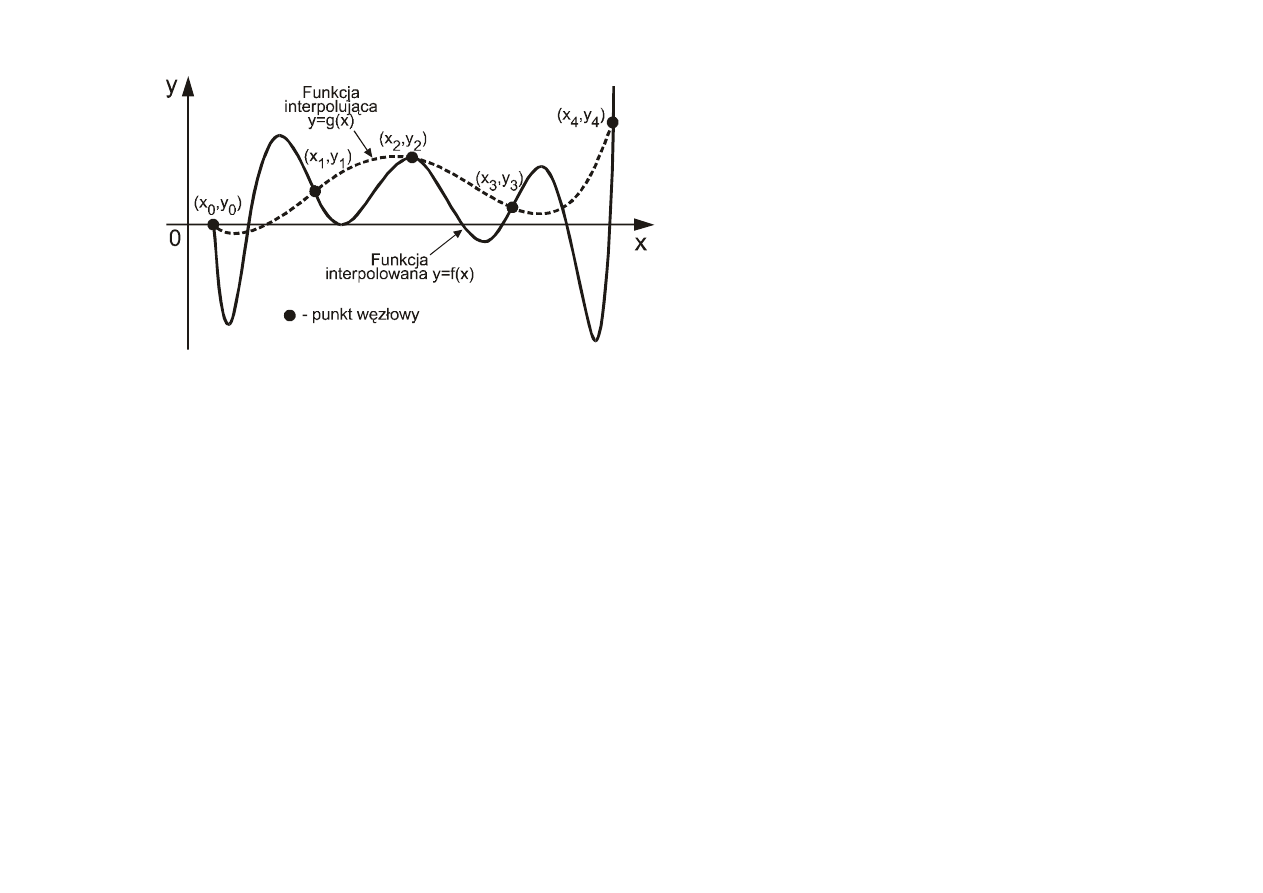
4

Dane s

ą

to warto

ś

ci funkcji f (x)

zapisane jako

n

i

x

f

y

i

i

,...,

2

,

1

,

0

)

(

=

=

Nale

ż

y znale

źć

funkcj

ę

F (x) okre

ś

lonej klasy, która przyjmuje w w

ę

złach

interpolacji te same warto

ś

ci co funkcja interpolowana

n

i

x

f

y

i

i

,...,

2

,

1

,

0

)

(

=

=

n

i

y

x

F

i

i

...,

,

1

,

0

)

(

=

=

czyli

Interpolacja: odcinkami, wielomianami pot

ę

gowymi Lagrange’a, wielomianami

Newtona, ró

ż

nicami sko

ń

czonymi, funkcjami sklejanymi

5

Interpolacja wielomianami Lagrange’a

Nale

ż

y znale

źć

dla danej funkcji f (·) taki wielomian pot

ę

gowy stopnia nie wy

ż

szego ni

ż

n oznaczanego przez

)

(

⋅

n

L

którego warto

ś

ci w n + 1 zadanych punktach

n

i

x

i

...,

,

1

,

0

,

=

s

ą

równe odpowiednim warto

ś

ciom funkcji, co oznacza,

ż

e

n

i

dla

x

f

x

L

i

i

n

...,

,

1

,

0

)

(

)

(

=

=

n

i

x

i

...,

,

1

,

0

,

=

Punkty

w

ę

zły interpolacji

6

Wielomiany Lagrange’a

)

(

)

(

)

(

0

x

L

y

x

L

n

i

n

i

i

n

⋅

=

∑

=

)

)...(

)(

)...(

)(

(

)

)...(

)(

)....(

)(

(

)

(

1

1

1

0

1

1

1

0

)

(

n

i

i

i

i

i

i

i

n

i

i

n

i

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

L

−

−

−

−

−

−

−

−

−

−

=

+

−

+

−

Dla n = 2 i = 0, 1, 2 mamy

)

)(

(

)

)(

(

)

(

2

0

1

0

2

1

)

2

(

0

x

x

x

x

x

x

x

x

x

L

−

−

−

−

=

)

)(

(

)

)(

(

)

(

2

1

0

1

2

0

)

2

(

1

x

x

x

x

x

x

x

x

x

L

−

−

−

−

=

)

)(

(

)

)(

(

)

(

1

2

0

2

1

0

)

2

(

2

x

x

x

x

x

x

x

x

x

L

−

−

−

−

=

7

Przykład

Dane

i

0

1

2

i

x

0

1

2

i

y

-1

0

3