1

Wykład 1

Część 1

Badania operacyjne

jako dziedzina wiedzy

Definicja i krótki zarys historii

badań operacyjnych (1)

Badania operacyjne - dyscyplina naukowa

uważana najczęściej za jedną z dziedzin
nauk o zarządzaniu (ang. management
science), łącząca elementy

• ekonomii,
• matematyki
• naukowych metod organizacji,
.

Definicja i krótki zarys historii

badań operacyjnych (2)

a zajmująca się tworzeniem
• modeli,
• metod,
• reguł postępowania
prowadzących do podejmowania racjonalnych

decyzji.

Definicja i krótki zarys historii

badań operacyjnych (3)

Polska nazwa „badania operacyjne” jest

tłumaczeniem angielskich terminów
operational research (UK)/operations
research (USA). Pochodzi ona od badań
na efektywnością operacji wojskowych
(przede wszystkim o charakterze
logistycznym) podczas drugiej wojny
ś

wiatowej.

Zastosowanie badań

operacyjnych w praktyce

Przedmiotem zainteresowania w badaniach

operacyjnych są najczęściej problemy, które,
niezależnie od ich szczegółowej natury, można
scharakteryzować na dwa podstawowe sposoby:

•

maksymalizacja efektywności (maksymalizacja
zysku, stosunku przychodów do kosztów,
wydajności procesu produkcyjnego,
przepustowości sieci, szybkości obsługi klientów)

•

minimalizacja nakładów (minimalizacja kosztów,
czasu pracy/podróży, przebytej drogi, zużycia
surowców i energii, minimalizacja ryzyka)

6

Podstawowe pojęcia (1)

Parametrami modeli matematycznych

występujących w badaniach operacyjnych
nazywamy

ustalone tzn. niezmienne

podczas obliczeń liczby oznaczające np.

• parametry techniczne maszyn,
• koszty/przychody/zyski jednostkowe,
• opisane liczbowo wymogi prawne,

zapotrzebowania na towary/usługi,

• parametry rozkładów prawdopodobieństwa.

7

Podstawowe pojęcia (2)

Zmienne w modelach matematycznych

występujących w badaniach operacyjnych
nazywa się często

zmiennymi decyzyjnymi.

W sensie matematycznym są to zwykłe
zmienne, a określenie „decyzyjne” ma
jedynie na celu podkreślenie faktu, że
oznaczają one wielkości, które, w
przeciwieństwie do parametrów modelu,
można zmieniać (np. wielkość produkcji,
ilość przewiezionych towarów).

8

Podstawowe pojęcia (3)

Poza zmiennymi decyzyjnymi w modelach

matematycznych mogą też pojawić się tzw.
zmienne pomocnicze. Zmienne te nie
reprezentują wielkości, co do których są
podejmowane decyzje opisywane przez
model. Mogą one służyć do uproszczenia
zapisu modelu lub być wykorzystywane
przez algorytmy rozwiązujące problem.

9

Wykład 1

Część 2

Programowanie liniowe -

informacje wstępne

10

Programowanie liniowe

- definicja słowna

Programowanie liniowe jest to maksymalizacja lub
minimalizacja liniowej funkcji wielu zmiennych

1

x

,

2

x

,…,

n

x

(zwanej funkcją celu), gdy zmienne te podlegają liniowym
warunkom ograniczającym w postaci równań lub
nierówności ≤, ≥.

Słowo „liniowy” oznacza, iż funkcja celu oraz lewe strony
warunków ograniczających mogą być zapisane jako

parametr_1∙

1

x

+ parametr_2∙

2

x

+…+ parametr_n∙

n

x

a prawe strony warunków ograniczających to liczby.

Programowanie liniowe

- wyjaśnienie nazwy

Słowo

"programowanie" występujące w nazwie

„programowanie liniowe” (a także w innych
nazwach poddziedzin badań operacyjnych)

nie

oznacza programowania w sensie tworzenia
programów komputerowych. Słowo to jest
używane jako

synonim słowa „planowanie”

(ang. planning) i wywodzi się z terminologii
stosowanej w początkach badan operacyjnych w
czasie drugiej wojny światowej.

11

Programowanie liniowe

- stosowane skróty

Programowanie liniowe jako jeden z rodzajów
optymalizacji jest niekiedy oznaczane skrótem
PL (albo LP od ang. linear programming).
Konkretny liniowy problem optymalizacyjny
czyli zadanie programowania liniowego jest
oznaczane skrótem

ZPL.

12

13

Programowanie liniowe - postać ogólna (1)

min

max/

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

(funkcja celu)

przy ograniczeniach

i

n

in

i

i

b

x

a

x

a

x

a

≤

+

+

+

...

2

2

1

1

p

i

,...,

2

,

1

=

i

n

in

i

i

b

x

a

x

a

x

a

≥

+

+

+

...

2

2

1

1

.…

q

p

i

,...,

2

,

1

+

=

i

n

in

i

i

b

x

a

x

a

x

a

=

+

+

+

...

2

2

1

1

….

m

q

i

,...,

2

,

1

+

=

(ograniczenia funkcyjne)

0

≥

j

x

1

,...,

2

,

1

n

j =

,

n

n ≤

1

(warunki nieujemności zmiennych)

14

Programowanie liniowe - postać ogólna (2)

ij

a ,

i

b ,

j

c są to parametry

zadania/modelu programowania liniowego

j

x - są to zmienne

zadania/modelu programowania liniowego

15

Czy warunki nieujemności zmiennych są

liniowymi warunkami ograniczającymi?

Tak. Każdy warunek nieujemności zmiennej
można zapisać następująco:

⇔

≥

0

1

x

0

0

...

0

1

2

1

≥

+

+

+

n

x

x

x

⇔

≥

0

2

x

0

0

...

1

0

2

1

≥

+

+

+

n

x

x

x

M

⇔

≥

0

n

x

0

1

...

0

0

2

1

≥

+

+

+

n

x

x

x

16

Dlaczego warunki nieujemności zmiennych

są „wyróżnione” w postaci ogólnej ZPL?

1. Najważniejsza metoda rozwiązywania

ZPL, tzw. metoda simpleks wymaga
nieujemności zmiennych (gdy któraś z
nich może przyjmować wartości
ujemne, wymagane są pewne
przekształcenia ZPL).

2. W zastosowaniach praktycznych PL

zmienne muszą być najczęściej
nieujemne, ponieważ opisują wielkości
przyjmujące wartości nieujemne.

17

Czy jest możliwe zapisane ogólnej

postaci ZPL w prostszej postaci?

Tak. Każde ZPL można sprowadzić do postaci zwanej
niekiedy

postacią standardową.

Występują dwa warianty postaci standardowej:
• z

maksymalizacją funkcji celu i wszystkimi

ograniczeniami funkcyjnymi typu ≤ ;

• z

minimalizacją funkcji celu i wszystkimi

ograniczeniami funkcyjnymi typu ≥.

Nierówności w ograniczeniach funkcyjnych typu ≤
w zadaniach maksymalizacji oraz typu ≥ w zadaniach
minimalizacji nazywane są nierównościami typowymi.

18

Programowanie liniowe - postać

standardowa dla maksymalizacji

max

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

(funkcja celu)

przy ograniczeniach

1

1

2

12

1

11

...

b

x

a

x

a

x

a

n

n

≤

+

+

+

2

2

2

22

1

21

...

b

x

a

x

a

x

a

n

n

≤

+

+

+

M

m

n

mn

m

m

b

x

a

x

a

x

a

≤

+

+

+

...

2

2

1

1

(ograniczenia funkcyjne)

0

≥

j

x

n

j

,...,

2

,

1

=

(warunki nieujemności zmiennych)

19

Programowanie liniowe - postać

standardowa dla minimalizacji

min

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

(funkcja celu)

przy ograniczeniach

1

1

2

12

1

11

...

b

x

a

x

a

x

a

n

n

≥

+

+

+

2

2

2

22

1

21

...

b

x

a

x

a

x

a

n

n

≥

+

+

+

M

m

n

mn

m

m

b

x

a

x

a

x

a

≥

+

+

+

...

2

2

1

1

(ograniczenia funkcyjne)

0

≥

j

x

n

j

,...,

2

,

1

=

(warunki nieujemności zmiennych)

20

Zbiór rozwiązań dopuszczalnych zadania

programowania liniowego - definicja

Zbiór wszystkich

n

n

x

x

x

x

R

∈

=

)

,...,

,

(

2

1

spełniających

wszystkie warunki ograniczające danego zadania
programowania liniowego nazywamy zbiorem
rozwiązań dopuszczalnych (lub krótko: zbiorem
dopuszczalnym) D a jego elementy rozwiązaniami
dopuszczalnymi.

21

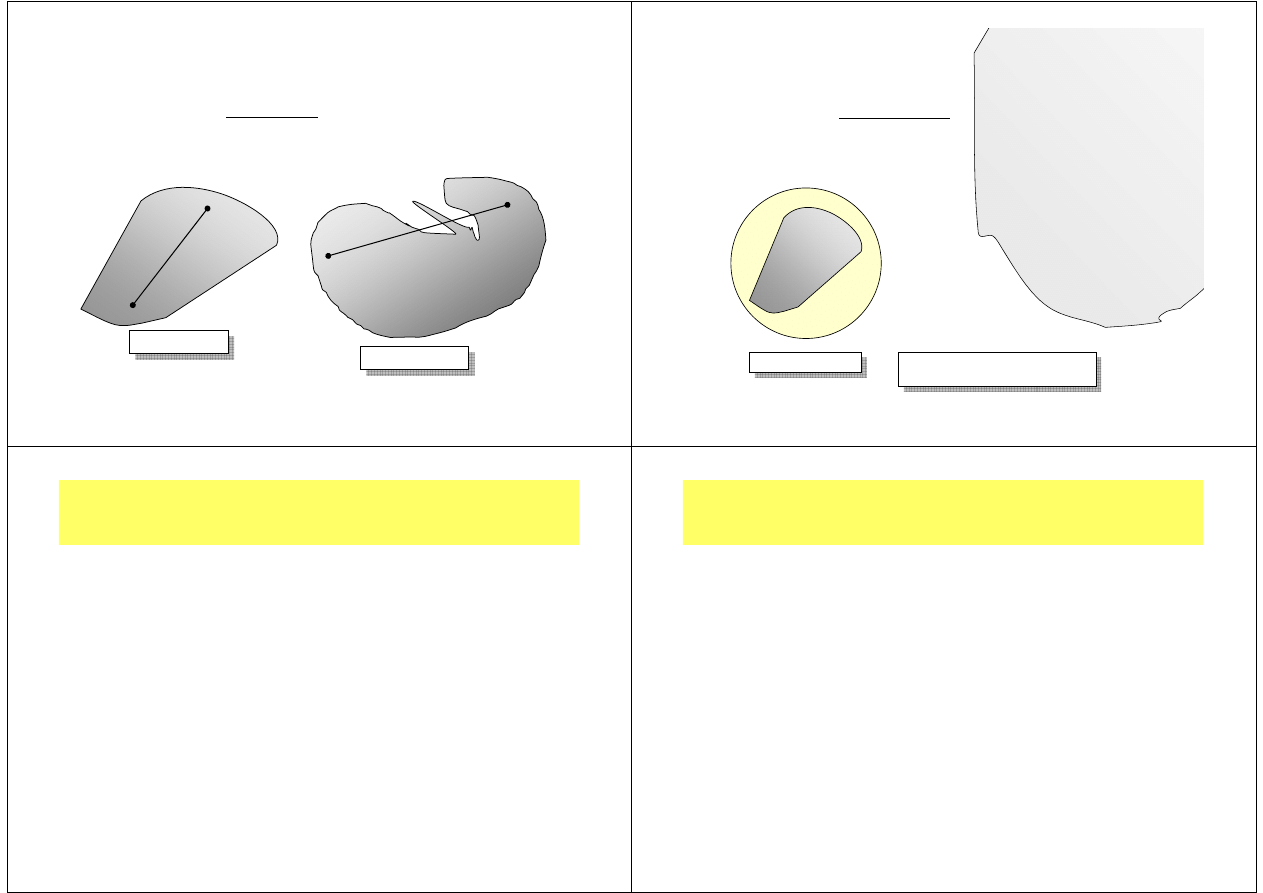
Zbiór wypukły - definicja

Zbiór nazywamy wypukłym, jeżeli dla dowolnych
dwóch punktów należących do tego zbioru, jest w nim
zawarty cały odcinek łączący te punkty.

Zbiór wypukły

Zbiór niewypukły

22

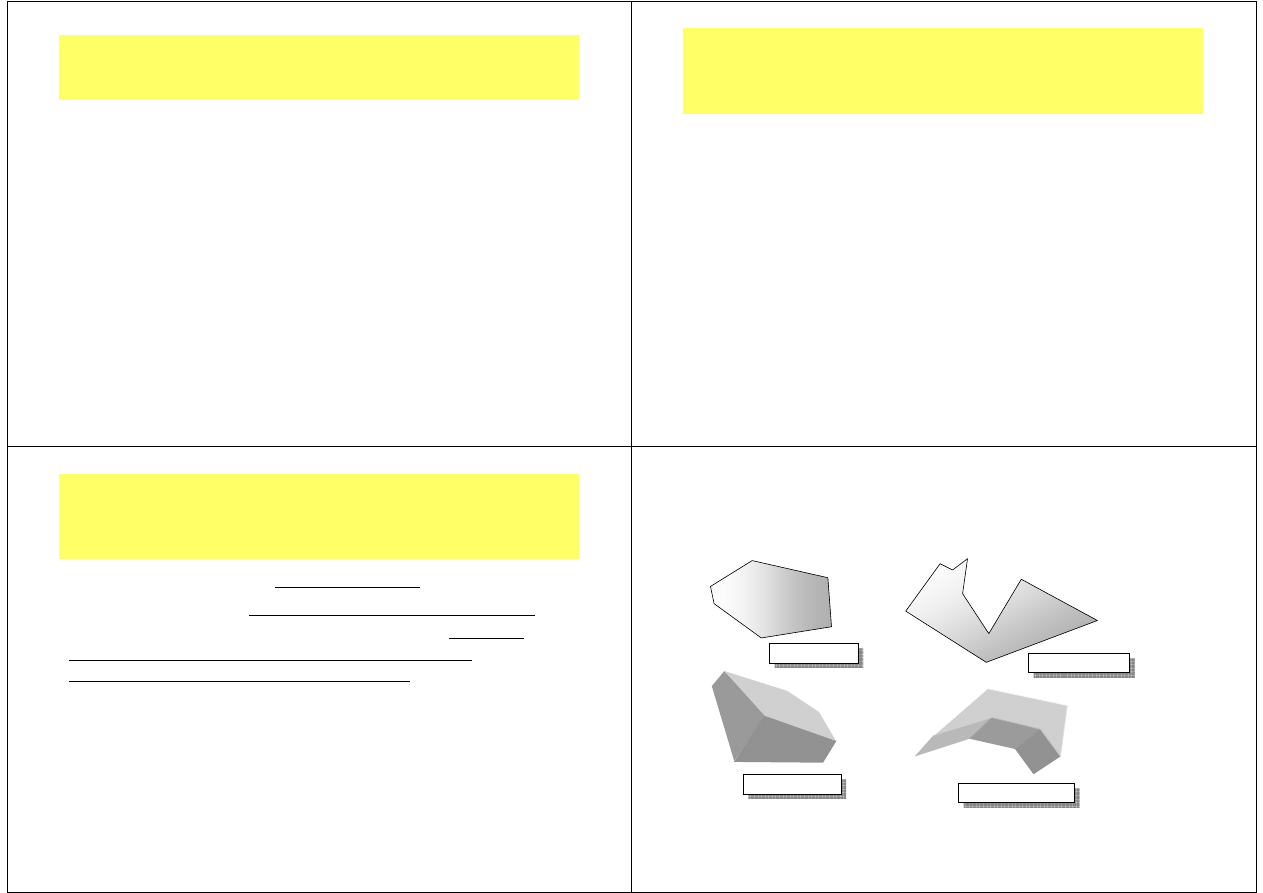
Zbiór ograniczony –
definicja

Zbiór nazywamy ograniczonym,
jeżeli istnieje kula
(na płaszczyźnie koło)
zawierająca ten zbiór

Zbiór ograniczony

Zbiór nieograniczony

– „rozciąga się do nieskończoności”

23

Zbiór rozwiązań dopuszczalnych ZPL –

twierdzenie o kształcie zbioru (1)

Niech n oznacza liczbę zmiennych

decyzyjnych. Wtedy z geometrycznego

punktu widzenia zbiór rozwiązań

dopuszczalnych D zadania programowania

liniowego może być

1) zbiorem ograniczonym:

dla

n=2 - wielokątem wypukłym;

dla

n=3 - wielościanem wypukłym;

dla

n>3 - n-wymiarowym „wielościanem”

wypukłym.

24

2) zbiorem nieograniczonym:
dla

n=2 - nieograniczonym wypukłym

podzbiorem płaszczyzny, którego krawędzie

są półprostymi i ewentualnie odcinkami;
dla

n≥3 - nieograniczonym wypukłym

podzbiorem przestrzeni n-wymiarowej,

którego krawędzie są półprostymi i

ewentualnie

odcinkami.

Zbiór rozwiązań dopuszczalnych ZPL –

twierdzenie o kształcie zbioru (2)

25

Dla pewnych zestawów warunków

ograniczających zbiór dopuszczalny D
może mieć szczególną postać:

• Jest

figurą o niższym wymiarze niż

wymiar przestrzeni (np. jest wielokątem
lub nieograniczonym podzbiorem
płaszczyzny w przestrzeni 3-wymiarowej),
a w szczególności półprostą, odcinkiem
czy wręcz pojedynczym punktem.

• Jest

zbiorem pustym (przypadek

sprzeczności warunków ograniczających).

Zbiór rozwiązań dopuszczalnych ZPL –

twierdzenie o kształcie zbioru (3)

26

W

ogólnym przypadku jest to niemożliwe.

Jednakże istnieją istotne z praktycznego punktu

widzenia typy ZPL, dla których przy realistycznych
parametrach można orzec, że zbiór dopuszczalny D
jest niepusty i, odpowiednio, ograniczony albo
nieograniczony.

Niekiedy można również stwierdzić bez obliczeń, że

zbiór dopuszczalny D jest pusty. Można ten fakt
wywnioskować z wartości niektórych parametrów w
warunkach ograniczających albo z występowania
jednocześnie warunków ograniczających w oczywisty
sposób sprzecznych, jak np.

Czy można stwierdzić bez obliczeń, czy

zbiór dopuszczalny jest ograniczony/

nieograniczony/pusty?

5

1

,

4

7

3

3

2

1

≤

+

+

x

x

x

8

1

,

4

7

3

3

2

1

≥

+

+

x

x

x

27

Jak można stwierdzić, czy dane liczby są

rozwiązaniem dopuszczalnym?

W ogólnym przypadku sprawdzenie czy dane

n

n

x

x

x

x

R

∈

=

)

,...,

,

(

2

1

jest rozwiązaniem dopuszczalnym

danego zadania programowania liniowego wymaga
podstawienia wszystkich powyższych liczb do
wszystkich warunków ograniczających.

Sprawdzenie niektórych warunków takich jak np.
warunki nieujemności zmiennych jest naturalnie
trywialne, ale oczywiście rozbudowane ograniczenia
funkcyjne wymagają szczegółowych obliczeń.

28

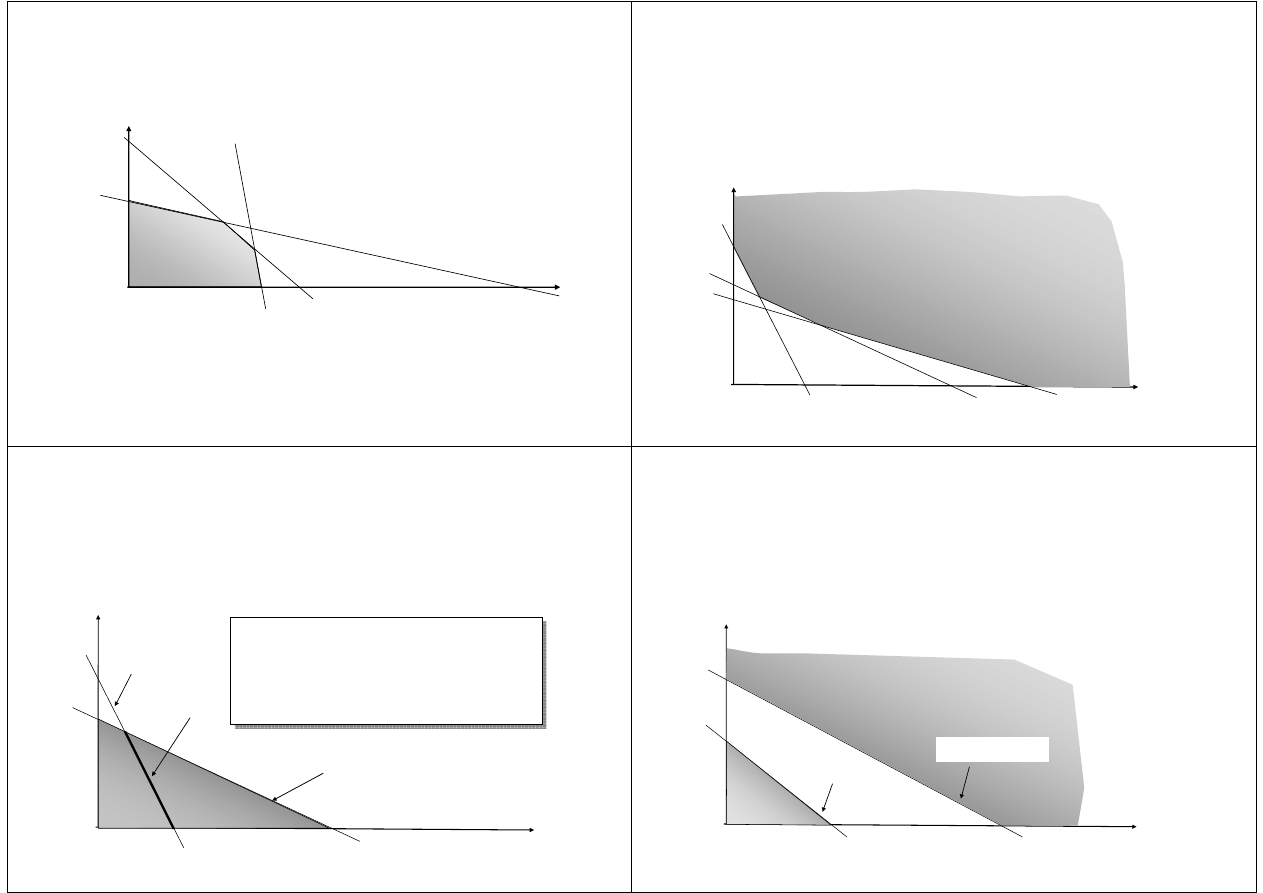
Zbiór rozwiązań dopuszczalnych

kształt zbioru c.d.

Przykłady wielokątów i wielościanów wypukłych i niewy-
pukłych

Wielokąt wypukły

Wielokąt niewypukły

Wielościan wypukły

Wielościan niewypukły

29

Zbiór rozwiązań dopuszczalnych - przykłady

Przykład 1 - zbiór dopuszczalny jest wielokątem
(zbiór ograniczony).

Zbiór rozwiązań dopuszczalnych D dla przypadku n=2.
Zbiór dopuszczalny może mieć taki kształt, gdy wszystkie

ograniczenia funkcyjne mają postać

k

k

k

b

x

a

x

a

≤

+

2

2

1

1

z

dodatnimi parametrami.

x

1

x

2

D

30

Zbiór rozwiązań dopuszczalnych - przykłady

Przykład 2 - zbiór rozwiązań dopuszczalnych jest
nieograniczonym podzbiorem płaszczyzny
(zbiór nieograniczony).
Zbiór dopuszczalny może mieć taki kształt np. gdy wszystkie

ograniczenia funkcyjne mają postać

k

k

k

b

x

a

x

a

≥

+

2

2

1

1

z dodatnimi

parametrami

x

1

x

2

D

D

31

Zbiór rozwiązań dopuszczalnych-przykłady

Przykład 3 - zbiór dopuszczalny na płaszczyźnie (czyli w przestrzeni
2-wymiarowej) jest odcinkiem (czyli jest jednowymiarowy). Zbiór
dopuszczalny może mieć taki kształt np. gdy w modelu występują

ograniczenia „równościowe” czyli typu

j

j

j

b

x

a

x

a

=

+

2

2

1

1

.

x

1

x

2

D

k

k

k

b

x

a

x

a

≤

+

2

2

1

1

j

j

j

b

x

a

x

a

=

+

2

2

1

1

Zbiór D (odcinek) jest częścią wspólną prostej

j

j

j

b

x

a

x

a

=

+

2

2

1

1

oraz części wspólnej 3 pół-

płaszczyzn (wyznaczonych przez warunki
nieujemności zmiennych oraz nierówność

k

k

k

b

x

a

x

a

=

+

2

2

1

1

. Część wspólna w/w 3 półpłasz-

czyzn jest oznaczona jako szary trójkąt.

32

Zbiór rozwiązań dopuszczalnych

Przykład 4 - zbiór rozwiązań dopuszczalnych D jest pusty.
Taka sytuacja może mieć miejsce, gdy w warunkach ograniczających

występują wzajemnie się wykluczające nierówności

k

k

k

b

x

a

x

a

≤

+

2

2

1

1

oraz

j

j

j

b

x

a

x

a

≥

+

2

2

1

1

.

x

1

x

2

k

k

k

b

x

a

x

a

≤

+

2

2

1

1

j

j

j

b

x

a

x

a

≥

+

2

2

1

1

33

Rozwiązanie optymalne zadania

programowania liniowego - definicja

Rozwiązaniem optymalnym (lub krótko – rozwiązaniem)
zadania programowania liniowego nazywamy każdy zbiór
n liczb należących do zbioru rozwiązań dopuszczalnych D:

D

x

x

x

x

n

∈

=

)

,...,

,

(

*

*
2

*

1

*

dla których funkcja celu

n

n

x

c

x

c

x

c

+

+

+

...

2

2

1

1

osiąga maksimum

albo minimum.
Rozwiązanie optymalne:
•

istnieje, jeżeli D jest zbiorem ograniczonym.

•

może nie istnieć, jeżeli D jest zbiorem nieograniczonym

•

nie istnieje, jeżeli D jest zbiorem pustym

Uwaga: Symbole:

n

i

x

i

,...,

1

,

*

=

oznaczają konkretne liczby

będące rozwiązaniem, a nie zmienne!

34

Twierdzenie o rozwiązaniach

optymalnych zadania progr. liniowego

Jeżeli istnieje rozwiązanie optymalne zadania

programowania liniowego, to są to

współrzędne

przynajmniej jednego z wierzchołków zbioru
dopuszczalnego D.

Rozwiązaniami optymalnymi ZPL mogą być

również

współrzędne dwóch lub więcej

wierzchołków zbioru dopuszczalnego D. Jest to
przypadek tzw. rozwiązań wielokrotnych/
alternatywnych.
Wówczas rozwiązaniami są również współrzędne
wszystkich punktów (jest ich nieskończenie wiele)
położonych pomiędzy w/w punktami.

35

Rozwiązania wierzchołkowe

i niewierzchołkowe zadania

programowania liniowego - definicja

Rozwiązaniem wierzchołkowym zadania

programowania liniowego nazywane jest każde
rozwiązanie optymalne, które jest
współrzędnymi jednego z wierzchołków
zbioru dopuszczalnego D.

Każde inne rozwiązanie optymalne nazywane

jest

rozwiązaniem niewierzchołkowym

zadania programowania liniowego.

36

Czy każde ZPL ma rozwiązanie?

1. Tak, jeżeli zbiór rozwiązań dopuszczalnych D jest

zbiorem ograniczonym tzn. punktem, odcinkiem,
wielokątem wypukłym, wielościanem wypukłym lub
n-wymiarowym „wielościanem”.

2. Może nie mieć, jeżeli zbiór rozwiązań

dopuszczalnych D jest zbiorem nieograniczonym
tzn. półprostą, nieograniczonym wypukłym
podzbiorem płaszczyzny lub przestrzeni n-
wymiarowej (n>3), którego krawędzie są półprostymi
i ewentualnie odcinkami. W takim przypadku nie
istnieje maksimum (tzn. funkcja celu dąży do +∞)
albo minimum (tzn. funkcja celu dąży do -∞).

3. Nie, jeżeli zbiór rozwiązań dopuszczalnych D jest

zbiorem pustym.

37

Ile rozwiązań może mieć ZPL?

1. Zero - zawsze gdy zbiór dopuszczalny jest

pusty oraz dla niektórych zbiorów
nieograniczonych (wtedy funkcja celu dąży do
+∞ albo -∞ )

2. Jedno - gdy zbiór dopuszczalny jest niepusty.

3. Nieskończenie wiele - gdy zbiór dopuszczalny

jest niepusty.

38

Wnioski z twierdzenia

o rozwiązaniach optymalnych ZPL

W praktyce powyższe twierdzenie oznacza, że

aby

znaleźć rozwiązanie ZPL, trzeba sprawdzić wartości
funkcji celu jedynie dla współrzędnych każdego z
wierzchołków zbioru dopuszczalnego D tzn.

podstawić współrzędne wierzchołków zbioru

dopuszczalnego D do funkcji celu i sprawdzić, dla

którego z wierzchołków zostanie osiągnięte

maksimum lub minimum.

Takie sprawdzanie może jednak zawieść w przypadku

gdy zbiór dopuszczalny jest nieograniczony, a funkcja
celu dąży do +∞ albo -∞. Metody obliczeniowe
używane w praktyce pozwalają jednak na wykrycie
takiej sytuacji. Ponadto, poprawnie przygotowane
modele rzeczywistych sytuacji decyzyjnych niemal
nigdy nie mają nieskończonego max/min.

39

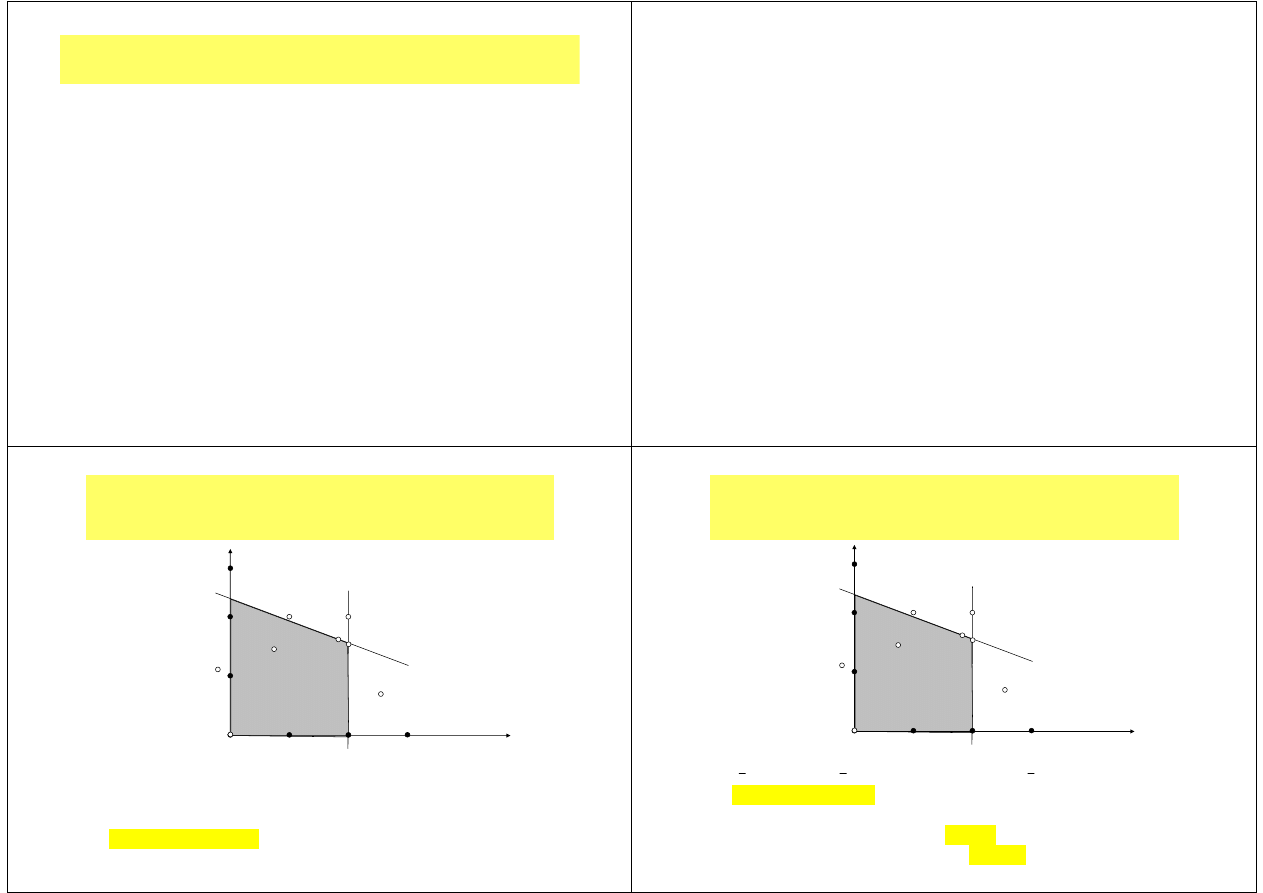
Przykład sprawdzania

dopuszczalności rozwiązań ZPL (1)

max

10

4

2

1

→

+

x

x

przy ograniczeniach

23

10

5

,

3

2

1

≤

+

x

x

2

1

≤

x

0

1

≥

x

,

0

2

≥

x

1

x

,

2

x

-całkowite

Zbiór dopuszczalny
to czworokąt
o wierzchołkach:
(0,0), (2,0), (0;2,3)
oraz (2;1,6).

Podstawienie do warunków ograniczających

A(0,0)

23

0

0

10

0

5

,

3

≤

=

⋅

+

⋅

,

2

0 ≤

,

0

0 ≥

,

0

0 ≥

dopuszcz.

B(0,8;1,5)

23

8

,

17

5

,

1

10

8

,

0

5

,

3

≤

=

⋅

+

⋅

,

2

8

,

0

≤

,

0

8

,

0 ≥

,

0

5

,

1 ≥

dopuszcz.

C(1;2)

23

5

,

23

2

10

1

5

,

3

>

=

⋅

+

⋅

,

2

8

,

0

≤

,

0

8

,

0 ≥

,

0

5

,

1 ≥

nie jest dopuszcz.

x

2

x

1

0

1

2

3

1

2

3

A

D

G

E

B

C

F

H

40

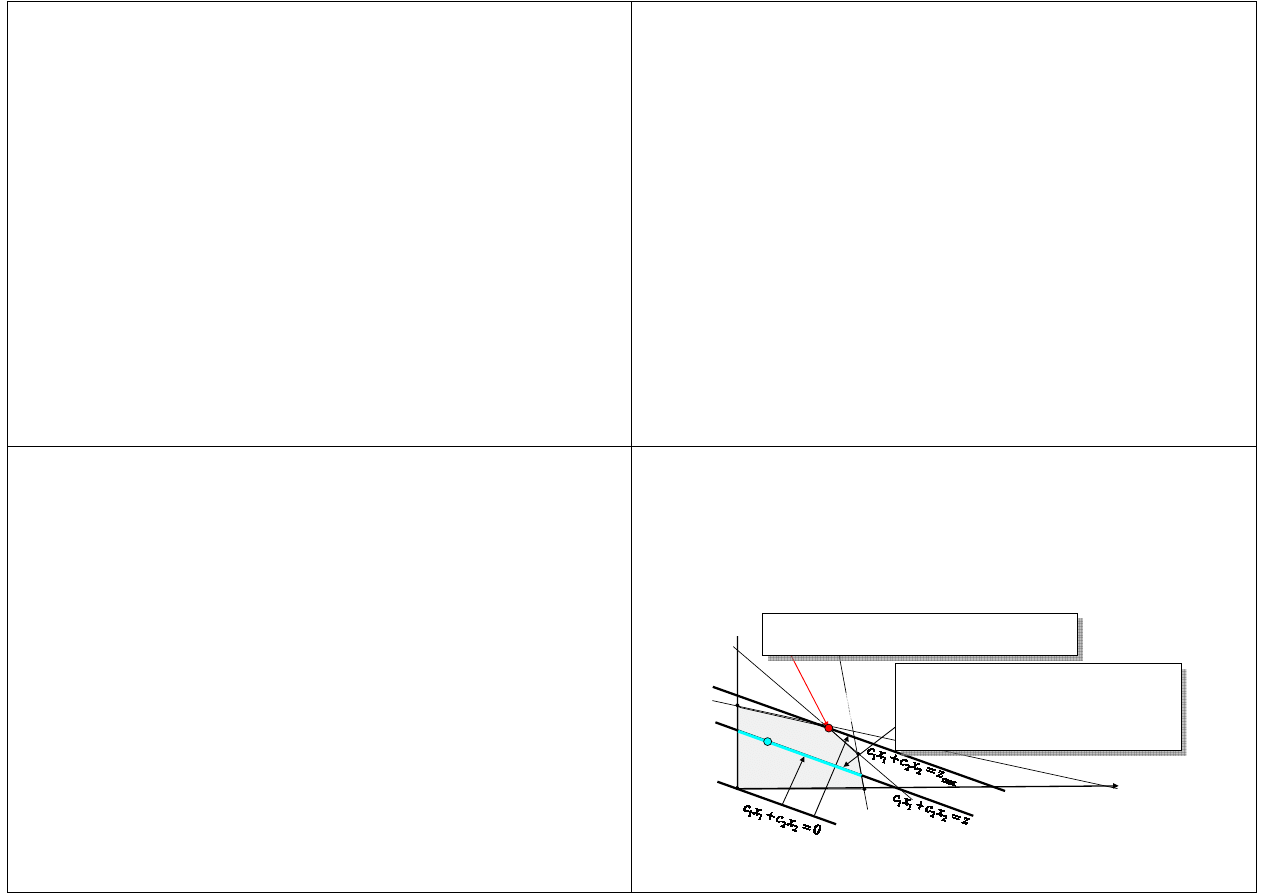
Przykład sprawdzania

dopuszczalności rozwiązań ZPL (2)

max

10

4

2

1

→

+

x

x

przy ograniczeniach

23

10

5

,

3

2

1

≤

+

x

x

2

1

≤

x

0

1

≥

x

,

0

2

≥

x

1

x

,

2

x

-całkowite

Podstawienie do warunków ograniczających

D(1,8;1

3

2

)

23

23

1

10

8

,

1

5

,

3

3

2

≤

=

⋅

+

⋅

,

2

8

,

1 ≤

,

0

8

,

1 ≥

,

0

1

3

2

≥

dopuszcz.

E(2;2)

23

27

2

10

2

5

,

3

>

=

⋅

+

⋅

,

2

8

,

0

≤

,

0

8

,

0 ≥

,

0

5

,

1 ≥

nie jest dopuszcz.

F(2;1,6)

23

23

5

10

2

5

,

3

≤

=

⋅

+

⋅

,

2

8

,

0

≤

,

0

8

,

0

≥

,

0

5

,

1 ≥

dopuszcz.

G(2,5;0,8)

23

75

,

16

8

,

0

10

5

,

2

5

,

3

≤

=

⋅

+

⋅

,

2

5

,

2

>

nie jest dopuszcz.

H(-0,2;1,1)

23

23

5

10

2

5

,

3

≤

=

⋅

+

⋅

,

2

8

,

0

≤

,

0

2

,

0

<

−

nie jest dopuszcz.

x

2

x

1

0

1

2

3

1

2

3

A

D

G

E

B

C

F

H

41

Programowanie liniowe

Rozwiązywanie zadań (1)

Rozwiązywanie zadań programowania

liniowego

nie może być oparte o

obliczanie pochodnych, ponieważ
pochodna funkcji celu po każdej ze
zmiennych jest stałą liczbą, a zatem nie
ma sensu przyrównywanie jej do zera.

42

Programowanie liniowe

Rozwiązywanie zadań (2)

Zadania programowania liniowego z 2

zmiennymi decyzyjnymi można
rozwiązywać przy pomocy tzw.

metody

graficznej. Zostanie ona przedstawiona
później w celu zilustrowania pewnych
charakterystycznych własności
programowania liniowego.

43

Programowanie liniowe

Rozwiązywanie zadań (3)

Uniwersalną metodą rozwiązywania zadań

programowania liniowego jest

algorytm

simpleks (metoda simpleks). Nie będziemy
go jednak omawiać, ponieważ jest on bardzo
pracochłonny, a osoby używające w praktyce
programowania liniowego mają do dyspozycji
bardzo wiele programów komputerowych,
które wykonają niezbędne obliczenia.

44

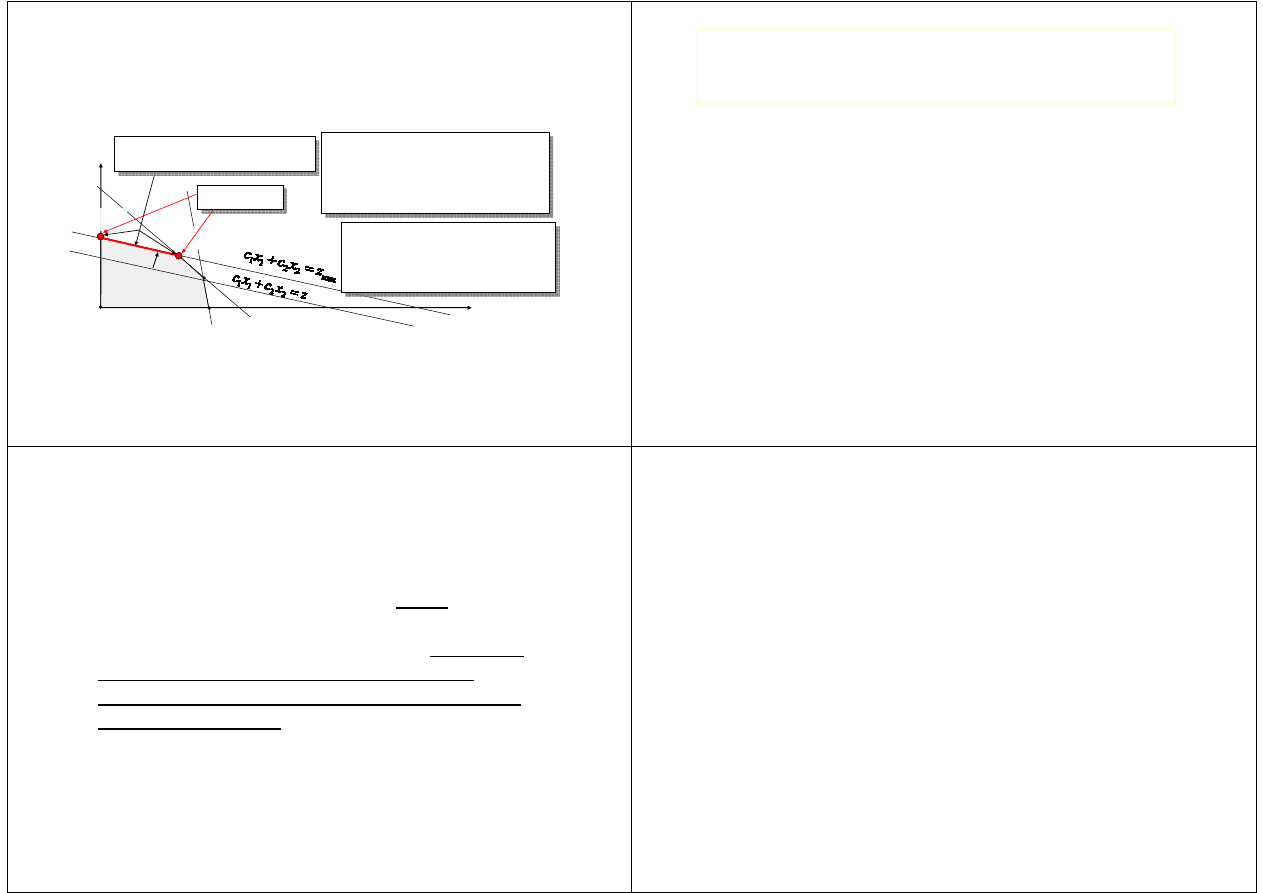
Metoda graficzna rozwiązywania

zadania programowania liniowego

Przykład
Zadanie z maksymalizacją funkcji celu (wszystkie
współczynniki funkcji celu i ograniczeń są dodatnie)

x

1

x

2

D

)

,

(

*

2

*

1

x

x

)

,

(

2

1

X

X

Dla współrzędnych tego punktu funkcja
celu osiąga maksimum równe z

max

.

Niebieski odcinek jest geometryczną re-
prezentacją wszystkich par liczb X

1

, X

2

należących do zbioru dopuszczalnego
D, dla których, po ich podstawieniu do
funkcji celu, przyjmie ona wartość

z

.

45

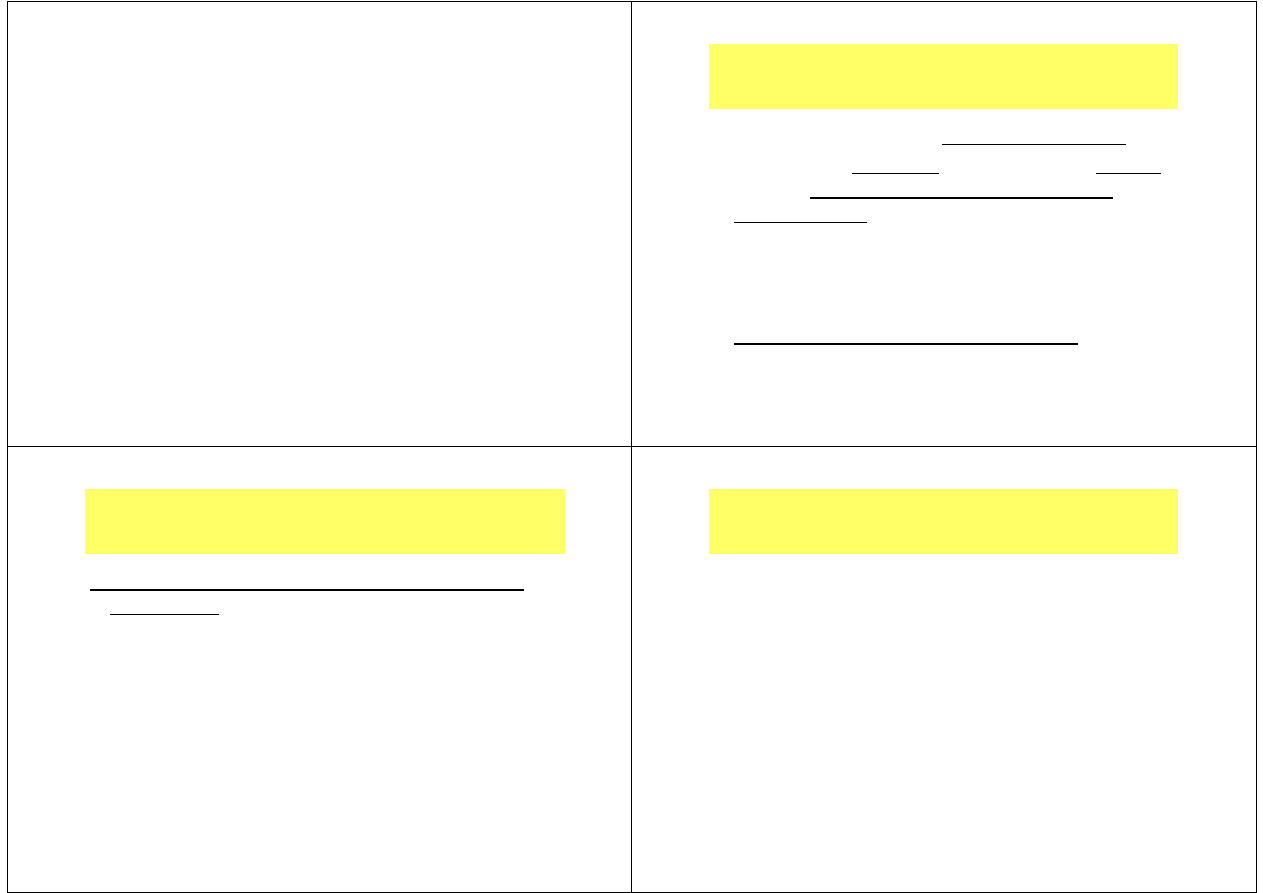
Rozwiązania wielokrotne zadania

programowania liniowego

Przykład

Funkcja celu osiąga maksimum również dla współrzędnych wszystkich

punktów odcinka o końcach

)

,

(

*
21

*

11

*

1

x

x

x =

oraz

)

,

(

*
22

*

12

*
2

x

x

x =

.

x

1

x

2

D

)

,

(

*
21

*

11

x

x

)

,

(

*
22

*

12

x

x

Zbiór rozwiązań wielokrotnych
(geometr. jest to odcinek)

Rozwiązania wielokrotne.
Przypadek n=2 (2 zmienne decy-
zyjne) dla standardowej postaci
zadania programowania liniowego
z dodatnimi parametrami.

Rozwiązania

wierzchołkowe

Dla współrzędnych punktów

)

,

(

*
21

*

11

*

1

x

x

x =

oraz

)

,

(

*
22

*

12

*
2

x

x

x =

funkcja celu osiąga maksimum

tzn.

max

*
22

2

*

12

1

*
21

2

*

11

1

z

x

c

x

c

x

c

x

c

=

+

=

+

.

46

Twierdzenie o kształcie zbioru

rozwiązań wielokrotnych ZPL (1)

Zbiór wszystkich rozwiązań wielokrotnych ZPL może

mieć następującą postać geometryczną

• dla n=2 - odcinek

• dla n=3 - wielokąt wypukły lub odcinek

• dla n>3 – co najwyżej (n-1)-wymiarowy „wielościan”

wypukły, wielokąt wypukły lub odcinek.

47

Twierdzenie o kształcie zbioru

rozwiązań wielokrotnych ZPL (2)

Jeżeli

zbiór dopuszczalny D jest nieograniczony, to

zbiór rozwiązań wielokrotnych może mieć postać
zbioru nieograniczonego o wymiarze co najwyżej o
1 mniejszym niż liczba zmiennych n: półprostej,
nieograniczonego podzbioru płaszczyzny/
przestrzeni, którego krawędziami są półproste i
ewentualnie odcinki,.

Przypadki te są jednak

nieistotne z praktycznego

punktu widzenia, ponieważ modele dla realnych
sytuacji decyzyjnych w zasadzie nigdy nie mają
rozwiązań o takiej postaci.

48

Rozwiązania wielokrotne zadania

programowania liniowego a

oprogramowanie optymalizacyjne

W przypadku, gdy istnieją rozwiązania wielokrotne

zadania programowania liniowego, wiele
programów komputerowych, w tym dodatek do
Excela o nazwie Solver niestety nie pokazuje
wszystkich rozwiązań „wierzchołkowych”, a
jedynie jedno z nich.

Można co prawda stwierdzić, że rozwiązania

alternatywne istnieją, ale wszelkie metody
postępowania, które to umożliwiają, są dość
niewygodne w użyciu.

49

Wykład 1

Część 3

Programowanie liniowe:

Wybór optymalnego planu

(asortymentu) produkcji przy

ograniczonej dostępności

ś

rodków produkcji

50

Wybór optymalnego planu produkcji –

sformułowanie słowne (1)

Firma może produkować n rodzajów wyrobów.

Zakładamy, że wszystkie wyprodukowane wyroby

zostaną sprzedane i to ze stałymi zyskami
jednostkowymi (tzn. nie zależącymi od wielkości
produkcji/sprzedaży). Do produkcji wyrobów
zużywanych jest m różnych rodzajów środków
produkcji (surowce, energia, maszyny, siła
robocza, powierzchnia magazynowa etc.),
dostępnych w ograniczonych ilościach w
pewnym ustalonym okresie czasu.

51

Wybór optymalnego planu produkcji –

model ogólny - sformułowanie słowne (2)

Należy określić, które wyroby i w jakich ilościach

produkować, aby nie przekraczając posiadanych
zasobów środków produkcji, zmaksymalizować
zysk ze sprzedaży tychże wyrobów w pewnym
ustalonym okresie czasu.

52

Wybór optymalnego planu produkcji –

parametry modelu (1)

Dane są:
•

- jednostkowe zużycie i-tego środka produkcji

tzn. ilość tego środka zużywana na wytworzenie
jednej jednostki j-tego wyrobu, liczona np. w
g/kg, mg/l, kg/m

3

, kWh/t, h/t itp.

(i=1,...,m; j = 1,...,n);

•

- maksymalne dostępne zasoby i-tego środka

produkcji w rozważanym okresie czasu, liczone
np. w kg, l, hl, t, m

2

, m

3

, m (i=1,...,m);

ij

a

i

b

53

Wybór optymalnego planu produkcji –

parametry modelu (2)

•

- zysk jednostkowy dla wyrobu j-tego rodzaju

tzn. zysk pochodzący ze sprzedaży jednej
jednostki wyrobu, liczony w PLN/m, PLN/kg,
PLN/m

3

, PLN/t itp. (zamiast PLN może być

oczywiście dowolna inna waluta, ale dla
wszystkich wyrobów jednakowa) (j = 1,...,n).

j

c

54

Wybór optymalnego planu produkcji –

zmienne decyzyjne

Zmiennymi decyzyjnymi w tym zagadnieniu są

wielkości produkcji i sprzedaży wyrobów:

•

- wielkość produkcji j-ego wyrobu liczona np.

w kg, l, hl, t, m

3

,m

2

, m, szt. (naturalnie wyroby

różnych rodzajów mogą być liczone w różnych
jednostkach np. niektóre w kg a inne w litrach).

j

x

55

Wybór optymalnego planu produkcji –

ogólny model matematyczny

max

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

- łączny zysk ze sprzedaży wyrobów

przy ograniczeniach

rzeczywiste zużycie

maksymalne dostępne zasoby

środków produkcji

środków produkcji

1

1

2

12

1

11

...

b

x

a

x

a

x

a

n

n

≤

+

+

+

2

2

2

22

1

21

...

b

x

a

x

a

x

a

n

n

≤

+

+

+

M M

m

n

mn

m

m

b

x

a

x

a

x

a

≤

+

+

+

...

2

2

1

1

0

1

≥

x

,

0

2

≥

x

,....,

0

≥

n

x

ilości wyrobów nie mogą być ujemne

56

Programowanie liniowe -

wybór optymalnego planu produkcji

57

Wybór optymalnego planu produkcji – uwagi:

wielkość produkcji a wielkość sprzedaży

W modelu występuje założenie

wielkość produkcji =

wielkość sprzedaży (zmienne decyzyjne w
funkcji celu oznaczają de facto wielkości
sprzedaży natomiast w warunkach
ograniczających - wielkości produkcji).

W rzeczywistości albo:

wszystkich wyprodukowanych wyrobów nie
uda się sprzedać (zatem te niesprzedane nie
przynoszą zysku)

albo:

produkcja jest realizowana w ramach
konkretnych zamówień, które nie muszą się
pokrywać z wyliczonym, optymalnym (tzn.
maksymalizującym zysk)

planem produkcji.

58

Istnienie rozwiązania dla zadania

optymalnego planu produkcji

Rozważany model wyboru planu produkcji

gwarantuje

istnienie rozwiązania

optymalnego dla dowolnych realistycznych
parametrów tzn.

nieujemnych , dodatnich (wartości
parametrów funkcji celu nie mają znaczenia ).
Jest tak, ponieważ dla parametrów takich jak
wyżej zbiór rozwiązań dopuszczalnych jest
niepusty

ij

a

i

b

j

c

59

Wybór optymalnego planu produkcji

a kwestia podzielności wyrobów

Jeżeli choć

jeden z rodzajów wyrobów musi być (ze

względu na swoją niepodzielność, np. jest to
urządzenie, maszyna, produkt odzieżowy itp.)

liczony w

sztukach, to wtedy może być konieczne dodanie
warunków całkowitoliczbowości zmiennej/ych,
ponieważ nie ma żadnej gwarancji, że rozwiązanie
przyjmie wartości całkowitoliczbowe.
Oznacza to, że rozważane zadanie stanie się

zadaniem

tzw. liniowego programowania całkowitoliczbowego.
Niepodzielność wyrobów występuje częściej niż to się
na pozór wydaje, ponieważ nawet wyroby podzielne (np.
soki, sery, proszek do prania) z reguły są pakowane w
niepodzielne opakowania o ustalonych rozmiarach

60

Wybór optymalnego planu produkcji

a postać standardowa ZPL

Ogólne wzory dla zadania wyboru

optymalnego planu (asortymentu)
produkcji

są identyczne jak podana

wcześniej

postać standardowa zadania

programowania liniowego dla
maksymalizacji.

Wykład 1

Część 4

Programowanie liniowe:

zadanie optymalnej diety

62

Wybór optymalnej diety –

sformułowanie słowne

Zakładamy, że w pewnym ustalonym okresie

czasu (najczęściej 1 dnia) należy spożyć

co

najmniej minimalne wymagane ilości m
różnych

składników odżywczych (takich jak

białko, węglowodany, tłuszcze, witaminy, sole
mineralne itp. a także odpowiednią ilość kalorii)

zawartych w dostępnych produktach n

rodzajów.

Zakładamy ponadto, że

koszty jednostkowe

produktów

są stałe i nie zależą od wielkości

zakupu a

ilość zakupiona = wielkość

spożycia.

63

Wybór optymalnej diety –

sformułowanie słowne cd.

Należy zaplanować, które produkty spożywcze

i w jakich ilościach należy zakupić aby
zminimalizować łączne koszty ich zakupu w
rozważanym okresie,

dostarczając przy tym co

najmniej tyle składników odżywczych, ile
wymagają normy.

64

Wybór optymalnej diety –

parametry modelu

•

ij

a

- zawartość i-tego składnika

odżywczego na jednostkę j-tego
produktu np. ilość gramów białka na kg
kiszonki w mieszance paszowej, gramów
węglowodanów na kg dżemu, dekagra-
mów tłuszczu na kg mięsa, miligramów
witaminy C na litr soku itp. (czyli
zawartości te są liczone w takich
jednostkach jak g/kg, dag/kg, mg/l,
kcal/kg) (i= 1,...,m; j = 1,...,n);

65

Wybór optymalnej diety –

parametry modelu c.d.

•

i

b

- minimalne wymagane spożycie i-tego

składnika odżywczego w rozważanym
okresie (liczone w takich jednostkach jak mg,
g, kg, ml, l, cm

3

, kcal) (i=1,...,m);

•

j

c

- cena jednostkowa dla j-tego

produktu (j = 1,...,n) (liczona w PLN/l,
PLN/kg, PLN/m

3

, PLN/t itp. – zamiast PLN

może być oczywiście dowolna inna waluta, ale
dla wszystkich produktów jednakowa).

66

Wybór optymalnej diety –

zmienne decyzyjne

Zmiennymi decyzyjnymi w tym zagadnieniu są

ilości produktów spożywczych:

•

-

wielkość zakupu (i spożycia) j-ego

produktu spożywczego.

j

x

67

Wybór optymalnej diety –

ogólny model matematyczny

min

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

łączny koszt zakupu produktów

przy ograniczeniach

rzeczywiste spożycie

minimalne wymagane spożycie

składników odżywczych

składników odżywczych

1

1

2

12

1

11

...

b

x

a

x

a

x

a

n

n

≥

+

+

+

2

2

2

22

1

21

...

b

x

a

x

a

x

a

n

n

≥

+

+

+

M

M

m

n

mn

m

m

b

x

a

x

a

x

a

≥

+

+

+

...

2

2

1

1

0

1

≥

x

,

0

2

≥

x

,....,

0

≥

n

x

ilości produktów nie mogą być

ujemne

68

Programowanie liniowe -

wybór optymalnej diety

Wybór optymalnej (najtańszej) diety - model ogólny

Wyboru diety można dokonać zakupując niektóre lub wszystkie spośród
n różnych dostępnych produktów spożywczych.

…

?

1

x

kg

?

2

x

kg

?

3

x

kg

?

4

x

l

…

?

n

x

kg

69

Wybór optymalnej diety – aspekty

praktyczne żywienia ludzi

Choć nie ma to znaczenia z punktu widzenia

złożoności obliczeń, z praktycznego punktu
widzenia ten model jest stosowany raczej do
układania planów żywienia dla zwierząt niż
dla ludzi, a to ze względu na

pominięcie

kwestii walorów smakowych oraz nieuchronną
monotonię tak ułożonej diety.

70

Czy zadanie optymalnej diety ma

zawsze rozwiązanie?

Zadanie optymalnej diety w podanej wyżej

(„podręcznikowej”)

postaci (tzn. wyłącznie z

dolnymi limitami spożycia składników), gdzie
parametry , , są dodatnie (ewentualnie
niektóre mogą wynosić 0, jeżeli składnik i
nie jest zawarty w produkcie j)

ma zawsze

rozwiązanie.
Rozwiązanie to jednak

może mieć znaczne

przekroczone minimalne limity spożycia dla
niektórych składników.

ij

a

i

b

j

c

ij

a

71

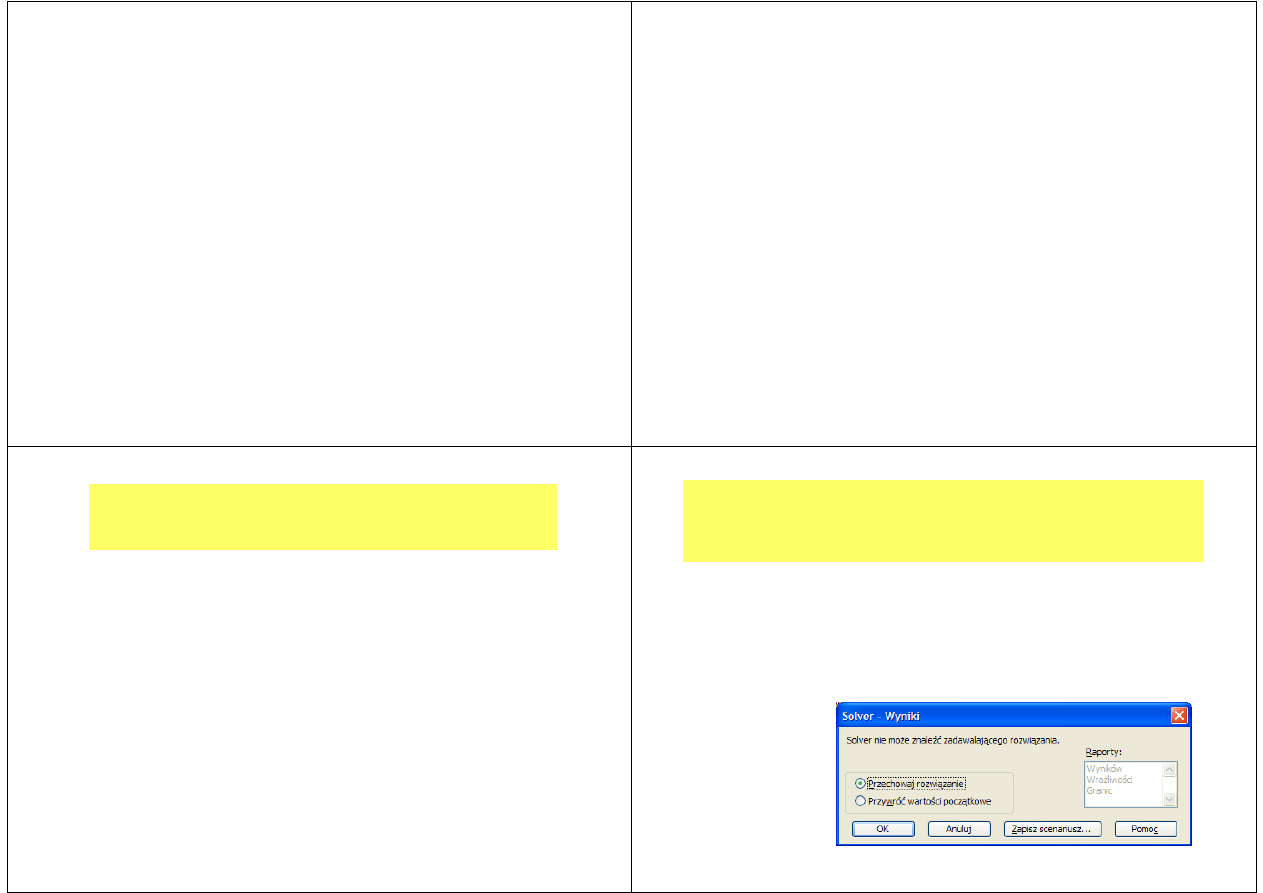
Czy w zadaniu optymalnej diety

istnieje maksimum funkcji celu?

Zadanie optymalnej diety w wersji tylko z dolnymi

limitami spożycia składników jest przykładem
zadania, w którym

nie istnieje maksimum funkcji

celu (alternatywnie można powiedzieć, że
maksimum to wynosi „plus nieskończoność”).

Konsekwencją tego faktu jest np. komunikat błędu
przy rozwiązywaniu zadania Solverem, jeśli parametr
„Równa” jest ustawiony omyłkowo na Maks zamiast
na Min

72

73

Wybór optymalnej diety –

przekroczenie spożycia składników

Jak już wspomniano wcześniej najtańsza

dieta może mieć znacznie przekroczone

spożycie niektórych składników. Wynika

stąd, iż

„realne” zadanie optymalnej diety

powinno uwzględnić nie tylko minimalne

wymagane spożycie składników, ale

także

maksymalne dopuszczalne ze względów

zdrowotnych spożycie składników

(zasada „co za dużo to niezdrowo”).

74

Wybór optymalnej diety – rozszerzenie

modelu o górne normy spożycia

Jeżeli istnieją górne normy zawartości składników

i

d

to

do zadania należy dołączyć następującą grupę warunków
ograniczających:

rzeczywiste spożycie

maks.dopuszczalne spożycie

składników odżywczych składników odżywczych

1

1

2

12

1

11

...

d

x

a

x

a

x

a

n

n

≤

+

+

+

2

2

2

22

1

21

...

d

x

a

x

a

x

a

n

n

≤

+

+

+

M

M

m

n

mn

m

m

d

x

a

x

a

x

a

≤

+

+

+

...

2

2

1

1

75

min

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

- łączny koszt zakupu produktów

przy ograniczeniach

rzeczywiste spożycie

minimalne wymagane spożycie

składników odżywczych

składników odżywczych

1

1

2

12

1

11

...

b

x

a

x

a

x

a

n

n

≥

+

+

+

M

M

m

n

mn

m

m

b

x

a

x

a

x

a

≥

+

+

+

...

2

2

1

1

rzeczywiste spożycie

maksymalne dopuszczalne spożycie

składników odżywczych

składników odżywczych

1

1

2

12

1

11

...

d

x

a

x

a

x

a

n

n

≤

+

+

+

M

M

m

n

mn

m

m

d

x

a

x

a

x

a

≤

+

+

+

...

2

2

1

1

0

1

≥

x

,

0

2

≥

x

,....,

0

≥

n

x

ilości produktów

nie mogą być ujemne

Wybór optymalnej diety –

ogólny model matematyczny z dolnymi i

górnymi normami spożycia

76

Czy zadanie optymalnej diety z górnymi

normami spożycia składników ma

zawsze rozwiązanie?

Nie, ponieważ warunki ograniczające z górnymi i

dolnymi limitami (normami) mogą się okazać

sprzeczne, zwłaszcza jeżeli do stworzenia diety
użyte są produkty o mało zróżnicowanym
składzie.

Próba rozwiązania w Excelu skutkuje następującym
komunikatem:

77

Wybór optymalnej diety –

uwagi historyczne

Zadanie optymalnej diety jest historycznie rzecz biorąc

jednym z pierwszych modeli programowania
liniowego zastosowanym w praktyce. Co ciekawe,
zostało ono pierwotnie użyte do ułożenia diety dla
ludzi.

Rozwiązanie przy pomocy metody simpleks

zadania

optymalnej diety z:

•

77 zmiennymi (n=77 - wybór dotyczył 77 produktów
spożywczych),

•

9 ograniczeniami funkcyjnymi (m=9 -
uwzględniono

9 składników odżywczych)

zajęło

jesienią 1947 roku:

78

Wybór optymalnej diety –

uwagi historyczne c.d.

10 pracownikom korzystającym z

mechanicznych kalkulatorów

łączny czas
120 roboczodniówek czyli ok. 1000 godzin.

79

Wybór optymalnej diety –

uwagi historyczne

80

Wybór optymalnej diety –

uwagi historyczne

Wykład 1

Część 5

Programowanie liniowe:

zadanie optymalnej mieszanki

(ang. blending problem)

82

Programowanie liniowe -

zadanie optymalnej mieszanki

Model matematyczny identyczny jak w zadaniu

optymalnej diety może również być użyty przy
wyborze najtańszej mieszanki „docelowej”
dowolnych substancji (niekoniecznie produktów
spożywczych) spełniającej dolne i ewentualnie
górne normy zawartości składników.

Substancje te są dalej nazywane roboczo

mieszankami „składowymi”, czyli jednorodnymi
mieszaninami związków chemicznych i/lub
pierwiastków (przykładem są produkty spożywcze
w zadaniu optymalnej diety).

83

Programowanie liniowe -

zadanie optymalnej mieszanki

Zadanie optymalnej mieszanki może być również

sformułowane w taki sposób, że zarówno:

•

zawartości składników w mieszankach

„składowych”

jak i

•

wymagane ilości składników zawartych w
mieszance „docelowej”

mogą być wyrażone nie w liczbach bezwzględnych,

ale

w procentach.

Funkcja celu oznacza wtedy łączny koszt jednej

jednostki mieszanki „docelowej”.

84

Zadanie optymalnej mieszanki (podejście

„procentowe”) – sformułowanie słowne

Należy zaplanować, które mieszanki

„składowe” i w jakich ilościach (lub

udziałach procentowych) należy zakupić

aby

zminimalizować łączny koszt 1

jednostki mieszanki „docelowej”,

zapewniając przy tym, że

zawartości

składników w mieszance „docelowej” będą

takie jak przewidują wymagania (dolne lub

górne normy). Ponadto, ilości mieszanek

„składowych” muszą się sumować do 1

jednostki (np. do 1 kilograma), w której to

jednostce są mierzone zarówno mieszanki

„składowe” jak i mieszanka „docelowa”.

85

Model matematyczny dla zadania optymalnej

mieszanki (podejście „procentowe”) - parametry

•

-

zawartość procentowa i-tego składnika w j-

tej mieszance „składowej” (i= 1,...,m; j = 1,...,n) –
ilość procent każdego ze składników zawartych w
mieszance „składowej”.

Ilości „procentowe” są

liczbowo równe ilości dag składnika na kg
mieszanki „składowej” (dag/kg) albo centylitrów
składnika na litr mieszanki „składowej” (cl/l, cl –
centylitr=0,01 litra), oczywiście pod warunkiem, że
jednostkami, w których liczone są mieszanki
„składowe” są odpowiednio kilogramy czy litry.

ij

a

86

Model matematyczny dla zadania optymalnej

mieszanki (podejście „procentowe”) –

parametry cd.

•

-

minimalne wymagane/maksymalne

dopuszczalne zawartości procentowe i-tego
składnika w mieszance „docelowej”
(i=1,...,m). Są one liczbowo równe wymaganej
liczbie dag czy cl przypadającej na kg/litr
mieszanki „docelowej”.

•

-

cena jednostkowa dla j-tej mieszanki

„składowej” (j = 1,...,n), liczona np. w PLN/l,
PLN/kg, PLN/m

3

, PLN/t itp. – zamiast PLN może

być oczywiście dowolna inna waluta, ale dla
wszystkich mieszanek „składowych” jednakowa.

i

i

d

b

/

j

c

87

Model matematyczny dla zadania optymalnej

mieszanki (podejście „procentowe”) –

zmienne decyzyjne

Zmiennymi decyzyjnymi są ilości mieszanek

składowych:

•

- ilość j-tej mieszanki „składowej” liczona np.

w kg (po przemnożeniu przez 100% ilość ta jest
równa udziałowi procentowemu j-tej mieszanki
„składowej” w mieszance „docelowej”).

j

x

88

Zadanie optymalnej mieszanki (podejście

„procentowe”) - model matematyczny (1)

min

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

łączny koszt 1 jedn. (np. kg, l, t) mieszanki „docelowej”

przy ograniczeniach

rzeczywiste % zawart. składn. minimalne wymagane % zawart.
w mieszance „docelowej” składn.w mieszance „docelowej”

1

1

2

12

1

11

...

b

x

a

x

a

x

a

n

n

≥

+

+

+

M

M

m

n

mn

m

m

b

x

a

x

a

x

a

≥

+

+

+

...

2

2

1

1

rzeczywiste % zawart. składn maksymalne dopuszczalne zawart.
w mieszance „docelowej”

składn.w mieszance „docelowej”

1

1

2

12

1

11

...

d

x

a

x

a

x

a

n

n

≤

+

+

+

M

M

m

n

mn

m

m

d

x

a

x

a

x

a

≤

+

+

+

...

2

2

1

1

89

Zadanie optymalnej mieszanki (podejście

„procentowe”) - model matematyczny (2)

1

...

2

1

=

+

+

+

n

x

x

x

ilości mieszanek „składowych”

muszą się sumować do 1 (1 jednostki mieszanki
„docelowej”)

0

1

≥

x

,

0

2

≥

x

,....,

0

≥

n

x

ilości mieszanek „składowych”

nie mogą być ujemne.

90

Parametry

i

b

mogą również w szczególności

oznaczać dokładne procentowe zawartości
składników w mieszance docelowej.

Jeżeli wszystkie procentowe zawartości składników
w mieszance docelowej mają postać równości, to
model matematyczny przybiera wtedy postać
podaną na następnym slajdzie.

Zadanie optymalnej mieszanki (podejście

„procentowe”) - „dokładne” normy

zawartości składników

91

Zadanie optymalnej mieszanki (podejście

„procentowe”) - model matematyczny:

„dokładne” normy zawartości składników

min

...

2

2

1

1

→

+

+

+

n

n

x

c

x

c

x

c

łączny koszt 1 jedn. (np. kg, l, t) mieszanki „docelowej”

przy ograniczeniach

rzeczywiste zawartości

wymagane zawartości

składników w mieszance

składników w mieszance

„docelowej”

„docelowej”

1

1

2

12

1

11

...

b

x

a

x

a

x

a

n

n

=

+

+

+

M

M

m

n

mn

m

m

b

x

a

x

a

x

a

=

+

+

+

...

2

2

1

1

1

...

2

1

=

+

+

+

n

x

x

x

ilości mieszanek „składowych” muszą

się sumować do 1 (1 jednostki mieszanki „docelowej”)

0

1

≥

x

,

0

2

≥

x

,....,

0

≥

n

x

ilości mieszanek „składowych” nie

mogą być ujemne.

92

Jeżeli parametry

ij

a

i

i

b

opisują „pełne”

zawartości mieszanek składowych i docelowej
tzn. opisują zawartości wszystkich ich
składników, co matematycznie można zapisać
jako:

1

1

=

∑

=

m

j

ij

a

oraz

1

1

=

∑

=

m

j

j

b

albo równoważnie:

%

100

1

=

∑

=

m

j

ij

a

oraz

%

100

1

=

∑

=

m

j

j

b

Zadanie optymalnej mieszanki (podejście

„procentowe”) z „dokładnymi” normami

zawartości składn. – uwagi (1)

93

Zadanie optymalnej mieszanki (podejście

„procentowe”) z „dokładnymi” normami

zawartości składn. – uwagi (2)

a warunki ograniczające związane z zawartością
składników mają postać równości, to wtedy
można zrezygnować z warunku

1

...

2

1

=

+

+

+

n

x

x

x

ponieważ warunki związane z zawartością
gwarantują jego spełnienie.

94

Zadanie optymalnej mieszanki (podejście

„procentowe”) – zadanie przykładowe

Należy wymieszać ze sobą 6 stopów ołowiu, cynku i cyny o ró-
żnych zawartościach składników i cenach za kg tak, aby
otrzymać nowy stop o zadanym składzie procentowym i jak
najniższej cenie za kg. Dane liczbowe są zawarte w tabeli.

Stopy „składowe”

S1 S2 S3 S4 S5 S6

Ceny jednostko-
we stopów
„składowych”
(PLN/kg)

5,50 5,70 5,80 6,00 6,10 5,30

Składniki stopów

Zawartości składników w sto-

pach „składowych”(w % lub

alternatywnie w dag/kg)

Zawartość

składników

w stopie

„docelowym”

(w % lub

alternatywnie

w dag/kg)

ołów (Pb)

33

28 40

50 20

20

30

cynk (Zn)

17

30 50

20 49

50

30

cyna (Sn)

50

42 10

30 31

30

40

95

Zadanie optymalnej mieszanki (podejście

„procentowe”) – zadanie przykładowe:

tworzenie modelu

6

5

4

3

2

1

,

,

,

,

,

x

x

x

x

x

x

- ilości stopów „składowych”

(odpowiednio S1, S2,…,S6) w kg

min

3

,

5

1

,

6

6

8

,

5

7

,

5

5

,

5

6

5

4

3

2

1

→

+

+

+

+

+

x

x

x

x

x

x

-

łączny koszt 1 kg stopu „docelowego

”

przy ograniczeniach

rzeczywiste zawartości

wymagane zawartości składn.

składn. w stopie „docelowym”

w stopie „docelowym”

30

20

20

50

40

28

33

6

5

4

3

2

1

=

+

+

+

+

+

x

x

x

x

x

x

30

50

49

20

50

30

17

6

5

4

3

2

1

=

+

+

+

+

+

x

x

x

x

x

x

40

30

31

30

10

42

50

6

5

4

3

2

1

=

+

+

+

+

+

x

x

x

x

x

x

1

...

6

2

1

=

+

+

+

x

x

x

ilości stopów w sumie wynoszą 1 kg

0

1

≥

x

,

0

2

≥

x

,....,

0

6

≥

x

ilości stopów „składowych”

nie mogą być ujemne.

96

Zadanie optymalnej mieszanki (podejście

„procentowe”) – zadanie przykładowe:

tworzenie modelu

1.Ograniczenie

1

...

6

2

1

=

+

+

+

x

x

x

jest de facto zbędne,

ponieważ dodanie stronami 3 ograniczeń na ilości
składników prowadzi do równoważnej mu równości

100

100

100

100

100

100

100

6

5

4

3

2

1

=

+

+

+

+

+

x

x

x

x

x

x

.

Jest to przypadek zadania, gdy parametry

ij

a

i

i

b

opisują

„pełne” zawartości mieszanek „składowych” (czyli
zawartości wszystkich składników).

2. Funkcja celu „rozpisana” z jednostkami miar to:

6

6

3

,

5

...

2

2

7

,

5

1

1

5

,

5

6

2

1

S

kg

x

S

kg

PLN

S

kg

x

S

kg

PLN

S

kg

x

S

kg

PLN

+

+

+

.

Zatem po „skróceniu” kg stopów „składowych” jednostka
funkcji celu to PLN.

97

Zadanie optymalnej mieszanki (podejście

„procentowe”) – zadanie przykładowe:

tworzenie modelu

3. Procentowy skład stopu „docelowego” to:

30% Pb, 30% Zn i 40% Sn.

W przeliczeniu na jednostki bezwzględne oznacza to, że
1 kg stopu „docelowego” składa się z 30 dag Pb, 30 dag
Zn i 40 dag Sn (czyli

wartości liczbowe w jednostkach

bezwzględnych są takie same jak wartości
procentowe).
Analogicznie, jeżeli chodzi o zawartości składników w
stopach „składowych” to np. 33% zawartości Pb w 1-ym
stopie składowym (S1) oznacza dokładnie to samo co
zawartość 33 dag ołowiu na 1 kg S1.

98

Zadanie optymalnej mieszanki (podejście

„procentowe”) – zadanie przykładowe:

tworzenie modelu

Biorąc pod uwagę w/w rozważania, można „rozpisać”
warunki ograniczające z jednostkami miar (przykładowo
podany jest pierwszy z nich):

Pb

dag

S

kg

x

S

kg

Pb

dag

S

kg

x

S

kg

Pb

dag

S

kg

x

S

kg

Pb

dag

30

6

6

20

...

2

2

28

1

1

33

6

2

1

=

+

+

+

Po „skróceniu” kg stopów „składowych” widać, że obie
strony nierówności wyrażają się w dag składnika
(np.dag Pb). Co ważniejsze jednak, współczynniki w
warunkach ograniczających liczone w dag na kg mają
te same wartości liczbowe co współczynniki
„procentowe”, dlatego też nie wymagają one żadnych
dodatkowych przeliczeń.

99

Zadanie optymalnej mieszanki (podejście

„procentowe”) – zadanie przykładowe:

rozwiązanie

Minimalny koszt 1 kg stopu „docelowego” wynosi 5,474 PLN.
W tym celu należy zmieszać stopy „składowe” w ilościach:

=

*

1

x

0,606 kg (60,6%),

=

*
2

x

0 kg

(0%),

=

*

3

x

0,106 kg (10,6%)

=

*
4

x

0 kg

(0%),

=

*

5

x

0 kg

(0%),

=

*

6

x

0,288 kg (28,8%).

Odpowiada to zawartościom procentowym stopów „składowych”
w stopie „docelowym” w następujących proporcjach: 60,6%
pierwszego, 10,6% trzeciego oraz 28,8% szóstego. Oznacza to
zatem, że mieszanka stopów „składowych” o dowolnej masie
m kg wymieszana w w-w proporcjach będzie miała dla wyma-
ganych procentowych zawartości składników najniższy możliwy
koszt równy 5,474∙m PLN.