OBLICZANIE ŁAW SZEREGOWYCH NA PODŁOŻU SPRĘŻYSTYM

ZA POMOCĄ METODY ANALITYCZNEJ

(model Winklera, metoda Bleicha)

1. Założenia i dane

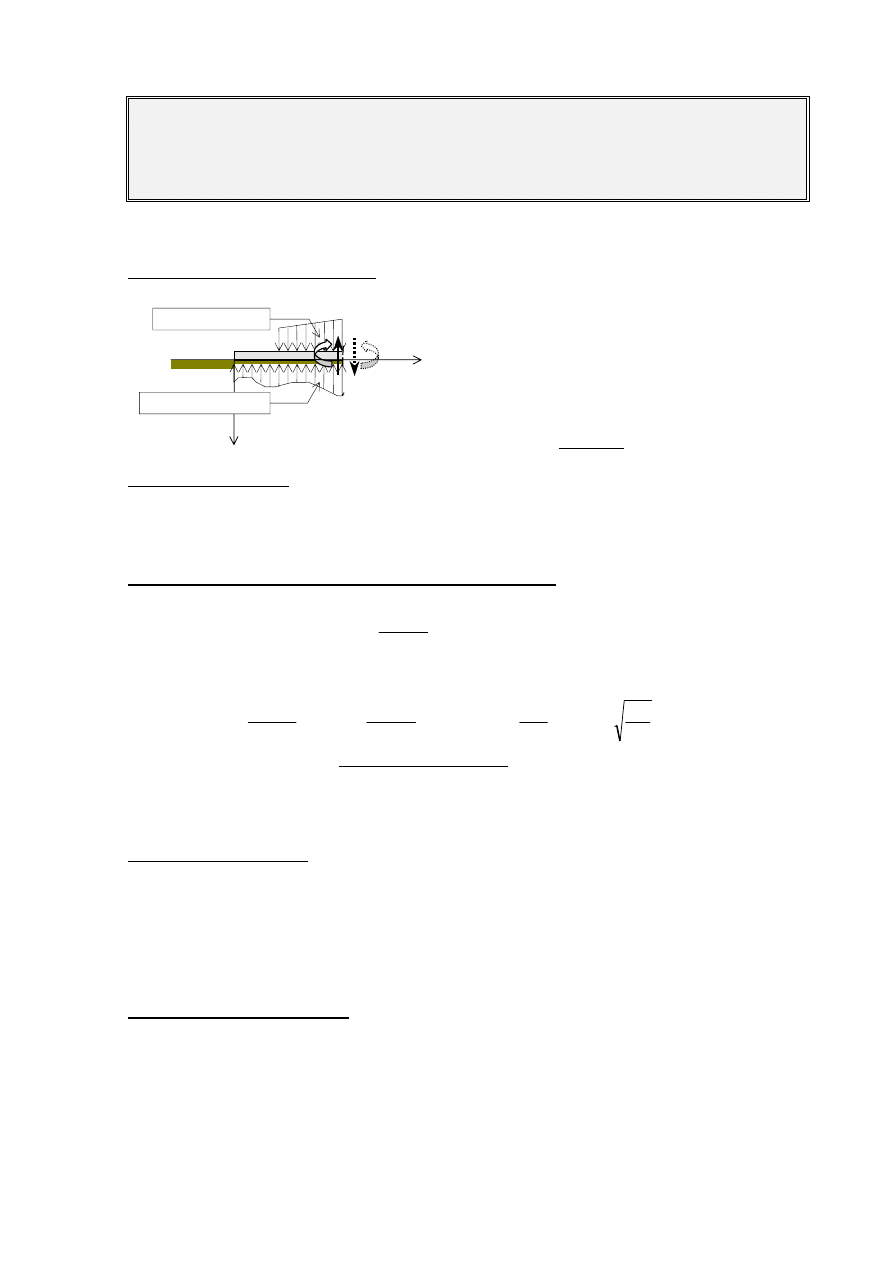
1.1. Oznaczenia sił wewnętrznych

Na rysunku obok przedstawiono zwroty dodatnich
obciążeń zewnętrznych, działających na ławę
q

o

(x), r(x) i reakcji równoważących siły

wewnętrzne M(x), Q(x) w przekroju o
współrzędnej x, liczonej od lewego końca ławy
(punkt x = 0).
Osiadanie przekroju x wynosi y(x), natomiast
szerokość ławy jest stała i wynosi B.

1.2. Związki statyczne
• dla obciążenia wypadkowego q(x) = r(x) - q

o

(x) zachodzi: dQ/dx = q, dM/dx = Q

• warunek Eulera-Bernoulliego: M = -EI/ρ ≈ -EI d

2

y/dx

2

• założenie Winklera: r(x) = C B y(x) , gdzie C - współczynnik podłoża [MN/m

3

], r [MN/m]

1.3. Równanie osi odkształconej belki na podłożu Winklera
Związki statyczne z p.1.2. prowadzą do równania różniczkowego zwyczajnego (1):

)

(

)

(

)

(

4

4

x

y

B

C

x

q

dx

x

y

d

EI

o

−

=

(1)

gdzie EI, B, C nie zależą od x. Szukane jest przemieszczenie osi obojętnej belki y(x).
Równanie można uprościć stosując zmienne bezwymiarowe

ξ zamiast x:

4

4

4

4

,

,

)

(

4

)

(

4

)

(

BC

EI

L

L

x

gdzie

BC

q

y

d

y

d

W

W

o

=

=

ξ

ξ

=

ξ

+

ξ

ξ

(2)

Parametr L

w

[m] nazywa się cechą sztywność belki.

2. Rozwiązanie ogólne i podstawowe

2.1. Rozwiązanie ogólne
Na odcinku nieobciążonym, gdzie q

o

≡ 0, rozwiązaniem równania (2) jest funkcja:

)

sin

cos

(

)

sin

cos

(

)

(

4

3

2

1

ξ

+

ξ

ξ

+

ξ

+

ξ

ξ

−

=

ξ

C

C

e

C

C

e

y

(3)

Do wyznaczenia czterech stałych C

i

, i=1,2,3,4, konieczne są cztery warunki nałożone na

funkcjê y(x) lub jej pochodne (siły wewnętrzne).

2.2. Rozwiązanie podstawowe
Najważniejsze znaczenie ma rozwiązanie szczególne równania (3) dla belki nieskończonej
(

−∞; +∞), obciążonej siłą skupioną:

• wystarczy rozwiązać belkę, tj. znaleźć y(ξ), dla jednej siły P skupionej w punkcie x/L

w

=

ξ

= 0, ponieważ dowolne obciążenie q

o

(x) jest sumą (całką) takich sił dP = q

o

dx a

przemieszczenia y(x) też się odpowiednio sumują (całkują),

• wystarczy rozwiązać zagadnienie dla ξ > 0, bo osiadania y(ξ) muszą być funkcją

parzystą; na tej półosi

ξ > 0 nie ma żadnego obciążenia belki, a więc q

o

≡ 0 w równaniu

(2).

0

obciążenie q

o

(x) > 0

M(x) > 0

Q(x) > 0

odpór podłoża r(x) > 0

y > 0

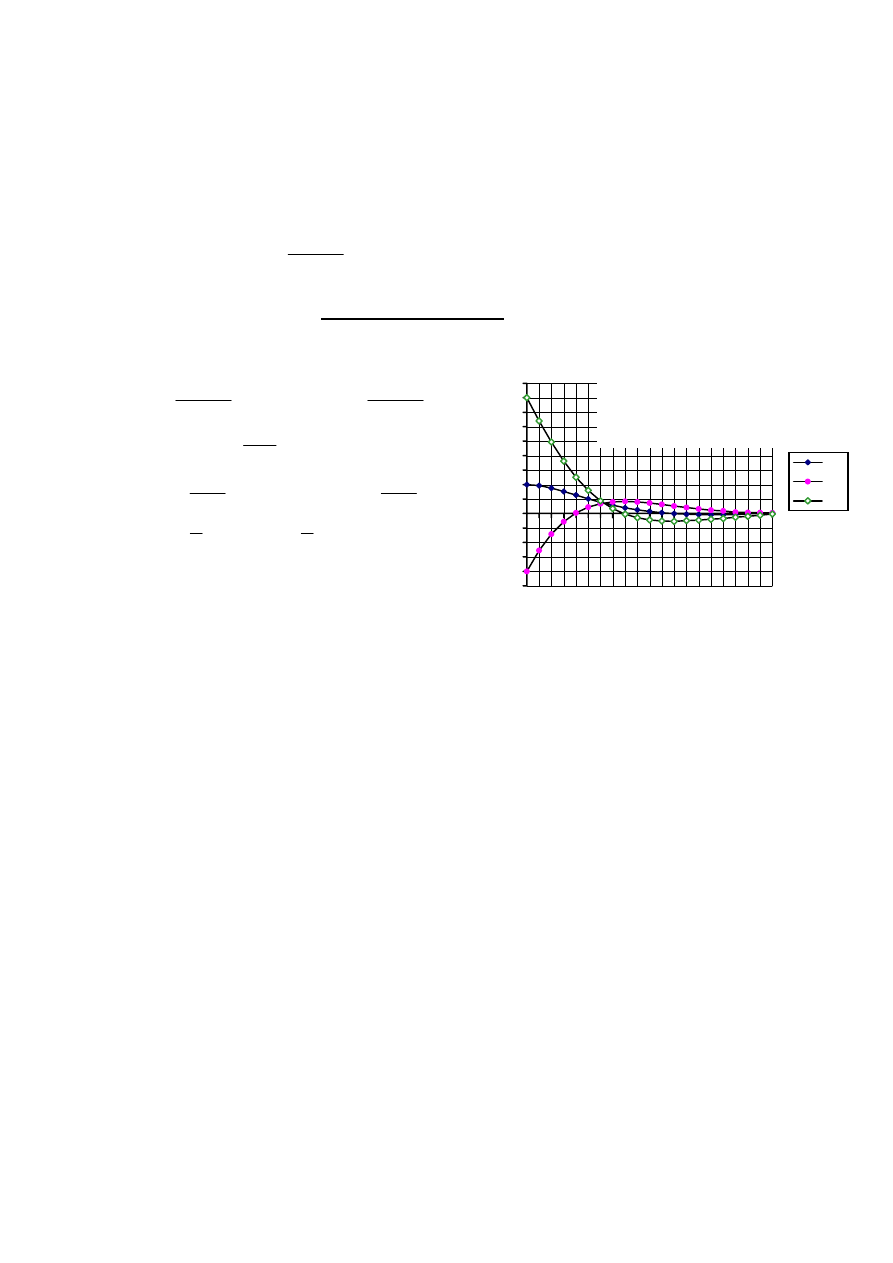
Przy tych spostrzeżeniach formułuje się następujące trzy warunki brzegowe.

1) Warunek Boussinesqa:

ξ → ∞ ⇒ y(ξ) → 0

..... stąd C

4

= C

3

= 0 w rozwiązaniu (3)

2) warunek symetrii (funkcja parzysta):

ξ = 0 ⇒ dy/dξ = 0

..... stąd C

2

= C

1

3) warunek antysymetrii:

ξ → 0+ (tj. ξ → 0, ξ > 0) ⇒ Q(ξ) → −P/2

..... stąd C

1

=

w

BCL

P

2

.

Ostatecznie otrzymuje się rozwiązanie podstawowe (4) dla półosi

ξ > 0.

(4)

Dla

ξ < 0 rozwiązanie jest odpowiednio symetrycznym albo antysymetrycznym odbiciem

rozwiązania (4) dla

ξ > 0.

Uwaga 1:

Y

o

’ = -2e

-

ξ

sin

ξ, Y

o

’’ = M

o

, Y

o

’’’ = Q

o

, Y

o

IV

= -4Y

o

.

dy(

ξ)/dx = dy(ξ)/dξ dξ/dx = y’/L

W

,

d

2

y(

ξ)/dx

2

= d[y’(

ξ)/L

W

]/d

ξ dξ/dx = y’’/(L

W

)

2

, itd.

więc:
M = -EI d

2

y(x)/dx

2

= = -EI d

2

y(

ξ)/dξ

2

/(L

W

)

2

Q = -EI d

3

y(x)/dx

3

= = -EI d

3

y(

ξ)/dξ

3

/(L

W

)

3

Rozwiązując własne zadania Studenci często zapominają o tym dzielniku L

W

!

Uwaga 2:

ξ jest bezwymiarową współrzędną przekroju liczoną od działającej siły

skupionej, siła ta więc nie musi być przyłożona w przekroju x

o

= 0, ale wtedy

ξ

w rozwiązaniu (4) należy zastąpić przez

ξ - ξ

o

, gdzie

ξ

o

= x

o

/L

W

Uwaga 3:

obowiązuje zasada superpozycji, tj. efekty działania kilku sił skupionych
rozpatruje się osobno, a wyniki sumuje się w danym przekroju.

-2,5

-2

-1,5

-1

-0,5

0

0,5

1

1,5

2

2,5

3

3,5

4

4,5

0

1

2

3

4

Yo
Mo
Qo

Yo - funkcja parzysta
Mo - funkcja parzysta
Qo- funkcja nieparzysta

)

(

8

cos

4

8

)

(

)

(

8

)

cos

(sin

2

8

)

(

)

(

2

)

(

)

(

)

(

2

)

sin

(cos

2

)

(

ξ

−

=

ξ

−

=

ξ

ξ

−

=

ξ

−

ξ

ξ

−

−

=

ξ

ξ

=

ξ

=

ξ

ξ

=

ξ

+

ξ

ξ

−

=

ξ

ξ

−

o

o

w

w

o

w

o

w

w

Q

P

e

P

Q

M

PL

e

PL

M

Y

L

P

y

C

B

r

Y

BCL

P

e

BCL

P

y

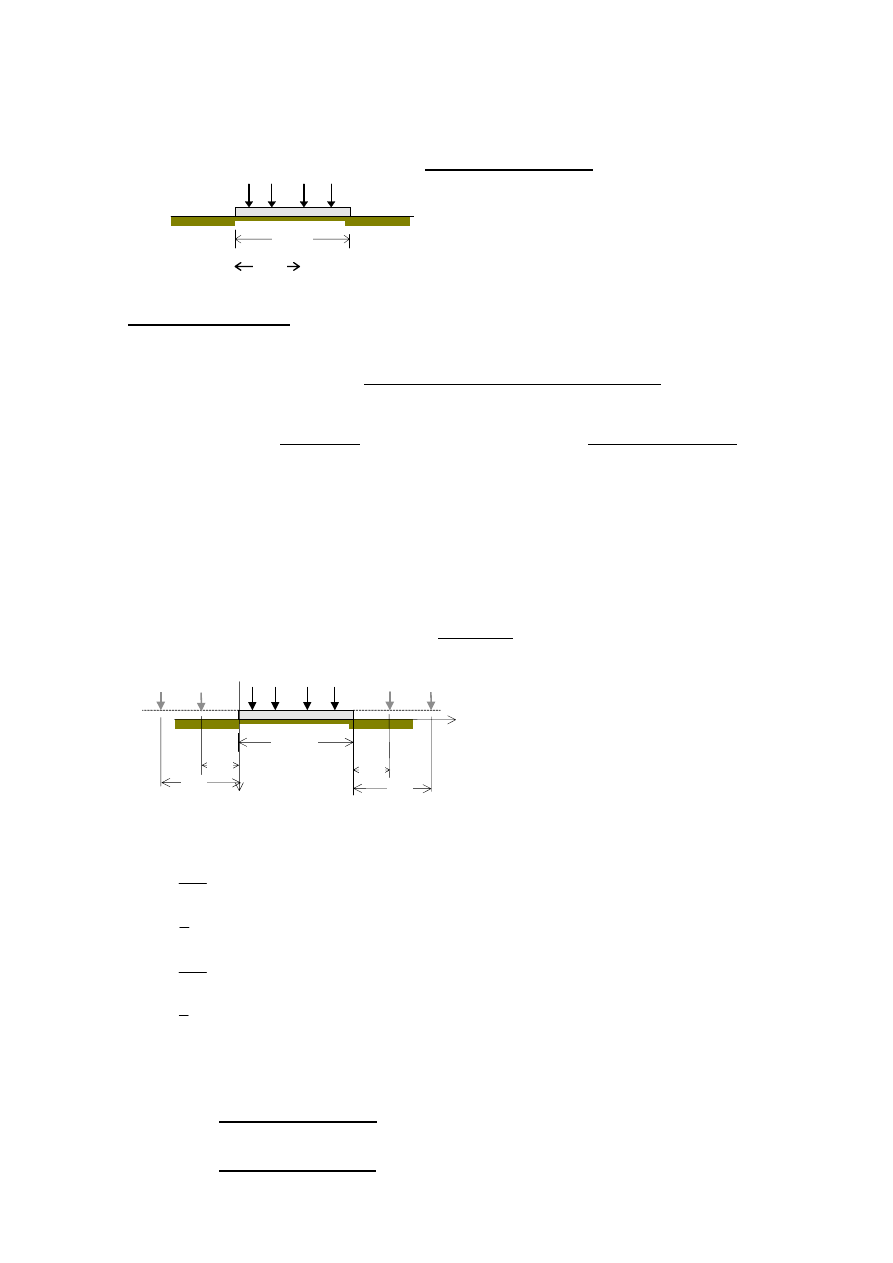
3. Rozwiązanie dla belki o skończonej długości za pomocą metody Bleicha

3.1. Warunki brzegowe

0

≤ x ≤ L, 0 ≤ ξ ≤ L/L

W

na swobodnym końcu A:

Σ M

i

= 0 ,

Σ Q

i

= 0

(5)

na swobodnym końcu B:

Σ M

i

= 0 ,

Σ Q

i

= 0

3.2. Metoda H.Bleicha
• Punkt A o współrzędnej ξ = 0 jest początkiem belki, a punkt B o współrzędnej ξ = L jest jej

końcem.

• Zamiast skończonej belki AB rozpatruje się belkę nieskończenie długą, fikcyjnie

przedłużoną do

±∞. Mają więc zastosowanie wzory (4),

• warunki brzegowe (5) nie są wówczas na ogół spełnione w przekrojach A, B

• belkę obciąża się dodatkowo czterema siłami skupionymi T

i

poza odcinkiem AB; są to

tzw. siły fikcyjne,

• wartości tych sił T

i

dobiera się w taki sposób, żeby były spełnione warunki brzegowe (5)

dla układu sił P

1

, P

2

, ... , P

n

, T

1

, T

2

, T

3

, T

4

,

• suma rozwiązań od tego układu n+4 sił skupionych stanowi ścisłe rozwiązanie

zagadnienia rozpatrywane w przedziale 0

≤ x ≤ L ( 0 ≤ ξ ≤ λ= L/L

W

), ponieważ

- jest postaci (3),

-

są odpowiednie skoki wartości sił poprzecznych Q

i

o P

i

w punktach x

i

- spełnione są warunki brzegowe (5),

-

rozwiązanie o tej własności jest tylko jedno (teoria równań różniczkowych!).

• Nieznane siły fikcyjne T

i

przykłada się zazwyczaj w następujących odległościach:

ξ

A1

=

ξ

B3

=

π/4 ,

ξ

A2

=

ξ

B4

=

π/2 ,

bo wtedy niektóre współczynniki wg (4) się
zerują.

Dla belki o swobodnych końcach siły fikcyjne T

i

oblicza się z układu równań (5), tj.:

[

]

0

)

(

)

(

)

(

)

(

8

4

4

3

3

2

2

1

1

=

=

ξ

+

λ

⋅

+

ξ

+

λ

⋅

+

ξ

⋅

+

ξ

⋅

−

∑

∞

i

B

o

B

o

A

o

A

o

W

P

A

M

M

T

M

T

M

T

M

T

L

M

[

]

0

)

(

)

(

)

(

)

(

8

1

4

4

3

3

2

2

1

1

=

=

ξ

+

λ

⋅

−

ξ

+

λ

⋅

−

ξ

⋅

+

ξ

⋅

−

∑

∞

i

B

o

B

o

A

o

A

o

P

A

Q

Q

T

Q

T

Q

T

Q

T

Q

[

]

0

)

(

)

(

)

(

)

(

8

4

4

3

3

2

2

1

1

=

=

ξ

⋅

+

ξ

⋅

+

ξ

+

λ

⋅

+

ξ

+

λ

⋅

−

∑

∞

i

B

o

B

o

A

o

A

o

W

P

B

M

M

T

M

T

M

T

M

T

L

M

[

]

0

)

(

)

(

)

(

)

(

8

1

4

4

3

3

2

2

1

1

=

=

ξ

⋅

−

ξ

⋅

−

ξ

+

λ

⋅

+

ξ

+

λ

⋅

−

∑

∞

i

B

o

B

o

A

o

A

o

P

B

Q

Q

T

Q

T

Q

T

Q

T

Q

gdzie

λ = L/L

W

, stosuje się funkcje M

o

, Q

o

z rozwiązania (4) oraz:

P

A

M

∞

,

P

B

M

∞

- wypadkowe momenty w przekrojach A(x=0), B(x=L)

belki nieskończenie długiej od wszystkich sił rzeczywistych P

i

, i =1,2,...,n

P

A

Q

∞

,

P

B

Q

∞

- wypadkowe siły poprzeczne w przekrojach x = 0, x = L

belki nieskończenie długiej od wszystkich sił rzeczywistych P

i

, i=1,2,...,n .

B

A

L

P

i

x

i

B

A

λ=L/L

W

P

i

T

2

T

1

T

3

T

4

ξ

A1

ξ

ξ

A2

ξ

B3

ξ

B4

Uwaga 1:

dla „dużych” odległości sił T

1

, T

2

od prawego końca belki (np.

ξ > 4÷5) wpływ tych sił można

zwykle pominąć, ze względu na bardzo małe wartości czynnika exp{-

ξ}. Analogicznie dla

dwóch pozostałych sił i lewego końca belki.

Uwaga 2:

nie są to zagadnienia trudne, ale wymagają pewnej wprawy i biegłości rachunkowej. Samą
ideę obciążeń fikcyjnych warto sobie dobrze przemyśleć, bo występuje ona w bardzo wielu
działach mechaniki, metod numerycznych i in. Jest to podejście w pełni poprawne
matematycznie.

Zaleca się przeanalizowanie różnych pytań i zadań zamieszczonej w kilku miejscach na tej
stronie www.

4. Pytania sprawdzające

1. Obciążenie belki wynosi q

o

(x). Ile wynosi osiadanie powierzchni ośrodka Winklera poza

belką (nieobciążona powierzchnia). Czy odpowiedź zależy od sztywności belki EI?

2. Sprawdzić, że równomierne obciążenie belki na podłożu Winklera powoduje jej
równomierne osiadanie, niezależnie od sztywności 0

≤ EI ≤ +∞.

3. Czy siły fikcyjne T

i

mogą być w dowolnej odległości od siebie?

4. Czy teoretycznie można rozmieścić je wszystkie po jednej stronie punktu B?
A

praktycznie?

5. Czy wystarczy użyć 3 zamiast 4 sił fikcyjnych? Czy 6 sił fikcyjnych T

i

zapewni większą

dokładność wyników?

6. Jak przyjąć siły fikcyjne, gdy belka jest jednostronnie nieskończenie długa?

7. Czy metodę Bleicha można stosować, jeśli obciążenie belki stanowią wyłącznie momenty

skupione M

i

a nie siły skupione P

i

?

8. Co zrobić, jeżli na końcu belki działa moment skupiony M

A

?

9. Zaproponować sposób analitycznego rozwiązania belki o odcinkowo zmiennej sztywności
EI = Ei

i

≠ const(i) lub B

i

≠ const(i) lub C

i

≠ const(i) (metoda Bleicha nie jest tu

najprostsza).

10. Rozwiązanie podstawowe dla belki nieskończenie długiej obciążonej momentem
skupionym

M ma postać:

)

sin(

)

(

2

ξ

ξ

−

=

ξ

e

L

C

B

M

y

W

Wyprowadzić to rozwiązanie odpowiednio modyfikując metodę z p.2.2.

11. Czy można wymyślić „własną metodę Bleicha”, która będzie używała momentów
fikcyjnych

skupionych M

i

zamiast fikcyjnych sił skupionych T

i

(czyli rozwiązania z

pyt.10) ?

12. Czy prawdą jest stwierdzenie, że metoda Bleicha jest metodą przybliżoną?

Wskazówki i odpowiedzi:

1.
Poza belką osiadanie jest wszędzie zerowe, niezależnie od q

o

i niezależnie od EI, co wynika

z definicji ośrodka Winklera (niezależnie od rodzaju fundamentu, czy jego braku).
2.
Jeśli q

o

= const , to w równaniu (1) rozwiązaniem jest odpowiednie y = const.

3.
Mogą, ale oczywiście nie mogą być w tym samym przekroju, bo de facto oznaczałoby to
jedną siłę.
4.
Teoretycznie mogą być m.in. wszystkie siły z jednej strony belki. W praktyce jednak trzeba
tutaj zachować pewną ostrożność. Gdyby np. siły fikcyjne były b.b.daleko od końców belki
(np. 10 x L

W

lub więcej), to musiałyby one mieć b.duże wartości, aby skorygować do zera siły

przekrojowe w odpowiednich przekrojach. Mała niedokładność w wyznaczeniu wartości sił
fikcyjnych (np. błędy zaokrągleń rzędu E-05) mogłaby istotnie rzutować na dokładność
rozwiązania pomiędzy tymi przekrojami. Jest to tzw. problem dobrego/złego uwarunkowania
numerycznego metody.
5.
Dla skończonej belki są 4 równania liniowe, więc muszą być dokładnie 4 siły fikcyjne. Tyle
tylko, że czasem może wyjść zerowa wartość siły fikcyjnej i wygląda jakby tej siły nie było...
6.
Dla nieskończonej belki są tylko dwa warunki brzegowe do spełnienia, więc będą 2 siły
fikcyjne. Pozostałe warunki „zerowania się w nieskończoności” są automatycznie spełnione
przez wykorzystywane rozwiązanie podstawowe.
7.
Można i to dokładnie w ten sam sposób, bo koryguje się wartości sił w przekrojach A,B i nie
jest istotne co powoduje siły wewnętrzne w tych przekrojach.
8.
Podstawić tę wartość zamiast 0 po prawej stronie w pierwszym z czterech równań w p.3.2.
9.
Można rozwiązywać osobno każdy z n odcinków pryzmatycznych, na którym L

W

= const.

Rozwiązania podstawowe (3) dają wtedy 4n stałych C

i

do wyznaczenia. Wyznacza się je z

4n równań: 2 warunki na lewym końcu belki, 2 warunki na prawym końcu, 4(n-1) warunków
ciągłości na „sklejeniu” n-1 segmentów pryzmatycznych. Te warunki sklejenia to: ciągłość linii
ugięcia y (bo belka się nie przerywa), ciągłość pochodnej y (kąt obrotu), ciągłość momentów
(brak momentu skupionego w przekroju) i ciągłość sił poprzecznych (brak siły poprzecznej
skupionej w przekroju). Te cztery warunki ciągłości są zupełnie oczywiste, może jednak nie
do końca, jeśli chodzi o ciągłość kąta obrotu. Po prostu zakładamy, że linia ugięcia jest
gładka (nie ma nieróżniczkowalnych „dziubków” w miejscach sklejenia).
10.
To trochę żmudne zadanie rachunkowe, rozwiązywane też oczywiście najpierw na odcinku
ξ > 0. Jest ono przedstawione w innym miejscu na stronie www dla IVr.
11.
Można. Można też brać np. dwie siły skupione i dwa momenty skupione, itp.
12.
Metoda Bleicha jest metodą ścisłą.