Dr Arkadiusz Kijek
Ekonometria

1

Wykłady 2009/2010

EKONOMETRIA

WYKŁADY 2009/2010

Przedmiot i cel ekonometrii

Pawłowski (1978): Ekonometria jest nauką o metodach badania ilościowych prawidłowości występujących w
zjawiskach ekonomicznych, za pomocą odpowiednio wyspecjalizowanego aparatu matematyczno-
statystycznego.

Chow (1995): Ekonometria jest nauką i sztuką stosowania metod statystycznych do mierzenia relacji
ekonomicznych.

Z tych definicji wynika, że ekonometria zajmuje się analizą ekonomicznych. Ze względu na złożonośd tych
zjawisk i skomplikowany charakter powiązao między nimi, zachodzi koniecznośd stosowania metod
ilościowych.

Celem ekonometrii jest analiza ilościowa systemu ekonomicznego i w konsekwencji dostarczanie
decydentom informacji potrzebnych do przewidywania i sterowania procesami gospodarczymi.

Model ekonometryczny – jest podstawowym narzędziem w ekonometrii, wykorzystywanym do analizy
zależności zachodzących między zjawiskami. Stanowi on formalną konstrukcję, która za pomocą
pojedynczego równania bądź układu równao opisuje zasadnicze powiązania
pomiędzy rozpatrywanymi zjawiskami ekonomicznymi (Pawłowski).

Ogólna postad modelu:

𝑌 = 𝑓 𝑋

1

, 𝑋

2

, … , 𝑋

𝑘

, 𝜀

𝑌 – zmienna objaśniana modelu

𝑋

1

, 𝑋

2

– zmienne objaśniające

𝜀 – składnik losowy

𝑓 – postad analityczna funkcji obrazującej zależnośd pomiędzy zmienną objaśnianą, a zmiennymi
objaśniającymi oraz składnikami losowymi.



Rodzaje danych statystycznych

I.

Dane przekrojowe (𝑦

𝑖

, 𝑖 = 1, 2, … , 𝑁). Dotyczą zbioru obiektów ekonomicznych (np. przedsiębiorstw)

w jednej jednostce czasu.

II.

Szeregi czasowe (𝑦

𝑡

, 𝑡 = 1, 2, … , 𝑇). Dotyczą zbioru obiektów ekonomicznych w kolejnych

jednostkach czasu z ustalonego przedziału czasowego.

III.

Dane panelowe (𝑦

𝑖𝑡

, 𝑖 = 1, 2, … , 𝑁; 𝑡 = 1, 2, … , 𝑇). Dotyczą zbioru obiektów w kolejnych jednostkach

czasu.

Dr Arkadiusz Kijek
Ekonometria

2

Wykłady 2009/2010

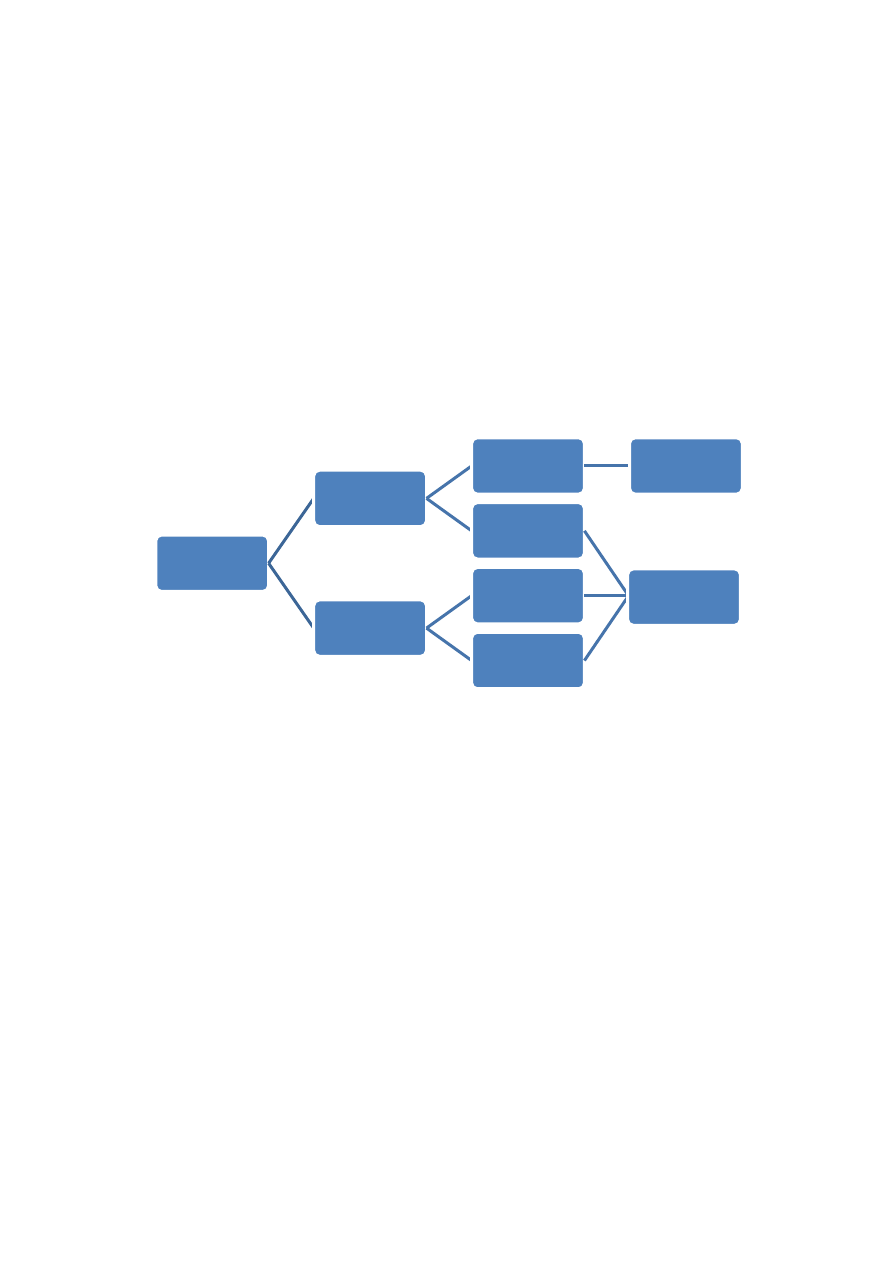
zmienne

endogeniczne

nieopóźnione

objaśniane

opóźnione

egzogeniczne

nieopóźnione

opóźnione

nieobjaśniane

Rodzaje zmiennych w modelu

Zmienne endogeniczne – zjawisko wyjaśniane przez model

Zmienne egzogeniczne – zjawisko nie wyjaśniane przez model

Zjawiska endogeniczne i egzogeniczne mogą byd opóźnione lub nieopóźnione (bieżące).

Zmienne objaśniane – wyjaśniane przez zmienne objaśniające w równaniach modelu, w ich roli występują
nieopóźnione zmienne endogeniczne.

Zmienne objaśniające – wyjaśniają zmienne objaśniane w równaniach modelu, w ich roli występują
opóźnione zmienne endogeniczne lub opóźnione i nieopóźnione zmienne egzogeniczne.

Składnik losowy i jego własności

Składnik losowy uwzględniany jest w modelu, by wyjaśnid rozbieżnośd pomiędzy zaobserwowanymi
metodami zmiennej objaśnianej, a wartościami teoretycznymi wynikającymi z teoretycznej konstrukcji
modelu.

Składnik zakłócający jest zmienną losową i charakteryzuje się określonym rozkładem prawdopodobieostwa.
Składnik losowy jest ważnym elementem modelu ekonometrycznego, a własności jego rozkładu
prawdopodobieostwa podlegają dokładnemu badaniu.



Przyczyny występowania składnika losowego

 błąd specyfikacji, czyli pominięcie istotnej zmiennej lub włączenie zmiennej nieistotnej

 błąd aproksymacji, czyli przyjęcie niewłaściwej postaci analitycznej funkcji błąd pomiaru zmiennych

ekonomicznych

 czynniki losowe wpływające na zmienną endogeniczną i wynikający z tego losowy charakter

Dr Arkadiusz Kijek
Ekonometria

3

Wykłady 2009/2010

Klasyfikacja modeli ekonometrycznych

I.

Ze względu na liczbę równao w modelu

a. jednorównaniowe
b. wielorównaniowe

II.

Ze względu na postad analityczną

a. liniowe
b. nieliniowe, sprowadzalne do liniowych
c. nieliniowe, niesprowadzalne do liniowych

III.

Ze względu na udział czynnika czasu

a. statyczne, nie uwzględniające czynnika czasu, w których nie występuje zmienna czasowa ani

zmienne opóźnione

b. dynamiczne, uwzględniające czynnik czasu, w których występują zmienna czasowa lub

zmienne opóźnione

IV.

Ze względu na charakter poznawczy

a. przyczynowo-skutkowe, opisowe, wyrażające związki przyczynowo-skutkowe pomiędzy

zmiennymi

b. symptomatyczne, równanie lub częśd równania nie ma interpretacji przyczynowo skutkowej,

w której zmiennymi objaśniającymi są zmienne skorelowane w sensie statystycznym ze
zmiennymi objaśniającymi

c. tendencji rozwojowej, trendu, w których rolę zmiennej objaśniającej pełni zmienna czasowa

Etapy budowy modelu ekonometrycznego

I.

Określenie celu i zakresu badania

II.

Specyfikacja modelu

a. określenie badanego zjawiska – zmiennej endogenicznej
b. dobór zmiennych objaśniających spośród czynników wpływających na zmienną objaśnianą
c. wybór postaci analitycznej, czyli określonej funkcji matematycznej, wyrażającej zależnośd

między zmienną objaśnianą a zmiennymi objaśniającymi

III.

Zebranie i opracowanie danych statystycznych

IV.

Szacowanie parametrów modelu

V.

Weryfikacja modelu pod względem formalnym (spełnienie założeo) oraz merytorycznym

VI.

Praktyczne zastosowanie modelu, a więc wykorzystywanie go do analizy ekonomicznej i
prognozowania

Prognozowanie na podstawie modeli ekonometrycznych

Prognozowanie ekonometryczne prowadzone jest na podstawie modelu wyjaśniającego kształtowanie się
badanej zmiennej endogenicznej. Punktem wyjścia jest dobór odpowiedniego modelu. Do najczęściej
wykorzystywanych modeli zaliczamy:

a. klasyczne modele tendencji rozwojowej
b. jednorównaniowe modele typu przyczynowo-skutkowego
c. modele symptomatyczne o charakterze autoregresyjnym
d. adaptacyjne
e. wielorównaniowe

Dr Arkadiusz Kijek
Ekonometria

4

Wykłady 2009/2010

Zastosowanie klasycznych modeli tendencji rozwojowej polega na ekstrapolacji funkcji trendu 𝑓(𝑡). W tej
metodzie wymagane jest przyjęcie założenia o stabilności przyjętej lub oszacowanej funkcji trendu, tak aby
jej postad analityczna i parametry nie uległy istotnej prognozy obarczone są dużymi błędami.

Jednorównaniowe modele przyczynowo-skutkowe pozwalają na budowę średnio i długookresowych
prognoz. Ich przydatnośd zależy od wyników etapów cząstkowych. Prawidłowo przeprowadzone etapy dają
możliwośd uzyskania trafnych prognoz.

Modele symptomatyczne o charakterze autoregresyjnym wykorzystywane są, gdy występują problemy
związane z doborem zmiennych objaśniających. Są one podstawą budowy prognoz krótkookresowych.

Modele adaptacyjne znajdują zastosowanie w sytuacji, gdy spełnione są założenia o niezmienności
mechanizmu rozwojowego badanych zjawisk dla modeli tendencji rozwojowej i modeli przyczynowo-
skutkowych. Charakteryzują się dużą elastycznością i możliwościami dostosowawczymi.

Modele wielorównaniowe są stosowane w przypadku zjawisk złożonych, które charakteryzują się
wielokierunkowymi powiązaniami. Stanowią one podstawę głównie prognozowania makroekonomicznego.

Linowy model ekonometryczny

𝑌 = 𝛼

0

+ 𝛼

1

𝑋

1

+ 𝛼

2

𝑋

2

+ … + 𝛼

𝑘

𝑋

𝑘

+ 𝜀

𝑌 – zmienna objaśniana

𝑋

1

, 𝑋

2

, … , 𝑋

𝑘

– zmienne objaśniające

𝜀 – składnik losowy

𝛼

0

, 𝛼

𝑎

, … , 𝛼

𝑘

– parametry strukturalne, wyrażające liniowy wpływ zmiennych objaśniających na zmienną

objaśnianą

Dobór zmiennych objaśniających

W metodach doboru zmiennych punkt wyjścia stanowi zbiór potencjalnych zmiennych objaśniających
(𝑋

1

, 𝑋

2

, … , 𝑋

𝑘

).

Z tego zbioru wybierany jest podzbiór zmiennych, którego elementy będą charakteryzowały się:

 wysokim stopniem zmienności

 silnym skorelowaniem ze zmienną objaśnianą

 słabym skorelowaniem między sobą zmiennych w celu wyeliminowania zjawiska powtarzania się

informacji

 silnym skorelowaniem ze zmiennymi nie wchodzącymi do zespołu diagnostycznego, których są

reprezentantami

Dr Arkadiusz Kijek
Ekonometria

5

Wykłady 2009/2010

Wstępną ocenę przydatności zmiennych stanowi analiza stopnia ich zmienności. Selekcję zmiennych w tym
zakresie przeprowadza się przy pomocy współczynnika zmienności, który obliczany jest zgodnie z
następującym wzorem:

𝑉

𝑖

=

𝑆(𝑥

𝑖

)

𝑥

𝑖

(𝑖 = 1, 2, … , 𝑚)

𝑥

𝑖

– średnia arytmetyczna

𝑆(𝑥

𝑖

) – odchylenie standardowe zmiennej 𝑥

𝑖

Ze zbioru potencjalnych zmiennych objaśniających eliminuje się te, dla których wielkośd współczynnika jest
mniejsza od przyjętej z góry wartości krytycznej 𝑉′. Warunek ten zapisujemy w poniższy sposób:

𝑉

𝑖

< 𝑉′

Z kolei zmienne, dla których współczynnik jest większy od wartości krytycznej poddawane są dalszej analizie.

Stopieo korelacji pomiędzy zmiennymi ocenia się na podstawie współczynnika korelacji. Wzór na obliczanie
współczynnika korelacji liniowej pomiędzy zmiennymi 𝑋 i 𝑌 jest następujący:

𝑟

𝑥𝑦

=

𝑐𝑜𝑣(𝑥, 𝑦)
𝑆 𝑥 𝑆(𝑦)

=

(𝑥

𝑖

− 𝑥 )(𝑦

𝑖

− 𝑦 )

(𝑥

𝑖

− 𝑥 )

2

(𝑦

𝑖

− 𝑦 )

2

Współczynnik korelacji zestawia się w wektor korelacji 𝑹

𝑜

oraz macierz korelacji 𝑹 o postaci

𝑹

𝑜

=

𝑟

1

𝑟

2

⋮

𝑟

𝑚

𝑹 =

1

𝑟

11

⋯

𝑟

1𝑛

𝑟

21

1

⋯

𝑟

2𝑛

⋮

⋮

⋱

⋮

𝑟

𝑚1

𝑟

𝑚 2

⋯

1

gdzie:

𝑟

𝑖

– współczynnik korelacji między zmiennymi 𝑋

𝑖

i 𝑌

𝑟

𝑖𝑗

– współczynnik korelacji między zmiennymi 𝑋

𝑖

i 𝑋

𝑗

Dr Arkadiusz Kijek
Ekonometria

6

Wykłady 2009/2010

Metoda wskaźników pojemności informacyjnej Hellwiga

Rozpatruje się wszystkie kombinacje potencjalnych zmiennych objaśniających, których liczba wynosi 2

m

-1.

Dla każdej kombinacji 𝐶

𝑠

(𝑠 = 1, 2, … , 2

𝑚

− 1) oblicza się indywidualną pojemnośd informacyjną nośników

wchodzących w jej skład wg wzoru:

𝑕

𝑠𝑗

=

𝑟

𝑗

2

1+

𝑟

𝑖𝑗

𝑖𝜖 𝐶𝑠

𝑖≠𝑗

lub

𝑕

𝑠𝑗

=

𝑟

𝑗

2

𝑟

𝑖𝑗

𝑖𝜖 𝐶𝑠

Następnie wyznacza się integralną pojemnośd informacyjną dla wszystkich kombinacji 𝐶

𝑠

, zgodnie ze wzorem

𝐻

𝑠

= 𝑕

𝑠𝑗

𝑗 ∈𝐶

𝑠

Indywidualne i integralne wskaźniki pojemności informacyjnej unormowane są w przedziale [0,1]. Ich
wartośd jest tym wyższa, im zmienne objaśniające wchodzące w skład kombinacji są silniej skorelowane ze
zmienną objaśnianą oraz słabiej skorelowane między sobą.

Kryterium doboru kombinacji zmiennych stanowi wartośd integralnej pojemności informacyjnej, który jest
miarą zasobu informacji dostarczanej przez zmienne objaśniające o zmiennej objaśnianej. Do modelu
przyjmuje się tą kombinację, dla której wskaźnik jest największy, czyli:

𝐶

𝑜𝑝𝑡

: 𝐻

𝑜𝑝𝑡

= max {𝐻

𝑠

= 𝑠 = 1, 2, … , 2

𝑚

− 1}

Jako miarę zasobu informacji brakującej do pełnego wyjaśnienia zachowania zmiennej objaśnianej przez
daną kombinację zmiennych objaśniających można przyjąd dopełnienie integralnego wskaźnika pojemności
informacyjnej do jedności, co zapisuje się następująco:

𝐺

𝑠

= 1 − 𝐻

𝑠

Zaletą metody Hellwiga jest możliwośd wyboru zmiennych spośród wszystkich możliwych kombinacji. Wadą
jest duża pracochłonnośd, np. przy 6 potencjalnych zmiennych rozpatrywane są 63 kombinacje zmiennych.

Metoda współczynnika korelacji wielorakiej

Współczynnik korelacji wielorakiej wykorzystywany jest jako miara siły zależności liniowej pomiędzy zmienną
objaśniającą a zmiennymi objaśniającymi. Oblicza się go wg następującego wzoru:

𝑅 = 1 −

det (𝐖)

det (𝑹)

gdzie:

𝑾 =

1

𝑹

0

𝑇

𝑹

𝟎

𝑹

Dr Arkadiusz Kijek
Ekonometria

7

Wykłady 2009/2010

Współczynnik korelacji wielorakiej przyjmuje wartości z przedziału *0,1+. Jego wartośd bliska jedności oznacza
silniejszy związek pomiędzy zmiennymi objaśniającymi a zmienną objaśnianą. Jednakże należy pamiętad, że
wartośd WKW nigdy nie spada, jeśli dodawane są nowe zmienne objaśniające, niezależnie od tego czy mają
istotny wpływ na zmienną objaśnianą. Dlatego może byd on wykorzystywany jako kryterium doboru
zmiennych jedynie w przypadku jednakowo licznych kombinacji. Wybiera się kombinacje, dla których jest on
maksymalny.

Estymacja parametrów modelu liniowego

Założenia klasycznej metody najmniejszych kwadratów

1) 𝑦 = 𝑋

𝑎

+ 𝜀

𝒚

[𝑛∗1]

=

𝑦

1

𝑦

2

…

𝑦

𝑛

𝑿

[𝑛∗ 𝑘+1 ]

=

1

𝑥

11

𝑥

12

⋯

𝑥

1𝑘

1

𝑥

21

𝑥

22

…

𝑥

2𝑘

⋮

⋮

⋮

⋱

⋮

1 𝑥

𝑛1

𝑥

𝑛2

⋯ 𝑥

𝑛𝑘

𝒂

[(𝑘+1)∗1]

=

𝛼

0

𝛼

1

…

𝛼

𝑘

𝜺

[𝑛∗1]

=

𝜀

1

𝜀

2

…

𝜀

𝑛

𝒚 – wektor obserwacji na zmiennej objaśnianej 𝑌, zarejestrowane wartości są realizacjami zmiennej
losowej co oznacza, że jest to wektor losowy

𝑿 – macierz wartości na zmiennych objaśniających, w kolejnych kolumnach znajdują się wartości
zmiennych objaśniających: 1, x

1

, x

2

, … , x

k

, pierwsza kolumna zawiera same jedynki, co wynika z

uwzględniania wyrazu wolnego

𝒂 – wektor parametrów strukturalnych modelu

𝜺 – wektor składników losowych

𝑛 – liczba obserwacji na zmiennej objaśnianej i zmiennych objaśniających

𝑘 – liczba zmiennych objaśniających

W zapisie skalarnym model można zapisad w następujący sposób jako układ równao liniowych:

𝑌

𝑡

= 𝛼

0

+ 𝛼

1

𝑥

𝑡1

+ ⋯ + 𝛼

𝑘

𝑥

𝑡𝑘

+ 𝜀

𝑡

(𝑡 = 1, 2, … , 𝑛)

Dr Arkadiusz Kijek
Ekonometria

8

Wykłady 2009/2010

Każda zaobserwowana wartośd 𝑦

𝑡

(𝑡 = 1, 2, … , 𝑛) zmiennej objaśniającej 𝑌 jest liniową funkcją

zaobserwowanych wartości 𝑥

𝑡1

, … , 𝑥

𝑡𝑘

zmiennych objaśniających 𝑥

1

, … , 𝑥

𝑘

z dokładnością do

składnika losowego 𝜀

𝑡

.

2) 𝑿 jest znaną macierzą nielosową

Założenie to oznacza, że zmienne objaśniające nie są zmiennymi losowymi. Dla znanych z góry
wartości 𝑥

𝑡1

, … , 𝑥

𝑡𝑘

zmiennych objaśniających 𝑥

1

, … , 𝑥

𝑘

dokonuje się obserwacji zmiennej

objaśniającej 𝑌.

3) 𝑟𝑧 𝑿 = 𝑘 + 1 ≤ 𝑛

Kolumny macierzy 𝑿 są liniowo niezależne, czyli wartości zmiennych objaśniających nie stanowią
liniowej kombinacji pozostałych zmiennych. Dodatkowo postawiony jest warunek co do liczby
obserwacji, która nie może byd mniejsza od k+1. Przyjęcie tego założenia wymagane jest z uwagi na
potrzebę wielokrotnego odwracania macierzy 𝑿

𝑇

𝑿.

4) 𝐸 𝜺 = 0

Wartośd oczekiwana wektora losowego 𝜺 jest wektorem zerowym 𝟎

[𝑛∗1]

. Wartośd oczekiwana

odchyleo spowodowanych oddziaływaniem czynników przypadkowych powinna byd równa zero.

5) 𝐷

2

𝜀 = 𝐸 𝜺𝜺

𝑻

= 𝜎

2

𝑰

gdzie:

𝑰 – macierz jednostkowa stopnia n (ma na przekątnej 1, a na pozostałych miejscach 0)

𝜎

2

– wariancja składnika losowego

𝐷

2

𝜀 – macierz wariancji i kowariancji wektora składników losowych (zwana w dalszej części

macierzą kowariancji)

Założenie to można podzielid na dwie części:

a) 𝐷

2

𝜀

𝑖

= 𝐸 𝜀

𝑡

2

= 𝜎

2

𝑰 (𝑡 = 1, 2, … , 𝑛)

Założenie o jednorodności wariancji składnika losowego. Jednorodnośd oznacza, że wariancja
składnika losowego jest stała i określona jest jako homoskedastycznośd.

Dr Arkadiusz Kijek
Ekonometria

9

Wykłady 2009/2010

b) 𝑐𝑜𝑣 𝜀

𝑡

, 𝜀

𝑠

= 𝐸 𝜀

𝑡

, 𝜀

𝑠

= 0 (𝑡 ≠ 𝑠)

𝑝 𝜀

𝑡

, 𝜀

𝑠

=

𝑐𝑜𝑣 𝜀

𝑡

, 𝜀

𝑠

𝐷

2

𝜀

𝑡

∗ 𝐷

2

𝜀

𝑠

=

0

𝜎

2

= 0 (𝑡 ≠ 𝑠)

Założenie o braku autokorelacji składników losowych różnych obserwacji. Kombinacje i
korelacje różnych obserwacji wynoszą zero. Wynika z tego, że pomiędzy składnikami
losowymi poszczególnych obserwacji nie istnieje zależnośd korelacyjna liniowa.

Założenia 1) – 5) są założeniami klasycznej metody najmniejszych kwadratów.

Założenia 1) – 4) powodują, że estymator otrzymany KMNK jest estymatorem liniowym, nieobciążonym i
zgodnym. Natomiast założenie 5) sprawia, że estymator jest również najefektywniejszy.

Dodatkowo wprowadza się następne założenie:

6) 𝜺 ~ 𝑁

𝑛

(0, 𝜎

2

𝐼)

Wektor składników losowych 𝜺 ma n-wymiarowy rozkład normalny i wartością oczekiwaną będącą
wektorem zerowym oraz macierzą kowariancji 𝜎

2

𝐼.

Klasyczna metoda najmniejszych kwadratów

MNK polega na wyznaczeniu wektora ocen 𝒂 parametrów strukturalnych 𝛼, w taki sposób aby suma
kwadratów odchyleo teoretycznych wartości zmiennej objaśniającej od empirycznych wartości była jak
największa.

𝑦

𝑡

– empiryczna wartośd zmiennej objaśnianej otrzymana na podstawie badania

𝑦

𝑡

– teoretyczna wartośd zmiennej objaśnianej obliczana jako:

𝑦

𝑡

= 𝛼

0

+ 𝛼

1

𝑥

𝑡1

+ 𝛼

2

𝑥

𝑡2

+ ⋯ + 𝛼

𝑘

𝑥

𝑡𝑘

(𝑡 = 1, 2, … , 𝑛)

𝑒

𝑡

– reszta dla obserwacji t, czyli różnica między wartością empiryczną a teoretyczną zmiennej objaśnianej,

szacowana wg wzoru:

𝑒

𝑡

= 𝑦

𝑡

− 𝑦

𝑡

(𝑡 = 1, 2, … , 𝑛)

Dr Arkadiusz Kijek
Ekonometria

10

Wykłady 2009/2010

Zapis macierzowy równania dla wektora wartości teoretycznych zmiennej objaśnianej oraz wektora reszt:

𝒚

= 𝑿𝒂 oraz 𝒆 = 𝒚 − 𝒚

= 𝒚 − 𝑿𝒂

gdzie:

𝒚

[𝑛∗1]

=

𝑦

1

𝑦

2

⋮

𝑦

𝑛

𝒂

[(𝑘+1)∗1]

=

𝛼

0

𝛼

1

⋮

𝛼

𝑘

𝒆

[𝑛∗1]

=

𝑒

1

𝑒

2

⋮

𝑒

𝑛

Funkcję celu 𝑆(𝒂) równą sumie kwadratu reszt zapisujemy następująco:

𝑆 𝒂 = 𝒆

𝑇

𝒆 = 𝒚 − 𝑿𝒂

𝑻

𝒚 − 𝑿𝒂 = 𝒚

𝑻

𝒚 − 𝒚

𝑻

𝑿𝒂 − 𝒂

𝑻

𝑿

𝑻

𝒚 + 𝒂

𝑻

𝑿

𝑻

𝑿𝒂 = 𝒚

𝑻

𝒚 − 2𝒂

𝑻

𝑿

𝑻

𝒚 + 𝒂

𝑻

𝑿

𝑻

𝑿𝒂

Warunkiem koniecznym istnienia ekstremum lokalnego funkcji jest zerowanie się wektora pierwszych
pochodnych cząstkowych (gradientu):

𝜕𝑆(𝒂)

𝜕𝒂

= −2𝑿

𝑻

𝒚 + 2𝑿

𝑻

𝑿𝒂 = 0

Po przekształceniach otrzymujemy układ równao, zwany układem równao normalnych:

𝑿

𝑇

𝑿𝒂 = 𝑿

𝑻

𝒚

Rozwiązując go względem 𝒂 otrzymujemy wzór na estymator MNK:

𝒂 = (𝑿

𝑻

𝑿)

−𝟏

𝑿

𝑻

𝒚

Warunkiem wystarczającym by uznad go za minimum, jest dodatnio określona macierz drugich pochodnych
(Hessianu):

𝜕𝑆

2

(𝒂)

𝜕𝒂𝜕𝒂

𝑻

= 2𝑿

𝑻

𝑿

Ponieważ macierz 𝑿

𝑻

𝑿 jest zawsze dodatnio określona, funkcja 𝑆(𝒂) osiąga w punkcie 𝑎 minimum lokalne.

Dr Arkadiusz Kijek
Ekonometria

11

Wykłady 2009/2010

Estymator wariancji składnika losowego

Nieobciążonym i zgodnym estymatorem wariancji składnika losowego 𝝈

2

jest wariancja resztowa zadana

wzorem:

𝑆

2

=

𝒚 − 𝑿𝒂

𝑻

(𝒚 − 𝑿𝒂)

𝑛 − 𝑘 − 1

=

𝒚

𝑻

𝒚 − 𝒂

𝑻

𝑿

𝑻

𝒚

𝑛 − 𝑘 − 1

=

𝒆

𝑇

𝒆

𝑛 − 𝑘 − 1

=

𝒆

𝑡

𝟐

𝑛

𝑡=1

𝑛 − 𝑘 − 1

Odchylenie standardowe składnika resztowego oblicza się jako pierwiastek z wariancji, według wzoru:

𝑆 = 𝑆

2

Odchylenie standardowe składnika resztowego informuje o poziomie przeciętnego odchylenia
zaobserwowanych wartości zmiennej objaśnianej od wartości teoretycznych tej zmiennej wyznaczonych z
modelu.

Estymator macierzy kowariancji estymatora 𝒂 parametrów strukturalnych modelu

Macierz kowariancji estymatora 𝑎:

𝑫

2

𝒂 = 𝜎

2

(𝑿

𝑻

𝑿)

−1

Nieobciążonym i zgodnym estymatorem kowariancji estymatora 𝑎 parametrów strukturalnych modelu jest:

𝑫

𝟐

𝒂 = 𝑆

2

(𝑿

𝑻

𝑿)

−𝟏

W macierzy 𝑫

𝟐

𝒂 elementy na głównej przekątnej są wariancjami estymatorów parametrów strukturalnych

𝑫

𝟐

𝒂

𝒊

.

Pierwiastki z wariancji estymatorów parametru:

𝑫

𝒂

𝒊

= 𝑫

𝟐

𝒂

𝒊

(𝑖 = 1, 2, … , 𝑘)

są odchyleniami standardowymi estymatorów parametrów. Określa się je mianem średnich błędów
szacunku parametrów modelu i informują one o ile przeciętnie oceny parametrów strukturalnych uzyskane
na podstawie próby różnią się od nieznanych wartości parametrów w populacji.

Dr Arkadiusz Kijek
Ekonometria

12

Wykłady 2009/2010

Średnie błędy szacunku parametrów odnoszą się do wartości bezwzględnej z ocen parametrów i w ten
sposób oblicza się względne błędy szacunku parametrów:

𝑾

𝒂

𝒊

=

𝑫

𝒂

𝒊

𝒂

𝒊

∙ 100% (𝑖 = 1, 2, … , 𝑘)

Ustalając z góry kryteria można dokonad oceny wielkości błędów i na tej podstawie ocenid jakośd
oszacowania parametrów.

Miary dopasowania modelu do danych empirycznych

1. Współczynnik determinacji, współczynnik zbieżności

Dla każdej obserwacji t (𝑡 = 1, 2, … , 𝑛) można zapisad następującą tożsamośd:

𝑦

𝑡

− 𝑦 = 𝑦

𝑡

− 𝑦

𝑡

+ (𝑦

𝑡

− 𝑦 )

Po odpowiednich przekształceniach można otrzymad

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

= (𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

= (𝑦

𝑡

− 𝑦

𝑡

)

2

𝑛

𝑡=1

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

– całkowita zmiennośd zmiennej objaśnianej, suma kwadratów odchyleo wartości

empirycznych od siebie

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

– zmiennośd wyjaśniana przez model, suma kwadratów odchyleo wartości teoretycznych

od średniej

(𝑦

𝑡

− 𝑦

𝑡

)

2

𝑛

𝑡=1

– zmiennośd nie wyjaśniana przez model, suma kwadratów reszt

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

+

(𝑦

𝑡

− 𝑦

𝑡

)

2

𝑛

𝑡=1

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

= 1

𝑅

2

𝜑

2

0 ≤ 𝑅

2

, 𝜑

2

≤ 1

Dr Arkadiusz Kijek
Ekonometria

13

Wykłady 2009/2010

𝑅

2

– współczynnik determinacji; informuje jaka częśd całkowitej zmienności zmiennej objaśnianej jest

wyjaśniana przez zmiennośd zmiennych objaśniających, dopasowanie modelu jest tym lepsze, im
współczynnik jest bliższy 1.

𝑅

2

=

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

=

𝒂

𝑻

𝑿

𝑻

𝒚 −

1
𝑛 (𝟏

𝑇

𝑦)

2

𝒚

𝑻

𝒚 −

1
𝑛 (𝟏

𝑇

𝑦)

2

= 1 − 𝜑

2

𝜑

2

– współczynnik zbieżności; informuje jaka częśd całkowitej zmienności zmiennej objaśnianej nie jest

wyjaśniana przez zmiennośd zmiennych objaśniających, dopasowanie modelu jest tym lepsze, im
współczynnik jest bliższy 0.

𝜑

2

=

(𝑦

𝑡

− 𝑦

𝑡

)

2

𝑛

𝑡=1

(𝑦

𝑡

− 𝑦 )

2

𝑛

𝑡=1

=

𝒆

𝑻

𝒆

𝒚

𝑻

𝒚 −

1
𝑛 (𝟏

𝑇

𝑦)

2

=

𝒚

𝑻

𝒚 − 𝒂

𝑻

𝑿

𝑻

𝒚

𝒚

𝑻

𝒚 −

1
𝑛 (𝟏

𝑇

𝑦)

2

= 1 − 𝑅

2

Suma kwadratów reszt zależy od liczby zmiennych objaśniających w modelu i nigdy nie rośnie (zwykle
maleje) wraz ze wzrostem liczny zmiennych objaśniających. Dlatego wartośd współczynnika determinacji
nigdy nie będzie malała (zwykle będzie rosła) wraz z dodawaniem nowych zmiennych objaśniających,
niezależnie od tego czy dana zmienna istotnie czy nieistotnie wpływa na zmienną objaśnianą.
Dodatkowo w przypadku małej liczby szacowanych parametrów, suma kwadratów jest mała i powoduje,
że obraz dopasowania jest zbyt optymistyczny – w takich sytuacjach stosuje się skorygowane o liczbę
stopni swobody współczynniki zbieżności i determinacji.

𝜑

2

=

𝑛 − 1

𝑛 − 𝑘 − 1

𝜑

2

𝑅

2

= 1 − 𝜑

2

= 𝑅

2

−

𝑘

𝑛 − 𝑘 − 1

(1 − 𝑅

2

)

Wadą powyższych współczynników jest brak ich unormowania, co utrudnia ich interpretację i ocenę
dopasowania modelu.

2. Współczynnik zmienności resztowej

𝑊 =

𝑆
𝑦

∙ 100%

Informuje jaki procent średniej wartości zmiennej objaśnianej stanowi odchylenie standardowe reszt
modelu. Dopasowanie modelu do danych empirycznych jest tym lepsze, im 𝑊 jest bliższy 0.

Dr Arkadiusz Kijek
Ekonometria

14

Wykłady 2009/2010

Predykcja na podstawie liniowego modelu ekonometrycznego

Prognozy ilościowe mogą byd dwojakiego rodzaju: punktowe lub przedziałowe. Prognoza punktowa jest
liczbą uznaną za najwiarygodniejszą ocenę wartości zmiennej w okresie prognozowanym (zasada
największego prawdopodobieostwa) lub jest równa wartości oczekiwanej zmiennej prognozowanej (zasada
predykcji nieobciążonej). Prognoza przedziałowa jest przedziałem liczbowym, który ze z góry zadanym
prawdopodobieostwem (wiarygodnośd prognozy) pokrywa wartośd zmiennej w okresie prognozowanym.

Prognoza punktowa zmiennej endogenicznej w okresie T wyznacza się wg wzoru:

𝑌

𝑇

∗

= 𝛼 + 𝛼

1

𝑥

1𝑇

∗

+ 𝛼

2

𝑥

2𝑇

∗

+ ⋯ + 𝛼

𝑘

𝑥

𝑘𝑇

∗

gdzie

𝑥

1𝑇

∗

, 𝑥

2𝑇

∗

, … , 𝑥

𝑘𝑇

∗

– wartości zmiennych objaśniających w okresie T.

Prognozę punktową można również wyznaczyd ze wzoru macierzowego

𝑌

𝑇

∗

= 𝒙

𝑇

𝑇

𝒂

gdzie

𝒙

𝑇

𝑇

= 1 𝑥

1𝑇

∗

𝑥

2𝑇

∗

⋯ 𝑥

𝑘𝑇

∗

Wartości zmiennych objaśniających w okresie prognozowanym

W przypadku prognoz wyznaczanych na podstawie modelu ekonometrycznego istotną rzeczą jest, by przyjąd
właściwe wartości zmiennych objaśniających w okresie prognozy, ponieważ przyjęcie trafnych wartości
zmiennych objaśniających w okresie prognozowanym zapewnia najlepszą prognozę zmiennej prognozowanej
(najbliższą realizacji względnej).

W niektórych przypadkach wartości zmiennych objaśniających w okresie prognozowanym są zmiennymi
decyzyjnymi. W tej sytuacji ich wartośd zależy od planów przyjętych przez odpowiednie podmioty. Jeżeli
prognozy mają charakter makroekonomiczny, wartości niektórych zmiennych objaśniających ustalane są
przez odpowiednie organy rządowe lub inne instytucje centralne. Natomiast jeżeli prognozowanie odbywa
się na szczeblu mikroekonomicznym, poziom niektórych zmiennych objaśniających przyjmowany jest przez
decydentów odpowiedzialnych za budżetowanie w przedsiębiorstwach.

Wartości zmiennych objaśniających mogą byd również prognozowane za pomocą innych modeli
ekonometrycznych. W tym przypadku najczęściej wykorzystywane są modele autoregresyjne oraz modele
tendencji rozwojowej dla tych zmiennych.

Dr Arkadiusz Kijek
Ekonometria

15

Wykłady 2009/2010

Modele szeregów czasowych

Kształtowanie zjawisk ekonomicznych w czasie jest wypadkową działania przyczyn głównych oraz
przypadkowych. W stosunkowo długim okresie czasu przyczyny główne wpływają na zarysowanie się
tendencji rozwojowej (trendu) badanego zjawiska. W szczególnym przypadku, gdy długookresowa analiza nie
dowodzi zarysowania się wyraźnej tendencji, mamy do czynienia ze stałym poziomem zjawiska w czasie.

Poza tendencją rozwojową na zmiany w poziomie zjawiska wpływa okresowośd. Wahania okresowe
ujawniają się co pewien okres podobnymi co do wielkości zmianami poziomów badanego zjawiska. Odstęp
czasu, w którym występują wszystkie fazy wahao, określany jest mianem cyklu. Najczęściej występującym
cyklem jest cykl roczny i wtedy wahania nazywane są wahaniami sezonowymi. Z kolei wahania
nieprzypadkowe (losowe) są efektem działania czynników o nieprzewidywalnym charakterze i powodują one
odchylenia w różnych kierunkach z różną siłą.

Równanie opisujące kształtowanie się określonego zjawiska jako funkcję trendu nosi nazwę modelu
tendencji rozwojowej.

Model tendencji rozwojowej

MTR jest modelem, w którym rolę zmiennej objaśniającej pełni zmienna czasowa 𝑡. Znajduje on
zastosowanie, gdy w szeregu czasowym można wyodrębnid tendencję rozwojową oraz wahania
przypadkowe. Postad analityczną tego modelu najczęściej dobiera się na podstawie analizy rozkładu punktów
empirycznych, odpowiadających zaobserwowanym realizacjom zmiennej objaśnianej w kolejnych okresach w
układzie współrzędnych. W ten sposób określa się jej matematyczną funkcję najlepiej pasującą do kształtu
rozkładu punktów empirycznych.

Najprostszą postacią modelu jest postad liniowa:

𝑌 = 𝛼

0

+ 𝛼

1

∙ 𝑡 + 𝜀

𝑡

Do oszacowania parametrów liniowego modelu tendencji rozwojowej wykorzystuje się następujący
estymator:

𝒂 = (𝑻

𝑻

𝑻)

−𝟏

𝑻

𝑻

𝒚

Weryfikacja MTR odbywa się zgodnie z regułami dotyczącymi modelu ekonometrycznego.

Predykcja na podstawie modelu tendencji rozwojowej

Ekstrapolacja funkcji trendu może byd wykorzystywana do sporządzania prognoz w przypadku, gdy postad
analityczna funkcji trendu i wartośd jej parametrów strukturalnych w okresie 𝑇, na której dokonuje się
prognozy, nie mogą ulec istotnej zmianie w porównaniu z okresem, którego dotyczyły informacje liczbowe
służące do oszacowania funkcji trendu. W przypadku istotnych zmian w kształtowaniu się zjawisk,
zastosowanie ekstrapolacji trendu może przynieśd duże błędy.

Dr Arkadiusz Kijek
Ekonometria

16

Wykłady 2009/2010

Prognozę punktową zmiennej endogenicznej w okresie 𝑇 wyznacza się wg wzoru:

𝑦

𝑇

∗

= 𝛼

0

+ 𝛼

1

∙ 𝑇

Miary dokładności predykcji ex ante

Ostatnim etapem predykcji jest ocena dokładności prognoz. Ocena taka może byd dokonywana na podstawie
błędów prognozy ex ante. Mierniki te pozwalają na oszacowanie oczekiwanej wielkości odchylenia prognozy
od rzeczywistej wartości zmiennej prognozowanej.

W przypadku modelu ekonometrycznego bezwzględny błąd prognozy punktowej ex ante szacuje się
następująco:

I sposób

𝐷

𝑇

= 𝑆

2

+ 𝒙

𝑻

𝑻

𝑫

𝟐

𝒂 𝒙

𝑇

= 𝑆 1 + 𝒙

𝑻

𝑻

(𝑿

𝑻

𝑿)

−1

𝒙

𝑇

𝒙

𝑻

𝑻

= 1 𝑥

1𝑇

∗

𝑥

2𝑇

∗

⋯ 𝑥

𝑘𝑇

∗

II sposób

𝐷

𝑇

= 𝑥

𝑖𝑇

2

𝐷

2

𝛼

𝑖

+ 2 𝑥

𝑖𝑇

𝑥

𝑗𝑇

∙ 𝑐𝑜𝑣 𝛼

𝑖

> 𝛼

𝑗

+ 𝑆

2

𝑗 >𝑖

𝑘−1

𝑖=0

𝑘

𝑖=0

W przypadku modelu tendencji rozwojowej, bezwzględny błąd prognozy punktowej ex ante wyznacza się
następująco:

I sposób

𝐷

𝑇

= 𝑆 1 +

1
𝑛

+

(𝑇 − 𝑡)

2

(𝑡 − 𝑡)

2

𝑛

𝑡=1

II sposób

𝐷

𝑇

= 𝑆

2

+ 𝐷

2

𝛼

0

+ 𝑇

2

𝐷

2

𝛼

1

+ 2𝑇 ∙ 𝑐𝑜𝑣 𝛼

𝑖

> 𝛼

𝑗

Dr Arkadiusz Kijek
Ekonometria

17

Wykłady 2009/2010

Ocenę wielkości błędu predykcji przeprowadza się na podstawie względnego błędu prognozy ex ante, który
oblicza się wg wzoru:

𝑉

𝑇

=

𝐷

𝑇

𝑦

𝑇

∗

∙ 100%

Ustalając z góry kryteria można dokonad oceny wielkości błędów i na tej podstawie ocenid dopuszczalnośd
wyznaczonych prognoz.

Modele optymalizacyjne

Osiągnięcie określonego celu ekonomicznego wymaga podjęcia odpowiednich decyzji odnośnie
zaangażowania określonych zasobów. W przypadku wystąpienia więcej niż jednego wariantu decyzyjnego
mówimy o istnieniu problemu decyzyjnego. Decyzja, która jest najlepsza z punktu widzenia przyjętego celu,
oraz występujących ograniczeo nazywana jest decyzją optymalną.

Model służący do rozwiązywania problemu decyzyjnego, nazywany jest modelem decyzyjnym lub modelem
optymalizacyjnym. Dziedziną zajmującą się rozstrzyganiem problemów decyzyjnych określa się mianem
badao operacyjnych. Ważną klasą modeli optymalizacyjnych są modele programowania matematycznego, a
w szczególności ich podklasa – programy liniowe.

Charakterystyczną cechą programów liniowych jest występowanie w nich liniowych warunków
ograniczających oraz liniowej funkcji celu. Jeżeli w modelach optymalizacyjnych występuje co najmniej jeden
nieliniowy warunek ograniczający lub nieliniowa funkcja celu, taki model określany jest mianem modelu
nieliniowego.

Konstrukcja modeli programowania matematycznego

Zmienne decyzyjne 𝑥

1

, 𝑥

2

, … , 𝑥

𝑛

odpowiadają wielkości ograniczonych zasobów, które mogą zostad

wykorzystane w do osiągnięcia zamierzonego celu. Optymalna wartośd tych zmiennych ustalana jest przy
rozwiązywaniu problemu decyzyjnego. Dowolny wektor n-wymiarowy, którego współrzędnymi są wartości
zmiennych decyzyjnych:

𝒅 = 𝑥

1

𝑥

2

⋯ 𝑥

𝑛

𝑇

nazywany jest decyzją.

Warunki ograniczające są restrykcjami nałożonymi na zmienne decyzyjne, które wynikają z ograniczoności
zasobów oraz zobowiązao decydentów. Warunki ograniczające dzielą się na warunki elementarne i
nieelementarne.

Dr Arkadiusz Kijek
Ekonometria

18

Wykłady 2009/2010

Warunki elementarne są to warunki typu:

𝑥

𝑗

> 0 dla 𝑗 = 1, 2, … , 𝑛

1

𝑥

𝑗

< 0 dla 𝑗 = 𝑛

1

+ 1, 𝑛

1

+ 2, … , 𝑛

2

𝑥

𝑗

∈ ℝ dla 𝑗 = 𝑛

2

+ 1, 𝑛

2

+ 2, … , 𝑛

Pozostałe warunki określane są jako warunki nieelementarne.

Warunki nieelementarne są to warunki typu:

𝑔

𝑖

𝑥 ≤ 𝑏

𝑖

dla 𝑖 = 1, 2, … , 𝑚

1

𝑔

𝑖

𝑥 ≥ 𝑏

𝑖

dla 𝑖 = 𝑚

1

+ 1, 𝑚

1

+ 2, … , 𝑚

2

𝑔

𝑖

𝑥 = 𝑏

𝑖

dla 𝑖 = 𝑚

2

+ 1, 𝑚

2

+ 2, … , 𝑚

gdzie:

𝑔

𝑖

𝑥 – funkcja określona na wektorze zmiennych decyzyjnych 𝒙.

Zbiór decyzji 𝒅 spełniających warunki ograniczające nazywany jest zbiorem decyzji dopuszczalnych 𝐷.

Funkcja celu 𝑓(𝑥) jest sformalizowanym zapisem celu do którego dąży decydent przy użyciu posiadanych
zasobów. W procesie decyzyjnym dokonywana jest optymalizacja funkcji celu, która polega na jej
maksymalizacji lub minimalizacji, co zapisuje się następująco:

𝑓(𝑥) → 𝑚𝑎𝑥 lub 𝑓(𝑥) → 𝑚𝑖𝑛

Zadanie programowania matematycznego polega na znalezieniu takiego punktu (punktów) 𝒙

0

należącego do

zbioru 𝐷, w którym funkcja 𝑓 osiąga wartośd maksymalną:

𝐷

𝒐𝒑𝒕

= {𝒙

0

∈ 𝐷: 𝑓(𝑥) ≤ 𝑓(

𝑥∈𝐷

𝒙

0

)}

lub minimalną:

𝐷

𝒐𝒑𝒕

= {𝒙

0

∈ 𝐷: 𝑓(𝑥) ≥ 𝑓(

𝑥∈𝐷

𝒙

0

)}

Punkt (punkty) tworzy zbiór decyzji optymalnych.

Dr Arkadiusz Kijek
Ekonometria

19

Wykłady 2009/2010

Szczególny przypadek zadao programowania matematycznego stanowią zadania programowania liniowego.
Mamy z nim do czynienia, gdy funkcje 𝑓 oraz 𝑔

𝑖

dla 𝑖 = 1, 2, … , 𝑚 są liniowe:

𝑓 𝑥

1

, 𝑥

2

, … , 𝑥

𝑛

= 𝑐

𝑗

𝑥

𝑗

𝑛

𝑗 =1

𝑔

𝑖

𝑥

1

, 𝑥

2

, … , 𝑥

𝑛

=

𝑎

𝑖𝑗

𝑥

𝑖

𝑛

𝑗 =1

dla 𝑖 = 1, 2, … , 𝑚

przy czym 𝑎

𝑖𝑗

dla 𝑖 = 1, 2, … , 𝑚; 𝑗 = 1, 2, … , 𝑛 są współczynnikami warunków organizacyjnych, a parametry

𝑐

𝑗

dla 𝑗 = 1, 2, … , 𝑛 określane są jako współczynniki funkcji celu.

Każdy program liniowy można sprowadzid do postaci klasycznej

𝑐

1

𝑥

1

+ 𝑐

2

𝑥

2

+ ⋯ + 𝑐

𝑛

𝑥

𝑛

→ 𝑚𝑎𝑥

𝑎

11

𝑥

1

+ 𝑎

12

𝑥

2

+ ⋯ + 𝑎

1𝑛

𝑥

𝑛

≤ 𝑏

1

𝑎

21

𝑥

1

+ 𝑎

22

𝑥

2

+ ⋯ + 𝑎

2𝑛

𝑥

𝑛

≤ 𝑏

2

⋯

𝑎

𝑚 1

𝑥

1

+ 𝑎

𝑚 2

𝑥

2

+ ⋯ + 𝑎

𝑚𝑛

𝑥

𝑛

≤ 𝑏

𝑚

𝑥

1

+ 𝑥

2

+ ⋯ + 𝑥

𝑛

≤ 0

Zapis macierzowy postaci klasycznej:

𝑪

𝑇

𝒙 → 𝑚𝑎𝑥

𝑨𝒙 ≤ 𝒃

𝒙 ≥ 𝟎

gdzie 𝒙 jest wektorem zmiennych decyzyjnych, 𝑨 jest macierzą współczynników warunków ograniczających,
𝒃 jest wektorem wyrazów wolnych warunków ograniczających, 𝟎 jest wektorem zerowym (𝒂 ≤ 𝒃 oznacza,
że współrzędne wektora 𝒂 są nie większe, niż odpowiadające im współrzędne wektora 𝒃).

Przy kryterium maksymalizacji, nieelementarne warunki ograniczające są nierównościami typu „≤”
(nierówności typowe), a przy kryterium minimalizacji nierównościami typu „≥” (nierówności typowe).
Natomiast warunki nieelementarne w obydwu przypadkach zakładają nieujemności zmiennych (nierówności
typowe).

Inną ważną postacią zadania programowania liniowego jest postad standardowa, w której wszystkie warunki
mają postad równości i na wszystkie zmienne decyzyjne nałożony jest warunek nieujemności. Każde zadanie
w postaci klasycznej można sprowadzid do postaci standardowej poprzez odpowiednie przekształcenie
warunków nieelementarnych.

Dr Arkadiusz Kijek
Ekonometria

20

Wykłady 2009/2010

Sprowadzanie do postaci standardowej

W przypadku warunku:

𝑔

𝑖

𝒙 ≤ 𝑏

𝑖

Należy do lewej strony dodad zmienną swobodną 𝑥

𝑛+1

:

𝑔

𝑖

𝒙 + 𝑥

𝑛+1

= 𝑏

𝑖

W przypadku warunku:

𝑔

𝑖

𝒙 ≥ 𝑏

𝑖

Należy od lewej strony odjąd zmienną swobodną 𝑥

𝑛+1

:

𝑔

𝑖

𝒙 − 𝑥

𝑛+1

= 𝑏

𝑖

W pierwszym przypadku zmienną swobodną 𝑥

𝑛+1

określa się jako zmienną niedoboru, natomiast w drugim

przypadku zmienną nadmiaru. Zmienna ta również spełnia warunek nieujemności.

Etapy formułowania zadania programowania matematycznego

1. Zdefiniowanie zmiennych decyzyjnych

2. Ustalenie wielkości parametrów

3. Sformułowanie funkcji celu

4. Sformułowanie warunków ograniczających

Klasy problemów decyzyjnych

W zależności od rodzaju problemu decyzyjnego, jego funkcji celu oraz warunków ograniczających będziemy
rozpatrywad następujące klasy problemów decyzyjnych:

a) optymalizacja struktury produkcji

b) problem mieszanek

c) wybór procesu technologicznego

Dr Arkadiusz Kijek
Ekonometria

21

Wykłady 2009/2010

a) optymalizacja struktury produkcji

Optymalizacja struktury produkcji polega na określeniu rodzaju oraz ilości wyrobów jakie powinno
produkowad przedsiębiorstwo przy posiadanych zasobach produkcji oraz innych ograniczeniach, aby
zmaksymalizowad zysk albo przychody ze sprzedaży.

Przykład.

Przedsiębiorstwo MPJ produkuje dwa wyroby 𝑊

1

i 𝑊

2

, do wytwarzania których wykorzystuje dwa

limitowane surowce 𝑆

1

i 𝑆

2

. Limity miesięcznego zużycia surowców wynoszą: 𝑆

1

– 2100 kg , 𝑆

2

– 2600

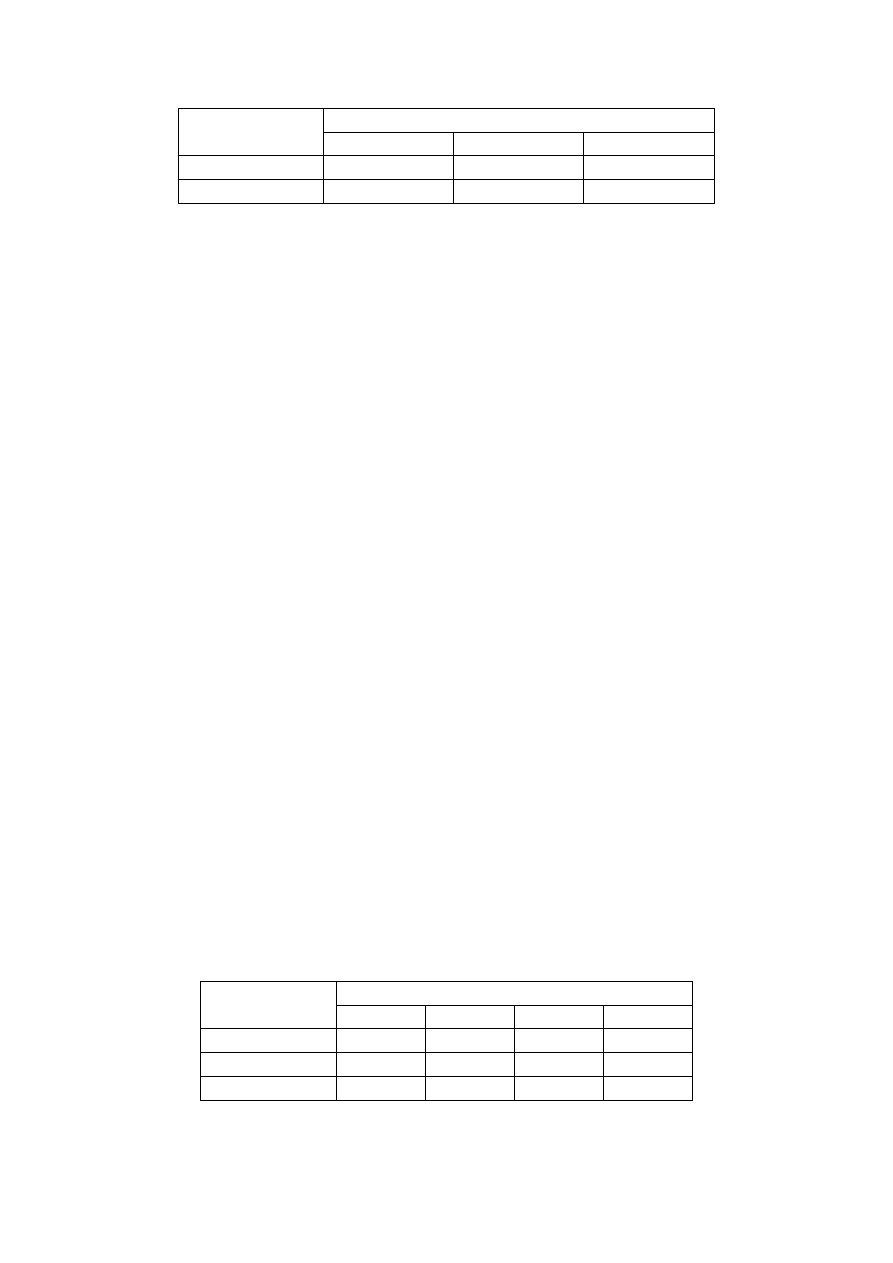
kg. Jednostkowe zużycie tych surowców do produkcji poszczególnych wyrobów podane są w poniższej tabeli.

surowce

wyroby

𝑊

1

𝑊

2

𝑆

1

6

3

𝑆

2

4

4

Zysk osiągany na jednostce wyrobu 𝑊

1

wynosi 40 zł, a na jednostce wyrobu 𝑊

2

wynosi 50 zł. Ile wyrobów

miesięcznie ma produkowad przedsiębiorstwo, aby osiągnąd maksymalny zysk?

Zmienne decyzyjne:

𝑥

1

– miesięczna produkcja wyrobu 𝑊

1

(w szt.)

𝑥

2

– miesięczna produkcja wyrobu 𝑊

2

(w szt.)

𝑓 𝑥

1

, 𝑥

2

= 40𝑥

1

+ 50𝑥

2

→ 𝑚𝑎𝑥

6𝑥

1

+ 3𝑥

2

≤ 2100 ; 4𝑥

1

+ 4𝑥

2

≤ 2600

𝑥

1

, 𝑥

2

≥ 0

b) problem mieszanek

Problem mieszanek polega na określeniu rodzaju oraz ilości surowców jakie należy zakupid, aby otrzymad
produkt o podanym składzie przy możliwie najniższych kosztach zakupu surowców.

Przykład.

Racjonalne odżywianie wymaga przyjmowania dwóch składników odżywczych w odpowiednich ilościach: 𝑆

1

– co najmniej 2 kg miesięcznie oraz 𝑆

2

– co najmniej 2,5 kg miesięcznie. Zawartośd tych składników w trzech

produktach odżywczych przedstawia tabela:

Dr Arkadiusz Kijek
Ekonometria

22

Wykłady 2009/2010

Składniki odżywcze

Zawartośd składników odżywczych w 1 kg produktu

𝑃

1

𝑃

2

𝑃

3

𝑆

1

0,2

0,15

0,1

𝑆

2

0,05

0,1

0,2

Wiedząc, że ceny poszczególnych produktów wynoszą: 𝑃

1

– 30 zł, 𝑃

2

– 50 zł oraz 𝑃

3

– 40 zł dobrad optymalne

ilości produktów, tak aby zminimalizowad koszt stosowania diety.

Zmienne decyzyjne:

𝑥

1

– waga produktu 𝑃

1

(w kg)

𝑥

2

– waga produktu 𝑃

2

(w kg)

𝑥

3

– waga produktu 𝑃

3

(w kg)

𝑓 𝑥

1

, 𝑥

2

, 𝑥

3

= 30𝑥

1

+ 50𝑥

2

+ 40𝑥

3

→ 𝑚𝑖𝑛

0,2𝑥

1

+ 0,15𝑥

2

+ 0,1𝑥

3

≥ 2

0,05 + 0,1𝑥

2

+ 0,2𝑥

3

≥ 2,5

𝑥

1

, 𝑥

2,

, 𝑥

3

≥ 0

c) wybór procesu technologicznego

Wybór procesu technologicznego polega na określaniu skali zastosowania możliwych procesów
wytwórczych, aby wyprodukowad określone ilości produktów przy możliwie najniższych kosztach.

Przykład.

Przedsiębiorstwo MWM produkuje dwa wyroby 𝑊

1

i 𝑊

2

, do wytwarzania których wykorzystuje cztery

rodzaje płyt: 𝑃

1

, 𝑃

2

, 𝑃

3

i 𝑃

4

. Ilośd możliwych do uzyskania wyrobów oraz odpad z poszczególnych rodzajów

płyt zawiera poniższa tabela:

Wyroby

Płyty

𝑃

1

𝑃

2

𝑃

3

𝑃

4

𝑊

1

6

4

3

0

𝑊

2

1

2

4

6

Odpad (w m

2

)

0,3

0,5

0,4

0,6

Dr Arkadiusz Kijek
Ekonometria

23

Wykłady 2009/2010

Dobrad optymalną dostawę płyt potrzebnych do wyprodukowania co najmniej 1500 szt. wyrobu 𝑊

1

oraz co

najmniej 2000 szt. wyrobu 𝑊

2

, aby zminimalizowad odpad z wykorzystanych płyt.

Zmienne decyzyjne:

𝑥

1

– liczba płyt 𝑃

1

𝑥

2

– liczba płyt 𝑃

2

𝑥

3

– liczba płyt 𝑃

3

𝑥

4

– liczba płyt 𝑃

4

𝑓(𝑥

1

, 𝑥

2

, 𝑥

3

, 𝑥

4

) = 0,3𝑥

1

+ 0,5𝑥

2

+ 0,4𝑥

3

+ 0,6𝑥

4

→ 𝑚𝑖𝑛

6𝑥

1

+ 4𝑥

2

+ 3𝑥

3

≥ 1500

𝑥

1

+ 2𝑥

2

+ 4𝑥

3

+ 6𝑥

4

≥ 2000

𝑥

1

, 𝑥

2

, 𝑥

3

, 𝑥

4

≥ 0

Metoda geometryczna

Rozwiązywanie zadao programowania liniowego metodą geometryczną, polega na wyznaczeniu w
skonstruowanym graficznie zbiorze rozwiązao dopuszczalnych punktu lub punktów, dla których funkcja celu
przyjmuje wartości najkorzystniejsze (minimalne lub maksymalne). Punkt (punkty) ten nosi nazwę punktu
optymalnego.

Metodę graficzną można zastosowad do rozwiązywania zadao z co najwyżej trzema zmiennymi decyzyjnymi.
Wiąże się to z koniecznością wykorzystywania przestrzeni dwuwymiarowych, ewentualnie trójwymiarowych.

Tworząc przestrzeo decyzji dopuszczalnych 𝐷, należy zobrazowad każdy z warunków w układzie
współrzędnych. W przypadku układów dwuwymiarowych odwzorowaniem warunku jest:

a) prosta dla równości

b) półpłaszczyzna z prostą ograniczającą dla nierówności słabych

c) półpłaszczyzna bez prostej ograniczającej dla nierówności ostrych

Częśd wspólna dla wszystkich warunków ograniczających tworzy zbiór decyzji dopuszczalnych 𝐷.

Izokwantą funkcji celu jest prosta, zawierająca punkty o tej samej wartości funkcji celu 𝑐

1

𝑥

1

+ 𝑐

2

𝑥

2

= 𝑧.

Należą do niej wszystkie argumenty, dla których wartośd funkcji celu wynosi 𝑧.

Gradient jest wektorem wskazującym kierunek wzrostu wartości funkcji celu [𝑐

1

, 𝑐

2

] (izokwanta jest

prostopadła do gradientu). Z kolei wektor przeciwny do gradientu wskazuje kierunek spadku wartości funkcji

Dr Arkadiusz Kijek
Ekonometria

24

Wykłady 2009/2010

celu. Jeśli funkcja celu dąży do maksimum, przesuwamy izokwantę zgodnie z gradientem; gdy do minimum,
w kierunku przeciwnym do gradientu.

Rozwiązanie zadania programowania liniowego stanowi punkt lub punkty zbioru 𝐷 należące do izokwanty o
najmniejszej wartości 𝑧 (dla minimum) lub największej (dla maksimum). Inaczej mówiąc, rozwiązaniem
zadania programowania liniowego jest punkt lub punkty należące do najwyżej (dla maksimum) lub najniżej
(dla minimum) położonej izokwanty znajdujące się w zbiorze 𝐷.

Jeżeli zadanie programowania liniowego ma rozwiązanie optymalne, to znajduje się ono w co najmniej
jednym wierzchołku zbioru 𝐷.

Rozwiązanie zadania programowania liniowego jest jednym z następujących przypadków:

a) zbiór pusty, gdy zbiór 𝐷 jest pusty lub funkcja celu nie jest ograniczona z góry (dołu) na zbiorze 𝐷:

𝐷

𝑜𝑝𝑡

= ∅

b) jedno rozwiązanie, którym jest wierzchołek zbioru 𝐷:

𝐷

𝑜𝑝𝑡

= 𝑑

1

𝑑

2

𝑇

c) nieskooczenie wiele rozwiązao, które stanowi odcinek łączący dwa wierzchołki 𝑑

1

i 𝑑

2

zbioru 𝐷

𝐷

𝑜𝑝𝑡

= { 𝑑

𝑜𝑝𝑡

= 𝜆𝑑

1

+ 1 − 𝜆 𝑑

2

∶ 𝜆 ∈ < 0,1 > }

d) lub półprosta wychodząca z wierzchołka 𝑑 zbioru 𝐷 w kierunku wektora 𝑕 (wyznacza on kierunek

półprostej ograniczającej zbioru 𝐷 wychodzącej z punktu 𝑑):

𝐷

𝑜𝑝𝑡

= { 𝑑

𝑜𝑝𝑡

= 𝑑 + 𝜆𝑕 ∶ 𝜆 ∈ < 0, +∞ > }

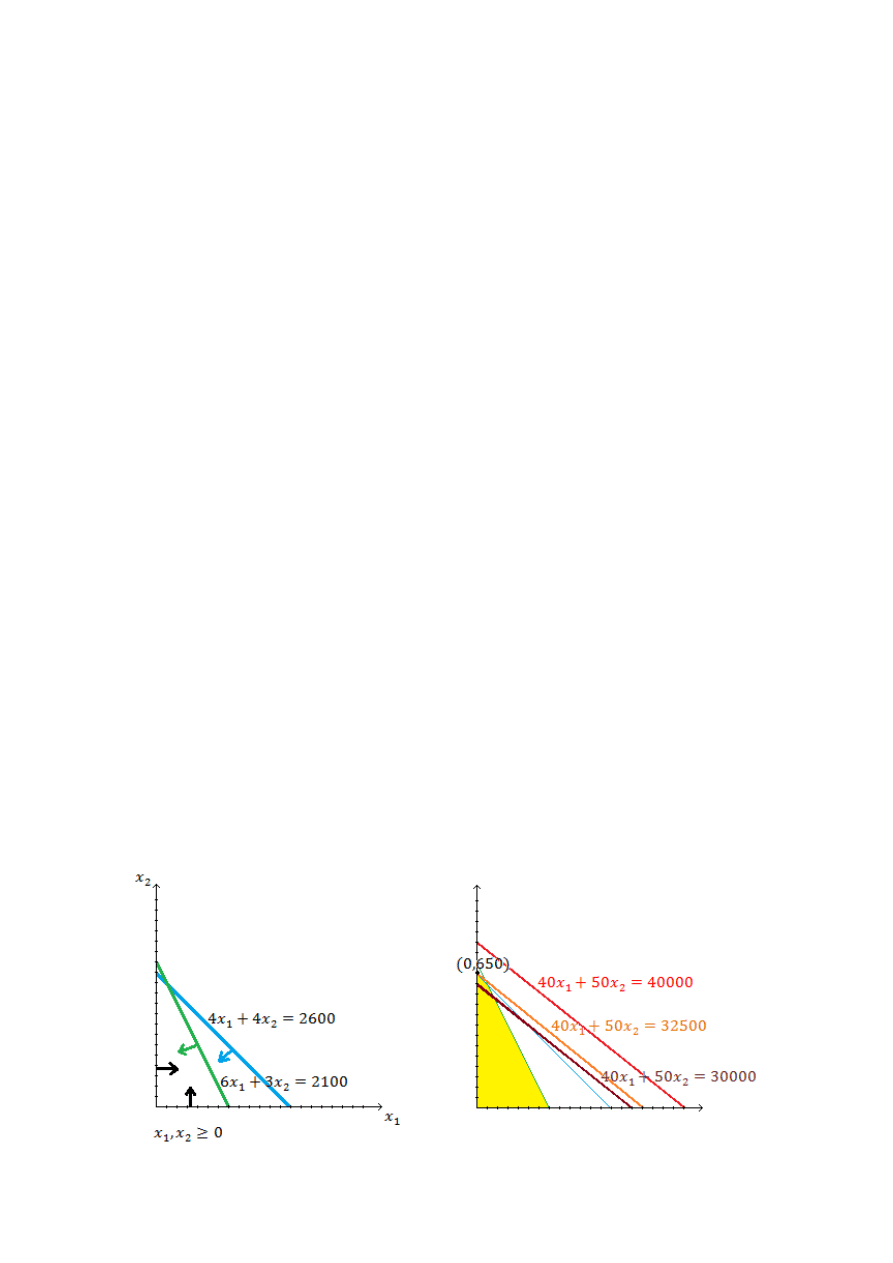
Przykład (cd.)

a) optymalizacja struktury produkcji

Dr Arkadiusz Kijek
Ekonometria

25

Wykłady 2009/2010

𝑑

𝑜𝑝𝑡

=

0

650

𝑓 𝑑

𝑜𝑝𝑡

= 32500

Metoda Simpleks

Opracowana przez G. B. Dantziga metoda rozwiązywania zadao programów liniowych. Polega ona na
poszukiwaniu rozwiązao optymalnych poprzez badanie sąsiednich bazowych rozwiązao dopuszczalnych w
taki sposób, aby kolejne rozwiązane było nie gorsze od poprzedniego pod względem wartości funkcji celu.
Postępowanie kooczy się w momencie wyznaczenia rozwiązania optymalnego lub stwierdzenia o braku jego
istnienia. Algorytm Simpleks jest procedurą etapową, a wyniki w kolejnych krokach różnią się od siebie.

Podstawą procedury jest program liniowy w postaci standardowej:

𝑐

𝑇

𝑥 → 𝑚𝑎𝑥

𝐴𝑥 = 𝑏

𝑥 ≥0

Postad bazowa programu liniowego występuje w sytuacji gdy macierz 𝐴 jest w postaci bazowej, czyli wśród
jej kolumn znajduje się 𝑚 kolumn będących liniowo niezależnymi wektorami jednostkowymi. Z kolei jeżeli
wektor wyrazów wolnych 𝑏 ma nieujemne współrzędne oznacza to, że mamy do czynienia z postacią
dopuszczalną. Spełnienie obu warunków daje dopuszczalną postad bazową zadania.

Macierz 𝐴 dzieli się na dwa bloki 𝐵 i 𝑃:

𝐴 = 𝐵 𝑃

W macierzy 𝐵 znajduje się 𝑚 liniowo niezależnych kolumn macierzy 𝐴 = (𝑎

𝑗 1

, … , 𝑎

𝑗𝑚

)

.

Macierz 𝑃 tworzą

pozostałe kolumny macierzy 𝐴 = (𝑎

𝑗𝑛 +1

, … , 𝑎

𝑗𝑛

). Macierz 𝐵 nazywana jest macierzą bazową lub bazą.

Zbiór indeksów zmiennych bazowych 𝐵 = (𝑗

1

, … , 𝑗

𝑚

) nazywamy zbiorem bazowym.

Analogiczny podział macierzy 𝐴 na bloki 𝐵 i 𝑃, dzieli wektor zmiennych 𝑥 na dwie części 𝑥

𝐵

𝑖 𝑥

𝑃

:

𝑋 =

𝑥

𝐵

𝑥

𝑃

𝑋

𝐵

= 𝑥

𝑗 1

… … … 𝑥

𝑗𝑚

T

𝑋

𝑃

= 𝑥

𝑗 𝑚 +1

… … … 𝑥

𝑗𝑚

T

Dr Arkadiusz Kijek
Ekonometria

26

Wykłady 2009/2010

oraz wektor współczynników funkcji celu 𝑐 na 𝑐

𝐵

i 𝑐

𝑃

.

𝑐 =

𝑥

𝐵

𝑥

𝑃

𝑐

𝐵

= 𝑥

𝑗 1

… … … 𝑥

𝑗𝑚

T

𝑐

𝑃

= 𝑥

𝑗 𝑚 +1

… … … 𝑥

𝑗𝑚

T

Po powyższych przekształceniach układ nieelementarny warunków ograniczających można zapisad:

𝐵 𝑃

𝑥

𝐵

𝑥

𝑃

, 𝐵𝑥

𝐵

+ 𝑃𝑥

𝑃

= 𝑏

Jeżeli podstawimy 𝑥

𝑃

= 0 otrzymamy rozwiązanie bazowe programu liniowego:

𝑥

𝐵

𝐵

=

𝑥

𝐵

𝑥

𝑃

= 𝐵

−1

𝑏

0

Zmienne wchodzące w skład wektora 𝑥

𝐵

określa się zmiennymi bazowymi, a pozostałe zmienne tworzące

wektor 𝑥

𝑃

zmiennymi niebazowymi.

Bazowym rozwiązaniem dopuszczalnym zadania PL nazywamy rozwiązanie bazowe, które spełnia warunek
nieujemności zmiennych bazowych.

𝐵

−1

𝑏 ≥ 0

Rozwiązanie bazowe 𝑥

𝐵

określa się jako niezdegradowane, jeżeli wszystkie zmienne bazowe mają wartośd

różną od zera; jeżeli co najmniej jedna zmienna bazowa jest równa zero to rozwiązanie nazywamy
zdegradowanym.

Dwa rozwiązania bazowe nazywamy sąsiednimi jeżeli różnią się dokładnie jedną zmienną bazową i w
konsekwencji jedną zmienną niebazową.

Wektor 𝑥

𝐵

jest bazowy rozwiązaniem dopuszczalnym wtedy i tylko wtedy gdy jest wierzchołkiem zbioru

rozwiązao dopuszczalnych 𝐷.

Warunkiem wystarczającym optymalności bazowej rozwiązania dopuszczalnego 𝑥

𝐵

odpowiadającym

macierzy bazowej 𝐵 jest:

𝑐

𝑃

𝑇

− 𝑐

𝑃

𝑇

𝐵

−1

𝑃 ≤ 0

𝑇

𝐻

𝑃

= 𝐵

−1

𝑃 𝑐

𝑝

− 𝑧

𝑃

≤ 0

𝑧

𝑃

𝑇

= 𝑐

𝐵

𝑇

𝐵

−1

Po wprowadzeniu analogicznych oznaczeo dla części bazowej:

𝐻

𝐵

= 𝐵

−1

𝐵 = 𝐼 𝑖 𝑧

𝐵

𝑇

= 𝑐

𝐵

𝑇

𝐻

𝐵

= 𝑐

𝐵

𝑇

Dr Arkadiusz Kijek
Ekonometria

27

Wykłady 2009/2010

Po wyznaczeniu analogicznego wyrażenia

𝑐

𝐵

− 𝑧

𝐵

= 0

Oraz połączeniu oznaczeo dla części bazowej i niebazowej:

𝑧

𝐵

=

𝑧

𝐵

𝑧

𝑃

𝐻

𝐵

= 𝐻

𝐵

𝐻

𝑃

Można zapisad warunek dostateczny optymalności bazowej rozwiązania dopuszczalnego 𝑥

𝐵

odpowiadającego macierzy bazowej B

𝑐 − 𝑧

𝐵

≤ 0 𝑒𝑙𝑒𝑚𝑒𝑛𝑡𝑦 𝑤𝑒𝑘𝑡𝑜𝑟𝑎 𝑐 − 𝑧

𝐵

: 𝑐

𝑗

− 𝑧

𝑗

𝐵

=𝑐

𝑗

− 𝑐

𝐵

𝑇

𝑕

𝑗

Gdzie 𝑕

𝑗

oznacza kolumnę macierzy 𝐻

𝐵

odpowiadającą zmiennej 𝑥

𝑗

, 𝑐

𝑗

to współczynniki funkcji celu przy

zmiennej 𝑥

𝑗

nazywane współczynnikami optymalności.

Ponieważ wskaźnik optymalności przy zmiennych bazowych jest równy 0, a więc badanie optymalności
bazowego rozwiązania dopuszczalnego, polega na sprawdzeniu czy wskaźniki optymalności przy zmiennych
niebazowych są niedodatnie

𝑐

𝑗

− 𝑧

𝑗

𝐵

≤ 0 𝑑𝑙𝑎 𝑗 ∉ 𝐵

Bazowe rozwiązanie dopuszczalne 𝑥

𝐵

jest rozwiązaniem optymalnym, gdy wszystkie wskaźniki optymalności

są niedodatnie: 𝑐 − 𝑧

𝐵

≤ 0

Bazowe rozwiązanie dopuszczalne będące rozwiązaniem optymalnym nazywane jest bazowym rozwiązaniem
optymalnym.

Bazowe rozwiązanie dopuszczalne 𝑥

𝐵

jest jedynym rozwiązaniem optymalnym, gdy wskaźniki optymalności

zmiennych niebazowych są ujemne

𝑐

𝑗

− 𝑧

𝑗

𝐵

< 0 𝑑𝑙𝑎 𝑗 ∉ 𝐵

Jeżeli dla zmiennej nie bazowej 𝑥

𝑘

wskaźnik optymalności przyjmuje wartości dodatnie, oznacza to że

zwiększenie wartości tej zmiennej o jedną jednostkę spowoduje przyrost wartości funkcji celu o 𝑐

𝑘

− 𝑧

𝑘

𝐵

. Z

kolei wartośd ujemna wskaźnika optymalności informuje o poziomie spadku wartości funkcji celu.

W metodzie Simpleks ważną rolę odgrywa macierz 𝐴 𝑏 oraz wyznaczona na jej podstawie przez ciąg
operacji elementarnych macierz 𝐻

𝐵

𝑕

0

𝐵

ostatnia kolumna tej macierzy zawiera wektor wartości

zmiennych bazowych x

B

odpowiadających bazie B, który oblicza się następująco:

𝑕

0

𝐵

=𝐵

−1

𝑏

Przy tych oznaczeniach bazowe rozwiązanie zapisuje się :

𝑥

𝐵

=

𝑥

𝐵

𝑥

𝑃

= 𝑕

0

𝐵

0

Dr Arkadiusz Kijek
Ekonometria

28

Wykłady 2009/2010

Wartośd funkcji celu dla bazowego rozwiązania dopuszczalnego 𝑥

𝐵

można wyznaczyd:

𝑓 𝑥

𝐵

= 𝑐

𝐵

𝑇

𝑥

𝐵=

𝑐

𝐵

𝑇

𝑕

0

𝐵

Obliczenia w metodzie Simpleks prezentowane są w tablicy simpleksowej:

𝑐

𝐵

𝑐

𝑗

Zmienne

bazowe

𝑐

1

, 𝑐

2

, … , 𝑐

𝑛

𝑥

𝐵

𝑥

1

, 𝑥

2

, … , 𝑥

𝑛

𝑐

𝐵

Nazwa

zmiennych

𝐻

𝐵

𝑕

0

𝐵

𝑧

𝑗

𝐵

𝑧

𝐵

𝑐

𝐵

𝑇

𝑕

0

𝐵

𝑐

𝑗

− 𝑧

𝑗

𝐵

𝑐 − 𝑧

𝐵

W kolejnych tablicach simpleksowych kolumny macierzy 𝐻

𝐵

zapisuje się wg kolejności zmiennych

Jeżeli sprowadzenie zadania PL do postaci standardowej wymaga aby w 𝑖-tym warunku nieelementarnym
𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

…..+𝑎

𝑖𝑛

𝑥

𝑛

≤ 𝑏

𝑖

dodana została zmienna swobodna 𝑥

𝑛+1

𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

…..+𝑎

𝑖𝑛

𝑥

𝑛

+ 𝑥

𝑛+1

= 𝑏

𝑖

to zmienna swobodna wprowadzana jest do pierwszej bazy.

Jeżeli potrzebne jest aby w 𝑖-tym warunku nieelementarnym 𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

…..+𝑎

𝑖𝑛

𝑥

𝑛

≤ 𝑏

𝑖

odjęta została

zmienna swobodna 𝑥

𝑛+1

:

𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

…..+𝑎

𝑖𝑛

𝑥

𝑛

− 𝑥

𝑛+1

= 𝑏

𝑖

oraz w macierzy 𝐴 nie można wyodrębnid m niezależnych liniowo kolumn, otrzymanie dopuszczalnej postaci
bazowej wymaga wprowadzenia zmiennej sztucznej 𝑆

𝑗

:

𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

…..+𝑎

𝑖𝑛

𝑥

𝑛

− 𝑥

𝑛+1

+ 𝑆

𝑖

= 𝑏

𝑖

zmienna ta również wprowadzana jest do pierwszej bazy.

Ponieważ zmienne sztuczne nie posiadają interpretacji dlatego nie mogą znaleźd się w koocowym
rozwiązaniu zadania PL. Sytuacja taka będzie miała miejsce jeżeli będą one równe 0. Osiąga się to poprzez
wprowadzenie do funkcji celu z kryterium maksymalizacji zmiennych sztucznych ze współczynnikiem −𝑀,
gdzie 𝑀 jest bardzo dużą liczbą 𝑀 → ∞. Powoduje to, że funkcja celu jest sztucznie zaniżana i dzięki temu
zmienne te nie znajdą się w zbiorze bazowym. Natomiast do funkcji celu z kryterium minimalizacji zmienne
sztuczne wprowadza się ze współczynnikiem +𝑀.

Dr Arkadiusz Kijek
Ekonometria

29

Wykłady 2009/2010

W sytuacji gdy 𝑖-ty warunek nieelementarny jest równością:

𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

…..+𝑎

𝑖𝑛

𝑥

𝑛

= 𝑏

𝑖

i w macierzy 𝐴 nie można wyodrębnid m niezależnych liniowo kolumn, wprowadza się również zmienną
sztuczną 𝑆

𝑗

:

𝑎

𝑖1

𝑥

1

+ 𝑎

𝑖2

𝑥

2

…..+𝑎

𝑖𝑛

𝑥

𝑛

+ 𝑆

𝑗

= 𝑏

𝑖

którą umieszcza się w pierwszej bazie.

Dzięki wprowadzeniu zmiennych swobodnych i sztucznych macierz 𝐴 zawiera 𝑚 liniowo niezależnych
kolumn jednostkowych co sprawia, że znajduje się ona w postaci bazowej.

Przykład:

3𝑥

1

+ 2𝑥

2

→ 𝑚𝑎𝑥

4𝑥

1

+ 𝑥

2

≤ 5

2𝑥

1

+ 5𝑥

2

≥ 2

𝑥

1

, 𝑥

2

≥ 0

Sprowadzenie do postaci standardowej:

4𝑥

1

+ 𝑥

2

+ 𝑥

3

= 5

2𝑥

1

+ 5𝑥

2

− 𝑥

4

+ 𝑆

2

= 2

𝑥

1

, 𝑥

2

, 𝑥

3

, 𝑥

4

, 𝑆

2

≥ 0

3𝑥

1

+ 2𝑥

2

− 𝑀𝑆

2

→ 𝑚𝑎𝑥

C

B

C

J

Zm. bazowe

3

2

0

0

-M

X

B

𝑥

1

𝑥

2

𝑥

3

𝑥

4

𝑆

2

0

𝑥

3

4

1

1

0

0

5

-M

𝑆

2

2

5

0

-1

1

2

𝑧

𝑗

𝐵

-2M

-5M

0

M

-M

-2M

𝑐

𝑗

− 𝑧

𝑗

𝐵

3+2M

2+5M

0

-M

0

*

-
-
-
-
-
-
-
b
n
v
g
f
h
f
g
h
-

=

=

=

Dr Arkadiusz Kijek
Ekonometria

30

Wykłady 2009/2010

Jeżeli bazowe rozwiązanie dopuszczalne 𝑥

𝐵

nie jest rozwiązaniem optymalnym wyznacza się kolejne bazowe

rozwiązanie dopuszczalne i sprawdza się jego optymalnośd. W tym celu należy ustalid zmienną nie bazową,
która będzie dołączona do zbioru zmiennych bazowych a następnie wskazad zmienną bazową, która zostanie
usunięta z tego zbioru.

Określenie zmiennej 𝑥

𝑠

, którą należy wprowadzid do zbioru bazowego odbywa się przy użyciu wskaźnika

optymalności. Jeżeli maksymalizuje się funkcje celu, właściwą zmienną jest ta, dla której wskaźnik jest
największy:

𝑥

𝑠

: 𝑐

𝑠

− 𝑧

𝑠

= 𝑚𝑎𝑥 𝑐

𝑗

− 𝑧

𝑗

: 𝑐

𝑗

− 𝑧

𝑗

> 0

Oznacza to, że wprowadzenie wybranej zmiennej w największym stopniu przyczynia się do wzrostu wartości
funkcji.

Jeżeli funkcja celu jest minimalizowana, to w kryterium wejścia wybiera się tą zmienną dla której wskaźnik
jest najmniejszy:

𝑥

𝑠

: 𝑐

𝑠

− 𝑧

𝑠

= 𝑚𝑖𝑛 𝑐

𝑗

− 𝑧

𝑗

: 𝑐

𝑗

− 𝑧

𝑗

< 0

W tym przypadku wprowadzenie wybranej zmiennej do zbioru bazowego w największym stopniu przyczynia
się do spadku wartości funkcji.

Wyznaczanie zmiennej 𝑥

𝑟

, którą należy usunąd ze zbioru bazowego, rozstrzyga się następująco:

𝑥

𝑟

:

𝑕

𝑟0

𝑕

𝑟𝑠

= 𝑚𝑖𝑛

𝑕

𝑖0

𝑕

𝑖𝑠

: 𝑕

𝑖𝑠

> 0

𝑕

𝑖0

to wartośd zmiennej bazowej znajdująca się w 𝑖-tym wierszu

𝑕

𝑖𝑠

jest elementem macierzy 𝐻 znajdująca się w 𝑖-tym wierszu i 𝑠-tej kolumnie odpowiadającej zmiennej

niebazowej 𝑥

𝑠

wybranej zgodnie z kryterium wyjścia.

Po zastosowaniu obydwu warunków dokonujemy wprowadzenia jednej zmiennej 𝑥

𝑠

do zbioru bazowego w

miejsce zmiennej 𝑥

𝑟

. Element znajdujący się na skrzyżowaniu wiersza zmiennej 𝑥

𝑟

oraz kolumny 𝑥

𝑠

określa

się jako element centralny. Doprowadzenie do nowej postaci bazowej zadanie wymaga wykonania
odpowiednich operacji elementarnych na wierszach macierzy 𝐻

𝐵

𝑕

0

𝐵

które doprowadzą do uzyskania

wektora jednostkowego w kolumnie 𝑆 przy zachowaniu wektorów jednostkowych przy pozostałych
zmiennych bazowych.

W przypadku gdy dla danego bazowego rozwiązania dopuszczalnego 𝑥

𝐵

istnieje taka zmienna niebazowa 𝑥

𝑘

,

dla której spełniona jest nierównośd: 𝑕

𝑘

𝐵

< 0 to zbiór 𝐷 jest nieograniczony, a wektor wyznacza kierunek

nieskooczonej krawędzi wychodzącej z wierzchołka odpowiadającego obszarowi BRP.

Jeżeli dodatkowo dla tej zmiennej jest spełniony warunek: 𝑐

𝑘

− 𝑧

𝑘

𝐵

> 0 to funkcja jest nieograniczona z góry.

W sytuacji gdy dla danego bazowego rozwiązania optymalnego 𝑥

𝐵

wskaźnik optymalności co najmniej jednej

zmiennej niebazowej jest równy 0 oznacza to, że zadanie ma więcej niż jedno rozwiązanie optymalne.

Dr Arkadiusz Kijek
Ekonometria

31

Wykłady 2009/2010

W przypadku gdy bazowe rozwiązanie optymalne 𝑥

𝐵

zadanie, w którym występują zmienne sztuczne zawiera

te zmienne to zadanie jest sprzeczne.

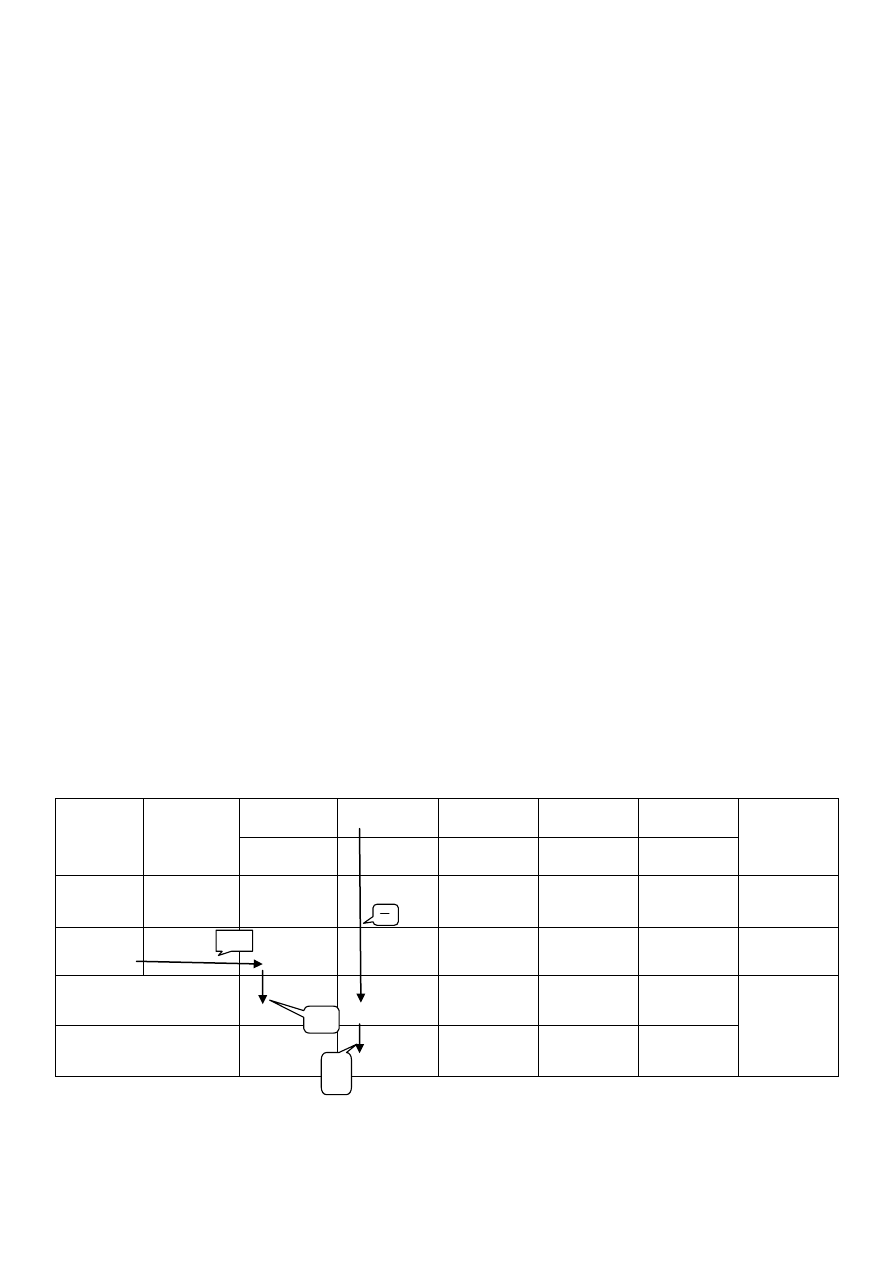
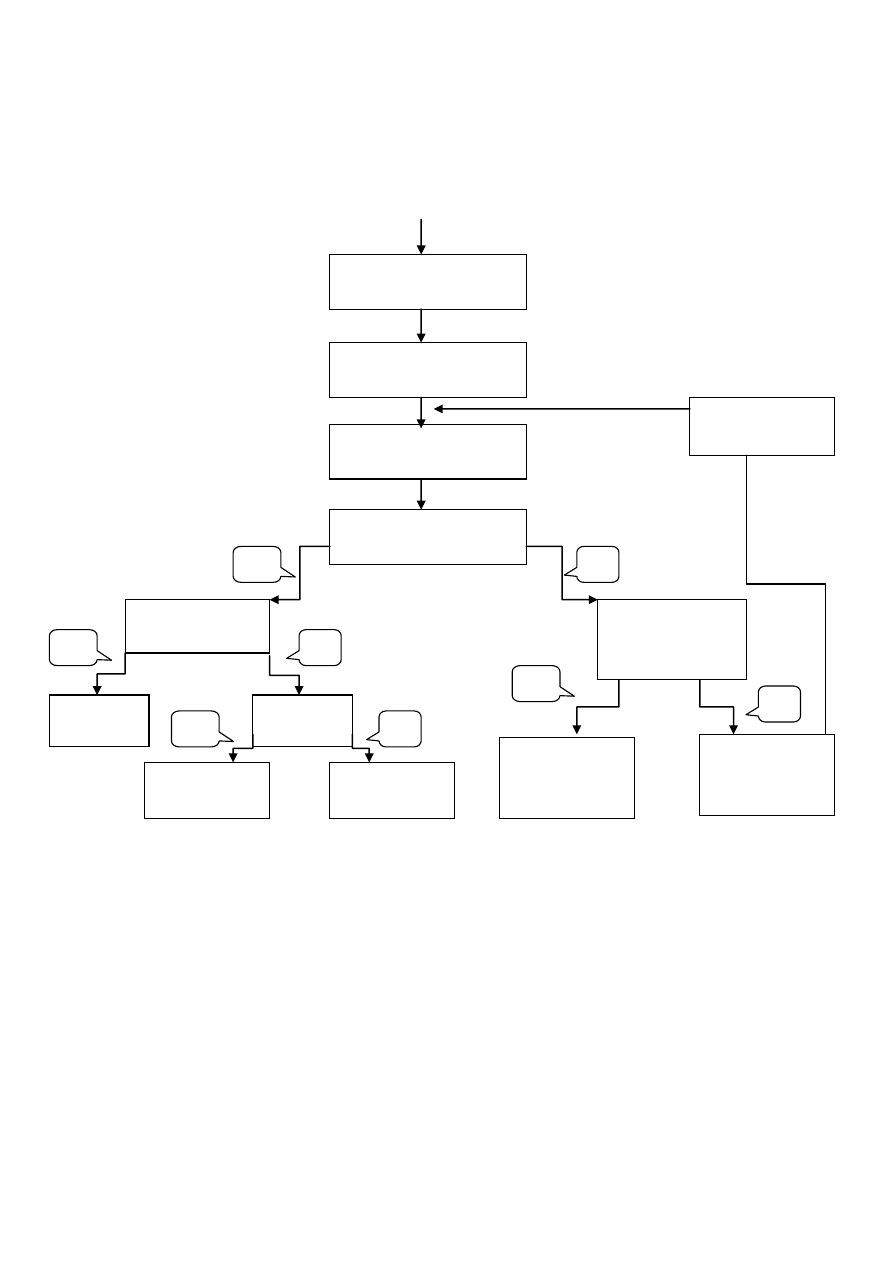
Zapisanie postaci

standardowej

Początkowe BRD

Wyznaczenie

wskaźników

optymalności

𝒄 − 𝒛 ≤ 𝟎

TAK

NIE

BRD zawiera

zmienne sztuczne

𝑐

𝑗

− 𝑧

𝐵

> 0

𝑕

𝑗

𝐵

≤ 0

NIE

Zadanie

sprzeczne

𝑐

𝑗

− 𝑧

𝑗

𝐵

< 0

TAK

NIE

Jednoznaczne

rozwiązanie

optymalne

Niejednoznaczne

rozwiązanie

optymalne

Funkcja celu

nieograniczona

z góry

Zastosowanie

kryterium

wejścia i wyjścia

NIE

TAK

Konsultacje

kolejnej BRD

TAK