Ćwiczenie 2. Matlab – tablice (macierze)

Tworzenie tablic i operacje tablicowe

Tablica jest programową reprezentacją macierzy. Może być jednowymiarowa (wektor) lub dwuwymiarowa, po-

siada rozmiar w każdym wymiarze.

Ćwiczenie

Utworzyć m- plik, wpisać, przetestować i zrozumieć poniższe operacje:

m=[1 2 3 ]

%przypisanie wartości elementom macierzy (wektor wierszowy)

m0= [1; 2; 1; 1; 0]

% przypisanie macierzy (wektor kolumnowy)

m1 = [1.1 2.1 3.55 ; -2 1 1; 1.44 0 0]

%macierz kwadratowa

m2=[1 1 1 1 1]
m3=[1 2 3 4 5]
m4 = m1 + m2

% dodanie macierzy (uwaga na wymiary i rozmiar)

m5 = m4*m0

% mnożenie macierzy (uwaga na wymiary i rozmiar)

m5t = m5'

% macierz transponowana

m5o = m5^(-1)

% macierz odwrotna

m5*m5o

% sprawdzenie - macierz jednostkowa

det(m1)

% funkcja obliczenia wyznacznika macierzy kwadratowej

m3(3)

% dostęp do elementu macierzy (indeks)

m1(2,3)

% dostęp do elementu macierzy (indeksy wiersz-kolumna)

Uwaga: po znaku % piszemy komentarze ignorowane przez Matlaba

Inny sposób definicji tablic:

M1=0:10:90

Uwaga: wartość_początkowa:krok:wartość_końcowa

Zadania

1.

Zinterpretować w m-pliku rezultat wypełnienia tablic:

M1=[0:0.1:2*pi]
M2=[M1; sin(M1)]

2.

Wypełnić dwie macierze dwuwymiarowe (wiersze, kolumny) rozmiarze m

x

n, a następnie:

a.

dodać je do siebie,

b.

pomnożyć je przez siebie.

3.

Jaki rozmiar w obu wymiarach powinny mieć macierze, żeby dozwolone było wykonanie obu operacji?

4.

Zastąpić operator mnożenia macierzy

*

operatorem dwuznakowym

.*

.

Zinterpretować wynik.

5.

Wykonać dzielenie elementowe macierzy przez macierz wykorzystując operator

./

(obie ten sam roz-

miar w obydwu wymiarach. Zinterpretować wynik.

6.

Jaką macierz da się podnieść do kwadratu? Wypróbować operatory:

^

i

.^

Wykresy 2D

Funkcja plot

Wykresy na płaszczyźnie tworzymy wykorzystując funkcję plot(x, y, kolor).

Definiujemy wektory x i y:

x= [0 1 2 3 4 5 6 7 8 9 10]

% wektor wartości x

albo:

x=0:10

%generowanie wektora co 1, wart_pocz:wart_konc

y=sqrt(x)

% wektor wartości y

title('Wykres')

%opcjonalnie tytuł wykresu

plot(x,y)

% narysowanie wykresu (w osobnym oknie)

Dwie krzywe w jednym układzie współrzędnych:

x=0:pi/50:6*pi

% definicja wektora x

y=cos(2*x)./sqrt(x+1)

% definicja wektora y(x)

z=sin(x)

% definicja wektora z(x)

plot(x,y,'b',x,z,'r')

% (b=blue, r=red)

grid

%dodanie siatki do wykresu

Uwaga: Stosujemy operator ./ dzielenie elementowe wektorów

Funkcja fplot

Dla funkcji fplot niepotrzebne są wektory zmiennych – jedynie wyrażenie tekstowe opisujące funkcję:

fplot ( ' wyrażenie arytmetyczne (x) ' , [ x_pocz , x_konc ] )

Przykład:

fplot('sin(x*x)/x',[0 4*pi])

% uwaga: punkt dzielenia przez 0 nie jest rysowany

Można również narysować więcej krzywych na wykresie:

fplot('[sin(x*x)/x, cos(x)]',[0 2*pi])

albo

fplot('sin(x*x)/x',[0 2*pi])
hold on
fplot('cos(x)',[0 2*pi])

Wykresy 3D

Krzywe 3D
Wykorzystujemy tu funkcję plot3(y,z,x). Przykładowo dla krzywej (helisy) danej równaniami:

y=sin(x)

z=cos(x)

Tworzymy m-plik:

t = 0:pi/50:10*pi;
plot3(sin(t),cos(t),t);

Powierzchnie 3D
Korzystamy z funkcji mesh(x,y,z). Dla powierzchni podanej równaniem:

z=cos3x siny

Piszemy m-plik:

clear

y = 0:0.01:pi

%wektor wierszowy

y = x'

%wektor kolumnowy!

z=cos(3*x) * sin(y)

%przeanalizować tablicę z (KWADRATOWA!)

mesh(x, y, z)

-1

-0.5

0

0.5

1

-1

-0.5

0

0.5

1

0

10

20

30

40

Zadania

1.

Sprawdzić działanie powyższych przykładów.

2.

Wykonać wykres funkcji

x

sin

e

3

x

−

w przedziale [-10,10] stosując funkcję plot i fplot.

3.

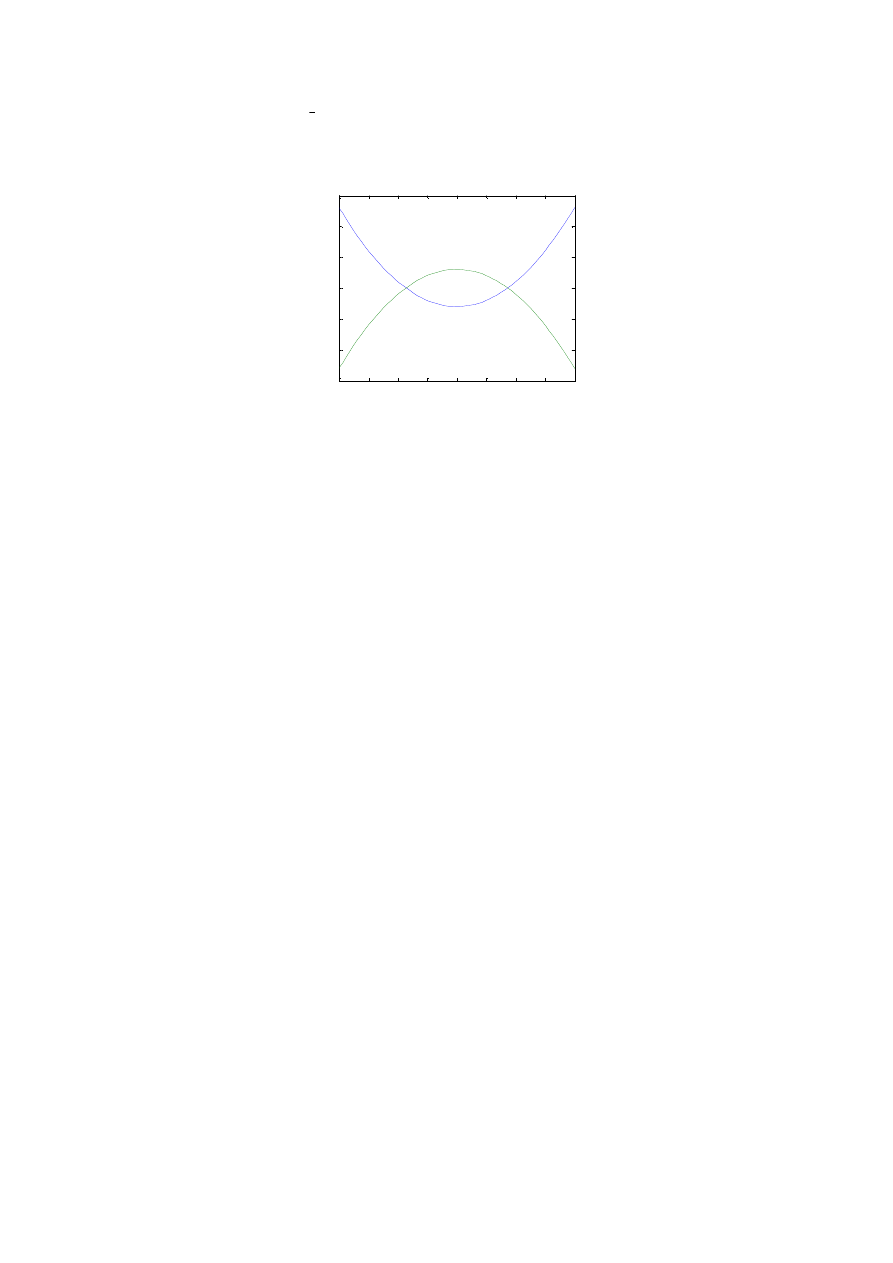
Wykonać w jednym układzie współrzędnych wykresy dwóch krzywych podanych równaniami drugiego

stopnia (parabole) o różnych współczynnikach. Tak dobrać współczynniki by uzyskać wykres jak poniżej:

4.

Napisać m-plik, w którym rysowany jest wykres funkcji a sin(bx+c), gdzie a, b, c oraz granice przedziału

zmiennej x podawane są interakcyjnie przez użytkownika.

5.

Narysować wykres półokręgu (równanie: x

2

+y

2

=R

2

).

6.

Bazując na powyzszym równaniu narysować wykres 3d dla półkuli.

Rozwiązanie układu równań liniowych

Przykładowy układ:

2x + 3y – 4 z = 5
x + y – z = 3,5
-4 y + 2,5 x – z = 2

Rozwiązujemy w m-pliku:

A = [2 3 -4 ; 1 1 -1 ; 2.5 -4 -1]

% Uwaga: zachować kolejność zmiennych

B = [ 5 ; 3.5 ; 2]
X= A^-1*B

%wektor rozwiązań

S=A*X

%sprawdzenie – wynikiem powinien być wektor wyrazów wolnych B

s1=A(1,1)*X(1)+ A(1,2)*X(2) + A(1,3)*X(3)

%sprawdzenie 1-szego równania

Zadanie

Rozwiązać samodzielnie układ równań:

–x + y – 4.3 z + 2 v= 15
3x + y – v = 35
4 x + 0,5 y + z – 4.5 v = 2,2
12,5 y – z – 5 v = 12

Użyteczne funkcje tablicowe

rand(n)

- losowo generowana tablica kwadratowa n

x

n

rand(n,m)

- losowo generowana tablica kwadratowa n

x

m

sum (A)

- wektor sum elementów w kolumnach macierzy A

sum(sum(A)) - suma wszystkich elementów macierzy dwuwymiarowej
max(A)

- wektor elementów maksymalnych w kolumnach macierzy A

max(max(A)) - element największy w macierzy dwuwymiarowej
min(A)

- wektor elementów minimalnych w kolumnach macierzy A

min(min(A)) - element najmniejszy w macierzy dwuwymiarowej
ndims(A)

- ile wymiarów macierzy

numel(A)

- liczba elementów macierzy

reshape(A,n,m) - rekonfiguracja macierzy
size(A)

- rozmiar macierzy

length(A)

- największy rozmiar

-4

-3

-2

-1

0

1

2

3

4

-15

-10

-5

0

5

10

15

Zadanie

Wypróbować i zrozumieć działanie powyższych funkcji. Można tu skorzystać z pomocy Matlaba, pisząc w li-

nii poleceń Command Window:

help funkcja

Zapis elementów tablicy do pliku ASCII i odczyt z pliku

clear

c = [8 6 4 2;4 -1 4 5]

save

(

'mydata.dat'

,

'c'

,

'-ASCII'

)

clear

load

(

'mydata.dat'

)

disp(

'Dane z pliku:'

);

mydata

Zapis danych do pliku typu

mat

i odczyt z pliku

a=rand(3)

b=6

save

(

'plik.mat'

,

'a'

,

'b'

)

clear

a

clear

b

load

(

'plik.mat'

)

disp(a)

disp(b)

Zadania

1.

Napisać m-plik o poniższych działaniach, wykorzystując poznane funkcje tablicowe:

a.

wygenerować losowo tablicę o rozmiarze 4x4 o elementach całkowitych z przedziału (-20, 20),

b.

zamienić drugi wiersz z czwartym,

c.

obliczyć i wyświetlić sumę elementów drugiej i trzeciej kolumny,

d.

następnie przekształcić tablicę w tablicę 2x8,

e.

utworzyć nową tablicę 1x8 o dowolnych elementach i dopisać ją jako nowy wiersz w tablicy

utworzonej w poprzednim podpunkcie,

f.

zapisać ostatnią tablicę o rozmiarach 1x9 do pliku ASCII o nazwie

plik1.txt i pliku mat o nazwie

plik2.mat.

2.

Utworzyć m-plik odczytujący dane zapisane w plikach

plik1.txt i plik.mat.