
1
XXV. MIERNICTWO GÓRNICZE
PODSTAWOWE WIADOMOSCI O MIERNICTWIE.
WYMAGANIA PODSTAWOWE
Wiadomo
ś
ci ogólne.
I/ Geodezja
–
nauka zajmuj
ą
ca si
ę
wykonywanie pomiarów okre
ś
laj
ą
cych:
a/ kształt i rozmiary Ziemi,
b/ wyznaczeniem wzajemnego poło
ż
enia punktów na jej
powierzchni.
Geodezj
ę
dzielimy na:
a/ geodezj
ę
wy
ż
sz
ą
,
– zajmuj
ą
c
ą
si
ę
pomiarami kształtów i rozmiarów Ziemi,
z uwzgl
ę
dnieniem jej wypukło
ś
ci. Do jej zada
ń
nale
ż
y
okre
ś
lenie poło
ż
enia punktów, stanowi
ą
cych podstaw
ę
dla szczegółowych pomiarów geodezji ni
ż
szej.
b/ geodezj
ę
ni
ż
sz
ą
- przyjmuj
ą
c
ą
zało
ż
enie,
ż
e powierzchnia Ziemi jest
płaszczyzn
ą
.
Korzystaj
ą
c z wyznaczonych przez geodezj
ę
wy
ż
sz
ą
punktów odniesienia,
geodezja ni
ż
sza dokonuje pomiarów wzajemnego poło
ż
enia punktów
zmierzaj
ą
cych do uzyskania szczegółowych planów i map
.
II/ Prawa dotycz
ą
ce miernictwa górniczego.
1/ USTAWA z dnia 4 lutego 1994 roku:
„Prawo Geologiczno – Górnicze”.
2/ Rozporz
ą
dzenie Ministra Gospodarki z 19 marca 2002 roku:
„W sprawie dokumentacji mierniczo – geologicznej”.
3/ „Prawo geodezyjne i kartograficzne” z 1989 roku, które okre
ś
la:
-ogólne zasady wykonywania prac geodezyjnych (obowi
ą
zuje wszystkich),
tzn. 1/ jednolity system miar,
2/ jednolity system odniesienia wyników pomiarów:
Tj. a/ poziomy układ odniesienia – układ współrz
ę
dnych płaskich,
(tzw. „system 2000”) – przyporz
ą
dkowanie punktom powierzchni
Ziemi odpowiednim punktom na płaszczy
ź
nie wg teorii
odwzorowania kartograficznego Gaussa Krugera,
b/ pionowy układ odniesienia – układ wysoko
ś
ci, który odnosi si
ę
do
ś
redniego poziomu Morza Bałtyckiego w Zatoce Fi
ń
skiej
wyznaczonego przez mareograf w Kronsztadzie
(koło Sanki Petersburga).
3/ okre
ś
lona przepisami tre
ść
, dokładno
ść
i forma opracowa
ń
.

2
Przepisy techniczne – obowi
ą
zuj
ą
ce wszystkich.
Instrukcje techniczne:
Grupa „0” – ogólne zasady wykonywania prac;
Grupa „G” – szczegółowe zasady wykonywania prac;
Grupa „K” - opracowania map;
ZAGADNIENIA
1/ Omówi
ć
cele i zadania miernictwa.
Miernictwo – dział geodezji obejmuj
ą
cy metody wykonywania terenowych
pomiarów powierzchni Ziemi i sporz
ą
dzania map.
Cele miernictwa górniczego:
a/ sporz
ą
dzanie map wyrobisk ZG,
b/ aktualizacj
ę
tych map,
c/ wyznaczanie projektowanych wyrobisk w kopalni.
Zadania miernictwa:
a/ pomiary wysoko
ś
ciowo sytuacyjno – wysoko
ś
ciowe na powierzchni
i w kopalni ,
b/ wyznaczanie filarów ochronnych, oporowych, bezpiecze
ń
stwa,
granicznych,
c/ pomiary ruchów powierzchni,
d/ obliczanie zasobów kopaliny,
e/ współpraca przy projektowaniu udost
ę
pnienia zło
ż
a,
f/ szkody górnicze, regulacja granic, wymiana gruntów.
2/ Umie
ć
zdefiniowa
ć
podstawowe jednostki miar u
ż
ywane w geodezji.
A/ Długo
ść
– podstawowa jednostka to 1m = około 1/10 000 000
cz
ęś
ci
ć
wiartki południka ziemskiego.
Miernictwo u
ż
ywa cz
ęś
ci lub wielokrotno
ś
ci 1m:
1km = 1000m;
1m = 10dm = 100cm = 1000mm;
1dm = 0,1m = 10cm = 100mm;
1cm = 0,01m = 0,1dm = 10mm;
1mm = 0,001m = 0,01dm = 0,1cm;
1 mikron = 1
µ
= 0,001mm;
Inne miary:
1 mila morska = 1,85 km;
1 mila geograficzna = 7,42 km;
B/ Miary powierzchni – podstawowa jednostka to 1m
2
; Inne miary:
1 ar to 1 a = 100m
2
;
1 hektar to 1 ha = 100 a = 10000m
2
;
1 km
2
= 1000000 m
2
;
3
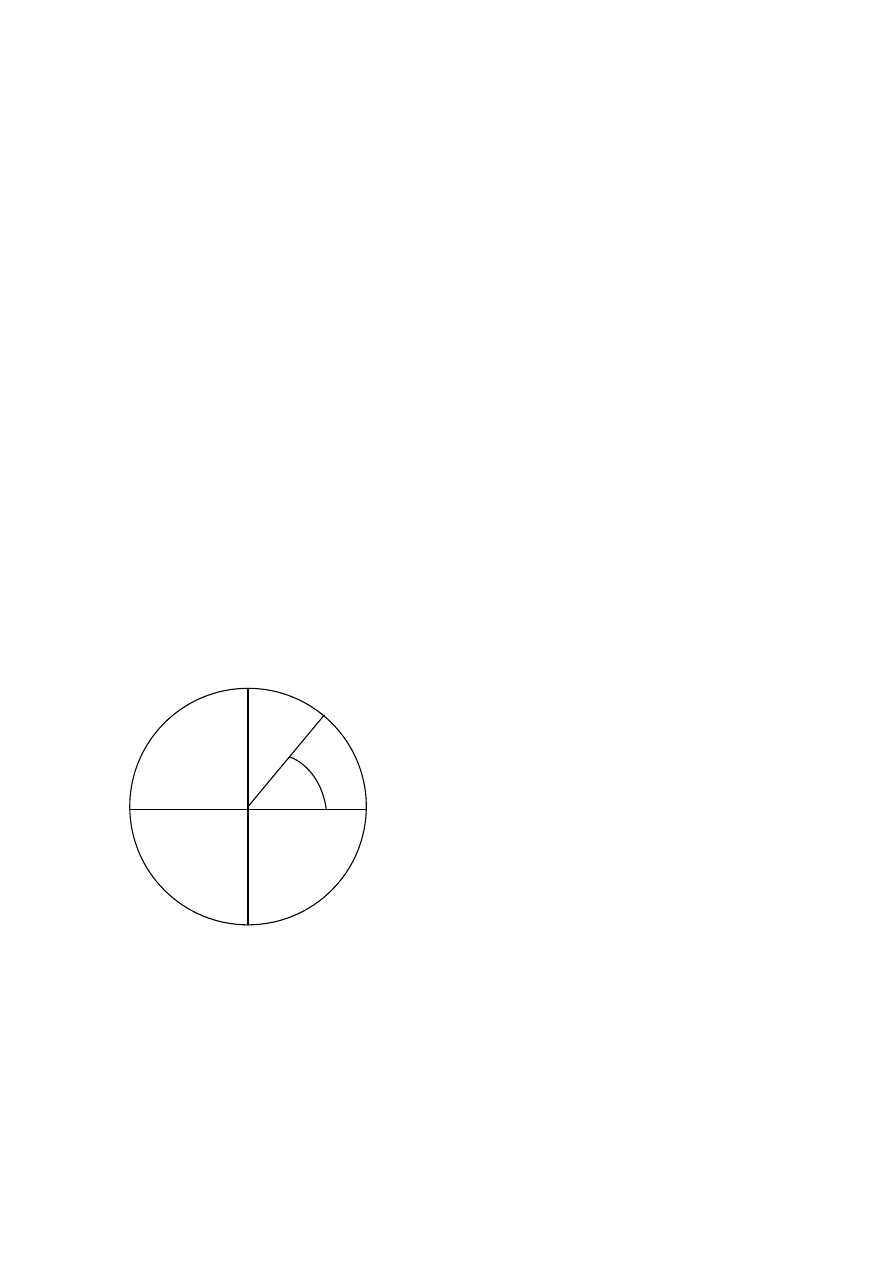
C/ Miary k
ą
towe – w miernictwie dzieli si
ę
obwód koła na stopnie.
S
ą
dwa rodzaje:
a/ SZE
ŚĆ
DZIESI
Ą
TKOWY – Stary podział.
Obwód koła dzieli si
ę
na 360°.
1° dzieli si
ę
na 60' (minut).
1' dzieli si
ę
na 60" (sekund).
- czyli 1° = 60' = 3600".
b/ SETKOWY (gradowy) – Nowy podział.
Obwód koła podzielono na 400
g
(stopni gradowych).
1
g
( 1 stopie
ń
gradowy) dzieli si
ę
na 100
c
(minut gradowych).
1
c
(minut
ę
gradow
ą
) podzielono na 100
cc
(sekund gradowych).
- czyli 1
g
= 100
c
= 10 000
cc
.
Przechodzenie ze sze
ść
dziesi
ą
tkowego na setkowy.
Czy nowy czy stary jest to obwód koła = 2
π
r.
Porównuj
ą
c:
360° = 400
g
/4 (dziel
ą
c obustronnie – 360: 4 = 90 i 400: 4= 100)
St
ą
d: 90° = 100
g
, czyli 100
g
= 90
o
1° = 10
g
/9 = 1
g
11
c
11cc, 1
g
= 9
o
/10 = 0
o
54',
1' = 100
c
/54 = 1
c
85
cc
, 1
c
= 54'/100 = 0'32,4",
1" = 1000
cc
/324 = 3
cc
, 1
cc
= 324"/1000= 0,3",
C/ K
ą
t miary łukowej (radian).
Mo
ż
emy napisa
ć
równanie:
ł : 2
π
r =
αααα
: 360
o
to: ł / 2
π
r =
αααα
/ 360
o
, mno
żą
c przez 2
π
r360
o
,
r ł
αααα
ł 360
o
=
αααα
2
π
r st
ą
d ł =
αααα
2
π
r/ 360
o
albo:
αααα
= ł 360
o
/2
π
r
Przyjmuj
ą
c:
ł = r otrzymamy:
αααα
= 360
o
/2
π
,
czyli :
αααα
= 180
o
/
π
, (
π
=3,14159265)
St
ą
d :
αααα
= 57
o
17'45", - jest to k
ą
t miary łukowej tzw. 1 rad (radian).
- przy zało
ż
eniu,
ż
e r = ł.
Oznaczaj
ą
c 1rad: w stopniach (
ρ
o
), minutach (
ρ
'), sekundach (
ρ
"),
Otrzymamy:
ρ
o
= 180
o
/
π
= 57,3
o
= 57
o
17'45",
ρ
' = 180
o
x 60/
π
= 3437,7' ,
ρ
" = 180
o
x 3600/
π
= 206264,8" ,
4
Aby k
ą
t wyra
ż
ony jest w radianach (
α
) przeliczy
ć
na k
ą
t w jednostkach
k
ą
towych (
α
o
) , nale
ż
y:
α
o
=
α
x
ρ
o
, lub
α
' =
α
x
ρ
' , lub
α
" =
α
x
ρ
" ,
Odwrotnie – przej
ś
cie z k
ą
towej na łukow
ą
:
α
=
α
o
/
ρ
o
=
α
' /
ρ
' =
α
" /
ρ
" .
WA
ś
NE:
ł = r x
α
– tzn. długo
ść
łuku równa si
ę
promieniowi pomno
ż
onemu
przez k
ą
t wyra
ż
ony w radianach.
Miar
ę
łukow
ą
stosujemy w miernictwie dla małych k
ą
tów ( do 10
o
), bo:
warto
ść
ich sinusów i tangensów w przybli
ż
eniu równa si
ę
k
ą
tom wyra
ż
onym
w mierze łukowej,
czyli: sin
α
o
= tg
α
o
=
α
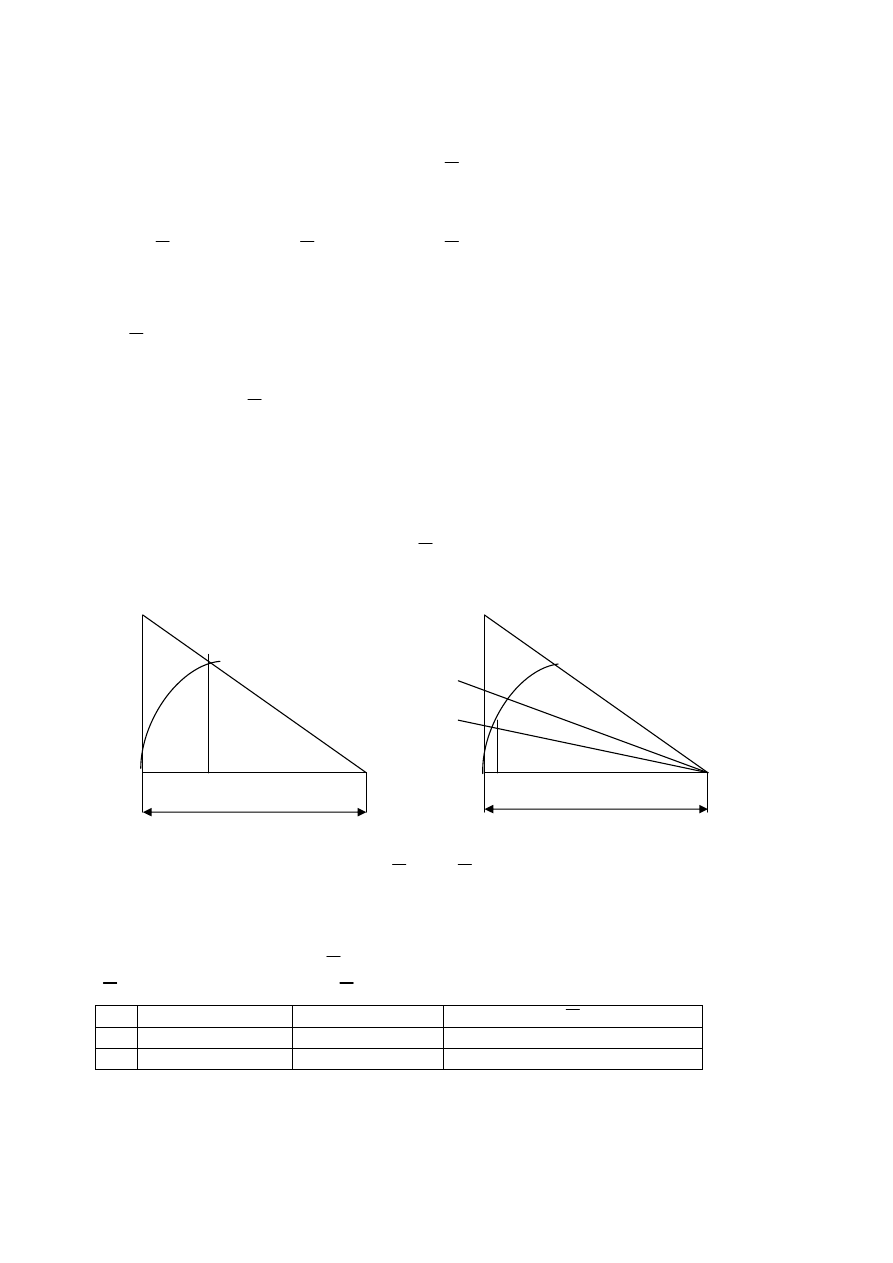
patrz rysunek poni
ż
ej:
D
B
ł
D
B
A
α
ł
α
C
0 c
A
Przyjmijmy,
ż
e
r = 1
przyjmijmy r = 1
Dla małych k
ą
tów (do 10
o
) przyjmuj
ą
c,
ż
e r = 1 mo
ż
emy zapisa
ć
sin
α
= AB, tg
α
=CD, a łuk ł =
α
x 1 =
α
, a ró
ż
nice odcinków AB, CD i ł
s
ą
małe - dlatego mo
ż
na przyj
ąć
,
ż
e AB = CD = ł ,
Z poni
ż
szej tabeli wida
ć
,
ż
e dla k
ą
tów do 10
o
(miary k
ą
towej) po przeliczeniu na
miar
ę
łukow
ą
wg zasad:
α
=
α
o
/
ρ
o
, czyli np. dla 1
o
, to:
α
= 1
o
/
ρ
o
= 1
o
/ 57,3
o
, st
ą
d
α
= 0,017452 ( bo
ρ
o
= 180
o
/
π
= 180
o
/3,14 = 57,3
o
).
1
o
Sin 1
o
= 0,01745 Tg 1
o
= 0,01745
W radianach (
α
) 1
o
= 0,01745
5
o
Sin 5
o
= 0,08715
Tg 5
o
= 0,08748
W radianach 5
o
= 0,08727
10
o
Sin 10
o
= 0,17364 Tg 10
o
= 0,17632 W radianach 10
o
= 0,17453
Przykładowe praktyczne zastosowania miary łukowej w miernictwie.

5
Zad.1
Jaka jest warto
ść
k
ą
ta
α
, którego sin
α
= 1/200 000 ?
Wiemy,
ż
e sin
α
= tg
α
=
α
, czyli w naszym przypadku
α
= sin
α
.
To:
α
=1/ 200 000
Wiemy te
ż
,
ż
e:
α
" =
α
x
ρ
" ,a
ρ
" = 180
o
x 3600/
π
= 206264,8" ,
To podstawiaj
ą
c:
α
" = (1/ 200 000) x 206265" = 1,03" – to jest warto
ść
k
ą
ta.
Zad.2
Ile wynosi tg 1' ?
tg
α
=
α
=
α
' /
ρ
' = 1' / 3438' = 0,00029,
3438' st
ą
d,
ż
e
ρ
' = (180
o
x 60')/ 3,14159265 = 10800'/ 3,14159265= 3437,7'.
Zad.3
Przekop prowadzono ze spadkiem 6mm na 1m.
Jaki jest k
ą
t nachylenia przekopu do poziomu?
α
= sin
α
= 6/1000
6mm
sin
α
= 6/1000
α
'
α
' =
α
x
ρ
' = (6/1000) x 3438' = 20,6' .
Zad. 4
Przy dr
ąż
eniu przekopu prostego o długo
ś
ci 2000m, wyznaczaj
ą
c kierunek jego
osi zało
ż
ono bł
ą
d 40" .
Jaki b
ę
dzie bł
ą
d na ko
ń
cu przekopu?
ł = r x
α
= r x (
α
" /
ρ
") = 2000 x (40"/ 206 265") = 0,3878m = 388mm.
Zad.5
Pochylni
ę
długo
ś
ci 600m trzeba przesun
ąć
o 1m.
O jaki k
ą
t trzeba zmieni
ć
jej kierunek, je
ż
eli punk pocz
ą
tkowy jej osi pozostaje
bez zmiany?
α
' = (ł / r) x
ρ
' = (1m/600m) x 3438' = 5,7' .
3/ Scharakteryzowa
ć
skale i podziałki.
1m = 1000mm

6
A/SKALA.
Mapy s
ą
wykonywane w pewnym zmniejszeniu – czyli skali.
Skala – to stosunek długo
ś
ci odcinka mapy do długo
ś
ci poziomego rzutu tego
samego odcinka w terenie.
Je
ż
eli przyjmiemy,
ż
e:
L – to jest rzeczywista długo
ść
rzutu poziomego odcinka w terenie,
l - długo
ść
odpowiadaj
ą
cego mu obrazu na mapie,
to stosunek l / L = N – jest skal
ą
mapy.
Np. l = 25 cm = 0,25m, L = 2500m to: N = 0,25/2500 = 1/ 10000, co zapisujemy
N = 1 : 10000.
Mianownik skali wskazuje ile razy zmniejszona została mapa w stosunku do
rzeczywisto
ś
ci.
Wynika z tego to,
ż
e mapa dokładna – bardziej szczegółowa to ta, która
mianownik ma mniejszy.
Tak wi
ę
c skala 1 : 100 jest 10 razy wi
ę
ksza ni
ż
skala 1 : 1000.
Je
ż
eli mamy map
ę
ze skal
ą
1 : 1000, tzn.
ż
e długo
ść
rzeczywista z terenu
jest 1000 razy pomniejszona.
St
ą
d długo
ść
odcinka 1m ( = 1000mm) w skali 1:1000 na mapie to:
1m/1000 = 1000mm/1000 = 1mm.
Odwrotnie 1mm na mapie w skali 1:1000 to w rzeczywisto
ś
ci 1mm x 1000 = 1m.
SKALE MAP GÓRNICZYCH:
1:500, 1:1000, 1:2000, 1:5000, 1:10000.
Mo
ż
na te
ż
stosowa
ć
mapy o wi
ę
kszych skalach.
Skale map podstawowych normuj
ą
instrukcje techniczne.
B/ PODZIAŁKI.
W Miernictwie u
ż
ywa si
ę
podziałki : LINIOWE i POPRZECZNE.
PODZIAŁKA LINIOWA.
S
ą
one sporz
ą
dzane w celu ułatwienia prac na mapami i ułatwiaj
ą
nanoszenie
na mapy lub odczytywanie z mapy długo
ś
ci, bez dokonywania oblicze
ń
.
Jest to odcinek prostej podzielony kreskami na cz
ęś
ci.
Najmniejszy odst
ę
p mi
ę
dzy dwoma kreskami nazywa si
ę
warto
ś
ci
ą
podziałki.
Np. warto
ś
ci
ą
podziałki w skali 1:1000, gdzie najmniejszy odst
ę
p to 1mm
jest 1m.
Podziałka opisana jest tak,
ż
e liczby podziałki odpowiadaj
ą
rzeczywistym
długo
ś
ci
ą
w naturze.
Na podziałce 1:1000 ko
ń
ce centymetrów podziałki s
ą
oznaczone:

7
10, 20, 30, 40 itd. metrów.
Na podziałce 1:2000 ko
ń
ce centymetrów podziałki s
ą
oznaczone:
20, 40, 60, 80 itd. metrów.
Na podziałce 1:5000 ko
ń
ce centymetrów podziałki s
ą
oznaczone:
50, 100,150,200 itd. metrów.
Liczby te okre
ś
laj
ą
rzeczywist
ą
długo
ść
w terenie.
Odst
ę
p mi
ę
dzy 2- a kreskami dobiera si
ę
tak aby nie był mniejszy ni
ż
0,5mm.
Okre
ś
laj
ą
c mniejsze długo
ś
ci ni
ż
warto
ś
ci podziałki liniowej popełnia si
ę
bł
ą
d.
Podziałki liniowe mo
ż
na kupi
ć
gotowe: metalowe, drewniane, papierowe.
PODZIAŁKI POPRZECZNE ( TRANSWERSALNE).
S
ą
one bardziej dokładne.
Zasady u
ż
ycia:
a/ cyrklem odbiera si
ę
z mapy długo
ść
mierzonego odcinka.
b/ przesuwa si
ę
równolegle cyrkiel, a
ż
drugi koniec przetnie lini
ę
uko
ś
n
ą
.
c/ dokonujemy odczytu. Przy pionowej kresce umieszczonej za lini
ą
okre
ś
laj
ą
c
ą
100m znajduj
ą
si
ę
od dołu do góry cyfry: 1,2,3,4,5,6,7,8,9.
Na linii oznaczonej 1 ( w skali podziałki 1:1000 znaczy to 1mm z mapy,
czyli 1m w rzeczywisto
ś
ci).
Podziałki te wykonuje si
ę
cz
ę
sto na mapach.
S
ą
te
ż
gotowe ( np. z metalu) w skalach: 1:500, 1:1000, 1:2000, 1:2500, 1:4000,
1:5000,
WYMAGANIA PONADPODSTAWOWE
1/ Obliczy
ć
długo
ś
ci odcinków w ró
ż
nych skalach.
2/ Umie
ć
narysowa
ć
podziałki liniowe i poprzeczne.
13. POMIARY LINIOWE, KATOWE I POLIGONOWE.
WYMAGANIA PODSTAWOWE
1/Umie
ć
ogólne zasady wykonywania pomiarów.
A/ Podstawowe poj
ę
cia.
a/ PUNKT POMIAROWY – punkt wyznaczony w terenie za pomoc
ą
znaku
lub sygnału.
Sygnał to np. wie
ż
a, kamie
ń
, rurka w ziemi, palik, tyczka, pion…
Sygnał mo
ż
e mie
ć
ró
ż
ne kształty i wymiary.
Punkt to idealny
ś
rodek sygnału.
Punkty mog
ą
by
ć
:
- stałe wyznaczone przy u
ż
yciu trwałych znaków lub sygnałów,
- stracone, wyznaczane na czas pomiarów.
W zale
ż
no
ś
ci do jakiego celu i jakiej metodzie pomiarowej słu
żą
rozró
ż
nia
8
si
ę
punkty: triangulacyjne, poligonowe, teodolitowe, kompasowe,
niwelacyjne….
b/ LINIA POMIAROWA – prosta wyznaczona w terenie przez min 2 punkty.
Linia pomiarowa lub te
ż
układ linii to podstawa pomiarów sytuacyjnych.
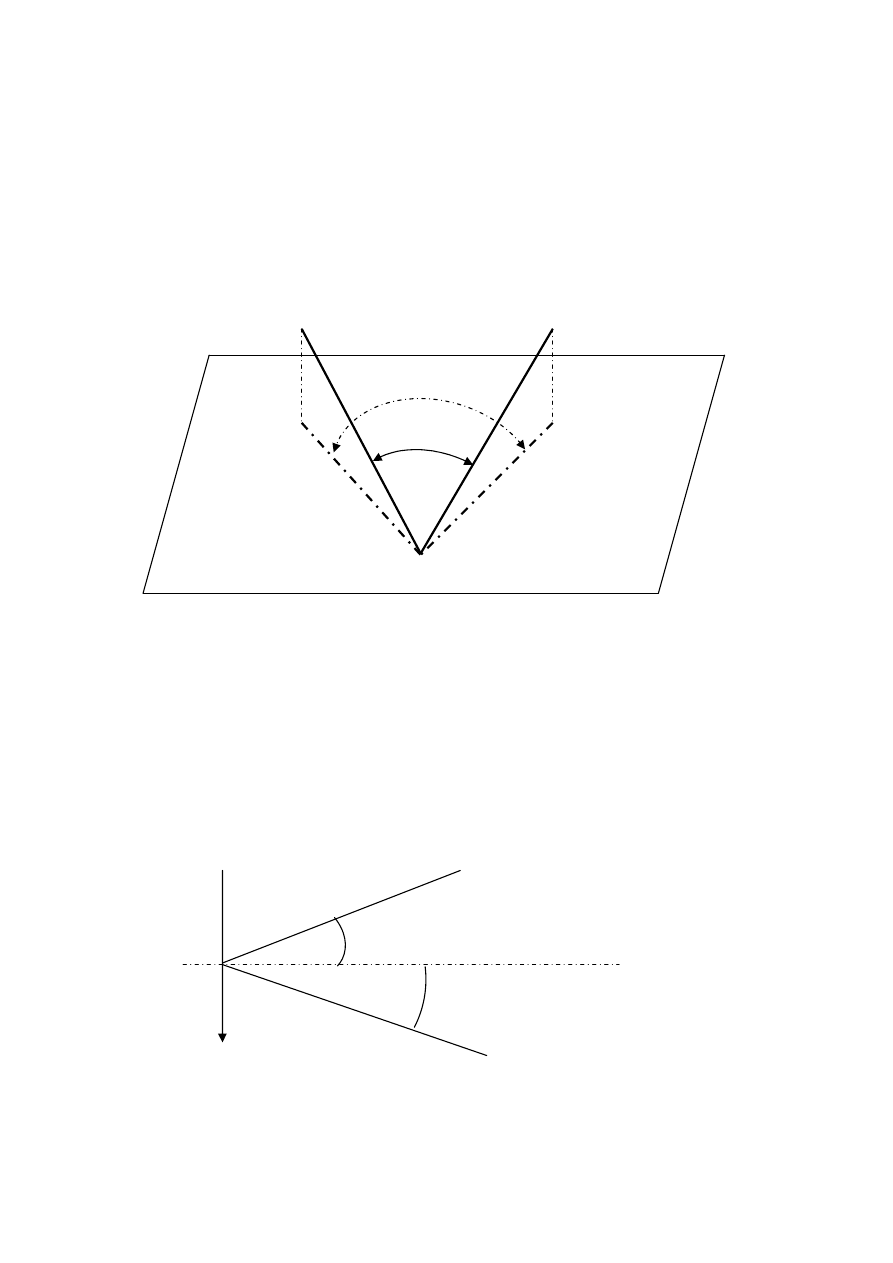
c/ K
Ą
T POZIOMY – k
ą
t zawarty mi
ę
dzy rzutami ramion na płaszczyzn
ę
poziom
ą
.
B C
β
B'
α
C'
Płaszczyzna pozioma
A
Skoro punkty A i B nie le
żą
na tej samej wysoko
ś
ci co punkt A.
Wobec tego k
ą
t
α
zawarty mi
ę
dzy punktami B, A i C nie jest k
ą
tem poziomym.
Musimy wykona
ć
rzuty punków B i C na płaszczyzn
ę
poziom
ą
.
Dopiero k
ą
t
β
(k
ą
t B' A C') zawarty mi
ę
dzy rzutami jest k
ą
tem poziomym.
d/ K
Ą
T PIONOWY – jest k
ą
t nachylenia mierzonego odcinka lub prostej do
płaszczyzny poziomej.
Mo
ż
e by
ć
dodatni (+), gdy le
ż
y nad płaszczyzn
ą
poziom
ą
;
lub ujemny ( - ), gdy le
ż
y pod płaszczyzn
ą
poziom
ą
.
+
α
poziom
-
α
Do pomiarów k
ą
tów poziomych i pionowych słu
ż
y teodolit.
e/ WYSOKO
ŚĆ
PUNKTU – pionowa odległo
ść
tego punku od poziomej
p
io
n

9
płaszczyzny odniesienia. S
ą
wysoko
ś
ci wzgl
ę
dne i bezwzgl
ę
dne.
WYSOKO
ŚĆ
BEZWZGL
Ę
DNA – wysoko
ść
do poziomu morza
( lub jego przedłu
ż
enia pod l
ą
dem).
Punkt le
żą
cy powy
ż
ej poziomu morza ma znak ( + ).
Punkt le
żą
cy poni
ż
ej poziomu morza ma znak ( - ).
Dla poziomu morza jako płaszczyzn
ę
odniesienia zakłada si
ę
wysoko
ść
± 0 (zero normalne).
WYSOKO
ŚĆ
WZGL
Ę
DNA – wysoko
ść
okre
ś
lona do dowolnie przyj
ę
tej
płaszczyzny poziomej.
B/ Metody pomiarowe.
Przy wykonywaniu pomiarów stosuje si
ę
zasad
ę
„od ogółu do szczegółu”.
Tzn. a/ z najwi
ę
ksz
ą
dokładno
ś
ci
ą
okre
ś
la si
ę
główne punkty pomiaru – ramy;
b/ dopiero w tych ramach wykonuje si
ę
szczegółowe pomiary nie
wymagaj
ą
ce du
ż
ej dokładno
ś
ci.
Dla głównych punktów pomiarowych na terenie kraju słu
ż
y tzw. metoda
„TRIANGULACJNA”- czyli trójk
ą
towanie – polega na:
- zało
ż
eniu w terenie sieci trójk
ą
tów o wspólnych bokach,
- okre
ś
leniu długo
ś
ci boków,
- poło
ż
enia wierzchołków ABCDE tych trójk
ą
tów
β
γ
α
A
C
E
Stosujemy w miernictwie dwa rodzaje dokładno
ś
ci pomiarów:
- wy
ż
szego rz
ę
du, dokładne,
- ni
ż
szego rz
ę
du – mniej dokładne.
W metodzie „triangulacji”,
ż
eby unikn
ąć
kosztów mo
ż
na dokona
ć
pomiarów:
- długo
ś
ci jednego boku – jest to tzw. baza (podstawa) triangulacji;
- pomiarów wszystkich k
ą
tów w sieci trójk
ą
tów;
- pozostałe boki obliczamy.
Np. Bok: AB = a (baza), CD = a x sin
γγγγ
/sin
αααα
, AC = a x sin
ββββ
/ sin
αααα
.
Punkty ABCDE wyznaczone t
ą
metod
ą
nazywamy trygonometrycznymi.
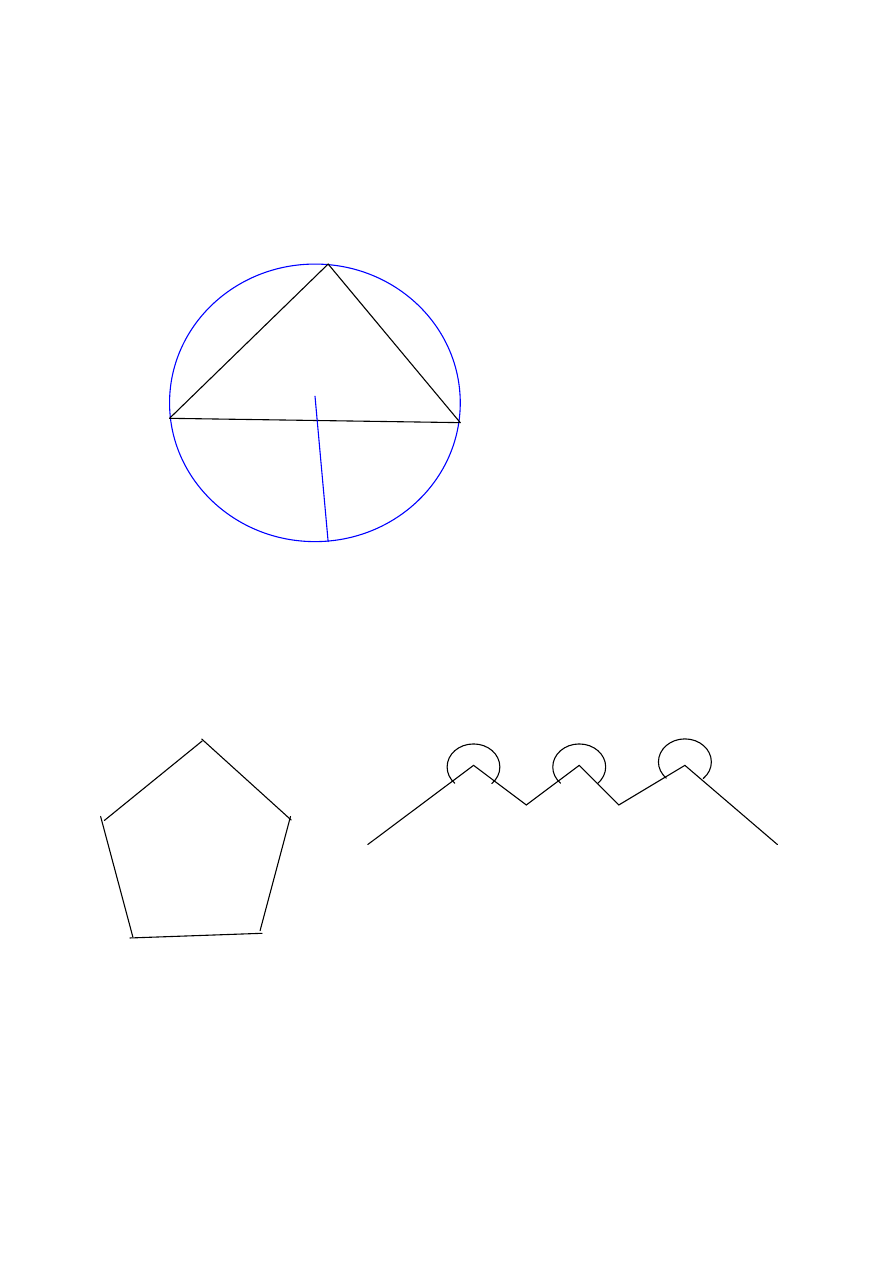
Korzystamy z metod obliczania trójk
ą
tów:
10
- np. a/ twierdzenia sinusów: AB/sin
γ
= BC/sin
α
= CA/sin
β
=2R,
b/ twierdzenie cosinusów :
a
2
= b
2
+c
2
– 2bc cos
α
, b
2
= c
2
+a
2
– 2ca cos
β
, c
2
= b
2
+a
2
– 2ba cos
γ
.
i inne.
C
γ
b
a
α
β
A
c
B
R
2/ POLIGONIZACJA – metoda polegaj
ą
ca na pomiarze boków i k
ą
tów linii
łamanej zało
ż
onej w terenie- tzw. poligonu.
Poligony nawi
ą
zuje si
ę
do punktów trygonometrycznych jako punktów
wy
ż
szego rz
ę
du.
W poligonie mierzy si
ę
długo
ś
ci boków i wielko
ś
ci k
ą
tów na załamaniach oraz
k
ą
ty nawi
ą
zania
ϕ
i
ψ
. K
ą
ty te nawi
ą
zuj
ą
poligon do sieci triangulacyjnej.
Daj
ą
mo
ż
liwo
ść
kontroli pomiarów.
T.R.II
β
2
T.R.III
l
2
α
3
l
3
ϕ
ψ
β
1
β
3
α
2
α
4
l
4
T.R.I
T.R.IV
l
1
α
1
α
5
Poligon nawi
ą
zany do punktów triangulacyjnych.
l
5
POLIGON
POMIAR SZCZEGÓŁÓW – pomiar opiera si
ę
na sieci poligonowej.
Poligony zakłada si
ę
blisko granic – charakterystyczne punkty domierza si
ę
do boków poligonu metod
ą
domiarów.
W razie potrzeby wi
ę
kszej dokładno
ś
ci zakłada si
ę
sie
ć
pomocniczych linii.
Linie te z bokami poligonu to osnowa geodezyjna dla szczegółów
11
sytuacyjnych mierzonego obszaru.
Zasada „od ogółu do szczegółu” to nast
ę
puj
ą
ca kolejno
ść
pomiarów:
- triangulacja;
- poligonizacja;
- zdj
ę
cie szczegółów.
Definicja mapy: map
ą
obszaru nazywamy wykre
ś
lon
ą
figur
ę
podobn
ą
do rzutu
poziomego tego obszaru.
Wynika z tego,
ż
e na mapy przenosi si
ę
rzut poziomy (nie wolno przenosi
ć
długo
ś
ci rzeczywistych – chyba,
ż
e znajduj
ą
si
ę
one na jednakowej wysoko
ś
ci.
PRZYKŁADY:
A'
l' B'
A
l
l
α
- przykład 1.
B
l
1
(długo
ść
przenoszona na map
ę
to:
rzut poziomy odcinka AB, czyli A
'
B
' = l
- przykład 2.
W tym przykładzie długo
ść
przenoszona na map
ę
to:
l
1
= l cos
α
, bo cos
α
= l
1
/ l .
Ogólnie mapy dzielimy na:
a/ geograficzne – w skalach od 1: 500 000 do 1: 50 000 000 i mniejsze.
Przedstawia si
ę
na nich: powierzchnie ziemi, krajów, mórz,
l
ą
dów, rzek, niziny, wy
ż
yny, góry, granice pa
ń
stw, klimaty...
b/ topograficzne – w skalach: 1:10 000, 1: 25 000, 1: 50 000, 1: 100 000,
1: 300 000 i 1: 500 000.
Przedstawia si
ę
na nich: miasta, osiedla, drogi, kolej, lasy,
rzeki, jeziora.
Na mapach 1: 100 000 i wi
ę
kszych (np. 1: 25 000) nanosi
si
ę
szczegóły jak: mosty, drogi, budowle, rze
ź
b
ę
terenu
przedstawion
ą
w postaci tzw. warstwic.
Na podstawie map wi
ę
kszych opracowuje si
ę
projekty
techniczne.
c/ techniczne – mapy opracowywane dla ró
ż
nych dziedzin gospodarki, np.:
- gleboznawcze podaj
ą
ce rozmieszczenie klas gleb,
- miejskie sporz
ą
dzane w małych skalach pokazuj
ą
ce ulice,
place, linie komunikacyjne. Mapy szczegółowe w skali
12
1: 1000, 1: 500przedstawiaj
ą
budynki, granice
nieruchomo
ś
ci, wodoci
ą
gi, sie
ć
elektryczn
ą
.
d/ katastralne – słu
żą
do wymiaru podatku. Ukazuj
ą
granice własno
ś
ci, u
ż
ytki
rolne, drogi, zabudowania…
e/ melioracyjne – w skali 1: 5000, 1: 2000, 1: 1000 podaj
ą
warstwice terenu,
drogi, zabudowania, u
ż
ytki, rzeki, rowy, dreny.
f/ geologiczne – np.:
- stratygraficzne podaj
ą
ce rozmieszczenie warstw geologicznych,
budow
ę
geologiczn
ą
uwzgl
ę
dniaj
ą
c wiek warstw,
- surowcowe podaj
ą
ce rozmieszczenie złó
ż
surowców i litologi
ę
warstw kraju,
- hydrogeologiczne: poło
ż
enie poziomów wód wgł
ę
bnych,
- geotechniczne: własno
ś
ci budowlane gruntów,
- zło
ż
owe: budowa złó
ż
, rozmieszczenie kopalin,
g/ górnicze – sytuacja na powierzchni, wyrobiska górnicze, sytuacj
ę
geologiczn
ą
.
2/ Wyja
ś
ni
ć
, na czym polega tyczenie linii prostej bez u
ż
ycia lunety.
Tyczenie linii prostej mi
ę
dzy dwoma danymi punktami polega na znalezieniu
punktów po
ś
rednich le
żą
cych w płaszczy
ź
nie pionowej przechodz
ą
cej przez
dwa dane punkty. Punkty po
ś
rednie s
ą
przej
ś
ciowe (na czas trwania
pomiaru) a wyznacza si
ę
je tyczkami mierniczymi.
Mog
ą
zaj
ść
dwa przypadki mi
ę
dzy punkami A i B :
1/ punkty A i B s
ą
widoczne;
2/ mi
ę
dzy punktami A i B jest przeszkoda;
W obu przypadkach tyczenie prostej zaczynamy od ustawienia tyczek
w punktach A i B. Tyczki trzeba wypionowa
ć
– za pomoc
ą
pionu.
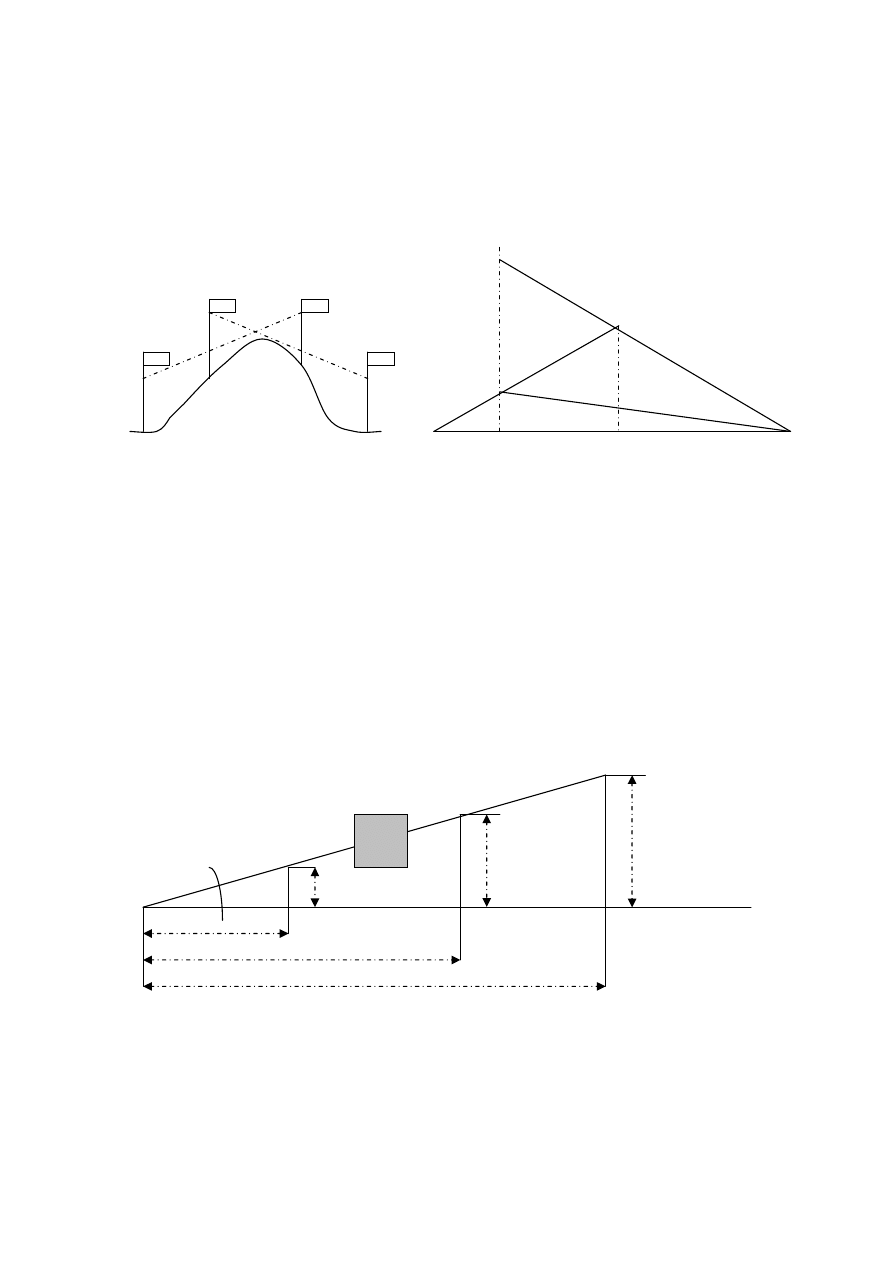
Przykład 1/.
- punkty A i B s
ą
widoczne
C
(teren płaski).
A B
- mierniczowie ustawiaj
ą
tyczki w punktach A i B.
- mierniczy 1 ustawia si
ę
2 ÷ 5m za tyczk
ą
A.
- patrz
ą
c przez tyczk
ę
A celuje na tyczk
ę
B.
- pomocnik z tyczk
ą
C znajduje si
ę
mi
ę
dzy punkami A i B.
- mierniczy naprowadza pomocnika, który trzyma tyczk
ę
C do momentu, a
ż
tyczki A, B, C znajd
ą
si
ę
w płaszczy
ź
nie pionowej (tzn. tyczka C zasłoni
13
tyczk
ę
B). Nast
ę
pne punkty po
ś
redni tyczy si
ę
podobnie.
Przykład 2/.
'
Mi
ę
dzy punkami A i B jest przeszkoda.
Rzut pionowy. C'
Rzut poziomy.
D'
C
D C'' D''
A
B
A C D B
Tyczenie prostej – gdy A i B s
ą
niewidoczne to trzeba co najmniej dwa punkty
po
ś
rednie C' i D' w przybli
ż
eniu linii AB, ALE tak aby stoj
ą
c
za tyczk
ą
C' widzie
ć
tyczki D' i B oraz stoj
ą
c za tyczk
ą
D'
widzie
ć
tyczki C' i A.
Mierniczy stoj
ą
c za tyczk
ą
C' przesuwa tyczk
ę
D'
pomocnika tak, a
ż
znajdzie si
ę
ona w płaszczy
ź
nie C' B.
Pomocnik tyczki D' naprowadza tyczk
ę
C' do punktu C''
na linii D' A.
Nast
ę
pnie obserwator C'' patrz
ą
c na B naprowadza tyczk
ę
D' do punktu D'' .
Czynno
ś
ci te powtarza si
ę
tak długo, a
ż
tyczki znajd
ą
si
ę
na linii A B.
Przypadek 3/ gdy na linii AB znajdzie si
ę
dom….
B
D
F
Y
B
Y
D
α
Y
F
A
F' D' B'
C
X
F
X
D
X
B
Gdy na prostej AB znajduje si
ę
przeszkoda (np. dom) to aby wyznaczy
ć
prost
ą
AB wytyczamy lini
ę
pomocnicz
ą
AC. Na prostej AC „w
ę
gielnic
ą
„ wyznaczamy
punkt B' le
żą
cy na prostej prostopadłej z punktu B do prostej AC.
Wyznaczamy dowolny punkt D'. Mierzymy odległo
ś
ci: X
B
X
D
Y
B .
Punkt D okre
ś
la si
ę
odmierzaj
ą
c na prostopadłej w punkcie D' odległo
ść
Y
D

14
obliczon
ą
na podstawie twierdzenia Talesa lub funkcji trygonometrycznych k
ą
ta
ostrego – w tym przypadku tg lub ctg.
Wzór na podstawie twierdzenia Talesa: X
B
/ Y
B
= X
D
/ Y
D .
St
ą
d: Y
D
= X
D
Y
B
/ X
B
Na podstawie funkcji tanges:
tg
α
= Y
D
/ X
D
= Y
B
/ X
B
.
czyli: Y
D
/ X
D
= Y
B
/ X
B
. St
ą
d: Y
D
= X
D
Y
B
/ X
B
.
Podobnie wyznaczamy inne punkty.
3/ Umie
ć
zmierzy
ć
długo
ś
ci linii prostych w terenie.
Długo
ść
Linii prostej mo
ż
emy metodami:
a/ bezpo
ś
rednimi – odmierzanie miar
ą
kolejnych odcinków;
b/ po
ś
rednimi – pomiar wielko
ś
ci dzi
ę
ki, którym wyznaczymy okre
ś
lon
ą
długo
ść
( metody trygonometryczne, optyczne).
Pomiar długo
ś
ci ta
ś
m
ą
stalow
ą
w terenie równym i poziomym:
- na ko
ń
cach punktów pomiarowych ustawia si
ę
tyczki,
- gdy długo
ść
przekracza 100m wyznacza si
ę
punkty po
ś
rednie.
Długo
ść
mierzy dwóch pomocników:
a/ 1- y z przodu ma szpilki, którymi zaznacza ilo
ść
przyło
ż
e
ń
ta
ś
my,
b/ 2- i przykłada zero do pocz
ą
tku prostej i naprowadza 1- go na kierunek,
c/ po osi
ą
gni
ę
ci długo
ś
ci miary (np. 20m) 1- y naci
ą
ga ta
ś
m
ę
i wbija szpilk
ę
,
d/ nast
ę
pnie obaj id
ą
wzdłu
ż
prostej – pomocnik 2- i przykłada ta
ś
m
ę
do
pierwszej szpilki – 1- y naci
ą
ga ta
ś
m
ę
i wbija drug
ą
szpilk
ę
, itd.,
e/ kolejne kroki s
ą
podobne – tylko 2- i zbiera na kółko szpilki.
Ostatni odcinek niepełny, ”reszt
ę
” (przy rozci
ą
gni
ę
tej ta
ś
mie 20m–np.15,6m)
odczytuje si
ę
z ta
ś
my a centymetry np. metrem.
Ilo
ść
szpilek zebranych przez II- go i reszt
ę
zapisuje si
ę
w dzienniku.
Ka
ż
da długo
ść
musi by
ć
mierzona 2- a razy (tam i z powrotem).
Dziennik pomiaru długo
ś
ci.
Bok
Liczba ta
ś
m
20 m
Reszta
m
Długo
ść
m
Ś
rednia
m
Uwagi
1 - 2
6
6
15,60
15,48
135,60
135,48
135,54
Ró
ż
nice pomiarów długo
ś
ci (1- go od 2- go) okre
ś
laj
ą
instrukcje pomiarowe.
Zale
ż
ne s
ą
od wa
ż
no
ś
ci pomiarów: np. dla boku = 100m poligonu kategorii A
- ró
ż
nica mi
ę
dzy 1- ym a 2- im pomiarem to 7cm.
15
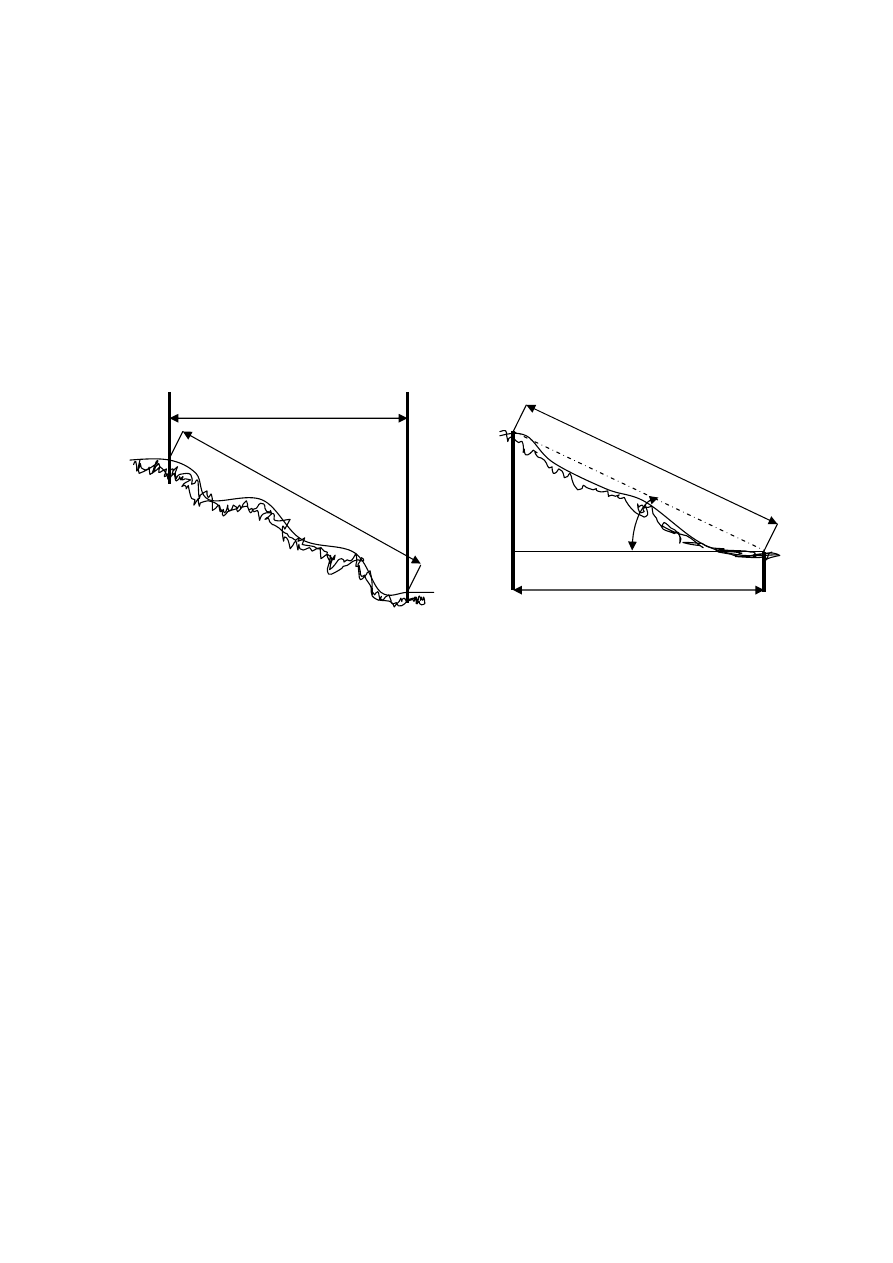
Pomiar ta
ś
m
ą
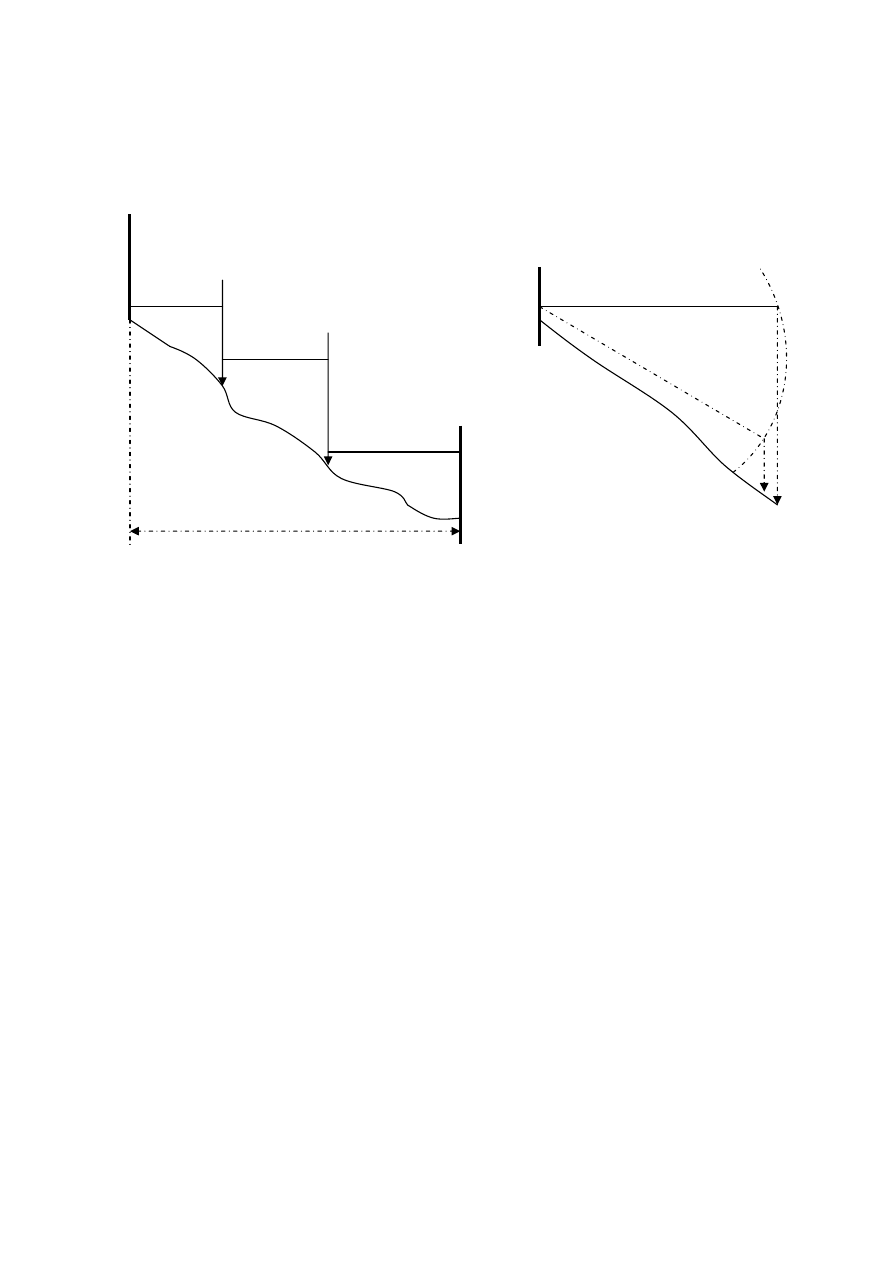
w terenie silnie nachylonym:
- metoda schodkowania dziel
ą
c na równo nachylone odcinki: L1, L2, L3.
L1
A B
A
L2
C
L3
C'
L = L1+L2+L3
B
B'
Poziomowanie ta
ś
my:
- przy pomocy libelli, - przez rzut poziomy punku B
przy braku libelli.
PRZYRZ
Ą
DY do pomiarów długo
ś
ci:
a/ drut inwarowy - wykonany ze stali i niklu słu
ż
y do precyzyjnych pomiarów
du
ż
ych odległo
ś
ci (np. bazy triangulacyjnej);
b/ ta
ś
ma miernicza stalowa – o długo
ś
ciach: 20, 30, 50m wi
ę
kszych:
500,1000 do pomiarów np. gł
ę
boko
ś
ci szybów;
Oznaczone odległo
ś
ci:
- odst
ę
py metrowe (płytki mosi
ęż
ne z cyframi – ilo
ść
m.),
- odst
ę
py dcm (otworki),
- półmetrowe (nity).
Odst
ę
py w cm i mm nie s
ą
oznaczone, odczytuje si
ę
je za pomoc
ą
podziałki.
Ta
ś
ma ma uchwyty do naci
ą
gania. Napinana jest sił
ą
10÷15 kG: r
ę
cznie,
dr
ąż
kami lub dynamometrem. Do zaznaczania długo
ś
ci mierzonych słu
żą
szpilki (jest ich 11).
Krótkie odcinki w powietrzu mierzy si
ę
ta
ś
m lekkich –ruletek.
S
ą
one: 20-o, 30-o, 50-o metrowe. Oznaczenia: cm, dcm i metry.
Ta
ś
my kopalniane: stalowe (stal szlachetna) i inwarowe. Mniej wa
żą
.
Do krótkich odległo
ś
ci (o małej dokładno
ś
ci) słu
żą
ta
ś
my parciane.

16
4/ Omówi
ć
budow
ę
w
ę
gielnicy oraz teodolitu górniczego stoj
ą
cego
i wisz
ą
cego.
W
Ę
GIELNICA – zwierciadlana, pryzmatyczna.
4.1W
ę
gielnica zwierciadlana składa si
ę
z:
- metalowego pudełka,
- dwóch małych lusterek ustawionych do siebie pod k
ą
tem 45
o
,
- od spodu do zamocowanego trzonka z uchem mo
ż
na zawiesi
ć
pion.
Przy jej u
ż
yciu mo
ż
na wykona
ć
nast
ę
puj
ą
ce czynno
ś
ci:
a/ wyznaczy
ć
prostopadł
ą
do prostej z punktu le
żą
cego na prostej:
C
A
D
B
- ustawiamy w
ę
gielnic
ę
nad punktem D (D le
ż
y na prostej AB) przy pomocy
pionu,
- obracamy w
ę
gielnic
ą
tak aby w lustrze zobaczy
ć
obraz tyczki A,
- z kolei patrz
ą
c przez okienko w
ę
gielnicy pomocnikowi pokazujemy,
aby przesuwał si
ę
z tyczk
ą
C do momentu, a
ż
tyczka C i obraz tyczki A
b
ę
d
ą
na jednej linii pionowej. Wtedy k
ą
t ADC=90
o
.
b/ znale
źć
rzut danego punktu na prost
ą
:
- ustawiamy tyczk
ę
w punkcie C,
- przesuwamy si
ę
wzdłu
ż
linii AB,
- patrz
ą
c przez okienko w
ę
gielnicy szuka si
ę
punktu, w którym obraz
tyczki A (lub B) znajduje si
ę
na jednej linii pionowej z tyczk
ą
C.
- opuszcza si
ę
pion nad ta
ś
m
ą
linii AB i zaznaczamy to miejsce szpilk
ą
.
- odczytujemy odległo
ść
tego punktu od pocz
ą
tku linii.
4.2W
ę
gielnica lustrzana – słu
ż
y głównie do tyczenia k
ą
tów prostych
Składa si
ę
z:
- pryzmatu szklanego w kształcie prostok
ą
tnego, równoramiennego
trójk
ą
ta,
-
ś
ciana le
żą
ca naprzeciw k
ą
ta prostego wyło
ż
ona jest amalgamatem rt
ę
ci,
i działa jak lustro.
17
C
α
O1
D
O2
β
A B
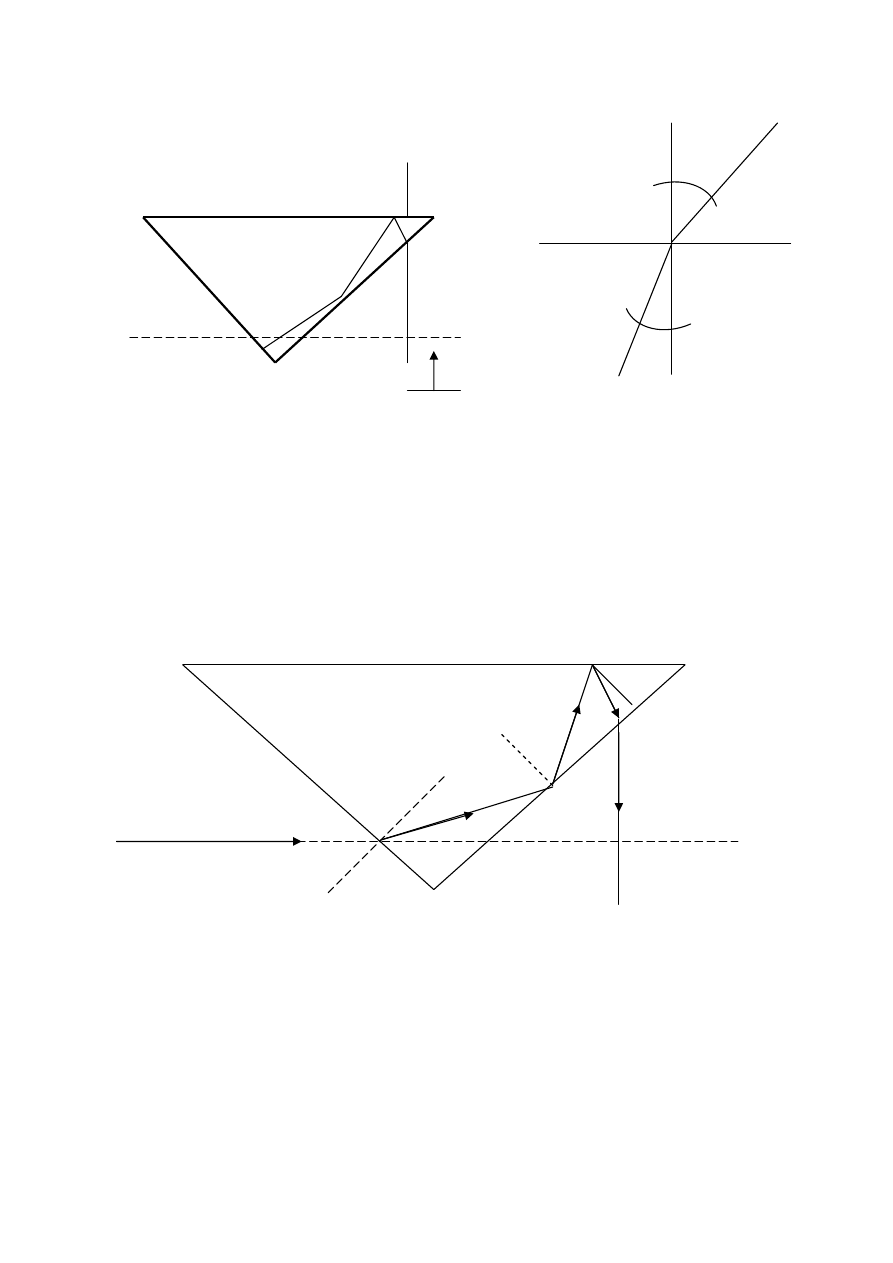
Tyczenie k
ą
ta prostego . Załamanie promienia przechodz
ą
cego
przez dwa o
ś
rodki O1 i O2.
Sin
α
/sin
β
= n – współczynnik załamania.
Dla szkła n = 1,5÷1,8
Zasada odbicia
ś
wiatła w w
ę
gielnicy pryzmatycznej:
45
o
β
β
β
β
α
4.3/ Teodolity – dziel
ą
si
ę
na stoj
ą
ce (na statywie) i wisz
ą
ce.
18
Je
ż
eli chodzi o odczyt k
ą
tów dziel
ą
si
ę
na:
- noniuszowe (dokładno
ść
odczytu koła poziomego - 30'',
- mikroskopowe (o dokładno
ś
ci odczytu 1' lub 6''.
Słu
żą
głównie pomiarów k
ą
tów poziomych i pionowych.
Najwa
ż
niejsz
ą
cech
ą
jest liczba osi obrotu teodolitów:
a/ jednoosiowe – zwykłe, b/ dwuosiowe – repetycyjne.
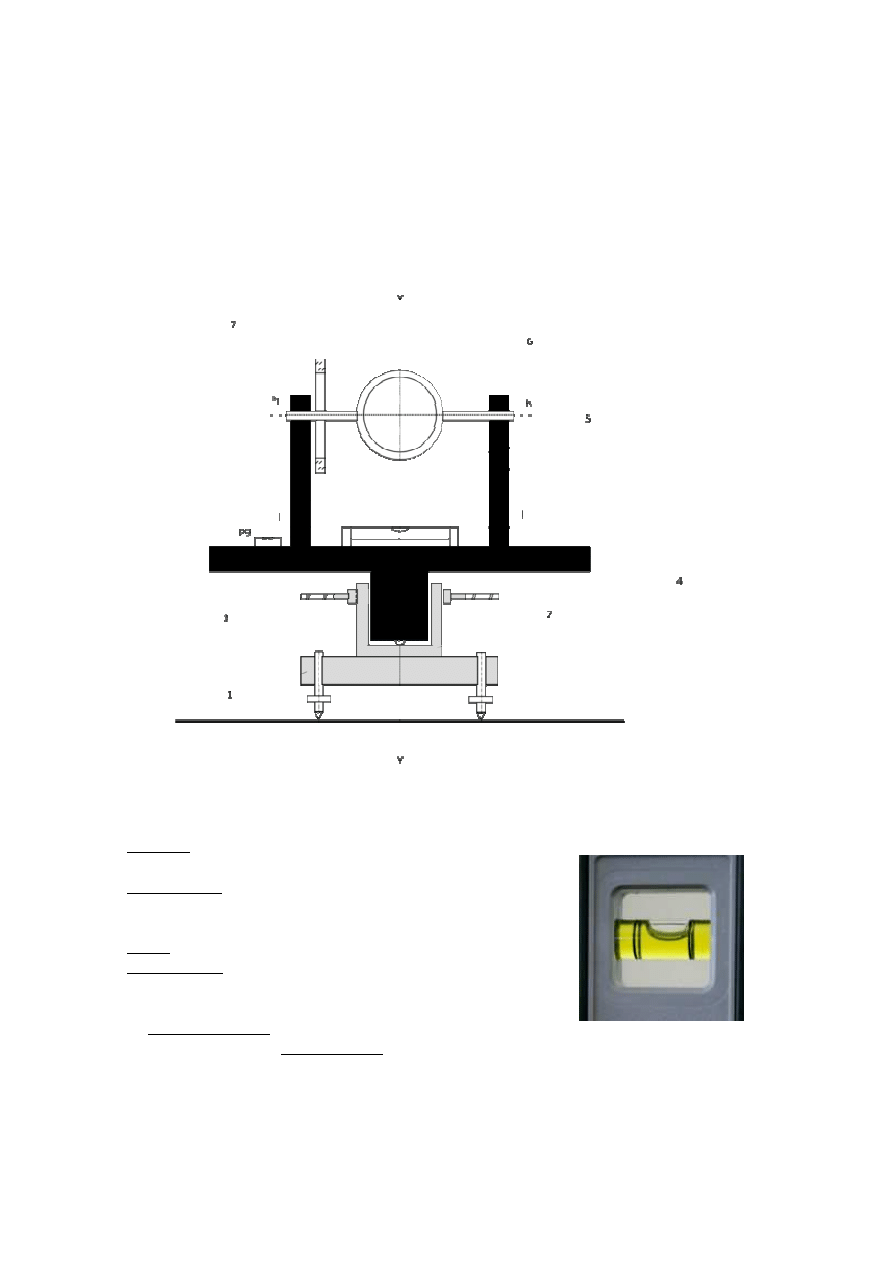
Układ osiowy bordy i podstawowe osie teodolitu:
LIBELLA RURKOWA
1 - spodarka
2 - tuleja złączona ze spodarką
3 - koło poziome
4 - alidada
5 - dźwigary lunety
6 - luneta
7 - koło pionowe sprzęgnięte z lunetą
vv - pionowa (inaczej główna lub obrotu alidady) oś teodolitu
hh - pozioma oś obrotu lunety
ll - oś libelli alidadowej (rurkowej)
pg - płaszczyzna główna libelli okrągłej
4.3.1 Teodolit stoj
ą
cy.

19
Budowa: spodarka, limbus, alidada z umocowan
ą
lunet
ą
geodezyjn
ą
, statyw.
1/ Spodarka – trójramienna podstawa z 3- ma
ś
rubami nastawczymi,
która pozwalaj
ą
na ustawienie przyrz
ą
du do podstawy.
2/ Limbus - ze spodark
ą
poł
ą
czone jest na stałe poziome koło limbusu.
W teodolitach dwuosiowych limbus osadza si
ę
na osobnej tulei,
jest nie zale
ż
ny od spodarki.
Na obwodzie limbusu wyryty jest podział k
ą
towy.
Na walcu ł
ą
cz
ą
cym spodark
ę
z limbusem osadzona jest
pionowa o
ś
alidady.
3/ Alidada – składa si
ę
z koła poziomego współ
ś
rodkowego z limbusem
i d
ź
wigarków mocuj
ą
cych lunet
ę
. Alidada obraca si
ę
dookoła
osi teodolitu.
4/ Luneta – o
ś
obrotu lunety spoczywa na d
ź
wigarkach.
Teodolity dostosowane do pomiarów k
ą
tów pionowych na osi
lunety maj
ą
koła pionowe( odczyt k
ą
ta pionowego).
5/ Noniusz (lub mikroskop) – słu
ż
y do odczytu na limbusie – s
ą
dwa.
Pionowo
ść
noniuszy ustawia si
ę
za pomoc
ą
libelli rurkowych.
Do unieruchomienia alidady wzgl
ę
dem spodarki (limbusu) słu
ż
y
ś
ruba
zaciskowa. Teodolit ustawia si
ę
na statywie (trójnogu), do którego mo
ż
na
przymocowa
ć
pion.
Teodolity górnicze ró
ż
ni
ą
si
ę
tylko konstrukcyjnie: s
ą
l
ż
ejsze, maj
ą
szczeln
ą
i zwi
ę
zł
ą
budow
ę
, zakryte koła podziałowe a lunet
ę
o stałej długo
ś
ci.
Do centrowania na lunecie (na przedłu
ż
eniu osi pionowej) otworek
lub sworze
ń
. Krzy
ż
nitkowy składa si
ę
z dwóch z dwóch nitek pionowych.
Na niektórych krzy
ż
ach s
ą
podziałki – do obserwacji waha
ń
pionu.
Nowe teodolity maj
ą
własne o
ś
wietlenie krzy
ż
a i kół podziałowych.
TEODOLIT WISZ
Ą
CY – ma te same cz
ęś
ci jak teodolit dwuosiowy: spodark
ę
,
limbus, alidad
ę
i lunet
ę
z kołem pionowym.
Spodarka ma kształt przegubu kulistego pozwalaj
ą
cego podwiesi
ć
teodolit.
Teodolit wisz
ą
cy ma limbus stale zł
ą
czony z alidad
ą
.
Noniusze osadzone s
ą
na osobnej tulei obracaj
ą
cej si
ę
dookoła głównej osi.
Noniusze i limbus mog
ą
si
ę
porusza
ć
niezale
ż
nie od siebie.
Podziałka limbusu (koło poziome) jest odwrotna do ruchu wskazówek
zegara i podzielona na 360 stopni lub 400 gradów.
Podziałka koła pionowego – koło podzielone jest na 4- y
ć
wiartki (0±90 st.),
ze znakami (+) czyli wznios i (-) czyli upad. Noniusze (lupy) słu
żą
do
odczytywania koła pionowego. Noniusze s
ą
poł
ą
czone z libell
ą
rurkow
ą
.
Do poziomowania przyrz
ą
du słu
ż
y libella rurkowa.
WARUNKI JAKIE MUSI SPEŁNIA
Ć
TEODOLIT.
20
a/ o
ś
główna powinna by
ć
prostopadła do osi libelli alidady
– o
ś
główna musi by
ć
pionowa;
b/ o
ś
obrotu lunety musi by
ć
prostopadła do osi głównej
- o
ś
lunety musi by
ć
pozioma;
c/ o
ś
celowa musi by
ć
prostopadła do osi obrotu lunety;
d/ o
ś
obrotu alidady musi by
ć
w
ś
rodku (centrycznie) do
ś
rodka limbusu;
e/ dokładny podział limbusu i noniuszów;
f/ centryczna o
ś
celowa lunety.
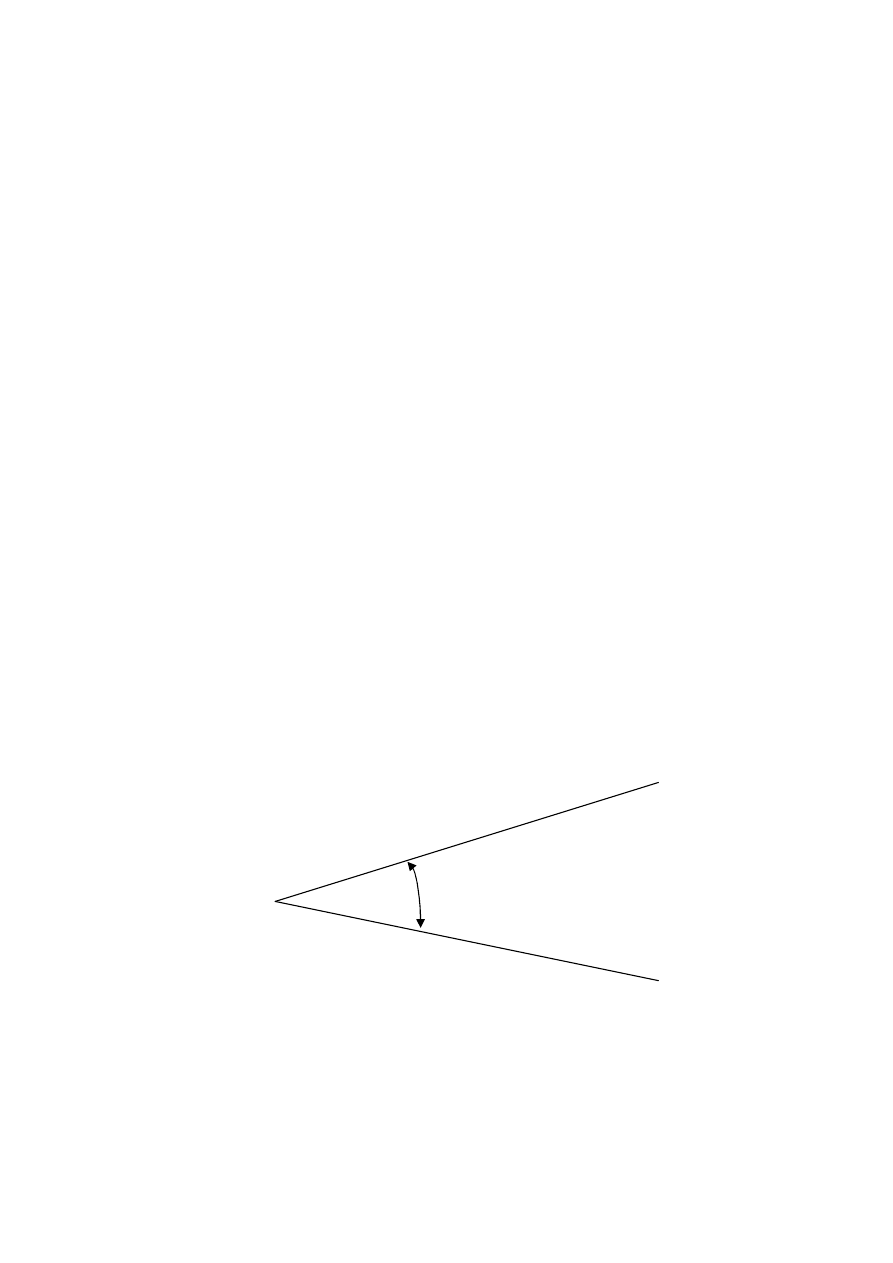
USTAWIENIE TEODOLITU.
Głowica statywu
płytka oporowa
Spr
ęż
yna
ś
ruby
Nakr
ę
tka wewn
ę
trzna
Ś
ruba centralna
Nakr
ę
tka zewn
ę
trzna
Hak do pionu
Przed pomiarem teodolit trzeba: spoziomowa
ć
i scentrowa
ć
teodolit.
Poziomowanie:
- za pomoc
ą
ś
rub nastawczych libell
ę
alidady ustawia si
ę
równolegle
(tzw. górowanie ba
ń
ki),
- pó
ź
niej obraca si
ę
alidad
ę
z libell
ą
o k
ą
t 90 stopni,
- przy pomocy trzeciej
ś
ruby doprowadza si
ę
ba
ń
k
ę
do „górowania”,
Po spoziomowaniu ba
ń
ka libelli przy obrocie alidady nie mo
ż
e si
ę
wychyla
ć
.
Centrowanie:
21
a/ nad punktem:
- statyw musi by
ć
ustawiony tak aby
ś
rodek głowicy był nad punktem,
(warunek – głowica musi by
ć
spoziomowana),
- zapina si
ę
teodolit mocuj
ą
c go
ś
rub
ą
centraln
ą
,
- na haczyk
ś
ruby zapina si
ę
pion,
- przesuwa si
ę
instrument po głowicy dot
ą
d a
ż
pion znajdzie si
ę
dokładnie nad punktem,
- nakr
ę
tk
ą
wewn
ę
trzn
ą
dociska si
ę
spr
ęż
yn
ę
ś
ruby centralnej stabilizuj
ą
c
poło
ż
enie teodolitu,
b/ pod punktem:
- opuszcza si
ę
pion z punktu tak aby był on w
ś
rodku głowicy
( spoziomowanej),
- zakr
ę
camy
ś
ruby statywu i ustawiamy teodolit,
- przykr
ę
camy go nakr
ę
tk
ą
zewn
ę
trzn
ą
ś
ruby centralnej,
- poziomujemy lunet
ę
,
- teraz przesuwamy na głowicy instrument, a
ż
ostrze pionu znajdzie si
ę
nad znaczkiem umieszczonym na lunecie.
Pami
ę
ta
ć
, aby p
ę
cherzyk libelli limbusu zajmował
ś
rodkowe poło
ż
enie.
5/ Zna
ć
metody pomiaru k
ą
ta poziomego i pionowego.
Metody pomiaru k
ą
ta poziomego:
- zwykła opisana poni
ż
ej,
- metoda repetycyjna ( n krotne pomiary k
ą
ta). K
ą
ty si
ę
dodaje.
Po wykonaniu n pomiarów dzieli si
ę
sum
ę
przez n pomiarów.
- metoda kierunkowa ( pomiar z jednego miejsca kilku kierunków).
Po spoziomowaniu i po scentrowaniu teodolitu sprz
ę
gamy limbus i spodark
ę
na stałe (efekt – teodolit zwykły jednoosiowy).
A
0
α
B
- lunet
ę
kierujemy na A, sprz
ę
gamy alidad
ę
, limbus i leniwk
ę
alidady
- naprowadzamy pionow
ą
nitk
ę
krzy
ż
a nitkowego ze znakiem(np. sznurkiem)
w punkcie A,
- zaciska si
ę
ś
rub
ę
sprz
ę
gow
ą
lunety i leniwk
ą
naprowadzamy na
ś
rodek
sygnału – odczytujemy na noniuszach (mikroskopach) wyniki,

22
- zwalniamy
ś
rub
ę
sprz
ę
gaj
ą
c
ą
alidad
ę
z limbusem kieruj
ą
c lunet
ę
na punkt B.
Lunet
ę
obracamy zgodnie z ruchem wskazówek zegara,
- ponownie sprz
ę
gamy alidad
ę
i lunet
ę
naprowadzaj
ą
c leniwkami nitk
ę
krzy
ż
a
na
ś
rodek sygnału w punkcie B,
- odczytujemy na noniuszach k
ą
ty i wpisujemy do dzienniczka,
- nast
ę
pnie robimy pomiary przesuwaj
ą
c lunet
ę
w płaszczy
ź
nie pionowej przez
„zenit”,
- zwalniamy
ś
rub
ę
zaciskow
ą
alidady i kierujemy lunet
ę
na punkt B.
- łapiemy
ś
rodek sygnału punktu B i zapisujemy odczyt,
- pó
ź
niej zwalniaj
ą
c
ś
rub
ę
zaciskow
ą
alidady celujemy na punkt A ustawiaj
ą
c
nitk
ę
krzy
ż
a na sygnał punku A i odczytujemy noniusze zapisuj
ą
c wynik,
Odczyty z punktu B do A wykonywane s
ą
przeciwnie do ruchu wskazówek.
Obliczamy
ś
redni
ą
arytmetyczn
ą
z dwóch odczytów dla punktu A i B.
Dla pomiarów zgodnie z ruchem wskazówek zegara ró
ż
nica
ś
redniej B i A daje
k
ą
t BA.
Dla kontroli cz
ę
sto mierzy si
ę
k
ą
t uzupełniaj
ą
cy ( 360
o
-
α
).
Metody pomiaru k
ą
ta pionowego:
K
ą
ty pionowe przewa
ż
nie mierzy si
ę
razem z kontami poziomymi.
Przebieg pomiaru.
- celujemy lunet
ą
na punkt,
- zaciskamy
ś
rub
ę
zaciskow
ą
lunety,
- przy pomocy leniwki nastawiamy poziom
ą
nitk
ę
krzy
ż
a na znak
wysoko
ś
ciowy sygnału,
- doprowadzamy libell
ę
koła pionowego do górowania i odczytujemy obydwa
noniusze,
- przerzucamy lunet
ę
przez „zenit” powtarzaj
ą
c pomiary,
-
ś
rednia z obydwu odczytów daje wielko
ść
k
ą
ta.
Wa
ż
ny jest tu podział koła pionowego.
Je
ż
eli koło czterokrotnie opisane jest od 0 do 90 stopni i linia zerowa le
ż
y
równolegle do osi celowania to
ś
rednia z odczytów da wła
ś
ciw
ą
warto
ść
.
W innym przypadku trzeba przelicza
ć
k
ą
ty.
6/ Wymieni
ć
rodzaje ci
ą
gów poligonowych.
23
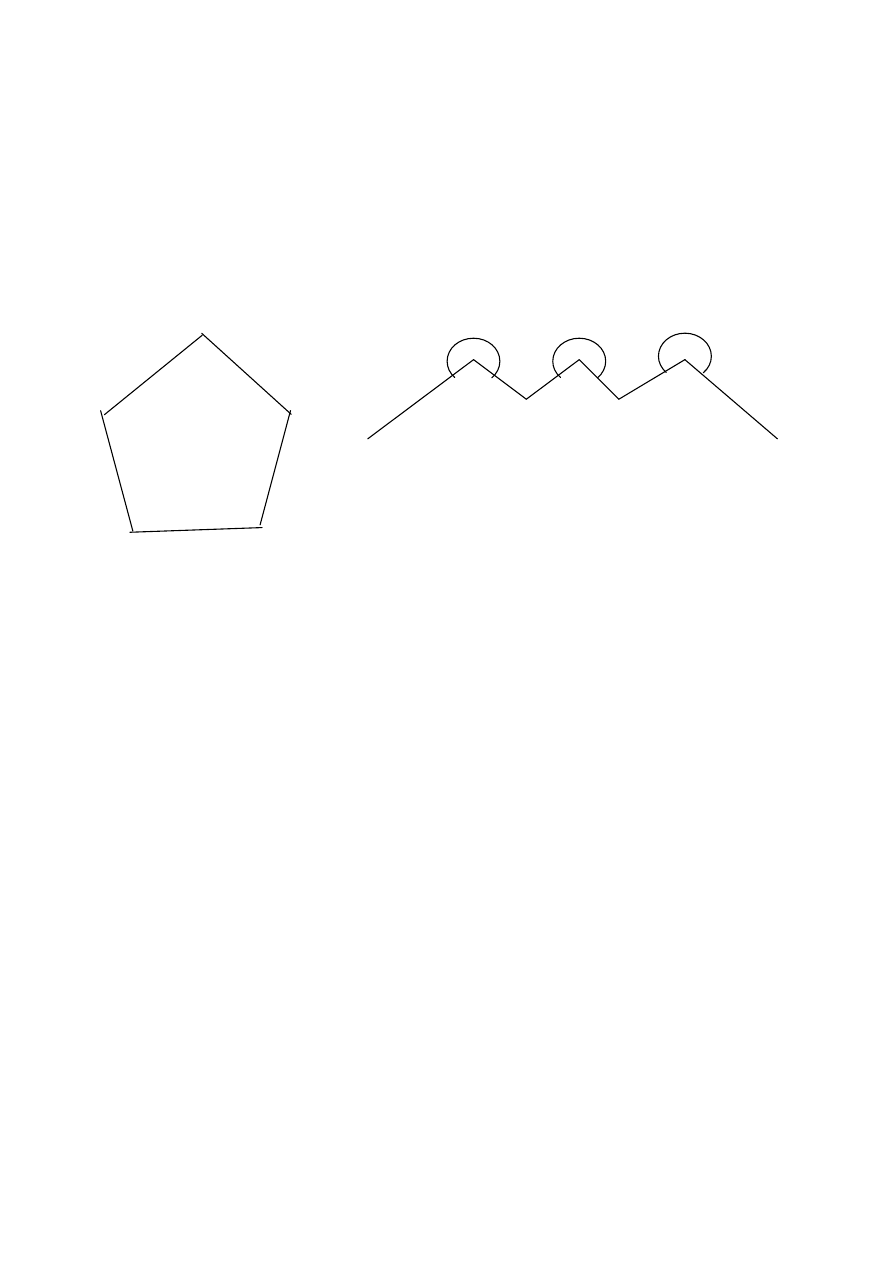
POLIGONIZACJA – metoda polegaj
ą
ca na pomiarze boków i k
ą
tów linii
łamanej zało
ż
onej w terenie- tzw. poligonu.
Poligony nawi
ą
zuje si
ę
do punktów trygonometrycznych jako punktów
wy
ż
szego rz
ę
du.
W poligonie mierzy si
ę
długo
ś
ci boków i wielko
ś
ci k
ą
tów na załamaniach oraz
k
ą
ty nawi
ą
zania
ϕ
i
ψ
. K
ą
ty te nawi
ą
zuj
ą
poligon do sieci triangulacyjnej.
Daj
ą
mo
ż
liwo
ść
kontroli pomiarów.
T.R.II
β
2
T.R.III
l
2
α
3
l
3
ϕ
ψ
β
1
β
3
α
2
α
4
l
4
T.R.I
T.R.IV
l
1
α
1
α
5
Poligon nawi
ą
zany do punktów triangulacyjnych.
l
5
Ci
ą
gi poligonowe – wieloboki zało
ż
one mi
ę
dzy punktami triangulacyjnymi celem
zag
ę
szczenia sieci punktów pomiarowych.
Sie
ć
ci
ą
gów jest podstaw
ą
do zdj
ę
cia dla wi
ę
kszych
obszarów.
Ci
ą
gi s
ą
:
a/ zamkni
ę
te - wielobok zamkni
ę
ty,
b/ otwarte – boki poligonu to łamana otwarta.
Poligony nawi
ą
zane do:
a/ dwóch punktów A i B o znanych współrz
ę
dnych i pomierzonych k
ą
tach
ϕ
i
ψ
to taki poligon nazywamy dwustronnie nawi
ą
zanym,
b/ poligon nawi
ą
zany do jednego punktu A to poligon jednostronnie nawi
ą
zany.
S
ą
jeszcze poligony nie nawi
ą
zane do
ż
adnego punktu – tzw. swobodne.
Powi
ą
zanie ze sob
ą
kilku ci
ą
gów poligonowych to – sie
ć
poligonowa.
Suma k
ą
tów wewn
ę
trznych w wieloboku zamkni
ę
tym wynosi - (n – 2)x180
o
, a
suma k
ą
tów zewn
ę
trznych w wieloboku o n bokach wynosi – (n + 2)x 180
o
.
Mo
ż
na w ten sposób sprawdzi
ć
pomiary k
ą
tów.
POLIGON
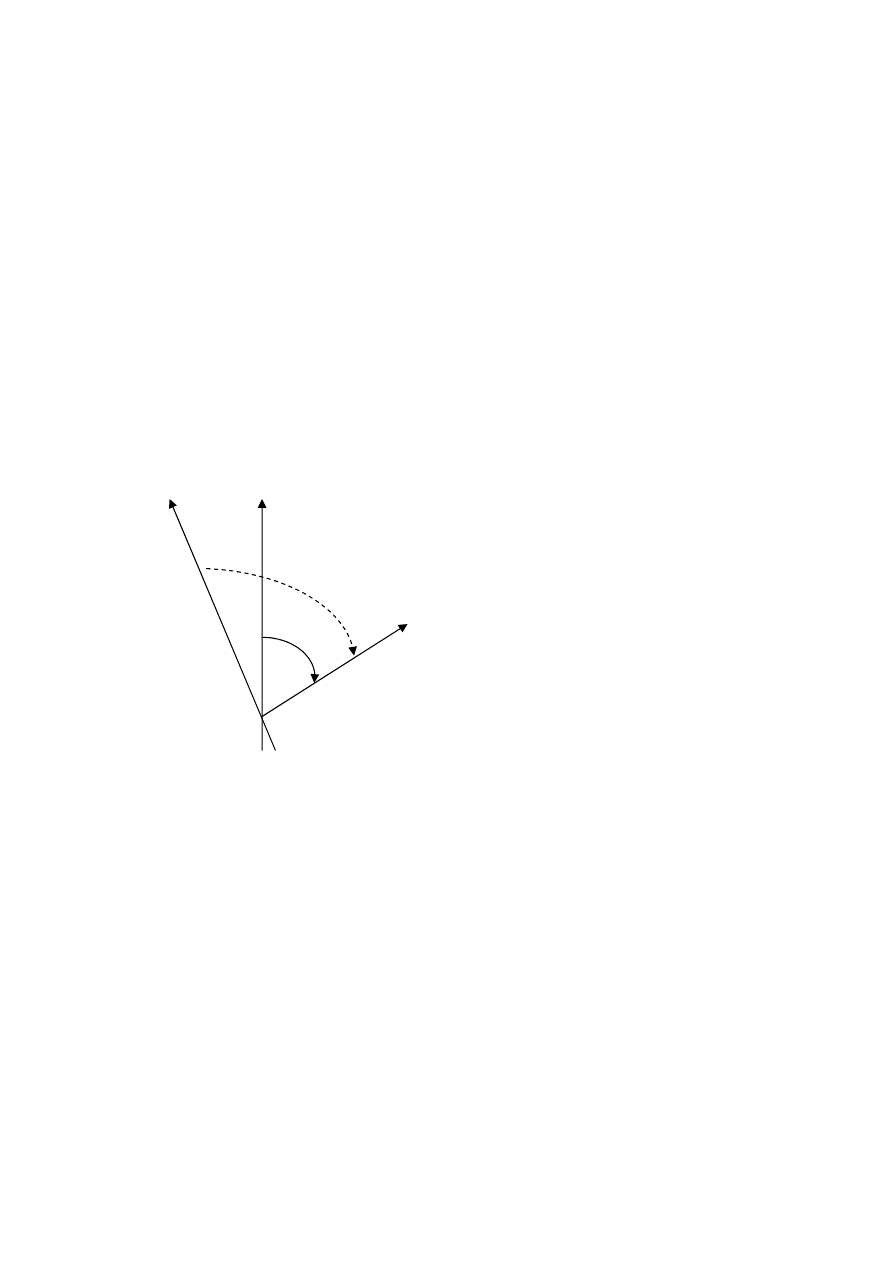
POMIAR SZCZEGÓŁÓW – pomiar opiera si
ę
na sieci poligonowej.
Poligony zakłada si
ę
blisko granic – charakterystyczne punkty domierza si
ę
do boków poligonu metod
ą
domiarów.
W razie potrzeby wi
ę
kszej dokładno
ś
ci zakłada si
ę
sie
ć
pomocniczych linii.
24
Linie te z bokami poligonu to osnowa geodezyjna dla szczegółów
sytuacyjnych mierzonego obszaru.
Zasada „od ogółu do szczegółu” to nast
ę
puj
ą
ca kolejno
ść
pomiarów:
- triangulacja;
- poligonizacja;
- zdj
ę
cie szczegółów.
7/ Omówi
ć
dzienniki pomiarowe.
8/ Zna
ć
poj
ę
cie azymutu i układy lokalne współrz
ę
dnych.
AZYMUT – to k
ą
t zawarty mi
ę
dzy mi
ę
dzy dowoln
ą
lini
ą
prost
ą
a kierunkiem
południka geograficznego lub magnetycznego.
Kierunek południka geograficznego lub kierunek północy wyznacza linia
ł
ą
cz
ą
ca ten punkt z biegunem północnym Ziemi lub nieba.
Kierunek północy wyznacza igła magnetyczna.
Południk geograficzny
Południk
γγγγ
Magnety,
β
ω
A
Azymut liczy si
ę
w prawo.
K
ą
t mierzony od południka geograficznego przechodz
ą
cego przez punkt A
- to azymut geograficzny,
K
ą
t liczony od południka magnetycznego to azymut magnetyczny- kierunek
prostej.
K
ą
t b
ę
d
ą
cy ró
ż
nic
ą
tych dwóch k
ą
tów – to deklinacja magnetyczna.
Układy współrz
ę
dnych.

25
W miernictwie o
ś
OX to kierunek północy, a o
ś
OY to kierunek na wschód.
Jest te
ż
układ odwrotny.
Pn
-X
+X
II
I
- Y
+Y (W)
+Y -Y
III
IV
-X
+X
Układ odwrotny „Sucha Góra”.
9/ Scharakteryzowa
ć
k
ą
t kierunkowy.
Kierunek osi X dla danego układu współrz
ę
dnych wyznacza południk
geograficzny przechodz
ą
cy przez pocz
ą
tek układu,
Kierunek osi Y wyznacza odpowiedni równole
ż
nik przechodz
ą
cy przez
pocz
ą
tek układu.
Południk przechodz
ą
cy przez pocz
ą
tek układu to południk zerowy.
Mi
ę
dzy południkiem geograficznym przechodz
ą
cym przez dowolny punkt a
równoległ
ą
do południka przechodz
ą
cego przez pocz
ą
tek układu
(równoległa do osi X) zawarty jest k
ą
t zbie
ż
no
ś
ci.
W układzie współrz
ę
dnych kierunek linii okre
ś
la k
ą
t kierunkowy.
Mierzony on jest od równoległej do południka zerowego poprowadzonej
przez punkt pocz
ą
tkowy danej linii.
Je
ż
eli o
ś
+X jest skierowana na PN – to k
ą
t północny, a je
ś
li o
ś
+X jest
skierowana na PD – to k
ą
t południowy.

26
WYMAGANIA PONADPODSTAWOWE
1/ Umie
ć
wytyczy
ć
k
ą
ty proste w
ę
gielnic
ą
.
W
ę
gielnica zwierciadlana składa si
ę
z:
- metalowego pudełka,
- dwóch małych lusterek ustawionych do siebie pod k
ą
tem 45
o
,
- od spodu do zamocowanego trzonka z uchem mo
ż
na zawiesi
ć
pion.
Przy jej u
ż
yciu mo
ż
na wykona
ć
nast
ę
puj
ą
ce czynno
ś
ci:
a/ wyznaczy
ć
prostopadł
ą
do prostej z punktu le
żą
cego na prostej:
C
A
D
B
- ustawiamy w
ę
gielnic
ę
nad punktem D (D le
ż
y na prostej AB) przy pomocy
pionu,
- obracamy w
ę
gielnic
ą
tak aby w lustrze zobaczy
ć
obraz tyczki A,
- z kolei patrz
ą
c przez okienko w
ę
gielnicy pomocnikowi pokazujemy,
aby przesuwał si
ę
z tyczk
ą
C do momentu, a
ż
tyczka C i obraz tyczki A
b
ę
d
ą
na jednej linii pionowej. Wtedy k
ą
t ADC=90
o
.
b/ znale
źć
rzut danego punktu na prost
ą
:
- ustawiamy tyczk
ę
w punkcie C,
- przesuwamy si
ę
wzdłu
ż
linii AB,
- patrz
ą
c przez okienko w
ę
gielnicy szuka si
ę
punktu, w którym obraz
tyczki A (lub B) znajduje si
ę
na jednej linii pionowej z tyczk
ą
C.
- opuszcza si
ę
pion nad ta
ś
m
ą
linii AB i zaznaczamy to miejsce szpilk
ą
.
- odczytujemy odległo
ść
tego punktu od pocz
ą
tku linii.
W
ę
gielnica lustrzana – słu
ż
y głównie do tyczenia k
ą
tów prostych
Składa si
ę
z:
- pryzmatu szklanego w kształcie prostok
ą
tnego, równoramiennego
trójk
ą
ta,
-
ś
ciana le
żą
ca naprzeciw k
ą
ta prostego wyło
ż
ona jest amalgamatem rt
ę
ci,
i działa jak lustro.
27
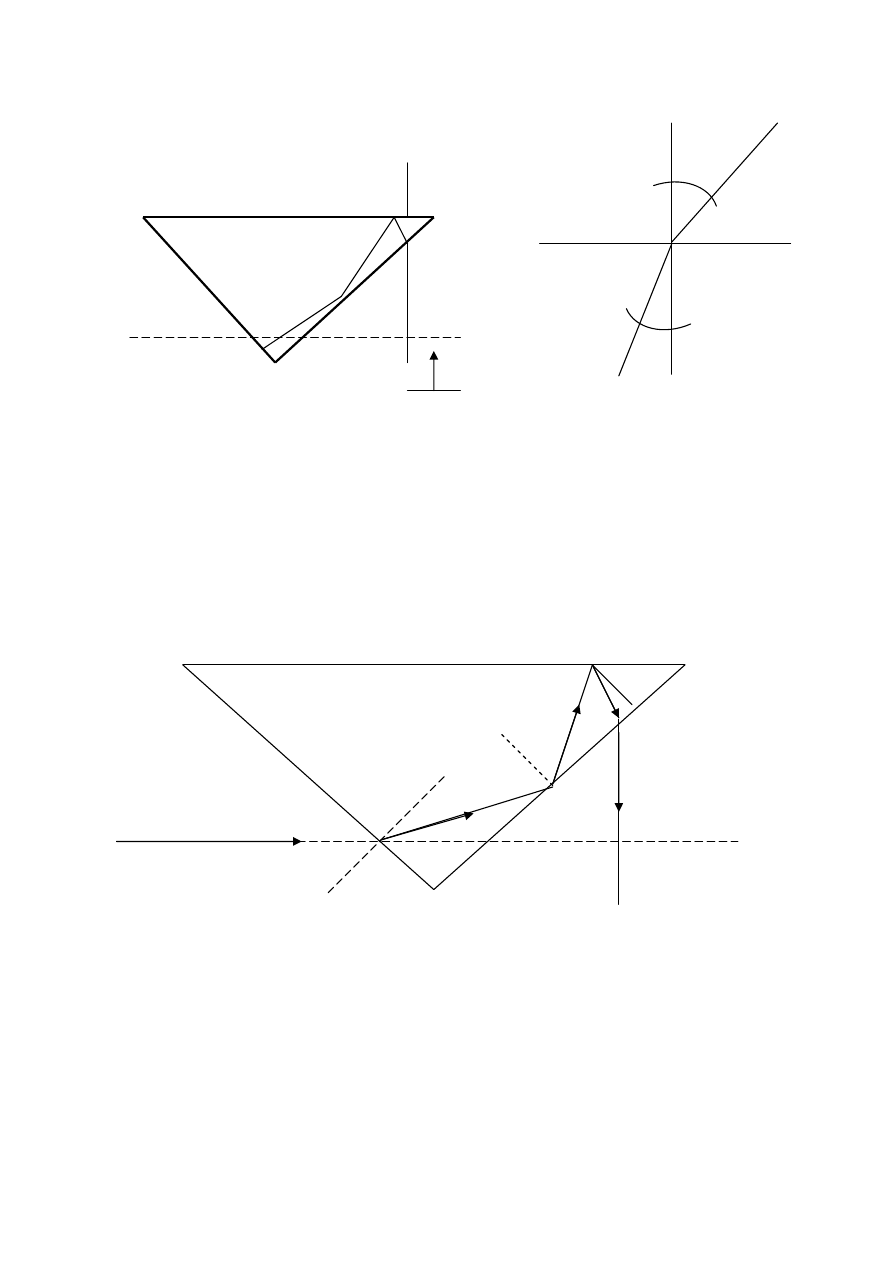
C
α
O1
D
O2
β
A B
Tyczenie k
ą
ta prostego . Załamanie promienia przechodz
ą
cego
przez dwa o
ś
rodki O1 i O2.
Sin
α
/sin
β
= n – współczynnik załamania.
Dla szkła n = 1,5÷1,8
Zasada odbicia
ś
wiatła w w
ę
gielnicy pryzmatycznej:
45
o
β
β
β
β
α
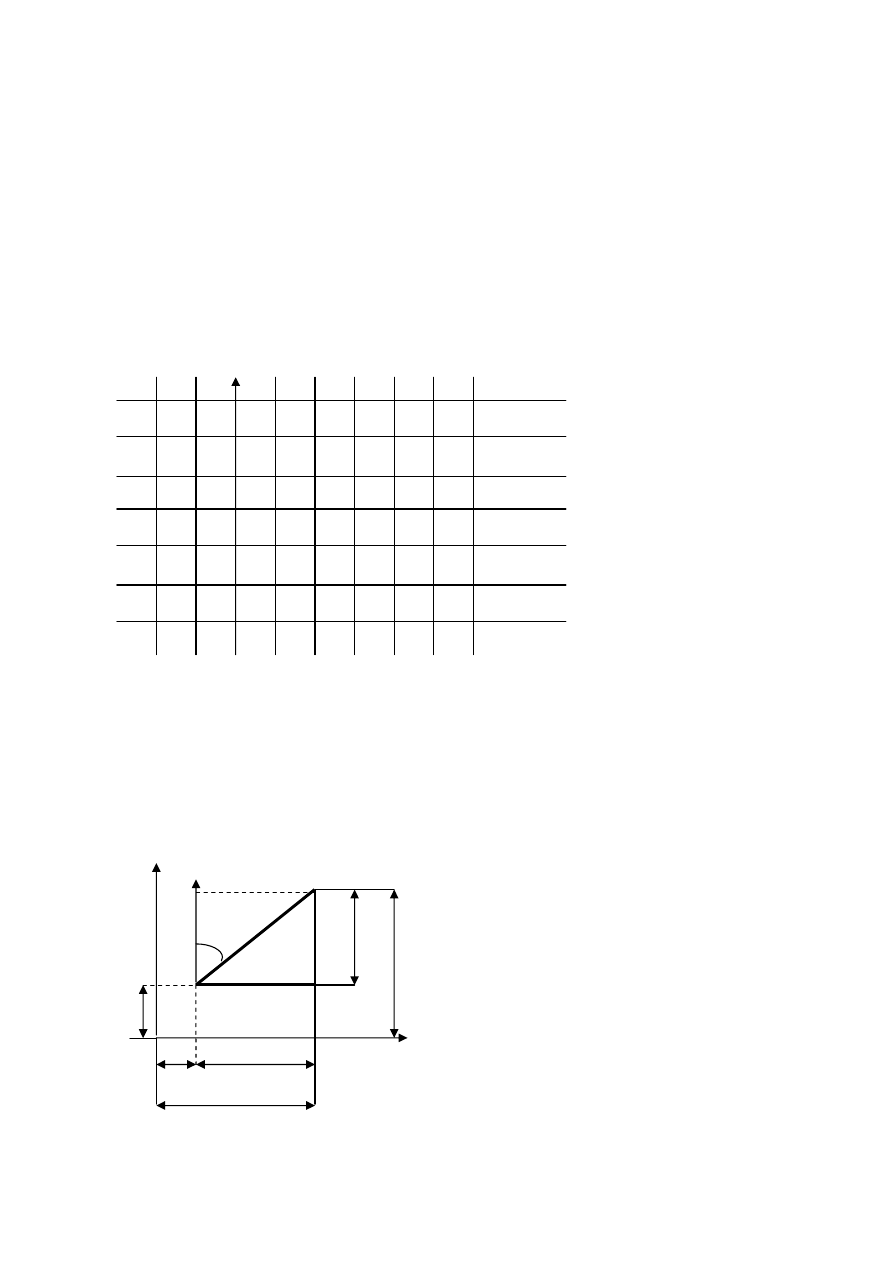
TROCH
Ę
MATEMATYKI.
28
MAPA.
A/ SIATKA WSPÓŁRZ
Ę
DNYCH.
- aby umiejscowi
ć
punkty na mapie przyj
ę
to,
ż
e co: 50, 100, 200 lub 500m
(oczywi
ś
cie w odpowiedniej skali mapowej) prowadzi si
ę
linie:
a/ poziome – równoległe do osi OY,
b/ pionowe – równoległe do osi OX.
Linie te tworz
ą
siatk
ę
współrz
ę
dnych.
Liczby przy liniach wskazuj
ą
ich odległo
ść
od pocz
ą
tku danego układu.
W granicach pa
ń
stwa jest zawsze kilka układów.
PN (o
ś
OX)
2700
2600
2500
2400
x P W
2300
2200
2100
-4000 -3900 -3800 -3700 – 3600 -3500 -3400 -3300 -3200
Np. punkt P ma współrz
ę
dne (2400; -3600).
PRZYROSTY WSPÓŁRZ
Ę
DNYCH.
S
ą
dwa punkty (A i B) o współrz
ę
dnych: A ( x1;y2) i B (x2;y2).
Ró
ż
nica odpowiednich współrz
ę
dnych x i y – to przyrost współrz
ę
dnych
∆∆∆∆
.
Czyli:
∆∆∆∆
x = x2 – x1; a
∆∆∆∆
y = y2 – y1;
X B c – odległo
ść
mi
ę
dzy punktami A i B.
ω
ω
ω
ω
AB
– azymut (k
ą
t kierunkowy) prostej AB.
c
ω
AB
∆
x
x2
A
x1
Y
y1
∆
y
y2
Korzystaj
ą
c z trygonometrii mamy:
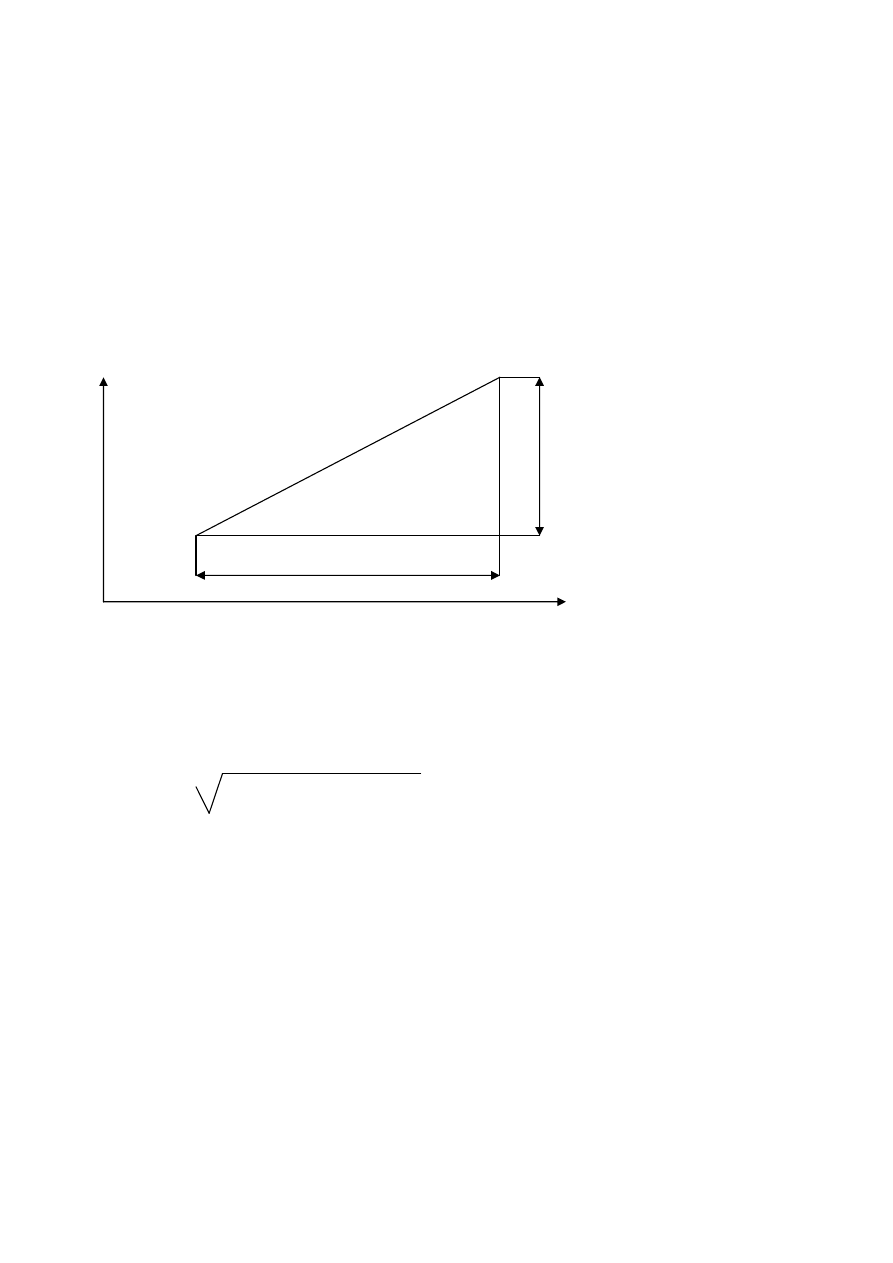
29
a/ sin
ω
ω
ω
ω
AB
=
∆
y/ c, czyli
∆
y= c sin
ω
ω
ω
ω
AB
,
b/ cos
ω
ω
ω
ω
AB
=
∆
x/ c, czyli
∆
x = c cos
ω
ω
ω
ω
AB
.
Znaj
ą
c współrz
ę
dne punktu A i długo
ść
boku AB =c oraz azymut linii AB
(k
ą
t kierunkowy linii AB) mo
ż
emy obliczy
ć
współrz
ę
dne punktu B:
x2 = x1+
∆
x = x1 + c cos
ω
ω
ω
ω
AB
;
y2 = y1+
∆
y = y1 + c sin
ω
ω
ω
ω
AB
;
Znaj
ą
c współrz
ę
dne A i B mo
ż
emy obliczy
ć
długo
ść
boku AB korzystaj
ą
c ze
twierdzenia Pitagorasa tj. wzoru: B (x2; y2)
X (Pn)
∆
x = x2 – x1
A
(x1; y1)
∆
y = y2 – y1
Y (W)
0
Suma kwadratów przyprostok
ą
tnych równa si
ę
kwadratowi przeciwprostok
ą
tnej.
Czyli:
(AB)
2
= (
∆
x)
2
+ (
∆
y)
2
, czyli (AB)
2
= (x2 – x1)
2
+ (y2 – y1)
2
,
To: AB = (x2 – x1)
2
+ (y2 – y1)
2
,
Gdy bok poligonu le
ż
y na płaszczy
ź
nie to mo
ż
e przyjmowa
ć
w układzie
współrz
ę
dnych ró
ż
ne poło
ż
enia.
Przyjmijmy,
ż
e 4- y boki przyjmuj
ą
poło
ż
enie w czterech
ć
wiartkach: I, II, III i IV.
Jeden punkt ka
ż
dego z tych boków le
ż
y w pocz
ą
tku układu współrz
ę
dnych.
Ka
ż
demu z poło
ż
e
ń
boków odpowiada odpowiedni azymut (k
ą
t kierunkowy).
Azymuty przyjmuj
ą
warto
ś
ci :
a/ I
ć
wiartka – 0
o
÷ 90
o
,
b/ II
ć
wiartka - 90
o
÷ 180
o
,
c/ III
ć
wiartka - 180
o
÷ 270
o
,
d/ IV
ć
wiartka - 270
o
÷ 360
o
.
Warto
ś
ci funkcji sin i cos przyjmuj
ą
warto
ś
ci w poszczególnych
ć
wiartkach dla
k
ą
tów 0
o
÷ 90
o
:
30
Ć
wiartka
I
II
III
IV
sin
ω
+
+
-
-
cos
ω
+
-
-
+
Dla k
ą
tów powy
ż
ej 90
o
stosujemy wzory redukcyjne:
Ć
wiartka
I
II
III
IV
Funkcja
ω
=
α
ω
= 180
o
-
α
ω
= 180
o
+
α
ω
= 360
o
-
α
sin
ω
+ sin
α
+ sin
α
- sin
α
- sin
α
cos
ω
+ cos
α
- cos
α
- cos
α
+ cos
α
tg
ω
+ tg
α
- tg
α
+ tg
α
- tg
α
Przebieg funkcji y = tg x
Przebieg funkcji y = ctg x
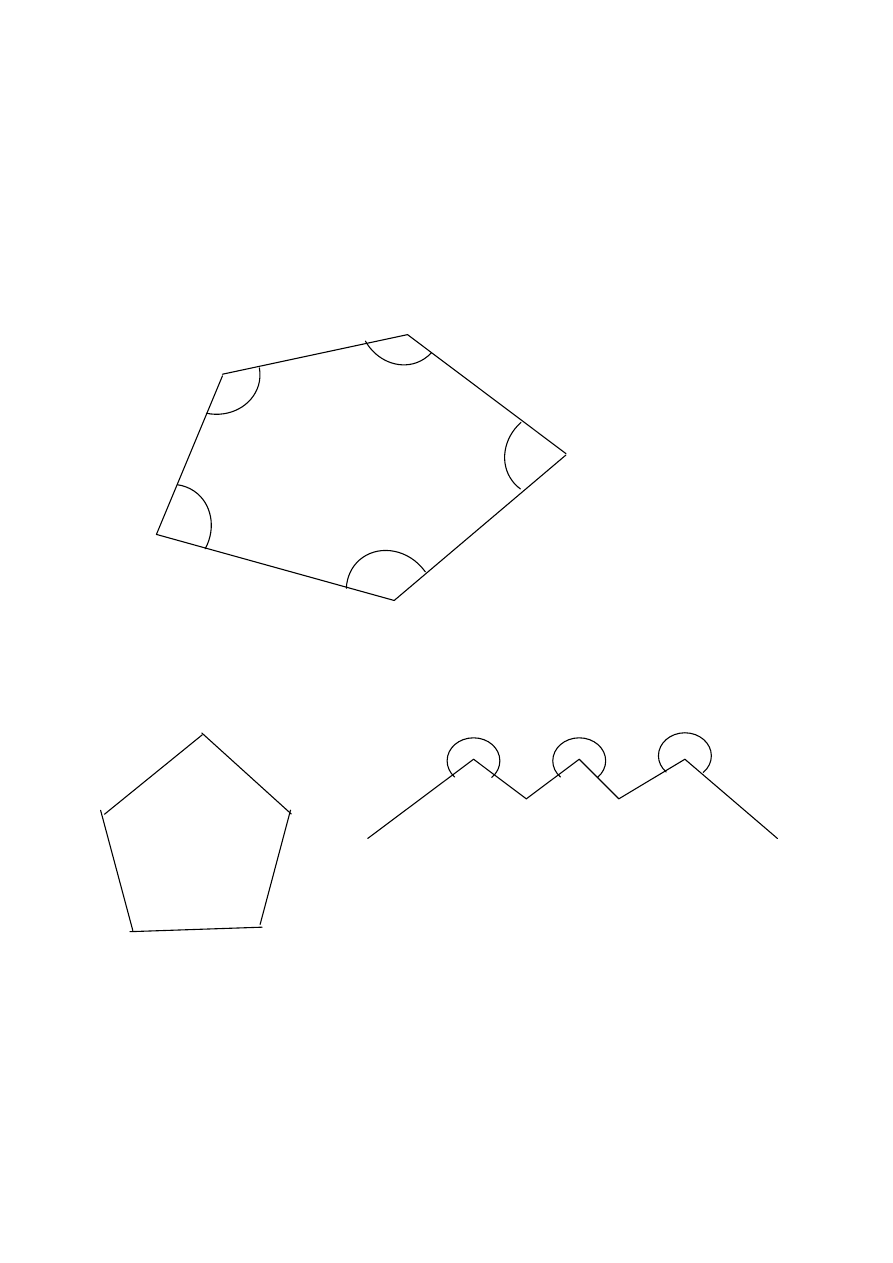
31
2/ Umie
ć
obliczy
ć
azymuty boków w ci
ą
gach poligonowych.
W CI
Ą
GACH ZAMKNI
Ę
TYCH ( wielobok zamkni
ę
ty).
Mo
ż
na korzysta
ć
ze wzorów na sum
ę
k
ą
tów.
K
ą
ty wewn
ę
trzne: S
w
= ( n – 2 )x 180
o
,
Dla k
ą
tów zewn
ę
trznych: S
z
= ( n + 2 ) x 180
o
Gdzie: n – suma k
ą
tów.
K
ą
ty zewn
ę
trzne
K
ą
ty wewn
ę
trzne
W poligonie mierzy si
ę
długo
ś
ci boków i wielko
ś
ci k
ą
tów na załamaniach oraz
k
ą
ty nawi
ą
zania
ϕ
i
ψ
. K
ą
ty te nawi
ą
zuj
ą
poligon do sieci triangulacyjnej.
Daj
ą
mo
ż
liwo
ść
kontroli pomiarów.
T.R.II
β
2
T.R.III
l
2
α
3
l
3
ϕ
ψ
β
1
β
3
α
2
α
4
l
4
T.R.I
T.R.IV
l
1
α
1
α
5
Poligon nawi
ą
zany do punktów triangulacyjnych.
l
5
Ci
ą
gi poligonowe – wieloboki zało
ż
one mi
ę
dzy punktami triangulacyjnymi celem
zag
ę
szczenia sieci punktów pomiarowych.
Sie
ć
ci
ą
gów jest podstaw
ą
do zdj
ę
cia dla wi
ę
kszych
obszarów.

32
X B c – odległo
ść
mi
ę
dzy punktami A i B.
ω
ω
ω
ω
AB
– azymut (k
ą
t kierunkowy) prostej AB.
c
ω
AB
∆
x
x2
A
x1
Y
y1
∆
y
y2
Korzystaj
ą
c z trygonometrii mamy:
a/ sin
ω
ω
ω
ω
AB
=
∆
y/ c, czyli
∆
y= c sin
ω
ω
ω
ω
AB
,
b/ cos
ω
ω
ω
ω
AB
=
∆
x/ c, czyli
∆
x = c cos
ω
ω
ω
ω
AB
.
3/ Wyznaczy
ć
współrz
ę
dne punktów poligonowych na mapie.
Po dokonaniu pomiarów otrzymujemy współrz
ę
dne punktów poligonowych
nanoszonych na map
ę
z naniesion
ą
siatk
ą
współrz
ę
dnych – linii
równoległych do osi X i Y
Mapy wykre
ś
la si
ę
na arkuszach (sekcjach), o wymiarach okre
ś
lonych w
instrukcjach.
Mapy kopalniane sporz
ą
dza si
ę
zwykle w kilku sekcjach o wymiarach
siatki 500x800mm. Wymiary oczek siatki w skali:
1:2000 to 5x5cm,
1: 500 i 1:1000 to 10x10cm.
Współrz
ę
dne punktów poligonowych na mapie wyznaczamy nast
ę
puj
ą
co:
- odczytujemy skal
ę
mapy,
- odczytujemy współrz
ę
dn
ą
x i y, k
ą
t kierunkowy.
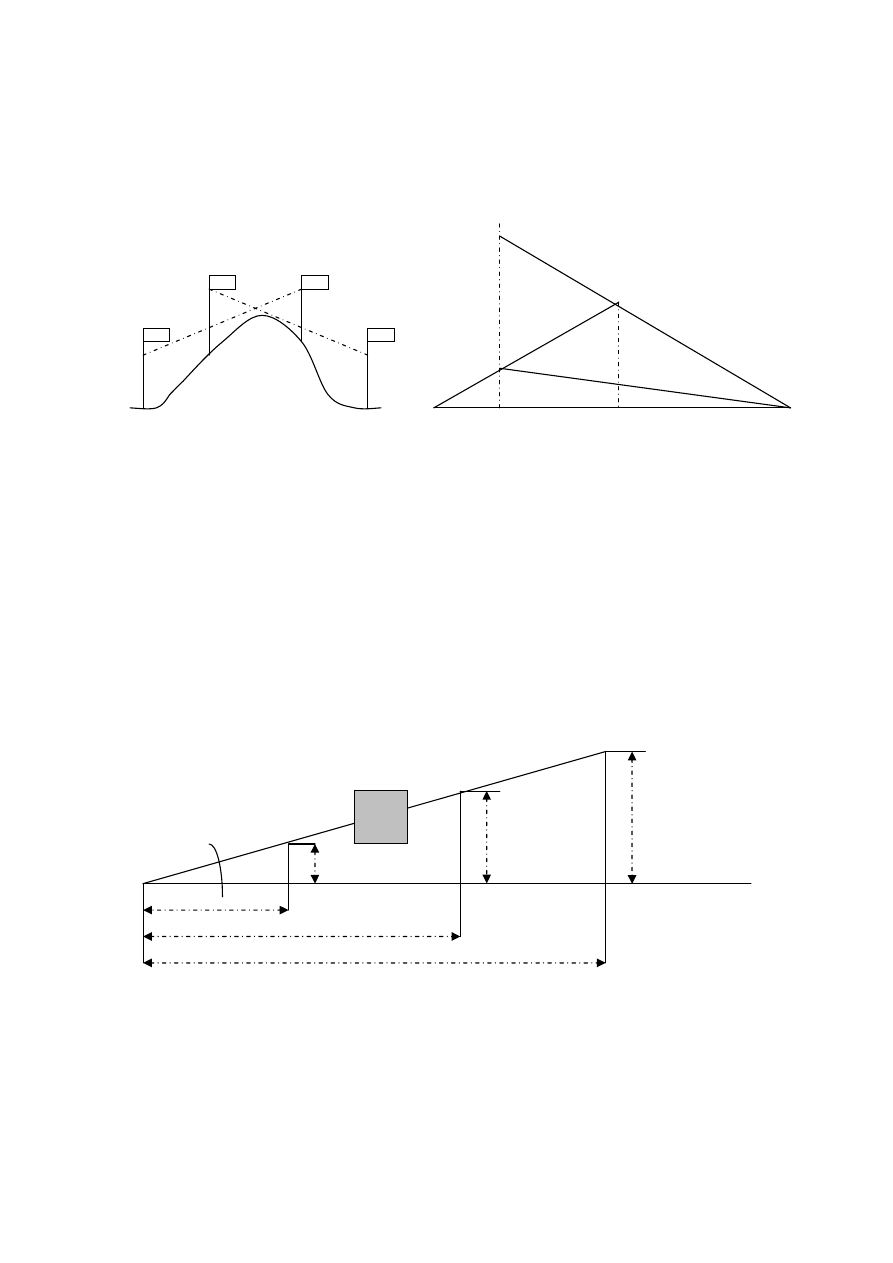
33
4/ Umie
ć
wytycza
ć
i oblicza
ć
długo
ś
ci odcinków linii prowadzonych przez
przeszkody terenowe.
4.1/ Mi
ę
dzy punkami A i B jest przeszkoda.
Rzut pionowy. C'
Rzut poziomy.
D'
C
D C'' D''
A
B
A C D B
Tyczenie prostej – gdy A i B s
ą
niewidoczne to trzeba co najmniej dwa punkty
po
ś
rednie C' i D' w przybli
ż
eniu linii AB, ALE tak aby stoj
ą
c
za tyczk
ą
C' widzie
ć
tyczki D' i B oraz stoj
ą
c za tyczk
ą
D'
widzie
ć
tyczki C' i A.
Mierniczy stoj
ą
c za tyczk
ą
C' przesuwa tyczk
ę
D'
pomocnika tak, a
ż
znajdzie si
ę
ona w płaszczy
ź
nie C' B.
Pomocnik tyczki D' naprowadza tyczk
ę
C' do punktu C''
na linii D' A.
Nast
ę
pnie obserwator C'' patrz
ą
c na B naprowadza tyczk
ę
D' do punktu D'' .
Czynno
ś
ci te powtarza si
ę
tak długo, a
ż
tyczki znajd
ą
si
ę
na linii A B.
4.2/ Gdy na linii AB znajdzie si
ę
dom….
B
D
F
Y
B
Y
D
α
Y
F
A
F' D' B'
C
X
F
X
D
X
B
Gdy na prostej AB znajduje si
ę
przeszkoda (np. dom) to aby wyznaczy
ć
prost
ą
AB wytyczamy lini
ę
pomocnicz
ą
AC. Na prostej AC „w
ę
gielnic
ą
„ wyznaczamy
punkt B' le
żą
cy na prostej prostopadłej z punktu B do prostej AC.
Wyznaczamy dowolny punkt D'. Mierzymy odległo
ś
ci: X
B
X
D
Y
B .
Punkt D okre
ś
la si
ę
odmierzaj
ą
c na prostopadłej w punkcie D' odległo
ść
Y
D
34
obliczon
ą
na podstawie twierdzenia Talesa lub funkcji trygonometrycznych k
ą
ta
ostrego – w tym przypadku tg lub ctg.
Wzór na podstawie twierdzenia Talesa: X
B
/ Y
B
= X
D
/ Y
D .
St
ą
d: Y
D
= X
D
Y
B
/ X
B
Na podstawie funkcji tanges:
tg
α
= Y
D
/ X
D
= Y
B
/ X
B
.
czyli: Y
D
/ X
D
= Y
B
/ X
B
. St
ą
d: Y
D
= X
D
Y
B
/ X
B
.
Podobnie wyznaczamy inne punkty.
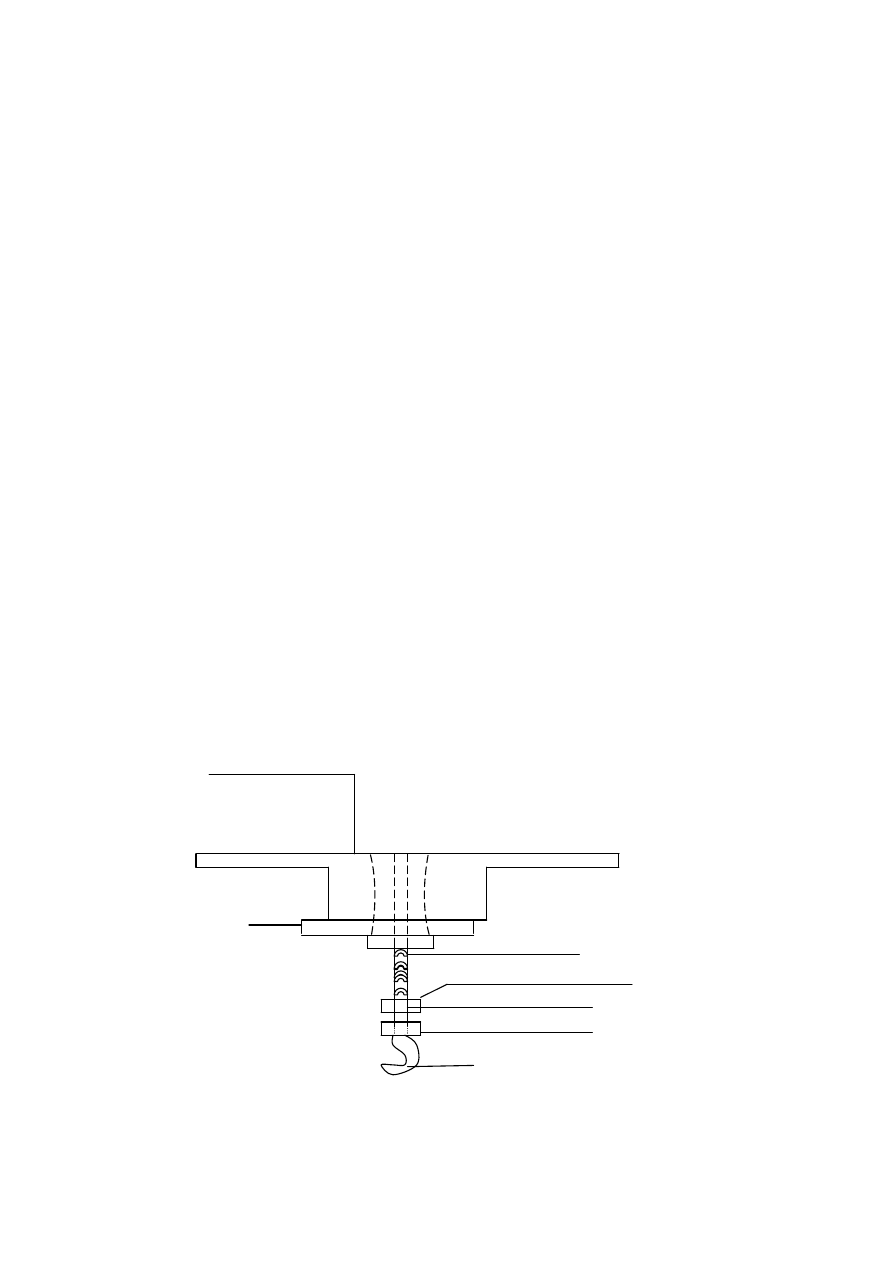
5/ Umie
ć
przygotowa
ć
teodolit do pomiaru.
WARUNKI JAKIE MUSI SPEŁNIA
Ć
TEODOLIT.
a/ o
ś
główna powinna by
ć
prostopadła do osi libelli alidady
– o
ś
główna musi by
ć
pionowa;
b/ o
ś
obrotu lunety musi by
ć
prostopadła do osi głównej
- o
ś
lunety musi by
ć
pozioma;
c/ o
ś
celowa musi by
ć
prostopadła do osi obrotu lunety;
d/ o
ś
obrotu alidady musi by
ć
w
ś
rodku (centrycznie) do
ś
rodka limbusu;
e/ dokładny podział limbusu i noniuszów;
f/ centryczna o
ś
celowa lunety.
USTAWIENIE TEODOLITU.
Głowica statywu
płytka oporowa
Spr
ęż
yna
ś
ruby
Nakr
ę
tka wewn
ę
trzna
Ś
ruba centralna
Nakr
ę
tka zewn
ę
trzna
Hak do pionu
Przed pomiarem teodolit trzeba: spoziomowa
ć
i scentrowa
ć
teodolit.

35
Poziomowanie:
- za pomoc
ą
ś
rub nastawczych libell
ę
alidady ustawia si
ę
równolegle
(tzw. górowanie ba
ń
ki),
- pó
ź
niej obraca si
ę
alidad
ę
z libell
ą
o k
ą
t 90 stopni,
- przy pomocy trzeciej
ś
ruby doprowadza si
ę
ba
ń
k
ę
do „górowania”,
Po spoziomowaniu ba
ń
ka libelli przy obrocie alidady nie mo
ż
e si
ę
wychyla
ć
.
Centrowanie:
a/ nad punktem:
- statyw musi by
ć
ustawiony tak aby
ś
rodek głowicy był nad punktem,
(warunek – głowica musi by
ć
spoziomowana),
- zapina si
ę
teodolit mocuj
ą
c go
ś
rub
ą
centraln
ą
,
- na haczyk
ś
ruby zapina si
ę
pion,
- przesuwa si
ę
instrument po głowicy dot
ą
d a
ż
pion znajdzie si
ę
dokładnie nad punktem,
- nakr
ę
tk
ą
wewn
ę
trzn
ą
dociska si
ę
spr
ęż
yn
ę
ś
ruby centralnej stabilizuj
ą
c
poło
ż
enie teodolitu,
b/ pod punktem:
- opuszcza si
ę
pion z punktu tak aby był on w
ś
rodku głowicy
( spoziomowanej),
- zakr
ę
camy
ś
ruby statywu i ustawiamy teodolit,
- przykr
ę
camy go nakr
ę
tk
ą
zewn
ę
trzn
ą
ś
ruby centralnej,
- poziomujemy lunet
ę
,
- teraz przesuwamy na głowicy instrument, a
ż
ostrze pionu znajdzie si
ę
nad znaczkiem umieszczonym na lunecie.
Pami
ę
ta
ć
, aby p
ę
cherzyk libelli limbusu zajmował
ś
rodkowe poło
ż
enie.
6/ Zna
ć
zasady obliczania k
ą
tów kierunkowych i współrz
ę
dnych punktów
poligonowych.
OMÓWIONE POWYśEJ.
14. POMIARY NIWELACYJNE I SYTUACYJNO WYSOKOSCIOWE.
WYMAGANIA PODSTAWOWE
36
1/ Omówi
ć
cele i rodzaje pomiarów wysoko
ś
ciowych .
Aby okre
ś
li
ć
wła
ś
ciwe poło
ż
enie punktów trzeba:
- okre
ś
li
ć
ich poło
ż
enie na płaszczy
ź
nie,
- tak
ż
e okre
ś
li
ć
ich wysoko
ść
nad poziomem morza.
Zasada obliczania wysoko
ś
ci.
B
H
B
= H
A
+ H
AB
h
AB
A
h
B
h
A
- poziom morza.
Rozró
ż
niamy nast
ę
puj
ą
ce rodzaje pomiarów wysoko
ś
ciowych:
a/ niwelacja trygonometryczna,
b/ niwelacja geometryczna,
c/ niwelacja barometryczna.
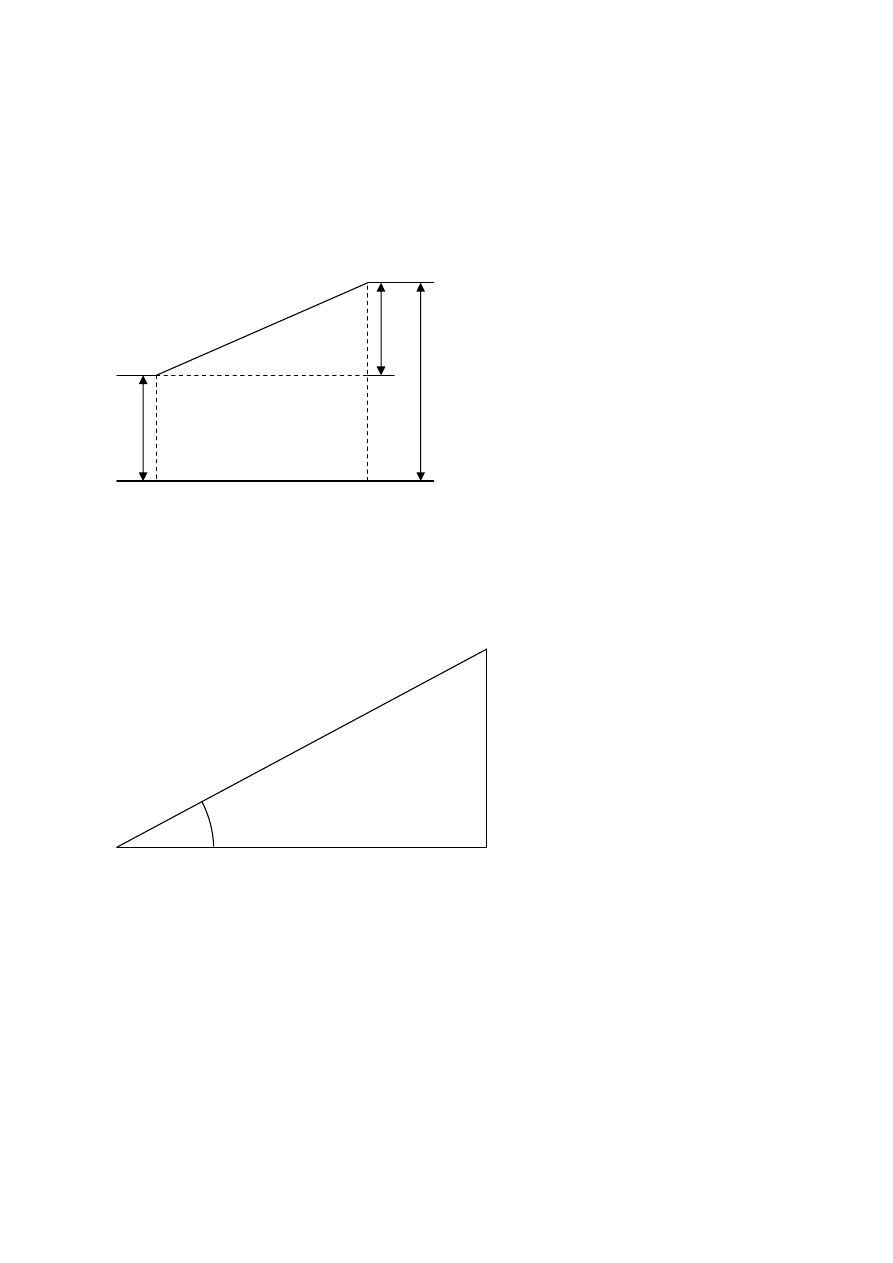
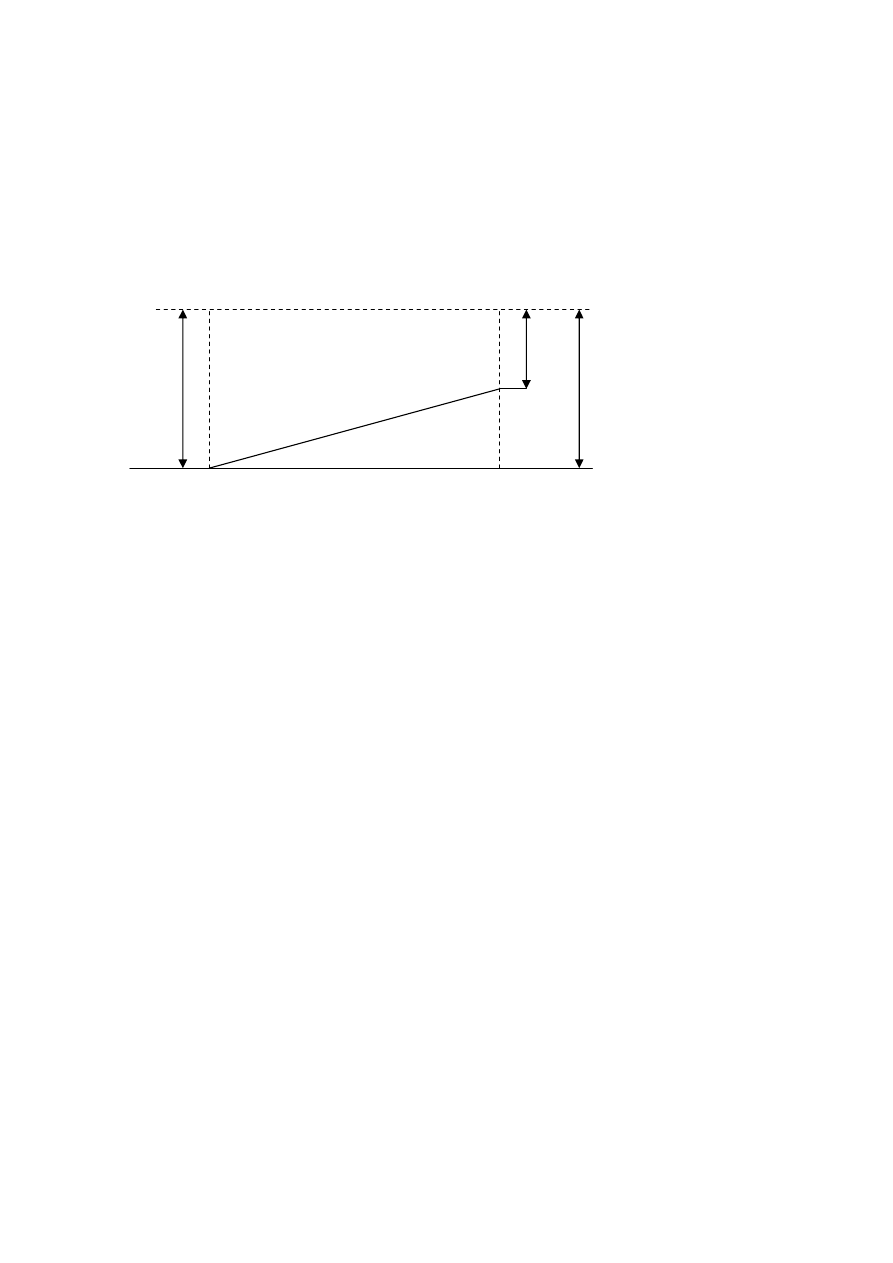
Ad.1.a/ niwelacja trygonometryczna.
B
l
h
α
A
l'
Metod
ę
t
ę
stosuje si
ę
dla punktów znacznie oddalonych od siebie i o du
ż
ej
ró
ż
nicy wysoko
ś
ci.
Mierzy my długo
ść
odcinka l (AB) lub odległo
ść
poziom
ą
l' oraz k
ą
t nachylenia
prostej l (AB). H wyznaczamy z równania:
1. sin
α
= h/ l lub 2. tg
α
= h/ l' ,
St
ą
d: h = l sin
α
lub h = l' tg
α
,
Czyli: h = l sin
α
= l' tg
α
.
37
Ad.1.b/ niwelacja geometryczna.
Stosuje si
ę
j
ą
przy małych ró
ż
nicach wysoko
ś
ci punktów.
Jest to pomiar bezpo
ś
redni odległo
ś
ci punktów od A i B od dowolnej
płaszczyzny lub linii poziomej.
Niwelacj
ę
geometryczn
ą
wykonuje si
ę
przy pomocy niwelatorów.
Zasada: poziom (linia pozioma) np. poziom zr
ę
bu.
h
B
h
A
h = h
A
– h
B
A
h = h
A
– h
B
Ad.1.c/ niwelacja barometryczna.
Korzystamy z ró
ż
nicy ci
ś
nie
ń
, tj.
Wykonujemy jednocze
ś
nie pomiary ci
ś
nienia nad punkami A i B barometrem.
Ci
ś
nienie powietrza zmniejsza si
ę
na wy
ż
szych wysoko
ś
ciach.
Spadek ci
ś
nienia o 1mm to około 11m ró
ż
nicy wysoko
ś
ci punktów A i B.
2/ Scharakteryzowa
ć
i opisa
ć
budow
ę
niwelatorów i łat niwelacyjnych.
2.1/ Budowa niwelatorów.
Niwelator składa si
ę
z: spodarki, alidady, lunety i libelli rurkowej.
Spodarka – trójramienna podstawa ze
ś
rubami nastawczymi i czopem,
w którym obraca si
ę
alidada,
Alidada - składa si
ę
z tulei i urz
ą
dzenia do zamocowania lunety,
Luneta - mo
ż
e by
ć
przymocowana bezpo
ś
rednio do alidady lub spoczywa
na d
ź
wigarkach.
Wysoko
ść
jednego d
ź
wigarka zmienia si
ę
ś
rub
ą
elewacyjn
ą
,
czyli o
ś
lunety mo
ż
e przesuwa
ć
si
ę
w pionie.
Libella pudełkowa – słu
ż
y do przybli
ż
onego poziomowania przyrz
ą
du,
umieszczona jest na alidadzie lub na spodarce.
Libella rurkowa – zł
ą
czona jest z lunet
ą
. Słu
ż
y do dokładnego ustawienia osi
celowej lunety w płaszczy
ź
nie poziomej.
Niwelatory u
ż
ywane w górnictwie s
ą
nast
ę
puj
ą
ce:
- z libell
ą
poł
ą
czon
ą
na stałe z lunet
ą
, która sztywno jest poł
ą
czona z alidad
ą
,
- niwelatory ze
ś
rub
ą
elewacyjn
ą
(mo
ż
na przesuwa
ć
w pionie osi lunety),
- z lunet
ą
obracaln
ą
wraz z libell
ą
dookoła osi geometrycznej lunety.
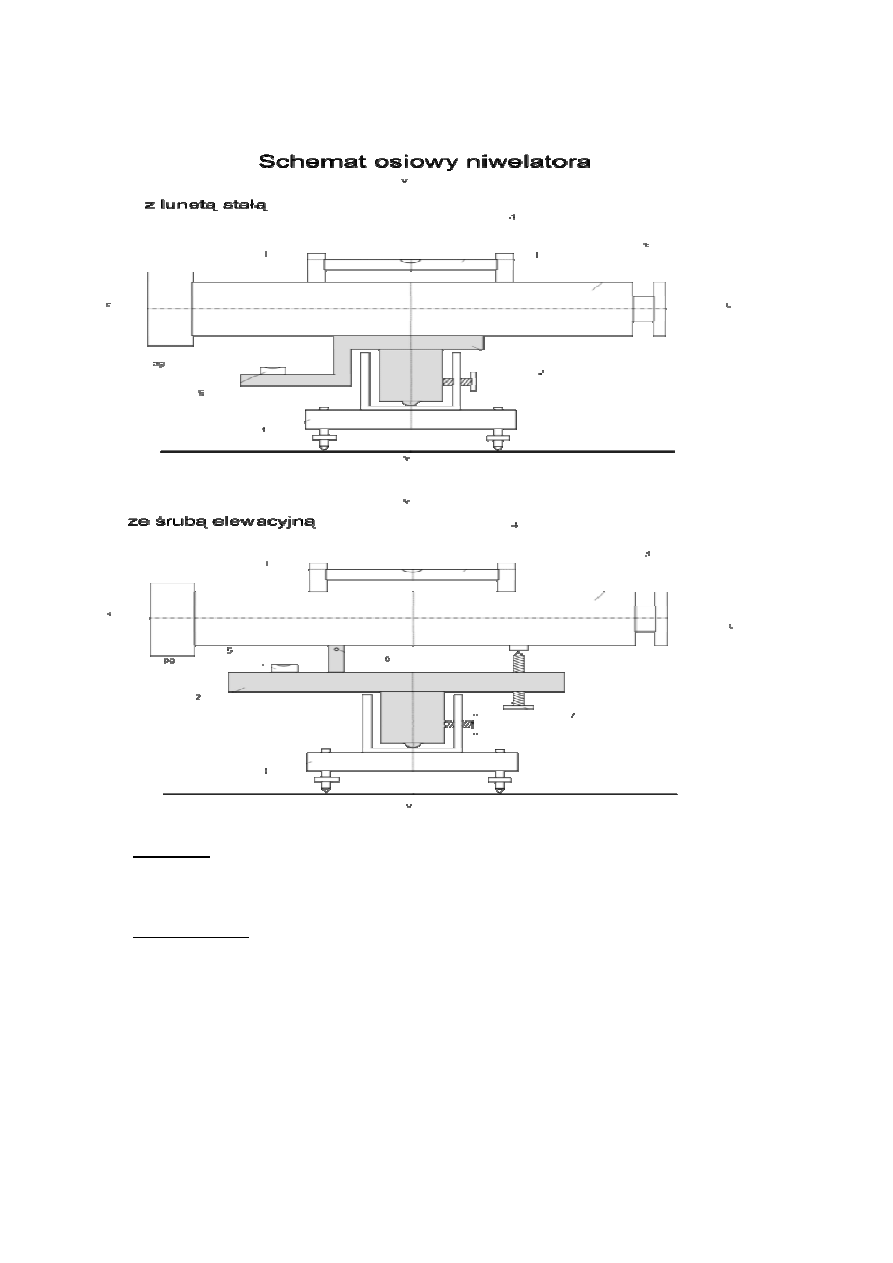
38
Schemat osiowy niwelatora z lunet
ą
stał
ą
i ze
ś
rub
ą
elewacyjn
ą
.
1 – spodarka
2 – alidada
3 – luneta geodezyjna
4 – libella niwelacyjna
5 – libella okr
ą
gła
6 – pozioma o
ś
obrotu zespołu luneta-libella niwelacyjna
7 –
ś
ruba elewacyjna
cc – o
ś
celowa lunety
vv – pionowa o
ś
główna instrumentu (o
ś
obrotu alidady)
ll – o
ś
libelli niwelacyjnej
pg – płaszczyzna główna libelli okr
ą
głej
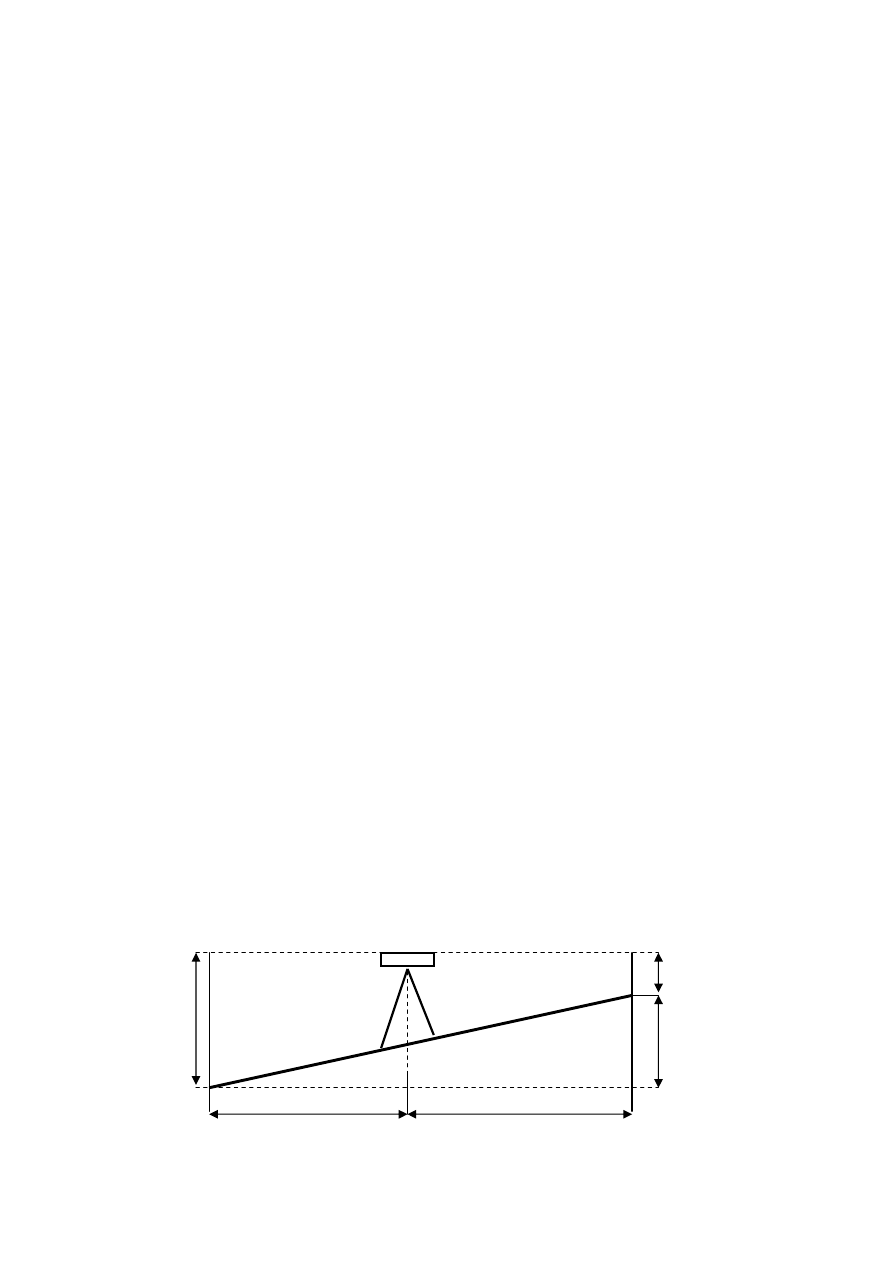
39
Najwa
ż
niejsza to luneta.
Budowa: dwie soczewki, obiektyw, okular.
Soczewki – rodzaje - obustronnie wypukłe:
- płasko wypukłe, wkl
ę
sło wypukłe, obustronnie wkl
ę
słe, płasko wkl
ę
słe,
wypukło wkl
ę
słe.
Do dokładnych pomiarów w kopalni u
ż
ywa si
ę
niwelatorów z 20 ÷ 30 krotnym
powi
ę
kszeniem lunety.
Niwelator ustawiamy na statywie i mocujemy go. Nast
ę
pnie poziomujemy.
Poziomowanie:
- obraca si
ę
instrument z libell
ą
do poło
ż
enia równoległego do 2- ch
ś
rub
nastawczych,
-
ś
rubami doprowadza si
ę
p
ę
cherzyk libelli do górowania,
- obracamy lunet
ę
o k
ą
t 90
o
i trzeci
ą
ś
rub
ą
poziomujemy libell
ę
,
- w obu poło
ż
eniach ba
ń
ka musi zaj
ąć
poło
ż
enie
ś
rodkowe,
- po spoziomowaniu dokr
ę
ca si
ę
nakr
ę
tk
ę
dociskaj
ą
c
ą
spr
ęż
yn
ę
.
S
ą
te
ż
niwelatory ustawiane na ramieniu – przy pomocy przegubu (górnicze).
2.2/ Łaty niwelacyjne – to podziałki słu
żą
ce do wyznaczania ró
ż
nic wysoko
ś
ci.
Na powierzchni u
ż
ywa si
ę
łat drewnianych 3, 4, 5m oraz 3m inwarowych.
Łaty górnicze maj
ą
długo
ść
1,2 do 1,6m i s
ą
drewniane lub z tworzywa.
Maj
ą
podział na centymetry – pola podziału s
ą
pomalowane na przemian na
czarny i czerwony kolor.
Podział jest opisany w odst
ę
pach decymetrowych cyframi odwróconymi,
bo luneta daje obraz odwrócony.
Milimetry si
ę
szacuje.
Przy pomiarze łaty ustawia si
ę
na podstawkach – „
ż
abkach”.
Rodzaje łat: stała długo
ść
, wysuwne, podwieszane na haczyku w łacie.
3/ Wymieni
ć
rodzaje ci
ą
gów niwelacyjnych.
Punkty o okre
ś
lonej wysoko
ś
ci za pomoc
ą
niwelacji to punkty niwelacyjne
(wysoko
ś
ciowe). Nawi
ą
zuje si
ę
je do punktów pa
ń
stwowych (tzw. punktów
niwelacji
ś
cisłej). Punkty, które maj
ą
słu
ż
y
ć
nam dłu
ż
ej stabilizuje si
ę
- s
ą
to repery. S
ą
to stalowe trzpienie osadzane w betonie.
Ci
ą
gi niwelacyjne:
a/ ze
ś
rodka – polega na pomiarze nachylenia odcinka w
ś
rodku:
P
B
W h
A
d
d
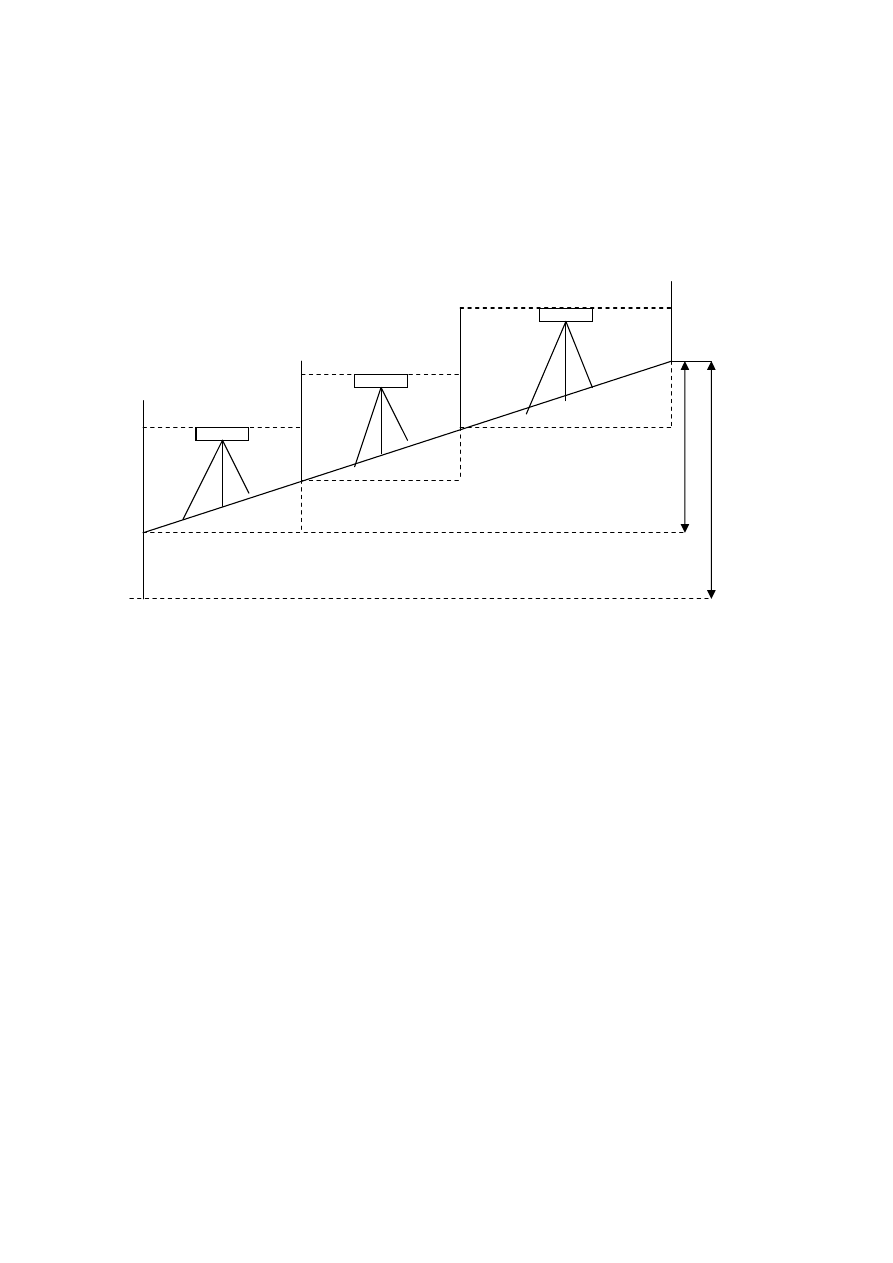
40
Jest stosowana do okre
ś
lenia ró
ż
nicy wysoko
ś
ci dwóch punktów A i B.
Wykonuje pomiary: wstecz i przód. H oblicza si
ę
ze wzoru:
h = w – p
Przy wi
ę
kszych odległo
ś
ciach i niemo
ż
liwo
ś
ci pomiaru punku ko
ń
cowego
dzielimy odcinek kilka odcinków dokonuj
ą
c pomiary podobnie.
B
A
- poziom punktu A
- poziom morza
W zale
ż
no
ś
ci od tego czy punkt pocz
ą
tkowy obierzemy A czy B to teren: mo
ż
e
by
ć
po wzniosie lub po upadzie.
4/ Zna
ć
zasady sporz
ą
dzania profili podłu
ż
nych i poprzecznych oraz map
warstwicowych.
5/ Wymieni
ć
zastosowanie kompasu górniczego i geologicznego do
pomiarów w kopalni.
6/ Omówi
ć
mo
ż
liwo
ś
ci zdj
ę
cia warstw geologicznych przy u
ż
yciu kompasu
górniczego.
7/ Umie
ć
zinterpretowa
ć
wykres łupno
ś
ci skał.
WYMAGANIA PONADPODSTAWOWE
1/ Umie
ć
przygotowa
ć
niwelator do pomiaru.
2/ Na wybranych przykładach wyja
ś
ni
ć
niwelacj
ę
w kopalni.
3/ Przedstawi
ć
sposób pomiaru gł
ę
boko
ś
ci szybu.
4/ Umie
ć
wykona
ć
projekt profilu podłu
ż
nego i poprzecznego sp
ą
gu
chodnika.
5/ Zna
ć
sposób wypełniania dziennika niwelacji.
6/ Obja
ś
ni
ć
sposoby pomiarów elementów geologicznych z odsłoni
ę
tych

41
warstw w wyrobiskach górniczych./grubo
ść
, nachylenie, rozci
ą
gło
ść
/.
7/ Zna
ć
sposób graficznego wyznaczania elementów uskoku.
8/ Umie
ć
wykona
ć
wykres łupnosci skał.
15. OBLICZANIA POWIERZCHNI I ORIENTACJA KOPALN.
WYMAGANIA PODSTAWOWE
1/ Wymieni
ć
sposoby pomiarów powierzchni.
2/ Obja
ś
ni
ć
stosowane metody obliczania powierzchni z pomiarów
wykonanych w terenie i na mapie.
3/ Budowa i zasada obliczania powierzchni planimetrem biegunowym.
4/ Omówi
ć
cele pomiarów orientacyjnych w kopalni i wymieni
ć
stosowane
metody.
WYMAGANIA PONADPODSTAWOWE
1/ Obja
ś
ni
ć
zasad
ę
obliczania powierzchni ze współrz
ę
dnych.
2/ Scharakteryzowa
ć
mechaniczny sposób przeniesienia kierunku
i współrz
ę
dnych z powierzchni do kopalni.
3/ Zna
ć
optyczne metody pomiarów orientacyjnych.
16. WYZNACZANIE KIERUNKÓW, TYCZENIE ŁUKÓW I POMIARY GEODEZYJNE
ROBÓT PRZEBITKOWYCH.
WYMAGANIA PODSTAWOWE
1/ Scharakteryzowa
ć
kierunki pionowe i poziome wyrobisk.
2/ Wymieni
ć
czynno
ś
ci w biurze geodezyjnym i w kopalni w celu nadania
kierunków i spadków dla wyrobisk za pomoc
ą
teodolitu.
3/ Wymieni
ć
rodzaje robót przebitkowych w kopalni.
Rodzaje przebitek: pionowe, poziome, przebicie pochylni.
PIONOWA – zadaniem jest aby współrz
ę
dne x,y
Szyb I
Szyb II
punktów M i P (osi szybu) musz
ą
by
ć
identyczne
Dokładno
ść
zbicia zale
ż
y od prawidłowego P
wyznaczenia współrz
ę
dnych x i y
punktu M.
M
POZIOMA – aby poł
ą
czy
ć
na zbicie przekopy (przecznice) ustalamy
współrz
ę
dne punktów A i B le
żą
cych na osi wyrobiska oraz
wyznaczy
ć
kierunek prostej AB.
NALE
ś
Y wykona
ć
:
1/ pomiary (poligonowe lub trygonometryczne) na powierzchni,
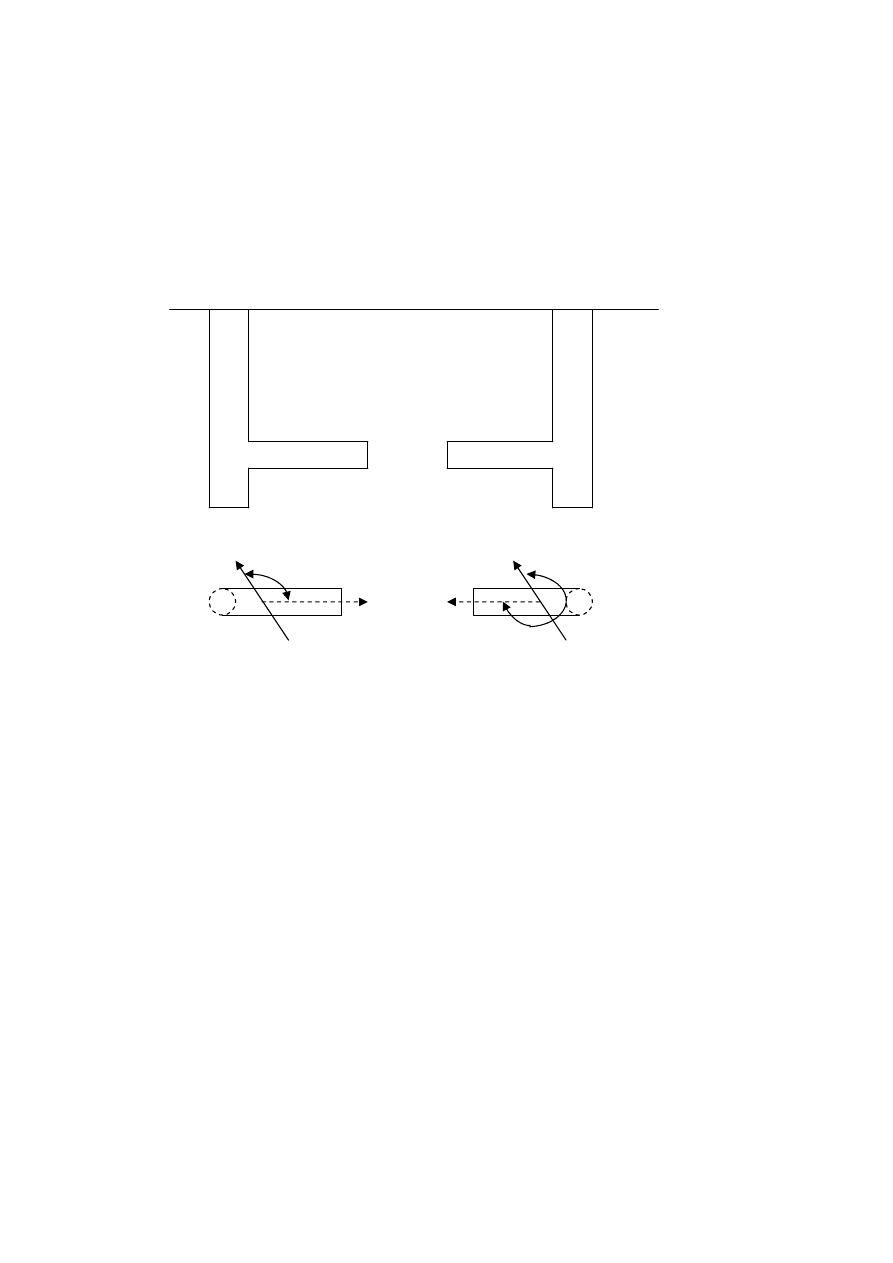
42
okre
ś
laj
ą
c x,y punktów zawieszenia pionów w szybach,
2/ pomiary orientacyjne w obu szybach,
3/ poligonizacj
ę
w kopalni dla okre
ś
lenia współrz
ę
dnych punktów A i B,
4/ pomiar gł
ę
boko
ś
ci szybów,
5/ niwelacj
ę
w kopalni aby okre
ś
li
ć
wysoko
ść
punktów A i B.
Po tych pomiarach nadaje si
ę
kierunki dla obu odcinków i wyznacza nachylenie.
- szyb I
- szyb II
- przecznica
A
B
Pn Pn
ω
AB
I II
Prowadzenie na zbicie chodnika w pokładzie:
Je
ż
eli punkty A i B poł
ą
czymy przez inne wyrobiska ci
ą
giem poligonowym to nie
trzeba robi
ć
pomiarów orientacyjnych.
Wówczas:
1/ wyznaczamy punkty A i B na wysoko
ś
ci projektowanego poziomu pomiarami
niwelacyjnymi,
2/ okre
ś
lamy współrz
ę
dne punktu A i B przez nawi
ą
zanie ich do sieci
poligonowej,
3/ okre
ś
lamy azymuty prostej ł
ą
cz
ą
cej punkty A i B,
WYMAGANIA PONADPODSTAWOWE
1/ Okre
ś
li
ć
zasady projektowania łuków w kopalni.
ŁUKI – aby prowadzi
ć
transport kołowy w kopalni (materiału, urobku, ludzi)
przy zmianach kierunku wyrobiska prowadzi si
ę
po łuku stosuj
ą
c łuki
(o jednym promieniu) – kołowe.
Torowiska te musz
ą
mie
ć
odpowiedni
ą
krzywizn
ę
.
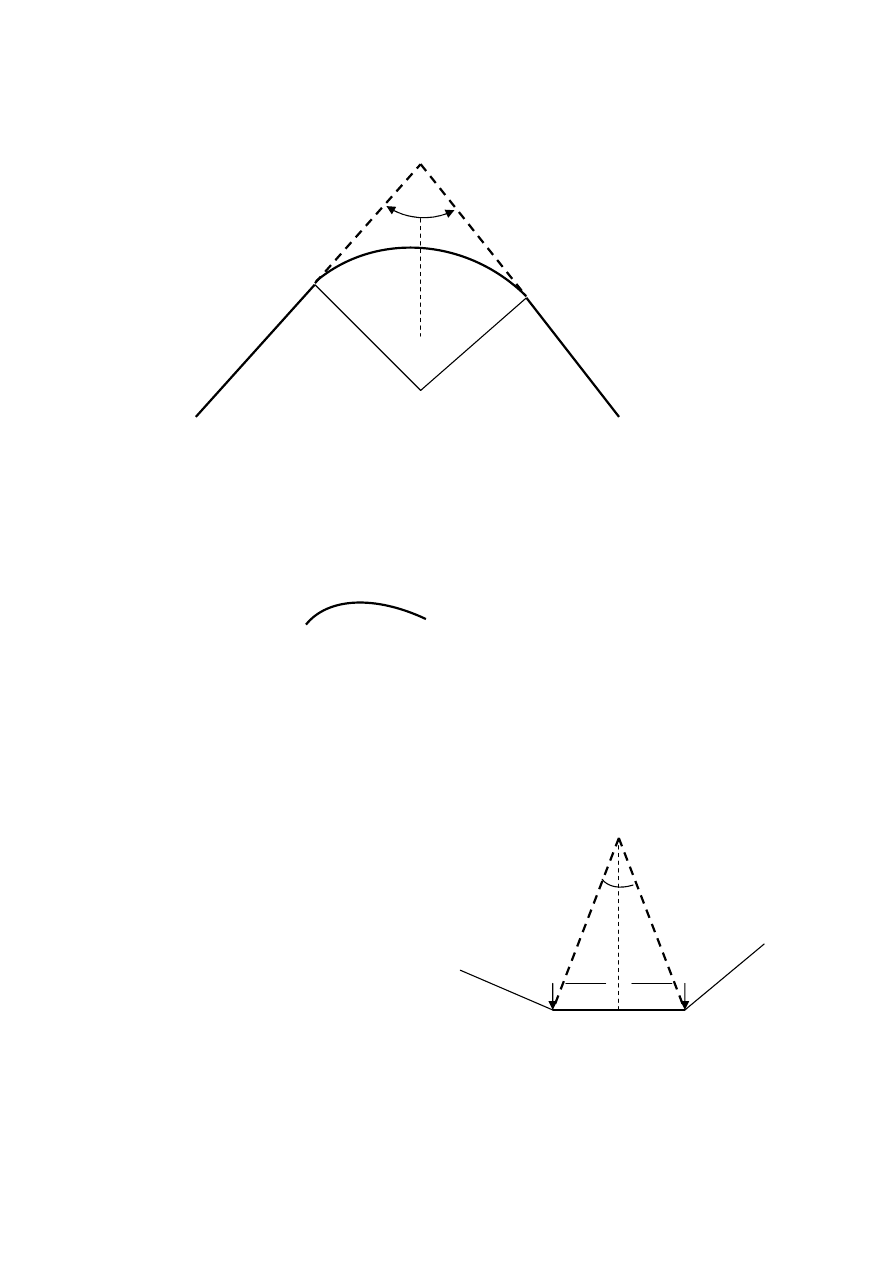
43
W
α
A
B
r r
90st
90st
180 -
α
O
A, B – punkty główne (pocz
ą
tkowy i ko
ń
cowy),
W – wierzchołek łuku,
OW = r/sin(
α
/2),
AW = r ctg(
α
/2).
Gdy łukiem o promieniu “r” nie da si
ę
przej
ść
od stycznej do stycznej, np. dla
łuku jak poni
ż
ej:
to stosuje si
ę
tzw. łuki koszowe – składaj
ą
ce si
ę
kilku łuków o ró
ż
nych
promieniach: r1, r2, r3…..
2/ Umie
ć
wykona
ć
projekt łuku kołowego w chodniku.
Projekt łuku:
- szkic w skali 1:100, 1:200,
- dzielimy łuk mi
ę
dzy punktem pocz
ą
tkowym i ko
ń
cowym na równe cz
ęś
ci,
- ł
ą
cz
ą
c punkty otrzymujemy poligon (wielobok)
wewn
ą
trz wyrobiska kołowego,
- z długo
ś
ci ci
ę
ciw oraz promienia krzywizny
oblicza si
ę
k
ą
ty załamania poligonu,
- k
ą
t
ś
rodkowy
β
oblicza si
ę
ze wzoru: r k
ą
t
β
sin(
β
/2) = S/(2r),
K
ą
t załamania poligonu wynosi (180 – (
β
/2).
polgon
A
S B
3/ Umie
ć
omówi
ć
rodzaje prac geodezyjnych przy prowadzeniu robót
przebitkowych
.
17. MAPY GÓRNICZE.

44
WYMAGANIA PODSTAWOWE
1/ Omówi
ć
znaczenie map górniczych dla racjonalnej gospodarki zło
ż
em.
2/ Zna
ć
podział map górniczych ich tematyk
ę
i charakterystyk
ę
.
3/ Obja
ś
ni
ć
proces tworzenia map górniczych i sposoby ich reprodukcji.
4/ Omówi
ć
metody powi
ę
kszania i pomniejszania map górniczych.
5/ Zna
ć
zasady przechowywania i ochrony map.
WYMAGANIA PONADPODSTAWOWE
1/ Umie
ć
rozpoznawa
ć
znaki umowne na mapach górniczych i czyta
ć
ich
tre
ś
ci.
2/ Zna
ć
przepisy dotyczace sporz
ą
dzania i uzupełniania map zgodnie z
obowi
ą
zuj
ą
cymi normami.
3/ Zna
ć
normy dotyczace doboru skali dla ró
ż
nych map.
4/ Umie
ć
zinterpretowa
ć
struktur
ę
przestrzenn
ą
kopalni na podstawie mapy
górniczej.
5/ Omówi
ć
nowe kierunki w sposobie opracowania i kartowania map
.
18. POMIARY WPŁYWÓW EKSPLOATACJI PODZIEMNEJ NA GÓROTWÓR I
POWIERZCHNIE, ZASADY WYZNACZANIA FILARÓW POMIARY ZWAŁÓW.
WYMAGANIA PODSTAWOWE
1/ Scharakteryzowa
ć
ogólnie wpływy eksploatacji górniczej na górotwór
i powierzchni
ę
.
2/ Zna
ć
sposoby ustalania wielko
ś
ci wpływów i stopnia uszkodze
ń
obiektów.
3/ Scharakteryzowa
ć
sposoby zabezpieczania obiektów przed skutkami
eksploatacji górniczej.
- wyznaczanie filarów ochronnych,
- wybieranie z podsadzk
ą
such
ą
+ doszczelnienie np. pyłami dymnicowymi
z cementem - bez zer podsadzkowych,
- stosowanie podsadzki hydraulicznej w pod wa
ż
nymi obiektami,
- stosowanie współczesnych technologii budowania obiektów.

45
4/ Zna
ć
zasady wyznaczania filarów ochronnych i oporowych.
Filar ochronny – chroni obiekty na powierzchni,
Filar oporowy - chroni wyrobiska górnicze.
4.1/ Filar ochronny – wyznacza si
ę
przy pomocy k
ą
ta wpływów
ψ
w zale
ż
no
ś
ci od wa
ż
no
ś
ci kategorii obiektu.
Kategoria K
ą
t wpływów
I
ψ
= 54 stopni
II
ψ
= 58 stopni
III
ψ
= 62 stopni
IV
ψ
= 66 stopni
Przy pokładach nachylonych do 10 stopni.
Do gł
ę
boko
ś
ci 180m wyznacza si
ę
pas ochronny wokół obiektu o szeroko
ś
ci
30m.
Przy pokładach zalegaj
ą
cych poni
ż
ej 180m filar wykre
ś
la si
ę
od granic obiektu.
Przy pokładach nachylonych powy
ż
ej 10 stopni.
Wyznacza si
ę
filar tak jak dla pokładów do 10 stopni a pó
ź
niej przesuwa si
ę
w
kierunku wzniosu pokładu:
P = H – tg(k
α
)
Gdzie:
H – mi
ąż
szo
ść
(grubo
ść
) pokładu,
k = 0,7 współczynnik ,
α
- k
ą
t nachylenia pokładu.
4.2/ Filar oporowy.
Szeroko
ść
filara wyznacza si
ę
ze wzoru:
S =2S
1
+ 2a , gdzie S
1
= H( 2,5 + 0,6g ) / f
H – gł
ę
boko
ść
wybierania,
f – współczynnik urabialno
ś
ci,
g – grubo
ść
pokładu,
2a – szeroko
ść
chronionego wyrobiska.
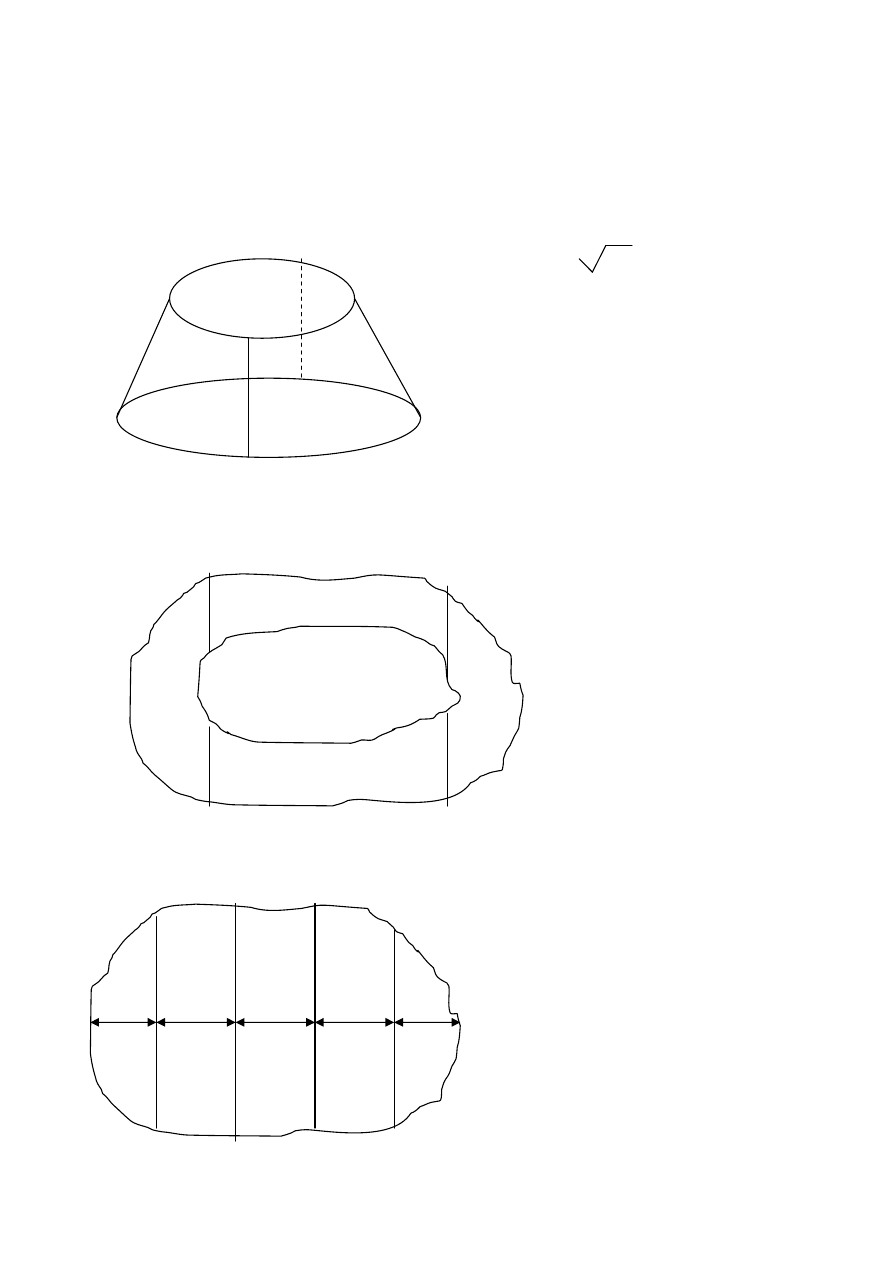
46
5/ Umie
ć
obliczy
ć
obj
ę
to
ś
ci zwałów metoda podziału na figury
geometryczne.
Metoda ta polega na podziale zwału na figury geometryczne:
- gdy zwał ma kształt ostrosłupa
ś
ci
ę
tego równolegle do podstawy liczymy
nast
ę
puj
ą
co:
V = h (b +B + b B )/ 3
b
h – wysoko
ść
zwału,
b, B – powierzchnie podstaw.
Pomiary powierzchni b i B wykonujemy planimetrem.
B
- inny sposób to podział zwału na pi
ęć
cz
ęś
ci
(stosujemy go gdy s
ą
bardzo wydłu
ż
one skarpy boczne C1 i C2).
Bryłę A – liczymy jak graniastosłup.
Skarpy boczne B1 i B2 jak
graniastosłupy o podstawie trójkąta.
B1
Skarpy czołowe C1 i C2 jak ostrosłupy.
A
h - stale
C1 C2
B2
- mo
ż
emy te
ż
stosowa
ć
metod
ę
przekrojów o poziomych równych
odległo
ś
ciach.
L
L
L
L
L
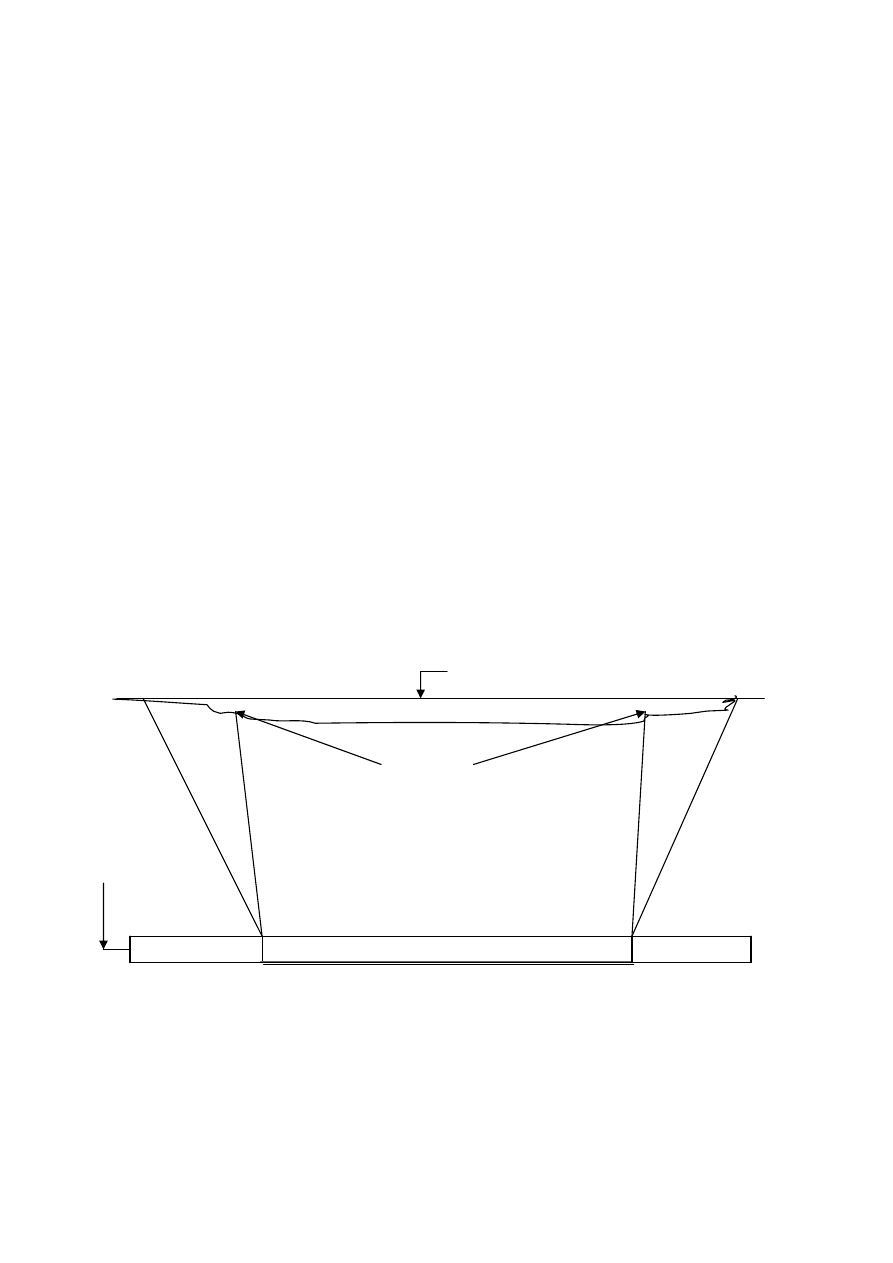
47
WYMAGANIA PONADPODSTAWOWE
1/ Umie
ć
scharakteryzowa
ć
geodezyjne metody pomiaru deformacji oraz
sposoby ustalania kryteriów stopnia zagro
ż
enia powierzchni.
Pomiary te przeprowadza si
ę
na powierzchni i na dole:
a/ na powierzchni :
- ustala si
ę
sie
ć
trwałych punktów rozmieszczonych poza wpływami,
- przeprowadza si
ę
na nich okresowe pomiary,
- przemieszczanie w pionie mierzy si
ę
niwelacj
ą
geometryczn
ą
,
- przemieszczanie w poziomie mierzymy przez pomiar odległo
ś
ci punktów,
- za pomoc
ą
pomiarów k
ą
tów okre
ś
lamy przestrzenne przesuni
ę
cie
punktów pomiarowych,
b/ na dole pomiary si
ę
nie ró
ż
ni
ą
.
Punkty pomiarowe zakłada si
ę
w sp
ą
gu lub stropie wyrobisk.
2/ Wykona
ć
i zinterpretowa
ć
szkic niecki osiadania.
Wielko
ść
osiadania zale
ż
y od grubo
ś
ci pokładu, gł
ę
boko
ś
ci wydobycia i rodzaju
skał nadkładu, k
ą
ta nachylenia.
przed eksploatacj
ą
obni
ż
enie
obni
ż
enie
zawalisko
grubo
ść
pokładu
.
pokład
Przestrze
ń
wybrana
pokład
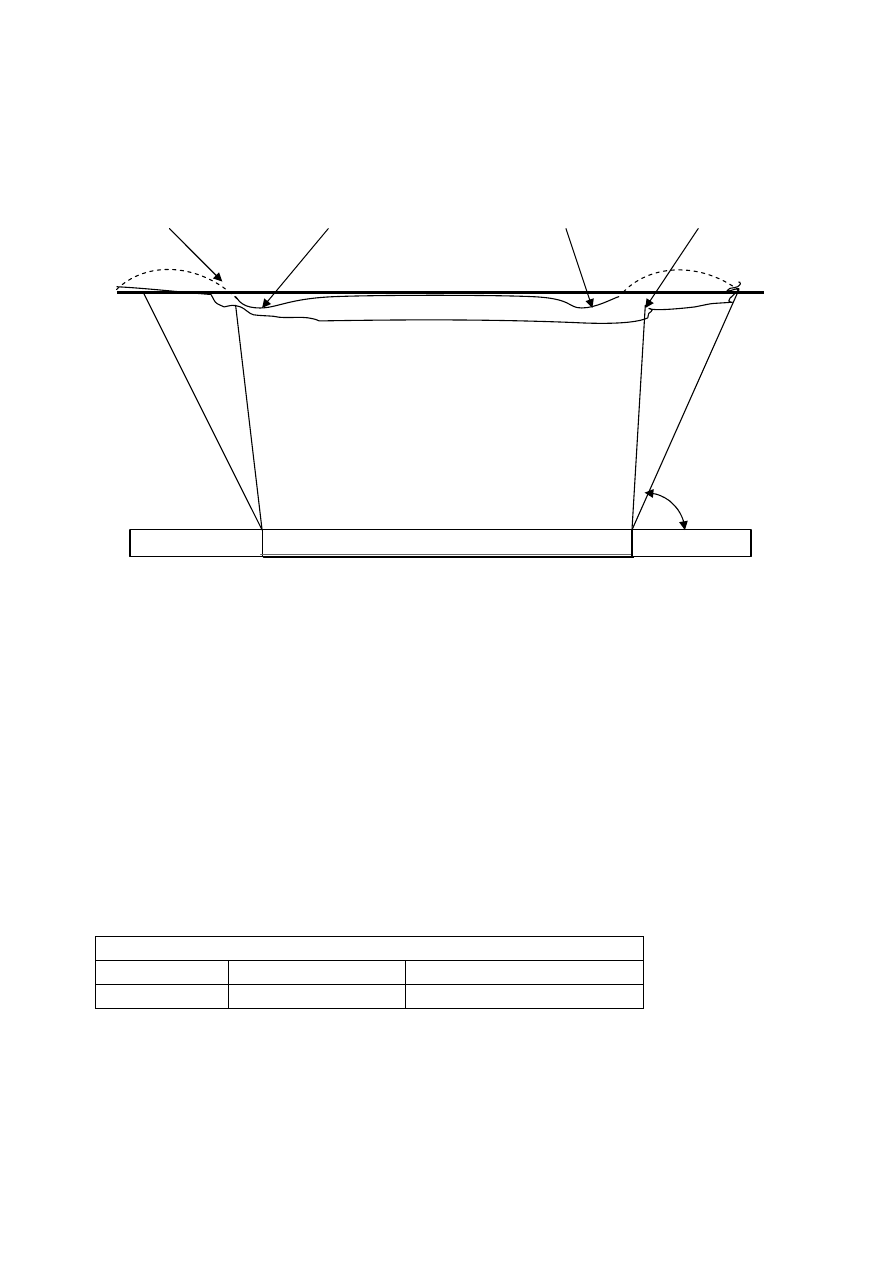
48
Niecka osiadania przy małych gł
ę
boko
ś
ciach wybierania.
rozrywanie
ś
ciskanie
ś
ciskanie rozrywanie
K
ą
t wpływów
pokład
Przestrze
ń
wybrana
pokład
3/ Umie
ć
obliczy
ć
wska
ź
niki odkształce
ń
powierzchni i klasyfikowa
ć
obiekty
w zale
ż
no
ś
ci od wa
ż
no
ś
ci i wra
ż
liwo
ś
ci na odkształcenia.
Dopuszczalne odkształcenia powierzchni oblicza si
ę
ze wzoru:
ε
= 1500W
max
/ H
Gdzie:
ε
– dopuszczane odkształcenia powierzchni,
H – gł
ę
boko
ść
eksploatacji,
W
max
= a g – maksymalne obni
ż
enie powierzchni, gdzie:
g – grubo
ść
pokładu,
a – współczynnik osiadania (zale
ż
y od sposobu prowadzenia stropu).
Warto
ść
współczynnika a
Zawał stropu Podsadzka sucha Podsadzka hydrauliczna
a = 0,7
a = 0,5
a = 0,02 ÷ 0,03
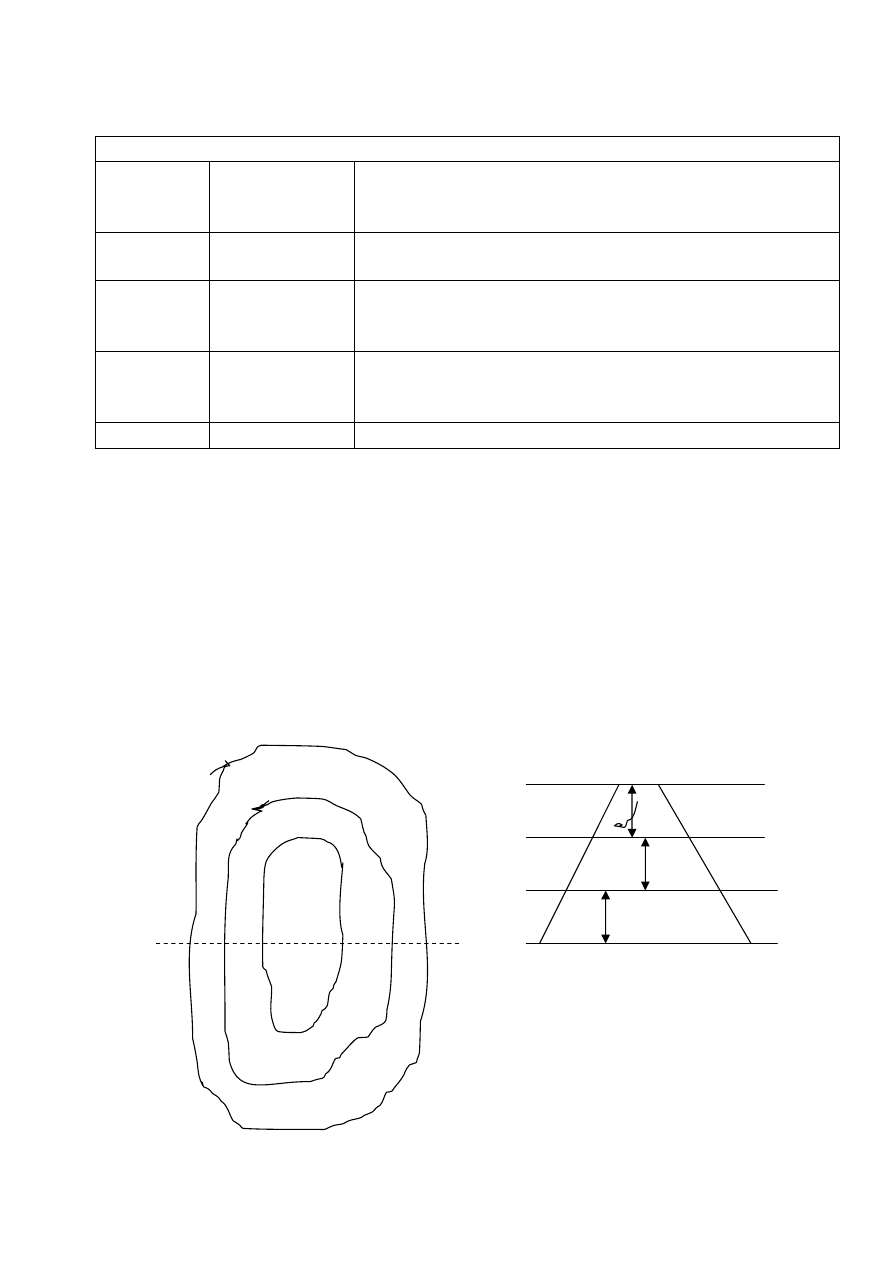
49
Dopuszczalne odkształcenia poziome w zale
ż
no
ś
ci od rodzajów obiektów
Kategoria
ochrony.
Dopuszczalne
odkształcenie
poziome.
Rodzaj obiektów
I
ε
≤
1,5mm
Główne gazoci
ą
gi, zbiorniki wodne, wa
ż
ne obiekty
przemysłowe, zabytki.
II
ε
≤
3mm
Piece hutnicze, koksownie, maszyny wyci
ą
gowe,
suwnice, obiekty publiczne, rzeki, zbiorniki wodne,
główne szlaki kolejowe, główna sie
ć
wodoci
ą
gów.
III
ε
≤
6mm
Drogi, szlaki kolejowe, kominy wysokie, ko
ś
cioły,
lotniska, ruroci
ą
gi, mniej podatne obiekty
przemysłowe.
IV
ε
≤
9mm
Stadiony, budynki do 10m, mniej wa
ż
ne obiekty.
4/ Umie
ć
obliczy
ć
obj
ę
to
ść
zwałów metoda izolinii.
Metod
ę
izolinii stosuje si
ę
do obliczania obj
ę
to
ś
ci du
ż
ych zwałów o łagodnie
nachylonych zboczach. Podstaw
ą
obliczenia jest mapa izolinii grubo
ś
ci
zwału, wykre
ś
lona na podstawie pomiarów sytuacyjno wysoko
ś
ciowych.
Metoda polega na podzieleniu sto
ż
ka na cz
ęś
ci o równej grubo
ś
ci np. co 1m.
Czyli rozcinamy zwał płaszczyznami poziomymi o grubo
ś
ci ustalonej.
Płaszczyzny te musz
ą
tworzy
ć
warstwice – punkty jednakowej wysoko
ś
ci.
3m
h3
2m
h2
1m
A
A
h1
0m
f2
f1
fo

50
Na postawie rz
ę
dnych podło
ż
a i powierzchni lub przekrojach zwału okre
ś
la si
ę
jego grubo
ść
w poszczególnych punktach.
Nast
ę
pnie kre
ś
limy izolinie grubo
ś
ci zwału.
Przybli
ż
on
ą
obj
ę
to
ść
segmentów liczymy ze wzoru na powierzchni
ę
trapezu.
Np. segmentu V1 = [(fo +f1)/2] h1,
Czyli w naszym przypadku całkowita obj
ę
to
ść
zwału to:
Vc = V1+ V2+ V3 = [(fo +f1)/2] h1+ [(f1 +f2)/2] h1+ [(f2 +f3)/2] h1,
Skoro: h1= h2= h3= h to:
Vc = h (fo/2 + f1+ f2 + f3/2).
Maj
ą
c obj
ę
to
ść
oraz z pobranych próbek ci
ęż
ar obj
ę
to
ś
ciowy lub nasypowy
γγγγ
wyra
ż
any w [t/m
3
] mo
ż
emy obliczy
ć
ci
ęż
ar ilo
ść
w
ę
gla na zwałach ze wzoru:
Q = V
γ
[t].
Podziałka.
Wyszukiwarka
Podobne podstrony:
kolo z miernictwa id 240039 Nieznany
miernictwo 5 id 299485 Nieznany
oznaczenia miernikow id 343361 Nieznany
miernictwo 7 id 299488 Nieznany
lab4 miernictwo id 259817 Nieznany
Miernictwo2Lab2013 id 299818 Nieznany
Miernik cewek id 299848 Nieznany
miernictwo1 wyklad 3 id 776866 Nieznany
Miernictwo 08 Oscyloskopy id 29 Nieznany
miernik tetna id 299924 Nieznany
miernik va6512 a4 cndA id 29992 Nieznany
miernictwo1 teoria bledow id 77 Nieznany
miernictwo1 niepewnosci id 7768 Nieznany
Miernik cewek id 299848 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
więcej podobnych podstron