Kwadratury Gaussa

Definicja całki w sensie Riemanna [1]:

Niech f będzie funkcja określoną i ograniczona na odcinku [a,b]. Całką oznaczoną funkcji f

na [a,b],

∫

b

a

dx

x

f

)

(

, nazywamy granicę sum:

(

)

∑

=

+

−

=

n

i

i

i

i

n

x

f

x

x

S

0

1

)

~

(

, gdzie a=x

0

<x

1

<…<x

n+1

=b jest dowolnym podziałem odcinka [a,b]

takim, że

0

max

1

0



 →



−

∞

→

+

≤

≤

n

i

i

n

i

x

x

, a

[

]

1

,

~

+

∈

i

i

i

x

x

x

są dowolnymi punktami pośrednimi.

Obliczenie wartości całek w sposób analityczny jest możliwy tylko dla niewielkiej klasy

funkcji. Dla zdecydowanej większości funkcji obliczenia te są zbyt skomplikowane i tutaj

znajdują zastosowanie kwadratury. Kwadratury służą do numerycznego (przybliżonego)

obliczania wartości całek. Najczęściej stosowane są kwadratury wykorzystujące jedynie

wartość funkcji f, są one postaci:

∑

∫

=

=

≈

n

i

i

i

b

a

x

f

A

f

Q

dx

x

f

0

)

(

)

(

)

(

.

Definicja rzędu kwadratury [1]:

Mówimy, że

kwadratura Q jest rzędu n, jeśli jest dokładna dla wszystkich wielomianów

stopnia mniejszego od n,

( )

∫

=

b

a

dx

x

w

w

Q

)

(

dla

1

−

∈

n

W

w

oraz istnieje wielomian w

n

stopnia n,

dla którego

( )

∫

≠

b

a

n

n

dx

x

w

w

Q

)

(

.

Kwadratury Gaussa przy ustalonej liczbie węzłów mają najwyższy rząd [1].

Wartość

( )

∫

−

=

b

a

dx

x

f

f

Q

f

R

)

(

)

(

nazywamy

resztą kwadratury.

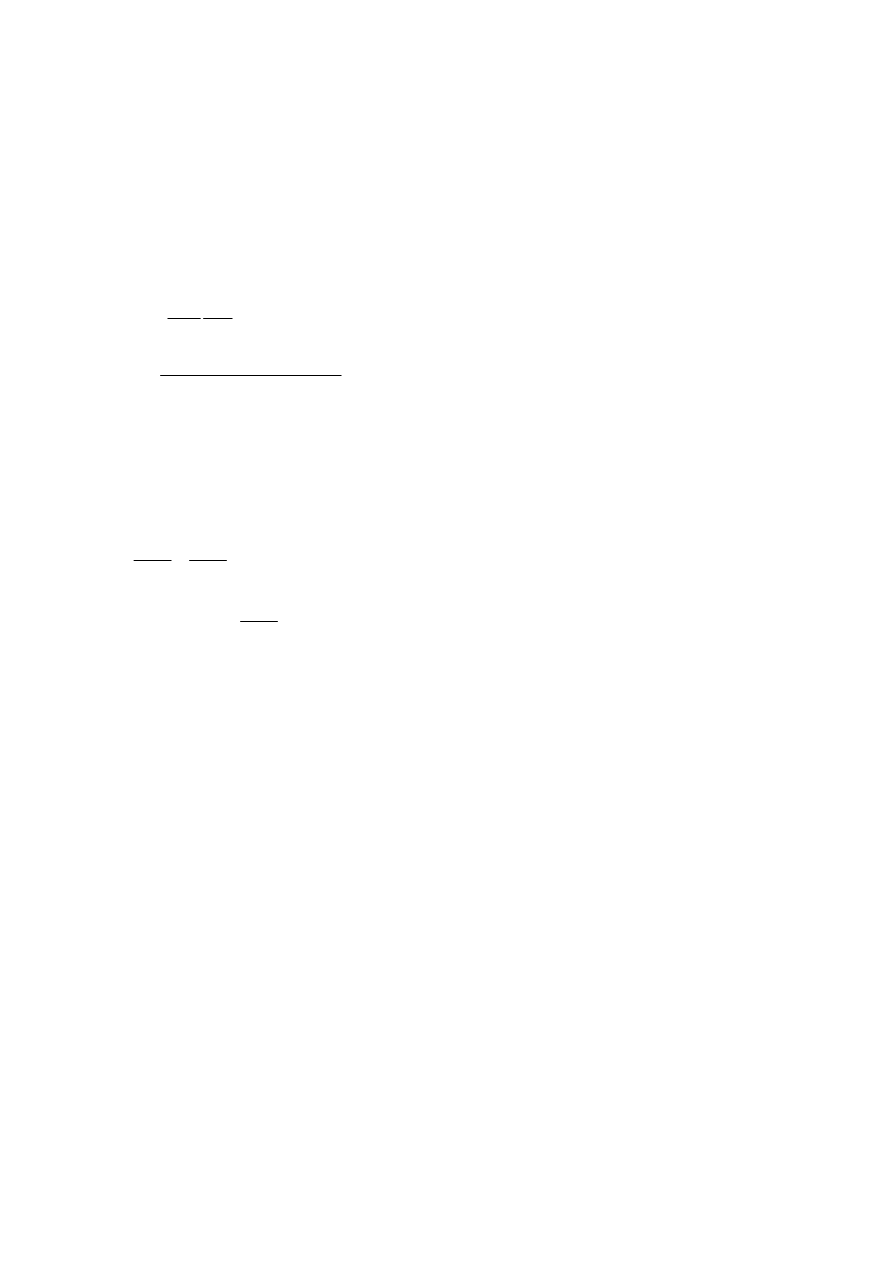
Kwadratury Gaussa to kwadratury postaci:

∑

=

=

N

k

k

k

x

f

A

f

S

0

)

(

)

(

, gdzie węzły

x

k

i

współczynniki

A

k

są dobrane w taki sposób, by rząd kwadratury był jak najwyższy (

2n+2).

Kwadratury Gaussa-Legendre’a:

[a,b]=[-1,1]

(

)

n

n

n

n

n

x

dx

d

n

x

P

1

!

2

1

)

(

2

−

=

)

(

)

(

)

2

(

2

'

1

2

k

N

k

N

k

x

P

x

P

N

A

+

+

+

−

=

Natomiast węzły kwadratury

x

k

to zera wielomianu

P

N+1

(x).

Aby zastosować powyższe wzory dla dowolnego przedziału

[a,b] należy dokonać

podstawienia:

x

a

b

b

a

t

2

2

−

+

+

=

,

∫

∑

=

−

=

≈

b

a

N

k

k

k

t

f

A

a

b

f

S

dt

t

f

0

)

(

2

)

(

)

(

.

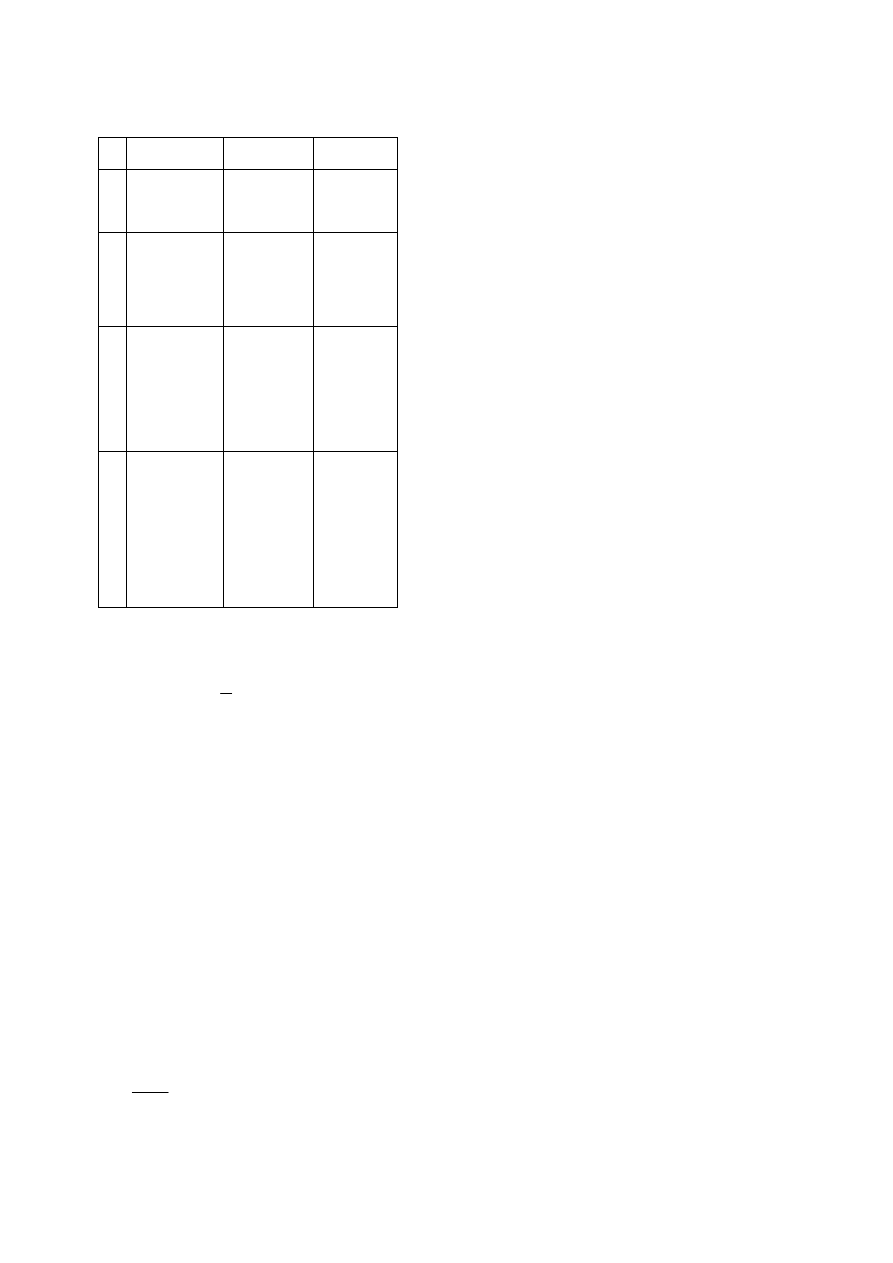
Współczynniki i węzły kwadratur Gaussa są stablicowane [2].

N

k

x

k

A

k

1

0, 1

0,577350

-0,577350

1

1

2

0, 1, 2

-0,774597

0

0,774597

5/9

8/9

5/9

3

0, 1, 2, 3

-0,861136

-0,339981

0,339981

0,861136

0,347855

0,652145

0,652145

0,347855

4 0, 1, 2, 3, 4

-0,906180

-0,538469

0

0,538469

0,906180

0,236927

0,478629

0,568889

0,478629

0,236927

Przykład:

Oblicz całkę

∫

2

1

1

dx

x

.

Rozwiązanie:

Zastosujemy kwadraturę Gaussa-Legendre’a dwu- i cztero-węzłową.

Dla dwuwęzłowej kwadratury:

N=2,

x

0

= 0,577350, t

0

=1,5+0,5*0,577350=1,788675

x

1

= - 0,577350, t

1

=1,5+0,5*(- 0,577350)=1,211325

A

0

= 1

A

1

= 1

f(t

0

) = 0,559073

f(t

1

) = 0,825542

Q=

∑

=

−

N

k

k

k

t

f

A

a

b

0

)

(

2

=0,5(0,559073+0,825542)=0,692308

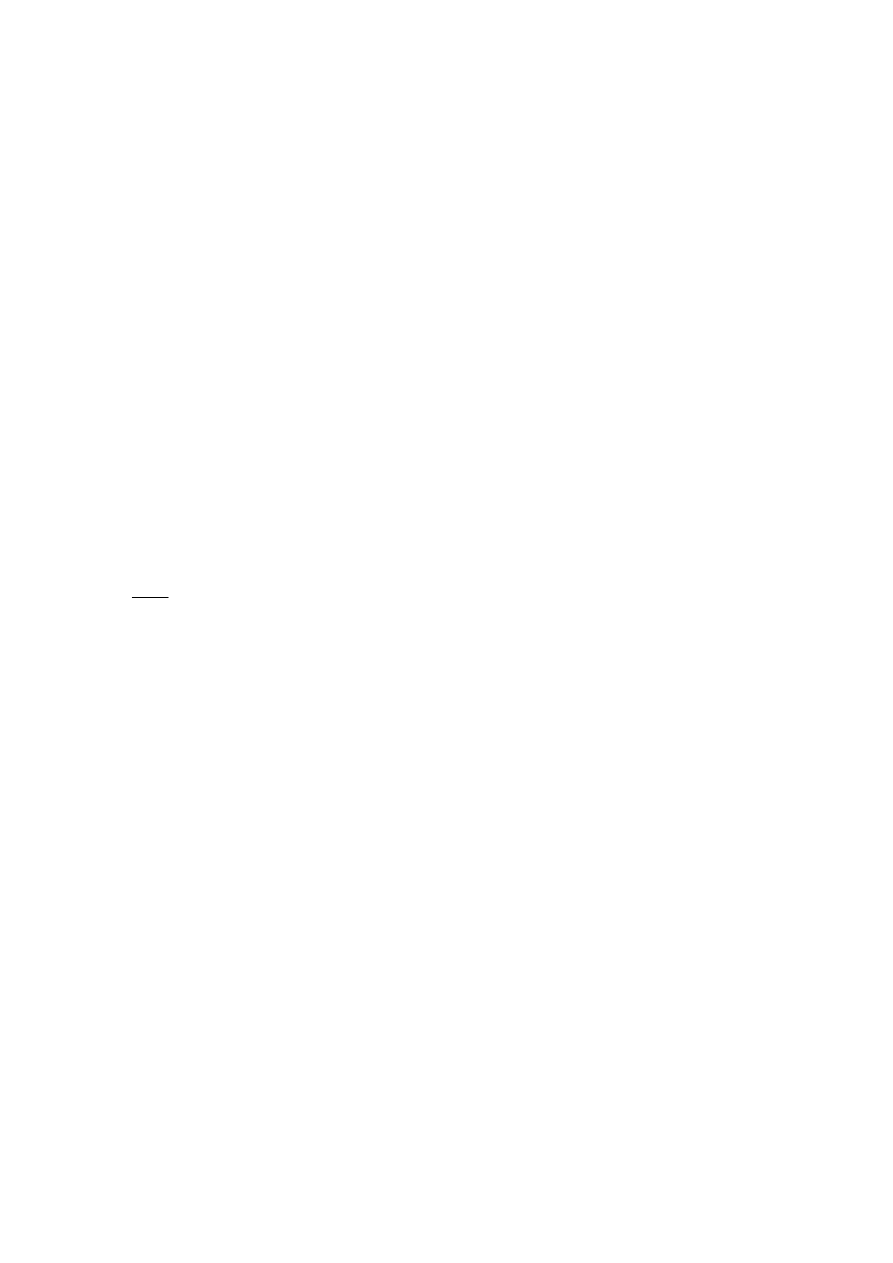
Dla kwadratury czterowęzłowej:

N=4,

x

0

= -0,861136,, t

0

=1,5+0,5*(-0,861136)=1,069432

x

1

=-0,339981, , t

1

=1,5+0,5*(-0,339981)=1,33001

x

2

=0,339981, , t

2

=1,5+0,5*0,339981=1,669991

x

3

= 0,861136,, t

3

=1,5+0,5*0,861136=1,930568

A

0

= 0,347855

A

1

= 0,652145

A

2

= 0,652145

A

3

= 0,347855

f(t

0

) = 0,935076

f(t

1

) = 0,751874

f(t

2

) = 0,598806

f(t

3

) = 0,517982

Q=

∑

=

−

N

k

k

k

t

f

A

a

b

0

)

(

2

=0,693146

1.

Jankowscy, Janina i Michał. Przegląd metod i algorytmów numerycznych, cz.1.

Warszawa : Wydawnictwa Naukowo-Techniczne, 1981. ISBN 83-204-0226-3.
2.

Fortuna Z., Macukow B., Wąsowski J. Metody Numeryczne. Warszawa : Wydawnictwa

Naukowo-Techniczne, 2005. ISBN 83-204-3245-6.