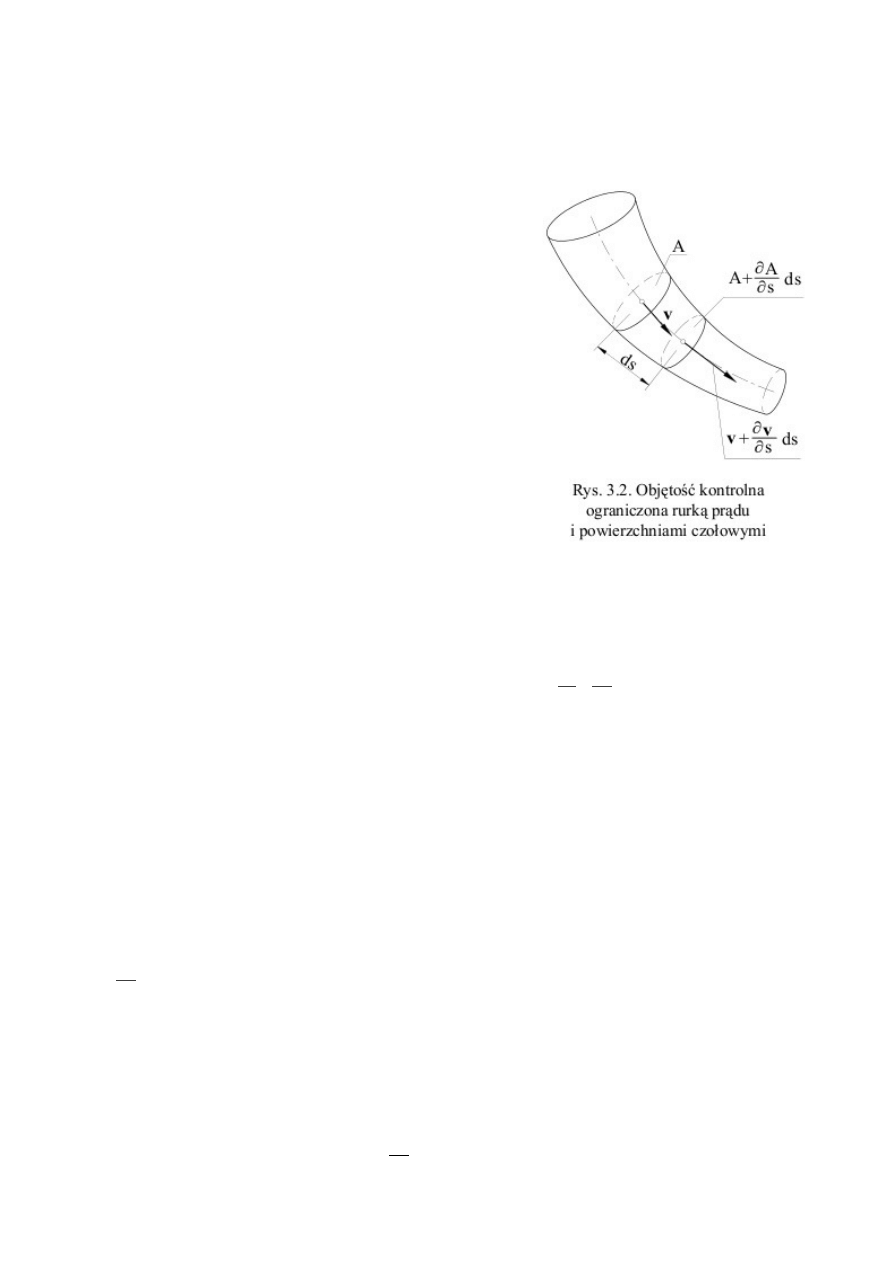
1.1 Podstawowe równania mechaniki płynów – zasada zachowania masy, pędu i 
energii.

1. Równanie ciągłości przepływu (zasada zachowania masy)

Zgodnie z zasadą zachowania masy, w żadnym punkcie pola masa 
nie może się tworzyć ani znikać. W płynie nieściśliwym (ρ = const) 
tylko takie pole prędkości będzie spełniało tę zasadę, w którym w 
każdej   chwili   do   obszaru   ograniczonego   powierzchnią   kontrolną 
będzie   wpływało   tyle   płynu,   ile   w   tej   samej   chwili   wypływa. 
Warunek   ten   jest   zatem   identyczny  dla   przepływów   ustalonych   i 
nieustalonych. 

W przypadku ruchu ustalonego (żadna wielkość nie zależy od czasu) 
zasadę przedstawiają równania: 

•

dla płynu ściśliwego  - 

⋅

A⋅v =const

•

dla płynu nieściśliwego - 

A⋅v=const ,

które można również napisać w postaci: 

•

dla płynu ściśliwego - 

ρ

1

⋅

A

1

⋅

v

1

=

ρ

2

⋅

A

2

⋅

v

2,

 

•

dla płynu nieściśliwego - 

A

1

⋅

v

1

=

A

2

⋅

v

2,

gdzie: 

v

1

– prędkość wpływu przez powierzchnię o polu

A

1

, 

v

2

– prędkość wypływu przez powierzchnię o polu

A

2

. 

Wielkość 

A⋅v

 oznacza strumień objętości przepływu:

q

V

=

∫

v⋅dA=A⋅v

śr

A po pomnożeniu przez gęstość dostajemy strumień masy:

q

m

=

∫

v⋅⋅dA= A⋅⋅v

śr

 

Stąd możemy wyliczyć wartość prędkości średniej:

v

śr

=

q

v

A

=

q

m

A



W  obliczeniach   inżynierskich   najczęściej   operuje   się   właśnie   prędkością   średnią,   sprowadzając   ruch   w 
rurach i kanałach do przepływu jednowymiarowego.

2. Zasada zachowania pędu

Opisana ogólnie: 

∑

m

i

a

i

=

∑

P

io



∑

P

ij

, gdzie:

P

io

 – siła zewnętrzna działająca na i-tą cząstkę o masie m

i

 i przyśpieszenie a

i

, 

P

ij

 – siła wewnętrzna, z jaką j-ta cząstka działa na i-tą 

W ośrodku ciągłym sumy zastępujemy całkami i otrzymujemy:

∫

dv

dt

⋅⋅

dV =

∫

f  dV 

∫



dA

, gdzie:

dv /dt – przyśpieszenie elementu o masie ρ dV ,

f i σ – jednostkowe siły :masowa i powierzchniowa

Równanie powyższe przedstawia zasadę zachowania pędu w niutonowskiej mechanice ośrodków ciągłych, 
które orzeka, że zmiana pędu w czasie jest spowodowana przez siły masowe i powierzchniowe. 

Ciecz doskonała jest nieściśliwa i nielepka, a zatem nie występują w niej naprężenia styczne , więc równanie 
zachowania pędu można zapisać w postaci równania Eulera (równanie cieczy doskonałej):

⋅

dv

dt

=⋅

f −grad p

3. Zasada zachowania energii dla cieczy nielepkiej i nieprzewodzącej (nn) ciepła oraz gazu 
doskonałego

Gaz doskonały oraz ciecz nn spełniają zależność na energię wewnętrzną: 

e=c

V

⋅

T

,

c

V

=

const

.

Równanie energii dla powyższych:

⋅

d

dt



v

2

2



c

V

⋅

T 

p



=⋅

f⋅v−



p



t

, gdzie 

c

V

⋅

T 

p



=

i

1.2. Równanie Bernoulliego dla płynu doskonałego i jego zastosowanie

v

2

2g



p



g



z =H =const

, gdzie H jest wysokością rozporządzalną oraz [H] = m 



v

2

2



pz⋅⋅g = p

rozp

=

const

, gdzie p

rozp

 jest to ciśnienie rozporządzalne podawane w Pa

Równanie   Bernoulliego   określa   przemiany   energetyczne   wzdłuż   strugi   elementarnej   o   przekroju 
poprzecznym   nieskończenie   małym   i   jest   szczególnym   przypadkiem   zasady   zachowania   energii   w 
przepływie   płynu   nielepkiego.   W   przepływach   płynów   rzeczywistych   ograniczonych   ścianami   stałymi 
(przepływy   przez   przewody   pod   ciśnieniem,   kanały   otwarte   itd.)   twierdzenie   Bernoulliego   prowadzi 
natomiast do wyników niezgodnych z doświadczeniem. Ale i w tych przypadkach posługujemy się tym 
równaniem,   powiększonym   o   składnik,   którego   wartość   liczbowa   odpowiada   wysokości   strat 
energetycznych. Uogólnione w ten sposób równanie Bernoulliego stanowi jedno z podstawowych równań 
hydrauliki .

Zastosowania równania Bernoulliego

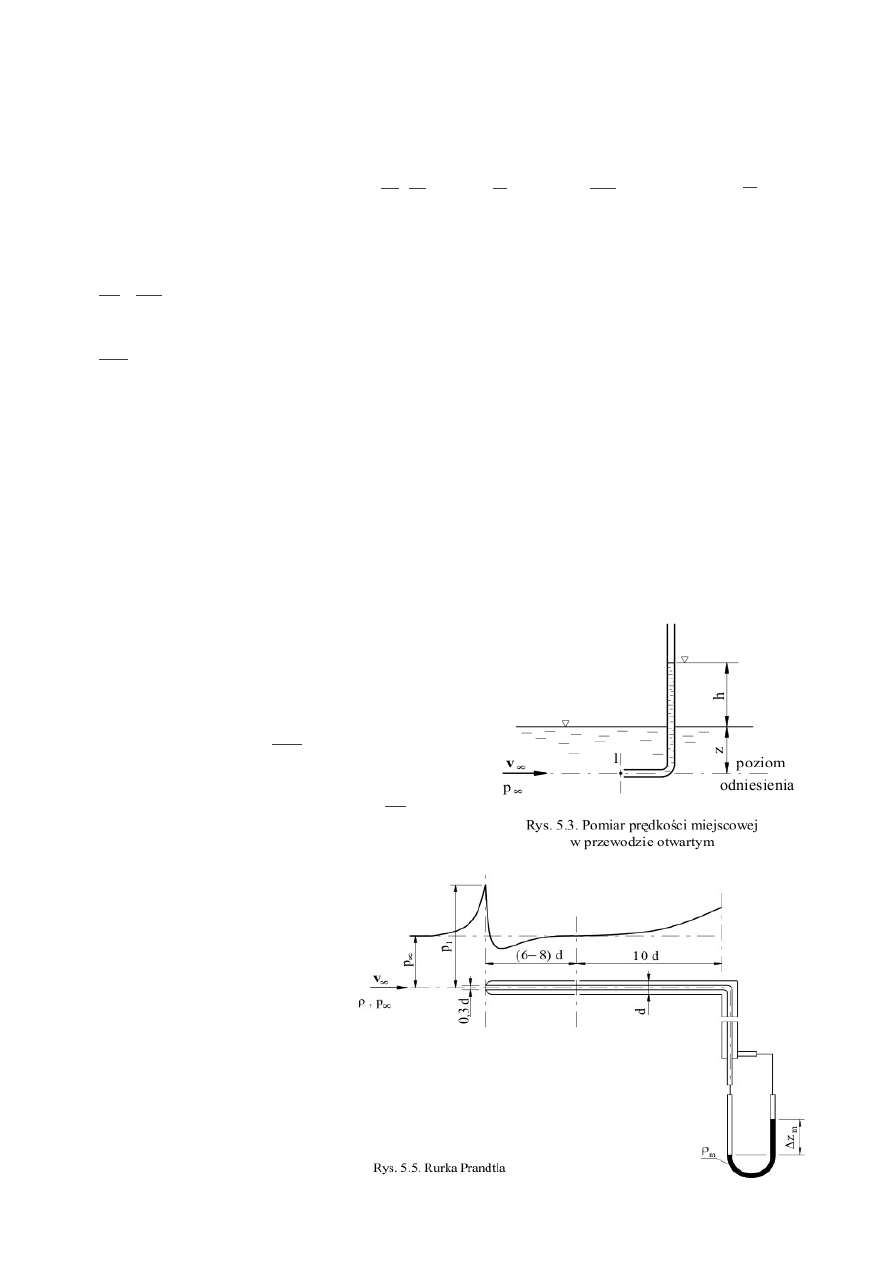
a) Pomiar prędkości miejscowej

•

Rurka   Pitota   -  najprostszy   przyrząd   służący   do 
pomiaru prędkości miejscowej. Jest to rurka zagięta 
pod  kątem  90

o

, której  jedno ramię   znajduje  się  w 

kanale, w którym dokonujemy pomiaru, a drugie jest 
otwarte lub podłączone do manometru. Prędkość v

∞ 

wynosi:

 

v

∞

=



2gh

,   ponieważ

 ciśnienie 

spiętrzenia

 

p

1

:

p

1

=

p

b



g hz = p

b



gz

v

∞

2

2g

.   Podczas 

pomiaru   prędkości   miejscowej   powietrza   należy 
pamiętać,   że   posiada   ono   inną   gęstość   niż   ciecz 
manometryczna!

•

Rurka   Prandtla   -   przyrząd 
pomiarowy   umożliwiający 
bezpośredni   pomiar   różnicy 
ciśnienia   spiętrzenia   i 
ciśnienia

 

statycznego 

przepływu   niezakłóconego 
jest rurka Prandtla (rys. 5.5). 
Odbiór ciśnienia statycznego 
p∞   odbywa   się   na 
pobocznicy   rurki   za 
pośrednictwem   otworków, 
których położenie zależy od 
rozkładu   ciśnienia   wzdłuż 
poziomej   gałęzi   rurki.   Jak 

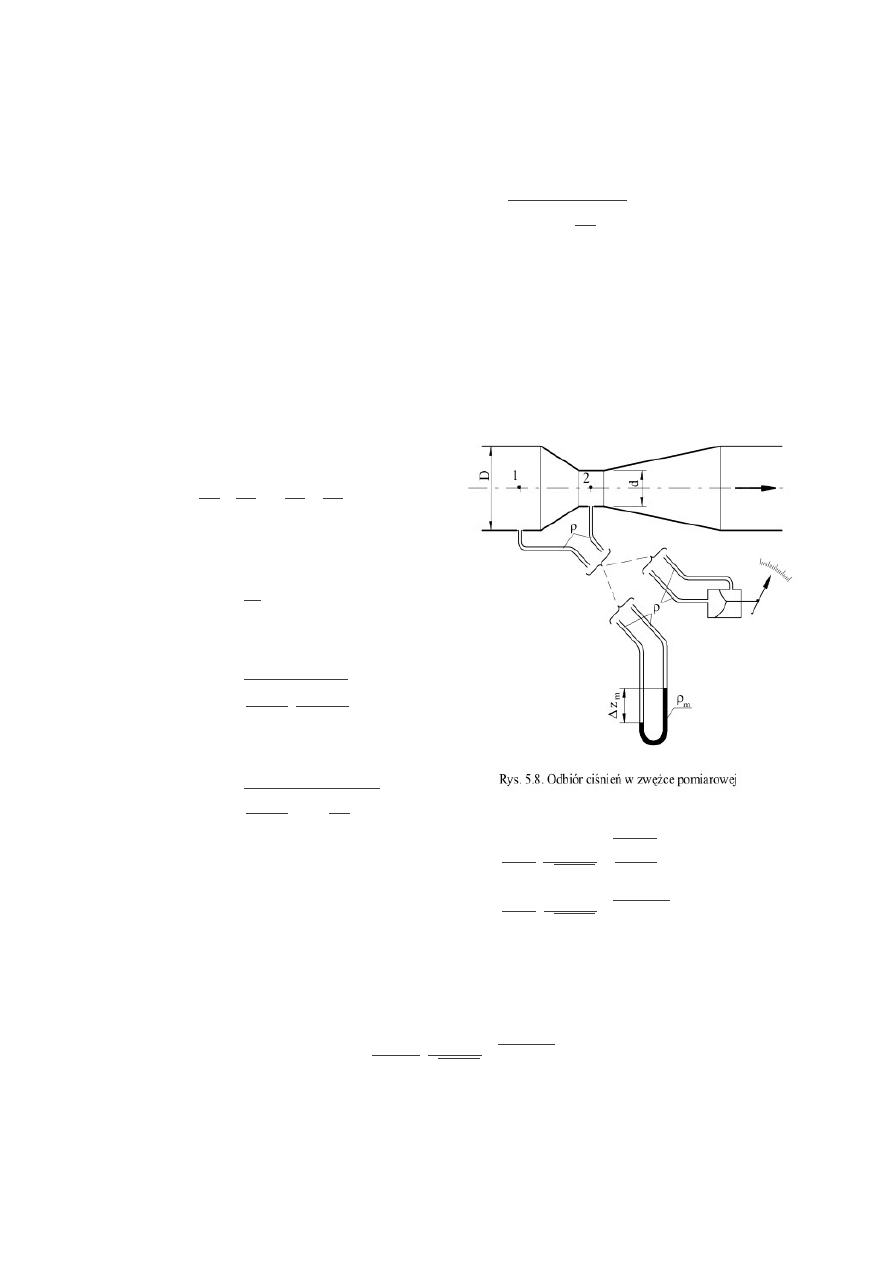
wynika z wykresu (rys. 5.5), ciśnienie przed rurką wzrasta, osiągając maksimum bezpośrednio u 
wlotu do rurki, potem raptownie maleje nieco poniżej wartości p∞, a następnie łagodnie wzrasta, 
osiągając w odległości (6–8)d od wlotu1) wartość p∞. W tym przekroju powinien następować odbiór 
ciśnienia statycznego. 

Jeżeli różnica ciśnień mierzona jest za pomocą manometru różnicowego to:

p

1

 – p

∞

 = g ∆z

m

 (ρ

m

 – ρ) , więc: 

v

∞

=



2 g  z

m





m



−

1

. 

Pomiary wykonywane za pomocą rurki Prandtla podłączonej do, np. mikromanometru  mają
niedokładność do 1%. Rurka powinna być wprowadzana do odcinka prostego kanału (nie 
mierzyć bezpośrednio za zwężkami, kolanami, zmianami średnic etc.).

b) Pomiar prędkości średniej i strumienia objętości metodą prędkościomierzową 

[1.2. Mechanika płynów.pdf, str.125-126]

c) Pomiar strumienia objętości metodą zwężkową 

Równanie Bernoulliego dla przekrojów 1 i 2:

v

1

2

2g



p

1

g

=

v

2

2

2g



p

2

g



A równanie ciągłości przepływu:

v

1

=

d

D



2

⋅

v

2

=

2

⋅

v

2

Rozwiązanie względem v

2

:

v

2

=



2g

1−

4

⋅

p

1

– p

2

g 

Często mierzymy manometrem różnicowym, więc:

v

2

=



2g

1−

4

⋅

z 



m



−

1

Z tego łatwo można policzyć strumień objętości:

q

v

=



d

2

4

⋅

1



1−

4

⋅



2  p



oraz masy:

q

v

=



d

2

4

⋅

1



1−

4

⋅



2  p⋅

W układach rzeczywistych należy jeszcze uwzględnić liczbę ekspansji ε, uwzględniającą spadek ciśnienia na 
zwężce (dla płynów nieściśliwych  ε=1, dla ściśliwych  ε<1) oraz współczynnika przepływu C zależnego od 
liczby Reynoldsa w zwężce. Ostatecznie dla układów rzeczywistych:

q

m

=

⋅

d

2

4

⋅

C



1−

4

⋅



2  p⋅

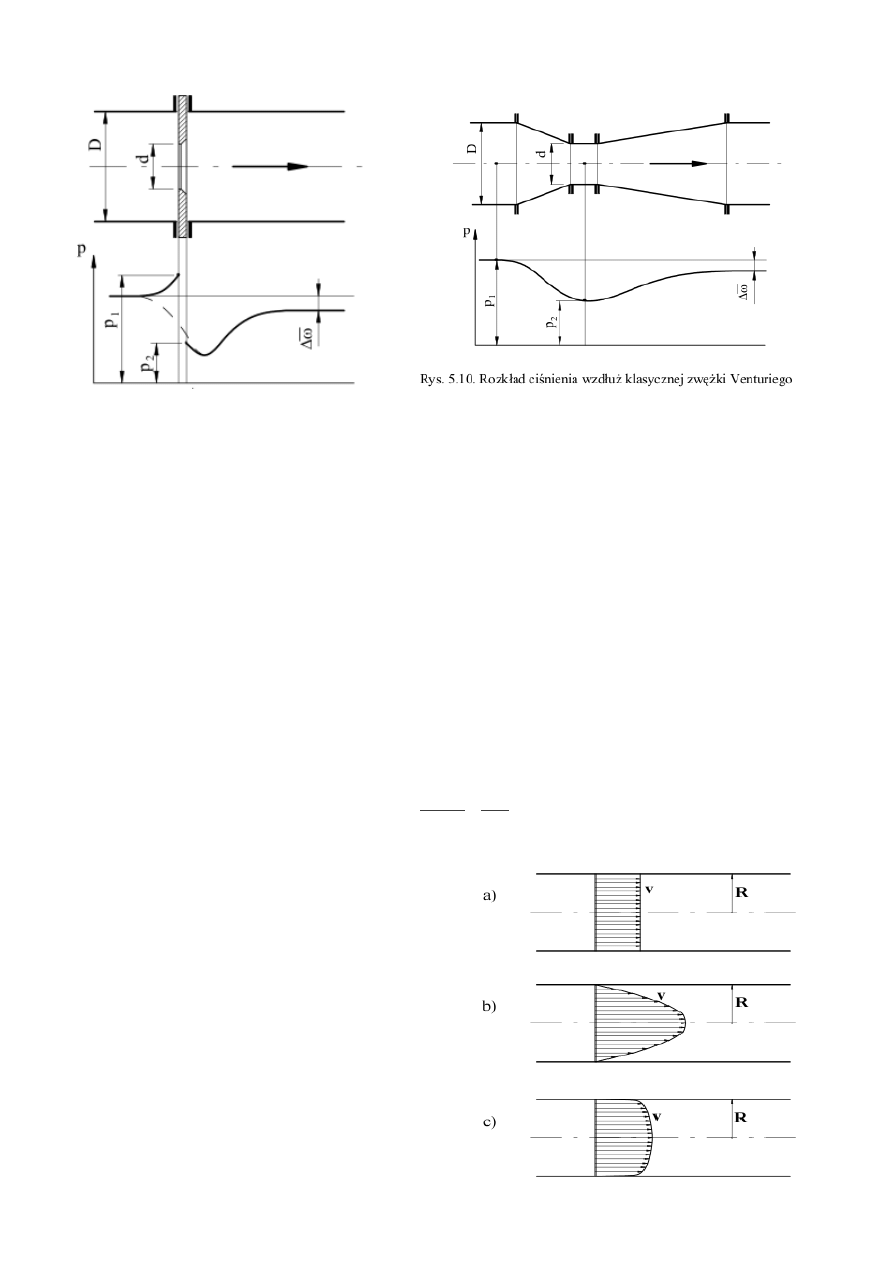
Na rysunkach pokazano schemat wraz z rozkładem ciśnienia zwężki pomiarowej (strona lewa) oraz zwężki 
Venturiego (strona prawa). Zwężka Venturiego powoduje mniejsze straty hydrauliczne jednak w praktyce 
stosuje się kryzy pomiarowe.

d) Wypływy przez otwory, przelewy etc. [1.2. Mechanika płynów.pdf, str.130]

1.3. Przepływy laminarne i turbulentne. Rozkład prędkości przepływu w 
przewodzie.

Przepływ  jest laminarny (uwarstwiony),  gdy elementy płynu poruszają  się  w warstwach.  W przepływie 
turbulentnym   (burzliwym),   oprócz   ruchu   głównego   (w   kierunku   przepływu),   występują   fluktuacje 
parametrów   hydrodynamicznych   (prędkości,   ciśnienia).  Analizę   przejścia   przepływu   laminarnego   w 
turbulentny przeprowadził Reynolds (1883), obserwując przepływ w przewodzie kołowym. Reynolds badał 
właściwości przepływu laminarnego i turbulentnego, wprowadzając strugę barwnika (aniliny) wzdłuż osi 
rury, którą przepływała woda z niewielką prędkością. W przepływie laminarnym nierozmyta struga barwnika 
poruszała się wzdłuż osi, natomiast w przepływie turbulentnym barwnik był szybko rozpraszany. Reynolds 
zauważył, że na charakter przepływu wpływają następujące parametry: prędkość średnia (v), gęstość (ρ) i 
lepkość (μ) cieczy oraz średnica rury (d). Kryterium decydującym o rodzaju ruchu jest bezwymiarowa liczba 
ρvd/μ utworzona z tych parametrów i nazwana później liczbą Reynoldsa (Re).

Re=

⋅

v⋅d


=

v⋅d



Umownie u przepływie laminarnym mówi, gdy Re<2300, jednak jest to wartość nieprecyzyjna, gdyż przy 
zachowaniu   odpowiednich   warunków   przepływu 
(powolny   przyrost   prędkości)   ruch   laminarny   może 
utrzymywać się nawet przy Re wielokrotnie wyższej.

Przedstawione profile dotyczą przepływów 
jednowymiarowych: 

a) o płaskim rozkładzie prędkości ( jak w modelu płynu 
nielepkiego, przyjmowany najczęściej w koncepcji 
przepływu jednowymiarowego), 
b) o parabolicznym rozkładzie prędkości ( przy przepływie 
laminarnym), 
c) o w pełni uformowanym profilu turbulentnym. 

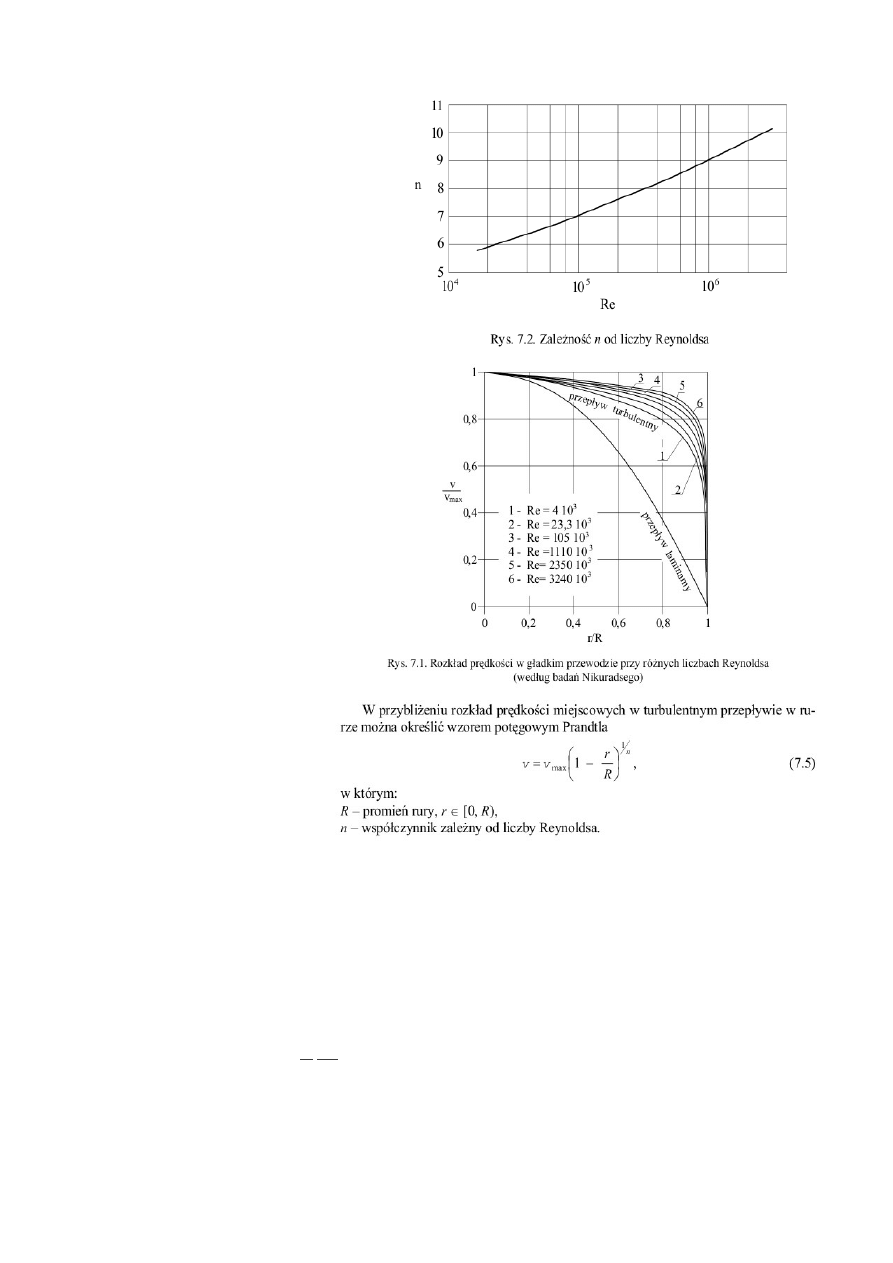
Przejście   ruchu   laminarnego   w   turbulentny 
następuje wskutek utraty stateczności przepływu 
laminarnego. Drobne wszechobecne zaburzenia 
generujące   fluktuacje   elementów   płynu 
występują   zawsze   podczas   przepływu.   W 
przepływie   laminarnym,   w   którym   siły 
bezwładności   są   małe   w   porównaniu   z   siłami 
lepkości,   są   one   jednak   tłumione   przez   te 
ostatnie. Wzrost sił bezwładności, np. wskutek 
przyrostu   prędkości   przepływu,   powoduje,   że 
tłumiące

 

działanie

 

lepkości

 

jest 

niewystarczające,   co   wywołuje   utratę 
stateczności ruchu laminarnego i jego przejście 
w ruch turbulentny. 

Rozróżnia   się   dolną   wartość 
krytyczną   liczby   Reynoldsa   Re

kr   d 

(poniżej której nigdy nie występuje 
ruch   turbulentny)   i   górną   wartość 
krytyczną   liczby   Reynoldsa   Re

kr   g 

( powyżej której nie występuje ruch 
laminarny),   przy   czym   tylko 
pierwsza z nich jest dość dokładnie 
określona,   np.   w   przypadku 
przepływu

 

przez

 

długą 

cylindryczną   rurę   o   przekroju 
kołowym   Re

kr   d

 

  2300.   Górna

≅

 

wartość krytyczna liczby Reynoldsa 
zależy   od   wielu   czynników 
ubocznych,   jak   np.   kształtu   wlotu 
do  przewodu,  wstępnych  zaburzeń 
mechanicznych

 

płynu 

wpływającego   do   przewodu, 
stopnia   gładkości   ścian   przewodu, 
drgań   przewodu.   Wszystkie   te 
czynniki   mogą   spowodować,   że 
przejście przepływu laminarnego w 
turbulentny   może   nastąpić   przy 
różnych   wartościach   liczby 
Reynoldsa. 

1.4. Charakterystyka przepływu  w pojedynczym przewodzie i szeregowym systemie 
hydraulicznym. Rozkład energii wzdłuż rurociągu – wykres Ancony.

1. Straty hydrauliczne wywołane tarciem.

•

Straty liniowe

Wysokość strat liniowych liczymy ze wzoru Darcy’ego–Weisbacha:



h

l

=

l

d

v

2

2g

, gdzie 



– współczynnik oporuliniowego

l – długość przewodu

d – średnica przewodu

v – średnia prędkość przepływu

Współczynnik   oporu   liniowego   jest   w   ogólnym   przypadku   funkcją   liczby   Reynoldsa   Re   i 

chropowatości   względnej   k/d   (k   –   średnia   wysokość   nierówności   na   ścianie   rury).   Wartość   tego 
współczynnika   bywa   najczęściej   wyznaczana   z   wykresów   opracowanych   na   podstawie   badań 

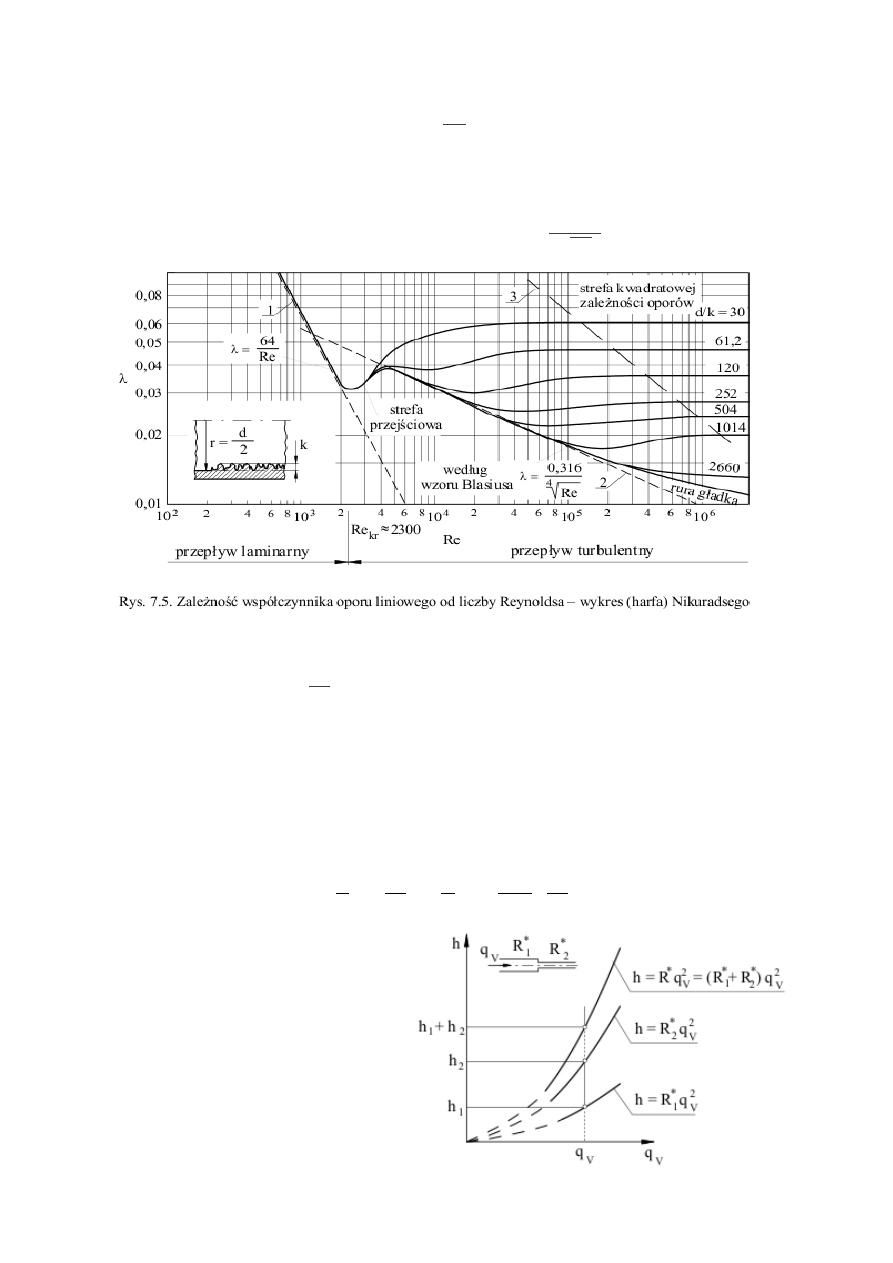
doświadczalnych,   z   formuł   empirycznych   lub   pół-empirycznych.   Jedynie   w   przypadku   przepływu 

laminarnego można teoretycznie ze wzoru:

=

64
Re

  wyznaczyć   zależność   między  λ   i   Re.  Wynika 

stąd, że w przepływie laminarnym przez przewody o przekroju kołowym współczynnik oporu liniowego jest 
odwrotnie proporcjonalny do liczby Reynoldsa. Zależność (7.3) została potwierdzona licznymi wynikami 
doświadczalnymi. 

Dla Re < 100000 często stosuje się empiryczny wzór Blasiusa:

=

0,3614

4



Re

=

100 Re

−

0,25

•

Straty miejscowe

Wysokość strat miejscowych liczymy ze wzoru Darcy’ego–Weisbacha:



h

m

=

v

2

2g

, gdzie 



– współczynnik oporuliniowego

v – średnia prędkość przepływu

ζ jest współczynnikiem strat miejscowych zależnych od liczby Reynoldsa i rodzaju przeszkody odniesiony 
najczęściej   do   średniej   prędkości   za   nią.  Współczynnik   strat   miejscowych   najczęściej   wyznaczany  jest 
doświadczalnie.

2. Pojedynczy przewód.

Dla pojedynczego przewodu zawierającego opory miejscowe można napisać równanie na wysokość strat 
hydraulicznych:



h

s

=

l

d



v

2

2g

=

l

d



4q

v



d

2



2

1

2g

=

R

∗

q

v

2

, gdzie R

8

 jest opornością hydrauliczną 

przewodu.

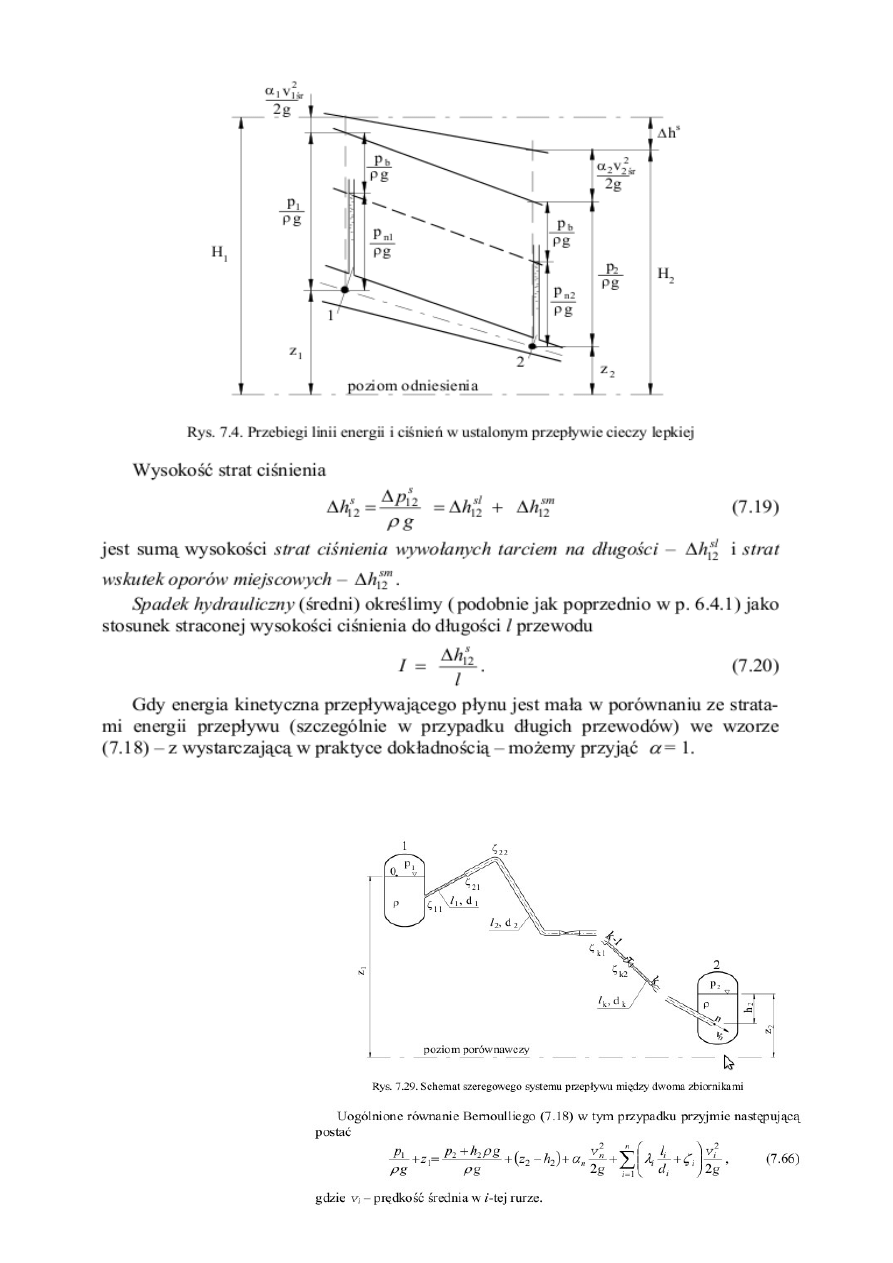
3. Szeregowy system 
hydrauliczny



jest to współczynnik 

Coriolisa uwzględniający 
nierównomierny rozkład 
prędkości w przekroju 
poprzecznym strugi. Dla 
przepływu laminarnego jest on 2 
a dla turbulentnego >1.

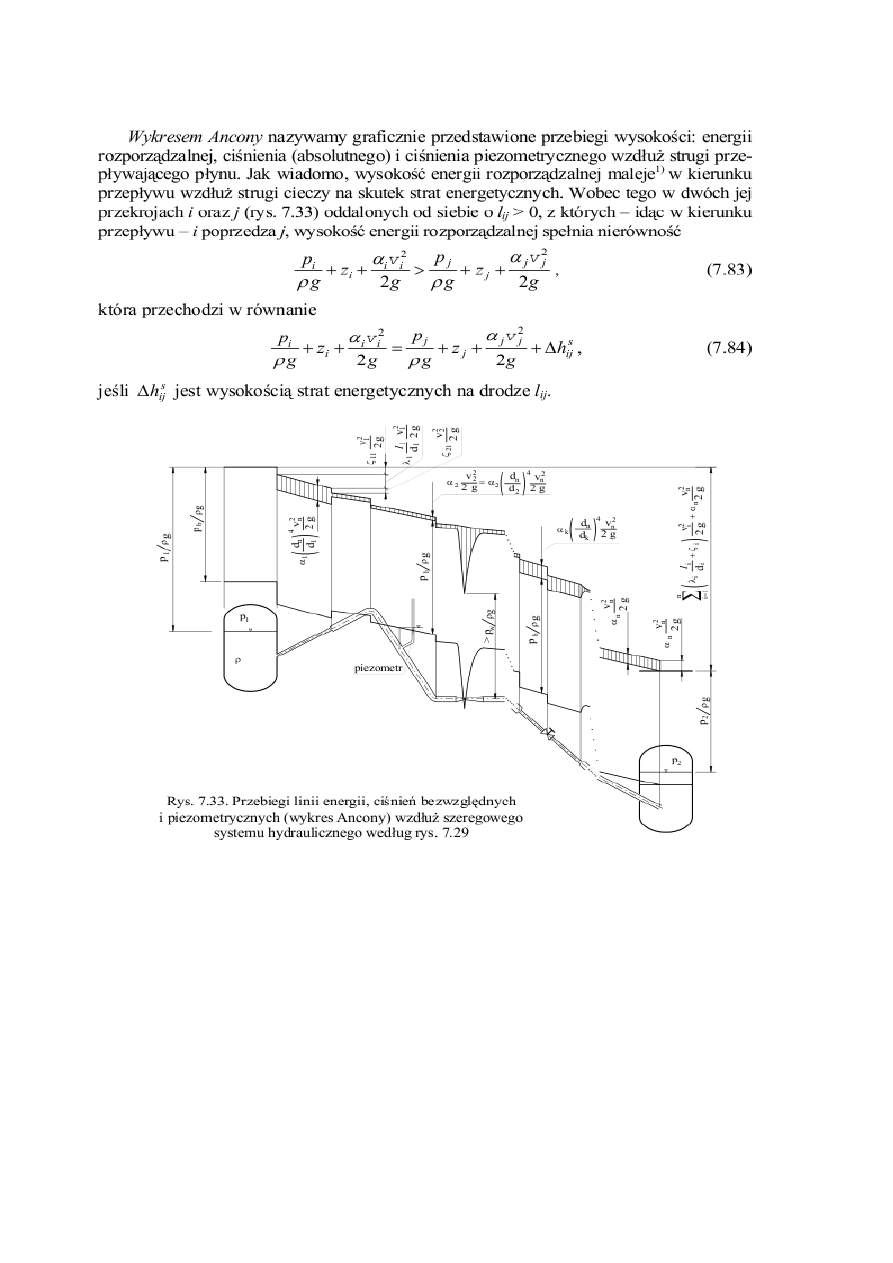
4. Wykres Ancony

Znając zatem wartość energii w pewnym przekroju strugi, możemy znaleźć tę wartość w dowolnym jej 
przekroju, jeśli potrafimy obliczyć straty energetyczne między tymi przekrojami. Pozwoli to uzyskać linię 
energii, która nie może nigdzie wznosić się w kierunku przepływu płynu. Przeciwnie, podczas przepływu 
płynów lepkich linia energii zawsze opada w kierunku przepływu. Wysokość  ciśnienia (absolutnego) w 
dowolnym przekroju strugi otrzymujemy, odejmując – od wysokości energii – wysokość prędkości. Znając 
wysokość   ciśnienia   w   każdym   przekroju   strugi,   możemy   wykreślić   linię   ciśnień   i   linię   ciśnień 
piezometrycznych,   która   przebiega   równolegle   do   linii   ciśnień,   ale   niżej   od   niej   o   wysokość   ciśnienia 
barometrycznego pb /ρ g. Linie ciśnień i ciśnień piezometrycznych kształtują się w zależności od wymiarów 
geometrycznych przewodu i strumienia objętości, ale nie muszą opadać w kierunku ruchu. Na rysunku 7.33 
przedstawiono   wykres   Ancony   ilustrujący   przebieg   wysokości   energii   i   ciśnień   między   zbiornikami 
rozważanymi   w   poprzednich   punktach.   Łatwo   spostrzec,   że   linie   energii   i   ciśnień   nie   mogą   przecinać 
rurociągu1), a dla zapobieżenia odparowaniu cieczy ciśnienie w rurze musi przekraczać ciśnienie parowania 
pw.   Wynika   stąd,   że   linia   ciśnień   piezometrycznych   nie   może   przebiegać   pod   rurociągiem   niżej 
niż (pb – pw)/ρ g. 

1.5. Pierwsza i druga zasada termodynamiki (entropia, zjawiska odwracalne i 
nieodwracalne).

1.  Pierwsza   zasada   termodynamiki –   jedno   z   podstawowych   praw termodynamiki,   jest 
sformułowaniem zasady   zachowania   energii dla układów   termodynamicznych.   Zasada   stanowi 
podsumowanie równoważności ciepła i pracy oraz stałości energii układu izolowanego.

Dla układu   zamkniętego (nie   wymienia   masy   z   otoczeniem,   może   wymieniać   energię)   zasadę   można 
sformułować w postaci: zmiana energii wewnętrznej układu zamkniętego jest równa energii, która przepływa 
przez jego granice na sposób ciepła lub pracy.

, 

gdzie:

ΔU – zmiana energii wewnętrznej układu,
Q – energia przekazana do układu jako ciepło,
W – praca wykonana na układzie.

W powyższym sformułowaniu przyjmuje się konwencję, że gdy:

•

W > 0 – do układu przepływa energia na sposób pracy,

•

W < 0 – układ traci energię na sposób pracy,

•

Q > 0 – do układu przepływa energia na sposób ciepła,

•

Q < 0 – układ traci energię na sposób ciepła.

W przypadku układu termodynamicznie izolowanego układ nie wymienia energii z otoczeniem na sposób 
pracy (W = 0) ani na sposób ciepła (Q = 0), wówczas:

W   układzie   zamkniętym   zawierającym   ciało   proste   zmiana   energii   wewnętrznej   równa   jest   sumie 
algebraicznej pracy oraz ciepła wymienianego z otoczeniem, o ile nie występuje zmiana energii kinetycznej 
oraz   energii   położenia   układu.  Pierwsza   zasada   termodynamiki  stwierdza  możliwość   zamiany  ciepła   na 
pracę.

Energia wewnętrzna ciała jest sumą energii cząstek oraz energii ich wzajemnego oddziaływania. Energia 
wewnętrzna zawsze rośnie wraz ze wzrostem temperatury.

Przemiana   termodynamiczna   jest   zbiorem   kolejnych   stanów   substancji,   ciała   lub   układu 
termodynamicznego. Przemiana jest odwracalna, jeżeli od jej stanu końcowego do początkowego można 
powrócić w taki sposób, że i otoczeniu przywrócony będzie stan pierwotny. Nieodwracalność przemiany 
związana jest z rozpraszaniem energii w takich zjawiskach, jak tarcie czy wydzielanie ciepła Joule'a w 
przepływie prądu.

Praca zewnętrzna jest pracą sił zewnętrznych jakimi działa otoczenie na układ.

∫

=

2

1

V

V

1,2

dV

 

p(V)

L

.

Jeżeli we wzorze określającym I zasadę termodynamiki zastąpić zmianę energii wewnętrznej zmianą entalpii 
to zamiast pracy zewnętrznej W we wzorze pojawi się praca techniczna W

tech

L

t1,2

 = 

∫

−

2

1

p

p

dp

 

V(p)

Entalpię definiuję się jako: 

I =U  pV

, 

czyli entalpia jest sumą energii wewnętrznej układu i pracy zewnętrznej.

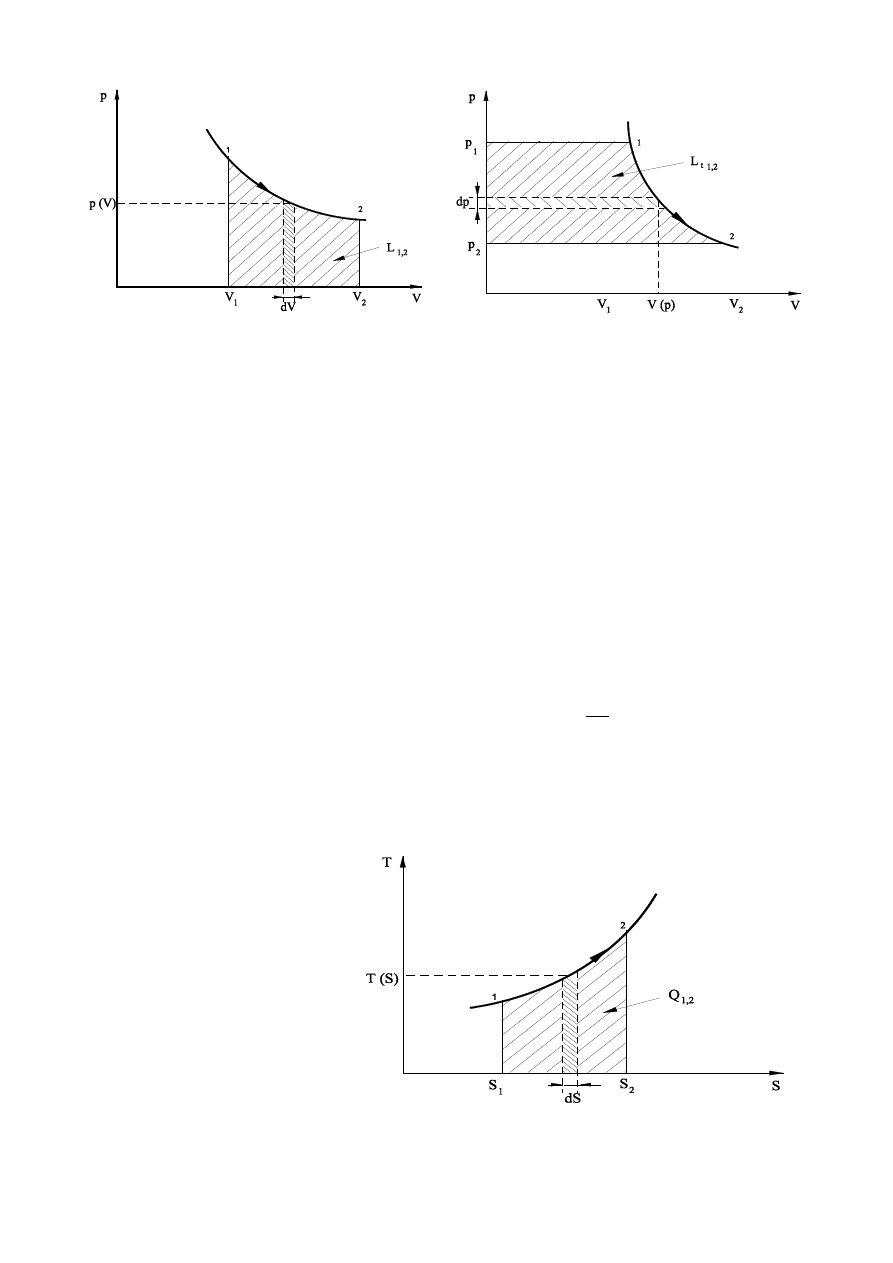
Rys.1. Interpretacja graficzna pracy zewnętrznej.

Rys. 2. Interpretacja graficzna pracy technicznej.

2. Druga zasada termodynamiki

Pierwsza zasada termodynamiki stwierdza, że w ogóle można zamienić ciepło na pracę, natomiast druga 
zasada podaje warunki, w jakich można zamienić ciepło na pracę oraz jak należy przeprowadzić proces, aby 
z danej ilości ciepła uzyskać maksymalną pracę. 

Trzy sformułowania II zasady termodynamiki:
a) aby zamienić ciepło na pracę muszą istnieć dwa źródła ciepła o różnych  
    temperaturach,
b) sprawność termiczna procesu (obiegu silnika) nie może osiągnąć jedności,
c) w przyrodzie możliwe są tylko takie przemiany, podczas których entropia
    układu wzrasta. 

Praktycznie oznacza to, że entropia układu zamkniętego i izolowanego nie może maleć podczas dowolnej 
przemiany   i   wzrasta   przy   przemianach   nieodwracalnych.   W   praktyce   stosuje   się   najczęściej   przyrosty 
entropii lub względne wartości entropii ponad stan przyjęty umownie za zerowy.
Przyrost entropii dla substancji stałych i ciekłych o stałym cieple właściwym

cpcv =c=const

 można zapisać w postaci:

 

1

2

1

2

T

T

 

ln

 

Mc

 

 

S

 

-

 

S

=

.

Ze wzoru na entropię ciepło przemiany jest równe:

 

∫

=

2

1

S

S

1,2

dS

 

T(S)

 

 

Q

.

Rys.3.   Interpretacja   ciepła   przemiany 
na wykresie T-S

Może   ono   być   przedstawione   na 
wykresie o współrzędnych T – S  (rys. 
3)   w   taki   sam   sposób   jak   praca 
zewnętrzna   przemiany   na   wykresie   o 
współrzędnych   p   –   V   (rys.1).   Ciepło 
przemiany  jest   dodatnie,   gdy  entropia 
rośnie, a ujemne gdy entropia maleje. 
Podstyczna   na   wykresie   o 
współrzędnych   T   –S   przedstawia 
rzeczywiste ciepło właściwe przemiany 
w   stanie   odpowiadającym   punktowi 
styczności. Ponieważ dla gazów i par c

p 

>   c

v

,   na   wykresie   o   współrzędnych   T-S   izobara   przebiega   łagodniej   od   izochory.   Podobnie   jak   pracę 

przedstawia pole pod krzywą przemiany na wykresie p-V, ciepło może być przedstawione w postaci pola pod 

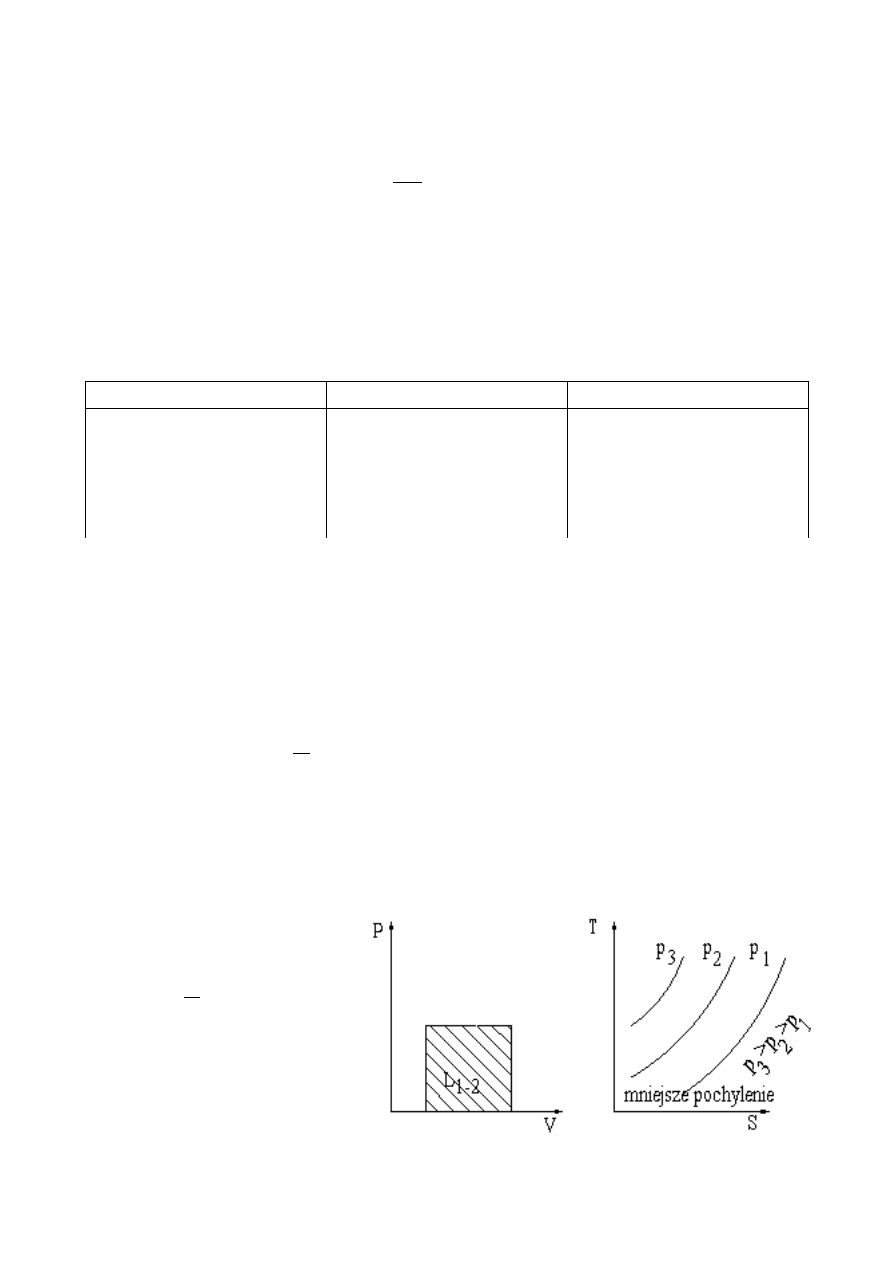
krzywą przemiany na wykresie T-S.  W przemianach odwracalnych pole to jest miarą ciepła wymienianego z 
otoczeniem, natomiast dla przemian nieodwracalnych z tarciem przedstawia sumę ciepła wymienianego z 
otoczeniem oraz ciepła Q

f

  doprowadzonego nieodwracalnie. Przyrost entropii układu można rozdzielić na 

część spowodowaną wymianą ciepła z otoczeniem:

0

 

T

dQ

 

 

dS

≥

=

gdzie:   dQ   –   ciepło   wymienione   z   otoczeniem   oraz   zawsze   dodatnie   wytworzenie   entropii   wewnątrz 
rozpatrywanej części układu spowodowane zjawiskami nieodwracalnymi np. praca tarcia zostaje zamieniona 
na ciepło tarcia (dQ

f

 = dL

f

). Entropia układu adiabatycznego na skutek przemian nieodwracalnych wzrastaa 

w przypadku przemian odwracalnych nie zmienia się.

1.6. Przemiany charakterystyczne  gazu doskonałego. Równanie stanu gazu. 

1. Równanie stanu gazu.

Gaz doskonały

Gaz półdoskonały

Gaz rzeczywisty

- drobiny nie oddziałują między 
sobą, 
- drobiny mają zerową objętość, 
- drobiny są sztywne (nie drgają), 
-stałe ciepło właściwe 

c

p

 i 

c

v

- drobiny posiadają energię 
kinetyczną (ruch postępowy, 
obrotowy, oscylacyjny, 
- drobiny mogą drgać, 
- ciepło właściwe 

c

p

 i 

c

v

 

zależne od temperatury

- drobiny oddziałują na siebie, 
- drobiny mają własną objętość,  
- drobiny w ciągłym ruchu, 
- stanu nie opisuje równanie 
Clapeyrona

Równaniem stanu gazu doskonałego i półdoskonałego jest równanie Clapeyrona postaci:

p⋅V =m⋅R⋅T

   lub   

p⋅V =n⋅M⋅R⋅T

gdzie: 

R

 - indywidualna stała gazowa, 

J / kg⋅K 

, 

M⋅R

 - uniwersalna stała gazowa, 

J / kg⋅K 

, 

n

 - liczba moli.

Równaniem stanu gazu rzeczywistego jest równanie:

–

van der Waalsa



p

a

v

2

⋅

v−b=R⋅T

,

–

Redlicha - Kwanga, 

–

wirialne (szereg potęgowy) - grupa równań

2. Przemiany termodynamiczne.

•

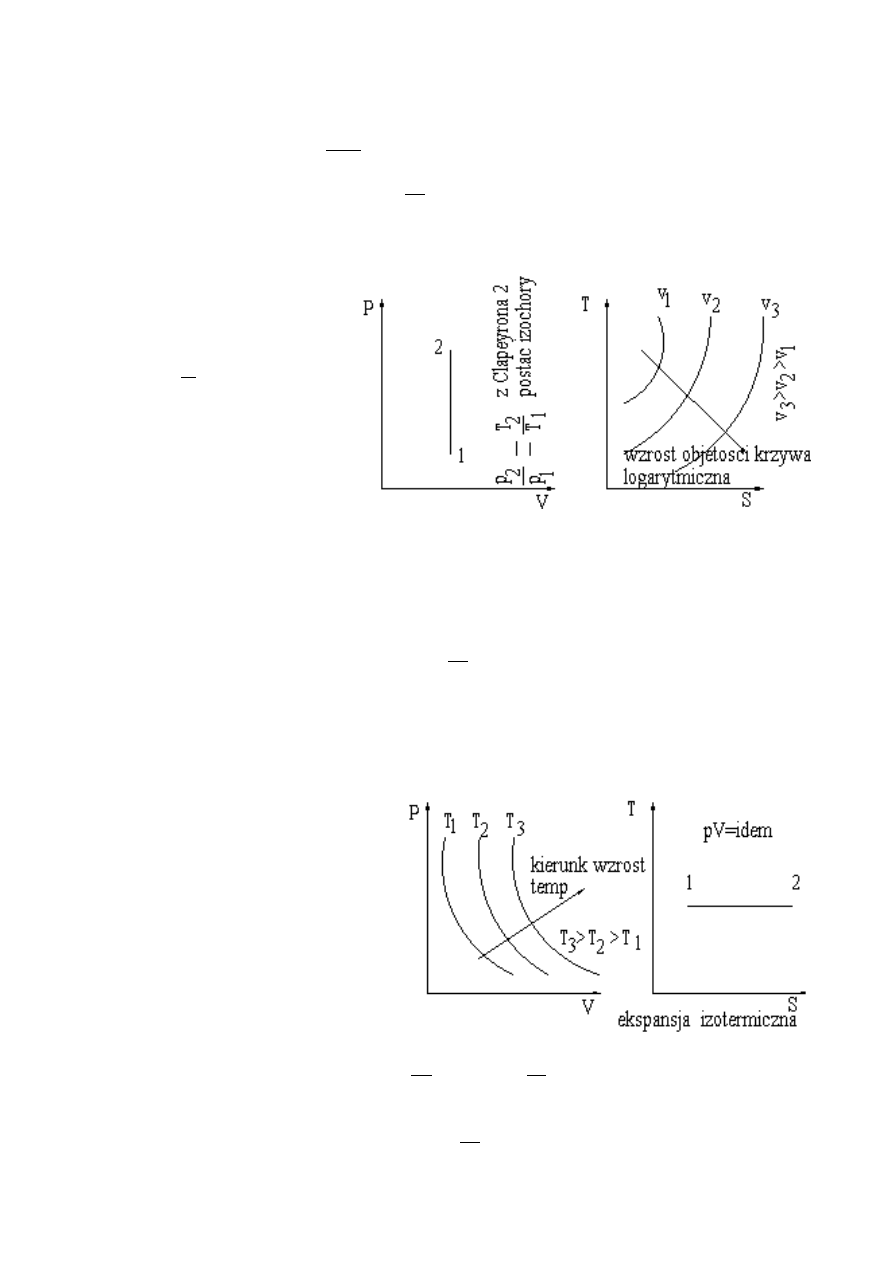
izobaryczna

p = idem

–

równanie przemiany (prawo 
Gay-Lusaca):

 

p=

V
T

=

idem

–

przemiany izobaryczne:
ekspansja, kompresja

–

praca zewnętrzna: 

L= p⋅V

2

– V

1

=

M⋅R⋅T

2

– T

1



–

 praca techniczna: 

L

t

=

V⋅ p

1

– p

2

=

0

–

ciepło: 

Q=M⋅c

p

⋅

T

2

−

T

1



–

sprawność termiczna: 

=

−

1



–

przyrost entropii: 

S

2

−

S

1

=

M⋅c

p

⋅

ln

T

2

T

1



•

izochoryczna

V = idem

–

równanie przemiany (prawo 
Charlesa): 

V =

p

T

=

idem

–

przemiany izochoryczne: 
sprężanie, rozprężanie

–

praca zewnętrzna: 

L=0

, bo 

dV =0

–

 praca techniczna: 

L

t

=

V⋅ p

1

−

p

2



–

ciepło: 

Q=M⋅c

v

⋅

T

2

−

T

1



–

przyrost entropii: 

S

2

−

S

1

=

M⋅c

V

⋅

ln

T

2

T

1



•

izotermiczna

T = idem

–

równanie przemiany (prawo Boyla-
Mariotta): 

T = p⋅V =idem

–

przemiany izotermiczne: 
ekspansja=rozprężanie, 
kompresja=sprężanie

–

praca zewnętrzna: 

L= p

1

⋅

V

1

⋅

ln

V

2

V

1

=

p

1

⋅

V

1

⋅

ln

p

1

p

2



–

 praca techniczna: 

L

t

=

L=M⋅R⋅T

1

⋅

ln

p

1

p

2



–

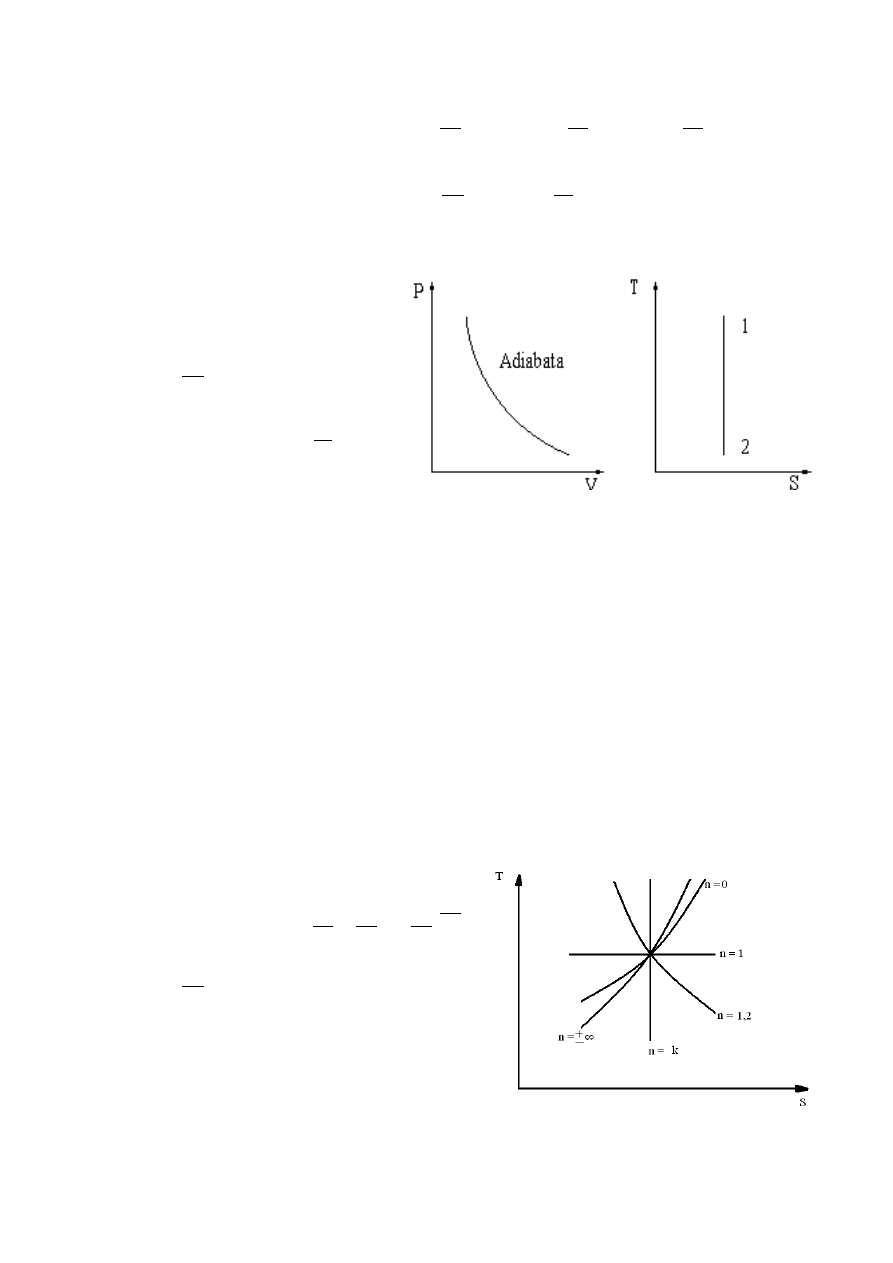
ciepło: 

Q= L= p

1

⋅

V

1

⋅

ln

V

2

V

1

=−

p

1

⋅

V

1

⋅

ln 

p

2

p

1

=

p

1

⋅

V

1

⋅

ln

p

1

p

2



–

przyrost entropii: 

S

2

−

S

1

=

M⋅R⋅ln 

V

2

V

1

=

M⋅R⋅ln

p

1

p

2



•

adiabatyczna



= idem

–

równanie przemiany: 

p⋅V



=

idem

, 

T⋅V

−

1

=

idem

, 

T⋅p

1−



=

idem

–

wykładnik izentropy

=

c

p

c

v

=

idem

.

–

charakteryzuje się brakiem wymiany 
ciepła pomiędzy czynnikiem a źródłami 
zewnętrznymi,

–

wytworzone ciepło tarcia powoduje podwyższenie energii wewnętrznej czynnika,

–

praca zewnętrzna: 

L=U

1

−

U

2

=

M⋅c

V

⋅

T

1

−

T

2



–

praca techniczna: 

L

t

=⋅

L=I

1

−

I

2

=

M⋅c

p

⋅

T

1

−

T

2

=

M⋅⋅c

v

⋅

T

1

−

T

2



•

izentropowa

S = idem

–

jest przemianą adiabatyczną odwracalną, podczas której entropia jest stała
(

dQ=0

 i 

Q=0

, a przy 

T 0

 

dS =0

 i 

S=idem

)

•

izentalpowa

I = const

•

politropowa

n = const

–

równanie przemiany:

p⋅V

n

=

idem

,  

p

2

p

1

=

V

1

V

2



n

=

T

2

T

1



n

n−1

T⋅V

n−1

=

idem ,

,

T⋅p

1−n

n

=

idem

–

wykładnik politropy n - stały dla danej rodziny 
przemian, może być dowolną liczbą rzeczywistą 
większą lub mniejszą od 



, 

n=idem

–

istnieje wymiana ciepła 

dQ=M⋅c⋅dT

, przy czym średnie ciepło właściwe „c” dla danej 

politropy jest stałe i równe:

c=c

v



p⋅dV

dt

=

c

v

⋅

n−
n−1

–

praca techniczna: 

L

t

=

n⋅L=I

1

−

I

2

–

ciepło: 

Q=M⋅c⋅T

2

−

T

1



–

przyrost entropii: 

S

2

−

S

1

=

M⋅c⋅ln

T

2

T

1



–

wykładnik politropy można wyznaczyć analitycznie:

n=lg

p

2

p

1

/

lg

V

1

V

2



–

typowe przemiany politropowe:

Wykładnik
 politropy

  Ciepło 
właściwe

  Równanie
   przemiany

              Przemiany

        0
        1
      



      

∞

     c

p

   

∞

      0
     c

v

   p = const
  pV=RT=const
  pV



 = const

    V = const

 izobaryczne substancji dowolnych
 izotermiczne gazów doskonałych
 izentropowe gazów doskonałych
 izochoryczne substancji dowolnych

3. Gaz wilgotny.

Teoria gazów wilgotnych dotyczy gazów, które w sąsiedztwie cieczy wchłaniają pary cieczy i stają 

się wilgotne. Zmiana warunków powoduje, że część pary ulega skropleniu. 
Najbardziej   typowym   przykładem  jest  powietrze   wilgotne  –  mieszanina   gazów   i   par   (gaz   suchy  -  nie 
skroplone w atmosferze cząstki azotu, tlenu, argonu +  woda  występująca w powietrzu w różnych stanach 
fazowych).

Ciśnienie   cząstkowe   pary   wodnej   w   powietrzu   jest   nieznaczne   i   dlatego   można   z   pewnym 

ograniczeniem stosować w tym przypadku prawa gazów doskonałych i prawo Daltona (każdy składnik w 
roztworze gazowym zachowuje się tak, jakby znajdował się sam w przestrzeni zajętej przez roztwór). Zatem 
ciśnienie cząstkowe pary wodnej w powietrzu wilgotnym jest równe:

p

p

=

p

a

−

p

s

            

gdzie:

p

p

 – ciśnienie cząstkowe pary wodnej, 

          

p

a

– ciśnienie atmosferyczne, 

          

p

s

- ciśnienie cząstkowe gazu suchego. 

Wyróżnia się powietrze:

–

suche   nienasycone   wilgocią,   zawierające   parę   wodną   przegrzaną,     zdolne   do   wchłonięcia   pary 
wodnej w danej temperaturze

–

wilgotne nasycone wilgocią, zawierające suchą parę nasyconą, 

–

wilgotne przesycone wilgocią (zamglone), zawierające parę mokrą.

Gaz suchy oraz parę wodną w gazie wilgotnym (niskie ciśnienie pary) można traktować jak gaz doskonały.

Stan powietrza wilgotnego określają:

•

wilgotność bezwzględna 

ρ

p

=

m

p

V

 - masa pary wodnej zawarta w jednym metrze sześciennym 

powietrza wilgotnego, co jednoznacznie odpowiada gęstości pary, 

•

wilgotność względna 

=



p



nas



p ,T

=

p

p

p

nas



T

 – stosunek gęstości pary wodnej do gęstości pary 

suchej nasyconej, 

•

stopień suchości 

x=

m

p

m

p



m

c

 - masa pary wodnej (nasyconej suchej) zawartej w parze mokrej 

(ciecz nasycona + para nasycona), 

•

stopień zawilżenia 

X =

m

p

m

gs

 - masa pary zawartej w gazie suchym,

•

przedstawienie graficzne - wykres Moliera (i - X), 

•

równanie Clapeyrona: 

p⋅V =m

gs

⋅

1 X ⋅R⋅T

.

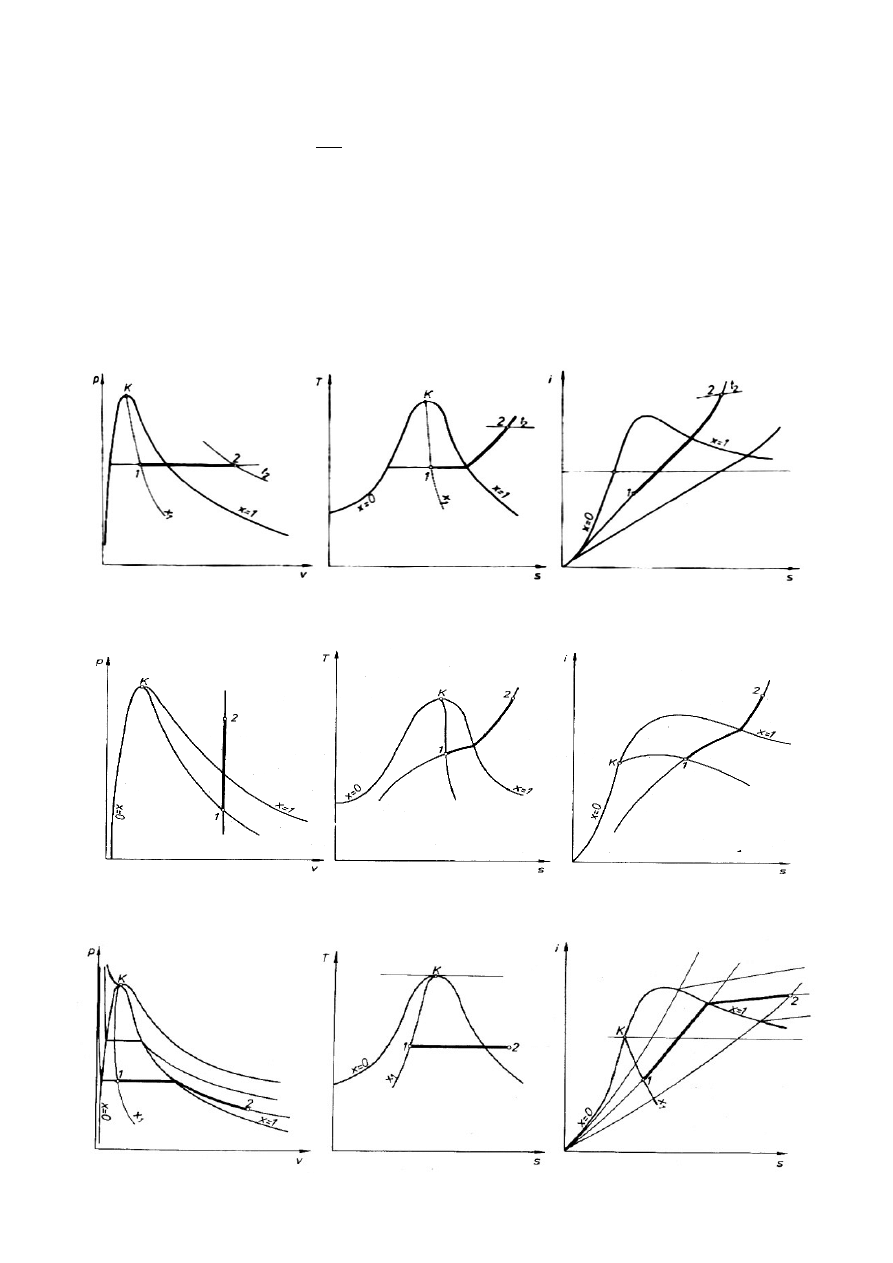
1.7. Przemiany charakterystyczne pary wodnej (układ p-v, T-s, i-s)

•

przemiana izobaryczna p = idem

•

przemiana izochoryczna V = idem

•

przemiana izotermiczna T = idem

•

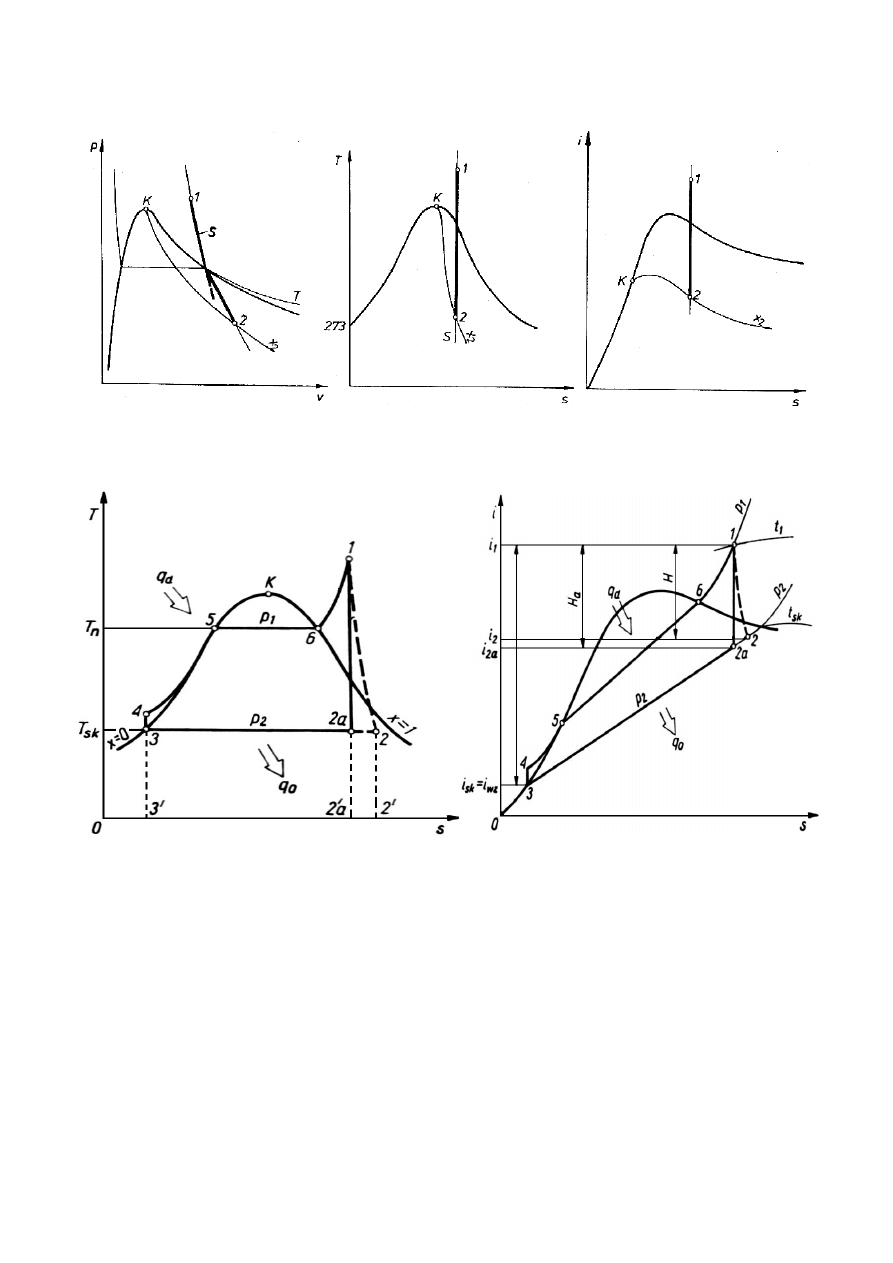
przemiana izentropowa (adiabatyczna bez tarcia) 

p⋅V



=

idem

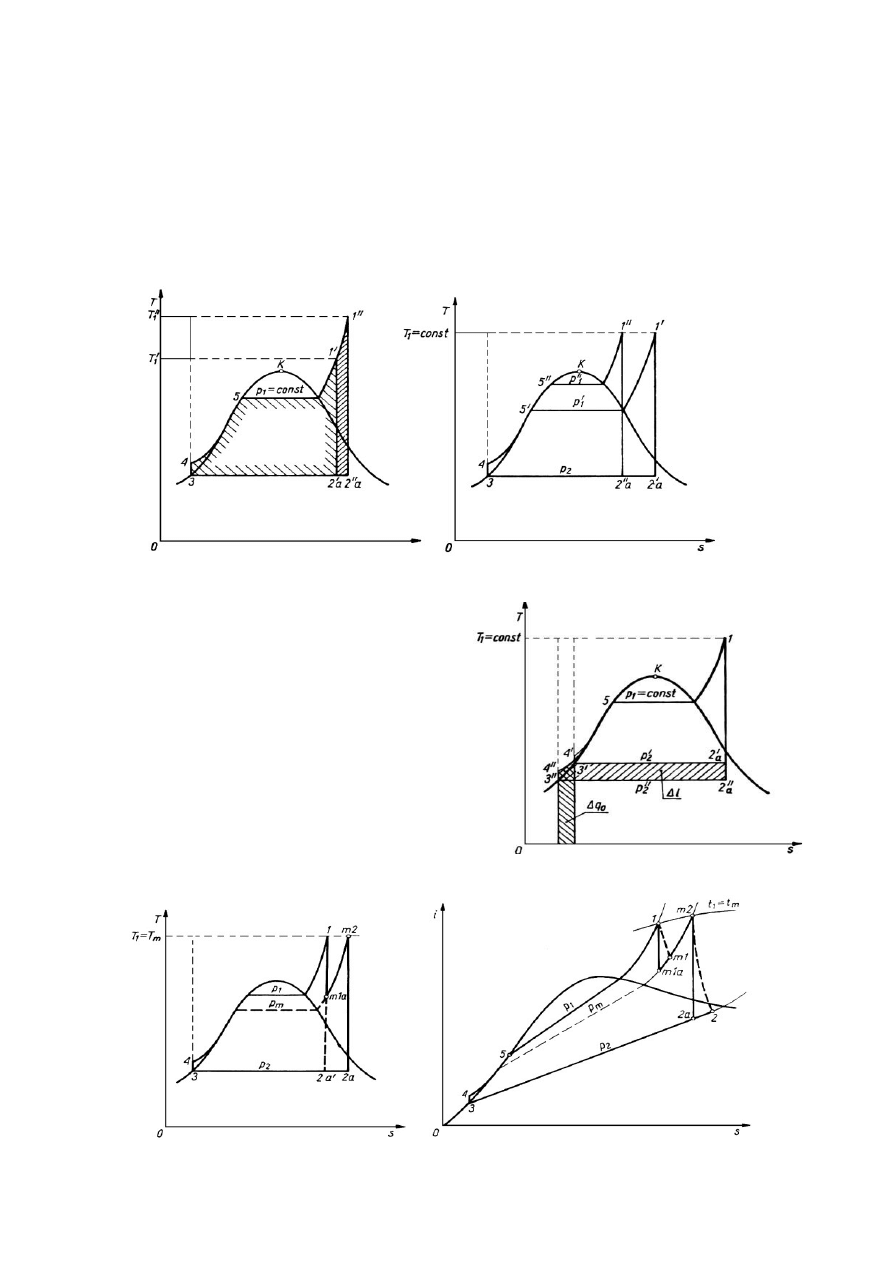
1.8. Obieg Clausiusa - Rankine'a. Metody podwyższania sprawności obiegu C-R.

[Pawlik, Strzelczyk, Elektrownie. str. 32]

Obieg Rankine’a elektrowni parowej 

kondensacyjnej: a) w układzie T-s; b) w układzie i-s

gdzie:  3 – 4 izentropowe sprężanie wody zasilającej przez pompę wody zasilającej;

4 – 5 podgrzewanie wody w kotle;
5 – 6 odparowanie wody;
6 – 1 przegrzewanie pary;
1 – 2 rozprężanie pary w turbinie;
2 – 3 skraplanie pary w skraplaczu;
qd – ciepło doprowadzone do obiegu;
qo – ciepło odprowadzone z obiegu.

Obieg Rankine’a jest obiegiem idealnej siłowni parowej i służy on do oceny pracy rzeczywistej siłowni. 
Idealna siłownia parowa jest to taka, w której: 

•

nie występuje tarcie, nie ma spadu ciśnienia podczas przepływu płynu rurociągiem i nie ma strat 
pracy przez tarcie w silniku i pompie; 

•

nie występują straty ciepła, ponieważ izolacja turbiny i rurociągów jest idealna; 

•

występuje izentropowa ekspansja, ponieważ turbina jest idealna; 

•

pompa zasilająca spręża kondensat izentropowo do ciśnienia kotłowego, nie występuje dławienie; 

•

całe ciepło spalania paliwa jest przekazywane czynnikowi obiegowemu, ponieważ kocioł jest 
idealny. 

Ogólnie zwiększenie sprawności realizuje się przez: zwiększenie sprawności termicznej obiegu, zwiększenie 
sprawności   poszczególnych   urządzeń,   zmniejszenie   zużycia   energii   na   potrzeby   własne.   Sposoby 
zwiększania sprawności obiegu CR:

•

zwiększenie parametrów pary świeżej doprowadzonej do turbiny = większa sprawność obiegu i 
mniejsze jednostkowe zużycie paliwa.

•

obniżenie parametrów w skraplaczu (ciśnienia pary wylotowej), realizowane przez:

- zwiększenie powierzchni kondensatora;
- zwiększenia przepływu wody przez 
kondensator;
- obniżenie temperatury wody chłodzącej.

•

międzystopniowe przegrzewanie pary

•

regeneracyjne podgrzewanie wody zasilającej - podgrzewanie kondensatu i wody zasilającej parą, 
która już częściowo wykonała pracę w turbinie. Liczba stopni podgrzewania = 7 - 9.

•

zwiększenie sprawności wewnętrznej turbiny, 

•

zwiększenie sprawności kotła, 

•

skojarzone wytwarzanie energii elektrycznej i cieplnej, 

•

zmniejszenie zużycia energii na potrzeby własne, 

•

skojarzenie obiegów o różnych czynnikach roboczych.

1.9.  Przewodzenie   i   przenikanie   ciepła.   Promieniowanie   cieplne.   Rodzaje 
wymiany ciepła – równania. Przekazywanie ciepła.

1.   Przewodzenie   ciepła  -   wymiana   ciepła   między   bezpośrednio   stykającymi   się   częściami   ciał,   brak 
makroskopowego ruchu substancji.

Prawo   Fouriera  -   gęstość   strumienia   przewodzonego   ciepła   jest   wprost   proporcjonalna   do   gradientu 
temperatury w kierunku prostopadłym do powierzchni izotermicznej.

q=−⋅grad⋅t=−⋅

dt

dn

, gdzie 



 - współczynnik przewodzenia ciepła, 

W

m⋅K

.

Największa wartość  



  mają metale (srebro, złoto, miedź), im lepszy przewodnik tym wartość  



 

rośnie.   Izolatory,   mają   strukturę   porowatą,   duży   udział   gazu,   np.   dla   styropianu   rzędu   setnych   części 

W / m⋅K 

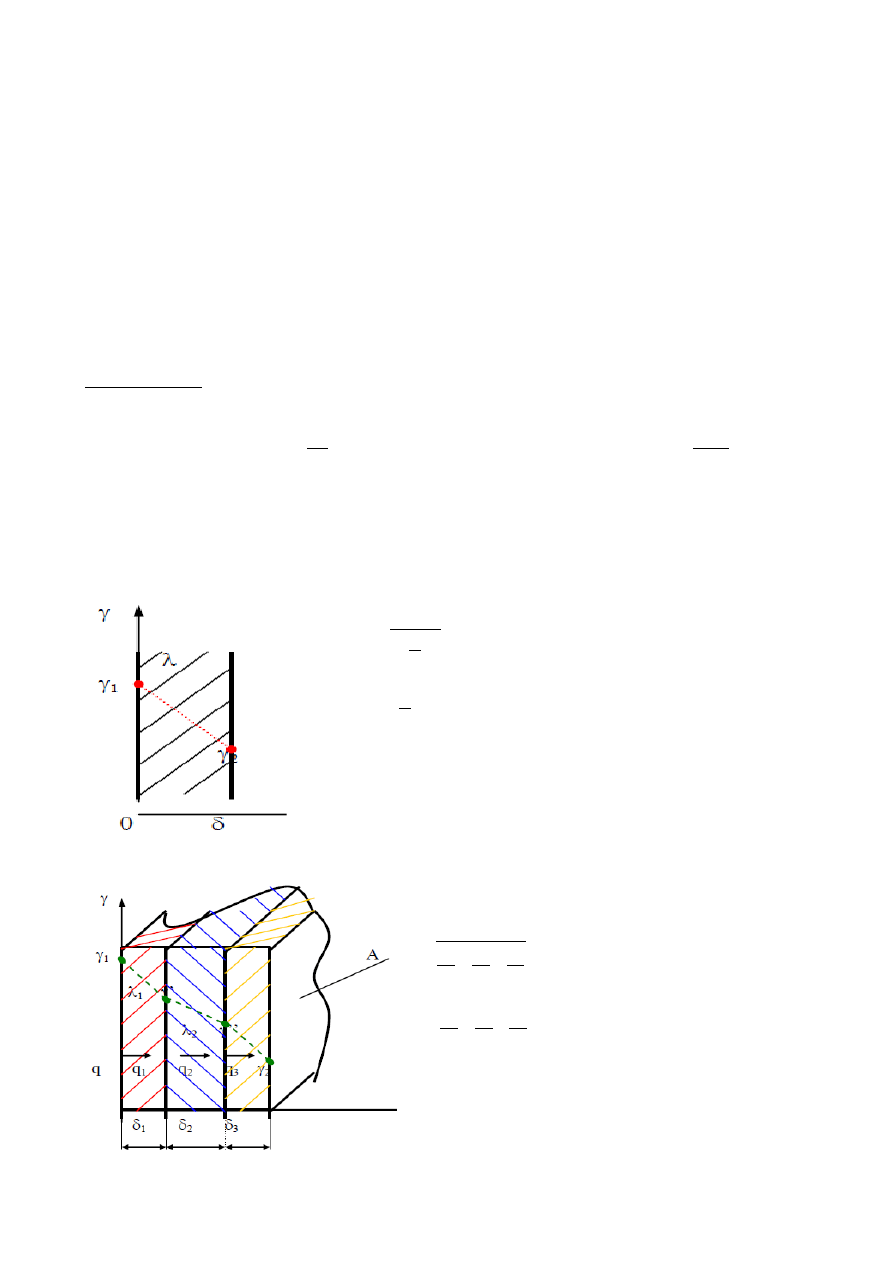
a) jednowymiarowe, ustalone przewodzenie przez ścianę płaską.

q=



1

−

2




   - gęstość strumienia ciepła

R



=




   - opór przewodzenia

b) przewodzenie przez warstwy o różnych 



 i różnych 



.

q=



1

−

2



1



1





2



2





3



3

   - gęstość strumienia ciepła

r



=



1



1





2



2





3



3

   - opór przewodzenia

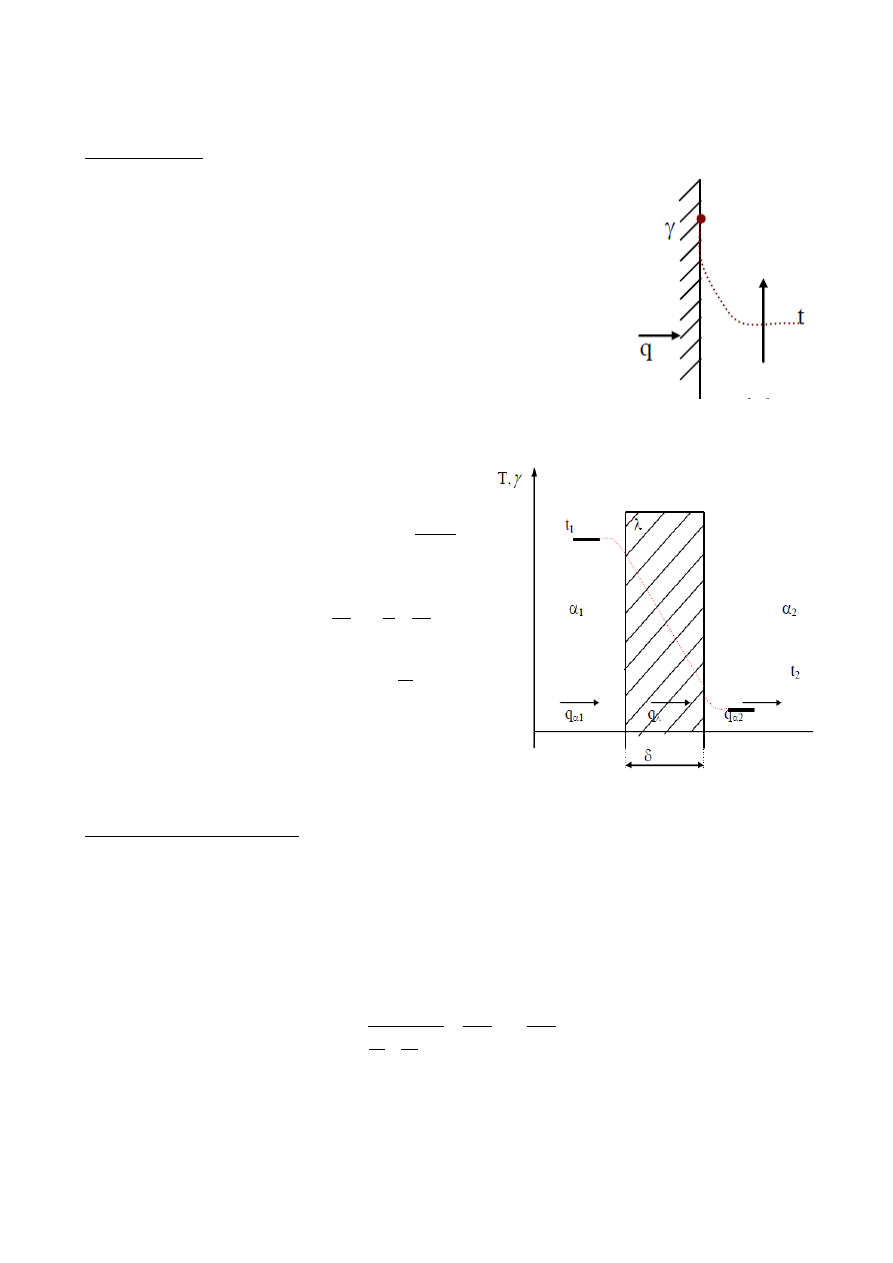
2. Przejmowanie ciepła (wnikanie) - wymiana ciepłą między powierzchnią ciała stałego a omywającym go 
płynem.

Prawo   Newtona  -   gęstość   strumienia   przejmowanego   ciepła   jest   wprost   proporcjonalny   do   różnicy 
temperatur powierzchni ciała stałego i płynu.

q=⋅t

s

−

t

p



, gdzie 



- wsp. przejmowania ciepła, 

W /m

2



  zależny  od   charakteru   przepływu   (liczba   Reynoldsa,   liczba   Prandtla), 

rodzaju płynu, kształtu opływanej powierzchni.
Największe



- przepływ ze zmienną fazą (wrzenie, skraplanie),  najmniejsze



- konwekcja naturalna, gdy czynnikiem jest gaz, 

(5,6 W/m

2

).

3. Przenikanie ciepła  - wymiana ciepła między dwoma płynami rozdzielonymi ścianką (ściankę płaską i 
walcową).

•

gęstość   strumienia   ciepła   przenikającego   przez 

ściankę płaską rozdzielającą płyny: 

q=

t

1

−

t

2

R

p

•

opór   przenikania   =   suma   oporów   przejmowania   i 

przewodzenia ciepła: 

R

p

=

1



1








1



2

•

współczynnik przenikania ciepła 

k =

1

R

•

strumień ciepła: 

Q= A⋅q= A⋅k⋅t

1

−

t

2



4. Promieniowanie cieplne (fale elektromagnetyczne).

Prawo Stefana  

 

 –  

   Boltzmanna

 

   – wielkość  strumienia energii przenoszonego w wyniku promieniowania 

cieplnego jest proporcjonalna do temperatury w czwartej potędze:

=⋅⋅

T

4

, 

W /m

2

, gdzie:



 - stała Stefana - Bolzmanna (promieniowania ciała doskonale czarnego 

5,67⋅10

−

8

W /m

2

⋅

K

4

),



 = 0 – 1 – emisyjność (0 – ciało białe; 1 – ciało doskonale czarne).

•

gęstość   strumienia   ciepła   wymienianego   przez   promieniowanie   pomiędzy   równoległymi 

powierzchniami płaskimi: 

q

1,2

=

C

0

1



1



1



2

−

1

⋅[

T

1

100



4

−

T

2

100



4

]

, 

gdzie 

C

0

 - stała promieniowania powierzchni doskonale czarnej, 



 - emisyjność względna.

•

temperaturę płomienia wylicza się z średniej temperatury w całym palenisku.

1.10.   Spalanie   paliw   stałych,   ciekłych,   gazowych   -   specyfika   spalania, 
stechiometria.

Zapłon - intensywna reakcja egzotermiczna wywołana w mieszaninie palnej, najpowszechniejszy sposób 
doprowadzania mieszaniny palnej do procesu spalania. Wyróżnia się:
zapłon wymuszony - iskra elektryczna, płomień pilotujący, gorące ścianki lub spaliny, 
samozapłon - równomierne podgrzewania całej masy mieszaniny palnej.

1.10.1.  Paliwa stałe  (1.10. A. pdf).w energetyce: węgiel, muły węglowe, koks petrochemiczny, biomasa, 
odpady.

Organizacja spalania węgla (1.10.A str. 1 -2):
a) paleniska rusztowe: 

•

z rusztem stałym (muł, miał, drobny groszek, orzech, gruby), 

•

z rusztem ruchomym (groszek, orzech 10 - 30 mm),

b) złoże fluidalne:

•

pęcherzykowe (< 25 mm) - kotły mniejszej mocy, 

•

cyrkulujące (< 6 mm) - energetyka zawodowa,

c)płomień pyłowy (węgiel kamienny: R

90

 = 25-30%, R

200

 < 8%, węgiel brunatny: R

90

 = 48-55%, R

200

 = 25-

32%, R

1000

 = 3-5%)

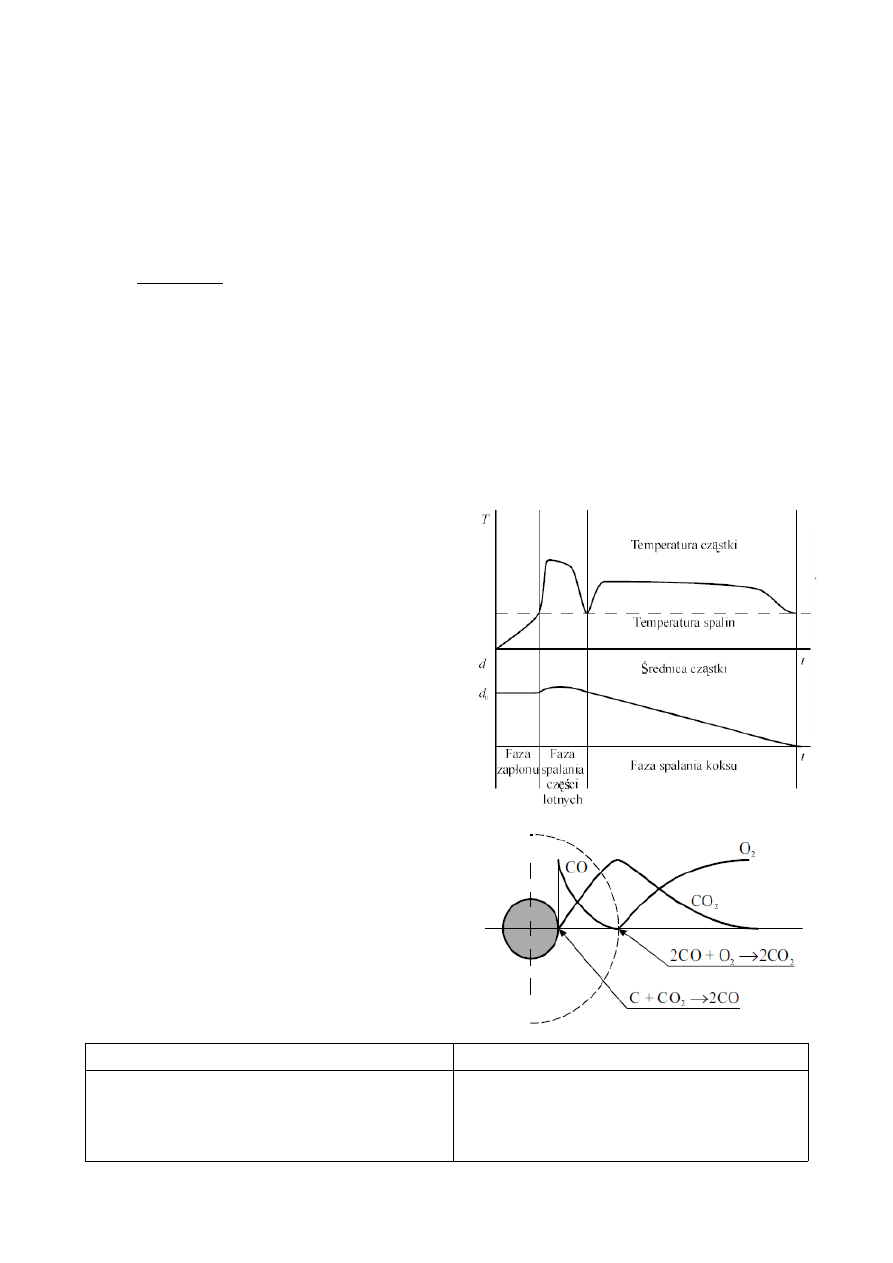
1. Spalanie pojedynczej cząstki węgla, etapy:

•

nagrzewanie   -   po   utracie   wody   temperatura 
cząstki   wzrasta,   aż   do   zapoczątkowania 
termicznego   rozkładu   węgla   (pirolizy).     Czas 
potrzebny   do   uzyskania   temperatury   zapłonu   - 
czas indukcji zapłonu.

•

zapłon części lotnych

•

wydzielenie   i   spalenie   części   lotnych   - 
wydzielone   z   węgla   części   lotne   ulegają 
zapłonowi i spalają się w płomieniu gazowym, a 
przekazywane   od   płomienia   ciepło   przyspiesza 
pirolizę węgla.

•

spalanie pozostałości koksowej - pozostałość 
koksowa   po   odgazowaniu   węgla, 
bezpłomieniowy   charakter   reagowania   z 
tlenem   z   powietrza,   spala   się   powoli   czas 
spalania   pozostałości   koksowej   jest   o   rząd 
wielkości większy od czasu spalania części 
lotnych), temperatura spalania cząstki węgla: 
1300-1700

o

C.

Procesy fizyczne

Procesy chemiczne

•

parowanie wody (suszenie)

•

pęcznienie (dylatacja) cząstek węgla

•

powstawanie porowatej struktury karbonizatu

•

przemiany fizyczne substancji mineralnej

•

piroliza węgla

•

spalanie części lotnych

•

spalanie pozostałości koksowej

•

przemiany chemiczne substancji mineralnej

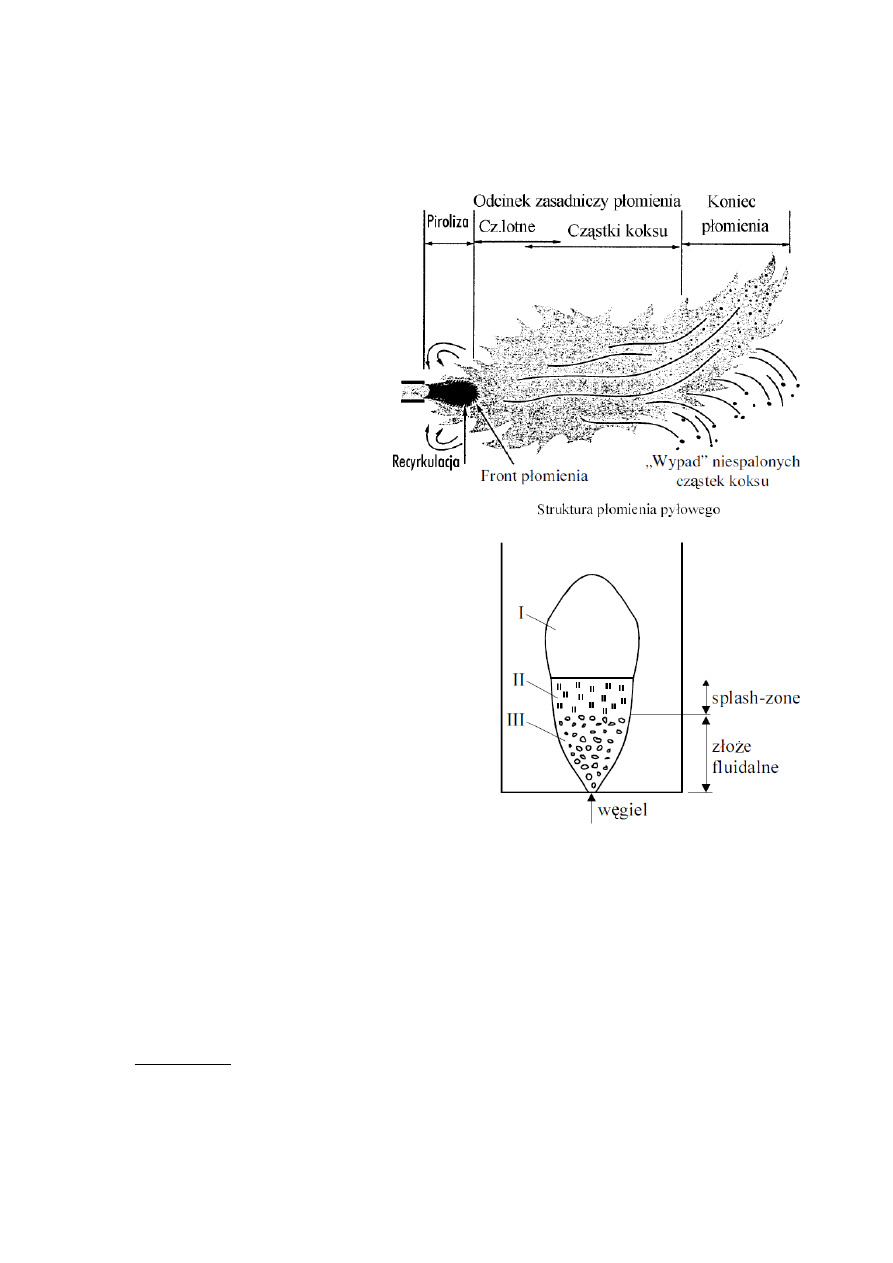
2. Spalanie pyłu węglowego (1.10.A str. 19).

Płomień pyłowy - wypływające z dyszy palnika pyłowego turbulentna struga mieszanki pyłowo-gazowej. 
Wstępujące do warstwy granicznej gorące spaliny mieszają się ze świeżą mieszanką, przyczyniając się do 
zapłonu cząstek węgla. 
I - rdzeń gęstej strugi mieszanki, w której 
następuje   wydzielenie   części   lotnych,   na 
którego   brzegu   formuje   się   front   spalania 
części   lotnych   i   mikronowych   cząstek 
węgla.

II   -   strefa   spalania   części   lotnych, 
charakteryzujący   się   silnym   promieniem. 
Strefy spalania części lotnych i pozostałości 
koksowej   stanowią   zasadniczy   odcinek 
płomienia pyłowego.

III   -   koniec   tworzy   strefa   dopalania 
większych cząstek węgla.

3.  Spalanie   w   warstwie   fluidalnej   (1.10.A 
str. 28).

Zróżnicowanie uziarnienie złoża = segregacja złoża. Dolną 
gęstą   część   warstwy   fluidalnej   o   charakterze 
pęcherzykowym tworzą grubsze frakcje cząstek, drobniejsze 
frakcje - część górną, a frakcje najdrobniejsze - wynoszone 
do górnej części paleniska zakończonego separatorem pyłu, 
z   którego   cząstki   są   zawracane   do   dolnej   części   kotła. 
Materiał złoża składa się z:

•

węgla (3% na dole, 5% u góry), 

•

popiołu, 

•

sorbentu wapniowego, 

•

piasku (krzemionki) tworzącego złoże pierwotne.

Budowa złoża:
I - gęsta część, nagrzewanie i odgazowanie węgla, spalanie 
części   lotnych   w   formie   pęcherzy,   spalanie   większych 
cząstek pozostałości koksowej (charakter dyfuzyjny).
II - splash-zone, rzadka strefa pośrednia, kinetyczne spalanie części lotnych, 
III - dyfuzyjne spalanie części lotnych.

Zalety:

•

czas przebywania cząstek węgla w złożu zależny od wypalenia,

•

niska temperatura w warstwie (750-950

O

C), niższa od temp. mięknięcia popiołu; wiązanie SO

2

 przez 

sorbenty wapniowe w 850

O

C.

•

czas indukcji zapłonu o 50% krótszy niż w płomieniu pyłowym.

•

duża sprawność spalania, małą emisja NO

x

, SO

2

, możliwość spalania paliw odpadowych. 

1.10.2. Paliwa ciekłe (1.10. B. pdf).

Fazy spalania paliwa ciekłego:

•

odparowanie, 

•

spalanie par.

1. Spalanie pojedynczej kropli paliwa.

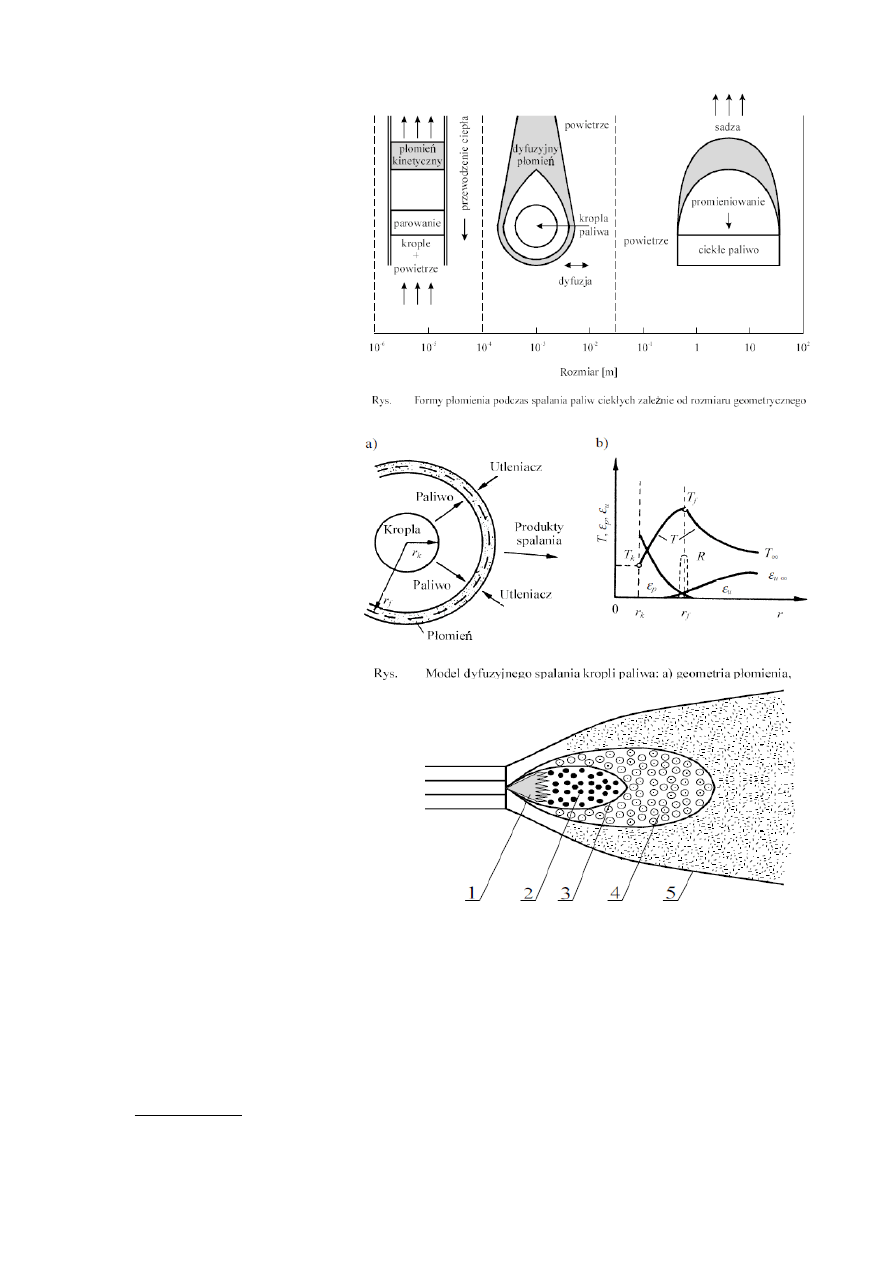
Spalanie   paliwa   ciekłego   polega 
głównie na rozpyleniu i spaleniu zbioru 
kropel,   wg   modelu   sferyczno   - 
symetrycznego.

a) małe krople szybko parują, a 

pary   tworzą   z   powietrzem 
homogeniczną   mieszaninę   palną. 
Płomień   ma   charakter   kinetyczny. 
Szybkość   spalania   =   prędkość 
propagacji płomienia.

b)   większe   krople   spalają   się 

indywidualnie. Wokół kropli tworzy się 
dyfuzyjny   płomień,   do   którego   tlen 
dopływa z otoczenia, a pary dopływają 
z   powierzchni   kropli.   Szybkość 
spalania = szybkość parowania.

c) największe krople: unoszące 

się gorące produkty spalania powodują 
napływ   na   powierzchnię   cieczy 
chłodniejszego powietrza zmniejszając 
gradient temperatury. Dostęp powietrza 
do par jest utrudniony, dlatego płomień 
jest bogaty i produkuje szadzę. Ciepło 
od płomienia do paliwa przekazywane 
głównie przez promieniowanie.

2. Płomień rozpylonego paliwa.

1 - strefa rozpylonej cieczy, 
2 - strefa parowania -duża koncentracja kropel, 
brak spalania, płomień na granicy strefy, 
3   -   strefa   zapłonu   (zapłon   par   i   spalanie 
homogeniczne),  
4   -   strefa   spalania   indywidualnego   kropel 
(heterogeniczne), 
5 - granice płomienia.

W   celu   zwiększenia   szybkości   spalania   i   poprawy  stabilności   płomienia   tworzy  się   wewnętrzne   strefy 
recyrkulacji   spalin   wzbogaconych   paliwem   poprzez   zawirowanie   strugi   powietrza.   Rozpylanie   paliw 
ciekłych za pomocą rozpylaczy:

•

strumieniowych,

•

wirowych, 

•

strumieniowo - wirowych, 

•

pneumatycznych, 

•

rotacyjnych.

1.10.3. Paliwa gazowe (1.10. C. pdf).

1.10.4. Stechiometria.

1. Znajomość składu paliwa oraz mas molowych podstawowych pierwiastków i ich związków (C, 
H, N, S, O, CH4, C2H6, SO2, etc.)

a) Paliwa gazowe: metan, etan, propan, butan – wzór C

n

H

2n+2

2. Umiejętność zapisu i uzgodnienia reakcji spalania

a) Reakcje utleniania wszystkich składników palnych paliwa w celu wyznaczenia teoretycznego 
zapotrzebowania na tlen

m

O2

=

∑



m

i

⋅

X

i



– udział masowy O

2

w paliwie

, 

gdzie:

m

i

– ilość tlenu potrzebna do spalenia składnika i

X

i

−

udział składnika i w paliwie

b) Uogólnione równanie spalanie:

1 mol  paliwamO

2



3,76⋅N

2

=

n

1

⋅

CO

2



n

2

⋅

H

2

On

3

⋅

COn

4

⋅

H

2



n

5

⋅

O

2



n

6

⋅

N

2



n

7

⋅

SO

2

Należy   zapamiętać,   że   dla   paliwa   gazowego   podawane   są   udziały   objętościowe,   które   są 
równoważne udziałom molowym, natomiast dla paliwa stałego podaje się udziały masowe, które w 
uogólnionym   równaniu   spalania   należy   podzielić   przez   masy   molowe   poszczególnych 
pierwiastków.

c) W zależności od warunków spalania:

•

λ<1 nie występuje człon  n

5

O

2

•

λ=1 nie występują człony n

5

O

2

,

  

n

3

CO,  n

4

H

2

•

λ>1 nie występują człony n

3

CO,  n

4

H

2