L

ABORATORIUM FIZYCZNE

Instytut Fizyki Politechniki Krakowskiej

ĆWICZENIE

7

Wyznaczanie współczynnika lepkości cieczy

Ćwiczenie 7

2

ĆWICZENIE

7

Wyznaczanie współczynnika lepkości cieczy

Anna Foryś

O p r a w ę g r a f i c z n ą i p r z y g o t o w a n i e n a p l a t f o r m i e M o o d l e w y k o n a ł a B o ż e n a B u r t a n

1.

Wprowadzenie

Celem ćwiczenia jest wyznaczenie wartości współczynnika lepkości cieczy (oleju) na podstawie

prawa Stokesa.

Lepkość

– tarcie wewnętrzne, to właściwość nie tylko cieczy, ale także gazów. Ciecze

i gazy nazywamy płynami . Tarcie wewnętrzne polega na oddziaływaniach występujących przy wza-
jemnym przesuwaniu się elementów (obszarów) płynu. Miarą tych oddziaływań są

siły tarcia

we-

wnętrznego lub lepkości występujące przy wzajemnym przesuwaniu się elementów cieczy lepkich
lub gazu. Jak wiele innych zjawisk w fizyce, zjawisko to wiąże się z charakteryzującym je współczyn-
nikiem, zwanym

współczynnikiem lepkości

.

W naszym ćwiczeniu zajmiemy się wyznaczeniem współczynnika lepkości cieczy. Elementy cie-

czy mogą przesuwać się nawzajem względem siebie przy różnego rodzaju przepływach ( np.

prze-

pływ laminarny czy turbulentny

). W przepływie laminarnym ciecz płynie równoległymi warstwami z

różnymi prędkościami, w odróżnieniu od przepływu burzliwego (inaczej turbulentnego), w którym
wektor prędkości elementów cieczy zmienia się chaotycznie.

Gdy różnego rodzaju ciała stałe przemieszczają się w spoczywającej cieczy lepkiej, również po-

wodują one przemieszczanie się wzajemne elementów cieczy, co powoduje wystąpienie sił oporu
lepkiego. W tym ostatnim przypadku mówimy o oporach ruchu, jakich doznają poruszające się ciała
stałe w płynach. Opory ruchu nie tylko zależą od właściwości lepkich cieczy, ale również zależą
istotnie od kształtu poruszającego się ciała i jego prędkości. Hydrodynamika jest tą dziedziną wie-
dzy, która zajmuje się zarówno prawami rządzącymi przepływami różnego typu płynów, jak również
prawami opisującymi zjawisko oporu ciał stałych poruszających się w płynach.

Wielkością, pozwalającą scharakteryzować rodzaj przepływu lub zakres stosowalności praw opi-

sujących opory ruchu, jest bezwymiarowy parametr Re zwany

liczbą Reynoldsa

:

(1.1)

a)

b)

Rys.1. Przepływ cieczy (a) przepływ laminarny (b) przepływ turbulentny

Źródło:

http://www.if.pw.edu.pl/~bibliot/archiwum/adamczyk/WykLadyFO/FoWWW_18.html

3

gdzie:

ρ

jest gęstością cieczy, – średnią (w przekroju poprzecznym) prędkością strugi,

η

– współ-

czynnikiem lepkości, a – charakterystycznym rozmiarem liniowym przekroju poprzecznego strugi
cieczy (np. promieniem rurki) lub ciała poruszającego się w cieczy (np. promieniem kulki). Poniżej
krytycznej wartości liczby Reynoldsa przepływ ma charakter laminarny, natomiast w przypadku ruchu
ciał w cieczach poprawność stosowania praw rządzących oporami ruchu zależy od wartości parame-
tru

.

W punkcie 1.1 wprowadzimy definicję współczynnika lepkości cieczy. W wyniku wzajemnego prze-

suwania się elementów cieczy (w ruchu laminarnym warstw) występują w cieczy lepkiej naprężenia
wewnętrzne . Rozważmy małą, płaską powierzchnię warstwy cieczy o polu w ruchu laminarnym
(rys. 2).W wyniku sił tarcia wewnętrznego na powierzchnię tę stycznie do niej działa siła o wartości .

Naprężeniem stycznym

wywołanym siłą

tarcia wewnętrznego

nazywamy z definicji iloraz wartości tej

siły przez pole powierzchni warstwy

1.1

Definicja współczynnika lepkości cieczy

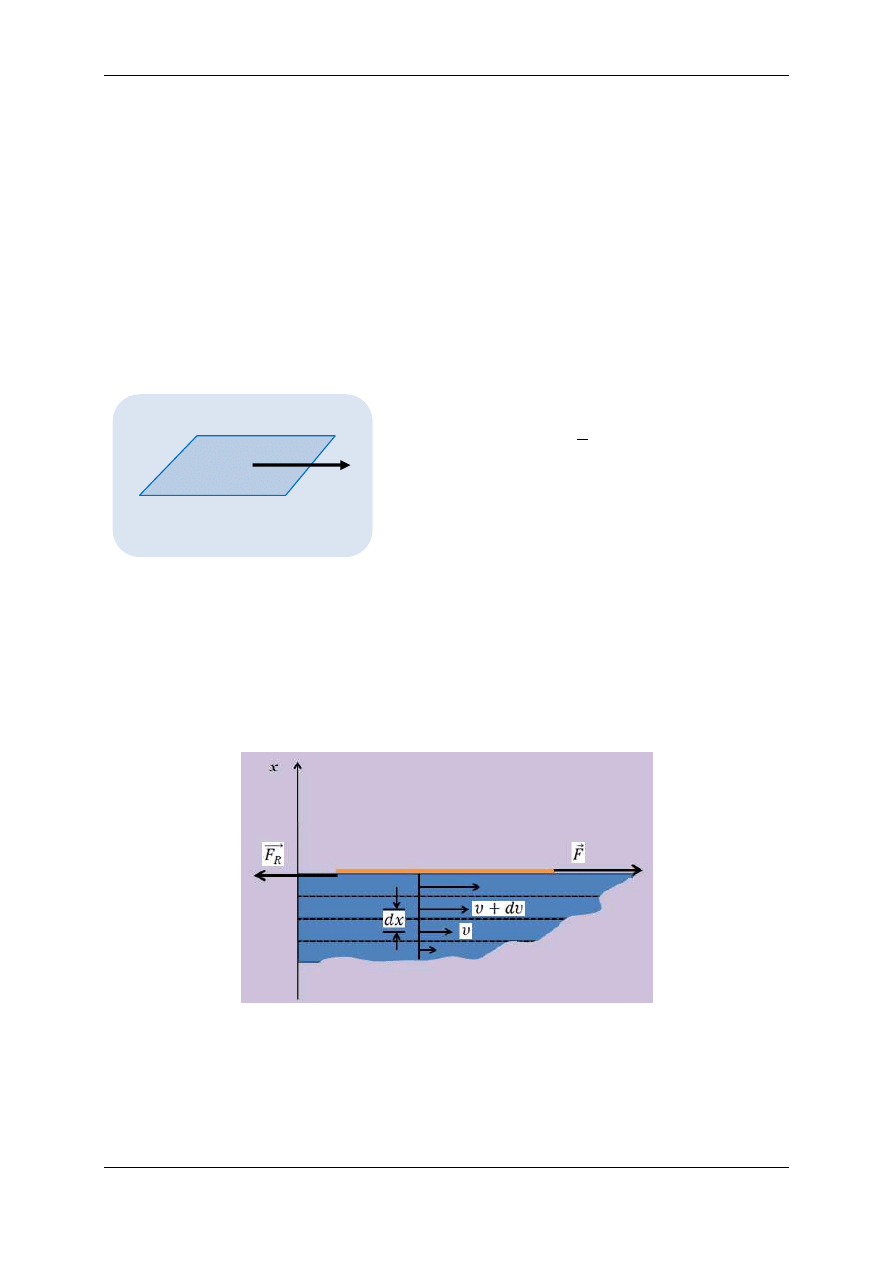
Aby zilustrować zjawisko tarcia wewnętrznego i zrozumieć definicję współczynnika lepkości, wy-

obraźmy sobie obszar cieczy, w którym przepływ jest warstwowy (laminarny), rys.3. Można to na
przykład zrealizować przesuwając po powierzchni cieczy bardzo cienką, doskonale zwilżalną płytkę ze
stałą prędkością, równoległą do tej powierzchni.

Rys.3. Rozkład prędkości w warstwie cieczy.

Doświadczenia wykazują, że do płytki należy wówczas przyłożyć stałą siłę

,

równoległą do po-

wierzchni cieczy. Siłę równoważy siła lepkości

. Siła lepkości występuje między warstewką przy-

legającą do płytki i warstewką następną oraz między każdą sąsiednią parą warstewek. Poszczególne

(1.2)

Rys.2. Definicja naprężenia stycznego

Ćwiczenie 7

4

Rys.4. Przechodzenie cząsteczek cieczy
między warstwami (transport cząsteczek)

warstewki cieczy przesuwają się (ślizgają się) równolegle względem siebie, przy czym rozkład prędko-
ści w zależności od współrzędnej przedstawiono na rys.3. Doświadczalnie stwierdzono, że dla więk-
szości cieczy (nazywanych

cieczami niutonowskimi

) wartość siły lepkości jest proporcjonalna do pola

powierzchni elementu warstewki oraz do wartości bezwzględnej pochodnej

.

Wobec tego po skorzystaniu z (1.2) mamy:

(1.3)

gdzie

jest przyrostem prędkości warstewek cieczy znajdujących się w odległości

.

Współczynnik proporcjonalności

η

we wzorze (1.3) nazywamy

współczynnikiem lepkości

.

DEFINICJA:

Wzór (1.3) jest definicją współczynnika lepkości η cieczy (lub gazu). Jego wymiarem jest

:

N ∙ s ∙ m

Pa ∙ s.

Współczynnik lepkości zależy od rodzaju cieczy, temperatury oraz ciśnienia. Wyżej opisane doświad-
czenie może być wykorzystane do opracowania metody jego pomiaru.

Postaramy się teraz krótko wyjaśnić mechanizm tarcia wewnętrznego. Siła lepkości uwarunko-

wana jest dwoma czynnikami: istnieniem sił spójności (w gazie nie występują) oraz ruchem termicz-
nym cząsteczek, który zachodzi również między warstewkami cieczy o różnych prędkościach. Prze-
chodzenie cząsteczek między warstewkami nie zmienia charakteru ruchu tzn. ruch pozostaje lami-
narny. Cząsteczki z warstwy o większej prędkości przechodzą do warstwy o mniejszej prędkości, przy-
spieszając ją. Średnio taka sama liczba cząsteczek przechodzi z warstwy o mniejszej prędkości do
warstwy o większej prędkości, spowalniając ją. W miarę wzrostu temperatury siły spójności maleją.
Stąd w cieczach ze wzrostem temperatury współczynnik lepkości maleje. Przeciwnie jest dla gazów.

Zjawisko tarcia wewnętrznego jest jednym z przykładów

zjawisk transportu

, kiedy gradient jednej

wielkości fizycznej jest przyczyną transportu (przenoszenia się) innej wielkości fizycznej. W przypadku
tarcia wewnętrznego gradient prędkości jest przyczyną transportu pędu cząsteczek.

5

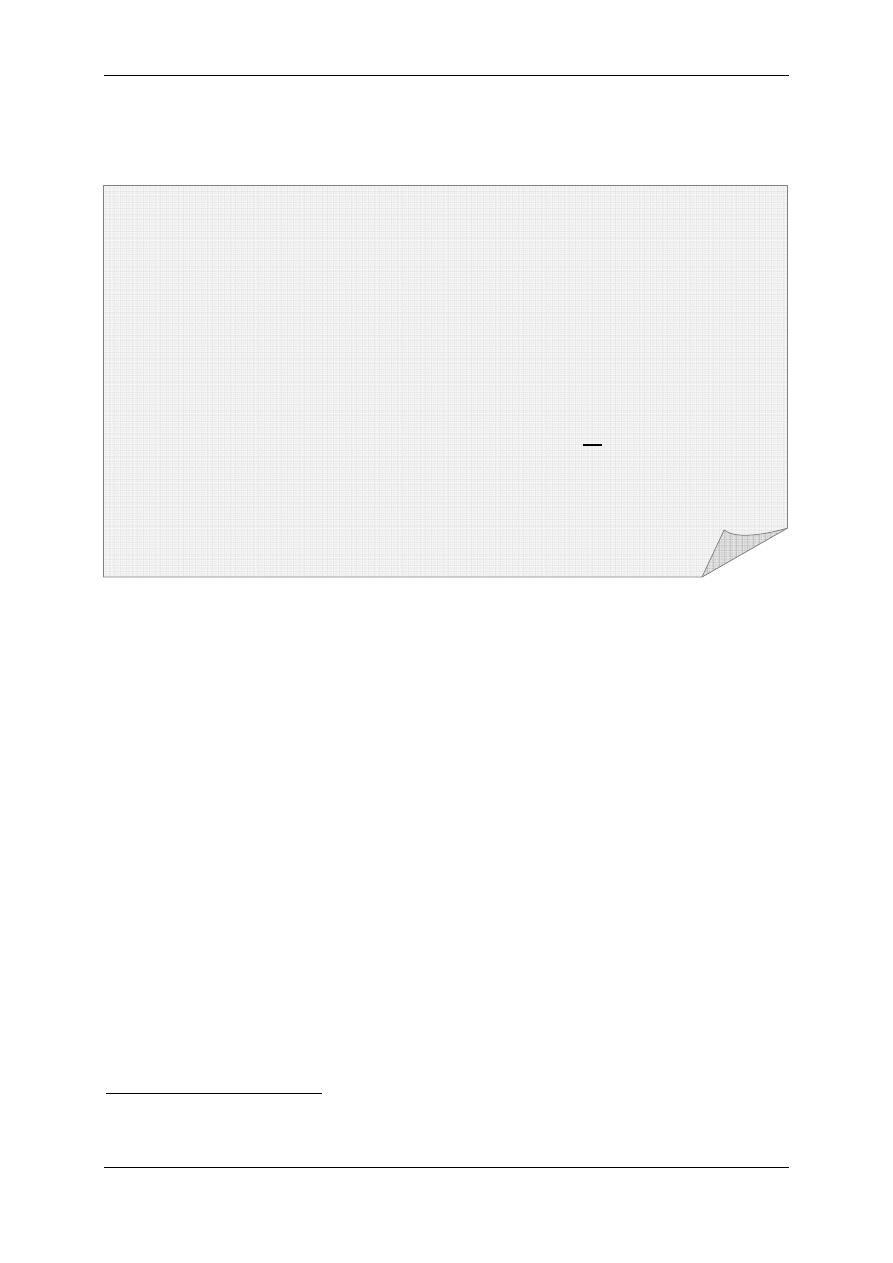
Rys.5. Siły działające na kulkę

spadającą w lepkiej cieczy

1.2

Opory ruchu. Prawo Stokesa

Opory ruchu występują podczas ruchu dowolnego ciała w płynie. Występują przy ruchu samo-

chodu czy samolotu w powietrzu. Występują również przy spadaniu dowolnych ciał, na przykład
kropli deszczu w powietrzu, kuli w cieczy itd.

Współczynnik lepkości cieczy wyznaczymy w tym ćwiczeniu opierając się na prawie Stokesa. Pra-

wo to podaje wzór na siłę oporu w przypadku ruchu kuli w cieczy lub gazie.

Przyjmijmy, że w cieczy lepkiej, dla której

≪ 1, spada kulka z niewielką prędkością .

Spadająca kulka pociąga za sobą, z powodu ist-
nienia sił międzycząsteczkowych, sąsiadujące z
kulką warstwy cieczy. Układ warstw cieczy ślizga-
jących się po sobie posiada różne prędkości.
Kulka razem z warstewką cieczy do niej przy-

legającą doznaje działania siły oporu lepkiego

4

5

. Oprócz siły oporu 4

5

na spadającą kulkę

działają: siła ciężkości = oraz siła wyporu >,

dana prawem Archimedesa (rys.5). Punktem
zaczepienia wszystkich sił jest środek kulki.

Wartość siły oporu F

0

zależy od wielkości i kształtu poruszającego się ciała, od prędkości ciała

oraz od rodzaju cieczy, w której ciało porusza się. Dla kulki o promieniu

@ jest ona określona prawem

Stokesa:

A

= 6C @ .

(1.4)

Można wykazać, że po pewnym czasie ustali się ruch jednostajny kulki (patrz: Uzupełnienie).

Zgodnie z

ІІ zasadą dynamiki Newtona mamy wówczas:

E + G +

A

= 0.

(1.5)

czyli

4

3 C@

K

L

M −

4

3 C@

K

M − 6C @ = 0.

(1.6)

gdzie:

L

, są odpowiednio gęstością kulki i gęstością cieczy, M jest przyspieszeniem ziemskim. Wy-

znaczony na podstawie wzoru (1.6) współczynnik lepkości jest równy:

=

(

L

− )M

18

,

(1.7)

gdzie

= 2@.

Liczba Reynoldsa

dla kulki o promieniu r poruszającej się w cieczy określona jest wzorem:

=

@

.

(1.8)

Ćwiczenie 7

6

Prawo Stokesa jest słuszne dla

< 0,4. Wówczas otaczająca kulkę ciecz tworzy warstwy przesuwa-

jące się względem kulki, gdy kulka spada (laminarny ruch względny cieczy).

2.

Metoda pomiaru. Wykonanie ćwiczenia

Aby wyznaczyć współczynnik lepkości cieczy (często w podręcznikach zwanym współczynnikiem

lepkości dynamicznej) stosujemy wzór Stokesa. Metoda pomiaru została podana w punkcie 1.2. Po-
służymy się wyprowadzonym tam wzorem 1.7. Używamy kuleczek polistyrenowych. Sprawdzamy
przed pomiarem, czy wybrana kulka nie zawiera pęcherzyków powietrza

.

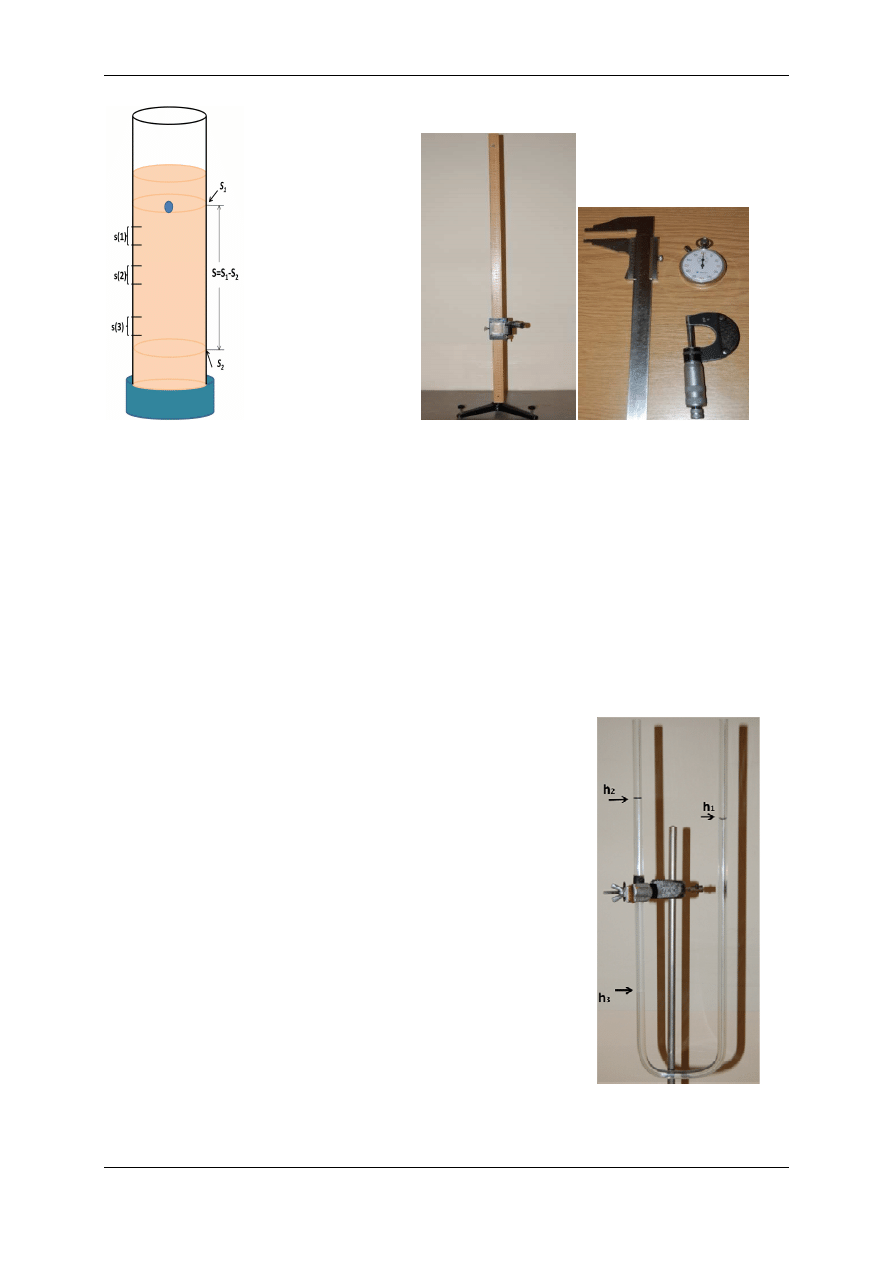
Stanowisko pomiarowe składa się ze szklanego cylindra z zaznaczonymi poziomami poniżej pew-

nej warstwy oleju (rys. 6 ), katetometru

1

, stopera, śruby mikrometrycznej oraz suwmiarki (fot.1).

Konieczny jest również przy stanowisku pomiarowym termometr. Cylinder wypełniono cieczą - ole-
jem. Należy wyznaczyć jego gęstość

ρ

2

.

Zaproponowana w ćwiczeniu metoda pomiaru współczynnika lepkości cieczy wymaga spełnienia

pewnych warunków, aby pomiar był wykonany poprawnie i można było zastosować wzór (1.7) ( po-
równaj wyprowadzenie w punkcie 1.2 ). Sprawdzenia tego dokonamy w punktach 1* i 2*:

1

*

. Sprawdzimy, czy na drodze

T odbywa się ruch jednostajny

2

*

. Sprawdzimy, czy

< 0,4, aby można stosować prawo Stokesa

W pomiarach sprawdzających wyznaczamy tylko raz lub dwa razy wielkości mierzone bezpośrednio.
W punktach 1*, 2* nie obliczamy niepewności.

1

Katetometr jest przyrządem pozwalającym mierzyć odległości pionowe lub przesunięcia pionowe z pewnej

odległości. Opis budowy i posługiwania się katetometrem dołączony jest do instrukcji znajdującej się na stole
laboratoryjnym.

Pamiętaj

W cieczach rzeczywistych występuje zjawisko lepkości, czyli tarcia wewnętrznego.

Przepływy laminarne zachodzą wówczas, gdy elementy cieczy poruszają się w warstwach, z
których każda ma inną, ale stałą prędkość.

W przepływach turbulentnych nie można wyróżnić takich warstw, elementy cieczy poruszają
się chaotycznie.

Wartość liczby Reynoldsa pozwala określić czy ruch będzie laminarny czy turbulentny oraz
jej odpowiednia wartość pozwala na zastosowanie prawa Stokesa.

Dla cieczy lepkich, niutonowskich naprężenie styczne powstające przy przesuwaniu się

sąsiednich warstw w ruchu laminarnym jest proporcjonalne do

U U.

Współczynnik lepkości charakteryzuje ciecz i jest zdefiniowany wzorem (1.3)

.

Współczynnik lepkości cieczy zależy od rodzaju cieczy i wyraźnie od temperatury.

7

Rys. 6. Cylinder

.

Fot.1. Przyrządy używane w pomiarach: katetometr, stoper,

śruba mikrometryczna oraz suwmiarka

.

Proponujemy

następującą kolejność wykonania pomiarów:

Zadanie 1. Wyznaczamy gęstość oleju

Zadanie 2. Wyznaczamy współczynnik lepkości

2.1

Wykonanie zadania 1.

Do wyznaczenia gęstości

ρ

2

oleju za pomocą naczyń połączo-

nych (patrz: ćwiczenie poświęcone metodom wyznaczania tej
wielkości) dokonujemy pomiaru położenia: h

1

- swobodnej po-

wierzchni wody destylowanej, h

2

- swobodnej powierzchni oleju,

h

3

-powierzchni zetknięcia oleju i wody destylowanej. Wielkości te

mierzymy posługując się katetometrem.

Mierzymy temperaturę t oleju. Gęstość

ρ

w

wody destylowa-

nej w tej temperaturze odczytujemy z tablic.

Szacujemy wielkość przedziału granicznego

∆W związanego z

odczytem poziomów.

Wyniki zapisujemy w tabeli 1.

Rys.7. Naczynie połączone, tzw.
U-rurka stosowane do wyzna-
czenia gęstości oleju

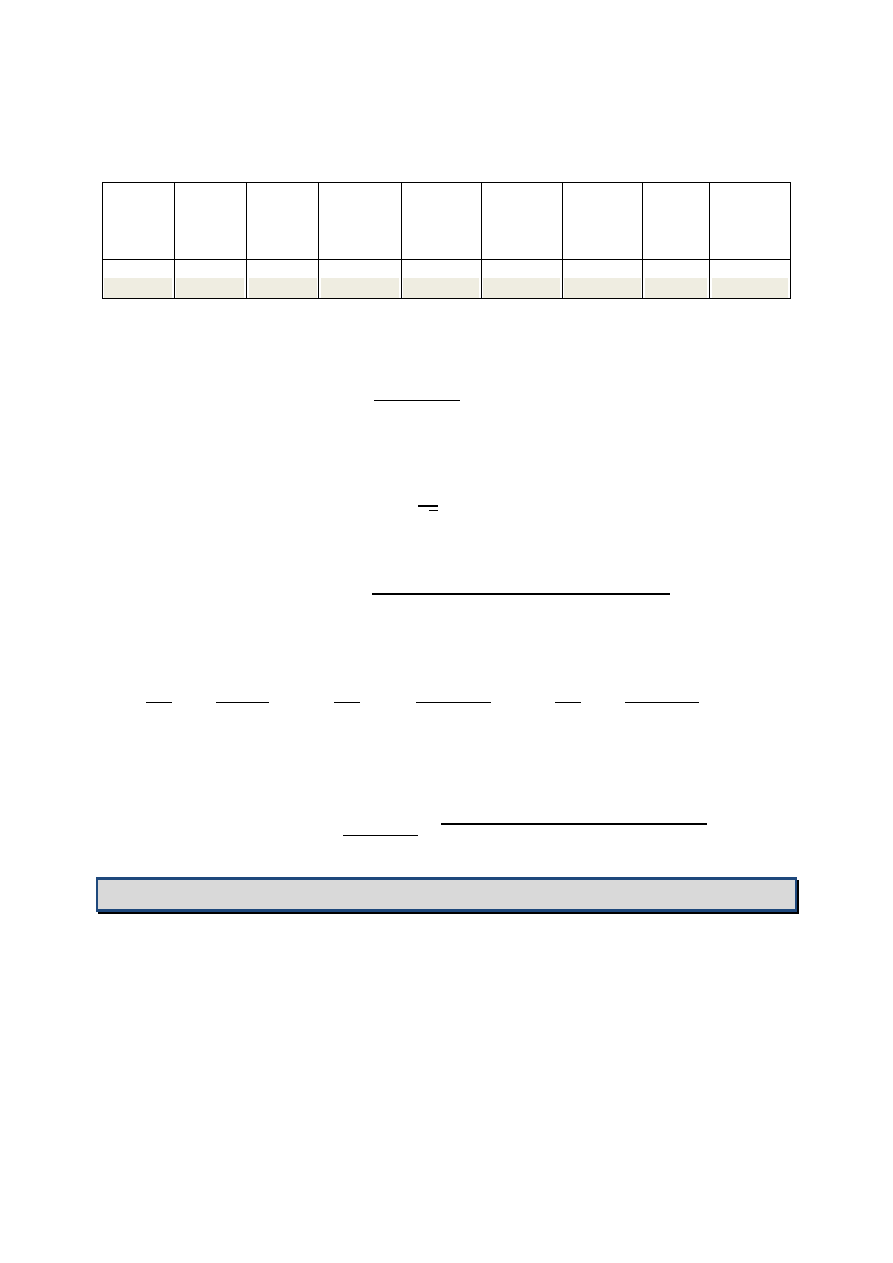
Tabela 1

W

L

[cm]

W

[cm]

W

K

[cm]

Połowa

przedziału

granicznego

∆ℎ [cm]

ℎ

L

− ℎ

K

[cm]

ℎ − ℎ

K

[cm]

X

[kg/m

3

]

t

[

o

C]

[kg/m

3

]

Gęstość

oleju obliczamy ze wzoru wynikającego z równości ciśnień hydrostatycznych na pozio-

mie zetknięcia cieczy i oleju (rys.8).

X

(ℎ

L

− ℎ

K

)

ℎ − ℎ

K

.

(2.1)

Oceniamy niepewność standardową metodą B,

Y

Z

(ℎ), pomiaru poziomu cieczy (zakładając rozkład

trójkątny prawdopodobieństwa):

Y

Z

(ℎ)

∆ℎ
√6

.

(2.2)

Następnie obliczamy złożoną niepewność standardową pomiaru pośredniego gęstości

\

]

z prawa

propagacji niepewności:

Y

^

( ) _ `a

L

Y

Z

(ℎ

L

)b + `a Y

Z

(ℎ )b + `a

K

Y

Z

(ℎ

K

)b . (]. c)

Współczynniki wrażliwości

a

d

, e 1,2,3 we wzorze (2.3) są równe pochodnym cząstkowym z funkcji

(ℎ

L

, ℎ , ℎ

K

) danej wzorem (2.1):

a

L

f

fℎ

L

X

1

ℎ − ℎ

K

, a

f

fℎ

−

X

ℎ

L

− ℎ

K

(ℎ − ℎ

K

) , a

K

f

fℎ

K

X

ℎ

L

− ℎ

(ℎ − ℎ

K

) .

Możemy przyjąć, że niepewność pomiaru każdego z trzech poziomów jest taka sama i równa

Y

Z

(ℎ).

Po podstawieniu wyrażeń na współczynniki wrażliwości do wzoru (2.3) i prostych przekształceniach
otrzymujemy standardową niepewność złożoną gęstości oleju

Y

^

( )

X

Y

Z

(ℎ)

(ℎ − ℎ

K

) ∙ _ (ℎ − ℎ

K

) + (ℎ

L

− ℎ

K

) + (ℎ

L

− ℎ ) . (2.4)

UWAGA:

Po uzgodnieniach z prowadzącym ćwiczenia można opuścić część lub cały punkt 2.2.

2.2

Sprawdzenie warunków 1* oraz 2*

1*. Sprawdzamy, czy na drodze

T ruch jest jednostajny.

Wykazano (por. Uzupełnienie), że po pewnym czasie, to znaczy po przebyciu warstwy cieczy o odpo-
wiedniej grubości, ruch kuleczki ustali się i będzie jednostajny. W tym celu wybierzemy kilka równych
odcinków

T(1), T(2), T(3) na skali cylindra, między naklejonymi paskami wyznaczającymi drogę s

(rys.7) i sprawdzimy, czy czasy w jakich są one pokonywane przez spadającą kulkę są równe, tj. czy
g(1) = g(2) = g(3). Jeżeli tak, to ustalił się ruch jednostajny ze stałą prędkością

9

=

T

g =

T(1)

g(1) =

T(2)

g(2) =

T(3)

g(3).

2*. Sprawdzamy czy

< 0,4, tzn. czy można stosować prawo Stokesa.

Zgodnie ze wzorem (1.1) mamy

= 2 ,

Mierzymy jeden raz średnicę

kuleczki. Obliczamy wartość współczynnika lepkości na podstawie

(1.7), wstawiając wyznaczoną wartość gęstości oleju i wartość prędkości wyznaczoną w pomiarze
sprawdzającym 1*. Dane do obliczenia liczby

zamieszczamy w tabeli pomocniczej, umieszczając

tam również wartość przyspieszenia ziemskiego. Jeżeli

< 0,4, to przystępujemy do zadania 2.

Jeżeli natomiast liczba Re jest za duża wybieramy inną kuleczkę (dokonujemy raz pomiaru średnicy),
aby spełnić warunek.

[mm]

L

h

kg

m

K

i

h

kg

m

K

i

g

j

m

s k

j

cm

s k

=

(

L

− )M

18

[Pa ∙ s]

2.3

Zadanie 2. Wyznaczenie współczynnika lepkości cieczy na pod-
stawie prawa Stokesa.

•

Używając śruby mikrometrycznej 10 razy wyznaczamy średnicę wybranej kulki.

•

Odpowiednio wysoki cylinder o średnicy D, znacznie większej od średnicy używanych kulek
został wypełniony badaną cieczą. Na ścianie cylindra zaznaczono paskami papieru odcinek
drogi spadającej kulki. Pierwszy pasek w położeniu

T

1

powinien znajdować się kilka centyme-

trów poniżej poziomu cieczy, aby ustalił się ruch jednostajny kulki.

•

Za pomocą katetometru wyznaczamy drogę:

T = T

L

− T . Najczęściej około 5-ciu razy.

•

Mierzymy stoperem czas

τ

ruchu kulki na drodze

T uważając, aby nie popełniać błędu para-

laksy. Kulka powinna spadać blisko osi cylindra. Po każdym pomiarze (również ok. 5 pomia-
rów) należy wyłowić kulkę za pomocą sitka, osuszyć na bibule i przed kolejnym pomiarem
chwilę odczekać, aby wydostały się na powierzchnię cieczy pęcherzyki powietrza oraz aby
ustał ruch cieczy.

•

Obliczamy średnią prędkość

̅ kulki.

•

Obliczamy wartość średnią średnicy kulki

̅.

•

Przy użyciu suwmiarki wyznaczamy średnicę

m cylindra (1 lub 2 razy). Pomiar ten jest po-

trzebny do obliczenia poprawki.

•

Zapisujemy wyniki w tabeli 2.

Ćwiczenie 7

10

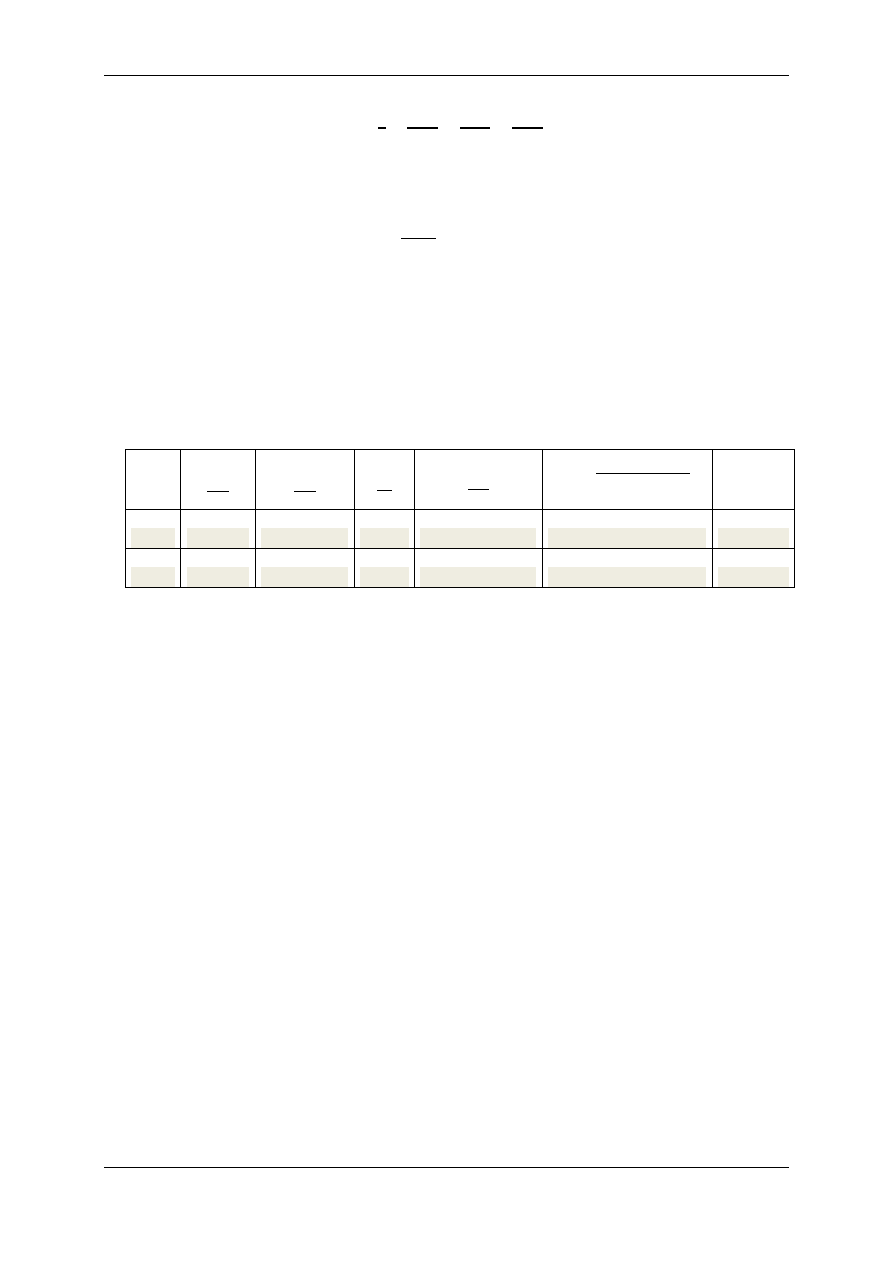
Tabela 2

Lp.

= 2@

[mm]

T

L

[cm]

T

[cm]

T = T

L

− T

[cm]

[s]

m = 2

[cm]

1.

…

Przedziały graniczne

∆ [mm]

∆ T

L

[cm]

∆ T [cm]

∆ [s]

∆

n

m[cm]

UWAGA:

Prawo Stokesa zostało wyprowadzone dla cieczy rozciągającej się nieograniczenie. Gdy

kulka spada w cieczy, która znajduje się w naczyniu o dużych wymiarach, to można pominąć wpływ
ścian na ruch kulki. W naszym ćwiczeniu należy dokonać poprawki ze względu na wpływ ścian cylin-
dra o promieniu R na prędkość spadającej kulki.

Według Ladenburga wzór na prędkość kulki po uwzględnieniu poprawki na wpływ ścianek cy-

lindra ma postać:

o

p1 + 2,4 · mr,

(2.5)

gdzie jest zmierzoną prędkością spadającej kulki, – średnicą kulki,

m – średnicą cylindra. Podsta-

wiając wyrażenie (2.5) do wzoru (1.7) dostajemy wzór na współczynnik lepkości, uwzględniający
wpływ ścianek cylindra na ruch kuleczki

o =

s1 + 2,4 · mt

=

m

m + 2,4 ,

(2.6)

gdzie

η

jest wyznaczonym przez nas współczynnikiem lepkości cieczy.

1. Dokonujemy obliczenia wartości współczynnika lepkości wstawiając średnie wartości wyliczone
powyżej oraz wartość gęstości oleju

z zadania 1.

2. Obliczamy współczynnik lepkości

o

ze wzoru (2.6) uwzględniającego poprawkę Landenburga.

3. Zgodnie z poleceniem prowadzącego ćwiczenie przeprowadzamy dyskusję poprawności pomiaru
wielkości

η

oraz wielkości

o, obliczając niepewności pomiarów. W tym celu musimy najpierw osza-

cować niepewności wielkości mierzonych bezpośrednio.

W przypadku pomiaru średnicy kulki szacujemy składniki niepewności:

•

obliczamy niepewność metodą typu A:

11

Y

u

( ) = v

∑ (

d

− ̅)

x

yzL

{({ − 1)

(2.7)

•

Oceniamy niepewność metodą typu B przyjmując, że szerokość przedziału granicznego jest
równa działce skali. W przypadku śruby mikrometrycznej działka ta wynosi 0,01 mm. Niech
Δ oznacza połowę szerokości przedziału granicznego, czyli w tym przypadku połowę działki
skali

Δ =

L

∙ 0,01mm = 0,005 mm. Obliczamy niepewność pomiaru Y

Z

( ) zgodnie ze wzo-

rem dla rozkładu trójkątnego prawdopodobieństwa

Y

Z

( ) =

Δ

2√6

(2.8)

•

Sumujemy składniki niepewności

Y

^

( ) = ~Y

u

+ Y

Z

(2.9)

Następnie wyznaczamy niepewność pomiaru prędkości

̅ = T̅/ ̅.

•

W tym celu najpierw oceniamy składniki niepewności drogi

T oraz czasu metodą A oraz me-

todą B, podobnie jak przy szacowaniu niepewności średnicy kulki . Zauważmy, że składnik
niepewności drogi liczony metodą typu B jest równy

Y

Z

(T) = √2 · Y(T

L

) , gdzie

Y(T

L

) = Y(T ) =

ΔT

L

√6

(2.11)

•

Obliczamy niepewności pomiaru czasu spadania metodą B (przyjmując rozkład prostokątny
prawdopodobieństwa)

Y( ) =

Δ

√3

. (2.12)

•

Sumujemy składniki niepewności, podobnie jak we wzorze (2.9) w celu otrzymania niepew-
ności

Y(T)

oraz

Y( ).

•

Złożoną niepewność standardową obliczymy korzystając z tego, że funkcja jest ilorazem

T

oraz i można w związku z tym uniknąć liczenia pochodnych cząstkowych, aby wyprowadzić
wzór na niepewność względną. Po przekształceniach dostajemy z niego

Y

^

( )

€

Y (T)

T +

Y ( )

•

(2.13)

W następnej kolejności obliczamy niepewność współczynnika lepkości cieczy.

•

Na podstawie wzoru (1.7) wyprowadzamy wyrażenie na standardową niepewność względną:

Y

^

( ) v Y

^

( )

(

L

− ) +

4Y

^

( )

+

Y

^

( )

. (2.14)

Można również podać niepewność wyrażoną w procentach.

Ćwiczenie 7

12

•

Ze wzoru (2.14) obliczamy standardową niepewność złożoną współczynnika lepkości

Y

^

( ) i

podajemy ją wraz z obliczoną wartością .

Obliczamy niepewność pomiaru współczynnika lepkości

‚ wyznaczonego z uwzględnieniem po-

prawki Landenburga. Ze względu na konieczność obliczenia współczynników wrażliwości za pomocą
pochodnych, podajemy gotowy wzór (w przekształconej postaci):

Y

^

(‚) = ‚ ∙ v€

Y

^

( )

• + p

2,4

m + 2,4 r ƒ€

Y

^

(m)

m • + €

Y

^

( )

• „ .

•

Zapisujemy wynik

‚ oraz Y

^

(‚).

3.

Uzupełnienia

3.1

Ruch kulki w cieczy lepkiej

Równanie ruchu kulki o masie m spadającej w lepkiej cieczy ma postać równania różniczkowego

(pionowa oś układu odniesienia jest zwrócona w dół):

… g

− † .

(3.1)

gdzie wartości sił: ciężkości

E oraz wyporu P nie zależą od prędkości v poruszającej się kulki, a więc

ich różnica:

E – G również nie zależy od prędkości. Natomiast siła oporu

0

jakiego doznaje kul-

ka w lepkiej cieczy dla małych prędkości jest proporcjonalna do prędkości i dana jest prawem Sto-
kesa

A

6C @

† , gdzie wprowadziliśmy oznaczenie † 6C @. Równanie (3.1) można przed-

stawić w postaci:

g −

†

… p − †r.

(3.2)

Wprowadzając nową zmienną:

ˆ s −

‰

Š

t uzyskujemy następujące równanie o zmiennych

rozdzielonych:

ˆ

ˆ

−

†

… g.

(3.3)

Po scałkowaniu oraz przyjęciu warunku, że w chwili początkowej

g 0 prędkość (0)

A

(g) † + p

A

− †r ·

Š‹

Œ

.

(3.4)

Po dostatecznie długim czasie drugi składnik jest bliski zeru i kulka porusza się z szybkością bliską
wartości granicznej:

(g) † + p

A

− †r ·

Š‹

Œ

.

(3.5)

•Ž

†

(… − …‚)M

6C @ .

(3.6)

gdzie przez

…‚ oznaczono masę cieczy wypartej przez kulkę.

13

4.

Literatura

[1] A.K.Wróblewski, J.A.Zakrzewski: Wstęp do fizyki, t.1. PWN, Warszawa 1976.

[2] I.W.Sawieliew: Kurs fizyki, t.I. PWN, Warszawa 1987.

[3] Praca zbiorowa: Słownik fizyczny. Wiedza Powszechna, Warszawa 1984.

[4] T.Dryński: Ćwiczenia laboratoryjne z fizyki. PWN, Warszawa 1977.

[5] H.Szydłowski: Pracownia fizyczna. PWN, Warszawa 1966.

[6] J.Kurzyk: Wprowadzenie do metod opracowania danych pomiarowych.

[7] B.Oleś, M.Duraj: Ćwiczenia laboratoryjne z fizyki, część 1.

5.

Jeśli chcesz wiedzieć więcej

http://www.fizyka.net.pl/index.html?menu_file=ciekawostki%2Fm_ciekawostki.html&former_url=http%3A%2F
%2Fwww.fizyka.net.pl%2Fciekawostki%2Fciekawostki_t3.html