1

Jolanta Dymkowska

Centrum Nauczania Matematyki

i Kształcenia na Odległość

al. Zwycięstwa 25 - pokój 102

http://www.pg.gda.pl/snm/pracownicy/jolanta.dymkowska

http://www.moodle.pg.gda.pl

2

Literatura

• Matematyka - Podstawy z elementami matematyki wyższej, Praca

zbiorowa, PG, Gdańsk 2007

• K. Jankowska, T. Jankowski, Zbiór zadań z matematyki, PG,

Gdańsk 1997

• Praca zbiorowa pod red. E. Mieloszyka, Matematyka – Materiały

pomocnicze do ćwiczeń, PG, Gdańsk 2004

• R. Leitner, Zarys matematyki wyższej I i II, Wydawnictwo Naukowo-

Techniczne, Warszawa 2001

• R. Leitner, W. Matuszewski, Z. Rojek, Zadania z matematyki

wyższej I i II, Wydawnictwo Naukowo-Techniczne, Warszawa 1999

• M. Gewert, Z. Skoczylas, Analiza matematyczna 1 – Definicje,

twierdzenia, wzory, Oficyna Wydawnicza GiS, Wrocław 2001

3

• M. Gewert, Z. Skoczylas, Analiza matematyczna 1 – Przykłady i

zadania, Oficyna Wydawnicza GiS, Wrocław 2001

• T. Jankowski, Linear algebra, PG, Gdańsk 2001

• T. Jurlewicz, Z. Skoczylas, Algebra liniowa 1 – Definicje, twierdzenia,

wzory, Oficyna Wydawnicza GiS, Wrocław 2002

• T. Jurlewicz, Z. Skoczylas, Algebra liniowa 1 – Przykłady i zadania,

Oficyna Wydawnicza GiS, Wrocław 2002

• E. Mieloszyk, Liczby zespolone, PG, Gdańsk 2003

• E. Mieloszyk, Macierze, wyznaczniki i układy równań, PG, Gdańsk

2003

• W. Krysicki, L. Włodarski, Analiza matematyczna w zadaniach I

i II, Wydawnictwo Naukowe PWN, Warszawa 1998

4

Podstawowe pojęcia i oznaczenia algebry zbiorów

X, Y, Z

- zbiory

x, y, z

- elementy zbioru

x ∈ X

-

x

”należy” do zbioru

X

,

x

jest elementem zbioru

X

X ⊂ Y

- zbiór

X

”zawiera się” w

Y

,

X

jest podzbiorem

Y

Zbiory liczbowe

N

-

zbiór liczb naturalnych

Z

-

zbiór liczb całkowitych

Q

-

zbiór liczb wymiernych

R

-

zbiór liczb rzeczywistych

N   Z   Q   R

5

Kwantyfikatory

∀

−

kwantyfikator ogólny

( ∧ )

∃

−

kwantyfikator szczególny

( ∨ )

Przykład

Czy prawdziwe są zdania?

∀

x∈R

x

2

+ 1 > 0

∃

x∈R

x

2

+ 1 > 0

∀

x∈R

x

2

− 1 = 0

∃

x∈R

x

2

− 1 = 0

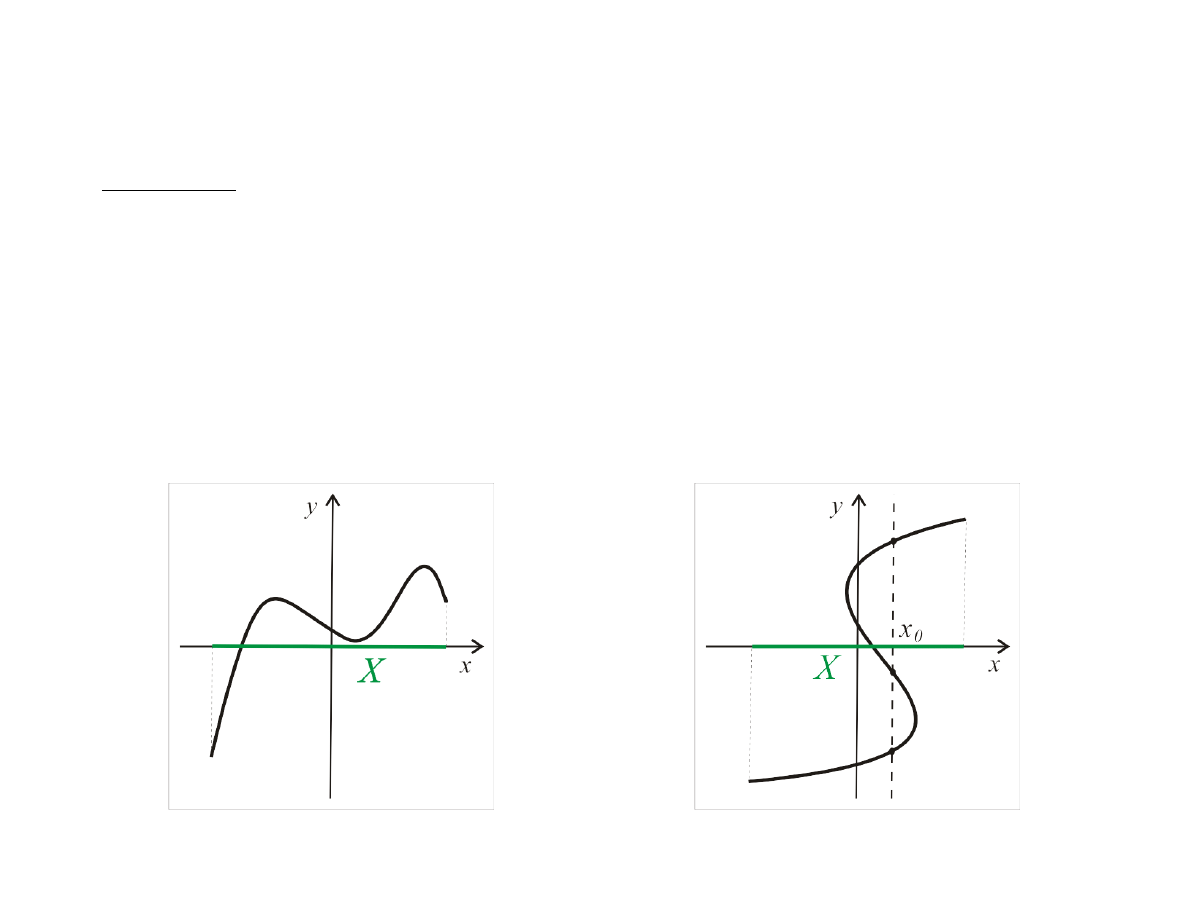
6

Funkcje - podstawowe pojęcia i własności

Definicja

Jeżeli każdemu elementowi zbioru

X

został przypo-

rządkowany dokładnie jeden element zbioru

Y

, to mówimy, że

zostało określone odwzorowanie zbioru

X

w zbiór

Y

. Zamiast

”odwzorowanie” mówimy też: ”przekształcenie” lub ”funkcja”, odwzo-

rowująca zbiór

X

w zbiór

Y

a piszemy

f : X → Y

.

Wykres funkcji f : X → Y

Krzywa nie będąca wykresem funkcji

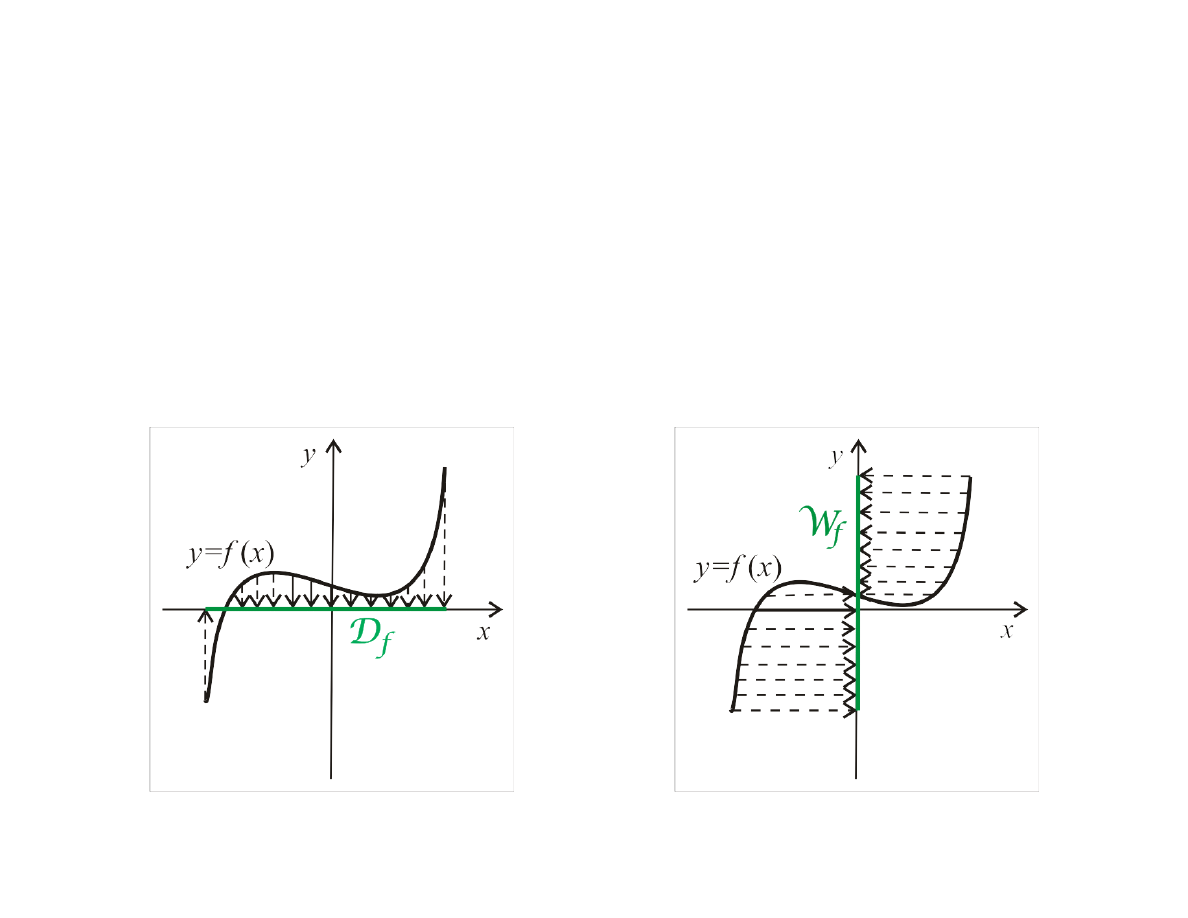
7

•

X

- dziedzina funkcji

f

(ozn.

X = D

f )

•

x ∈ X

- argument funkcji

f

•

f (x) ∈ Y

- wartość funkcji

f

w punkcie

x

(ozn.

y = f (x)

)

•

W

f

=

{ y ∈ Y

:

y = f (x), x ∈ X } ⊂ Y

-

przeciwdziedzina funkcji

f

, zbiór wartości funkcji

f

8

Uwaga

Jeżeli dany jest tylko wzór określający funkcję (rzeczywistą

zmiennej rzeczywistej), to zbiór tych liczb rzeczywistych, dla których

wzór ten ma sens, nazywamy dziedziną naturalną funkcji.

Przykład

Niech

f

będzie funkcją, której wartości są dane

wzorem

f (x) = 3 −

v
u
u
t

2 − (x + 1)

2

.

Wyznaczmy dziedzinę naturalną funkcji

f

oraz jej przeciwdziedzinę.

Naszkicujmy wykres funkcji

f

, wiedząc, że wykresem funkcji rze-

czywistej zmiennej rzeczywistej nazywamy zbiór







(x, y) ∈ R

2

: x ∈ D

f

, y = f (x)







.

9

Definicja

Funkcje

f : D

f

→ Y

i

g : D

g

→ Y

są równe, co

zapisujemy

f = g

, wtedy i tylko wtedy, gdy

D

f

= D

g

∧

∀

x∈D

f

f (x) = g(x).

Przykład

Zbadajmy, czy podane funkcje są równe

•

f (x) = x

2

+ x + 1,

g(x) =

x

3

−1

x−1

•

f (x) =

√

2x

2

+ x,

g(x) =

√

x ·

√

2x + 1

.

10

Definicja

Niech X, Y ⊂ R .

•

Funkcję

f : X → Y

nazywamy funkcją ograniczoną, jeżeli

∃

m,M ∈R

∀

x∈X

m 6 f (x) 6 M.

•

Funkcję

f : X → Y

nazywamy

funkcją rosnącą,

funkcją malejącą,

funkcją nierosnącą,

funkcją niemalejącą,



















































































jeżeli dla x

1

< x

2

,



















































































f (x

1

) < f (x

2

)

f (x

1

) > f (x

2

)

f (x

1

)

> f (x

2

)

f (x

1

)

6 f (x

2

),

dla dowolnych

x

1

, x

2

∈ X

•

Funkcję

f : X → Y

nazywamy funkcją okresową, jeżeli

∃

T >0

∀

x∈X

 

x ± T ∈ X

∧

f (x + T ) = f (x)

!

.

11

Definicja

Niech X, Y ⊂ R .

•

Funkcję

f : X → Y

nazywamy funkcją parzystą, jeżeli

∀

x∈X

 

− x ∈ X

∧

f (−x) = f (x)

!

.

•

Funkcję

f : X → Y

nazywamy funkcją nieparzystą, jeżeli

∀

x∈X

 

− x ∈ X

∧

f (−x) = −f (x)

!

.

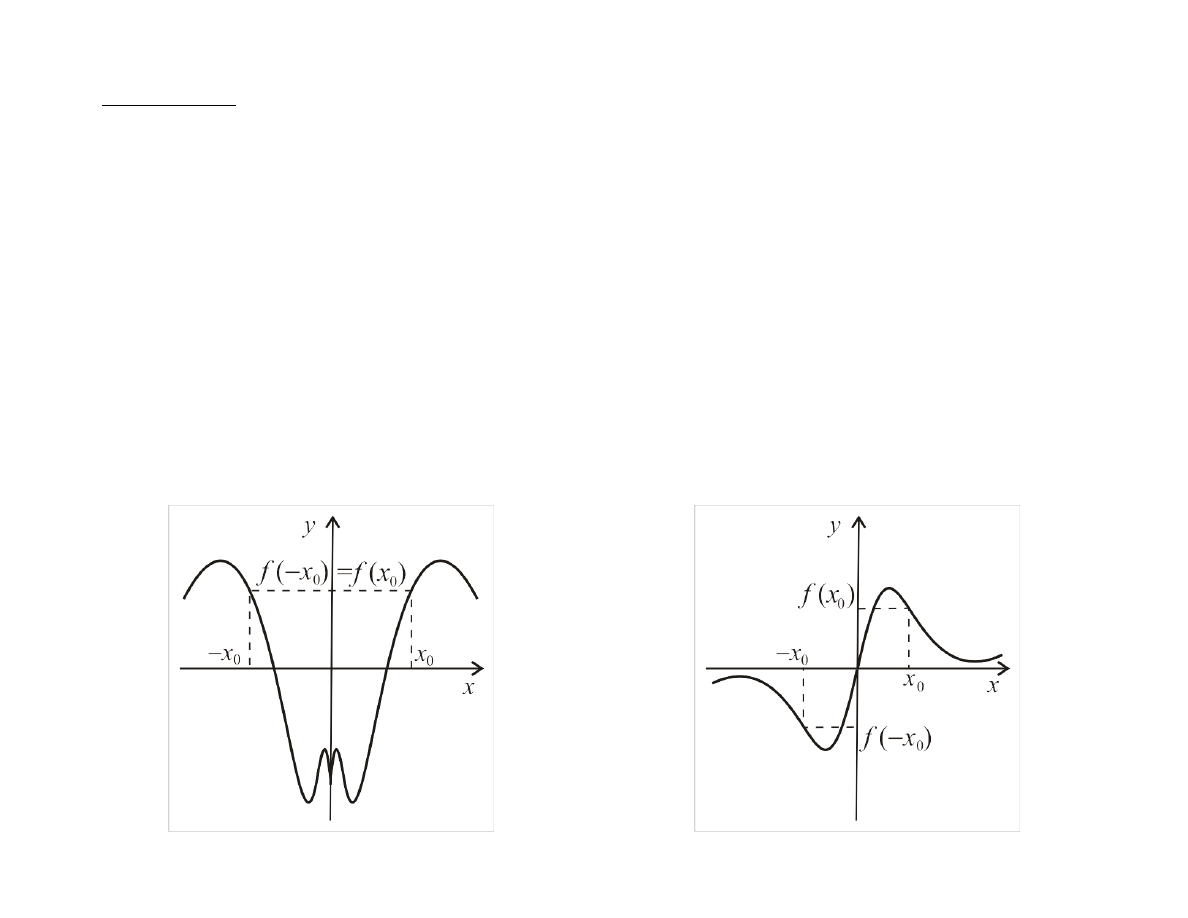
Wykres funkcji parzystej

Wykres funkcji nieparzystej

12

Przykład

Wykazać, że funkcja

f (x) =

√

2x − 1

jest funkcją rosnącą.

Przykład

Zbadać, czy podane funkcje są parzyste, czy nieparzyste.

•

f (x) = |3x − 8| + |3x + 8|

•

f (x) = (x

6

+ 2x

2

) · sgn x