
Przekształcenie Laplace’a
Definicja i własności, transformaty
podstawowych sygnałów

)]
(
[
)
(
t
f
L
s
F
=
Transformatą Laplace’a funkcji f(t) jest funkcja F(S) zmiennej zespolonej,
którą oznacza się następująco:
dt
e
t
f
s
F
st
−
∞
∫
=
)
(
)
(
Funkcja F(S) nazywana bywa również funkcją przekształconą lub
obrazem f(t). To przekształcenie całkowe zdefiniowane jest wzorem:
Aby przekształcenie to miało sens, całka występująca po prawej stronie
wzoru musi być zbieżna, tj.
∞
<
∫
∞
−
0
)
(
dt
e
t
f
st
dt
e
t
f
s
F
∫
=
0
)
(
)
(

∫
+
−
=
ω
ω
π
j
c
j
c
st
ds
e
s
F
j
t
f
)
(
2
1
)
(
Odwrotnie, mając daną F(S) możemy dokonując przekształcenia
odwrotnego wyznaczyć f(t).
przy czym c jest stałą większą od odciętej zbieżności funkcji F(S).
przy czym c jest stałą większą od odciętej zbieżności funkcji F(S).
Piszemy wtedy, że:
Funkcja f(t) nazywana jest również oryginałem funkcji F(s) lub funkcją
oryginalną.
)]
(
[
)
(
1
s
F
L
t
f
−
=

Własności przekształcenia Laplace’a.
1. Liniowość
gdzie a, b są stałymi
)
(
)
(
)]
(
)
(
[
)
(
)
(
s
G
b
s
F
a
t
g
b
t
f
a
L
s
F
a
t
f
a
⋅
+
⋅
=
⋅
+
⋅
⋅
=
⋅
gdzie a, b są stałymi
2. Całkowanie w dziedzinie rzeczywistej
)
(
1
]
)
(
[
0
s
F
s
dt
t
f
L
=
∫
τ

3. Różniczkowanie w dziedzinie rzeczywistej
W szczególności dla n=1 otrzymujemy
)
0
(
)
(
)]
(
[
1
0
)
(
1
d
f
s
s
F
s
t
f
dt
d
L
n
k
k
k
n
n
n
n
+
−
=
+
−
−
−
⋅
=
−
=
∑
gdzie:
granica prawostronna
)
(
lim
)
0
(
)
0
(
)
(
)]
(
[
0
t
f
f
f
s
F
s
t
f
dt
d
L
t
def
→
+
+
=
−
⋅
=

4. Całkowanie w dziedzinie zespolonej zmiennej s
O ile funkcja jest transformowalna wg Laplace’a
]
)
(
[
)
(
t
t
f
L
ds
s
F
s
∫
∞
=
t
f
)
(
O ile funkcja jest transformowalna wg Laplace’a
t
t
f
)
(
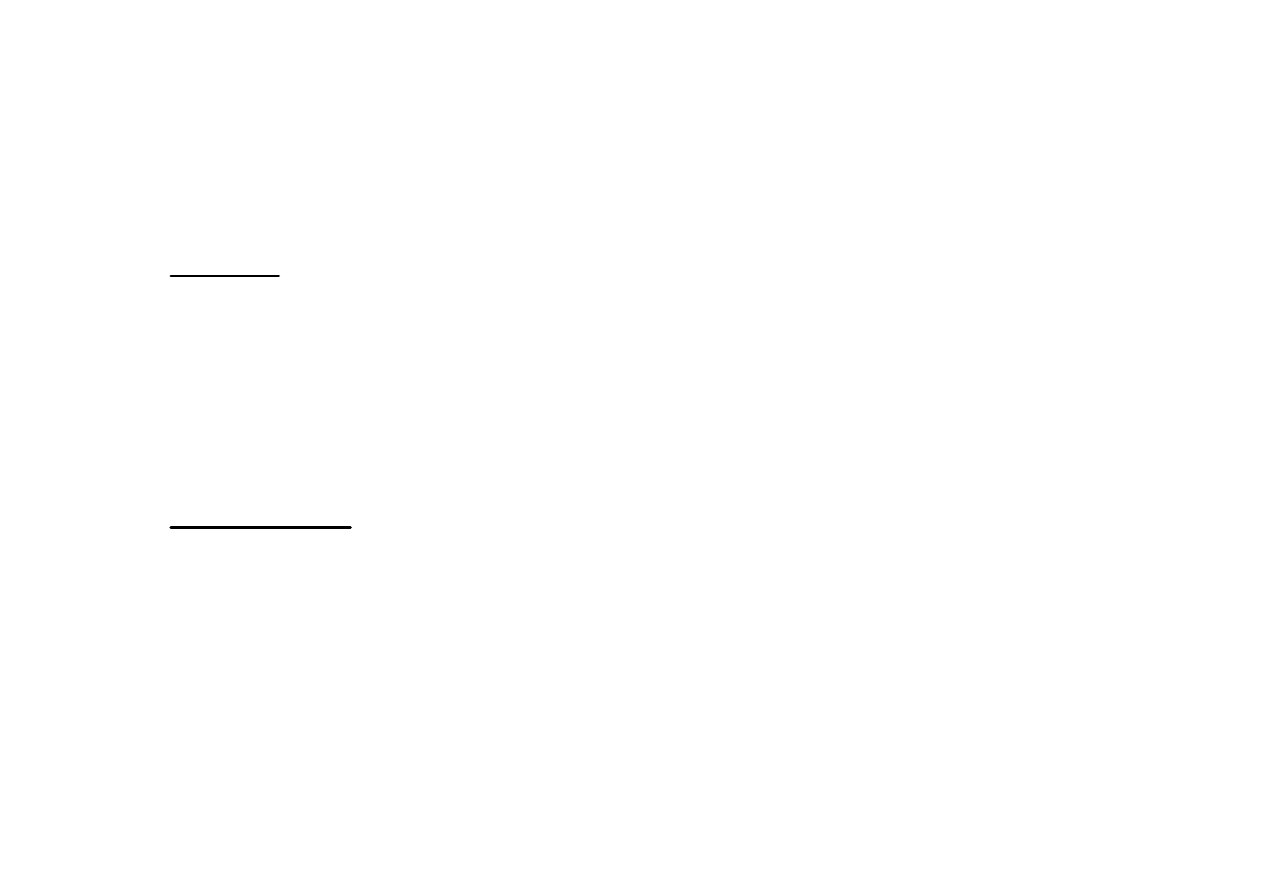
5. Różniczkowanie w dziedzinie zespolonej
W szczególności dla n=1 mamy:
)],
(
[
)
1
(
)
(
t
f
t
L
s
F
ds
d
n
n
n
n
−
=
)]
(
[
)
(
t
tf
L
ds
s
dF
−
=

6. Przesunięcie w dziedzinie rzeczywistej
Przez funkcję f
1
(t) przesuniętą w dziedzinie rzeczywistej (czasu)
względem funkcji f(t) o odcinek t
0
rozumiemy funkcję f
1
(t)=f(t-t
0
).
Ponieważ w przekształceniu Laplace’a dokonujemy całkowania w
granicach (0,∞), część funkcji f(t) dla argumentu t<0 musi być w funkcji
przesuniętej równa zeru. To znaczy, że funkcja f
1
(t) musi być postaci:
<
=
0
0
)
(
t
t
dla
t
f
>
−
<
=
0
0
0
1
)
(
0
)
(
t
t
dla
t
t
f
t
t
dla
t
f
Można to osiągnąć poprzez pomnożenie funkcji f(t-t
0
) przez przesuniętą
funkcję skoku jednostkowego
1
(t-t
0
).

Jak wiadomo, funkcja
1
(t) jest określona jako:
>
<
=
0
1
0
0
)
(
1
t
dla
t
dla
t
Zatem
>
<
=
−
0
0
0
1
0
)
(
1
t
t
dla
t
t
dla
t
t

Ostatecznie transformata funkcji przesuniętej wyraża się zależnością
)
(
)]
(
1
)
(
[
0
0
0
s
F
e
t
t
t
t
f
L
st
−
=
−
⋅
−
7. Przesunięcie w dziedzinie zespolonej
)]
(
[
)
(
t
f
e
L
a
s
F
at
=
−
)]
(
[
)
(
t
f
e
L
a
s
F
at
=
−

8. Zmiana skali
9. Splot funkcji (twierdzenie Borela)
)
(
1
)]
(
[
a
s
F
a
at
f
L
=
)
(
)
(
)]
(
*
)
(
[
2
1
2
1
s
F
s
F
t
f
t
f
L
⋅
=

Gdzie splot
τ
τ
τ
τ
τ
τ
d
f
t
f
d
t
f
f
t
f
t
f
t
t
)
(
)
(
)
(
)
(
)
(
*
)
(
2
0
1
2
1
∫
∫
−
=
=
−
=
τ
τ
τ
d
f
t
f
)
(
)
(
2
0
1
∫
−
=
jest operacją przemienną, łączną, rozdzielną względem dodawania. Splot
jest równy zeru wtedy i tylko wtedy, gdy co najmniej jedna z funkcji f
1
(t)
lub f
2
(t) jest funkcją zerową.

Znaczenie praktyczne ma związana z pojęciem splotu całka Duhamela
)
(
)
(
]
)
(
)
(
[
2
1
0
2
1
s
F
s
sF
d
t
f
f
dt
d
L
t
⋅
=
−
∫
τ
τ
τ
Z zależności
)
(
)
(
)]
(
*
)
(
[
2
1
2
1
s
F
s
F
t
f
t
f
L
⋅
=
Z zależności
wynika oczywisty fakt, że iloczyn transformat nie jest transformatą
iloczynu funkcji. Wzór na transformatę iloczynu jest skomplikowany na
tyle, że nie znalazł szerszego zastosowania.

Transformaty funkcji impulsowych
Funkcją impulsową
δ
(t) – impulsem Diraca – nazywamy „funkcję”
określoną następująco:
=
∞
≠
=
0
0
0
)
(
t
dla
t
dla
t
δ
=
∞
0
t
dla
przy czym
Jest to więc matematyczny zapis impulsu o nieskończenie krótkim czasie
trwania i jednostkowej energii.
1
)
(
=
∫
∞
∞
−
t
δ

Typowe wymuszenia w badaniu układów automatyki
Funkcja impulsowa
δ
(t)– „delta” Diraca
0
∞
t
δ
(t)
0
t
1111
(t)
0
t
0
1111
(t-t
0
)
Funkcja skoku jednostkowego 1(t)
t

1
)
(
=
∫
∞
∞
−
t
δ
Z zależności
wynika, że
0
1
0
0
)
(
t
dla
t
dla
dt
t
t
>
<
=
∫
δ
a zatem
)
(
1
)
(
0
1
t
dt
t
t
dla
t
=
>
∫
∫
∞
−
∞
−
δ
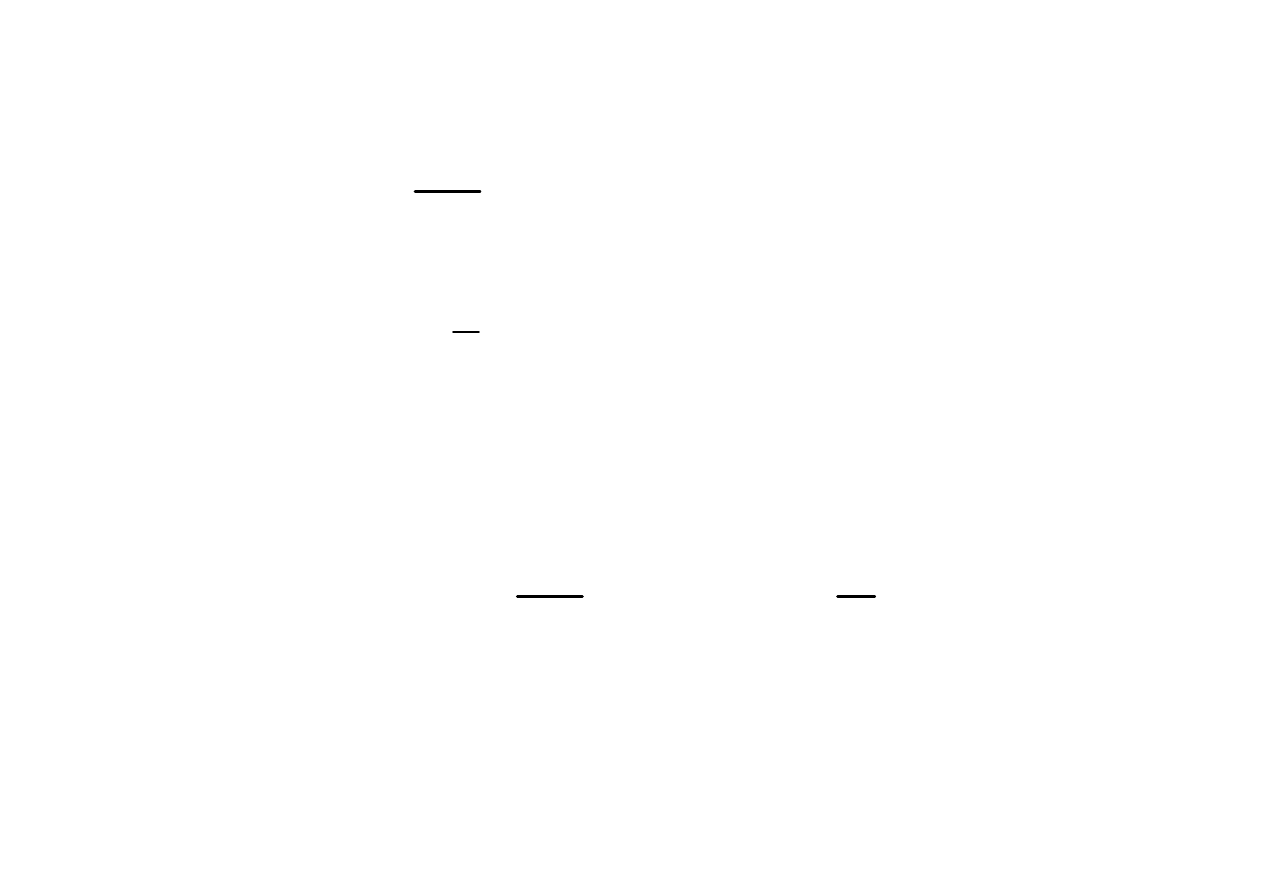
)
(
)
(
1
t
t
dt
d
δ
=
Stąd otrzymujemy następujący związek między funkcją skokową a
funkcją impulsową
Ponieważ
s
t
1
)]
(
1
[
L
=
więc korzystając z zależności na transformatę pochodnej otrzymamy
więc korzystając z zależności na transformatę pochodnej otrzymamy
1
1
)]
(
1
L[
]
)
(
L[
=
⋅
=
=
s
s
t
dt
d
t
δ

Transformata funkcji okresowej
Transformata funkcji okresowej f(t) o okresie T dana jest wzorem
sT
T
e
s
F
t
f
−
−
=
1
)
(
]
)
(
L[
gdzie:
gdzie:
∫
−
=
T
sT
T
dt
e
t
f
s
F
0
)
(
)
(

Transformaty najczęściej spotykanych funkcji
Oryginał f(t)
Obraz F(s)
δ
(t)
1
1(t)
t
t
n
e
α
t
s
1
2
1
s
1
!
+
n
s
n
1
e
α
t
t e
α
t
sin(
ω
t)
cos(
ω
t)
α
−
s
1
2
)
(
1
α
−
s
2
2
ω
ω
+
s
2
2
ω
+
s
s

Oryginał f(t)
Obraz F(s)
sin(
ω
t+
ϕ
)
cos(
ω
t+
ϕ
)
e
α
t
sin(
ω
t+
ϕ
)
2
2
cos
sin
ω
ϕ
ω
ϕ
+
+
s
s
2
2
sin
cos
ω
ϕ
ω
ϕ
+
−
s
s
2
2
)
(
ω
α
ω
+
−
s
e
α
t
cos(
ω
t+
ϕ
)
2
2
)
(
ω
α
α
+
−
−
s
s
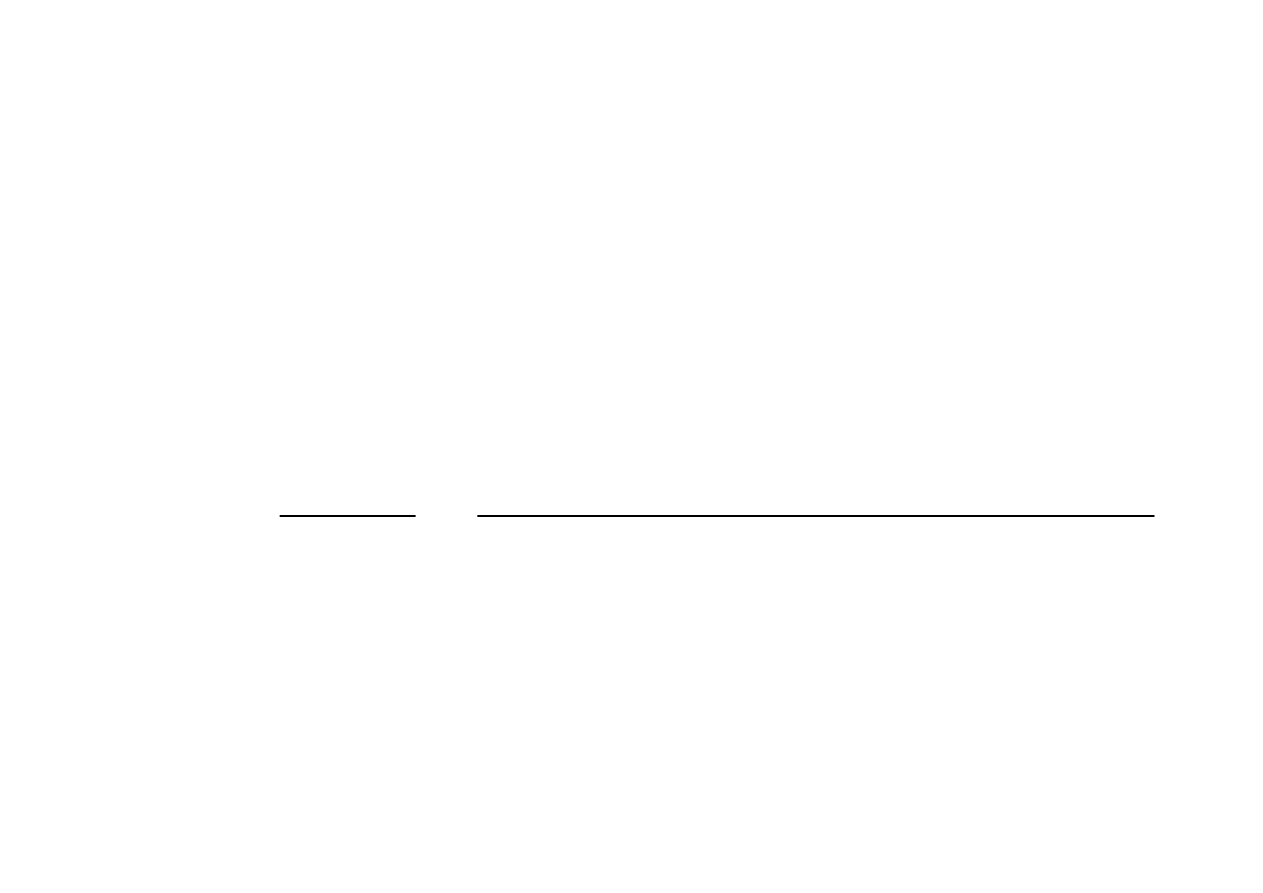
Wyznaczanie transformaty odwrotnej (oryginału)
Do wyznaczenia oryginału funkcji stosuje się dwie metody:
1. Metoda rozkładu na ułamki proste
2. Metoda residuów
Najczęściej transformata funkcji ma postać:
1
1
...
)
(
a
s
a
s
a
s
a
s
L
n
n
+
+
+
+
−
0
1
1
1
1
0
1
1
1
1
...
...
)
(
)
(
)
(
b
s
b
s
b
s
a
s
a
s
a
s
a
s
M
s
L
s
F
m
m
m
n
n
n
n
+
+
+
+
+
+
+
+
=
=
−
−
−
−
Załóżmy dodatkowo, że stopień licznika jest mniejszy od stopnia
mianownika, tzn. n < m (praktycznie występuje zależność n≤m)
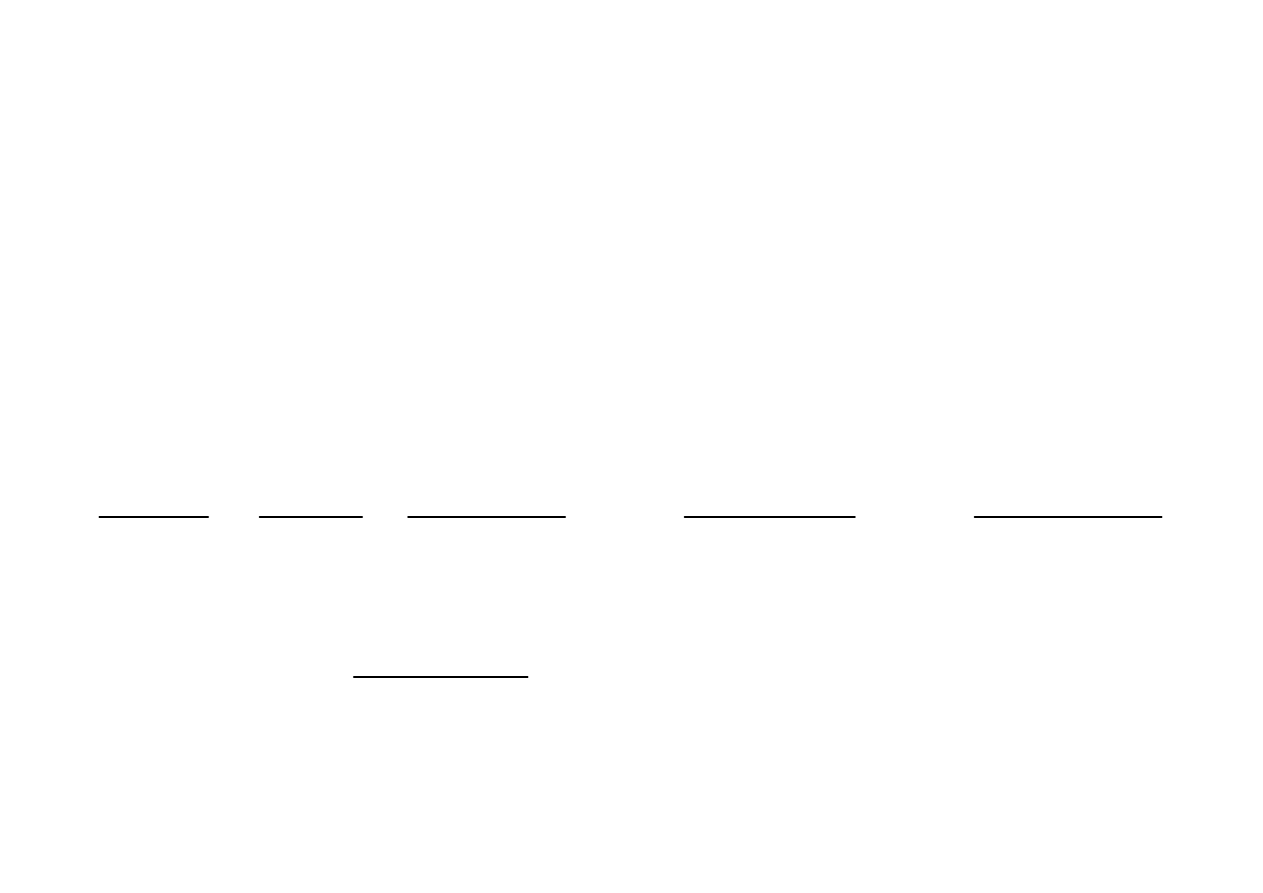
Metoda rozkładu na ułamki proste
Mianownik, jako wielomian m-tego stopnia ma m pierwiastków
(zwanych biegunami), w ogólności zespolonych, przy czym niektóre
mogą się powtarzać. Niech różnych pierwiastków mianownika będzie
p≤m, krotność i-tego pierwiastka oznaczamy przez
α
i
. Wówczas funkcję
F(s) można przedstawiać w postaci sumy ułamków prostych, tj. takich,
których mianownik jest pewną potęgą dwumianu (s-s
i
)
rj
.
A
∑∑
=
=
−
=
−
+
+
−
+
+
−
+
−
=
p
i
j
i
ij
p
p
i
j
p
p
i
s
s
A
s
F
s
s
A
s
s
A
s
s
A
s
s
A
s
M
s
L
1
1
1
1
2
1
12
1
11
)
(
)
(
)
(
...
)
(
...
)
(
)
(
)
(
1
α
α
α
α
α
α

18
30
14
2
8
4
)
(
2
3
+
+
+
+
=
s
s
s
s
s
F
Przykład
9
15
7
4
2
)
(
2
3
+
+
+
+
=
s
s
s
s
s
F
Jeżeli powyższą zależność doprowadzimy do postaci pożądanej (dzieląc
licznik i mianownik przez współczynnik przy najwyższej potędze
mianownika – czyli w naszym przykładzie 2) otrzymamy
9
15
7
)
(
2
3
+
+
+
=
s
s
s
s
F
W tym przypadku n=1, m=3
a
1
=2,
a
0
=4,
b
2
=7,
b
1
=15,
b
0
=9
Pierwiastki mianownika są równe: s
1
= -1, s
2
= -3, przy czym pierwszy z
nich jest jednokrotny a drugi dwukrotny.

2
22
21
11
)
3
(
3
1
)
(
+
+
+
+
+
=
s
A
s
A
s
A
s
F
Rozkład więc będzie typu:
Współczynniki A
ij
można wyznaczyć różnymi metodami. Przedstawiona
będzie jedna z nich. Jeżeli powyższą zależność sprowadzimy do
wspólnego mianownika i przyrównamy liczniki do siebie, otrzymamy:
A
11
(s+3)
2
+A
21
(s+1)(s+3)+A
22
(s+1)=2s+4
czyli
(A
11
+A
21
)s
2
+(6A
11
+4A
21
+A
22
)s+9A
11
+3A
21
+A
22
=2s+4
stąd:
=
+
+
=
+
+
=
+
4
3
9
2
4
6
0
22
21
11
22
21
11
21
11
A
A
A
A
A
A
A
A
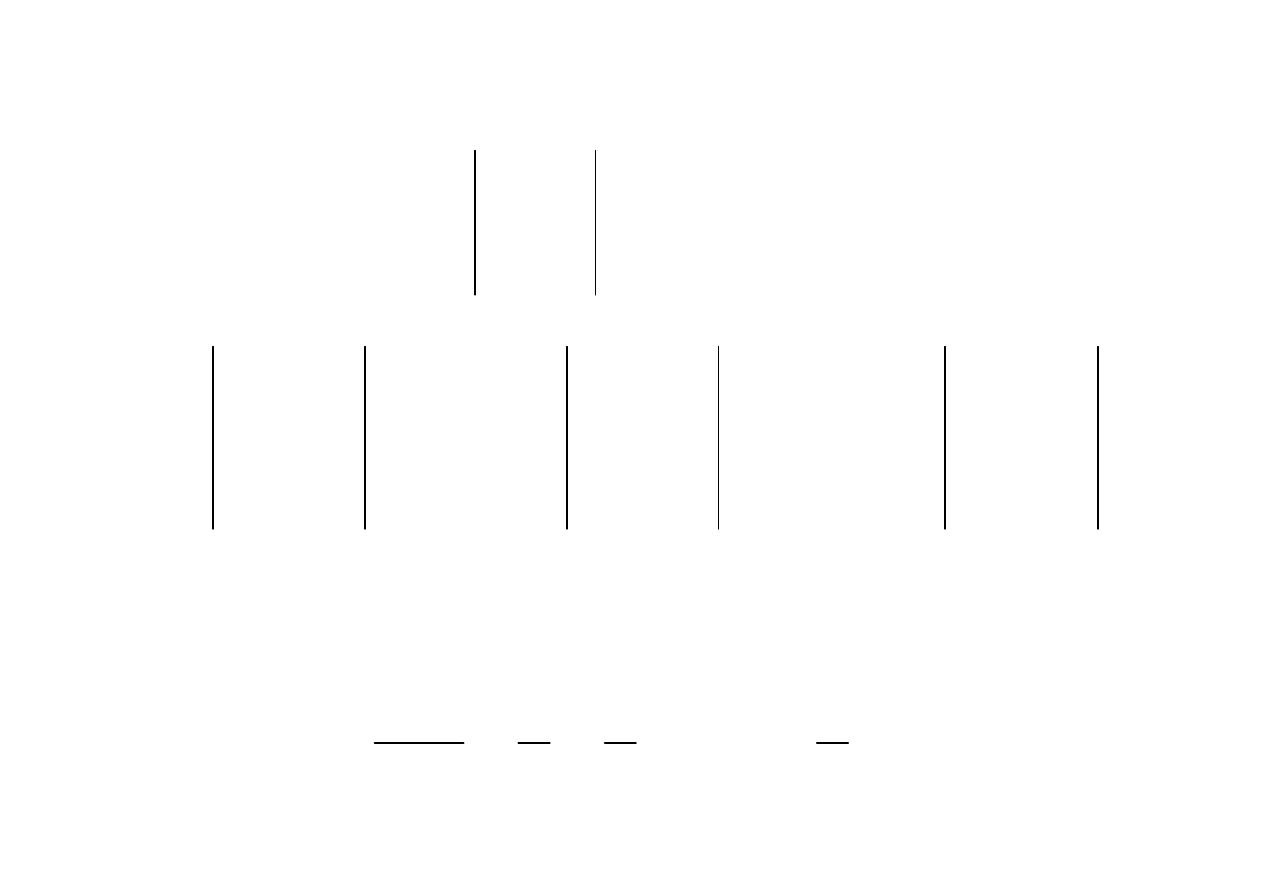
Rozwiązując ten układ równań dowolną metodą (np. Cramera)
otrzymamy:
4
3
1
1
3
9
1
4
6
0
1
1
=
+
=
=
W
4
2
4
6
0
1
1
;
2
1
2
6
0
0
1
;
2
1
4
2
0
1
0
=
=
−
=
=
=
=
A
A
A
W
W
W
4
4
3
9
2
4
6
;
2
1
4
9
1
2
6
;
2
1
3
4
1
4
2
22
21
11
=
=
−
=
=
=
=
A
A
A
W
W
W
1
;
2
1
;
2
1
4
2
22
21
11
11
=
−
=
=
=
=
A
A
W
W
A
A
Stąd:
2
)
3
(
1
3
2
1
1
2
1
)
(
+
+
+
−
+
+
=
s
s
s
s
F
W rezultacie otrzymujemy rozkład na ułamki proste
Ponieważ
(
)
t
s
k
k
i
e
k
t
s
s
L
⋅
−
=
−
−
−
!
1
)
(
1
1
1
więc po dokonaniu na ułamki proste otrzymujemy natychmiast
transformatę odwrotną w postaci
(
)
k
i
k
s
s
−
−
!
1
)
(
[
]
∑∑
=
=
−
−
⋅
−
=
=
p
i
j
t
s
j
ij
i
i
e
t
j
A
s
F
L
t
f
1
1
1
1
)!
1
(
)
(
)
(
α

Metoda Residuów
Przez residuum funkcji F(s) w biegunie s=s
i
rozumiemy współczynnik A
i1
rozwinięcia funkcji F(s) w szereg Laurenta w otoczeniu punktu s=s
i
, tzn.
rozwinięcia
∑
−
=
n
n
i
in
s
s
A
s
F
)
(
)
(
gdzie n przyjmuje wartości od - ∞ do + ∞.
Część sumy dla n>0 nazywamy częścią główną rozwinięcia. Współczynnik
A
i1
jest tożsamy ze współczynnikiem występującym w metodzie rozkładu
na ułamki proste i w zależnościach następnych.

Metoda residuów jest ogólniejsza od metody rozkładu na ułamki proste,
gdyż ma zastosowanie także do transformat nie będących funkcjami
wymiernymi. Fundamentalnym wzorem tej metody jest
]
)
(
[
)]
(
[
1
st
i
s
s
e
s
F
res
s
F
L
i
∑
=
−
=
gdzie s
i
– bieguny funkcji F(s)
i
Jeśli F(s) jest funkcją wymierną, to
[
]
(
)
−
−
=
−
−
→
=
st
i
s
s
i
st
s
s
e
s
s
s
F
ds
d
e
s
F
res
i
i
i
i
i
α
α
α
α
)
)(
(
lim
!
1
1
)
(
1
1

]
)
(
[
]
)
(
[
)
(
t
s
s
s
s
s
st
s
s
i
i
i
i
e
s
F
res
e
s
F
res
−
=
=
=
W przypadku, gdy biegun jest jednokrotny otrzymamy:
Przykład:
Znaleźć
metodą residuów.
]
)
)(
(
[
1
c
s
b
s
a
L
+
+
−
Rozpatrywana transformata ma dwa bieguny pojedyncze: s
1
=-b, s
2
=-c
Residua w tych biegunach obliczamy ze wzoru powyżej otrzymując:
ct
st
s
s
bt
st
b
s
st
s
s
e
c
b
a
e
s
F
res
e
b
c
a
e
c
s
a
e
s
F
res
−
=
−
−
→
=
−
=
−
=
+
=
]
)
(
[
lim
]
)
(
[
2
1

Na naszych zajęciach nie będziemy wykorzystywać metody residuów i
ograniczymy się do metody rozkładu na ułamki proste.
Na dzisiaj
Na dzisiaj
DZIĘKUJĘ ZA UWAGĘ!
Wyszukiwarka
Podobne podstrony:
8838
ped.wykl3, PEDAGOGIKA
8838
SOUP wykl3
Mima i pantomima cz1, ALTERNATYWNE METODY KOMUNIKACJI
Neurologia wykl3
3690 Mima wykl4 id 36210 Nieznany
Podstawy metr wykł3 2008
Silniki spal.-wykł3, III rok, Samochodowe silniki spalinowe
8838
Mima i pantomima cz 1(1)(1)
sciaga 8838
8838
więcej podobnych podstron