Analizując roztwór jodku kadmu(II) ustalono między innymi, że z 12,1063 g tego
roztworu wytrącono 1,0492 g tlenku kadmu(II). Roztwór ten poddano następnie
elektrolizie w aparacie Hittorfa wyposażonym anodę wykonaną z czystego kadmu
oraz katodę sporządzoną ze srebra. Aparat Hittorfa połączono szeregowo z
kulometrem srebrowym. Po zakończeniu elektrolizy stwierdzono, że w kulometrze
wydzieliło się 671,2 mg srebra. Następnie analizie poddano zawartość przestrzeni
anodowej. Analiza polegała na tym, że do roztworu wprowadzono azotan srebra
wytrącając w sposób jodek srebra, który następnie odsączono, przemyto wodą,
wysuszono i zważono. Masa anolitu wynosiła 17,0938 g, a masa wytrąconego jodku
srebra 6,722. Wyznacz liczbę przenoszenia jonów kadmu oraz jonów jodkowych.


Punktem wyjścia do rozwiązania zadania jest bilans zmian zachodzących w
przestrzeni anodowej związanych z reakcją elektrodową oraz migracją jonów.

Reakcją anodową jest roztwarzanie się materiału elektrodowego, w tym przypadku
kadmu:

−

+

+

→

e

2

Cd

.)

st

(

Cd

2

W przestrzeni anodowej przybywa więc pewna ilość jonów kadmowych. Ilość ta jest
proporcjonalna do ładunku który przepłynął przez elektrolizer, a który warto wyrazić w
w faradajach (F), czyli w jednostkach ładunku równych ładunkowi jednego mola
elektronów. Ze względu na to, że liczba ładunkowa jonu kadmowego wynosi 2+ to
przyrost ilości jonów kadmowych w przestrzeni anodowej równy jest

+

2

Cd

jonów

mola

F

Q

2

1

Jednocześnie do przestrzeni anodowej w wyniki migracji w polu elektrycznym

przybywają jony jodkowe, a ich ilość jest proporcjonalna do ładunku oraz liczby
przenoszenia anionów

−

−

+

I

jonów

mola

F

Q

t

Towarzyszy temu ubytek odpowiedniej ilości kationów

+

+

−

2

Cd

jonów

mola

F

Q

t

2

1

Razem więc

−

−

+

+

+

+

−

I

jonów

mola

F

Q

t

Cd

jonów

mola

F

Q

t

2

1

Cd

jonów

mola

F

Q

2

1

2

2

co można sprowadzić do postaci

−

−

+

−

+

I

jonów

mola

F

Q

t

Cd

jonów

mola

F

Q

t

2

1

2

Równoważny zapis ma postać

mola

F

Q

t

2

1

n

2

CdI

−

=

∆

Ładunek, który przepłynął przez elektrolizer i kulometr srebrowy łatwo

obliczyć. Znana jest masa srebra wydzielonego w kulometrze. Można więc obliczyć
ile to moli

mola

10

2223

,

6

87

,

107

6712

,

0

M

m

n

3

Ag

Ag

Ag

−

⋅

=

=

=

a ładunek wyrazić w faradajach

F

10

2223

,

6

Q

3

−

⋅

=

co można również przedstawić jako

mol

10

2223

,

6

F

Q

3

−

⋅

=

Kolejnym etapem jest wyznaczenie składu roztworu wyjściowego. Trzeba

przecież obliczyć początkową ilość moli soli w anolicie.

Znana jest masa tlenku kadmu wytrąconego z danej ilości roztworu. Ilość

tlenku kadmu równoważna jest ilości jodku kadmu.

CdO

CdI

n

n

3

=

Łatwo obliczyć ilość moli tlenku kadmu

mola

10

171

,

8

40

,

128

0492

,

1

M

m

n

3

CdO

CdO

CdO

−

⋅

=

=

=

masę jodku kadmu

g

9924

,

2

21

,

366

10

171

,

8

M

n

m

3

CdI

CdI

CdI

2

2

2

=

⋅

⋅

=

⋅

=

−

oraz masę wody w analizowanej próbce roztworu

g

1139

,

9

9924

,

2

1063

,

12

m

m

m

2

2

CdI

1

O

H

=

−

=

−

=

Skład roztworu można więc wyrazić jako molalność, czyli ilość moli soli przypadającą
na 1 kg wody

1

1

3

O

H

CdI

kg

mol

89658

,

0

g

1139

,

9

kg

g

1000

mol

10

171

,

8

m

n

m

2

2

−

−

−

⋅

=

⋅

⋅

⋅

=

=

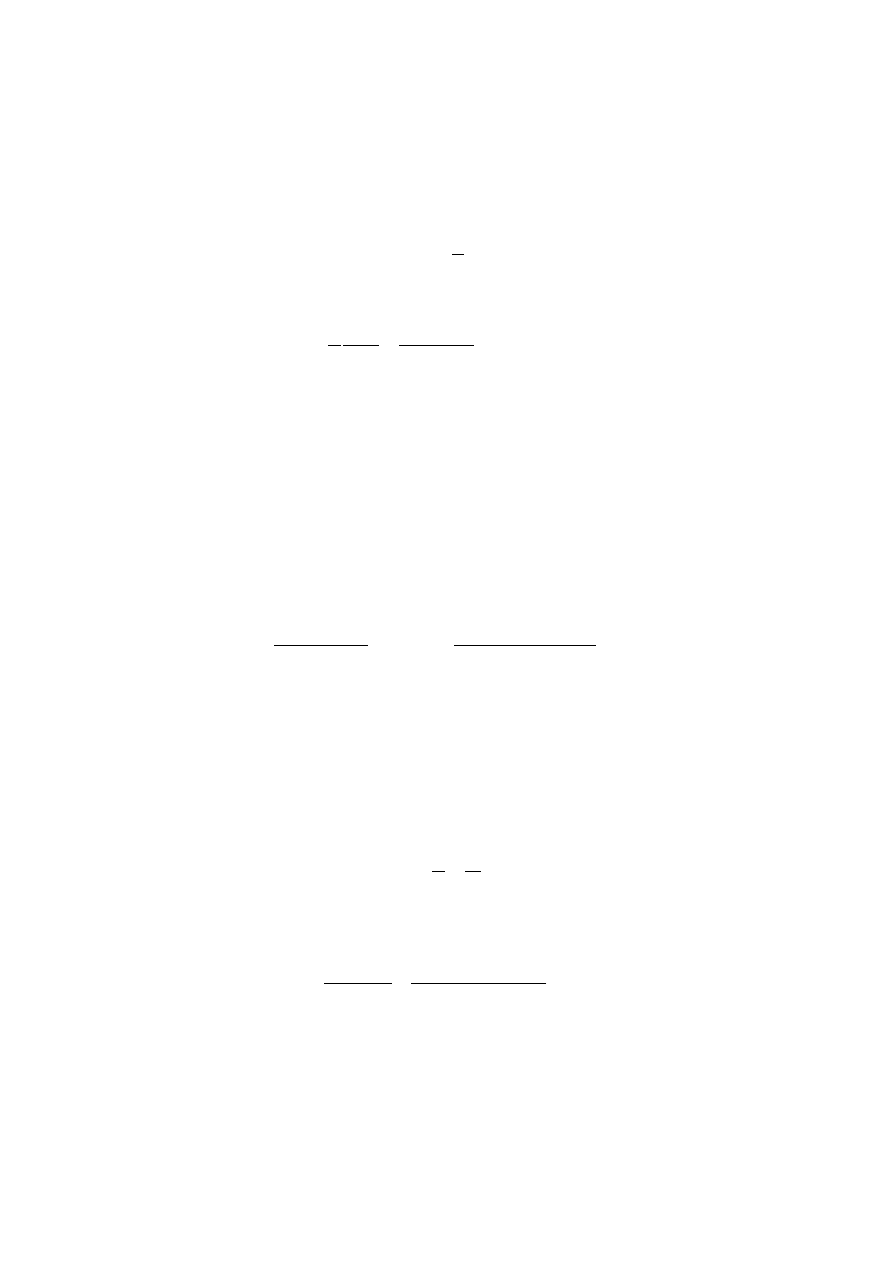
Znając masę wody w roztworze anodowym będzie można obliczyć wyjściową
ilość soli.
Znając masę AgI wytrąconego z roztworu anodowego po zakończeniu
elektrolizy należy obliczyć równoważną ilość moli CdI

2

. Trzeba tylko pamiętać, że

jeden mol CdI

2

równoważny jest dwóm molom AgI, czyli

AgI

CdI

n

2

1

n

2

=

Można więc obliczyć ilość moli

mol

10

4316

,

1

77

,

234

2

722

,

6

M

m

2

1

n

2

AgI

AgI

CdI

2

−

⋅

=

⋅

=

=

następnie masę jodku kadmu

g

2427

,

5

21

,

366

10

4316

,

1

M

n

m

2

CdI

CdI

CdI

2

2

2

=

⋅

⋅

=

⋅

=

−

i masę wody

g

8511

,

11

2427

,

5

0938

,

17

m

m

m

2

2

CdI

2

O

H

=

−

=

−

=

w roztworze anodowym po zakończeniu elektrolizy.

Należy teraz odpowiedzieć na pytanie: ile moli jodku kadmu znajdowało w tej

ilości wody przed rozpoczęciem elektrolizy?

mol

010625

,

0

kg

g

1000

kg

mol

89658

,

0

8511

,

11

kg

g

1000

m

m

n

1

1

1

O

H

CdI

2

2

=

⋅

⋅

⋅

=

⋅

⋅

=

−

−

−

Można więc obliczyć ile moli CdI

2

przybyło podczas elektrolizy

mol

10

691

,

3

010625

,

0

014316

,

0

n

3

CdI

2

−

⋅

=

−

=

∆

i wykorzystując ostatnie równanie wynikające z bilansu

mola

F

Q

t

2

1

n

2

CdI

−

=

∆

obliczyć liczbę przenoszenia anionu

186

,

1

mol

10

2223

,

6

mol

10

691

,

3

2

F

/

Q

n

2

t

3

3

CdI

2

=

⋅

⋅

⋅

=

∆

⋅

=

−

−

−

Jak wytłumaczyć ten niezwykły na pozór wynik? Przecież liczba przenoszenia

winna być mniejsza od jedności. Co więcej, każdy wie, że

1

t

t

=

+

−

+

a wynika z tego, że liczba przenoszenia kationu kadmowego jest ujemna

186

,

0

t

1

t

−

=

−

=

−

+

Jon kadmowy tworzy z jonami trwałe jony kompleksowe i w roztworze w

którym znajdują się obok siebie oba te jony powstają kolejno kompleksy CdI

+

, CdI

2

,

−

−

2
4

3

CdI

oraz

CdI

. Tylko pierwszy z nich jest kationem i porusza się w kierunku katody.

Dwa ostatnie są posiadają ładunek ujemny – są więc anionami - i poruszają się w
kierunku anody. Co więcej, trwałość kompleksów tetrajodkowych jest na tyle duża, że
przy odpowiednim stężeniu soli zachodzi zjawisko znane jako dysproporcjonacja
koordynacyjna, które można opisać reakcją

−

+

+

→

2
4

2

2

CdI

Cd

CdI

2

Jak widać, 50% jonów kadmowych może istnieć w postaci kompleksów
tetrajodkowych o ładunku ujemnym poruszających się w kierunku anody. Formalnie
poprawna analiza procesów zachodzących podczas elektrolizy musi prowadzić do
„dziwacznych” wartości liczb przenoszenia. Takie właśnie wartości liczb przenosze-
nia doprowadziły swego czasu badaczy do odkrycia zjawiska „dysproporcjonacji
koordynacyjnej”.

© W.Grzybkowski, 2003