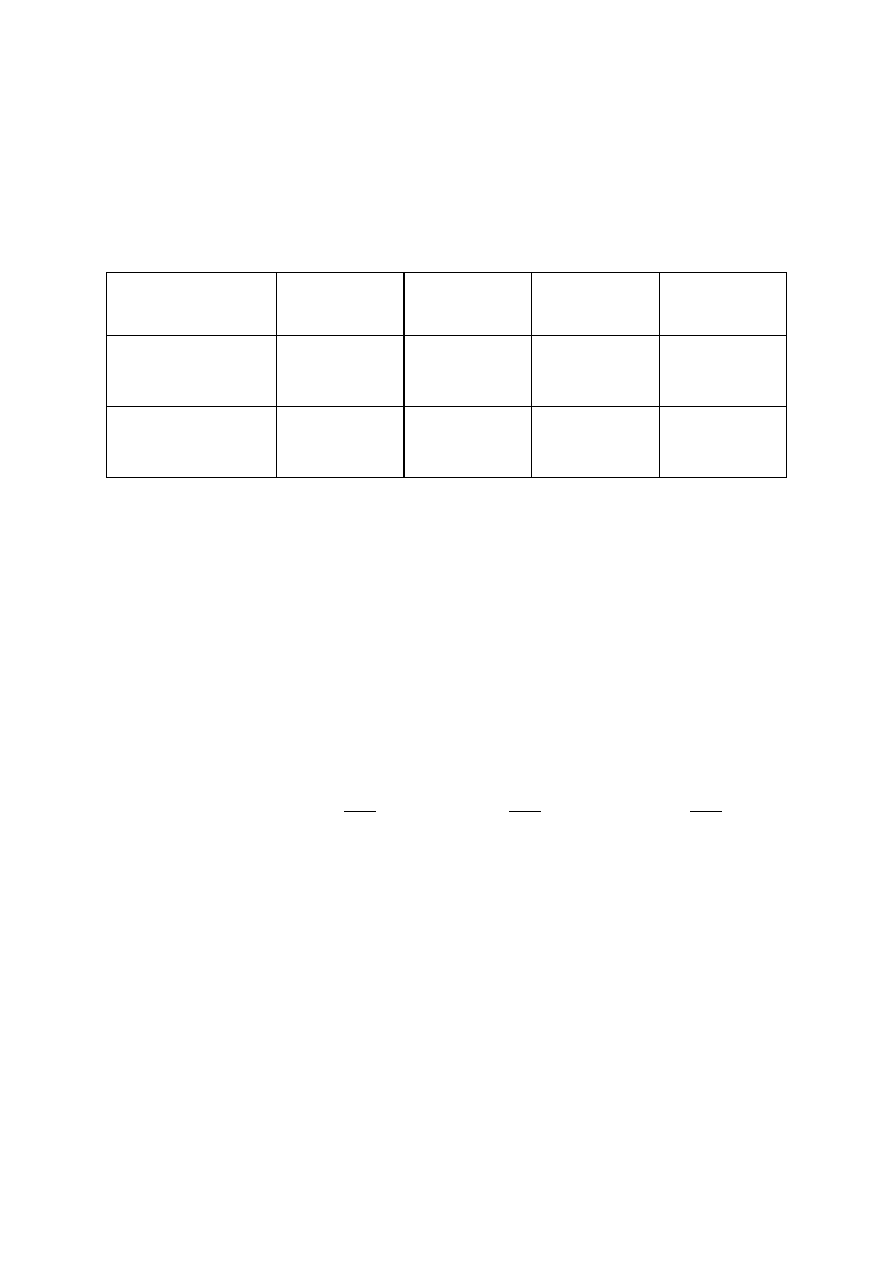
CYKLE TERMOCHEMICZNE SPALANIA METANU
W oparciu o podane w tabeli dane oblicz standardową entalpię reakcji
spalania metanu w temperaturze 25
0
C oraz w temperaturze 90
0
C. Przyjmij, że w
interesującym nas zakresie temperatur molowe pojemności cieplne substratów i
produktów są niezależne od temperatury.
)
g
(
CH
4
)
g
(
O
2
)
g
(
CO
2
)
c
(
O
H
2
0
298
,
f
H
∆
/
1
mol
kJ
−
- 74,81
- - - - -
- 393,51
- 285,83
1
1
0
298
,
P
mol
JK
/
C
−
−
35,11
29,355
37,11
75,291
Standardową entalpię reakcji spalania gazowego metanu w temperaturze 25
0
C, czyli
298,15 K
( )
c
O
H
)
g
(
CO
)
g
(
O
)
g
(
CH
2
2
2
4
2
2
+
→
+
można obliczyć wykorzystując podane w tabeli wartości standardowych entalpii
tworzenia substratów i produktów.
[
]
[
]
[
]
)
g
(
CH
H
)
c
(
O
H
H
)
g
(
CO
H
H
f
f
f
4
0
2
0
2
0
0
2
∆
−
∆
+
∆
=
∆
Po podstawieniu
−
⋅
−
−
⋅
+
−
⋅
=
∆
mol
kJ
81
,
74
mol
1
mol
kJ
83
,
285
2
mol
kJ
51
,
393
mol
1
H
0
kJ
36
,
890
H
0
−
=
∆
Entalpię reakcji w temperaturze 90
0
C można obliczyć w oparciu o znane równanie
Kirchhoff’a
∫
∆
+
∆
=
∆
2
1
T
T
0
P
1
0
2
0
dT
C
)
T
(
H
)
T
(
H
które przy założeniu niezależności molowych pojemności cieplnych od temperatury
przybiera postać
(
)
1
2
0
1
0
2
0
T
T
C
)
T
(
H
)
T
(
H
P
−
⋅
∆
+
∆
=
∆
Po obliczeniu wartości
0
P
C
∆
określonej jako
[
]
[
]
[
]
[
]
)
g
(
O
C
2
)
g
(
CH
C
)
c
(
O
H
C
2
)
g
(
CO
C
C
2
0
P
4
0
P
2
0
P
2
0
P
0
P
−
−
+
=
∆
⋅
⋅
−
⋅
⋅
−
⋅
⋅
+
⋅
⋅
=
∆
mol
K
kJ
355
,
29
mol
2
mol
K
kJ
31
,
35
mol
1
mol
K
kJ
291
,
75
mol
2
mol
K
kJ
11
,
37
mol
1
C
0
P
1
0
P
JK
67
,
93
C
−
=
∆
można dokonać ostatecznego przeliczenia entalpii reakcji z temperatury 25
0
C na
temperaturę 90
0
C, czyli
(
)
15
,
298
15
,
363
C
)
K
15
,
298
(
H
)
K
15
,
363
(
H
0
P
0
0
−
⋅
∆
+
∆
=
∆
kJ
27
,
884
J
1000
kJ
1
K
65
K
J
67
,
93
kJ
36
,
890
)
K
15
,
363
(
H
0
−
=
⋅
⋅
+
−
=
∆
Istnieje inny sposób rozwiązania tego problemu. Sposób ten będzie użyteczny
dla osób nie znających zastosowanego wyżej równania Kirchhoff’a. Jest to nieco
dłuższa droga będąca prostym zastosowaniem prawa Hess’a. Ilustruje to
przedstawiony niżej cykl termodynamiczny
(
)
K
363
,
c
O
H
2
)
K
363
,
g
(
CO
)
K
363
,
g
(
O
2
)
K
363
,
g
(
CH
2
2
K
363
2
4
+
→
+
↑
↓
(
)
K
298
,
c
O
H
2
)
K
298
,
g
(
CO
)
K
298
,
g
(
O
2
)
K
298
,
g
(
CH
2
2
K
298
2
4
+
→
+
Łatwo zauważyć, że polega to na zastąpieniu procesu zachodzącego w
temperaturze 363,15 K trzema procesami, a mianowicie:
1 – ochłodzeniem substratów o temperaturze 363,15 K to temperatury 298,15;
2 – reakcją zachodzącą w temperaturze 298,15 K
3 – ogrzaniem produktów reakcji do temperatury 363,15 K.
Jest chyba rzeczą dość oczywistą, że
(
)
(
)
3
0
1
0
H
K
15
,
298
H
H
K
15
,
363
H
∆
+
∆
+
∆
=
∆
Pozostaje więc obliczyć dwa tylko efekty cieplne,
3
1
H
oraz
H
∆
∆
. Pierwszy z nich dany
∫ ∑
=
∆
298
363
i
i,
P
1
dT
.)
subst
(
C
H
(
)
( )
(
)
[
]
(
)
( )
(
)
[
]
(
)
15
,
363
15
,
298
g
O
C
2
)
g
(
CH
C
dT
g
O
C
2
)
g
(
CH
C
H
2
0
P
4
0
P
298
363
2
0
P
4
0
P
1
−
⋅
+
=
+
=
∆
∫
(
)
J
2
,
6115
K
15
,
363
15
,
298
mol
K
J
08
,
94
H
1
−
=
−
⋅
=
∆
Podobnie drugi, związany z ogrzaniem produktów
∫ ∑
=
∆
363
298
i
i,
P
3
dT
.)
prod
(
C
H
(
)
( )
(
)
[
]
(
)
( )
(
)
[
]
(
)
15
,
298
15
,
363
c
O
H
C
2
)
g
(
CO
C
dT
c
O
H
C
2
)
g
(
CO
C
H
2
0
P
2
0
P
363
298
2
0
P
2
0
P
3
−
⋅
+
=
+
=
∆
∫
(
)
J
98
,
12199
K
15
,
298
15
,
363
mol
K
J
692
,
187
H
3
=
−
⋅
=
∆
Zsumowanie obliczonych wartości
(
)
J
1000
kJ
1
J
98
,
12199
kJ
36
,
890
J
1000
kJ
1
J
2
,
115
6
K
15
,
363
H
0
+
−
⋅
−
=
∆
prowadzi do
(
)
kJ
27
,
884
K
15
,
363
H
0
−
=
∆
Obliczenia termochemiczne są stosunkowo proste gdy analizowanym
reakcjom nie towarzyszą przemiany fazowe. Należy pamiętać, że punktem
odniesienia są standardowe ciepła tworzenia podane dla temperatury 298,15 K.
Chcąc obliczyć efekt cieplny reakcji spalania metanu w temperaturze wyższej
od temperatury 100
0
C, na przykład 150
0
C, należy więc uwzględnić efekt
energetyczny związany z zamianą wody ciekłej w parę wodną. Zamiast trzech należy
uwzględnić więc aż 6 etapów. Są to:
1 – ochłodzenie obu substratów, to jest 1 mola metanu i 2 moli tlenu do
temperatury 25
0
C;
2 – reakcja zachodząca w temperaturze 25
0
C;
3 – ogrzanie 1 mola gazowego CO
2
(g) wyższej temperatury 150
0
C;
4 – ogrzanie 2 moli ciekłej wody do100
0
C;
5 – przeprowadzenie 2 moli wody w stan pary o temperaturze 100
0
C;
6 – ogrzanie 2 moli pary wodnej do temperatury 150
0
.
Ilustruje to cykl termodynamiczny w którym temperatura podawana jest w
Kelwinach, podczas gdy w powyższym opisie dla jasności i orientacji użyte były
stopnie Celsjusza.
(
)
K
423
,
g
O
H
2
)
K
423
,
g
(
CO
)
K
423
,
g
(
O
2
)
K
423
,
g
(
CH
2
2
K
423
2
4
+
→
+
↑
↓
(
)
(
)
K
373
,
g
O
H
K
373
,
c
O
H
2
2
→
↓
↑
↓
(
)
K
298
,
c
O
H
2
)
K
298
,
g
(
CO
)
K
298
,
g
(
O
2
)
K
298
,
g
(
CH
2
2
K
298
2
4
+
→
+
Jak widać do wykonania obliczeń potrzebne są dodatkowe dane, entalpia
parowania wody oraz molowa pojemność cieplna wody w stanie gazowym.
© W. Grzybkowski 2002