Ć w i c z e n i e 18

WYZNACZANIE PRZERWY ENERGETYCZNEJ GER-

MANU

18.1. Opis teoretyczny

18.1.1. Pasmowa teoria ciał stałych

Elektronowe poziomy energetyczne odosobnionego atomu są ostro określone co do wartości. Natu-
ralna szerokość poziomu energetycznego wynikająca z zasady nieoznaczoności Heisenberga wyno-
si tylko 10

-7

eV. W ciele stałym atomy są położone bardzo blisko siebie, co umożliwia oddziaływa-

nia między nimi .
Gdy zaczniemy zbliżać atomy do siebie wówczas siły ich wzajemnego oddziaływania będą stop-
niowo rosły. W ciele stałym atomy są już ułożone bardzo blisko siebie, a ich struktura elektronowa
tworzy nową jakość. Ze zbliżaniem się atomów w wyniku oddziaływań międzyelektronowych na-
stępuje rozszczepienie się poszczególnych poziomów elektronowych na wiele blisko położonych
podpoziomów. Temu efektowi szczególnie łatwo ulegają poziomy zewnętrznych elektronów atomu.
Ich stany energetyczne zostają rozszczepione w ciele stałym aż na 2N (2l+1) podpoziomy (gdzie N-
ilość atomów w krysztale, l-poboczna liczba kwantowa stanu) położone bardzo blisko siebie (ich
wzajemne odległości są rzędu 10

-22

eV ).

Następnym efektem zmniejszenia odległości międzyatomowych jest uwspólnienie się rozszczepio-
nych stanów (w wyniku tunelowania) i utworzenie rozmytych stanów elektronowych wspólnych dla
wszystkich atomów w krysztale tzw. pasm energetycznych. Wpływ atomów sąsiednich jest naj-
mniejszy na elektrony wewnętrzne w atomie. Znajdują się one blisko jądra i są silnie z nim związa-
ne. Dlatego pasma energii elektronów wewnętrznych są bardzo wąskie i praktycznie odpowiadają
poziomom w odosobnionym atomie. Natomiast wysokoenergetyczne poziomy elektronów ze-
wnętrznych tworzą szerokie pasma. W efekcie istnieją dwa pasma wspólne dla całego kryształu.
Niższe energetycznie zwane podstawowym lub walencyjnym, a wyższe – dozwolonym lub prze-
wodnictwa. Szerokość tych pasm jest duża – rzędu 1eV.
Reasumując, istnienie pasm energetycznych można wytłumaczyć silnym oddziaływaniem ze-
wnętrznych elektronów danego atomu z zewnętrznymi elektronami sąsiedniego atomu, a za ich
pośrednictwem ze wszystkimi innymi zewnętrznymi elektronami znajdującymi się w krysztale.
W temperaturze T=0K pasmo walencyjne ciała stałego jest całkowicie zapełnione elektronami, na-
tomiast pasmo przewodnictwa jest całkowicie puste.

18.1.2. Półprzewodniki samoistne

Ciała stałe ze względu na ich właściwości elektryczne dzielimy na trzy grupy:
1. przewodniki, w których stany zapełnione sąsiadują bezpośrednio ze stanami pustymi (np. meta-

le),

2. izolatory, w których najmniejsza energetyczna odległość między stanami zapełnionymi elek-

tronami i pustymi zwana przerwą energetyczną (E

g

) jest duża, tzn. większa niż 2 eV (np. dla

diamentu wynosi ona 5,4 eV),

3. Półprzewodniki, w których przerwa energetyczna jest mniejsza niż 2 eV (np. dla krzemu wyno-

si 1,1 eV). Na rys. 18.1 przedstawiono schematycznie strukturę pasmową tych materiałów oraz
ich obsadzenie elektronami w temperaturze zera bezwzględnego.

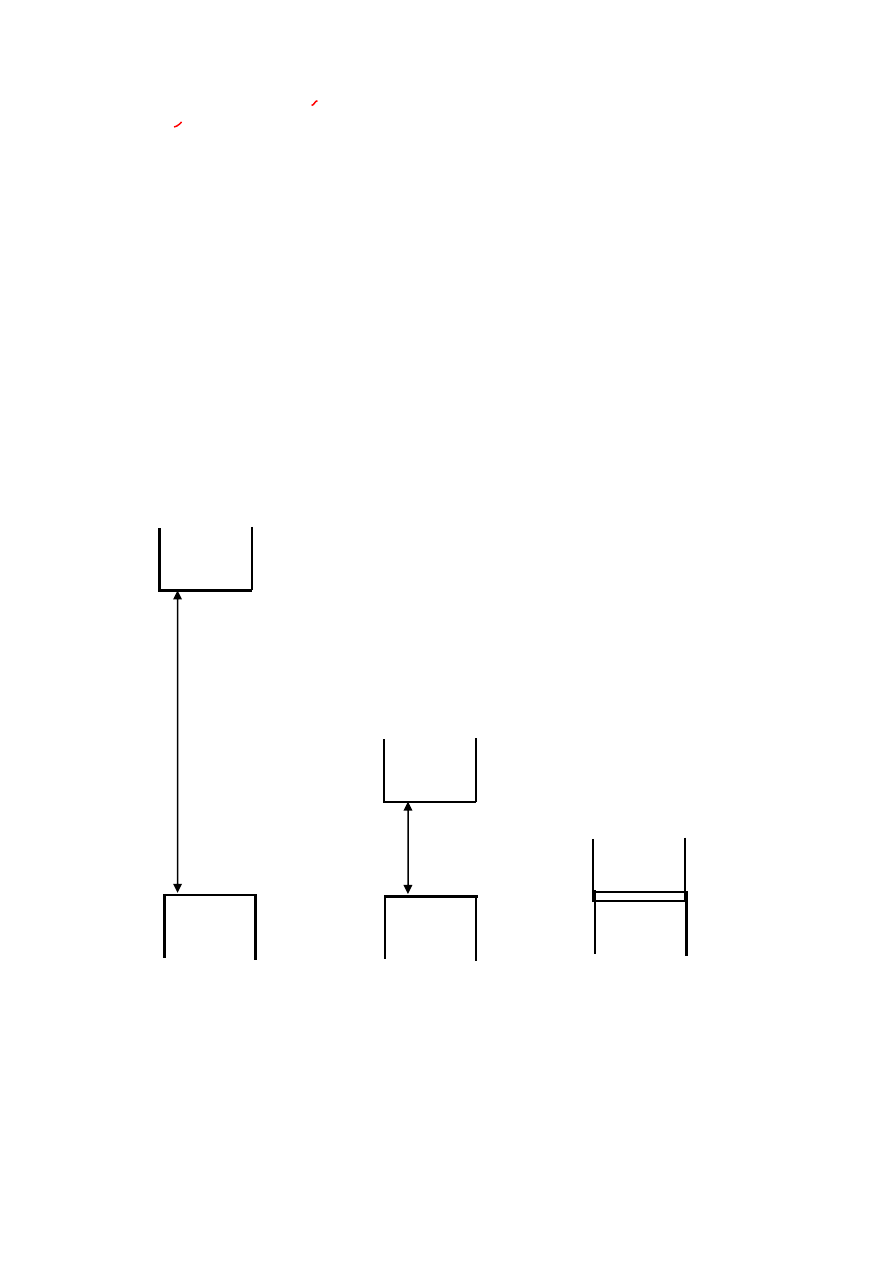
W wyższych temperaturach wskutek oddziaływania elektronów z termicznymi drganiami sieci
kryształu część z nich może uzyskać energię wystarczająco dużą by przejść z pasma walencyj-
nego do pasma przewodnictwa i brać udział w przewodnictwie prądu elektrycznego. Aby elek-
tron uczestniczył w przewodnictwie prądu elektrycznego musi pobierać energię od przyłożone-
go z zewnątrz pola elektrycznego, a to jest możliwe tylko wówczas gdy znajdzie się on w pa-
śmie przewodnictwa. Elektrony takie nazywamy swobodnymi, gdyż mogą poruszać się po ca-
łym krysztale.

Wydajność opisanego termicznego procesu wzbudzenia elektronu do pasma przewodnictwa bardzo
silnie zależy od wartości przerwy energetycznej:

- przy jej praktycznym braku (jak w przewodnikach) już w temperaturze kilkudziesięciu K
wszystkie elektrony biorą udział w przewodnictwie,
- gdy jest ona bardzo duża (jak w izolatorach) nawet w temperaturach rzędu kilkuset stopni
Celsjusza elektronów swobodnych w ciele stałym jest tak mało, że praktycznie nie przewodzi on
prądu,
- natomiast w półprzewodnikach, gdzie przerwa energetyczna jest mniejsza, już w temperaturze
pokojowej część elektronów jest przeniesiona do pasma przewodnictwa, co umożliwia przepływ
prądu.

a)
Stany
pp

puste

b)

E

g

Stany

pp

puste

c)

E

g

Stany

pp

puste

pv

Stany

pv

Stany

pv

Stany

zapełnione

zapełnione

zapełnione

Rys. 18.1. Struktura pasmowa ciał stałych w T=0K: a) izolatorów, b) półprzewodników, c)

przewodników (nałożenie się dwu pasm): pp – pasmo przewodnictwa, pv – pasmo walen-

cyjne, Eg – przerwa zabroniona.

Należy zaznaczyć, że ilość swobodnych elektronów w półprzewodniku jest stosunkowo mała i dla-
tego dalsze ogrzewanie półprzewodnika wymusza generację dalszych elektronów swobodnych.
Następuje dalszy silny wzrost przewodnictwa, np. ogrzewając czysty krzem od 0 do 200

o

C obser-

wujemy wzrost jego przewodnictwa od 10

-7

do 10

-2

[

Ω

-1

cm

-1

], a więc o pięć rzędów wielkości. Ta

silna zależność koncentracji nośników ładunku od temperatury jest specyficzną właściwością pół-

przewodników odróżniającą je od metali, w których koncentracja swobodnych elektronów jest
praktycznie stała, niezależna od temperatury.

pp

E

g

pv

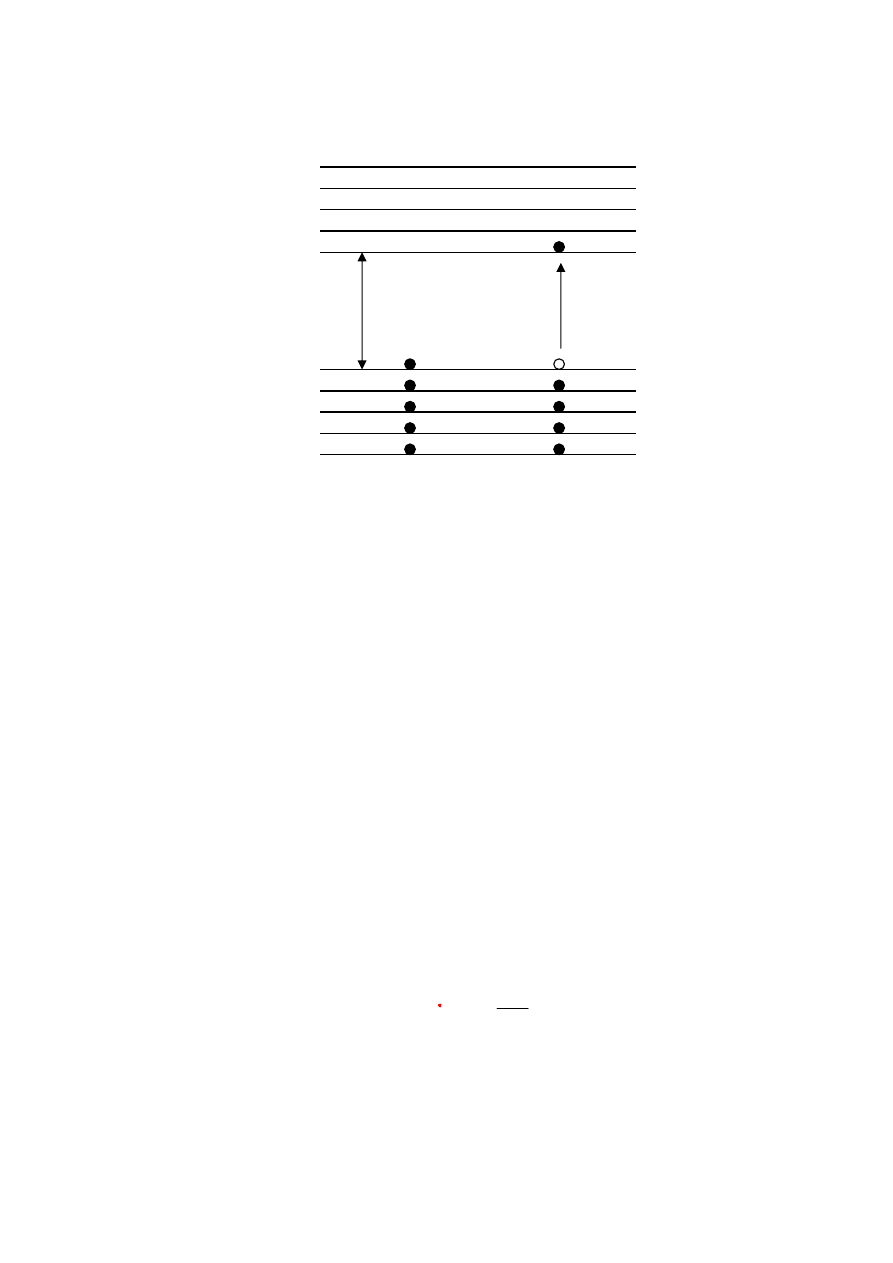
Rys. 18.2. Termiczna generacja nośników ładunku w półprzewodniku samoistnym (model

pasmowy). Na danym poziomie energetycznym mogą przebywać tylko dwa elektrony o róż-

nych spinach.

Przejście elektronu z pasma walencyjnego w półprzewodniku do pasma przewodnictwa oznacza w
modelu energetycznym (rys. 18.2 ) pojawienie się w paśmie walencyjnym wolnego stanu nie obsa-
dzonego elektronem zwanego dziurą. Wytworzona dziura może zostać zajęta przez jeden z sąsied-
nich związanych elektronów i w rezultacie przesunąć się w inne miejsce. Jest więc ona nośnikiem
nieskompensowanego dodatniego ładunku elementarnego. W obecności zewnętrznego pola elek-
trycznego dziury będą poruszać się w kierunku pola, a wolne elektrony w kierunku przeciwnym. W
ten sposób w półprzewodniku występują obok siebie dwa niezależne nośniki prądu. Z omówionego
mechanizmu generacji nośników ładunku (rys. 18.2 ) wynika, że w półprzewodniku powinno być
tyle samo elektronów w paśmie przewodnictwa, jak i dziur w paśmie walencyjnym, gdyż w wyniku
każdego pojedynczego aktu generacji powstaje para nośników elektron-dziura. Właściwość tę ma
każdy czysty materiał półprzewodnikowy o nie zaburzonej strukturze krystalicznej. Półprzewodniki
takie nazywamy samoistnymi. W ćwiczeniu badamy właśnie elektryczne właściwości samoistnego
kryształu germanu.
Wielkością fizyczną określającą ilość nośników ładunku jest ich koncentracja. I tak koncentracją
swobodnych elektronów (n) nazywamy liczbę elektronów w paśmie przewodnictwa przypadającą
na jednostkę objętości ciała, a koncentracją dziur (p) nazywamy liczbę dziur w paśmie walencyj-
nym w jednostce objętości ciała. Szczegółowa teoria samoistnych półprzewodników pokazuje, że
koncentracja nośników ładunku wykładniczo rosną z temperaturą (T) wyrażoną w stopniach K.













−

=

=

2kT

E

exp

n

n

p

g

0

(18.1)

gdzie n

0

możemy traktować jak stałą niezależną od temperatury.

18.1.3. Przewodnictwo półprzewodników samoistnych

Jeżeli do półprzewodnika przyłożymy pewne stałe napięcie, to w wyniku przyspieszającego działa-
nia tego zewnętrznego pola elektrycznego oraz hamującego oddziaływania ze strukturą sieci krysz-
tału, ustali się pewna średnia prędkość ruchu nośników ładunków kierunku pola.
Gęstość prądu w półprzewodnikach, jak wynika z definicji tej wielkości, wyniesie w ogólnym
przypadku

(

)

p

n

v

p

v

n

e

j

+

=

(18.2)

gdzie: j – gęstość prądu, e – ładunek elektronu, v

n

, v

p

– średnie prędkości elektronów i dziur.

Wprowadzając pojęcie ruchliwości nośników zdefiniowanej wzorami

E

v

n

=

n

µ

E

v

p

=

p

µ

(18.3)

(np. dla germanu

/Vs

cm

3900

2

=

n

µ

i

s

p

/V

cm

1900

2

=

µ

) otrzymujemy

(

)

E

p

n

e

j

p

n

µ

µ

+

=

(18.4)

gdzie E – natężenie przyłożonego pola elektrycznego.

Porównując ostatni wzór z prawem Ohma:

E

σ

j

=

otrzymujemy wyrażenie na przewodnictwo elek-

tryczne półprzewodników:

(

)

p

n

p

n

e

µ

µ

σ

+

=

(18.5)

Ponieważ dla półprzewodników samoistnych słuszna jest zależność (18.1), a więc możemy dla nich
napisać:

(

)













−

+

=

2kT

E

exp

n

e

g

0

p

n

µ

µ

σ

(18.6)

lub













−

=

2kT

E

exp

g

0

σ

σ

(18.7)

gdzie

0

σ

można traktować jak stałą niezależną od temperatury.

W ćwiczeniu wyznaczamy przerwę energetyczną germanu z pomiarów zależności rezystancji pół-
przewodnika samoistnego od temperatury. Jak wynika ze wzoru (18.7) zależność tę można zapisać
w postaci:













=

2kT

E

exp

g

0

R

R

(18.8)

gdzie: R

0

- jest z dobrym przybliżeniem stałą rezystancją zależna od rodzaju półprzewodnika i jego

wymiarów geometrycznych.
Logarytmując to wyrażenie otrzymujemy:

T

1

2k

E

0,4343

lg

lg

g

0

+

=

R

R

(18.9)

a więc zależność













=

T

1

lg

f

R

jest prostą, a jej nachylenie wynosi

2k

E

4343

,

0

g

.

U w a g a: Funkcja lgR =f(1/T) otrzymana z eksperymentu nie jest proporcjonalna w całym zakresie
stosowanych temperatur. Warunek (18.9) jest spełniony tylko dla wystarczająco wysokich tempera-
tur, ponieważ w doświadczeniu użyto półprzewodnika domieszkowanego

(

)

p

n

≠

. W wysokich

temperaturach intensywność termicznej generacji nośników ładunku (patrz rys. 18.2) osiąga tak
dużą wydajność (jednocześnie nośników domieszkowanych z temperaturą nie przebywa), że pół-
przewodnik staje się samoistnym

.

T a b e l a 18.1

Właściwości materiałów półprzewodnikowych

Związek

E

g

[eV]

293 K

µ

n

[ cm

2

/Vs ]

µ

p

[ cm

2

/Vs ]

C-diament

(izolator)

Si

Ge

α Sn

β SiC

AlP

AlAs

AlSb

GaP

GaAs

GaSb

InP

InAs

InSb

5,4

1,107

0,67
0,08

2,3
2,5

2,16

1,6

2,24
1,35
0,67
1,27
0,36

0,165

1800
1900
3800
2500
4000

-

1200

200 – 400

300

8800
4000
4600

33000
78000

1400

500

1820
2400

-
-

420
500
100
400

1400

150
460
750

18.2. Opis układu pomiarowego

Badana próbka o wymiarach 2×2×20 mm

3

została wycięta z monokrystalicznego walca germanu.

Po mechanicznym wypolerowaniu i obróbce chemicznej wykonywano kontakty elektryczne. W tym
celu na dłuższym jej boku wtopiono próżniowo stop Pb+10% In w temperaturze 600

o

C. Próbka

germanu jest monokryształem o rezystywności 0,60

Ωm.

Badana próbka germanu umieszczona jest wewnątrz pieca rezystorowego. Cienkie druciki przylu-
towane do kontaktów elektrycznych próbki połączone są z precyzyjnym cyfrowym miernikiem re-
zystancji. Temperatura próbki mierzona jest za pomocą przecechowanej termopary Cu – konstantan

podłączonej do woltomierza cyfrowego. Temperaturę pieca można regulować zmieniając natężenie
prądu płynącego przez taśmę rezystorową pieca.

18.3. Przebieg pomiarów

1. Zaznajomić się z układem pomiarowym.
2. Przełącznik ustawić w jednym z trzech położeń umożliwiających pomiar rezystancji próbki
( R

12

, R

23

, R

13

).

3. Zmierzyć rezystancję półprzewodnika w temperaturze pokojowej.
4. Włączyć zasilacz i regulować prądem płynącym przez piec tak, aby uzyskać szybkość ogrzewa-
nia około 3

o

C/min.

U w a g a :

Można wybrać jeden z dwóch sposobów zmian temperatury próbki:

• szybko podnosić jej temperaturę; wówczas należy wykonać pomiary podczas ogrzewania i
schładzania oraz obliczyć wartość średnią,
• powoli podnosić jej temperaturę; wówczas pomiar przy schładzaniu pieca jest zbyteczny (nie
obserwuje się „histerezy” otrzymanych wyników). Optymalny sposób powolnego ogrzewania do:
50

o

C – prąd 0,5 A; od 50

o

C do 70

o

C – I = 0,7 A; od 70

o

C do 100

o

C – I = 0,9 A; od 100

o

C do 120

o

C

– I = 1,1 A. Nie przekraczać I = 1,25 A !!

5. Notować wskazania miernika rezystancji co 5

o

C, aż do uzyskania temperatury około 125

o

C.

18.4. Opracowanie wyników pomiarów.

1. Zaznaczyć punkty pomiarowe zależności













=

T

1

lg

f

R

na wykresie. Zinterpretować

przebieg wykresu.
2. Wybrać 5 - 7 punktów z zakresu liniowego powyższej zależności i poprowadzić przez nią
prostą w optymalny sposób.
3. Określić nachylenie prostej oraz błąd jego wyznaczenia.

4. Na podstawie wzoru (18.9) obliczyć E

g

i

g

E

σ

.

18.5. Pytania kontrolne

1. Omówić mechanizm powstawania pasm w ciałach stałych.
2. Podać podział ciał stałych ze względu na ich właściwości elektryczne.
3. Omówić strukturę pasmową półprzewodnika samoistnego.
4. Zinterpretować zależność konduktywności półprzewodnika od temperatury.
5. Jak wyznaczyć przerwę energetyczną półprzewodnika.

L i t e r a t u r a

[1] Kittel C.: Wstęp do fizyki ciała stałego. PWN, Warszawa 1970.

[2] Massalski J.M.: Fizyka dla inżynierów, cz.2, WNT, Warszawa 1975.
[3] Wolf H.: Półprzewodniki. WNT, Warszawa 1975.