Ekonometria

WYKŁAD 2

Piotr Ciżkowicz

Katedra Międzynarodowych Studiów Porównawczych

Plan

Czym się zajmiemy:

1. Miary dopasowania modelu do danych

2.

Błędy szacunku parametrów

3.

Testowanie istotności parametrów

Postać liniowego modelu ekonometrycznego

►

Analizujemy model regresji, w którym stosujemy k
zmiennych objaśniających (wyraz wolny stanowi jedną ze
zmiennych) postaci…

►

…lub w postaci macierzowej

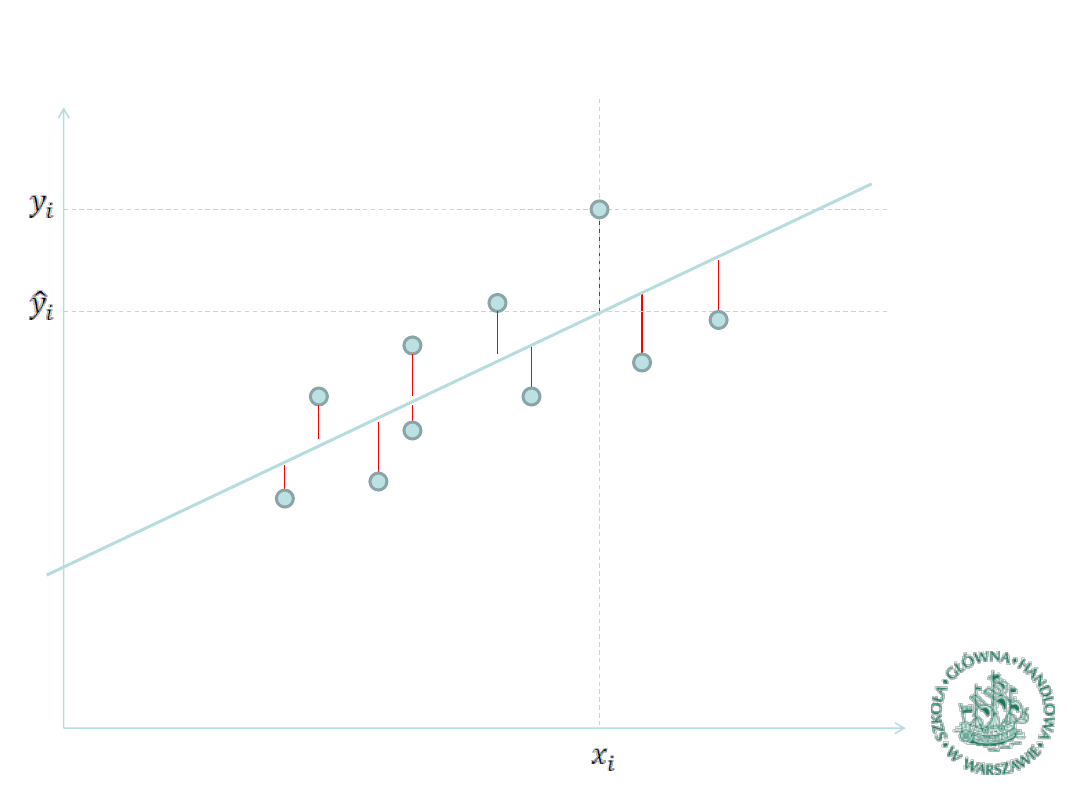
MNK

– idea (1)

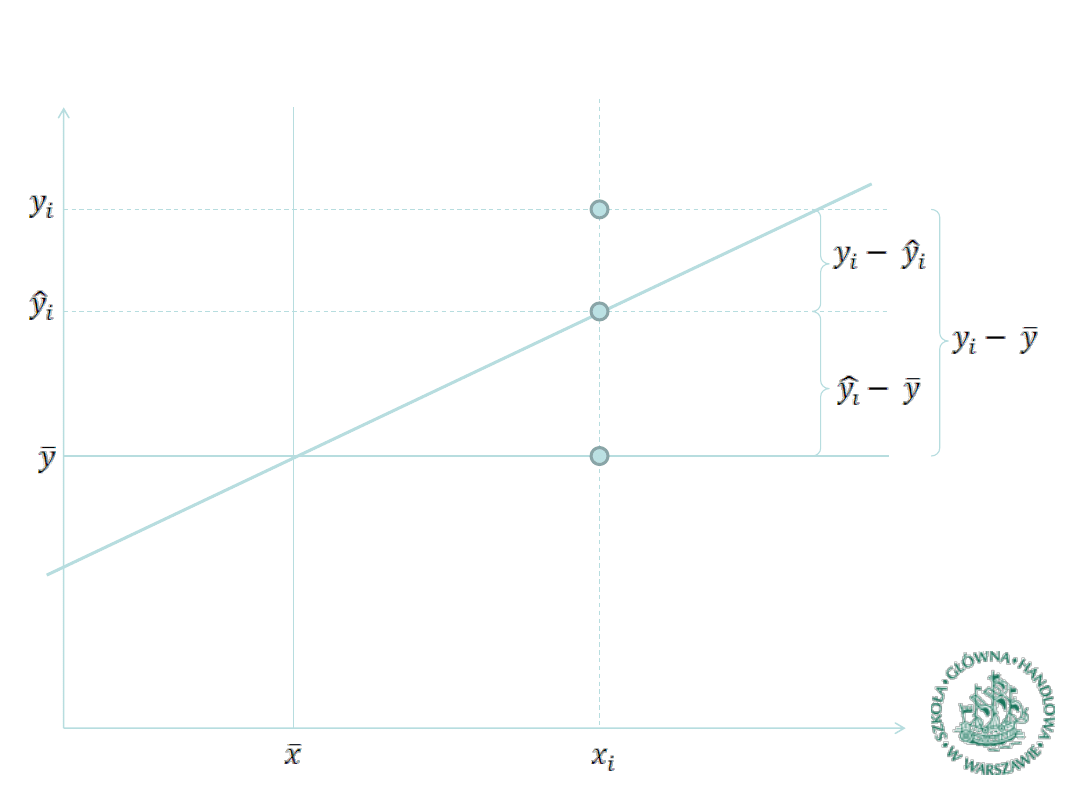
MNK

– idea (2)

►

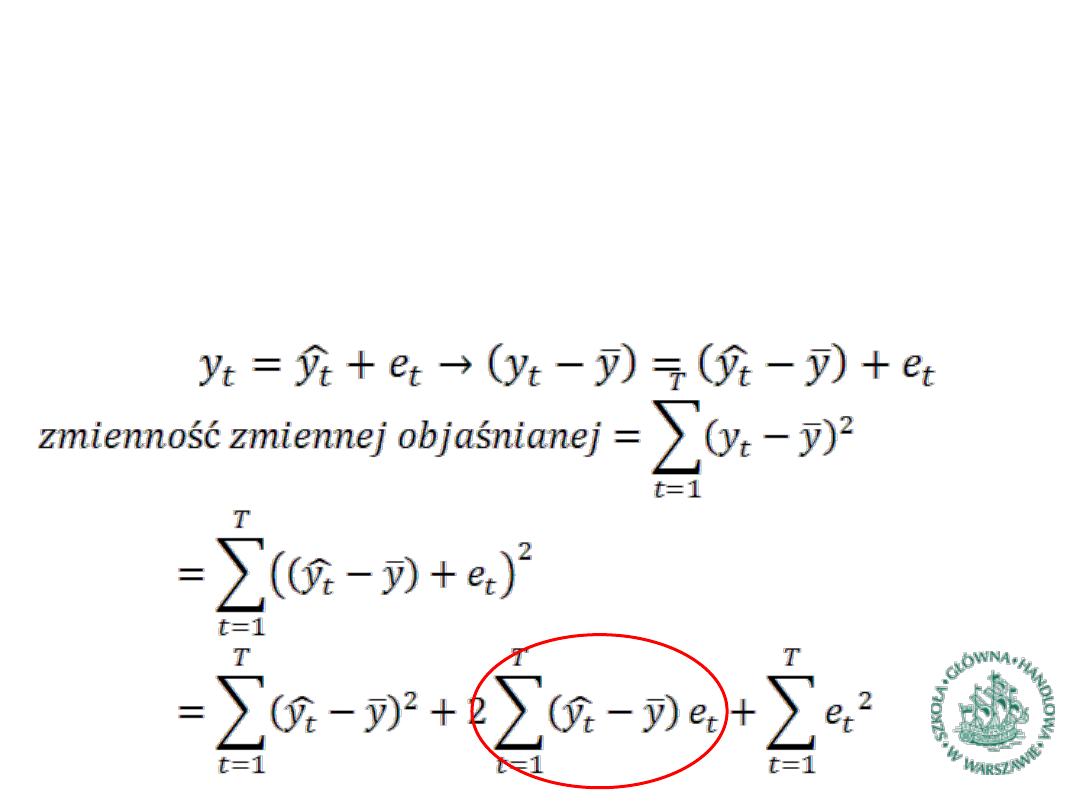
Współczynnik determinacji (R^2) jest naturalna miarą jakości
dopasowania modelu do danych empirycznych

►

Informuje w jakim stopniu zmienność zmiennej objaśnianej jest
wyjaśniona przez model

►

Wyprowadzenie wzoru

Współczynnik determinacji (1)

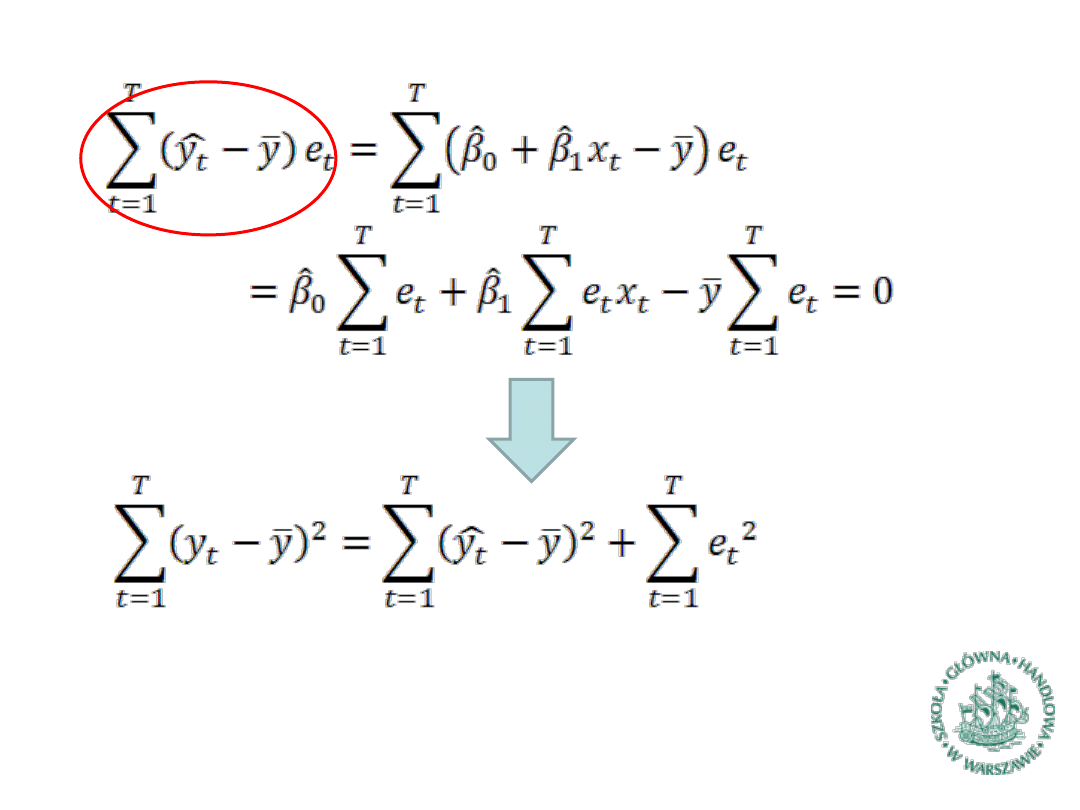
Współczynnik determinacji (2)

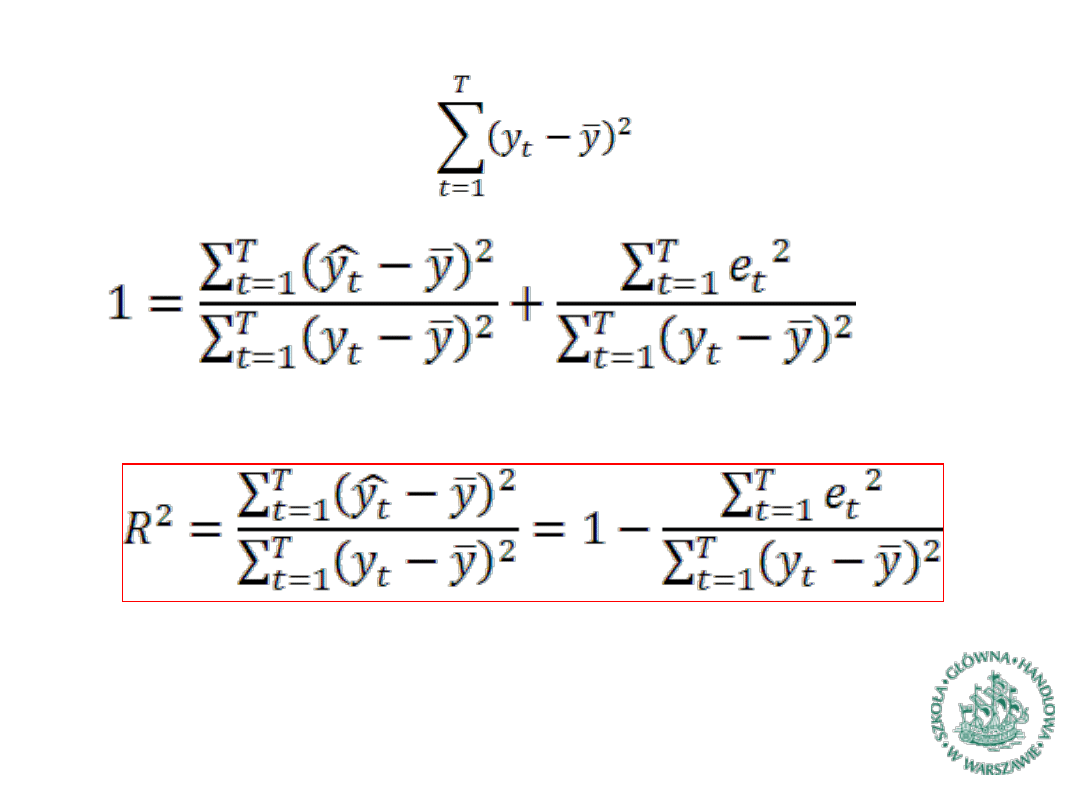
Współczynnik determinacji (3)

►

Dzieląc stronami przez otrzymujemy:

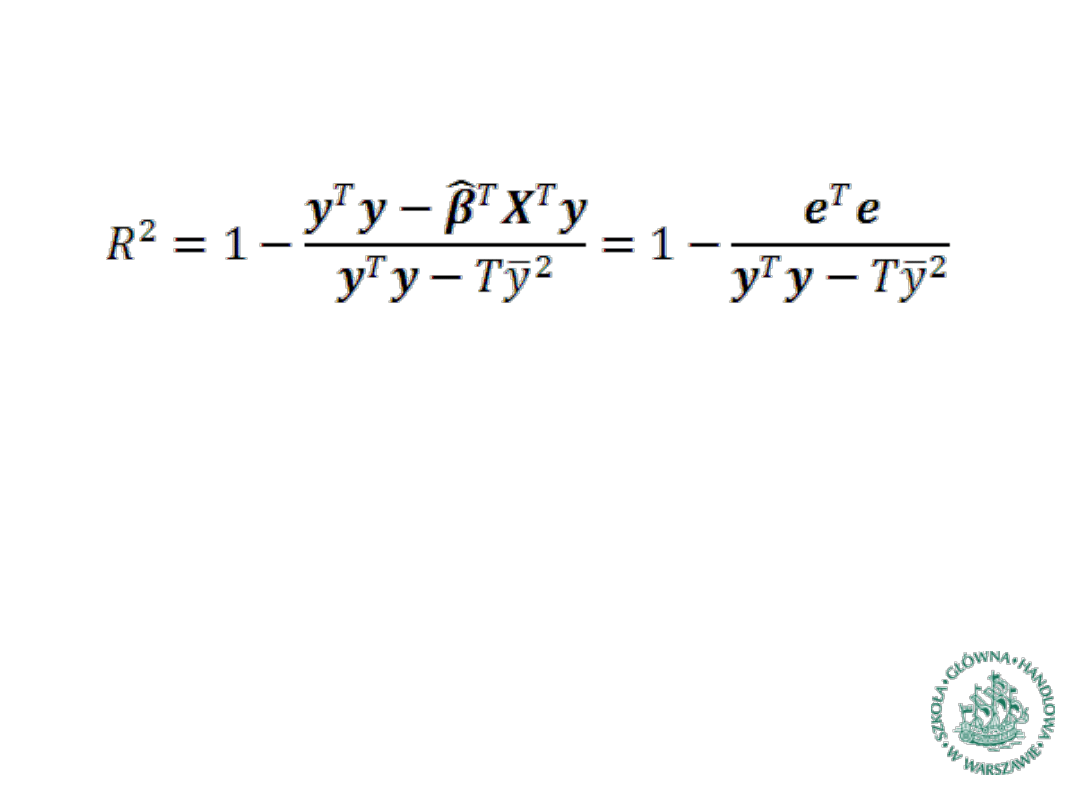
Współczynnik determinacji (4)

►

Inne postacie wzorów (w zapisie macierzowym):

►

Współczynnik determinacji przyjmuje wartości z przedziału <0;1>

►

Interpretacja: współczynnik determinacji informuje, ile procent
zmienności zmiennej objaśnianej zostało wyjaśnione przez
model.

►

Ograniczenia współczynnika determinacji:

►

Nadaje się do oceny dopasowania modelu, w którym relacja
między zmiennymi objaśniającymi a objaśnianą jest liniowa, a
parametry zostały wyestymowane MNK

Współczynnik determinacji (5)

►

Ograniczenia współczynnika determinacji:

►

nadaje się do oceny dopasowania modelu, w którym relacja
między zmiennymi objaśniającymi a objaśnianą jest liniowa, a
parametry zostały wyestymowane MNK;

►

przyjmuje wartości unormowane (od 0 do 1), jeśli w modelu
jest wyraz wolny

►

jest on rosnącą funkcją liczby zmiennych objaśniających
modelu (dlaczego?), stąd nie nadaje się do porównywania
jakości dopasowania modeli o różnej liczbie zmiennych

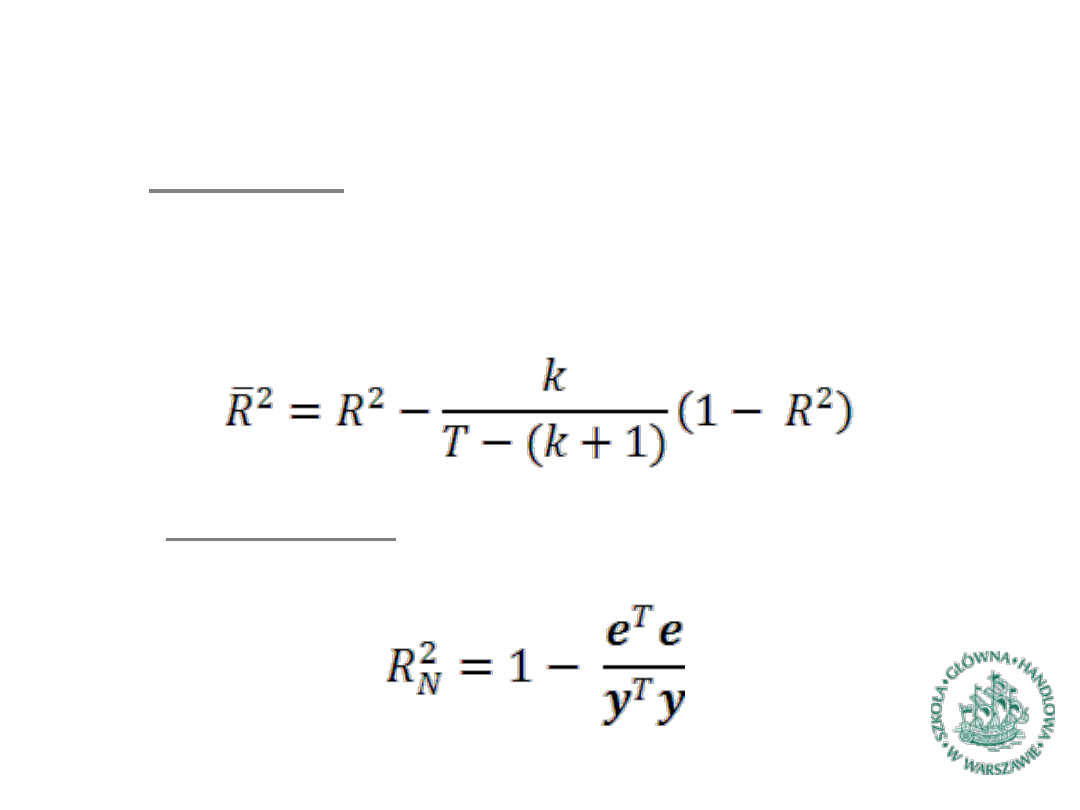
Współczynnik determinacji (6)

►

Inne postacie współczynnika determinacji:

►

Skorygowany

: koryguje wpływ różnej liczby zmiennych na

R^2 nakładając „karę” za każdą dodatkową zmienną; stosuje
się go przy porównywaniu modeli o różnej liczbie zmiennych;
współczynnik ten nie jest unormowany i może przyjmować
ujemne wartości

►

Niescentrowany: stosowany do oceny dopasowania modeli
bez wyrazu wolnego; przyjmuje wartość z przedziału <0;1>

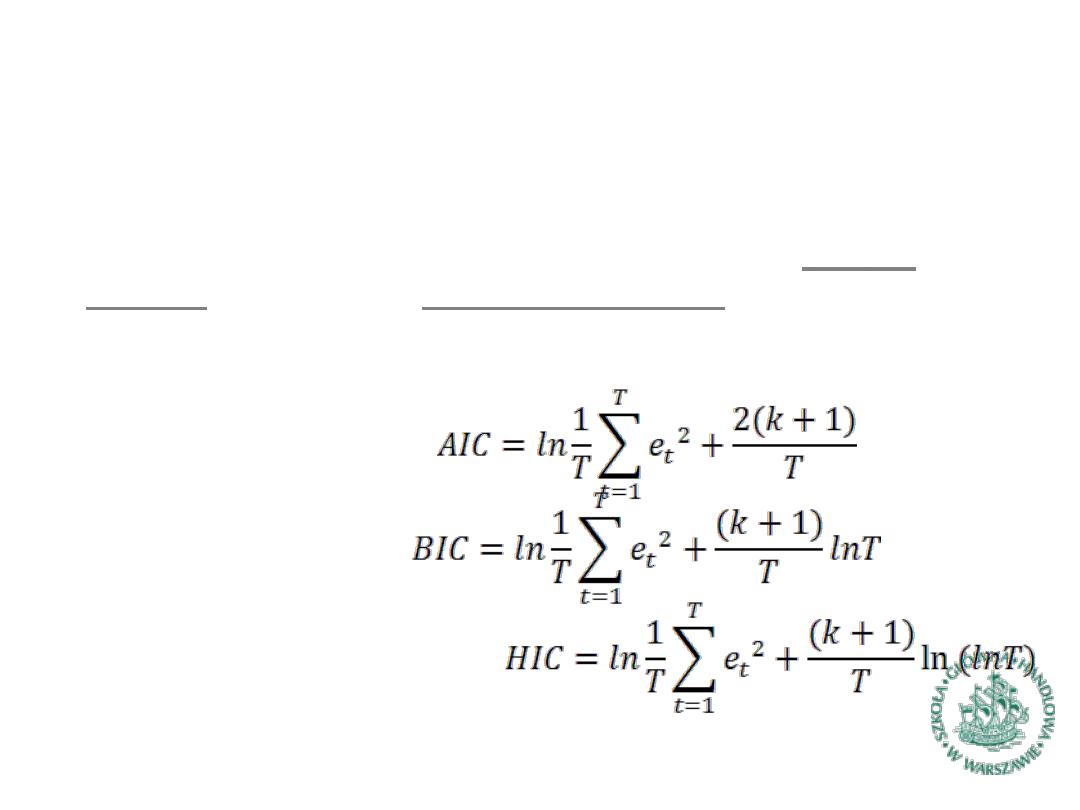
Alternatywne miary dopasowania modelu

– kryteria

informacyjne

►

Kryteria informacyjne bazują na koncepcji, w której z jednej
strony brana jest pod uwagę ilość informacji zawarta w modelu
(mierzona logarytmem funkcji wiarygodności), z drugiej zaś
poziom złożoności (liczba zmiennych modelu). Im większa
wartość kryterium, tym gorsze dopasowanie modelu.

►

Kryterium

Akaike’a:

►

Kryterium Schwarza:

►

Kryterium Hannana-Quinna:

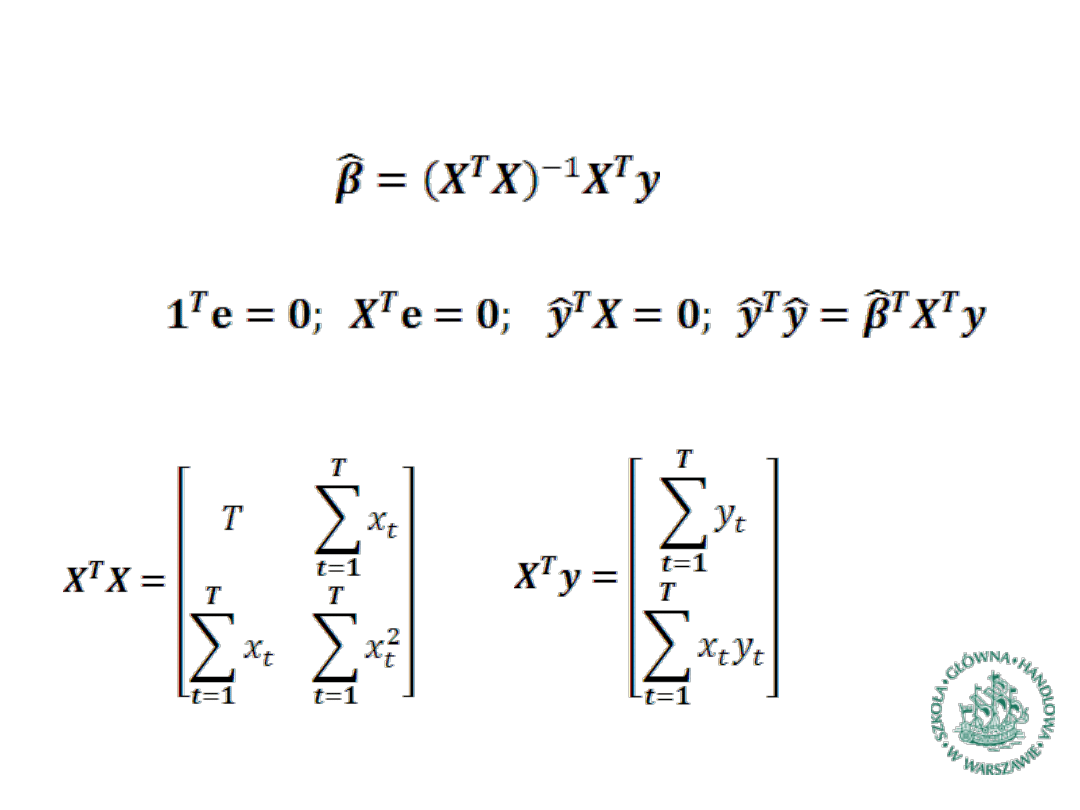
MNK

– Własności arytmetyczne estymatora MNK (1)

►

Przy oznaczeniach jak na slajdzie 4 estymator MNK dany jest
wzorem:

►

Obowiązują przy tym następujące zależności:

►

Ponadto dla modelu z wyrazem wolnym i jedną zmienną
objaśniającą odpowiednie macierze mają następującą postać:

MNK

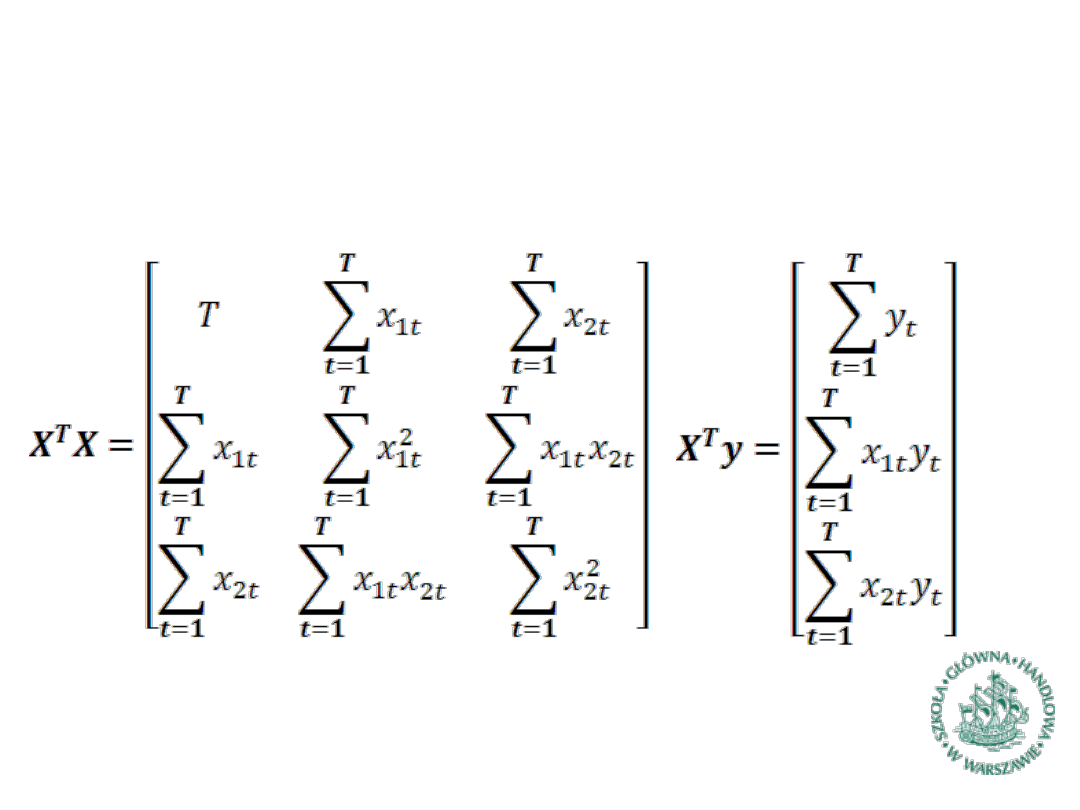
– Własności arytmetyczne estymatora MNK (2)

►

Dla modelu z wyrazem wolnym i dwiema zmiennymi
objaśniającymi macierze te mają postać:

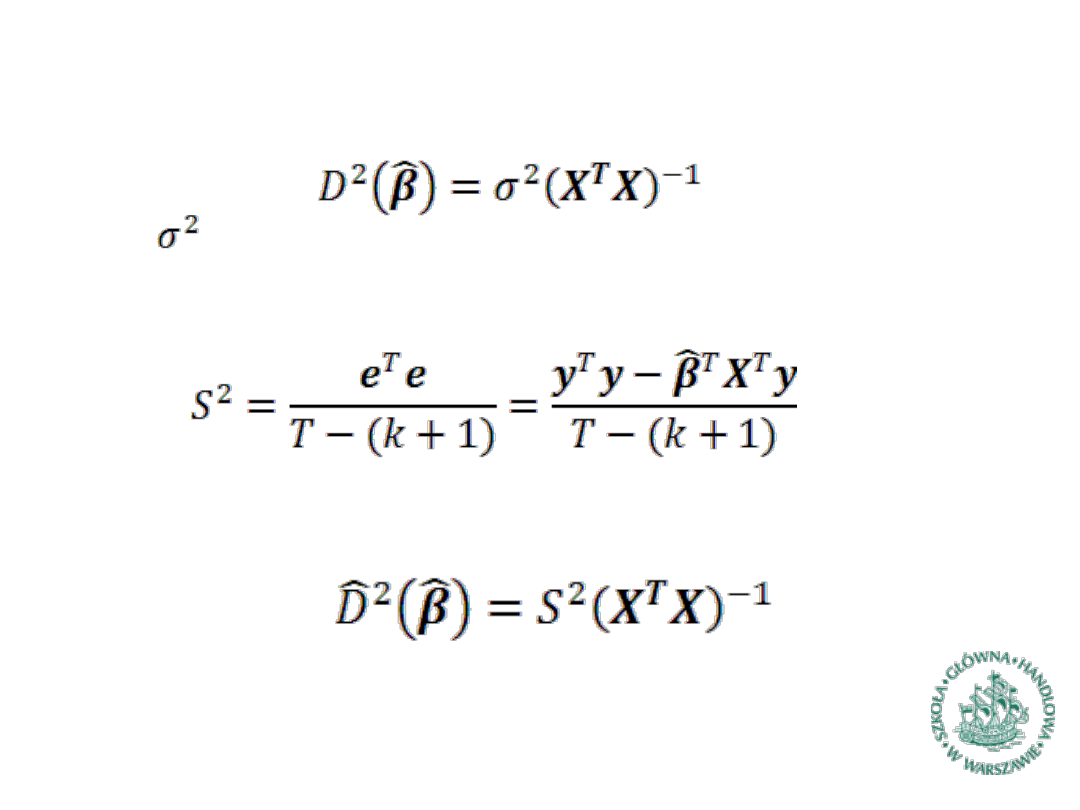
MNK

– Macierz kowariancji estymatora MNK (1)

►

Macierz kowariancji estymatora MNK dana jest wzorem

gdzie jest wariancją składnika losowego, która nie jest znana

►

Estymator wariancji składnika losowego dany jest wzorem:

stąd estymator macierzy kowariancji estymatora MNK

przybiera postać:

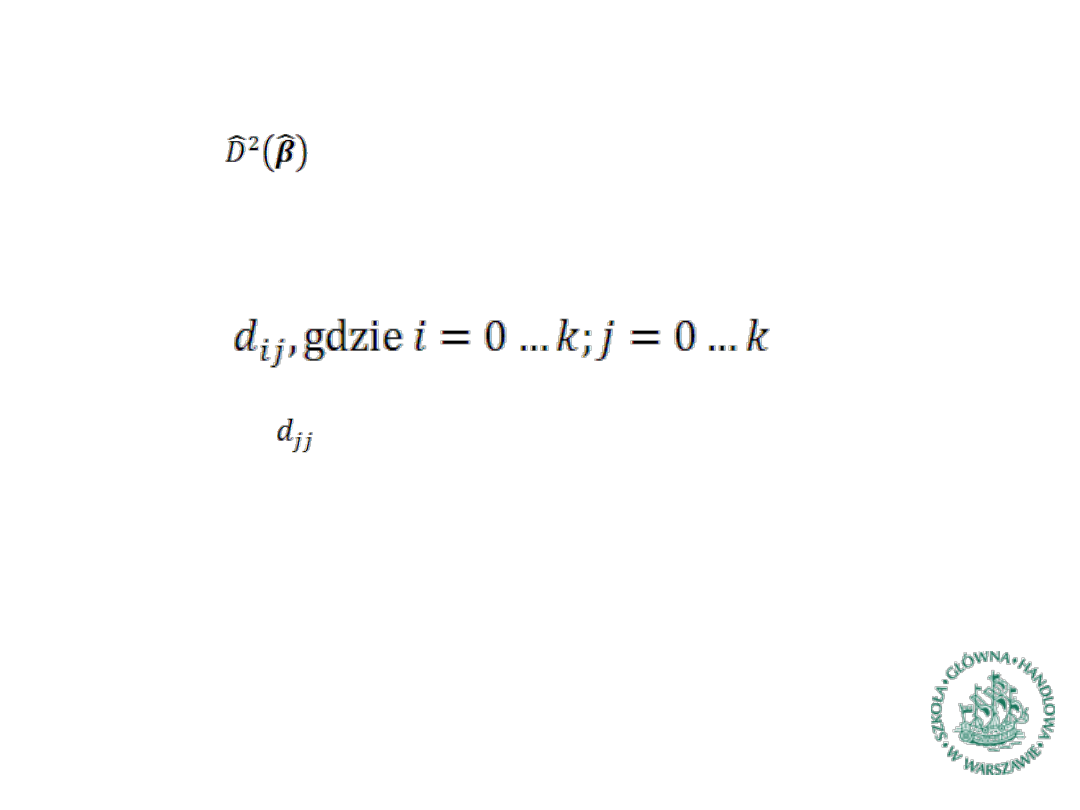
MNK

– Macierz kowariancji estymatora MNK (2)

►

Macierz jest macierzą kwadratową i symetryczną o
wymiarze równym liczbie szacowanych parametrów tzn. k+1

►

Jeśli poszczególne elementy macierzy oznaczymy jako

to elementy stanowią oszacowania wariancji estymatorów
poszczególnych parametrów strukturalnych.

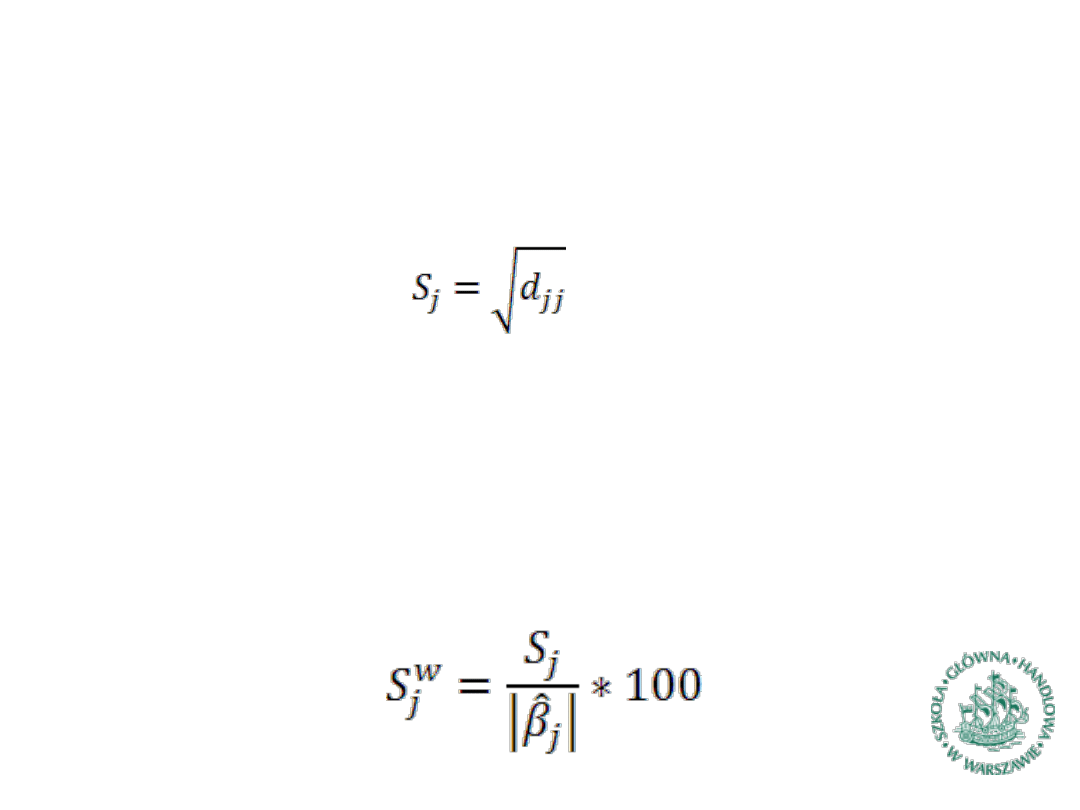
Błędy szacunków parametrów

►

Do wnioskowania o dokładności szacunków parametrów
strukturalnych stosuje się odchylenia standardowe
estymatora tych parametrów czyli:

►

Wartość te nazywa się średnim błędem szacunku parametru j.
Wartość ta stanowiłaby przeciętne odchylenie wartości
wyestymowanego

parametru, jeśli możnaby dokonać estymacji na

innych próbach o tej samej liczebności.

►

Do wnioskowania wygodniejszy jest tzw. średni względny błąd
szacunku wyrażony w procentach wyestymowanej wartości
parametru i opisany wzorem:

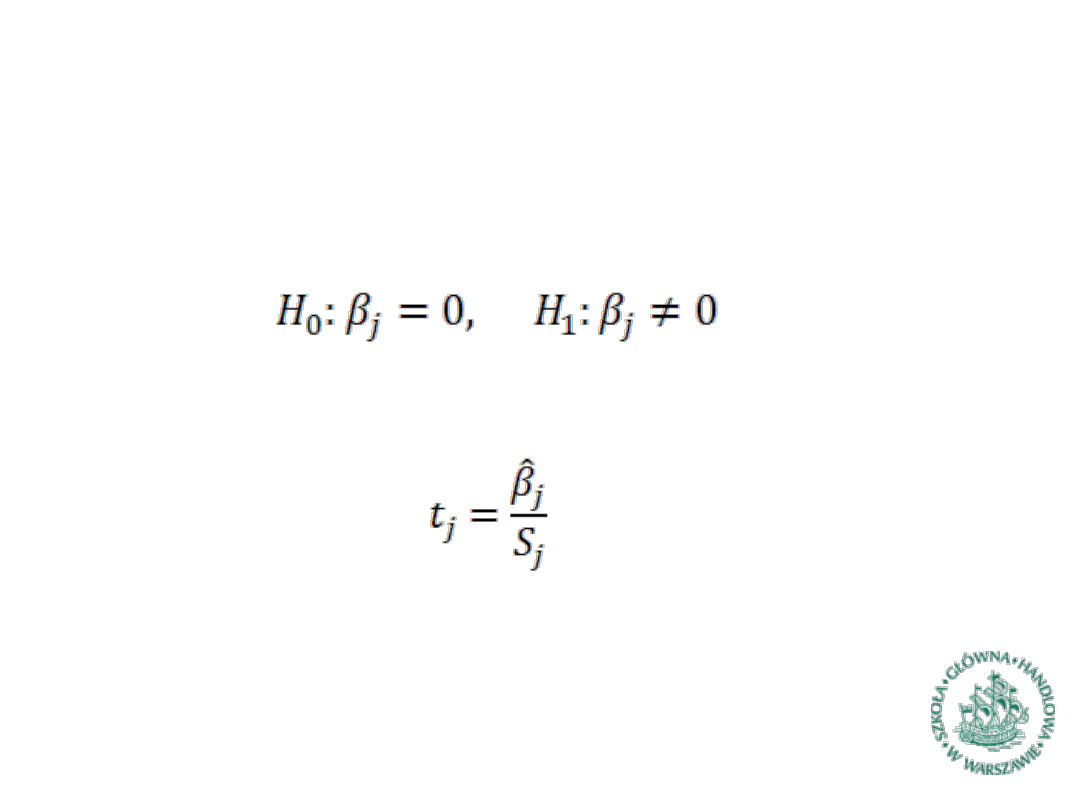
Testy istotności parametrów (1)

►

Podstawowym testem stosowany do oceny istotności
oszacowań parametrów strukturalnych jest test bazujący na
statystyce t-Studenta.

►

Testowany jest zestaw hipotez postaci:

►

Przy prawdziwości hipotezy zerowej statystyka

ma rozkład t- Studenta z T-(k+1) stopniami swobody

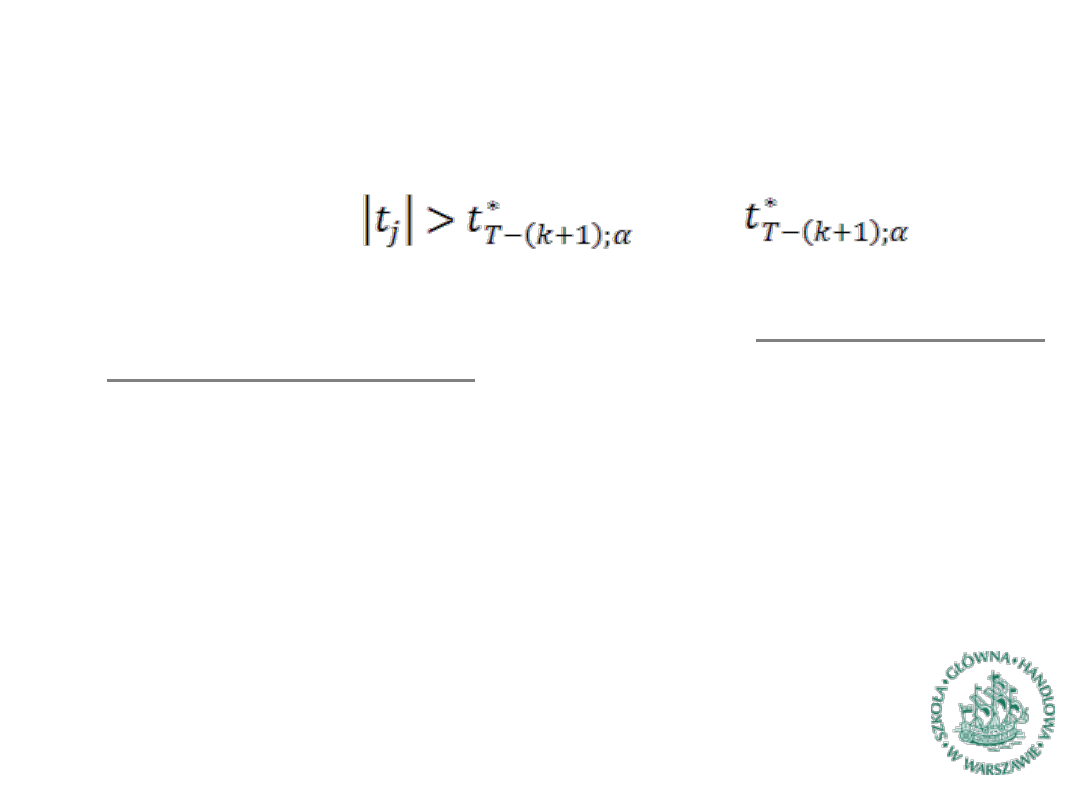
Testy istotności parametrów (2)

►

Sposoby testowania:

a) Jeśli zachodzi gdzie

to wartość odczytana z tablic rozkładu dla zadanej liczby stopni
swobody i ustalonego poziomu istotności, to odrzucamy hipotezę
zerową o braku istotności, zaś w przeciwnym przypadku nie mamy
podstaw do jej odrzucenia

b) W praktyce łatwiej posługiwać się tzw. empirycznym poziomem

istotności oznaczanym jako „wartość p” lub „p- value”. Jest to
najniższy poziom istotności, przy którym odrzucalibyśmy hipotezę
zerową. Jeśli wartość empirycznego poziomu istotności jest niższa
od ustalonej do testowania wartości poziomu istotności to
odrzucamy hipotezę zerową.

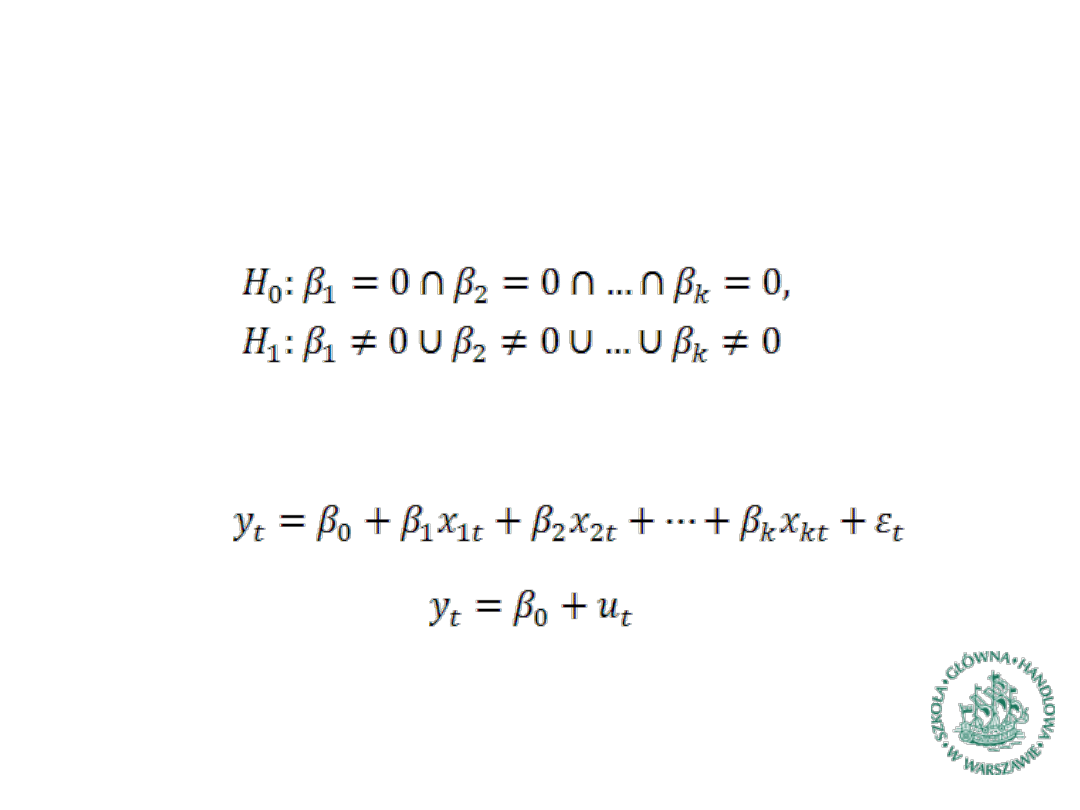
Testy łącznej istotności parametrów (test Walda) (1)

►

Test Walda

służy do testowania łącznej istotności zmiennych

ujętych w modelu

►

Testowany jest zestaw hipotez postaci:

►

Ujmując to inaczej jest to test porównujący jakość
dopasowania do danych dwóch modeli:

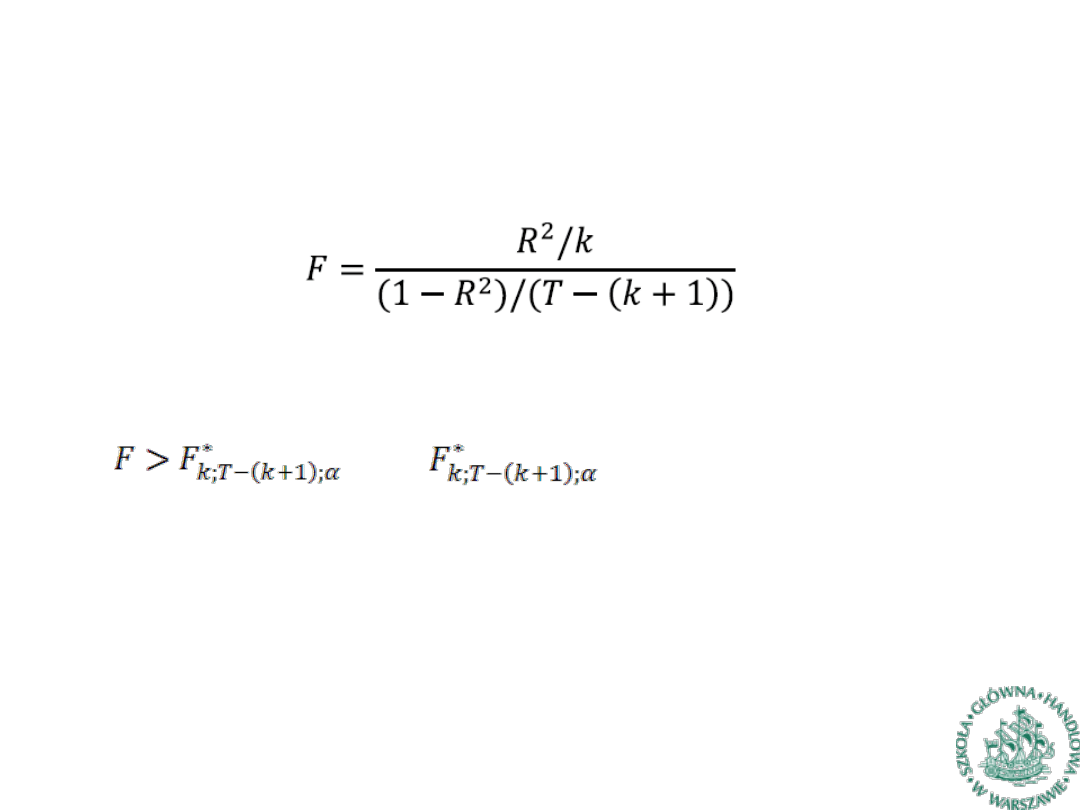
Testy łącznej istotności parametrów (test Walda) (2)

►

Przy prawdziwości hipotezy zerowej statystyka

ma rozkład F-Snedecora przy liczbie stopni swobody k i T-(k+1)

►

Hipotezę zerową o braku istotności należy odrzucić jeśli

gdzie to wartość statystyki odczytana

z tablic rozkładu

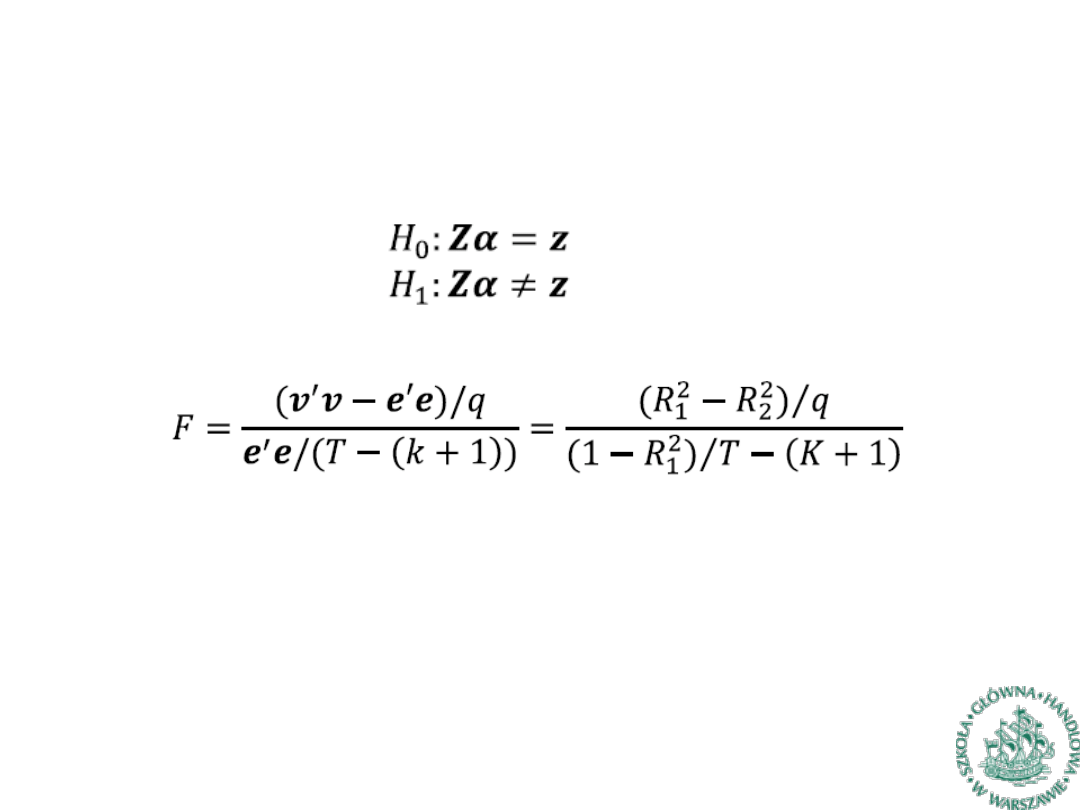
Uogólniony test Walda dla restrykcji liniowych

►

Test Walda

łącznej istotności parametrów jest szczególnym

przypadkiem ogólniejszego testu, gdzie weryfikacji poddawany jest
zestaw hipotez

►

Przy prawdziwości hipotezy zerowej statystyka

ma rozkład F-Snedecora przy liczbie stopni swobody q i T-(k+1),
gdzie q

liczba nałożonych restrykcji, e i v to wektory reszt dla

modeli, odpowiednio, bez i z resrykcjami

►

Ta postać testu wykorzystywana jest m. in. do testowania postaci
funkcyjnej modelu (test RESET), stabilności strukturalnej (test
Chowa), kompletności zestawu zmiennych objaśniających (test
Davidsona

–MacKinona)

Dziękuję za uwagę