1

Prawdopodobieństwo. Rozkład prawdopodobieństwa

Dana jest przestrzeń zdarzeń elementarnych Ω i rodzina S podzbiorów tej przestrzeni.
Na rodzinie S określamy funkcję rzeczywistą P, o której zakładamy, że spełnia następujący układ aksjomatów:

1. Dla każdego zdarzenia

S

A

∈

P( A ) ≥ 0, czyli funkcja P() jest nieujemna.

2. Prawdopodobieństwo zdarzenia pewnego jest równe jedności: P ( Ω ) = 1.

3. Dla każdego ciągu A

1

, A

2

, ... zdarzeń parami rozłącznych, tzn.

0

)

(

=

∩

j

i

A

A

dla i, j=1,2,..; i ≠ j

prawdziwa jest równość:

∑

∞

=

∞

=

=

1

1

)

(

)

(

i

i

i

i

A

P

A

P

U

czyli P jest przeliczalnie addytywną funkcją zbioru.

Funkcję P spełniającą układ tych 3-ch aksjomatów nazywamy rozkładem prawdopodobieństwa na rodzinie S.
Rozkład prawdopodobieństwa jest to więc funkcja, której argumentami są zdarzenia losowe, wartościami zaś
liczby.
Wartość zaś tej funkcji dla jednego zdarzenia będziemy nazywać prawdopodobieństwem tego zdarzenia.
Sformułowanie:
„obliczyć prawdopodobieństwo” będzie na ogół oznaczać obliczenie konkretnej wartości liczbowej.
Natomiast sformułowanie:
„znaleźć rozkład prawdopodobieństwa” będzie oznaczać, że należy określić funkcję P.

Podstawowe własności rozkładu prawdopodobieństwa ( funkcji

P )

Twierdzenie 1.1.
Prawdopodobieństwo zdarzenia niemożliwego wynosi 0: P(

∅

) = 0 .

Twierdzenie odwrotne nie jest prawdziwe, tzn. z faktu, że P( A ) = 0 nie wynika, że zdarzenie A jest
zdarzeniem niemożliwym.

Twierdzenie 1.2.
Funkcja P jest funkcją addytywną, tzn. dla dowolnego układu zdarzeń A

1

, A

2

,..., A

n

parami

rozłącznych, zachodzi:

∑

=

=

=

n

i

i

i

n

i

A

P

A

P

1

1

)

(

)

(

U

Twierdzenie 1.3.

Prawdopodobieństwo zdarzenia przeciwnego wyraża się wzorem:

)

(

1

)

(

A

P

A

P

−

=

Twierdzenie 1.4.
Dla dowolnych zdarzeń A oraz B, zachodzi:

)

(

)

(

)

(

)

(

B

A

P

B

P

A

P

B

A

P

∩

−

+

=

∪

Twierdzenie to metodą indukcji matematycznej można uogólnić na przypadek dowolnej liczby n
składników.

Twierdzenie 1.4a

Dla ciągu n zdarzeń elementarnych

Ω

∈

n

A

A

A

,...,

,

2

1

, otrzymamy:

∑

∑

∑

≤

≤

<

<

≤

≤

<

<

≤

=

−

∩

∩

+

∩

−

=











∪

n

i

n

j

i

n

k

j

i

k

j

i

j

i

i

i

n

i

A

A

A

P

A

A

P

A

P

A

P

1

1

1

1

)

(

)

(

)

(

)

...

(

)

1

(

2

1

1

n

n

A

A

A

P

∩

∩

∩

−

−

+

Jest to tzw. wzór włączeń i wyłączeń.

2

Przykładowo, dla n = 3, otrzymamy:

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

C

B

A

P

C

B

P

C

A

P

B

A

P

C

P

B

P

A

P

C

B

A

P

∩

∩

+

∩

−

∩

−

∩

−

+

+

=

∪

∪

Twierdzenie 1.5.

Dla zdarzenia

B

A

⊂

, zachodzi:

)

(

)

(

B

P

A

P

≤

Twierdzenie 1.6.

Dla każdego zdarzenia A:

1

)

(

≤

A

P

Twierdzenie 1.7.

Jeżeli zdarzenia A

1

, A

2

, ... stanowią wstępujący ciąg zdarzeń, tzn. jeśli

...

(

2

1

⊂

⊂

A

A

i jeśli

i

i

A

A

U

=

, to

)

(

)

(

lim

n

n

A

P

A

P

∞

→

=

Twierdzenie 1.7a.

Jeśli zdarzenia A

1

, A

2

, ... stanowią wstępujący ciąg zdarzeń, i zachodzi

Ω

=

i

A

i

U

, to:

1

)

(

lim

=

∞

→

n

n

A

P

Twierdzenie 1.8.

Jeżeli zdarzenia A

1

, A

2

, ... stanowią zstępujący ciąg zdarzeń, tzn. jeśli

...

(

2

1

⊃

⊃

A

A

i jeśli zachodzi:

i

A

A

i

I

=

, to zachodzi:

)

(

)

(

lim

n

n

A

P

A

P

∞

→

=

Twierdzenie 1.8a.

Jeżeli zdarzenia A

1

, A

2

, ... stanowią zstępujący ciąg zdarzeń i zachodzi:

0

1

=

=

i

n

i

A

I

, to:

0

)

(

lim

=

∞

→

n

n

A

P

Przestrzeń probabilistyczna

Przestrzeń Ω z określoną na niej rodziną podzbiorów S i rozkładem prawdopodobieństwa P nazywamy
przestrzenią probabilistyczną i oznaczamy ją: (Ω, S, P ).

Rozkład prawdopodobieństwa w skończonej przestrzeni zdarzeń

Niech Ω będzie przestrzenią przeliczalną: Ω = { ω

1

, ω

2

, ... }.

Dla zdarzeń jednoelementowych funkcję P określamy następująco: P( { ω

i

} ) = p

i

gdzie: p

i

≥ 0 i

1

=

∑

i

i

p

Z tego określenia i układu aksjomatów o prawdopodobieństwie wynika, że jeśli

Ω

⊂

A

i A = { ω

i1

, ω

i2

, ... },

to:

P(A) = P({ ω

i1

, ω

i2

, ... }) =

...)

}

{

}

({

2

1

∪

∪

i

i

P

ω

ω

=

})

({

1

i

P

ω

+

})

({

2

i

P

ω

+ ... = p

i1

+ p

i2

+ ...

3

Dla przestrzeni skończonej N – wymiarowej, tzn. Ω = { ω

1

, ω

2

, ..., ω

N

}

i jeśli P({ω

1

}) = P({ω

2

}) = ... = P({ω

N

}) = 1/N

Jeśli

Ω

⊂

A

i A = { ω

i1

, ω

i2

, ..., , ω

in

}, to zachodzi:

})

,...,

,

({

)

(

2

1

in

i

i

P

A

P

ω

ω

ω

=

=

})

({

1

i

P

ω

+

})

({

2

i

P

ω

+ ...+

N

n

P

in

=

})

({

ω

Jest to tzw. wzór Laplace’a – przyjmowany za klasyczną definicję prawdopodobieństwa. Traktowanie tego
wzoru jako definicji prawdopodobieństwa nie jest poprawne, natomiast można go stosować do obliczania
prawdopodobieństw w przypadku gdy przestrzeń Ω jest skończona, N- elementowa i zachodzi:

N

P

i

1

})

({

=

ω

gdzie i = 1, 2, ..., N

We wzorze Laplace’a N jest liczbą wszystkich zdarzeń elementarnych, zaś n – nazywamy liczbą zdarzeń
sprzyjających zdarzeniu A.

Przykład:
Rzucamy 1 raz monetą. Wówczas: Ω = { O, R }, rodzina S = {

∅

, {O}, {R}, Ω }, P(O)=P(R)=1/2.

W ten sposób określiliśmy przestrzeń probabilistyczną ( Ω, S, P ).

Obliczanie prawdopodobieństw

Schemat 1

Każdy z n elementów może być zaklasyfikowany do jednego z m różnych zbiorów ( n < m ). Każdemu

z m

n

różnych rozmieszczeń elementów przyporządkowujemy prawdopodobieństwo: 1 / m

n

.

Prawdopodobieństwo tego , że żadne 2 elementy nie zostaną zaklasyfikowane do tego samego zbioru wynosi:

n

m

n

m

m

m

m

)

1

(

...

)

2

(

)

1

(

+

−

⋅

⋅

−

⋅

−

⋅

Przykład:
Siedmiu studentów wyjedzie na jeden z 10-ciu obozów wakacyjnych. Obliczyć prawdopodobieństwo
zdarzenia A polegającego na tym, że żadnych dwóch studentów nie pojedzie na ten sam obóz. Zakładamy, że
rozmieszczenia studentów na obozach są jednakowo prawdopodobne.

Ω – zbiór 10

7

elementowy. Każdy element ma prawdopodobieństwo: p = 10

-7

.

Aby znaleźć liczność zbioru A (moc zbioru), należy zauważyć, że:
A – oznacza: - 1-szy student jedzie na dowolny z 10 obozów,
- 2-gi student jedzie na dowolny z pozostałych 9-ciu,

- itd.

Czyli:

06048

,

0

10

4

5

6

7

8

9

10

)

(

7

=

⋅

⋅

⋅

⋅

⋅

⋅

=

A

P

Schemat 2

B

A

∪

=

Ω

, liczność zbioru A: Card A = n, liczność zbioru B: Card B = m.

Ze zbioru Ω wybieramy losowo s elementów ( s <= n ).
Prawdopodobieństwo tego, że wszystkie wybrane elementy są elementami zbioru A, wynosi:

4







 +









=

s

m

n

s

n

p

Przykład:
W urnie jest 7 kul białych i 3 czarne. Wybieramy losowo 2 kule. Obliczyć prawdopodobieństwo tego, że
obie wybrane kule są czarne.

Przestrzeń Ω jest zbiorem

45

2

10

=













- elementowym. Każdemu elementowi zbioru Ω przyporządkowujemy

prawdopodobieństwo p= 1/45.

Zdarzenie A – polegające na wylosowaniu dwóch kul czarnych jest zbiorem

3

2

3

=













- elementowym.

Zatem:

0666

,

0

15

1

45

3

)

(

=

=

=

A

P

.

Schemat Bernoulli’ego

Niech doświadczenie składa się z n prób. Wyniki tych prób nie zależą od siebie. Każda próba

może zakończyć się sukcesem lub porażką.
Próbą Bernoulli’ego nazywamy doświadczenie, w którym możliwe jest otrzymanie jednego z dwóch
wyników. Jeden z tych wyników, o prawdopodobieństwie

)

1

,

0

(

∈

p

, nazywamy sukcesem, a drugi, o

prawdopodobieństwie q =1-p porażką.

Schemat Bernoulli’ego jest ciągiem niezależnych powtórzeń prób Bernoulli’ego.
Prawdopodobieństwo uzyskania r sukcesów w n próbach określone jest wzorem:

r

n

r

n

q

p

r

n

r

P

−









=

)

(

Drzewo stochastyczne

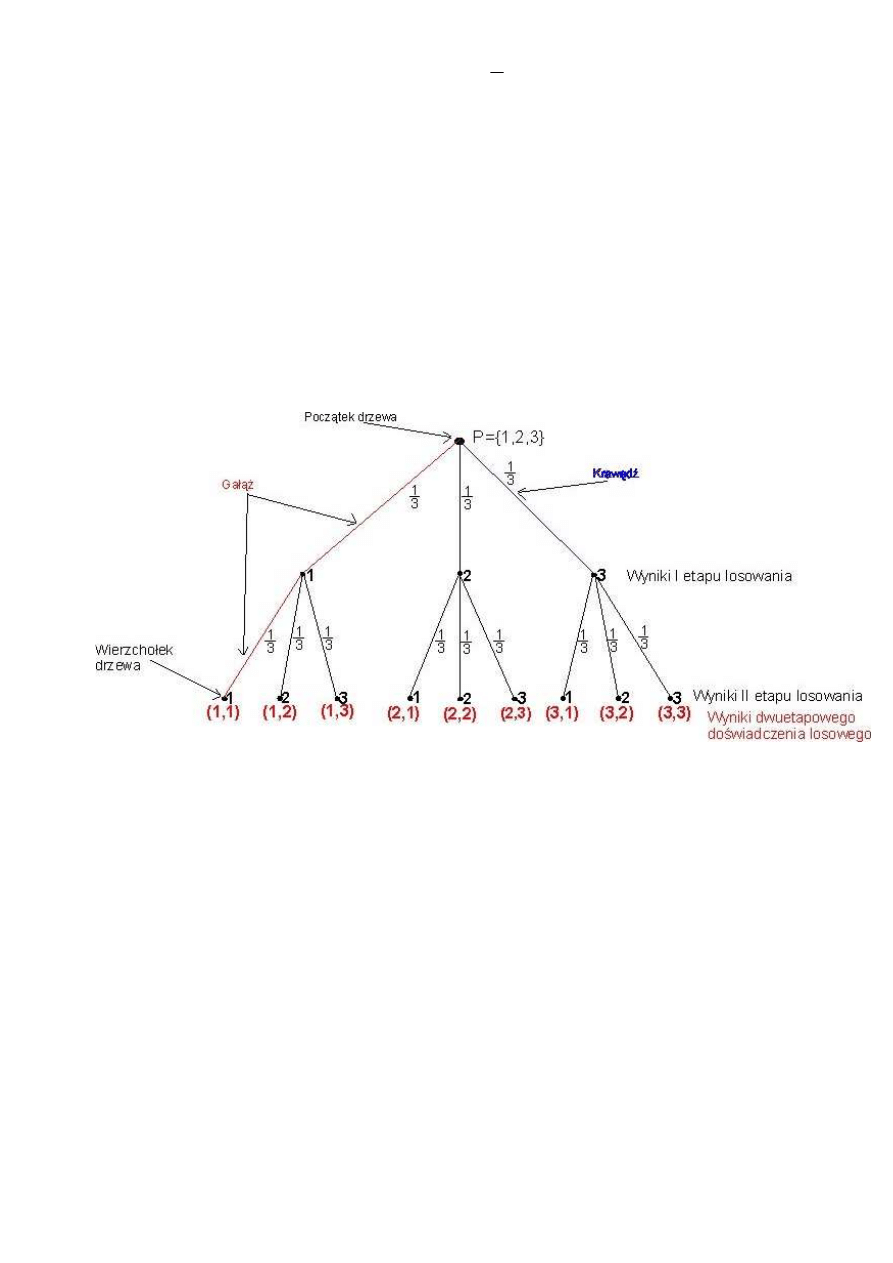
Drzewem stochastycznym nazywamy graf ilustrujący przebieg wieloetapowego doświadczenia losowego.
Wierzchołkom drzewa stochastycznego przyporządkowane są wyniki poszczególnych etapów doświadczenia, a
krawędziom prawdopodobieństwa uzyskania tych wyników. Suma prawdopodobieństw przyporządkowanych
krawędziom wychodzącym z tego samego wierzchołka jest równa 1.

Przykład 1:

1. W pudełku mamy trzy piłki oznaczone cyframi kolejno 1, 2, 3. Wyciągamy z pudełka w sposób

losowy jedną piłkę i zapisujemy cyfrę na niej napisaną (niech będzie to cyfra dziesiątek pewnej liczby
dwucyfrowej). Następnie piłkę wkładamy do pudełka i ciągniemy znów w sposób losowy piłkę i
zapisujemy cyfrę na niej napisaną (będzie to cyfra jedności liczby dwucyfrowej). Otrzymaliśmy w
wyniku losowania uporządkowaną parę cyfr, która wyznacza liczbę dwucyfrową.

Określ przestrzeń wyników opisanego doświadczenia. Ile elementów liczy ta przestrzeń? Oblicz
prawdopodobieństwo otrzymania liczby pierwszej.

Ω = { (x, y ) :

}

3

,

2

,

1

{

,

∈

y

x

} gdzie: ( x, y ) – zdarzenia elementarne: wylosowano za pierwszym

razem cyfrę x i za drugim razem cyfrę y.

5

Moc zbioru Ω: Card Ω = 3

2

= 9. Więc:

9

1

)

,

(

=

y

x

P

, dla każdego

}

3

,

2

,

1

{

,

∈

y

x

Niech A – zdarzenie polegające na otrzymaniu w wyniku losowania liczby pierwszej. Czyli:

A = { (1,1), (1,3), (2,3), (3,1) }, moc zbioru A: Card A = 4, P(A) = Card A/ Card Ω = 4/9

Przedstawmy powyższe doświadczenie losowe za pomocą grafu czyli drzewa stochastycznego:

Ustalmy terminologię jaka będzie nas obowiązywać przy opisie drzewa.

Drzewem stochastycznym nazywamy graf ilustrujący przebieg wieloetapowego doświadczenia losowego. Graf
składa się z odcinków, które nazywamy krawędziami. Każda z krawędzi wychodzących z tego samego węzła
odpowiada innemu wynikowi jednoetapowego doświadczenia losowego. Na końcu każdej krawędzi będziemy
wypisywać litery(cyfry), pary liter, względnie trójki liter(cyfr) – które oznaczają możliwe wyniki w pierwszym,
drugim, trzecim,...etapie doświadczenia losowego. Obok każdej krawędzi zapiszemy prawdopodobieństwo
uzyskania danego wyniku. Pamiętamy, że suma prawdopodobieństw przypisanych krawędziom wychodzących
ze wspólnego węzła jest równa 1. Gałąź drzewa stochastycznego – jest to ciąg krawędzi prowadzących od
początku drzewa do jednego z ostatnich jego wierzchołków. Na każdym wierzchołku znajduje się w pewien
sposób zakodowany wynik doświadczenia losowego.

Przestrzenią wyników doświadczenia losowego jest:

Ω={ (1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)}, Card Ω = 9.

Przypiszmy każdej gałęzi liczbę równą iloczynowi prawdopodobieństw przypisanych kolejnym krawędziom tej
gałęzi. Liczbę przypisaną w ten sposób traktujemy jako prawdopodobieństwo wyniku „wiszącego” na tej
gałęzi. Nazwiemy to regułą mnożenia prawdopodobieństw dla drzew.

6

Reguła iloczynów

– prawdopodobieństwo zdarzenia reprezentowanego przez jedną gałąź drzewa jest równe

iloczynowi prawdopodobieństw przyporządkowanych krawędziom, z których składa się rozważana gałąź.
Reguła wynika ze wzoru na prawdopodobieństwo iloczynu.

Korzystając z drzewa obliczymy prawdopodobieństwo tego, że w wyniku losowania opisanego w ćwiczeniu 1
otrzymamy liczbę pierwszą. Zdarzenie to jest opisane przez kilka gałęzi powyższego grafu.

Reguła sum

– Prawdopodobieństwo danego zdarzenia opisanego przez kilka gałęzi jest równe sumie

prawdopodobieństw otrzymanych regułą iloczynów dla tych gałęzi. Reguła wynika z twierdzenia o
prawdopodobieństwie całkowitym.

A – zdarzenie, że w wyniku losowania otrzymamy liczbę pierwszą, zatem zgodnie z regułą mnożenia i
korzystając z reguły dodawania mamy:

P(A) = P(11)+P(13)+P(23)+P(31) =

9

4

3

1

3

1

3

1

3

1

3

1

3

1

3

1

3

1

=

⋅

+

⋅

+

⋅

+

⋅

Przykład 2:

W urnie znajdują się dwie kostki zielone (z) i dwie kostki czerwone (c). Losujemy „na chybił trafił”
trzykrotnie bez zwracania kostkę, budując z kolejno wyciągniętych kostek wieżę. Interesujemy się kolorem
kolejnych kondygnacji wieży. Narysuj drzewo opisujące jak etapami może powstawać wieża. Oblicz
prawdopodobieństwo zdarzenia, że wieża jaka powstanie, będzie się składać z dwu kondygnacji zielonych i
jednej czerwonej.

Drzewo stochastyczne ilustrujące przebieg tego doświadczenia:

Ω = { (z,z,c), (z,c,z), (z,c,c), (c,z,z), (c,z,c), (c,c,z) }

Niech A – oznacza zdarzenie, że wieża będzie się składać z dwu kondygnacji zielonych i jednej czerwonej.
Zdarzenie to opisane jest przez kilka gałęzi powyższego drzewa. Zatem zgodnie z regułą mnożenia i
dodawania dla drzew otrzymamy:

7

P(A) = P(zzc) + P(zcz) + P(czz) =

2

1

2

1

3

2

4

2

2

1

3

2

4

2

1

3

1

4

2

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

Rozkład prawdopodobieństwa w jednowymiarowej przestrzeni euklidesowej

Niech Ω – jednowymiarowa przestrzeń euklidesowa

1

ℜ

. Wprowadźmy pomocniczą funkcję rzeczywistą F

określoną na

1

ℜ

i mającą następujące własności:

1. F jest funkcją niemalejącą,
2.

0

)

(

lim

=

−∞

→

x

F

x

,

1

)

(

lim

=

∞

→

x

F

x

3. Funkcja F jest lewostronnie ciągła.

Funkcja F jest niemalejąca, to oznacza, że dla a < b, zachodzi:

∫

≥

=

−

b

a

x

f

a

F

b

F

0

)

(

)

(

)

(

,

czyli, że całka z

pewnej funkcji f() po dowolnym przedziale ( a, b ) jest nieujemna.
Funkcję F o powyższych własnościach nazywamy dystrybuantą.
Funkcję P czyli rozkład prawdopodobieństwa wyznaczamy za pomocą funkcji F następująco:

)

(

)

(

))

,

([

a

F

b

F

b

a

P

b

a

−

=

∧

<

Zatem wniosek: dystrybuanta wyznacza jednoznacznie rozkład prawdopodobieństwa P.
I odwrotnie: każdy rozkład prawdopodobieństwa wyznacza jednoznacznie pewną dystrybuantę:

Twierdzenie 1.9:

Jeżeli P jest rozkładem prawdopodobieństwa w przestrzeni

1

ℜ

, to funkcja F określona wzorem:

))

,

((

)

(

x

P

x

F

−∞

=

jest dystrybuantą i ma własności 1 – 3.

Prawa wielkich liczb

Przeprowadzając n obserwacji jakiegoś zjawiska zaobserwujemy interesujące nas zjawisko k razy, to
prawdopodobieństwo zajścia tego zjawiska powinno wynosić k / n.
Iloraz ten często jest przyjmowany za tzw. „statystyczną definicję prawdopodobieństwa”.
Określenie to nie jest całkiem poprawne, ale intuicyjnie uzasadnione, a poniższe twierdzenie nadaje mu ścisły
matematyczny charakter.


Twierdzenie 1.10: Mocne prawo wielkich liczb.

Niech ( Ω, S, P ) – przestrzeń probabilistyczna, a

∞

=

∈

1

}

{

i

i

S

A

będzie nieskończonym ciągiem zdarzeń

niezależnych o tym samym prawdopodobieństwie P( A

i

) = p.

Niech

Ω

∈

ω

- dowolne, ale ustalone zdarzenie. Oznaczmy przez

)

,

(

ω

n

N

liczbę tych zdarzeń A

i

spośród

zdarzeń A

1

, ..., A

n

, dla których

i

A

∈

ω

, gdzie i = 1, 2,..., n.

Wówczas:

1

})

)

,

(

lim

:

({

=

=

∞

→

p

n

n

N

n

P

ω

ω

8

Twierdzenie 1.11: Słabe prawo wielkich liczb.
Przy założeniach z twierdzenia 1.10 wynika, że:

0

})

|

)

,

(

:|

({

lim

0

=

>

−

∧

∞

→

>

ε

ω

ω

ε

p

n

n

N

P

n

Interpretacja twierdzenia 1.10.

Równość we wzorze mówi, że stosunek liczby zjawisk zaobserwowanych w n obserwacjach do
całkowitej liczby obserwacji n, dąży do prawdopodobieństwa zaobserwowania zjawiska przy jednej obserwacji
dla prawie wszystkich doświadczeń.

Interpretacja twierdzenia 1.11.
Mówi ono, że stosunek liczby zjawisk zaobserwowanych w n obserwacjach do liczby obserwacji różni
się niewiele od prawdopodobieństwa zaobserwowania zjawiska przy jednej obserwacji jeśli tylko weźmiemy
dostatecznie duże n.

Inny wniosek z twierdzeń: Zdarzenie prawie pewne.

Jeśli P(A) = 1, to mówimy, że zdarzenie A zachodzi prawie na pewno (może być tak, że A ≠ Ω, chociaż
P(A)=1 ).

Prawdopodobieństwo warunkowe

Prawdopodobieństwo warunkowe zajścia zdarzenia A pod warunkiem zajścia zdarzenia B, oznaczamy

symbolem:

)

( B

A

P

i jest to prawdopodobieństwo zajścia zdarzenia A obliczone przy założeniu, że

zdarzenie B nastąpiło.

Przykład:

W magazynie są elementy pochodzące z dwóch fabryk: I i II. Elementy są klasyfikowane jako dobre i
złe.

Oznaczmy przez:

A

- zdarzenie: „wybrany losowo element jest dobry”,

A

- zdarzenie: „wybrany losowo element jest zły”,

B

- zdarzenie: „wybrany losowo element pochodzi z fabryki I”,

B

- zdarzenie: „wybrany losowo element pochodzi z fabryki II”.

zdarzenie dobre

A

złe

A

razem:

Fabr. I

B

a

b

a + b

Fabr II

B

c

d

c + d

razem:

a + c

b + d a+b+c+d=n

Zauważmy, że:

n

a

B

A

P

=

∩

)

(

,

n

c

B

A

P

=

∩

)

(

,

n

b

B

A

P

=

∩

)

(

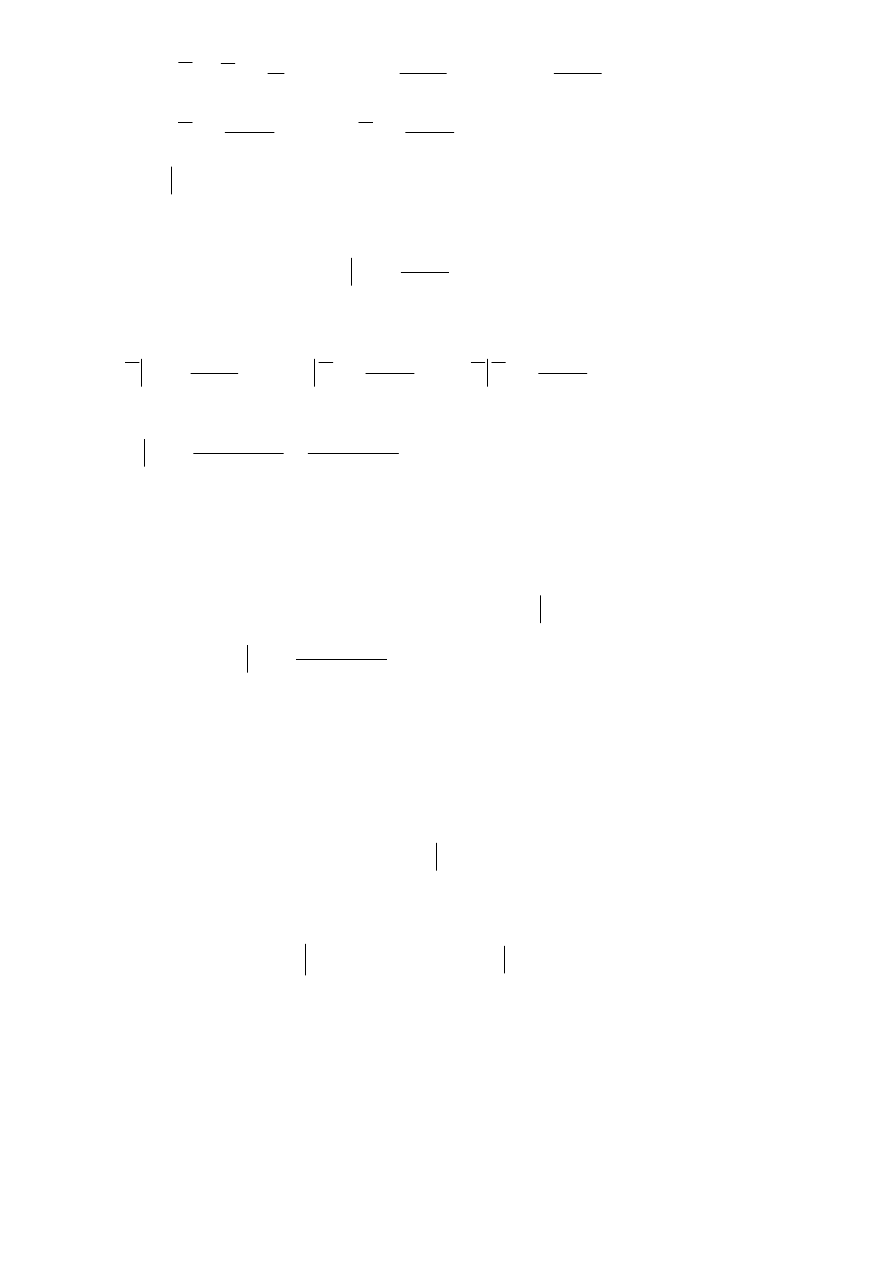
9

n

d

B

A

P

=

∩

)

(

,

n

c

a

A

P

+

=

)

(

,

n

b

a

B

P

+

=

)

(

,

n

d

b

A

P

+

=

)

(

,

n

d

c

B

P

+

=

)

(

.

Obliczmy:

)

( B

A

P

- bierzemy pod uwagę jedynie elementy z fabryki I (B). Jest to więc

prawdopodobieństwo wylosowania elementu dobrego przy założeniu, że losujemy tylko spośród elementów z
fabryki I ( tylko pierwszy wiersz w tabeli). Elementów z fabryki I jest a+b, a dobrych jest „a”, więc:

b

a

a

B

A

P

+

=

)

(

Analogicznie:

b

a

b

B

A

P

+

=

)

(

,

d

c

c

B

A

P

+

=

)

(

,

d

c

d

B

A

P

+

=

)

(

,

czyli:

)

(

)

(

/

)

(

/

)

(

B

P

B

A

P

n

b

a

n

a

B

A

P

∩

=

+

=

Definicja 1.1

Jeśli

0

)

(

>

B

P

, to prawdopodobieństwo warunkowe

)

( B

A

P

zdarzenia A pod warunkiem B,

wynosi:

)

(

)

(

)

(

B

P

B

A

P

B

A

P

∩

=

Uwaga: zdarzenie B jest tutaj ustalone. Argumentem jest zdarzenie A.

Definicja 1.2

Prawdopodobieństwo iloczynu zdarzeń, wynosi:

)

(

)

(

)

(

B

P

B

A

P

B

A

P

⋅

=

∩

Uogólnienie na przypadek n zdarzeń (można wykazać metodą indukcji):

)

(

(

)...

...

(

...

(

1

1

2

1

1

)

2

1

A

P

A

A

P

A

A

A

P

A

A

A

P

n

n

n

−

∩

∩

=

∩

∩

∩

przy założeniu, że:

0

)

...

(

1

2

1

>

∩

∩

∩

−

n

A

A

A

P

Zdarzenia niezależne

Zdarzenie A nie zależy od zdarzenia B jeśli informacja, że zaszło zdarzenie B nie wpływa na
prawdopodobieństwo zajścia zdarzenia A. Czyli:

10

)

(

)

(

A

P

B

A

P

=

Definicja 1.3

Niech ( Ω, S, P ) – przestrzeń probabilistyczna i niech zdarzenia

S

B

A

∈

,

.

Mówimy, że zdarzenia A i B są niezależne jeśli:

)

(

)

(

)

(

B

P

A

P

B

A

P

⋅

=

∩

Wnioski:

1. Jeśli P(A) > 0, to:

)

(

)

(

B

P

A

B

P

=

.

2. Jeśli P(B) > 0, to:

)

(

)

(

A

P

B

A

P

=

.

3. Jeśli zdarzenia A i B są niezależne, to zdarzenia

A

i

B

są również niezależne.

4. Jeśli zdarzenia A i B są niezależne, to zdarzenia

A

i

B

są również niezależne.

5. Jeśli zdarzenia A i B są niezależne, to zdarzenia

A

i

B

są również niezależne.

Wprowadzone pojęcia niezależności dwóch zdarzeń uogólnia się na przypadek dowolnej, skończonej liczby
zdarzeń:

Definicja 1.4

Zdarzenia A

1

, A

2

, ..., A

n

są niezależne, jeśli dla dowolnych wskaźników k

1

, k

2

,..., k

s

, gdzie:

1 ≤ k

2

< k

2

< ... < k

s

≤ n zachodzi równość:

)

(

...

)

(

)

(

)

...

(

2

1

2

1

ks

k

k

ks

k

k

A

P

A

P

A

P

A

A

A

P

⋅

⋅

⋅

=

∩

∩

∩

Warunek ten może być spełniony dla pewnych układów wskaźników, a dla innych nie. Jeżeli dla pewnego
układu wskaźników k

1

, k

2

,..., k

s

, ( s < n ) ten warunek nie jest spełniony,

to zdarzenia A

1

, A

2

, ..., A

n

nazywamy zależnymi.

Prawdopodobieństwo całkowite (zupełne). Wzór Bayesa.

Często mamy do czynienia z doświadczeniami wieloetapowymi i interesuje nas, jak liczyć
prawdopodobieństwa zdarzeń, które zaszły we wcześniejszych etapach naszych doświadczeń.
Posłuży nam do tego wzór na prawdopodobieństwo całkowite. Do jego sformułowania potrzebne nam będzie
pojęcie układu zupełnego zdarzeń.

Definicja 1.5

Zdarzenia H

1

, H

2

, ..., H

n

S

∈

tworzą układ zupełny zdarzeń w przestrzeni probabilistycznej

(Ω, S, P ), jeśli spełniają następujące warunki:

1.

Ω

=

∪

∪

∪

n

H

H

H

...

2

1

,

11

2

.

0

=

∩

j

i

H

H

dla i ≠ j – zdarzenia są parami rozłączne,

3.

0

)

(

>

i

H

P

, dla i = 1, 2, ..., n.

Twierdzenie o prawdopodobieństwie zupełnym (całkowitym )

Jeśli zdarzenia H

1

, H

2

, ..., H

n

S

∈

tworzą układ zupełny zdarzeń w przestrzeni probabilistycznej

(Ω, S, P ), to dla dowolnego zdarzenia A

S

∈

, zachodzi:

∑

=

⋅

=

n

i

i

i

H

P

H

A

P

A

P

1

)

(

)

(

)

(

Twierdzenie to interpretuje się następująco:

Jeżeli skutek A może zajść w wyniku jednej z n przyczyn

H

1

, H

2

, ..., H

n

,

to prawdopodobieństwo

wystąpienia skutku A wyraża się powyższym wzorem.
Wyobraźmy sobie, że znamy wynik drugiego etapu doświadczenia i pytamy o to co stało się w jego pierwszym
etapie. W takich sytuacjach stosujemy wzór Bayesa.

Twierdzenie Bayesa

Niech zdarzenia H

1

, H

2

, ..., H

n

S

∈

tworzą układ zupełny zdarzeń w przestrzeni probabilistycznej

(Ω, S, P ) i niech A

S

∈

będzie dowolnym ustalonym zdarzeniem o dodatnim prawdopodobieństwie P( A )>0.

Wówczas prawdziwy jest wzór:

∑

=

⋅

⋅

=

∩

=

n

i

i

i

k

k

k

k

H

P

H

A

P

H

P

H

A

P

A

P

A

H

P

A

H

P

1

)

(

)

(

)

(

)

(

)

(

)

(

)

(

gdzie: k = 1, 2, ..., n

Interpretacja:

Jeśli skutek A nastąpił w wyniku zajścia jednej z n przyczyn H

1

, H

2

, ..., H

n

(jedynie możliwych i

wzajemnie się wykluczających), to prawdopodobieństwo tego, że H

k

było przyczyną zajścia A wyraża się

powyższym wzorem.