Zmienne losowe
1. Zmienne losowe dyskretne i ciągłe. Rozkłady zmiennych losowych. Dystrybuanta zmiennej losowej.
2. Momenty zmiennych losowych – zwykłe, centralne, mieszane.
3. Współczynnik korelacji. Ilość informacji. Entropia.
4. Funkcje zmiennych losowych dyskretnych i ciągłych. Wielowymiarowe zmienne losowe.
Nieliniowe przekształcenie tych zmiennych.
5. Nierówność Markowa i Czebyszewa. Prawa wielkich liczb. Funkcja charakterystyczna.
Wyznaczanie podstawowych parametrów probabilistycznych za pomocą funkcji charakterystycznej.
Literatura
1.
Z. Hellwig Elementy rachunku prawdopodobieństwa i statystyki matematycznej. Warszawa 1977.
2.
H. Jasiulewicz, W. Kordecki Rachunek prawdopodobieństwa i statystyka matematyczna.
Wrocław 2001.
3.
W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska. M. Wasilewski Rachunek prawdopodobieństwa
i statystyka matematyczna w zadaniach. Część 1 i część 2. Warszawa 1986.
Określenie zmiennej losowej
W różnych zagadnieniach praktycznych przestrzeń zdarzeń elementarnych Ω może mieć bardzo
różne postacie. Przykładowo, przestrzeń zdarzeń elementarnych Ω może być:
- zbiorem wszystkich możliwych ocen na egzaminie,
- zbiorem serii n strzałów, z których każdy jest celny lub niecelny,
- zbiorem układów n zdarzeń postaci: przekaźnik zadziałał, przekaźnik nie zadziałał
( n liczba przekaźników) itd.
Aby ujednolicić sposób rozważań dla różnych przestrzeni zdarzeń elementarnych Ω, dokonujemy
przekształcenia przestrzeni zdarzeń elementarnych Ω w przestrzeń
1
ℜ
lub jej podzbiór:
Zamiast mówić o zdarzeniach elementarnych ω mających bardzo różne interpretacje praktyczne,
odwzorowujemy je na liczby i w ten sposób uzyskujemy możliwość liczbowego opisu w przypadku
dowolnej przestrzeni zdarzeń elementarnych Ω.
Przykładami zjawisk o charakterze losowym, dla których nie ma ujednoliconego sposobu liczbowego ich
przedstawiania są np.:
- samopoczucie osoby,
- stan zdrowia osoby,
- stan techniczny urządzenia,
- barwa rośliny,
- korozja metali,
- zakłócenia przyjmowanych sygnałów,
- zniszczenie banknotów, itp.
Dla pewnych określonych celów możemy takim zjawiskom przyporządkować liczby, tak aby można było
np. porównać ze sobą dwa elementy ze względu na interesującą nas cechę czy zespół cech, czyli:
Ω
1
ℜ
przekształcamy nieliczbową przestrzeń
Ω w przestrzeń liczbową
1
ℜ
.
Funkcję przekształcającą przestrzeń Ω w przestrzeń
1
ℜ
nazywamy zmienną losową jednowymiarową.
Zakładamy oczywiście, że każdemu zdarzeniu elementarnemu ω
i
jest przyporządkowane
prawdopodobieństwo P( ω
i
). Zmienna losowa jest więc funkcją określoną na zbiorze zdarzeń
elementarnych, a więc argumentami są zdarzenia elementarne.
Definicja
Niech będzie dana przestrzeń probabilistyczna (Ω, S, P ). Zmienną losową nazywamy funkcję
rzeczywistą X określoną na przestrzeni zdarzeń elementarnych Ω i przyjmującą wartości rzeczywiste:
1
:
ℜ
→
Ω
X
i spełniającą warunek: dla każdej liczby rzeczywistej x zbiór zdarzeń elementarnych ω, dla których:
X(ω ) < x jest zdarzeniem, czyli jest elementem rodziny S . Własność tę można zapisać jako:
S
x
X
x
∈
<
∧
ℜ
∈
}
)
(
:
{
1
ω
ω
Zmienne losowe będziemy oznaczać dużymi literami X, Y, Z , zaś jej wartości liczbowe, czyli realizacje,
małymi literami x, y, z.
Realizacje zmiennych losowych
Zmienna losowa typu skokowego – jest to zmienna, która posiada skończony lub przeliczalny zbiór
wartości, najczęściej są to liczby naturalne ( np. liczba oczek kostki do gry ).
Zmienna losowa typu ciągłego
– jest to zmienna, która może przybierać dowolne wartości liczbowe,
rzeczywiste z pewnego przedziału, nieskończonego i nieprzeliczalnego.
Zmienna losowa typu skokowego (dyskretna)
Mówimy, że zmienna losowa X jest typu skokowego, jeśli istnieje zbiór przeliczalny
1
ℜ
∈
χ
taki,
że
1
)
(
=
χ
X
P
.
Elementy
z
bioru
χ
oznaczamy przez x
k
, czyli:
}
,...
,
{
2
1
x
x
=
χ
lub
}
,...,
,
{
2
1
n
x
x
x
=
χ
. Liczby x
k
nazywamy wartościami zmiennej losowej X.
Dla zmiennej losowej skokowej X, która przybiera wartości: x
1
, x
2
, ... , x
n
definiuje się:
1. Funkcję rozkładu prawdopodobieństwa – która przyporządkowuje wartościom { x
1
, x
2
, ... , x
n
}
zmiennej losowej X prawdopodobieństwa: p
1
, p
2
, ... , p
n
:
P( X = x
i
) = p
i
gdzie i = 1, 2, ... , n ; p
i
≥ 0 ;
zmienne losowe
zmienne losowe typu skokowego
(dyskretne)
zmienne losowe typu ciągłego

Funkcja ta ma własność:
1
1
=
∑
=
n
i
i
p
dla i = 1, 2, ... , n
Funkcja ta może być określona:
- wzorem,
- tabelką,
- wykresem.
2. Dystrybuantą zmiennej losowej typu skokowego X - nazywamy funkcję F( x ) zmiennej
rzeczywistej x, która wyznacza prawdopodobieństwo tego, że zmienna losowa X przyjmie w
uporządkowanym zbiorze:
n
n
i
x
x
x
x
x
≤
≤
≤
≤
≤
≤
−
1
2
1
...
...
wartość mniejszą od x:
)
(
)
(
x
X
P
x
F
def
<
=
dla
1
ℜ
∈
∧
x
lub inaczej:
∑
<
=
x
X
i
p
x
F
)
(
Pojęcie zmiennej losowej typu skokowego wiąże się z postacią dystrybuanty. Dla zmiennych losowych
typu skokowego dystrybuanta jest przedziałami stała, a w punktach nieciągłości x
k
ma skoki o wielkości
p( x
k
) i suma wszystkich skoków jest równa 1.
Inna definicja zmiennej losowej typu skokowego:
Jest to zmienna losowa , której suma wszystkich skoków jej dystrybuanty jest równa 1.
Własności dystrybuanty:
1. Jest funkcją niemalejącą, tzn. dla x
1
< x
2
zawsze jest F( x
1
) ≤ F( x
2
),
2.
0
)
(
lim
=
−∞
→
x
F
x
,
1
)
(
lim
=
∞
→
x
F
x
, czyli przyjmuje wartości z przedziału:
1
)
(
0
≤
≤
x
F
dla
)
,
(
∞
−∞
∈
x
,
3. jest funkcją lewostronnie ciągłą, tzn.
)
(
)
(
lim
0
0
x
F
x
F
x
x
=
−
→
Przy pomocy dystrybuanty można określić prawdopodobieństwa zdarzeń:
1.
)
(
)
(
)
(
0
0
0
x
X
P
x
F
x
X
P
=
+
=
≤
2. Prawdopodobieństwo przyjęcia przez zmienną losową X wartości z przedziału: [ x
1
, x
2
) :
)
(
)
(
)
(
1
2
2
1
x
F
x
F
x
X
x
P
−
=
<
≤
3. Prawdopodobieństwo przyjęcia przez zmienną losową X wartości x
0
:
)
(
)
(
)
(
0
0
0
x
F
x
F
x
X
P
−
=
=
+
gdzie
)
(
lim
)
(
0
0
t
F
x
F
x
t
+
→
+
=
4.
)
(
1
)
(
0
0
+
−
=
>
x
F
x
X
P

5.
)
(
)
(
)
(
)
(
2
1
2
2
1
x
X
P
x
F
x
F
x
X
x
P
=
+
−
=
≤
≤
6.
)
(
)
(
0
0
x
F
x
X
P
def
=
<
7.
)
(
1
)
(
0
0
x
F
x
X
P
−
=
≥
8.
)
(
)
(
)
(
)
(
1
1
2
2
1
x
X
P
x
F
x
F
x
X
x
P
=
−
−
=
<
<
Przykład:
Określmy zmienną losową na podstawie rzutów symetryczną kostką do gry. Zbiór zdarzeń
elementarnych zawiera 6 elementów odpowiadających sześciu ściankom kostki. Prawdopodobieństwa
poszczególnych zdarzeń elementarnych są jednakowe i równe 1/6.
Z każdym zdarzeniem elementarnym możemy związać liczbę równą np. liczbie oczek na odpowiedniej
ściance kostki. Przyporządkowanie takie jest przykładem zmiennej losowej dyskretnej, przyjmującej
wartości 1, 2, 3, 4, 5, 6 z jednakowym prawdopodobieństwem 1/6:
Ω = { ω
1
, ω
2
, ... , ω
6
} – przestrzeń zdarzeń elementarnych
X( x
i
) = { 1, 2, ... , 6 } - zmienna losowa skokowa, P( X =x
i
) = p
i
= 1/6
Oczywiście na tym zbiorze sześciu zdarzeń elementarnych odpowiadających rzutom kostką, można określić
inne zmienne losowe. Można np. przyporządkować każdej ściance kostki liczbę równą liczbie oczek
pomnożonej np. przez 3. Otrzymamy wówczas zmienną losową dyskretną o następujących wartościach i
prawdopodobieństwach:
Ω = { ω
1
, ω
2
, ... , ω
6
} – przestrzeń zdarzeń elementarnych
Y( y
i
) = { 3, 6, ... ,18 } - zmienna losowa skokowa, P( Y =y
i
) = p
i
= 1/6
Określmy rozkład prawdopodobieństwa i dystrybuantę dla zmiennej losowej X:
Rozkład prawdopodobieństwa zmiennej losowe X w postaci tabelarycznej:
x
i
1
2
...
6
p
i
1/6
1/6
...
1/6
0
1/6
P(X=x)
1
2
3
4
5
6
x
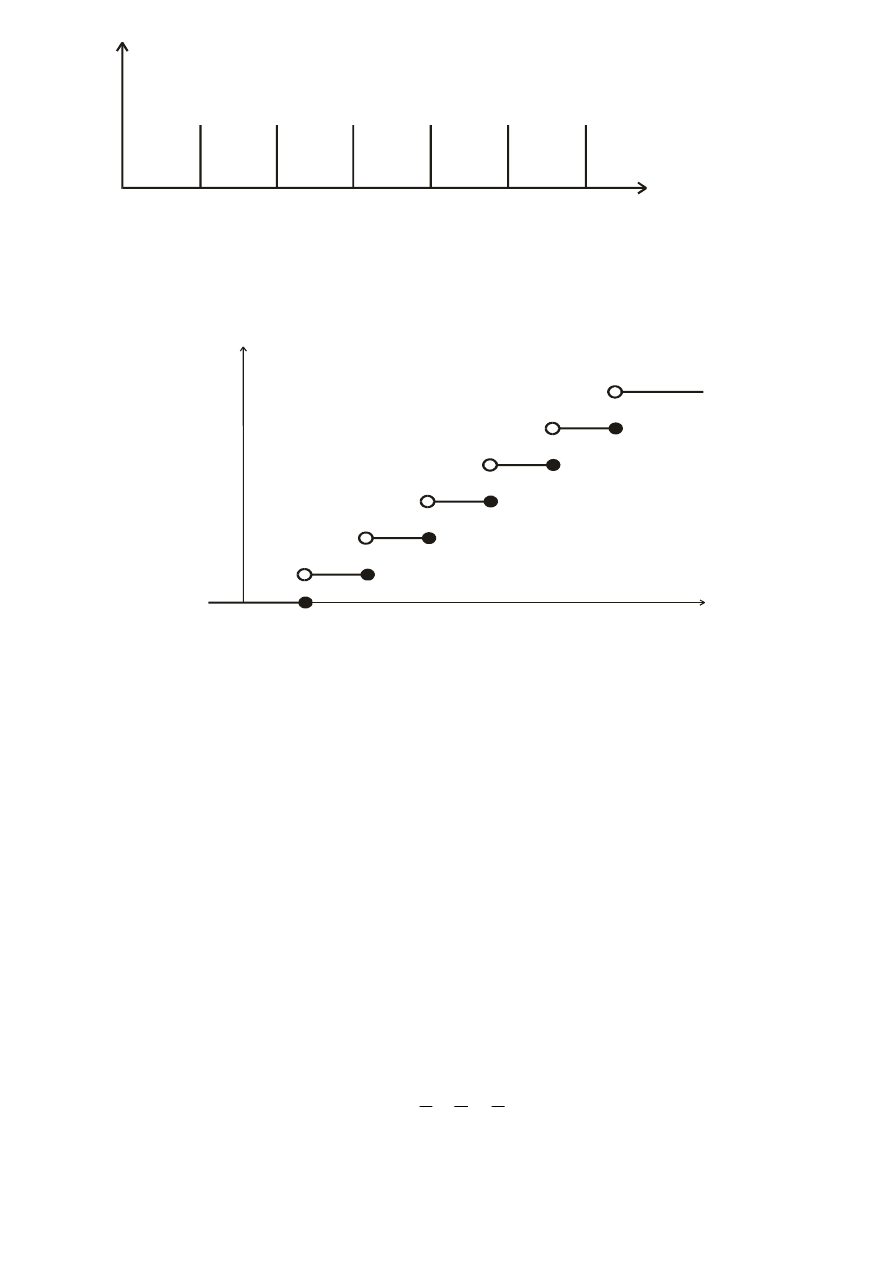
Z definicji dystrybuanty, otrzymujemy:
∑
<
=
<
=
x
X
i
def
p
x
X
P
x
F
)
(
)
(
0
1/6
2/6
3/6
4/6
5/6
1
F(x)
1
2
3
4
5
6
x
∞
∈
∈
∈
∈
∈
∈
−∞
∈
=
)
,
6
(
1
]
6
,
5
(
6
/
5
]
5
,
4
(
6
/
4
]
4
,
3
(
6
/
3
]
3
,
2
(
6
/
2
]
2
,
1
(
6
/
1
]
1
,
(
0
)
(
x
dla
x
dla
x
dla
x
dla
x
dla
x
dla
x
dla
x
F
Obliczanie prawdopodobieństw:
1. Obliczyć prawdopodobieństwo, że:
6
1
6
4
6
5
)
5
(
)
5
(
})
({
)
5
(
5
=
−
=
−
=
=
=
+
F
F
P
X
P
ω
2. Obliczyć prawdopodobieństwo, że:

6
3
6
1
6
4
)
2
(
)
5
(
})
,
,
({
)
5
2
(
4
3
2
=
−
=
−
=
=
<
≤
F
F
P
X
P
ω
ω
ω
3. Obliczyć prawdopodobieństwo, że:
6
4
)
5
(
})
,
,
,
({
)
5
(
4
3
2
1
=
=
=
<
F
P
X
P
ω
ω
ω
ω
4. Obliczyć prawdopodobieństwo, że:
1
6
1
0
6
5
)
6
(
)
1
(
)
6
(
)
(
)
6
1
(
=
+
−
=
=
+
−
=
Ω
=
≤
≤
X
P
F
F
P
X
P
5. Obliczyć prawdopodobieństwo, że:
0
1
1
)
7
(
1
)
(
)
7
(
=
−
=
−
=
∅
=
≥
F
P
X
P
Zmienna losowa typu ciągłego
Zmienna losowa typu skokowego może być stosowana tylko do charakteryzowania pewnych
wielkości losowych, przyjmujących przeliczalną liczbę wartości. Mogą to być np.:
- liczby uszkodzeń badanych elementów czy urządzeń w pewnym określonym przedziale
czasu,
- liczby sztuk wadliwych w badanej próbie,
- liczby cząstek rejestrowanych przez licznik itp.
W przyrodzie i technice występuje jednak wiele zjawisk, do których opisu nieodzowne jest wprowadzenie
zmiennej, mogącej przyjmować dowolną wartość z jednego lub kilku przedziałów, a więc zmiennej, która
przyjmuje nieprzeliczalną liczbę wartości.
Wprowadzenie takiej zmiennej losowej jest konieczne np. przy:
- badaniu błędów obróbki,
- błędów pomiarów,
- szumów w odbiornikach telekomunikacyjnych,
- współrzędnych molekuł gazu umieszczonych w naczyniu itp.
Mówimy, że zmienna losowa X o dystrybuancie F jest typu ciągłego, jeśli istnieje taka funkcja
0
)
(
≥
u
f
,
że:
∧
ℜ
∈
1
x
zachodzi:
∫
∞
−
=
x
du
u
f
x
F
)
(
)
(
oraz:
∫
∞
∞
−
=
1
)
(
dx
x
f
Funkcję f(u) nazywamy funkcją gęstości prawdopodobieństwa zmiennej losowej X lub w skrócie gęstością.
W analizie matematycznej taką funkcję F, która dla każdego x może być przedstawiona w postaci:
∫
∞
−
+
=
x
C
u
f
x
F
)
(
)
(
gdzie: f – funkcja całkowalna, C – pewna stała,
nazywamy funkcją bezwzględnie ciągłą, to zmienną losową X nazywamy funkcją typu ciągłego.
W punktach, w których funkcja f( ) jest ciągła, zależność:
∫
∞
−
=
x
du
u
f
x
F
)
(
)
(
możemy zróżniczkować stronami względem x i wówczas otrzymamy:
)
(
)
(
'
x
f
x
F
=
W punktach, w których funkcja f( ) jest ciągła, pochodna dystrybuanty równa się gęstości
prawdopodobieństwa.
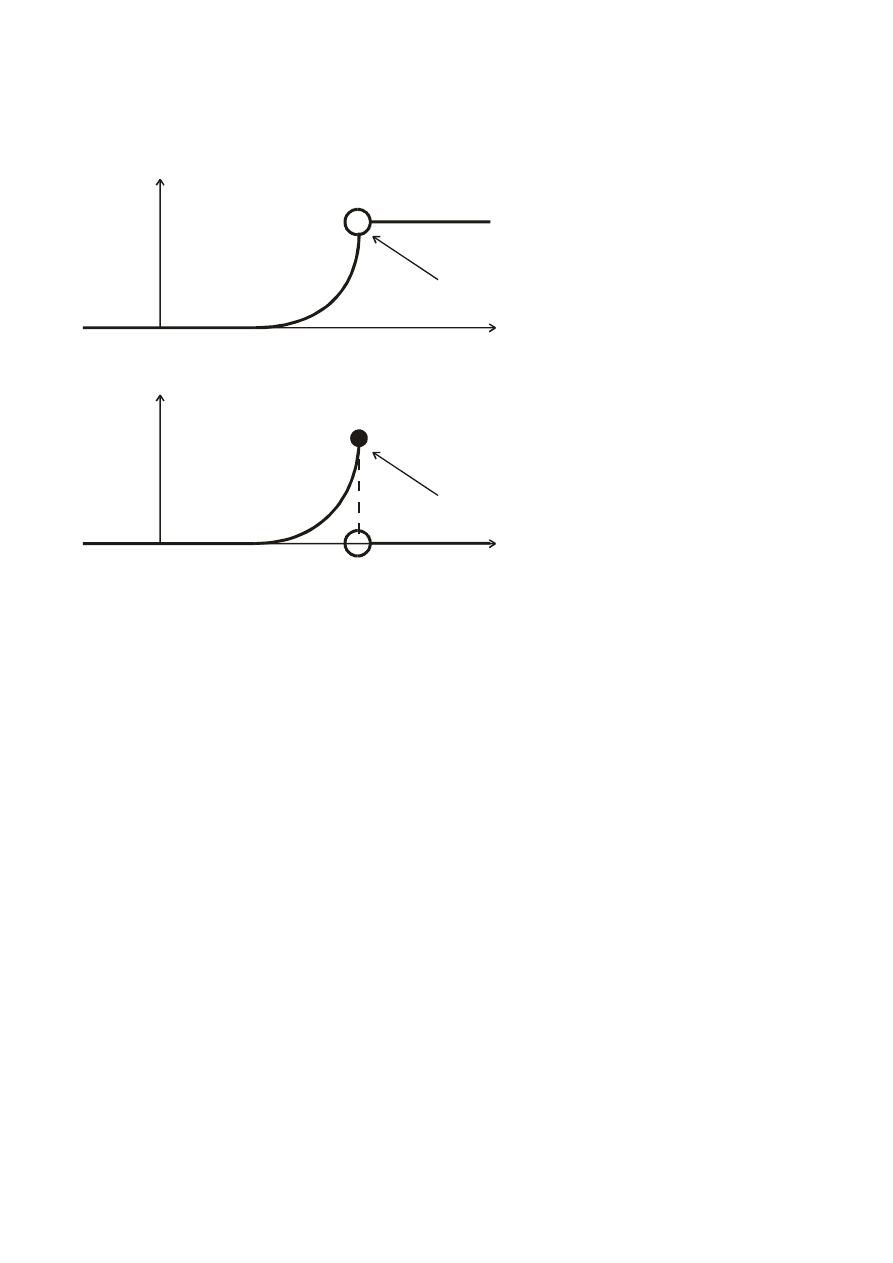
Przykład:
0
x
1
F(x)
punkt
nieciągłości
Y=x
n
0
x
f(x)
punkt
nieciągłości
nx
n-1
Nie każda funkcja może być przyjęta za funkcję gęstości prawdopodobieństwa, ale tylko taka, dla której
zachodzi:
0
)
(
≥
x
f
oraz
∫
∞
∞
−
=
1
)
(
dx
x
f
Prawdziwe jest również stwierdzenie odwrotne:
Każda funkcja gęstości prawdopodobieństwa
0
)
(
≥
x
f
, nieujemna i spełniająca warunek:
∫
∞
∞
−
=
∞
=
1
)
(
)
(
F
dx
x
f
,
wyznacza za pomocą wzoru:
∫
∞
−
=
x
du
u
f
x
F
)
(
)
(
pewną dystrybuantę, a tym samym i rozkład prawdopodobieństwa pewnej zmiennej losowej.
Obliczanie prawdopodobieństw dla zmiennej losowej typu ciągłego
1. Aby obliczyć prawdopodobieństwo, że zmienna losowa X znajdzie się w przedziale [ a, b ), stosujemy
wzór:
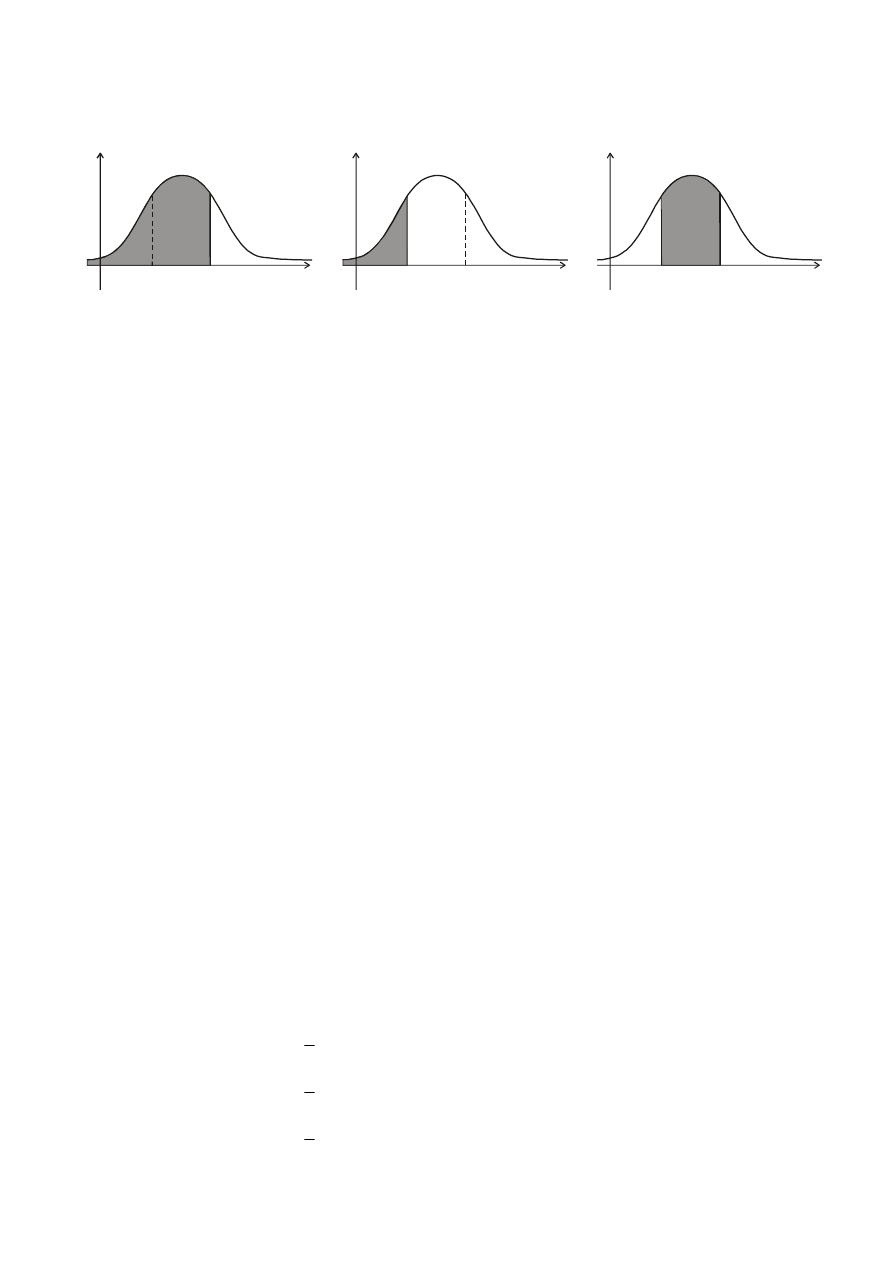
∫
∫
∫
∞
−
∞
−
−
=
=
−
=
<
≤
b
a
b
a
a
F
b
F
du
u
f
du
u
f
du
u
f
b
X
a
P
)
(
)
(
)
(
)
(
)
(
)
(
f(x)
-
=
f(x)
f(x)
x
x
x
b
b
b
a
a
a
2. Prawdopodobieństwo tego, że zmienna losowa ciągła X przyjmie dokładnie wartość a (gdzie a jest
dowolną stałą) jest równe zeru:
0
)
(
)
(
)
(
lim
=
∫
→
=
=
=
≤
≤
a
a
a
b
a
X
P
dx
x
f
b
X
a
P
Nie oznacza to, że zdarzenie x = a jest niemożliwe, jest tylko bardzo mało prawdopodobne, ponadto,
prawdopodobieństwo tego, że zmienna losowa X przyjmie wartość inną niż x = a jest równe jedności,
co nie świadczy o tym, że jest ono pewne, jest tylko wysoce prawdopodobne.
Zadania
1. Niech doświadczenie losowe polega na trzykrotnym rzucie monetą. Określić przestrzeń zdarzeń
elementarnych, zmienną losową, jej rozkład prawdopodobieństwa i dystrybuantę.
2. Określić rozkład prawdopodobieństwa i dystrybuantę zmiennej losowej określonej na doświadczeniu
losowym: w rzucie kostką wypadła parzysta liczba oczek lub nieparzysta liczba oczek.
3. Określić rozkład prawdopodobieństwa i dystrybuantę zmiennej losowej określonej na doświadczeniu
losowym: w rzucie kostką wypadła liczba oczek większa od 2 lub co najwyżej 2.
4. Określić rozkład prawdopodobieństwa i dystrybuantę zmiennej losowej określonej jako: suma oczek
na dwóch kostkach przy niezależnych rzutach.
5. Dana jest dystrybuanta pewnej zmiennej losowej X typu skokowego:
∞
≤
<
≤
<
≤
<
≤
<
≤
=
x
dla
x
dla
x
dla
x
dla
x
dla
x
F
10
1
10
5
7
6
,
5
2
7
3
,
2
1
7
1
,
1
0
)
(
Określić rozkład prawdopodobieństwa tej zmiennej losowej oraz obliczyć prawdopodobieństwa:
)
8
5
(
<
≤
X
P
oraz
)
8
5
(
≤
≤
X
P
.
6. Funkcja
∞
≤
<
≤
<
≤
<
−
−
≤
<
−
−
≤
=
x
dla
x
dla
x
dla
x
dla
x
dla
x
F
3
1
3
1
7
,
0
,
1
1
3
,
0
,
1
3
1
,
0
,
3
0
)
(
jest dystrybuantą pewnej zmiennej losowej X.
Obliczyć prawdopodobieństwa:
a)
),
1
(
=
X
P
b)
)
1
1
(
<
≤
−
X
P
,
c)
)
1
1
(
≤
≤
−
X
P
.
7. W pudełku jest 10 losów ponumerowanych od 1 do 10. Na los z numerem 1 pada główna wygrana
10 zł, na losy z numerami 2 i 3 wygrana pocieszenia 1 zł, a za wyciągnięcie pozostałych płacimy 2
zł (wygrywamy –2 zł). Załóżmy, że wyciągnięcie każdego z losów jest jednakowo prawdopodobne.
Określić zmienną losową oraz jej rozkład prawdopodobieństwa.
8. Określić stałą A tak, aby tabela przedstawiała rozkład prawdopodobieństwa pewnej zmiennej
losowej X :
i
x
0 1 3 6
i
p
3
1
A
3
1
6
1
Wyznaczyć dystrybuantę tej zmiennej losowej.
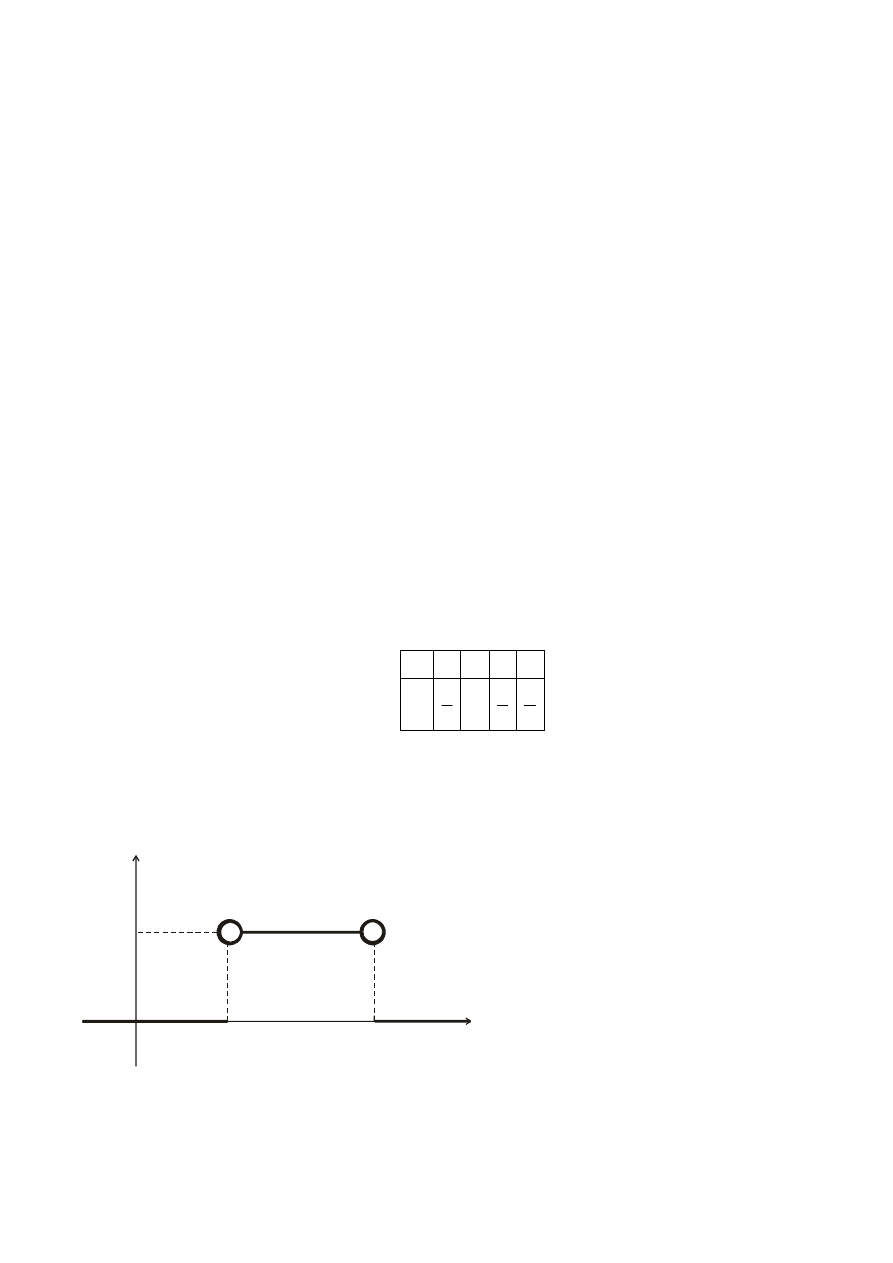
9. Wyznaczyć stałą A tak, aby funkcja przedstawiona na rysunku była rozkładem równomiernym.
Określić dystrybuantę tego rozkładu.
A
f(x)
x
a
b
10. Sprawdzić, czy funkcja określona następująco:
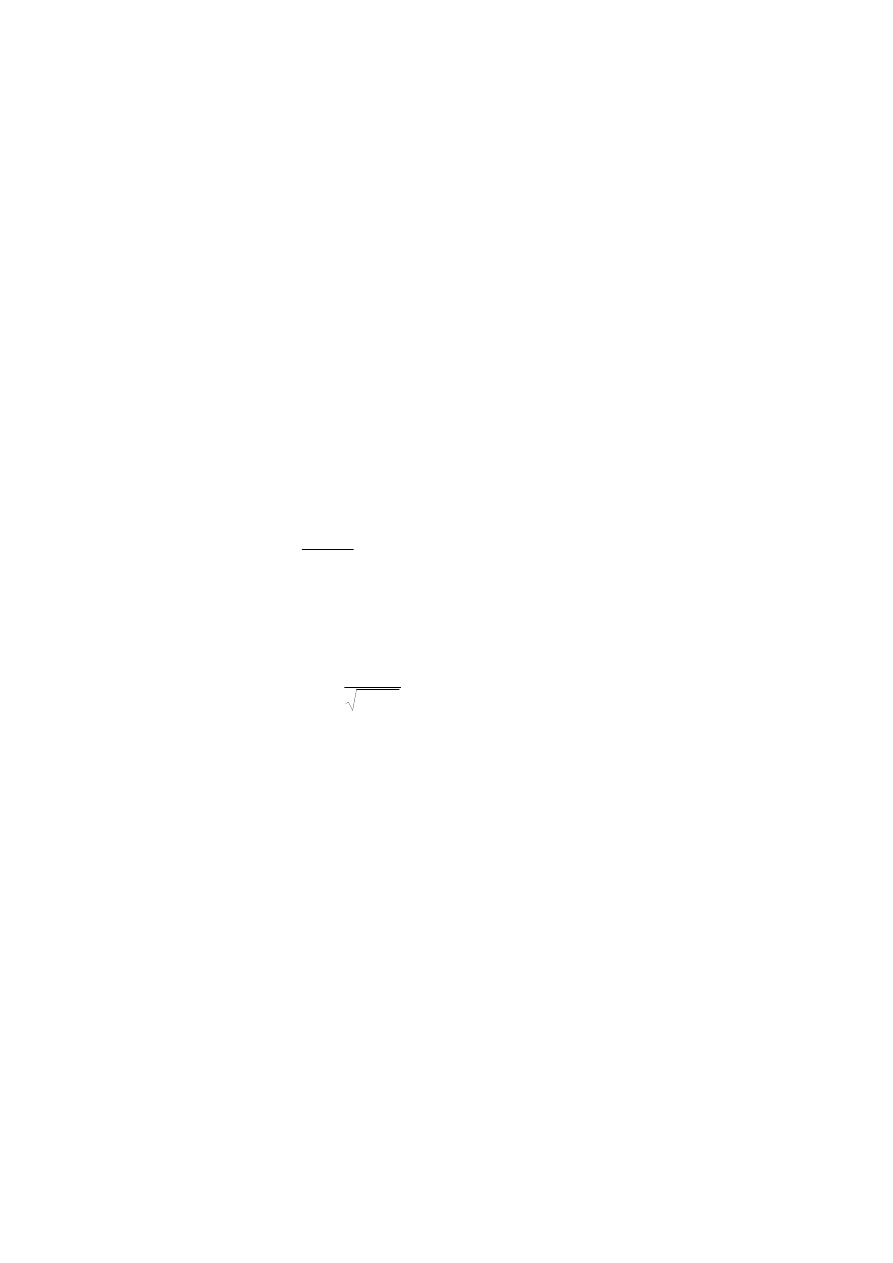
≥
<
=
−
,
0
,
0
0
)
(
x
dla
e
x
dla
x
f
x
a) jest funkcją gęstości prawdopodobieństwa pewnej zmiennej losowej,
b) jeśli jest, to obliczyć dystrybuantę tej zmiennej losowej,
c) obliczyć prawdopodobieństwa:
2
/
1
(
<
X
P
oraz
)
2
1
(
<
≤
X
P
.
11. Wyznaczyć dystrybuantę rozkładu wykładniczego o funkcji gęstości prawdopodobieństwa:
≥
<
=
−
,
0
2
,
0
0
)
(
2
x
dla
e
x
dla
x
f
x
12. Wyznaczyć stałą A taką, aby funkcja:
≥
<
=
−
,
0
,
0
0
)
(
3
x
dla
Ae
x
dla
x
f
x
była funkcją gęstości prawdopodobieństwa pewnej zmiennej losowej X. Obliczyć
prawdopodobieństwo:
)
1
(
>
X
P
.
13. Wyznaczyć stałą A taką, aby funkcja f(x) była funkcją gęstości prawdopodobieństwa rozkładu
Couchy’ego:
2
1
)
(
x
A
x
f
+
=
. Wyznaczyć dystrybuantę.
14. Wyznaczyć stałą A taką, aby funkcja f(x) była funkcją gęstości prawdopodobieństwa rozkładu
arcus sinusa:
∞
<
≤
<
<
−
−
≤
<
∞
−
=
x
x
x
A
x
x
f
1
0
1
1
1
1
0
)
(
2
Wyznaczyć dystrybuantę.
Wyszukiwarka
Podobne podstrony:
jurlewicz,probabilistyka, rozkl Nieznany
ProbabilistykaEND SprawozdanieA Nieznany
jurlewicz,matematyka ,szeregi f Nieznany
jurlewicz,probabilistyka, zdarzenia i elementy kombinatoryki
jurlewicz,probabilistyka, zmienne losowe wielowymiarowe
jurlewicz,probabilistyka, zmienne losowe wielowymiarowe
jurlewicz,probabilistyka, zadania
jurlewicz,probabilistyka, twierdzenia graniczne
jurlewicz,probabilistyka, rozkład typu skokowego
jurlewicz,probabilistyka, test
Jednookresowy probabilistyczny Nieznany
Probabilistyka i Statystyka id Nieznany
15 Wnioskowanie probabilistyczn Nieznany (2)
Gor±czka o nieznanej etiologii
więcej podobnych podstron