Jednookresowy probabilistyczny model zapasów
(single period stochastic problem, newsboy problem)

Dane

D – popyt w rozpatrywanym okresie, zmienna losowa o rozkładzie dyskretnym

j

p

}

j

D

{

P





, j = 0, 1, 2,...

(1)

n

s - jednostkowa strata z powodu niedoszacowania popytu, tzn. strata z powodu

jednego nie obsłużonego klienta,

0



n

s

p

s

- jednostkowa strata z powodu przeszacowania popytu, tzn. strata z powodu

nie sprzedanej jednostki towaru,

0



p

s

Optymalizacja

x - wielkość zapasu, zmienna decyzyjna

Y - strata w rozpatrywanym okresie, zmienna losowa zależna od wielkości

zapasu x przy danych D,

n

s ,

p

s

K(x) - oczekiwana strata przy zapasie x

)

Y

(

E

)

x

(

K



(2)

Kryterium optymalności

)}

x

(

K

{

min

)

x

(

K

:

x

x

,...

,

,

x

opt

opt

2

1

0







(3)

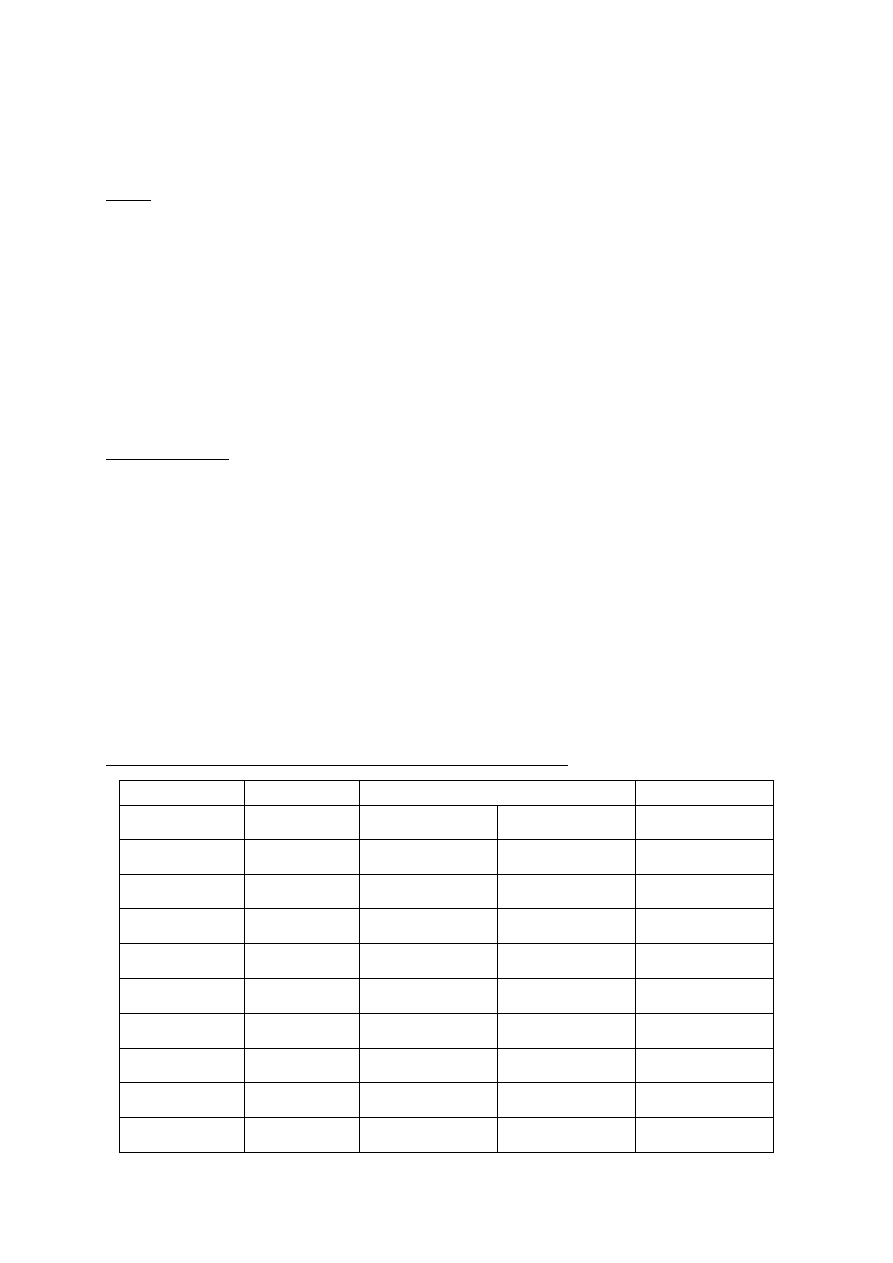
Wyznaczenie rozkładu i wartości oczekiwanej straty Y

Liczba jednostek

Popyt

j

D



}

j

D

{

P



zbędnych

brakujących

Strata

j

y

Y



0

0

p

x

0

p

s

x



1

1

p

x-1

0

p

s

)

x

(





1

2

2

p

x-2

0

p

s

)

x

(





2

...

...

...

...

...

x-1

1



x

p

1

0

p

s



1

x

1



x

p

0

0

0

x+1

1



x

p

0

1

n

s



1

x+2

2



x

p

0

2

n

s



2

...

...

...

...

...

2

}

y

Y

{

P

j



=

}

j

D

{

P







































1

2

1

0

1

2

1

x

p

p

p

p

p

s

...

p

s

)

x

(

p

s

)

x

(

p

s

x

)

Y

(

E

...

p

s

p

s

x

n

x

n



















2

1

2

1

























1

1

0

x

j

j

n

x

j

j

p

p

)

x

j

(

s

p

)

j

x

(

s

)

Y

(

E

(4)

(2)

























1

1

0

x

j

j

n

x

j

j

p

p

)

x

j

(

s

p

)

j

x

(

s

)

x

(

K

(5)

Funkcja K(x) ma w punkcie x minimum lokalne, jeśli x spełnia układ
nierówności















)

x

(

K

)

x

(

K

)

x

(

K

)

x

(

K

1

1

(6)

Rozwiązaniem powyższego układu jest nierówność (praca domowa, oddaj na
kartce, jeśli chcesz)

















x

j

j

p

n

n

x

j

j

p

s

s

s

p

0

1

0

(7)

Bez trudu zauważamy, że

)

x

(

F

}

x

D

{

P

p

x

j

j











0

,

(8)

gdzie F oznacza dystrybuantę zmiennej losowej D.

(7), (8)



)

x

(

F

s

s

s

)

x

(

F

p

n

n









1

(9)

1) Skoro

0



n

s

i

0



p

s

, więc

1

0







p

n

n

s

s

s

(10)

2) Skoro F jest funkcją niemalejącą, więc nierówność (9) albo ma jedno
rozwiązanie i wtedy istnieje jedno minimum (lokalne = globalne) w punkcie

opt

x

x



, albo istnieje kilka kolejnych wartości x takich, że

...

)

x

(

F

)

x

(

F







1

i

wtedy istnieją alternatywne rozwiązania optymalne

,...

x

,

x

x

opt

1





3

3) Optymalna wielkość zapasu jest więc rozwiązaniem nierówności

)

x

(

F

s

s

s

)

x

(

F

opt

p

n

n

opt









1

(11)

Uwaga: jeśli popyt D jest zmienną losową typu ciągłego, wtedy warunek (11)
ma postać (praca domowa, oddaj na kartce, jeśli chcesz)

n

p

n

opt

s

s

s

)

x

(

F





(12)